Abstract
Identifying statistical associations between biological variables is crucial to understanding molecular mechanisms. Most association studies are based on correlation or linear regression analyses, but the identified associations often lack reproducibility and interpretability due to the complexity and variability of omics datasets, making it difficult to translate associations into meaningful biological hypotheses. We developed StableMate, a regression framework, to address these challenges through a process of variable selection across heterogeneous datasets. Given datasets from different environments, such as experimental batches, StableMate selects environment-agnostic (stable) and environment-specific predictors in predicting the response of interest. Stable predictors represent robust functional dependencies with the response, and can be used to build regression models that make generalizable predictions in unseen environments. We applied StableMate to (i) RNA sequencing data of breast cancer to discover genes that consistently predict estrogen receptor expression across disease status; (ii) metagenomics data to identify microbial signatures that show persistent association with colon cancer across study cohorts; and (iii) single-cell RNA sequencing data of glioblastoma to discern signature genes associated with the development of pro-tumour microglia regardless of cell location. Our case studies demonstrate that StableMate is adaptable to regression and classification analyses and achieves comprehensive characterization of biological systems for different omics data types.
Introduction
Inferring relationships between biological variables is a critical problem in systems biology. Among different types of biological relationships, causal relationships are of high interest as they enable a deeper understanding of the function and regulatory mechanism of fundamental biological processes. However, this type of relationship is extremely difficult to identify based on observational studies alone, without further investment in experimental design. In contrast, statistical associations (e.g. based on correlation or linear regression analyses) can be easily computed, but these associations may lead to spurious findings. In recent years, a large number of methods have been proposed for statistical association analysis. Most of these methods are network modelling approaches that infer gene regulation by identifying associations between genes through their expression levels (1–8). However, these approaches result in associations that are not robust against small variations in the data, are not reproducible or lack interpretability (9–11).
An important concept pertinent to the reproducibility of statistical associations is stability. A statistical association is considered stable if it is invariant under small perturbations of the data, and hence, more likely to be reproducible across different studies or conditions. Stability analysis in this context allows us to gain unique biological insights that are not accessible with conventional inference association methods. While the concept of stability has been applied ubiquitously in meta-analysis studies to recover truly significant biomarkers associated with traits (12,13), it is only in recent years that statisticians have established a formal framework explaining the connection between stability and causality (14). Indeed, biological variables that show stable associations are more likely to be closely or even have a causal relationship compared to those with unstable associations. While stability is not sufficient to establish causality, a causal relationship is necessarily stable in some sense (15). Thus, identifying stable associations may serve as a first step towards the inference of causal relationships. It is also enlightening to identify associations that are unstable as they are sensitive to a change of study and experimental conditions and provide insights into how these conditions influence a biological system (16).
We developed StableMate, a statistical framework, to identify both stable and unstable associations through variable selection in a regression context. Inherent to variable selection is the motivation to infer regression function that encapsulates potential functional dependencies between the response and selected predictors beyond using simple correlations. StableMate is based on the recent theoretical development of stabilized regression (SR) (17). SR considers data collected from different ‘environments’ or experiments, including technical or biological conditions. Typical environments can be batches, cohorts, and also disease states. Given a response variable and a set of predictors measured on samples in multiple environments, there are two goals in SR. The first goal is to distinguish stable predictors from unstable predictors, based on whether these predictors are able to make consistent or inconsistent predictions of the response across multiple environments. More specifically, a prediction is defined as the predictors’ functional dependency on the response learned from a regression model (e.g. linear model). To measure the consistency of a prediction, we fit a regression model per environment and compare the functional dependencies between the fitted models (e.g. linear model regression coefficients). The second goal is to build regression models using stable predictors that are generalizable to unseen environments.
While the original approach from Pfister et al. (17) provides an elegant framework for SR, its application is computationally inefficient for high-dimensional biological data. We showed in our simulation study that it can lead to inaccurate results. StableMate provides a new version of SR. While SR selects stable predictors by performing stability tests on every possible predictor subset, StableMate optimizes efficiency with a greedy search based on our improved stochastic stepwise selection algorithm. Moreover, StableMate provides the flexibility to perform stability analysis with any regression model. This greatly generalizes SR, which has been designed for simple linear regression only.
We illustrate the broad applicability and flexibility of StableMate through three case studies across a broad range of biological questions and data types. We show that StableMate is able to (i) identify genes and gene modules involved in the trancriptional regulation of a critical breast cancer (BC) gene (see the 'StableMate identifies genes associated with ESR1 expression in ER+ breast cancer using RNA-seq data' section); (ii) identify faecal microbial markers for prediction of colon cancer while accounting for batch effects in a multi-cohort data (see the ‘StableMate discerns global microbial signatures for colon cancer in multi-cohort metagenomics data’ section); and (iii) characterize changes of microglia transcriptional identity during their transitions to a pro-tumour phenotype (see the ‘StableMate characterizes cell identity transition of glioblastoma-associated microglia with scRNA-seq data’ section). In both simulated and real data (Section 5, Supplementary Figures S1 and S2), we benchmarked the prediction and the variable selection performances of StableMate against other commonly used regression methods, including the original SR algorithm in Pfister et al. (17). The results show that StableMate yields superior performances compared to competing methods.
Materials and methods
Data and preprocessing
A summary of the data and StableMate analysis from the case studies is presented in Table 1.
Table 1.
Summary of case studies
| Data | Samples | Response | Predictors | Environment | Used in |
|---|---|---|---|---|---|
| BC RNA-seq data from The Cancer Genome Atlas (TCGA-BRCA) | N = 1207 = 113 normal samples + 1094 ER+ BC samples | ESR1 gene expression | P = 19 937 protein-coding genes, pre-filtered, further see the ‘StableMate to identify stable and environment-specific statistical associations’ section P = 50 principal components learnt on the 19,937 genes excluding ESR1 | Disease status (ER+ BC or normal) | ‘StableMate identifies genes associated with ESR1 expression in ER+ breast cancer using RNA-seq data’ section, pooled StableMate analysis (ESR1 versus genes) ‘StableMate identifies genes associated with ESR1 expression in ER+ breast cancer using RNA-seq data’ section, pooled StableMate analysis (ESR1 versus PCs) |
| RNA-seq data of normal breast tissue from GTEx | N = 980 normal samples | ‘StableMate identifies genes associated with ESR1 expression in ER+ breast cancer using RNA-seq data’ section, external validation | |||
| Microarray data of BC from METABRIC | N = 2509 ER+ BC samples | ‘StableMate identifies genes associated with ESR1 expression in ER+ breast cancer using RNA-seq data’ section, external validation | |||
| Metagenomics studies of colon cancer collected from | N = 1429 = 107 (61 controls, 46 cases) samples from an Austrian cohort + 128 (54 controls, 74 cases) samples from a Chinese cohort + 114 (61 controls, 53 cases) samples from a French cohort + 125 (65 controls, 60 cases) samples from a German cohort + 53 (24 controls, 29 cases) samples from an Italian cohort A + 60 (28 controls, 32 cases) samples from an Italian cohort B + 509 (251 controls, 258 cases samples from a Japanese cohort + 104 (52 controls, 52 cases) samples from a US cohort | Colon cancer incidence (cancerous or normal) | P = 313, species detected in all cohorts P = 431, pathways detected in all cohorts | Study cohort | ‘StableMate discerns global microbial signatures for colon cancer in multi-cohort metagenomics data’ and ‘Benchmarking StableMate variable selection and prediction on metagenomics data’ sections, pooled StableMate analysis (disease status versus species) ‘StableMate discerns global microbial signatures for colon cancer in multi-cohort metagenomics data’ section, environment-specific StableMate analysis (disease status versus species) ‘Benchmarking StableMate variable selection and prediction on metagenomics data’ section, pooled StableMate analysis (disease status versus pathways) Supplementary Section S1.2, environment-specific StableMate analysis (disease status versus pathways) |
| scRNA-seq data of glioblastoma | N = 1847 = 1329 cells from tumour core + 518 cells from tumour periphery | DPT Each of CCL3, CCL4 TNF, IL1B, CSF1, CCL2 gene expression | P = 23 368, protein-coding genes, pre-filtered; further see the ‘Materials & methods’ section | Cell location (periphery or core) | ‘StableMate characterizes cell identity transition of glioblastoma-associated microglia with scRNA-seq data’ section, environment-specific and pooled StableMate analysis (DPT versus genes) ‘StableMate characterizes cell identity transition of glioblastoma-associated microglia with scRNA-seq data’ section, pooled StableMate analysis (each cytokine versus genes) |
| Bulk transicriptional atlas of myeloid cells | N = 901 myeloid cells | ‘StableMate characterizes cell identity transition of glioblastoma-associated microglia with scRNA-seq data’ section, for cell identify profiling |
Sample breakdown per environment, response, predictors and the environment variables are described for StableMate regression. We performed two types of StableMate analysis based on how predictive variables were defined. In the first type, we pooled environments to select predictive variables and assess their stability across environments. In the second type, we select predictive variables in each environment and tested the stability of the predictor selected in the remaining combined environments. These two types of StableMate analysis are referred to as pooled and environment-specific.
BC gene expression data
We analysed the RNA-seq dataset from The Cancer Genome Atlas Program (TCGA-BRCA) to study the transcriptional regulation of ESR1 in ER+ BC, available from the R package TCGAbiolinks (18). The dataset includes the expression quantification of 60 660 genes on 113 normal samples and 1094 BC samples. We focused on the log-transcript-per-million (logTPM) of 19 937 protein-coding genes for analysis.
We used two other gene expression studies as validation: the microarray data of 2509 BC samples from the METABRIC cohort (19,20), available from cBioProtal (21) in the form of z-score relative to all samples (log), and RNA-seq data of 980 normal breast samples from GTEx (22) in the form of logTPM.
Colon cancer metagenomics data
We obtained nine colorectal cancer (CRC) case-control studies of faecal metagenome from the R package curatedMetagenomicData (23). We excluded two studies with a sequencing depth lower than the average 10 million reads per sample. The remaining studies included curated microbial species abundance and pathway abundance data from seven different countries and eight different cohorts: including 107 samples from Austria (24), 104 samples from the USA (25), 125 samples from Germany (26), 509 samples from Japan (27), 128 samples from China (28) and 114 samples from France (29), as well as two cohorts containing 53 and 60 samples from Italy (30). In total, all cohorts included 1429 samples. We filtered the species and pathway abundance data from each cohort down to 313 species and 431 pathways that were detected across all cohorts.
To normalize the abundance data, we applied rank transformation by calculating the within-sample ranking quantile of the abundance of each species (or pathway). A species ranked the qth most abundant in a sample is assigned the value (1 − q)/(p − 1), where p is the total number of species analysed. Therefore, the most abundant species of a sample has a rank transformed value of 1, and the least abundant species has a value of 0.
Glioblastoma single-cell RNA sequencing data
We analysed the glioblastoma (GBM) single-cell RNA sequencing (scRNA-seq) data from Darmanis et al. (31), who sequenced single cells sampled from four GBM patients at their tumour cores and surrounding peripheral tissues. The raw and curated read count data included 3589 cells measured on 23 368 genes available from http://gbmseq.org/. We retained 1874 cells of myeloid cell types, including 1329 cells sequenced from the core and 518 cells sequenced from the periphery for analysis. We used the R package Seurat to log-normalize the data and identify the most variable 2000 genes with the FindVariableFeatures function (32). We then imputed the log normalized data using Sincast imputation with default tuning (33) for StableMate variable selection and single-cell projection. Diffusion map (DM) and diffusion pseudotime (DPT) learning were performed on the original log-normalized data (without imputation).
StableMate to identify stable and environment-specific statistical associations
We developed a variable selection method based on the SR framework proposed by Pfister et al. (17), where the predictors and response are measured in different biological environments. The goal is to select stable and environment-specific (unstable) predictors that, respectively, make consistent and inconsistent predictions of the response across environments. A final model is built on the stable predictors and is generalizable to unseen environments.
The original SR
Briefly, SR examines all possible subsets of predictors in a brute force search, fits a regression function on each subset, and evaluates the subset’s stability across environments and its prediction ability. First, the stability of predictor subsets is constructed based on either a Chow test (testing for equal regression coefficients of the predictors between regression functions fitted in a specific environment) or a resampling approach. Subsequently, the prediction ability of stable subsets is evaluated based on negative mean squared prediction error combined with bootstrapping to define a cut-off for selecting the most predictive sets. The importance of each variable with respect to their stability, instability, and prediction ability is then assessed via frequency of selection. The final SR model is obtained as a weighted average of the regression functions fitted on the stable and predictive subsets [refer to (17) for more details].
We identified several limitations of SR in its current form.
It is computationally infeasible to enumerate every possible subset of predictors in omics data where the number of predictors P is very large (i.e. >30). Pfister et al. (17) proposed the following solution: (i) pre-filter data to tens of predictors. Then from the pre-filtered predictor sets, (ii) randomly sample thousands of subsets to test for stability and subsequently prediction ability. However, we argue that this solution is inefficient, as thousands of subsets are not sufficient to represent the subset space of many predictors. A drastic pre-filtering is therefore required but can result in filtering out important predictors.
Identifying first the stable predictor sets, and then assessing their prediction ability is not efficient. This is not only because the stable and predictive sets are included in the predictive sets, as we describe in Supplementary Section S3.1, but also because stability is more difficult to compute compared to prediction ability.
Because of these limitations, SR results lack both variable selection and prediction accuracy for large datasets, as we highlight in our simulation (Supplementary Figure S2).
The StableMate approach
StableMate addresses these issues by (i) implementing a greedy rather than a brute force approach to select predictor sets based on an improved version of stochastic stepwise regression (ST2*), which is a stochastic selector, (ii) building a variable selection ensemble using repeated ST2*, (iii) pre-screening predictors before each ST2* using random Lasso to enable a much larger starting set of predictors than SR, (iv) identifying first the predictive variables and then narrowing down to the stable predictors to be more efficient in the search, and (v) developing the concept of pseudo-predictor to benchmark ST2* selections. The full methodological details are available in Supplementary Section S3.1.
Main steps of StableMate
We summarize the main steps of StableMate; a more detailed algorithm is presented in Algorithm 1 in Supplementary Section S3.1.
Depending on the type of analysis, a base regressor for ST2* is first specified, for example, we used ordinary least square regression (OLS) for case studies in the ‘StableMate identifies genes associated with ESR1 expression in ER+ breast cancer using RNA-seq data’ and ‘StableMate characterizes cell identity transition of glioblastoma-associated microglia with scRNA-seq data’ sections and generalized linear models in the ‘StableMate discerns global microbial signatures for colon cancer in multi-cohort metagenomics data’ section.
-
For each iteration k, k = 1, …, K
Apply random Lasso pre-screening, then add pseudo-predictor.
Run ST2* to select the most predictive predictor set denoted
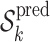 .
.Run ST2*to select the stable predictors within
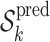 such that
such that 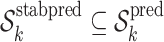 .
.
Define importance score for prediction and stability.
Calculate significance cut-off scores to define stable, unstable and non-significant variables.
Fit the final ensemble regression model as the weighted average of the fitted regressions on
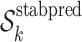 .
.
Pre-screening predictors based on random Lasso
We first pre-filter predictors based on a random Lasso procedure. For each ST2* run (described below), we randomly sample one-half of the samples to select the top p predictors with Lasso (34). As an example, we chose p = 100 for the ‘StableMate identifies genes associated with ESR1 expression in ER+ breast cancer using RNA-seq data’ and ‘StableMate characterizes cell identity transition of glioblastoma-associated microglia with scRNA-seq data’ sections. The advantages are of 2-fold. First, across the different resampling runs, the top p predictors are expected to differ, thus enabling us to cover a large and diverse range of predictors in our overall search. Second, we improve the stability of Lasso pre-screening when subjected to sample perturbation (35) (see more details in Supplementary Section S3.1).
ST2*: a new stochastic stepwise variable selection procedure
We improved the ST2 algorithm proposed by Xin and Zhu (36). ST2 is a stochastic version of the classic stepwise variable selection. ST2 searches for a set of predictors maximizing a particular objective function to quantify the predictive ability or stability of predictor sets. It uses a greedy approach with iterative forward and backward searching steps. ST2 starts with an initial predictor set (which can be empty). In the forward step, a collection of predictor sets is randomly sampled from predictors that are not included in the current model. The predictor set that yields the largest increase in the objective function is then added to the current model. In the backward step, a collection of predictor sets is randomly sampled from predictors that are included in the current model. The set that yields the largest increase of the objective function is then removed from the current model. The forward and backward steps alternate until the objective function does not improve further. However, the major drawback of ST2 is that it samples subsets of a fixed size that is randomized at each step. If a wrong size is sampled, ST2 may stop prematurely, leading to inaccurate variable selection.
In ST2*, we follow the ST2 algorithmic framework but we improved the procedure to sample different predictor subset sizes at each step (refer to Supplementary Section S3.1 for a detailed description of the ST2* algorithm). We also added objective functions that are well suited to assess prediction and stability; namely, we used the negative Bayesian information criterion (NBIC) and negative prediction sum of squares (NPSS) (Supplementary Section S3.1).
Finally, we run ST2* on K iterations (e.g. K = 2000 in our case studies) first to identify the predictive subsets of predictors, and second to identify the stable subsets within each predictive subset. As a result, we select an ensemble of stable and predictive predictor sets. These iterations address the stochastic nature of ST2*, which can yield potentially different predictor sets for each iteration. The sets of stable predictors are then used to build the final regression model (described below).
Cut-off prediction and stability scores
We calculate a prediction score for each predictor based on how often the predictor is selected as predictive across the ensembles. We do similarly for the stability score. The output can be represented in a variable selection plot such as Figure 2A, where the scores are represented on the x-axis (prediction) and y-axis (stability).
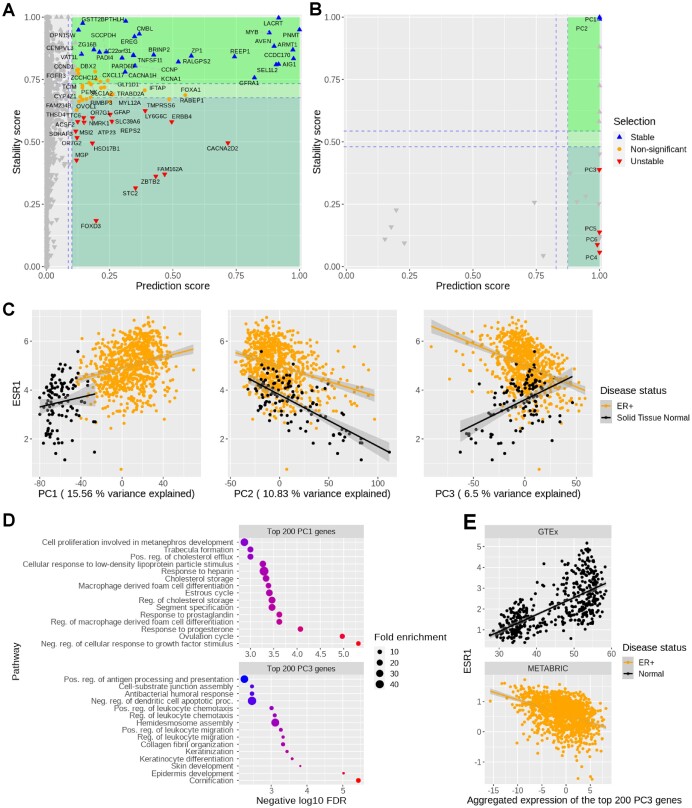
Figure 2.
StableMate selects genes from the TCGA-BRCA dataset which predict ESR1 expression across normal and ER+ samples. We used (A) gene expression or (B) principal components (PCs) of gene expression as predictors. The stability score (y-axis) of a gene is a measure of how consistently this gene predicts ESR1 regardless of the disease status (normal or ER+). Stable and disease-specific genes/PCs are labelled as up and down triangles, respectively. (C) ESR1 expression (y-axis) against PC scores (x-axis). The correlation between ESR1 with the highly disease-specific PC3 changed from positive to negative between normal and ER+ samples, whereas the sign of the correlations between ESR1 and the stable PC1 and PC2 remained unchanged between normal and ER+ samples. We analysed PC1 (i.e. the most important stable PC) and PC3 (i.e. the most important disease-specific PC) as an example. (D) Gene ontology enrichment on the top 200 genes from PC1 (top) and PC3 (bottom) suggested biological activities related to hormonal regulation and epidermis development, respectively. The predictive ability and stability of PC1 suggest that ESR1 may directly participate in hormonal regulation, which is corroborated by the knowledge that ESR1 is a transcriptional factor activated by estrogen binding. (E) Reproducibility of StableMate results using external databases, GTEx for normal breast tissue and the METABRIC data from cBioPortal for ER+ BC: ESR1 expression against the expression of the metagene defined by the top 200 genes contributing to PC3 (i.e. linear combination of these 200 genes according to the loading vector of PC3) confirm the opposite trends we observed in (C) of ESR1 against PC3 in normal and ER+ samples.
To define a significance cut-off of these scores, we create a pseudo-predictor as a negative control. A pseudo-predictor is represented as an artificial index P + 1 so that its inclusion in the regression model does not affect the model fitting nor the value of the objective function in ST2*, but it is still taken into account when calculating the scores of all predictor sets.
We applied a bootstrap procedure on the variable selections to compare the distributions of the prediction and stability scores of the predictors to that of the pseudo-predictor to assess their significance. A predictor with a prediction score larger than the pseudo-predictor’s in more than 97.5% times of the bootstrap iterations is considered as significantly predictive. We do similarly for the cut-off stability score. A predictor is considered environment-specific (unstable) if its stability score is lower than that of the pseudo-predictor. Finally, the rest of the predictors are assigned as ‘non-significant’, as shown in plot Figure 2A. Note that since these cut-off scores are based on the bootstrap of variable selections, the significance indicates the variability in the ST2* selections, and hence provide a reference on whether more ST2* runs need to be performed.
Final ensemble regression model generalizable to unseen environments
The final regression model is then built on the different sets of stable and predictive predictors. Each regression model is fitted by regressing the response variable on each stable and predictive subset in the ensemble. We then aggregate these models as the average of the fitted regression weighted by the ranking of objective functions NBIC and NPSS.
Principal component analysis
We used the prcomp function from the R package stats (37) to perform principal component analysis (PCA).
Gene modules
PCA (centred but unscaled) was used to identify metagenes in the form of PCs that represent gene modules from the TCGA BC RNA-seq data. The 23 most variable metagenes selected by the elbow method were then used as the predictors of ESR1 expression for the subsequent StableMate analysis (38). To avoid overfitting, ESR1 was removed from the data.
Aggregation of gene expression with similar expression patterns
We applied PCA (not centred nor scaled) on the set of genes, and extracted the loading coefficients of each gene on the first PC using a soft-thresholding approach to identify the top contributing genes with loading coefficients of the same sign. We then considered the absolute value of the loading coefficients of these top genes to obtain positive weights, which we then used for aggregating their expression by a linear combination.
Principal coordinate analysis
We used the cmdscale function from the R package stats (37) to perform principal coordinate analysis (PCoA). PCoA was performed on the combined colon cancer case-control studies with classical multidimensional scaling on Euclidean distance between samples. We calculated two distances matrices on either the 313 species of the full data and the 23 species selected by StableMate. Permutational multivariate analysis of variance (PERMANOVA) was then used to test the separation of the sample groups based on disease status or cohorts. We used the adonis function from the R package vegan (39).
Methods’ benchmark
We benchmarked the prediction performance of StableMate against other commonly used methods, including OLS, generalized linear model (GLM or logistic regression), Lasso regression (Lasso) (34), and random forest (RF) (40).
The regression models were trained for the different benchmarking tasks described below on the pooled data of training environments. For predicting continuous responses in the simulation study, we used GLM Lasso with a Gaussian family. For the binary classification of colon cancer in the second case study, we used GLM Lasso with a binomial family. StableMate requires to specify the different sample environments, while in RF samples were weighted according to the inverse of the size of the environment each sample belongs to. Lasso penalties were tuned using cross-validation, where each environment is used as a fold to minimize the averaged mean squared error. We used the functions lm for OLS, glm for GLM, cv.glmnet from the package caret for Lasso (41), and the R package randomForest for RF (42).
Simulation study
The benchmark results are shown in Supplementary Figures S1 and S2.
We simulated systems of variables observed from four environments. A system is a model that describes the causal relationships between variables, and an environment is the probability distribution of variables that generates data. Therefore, a system of variables in different environments are generated by different probability distributions but with the same causal relationships. The simulations are described in Supplementary Section S3.2. For each simulation run, a variable in the system was randomly sampled as the response while the remaining variables were set as predictors. The regression models were trained on data generated in the first three environments to predict the response. The data of the fourth environment were used for testing.
Metagenomics case study (‘StableMate discerns global microbial signatures for colon cancer in multi-cohort metagenomics data’ section)
We trained each regression model to predict colon cancer disease status. We performed leave-one-dataset-out (LODO) cross-validation. We considered either all 313 species or 431 pathway abundances (no pre-filtering). In addition, we also performed LODO validation to evaluate the performance of the RF models trained using the different sets of predictors selected by either StableMate, Lasso, or RF.
Diffusion map and diffusion pseudotime
Diffusion map
In case study 3 (see the ‘StableMate characterizes cell identity transition of glioblastoma-associated microglia with scRNA-seq data’ section) we visualized the scRNA-seq data using DM, which is a non-linear dimension reduction method highly suitable for single-cell data with potential cell state transitions. DM learns transition probabilities between cells and projects cells into a lower dimensional Euclidean space that approximates the ‘diffusion distances’ between cells accordingly. DM was run on the 2000 most variable genes of the log normalized data using the R function DiffusionMap with default parameters from the package destiny (43).
Diffusion pseudotime
DPT inference was then applied following DM learning (44). The cell that has the largest DC1 score in the tumour periphery was chosen as the root of the cell trajectory. The distance between the cumulative transition probabilities of any cell with the root cell is defined as its pseudotime.
Sincast projection of scRNA-seq onto a reference atlas of myeloid cells
We used Sincast (33) available at https://github.com/meiosis97/Sincast to impute scRNA-seq data and to query GBM cell types and cell states. We queried the identity of a specific subset of GBM cells, namely myeloid cells classified by Darmanis et al. (31). The reference myeloid atlas was from Rajab et al. (45) who compiled bulk RNA-seq and microarray data of myeloid cells from 44 independent studies. Sincast projects the query scRNA-seq cells onto the atlas by calculating the predicted PCs of the cells, which are then represented on the PCA of the reference atlas. The result is a 3D PCA plot (i.e. Figure 4A) where we can infer the identity of the query cells according to the biology of their surrounding atlas samples.
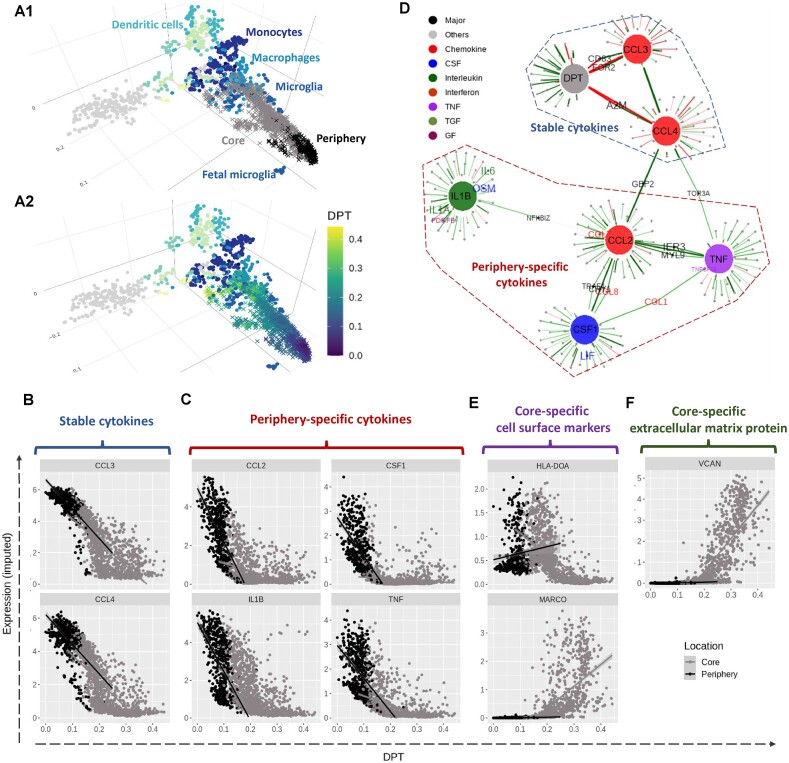
Figure 4.
Characterizing transition of microglia cell identity from periphery to core in GBM tumour with scRNA-seq data. (A1) Sincast projection of the query single cells (crosses) onto a bulk RNA-seq reference atlas of myeloid cells (dots) to assign cell identity. The cells from the tumour periphery were located close to the reference foetal microglia, while the cells from the tumour core showed a transition towards the reference monocytes and macrophages. Panel (A2) is identical to panel (A1) except that cells are coloured according to DPT, representing a cell state transition. StableMate was applied to select genes predictive of DPT, where cell location (core and periphery) was set as the environmental variable. (B)–(F) The expression of the cytokines was imputed based in Sincast. We identified several cytokines that are typical microglia activation and polarization markers, including (B) CCL3 and CCL4, which are stable, and (C) TNF, IL1B, CCL2, and CSF1, which are periphery-specific. (D) A gene regulatory network was built by running StableMate on each of the seven response variables, namely DPT and six cytokines CCL3, CCL4, TNF, IL1B, CCL2, and CSF1 (represented as large nodes). The aim was to select stable and predictive genes associated with each of these response variables. The cell location was still set as the environment variable. An edge indicates that a gene is stable and predictive of a response variable. We found that CCL3 and CCL4 were stable and predictive of DPT as a separate graphical community from TNF, IL1B, CCL2, and CSF1, which were predictive but unstable of DPT. (E) The expression levels of MHC-II molecule HLA-DOA and the macrophage marker MARCO. (F) The expression levels of large extracellular matrix protein VCAN. MARCO, VCAN and HLA-DOA were all identified as core-specific. The upregulation of MARCO, VCAN, and the downregulation of HLA-DOA suggest a development of M2-like immunosuppressive macrophage.
Sincast imputation
The log-normalized scRNA-seq data was imputed using the sincastImp function with its default parameters, where the imputation of any cell is based on its nearest neighbouring cells.
Sincast projection
Only the most 2000 most variable genes of the query scRNA-seq data were considered. The query data were projected onto the reference PCA atlas after rank transformation. The projection is then reorganized and visualized via DM.
Quantification of query cell identity
To quantify the identity of each query cell based on the reference cell types, we used Sincast modified version of the Capybara cell score of Kong et al. (46). The approach is based on weighted restricted least square regression (33).
Results
Illustration of StableMate on toy example
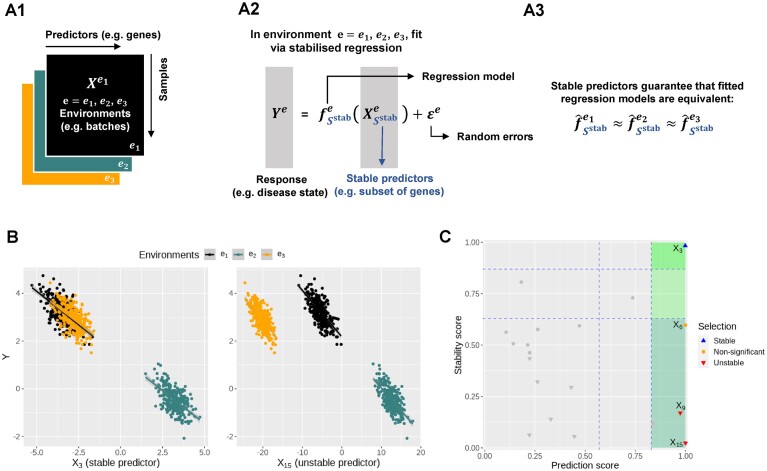
We simulated 900 samples measured on 20 variables from three environments e = e1, e2, e3, with 300 samples in each environment. Denote by Ye the response variable of interest we wish to predict. We use the remaining 19 variables 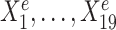 as predictors (see Figure 1A). In particular,
as predictors (see Figure 1A). In particular, 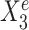 is a causal parent of Ye and is expected to be stable, whereas
is a causal parent of Ye and is expected to be stable, whereas 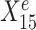 is a causal child of Ye and hence is expected to be environment-specific (see details in Supplementary Section S3.2). To illustrate StableMate results we plotted Ye against
is a causal child of Ye and hence is expected to be environment-specific (see details in Supplementary Section S3.2). To illustrate StableMate results we plotted Ye against 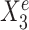 and
and 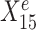 in Figure 1B. Here,
in Figure 1B. Here, 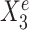 is stable in the sense that its relationship with Ye can be described by the same linear equation for e = e1, e2, e3, whereas X15 is environment-specific as its relationship with Ye varies for different e.
is stable in the sense that its relationship with Ye can be described by the same linear equation for e = e1, e2, e3, whereas X15 is environment-specific as its relationship with Ye varies for different e.
Figure 1.
Toy example for StableMate analysis. (A) Stable predictors. Consider a regression problem where the response Ye and predictors Xe were generated from three different environments (e.g. batches, cohorts) e = e1, e2, e3, as represented in panel (A1). Stable predictors are a subset of all predictors that are useful for predicting Ye and whose association with the response Ye does not change with e. If we fit a regression model in each environment to predict the response using only the stable predictors (A2), then the fitted models should be approximately the same across all environments (A3). Thus identifying stable predictors is useful for constructing regression models that are agnostic to environments and hence may be more generalizable to unseen environments. On the other hand, predictive but unstable (referred to as ‘environment-specific’) predictors may be useful for understanding environment-specific regulatory mechanisms of the response Ye. (B) Difference between stable and environment-specific predictors. We simulated 900 samples, each with response Ye and predictors 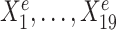 across environments e = e1, e2, e3. Left panel plots Ye against a stable predictor
across environments e = e1, e2, e3. Left panel plots Ye against a stable predictor 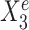 ; right panel plots Ye against an environment-specific predictor
; right panel plots Ye against an environment-specific predictor 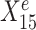 . Linear regression lines were fitted per environment. Both
. Linear regression lines were fitted per environment. Both 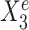 and
and 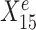 are useful for predicting Ye since they are both strongly negatively correlated with Ye in each environment. However, for the stable predictor
are useful for predicting Ye since they are both strongly negatively correlated with Ye in each environment. However, for the stable predictor 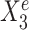 , the regression lines have the same slope and intercept in all three environments. For the environment-specific predictor
, the regression lines have the same slope and intercept in all three environments. For the environment-specific predictor 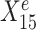 , the regression lines have the same slope but differ in their intercepts. (C) StableMate variable selection plot. StableMate takes as input the predictors
, the regression lines have the same slope but differ in their intercepts. (C) StableMate variable selection plot. StableMate takes as input the predictors 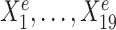 measured from the 900 samples across all environments, where the environment index e is known for each sample, and the response Ye for each sample. The variable selection plot shows the prediction score (x-axis) and the stability score (y-axis) assigned to each predictor. Vertical and horizontal dashed lines represent the significance thresholds for prediction and stability respectively based on bootstrap, as defined in the ‘Materials and methods’ section. The predictive variables are further labelled as stable (up triangles) or environment-specific (down triangles), where, in particular,
measured from the 900 samples across all environments, where the environment index e is known for each sample, and the response Ye for each sample. The variable selection plot shows the prediction score (x-axis) and the stability score (y-axis) assigned to each predictor. Vertical and horizontal dashed lines represent the significance thresholds for prediction and stability respectively based on bootstrap, as defined in the ‘Materials and methods’ section. The predictive variables are further labelled as stable (up triangles) or environment-specific (down triangles), where, in particular, 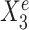 and
and 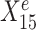 are both correctly labelled.
are both correctly labelled.
Briefly, the StableMate procedure first pools samples from all environments to identify the variables that are most predictive of the response regardless of the environment. Then, among these predictive variables, stable and unstable (environment-specific) variables are further differentiated. Both procedures involve fitting regression models with a base regressor, which is set as simple linear regression by default. More complex relationships can be modelled by choosing non-linear models as the base regressor in StableMate.
The variable selection results from a default StableMate analysis can be summarized in Figure 1C, where every variable is assessed in terms of prediction and stability. First, all variables with low prediction scores are filtered out. They are evaluated based on their prediction ability from the fitted regression models. Second, among the predictive variables, we further differentiate between those that are significantly stable, unstable, or indeterminate. The stability score of a given predictor measures the probability of a predictor being present in regression models that are generalizable across environments. In this example, 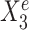 , which was expected to be stable, received the highest prediction and stability score, whereas
, which was expected to be stable, received the highest prediction and stability score, whereas 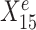 , which was expected to be environment-specific, received a high prediction score but the lowest stability score. We further detail in the ‘Materials and methods’ section (see the ‘StableMate to identify stable and environment-specific statistical associations’ section) how we defined these scores and significance thresholds.
, which was expected to be environment-specific, received a high prediction score but the lowest stability score. We further detail in the ‘Materials and methods’ section (see the ‘StableMate to identify stable and environment-specific statistical associations’ section) how we defined these scores and significance thresholds.
We evaluated the ability of StableMate to accurately identify stable and environment-specific predictors in a benchmark study where we compared our performance with existing approaches including the original SR algorithm. Our results show that StableMate leads to superior accuracy and computational efficiency, as detailed in Supplementary Figures S1 and S2.
The next sections highlight the flexibility of StableMate to identify stable and environment-specific predictors in different analytical settings. The different types of analyses are described in Table 1.
StableMate identifies genes associated with ESR1 expression in ER+ BC using RNA-seq data
In the first case study, we illustrate the application of StableMate to identify genes and gene modules associated with the regulation of the ESR1 gene based on BC transcriptomics data. ESR1 is one of the marker genes of the ER+ subtype of BC, characterized by the high expression of the estrogen receptor (ER) (47). By leveraging abundant prior knowledge of ESR1’s role in BC progression, our aim is to validate StableMate results within a biological context. We are interested in the association between ESR1 and other genes across normal and ER+ samples. In particular, we expect that genes identified as stable for predicting ESR1 expression are not confounded by disease status, suggesting a close or potential causal relationship with ESR1 in its transcriptional regulation. In contrast, genes identified as disease-specific might be interacting with ESR1 indirectly, e.g. at downstream of ER regulation or by co-regulating with ER.
Data and StableMate setting.
We used the publicly available BC gene expression (BRCA) data from The Cancer Genome Atlas (TCGA) (48). We filtered the dataset to retain 113 normal and 778 ER+ tumour samples.
Since we were interested in the regulation of ESR1, we set ESR1 as the response and all other genes as predictors and fit simple linear regressions for StableMate analysis. We set the disease status (normal or ER+) as the environment variable so that we could identify stable genes, whose association with ESR1 did not change significantly between normal versus ER+ samples, and disease-specific genes, whose association with ESR1 significantly varied significantly between disease status. In addition to identifying individual genes, we also combined StableMate with PCA to identify stable and disease-specific gene modules. Namely, we still took ESR1 as the response and disease status as the environment variable, but we used meta genes (first a few PCs of all genes except ESR1) as predictors. Then, we defined the stable and disease-specific gene modules as the most important genes of stable and disease-specific metagenes.
StableMate selected genes proxy to ESR1 regulation
The StableMate variable selection results are summarized in Figure 2A. Among the most stable genes predictive of the ESR1 expression, CCDC170 and ARMT1 are the closest genes located to the upstream genomic region of ESR1 (Supplementary Figure S3A) and have been reported to fuse with ESR1 (49). Their proxy to ESR1 suggests that they might be subject to the same transcriptional regulation as ESR1, thus explaining their stability. On the other hand, the STC2 gene was identified as disease-specific. This might be explained by the fact that STC2 has been identified as a downstream target of ER signalling (50,51). In addition, the proximal promotor region of STC2 is not directly subject to ER binding but is dominated by other transcriptional activities such as hypoxia induced stress response (52,53). As a result, ER signalling is indirectly involved in the STC2 activation (51). This evidence supports our hypothesis that STC2 and ESR1 should be indirectly or distally related in transcriptional regulation as indicated by their environment-specific associations.
StableMate with PCA identified gene modules associated with ESR1
Feature selection from transcriptional data is often followed by gene set enrichment analysis. While the stability analysis on individual genes gave us some insights into ER regulation, we selected relatively few genes as either stable or disease-specific—this was insufficient for statistically meaningful enrichment analysis. To overcome this issue, we used the first 23 most significant PCs (selected by the elbow method) (38) of all genes (except ESR1) as predictors for ESR1 expression rather than individual genes. In this context, each PC is a linear combination of the expression of all genes except ESR1, and can be viewed as a metagene, which is useful for quantifying the activities of gene modules (54). Similar to our previous analysis, disease status (normal and ER+) was set as the environmental variable. Of note, we observed similar results with the metagene construction method of weighted gene co-expression network analysis (1), which identifies gene modules with hierarchical clustering first and then computes a metagene on each gene module by eigen decomposition, akin to PCA (see Supplementary Methods S1.1 and Supplementary Figures S4 and S5).
The StableMate variable selection results are summarized in Figure 2B. PC1 and PC2 were found to be highly stable and predictive, suggesting that the major source of variation they explain (15.56% and 10.83%, respectively) is closely related to ER regulation. All subsequent PCs up to PC6 were predictive but disease-specific. We considered the top 200 genes contributing to PC1 (most stable) and PC3 (disease-specific) and conducted an enrichment analysis. Genes from PC1 were mainly associated with biological processes related to hormone regulation (Figure 2C). The ESR1-mediated estrogen signalling is at the centre of hormone regulation, and hence the high prediction ability and stability of PC1 are manifest. Genes from PC3 were associated with basal cell-like transcriptional activities in epidermis development. The top genes contributing to PC3 (see details in Supplementary Figure S3B) included a high proportion of basal cytokeratins (BCKs), such as KRT5, KRT7, KRT14, and KRT17, suggesting that PC3 may reflect the ‘basalness’ of samples (Figure 2C). Interestingly, PC3 scores were positively correlated with ESR1 expression in normal samples but negatively correlated with ESR1 in ER+ samples (Figure 2C). This trend was also observed between the basal BC enriched genes [listed in Li et al. (55)] and ESR1 expression (Supplementary Figure S3C), confirming the PC3 characterization of basalness.
To validate the reproducibility of our findings, we queried the gene expression portals GTEx (22) for normal breast tissue and the METABRIC data from cBioPortal (21) for ER+ BC. Our analysis using these external datasets showed similar trends between ESR1 and PC3 (Figure 2E). The negative correlation between BCKs (contributing to PC3) and ESR1 expression may be explained by the fact that the BCK induction in ER+ BC requires low ER expression (55). However, to the best of our knowledge, no study so far has reported that this correlation may turn positive in normal breast tissues.
StableMate discerns global microbial signatures for colon cancer in multi-cohort metagenomics data
There has been considerable research interest in using faecal microbiome as biomarkers for CRC. If successful, this non-invasive way of screening for CRC may reduce the mortality rate through early intervention (56,57). By pooling faecal metagenomics data from a large number of independent CRC–control studies, several meta-analyses have been conducted to identify cross-cohort microbial signatures of CRC and to build predictive models for its diagnosis (26,30,58). However, these analyses ignored the technical differences between cohorts, which could have confounded their results. We addressed this problem by conducting a meta-analysis based on StableMate using the cohort as the environmental variable. In particular, we selected stable microbial signatures that make consistent predictions of CRC across cohorts, as well as cohort-specific signatures that highlight confounding factors in CRC prediction. Our results showed better prediction accuracy compared to the methods used in these studies.
Data and StableMate setting
We retrieved eight CRC case-control faecal metagenomic datasets from the R package curatedMetagenomicData (23). The datasets were generated by eight different cohorts from seven countries (refer to Table 1 for the cohort used and for the number of CRC and controls in each cohort). Data were curated into abundance data using a standardized data processing pipeline by Pasolli et al. (23). In total, we collected 604 CRC and 596 control samples. Our analysis focused on the species abundance data measured on 313 microbial species. The analysis of pathway abundance data measured on 431 pathways is detailed in Supplementary Figure S6.
Since we were interested in the CRC diagnosis using metagenomics data, we set the disease status (CRC or normal) as the response and the microbial species as predictors and performed logistic regression in StableMate analysis. We implemented StableMate using the following two strategies. In the first analysis, we applied StableMate as in the toy example (see ‘Illustration of StableMate on toy example’ section) and our first case study (see the ‘StableMate identifies genes associated with ESR1 expression in ER+ breast cancer using RNA-seq data’ section), where all cohorts were pooled to select predictive species and assessed their stability by setting cohort as the environment variable. From this analysis, we found that the majority of the selected predictive species were stable and none of them was cohort-specific (as discussed later in the ‘StableMate discerns global microbial signatures for colon cancer in multi-cohort metagenomics data’ section). Therefore, in a second analysis, we applied StableMate on each cohort to identify cohort-specific predictive species and tested the stability of the species selected in the remaining seven cohorts combined. There we considered only two environments: the specific cohort and the remaining cohorts combined. These ‘cohort-specific analyses’ are useful for identifying species that are highly predictive in a specific cohort but their association with CRC in the specific cohort cannot be generalized to other cohorts.
StableMate identified stable microbial species predictive of colon cancer
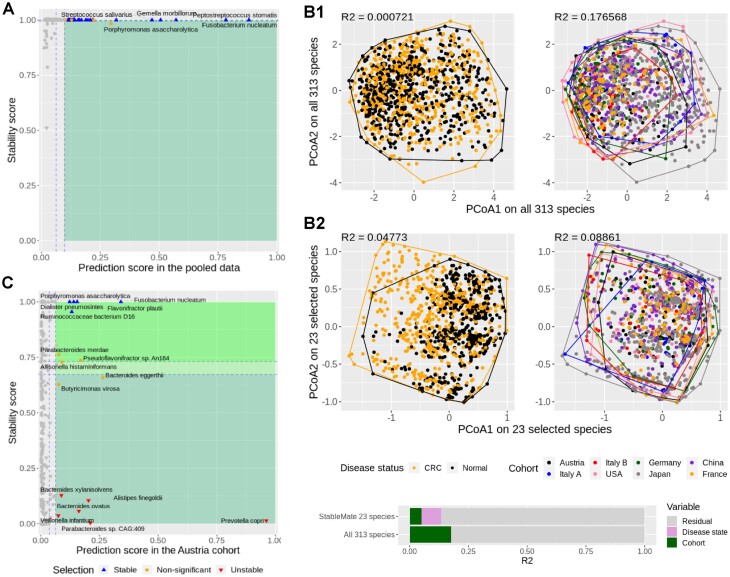
From the pooled analysis, we identified 23 stable species to predict disease status (CRC or normal) (Figure 3A). To illustrate the strong cohort effect of the data and the ability of StableMate selection to identify predictors with a mild cohort effect, we used PCoA with all 313 species versus the 23 stable species. The PCoA results combined with a permutation ANOVA showed that the main source of variation was the cohort effect rather than disease status (Figure 3B1) when all species were used. This implies that a predictive model built using all species is likely to be affected by cohort (batch) effects. In contrast, the PCoA and ANOVA results of the 23 stable species selected by StableMate showed a decrease in cohort effects and an increase in the effects of disease status (Figure 3B2). In particular, the CRC and normal samples were better separated in the PCoA when using only the 23 stable species (left panel of Figure 3B2). A formal evaluation of the goodness of variable selection is presented in the ‘Benchmarking StableMate variable selection and prediction on metagenomics data’ section.
Figure 3.
StableMate meta-analysis of metagenomic data reveals key species predictive of CRC across eight independent study cohorts. (A) StableMate variable selection plot of the pooled analysis. The majority of highly predictive species were found stable, and none was identified as cohort-specific. (B) PCoA with samples coloured by either disease status (left column) or cohorts (right column). (B1) Using all 313 species shared by all cohorts, regardless of their stability; (B2) using only the 23 stable species selected by StableMate. PERMANOVA R2 statistic on the first two principal coordinates is shown in the top left corner of each panel. The coloured bar at the bottom shows the composition of the total variance. When considering all 313 species, the cohort effect is much larger than the disease effect (almost negligible); with 23 species identified as stable, the cohort effect is still present but smaller than the disease effect. (C) StableMate variable selection plot of the Austria cohort-specific analysis (one of the eight cohort-specific analyses). Prevotella copri was found to be an Austria-specific species for predicting CRC, since it has a high prediction score but a low stability score. Such species are interesting for studying cohort-specific effects that may confound the CRC diagnosis.
StableMate identified cohort-specific microbial species predictive of colon cancer
We conducted cohort-specific analyses for each of the eight cohorts to identify predictors with high cohort specificity. As an example, Figure 3C shows the results for the Austrian cohort. A number of species were found to be highly predictive in the Austrian cohort but with a very low stability score and, therefore, were identified as cohort-specific. Among them, P. copri was the most predictive and one of the most cohort-specific species, suggesting that P. copri might be a marker for CRC specific to the Austrian cohort only. It should be noted, however, that diet could be a confounder, as the Austria-specific species might be related to the low-fibre diet in that population (see Supplementary Section S1.2 for details).
Pooling data improves generalizability of prediction models
Most of the predictive species selected on the pooled data were stable (Figure 3A), whereas predictive species selected in the individual cohorts showed less stability (Supplementary Figure S7). This can be explained as the stability score of a predictor is correlated with the predictor’s influence on the generalizability of regression models. As the number of cohorts increases, regression models tend to put less weight on unstable predictors. As a result, unstable predictors have less influence on model fitting. Hence, we obtained high stability scores for these predictors. This analysis quantitatively confirms a common perception in classical meta-analysis that training regression models on pooled data rather than individual datasets can yield improved generalizability (26,30,58).
However, aside from pooling data, we were able to further improve generalizability of prediction models by taking into account the cohort effect through stability analysis. We conducted a benchmark study in the ‘Benchmarking StableMate variable selection and prediction on metagenomics data’ section, where we showed that the StableMate model built using the stable species outperformed several commonly used regression methods in the pooled analysis.
StableMate characterizes cell identity transition of GBM-associated microglia with scRNA-seq data
GBM is the most invasive type of brain tumour that presents significant therapeutic challenges. GBM harbors a heterogeneous tumour microenvironment dominated by tumour-associated macrophages (TAM) and microglia, which were recruited by GBM to promote tumour growth, migration, recurrence, and resistance to immunotherapy (59). Since the majority of TAM in GBM are thought to be derived from microglia (i.e. tissue-resident macrophages in the brain) infiltrating the tumour, identifying key genes involved in this process could have therapeutic potential.
In this case study, we analysed a scRNA-seq dataset of myeloid cells at the periphery (migrating front) and the core of the GBM tumour. These locations represent the start and the end points of the transition from microglia to TAM. We used StableMate to extract the key genes involved in this transition while taking location into account. Hence, we were able to investigate how the transition differs between the locations and reveal location-agnostic and -specific immune activities.
Data and StableMate setting
From the scRNA-seq dataset from Darmanis et al. (31) of four GBM tumours, we extracted and analysed 1847 myeloid cells from the tumour core (1329 cells) and from the tumour periphery (518 cells) with the cell annotation provided by the authors of the study.
We visualized the scRNA-seq data and observed a clear cell trajectory between the two locations, which may represent the cellular transition of microglia to TAM. We conducted a pseudotime analysis to quantify this trajectory and used StableMate to predict as a response the pseudotime based on expression of the genes as predictors. The base regressor used for StableMate analysis was simple linear regression. The cell location, core or periphery, was set as the environment variable. StableMate selected several cytokines as being predictive of the pseudotime. To further investigate the possible mechanism of these cytokines, we performed a second analysis to build a gene regulatory network for these cytokines. More specifically, we applied StableMate on each of the cytokines as a response and all other genes as predictors. We then summarized the selection results in the form of a network, where the cytokines are connected to their stable predictor genes.
DPT tumour periphery to core
We first visualized the myeloid cells projected onto a bulk RNA-seq reference atlas of myeloid cells (45) to assign the identity of the cells. We performed this using Sincast (33) (Figure 4A1). The projection showed that the cells from the periphery of the tumour closely matched foetal microglia in the reference, and the cells from the core of the tumour matched a wider range of monocytes and macrophages (Supplementary Figure S8A). The projection also showed a continuous state of transition, rather than discrete clusters. We also confirmed the transition by a separate DM analysis in Supplementary Figure S8B. This exploration suggested that the data were suitable for DPT analysis (Figure 4A2), where we set the cells at the tumour periphery as the root (start) of the trajectory (44). The inferred DPT was then used as the response for our first StableMate analysis described below.
StableMate analysis identifies cytokines that signify microglia pre-activation and polarization in tumour periphery
Among the genes selected by StableMate as predictive of DPT, we identified six cytokines whose expression were all negatively correlated with DPT (Supplementary Figure S8C). Among these cytokines, CCL3 and CCL4 were identified as stable (Figure 4B), while TNF, IL1B, CCL2, and CSF1 were identified as periphery-specific (Figure 4C). The selection of the six cytokines is interesting as they are important markers of microglia activation in response to disease (60).
In order to visualize the relationships of these cytokines, we ran StableMate on each cytokine as a response, where all the other genes were used as predictors, and built a gene regulatory network (Figure 4D—DPT was included as a ‘pseudo gene’ here to incorporate the result from the first analysis). This network showed that the two stable cytokines (CCL3 and CCL4) formed a community with DPT, whereas the four periphery-specific cytokines (TNF, IL1B, CCL2, and CSF1) formed another community.
Other stable genes predictive of DPT represented on this network include EGR2 and CD83, which were connected to both DPT and CCL3 (Supplementary Figure S8D). CCL3, CCL4, CD83, and EGR2 are all known to be associated with an immediate early inflammatory response by microglia in a pre-activated state, which is in between homeostasis to those fully activated under pathological conditions (61–66). These four genes showed consistent downregulation during the transition regardless of cell location. On the contrary, the periphery-specific cytokines, which are known markers for microglia polarization to either the pro-inflammatory M1 or anti-inflammatory M2 phenotype (60), exhibited stronger negative association with DPT in the periphery—resulting in low expression levels—and weak association with DPT in the core (Figure 4C).
Core-specific genes revealed reprogramming of tumour-infiltrating microglia into immunosuppressive TAM in GBM tumours
The core-specific genes identified by StableMate included two interesting cell surface markers: the macrophage marker MARCO and MHC class II antigen HLA-DOA (Supplementary Figure S8C). MACRO was lowly expressed in the tumour periphery but upregulated along the DPT trajectory towards the tumour core (Figure 4E, upper). HLA-DOA expression levels had a low–high–low pattern along the trajectory, with high expression levels at the boundary of tumour periphery and core (Figure 4E, lower; other MHC-II genes were also examined in Supplementary Figure S8E). The upregulation of MARCO and the downregulation of HLA-DOA towards the core may indicate the presence of MARCOhi, MHC-IIlo macrophages, which are characteristic of the M2-like immunosuppressive TAM (67,68). In addition to these two cell surface markers, many pro-tumour markers were also identified by StableMate as core-specific and showed similar expression patterns as MACRO (Supplementary Figure S9A). One example is VCAN, which encodes a large extracellular protein contributing to the establishment of tumour microenvironments (Figure 4F). The expression patterns of these core-specific pro-tumour markers suggest that they responded specifically to the tumour microenvironment and hence are potentially good therapeutic targets.
In addition, we examined the immune activation state of the cells at the beginning of the core stage of the transition. We observed high expression of the stable cytokines CCL3 and CCL4 (Figure 4C), as well as the microglia marker TMEM119, which were all then gradually suppressed in the core (Supplementary Figure S8F). This may imply the reprogramming of activated microglia in the early stages of the core transition to TAMs.
Benchmarking StableMate variable selection and prediction on metagenomics data
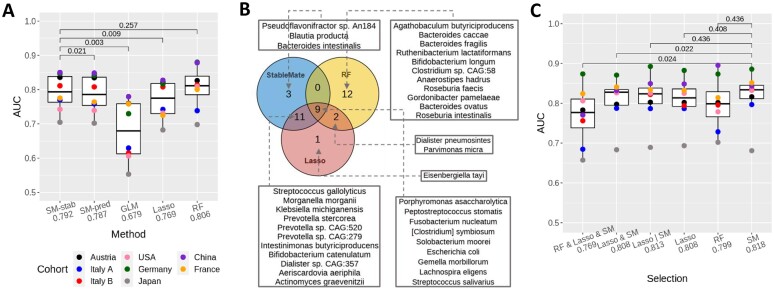
We used the species abundance data from eight metagenomics studies of CRC described in the ‘StableMate discerns global microbial signatures for colon cancer in multi-cohort metagenomics data’ section to benchmark the variable selection and prediction performances of StableMate (using logistic regression model as the base model) against GLM (with logistic regression using all predictors), Lasso regression (34) and RF (40). To assess the prediction performance of these methods, we used a LODO cross-validation strategy. That is, in each of the eight cross-validation iterations, we left out one of the cohorts and trained the different regression models using the other seven cohorts (based on all 313 species). The left-out cohort was then used as a test dataset on which the AUC was calculated for each regression model. Since the left-out cohort represents an unseen environment, regression models receiving higher AUCs can be considered as more generalizable. To assess the variable selection performance of StableMate, recall that we have already applied StableMate to do a pooled meta-analysis as described in the ‘StableMate discerns global microbial signatures for colon cancer in multi-cohort metagenomics data’ section and identified 23 stable species. We applied Lasso and RF to the same pooled data with eight cohorts to select 23 species (for RF, we ranked all species by their importance scores in descending order, and then selected the top 23). We use these three lists of species to build RF models and assess their generalizability using LODO.
StableMate based on logistic regression outperformed Lasso and performed comparably to RF in CRC classification
The LODO AUC values for all competing methods are shown in boxplots in Figure 5A. To illustrate the benefits of using stable predictors to build regression models, we considered two versions of the StableMate prediction model, one built using all selected predictive variables, the other using only the stable predictors. To further investigate if the differences in AUC values were statistically significant, we conducted a series of two-sided paired t-tests, and the P-values of these tests are shown in Figure 5A.
Figure 5.
StableMate outperforms commonly used regression methods in prediction and variable selection based on the colon cancer case study. (A) We used LODO cross-validation to calculate area under the curve (AUC, y-axis) and assess the generalizability of the classification when applied to an unseen cohort. Paired t-tests compare the AUC values and adjusted P-values (69) are shown. Each point presents the AUC value calculated on a left-out cohort. Methods include GLM (logistic regression), Lasso (Lasso logistic regression), RF, and two versions of StableMate (logistic regression): SM-Stab-based stable predictors only and SM-Pred using all predictive variables. Among all linear methods (all except RF), SM-Stab obtained the highest mean AUC (the difference is statistically significant). Compared to RF, SM-Stab had a slightly lower mean AUC, but this difference was not statistically significant. Note that RF is a more flexible non-linear classification method. (B) Venn diagram to compare the three lists of species (each containing 23 species) selected by StableMate, Lasso, and RF. StableMate and Lasso made similar selections, with 20 species selected by both. The RF selection was quite different from the other two methods. Nine species were selected by all three methods, all of which are known to be associated with CRC (70). In addition, two species, also known to be associated with CRC, were selected by both Lasso and RF but not by StableMate. This is because these two species were not significantly stable as suggested by StableMate selection. (C) Generalizability of six sets of species: top 23 species selected by StableMate (‘SM’), Lasso and RF, the 9 species selected by all the methods (‘RF & Lasso & SM’), the 20 species selected by both Lasso and StableMate (‘Lasso & SM’) and the 26 species selected by either Lasso or StableMate (‘Lasso | SM’). We built six RF classifiers using these six sets of species and reported their AUC values (mean AUC on the x-axis). The stable species selected by StableMate led to the best RF model, with a higher AUC than RF trained with all 313 species in (A).
We first compared the performances of all methods except RF, since they all use variants of linear models to make predictions, whereas RF is a non-linear approach. From Figure 5A, we observed that the StableMate prediction using only stable predictors was significantly better than GLM, Lasso, and StableMate using all predictive variables. Among these methods, GLM had the worst generalizability. As GLM does not perform variable selection, the prediction model potentially included many noisy features. Lasso’s selected variables led to poorer prediction compared to the two variants of StableMate. The version of StableMate using only stable predictors led to slightly higher mean AUC compared to StableMate using all predictive variables, with a P-value indicating a significant difference. The superior performance of StableMate based on stable predictors highlighted the benefits of using such type of predictors to build prediction models.
Finally, we observed that the AUC performance of StableMate based on the stable predictors was indistinguishable from RF. This can be explained as StableMate only uses an ensemble of stringent logistic models to make predictions (see the ‘Materials and methods’ and ‘StableMate to identify stable and environment-specific statistical associations’ sections), whereas RF uses an ensemble of non-linear and highly flexible decision trees targeted for classification tasks.
One can also use StableMate as a variable selection method only and then separately build regression models based on the stable predictors. Filtering out irrelevant and unstable predictors in data can benefit model fitting by improving generalizability (71). Therefore, the notable classification performance of RF motivated the second benchmark study below, in which we evaluated whether StableMate can select predictors that lead to more generalizable RF models.
Species selected by StableMate lead to more generalizable prediction models
We applied StableMate, Lasso, and RF to select three species lists, each containing 23 species. Figure 5B shows a Venn diagram that compares these three lists (see also Supplementary Figure S10A for a more comprehensive comparison). The three lists included an overlap of nine species, all of which are well-known species associated with CRC (70). Among these three methods, StableMate and Lasso shared 20 species, many more than with RF species selection. Of note, StableMate selected three species that were neither selected by Lasso nor by RF (Figure 5B), including Bacteroides intestinalis whose connection with CRC has not been widely reported. Bacteroides intestinalis, along with its metabolic product, is considered as an important biomarker for human gastrointestinal health (72). Under carcinogenetic stress, B. intestinalis has been shown to exhibit increased activity in enhancing DNA integrity maintenance and suppressing central metabolic activities, suggesting B. intestinalis’ protective role against CRC (73,74). This hypothesis is concordant with our observation of a decreased abundance of B. intestinalis in CRC samples across cohorts (Supplementary Figure S11A).
For a quantitative evaluation, we built RF models using six different selections of species and computed their AUC using the LODO cross-validation approach. The results are summarized in Figure 5C, where the 23 stable species selected by StableMate led to the highest mean AUC (0.818). StableMate and Lasso selections had high AUC values since their selections were similar. The difference between StableMate and RF selections was not statistically significant, probably due to a lack of cohorts and statistical power. However, the StableMate selection led to less variable prediction performances (smaller interquartile range) compared to RF. Two species, Dialister pneumosintes and Parvimonas micra, were selected by Lasso and RF but not by StableMate (Figure 5B). In particular, P. micra is known to be associated with CRC as it promotes tumourigenesis (75,76). However, StableMate identified these two species as predictive but not significantly stable. The fact that there was no improvement in the prediction performance of RF trained on the StableMate selection with these two additional species (comparing ‘Lasso | SM’ and ‘SM’ in Figure 5C) justifies why StableMate did not select these two species.
Benchmark based on pathway abundance data
A similar benchmarking analysis based on the pathway abundance data showed that StableMate outperformed the other methods, including RF, in predicting CRC (highest mean AUC; see Supplementary Figure S6B). However, the pathway abundance data were less stable and less predictive of CRC compared to the species abundance data. All methods obtained lower AUC scores in LODO assessment. We observed strong differences in variable selections between the cohorts and the methods (Supplementary Figures S6A and S10).
Discussion
The unbiased characterization of a biological system requires a comprehensive understanding of the relationships between biological variables. Current methods that infer biological relationships attempt to define and identify statistical associations but often lack generalizability or biological interpretability (9–11). We developed StableMate, a new regression framework based on SR (17) to address these challenges.
StableMate selects stable and environment-specific (unstable) predictors of the response variable to represent statistical associations across different technical or biological environments. Discerning the stability of associations allows us to make interpretable inferences on biological relationships. On the one hand, stable predictors suggest closer relationships with the response compared to environment-specific predictors. On the other hand, environment-specific predictors are useful for characterizing the environmental differences in the biological system under study.
In the three case studies dealing with different types of cancer omics data, we showed that StableMate brings novel biological insights. In the simulation study, we showed the benefit of using StableMate for better prediction accuracy, computational efficiency, and accuracy of variable selection compared to existing methods.
In the first case study, we analysed the RNA-seq data of BC. Stability analysis allowed us to identify genes and gene modules that directly or indirectly relate to ESR1 regulation.
In the second case study, we conducted a meta-analysis of eight metagenomic studies of colon cancer. StableMate analysis revealed global microbial signatures that can make consistent prediction of colon cancer regardless of the cohorts, as well as cohort-specific microbial signatures that can shed light on confounders in colon cancer prediction. In this study, we also benchmarked the performance of different existing methods in making cross-cohort predictions, showing that StableMate is highly competitive. We noted that StableMate did not significantly outperform RF, probably due to either a small number of cohorts affecting statistical power, or because of the difference between a linear logistic regression (StableMate) and a non-linear classification method (RF). This, therefore, also motivated our simulation study, where we considered a continuous response and generated enough repetition of experiments (Supplementary Figures S1 and S2).
In the third case study, we analysed scRNA-seq data of myeloid cells residing in the core and the surrounding periphery tissues of GBM. We first identified a trajectory of continuous cell state transition between the cells at the two locations and then applied StableMate to identify stable and location-specific genes associated with this cell state transition. By analysing periphery- and core-specific genes, we hypothesized that microglial polarization seems to occur primarily in the tumour periphery, and the reprogramming of microglia into pro-tumour TAM happens after microglia infiltrate the tumour core. The stable genes exhibited consistent expression patterns in both the locations, hence ubiquitously involved in the development of both the pro- and the anti-inflammatory microglia.
In these case studies, the biological interpretation of the variable selections mainly focused on significant genes or microbial signatures. However, further experimental validations could hypothesize on the causal implication of stable predictors to the response.
StableMate is based on SR but implements a different algorithm for stochastic stepwise variable selection to select stable and environment-specific predictors with higher computational efficiency and accuracy. The stepwise framework of StableMate can be implemented with different base regressors to address different regression problems, such as OLS and logistic regression, as we illustrated in our case studies. StableMate is available in R and can flexibly implement user-defined regression methods. One such extension could, for example, include non-linear regression methods, as well as penalized regression to avoid the pre-screening step currently proposed in StableMate.
Supplementary Material
Acknowledgements
We thank Miguel Ángel Berrocal Rubio and Patrick Lichtner for their helpful insights regarding the variable selection results from the GBM case study, and Kris Sankaran for his feedback on the manuscript.
Notes
Present address: Jarny Choi, Bioinformatics and Cellular Genomics, St Vincent’s Institute, 9 Princes Street, Melbourne, 3065, Australia.
Contributor Information
Yidi Deng, Melbourne Integrative Genomics, School of Mathematics and Statistics, The University of Melbourne, Royal Parade, Melbourne, 3052, Australia; Department of Anatomy and Physiology, Faculty of Medicine, Dentistry and Health Sciences, The University of Melbourne, Grattan Street, Melbourne, 3010, Australia.
Jiadong Mao, Melbourne Integrative Genomics, School of Mathematics and Statistics, The University of Melbourne, Royal Parade, Melbourne, 3052, Australia.
Jarny Choi, Department of Anatomy and Physiology, Faculty of Medicine, Dentistry and Health Sciences, The University of Melbourne, Grattan Street, Melbourne, 3010, Australia.
Kim-Anh Lê Cao, Melbourne Integrative Genomics, School of Mathematics and Statistics, The University of Melbourne, Royal Parade, Melbourne, 3052, Australia.
Data availability
The StableMate R code and data analysis are available at https://github.com/meiosis97/StableMate and https://doi.org/10.5281/zenodo.13626593.
Supplementary data
Supplementary Data are available at NARGAB Online.
Funding
Australian Research Council Discovery Project (DP200102903 to J.M.); National Health and Medical Research Council Investigator Grant (GNT2025648 to K.A.L.C.); Melbourne Graduate Research Scholarship, University of Melbourne (to Y.D.).
Conflict of interest statement. None declared.
References
- 1. Langfelder P., Horvath S. WGCNA: an R package for weighted correlation network analysis. BMC Bioinformatics. 2008; 9:559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Huynh-Thu V.A., Irrthum A., Wehenkel L., Geurts P. Inferring regulatory networks from expression data using tree-based methods. PLoS One. 2010; 5:e12776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Moerman T., Aibar Santos S., Bravo González-Blas C., Simm J., Moreau Y., Aerts J., Aerts S. GRNBoost2 and Arboreto: efficient and scalable inference of gene regulatory networks. Bioinformatics. 2019; 35:2159–2161. [DOI] [PubMed] [Google Scholar]
- 4. Aibar S., González-Blas C.B., Moerman T., Huynh-Thu V.A., Imrichova H., Hulselmans G., Rambow F., Marine J.-C., Geurts P., Aerts J. et al. SCENIC: single-cell regulatory network inference and clustering. Nat. Methods. 2017; 14:1083–1086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Faith J.J., Hayete B., Thaden J.T., Mogno I., Wierzbowski J., Cottarel G., Kasif S., Collins J.J., Gardner T.S. Large-scale mapping and validation of Escherichia coli transcriptional regulation from a compendium of expression profiles. PLoS Biol. 2007; 5:e8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Chan T.E., Stumpf M.P., Babtie A.C. Gene regulatory network inference from single-cell data using multivariate information measures. Cell Syst. 2017; 5:251–267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Chickering D.M. Optimal structure identification with greedy search. J. Mach. Learn. Res. 2002; 3:507–554. [Google Scholar]
- 8. Spirtes P., Glymour C., Scheines R., Kauffman S., Aimale V., Wimberly F. Constructing Bayesian network models of gene expression networks from microarray data. 2018; https://doi.org/10.1184/R1/6491291.v1.
- 9. Pratapa A., Jalihal A.P., Law J.N., Bharadwaj A., Murali T. Benchmarking algorithms for gene regulatory network inference from single-cell transcriptomic data. Nat. Methods. 2020; 17:147–154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Nguyen H., Tran D., Tran B., Pehlivan B., Nguyen T. A comprehensive survey of regulatory network inference methods using single cell RNA sequencing data. Brief. Bioinformatics. 2021; 22:bbaa190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Kang Y., Thieffry D., Cantini L. Evaluating the reproducibility of single-cell gene regulatory network inference algorithms. Front. Genet. 2021; 12:362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Xiang R., van den Berg I., MacLeod I.M., Daetwyler H.D., Goddard M.E. Effect direction meta-analysis of GWAS identifies extreme, prevalent and shared pleiotropy in a large mammal. Commun. Biol. 2020; 3:88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Austin-Zimmerman I., Levey D.F., Giannakopoulou O., Deak J.D., Galimberti M., Adhikari K., Zhou H., Denaxas S., Irizar H., Kuchenbaecker K. et al. Genome-wide association studies and cross-population meta-analyses investigating short and long sleep duration. Nat. Commun. 2023; 14:6059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Bühlmann P. Invariance, causality and robustness. Stat. Sci. 2020; 35:404–426. [Google Scholar]
- 15. Pearl J. An introduction to causal inference. Int. J. Biostat. 2010; 6:Article 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Shojaie A. Differential network analysis: a statistical perspective. Wiley Interdiscip. Rev. Comput. Stat. 2021; 13:e1508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Pfister N., Williams E.G., Peters J., Aebersold R., Bühlmann P. Stabilizing variable selection and regression. Ann. Appl. Stat. 2021; 15:1220–1246. [Google Scholar]
- 18. Colaprico A., Silva T.C., Olsen C., Garofano L., Cava C., Garolini D., Sabedot T.S., Malta T.M., Pagnotta S.M., Castiglioni I. et al. TCGAbiolinks: an R/Bioconductor package for integrative analysis of TCGA data. Nucleic Acids Res. 2016; 44:e71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Curtis C., Shah S.P., Chin S.-F., Turashvili G., Rueda O.M., Dunning M.J., Speed D., Lynch A.G., Samarajiwa S., Yuan Y. et al. The genomic and transcriptomic architecture of 2,000 breast tumours reveals novel subgroups. Nature. 2012; 486:346–352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Pereira B., Chin S.-F., Rueda O.M., Vollan H.K.M., Provenzano E., Bardwell H.A., Pugh M., Jones L., Russell R., Sammut S.-J. et al. The somatic mutation profiles of 2,433 breast cancers refine their genomic and transcriptomic landscapes. Nat. Commun. 2016; 7:11479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Cerami E., Gao J., Dogrusoz U., Gross B.E., Sumer S.O., Aksoy B.A., Jacobsen A., Byrne C.J., Heuer M.L., Larsson E. et al. The cBio Cancer Genomics Portal: an open platform for exploring multidimensional cancer genomics data. Cancer Discov. 2012; 2:401–404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Lonsdale J., Thomas J., Salvatore M., Phillips R., Lo E., Shad S., Hasz R., Walters G., Garcia F., Young N. et al. The genotype-tissue expression (GTEx) project. Nat. Genet. 2013; 45:580–585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Pasolli E., Schiffer L., Manghi P., Renson A., Obenchain V., Truong D.T., Beghini F., Malik F., Ramos M., Dowd J.B. et al. Accessible, curated metagenomic data through ExperimentHub. Nat. Methods. 2017; 14:1023–1024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Feng Q., Liang S., Jia H., Stadlmayr A., Tang L., Lan Z., Zhang D., Xia H., Xu X., Jie Z. et al. Gut microbiome development along the colorectal adenoma–carcinoma sequence. Nat. Commun. 2015; 6:6528. [DOI] [PubMed] [Google Scholar]
- 25. Vogtmann E., Hua X., Zeller G., Sunagawa S., Voigt A.Y., Hercog R., Goedert J.J., Shi J., Bork P., Sinha R. Colorectal cancer and the human gut microbiome: reproducibility with whole-genome shotgun sequencing. PLoS One. 2016; 11:e0155362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Wirbel J., Pyl P.T., Kartal E., Zych K., Kashani A., Milanese A., Fleck J.S., Voigt A.Y., Palleja A., Ponnudurai R. et al. Meta-analysis of fecal metagenomes reveals global microbial signatures that are specific for colorectal cancer. Nat. Med. 2019; 25:679–689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Yachida S., Mizutani S., Shiroma H., Shiba S., Nakajima T., Sakamoto T., Watanabe H., Masuda K., Nishimoto Y., Kubo M. et al. Metagenomic and metabolomic analyses reveal distinct stage-specific phenotypes of the gut microbiota in colorectal cancer. Nat. Med. 2019; 25:968–976. [DOI] [PubMed] [Google Scholar]
- 28. Yu J., Feng Q., Wong S.H., Zhang D., yi Liang Q., Qin Y., Tang L., Zhao H., Stenvang J., Li Y. et al. Metagenomic analysis of faecal microbiome as a tool towards targeted non-invasive biomarkers for colorectal cancer. Gut. 2017; 66:70–78. [DOI] [PubMed] [Google Scholar]
- 29. Zeller G., Tap J., Voigt A.Y., Sunagawa S., Kultima J.R., Costea P.I., Amiot A., Böhm J., Brunetti F., Habermann N. et al. Potential of fecal microbiota for early-stage detection of colorectal cancer. Mol. Syst. Biol. 2014; 10:766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Thomas A.M., Manghi P., Asnicar F., Pasolli E., Armanini F., Zolfo M., Beghini F., Manara S., Karcher N., Pozzi C. et al. Metagenomic analysis of colorectal cancer datasets identifies cross-cohort microbial diagnostic signatures and a link with choline degradation. Nat. Med. 2019; 25:667–678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Darmanis S., Sloan S.A., Croote D., Mignardi M., Chernikova S., Samghababi P., Zhang Y., Neff N., Kowarsky M., Caneda C. et al. Single-cell RNA-seq analysis of infiltrating neoplastic cells at the migrating front of human glioblastoma. Cell Rep. 2017; 21:1399–1410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Butler A., Hoffman P., Smibert P., Papalexi E., Satija R. Integrating single-cell transcriptomic data across different conditions, technologies, and species. Nat. Biotechnol. 2018; 36:411–420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Deng Y., Choi J., Lê Cao K.-A. Sincast: a computational framework to predict cell identities in single-cell transcriptomes using bulk atlases as references. Brief. Bioinformatics. 2022; 23:bbac088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Tibshirani R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. B Methodol. 1996; 58:267–288. [Google Scholar]
- 35. Meinshausen N., Bühlmann P. Stability selection. J. R. Stat. Soc. B Stat. Method. 2010; 72:417–473. [Google Scholar]
- 36. Xin L., Zhu M. Stochastic stepwise ensembles for variable selection. J. Comput. Graph. Stat. 2012; 21:275–294. [Google Scholar]
- 37. R Core Team R: a language and environment for statistical computing. R Foundation for Statistical Computing Vienna. 2013; Austria: R version 4.2.1http://www.R-project.org/. [Google Scholar]
- 38. Ledesma R., Valero-Mora P., Macbeth G. The scree test and the number of factors: a dynamic graphics approach. Span. J. Psychol. 2015; 18: 10.1017/sjp.2015.13. [DOI] [PubMed] [Google Scholar]
- 39. Oksanen J., Simpson G.L., Blanchet F.G., Kindt R., Legendre P., Minchin P.R., O’Hara R., Solymos P., Stevens M.H.H., Szoecs E. et al. vegan: community ecology package. 2022; R package version 2.6-4https://CRAN.R-project.org/package=vegan.
- 40. Breiman L. Random forests. Mach. Learn. 2001; 45:5–32. [Google Scholar]
- 41. Kuhn M. caret: classification and regression training. 2022; R package version 6.0-93https://CRAN.R-project.org/package=caret.
- 42. Liaw A., Wiener M. Classification and regression by randomForest. R. News. 2002; 2:18–22. [Google Scholar]
- 43. Haghverdi L., Buettner F., Theis F.J. Diffusion maps for high-dimensional single-cell analysis of differentiation data. Bioinformatics. 2015; 31:2989–2998. [DOI] [PubMed] [Google Scholar]
- 44. Haghverdi L., Büttner M., Wolf F.A., Buettner F., Theis F.J. Diffusion pseudotime robustly reconstructs lineage branching. Nat. Methods. 2016; 13:845–848. [DOI] [PubMed] [Google Scholar]
- 45. Rajab N., Angel P.W., Deng Y., Gu J., Jameson V., Kurowska-Stolarska M., Milling S., Pacheco C.M., Rutar M., Laslett A.L. et al. An integrated analysis of human myeloid cells identifies gaps in in vitro models of in vivo biology. Stem Cell Rep. 2021; 16:1629–1643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Kong W., Fu Y.C., Holloway E.M., Garipler G., Yang X., Mazzoni E.O., Morris S.A. Capybara: a computational tool to measure cell identity and fate transitions. Cell Stem Cell. 2022; 29:635–649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Johnson K.S., Conant E.F., Soo M.S. Molecular subtypes of breast cancer: a review for breast radiologists. J. Breast Imaging. 2021; 3:12–24. [DOI] [PubMed] [Google Scholar]
- 48. Weinstein J.N., Collisson E.A., Mills G.B., Shaw K.R., Ozenberger B.A., Ellrott K., Shmulevich I., Sander C., Stuart J.M. The cancer genome atlas pan-cancer analysis project. Nat. Genet. 2013; 45:1113–1120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Vitale S.R., Ruigrok-Ritstier K., Timmermans A.M., Foekens R., Trapman-Jansen A.M., Beaufort C.M., Vigneri P., Sleijfer S., Martens J.W., Sieuwerts A.M. et al. The prognostic and predictive value of ESR1 fusion gene transcripts in primary breast cancer. BMC Cancer. 2022; 22:165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Bouras T., Southey M.C., Chang A.C., Reddel R.R., Willhite D., Glynne R., Henderson M.A., Armes J.E., Venter D.J. Stanniocalcin 2 is an estrogen-responsive gene coexpressed with the estrogen receptor in human breast cancer. Cancer Res. 2002; 62:1289–1295. [PubMed] [Google Scholar]
- 51. Raulic S., Ramos-Valdes Y., DiMattia G.E. Stanniocalcin 2 expression is regulated by hormone signalling and negatively affects breast cancer cell viability in vitro. J. Endocrinol. 2008; 197:517–530. [DOI] [PubMed] [Google Scholar]
- 52. Law A.Y., Wong C.K. Stanniocalcin-2 is a HIF-1 target gene that promotes cell proliferation in hypoxia. Exp. Cell Res. 2010; 316:466–476. [DOI] [PubMed] [Google Scholar]
- 53. Law A.Y., Lai K.P., Ip C.K., Wong A.S., Wagner G.F., Wong C.K. Epigenetic and HIF-1 regulation of stanniocalcin-2 expression in human cancer cells. Exp. Cell Res. 2008; 314:1823–1830. [DOI] [PubMed] [Google Scholar]
- 54. Langfelder P., Horvath S. Eigengene networks for studying the relationships between co-expression modules. BMC Syst. Biol. 2007; 1:54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Li Z., McGinn O., Wu Y., Bahreini A., Priedigkeit N.M., Ding K., Onkar S., Lampenfeld C., Sartorius C.A., Miller L. et al. ESR1 mutant breast cancers show elevated basal cytokeratins and immune activation. Nat. Commun. 2022; 13:2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Labianca R., Beretta G.D., Kildani B., Milesi L., Merlin F., Mosconi S., Pessi M.A., Prochilo T., Quadri A., Gatta G. et al. Colon cancer. Crit. Rev. Oncol./Hematol. 2010; 74:106–133. [DOI] [PubMed] [Google Scholar]
- 57. Sears C.L., Garrett W.S. Microbes, microbiota, and colon cancer. Cell Host Microbe. 2014; 15:317–328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Dai Z., Coker O.O., Nakatsu G., Wu W.K., Zhao L., Chen Z., Chan F.K., Kristiansen K., Sung J.J., Wong S.H. et al. Multi-cohort analysis of colorectal cancer metagenome identified altered bacteria across populations and universal bacterial markers. Microbiome. 2018; 6:70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Andersen R.S., Anand A., Harwood D. S.L., Kristensen B.W. Tumor-associated microglia and macrophages in the glioblastoma microenvironment and their implications for therapy. Cancers. 2021; 13:4255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Jurga A.M., Paleczna M., Kuter K.Z. Overview of general and discriminating markers of differential microglia phenotypes. Front. Cell. Neurosci. 2020; 14:198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Kohno H., Maeda T., Perusek L., Pearlman E., Maeda A. CCL3 production by microglial cells modulates disease severity in murine models of retinal degeneration. J. Immunol. 2014; 192:3816–3827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62. Masuda T., Sankowski R., Staszewski O., Prinz M. Microglia heterogeneity in the single-cell era. Cell Rep. 2020; 30:1271–1281. [DOI] [PubMed] [Google Scholar]
- 63. Masuda T., Sankowski R., Staszewski O., Böttcher C., Amann L., Scheiwe C., Nessler S., Kunz P., van Loo G., Coenen V.A. et al. Spatial and temporal heterogeneity of mouse and human microglia at single-cell resolution. Nature. 2019; 566:388–392. [DOI] [PubMed] [Google Scholar]
- 64. Sinner P., Peckert-Maier K., Mohammadian H., Kuhnt C., Draßner C., Panagiotakopoulou V., Rauber S., Linnerbauer M., Haimon Z., Royzman D. et al. Microglial expression of CD83 governs cellular activation and restrains neuroinflammation in experimental autoimmune encephalomyelitis. Nat. Commun. 2023; 14:4601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65. Veremeyko T., Yung A.W., Anthony D.C., Strekalova T., Ponomarev E.D. Early growth response gene-2 is essential for M1 and M2 macrophage activation and plasticity by modulation of the transcription factor CEBPβ. Front. Immunol. 2018; 9:2515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66. O’Donovan K.J., Tourtellotte W.G., Millbrandt J., Baraban J.M. The EGR family of transcription-regulatory factors: progress at the interface of molecular and systems neuroscience. Trends Neurosci. 1999; 22:167–173. [DOI] [PubMed] [Google Scholar]
- 67. Wang B., Li Q., Qin L., Zhao S., Wang J., Chen X. Transition of tumor-associated macrophages from MHC class IIhi to MHC class IIlow mediates tumor progression in mice. BMC Immunol. 2011; 12:43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68. Georgoudaki A.-M., Prokopec K.E., Boura V.F., Hellqvist E., Sohn S., Östling J., Dahan R., Harris R.A., Rantalainen M., Klevebring D. et al. Reprogramming tumor-associated macrophages by antibody targeting inhibits cancer progression and metastasis. Cell Rep. 2016; 15:2000–2011. [DOI] [PubMed] [Google Scholar]
- 69. Benjamini Y., Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. R. Stat. Soc. B Methodol. 1995; 57:289–300. [Google Scholar]
- 70. Ternes D., Karta J., Tsenkova M., Wilmes P., Haan S., Letellier E. Microbiome in colorectal cancer: how to get from meta-omics to mechanism?. Trends Microbiol. 2020; 28:401–423. [DOI] [PubMed] [Google Scholar]
- 71. Chen R.-C., Dewi C., Huang S.-W., Caraka R.E. Selecting critical features for data classification based on machine learning methods. J. Big Data. 2020; 7:52. [Google Scholar]
- 72. Huang H.-J., Zhang A.-Y., Cao H.-c., Lu H.-F., Wang B.-H., Xie Q., Xu W., Li L.-J. Metabolomic analyses of faeces reveals malabsorption in cirrhotic patients. Digest. Liver Dis. 2013; 45:677–682. [DOI] [PubMed] [Google Scholar]
- 73. Ocvirk S., O’Keefe S.J. Influence of bile acids on colorectal cancer risk: potential mechanisms mediated by diet-gut microbiota interactions. Curr. Nutr. Rep. 2017; 6:315–322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74. Sun Z., Wang Y., Su X., Yang X., Luo Q. et al. Proteomic characterization of human gut habitual bacteroides intestinalis against common intestinal bile acid stress. Adv. Gut Microbiome Res. 2023; 2023:8395946. [Google Scholar]
- 75. Chang Y., Huang Z., Hou F., Liu Y., Wang L., Wang Z., Sun Y., Pan Z., Tan Y., Ding L. et al. Parvimonas micra activates the Ras/ERK/c-Fos pathway by upregulating miR-218-5p to promote colorectal cancer progression. J. Exp. Clin. Cancer Res. 2023; 42:13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76. Zhao L., Zhang X., Zhou Y., Fu K., Lau H. C.-H., Chun T.W.-Y., Cheung A.H.-K., Coker O.O., Wei H., Wu W.K.-K. et al. Parvimonas micra promotes colorectal tumorigenesis and is associated with prognosis of colorectal cancer patients. Oncogene. 2022; 41:4200–4210. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The StableMate R code and data analysis are available at https://github.com/meiosis97/StableMate and https://doi.org/10.5281/zenodo.13626593.