Abstract
Proteins can collapse into compact globules or form expanded, solvent-accessible coil-like conformations. Additionally, they can fold into well-defined three-dimensional structures or remain partially or entirely disordered. Recent discoveries have shown that the tendency for proteins to collapse or remain expanded is not intrinsically coupled to their ability to fold. These observations suggest that proteins do not have to form compact globules in aqueous solutions. They can be intrinsically disordered, collapsed, or expanded, and even form well-folded, elongated structures. This ability to decouple collapse from folding is determined by the sequence details of proteins. In this review, we highlight insights gleaned from studies over the past decade. Using a polymer physics framework, we explain how the interplay among sidechains, backbone units, and solvent determines the driving forces for collapsed versus expanded states in aqueous solvents.
Keywords: collapse, intrinsically disordered proteins, solvent quality, unfolded states, polymer physics
INTRODUCTION
Polypeptide chains undergo either collapse or expansion transitions in response to stimuli (20). These stimuli include changes to temperature and pressure, and changes to concentrations of osmolytes, salts, and pH (18, 38, 42, 73, 109, 139, 143). Other stimuli include mechanical forces that can be applied directly in vitro or through work done by molecular machines in vivo (52). The conformational response of compaction/expansion to various stimuli is fundamental to disorder–order transitions of proteins. It is also central to the various reactions and quality control programs that regulate the concentrations of proteins in vivo.
Uncovering the physicochemical details of collapse/expansion transitions of polypeptide chains remains at the forefront of protein biophysics. The emergence of insights over the past decade has required the deployment of advanced methodologies for experimental investigations that have gone hand in hand with synergistic advances in theory and computation. Through concerted efforts from many labs, built on pioneering earlier work, there appears to be a coherent set of answers to questions regarding the generic and sequence-specific molecular driving forces for the collapse/expansion transitions of proteins (20, 32, 33, 125, 127, 148).
Here, we review evidence suggesting that the driving forces for collapse/expansion originate from a fine interplay among backbone, sidechain, and solvent-mediated interactions. Further, simple extrapolations from studies of model systems fail to account for all the nuances of heteropolymeric collapse/expansion. Sequence-specific complexities must be embraced while simultaneously looking for universality. Indeed, the aphorism, often paraphrased and attributed to Einstein that “Everything [especially models] should be made as simple as possible, but not simpler” rather succinctly captures the emerging views regarding the molecular driving forces of collapse/expansion transitions.
POLYMER PHYSICS AS THE LINGUA FRANCA FOR COLLAPSE TRANSITIONS
Polypeptide chains can undergo collapse or expansion in response to stimuli (148). For brevity, we shall designate collapse/expansion transitions as collapse transitions. The conceptual foundations of polymer physics are helpful for describing the physics of collapse transitions. In the polymer physics literature, collapse transitions are referred to as coil-to-globule transitions (Figure 1a) (112). These transitions have been explored extensively in the context of protein folding (32). However, it is important to recognize that the collapse transition is in no way a protein-specific phenomenon and is observed with simple homopolymers as well as complex heteropolymers (30, 146).
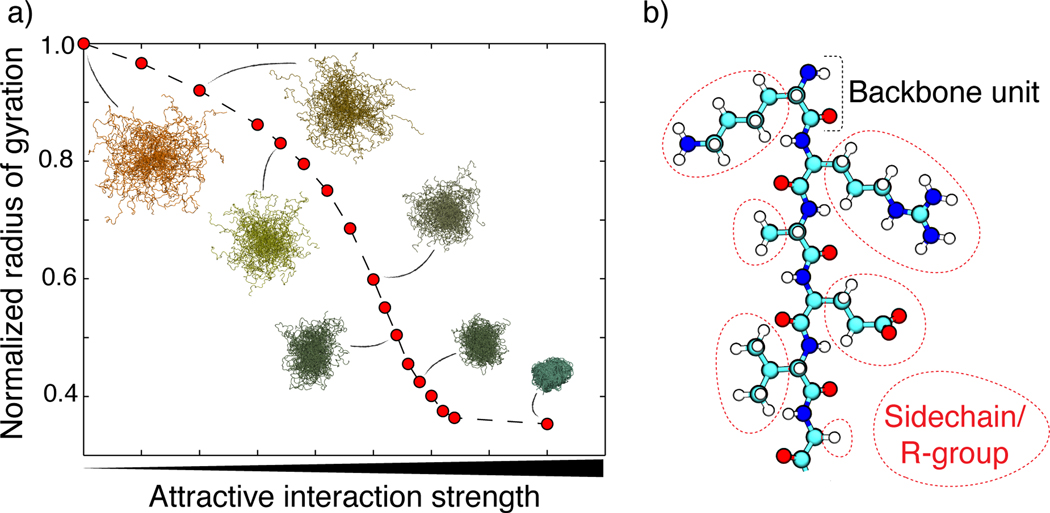
Figure 1.
(a) The coil-to-globule transition curve for a 100-residue homopolymer as a function of monomer–monomer interaction strength with representative ensemble snapshots. The sigmoidal shape is characteristic of a cooperative transition, as observed for complex heteropolymers and simple homopolymers alike. (b) The molecular structure of a polypeptide. A single backbone peptide unit is highlighted at the top; this structure repeats down the chain. Various sidechains are circled in red.
The dimensions of a chain, which define the extent of collapse or expansion vis-à-vis a well-defined reference state, such as a non-interacting Flory random coil, are governed by the interplay between intrachain and chain–solvent interactions (41). Bona fide order parameters for monitoring collapse transitions include the radius of gyration, the hydrodynamic radius , the radial density profile , and the scaling of spatial separation as a function of sequence separation (50, 77, 112, 126). Although, the mean end-to-end distance is often used, early theoretical work showed that can be a poor order parameter for describing global scaling behavior (50). In heteropolymers, a more pronounced decoupling of and can occur in both globule and coil-like states owing to the chemical heterogeneity of interactions (34, 43, 113, 124).
In mean-field and scaling theories, these order parameters are captured in terms of the excluded volume (, the chain length , the effective monomer size or Kuhn length , and the correlation length for the amplitude of conformational fluctuations quantified in terms of a scaling exponent (31, 40, 112). The excluded volume quantifies the effective volume set aside per residue for interactions with the surrounding solvent. It can be negative, zero, or positive depending on whether the effective interactions with the solvent are repulsive, indifferent, or attractive, respectively (53, 112). In physical chemistry, excluded volume is typically used to describe steric overlap. To avoid confusion, we follow recent precedent and use the term effective solvation volume for the polymer physics definition of excluded volume (53).
Generic proteins are unbranched, linear polymers of amino acids. In polymers, each repeating unit or monomer consists of a repeating backbone unit and an additional functional group (R-group). For homopolymers, each R-group is the same. For heteropolymers, the R-groups associated with different monomers along a single polymer are different. Polypeptides consist of a backbone peptide unit with sidechains as the polymer R-groups (Figure 1b). For a given set of solution conditions, we can decompose the determinants of collapse transitions into a combination of intrinsic backbone preferences and sequence-specific effects due to the sidechains. In this formulation, every protein sequence in solvent is, at a minimum, a three-component system consisting of the backbone repeating units, the sidechains, and the solvent (109). In biological systems, the solvent is typically a mixture of water, ions, and various organic and inorganic osmolytes.
Determinants of Chain Dimensions of Homopolymers
Physical descriptions of collapse transitions require a quantitative framework that captures the effects of the three-way interplay among polypeptide backbone units, sidechain moieties, and solvent components. The framework for describing this interplay can be borrowed from the polymer physics literature. Coil-to-globule transitions of flexible homopolymers can be described in terms of the interplay between effective intrachain and chain–solvent interactions. Mean-field theories provide a convenient route to arrive at phenomenological descriptions, and this is achieved in terms of the sign and magnitude of (112).
The effective, solvent-mediated potential of mean force denoted as is the free-energy change associated with bringing a pair of monomeric units from a noninteracting reference point to distance of one another in an aqueous solvent (112). If is small enough to allow direct interaction between the two monomeric units, then one of three possible scenarios will result: If the residues “like” one another more than they “like” the solvent, then the effective inter-residue interactions will be attractive. If the residues “like” the solvent more than they “like” one another, then the effective inter-residue interactions will be repulsive. If the residues “like” the solvent and one another equally, neither attractive nor repulsive interaction is experienced. The probability that a pair of chain monomers will be a distance from one another is proportional to , where , is the temperature, and is the ideal gas constant. Because residues cannot sterically overlap with one another, is zero for short inter-residue distances, while for large separations where the inter-residue interactions are effectively zero. Between these two limits, can be large and positive for separations where the inter-residue interactions are attractive. Conversely, is negligibly small at inter-residue separations where the effective interactions are repulsive (112).
For each pair of monomers, is defined as the negative of the integral of the Mayer -function over the volume available to the pair of residues (112). Here, , and the integral is performed over all pairs of inter-monomer separations. Depending on the inter-monomer separation and the type of interactions, the -function will be negative (short-range steric overlaps or effective inter-residue repulsions), positive (effective inter-residue attractions), or zero (large separations). The Mayer -function is dimensionless, and the integral has units of volume. It quantifies the effective pairwise inter-monomer interactions for the polymers in solution.
In a poor solvent, is negative; each monomer, on average, excludes itself from interactions with the solvent and instead interacts with other monomers. We can consider this to represent the fact that the chain relinquishes solvent in exchange for inter-residue interactions (i.e., the solvent now has a negative volume). In a good solvent, is positive because, on average, each residue interacts favorably with the solvent, such that there is a positive contribution . Depending on the sign, the magnitude of quantifies the poorness or the goodness of the solvent. If the inter-monomer interactions exactly counterbalance the monomer–solvent interactions, then and this is achieved in a theta solvent (20, 112).
The size of a chain, quantified in terms of , may be written as
| 1. |
Here, the pre-factor is a function of the effective solvation volume ; the three-body interaction parameter , which is defined by the thickness of the chain; and the effective monomer size (112). The three-body interaction parameter is always positive and represents the steric volume occupied by the chain, preventing this model from undergoing collapsing to a single point in the limit of . The effective monomer size (or Kuhn length) defines the chain persistence length. In this way, all the chemistry of the repeating units is subsumed in the pre-factor , which captures the effective bulk of the monomer as well as the chain connectivity. It should be clear form this formalism that will vary with .
In good, theta, and poor solvents, , 0.50, and 0.33, respectively (31, 40, 86). In poor solvents, homopolymers form compact globules, maximizing inter-residue contacts and minimizing the residue–solvent contacts. In good solvents, polymers adopt expanded coil-like conformations, minimizing inter–residue contacts and amplifying residue–solvent contacts in a way that maximizes chain entropy. In theta solvents, chain–solvent and chain–chain interactions are exactly counterbalanced and chain dimensions as well as the distribution of conformations are governed entirely by chain connectivity and conformational entropy (30, 31, 40).
Scaling laws hold for polymers that are infinitely long. Finite-size artifacts will lead to deviations from the canonical scaling exponents, and the presence of these artifacts can be discerned via analytical/numerical calculations or measurements as a function of chain length (126). For finite-length polymers, approaching the tricritical point, defined by the point where , sets a threshold to distinguish between good () and poor () solvent behavior. The inferred value of will represent a convolution of contributions from the apparent goodness versus poorness of the solvent as well the contributions to the amplitudes of fluctuations that come from the underlying chemical details and finite-size considerations.
Given a combination of polymer and solvent, how might we discern solvent quality? One approach is to quantify the sign and magnitude of from direct measurements, such as light scattering that yields estimates of the second virial coefficient, which is proportional to (102, 112). Alternatively, one can measure the scaling of or as a function of chain length using pulse-field gradient nuclear magnetic resonance (NMR), small angle X-ray scattering (SAXS), fluorescence correlation spectroscopy (FCS), two-focus FCS, or related measurements (4, 25, 56, 73, 139). If the accuracy and sampling of molecular mechanics–based simulations can be relied upon, then these provide a route to extracting the scaling exponent and in principle the sign and magnitude of (47, 53, 63, 91, 134, 147). Instead of simulating the conformational distributions for multiple chain lengths, it suffices to perform simulations for one suitably long chain length and compare the resultant conformational distributions to those obtained from simulations based on reference potentials (58, 86, 89). With these reference distributions in hand, one can compare a variety of order parameters from the simulation of interest with the reference to obtain inferences regarding solvent quality and even proxies for (53).
WATER IS A POOR SOLVENT FOR POLYPEPTIDE BACKBONES
A well-reasoned question to ask is whether water at room temperature is a good, indifferent, or poor solvent for polypeptide backbones? In order to answer this question, the constructs used should not yield confounding results due to the interplay between backbone and sidechain interactions. Over the past decade, several investigations have focused on glycine-rich sequences, including polyglycine of different chain lengths (2, 58, 64, 65, 128, 131). Results from these investigations may be summarized as follows: Polyglycine is a poly-secondary-amide. N-methylacetamide (NMA) is a model compound mimic of glycine, and vapor pressure osmometry measurements indicate a favorable free energy of solvation at room temperature of approximately –10 kcal/mol (141). The free energy of solvation quantifies the free-energy change associated with transferring the solute from the gas phase into water (10). Naive extrapolation predicts that polyglycine should be favorably solvated, and these molecules should favor expanded, coil-like conformations characterized by a scaling exponent of . However, molecular simulations, exceedingly poor solubility, and FCS experiments unequivocally show that polyglycine forms compact globules in water, implying that water is a poor solvent for polypeptide backbones (2, 58, 64, 65, 128).
What is the origin of the behavior of polyglycine in water? The free energy of solvation of model compounds does not account for the competition that arises from the high local concentration of other backbone moieties. Preference for compact, globular conformations derives from the ability of amides to solvate one another through favorable amide–amide interactions in globules, where the effective concentration of amides around one another is ~20 M (58). Pettitt and coworkers (2, 64, 65) have argued that the preference for self-solvation by polypeptide backbones is driven by amide mediated dipole–dipole interactions and a favorable entropic component through water release. Support for these inferences comes from denaturation experiments performed on polyglycine, which show that the extent of expansion that polyglycine undergoes in aqueous mixtures with 8 M urea () or 7 M GdmCl () is rather modest (58). Therefore, even high concentrations of a diamide such as urea are insufficient to outcompete the intrachain amide–amide interactions that give rise to the preference for compact globules in dilute solutions of polyglycine and the poor solubility of polyglycine in general.
Given that water is a poor solvent for polypeptide backbones, what does this result mean for protein sequences in general? Two diverging hypotheses emerge: According to the backbone- hypothesis, sidechains amplify the intrinsic properties of polypeptide backbones (3, 14, 111). Alternatively, the true nature of protein sequences derives from the three-way interplay among the intrinsic preferences of polypeptide backbones, sidechain-mediated interactions, and solvent-mediated effects (20, 32).
According to the backbone-centric view, the intrinsic preference for the collapse of globular proteins derives from the properties of polypeptide backbones in water. Sidechains essentially act as conformational selectivity filters, choosing the optimal collapsed backbone conformation that accommodates the partitioning between hydrophilic versus hydrophobic sidechains. This view is anchored by extrapolations from three sets of observations; dissection of the transfer free energies of model compounds from water into 1 M urea suggests that the backbone contributes most significantly to protein denaturation, whereas sidechains are passive bystanders (3). This is taken to mean that interactions other than intra-backbone interactions are refractory to stabilizing protein structures. Secondly, the hydrogen-bonding potential of backbone units is considered to be so strong that these amides would have to always hydrogen bond to themselves or to the surrounding solvent (111). And third, the coarse-grain tube model for polypeptide backbones, which is based on an elegant generalization of the Edwards continuum model for polymers, generates canonical hydrogen-bonded structures as so-called platonic folds of backbones without any consideration of sidechains (9, 35).
The backbone-centric model was introduced 2006 and was based on a synthesis of different types of data (14, 111). As discussed below, research over the past decade has diverged from the backbone-centric view. Although water is a poor solvent for polypeptide backbones, sidechains play a central role in modulating and even radically altering the intrinsic preferences of polypeptide backbones (29, 45, 85, 87, 98, 111a, 138).
HETEROPOLYMERIC PROTEIN SEQUENCES IN AQUEOUS SOLVENTS
Naturally occurring proteins are neither polyglycine nor simple homopolymers. Instead, they are finite-sized heteropolymers. How do concepts of solvent quality, effective solvation volumes, and scaling exponents transfer to finite-sized heteropolymeric sequences? The effective solvation volume per residue will be modified by the intrinsic and context-dependent free energies of solvation of each sidechain, the modulation of the backbone solvation by each sidechain, and the repulsive or attractive interactions between pairs of residues. Therefore, the effective solvation volume for a heteropolymeric sequence may be written as: where is the effective solvation volume of backbone units, is the signum function such that , 0, or +1, respectively, for , and > 0, and is a sequence-specific modifier that renormalizes the effective solvation volume. This leads to the approach of an apparent sequence-specific solvent quality, and the scaling relationship takes the form
| 2. |
The pre-factor captures the sequence- and composition-specific modulation of the effective solvation volume of the backbone, including sequence-specific solvation volume and the average size of a monomer unit . The difference beween Equations 1 and 2 is the appearance of a renormalized effective solvation volume and an apparent scaling exponent, , which can be quite different from the intrinsic scaling exponent of for polypeptide backbones in isolation. As in Equation 1, is also a function of .
The interplay among sidechain, solvent, and backbone interactions will be sequence is reflected in the values of and consequently . The major advance over the past decade has been the ability to uncover a set of heuristics that enable qualitative inferences regarding based on amino-acid compositions, although much work remains (29, 57).
CATEGORIES OF PROTEIN SEQUENCES
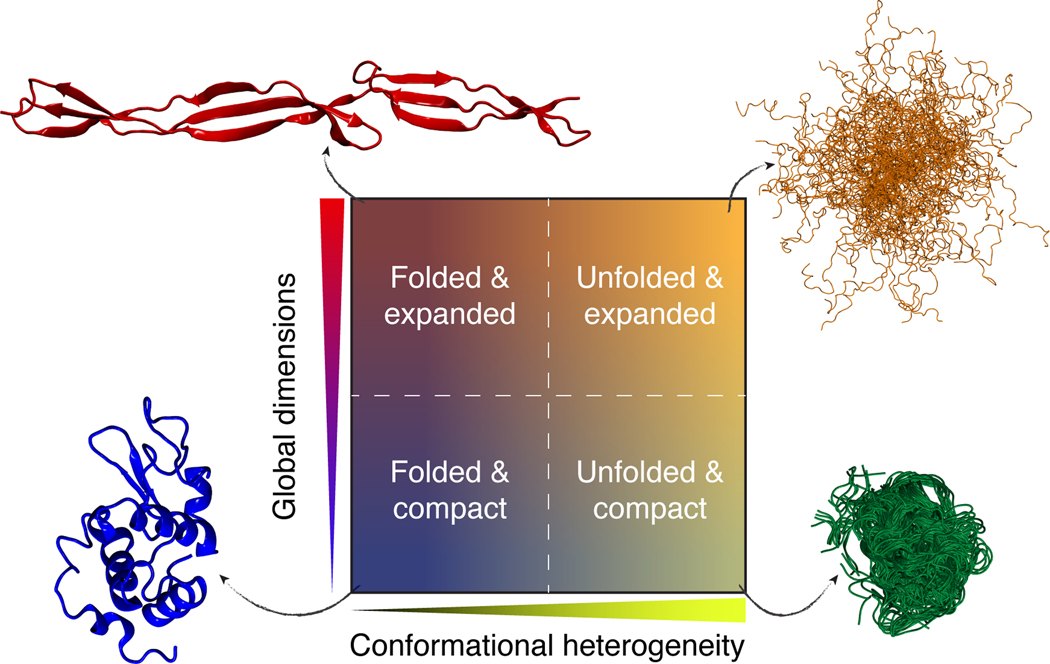
We propose that individual domains of proteins can be classified into one of four distinct ground states in aqueous solutions (17, 25, 60, 75, 104, 107, 108, 148). In dilute facsimiles of physiological milieus, which we refer to as native conditions, proteins can be (a) ordered (also known as folded) and collapsed; (b) disordered and collapsed; (c) ordered and expanded; or (d) disordered and expanded (Figure 2). Although this discretization is convenient, it is worth emphasizing that depending on the solution conditions, any chain can, in theory, adopt a continuum of values along both axes (e.g., the degree of order/disorder and global dimensions).
Figure 2.
Conformational classifications of polypeptides based on the two-dimensional space of conformational heterogeneity and global dimensions. Examples for each are the crystal structure of SasG (top left), the conformational ensemble of Ash1 (top right), the conformational ensemble for polyglutamine (bottom right), and the crystal structure of lysozyme (bottom left) (PDB: 1IEE) (51, 89, 140). The decoupling of global dimensions and conformational heterogeneity is formally addressed in Reference 82.
Proteins that Are Collapsed and Folded (Ordered) in Aqueous Solvents
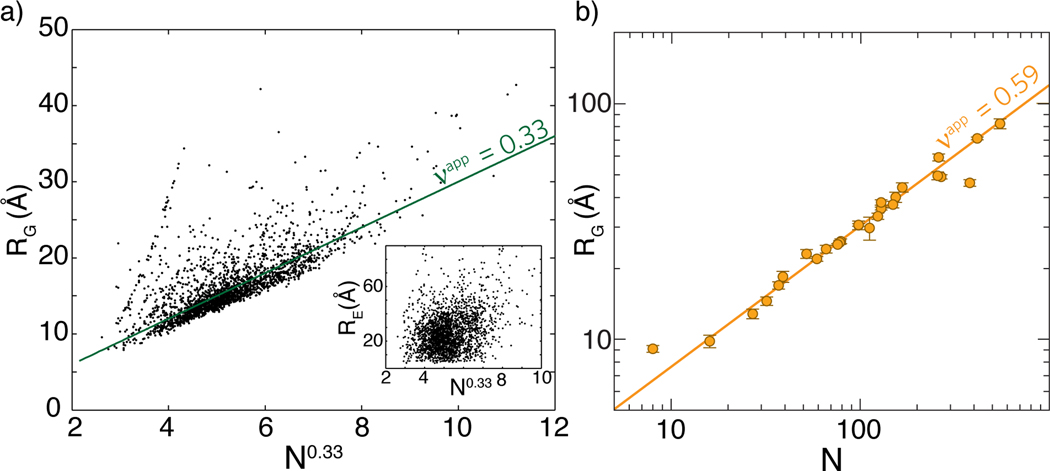
Dima & Thirumalai (34) showed that the scaling of with chain length for folded globular proteins yields values consistent with . This is concordant with the compact, globular nature of folded domains. We repeated this analysis with 2,392 nonredundant protein structures taken from PDBSELECT25 and found similar results, which are also consistent with other analyses (Figure 3a) (49, 87, 139). The inset in Figure 3a also demonstrates the decoupling between and , a result recently observed in flexible heteropolymers (43).
Figure 3.
(a) Scaling behavior for folded proteins based on ~2,400 nonredundant structures taken from PDBSELECT25 (49). While the radius of gyration shows reasonable agreement with , the end-to-end distance shows a poor correlation (inset). (b) Scaling behavior for chemically denatured proteins based on data from Reference 73. The unfolded state under strongly denaturing conditions is well described by a self-avoiding random chain ().
The similarity between and the scaling exponent derived for polyglycine suggests that, like polypeptide backbones, water is a poor solvent for folded states of globular proteins. Therefore, in the folded state, the sidechains maintain the intrinsic preference of backbones for collapse, although the accommodation of sidechains should change the packing density, degree of solvent penetration, and the surfaces of globules. As shown in Figure 3b, it is well established that foldable proteins under high concentrations of denaturant show conformational behavior consistent with a self-avoiding random coil () (73, 139). With this in mind, what does the scaling of with chain length for folded proteins tell us about the dimensions of unfolded proteins under folding conditions? The answer to this question is directly relevant to details of collapse transitions for autonomously foldable proteins. One might envisage two limiting behaviors.
The poorness of the solvent in the folded state could mean that is always approximately 0.33 for foldable proteins under native conditions, such that global dimensions of a foldable protein should be approximately equal irrespective of folding status. In this scenario, the folding transition is conceptualized as a conformational rearrangement between (wet or dry) molten globules and a compact folded globule, akin to a crystallization process (39, 121). The case for the distinct classes of molten globules, first introduced via theoretical work, has received some support from recent experiments (7, 17, 48, 55, 62, 99, 108, 115, 120, 148). Support for this model also comes from molecular dynamics simulations with compact unfolded states, although it is unclear whether these are legitimate observations or force-field artifacts (106). In this model, the poorness of the solvent for the backbone governs the dimensions of the folded and unfolded states, and these states are distinguishable mainly by the extent of internal hydration, the acquisition of secondary and tertiary structure, and the packing of sidechains. Given the finite-size nature of natural polypeptides, could be beyond the globule limit but still in the poor-solvent regime (0.33 < ), a prediction consistent with some data (24, 90, 93, 94).
Alternatively, if water is a good solvent for unfolded proteins, then we would expect scaling behavior consistent with . This could be at the limit of a self-avoiding random coil (), meaning the unfolded state in high concentrations of denaturant is identical to the unfolded state under native or near-native conditions. Inferences from SAXS-based experiments seem to support this model (60, 67, 107, 118, 119, 145, 111a). In this scenario, water is a good solvent for generic protein sequences. The tradeoff between chain–solvent hydrogen bonds for chain–chain hydrogen bonds can be accommodated through a combination of packing of specific elements such as foldons and the hydrophobic effect (36, 37, 59, 137).
Single-molecule Förster resonance energy transfer (smFRET) experiments and more recent simulation studies arrive at a somewhat different conclusion. These experiments show a continuous contraction of proteins upon dilution from denaturant (4, 15, 56, 83, 110, 117, 122, 129, 145, 147). This result is broadly consistent with water being a good or theta solvent for unfolded states () but suggests that a continuous worsening in solvent quality accompanies the dilution of denaturant. Although Hofmann et al. report of 0.46 ± 0.05, we suggest that within all reasonable expectations of experimental error this can be taken to imply that water is a generic theta-like () solvent for unfolded proteins under native conditions (56). The discrepancies between inferences based on SAXS and smFRET measures proved to be confounding and became the focus of intense scrutiny given the direct implications for the description of unfolded states under native conditions. Recent multiplexed experiments, numerical assessments, and analysis of SAXS/smFRET data on the same sets of molecules, aided by atomistic simulations, show that the discrepant inferences between SAXS and smFRET measurements originate, at least in part, from the decoupling between and , which is amplified for heteropolymeric sequences (43, 113, 124). When this is taken into account, SAXS and smFRET show reasonable agreement and suggest a general model for the unfolded state under native conditions. In this model, water is a theta-like or marginally good solvent for the unfolded state under native conditions (0.50 ≤ ), but there is a dependence of on the concentration of denaturant. It is noteworthy that recent analysis of full scattering curves taken from SAXS experiments using a novel approach (111a) suggests that unfolded proteins under native conditions are characterized by of 0.54. The for the unfolded state under native conditions is expected to show some sequence dependence, and the decoupling of and at lower denaturant concentrations may also be a confounding factor for the interpretation of certain experiments
Samanta et al. (114) recently developed a heteropolymeric theory for chain compaction parameterized using native-state topology. This predicts a continuous transition in chain dimensions as a function of denaturant concentration and that native-state topology has a significant impact on the so-called collapsibility of a given protein sequence. In this work, based on analysis of over two thousand structures, the authors make the important comment that one cannot arrive at proteome-wide inferences from experiments on a handful of systems. Nevertheless, there appears to be a growing consensus that water is a theta-like or marginally good solvent for unfolded states under native conditions.
There are numerous advantages that one can envisage for an unfolded state that behaves like it is in theta-like or marginally good solvents (70). These pertain to the amplitudes of conformational fluctuations, the ability to enable backtracking when folding errors are made, and direct encoding of cooperativity in folding–unfolding transitions by making the unfolded state distinct from the folded state (19, 69, 70). Such a result can reconcile numerous seemingly disparate observations, including the presence of foldons, the robustness of the linear extrapolation model for assessing protein stability, the impact of unfolded states on phi value analysis, and the modest global contraction observed in both SAXS and smFRET measurements when one accounts for the decoupling between and (22, 37, 103).
Proteins that Are Disordered and Collapsed in Aqueous Solvents
The discovery of intrinsically disordered proteins (IDPs) led to the recognition that proteins can be functional even while displaying significant conformational heterogeneity (132, 142). A surprising finding, arrived at via very different biophysical investigations, is that IDPs can form collapsed, globular ensembles while simultaneously exhibiting significant conformational heterogeneity (29, 132). Chain collapse in IDPs has been observed in many different systems. These include polyglutamine and polyglycine tracts, low-complexity sequences rich in Gly, Ser, Asn, and Gln, bacterial protamine-like domains, the amyloid beta peptides, the Islet amyloid polypeptide, and the P domain of Pab1 (58, 61, 85, 97, 101, 128, 133, 111b). These IDPs accentuate the intrinsic preferences of polypeptide backbones in water but do so without undergoing a folding transition. The energy landscapes associated with collapsed globules are expected to be rugged and resemble the topology of an egg carton, whereby distinct, albeit compact, conformations are of equivalent stability (134).
On the basis of heuristics gathered from simulations of a large number of sequences, a diagram of states was proposed for IDPs (28). According to this proposal, collapsed globules would be preferred for sequences with a fraction of charged residues (FCR) below 25%, which represent roughly 25% of all IDPs (29, 57). More recently, various lines of experimental evidence suggest that the determinants of collapse in IDPs are more complex than simple FCR-based thresholds. Many sequences with low FCR values are expanded relative to globules (43, 46, 89). Therefore, it seems likely that the fraction of sequences across the disordered proteome that form collapsed globules is smaller than would be predicted using composition-based heuristics. However, it is noteworthy that the study of IDPs that undergo collapse is inherently challenging. Techniques such as NMR and SAXS require high protein concentrations, and this opens the door to confounding inferences due to aggregation and poor solubility of globule-forming IDPs. In contrast, the observation of collapsed ensembles in simulations might not necessarily imply problems with force fields (12). IDPs that form globules readily become trapped in various metastable compact states, and broken ergodicity becomes a major challenge with respect to conformational sampling. These concerns emphasize the extant practical bias against studying collapsed IDPs. With this in mind, one should be cautious to not interpret the paucity of ensemble studies as evidence that these types of IDPs do not exist. In this context, single-molecule fluorescence and force spectroscopy measurements have a particularly useful role to play in concert with molecular simulations and theoretical analysis.
Proteins that Are Expanded and Folded in Aqueous Solvents
It is important to recognize that the folded states of proteins need not always be collapsed. As an example, while globular proteins are typically associated with a , the polypeptides that make up the collagen triple helix show scaling behavior consistent with a rod, (11). Other examples of folded structures that are more consistent with rodlike states in water include alpha helical rods formed by block copolypeptides of the form [(Glu)4-(Lys)4]n and the highly charged extracellular bacterial protein SasG (6). Various fibrous proteins or those with large coiled-coil segments are also inconsistent with global dimensions associated with chain collapse, although helices could be considered collapsed on an extremely local level (51, 81). Repeat proteins are another archetype of well-folded, highly stable, nonglobular proteins that lack the micellar organization of globular, folded proteins (1, 71, 72). Sequences that fold into elongated structures seem to bypass the collapse transition altogether, such that their folding likely involves a coil-to-rod transition, as opposed to coil-to-globule transition. There is much to learn from these systems that have the sequence characteristics or compositional biases of IDPs and yet fold into elongated structures via fundamentally different rules when compared to canonical globular proteins. A compact hydrophobic core is a convenient scaffold for protein stability, where that stability may help engender so-called evolvability (13). However, the discussion in this section emphasizes the point that a collapsed folded state is by no means the only mechanism through which a well-defined structure can be achieved.
Proteins that Are Expanded and Disordered in Aqueous Solvents
Many of the well-studied IDPs studied fall into this category. Marsh & Forman-Kay (87) found that, for a set of 32 IDPs, their global scaling behavior is consistent with an effective theta solvent (). In the eight years since that study, many more IDPs have been characterized, and this empirical scaling relationship seems to be reasonably robust. As for exceptions, we have already discussed the case of IDPs that are disordered albeit collapsed. Interestingly, there are many examples of IDPs that are considerably more expanded than the proteins in the Marsh & Forman-Kay data set. For these sequences, can be larger than even 0.6, and these sequences include IDPs with high fractions of charged residues (85, 98). These sequences are either polyelectrolytes or polyampholytes, and changes to their dimensions as a function of salt concentration are predictable using generalizations of mean-field theories (54, 85, 98). Sequences that show increased expansion may also be rich proline residues. The combination of local stiffness, a marginal charge density, and the context-dependent solvation properties are thought to drive expansion (16, 23, 46, 87, 89, 107a, 144).
It is worth emphasizing that heteropolymers with can have well-defined local and long-range attractive and repulsive interactions (21, 76, 89, 91, 123). As a result, should be thought of as a mean-field descriptor of the average polypeptide behavior but should not be taken as proof that the polypeptide is well described by a homopolymer model across all length scales. A prime example of this is the unfolded state of Ntl9, which under strongly denaturing conditions shows conformational behavior consistent with a scaling exponent of 0.59, yet complementary analysis by simulations and NMR find strong evidence for long-range and local interactions in the unfolded ensemble (91). Similarly, biophysical characterization of an intrinsically disordered region from the protein Ash1 found that although its expanded global dimensions are insensitive to phosphorylation, compensatory local changes lead to a reconfiguration of local and long-range intramolecular interactions (89).
We speculate that there may be an evolutionary bias toward expanded IDPs. According to conventional homopolymer theory, IDPs that undergo collapse would be expected to undergo aggregation, while those that show behavior consistent with a good solvent should remain soluble (112). If native environments were effective poor solvents for all disordered regions, then maintaining proteomic solubility would be an enormous energetic burden on the cell. Of course, this assumes that aggregation is detrimental. Recent work suggests the formation of biomolecular condensates through nonstoichiometric interactions among disordered proteins is a ubiquitous mechanism for cellular organization (8, 121a). Given the prevalence of polar-rich disordered regions in proteins that drive intracellular phase transitions, we suspect that at least in some cases the macroscopic self-assembly behavior of these disordered regions reflects a nanoscopic tendency for collapse (8, 95, 105).
THE INTERPLAY AMONG BACKBONE, SIDECHAINS, AND SOLVENT AS CAPTURED IN THE SIDECHAIN-PRIMING MODEL
The properties of IDPs that mimic the statistics of chains where can be attributed to a dominance of the sidechain properties over the intrinsic preferences of backbones in water. Surprisingly, this sidechain dominance can be manifest even in sequences with large glycine contents, such as the RGG domain of the Caenorhabditis elegans protein LAF-1 (35% Gly) or the glycine-rich snow-flea antifreeze protein (45% Gly), both of which show behavior that is consistent with (45, 138). How can glycine drive chain compaction in polyglycine, while showing little apparent impact on the dimensions of glycine-rich heteropolymers?
The sidechain-priming model provides a plausible explanation for this behavior (58). Here, the presence of sidechains has two effects on the properties of the backbone. First, sidechains can engage in either attractive or repulsive interactions with backbone, sidechains, and solvent. Second, the sidechains have a steric impact; they prevent compaction of the peptide backbone thus inhibiting the solvation of backbone amides by one another. This steric effect is significant. Starting with a maximally compact polyglycine globule as a reference, the sidechains can dilute the effective local concentration of backbone amides by ~10 M, thus reducing self-solvation of backbone amides and limiting backbone-driven collapse. Therefore, the key interplay is between the polyglycine effect intrinsic to all sequences, which concentrates backbone amides around one another, and the sidechain-mediated amplification or dilution of the effective backbone amide concentration. Hence, even the conformational properties of disordered ensembles such as unfolded states under native conditions and IDPs in physiological milieus will be determined by the amino acid composition and primary sequence. For example, certain sidechains can drive chain compaction via sidechain–sidechain and sidechain–backbone interactions, such as in the case of polyglutamine (25, 135, 140). Conversely, in other sequences, including those with glycine-rich stretches interrupted by nonglycine residues, the intrinsic tendency of the backbone to collapse on itself is reversed by the interplay among sidechain, backbone, and solvent units.
The sidechain-priming model also helps explain apparently confounding results regarding the effects of denaturants on protein collapse/expansion. Various models to explain the denaturation mechanism of GdmCl and urea have been proposed, each of which suggests that a different balance of denaturant–backbone and denaturant–sidechain interaction is key (3, 18, 78, 92). In the sidechain-priming model, denaturant–sidechain interactions enable interactions between denaturants and backbone amides, such that in the absence of sidechains, denaturant–backbone interactions are unable to outcompete backbone–backbone interactions. This model is consistent with a two-stage mechanism for protein unfolding in which denaturant–sidechain interaction leads to a so-called dry-molten globule before denaturant–backbone interactions occur, as proposed and predicted from theory and subsequently observed experimentally (62, 96, 136). While denaturant–backbone interactions play an important role, and could be the dominant mode of peptide–denaturant interaction, sidechain-based interactions are necessary to facilitate denaturant accessibility to the backbone.
THE OVERALL ROLE OF SIDECHAINS AS MODULATORS—EVEN DETERMINANTS OF COLLAPSE
Given our preceding discussion, it becomes clear that sidechains play a dominant role in dictating the apparent solvent quality for different protein states. Accordingly, the amino acids can be divided into distinct classes on the basis of their physicochemical properties.
Hydrophobic Residues
Arguably the most well-studied amino acid class, hydrophobic sidechains include Ala, Ile, Leu, Val, Met, Phe, Tyr, and Trp. As commonly described, the hydrophobic effect reflects the fact that there is an energetic penalty associated with the solvent exposure of hydrophobic moieties, driving them into more buried orientations. The role of hydrophobic residues in protein folding is well studied. The Matthews lab (44, 66, 100) has explored the impact of isoleucine, leucine, and valine residues in driving protein folding. Unsurprisingly, the impact of hydrophobic residues on the unfolded state is not limited to protein folding. The formation of hydrophobic clusters in the unfolded state has been observed in many proteins, both under native conditions and nonnative conditions (26, 68, 74, 84, 88). Although IDPs are generally depleted in hydrophobic residues, this need is not always the case. Riback et al. (111a) found a direct correlation between hydrophobicity and the degree of collapse in the hydrophobic and proline-rich P domain of Pab1. Similarly, work from the Schüler lab (98) has shown a direct relationship between hydrophobicity and chain dimensions.
Polar Residues
Although polar residues (Gly, Ser, Thr, Asn, Gln, and Cys) are typically abundant in IDPs, they are also found extensively in folded proteins. Experimental and computational analysis of polyglutamine found that, despite the absence of conventional hydrophobic residues, it undergoes robust collapse and shows scaling behavior consistent with a polymer in a poor solvent (25, 134). Although not directly characterized, the length-dependent self-assembly of polyasparagine is consistent with it undergoing nonspecific collapse (80). In agreement with this, the glutamine/asparagine-rich N-terminal domain of the yeast prion protein Sup35 forms compact ensembles, and many polar rich IDPs drive self-assembly, gelation, and phase separation (95, 97, 105). The drive for collapse associated with polar tracts appears to be a combination of intramolecular hydrogen bonding, dipole–dipole interactions, and an entropic component from water upon collapse as solvent–amide hydrogen bonds are replaced by amide–amide hydrogen bonds (2, 63–65). The impact of other polar residues, such as serine and threonine in particular, remains less well understood, although the absence of an amide group is expected to reduce their ability to drive collapse in the same manner as glutamine. Similarly, the interplay between different types of polar sidechains requires further study.
Charged Residues
The energy scales associated with the interactions mediated by charged residues (Asp, Glu, Lys, Arg, and His) imply that they play important roles as determinants of the conformational behavior of proteins. For unfolded proteins and IDPs, the net charge per residue shows a direct correlation with global dimensions of polypeptides, in agreement with polyelectrolyte theory (85, 87, 98). The origins of this expansion are twofold: the electrostatic repulsions of like-charge residues and the extremely favorable free energies of solvation of charged sidechains. In conjunction, these two factors drive unfolded proteins with a high net charge toward expanded, coil-like ensembles. However, charge interactions can also drive compaction. As a prime example of this, phosphorylation of an unfolded protein 4E-BP2 drives compaction and folding via the formation of a network of hydrogen bonds that drive protein folding and compaction (5).
For an IDP of fixed composition with approximately equal numbers of positively and negatively charged residues, the patterning of charged residues can also directly dictate the global dimensions and amplitudes of conformational fluctuations (27, 28, 116). Patches of oppositely charged residues will engender electrostatic attractions; in well-mixed sequences, the electrostatic repulsions are screened by attractions and the preference for chain solvation dominates typically lack the ability to overcome charge repulsion and favorable solvation. In naturally occurring proteins, the extent of charge patterning may be also be important for mediating intermolecular interactions (79, 101). Finally, the temperature dependence of charge interactions may also prove to be important. Highly charged chains can undergo compaction as temperature increases owing to the increase in entropic cost of solvating charged groups (143).
Proline
Proline imparts several distinct features. Despite its purported hydrophobicity, L-proline is the most soluble amino acid (3). This is true of high polymers of proline, which show lower critical solution temperature in that they are highly soluble below ~70°C and form liquid crystalline assemblies above this temperature (130). It has been proposed that the patterning of proline and charged residues may play a role in determining the degree of expansion in disordered proteins (89). Consistent with this hypothesis, several well-patterned proline sequences are highly expanded (16, 46, 107a, 144).
CONCLUDING REMARKS
In this review, we have highlighted emerging ideas regarding the collapse transitions of proteins. Our perspective has been guided by the recognition that the sequences of proteins are diverse enough to accommodate at least four distinct categories of states in aqueous solvents. Different flavors of IDPs and rod like protein sequences have led to the realization that there is more to the collapse/expansion transition than just the canonical hydrophobic effect. A topic not explored here, but of direct relevance to collapse transitions in the cell, is how different types of osmolytes influence conformational behavior (29a, 109). As new approaches and combinations of theory and experiments are deployed, ideally in a high-throughput manner, we will learn more about the intricate details of the interplay among backbone units, sidechain moieties, and solvent molecules and the extent of coupling/decoupling between collapse/expansion and folding. The authors are not aware of any affiliations, memberships, funding, or financial holdings that might be perceived as affecting the objectivity of this review.
ACKNOWLEDGMENTS
We acknowledge funding from the National Science Foundation (NSF) (MCB-1614766, MCB-0718924) and the National Institutes of Health (R01NS056114). We are grateful to Doug Barrick, Osman Bilsel, Hue Sun Chan, Rahul Das, Ken Dill, Hagen Hofmann, Edward Lemke, Nicholas Lyle, Susan Marqusee, Erik Martin, Bob Matthews, Tanja Mittag, Ivan Peran, Dan Raleigh, Josh Riback, Kiersten Ruff, Ben Schüler, Andrea Soranno, Tobin Sosnick, D. Thirumalai, and Andreas Vitalis for many stimulating discussions and insights. We also acknowledge fruitful discussions within the NSF-sponsored Protein Folding Consortium that have influenced our thinking about the collapse transitions of proteins.
LITERATURE CITED
- 1.Aksel T, Majumdar A, Barrick D. 2011. The contribution of entropy, enthalpy, and hydrophobic desolvation to cooperativity in repeat-protein folding. Structure 19:349–60 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Asthagiri D, Karandur D, Tomar DS, Pettitt BM. 2017. Intramolecular interactions overcome hydration to drive the collapse transition of Gly15. J. Phys. Chem. B 121:8078–84 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Auton M, Holthauzen LMF, Bolen DW. 2007. Anatomy of energetic changes accompanying urea-induced protein denaturation. PNAS 104:15317–22 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Aznauryan M, Delgado, Soranno A, Nettels D, Huang J-R, et al. 2016. Comprehensive structural and dynamical view of an unfolded protein from the combination of single-molecule FRET, NMR, and SAXS. PNAS 113:E5389–98 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bah A, Vernon RM, Siddiqui Z, Krzeminski M, Muhandiram R, et al. 2015. Folding of an intrinsically disordered protein by phosphorylation as a regulatory switch. Nature 519:106–9 [DOI] [PubMed] [Google Scholar]
- 6.Baker EG, Bartlett GJ, Crump MP, Sessions RB, Linden N, et al. 2015. Local and macroscopic electrostatic interactions in single α-helices. Nat. Chem. Biol 11:221–28 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Baldwin RL, Frieden C, Rose GD. 2010. Dry molten globule intermediates and the mechanism of protein unfolding. Proteins 78:2725–37 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Banani SF, Lee HO, Hyman AA, Rosen MK. 2017. Biomolecular condensates: organizers of cellular biochemistry. Nat. Rev. Mol. Cell Biol 18:285–98 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Banavar JR, Maritan A. 2007. Physics of proteins. Annu. Rev. Biophys. Biomol. Struct 36:261–80 [DOI] [PubMed] [Google Scholar]
- 10.Ben-Naim A. 2013. Solvation Thermodynamics. New York, NY: Springer Sci. Bus. Media [Google Scholar]
- 11.Berisio R, Vitagliano L, Mazzarella L, Zagari A. 2002. Crystal structure of the collagen triple helix model [(Pro-Pro-Gly)10]3. Protein Sci. 11:262–70 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Best RB, Zheng W, Mittal J. 2014. Balanced protein–water interactions improve properties of disordered proteins and non-specific protein association. J. Chem. Theory Comput 10:5113–24 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Bloom JD, Labthavikul ST, Otey CR, Arnold FH. 2006. Protein stability promotes evolvability. PNAS 103:5869–74 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Bolen DW, Rose GD. 2008. Structure and energetics of the hydrogen-bonded backbone in protein folding. Annu. Rev. Biochem 77:339–62 [DOI] [PubMed] [Google Scholar]
- 15.Borgia A, Zheng W, Buholzer K, Borgia MB, Schüler A, et al. 2016. Consistent view of polypeptide chain expansion in chemical denaturants from multiple experimental methods. J. Am. Chem. Soc 138:11714–26 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Boze H, Marlin T, Durand D, Pérez J, Vernhet A, et al. 2010. Proline-rich salivary proteins have extended conformations. Biophys. J 99:656–65 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Camacho CJ, Thirumalai D. 1993. Kinetics and thermodynamics of folding in model proteins. PNAS 90:6369–72 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Canchi DR, García AE. 2013. Cosolvent effects on protein stability. Annu. Rev. Phys. Chem 64:273–93 [DOI] [PubMed] [Google Scholar]
- 19.Capraro DT, Roy M, Onuchic JN, Jennings PA. 2008. Backtracking on the folding landscape of the β-trefoil protein interleukin-1β? PNAS 105:14844–48 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Chan HS, Dill KA. 1991. Polymer principles in protein structure and stability. Annu. Rev. Biophys. Biophys. Chem 20:447–90 [DOI] [PubMed] [Google Scholar]
- 21.Cho J-H, Meng W, Sato S, Kim EY, Schindelin H, Raleigh. 2014. Energetically significant networks of coupled interactions within an unfolded protein. PNAS 111:12079–84 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Cho J-H, Sato S, Raleigh DP. 2004. Thermodynamics and kinetics of non-native interactions in protein folding: a single point mutant significantly stabilizes the N-terminal domain of L9 by modulating non-native interactions in the denatured state. J. Mol. Biol 338:827–37 [DOI] [PubMed] [Google Scholar]
- 23.Chong PA, Ozdamar B, Wrana JL, Forman-Kay JD. 2004. Disorder in a target for the Smad2 Mad homology 2 domain and its implications for binding and specificity. J. Biol. Chem 279:40707–14 [DOI] [PubMed] [Google Scholar]
- 24.Choy W-Y, Mulder FAA, Crowhurst KA, Muhandiram DR, Millett IS, et al. 2002. Distribution of molecular size within an unfolded state ensemble using small-angle X-ray scattering and pulse field gradient NMR techniques. J. Mol. Biol 316:101–12 [DOI] [PubMed] [Google Scholar]
- 25.Crick SL, Jayaraman M, Frieden C, Wetzel R, Pappu RV. 2006. Fluorescence correlation spectroscopy shows that monomeric polyglutamine molecules form collapsed structures in aqueous solutions. PNAS 103:16764–69 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Crowhurst KA, Forman-Kay JD. 2003. Aromatic and methyl NOEs highlight hydrophobic clustering in the unfolded state of an SH3 domain. Biochemistry 42:8687–95 [DOI] [PubMed] [Google Scholar]
- 27.Das RK, Huang Y, Phillips AH, Kriwacki RW, Pappu RV. 2016. Cryptic sequence features within the disordered protein p27Kip1 regulate cell cycle signaling. PNAS 113:5616–21 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Das RK, Pappu RV. 2013. Conformations of intrinsically disordered proteins are influenced by linear sequence distributions of oppositely charged residues. PNAS 110:13392–97 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Das RK, Ruff KM, Pappu RV. 2015. Relating sequence encoded information to form and function of intrinsically disordered proteins. Curr. Opin. Struct. Biol 32:102–12 [DOI] [PMC free article] [PubMed] [Google Scholar]; 29a. Davis CM, Gruebele M, Sukenik S. 2018/2. How does solvation in the cell affect protein folding and binding? Curr. Opin. Struct. Biol 48:23–29 [DOI] [PubMed] [Google Scholar]
- 30.de Gennes PG. 1975. Collapse of a polymer chain in poor solvents. J. Phys. Lett 36:55–57 [Google Scholar]
- 31.de Gennes PG. 1979. Scaling Concepts in Polymer Physics. Ithaca, NY: Cornell Univ. Press [Google Scholar]
- 32.Dill KA. 1990. Dominant forces in protein folding. Biochemistry 29:7133–55 [DOI] [PubMed] [Google Scholar]
- 33.Dill KA, Shortle D. 1991. Denatured states of proteins. Annu. Rev. Biochem 60:795–825 [DOI] [PubMed] [Google Scholar]
- 34.Dima RI, Thirumalai D. 2004. Asymmetry in the shapes of folded and denatured states of proteins. J. Phys. Chem. B 108:6564–70 [Google Scholar]
- 35.Edwards SF. 1967. Statistical mechanics with topological constraints: I. Proc. Phys. Soc. Lond 91:513 [Google Scholar]
- 36.Englander SW. 2000. Protein folding intermediates and pathways studied by hydrogen exchange. Annu. Rev. Biophys. Biomol. Struct 29:213–38 [DOI] [PubMed] [Google Scholar]
- 37.Englander SW, Mayne L. 2014. The nature of protein folding pathways. PNAS 111:15873–80 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Fink AL, Calciano LJ, Goto Y, Kurotsu T, Palleros DR. 1994. Classification of acid denaturation of proteins: intermediates and unfolded states. Biochemistry 33:12504–11 [DOI] [PubMed] [Google Scholar]
- 39.Finkelstein AV, Shakhnovich EI. 1989. Theory of cooperative transitions in protein molecules. II. Phase diagram for a protein molecule in solution. Biopolymers 28:1681–94 [DOI] [PubMed] [Google Scholar]
- 40.Flory PJ. 1953. Principles of Polymer Chemistry. Ithaca, NY: Cornell Univ. Press [Google Scholar]
- 41.Flory PJ. 1969. Statistical Mechanics of Chain Molecules. New York: Oxford Univ. Press [Google Scholar]
- 42.Fossat MJ, Dao TP, Jenkins K, Dellarole M, Yang, et al. 2016. High-resolution mapping of a repeat protein folding free energy landscape. Biophys. J 111:2368–76 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Fuertes G, Banterle N, Ruff KM, Chowdhury A, Mercadante D, et al. 2017. Decoupling of size and shape fluctuations in heteropolymeric sequences reconciles discrepancies in SAXS vs. FRET measurements. PNAS 114:E6342–51 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Gangadhara BN, Laine JM, Kathuria SV, Massi F, Matthews CR. 2013. Clusters of branched aliphatic side chains serve as cores of stability in the native state of the HisF TIM barrel protein. J. Mol. Biol 425:1065–81 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Gates ZP, Baxa MC, Yu W, Riback JA, Li H, et al. 2017. Perplexing cooperative folding and stability of a low-sequence complexity, polyproline 2 protein lacking a hydrophobic core. PNAS 114:2241–46 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Gibbs EB, Lu F, Portz B, Fisher MJ, Medellin BP, et al. 2017. Phosphorylation induces sequence-specific conformational switches in the RNA polymerase II C-terminal domain. Nat. Commun 8:15233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Goldenberg DP. 2003. Computational simulation of the statistical properties of unfolded proteins. J. Mol. Biol 326:1615–33 [DOI] [PubMed] [Google Scholar]
- 48.Goluguri RR, Udgaonkar JB 2016. Microsecond rearrangements of hydrophobic clusters in an initially collapsed globule prime structure formation during the folding of a small protein. J. Mol. Biol 428:3102–17 [DOI] [PubMed] [Google Scholar]
- 49.Griep S, Hobohm U. 2010. PDBselect 1992–2009 and PDBfilter-select. Nucleic Acids Res. 38:D318–19 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Grosberg AY, Kuznetsov DV. 1992. Quantitative theory of the globule-to-coil transition. 1. Link density distribution in a globule and its radius of gyration. Macromolecules 25:1970–79 [Google Scholar]
- 51.Gruszka DT, Wojdyla JA, Bingham RJ, Turkenburg JP, Manfield, et al. 2012. Staphylococcal biofilm-forming protein has a contiguous rod-like structure. PNAS 109:E1011–18 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Guinn EJ, Jagannathan B, Marqusee S. 2015. Single-molecule chemo-mechanical unfolding reveals multiple transition state barriers in a small single-domain protein. Nat. Commun 6:6861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Harmon TS, Holehouse AS, Rosen MK, Pappu RV. 2017. Intrinsically disordered linkers determine the interplay between phase separation and gelation in multivalent proteins. bioRxiv 164301. 10.1101/164301 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Higgs PG, Joanny J-Fv. 1991. Theory of polyampholyte solutions. J. Chem. Phys 94:1543–54 [Google Scholar]
- 55.Hodsdon ME, Frieden C. 2001. Intestinal fatty acid binding protein: the folding mechanism as determined by NMR studies. Biochemistry 40:732–42 [DOI] [PubMed] [Google Scholar]
- 56.Hofmann H, Soranno A, Borgia A, Gast K, Nettels D, Schuler B. 2012. Polymer scaling laws of unfolded and intrinsically disordered proteins quantified with single-molecule spectroscopy. PNAS 109:16155–60 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Holehouse AS, Das RK, Ahad JN, Richardson MOG, Pappu RV. 2017. CIDER: resources to analyze sequence-ensemble relationships of intrinsically disordered proteins. Biophys. J 112:16–21 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Holehouse AS, Garai K, Lyle N, Vitalis A, Pappu RV. 2015. Quantitative assessments of the distinct contributions of polypeptide backbone amides versus side chain groups to chain expansion via chemical denaturation. J. Am. Chem. Soc 137:2984–95 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Hu W, Walters BT, Kan Z-Y, Mayne L, Rosen LE, et al. 2013. Stepwise protein folding at near amino acid resolution by hydrogen exchange and mass spectrometry. PNAS 110:7684–89 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Jacob J, Krantz B, Dothager RS, Thiyagarajan P, Sosnick TR. 2004. Early collapse is not an obligate step in protein folding. J. Mol. Biol 338:369–82 [DOI] [PubMed] [Google Scholar]
- 61.Jain N, Bhattacharya M, Mukhopadhyay S. 2011. Chain collapse of an amyloidogenic intrinsically disordered protein. Biophys. J 101:1720–29 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Jha SK, Marqusee S. 2014. Kinetic evidence for a two-stage mechanism of protein denaturation by guanidinium chloride. PNAS 111:4856–61 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Kang H, Vázquez FX, Zhang L, Das P, Toledo-Sherman L, et al. 2017. Emerging β-sheet rich conformations in supercompact Huntingtin exon-1 mutant structures. J. Am. Chem. Soc 139:8820–27 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Karandur D, Harris RC, Pettitt BM. 2016. Protein collapse driven against solvation free energy without H-bonds. Protein Sci. 25:103–10 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Karandur D, Wong K-Y, Pettitt BM. 2014. Solubility and aggregation of Gly5 in water. J. Phys. Chem. B 118:9565–72 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Kathuria SV, Chan YH, Nobrega RP, Özen A, Matthews CR. 2016. Clusters of isoleucine, leucine, and valine side chains define cores of stability in high-energy states of globular proteins: sequence determinants of structure and stability. Protein Sci. 25:662–75 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Kimura T, Uzawa T, Ishimori KI, Takahashi S, et al. 2005. Specific collapse followed by slow hydrogen-bond formation of β-sheet in the folding of single-chain monellin. PNAS 102:2748–53 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Klein-Seetharaman J, Oikawa M, Grimshaw SB, Wirmer J, Duchardt E, et al. 2002. Long-range interactions within a nonnative protein. Science 295:1719–22 [DOI] [PubMed] [Google Scholar]
- 69.Klimov DK, Thirumalai D. 1996. Criterion that determines the foldability of proteins. Phys. Rev. Lett 76:4070–73 [DOI] [PubMed] [Google Scholar]
- 70.Klimov DK, Thirumalai D. 1996. Factors governing the foldability of proteins. Proteins 26:411–41 [DOI] [PubMed] [Google Scholar]
- 71.Kobe B, Kajava AV. 2001. The leucine-rich repeat as a protein recognition motif. Curr. Opin. Struct. Biol 11:725–32 [DOI] [PubMed] [Google Scholar]
- 72.Kohl A, Binz HK, Forrer P, Stumpp MT, Plückthun A, Grütter MG. 2003. Designed to be stable: crystal structure of a consensus ankyrin repeat protein. PNAS 100:1700–5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Kohn JE, Millett IS, Jacob JB, Dillon TM, et al. 2004. Random-coil behavior and the dimensions of chemically unfolded proteins. PNAS 101:12491–96 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Kutyshenko VP, Prokhorov DA, Mikoulinskaia GV, Molochkov NV, Paskevich SI, Uversky VN. 2017. Evidence for the residual tertiary structure in the urea-unfolded form of bacteriophage T5 endolysin. J. Biomol. Struct. Dyn 35:1331–38 [DOI] [PubMed] [Google Scholar]
- 75.Li MS, Klimov DK, Thirumalai D. 2004. Finite size effects on thermal denaturation of globular proteins. Phys. Rev. Lett 93:268107 [DOI] [PubMed] [Google Scholar]
- 76.Lietzow MA, Jamin, Dyson HJ, Wright PE. 2002. Mapping long-range contacts in a highly unfolded protein. J. Mol. Biol 322:655–62 [DOI] [PubMed] [Google Scholar]
- 77.Lifshitz IM Grosberg AY, Khokhlov RA. 1978. Some problems of the statistical physics of polymer chains with volume interaction. Rev. Mod. Phys 50:683–713 [Google Scholar]
- 78.Lim WK, Rösgen J, Englander SW. 2009. Urea, but not guanidinium, destabilizes proteins by forming hydrogen bonds to the peptide group. PNAS 106:2595–600 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Lin Y-H, Song J, Forman-Kay JD, Chan HS. 2016. Random-phase-approximation theory for sequence-dependent, biologically functional liquid-liquid phase separation of intrinsically disordered proteins. J. Mol. Liq 228:176–93 [Google Scholar]
- 80.Lu X, Murphy RM. 2015. Asparagine repeat peptides: aggregation kinetics and comparison with glutamine repeats. Biochemistry 54:4784–94 [DOI] [PubMed] [Google Scholar]
- 81.Lupas AN, Bassler J, Dunin-Horkawicz S. 2017. The structure and topology of α-helical coiled coils. Subcell. Biochem 82:95–129 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Lyle N, Das RK, Pappu RV. 2013. A quantitative measure for protein conformational heterogeneity. J. Chem. Phys 139:121907 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Maity H, Reddy G. 2016. Folding of Protein L with implications for collapse in the denatured state ensemble. J. Am. Chem. Soc 138:2609–16 [DOI] [PubMed] [Google Scholar]
- 84.Mallamace F, Corsaro C, Mallamace D, Vasi S, Vasi C, et al. 2016. Energy landscape in protein folding and unfolding. PNAS 113:3159–63 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Mao AH, Crick SL, Vitalis A, Chicoine CL, Pappu RV. 2010. Net charge per residue modulates conformational ensembles of intrinsically disordered proteins. PNAS 107:8183–88 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Mao AH, Lyle N, Pappu RV. 2013. Describing sequence–ensemble relationships for intrinsically disordered proteins. Biochem. J 449:307–18 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Marsh JA, Forman-Kay JD. 2010. Sequence determinants of compaction in intrinsically disordered proteins. Biophys. J 98:2383–90 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Marsh JA, Neale C, Jack FE, Choy W-Y, Lee AY, et al. 2007. Improved structural characterizations of the drkN SH3 domain unfolded state suggest a compact ensemble with native-like and non-native structure. J. Mol. Biol 367:1494–510 [DOI] [PubMed] [Google Scholar]
- 89.Martin EW, Holehouse AS, Grace CR, Hughes A, Pappu RV, Mittag T. 2016. Sequence determinants of the conformational properties of an intrinsically disordered protein prior to and upon multisite phosphorylation. J. Am. Chem. Soc 138:15323–35 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Mayor U, Grossmann JG, Foster NW, Freund SMV, Fersht AR. 2003. The denatured state of Engrailed Homeodomain under denaturing and native conditions. J. Mol. Biol 333:977–91 [DOI] [PubMed] [Google Scholar]
- 91.Meng W, Luan B, Lyle N, Pappu RV, Raleigh DP. 2013. The denatured state ensemble contains significant local and long-range structure under native conditions: analysis of the N-terminal domain of ribosomal protein L9. Biochemistry 52:2662–71 [DOI] [PubMed] [Google Scholar]
- 92.Moeser B, Horinek D. 2014. Unified description of urea denaturation: backbone and side chains contribute equally in the transfer model. J. Phys. Chem. B 118:107–14 [DOI] [PubMed] [Google Scholar]
- 93.Mok KH, Kuhn LT, Goez M, Day IJ, Lin JC, et al. 2007. A pre-existing hydrophobic collapse in the unfolded state of an ultrafast folding protein. Nature 447:106–9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Mok YK, Kay CM, Kay LE, Forman-Kay J. 1999. NOE data demonstrating a compact unfolded state for an SH3 domain under non-denaturing conditions. J. Mol. Biol 289:619–38 [DOI] [PubMed] [Google Scholar]
- 95.. Molliex A, Temirov J, Lee J, Coughlin M, Kanagaraj AP, et al. 2015. Phase separation by low complexity domains promotes stress granule assembly and drives pathological fibrillization. Cell 163:123–33 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Mountain RD, Thirumalai D. 2003. Molecular dynamics simulations of end-to-end contact formation in hydrocarbon chains in water and aqueous urea solution. J. Am. Chem. Soc 125:1950–57 [DOI] [PubMed] [Google Scholar]
- 97.Mukhopadhyay S, Krishnan R, Lemke EA, Lindquist S, Deniz AA. 2007. A natively unfolded yeast prion monomer adopts an ensemble of collapsed and rapidly fluctuating structures. PNAS 104:2649–54 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Müller-Späth S, Soranno A, Hirschfeld V, Hofmann H, Rüegger S, et al. 2010. Charge interactions can dominate the dimensions of intrinsically disordered proteins. PNAS 107:14609–14 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Neumaier S, Kiefhaber T. 2014. Redefining the dry molten globule state of proteins. J. Mol. Biol 426:2520–28 [DOI] [PubMed] [Google Scholar]
- 100.Nobrega RP, Arora K, Kathuria SV, Graceffa R, Barrea RA, et al. 2014. Modulation of frustration in folding by sequence permutation. PNAS 111:10562–67 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Nott TJ, Petsalaki E, Farber P, Jervis D, Fussner E, et al. 2015. Phase transition of a disordered nuage protein generates environmentally responsive membraneless organelles. Mol. Cell 57:936–47 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Outer P, Carr CI, Zimm BH. 1950. Light scattering investigation of the structure of polystyrene. J. Chem. Phys 18:830–39 [Google Scholar]
- 103.Pace CN, Shaw KL. 2000. Linear extrapolation method of analyzing solvent denaturation curves. Proteins 41 (Suppl. 4):1–7 [DOI] [PubMed] [Google Scholar]
- 104.Pande VS, Grosberg AY, Tanaka T. 2000. Heteropolymer freezing and design: towards physical models of protein folding. Rev. Mod. Phys 72:259–314 [Google Scholar]
- 105.Patel A, Lee HO, Jawerth L, Maharana S, Jahnel M, et al. 2015. A liquid-to-solid phase transition of the ALS protein FUS accelerated by disease mutation. Cell 162:1066–77 [DOI] [PubMed] [Google Scholar]
- 106.Piana S, Klepeis JL, Shaw DE. 2014. Assessing the accuracy of physical models used in protein-folding simulations: quantitative evidence from long molecular dynamics simulations. Curr. Opin. Struct. Biol 24:98–105 [DOI] [PubMed] [Google Scholar]
- 107.Plaxco KW, Millett IS, Segel DJ, Doniach S, Baker D. 1999. Chain collapse can occur concomitantly with the rate-limiting step in protein folding. Nat. Struct. Biol 6:554–56 [DOI] [PubMed] [Google Scholar]; 107a. Portz B., Lu FEB, Mayfield JE, Rachel Mehaffey M, Zhang YJ, Brodbelt JS, Showalter SA, and Gilmour DS. 2017. Structural heterogeneity in the intrinsically disordered RNA polymerase II C-terminal domain. Nat. Commun 8: 15231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Ptitsyn OB, Uversky VN. 1994. The molten globule is a third thermodynamical state of protein molecules. FEBS Lett. 341:15–18 [DOI] [PubMed] [Google Scholar]
- 109.Record MT Jr., Guinn E, Pegram L, Capp M 2013. Introductory lecture: interpreting and predicting Hofmeister salt ion and solute effects on biopolymer and model processes using the solute partitioning model. Faraday Discuss. 160:9–44 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Reddy G, Thirumalai D. 2017. Collapse precedes folding in denaturant-dependent assembly of ubiquitin. J. Phys. Chem. B 121:995–1009 [DOI] [PubMed] [Google Scholar]
- 111.Rose GD, Fleming PJJRAJA, Bowman MA, Zmyslowski AM, Knoverek CR, Jumper JMJA, Katanski CD, Kear-Scott JL, Pilipenko EV, Rojek AE, et al. 2017. Stress-Triggered Phase Separation Is an Adaptive, Evolutionarily Tuned Response. Cell. 168(6):1028–40.e19 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Rubinstein M, Colby RH. 2003. Polymer Physics. New York: Oxford Univ. Press [Google Scholar]
- 113.Ruff KM, Holehouse AS. 2017. SAXS versus FRET: a matter of heterogeneity? Biophys. J 113:971–73 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Samanta HS, Zhuravlev PI, Hinczewski M, Hori N, Chakrabarti SD. 2017. Protein collapse is encoded in the folded state architecture. Soft Matter 13:3622–38 [DOI] [PubMed] [Google Scholar]
- 115.Sarkar SS, Udgaonkar JB, Krishnamoorthy G. 2013. Unfolding of a small protein proceeds via dry and wet globules and a solvated transition state. Biophys. J 105:2392–402 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Sawle L, Ghosh K. 2015. A theoretical method to compute sequence dependent configurational properties in charged polymers and proteins. J. Chem. Phys 143:085101 [DOI] [PubMed] [Google Scholar]
- 117.Schuler B, Lipman EA, Eaton WA. 2002. Probing the free-energy surface for protein folding with single-molecule fluorescence spectroscopy. Nature 419:743–47 [DOI] [PubMed] [Google Scholar]
- 118.Segel DJ, Fink AL, Hodgson KO, Doniach S. 1998. Protein denaturation: a small-angle X-ray scattering study of the ensemble of unfolded states of cytochrome c. Biochemistry 37:12443–51 [DOI] [PubMed] [Google Scholar]
- 119.Semisotnov GV, Kihara H, Kotova NV, Kimura K, Amemiya Y, et al. 1996. Protein globularization during folding. A study by synchrotron small-angle X-ray scattering. J. Mol. Biol 262:559–74 [DOI] [PubMed] [Google Scholar]
- 120.Sen S, Goluguri RR, Udgaonkar JB. 2017. A dry transition state more compact than the native state is stabilized by non-native interactions during the unfolding of a small protein. Biochemistry 56:3699–703 [DOI] [PubMed] [Google Scholar]
- 121..Shakhnovich EI, Finkelstein AV. 1989. Theory of cooperative transitions in protein molecules. I. Why denaturation of globular protein is a first-order phase transition. Biopolymers 28:1667–80 [DOI] [PubMed] [Google Scholar]; 121a. Shin Y, Brangwynne CP. 2017. Liquid phase condensation in cell physiology and disease. Science. 357(6357): [DOI] [PubMed] [Google Scholar]
- 122.Sherman E, Haran G. 2006. Coil-globule transition in the denatured state of a small protein. PNAS 103:11539–43 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123.Shortle DMS. 2001. Persistence of native-like topology in a denatured protein in 8 M urea. Science 293:487–89 [DOI] [PubMed] [Google Scholar]
- 124.Song J, Gomes G-N, Shi T, Gradinaru CC, Chan HS. 2017. Conformational heterogeneity and FRET data interpretation for dimensions of unfolded proteins. Biophys. J 113:1012–24 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Sosnick TR, Barrick D. 2011. The folding of single domain proteins–have we reached a consensus? Curr. Opin. Struct. Biol 21:12–24 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 126.Steinhauser MO. 2005. A molecular dynamics study on universal properties of polymer chains in different solvent qualities. Part I. A review of linear chain properties. J. Chem. Phys 122:094901. [DOI] [PubMed] [Google Scholar]
- 127.Tanford C. 1968. Protein denaturation. Adv. Protein Chem 23:121–282 [DOI] [PubMed] [Google Scholar]
- 128.Teufel DP, Johnson CM, Lum JK, Neuweiler H. 2011. Backbone-driven collapse in unfolded protein chains. J. Mol. Biol 409:250–62 [DOI] [PubMed] [Google Scholar]
- 129.Thirumalai D, Liu Z, O’Brien EP, Reddy G. 2013. Protein folding: from theory to practice. Curr. Opin. Struct. Biol 23:22–29 [DOI] [PubMed] [Google Scholar]
- 130.Tooke L, Duitch L, Measey TJ, Schweitzer-Stenner R. 2010. Kinetics of the self-aggregation and film formation of poly-L-proline at high temperatures explored by circular dichroism spectroscopy. Biopolymers 93:451–57 [DOI] [PubMed] [Google Scholar]
- 131.Tran HT, Mao A, Pappu RV. 2008. Role of backbone–solvent interactions in determining conformational equilibria of intrinsically disordered proteins. J. Am. Chem. Soc 130:7380–92 [DOI] [PubMed] [Google Scholar]
- 132.van der Lee R, Buljan M, Lang B, Weatheritt RJ, Daughdrill GW, et al. 2014. Classification of intrinsically disordered regions and proteins. Chem. Rev 114:6589–631 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 133.Vitalis A, Caflisch A. 2010. Micelle-like architecture of the monomer ensemble of Alzheimer’s amyloid-β peptide in aqueous solution and its implications for Aβ aggregation. J. Mol. Biol 403:148–65 [DOI] [PubMed] [Google Scholar]
- 134.Vitalis A, Wang X, Pappu RV. 2007. Quantitative characterization of intrinsic disorder in polyglutamine: insights from analysis based on polymer theories. Biophys. J 93:1923–37 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 135.Vitalis A, Wang X, Pappu RV. 2008. Atomistic simulations of the effects of polyglutamine chain length and solvent quality on conformational equilibria and spontaneous homodimerization. J. Mol. Biol 384:279–97 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 136.Wallqvist A, Covell DG, Thirumalai D. 1998. Hydrophobic interactions in aqueous urea solutions with implications for the mechanism of protein denaturation. J. Am. Chem. Soc 120:427–28 [Google Scholar]
- 137.Walters BT, Mayne L, Hinshaw JR, Sosnick TR, Englander. 2013. Folding of a large protein at high structural resolution. PNAS 110:18898–903 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 138.Wei M-T, Elbaum-Garfinkle S, Holehouse AS, Chen CC-H, Feric M, et al. 2017. Phase behaviour of disordered proteins underlying low density and high permeability of liquid organelles. Nat. Chem 10.1038/nchem.2803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 139.Wilkins DK, Grimshaw SB, Receveur V, Dobson CM, Jones, Smith LJ. 1999. Hydrodynamic radii of native and denatured proteins measured by pulse field gradient NMR techniques. Biochemistry 38:16424–31 [DOI] [PubMed] [Google Scholar]
- 140.Williamson TE, Vitalis A, Crick SL, Pappu RV. 2010. Modulation of polyglutamine conformations and dimer formation by the N-terminus of huntingtin. J. Mol. Biol 396:1295–309 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 141.Wolfenden R. 1978. Interaction of the peptide bond with solvent water: a vapor phase analysis. Biochemistry 17:201–4 [DOI] [PubMed] [Google Scholar]
- 142.Wright PE, Dyson HJ. 1999. Intrinsically unstructured proteins: re-assessing the protein structure-function paradigm. J. Mol. Biol 293:321–31 [DOI] [PubMed] [Google Scholar]
- 143.Wuttke R, Hofmann H, Nettels D, Borgia MB, Mittal, et al. 2014. Temperature-dependent solvation modulates the dimensions of disordered proteins. PNAS 111:5213–18 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 144.Yarawsky AE, English LR, Whitten ST, Herr AB. 2017. The proline/glycine-rich region of the biofilm adhesion protein Aap forms an extended stalk that resists compaction. J. Mol. Biol 429:261–79 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 145.Yoo TY, Meisburger SP, Hinshaw J, Pollack L, Haran G, et al. 2012. Small-angle x-ray scattering and single-molecule FRET spectroscopy produce highly divergent views of the low-denaturant unfolded state. J. Mol. Biol 418:226–36 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 146.Zhang G, Wu C. 2006. Folding and formation of mesoglobules in dilute copolymer solutions. In Conformation-Dependent Design of Sequences in Copolymers I, ed. Khokhlov AR, pp. 101–76. Berlin, Ger.: Springer-Verlag Berl. Heidelb. [Google Scholar]
- 147.Zheng W, Borgia A, Buholzer K, Grishaev A, Schuler, Best RB. 2016. Probing the action of chemical denaturant on an intrinsically disordered protein by simulation and experiment. J. Am. Chem. Soc 138:11702–13 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 148.Ziv G, Thirumalai D, Haran G. 2009. Collapse transition in proteins. Phys. Chem. Chem. Phys 11:83–93 [DOI] [PMC free article] [PubMed] [Google Scholar]