Skip to main content
PMC home page
Genome Research logoLink to Genome Research
. 2023 Mar;33(3):359–370. doi: 10.1101/gr.276705.122

Large haplotypes highlight a complex age structure within the maize pan-genome

Jianing Liu 1, R Kelly Dawe 1,2,✉
PMCID: PMC10078284  PMID: 36854668

Abstract

The genomes of maize and other eukaryotes contain stable haplotypes in regions of low recombination. These regions, including centromeres, long heterochromatic blocks, and rDNA arrays, have been difficult to analyze with respect to their diversity and origin. Greatly improved genome assemblies are now available that enable comparative genomics over these and other nongenic spaces. Using 26 complete maize genomes, we developed methods to align intergenic sequences while excluding genes and regulatory regions. The centromere haplotypes (cenhaps) extend for megabases on either side of the functional centromere regions and appear as evolutionary strata, with haplotype divergence/coalescence times dating as far back as 450 thousand years ago (kya). Application of the same methods to other low recombination regions (heterochromatic knobs and rDNA) and all intergenic spaces revealed that deep coalescence times are ubiquitous across the maize pan-genome. Divergence estimates vary over a broad timescale with peaks at ∼16 and 300 kya, reflecting a complex history of gene flow among diverging populations and changes in population size associated with domestication. Cenhaps and other long haplotypes provide vivid displays of this ancient diversity.

The origins of maize can be traced to stands of teosinte, a tall grass with many small ears that is native to Mexico (Doebley 2004). Teosintes are divided into four species, one of which is Zea mays, which is divided into three subspecies: Zea mays mays (cultivated maize), Zea mays parviglumis, and Zea mays mexicana. Genetic data suggest that maize originated from populations of parviglumis (Matsuoka et al. 2002) with lesser contributions from mexicana (Ross-Ibarra et al. 2009; Hufford et al. 2013; Calfee et al. 2021). Through selection for desirable traits such as fewer stems and larger ears with exposed kernels, early inhabitants transformed teosinte into a domesticated crop as early as 8700 yr ago (Piperno et al. 2009). Domesticated maize was then transported northward through the desert and into Canada, south through the Andes, and east to the islands of the Caribbean where at each point it was cultivated as local landraces (Ross-Ibarra et al. 2009; van Heerwaarden et al. 2011; Hufford et al. 2013). Although the process of domestication caused a loss of genetic diversity relative to ancestral teosinte (Tenaillon et al. 2004; Wang et al. 2017), the remaining variation has been sufficient to sustain decades of continuous improvement by breeders (Andorf et al. 2019; Haberer et al. 2020; Hufford et al. 2021).

Molecular data show that there remains extraordinary variation in genome size, gene content, methylation status, and repeat composition among maize lines (Chia et al. 2012; Sun et al. 2018; Haberer et al. 2020; Hufford et al. 2021). A large share of the diversity is a result of transposon insertion over the past 3 million yr, which inflated genome size by two- to fivefold (Sanmiguel and Bennetzen 1998) and altered gene spacing and arrangement (Fu and Dooner 2002; Brunner et al. 2005). Transposable elements make up ∼83% of any single assembled maize genome (Hufford et al. 2021) and exhibit extreme polymorphism among maize lines. In two divergent haplotypes of the bronze1 region there is an almost total absence of homology in the intergenic spaces: among 23 transposons annotated over ∼180 kb of combined sequence, only one transposon is conserved (Fu and Dooner 2002). Maize also contains several classes of tandem repeat arrays including those with CentC, a centromere repeat, and two interspersed repeats known as knob180 and TR-1 defining heterochromatic domains called knobs (Liu et al. 2020). The lengths of tandem repeat arrays vary over orders of magnitude and are highly polymorphic among lines (Albert et al. 2010). Much of this structural diversity is presumed to be a product of ancient haplotype divergence, predating speciation. Persistence of ancient haplotype diversity is attributable to a slow rate of genetic drift in large populations (Hilton and Gaut 1998; Clark et al. 2004) or gene flow across species and subspecies (Ross-Ibarra et al. 2009).

Highly repetitive, structurally divergent regions display reduced levels of recombination, allowing identification of large, often megabase-scale haplotypes that have persisted and diverged over thousands to millions of years. Well-known examples are the evolutionary strata on the human X Chromosome that reflect the timing of major structural rearrangements (Lahn and Page 1999). Outside of sex chromosomes and other special cases, recombination is lowest around centromeres where it trends toward zero (Shi et al. 2010; Nambiar and Smith 2016). In human, complete genome assemblies have shown that centromeres occur in large haplotypes (called cenhaps) that harbor rich and previously unknown genetic diversity (Langley et al. 2019; Altemose et al. 2022). Here we sought to thoroughly describe the structure and evolution of maize haplotype blocks around centromeres, knobs, and rDNA regions, and interpret the results in a pan-genome context.

Results

Whole-genome alignment over intergenic spaces

To investigate haplotype structure at genome scale, we analyzed 26 high-quality genomes from the maize Nested Association Mapping (NAM) population (Hufford et al. 2021), a rich collection including temperate lines, tropical lines, sweet corn, and popcorn (McMullen et al. 2009). The NAM genomes were assembled by integrating data from long Pacific Biosciences (PacBio) reads and Bionano optical maps. To confirm that the assemblies were accurate over the transposon-rich regions surrounding centromeres, we aligned PacBio and Illumina reads (from Hufford et al. 2021) to the B73 reference assembly (Zm-B73-REFERENCE-NAM-5.0) and measured the variation in coverage (Supplemental Fig. S1). We found that 99.85% (Illumina) and 99.56% (PacBio) of the genome showed coverage values within three standard deviations of the mean. These values are similar to what was reported for the human genome (99.86% [Nurk et al. 2022]). The assembly accuracy over centromere regions (excluding CentC repeats) matched the accuracy of the genome as a whole (99.87% Illumina, 99.56% PacBio). All 26 NAM founder inbreds were assembled using the same methods and are likely to be similarly accurate in TE-rich regions. The rDNA, CentC, and knob repeat arrays were generally not fully assembled. Nevertheless, the long stretches of repeat arrays that were included in the reference assemblies showed good agreement with the optical maps (Hufford et al. 2021). Further, as shown below, syntenic repeat arrays from different inbreds often showed good agreement at the sequence level.

To carry out whole-genome alignment over these highly repetitive regions, we implemented the longest increasing subsequence (LIS) algorithm (Abouelhoda and Ohlebusch 2005; Rani and Rajpoot 2016) in a two-step chaining procedure (Supplemental Fig. S2). This method resolved misalignment errors and effectively captured rearranged segments (Supplemental Fig. S3). The LIS method also revealed ∼19 million structural variations (Supplemental Figs. S4, S5; Supplemental Tables S1, S2); a greatly expanded list (relative to an earlier database of ∼0.79 million [Hufford et al. 2021]), which is available for use in mapping and association studies. By comparing genomes in an all-by-all manner and retaining the unique portions contributed by each, we estimated the total (genic and intergenic) pan-genome size to be ∼7.9 Gb (Supplemental Fig. S6A), which is ∼3.7 times larger than the average assembled size of any single genome (Hufford et al. 2021). Only ∼4.9% of the total pan-genome (0.38 Gb) is conserved among all lines with the remaining 7.5 Gb segregating among lines at various frequencies (Supplemental Fig. S6B).

Ancient haplotypes in centromeric regions

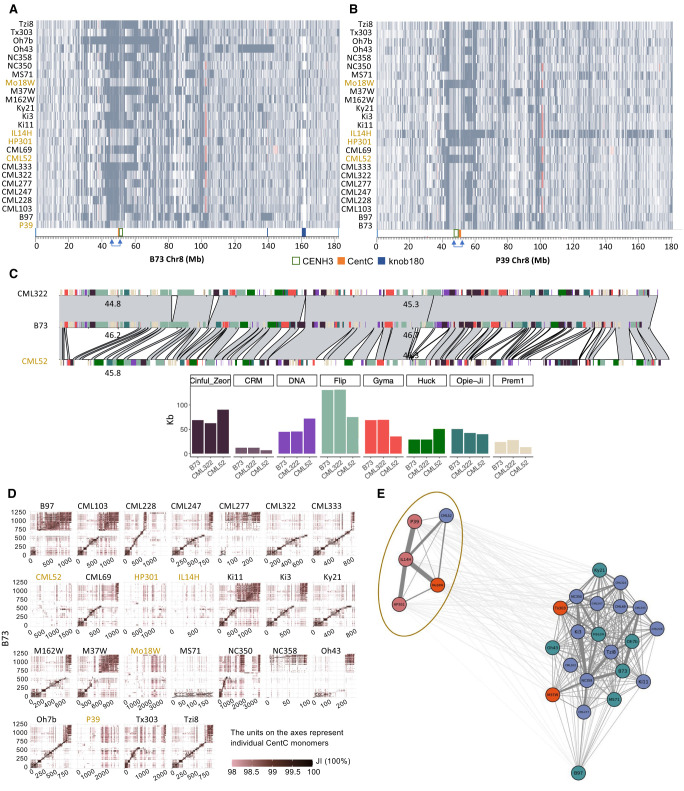
Alignments revealed megabase-scale cenhaps on seven chromosomes, including an ∼5 Mb region on Chromosome 2, an ∼10 Mb region on Chromosome 3, an ∼7 Mb region on Chromosome 5, an ∼10 Mb region on Chromosome 7, an ∼10 Mb region on Chromosome 8, an ∼7 Mb region on Chromosome 9, and an ∼8 Mb region on Chromosome 10 (Fig. 1A,B; Supplemental Figs. S7, S8). The segregating haplotype variants often include the functional centromere regions defined by the presence of Centromeric Histone H3 (CENH3) (Hufford et al. 2021; Wang et al. 2021) and extend well into flanking pericentromeric sequences. For example, five inbreds (CML52, HP301, IL14H, Mo18W, and P39) have cenhaps on Chromosome 8 that are clearly distinct from the cenhaps in all other inbreds (Fig. 1A,B). There is extreme variation in TE distribution between alternate Chromosome 8 cenhaps (such as B73 and CML52; Fig. 1C), mirroring the TE polymorphism previously described at the bronze1 locus (Fu and Dooner 2002). Cenhaps within a group (such as B73 and CML322) are similar but not identical, differing by multiple small insertions and deletions of retroelement sequences (Fig. 1C; Supplemental Fig. S9).

Figure 1.

Figure 1.

Open in a new tab

Cenhaps on Chromosome 8. (A) Alignments between NAM lines and B73 over Chromosome 8. Syntenic aligned regions (gray) and inverted segments (red) are shown. Blue arrows show the cenhap region with exceptional divergence. (B) Alignments between NAM lines and P39 over Chromosome 8. Annotation is the same as A. (C) Pairwise alignments and TE comparisons between CML322, CML52, and B73 over an ∼1 Mb region of Chromosome 8. Total kb of major TE families are shown below, in colors that match the annotation in the main panel (see Supplemental Fig. S9 for a more detailed view of TE subfamilies). This region does not include the CENH3 or CentC domains. (D) Pairwise alignments between NAM lines and B73 over CentC arrays on Chromosome 8. x- and y-axes show CentC monomers, and color intensity reflects the Jaccard index (JI) between each monomer pair. The non-B73 haplotypes are shaded in olive. (E) Clustering of CentC arrays on centromere 8. The colors over inbred names indicate varieties of corn: northern flint (pink), temperate (blue), mixed (red), and tropical (green).

Most maize centromeric regions contain long arrays of the ∼156-bp CentC repeat (Gent et al. 2017). To compare CentC arrays, individual monomers were aligned all-by-all and similarity was scored by Jaccard index (JI), which considers both SNPs and the size of the monomer. On Chromosome 8, the CentC array within the major cenhap group (the B73 type) and alternate type (the P39 group) show no collinear homology (Fig. 1D), suggesting a complete turnover of repeat arrays. Clustering of the Chromosome 8 data from different inbreds further supports the existence of two deeply divergent haplotype groups (Fig. 1E). Similarly divergent CentC arrays are observed on Chromosomes 2 and 3 (Supplemental Figs. S10, S11).

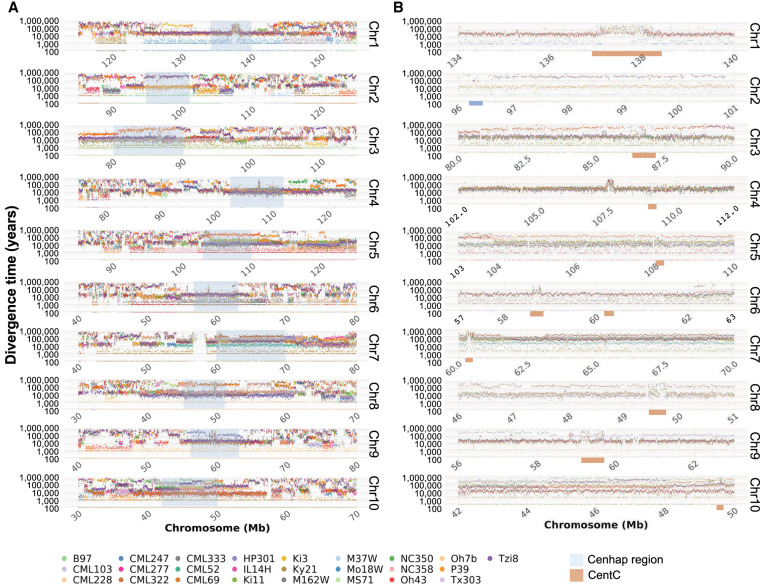
To compare the ages of maize cenhaps, we aligned all genomes to the B73 reference assembly, identified SNPs, and calculated the times of divergence (Fig. 2A,B; Supplemental Fig. S12; Clark et al. 2005). Before doing so, we masked all annotated genes and unmethylated (potential regulatory) regions under the assumption that intergenic sequences would be less likely to be constrained by selection (Lynch et al. 2016; Monroe et al. 2022). The divergence dating confirmed that cenhaps on seven chromosomes fall into two haplogroups with divergence times ranging from ∼130–450 kya. The divergence times estimated from adjacent 20-kb blocks were typically quite consistent (Fig. 2B), indicating that there were few local alignment errors that significantly impacted our age estimates (CentC arrays being an exception, Fig. 2B).

Figure 2.

Figure 2.

Open in a new tab

Divergence times of cenhaps. (A) Divergence times between NAM lines and B73 over pericentromeric regions. Dots represent estimated divergence times over 20-kb windows. The cenhap regions are highlighted in blue. (B) Cenhaps outlined in A. The divergence times over CentC regions (orange bars) are not reliable because of inaccurate alignment over CentC arrays and embedded retrotransposons within the arrays.

Retroelements that are present in one cenhap and absent in another are most likely to have been inserted after the two cenhaps diverged. The time of retroelement insertion can be estimated by comparing the sequences of the long terminal repeats (LTRs) (SanMiguel et al. 1998), and in previous work, the time of retroelement insertion has been used as a proxy for estimating haplotype divergence (e.g., Brunner et al. 2005). Our analysis of the B73 and CML322 cenhaps on Chromosome 8 indicated that they diverged very recently, ∼20 kya (Figs. 1C, 2B). To test whether the retroelements that differentiate these cenhaps are recent insertions, we compared the genome alignment with annotated retroelements and identified 19 retroelements that were present in the B73 Chromosome 8 cenhap but absent in CML322. Of these, 15 had an estimated age of zero, indicating no SNPs differentiate the LTRs of the retroelement. Four others had accumulated one or two SNPs, giving estimated ages ranging from 16,304 to 32,631 yr (Supplemental Table S3). These results indicate that whole-genome alignment provides estimates of haplotype divergence that are consistent with previously used methods.

The times of cenhap divergence coincide with the estimated origin of the Zea lineage (∼120 kya) (Chen et al. 2022). We tested whether the major cenhaps are present in teosintes by aligning Illumina data from 67 teosinte accessions including Zea mays ssp. parviglumis, ssp. mexicana, ssp. huehuetenangensis, and the related species Zea diploperennis to B73. The presence and absence of major cenhap groups could be scored based on the density of aligned reads, although there were ambiguous cases where the centromeres were heterozygous and sequence coverage was low (Supplemental Fig. S13). The data demonstrate that all major cenhap groups found in maize (Chromosomes 2, 3, 5, 7, 8, 9, 10) and two additional cenhaps on Chromosomes 1 and 6 occur as segregating polymorphism in parviglumis. Among the four mexicana accessions analyzed, there were alternate cenhaps on at least five chromosomes (Chromosomes 3, 4, 5, 7, 10). We also observed recombinant cenhaps in teosinte that are not observed in maize (see centromeres 2 and 3, Supplemental Fig. S13), consistent with the fact that maize is less diverse than its teosinte relatives (Hilton and Gaut 1998; Doebley 2004; Wang et al. 2017).

Ancient haplotypes in repeat arrays of knobs and NOR

Zea species contain many heterochromatic knobs with megabase-scale arrays of tandem repeats known as knob180 and TR-1. Knobs are found in mid-arm positions and are maintained by a meiotic drive mechanism (Dawe et al. 2018; Swentowsky et al. 2020). Recombination is suppressed within and around knobs (Ghaffari et al. 2013). Analysis of 10 large knobs in the NAM lines (Albert et al. 2010; Hufford et al. 2021) demonstrated that two (6L, 8L) fall into two clusters that have diverged for over 200 kya (Supplemental Figs. S14, S15). The knob on the short arm of Chromosome 9 (9S) separates into three clusters, where two diverged from B73 over 300 kya (Fig. 3A,B). In contrast, six knobs have divergence times of <100 kya consistent with a more recent emergence, presumably as an outcome of meiotic drive. We also analyzed the nucleolus organizer region (NOR), which contains megabase-scale arrays of rDNA (Fig. 3C; Supplemental Fig. S16). All-by-all alignment of the 6S knob linked to the NOR indicated three distinct clusters with progressive divergence times of 100, 220, and 300 kya (Fig. 3D). The analysis also corroborates the recent report of an ∼3 Mb insertion of non-rDNA sequence with homology to Tripsacum dactyloides (the sister genus to Zea; Supplemental Fig. S16) within the most common maize NOR haplotype (Huang et al. 2021), but minor NOR haplotypes do not include this insertion.

Figure 3.

Figure 3.

Open in a new tab

Ancient haplotypes in the 9S knob and NOR. (A) Dot-matrix alignments between 21 NAM lines and B73 over the knob180 array on Chromosome 9S (only 21 have the 9S knob). x- and y-axes show knob180 monomers, and color intensity reflects the Jaccard index between each monomer pair. (B) Clustering of 9S knobs based on repeat array alignments. Divergence times from B73 (kya) were calculated using syntenic SNPs in TEs that lie within the arrays. In panel A the non-B73 haplotypes are indicated in olive and green, and the corresponding clusters in B are circled in matching colors. (C) Dot-matrix alignments between 25 NAM lines and B73 over the NOR. x- and y-axes show 18S rDNA monomers, and color intensity reflects the Jaccard index (JI) between each monomer pair. (D) Clustering of the 6S knob180 array that is about 10 Mb from the NOR on Chromosome 6. The TEs in the knob were dated using syntenic SNPs. In B and D, the colors over individual inbred names indicate varieties of corn: northern flint (pink), temperate (blue), mixed (red), and tropical (green).

A pan-genome-wide burst of diversity at 10–30 kya

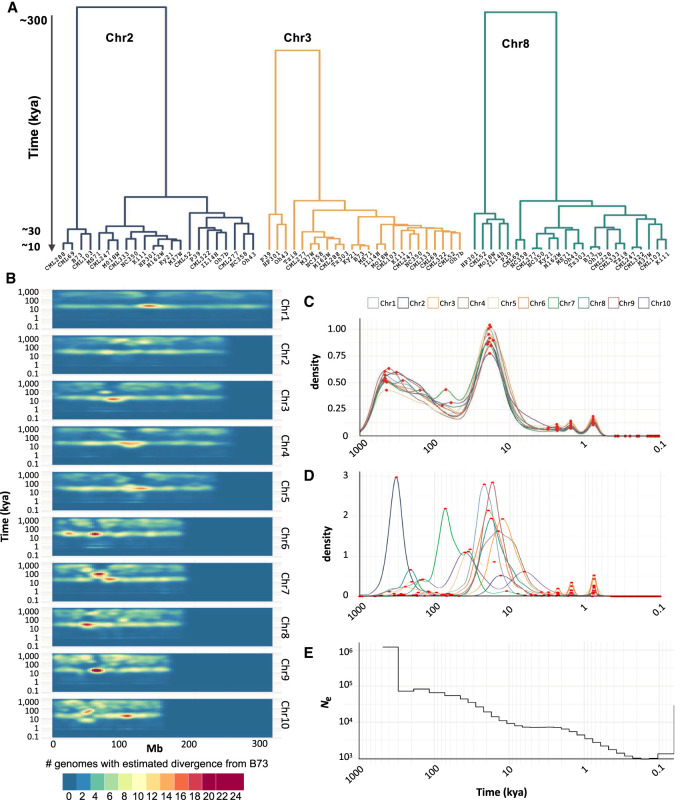
Our documentation of maize cenhaps (Fig. 2) reveals not only extreme cases of 100–300 kya of divergence between nonrecombining variants, but also a significant amount of divergence in the 10–30 kya range. These divergence times were estimated against a single reference genome. To gain a broader perspective we also performed hierarchical clustering using SNPs within cenhaps to interpret relative divergence in an all-by-all manner. The results confirm the deep separation of major haplotype groups and demonstrate that the majority of modern cenhap diversity evolved in the recent past (Fig. 4A; Supplemental Fig. S17), supporting previous conclusions (Schneider et al. 2016).

Figure 4.

Figure 4.

Open in a new tab

Whole-genome age distributions. (A) Hierarchical clustering of cenhaps from three chromosomes showing that most cenhap diversity dates to 10–30 kya. (B) Divergence times of intergenic spaces estimated from 20-kb windows represented in a density plot. (C) Density plot of all divergence times displayed in B. The x-axis shows probability densities, where the total area under the curve is 1. Local maxima are highlighted as red dots. When the B73 haplotype is compared to similar haplotypes, there is good alignment and few SNPs, giving discrete young peaks on the right of the curve (at ∼2.4, 1.6, and 0.8 kya, representing windows with 3, 2, or 1 SNP). When B73 is compared to more divergent haplotypes, there are more SNPs and the aligned regions may be smaller due to the presence of SVs (such as a deletion). In these cases, the denominators change to the size of the alignable sequence, causing the age distribution to become more continuous at older ages. (D) Density plot of cenhap divergence times only, annotated as in C. The two large peaks at older age represent cases where the B73 cenhap is in the minority group and diverged from most other cenhaps ∼220 kya (Chr 2) or ∼60 kya (Chr 7). (E) Effective population size (Ne) of maize over the past 0.5 million yr.

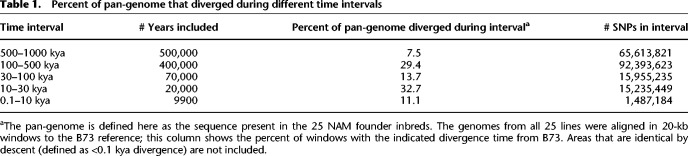
To determine whether these trends are unique to cenhaps, we plotted molecular age densities across all chromosomes of all NAM lines using B73 as a reference. This effort was designed to focus on the tens of thousands of smaller haplotypes between genes. The intergenic spaces in maize are about ∼50 kb on average (∼40,000 genes in ∼2.2 Gb genomes) and most recombination occurs within genes and areas with unmethylated DNA (Liu et al. 2009; Choi et al. 2018), which were omitted from our alignments. We chose to estimate divergence times using 20-kb sliding windows, but observed the same patterns with window sizes ranging from 10 to 100 kb (Supplemental Fig. S18). The results show that molecular age distributions are not uniform, with multiple bands of coalescence times in the 100–500 kya range and a rich layer of diversity dating to 10–30 kya (Fig. 4B). These general trends are more apparent when the genome-wide divergence data are displayed as a single age density plot (Fig. 4C; Table 1). In very broad terms, the age distributions can be seen as bimodal, with ∼29.4% of the total diversity originating between 100 and 500 kya, and ∼32.7% of the diversity originating in a burst-like pattern between 10 and 30 kya (Fig. 4C; Table 1). We observed similar trends when the analysis was performed on cenhaps alone (Fig. 4D), indicating that cenhaps, although large and conspicuous, are not otherwise unusual.

Table 1.

Percent of pan-genome that diverged during different time intervals

graphic file with name 359tb01.jpg

Open in a new tab

The peak of coalescence times in the 10–30 kya time frame is notable for its steep flanks on both sides. On the left side of the peak, the transition from relatively few alleles dating to 30–100 kya to an abundance at 10–30 kya can be explained as a natural outcome of genetic drift in populations with finite effective population sizes (Ne) (Wright 1951; Nordborg 2004). On average, two alleles will coalesce to their most recent common ancestor after 2Ne generations. Three prior estimates of historical Ne suggest a minimum Ne for maize of ∼6000 (Beissinger et al. 2016), a decreasing Ne starting at ∼50,000 and declining to ∼1000 during domestication (Wang et al. 2017), and a decreasing Ne starting at about ∼100,000 and declining to ∼10,000 during domestication (Tittes et al. 2021). All prior analyses were carried out using short-read alignments. We carried out a fourth analysis of historic Ne using our whole-genome alignments of 26 genomes (Fig. 4E). The results suggest that Ne dropped from a high of ∼90,000 to ∼1000 during domestication (the sudden change in Ne at ∼130 kya is probably spurious [Patton et al. 2019]). We infer from our data that the Ne stabilized at about 8000 individuals for several 1000 yr (in the period 2–6 kya). Applying 2Ne to this stable population size predicts an average coalescence time of ∼16 kya, which matches the observed peak in estimated allele age at ∼16–17 kya (Fig. 4E). Relatively little haplotype diversity dates directly to the domestication period when effective population sizes were at their lowest. Only about 11.1% of the 20-kb windows (Table 1) and 25 of the 260 cenhaps diverged from each other in the recent <10 kya past.

Mutation rates are known to vary across genomes and with respect to epigenetic features (e.g., Hodgkinson and Eyre-Walker 2011; Monroe et al. 2022). In our study we used a mutation rate of 3.3 × 10−8 substitutions/bp/yr, which is based on the frequency of mutations in an upstream region of the teosinte branched1 gene that swept to fixation during a known time interval (Clark et al. 2005). Although this mutation rate is widely accepted, the authors noted that it might be as low as 2.9 × 10−8 substitutions/bp/yr. Applying the 2.9 × 10−8 value would make all age estimates 13.7% older, such that the peak at 100–500 kya would be 114–568 kya, and the peak at 10–30 kya would be 11–34 kya (the historical Ne estimates will shift to the same 13.7% extent). More direct measurements of mutation frequencies (such has been done in Arabidopsis [Monroe et al. 2022]) will be required to confirm whether these estimates are accurate for maize intergenic spaces.

Discussion

Here we describe an approach for inferring evolutionary history based on SNP diversity within intergenic spaces, and through this analysis, document megabase-scale haplotypes in areas of low recombination, including cenhaps, knobs, and the NOR. These analyses allowed us to visualize and quantify ancient diversity on a scale that was not possible in early studies (Fu and Dooner 2002; Brunner et al. 2005). We show that ∼29.4% of the maize pan-genome is ancient, originating between 100–500 kya (Table 1). These regions are structurally very different, with long regions of differential TE insertions and relatively little alignable sequence (Fig. 1C). In cenhaps there are extreme differences in CentC arrays, to the point that in some cases there is no evident collinear homology (Fig. 1D). Another ∼32.7% of the diversity emerged in a burstlike pattern 10–30 kya. This period coincides with major changes in earth's climate (Williams 2003; Leyden et al. 2013) and the arrival of humans to the Americas (Ardelean et al. 2020; Becerra-Valdivia and Higham 2020). It is possible that some of the recent diversity accumulated as a result of demographic changes associated with these environmental events. However, the inferred reduction in population size to about 8000 during the 2–6 kya period is sufficient to explain the peak in coalescence times dating to 10–30 kya.

The evolutionary trendline of the maize pan-genome, with a significant amount of ancient diversity intermingled with a concentration of coalescence times at 10–30 kya, is clearly evident in the diversity of large haplotypes around the genome. Authors of a previous study argued that the apparent overabundance of recently evolved centromere haplotypes might be an outcome of domestication and selection (Schneider et al. 2016). Our analyses indicate that cenhap coalescence time distributions closely resemble and indeed accentuate genome-wide patterns of haplotype diversity (Fig. 4C,D). It has also been suggested that centromeres might evolve by meiotic drive, a process that could cause episodic sweeps of some cenhaps over others and reduce overall cenhap diversity (Malik 2009). Although centromere drive does occur in some species and lineages, it is likely rare (Lampson and Black 2017; Finseth et al. 2021) and drive-based sweeps are not evident in our maize cenhap data.

Given the small effective population sizes during domestication (Fig. 4E), we might expect that relatively little ancient polymorphism would have survived into modern maize, yet extensive ancient diversity persists (Fig. 4C; Table 1). A likely explanation for the high levels of ancient polymorphism in maize is admixture among species and subspecies populations (Ross-Ibarra et al. 2009; Hufford et al. 2013; Chen et al. 2022). Maize is thought to have been domesticated from Zea mays ssp. parviglumis with concurrent or subsequent intercrossing with ssp. mexicana (van Heerwaarden et al. 2011; Hufford et al. 2013). Subspecies parviglumis has maintained large effective population sizes over the last 10 kya (Wang et al. 2017; Chen et al. 2022) and contains substantially more genetic diversity than modern maize (Hufford et al. 2012; Beissinger et al. 2016). Additional complete genome assemblies from multiple Zea relatives will help to clarify these relationships and the extent of gene flow among species and subspecies.

Methods

Confirmation of assembly accuracy

30× PE150 Illumina and 57× error-corrected PacBio reads from Hufford et al. (2021) were aligned to the B73 assembly to validate the quality of assembly over centromere regions. Illumina reads were aligned using BWA-MEM (v.0.7.17) (-k50 -c1000000) and filtered using SAMtools (v.1.6) (-F 2308) (Li et al. 2009; Li 2013). Error-corrected PacBio reads were aligned using minimap2 (v.2.17) (-k19 -w 10) (Li 2018). Read depth over 1-kb bins was calculated with SAMtools (v.1.19) depth, and cenhap read depth was extracted using BEDTools (v.2.26) intersect (Quinlan and Hall 2010). Cenhap domains were defined using the same coordinates throughout the paper (see section on cenhap definition below).

Genome alignment and structural variant characterization

Previous studies of the NAM lines have interpreted structural variation by aligning resequencing data to the primary B73 reference genome, using both short and long reads (Gore et al. 2009; Chia et al. 2012; Hufford et al. 2021). However, this approach fails for insertions that are larger than the read length and preferentially recovers deletions. A partial solution to this problem is the merged alignment blocks method that was used to identify structural variants with whole-genome alignments across six European flint lines (Haberer et al. 2020). Although this approach identifies simple insertions and deletions accurately, it performs poorly in regions where the reference and query differ by multiple insertions/deletions. Another approach to improve mapping and variant detection is AnchorWave, which relies on gene annotation to anchor reference and query (Song et al. 2022). Our method was designed for regions with few genes and high TE content. In these areas, nonsyntenic alignments are frequently observed due to homology among similar transposons (Supplemental Fig. S2). To remove the alignment noise, we identified syntenic regions by identifying LIS (Abouelhoda and Ohlebusch 2005; Rani and Rajpoot 2016) in a two-step procedure (Supplemental Figs. S2, S3).

The workflow consisted of three phases: (1) Perform pairwise whole-genome alignment, (2) chain aligned segments with LIS in a two-step process, where the first step identified syntenic (collinear) segments and the second step resolved locally rearranged regions, and (3) characterize structural variants through identifying alignment gaps. Refer to https://github.com/dawelab/Age_Structure/tree/master/SV-calling.

Alignment

Genome assembly and annotation files were obtained from MaizeGDB (https://maizegdb.org/NAM_project). Pairwise genome alignments were carried out with minimap2 (Li 2018) (v2.17) using parameters: -c -cx asm5 ‐‐no-kalloc ‐‐print-qname ‐‐cs=long. The alignments were then sorted according to the position in the reference sequence.

Chaining

A two-round chaining procedure was implemented to identify the longest set of anchors, where the first round identifies the optimal chain and the second round finds lower-scoring anchors to fill the gaps in the first chain (Supplemental Fig. S2). During each round, we calculated the chaining score for individual anchors, and identified nonoverlapping anchors in the global optimal path using the backtracking approach. The computation of chaining score differed between the two rounds, as the second was carried out to incorporate anchors of lower mapping quality.

The chaining score of anchor i in the first round was calculated as f(i) = max{f(j) + len(i) × log10(q(i) + 0.001) − gap(i, j)/100}, i > j > 1, where len(i) and q(i) are, respectively, the length and the mapping quality of anchor i. Gap (i,j) is the distance between anchors i and j, which was computed as abs (ix − jy), and x and y are the start and end coordinates. After score calculation, the backtracking method was used by repeatedly finding the best predecessor of anchor i. After the first round, anchors identified in the optimal chain were combined with the remaining anchors larger than 15 kb and subjected to round two, where the score calculation of anchor i was modified from step1 as f(i) = max{f(j) + len(i) − gap(i, j)/100}, i > j > 1.

Structural variant characterization

In cases where two genomes differ by independent TE insertions in the same region, there can be unalignment gaps of different sizes. This special variant structure cannot be characterized by software developed to score small variants or variants with simple junctions. To accurately characterize structural changes in both reference and query genomes, we defined these variants as pairwise unaligned regions (Supplemental Fig. S4B). Translocations and tandem duplications were inferred from alignment chains and orientation. True variants were further filtered with a 20-kb cutoff for inversions, 10 kb for tandem duplications, and 50 kb for translocations.

All genome alignment and SV data, including files with pairwise syntenically aligned regions (syn.bed files) and separate files listing tandem duplications, inversions, and translocations (sv.bed files), can be found at GitHub (https://github.com/dawelab/Age_Structure/tree/master/SV-calling/MaizeNAM_SVoutput).

Variant identification among NAM lines

To identify structural changes among 26 NAM lines, we performed 325 pairwise alignments for each chromosome and carried out chaining and SV characterization with the workflow described above. Chaining was conducted with script “chaining.py” and SV calling was accomplished with “sv_detect.py.” The number and size of variants, including unalignments, tandem duplications, and inversions, were quantified for individual genomes and plotted with custom script using karyoploteR (Gel and Serra 2017). For each pair of unaligned regions, the region in the reference was defined as a deletion, and its counterpart in the query an insertion (Supplemental Fig. S4B).

All-by-all genome alignment across the 26 lines revealed a total of ∼19 million pairwise structural variants (Supplemental Tables S1, S2), among which 22.5% were simple deletions or insertions and 77.5% showed a reciprocal unalignment between reference and query (Supplemental Figs. S4, S5). We also identified 5314 large tandem duplications (>10 kb), including segmental duplications and nested duplications (Supplemental Fig. S5). Many large inversions and duplications have sustained additional insertions and rearrangements, suggesting ancient origins.

Pan-genome analysis

Pan-genome space

We employed the all-by-all syntenic alignments to calculate the pan-genome space (Supplemental Fig. S6A). The added nonredundant genome size was calculated upon the addition of each genome, which was subsequently used as the reference to investigate the expanded genomic space. Aligned segments between the nth genome and all its predecessor genomes (n−1) were merged, and unaligned segments of the nth genome were retained. The unaligned parts of each additional line are the novel regions added to the pan-genome space. The order of NAM lines was shuffled 1000 times, and pan-genome was calculated for every case. The pipeline for pan-genome computation and permutation was implemented in script pan-genome_cal.py.

Frequency of B73-like genome space in NAM population

The frequency distribution of B73-like genomic sequences (Supplemental Fig. S6B) was calculated by quantifying the presence/absence of every locus among 25 NAM lines. The start and end coordinates of each unit are intervals between adjacent alignment breakpoints of B73. For each chromosome, the SV breakpoints were extracted and sorted by position, and adjacent breakpoints smaller than 20 bp were merged as their midpoint. Intervals between breakpoints were derived, and the occurrences of each interval were counted across NAM based on genome alignment. B73 segments present in 25 lines were represented by an allele frequency of 26, and an allele frequency of 1 depicts B73-specific regions. The above steps were conducted with script allele_frequency_cal.py. Genes and UMRs that overlap with each interval were identified with BEDTools intersect (Quinlan and Hall 2010), and subsequently quantified for every allele frequency.

Defining cenhap regions

Cenhaps are fluid within populations and their boundaries are contingent on the reference chosen and the most divergent line in the comparison. We defined cenhaps by visual inspection. We scanned haplotype alignments by eye and chose regions that appeared to correspond to the areas of most restricted recombination and rounded the coordinates at the left and right borders to the nearest 1 Mb on the B73 reference assembly (Zm-B73-REFERENCE-NAM-5.0). The boundaries chosen are rough estimates. They are not meant to imply there are discrete boundaries at these coordinates. More accurate boundaries might be identified with larger data sets and additional effort.

The coordinates used were Chr 1 (134 to 140 Mb), Chr 2 (96 to 101 Mb), Chr 3 (80 to 90 Mb), Chr 4 (102 to 112 Mb), Chr 5 (103 to 110 Mb), Chr 6 (57 to 63 Mb), Chr 7 (60 to 70 Mb), Chr 8 (46 to 51 Mb), Chr 9 (56 to 63 Mb), and Chr 10 (42 to 50 Mb). The CENH3 domains of most but not all chromosomes lie within these cenhap regions. CENH3 domains are documented in Hufford et al. (2021).

Structural comparison among repeat arrays

To measure the genetic distance of syntenic repeat arrays, we employed the dot-matrix method to perform pairwise sequence alignment for repeat arrays, and calculated pairwise distance based on the number of monomer matches between reference and query. This pipeline was carried out for the structural comparison of ten CentC arrays, ten classical knobs, and the nucleolus organizer region (NOR) across 26 NAM lines. As large knobs are intermingled with knob180 and TR-1 monomers (Liu et al. 2020; Hufford et al. 2021), we performed alignment with the dominant monomer type in the array.

Repeat array and TE identification

The coordinates of syntenic knobs, CentC, and NOR arrays were obtained from a prior study (Hufford et al. 2021). We identified CentC arrays located within 5 Mb upstream and downstream of the active centromeres (defined by CENH3 ChIP-seq [Wang et al. 2021]) for each chromosome as true centromeric arrays. Classical knobs located on 2L, 3L, 4L, 5L, 6S1, 6S2, 6L, 7L, 8L, and 9S were selected for analysis. The NOR regions are present in syntenic areas on the short arm of Chromosome 6 in all lines.

Annotated transposable elements (Ou et al. 2019; Hufford et al. 2021) located in ∼1 Mb regions of Chromosome 8 (coordinates 46.10–47.10 Mb in B73, 44.70–45.70 Mb in CML322, and 45.57–46.71 Mb in CML52) were extracted and grouped by families. The total amount of DNA annotated for each TE family and subfamily in the selected windows was calculated with BEDTools (v2.29.2) (Quinlan and Hall 2010).

Pairwise alignment via dot matrix

As minimap2 failed to align tandem repetitive areas, we employed the dot-matrix approach to perform pairwise alignments between repeat arrays (Gibbs and McIntyre 1970). The traditional dot-matrix method compares two sequences through identifying nucleotide or amino acid matches on the main diagonal. In our pipeline, repeat arrays from reference and query were regarded as two sequences, where each repeat monomer was analyzed as a single residue. To identify the monomer pairs that share a common ancestor, we aligned all monomers from the reference array to those from the query array and measured their genetic distance. A match was assigned to a monomer pair when their similarity exceeded a certain threshold, and a dot was placed in the matrix. Structural similarity between the two repeat arrays was evaluated through manually inspecting the main diagonal in the dot matrix. The coordinates for CentC, knob, and rDNA repeat arrays were obtained from Hufford et al. (2021).

To construct the dot matrix, monomer indexes from reference and query arrays were written along the two axes, where n represents the nth monomer from each array. Sequences of indexed monomers were extracted with BEDTools getfasta (v2.29.2; -nameOnly -s). Genetic distance between any monomer pairs was measured through all-by-all alignments (i × j) with BLAT (v3.5; -minIdentity=70 -maxGap=10 -minScore=0 -repMatch=2147483647). The similarity score for each monomer alignment was calculated with the Jaccard index: Len(A, B) / {Len(A) + Len(B) − Len(A, B)}, where Len(A) and Len(B) represent the lengths of monomers A and B, and Len(A, B) is the number of matched nucleotides between them. Monomer pairs with a Jaccard index above 0.98 were classified as matches and marked in the matrix. Dot matrices were plotted with R (R Core Team 2021) and structural similarity evaluated manually.

Similarity calculation and clustering

To assess the overall similarity between two repeat arrays in a quantitative manner, we measured the total number of monomer matches for each alignment, and normalized it against the length of the smaller array to account for the difference in array length. The similarity of each pair of repeat arrays among NAM was calculated and used as input to construct a correlation matrix. This correlation matrix was visualized as a network through qgraph (Epskamp et al. 2012) in R.

Divergence-time estimation with the whole-genome alignment method

Whole chromosome intergenic spaces

As the syntenic anchors represent the true common ancestry between reference and query genomes, SNPs located in these syntenic regions could be used to accurately infer the divergence time for individual aligned segments. The syntenic aligned segments in a minimap2 PAF format were identified based on coordinates derived from the synteny identification step and subjected to variant calling with paftools.js call (v2.17) using parameters: -L50 -q0 -l50.

To obtain a more accurate estimation of divergence time, we excluded genes and unmethylated regions (UMRs) in each syntenic alignment (annotated in Hufford et al. 2021) and counted SNPs in remaining areas, which are true intergenic spaces. Accordingly, the effective alignment length for each region was calculated as follows: len(syntenic aligned region) − len(union(genes + UMRs)). Divergence time for each aligned segment was further estimated with equation d/u/2, where d is the total number of SNPs over individual effective alignment length, and u is the molecular clock of 3.3 × 10−8 (Clark et al. 2005).

The reference genome was divided into 20-kb nonoverlapping windows and syntenic SNPs were projected to each window with BEDTools (v2.29.2) (Quinlan and Hall 2010). The divergence time was calculated with a molecular clock of 3.3 × 10−8 by summarizing the total SNPs against an effective alignment length in window: 20,000 − sum(len(syntenic unaligned regions)) − sum(len(union(genes + UMRs))). This approach involves aligning nonoverlapping 20-kb windows to B73, however, the effective windows could be smaller than 20 kb due to the presence of genes, UMRs, and SVs such as deletions. We also tested a broader range of window sizes, including 10, 30, 40, 50, and 100 kb to estimate the effect of window size on divergence time profiling (Supplemental Fig. S18).

To validate the genome diversification times represented by syntenic SNPs, we estimated insertion times of retroelements that differentiate the B73 and CML322 Chromosome 8 cenhaps (46–51 Mb on the B73 reference). Insertion times were estimated using a database of B73 retroelements and their insertion times (Ou et al. [2022]; data available at https://ars-usda.app.box.com/v/maizegdb-public/folder/176803757412). We used the file B73.PLATINUM.pseudomolecules-v1.fasta.mod.pass.list. In this database the insertion times were estimated by comparison of LTR sequences using a mutation rate of 1.3 × 10−8 substitutions/bp/yr, which is slower than the 3.3 × 10−8 substitutions/bp/yr used in our analysis. Therefore, the ages from the public database were multiplied by 0.39394. We cross-referenced annotated B73 retroelements with our genome alignments, identifying retroelements within coordinates that did not align to CML322. However, this automated approach was imperfect due to alignment errors over the CentC array and nested insertions of the same class. We visually inspected all retroelements in the output and removed those that were not polymorphic due to these errors. See Supplemental Table S3, which includes the original and corrected data.

Knobs

As knobs are interspersed with a variety of transposable elements (Liu et al. 2020; Hufford et al. 2021), large portions of syntenic knobs could be uniquely aligned—mostly over syntenic TEs but also including many repeat monomers. To eliminate the effect of incorrect chaining of repeat sequences, we removed SNPs in TR-1 and knob180 repeat sequences with BEDTools intersect (v2.29.2) (Quinlan and Hall 2010) and computed the divergence time of each aligned segment with SNPs located in nontandem repetitive areas.

We were not able to estimate the times of divergence for CentC arrays by this method because most embedded TEs are of the CRM class and show high homology to each other, creating erroneous alignments. Divergence times for cenhaps were estimated with the selected pericentromeric regions as described above.

Hierarchical clustering over pericentromeric regions

To investigate the relative evolutionary distance among cenhaps, we used syntenic SNPs for clustering analysis. These SNPs were obtained through the divergence time estimation step described above. The B73 coordinates of cenhap regions are as follows: Chr 1 (134 to 140 Mb), Chr 2 (96 to 101 Mb), Chr 3 (80 to 90 Mb), Chr 4 (102 to 112 Mb), Chr 5 (103 to 110 Mb), Chr 6 (57 to 63 Mb), Chr 7 (60 to 70 Mb), Chr 8 (46 to 51 Mb), Chr 9 (56 to 63 Mb), and Chr 10 (42 to 50 Mb). All SNPs projected to B73 in each cenhap interval were cataloged and used as input for distance matrix construction. This matrix has a dimension of N × M, where N represents 26 NAM lines, and M is the total number of positions in B73 where SNPs were identified between any line and the reference genome. The absence of SNPs in the matrix could be accounted for by (1) high sequence divergence, where regions cannot be aligned to call SNPs, or (2) high sequence similarity, in which case no SNPs are found over aligned areas. To differentiate the two causes, we marked unaligned segments in the matrix as NA. Pericentromeric SNPs that are shared across all lines were subjected to hierarchical clustering with scikit-learn (Pedregosa et al. 2011).

Divergence-time estimation with short-read mapping

Source of data

Paired-end Illumina data of 49 parviglumis lines from Palmar Chico in Balsas river drainage of Mexico were obtained from the NCBI BioProject (https://www.ncbi.nlm.nih.gov/bioproject/) database under accession number PRJNA616247 (SRR11448786–SRR11448838). Illumina reads of 14 parviglumis lines, TIL01 (obtained from the NCBI Sequence Read Archive [SRA; https://www.ncbi.nlm.nih.gov/sra] under accession number SRR447882), TIL02 (SRA; SRR447886), TIL03 (SRA; SRR447894–SRR447895), TIL04 (SRA; SRR447962–SRR447964), TIL05 (SRA; SRR447755–SRR447757), TIL06 (SRA; SRR447827–SRR447829), TIL07 (SRA;SRR447960–SRR447961), TIL09 (SRA; SRR447954–SRR447955), TIL10 (SRA; SRR447825–SRR447826), TIL11 (SRA; SRR5976511), TIL12 (SRA; SRR447997), TIL14 (SRA; SRR447780–SRR447782), TIL15 (SRA; SRR447859–SRR447860), and TIL17 (SRA;SRR447896–SRR447898), were from HapMap II SRA accession number SRP011907. Paired-end reads of two mexicana lines, TIL08 (SRA; SRR447933–SRR447934) and TIL25 (SRA; SRR447936–SRR5976310), were obtained from SRA accession number SRP011907, and data from two other mexicana lines (SRA; SRR7758236 and SRR7758237) were downloaded from BioProject PRJNA487810. Reads for Zea mays huehuetenangensis samples Hue2 and Hue4 were downloaded from BioProject PRJNA384363, and data from Zea diploperennis (SRA; SRR13687522) were from BioProject PRJNA700589. Paired-end data for two Tripsacum dactyloides (sister genus of Zea) lines TDD39103 (SRA; SRR447804–SRR447807) and Trip_ISU_1 (SRA; SRR7758238) were from SRA accession number SRP011907 BioProject PRJNA487810. Short-read data from the NAM lines were obtained from BioProjects PRJEB31061 and PRJEB32225.

SNP calling

Illumina reads were trimmed with Trim Galore! (v0.6.5) (https://github.com/FelixKrueger/TrimGalore) and aligned to B73 RefGen_v5 with BWA-MEM (v0.7.17). Variant calling was conducted on BAM files with a mapping quality above 20 using BCFtools (Li 2011) mpileup (v1.6; -Ou -f -C50). To reduce the effect of read mapping errors on SNP calling, sites with too low or too high read depth were removed using BCFtools filter, where the lower and upper bounds were, respectively, defined as ¼ and 4 times of the mean read depth of input BAM files. High-confidence calls were obtained by further applying a quality cutoff of 20, and homozygous SNPs were extracted with BCFtools view.

Divergence calculation and normalization

To estimate the divergence of each line from the reference with short reads, we calculated the genetic distance between each sample and reference in a fixed window. The reference genomes were divided into 20-kb nonoverlapping windows with BEDTools (v2.29.2) (Quinlan and Hall 2010). Genetic distance was measured as the proportion of intergenic SNPs over effective SNPable lengths in each window. We applied the same coverage cutoff used for SNP calling to estimate effective length, which is between ¼ and 4 times of the mean read depth. The portion of SNPable segments that overlap with genes and UMRs were removed with BEDTools (v2.29.2) to account for intergenic regions. Divergence time over each window was estimated with d/2/u, where u = 3.3 × 10−8.

Multiple Sequentially Markovian Coalescent (MSMC)

To infer the dynamics of maize effective population size over the past million years, we employed the MSMC method to analyze syntenic intergenic SNPs between the 25 NAM lines and B73. As low residual heterozygosity was identified among NAM inbreds, one haplotype was used for each line for MSMC analysis. To generate input files for msmc2 (Schiffels and Durbin 2014; Schiffels and Wang 2020), SNPs in VCF format across 25 lines were merged with BCFtools (Li [2011]; v1.6; http://samtools.github.io/bcftools) and phased with Beagle (Browning et al. 2021). Syntenic aligned regions derived from the whole-genome alignment and SV calling section between NAM and B73 were used as mappability masks to define high-confidence mapping. Phased haplotypes and mask files for 25 lines were concatenated into a single file with generate_multihetsep.py, and used as input for msmc2 (Schiffels and Wang 2020). The time segment patterning parameter was set as 5 × 4 + 25 × 2 + 5 × 4 for MSMC2 analysis and a molecular clock of 3.3 × 10−8 was used for time estimation.

Data access

The code used in this study is available at GitHub (https://github.com/dawelab/Age_Structure). SV metadata (left and right breakpoint coordinates of each pairwise comparison in text file format) are available at GitHub (https://github.com/dawelab/Age_Structure/tree/master/SV-calling/MaizeNAM_SVoutput) and as Supplemental Material. The source code without SV metadata is also available as Supplemental Data.

Supplementary Material

Supplemental Material
supp_33_3_359__DC1.html (1.9KB, html)

Acknowledgments

We thank R. Piri for carrying out the work necessary to interpret sequence assembly accuracy over cenhap regions, for preparing Supplemental Figure S1, and for her patient help with GitHub. We also thank J. Leebens-Mack who provided encouragement, comments, and edits to the final manuscript, and M. Hufford, J. Gent, M. Stitzer, D. Wills, M. Brady, and R. Piri for comments to the manuscript. This work was supported by grants from the National Science Foundation, Division of Integrative Organismal Systems (No. IOS-174400 and No. IOS-2040218).

Footnotes

[Supplemental material is available for this article.]

Article published online before print. Article, supplemental material, and publication date are at https://www.genome.org/cgi/doi/10.1101/gr.276705.122.

Competing interest statement

The authors declare no competing interests.

References

  1. Abouelhoda MI, Ohlebusch E. 2005. Chaining algorithms for multiple genome comparison. J Discrete Algorithms 3: 321–341. 10.1016/j.jda.2004.08.011 [DOI] [Google Scholar]
  2. Albert PS, Gao Z, Danilova TV, Birchler JA. 2010. Diversity of chromosomal karyotypes in maize and its relatives. Cytogenet Genome Res 129: 6–16. 10.1159/000314342 [DOI] [PubMed] [Google Scholar]
  3. Altemose N, Logsdon GA, Bzikadze AV, Sidhwani P, Langley SA, Caldas GV, Hoyt SJ, Uralsky L, Ryabov FD, Shew CJ, et al. 2022. Complete genomic and epigenetic maps of human centromeres. Science 376: eabl4178. 10.1126/science.abl4178 [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Andorf C, Beavis WD, Hufford M, Smith S, Suza WP, Wang K, Woodhouse M, Yu J, Lübberstedt T. 2019. Technological advances in maize breeding: past, present and future. Theor Appl Genet 132: 817–849. 10.1007/s00122-019-03306-3 [DOI] [PubMed] [Google Scholar]
  5. Ardelean CF, Becerra-Valdivia L, Pedersen MW, Schwenninger J-L, Oviatt CG, Macías-Quintero JI, Arroyo-Cabrales J, Sikora M, Ocampo-Díaz YZE, Rubio-Cisneros II, et al. 2020. Evidence of human occupation in Mexico around the last glacial maximum. Nature 584: 87–92. 10.1038/s41586-020-2509-0 [DOI] [PubMed] [Google Scholar]
  6. Becerra-Valdivia L, Higham T. 2020. The timing and effect of the earliest human arrivals in North America. Nature 584: 93–97. 10.1038/s41586-020-2491-6 [DOI] [PubMed] [Google Scholar]
  7. Beissinger TM, Wang L, Crosby K, Durvasula A, Hufford MB, Ross-Ibarra J. 2016. Recent demography drives changes in linked selection across the maize genome. Nat Plants 2: 16084. 10.1038/nplants.2016.84 [DOI] [PubMed] [Google Scholar]
  8. Browning BL, Tian X, Zhou Y, Browning SR. 2021. Fast two-stage phasing of large-scale sequence data. Am J Hum Genet 108: 1880–1890. 10.1016/j.ajhg.2021.08.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Brunner S, Fengler K, Morgante M, Tingey S, Rafalski A. 2005. Evolution of DNA sequence nonhomologies among maize inbreds. Plant Cell 17: 343–360. 10.1105/tpc.104.025627 [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Calfee E, Gates D, Lorant A, Perkins MT, Coop G, Ross-Ibarra J. 2021. Selective sorting of ancestral introgression in maize and teosinte along an elevational cline. PLoS Genet 17: e1009810. 10.1371/journal.pgen.1009810 [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Chen L, Luo J, Jin M, Yang N, Liu X, Peng Y, Li W, Phillips A, Cameron B, Bernal JS, et al. 2022. Genome sequencing reveals evidence of adaptive variation in the genus Zea. Nat Genet 54: 1736–1745. 10.1038/s41588-022-01184-y [DOI] [PubMed] [Google Scholar]
  12. Chia J-M, Song C, Bradbury PJ, Costich D, de Leon N, Doebley J, Elshire RJ, Gaut B, Geller L, Glaubitz JC, et al. 2012. Maize HapMap2 identifies extant variation from a genome in flux. Nat Genet 44: 803–807. 10.1038/ng.2313 [DOI] [PubMed] [Google Scholar]
  13. Choi K, Zhao X, Tock AJ, Lambing C, Underwood CJ, Hardcastle TJ, Serra H, Kim J, Cho HS, Kim J, et al. 2018. Nucleosomes and DNA methylation shape meiotic DSB frequency in Arabidopsis thaliana transposons and gene regulatory regions. Genome Res 28: 532–546. 10.1101/gr.225599.117 [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Clark RM, Linton E, Messing J, Doebley JF. 2004. Pattern of diversity in the genomic region near the maize domestication gene tb1. Proc Natl Acad Sci 101: 700–707. 10.1073/pnas.2237049100 [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Clark RM, Tavaré S, Doebley J. 2005. Estimating a nucleotide substitution rate for maize from polymorphism at a major domestication locus. Mol Biol Evol 22: 2304–2312. 10.1093/molbev/msi228 [DOI] [PubMed] [Google Scholar]
  16. Dawe RK, Lowry EG, Gent JI, Stitzer MC, Swentowsky KW, Higgins DM, Ross-Ibarra J, Wallace JG, Kanizay LB, Alabady M, et al. 2018. A kinesin-14 motor activates neocentromeres to promote meiotic drive in maize. Cell 173: 839–850.e18. 10.1016/j.cell.2018.03.009 [DOI] [PubMed] [Google Scholar]
  17. Doebley J. 2004. The genetics of maize evolution. Annu Rev Genet 38: 37–59. 10.1146/annurev.genet.38.072902.092425 [DOI] [PubMed] [Google Scholar]
  18. Epskamp S, Cramer AOJ, Waldorp LJ, Schmittmann VD, Borsboom D. 2012. qgraph: network visualizations of relationships in psychometric data. J Stat Softw 48: 1–18. 10.18637/jss.v048.i04 [DOI] [Google Scholar]
  19. Finseth FR, Nelson TC, Fishman L. 2021. Selfish chromosomal drive shapes recent centromeric histone evolution in monkeyflowers. PLoS Genet 17: e1009418. 10.1371/journal.pgen.1009418 [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Fu H, Dooner HK. 2002. Intraspecific violation of genetic colinearity and its implications in maize. Proc Natl Acad Sci 99: 9573–9578. 10.1073/pnas.132259199 [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Gel B, Serra E. 2017. karyoploteR: an R/Bioconductor package to plot customizable genomes displaying arbitrary data. Bioinformatics 33: 3088–3090. 10.1093/bioinformatics/btx346 [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Gent JI, Wang N, Dawe RK. 2017. Stable centromere positioning in diverse sequence contexts of complex and satellite centromeres of maize and wild relatives. Genome Biol 18: 121. 10.1186/s13059-017-1249-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Ghaffari R, Cannon EKS, Kanizay LB, Lawrence CJ, Dawe RK. 2013. Maize chromosomal knobs are located in gene-dense areas and suppress local recombination. Chromosoma 122: 67–75. 10.1007/s00412-012-0391-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Gibbs AJ, McIntyre GA. 1970. The diagram, a method for comparing sequences. Its use with amino acid and nucleotide sequences. Eur J Biochem 16: 1–11. 10.1111/j.1432-1033.1970.tb01046.x [DOI] [PubMed] [Google Scholar]
  25. Gore MA, Chia J-M, Elshire RJ, Sun Q, Ersoz ES, Hurwitz BL, Peiffer JA, McMullen MD, Grills GS, Ross-Ibarra J, et al. 2009. A first-generation haplotype map of maize. Science 326: 1115–1117. 10.1126/science.1177837 [DOI] [PubMed] [Google Scholar]
  26. Haberer G, Kamal N, Bauer E, Gundlach H, Fischer I, Seidel MA, Spannagl M, Marcon C, Ruban A, Urbany C, et al. 2020. European maize genomes highlight intraspecies variation in repeat and gene content. Nat Genet 52: 950–957. 10.1038/s41588-020-0671-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Hilton H, Gaut BS. 1998. Speciation and domestication in maize and its wild relatives: evidence from the globulin-1 gene. Genetics 150: 863–872. 10.1093/genetics/150.2.863 [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Hodgkinson A, Eyre-Walker A. 2011. Variation in the mutation rate across mammalian genomes. Nat Rev Genet 12: 756–766. 10.1038/nrg3098 [DOI] [PubMed] [Google Scholar]
  29. Huang Y, Huang W, Meng Z, Braz GT, Li Y, Wang K, Wang H, Lai J, Jiang J, Dong Z, et al. 2021. Megabase-scale presence-absence variation with Tripsacum origin was under selection during maize domestication and adaptation. Genome Biol 22: 237. 10.1186/s13059-021-02448-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Hufford MB, Xu X, van Heerwaarden J, Pyhäjärvi T, Chia J-M, Cartwright RA, Elshire RJ, Glaubitz JC, Guill KE, Kaeppler SM, et al. 2012. Comparative population genomics of maize domestication and improvement. Nat Genet 44: 808–811. 10.1038/ng.2309 [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Hufford MB, Lubinksy P, Pyhäjärvi T, Devengenzo MT, Ellstrand NC, Ross-Ibarra J. 2013. The genomic signature of crop-wild introgression in maize. PLoS Genet 9: e1003477. 10.1371/journal.pgen.1003477 [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Hufford MB, Seetharam AS, Woodhouse MR, Chougule KM, Ou S, Liu J, Ricci WA, Guo T, Olson A, Qiu Y, et al. 2021. De novo assembly, annotation, and comparative analysis of 26 diverse maize genomes. Science 373: 655–662. 10.1126/science.abg5289 [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Lahn BT, Page DC. 1999. Four evolutionary strata on the human X chromosome. Science 286: 964–967. 10.1126/science.286.5441.964 [DOI] [PubMed] [Google Scholar]
  34. Lampson MA, Black BE. 2017. Cellular and molecular mechanisms of centromere drive. Cold Spring Harb Symp Quant Biol 82: 249–257. 10.1101/sqb.2017.82.034298 [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Langley SA, Miga KH, Karpen GH, Langley CH. 2019. Haplotypes spanning centromeric regions reveal persistence of large blocks of archaic DNA. eLife 8: e42989. 10.7554/eLife.42989 [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Leyden BW, Brenner M, Hodell DA, Curtis JH. 2013. Late pleistocene climate in the central American lowlands. In Climate change in continental isotopic records (ed. Swart PK, et al.), pp. 165–178. American Geophysical Union, Washington, DC. [Google Scholar]
  37. Li H. 2011. A statistical framework for SNP calling, mutation discovery, association mapping and population genetical parameter estimation from sequencing data. Bioinformatics 27: 2987–2993. 10.1093/bioinformatics/btr509 [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Li H. 2013. Aligning sequence reads, clone sequences and assembly contigs with BWA-MEM. arXiv:1303.3997 [q-bio.GN]. http://arxiv.org/abs/1303.3997
  39. Li H. 2018. Minimap2: pairwise alignment for nucleotide sequences. Bioinformatics 34: 3094–3100. 10.1093/bioinformatics/bty191 [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Li H, Handsaker B, Wysoker A, Fennell T, Ruan J, Homer N, Marth G, Abecasis G, Durbin R, 1000 Genome Project Data Processing Subgroup. 2009. The Sequence Alignment/Map format and SAMtools. Bioinformatics 25: 2078–2079. 10.1093/bioinformatics/btp352 [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Liu S, Yeh C-T, Ji T, Ying K, Wu H, Tang HM, Fu Y, Nettleton D, Schnable PS. 2009. Mu transposon insertion sites and meiotic recombination events co-localize with epigenetic marks for open chromatin across the maize genome. PLoS Genet 5: e1000733. 10.1371/journal.pgen.1000733 [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Liu J, Seetharam AS, Chougule K, Ou S, Swentowsky KW, Gent JI, Llaca V, Woodhouse MR, Manchanda N, Presting GG, et al. 2020. Gapless assembly of maize chromosomes using long-read technologies. Genome Biol 21: 121. 10.1186/s13059-020-02029-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Lynch M, Ackerman MS, Gout J-F, Long H, Sung W, Thomas WK, Foster PL. 2016. Genetic drift, selection and the evolution of the mutation rate. Nat Rev Genet 17: 704–714. 10.1038/nrg.2016.104 [DOI] [PubMed] [Google Scholar]
  44. Malik HS. 2009. The centromere-drive hypothesis: a simple basis for centromere complexity. Prog Mol Subcell Biol 48: 33–52. 10.1007/978-3-642-00182-6_2 [DOI] [PubMed] [Google Scholar]
  45. Matsuoka Y, Vigouroux Y, Goodman MM, Sanchez GJ, Buckler E, Doebley J. 2002. A single domestication for maize shown by multilocus microsatellite genotyping. Proc Natl Acad Sci 99: 6080–6084. 10.1073/pnas.052125199 [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. McMullen MD, Kresovich S, Villeda HS, Bradbury P, Li H, Sun Q, Flint-Garcia S, Thornsberry J, Acharya C, Bottoms C, et al. 2009. Genetic properties of the maize nested association mapping population. Science 325: 737–740. 10.1126/science.1174320 [DOI] [PubMed] [Google Scholar]
  47. Monroe JG, Srikant T, Carbonell-Bejerano P, Becker C, Lensink M, Exposito-Alonso M, Klein M, Hildebrandt J, Neumann M, Kliebenstein D, et al. 2022. Mutation bias reflects natural selection in Arabidopsis thaliana. Nature 602: 101–105. 10.1038/s41586-021-04269-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Nambiar M, Smith GR. 2016. Repression of harmful meiotic recombination in centromeric regions. Semin Cell Dev Biol 54: 188–197. 10.1016/j.semcdb.2016.01.042 [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Nordborg M. 2004. Coalescent theory. In Handbook of statistical genetics (ed. Balding DJ, et al. ). John Wiley & Sons, Ltd, Chichester. [Google Scholar]
  50. Nurk S, Koren S, Rhie A, Rautiainen M, Bzikadze AV, Mikheenko A, Vollger MR, Altemose N, Uralsky L, Gershman A, et al. 2022. The complete sequence of a human genome. Science 376: 44–53. 10.1126/science.abj6987 [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Ou S, Su W, Liao Y, Chougule K, Agda JRA, Hellinga AJ, Lugo CSB, Elliott TA, Ware D, Peterson T, et al. 2019. Benchmarking transposable element annotation methods for creation of a streamlined, comprehensive pipeline. Genome Biol 20: 275. 10.1186/s13059-019-1905-y [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Ou S, Collins T, Qiu Y, Seetharam AS, Menard CC, Manchanda N, Gent JI, Schatz MC, Anderson SN, Hufford MB, et al. 2022. Differences in activity and stability drive transposable element variation in tropical and temperate maize. bioRxiv 10.1101/2022.10.09.511471v1 [DOI] [PMC free article] [PubMed]
  53. Patton AH, Margres MJ, Stahlke AR, Hendricks S, Lewallen K, Hamede RK, Ruiz-Aravena M, Ryder O, McCallum HI, Jones ME, et al. 2019. Contemporary demographic reconstruction methods are robust to genome assembly quality: a case study in Tasmanian devils. Mol Biol Evol 36: 2906–2921. 10.1093/molbev/msz191 [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Prettenhofer P, Weiss R, Dubourg V, et al. 2011. Scikit-learn: machine learning in Python. J Mach Learn Res 12: 2825–2830. [Google Scholar]
  55. Piperno DR, Ranere AJ, Holst I, Iriarte J, Dickau R. 2009. Starch grain and phytolith evidence for early ninth millennium B.P. maize from the Central Balsas River Valley, Mexico. Proc Natl Acad Sci 106: 5019–5024. 10.1073/pnas.0812525106 [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Quinlan AR, Hall IM. 2010. BEDTools: a flexible suite of utilities for comparing genomic features. Bioinformatics 26: 841–842. 10.1093/bioinformatics/btq033 [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Rani S, Rajpoot DS. 2016. LIS using backtracking and branch-and-bound approaches. CSI Trans ICT 4: 87–93. 10.1007/s40012-016-0108-x [DOI] [Google Scholar]
  58. R Core Team. 2021. R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna. https://www.R-project.org/. [Google Scholar]
  59. Ross-Ibarra J, Tenaillon M, Gaut BS. 2009. Historical divergence and gene flow in the genus Zea. Genetics 181: 1399–1413. 10.1534/genetics.108.097238 [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Sanmiguel P, Bennetzen JL. 1998. Evidence that a recent increase in maize genome size was caused by the massive amplification of intergene retrotransposons. Ann Bot 82: 37–44. 10.1006/anbo.1998.0746 [DOI] [Google Scholar]
  61. SanMiguel P, Gaut BS, Tikhonov A, Nakajima Y, Bennetzen JL. 1998. The paleontology of intergene retrotransposons of maize. Nat Genet 20: 43–45. 10.1038/1695 [DOI] [PubMed] [Google Scholar]
  62. Schiffels S, Durbin R. 2014. Inferring human population size and separation history from multiple genome sequences. Nat Genet 46: 919–925. 10.1038/ng.3015 [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Schiffels S, Wang K. 2020. MSMC and MSMC2: the Multiple Sequentially Markovian Coalescent. Methods Mol Biol 2090: 147–166. 10.1007/978-1-0716-0199-0_7 [DOI] [PubMed] [Google Scholar]
  64. Schneider KL, Xie Z, Wolfgruber TK, Presting GG. 2016. Inbreeding drives maize centromere evolution. Proc Natl Acad Sci 113: E987–E996. 10.1073/pnas.1522008113 [DOI] [PMC free article] [PubMed] [Google Scholar]
  65. Shi J, Wolf SE, Burke JM, Presting GG, Ross-Ibarra J, Dawe RK. 2010. Widespread gene conversion in centromere cores. PLoS Biol 8: e1000327. 10.1371/journal.pbio.1000327 [DOI] [PMC free article] [PubMed] [Google Scholar]
  66. Song B, Marco-Sola S, Moreto M, Johnson L, Buckler ES, Stitzer MC. 2022. AnchorWave: sensitive alignment of genomes with high sequence diversity, extensive structural polymorphism, and whole-genome duplication. Proc Natl Acad Sci 119: e2113075119. 10.1073/pnas.2113075119 [DOI] [PMC free article] [PubMed] [Google Scholar]
  67. Sun S, Zhou Y, Chen J, Shi J, Zhao H, Zhao H, Song W, Zhang M, Cui Y, Dong X, et al. 2018. Extensive intraspecific gene order and gene structural variations between Mo17 and other maize genomes. Nat Genet 50: 1289–1295. 10.1038/s41588-018-0182-0 [DOI] [PubMed] [Google Scholar]
  68. Swentowsky KW, Gent JI, Lowry EG, Schubert V, Ran X, Tseng K-F, Harkess AE, Qiu W, Dawe RK. 2020. Distinct kinesin motors drive two types of maize neocentromeres. Genes Dev 34: 1239–1251. 10.1101/gad.340679.120 [DOI] [PMC free article] [PubMed] [Google Scholar]
  69. Tenaillon MI, U'Ren J, Tenaillon O, Gaut BS. 2004. Selection versus demography: a multilocus investigation of the domestication process in maize. Mol Biol Evol 21: 1214–1225. 10.1093/molbev/msh102 [DOI] [PubMed] [Google Scholar]
  70. Tittes S, Lorant A, McGinty S, Doebley JF, Holland JB, de Jesus Sánchez-González J, Seetharam A, Tenaillon M, Ross-Ibarra J. 2021. Not so local: the population genetics of convergent adaptation in maize and teosinte. bioRxiv 10.1101/2021.09.09.459637v1 [DOI]
  71. van Heerwaarden J, Doebley J, Briggs WH, Glaubitz JC, Goodman MM, de Jesus Sanchez Gonzalez J, Ross-Ibarra J. 2011. Genetic signals of origin, spread, and introgression in a large sample of maize landraces. Proc Natl Acad Sci 108: 1088–1092. 10.1073/pnas.1013011108 [DOI] [PMC free article] [PubMed] [Google Scholar]
  72. Wang L, Beissinger TM, Lorant A, Ross-Ibarra C, Ross-Ibarra J, Hufford MB. 2017. The interplay of demography and selection during maize domestication and expansion. Genome Biol 18: 215. 10.1186/s13059-017-1346-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
  73. Wang N, Liu J, Ricci WA, Gent JI, Dawe RK. 2021. Maize centromeric chromatin scales with changes in genome size. Genetics 217: iyab020. 10.1093/genetics/iyab020 [DOI] [PMC free article] [PubMed] [Google Scholar]
  74. Williams JW. 2003. Variations in tree cover in North America since the last glacial maximum. Glob Planet Change 35: 1–23. 10.1016/S0921-8181(02)00088-7 [DOI] [Google Scholar]
  75. Wright S. 1951. The genetical structure of populations. Ann Eugen 15: 323–354. 10.1111/j.1469-1809.1949.tb02451.x [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplemental Material
supp_33_3_359__DC1.html (1.9KB, html)
supp_gr.276705.122_Supplemental_Figures.pdf (49.7MB, pdf)
supp_gr.276705.122_Supplemental_Tables.docx (114.9KB, docx)
supp_gr.276705.122_SUPP_AgeStructure.zip (194.6KB, zip)
supp_gr.276705.122_SUPP_metadata_Chr1.zip (85.9MB, zip)
supp_gr.276705.122_SUPP_metadata_Chr2.zip (61.8MB, zip)
supp_gr.276705.122_SUPP_metadata_Chr3.zip (58.1MB, zip)
supp_gr.276705.122_SUPP_metadata_Chr4.zip (60.9MB, zip)
supp_gr.276705.122_SUPP_metadata_Chr5.zip (53.3MB, zip)
supp_gr.276705.122_SUPP_metadata_Chr6.zip (43.4MB, zip)
supp_gr.276705.122_SUPP_metadata_Chr7.zip (43.9MB, zip)
supp_gr.276705.122_SUPP_metadata_Chr8.zip (45.1MB, zip)
supp_gr.276705.122_SUPP_metadata_Chr9.zip (43.2MB, zip)
supp_gr.276705.122_SUPP_metadata_Chr10.zip (36.1MB, zip)

Articles from Genome Research are provided here courtesy of Cold Spring Harbor Laboratory Press

RESOURCES