Abstract
Cooperativity is a hallmark of protein folding, but the thermodynamic origins of cooperativity are difficult to quantify. Tandem repeat proteins provide a unique experimental system to quantify cooperativity, due to their internal symmetry and their tolerance to deletion, extension, and in some cases fragmentation into single repeats. Analysis of repeat proteins of different lengths with nearest-neighbor “Ising” models provides values for repeat folding (ΔGi) and inter-repeat coupling (ΔGi-1,i). Here we review the architecture of repeat proteins, and classify them in terms of ΔGi and ΔGi-1,i; this classification scheme groups repeat proteins according to their degree of cooperativity. We then present various statistical thermodynamic models, based on the one-dimensional Ising model, for analysis of different classes repeat proteins. We use these models to analyze data for highly and moderately cooperative and non-cooperative repeat proteins, and relate their fitted parameters to overall structural features.
Keywords: Repeat protein, Ising model, cooperativity, statistical thermodynamics, protein folding
Cooperativity is a defining feature of protein folding. Although the native states of proteins are structurally complex, many single-domain proteins, especially those less than 150 residues, fold in a concerted reaction in which distant regions of the polypeptide are coupled. If one segment of polypeptide chain is folded, a second segment is likely to be folded regardless of whether the two segments of the protein chain are close together or far apart. This cooperativity is likely to be an important property for biology, because it suppresses partly folded states which are prone to aggregation and may lead to pathological states. Cooperativity is also important for experimental biophysicists as it allows very simple two-state models to be used to analyze equilibrium protein folding data and extract energetic features of folding such as free energies, enthalpies, and heat capacities of folding.
However, this two-state folding mechanism makes it challenging to quantify folding cooperativity (and protein energy landscapes in general) in energetic terms. A quantitative molecular description of cooperativity would include relative free energies of partly folded states and the interaction or “coupling” energies between elements of structure. If partly folded states are not populated, these free energies cannot be experimentally quantified1. By its nature, cooperativity hides itself from view.
In the past few decades, protein families have been identified with architectures that facilitate quantification of cooperativity. These “tandem repeat proteins” are composed of two or (usually) more of the same sequence motif (or “repeat”) repeated in close proximity. Different families of repeat proteins show a broad range of repeat sizes, structures, and extent of long-range ordering. Many (but not all) of these proteins exhibit cooperativity as a result of thermodynamic coupling between repeats. Even when these repeats are very strongly coupled (i.e., when cooperativity is very high), cooperativity can be quantified as long as the number of repeats in the array can be varied.
This review will describe tandem repeat proteins and how they can be used to quantify cooperativity in protein folding. After introducing a useful thermodynamic classification scheme for tandem repeat proteins based on repeat stabilities and interaction energies, we will highlight sequence and structural features of various tandem repeat proteins. We will then introduce different nearest-neighbor models for quantifying cooperativity in repeat protein folding. These models are variations of the one-dimensional Ising model, which was developed a century ago to analyze the statistical thermodynamics of magnetization (19, 8). We will then present results from the literature, applying nearest-neighbor modeling to analyze the unfolding of different types of tandem repeat proteins to quantify intrinsic and nearest-neighbor coupling energies, and will compare cooperativities for different types of tandem repeat arrays.
1. TANDEM REPEAT PROTEINS
Proteins have long been known to contain direct sequence repeats. Two decades ago, a survey of genomes revealed that 14 percent of protein coding sequences contained a repeated sequence motif, and that repeats are enriched in eukaryotes (26). A more recent survey extended this study, and showed correlations between tandem sequence repeats, protein length, and intrinsic disorder (11).
Although structure determination of tandemly repeated protein domains can be challenging, especially when repeats are connected by flexible linkers, a large number of crystal structures of tandem repeat proteins have been determined in the last two decades. These structures have been surveyed by Kajava (21, 22), who developed a system for categorizing tandem repeat proteins based on repeat length, sequence, and structural features. Of particular interest to this review are the two classes of repeat proteins (classes III and V) that are unimolecular and have roughly linear (i.e., not circular or closed) structures. These two classes are distinguished by whether or not the repeats fold independently—a distinction that is not always easy to make from structural (rather than thermodynamic) analysis.
1.1. A thermodynamic classification of linear repeat proteins
Here we will expand this definition, focusing not only on whether repeats can fold independently, but also whether adjacent repeats stabilize (or in principle, destabilize) one another. We will use ΔGi to represent the free energy of folding of an individual repeat (for autonomously stable repeats, ΔGi < 0)2, and ΔGi-1,i to represent the free energy of coupling with its immediate N-terminal neighbor (for stabilizing interfaces, ΔGi-1,i < 0). From this bipartite definition, three useful classes emerge (Figure 1). On one end of the spectrum are tandem repeat proteins where the repeats fold autonomously (ΔGi < 0) and are uncoupled from their neighbors (ΔGi-1,i > 0). Proteins in this class, which we refer to as “fully-autonomous repeat proteins” (FARPs), should adopt “beads on a string” structures, corresponding to Kajava’s class V. On the other end of the spectrum are proteins where the repeats cannot fold autonomously (ΔGi > 0), requiring favorable coupling with their neighbors (ΔGi-1,i < 0) to drive their folding. Proteins in this class, which we refer to as “nonautonomous repeat proteins” (NARPs), should adopt rigid elongated structures (rods, arcs, or superhelices), corresponding to Kajava’s class III.
Figure 1. A thermodynamic classification of linear repeat proteins.
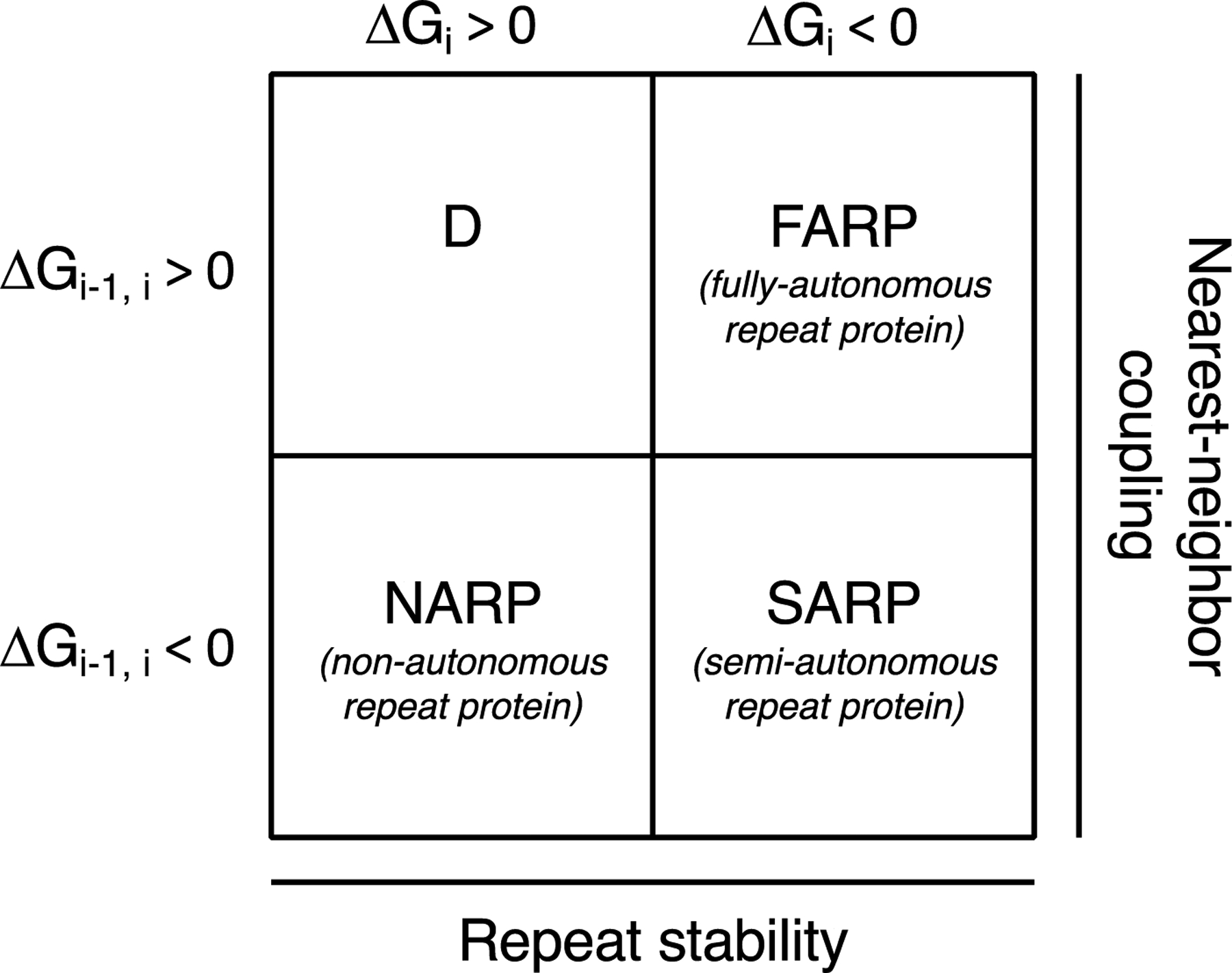
Using the sign of the two Ising energy terms as classifiers, four groups of tandem repeat proteins are generated. Non-autonomous repeat proteins have unstable repeats (ΔGi > 0) but stable interfaces (ΔGi-1,i < 0). Fully-autonomous repeat proteins have stable repeats (ΔGi < 0) but unstable interfaces (ΔGi-1,i > 0). Semi-autonomous repeat proteins have stable repeats and interfaces (ΔGi, ΔGi-1,i < 0). A fourth group, with unstable repeats and interfaces (ΔGi, ΔGi-1,i > 0) would not adopt a folded structure for any number of repeats.
The bipartite definition in Figure 1 generates two additional classes of linear repeat proteins. In one, repeats do not fold autonomously, and they are uncoupled from their neighbors (ΔGi > 0, ΔGi-1,i ≥ 0). This combination of free energies describes an intrinsically disordered polypeptide, but does not provide a means to study folding and cooperativity. However, the fourth class, where repeats fold autonomously and are favorably coupled to their neighbors (ΔGi < 0, ΔGi-1,i < 0), provides a rich opportunity to explore cooperativity in folding, as will be discussed below. These proteins, which we refer to as “semiautonomous repeat proteins” (SARPs), should also adopt rigid elongated structures. In a sense, SARPs are part way in between Kajava’s class III (exhibiting coupling between repeats) and class V (where Kajava classified them since individual spectrin repeats can fold in isolation).
1.2. Examples of proteins composed of tandem folded repeats.
Here we will describe the general properties of tandem repeat proteins that are amenable to nearest-neighbor analysis. These proteins are composed of folded repeats and have no obvious non-nearest neighbor interactions (which excludes globular and closed structures like TIM barrels). Some repeat proteins that match these criteria compiled in Table 1, along with some relevant features extracted from the Pfam database (12). Lengths of repeats selected in Table 1 range from around 20 to 100 residues. Most of these repeat protein families are represented by a large number of sequences (often in the tens of thousands), permitting precise bioinformatics analysis and sequence-based protein engineering. Within each type of repeat protein, sequences of repeats are quite variable, with pairwise identities typically in the low 20 percent range. This variability provides a rich source of variation to connect sequence and structural features to nearest-neighbor energy terms, yet conservation is adequate to create sequences with identical repeats if required for analysis (see section 3.2).
Table 1.
Tandem repeat protein families with large available alignmentsa
| Repeat name | Pfam familiesb | Median lengthb, c | # Unique sequencesb, c | Percent identityb, c | Taxonomy |
|---|---|---|---|---|---|
| Ankyrin repeat | Ank*, Ank_2, Ank_3, Ank_4, Ank_5 | 33 | ≥ 10,990 | 23.9 | Mostly eukarya, but also found in bacteria |
| Armadillo repeat | Arm*, Arm_2 | 41 | ≥ 23,055 | 22.0 | Eukarya |
| Cysteine rich repeat | Cys_rich_FGFR | 58 | 3588 | 19.5 | Metazoa, viridiplantae, and bacteria, mainly proteobacteria |
| HEAT repeat | HEAT*, HEAT_2, HEAT_EZ, HEAT_PDF | 31 | ≥ 2972 | 24.3 | Eukarya and Bacteria |
| Immunoglobulin domaind | C1-set, C2-set, C2-set_2, ig, Ig_2, Ig_3, Ig_7, Ig_C17orf99, I-set*, Izumo-Ig, Titin_Ig-rpts, V-set | 89 | ≥ 95,473 | 18.0 | Metazoa |
| Leucine-Rich Repeats (LRR) | LRR, LRR_2, LRR_3, LRR_4, LRR_5, LRR_6*, LRR_8, LRR_9, LRR_10, LRR_11, LRR_12, LRV | 24 | ≥ 57,589 | 25.0 | Mostly eukarya, but also found in bacteria |
| Membrane Occupation and Recognition repeat (MORN) | MORN* MORN_2 | 23 | ≥ 41,151 | 28.9 | Mostly eukarya, but also found in bacteria and viruses |
| Nebulin repeat | Nebulin | 28 | 5545 | 28.2 | Metazoa |
| Pentatricopeptide repeat (PPR) | PPR*, PPR_1, PPR_2, PPR_3 PPR_long | 30 | ≥ 127,520 | 27.8 | Streptophyta and fungi |
| Pumilio-family repeat (PUF) | PUF | 34 | 21,881 | 18.2 | Eukarya |
| Spectrin | Spectrin | 105 | 27,021 | 14.9 | Metazoa |
| Sushi | Sushi | 56 | 38,166 | 21.5 | Metazoa |
| TAL Effector (TALE) | TAL_effector | 34 | 308 | 57.3 | Proteobacteria |
| Tetratricopeptide repeat (TPR) | TPR_1 - TPR_12, TPR_14 - TPR_22, TPR_8* | 33 | ≥ 50,318 | 16.4 | Mostly eukarya and bacteria, and some archaea |
Data are from Pfam version 33.1 (May 2020). Analysis is restricted to families with only one repeat per motif; families two or more repeats per motif, e.g., Ank_2, were excluded from analysis.
For repeat types with multiple different Pfam families, the numbers of sequences and percent identities were calculated using the family with the largest number of sequences (marked with an asterisk).
Copies of sequences that were 100% identical were removed.
Only immunoglobulin domain families that contain tandem Ig repeats are included in this analysis.
Some structures of repeat proteins are given in Figure 2. Ankyrin repeats are rather small helical repeats that form extensive interfaces with their neighbors (16, 30), placing them in Kajava’s class III. Spectrin repeats are much larger helical repeats that form comparatively small interfaces with their neighbors (38, 18), placing them in Kajava’s class V; as has been noted extensively, adjacent spectrin repeats share a single continuous α-helix, which may couple adjacent repeats. Immunoglobulin repeats of some monomeric proteins such as titin are globular β-sheet domains that form elongated structures with limited nearest-neighbor contacts, suggesting largely autonomous and independent folding (10). Like spectrin repeats, the IgG binding repeats (E-, D-, A-, B-, and C-domains) of protein A fold into three-helix bundles (35); SAXS studies indicate that tandem B-domain (BdpA) repeats are structurally uncorrelated, and are best described by an excluded volume pearl necklace model (9).
Figure 2. Tandem repeat proteins structures.
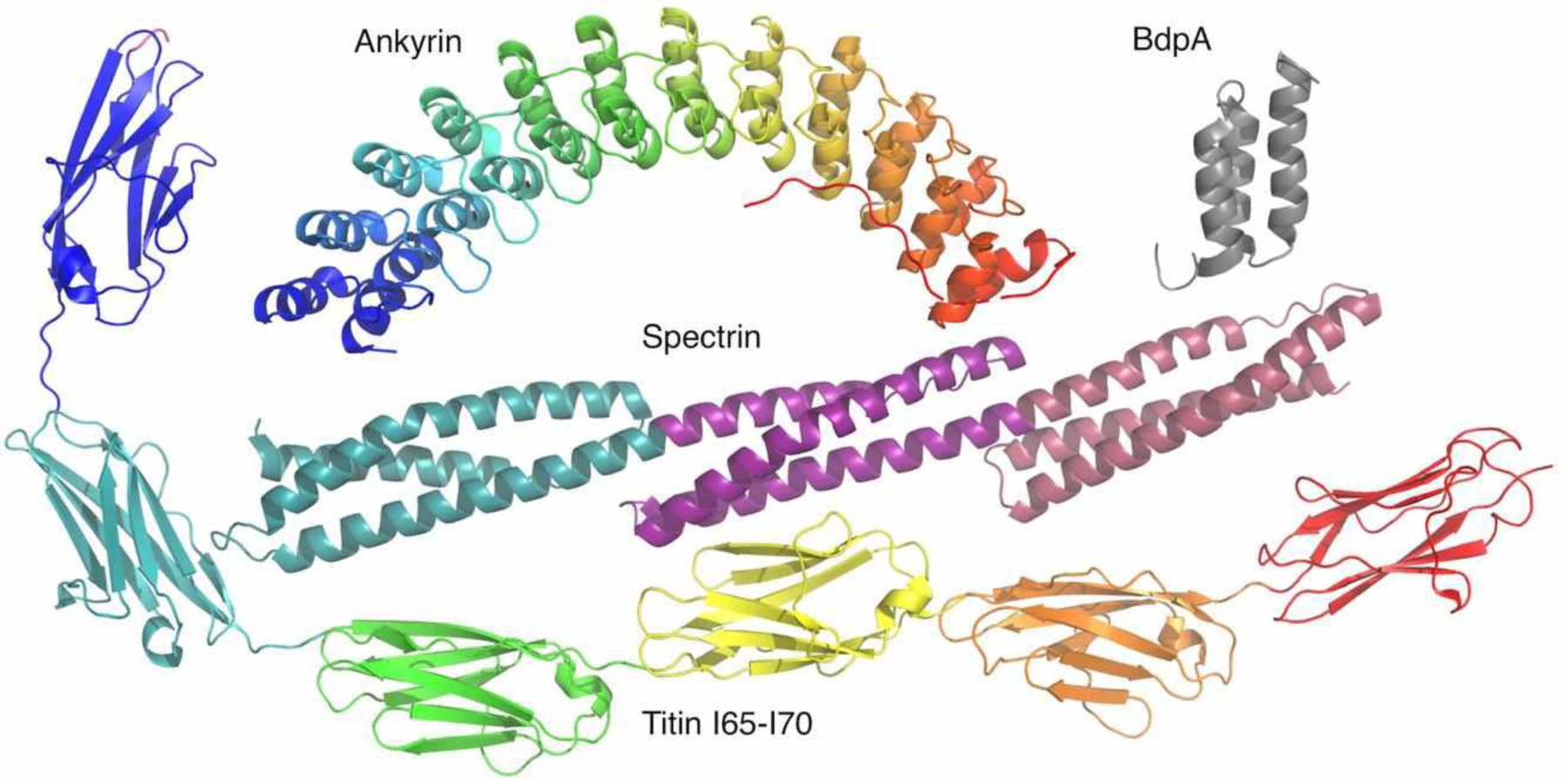
Ribbon diagrams of a 12-repeat ankyrin array (Michaely et al., 2002), a single repeat from protein A (36), a 3-repeat spectrin array (24), and a six-repeat Ig array from titin (10).
2. THERMODYNAMIC MODELS FOR COUPLING
In this section, models are presented for analysis of the thermodynamics of folding of tandem repeat proteins. Most of these are “nearest-neighbor” models3, where repeats are directly coupled to their two adjacent neighbors (or one, if they are a terminal repeat), but not to more distant repeats. These models are codified in molecular partition functions (4). Before constructing partition functions, which represent the probabilities of all conformational states included in the model, we will define the energy terms that make up nearest-neighbor models.
2.1. Nearest-neighbor models and their energy terms
The energy terms that are used to make up nearest-neighbor models for repeat protein folding are the intrinsic folding (ΔGi) and interfacial coupling free energies (ΔGi-1,i) introduced above (Figure 3). When repeat i folds and its nearest-neighbors (i-1 and i+1) are not folded (reactions i. and ii. Figure 3), the equilibrium constant and free energy for folding are κ and ΔGi. Equilibrium constants and free energies are related through the standard expression
| (1) |
Here we will typically omit the standard state symbol, but all free energies here are at standard state concentrations (one molar reactant and product).
Figure 3. Nearest-neighbor model energy terms and statistical weights.
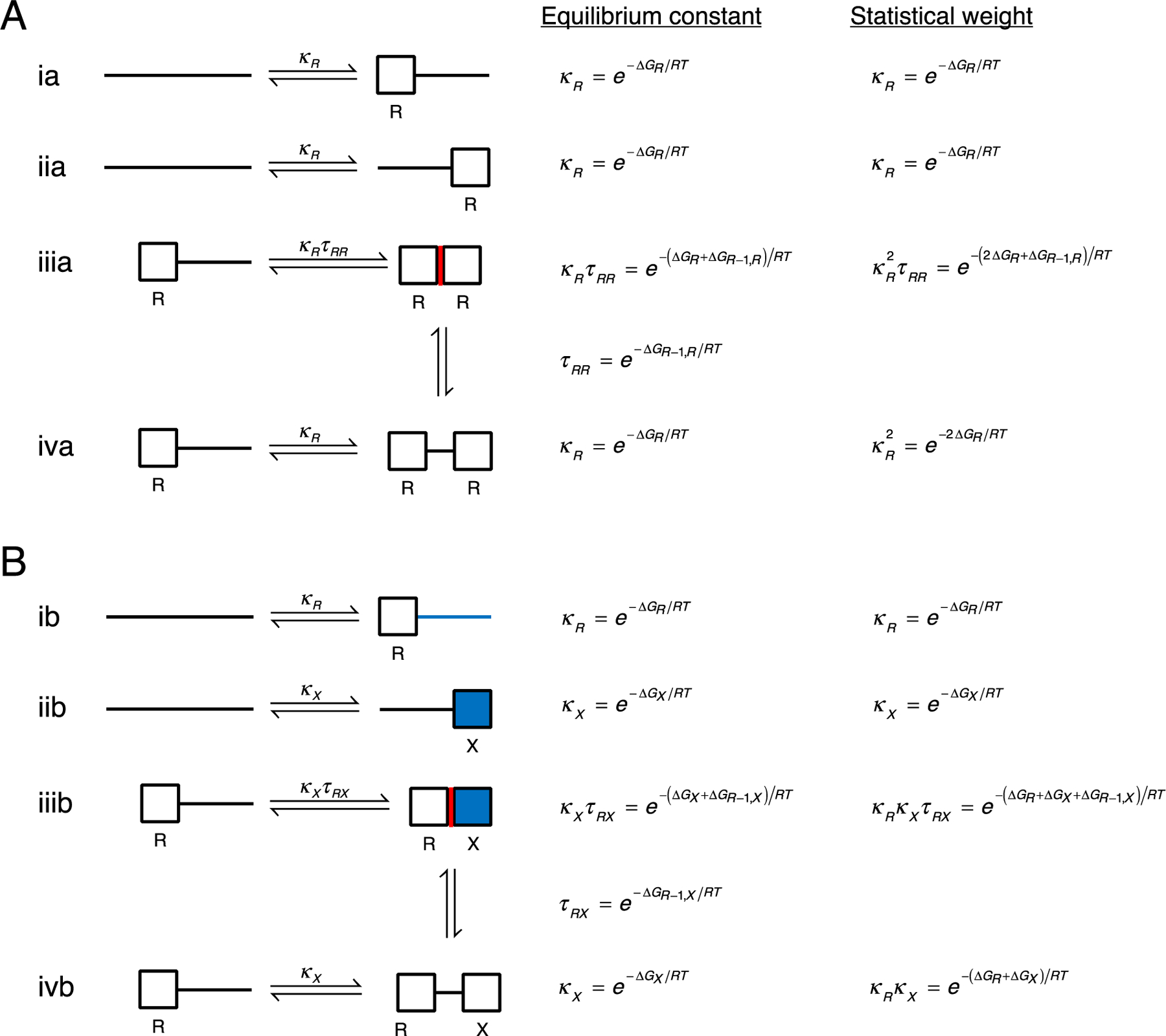
Unfolded and folded repeats are represented by lines and boxes, respectively. The left-hand column shows folding reactions for individual repeats for a two-repeat homopolymer (A; both repeats are labelled R) and a two-repeat heteropolymer (B; repeats are labelled R and X). The equilibrium constant for folding in the context of unfolded neighbors (reactions i and ii) is κR or κX. In the Ising model, the equilibrium constant for folding next to a folded neighbor (reaction iii) is κτ, where τ is the equilibrium constant for interface formation (illustrated by the two vertical transitions). The fractured Ising model permits additional states where adjacent repeats are folded but the interface is not formed (reaction iv). The right-hand column shows statistical weights relative to the reference (unfolded) state.
When repeat i folds and one of its nearest-neighbors is folded (for example, repeat i-1), an interface can be formed (reaction iii., Figure 3). The equilibrium constant for this coupled folding and interface formation is κiτi-1,i, where κi is as defined above. Expressed in this way, τi-1,i is an equilibrium constant for forming an interface between folded repeats i-1 and i.
Alternatively, it is possible that repeat i can fold next to a folded repeat but not form an interface (reaction iv. above); this is likely when the interface is weakly stabilizing or destabilizing, as is the case for FARPs. In such cases, the equilibrium constant for folding is κi, the same as for folding with unfolded neighbors. In addition to providing a means to analyze FARP unfolding, reaction iv. provides a clear definition of the equilibrium constant for interface formation, τi-1,i (vertical transitions, Figure 3). Because interfaces have contributions from two repeats, representing the type of interface requires two repeat types be specified. For example, for repeat types R and X, four types of interfaces can be formed: homopolymeric interfaces between R repeats and between X repeats (with equilibrium constants τRR and τXX), and heteropolymeric interfaces between R and X repeats (with equilibrium constants τRX and τXR, depending on the order of the repeats). When relevant, the type of interfacial free energy will be specified using labels such as ΔGR−1,X, which indicates an interface between an X repeat at position i and an R repeat at position i-1 (Figure 3B).
These equilibrium constants and free energies can be used to construct a partition function for a given repeat array. Here, the partition function is a sum of statistical weights for the fully folded state, each of the different partly folded states, and the unfolded state (which we use as a reference and assign a statistical weight of one). For each state, the statistical weight is simply the product of all the equilibrium constants that are needed to get from the reference state to that state (Figure 3, right-most column). The number of intrinsic κ constants in the product is equal to the number j of folded repeats (i.e., κj). However, the number of interfacial τ constants depends on the model and on the arrangement of the folded repeats.
2.2. Partition functions for different nearest-neighbor models
Here we will present several partition functions that model repeat protein folding and can be used to fit equilibrium folding data (Table 3). The models for these partition functions differ in the types of partly folded states they admit (see Appendix 1), and represent different levels of cooperativity. As such, some partition functions are more appropriate for FARPs, and others are more appropriate for NARPs (Table 3).
Table 3.
Partition functions for tandem repeat protein folding
| Correlation matrix | Two-repeat partition function | ℓ-repeat partition function | # states | ||
|---|---|---|---|---|---|
| NARP | Ising | ρI = 1 + 2κ + κ2τ | 2ℓ | ||
| FARP | Ising |
ρI = 1 + 2κ + κ2τ |
2ℓ | ||
| Fractured Ising |
ρFI = 1 + 2κ + κ2 + κ2τ |
||||
| Binomial | ρB = 1 + 2κ + κ2 | 2ℓ | |||
| SARP | Ising | ρI = 1 + 2κ + κ2τ | 2ℓ | ||
| Fractured Ising | ρFI = 1 + 2κ + κ2 + κ2τ |
The number ϕ is the golden ratio, with numeric value .
For the nearest-neighbor models presented here, partition functions are best represented as the product of a series of two-by-two correlation matrices W, with one matrix for each repeat. For a protein with ℓ repeats, the partition function ρ can be written
| (2) |
where n = [0 1] and c = [1 1]T are row and column vectors that convert the matrix product to a scalar and select the appropriate terms of the partition function. If the repeat array is homopolymeric (that is, if is composed of identical repeats), the partition function becomes
| (3) |
Details of this approach are presented elsewhere (32, 1).
The structure of the correlation matrix is shown in Table 2. The rows of matrix Wi represent whether or not repeat i-1 is folded, and the columns represent whether or not repeat i is folded. Thus, each matrix captures four i-1, i configurations, and the four elements are expressed as equilibrium constants for repeat i relative to the unfolded reference:
| (4) |
Because the left column represents repeat i in the folded state, both entries include the equilibrium constant κi. In the top row, the i-1 repeat is folded; although this does not modify the stability of the unfolded state of repeat i (right entry), it likely modifies the stability of the folded state of repeat i (left entry). This modidfication is represented in equation 4 by a general factor ϕi-1,i. The form of ϕ varies for different models, as described below.
Table 2.
Correlation matrix between repeat i-1 and i.
| i-1╲i | fi | ui |
|---|---|---|
| fi-1 | κϕ | 1 |
| ui-1 | κ | 1 |
2.2.1. The noncooperative or binomial model.
When there is no coupling between adjacent repeats—that is, repeats fold as if they are independent of each other, folding can be modeled with a binomial model. In this situation ϕ from equation (4) is equal to unity. For a homopolymeric repeat array, the partition function is given in Table 3; when the matrix product is multiplied out, the resulting terms can be factored into a single binomial:
| (5) |
This can be understood by recognizing that the partition function represents all combinations of folded and unfolded repeats, i.e., 1 + κ, and since each of the ℓ repeats is independent and identical, the ℓ (1 + κ) terms multiply.
For a heteropolymeric repeat array, the noncooperative (binomial) partition function factors into a product of sub-partition functions for each type of repeat, each with a binomial form (4). For the binomial model, there are a total of 2ℓ states, regardless of whether the repeat array is homo- or heteropolymeric (see Appendix 1).
2.2.2. The 1D-Ising model.
When adjacent repeats are coupled through strongly stabilizing interfaces (that is, when τ >>1 and ΔGi-1,i <<0), folding can be treated with a 1D-Ising model. In this model, the ϕ parameter in the correlation matrix (equation 4) takes the value τ. For a homopolymeric array of ℓ repeats, the partition function becomes
| (6) |
In the 1D-Ising model, when adjacent repeats are folded, they are required to form an interface—folded but unpaired adjacent repeats are not allowed. Unlike the binomial model, ρI does not factor into a simple form.
For a heteropolymeric repeat array, different repeats have different correlation matrices. The partition function is generated by multiplying these correlation matrices (equation 2), and they must be multiplied in the same order as they are found in the protein sequence. For example, for a repeat array composed of an N-terminal capping repeat, an internal R-type repeat, and internal X-type repeat, and a C-terminal capping repeat,
| (7) |
As with the binomial model, there are a total of 2ℓ states in the 1D-ising model of an ℓ repeat array, regardless of whether the repeat array is homo- or heteropolymeric (see Appendix 1).
2.2.3. The fractured 1D-Ising model.
When interfaces between repeats are either weak (τ ≈ 1, i.e, ΔGi−1,i ≈ 0) or unfavorable (τ ≈ 0 , i.e, ΔGi−1,i > 0), the requirement of the 1D-ising model that interfaces form between adjacent folded repeats is not satisfied. Thus, ρI is a poor representation of weakly coupled (or uncoupled) arrays. The missing states in which adjacent repeats are folded but their interfaces are not formed can be included by assigning the ϕ = κτ + κ in each correlation matrix. For a homopolymer, the fractured Ising model has the form
| (8) |
Recall that the upper left-hand element of the ith correlation matrix represents the situation in which both repeats i and i-1 are folded; the two terms κτ and τ represent configurations where the i-1, i interface is formed and broken, respectively, in relative proportions controlled by the value of τ. When τ is very large, the paired term dominates, and the fractured-Ising model converges to the simpler Ising model. When τ approaches zero, the model converges to the binomial model. For values of τ near unity the paired and fractured states have equal statistical weights, contributing equally within the ensemble of states.
As with the Ising model, the fractured Ising partition function for heteropolymeric sequences can be obtained by ordered multiplication of correlation matrices containing the additional fractured states. Owing to these extra terms in the partition function, there are more states represented by the fractured Ising model than the binomial and 1D-Ising models. As described in Appendix 1, the number of states for an ℓ repeat array is given by the Fibonacci number, F2ℓ+1.
3. ANALYSIS OF REPEAT PROTEIN FOLDING TRANSITIONS USING NEAREST-NEIGHBOR MODELS
In this section, the partition functions developed above are used to fit folding transitions to determine ΔGi and ΔGi-1,i values. To do so, we must derive equations that model equilibrium folding transitions. Fits of these equations to folding transitions for a series of NARPs, SARPs, and a FARP will be presented. Fitting is performed with a nonlinear least squares package that we have developed in python (27), which is freely available at https://github.com/barricklab-at-jhu/Ising_programs.
3.1. Expressions to fit repeat-protein folding transitions using nearest-neighbor models
The partition functions above describe the relative populations of all of the partly folded states along with the fully folded and fully unfolded states for a particular repeat protein array, given a set of nearest-neighbor (intrinsic and interfacial) free energies. However, these free energies are unknowns, and must be determined by analyzing experimental folding data. This requires an expression that gives the value of the observable used to monitor unfolding (Yobs below, often a spectroscopic observable such as far-UV circular dichroism or tryptophan fluorescence) as a function of the repeat protein conformations in solution. Typically, the populations of folded and unfolded conformations are modulated by a solution variable such as denaturant concentration or temperature, resulting in an equilibrium folding transition (colloquially, a “melt”). Thus, the equation used to fit a melt has the form
| (9) |
where the sum is over each of the c conformations in the set {s} of allowed states. Yc is the spectroscopic signal from conformation c, and pc is its population; pc depends on the intrinsic and interfacial free energies, which in turn depends on the solution variable x. When x represents denaturant concentration, the free energy terms are linearly dependent on denaturant concentration (see Greene & Pace, 1974; Marold et al., 2020).
To use equation 9 to analyze unfolding transitions, the populations pc must be given explicitly in terms of ΔGi and ΔGi-1,i. From statistical thermodynamics, the population of a particular configuration is given by the statistical weight divided by the partition function, such that
| (10) |
Because the partition function ρ is the same for all terms, it can be taken outside the sum. ΔGc is the free energy difference between conformation c and the unfolded reference state,4 and can be written as the sum of ΔGi and ΔGi-1,i values, weighted by the number of repeats folded (nf) and interfaces (nint) formed:
| (11) |
When Yc is proportional to the number of repeats that are folded, which is usually the case due to the high degree of structural similarity among repeats, a form of equation 9 can derived that depends on the fraction of repeats that are folded (ff):
| (12) |
where Yn and Yd are the spectroscopic signals from the fully-folded and fully-unfolded, arrays, and
| (13) |
In equation 13, the index j represents the different types of repeats (e.g., N, R, X, C). In the analyses below, data are fitted with equations 12 and 13, using whichever partition function (1D-Ising, fractured Ising, or binomial) is most appropriate. Because, as described in the next section, multiple folding transitions of different constructs are required, a global fit is performed in which different versions of equations 12 and 13, containing shared thermodynamic parameters, are fitted to transitions of different constructs.
3.2. Constructs required for determination of nearest-neighbor thermodynamic parameters
In its simplest form, nearest-neighbor analysis involves only two free energies: ΔGi and ΔGi-1,i. This occurs when all repeats are identical, as is sometimes the case with NARPS composed of consensus repeats. To extract values of these two parameters from experimental data, a minimum of two constructs that differ in repeat number are needed. However, homopolymeric consensus NARP arrays are often insoluble, and must be capped with N- and C-terminal repeats containing polar substitutions. This sequence heterogeneity increases the number of thermodynamic parameters that must be determined, and as a result, the number and types of constructs that need to be included in analysis (see (27).
Because individual repeats from NARPs are unstable, there are limits to the amount of heterogeneity that can be accommodated using nearest-neighbor analysis. However, the individual repeats of SARPS and FARPS are stable, allowing fully heterogeneous repeat arrays to be analyzed. In one approach, folding transitions of each individual repeat in an array is analyzed, along with transitions of overlapping pairs of adjacent repeats. For example, for a SARP composed of three repeats ABC, analysis of folding transitions of single-repeat constructs A, B, and C and two-repeat constructs AB and BC is sufficient to determine the five Ising parameters (ΔGA, ΔGB, ΔGC, ΔGA-1,B, ΔGB-1,C).
3.3. An example of a non-autonomous repeat protein: consensus ankyrin arrays
One of the first nearest-neighbor studies of a tandem repeat protein was that of an ankyrin repeat protein. Deletion studies using an ankyrin domain from the Drosophila Notch receptor demonstrated that at least three or four repeats were required for folding (29), indicating that ankyrin repeat proteins are NARPs. Thus, a 1D Ising model is appropriate for modeling ankyrin repeat protein unfolding. Though the Notch deletion study was not able to generate enough constructs to determine the Ising parameters for each repeat and interface as a result of the sequence variation among repeats, it did demonstrate that repeats were intrinsically unstable (ΔGi ≈ +7 kcal/mol) and that interfaces were strongly stabilizing (ΔGi−1,i ≈ −9 kcal/mol; (29).
Elegant studies using consensus ankyrin repeats confirmed and extended this thermodynamic partitioning (37, 2). An example of a global fit of folding transitions of consensus ankyrin repeat proteins with a 1D-Ising model is shown in Figure 4A. The data set includes eighteen melts for nine constructs that differ in repeat number and capping structure (see Aksel et al., 2011; Marold et al., 2020). The model contains four free energies (the intrinsic folding energies of the N-and C-terminal caps and the internal R repeats, ΔGN, ΔGR, and ΔGC, and an interfacial coupling energy, ΔGi-1,i) along with a shared denaturant dependence (m) for the three intrinsic free energy terms. Overall, the 1D-Ising model fits the folding transitions of these nine constructs very well, and determines the fitted Ising parameters with tight confidence intervals (2, 27).
Figure 4. Folding transitions of tandem repeat proteins fitted with nearest-neighbor folding models.
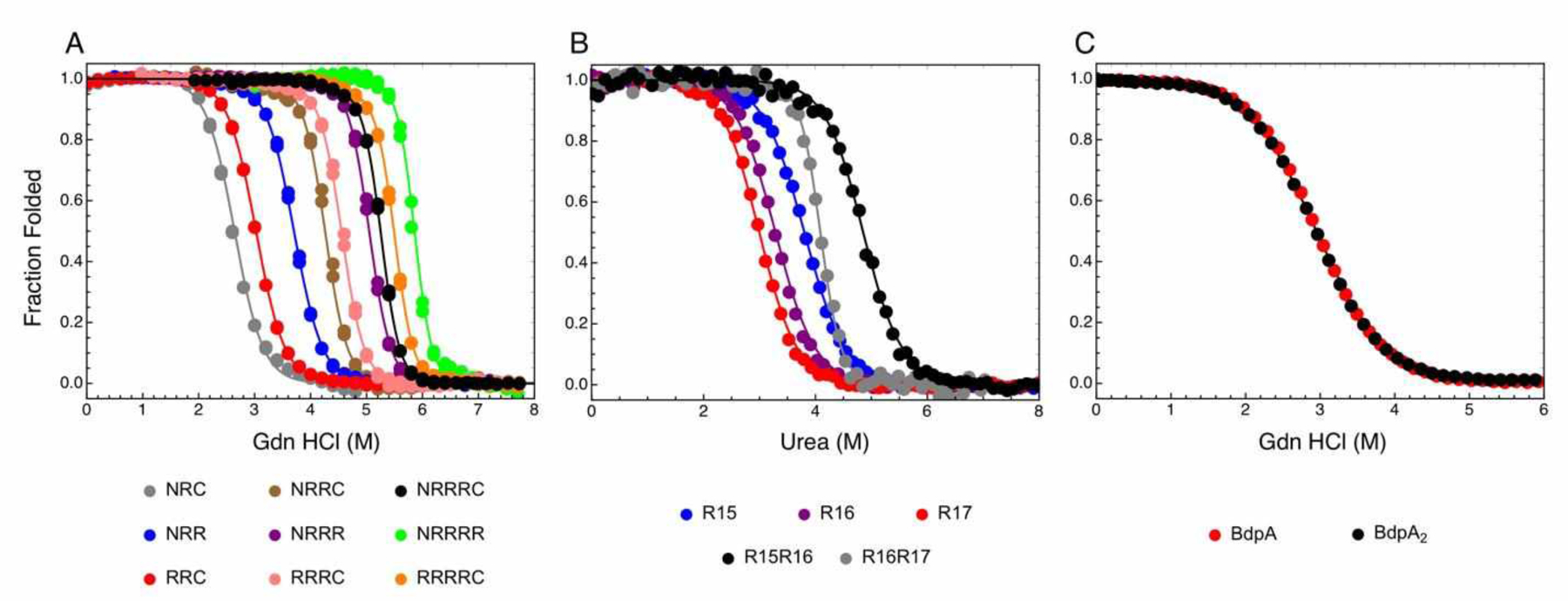
Fitted parameters for all data sets are given in Table 4. (A) Consensus ankyrin repeat arrays (a NARP) fitted with a 1D-Ising model. Data are from Aksel et al. (2011). (B) Spectrin repeats R15-R17 (a SARP) fitted with a 1D-ising model modified to include a stabilizing interaction between folded repeat R15 and unfolded repeat R16. Data are from (5). (C) B-domains of Staph. aureus protein A (a FARP) fitted with a fractured Ising model. Data are from (3).
3.4. An example of a semiautonomous repeat protein: naturally occurring spectrin arrays
Spectrin repeats are significantly larger (105 residues) than ankyrin repeats, and are known to fold autonomously. Therefore, depending on whether adjacent spectrin repeats interact thermodynamically, spectrin repeat proteins should either be classified as SARPs or FARPs. Jane Clarke’s laboratory has analyzed the folding of single spectrin repeats along with pairs of adjacent repeats and found the pairs to be more stable than the single-repeat constructs, demonstrating that spectrin arrays behave as SARPs (5, 6).
The folding transitions of three adjacent spectrin repeats, R15, R16, and R17, along with the two-repeat pairs, R15R16 and R16R17, are reproduced in Figure 4B. The three constructs involving R16, R17, and the tandem pair R16R17 are well-fitted by a 1D-Ising model, with a reduced sum of square residuals (RSSR)5 of 2.5×10−4. A fitted interfacial ΔG16,17 value of −3.32 kcal mol−1 is consistent with the classification of this repeat pair as a SARP, as is the goodness of fit. However, the transitions of R15, R16, and R15R16 are not as well-fitted by a 1D-ising model, with an RSSR of 4.8×10−4 and a nonrandom distribution of residuals (Figure S1A). Although the folding transition of the R15R16 tandem is centered at higher denaturant concentrations, indicating a favorable interfacial interaction, the transition is broad, which is inconsistent with a coupled two-repeat unfolding transition, and thus, inconsistent with a 1D-Ising model.
Although a variety of more complicated models can be fitted to the R15, R16, and R15R16 melts, a particularly good fit is obtained with a model that includes an interaction in which folded repeat R15 is stabilized by unfolded R16. This interaction can be introduced to the partition function for R15R16 using an equilibrium constant ω15f,16u as follows:
| (14) |
Using this model, the fit of R15, R16, and R15R16 melts gives a significantly improved RSSR of 2.2×10−4, and the resulting residuals appear more random (Figure S1B). A global fit of the five spectrin folding transitions in Figure 4B using the 1D Ising partition functions to fit R15, R16, R17, and R16R17, along with equation 14 to fit R15R16, gives a low RSSR (2.5×10−4; Table 4). The fitted free energy of stabilization of folded R15 by unfolded R166 is −2.0 kcal mol−1. This value is consistent with the observation by Batey and Clarke that the rate constant for unfolding of R15 is decreased by a factor of 28 in the context of unfolded R16 (5). Combined with a modest decrease in the folding rate constant, the analogous free energy deduced from the rate constants is −1.9 kcal mol−1, nearly the same as the value determined from the modified Ising fit. It should be noted that although it seems like the inclusion of the additional parameter might lead to an under-parameterization problem (six free energies are extracted from five curves), this problem is made less severe by the fact that an intermediate is populated in the unfolding transition of R15R16, directly constraining ω15f,16u.
Table 4.
Global thermodynamic parameters from Ising fitsa
| Consensus ankyrin (NARP) | |||||
| 1D-Ising (1.92×10−4) | ΔGN | 5.38 | 5.38 | 5.26 | 5.51 |
| ΔGR | 4.50 | 4.50 | 4.38 | 4.62 | |
| ΔGC | 6.94 | 6.94 | 6.79 | 7.09 | |
| ΔGR-1,R | −11.43 | −11.44 | −11.68 | −11.20 | |
| mR | 0.76 | 0.76 | 0.75 | 0.78 | |
| Spectrin (SARP) | |||||
| 1D-Ising with stabilized intermediate (2.48×10−4) | ΔGR15 | −6.07 | −6.08 | −6.48 | −5.73 |
| ΔGR16 | −5.43 | −5.44 | −5.78 | −5.11 | |
| ΔGR17 | −5.22 | −5.22 | −5.56 | −4.88 | |
| ΔGR15,R16 | −4.27 | −4.28 | −4.51 | −4.06 | |
| ΔGR16,R17 | −3.23 | −3.23 | −3.37 | −3.10 | |
| ΔGf15,u16 | −2.02 | −2.02 | −2.20 | −1.83 | |
| mR15 | 1.60 | 1.60 | 1.51 | 1.70 | |
| mR16 | 1.65 | 1.66 | 1.55 | 1.76 | |
| mR17 | 1.74 | 1.56 | 1.64 | 1.85 | |
| BdpA (FARP) | |||||
| 1D-Ising (4.25×10−6) | ΔGBdpA | −3.98 | −3.98 | −4.03 | −3.94 |
| ΔGBdpA,BdpA | 0.05 | 0.05 | 0.03 | 0.07 | |
| mBdpA | 1.35 | 1.35 | 1.33 | 1.36 | |
| Fractured 1D-Ising (5.13×10−6) | ΔGBdpA | −3.92 | −3.92 | −3.96 | −3.87 |
| ΔGBdpA,BdpA | 20.62 | 8.74 | 1.84 | 22.06 | |
| mBdpA | 1.33 | 1.33 | 1.32 | 1.34 | |
| Binomial (5.06×10−6) | ΔGBdpA | −3.92 | −3.92 | −3.96 | −3.88 |
| mBdpA | 1.33 | 1.33 | 1.32 | 1.34 | |
ΔG values in kcal mol−1; m values in kcal mol−1 M denaturant−1.
Values in parentheses are reduced sum of square residuals (RSSR=SSR/DOF) from the fit.
Values are from 2000 bootstrap iterations.
CI, confidence intervals.
The model for spectrin includes a stabilizing interaction between folded repeat 15 and unfolded repeat 16.
3.5. An example of a fully autonomous repeat protein: BdpA arrays
In full-length Staphylococcus aureus protein A, BdpA is one of five repeated domains with high sequence identity, sharing ~90% sequence identity with its nearest neighbors. Oas and coworkers have studied the folding of a single BdpA repeat and a tandem construct with two adjacent BdpA repeats (3). The equilibrium folding transitions of BdpA and BdpA2 are reproduced in Figure 4C. The two folding transitions are nearly identical, suggesting that BdpA2 behaves as a FARP. A 1D-Ising model fits well to the BdpA/BdpA2 folding transitions, and the fitted interfacial free energy is very close to zero (Table 4).
While a ΔGBdpA,BdpA value of zero is consistent with an interfacial interaction that is neither stabilizing nor destabilizing, it is inconsistent with the number of states in the 1D Ising model . An interfacial free energy of zero (equilibrium constant of one) would mean that when both repeats are folded, half of the population has an interface formed, and half has does not. However, the 1D Ising model does not allow for fractured interfaces. To account for this missing state, we fitted the BdpA curves using the fractured 1D-ising model. This model fits about as well as the standard 1D Ising model, and give a nearly identical ΔGBdpA (Table 4). However, ΔGBdpA,BdpA is poorly defined; though it has a lower bound of around +1 kcal/mol, it is essentially unbounded from above. This reflects the fact that unstable interfaces are not formed and thus have no influence on the folding transitions, regardless of whether interfacial stability is +1 or +10 kcal/mol. This is a manifestation of the thermodynamic maxim that things that are energetically unfavorable do not happen.
Although the fractured Ising partition function is a more appropriate description of the states of BdpA than the simpler 1D-Ising model, its poorly determined interfacial free energy is rather ungainly. The binomial model, which has the same form as the 1D-Ising model but treats adjacent folded repeats as unpaired, fits with about the same RSSR as the fractured 1D-Ising model, and gives identical ΔGBdpA and m-values to three significant figures (Table 4). The goodness-of-fit of the binomial model further supports the assignment of BdpA arrays to FARPs.
4. VALUES OF INTRINSIC AND INTERFACIAL COUPLING ENERGIES AND THEIR RELATIONSHIP TO COOPERATIVITY AND REPEAT PROTEIN STRUCTURE.
Using the nearest-neighbor models above, we and other groups have determined ΔGi and ΔGi-1,i values for a variety of repeat proteins. These values are displayed on the number lines in Figure 5. Values are color coded to indicate whether they are best described as NARPs, SARPs, or FARPs based on features of their folding transitions, fits from the different models, and the resulting ΔGi and ΔGi-1,i values.
Figure 5. Nearest-neighbor free energies of tandem repeat proteins.
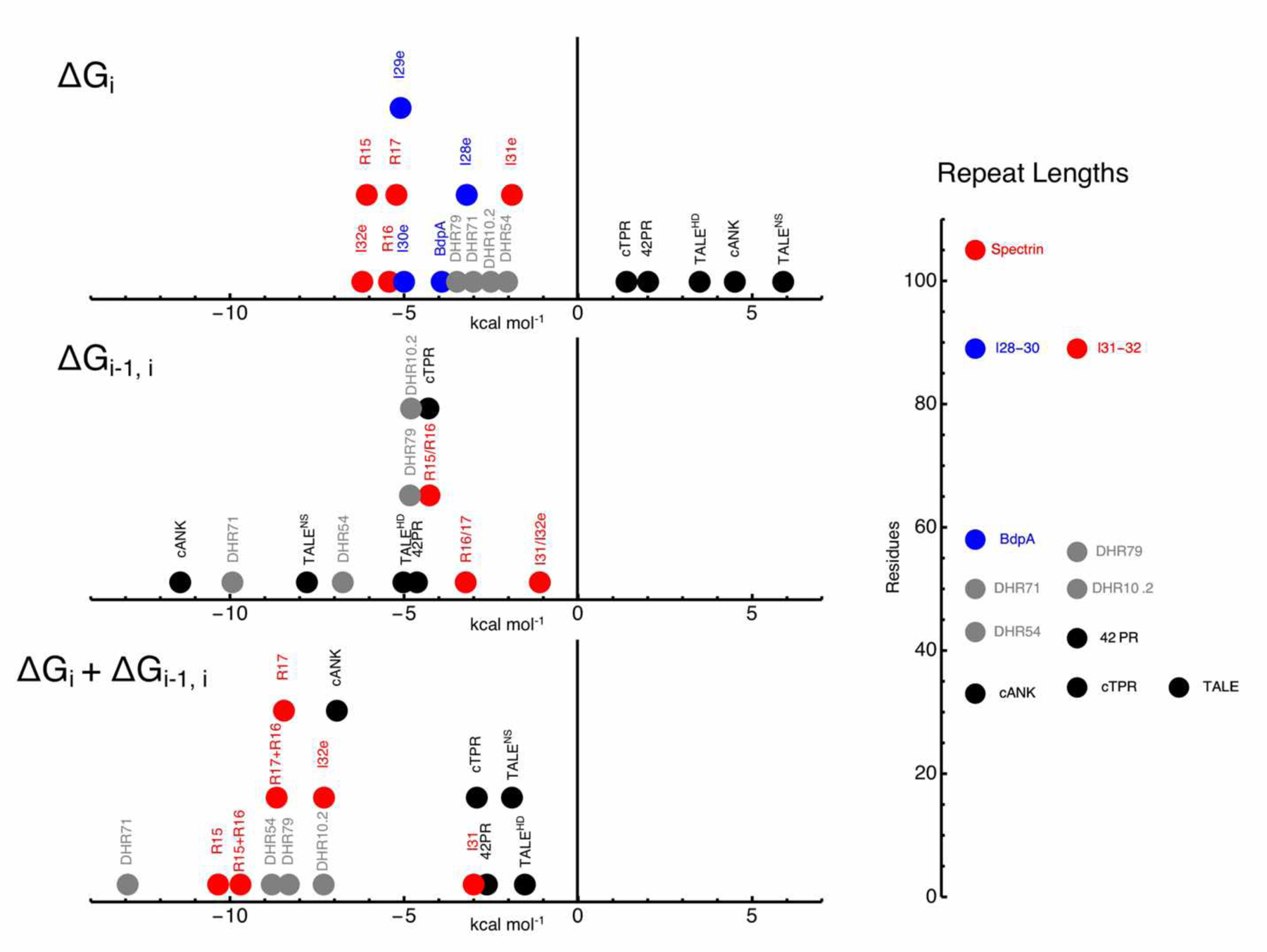
Negative values are stabilizing. Naturally occurring and consensus NARPs, SARPs, and FARPs are black, red, and blue, respectively. Rosetta-designed helical repeat proteins (DHRs) are grey. For cANK, values are for the internal (R) repeats. For spectrin, ΔGi and ΔGi-1,i values are from the model that includes a stabilizing interaction between folded repeat 15 and unfolded repeat 16. For BdpA, ΔGi is from the binomial model. For TALEs, ΔGi and ΔGi-1,i values are from Geiger-Schuller & Barrick (2016). For cTPR and 42PR , ΔGi and ΔGi-1,i values are from (20) and (28). For the titin I28e – I32e repeats, ΔGi (and for the I31/I32e pair, ΔGi-1,i) are from Scott et al. (2002). For the four DHR series, ΔGi and ΔGi-1,i values are from Geiger-Schuller et al. (2018). The number line on the right shows average repeat lengths.
NARPs show a minimum number of repeats required for folding—individual repeats are not structured. Above this minimum, folding transitions of NARPs shift to higher denaturant and become steeper as repeats are added. NARP arrays are well-fitted with the classic 1D-Ising model, and have positive ΔGi values and negative ΔGi-1,i values. Because the stabilities of individual (and usually pairs of) NARP repeats cannot be quantified, analysis of NARP arrays typically requires that most or all repeats have the same sequence. Thus, the five NARP families in Figure 5 (black circles) are all based on identical consensus repeats.
In contrast to NARPs, isolated repeats from SARPs are structured and display cooperative folding transitions. As with NARPS, as repeats are added to a SARP array, the folding transition shifts to higher denaturant and typically become steeper. The interfacial coupling energies of SARPs are generally lower than those of NARPs, indicating decreased cooperativity for the former. The fact that individual repeats are intrinsically stable isolation might also suggest decreased cooperativity; however, because denaturants destabilize intrinsic repeat folding, this stability is lost at the denaturant concentrations needed to bring about unfolding transitions. As described above, the ability to quantify stability of individual SARP repeats and pairs facilitates analysis of heteropolymeric repeat arrays.
Like SARPs, the individual repeats of FARPs are structured and display cooperative folding transitions. However, the folding transitions of FARPs are unperturbed by adding repeats (Figure 4C). Though the fractured 1D-Ising model includes all the populated states in FARP folding, ΔGi-1,i is poorly determined. Since the binomial partition function also includes all the populated states but lacks ΔGi-1,i, it seems best suited for describing FARPs. For the FARPs in Figure 5 (blue circles), those for BdpA are fitted using the binomial model, whereas those for the titin Ig domains I28e – I30e are obtained from two-state fits and kinetin measurements in Scott et al. (2002).
As with SARPs, the intrinsic stabilities of individual FARP repeats permits analysis of heteropolymeric arrays. This heterogeneity may be expected to lead to considerable variation in ΔGi and ΔGi-1,i along a repeat array; thus, some repeat arrays may be best modeled using a hybrid of the classic and fractured 1D-Ising models and the binomial model. The titin Ig repeats from Scott et al. (2002) show this type of hybrid behavior: repeats 28, 29 and 30 behave as FARPs, whereas repeats 31 and 32 are favorably coupled, thus behaving as a SARP (Figure 5). This hybrid thermodynamic behavior is consistent with a structural analysis of a different set of titin Ig repeats, which shows considerable variation in rigidity and flexibility between repeats, depending on their sequences and linkers (10). We have observed similar hybrid behavior in Ising parameters from a series of helix-hairpin-helix repeats (MP and DB, unpublished).
On the whole, there is considerable variation in the values of ΔGi and ΔGi-1,i, especially for the NARPs. These variations are somewhat anticorrelated: NARPs that have the most stable interfaces tend to have the least stable repeats. As a result, the sum of ΔGi and ΔGi-1,i, which reflects the stability change for adding a repeat to an already folded array, tends to show less variation (Figure 5).
Structurally, there are two features that distinguish NARPs from S/FARPs (SARPs and FARPs). First NARPs have large interfaces between adjacent repeats (Figure 1); these interfaces often bury a large number of hydrophobic side chains (2), but can also involve polar interactions that are important for stability (33, 23, 27). These large interfaces are a likely source of the favorable coupling energies needed to drive the folding of intrinsically unstable NARP repeats. Interfaces between spectrin and Ig repeats are considerably smaller. Second, the number of residues per repeat is lower for NARPs than for S/FARPs. For the naturally occurring repeat proteins in Figure 5, the NARPs are 42 residues or shorter, whereas the S/FARPs are 58 residues or longer. Presumably longer repeats are required to form autonomously folding domains.
One notable exception to these general trends comes from analysis of a series de novo designed helical repeat proteins referred to as DHRs (7). Ising analysis of four of these proteins reveals negative ΔGi values for all proteins, putting them in the S/FARP category (14). However, these Rosetta-designed DHR proteins also have strongly stabilizing interfaces comparable to NARPs (grey circles, Figure 5). Thus the free energy of propagation of DHR repeats (ΔGi + ΔGi-1,i) is unusually negative, reflecting the effectiveness of Rosetta in generating folded proteins with unusually high stability. Structurally the DHR proteins have large hydrophobic interfaces like those of naturally occurring NARPs; in terms of number of residues per repeat, they span the range between NARPs and S/FARPs, perhaps consistent with their chimeric thermodynamic behavior.
5. CONCLUSIONS AND FUTURE DIRECTIONS
Analysis of tandem repeat protein folding with nearest-neighbor models provides a unique way to quantify cooperativity. A range of intrinsic and interfacial stabilities are seen, giving rise to highly cooperative (NARP), moderately cooperative (SARP), and noncooperative (FARP) behavior. The ability of heterogeneous SARP arrays to be analyzed using classic and fractured 1D-Ising models gives access to complex energy landscapes, and provides a way to connect details of sequence and structure to folding cooperativity.
Linear nearest-neighbor models can also be extended to more complex geometries. One simple extension would be to analyze repeat proteins that are “closed”, that is, they have circular architectures in which terminal repeats interact with an interface equivalent to those of internal repeats. Examples of proteins with such archtectures are TIM barrels, β-trefoil domains, and WD-40 repeat proteins. A challlenge to such a study is that a circular protein would need to be composed of identical repeats, and non-circular fragments would need to be stable and soluble. Further extension to non-repeating (i.e., globular) proteins would provide tremendous insight into folding cooperativity, but would require a precise experimental approach to measure local stabilities and coupling energies.
Supplementary Material
APPENDIX 1. THE NUMBER OF STATES FOR VARIOUS TANDEM REPEAT PROTEIN FOLDING MODELS
The number of conformational states available to a repeat protein array grows geometrically with the number of repeats7. For the binomial distribution, it is fairly easy to see that the relationship between the number of states s and the number of repeats is s = 2ℓ. This is because each repeat has two states that are independent of its neighbors. Thus, the number of configurations per repeat (two) should multiply for each repeat in an array.
For the Ising model, although the values of the statistical weights depend on the conformational states of other repeats, the number of states per repeat do not—the fact that each repeat can either be folded or unfolded is not changed by interaction with neighboring repeats that shift the population to the folded state. Thus, there are s = 2ℓ states available in the 1D-Ising model, as with the binomial model.
For the fractured Ising model, there must be more than 2ℓ states available, since the model introduces additional (fractured) configurations. It is tempting to think that this additional third state would result in the relation s = 3ℓ; this would be obtained if there were three states for each repeat. However, this number independence is lost in the fractured Ising model—the additional fractured state is only available when the neighboring repeat is folded. Thus, for the fractured Ising model, 2ℓ < s < 3ℓ. The question is, what is the analytical expression s(ℓ)? Here, we will derive this expression by inspection of the number of states for a series of ℓ values.
The partition function provides an easy way to generate the number of states. In general, the numerical value of the partition function gives the average number of states populated. This value ranges from 1 to ℓ, depending on the values of κ and τ. By setting κ and τ to one, the statistical weight of each configuration is one, and the partition function becomes a count of the number of states.8 In this limit,
| (A.1A) |
| (A.1B) |
The first ten values of these matrix products are given below:
| ℓ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2ℓ | 2 | 4 | 8 | 16 | 32 | 64 | 129 | 256 | 512 | 1024 |
| ρB = ρI | 2 | 4 | 8 | 16 | 32 | 64 | 129 | 256 | 512 | 1024 |
| ρFI | 2 | 5 | 13 | 34 | 89 | 233 | 610 | 1597 | 4181 | 10946 |
| F2ℓ+1 | 2 | 5 | 13 | 34 | 89 | 233 | 610 | 1597 | 4181 | 10946 |
| 3ℓ | 3 | 9 | 27 | 81 | 243 | 729 | 2187 | 6561 | 19683 | 59049 |
Indeed, the number of states for the fractured Ising model is in between 2ℓ and 3ℓ, as expected. The pattern of the number of states for the fractured Ising model follows alternating terms in the Fibonacci series, starting with term 3 (F3=2). This is generalized by the formula
| (A.1C) |
where ϕ is the golden ratio and has the numerical value (25).
Footnotes
Amide hydrogen exchange methods provide an experimental route to determine the energies of partly folded states, though local stabilities and coupling energies are hard to resolve in this method.
Here, the subscript i denotes the position of a repeat within the array, and the i-1th repeat is the nearest-neighbor toward the N-terminus. When we discuss specific types of repeats, (N, R, C, … X), the position index i will be replaced by an index that denotes repeat type.
Although there are no nearest-neighbor interactions for FARPs, it is sometimes useful to analyze their folding transitions with a nearest-neighbor model, since as described below, full autonomy requires experimental verification.
For the fully unfolded state, ΔGc=0, giving the statistical weight of 1, as is expected for the reference state.
The reduced sum of square of residuals (RSSR) is the sum of square residuals divided by the number of degrees of freedom (the total number of data points in the unfolding transitions minus the number of fitted parameters.
Here, ΔGf15,u16 = −RTlnωf15,u16.
Note that the number of states is not the same as the number of states populated. The latter, which is given by the value of the partition function, depends on the values of the statistical weights (and ultimately on the values of κ and τ), whereas the number of states does not.
Alternatively, the temperature can be set to infinity.
LITERATURE CITED
- 1.Aksel T, Barrick D. 2009. Analysis of repeat-protein folding using nearest-neighbor statistical mechanical models. Meth. Enzymol 455:95–125 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Aksel T, Majumdar A, Barrick D. 2011. The contribution of entropy, enthalpy, and hydrophobic desolvation to cooperativity in repeat-protein folding. Structure. 19(3):349–60 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Arora P, Hammes GG, Oas TG. 2006. Folding Mechanism of a Multiple Independently-Folding Domain Protein: Double B Domain of Protein A†. Biochemistry. 45(40):12312–24 [DOI] [PubMed] [Google Scholar]
- 4.Barrick D 2017. Biomolecular Thermodynamics: From Theory to Application. Boca Raton: CRC Press. 552 pp. 1 edition ed. [Google Scholar]
- 5.Batey S, Clarke J. 2006. Apparent cooperativity in the folding of multidomain proteins depends on the relative rates of folding of the constituent domains. PNAS. 103(48):18113–18 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Batey S, Randles LG, Steward A, Clarke J. 2005. Cooperative folding in a multidomain protein. J. Mol. Biol 349(5):1045–59 [DOI] [PubMed] [Google Scholar]
- 7.Brunette TJ, Parmeggiani F, Huang P-S, Bhabha G, Ekiert DC, et al. 2015. Exploring the repeat protein universe through computational protein design. Nature. 528(7583):580–84 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Brush SG. 1967. History of the Lenz-Ising Model. Rev. Mod. Phys 39(4):883–89 [Google Scholar]
- 9.Capp JA, Hagarman A, Richardson DC, Oas TG. 2014. The Statistical Conformation of a Highly Flexible Protein: Small-Angle X-Ray Scattering of S. aureus Protein A. Structure. 22(8):1184–95 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Castelmur E von, Marino M, Svergun DI, Kreplak L, Ucurum-Fotiadis Z, et al. 2008. A regular pattern of Ig super-motifs defines segmental flexibility as the elastic mechanism of the titin chain. PNAS. 105(4):1186–91 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Delucchi M, Schaper E, Sachenkova O, Elofsson A, Anisimova M. 2020. A New Census of Protein Tandem Repeats and Their Relationship with Intrinsic Disorder. Genes (Basel). 11(4): [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.El-Gebali S, Mistry J, Bateman A, Eddy SR, Luciani A, et al. 2019. The Pfam protein families database in 2019. Nucleic Acids Res. 47(D1):D427–32 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Geiger-Schuller K, Barrick D. 2016. Broken TALEs: Transcription Activator-like Effectors Populate Partly Folded States. Biophysical Journal. 111(11):2395–2403 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Geiger-Schuller K, Sforza K, Yuhas M, Parmeggiani F, Baker D, Barrick D. 2018. Extreme stability in de novo-designed repeat arrays is determined by unusually stable short-range interactions. PNAS. 115(29):7539–44 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Geiger-Schuller K, Sforza K, Yuhas M, Parmeggiani F, Baker D, Barrick D. 2018. Extreme stability in de novo-designed repeat arrays is determined by unusually stable short-range interactions. PNAS. 115(29):7539–44 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Gorina S, Pavletich NP. 1996. Structure of the p53 Tumor Suppressor Bound to the Ankyrin and SH3 Domains of 53BP2. Science. 274(5289):1001–5 [DOI] [PubMed] [Google Scholar]
- 17.Greene RF, Pace CN. 1974. Urea and Guanidine Hydrochloride Denaturation of Ribonuclease, Lysozyme, α-Chymotrypsin, and β-Lactoglobulin. J. Biol. Chem 249(17):5388–93 [PubMed] [Google Scholar]
- 18.Grum VL, Li D, MacDonald RI, Mondragón A. 1999. Structures of Two Repeats of Spectrin Suggest Models of Flexibility. Cell. 98(4):523–35 [DOI] [PubMed] [Google Scholar]
- 19.Ising E 1925. Beitrag zur Theorie des Ferromagnetismus. Z. Physik. 31(1):253–58 [Google Scholar]
- 20.Kajander T, Cortajarena AL, Main ERG, Mochrie SGJ, Regan L. 2005. A New Folding Paradigm for Repeat Proteins. J. Am. Chem. Soc 127(29):10188–90 [DOI] [PubMed] [Google Scholar]
- 21.Kajava AV. 2001. Review: Proteins with Repeated Sequence—Structural Prediction and Modeling. Journal of Structural Biology. 134(2):132–44 [DOI] [PubMed] [Google Scholar]
- 22.Kajava AV. 2012. Tandem repeats in proteins: From sequence to structure. Journal of Structural Biology. 179(3):279–88 [DOI] [PubMed] [Google Scholar]
- 23.Klein SA, Majumdar A, Barrick D. 2019. A Second Backbone: The Contribution of a Buried Asparagine Ladder to the Global and Local Stability of a Leucine-Rich Repeat Protein. Biochemistry. acs.biochem.9b00355 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kusunoki H, Minasov G, MacDonald RI, Mondragón A. 2004. Independent Movement, Dimerization and Stability of Tandem Repeats of Chicken Brain α-Spectrin. Journal of Molecular Biology. 344(2):495–511 [DOI] [PubMed] [Google Scholar]
- 25.Livio M 2003. The Golden Ratio: The Story of PHI, the World’s Most Astonishing Number. New York, NY: Broadway Books. 294 pp. Reprint edition ed. [Google Scholar]
- 26.Marcotte EM, Pellegrini M, Yeates TO, Eisenberg D. 1999. A census of protein repeats11Edited by J. M. Thornton. Journal of Molecular Biology. 293(1):151–60 [DOI] [PubMed] [Google Scholar]
- 27.Marold J, Sforza K, Geiger-Schuller K, Aksel T, Klein S, et al. 2020. A collection of programs for one-dimensional Ising analysis of linear repeat proteins with point substitutions. bioRxiv. 2020.06.27.175224 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Marold JD, Kavran JM, Bowman GD, Barrick D. 2015. A Naturally Occurring Repeat Protein with High Internal Sequence Identity Defines a New Class of TPR-like Proteins. Structure. 23(11):2055–65 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Mello CC, Barrick D. 2004. An experimentally determined protein folding energy landscape. Proc Natl Acad Sci U S A. 101(39):14102–7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Michaely P, Tomchick DR, Machius M, Anderson RG. 2002. Crystal structure of a 12 ANK repeat stack from human ankyrinR. Embo J. 21(23):6387–96 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Michaely P, Tomchick DR, Machius M, Anderson RGW. 2002. Crystal structure of a 12 ANK repeat stack from human ankyrinR. The EMBO Journal. 21(23):6387–96 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Poland D, Scheraga HA. 1970. Theory of helix-coil transitions in biopolymers; statistical mechanical theory of order-disorder transitions in biological macromolecules. New York: Academic Press [Google Scholar]
- 33.Preimesberger MR, Majumdar A, Aksel T, Sforza K, Lectka T, et al. 2015. Direct NMR Detection of Bifurcated Hydrogen Bonding in the α-Helix N-Caps of Ankyrin Repeat Proteins. J. Am. Chem. Soc 137(3):1008–11 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Scott KA, Steward A, Fowler SB, Clarke J. 2002. Titin; a multidomain protein that behaves as the sum of its parts11Edited by J. Karn. Journal of Molecular Biology. 315(4):819–29 [DOI] [PubMed] [Google Scholar]
- 35.Tashiro M, Tejero R, Zimmerman DE, Celda B, Nilsson B, Montelione GT. 1997. High-resolution solution NMR structure of the Z domain of staphylococcal protein A. J. Mol. Biol 272(4):573–90 [DOI] [PubMed] [Google Scholar]
- 36.Tashiro M, Tejero R, Zimmerman DE, Celda B, Nilsson B, Montelione GT. 1997. High-resolution solution NMR structure of the Z domain of staphylococcal protein A11Edited by P. E. Wright. Journal of Molecular Biology. 272(4):573–90 [DOI] [PubMed] [Google Scholar]
- 37.Wetzel SK, Settanni G, Kenig M, Binz HK, Plückthun A. 2008. Folding and unfolding mechanism of highly stable full-consensus ankyrin repeat proteins. J. Mol. Biol 376(1):241–57 [DOI] [PubMed] [Google Scholar]
- 38.Yan Y, Winograd E, Viel A, Cronin T, Harrison SC, Branton D. 1993. Crystal structure of the repetitive segments of spectrin. Science. 262(5142):2027–30 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


