Abstract
The formation of membraneless organelles in cells commonly occurs via liquid-liquid phase separation (LLPS), and is in many cases driven by multivalent interactions between intrinsically disordered proteins (IDPs). Investigating the nature of these interactions, and their effect on dynamics within the condensed phase, is therefore of critical importance, but very challenging for either simulation or experiment. Here, we study these interactions and their dynamics by pairing a novel multiscale simulation strategy with microsecond all-atom MD simulations of a condensed, IDP-rich phase.We simulate two IDPs this way, the low complexity domain of FUS and the N-terminal disordered domain of LAF-1, and find good agreement with experimental information on average density, water content and residue-residue contacts. We go significantly beyond what is known from experiments by showing that ion partitioning within the condensed phase is largely driven by the charge distribution of the proteins and - in the cases considered - shows little evidence of preferential interactions of the ions with the proteins. Furthermore, we are able to probe the microscopic diffusive dynamics within the condensed phase, showing that water and ions are in dynamic equilibrium between dense and dilute phases, and their diffusion reduces by a factor of 2–3 in the dense phase. Despite their high concentration in the condensate, the proteins also remain mobile, explaining the observed liquid-like properties of this phase. We finally show that IDP self-association is driven by a combination of non-specific hydrophobic interactions, as well as hydrogen bonds, salt bridges, π−π and cation-π interactions. The simulation approach presented here allows the structural and dynamical properties of biomolecular condensates to be studied in microscopic detail, and is generally applicable to single and multi-component systems of proteins and nucleic acids involved in LLPS.
Graphical Abstract
Introduction
Biomolecular condensates are highly concentrated subcellular assemblies of biomolecules that occur naturally in biology, and may function as organelles, such as the nucleolus,1–3 ribonucleoprotein granules,4,5 and many others.6–10 The study of these bodies, often termed membraneless organelles (MLOs), has recently attracted tremendous research effort due to its novelty, and relevance to biological functions,11–14 pathologies such as neurodegenerative diseases15,16 and the design of biomimetic materials.17–19 It is now accepted that many MLOs are formed through a process of phase separation, commonly liquid-liquid phase separation (LLPS) in which a dynamic liquid-like condensate organizes biomolecules including proteins and nucleic acids and allows them to diffuse freely within the condensate, and to exchange rapidly with the surrounding environment.7 A physical understanding of the driving forces of biomolecular phase separation is essential for uncovering the mechanistic details of MLO formation and the pathology of relevant diseases.20–25
A frequent property of proteins involved in biomolecular phase separation is intrinsic disorder, which has been highlighted through estimates of enhanced disorder predicted within MLO-associated proteins.26 Indeed, intrinsically disordered proteins (IDPs) have been shown to phase separate at relatively low concentrations compared to most folded proteins,5,25,27 likely due to their polymeric nature, and consequent increased multivalent interactions.28 Additionally, IDPs are generally more solvent exposed29 than folded proteins, and thus more accessible to post-translational modifications, which provide an efficient mechanism of controlling the thermodynamic and dynamic properties of condensates.23,30,31 Recent work has highlighted that single-molecule behavior of IDPs may yield information relevant to their phase behavior, since the intramolecular interactions driving single-chain collapse are related to the intermolecular interactions driving its homotypic phase separation.32,33 This leads to the question of what exactly are the interactions that drive LLPS, how can they be determined, and how can they be manipulated to control phase behavior?25
Despite the advances in methodology for investigating structure formation inside LLPS droplets by experiment,22 it is still challenging to obtain high resolution, sequence-resolved information on structure and dynamics from experiment alone. All-atom molecular dynamics (MD) simulation with explicit solvent is a promising technique for generating detailed information on conformational ensembles of IDPs,34,35 and the contacts occurring within a condensate composed of IDP molecules.22,36,37 The approach has already been applied to simulating the condensed phase of disordered peptides and proteins.38–40 However, the large system sizes and timescales required to observe equilibrium coexistence of two phases pose a major challenge for all-atom simulations. We have previously overcome this difficulty by developing coarse-grained (CG) simulation models for LLPS.30,32,41–44 We have complemented CG simulations of LLPS with atomistic simulations of smaller fragments of the IDPs,5,22,24,36,45 which yield detailed interactions occurring between the relevant proteins in dilute solution, and in principle, within the condensed phase.32 In this work, we unify these two approaches, by using CG simulations to generate an initial, equilibrated configuration of phase-separated proteins, which is then mapped back to all-atom coordinates to investigate the details of atomic interactions occurring within a protein condensate.
Results and Discussion
As test systems, we have selected the low-complexity prion-like domain of FUS (hereafter, FUS LC),4 and the disordered N-terminal domain of LAF-1 (LAF-1 RGG).36,46To set up the system, we initially equilibrated 40 chains of FUS LC or LAF-1 RGG in a planar slab geometry using our previously developed CG model32,41 (Fig. 1a). The system size was chosen as it yields an atomic resolution system that is sufficiently small to run on Anton 2,47 while being sufficiently large that finite size effects are small. We verify this by comparing with a larger system as we have used previously with 100 chains32,41 and find similar coexistence densities (see supporting methods and Fig. S1). After setting up this system, we reconstructed all-atom coordinates from the Cα positions of the coarse-grained simulations by using a lookup table based on the protein structure database with the PULCHRA code48 (Fig. 1b). Any conflicts between sidechains of different chains were resolved via a short simulation with the CAMPARI Monte Carlo engine and ABSINTH implicit solvent model with fixed backbone49 (Fig. 1c). Finally, the system was solvated and equilibrated with explicit solvent using the Amber ff03ws50 force field, TIP4P/2005 water model,51 and ~100 mM NaCl52 (Fig. 1d). By utilizing the specialized software and hardware from Anton 2 supercomputer developed by DE Shaw Research,47 we equilibrated the system for 150 ns to relax it to its equilibrium density (Fig. S2) and collected a 2 μs trajectory in the NVT ensemble at 298 K for each sequence of interest (see supporting methods for details).
Figure 1:
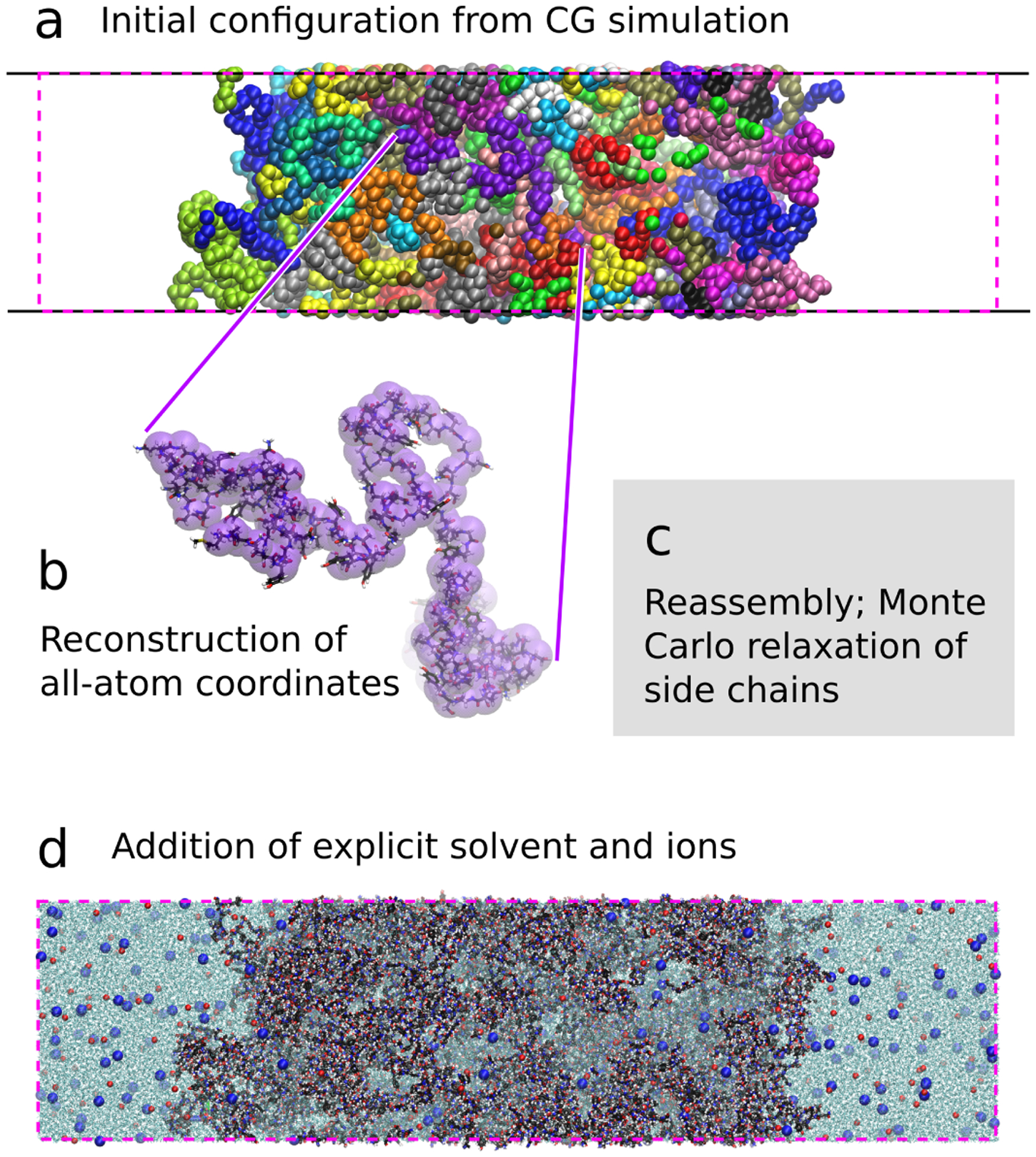
Procedure to set up all-atom simulations of dense phase. (a) An initial configuration is generated by CG simulations in a box with elongated z-dimension. (b) All-atom coordinates reconstructed from CG Cα coordinates templates for each chain using PDB database. (c) Reconstructed chains reassembled into condensed phase and sidechain clashes relieved using short Monte Carlo simulations with frozen backbone. (d) Addition of solvent and ions to generate complete system at all-atom resolution.
All-atom simulations with explicit solvent can provide a great deal of information not accessible from CG models, most obviously how the solvent and ions partition into the dense phase, and how this depends on protein sequence. The initial protein concentration in the dense phase for both proteins was selected based on the NMR measurement of condensed phase FUS LC to be ~477 mg/mL,22 and typical for protein LLPS.53 We note that there is also some indirect evidence for extremely low density condensates of LAF-1 RGG under certain conditions but it is not consistent with directly measured values for a human homolog ddx4 with very similar sequence which forms very high density phases.53,54 In both cases, the protein-rich phase has a higher total density than water (black lines), which agrees with the experimental observations that condensates of these proteins can be sedimented or separated using centrifugation.4,46 In our system size with 40 chains, the expected number of chains in the dilute phase is close to zero. We therefore designed the simulation to have all the chains in the condensed slab. The density of the dilute phase cannot be estimated due to the fact that the escape of one or two chains from the slab happens at a much longer time scale than our simulation length. However, the diffusion of solvent and ions is very rapid and so their equilibrium partitioning can be readily probed from our all-atom simulations, as shown in Fig. 2 for FUS LC and LAF-1 RGG protein condensates. The water content inside both FUS LC and LAF-1 RGG protein-rich regions is on the order of ~600 mg/mL (Figs. 2a and b), very similar despite significant differences in their sequence composition. The water content inside the FUS LC protein-rich phase from the simulation is consistent with the reported experimental estimate of 65% (by volume) by Murthy et al.22
Figure 2:
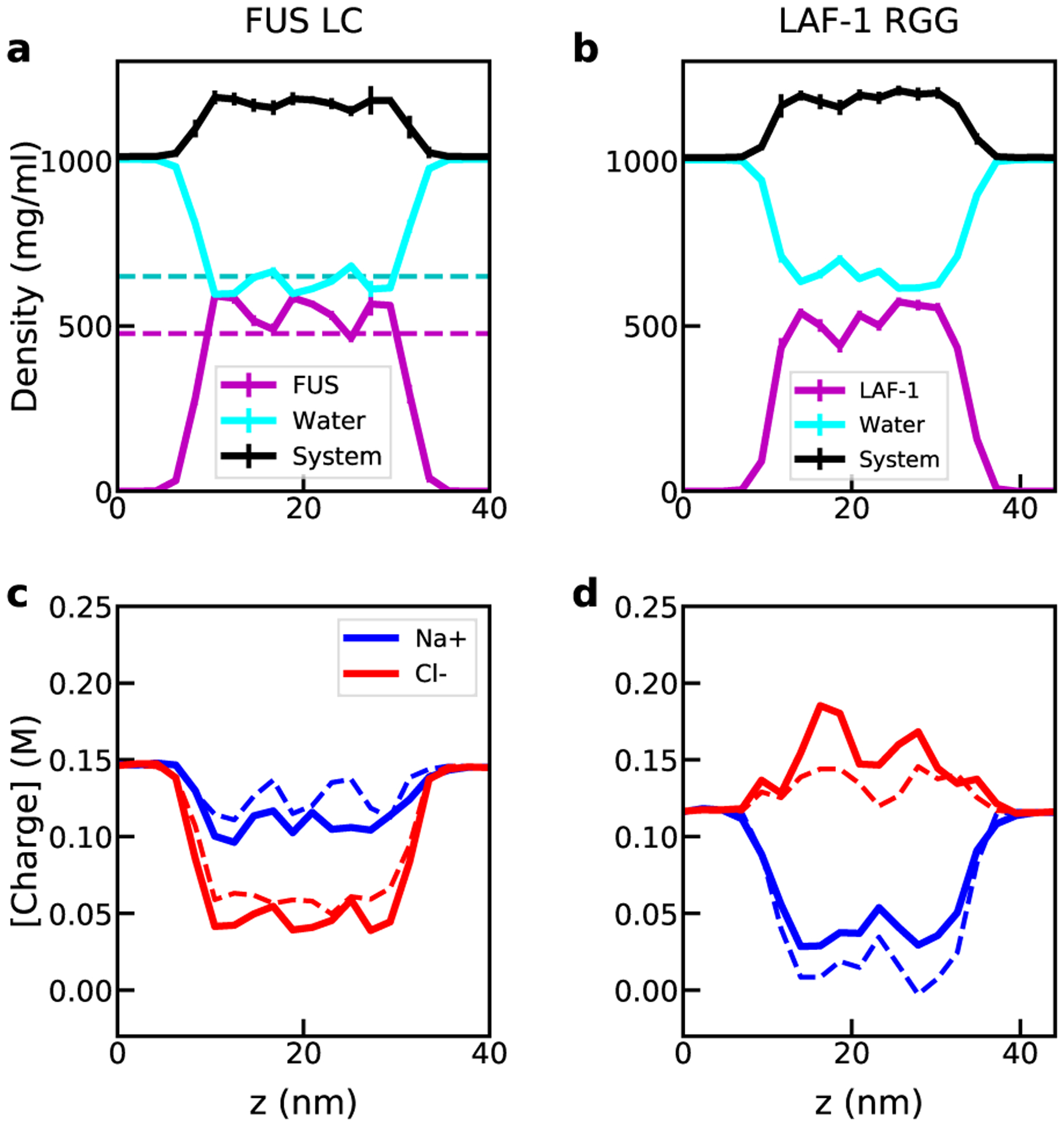
Density profiles from all-atom slab simulations of FUS LC (left) and LAF-1 RGG (right). Components are shown in the legend. Dashed lines in (a) indicate experimentally determined values22 and dashed lines in (c) and (d) indicate the predicted ion concentration using concentrations of protein cationic and anionic residues.
Despite very similar protein and water density profiles for FUS LC and LAF-1 RGG, the partitioning of Na+ and Cl− ions differs considerably between the two systems (Fig. 2c and d). In the case of FUS LC, which only has two anionic residues (Asp), the concentration of Cl− ions is greatly reduced inside the protein-rich phase, being preferentially excluded, while Na+ ion concentration is only slightly reduced in the protein-rich phase (Fig. 2c). For LAF-1 RGG (Fig. 2d), which contains a more significant fraction of anionic and cationic charged residues (26% of charged amino acids), the Cl− ions are preferentially incorporated into the protein-rich region, while the Na+ ions are excluded. This likely has to do with the net +4 charge per protein chain for LAF-1 RGG. The equilibrium partition coefficient of ions reflects an interplay of direct charge-charge interactions between charged amino acids and ions and the free energy of transferring the ions from a solvent-rich to a protein-rich environment. Using a simple model, we can predict the local concentration of Na+ and Cl− from the local concentration of cationic and anionic residues (Fig. S3) and bulk concentrations of ions and water. We set
| (1) |
to represent electroneutrality, and
| (2) |
which assumes negligible preferential interactions between ions and amino acids, as would be expected at these relatively low ion concentrations. The predicted Na+ and Cl− concentrations are plotted in Figs. 2c and d as dashed lines, and show good agreement with the concentrations obtained from the simulation. These results highlight the role of the charged amino acids in determining the density and composition of the protein condensates, which ultimately help to determine their function.
While equilibrium concentrations and compositions of MLOs are important to their function, another important factor is the dynamics within the dense phase, as it determines the rate at which components may pass through or rearrange within the condensate. Our MD simulations also provide detailed information on the dynamics within the condensed phase, and may be used to decouple the different components. The heterogeneous nature of our system with a distinct protein-rich environment, protein-poor bulk region, and an interfacial region poses some challenges to estimate diffusion coefficients unambiguously using the standard approach based on the mean square displacement. An alternative approach is to compute the probability distributions P(ξ(t0 + t) − ξ(t0)) for molecular displacement (i.e. propagators) in each direction ξ = x, y, z as a function of the lag time t between observations (see supporting methods and Fig. S4). Since the simulation box is not cubic, we report diffusivity (D) values based on only the longer z-axis, in order to minimize the finite size effects.55 We find it necessary to include more than one term (multiple D values) while fitting the propagator data from simulation to the expected distribution for one-dimensional diffusion. This behavior is consistent with the expected differences in the dynamics of solvent molecules within the protein-rich and bulk phases. We find that the observed behavior of water and ions is best accounted for by three D values whereas one D value is sufficient for fitting protein propagator data (Fig. S4).
The fastest D value for water (D1 ≈ 1.98 nm2/ns in FUS LC simulation) is consistent with the literature value (2.30 nm2/ns56), and its relative contribution to the propagators is also compatible with the number of water molecules in the bulk region (Table S2). The second mode is significantly slower, by a factor of 5 from the bulk diffusion, very close to the 6-fold decreased diffusivity reported for buffer molecules within FUS condensates.22 Based on this agreement, and its contribution to the propagator, we expect D2 reflects slower water diffusion inside the protein-rich region (Table S2). The slowest mode (~0.8% contribution) is difficult to pinpoint but is likely coming from a combination of factors, most importantly, water molecules directly interacting with protein atoms (Table S2). Similar to water diffusion, the dynamical behavior of ions reflects the presence of distinct populations. Most importantly, each mode’s contribution and its relative difference from bulk diffusion appear to depend on the protein sequence (Table S2).
The protein dynamics inside the condensed phase is closely connected to its liquid-like properties, needed for maintaining the biological function of the biomolecular condensate.57 To estimate the rate of relaxation of intramolecular protein degrees of freedom, we calculate the time autocorrelation function of the radius of gyration (Fig. S5) yielding average correlation times of 192 and 122 ns for FUS LC and LAF-1 RGG respectively. We note that relaxation timescales for LAF-1 RGG are somewhat shorter compared with those for FUS LC, and that they are comparable to experimental estimates for isolated IDPs of similar length.58,59 This suggests that formation of the condensed phase has only a modest effect on intramolecular dynamics. The 2 μs long MD simulations are at least 10 times longer than this relaxation timescale, which gives reasonable confidence in our ability to directly compute the diffusivity values of these two proteins (Fig. 3). The diffusion coefficient obtained for FUS LC is in excellent agreement with a previously determined value from FRAP and NMR diffusion experiments by Fawzi and co-workers4,22 (Fig. 3). Consistent with the faster chain relaxation time, the LAF-1 RGG diffusion coefficient is higher than that for the FUS LC. This may be explained because both the interchain and intrachain interactions governing frictional effects should have a similar dependence on the protein sequence.
Figure 3:
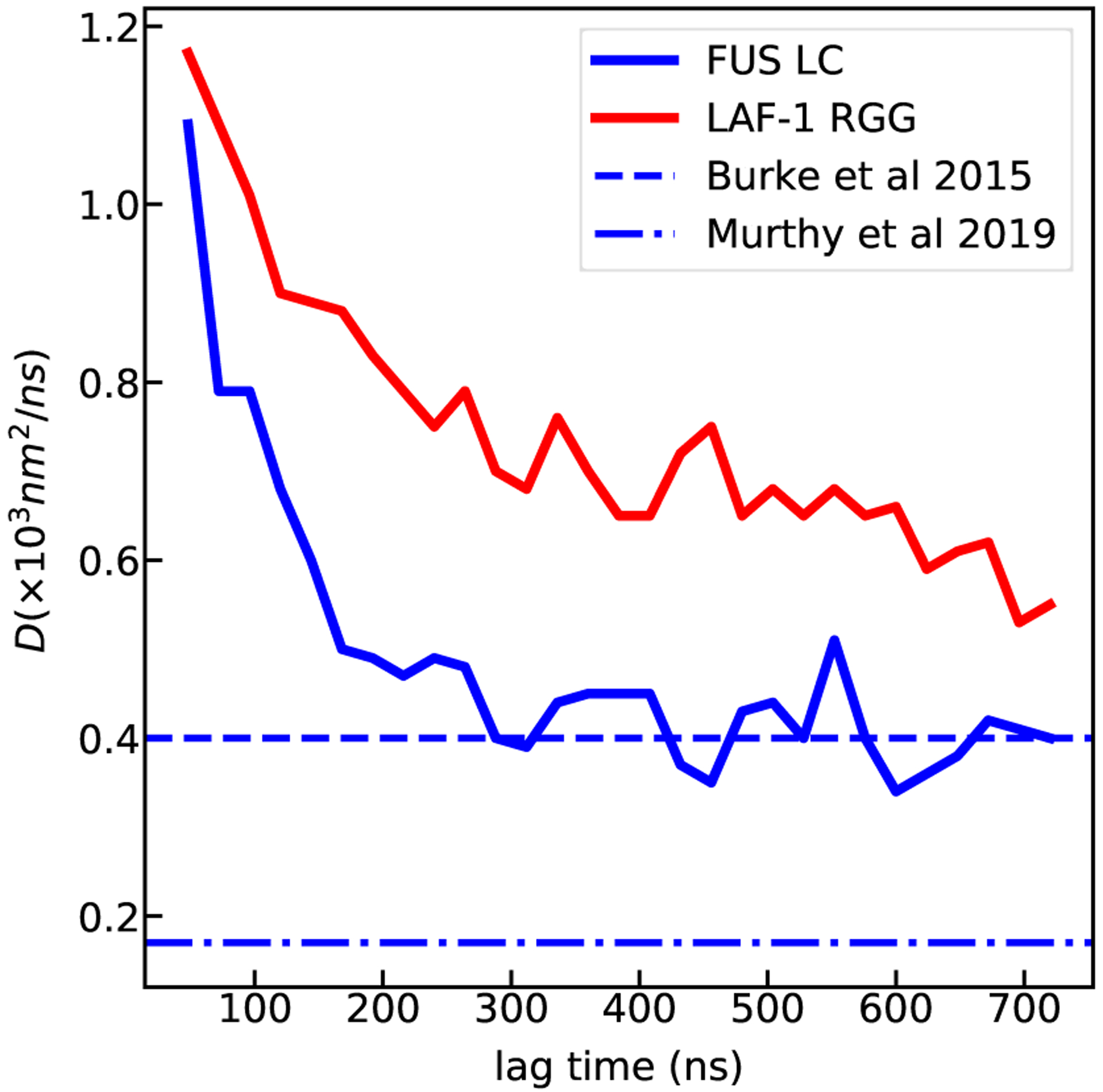
Protein self-diffusion coefficients within the slab along the z-axis, from all-atom slab simulations of FUS LC (blue) and LAF-1 RGG (red) are shown as a function of the lag time. Dashed horizontal line indicates experimentally determined diffusivity value for FUS LC.4
Because of the potential significance of secondary structure elements in mediating interactions in condensed phases,45 we examined the secondary structure populations of the proteins in the condensed phase using the DSSP algorithm60 (Fig. S6). From this analysis, we find that the protein chains are largely disordered, with more than 50% of residues in a coil conformation, with local helices being the most common type of structured state (Fig. S6). This is consistent with experimental NMR studies showing a lack of structure within FUS condensates,4,22,30 and condensates of a protein similar to LAF-1 IDR, Ddx4.53
The central goal of this work was to elucidate the atomic-resolution interactions stabilizing a condensed proteinaceous phase which cannot be accessed through lower-resolution CG simulations. This information is essential to gain a fundamental mechanistic understanding of molecular driving forces and developing theory for the sequence determinants of protein assembly. Previous studies have highlighted the role of various interaction modes that may be responsible for driving the LLPS of different protein sequences, such as salt bridges,28,53 cation-π interactions,61,62 hydrophobic interactions,22,39,63 sp2/π interactions between several residue pairs including the protein backbone,21,22 and hydrogen bonding interactions.22,39,64 There is still a limited understanding of the relative importance of these different interaction modes in the context of a particular type of amino acid pair, or a protein sequence. We attempt to provide answers to some of these questions here.
To characterize the regions of each sequence most involved in molecular interactions, we start by computing the number of intermolecular van der Waals (vdW) contacts (see supporting methods for definitions) formed as a function of protein residue number (Figs. 4a and b) per frame, averaged over the entire trajectory. We find that contacts are relatively evenly distributed throughout the FUS LC sequence (Fig. 4a), which is consistent with NMR data.22 One can observe intermittent peaks in the one-dimensional contact map data arising from the Tyr residues distributed throughout the FUS LC sequence (Fig. 4A, black dashed lines in the bottom panel). For LAF-1 RGG, the contacts are still distributed throughout the chain with a notable contact-prone region between residues 20–28 (Fig. 4b), which was identified previously from our CG model simulation and tested experimentally to be critical for promoting LLPS.36
Figure 4:
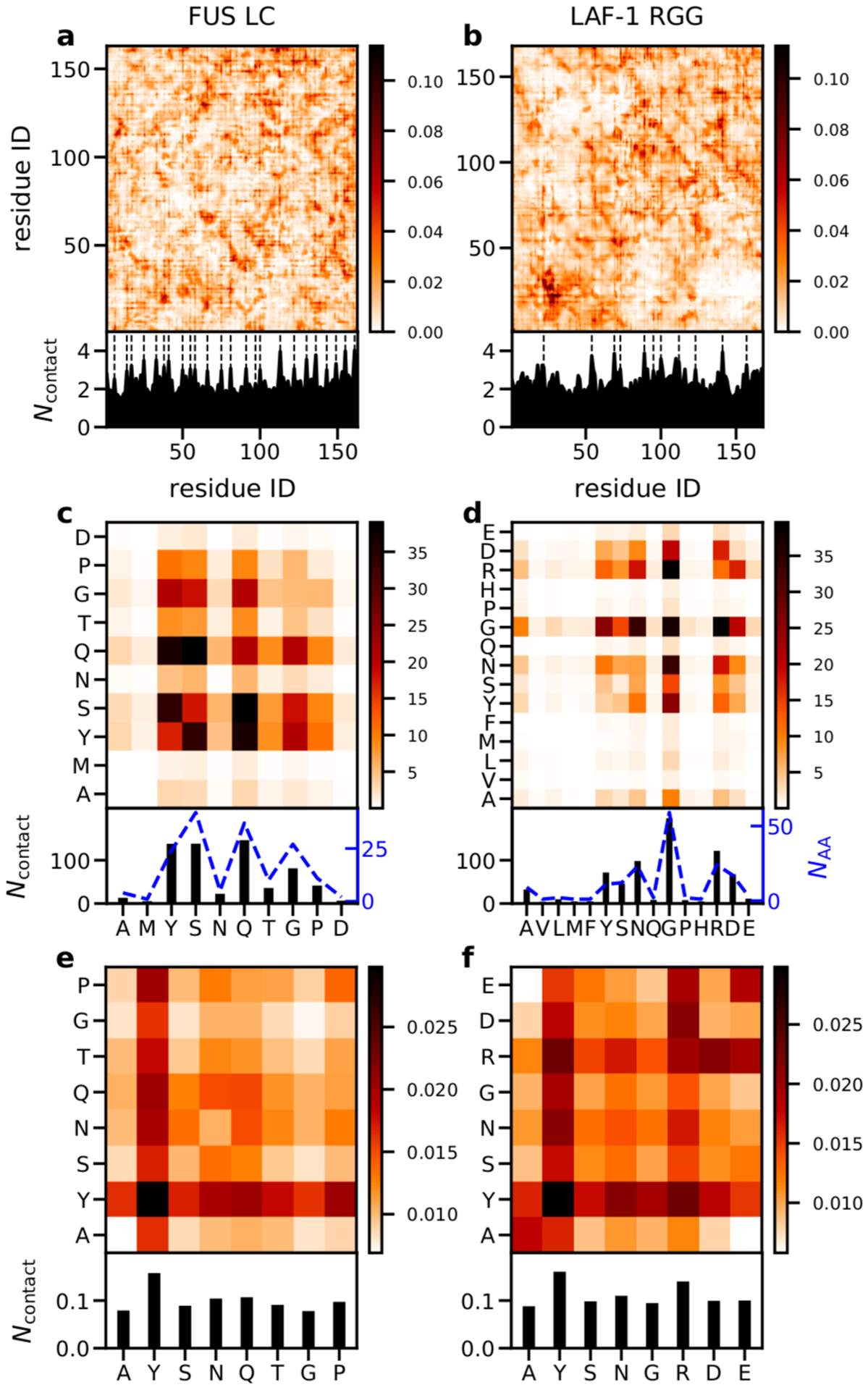
Intermolecular contacts within the condensed phase of FUS LC (left) and LAF-1 RGG (right), as a function of residue index (a and b) and amino acid types (c and d). The intermolecular contacts normalized by the relative abundance of each amino acid in the sequence are shown in e and f. In each of the figure, the bottom panel shows the one dimensional summation. The black dashed lines in a and b show the position of Tyr residues. The blues lines in c and d show the number of amino acids (NAA) in the sequence.
To obtain a better understanding of how different amino acid types contribute to the formation of intermolecular contacts between protein chains, we combine the contact data for different pairs of the same kind. From this data in Figs. 4c and d, one can identify important residue pairs as well as residue types that are primarily responsible for interchain interactions and for stabilizing the condensed protein-rich phase. For both FUS LC and LAF-1 RGG, Tyr interactions with itself and other residues are highly abundant and likely essential drivers of LLPS.21,22,28,37,62,64,65 Importantly, polar residues (Gln and Ser in the case of FUS LC and Asn in LAF-1 RGG ) also participate in significant contacts, consistent with a recent mutagenesis study highlighting their role in LLPS.22 Also, Gly residues appear to be forming contacts with many other residue types in both proteins; this is highly visible in the LAF-1 RGG data for interactions with Arg, Gly, Tyr, and Asn. Lastly, LAF-1 RGG contact formation is enhanced by interactions between oppositely-charged residue pairs such as Arg-Asp pairs (Fig. 4d). To obtain the intrinsic propensity for each amino acid to form a contact, we also normalize the contacts by the relative abundance of each amino acid in the sequence (Figs. 4e and f). The overall values are largely consistent between the FUS LC and LAF-1 RGG simulations, and supports the critical role of Tyr and Arg due to their intrinsic preference to form contacts while the Gly-involved contacts are present due to its abundance in both the sequences. Even though Gln and Ser contribute as many total contacts as Tyr, each individual Tyr contributes more. This is because there are more Ser and Gln than Tyr in FUS LC sequence. Additionally, Tyr is bigger than Ser and Gly, which may allow it to make more simultaneous contacts. We have also calculated the intramolecular interactions in the same way and obtained excellent agreement with the intermolecular interactions (Figs. S7 and S8), which supports our recent finding connecting the self-interaction properties of the single chain with LLPS behaviors.32 Data for residues that are an insignificant fraction of the protein composition (appearing ≤2 times) have been excluded from the plot due to higher uncertainty associated with their contacts. In addition, we have included a comparison of the residue-specific contacts between the all-atom simulations and the initial configuration reconstructed from the CG simulation (Fig. S9 and S10). We find for different pairs of amino acids, the contact difference is not uniform, suggesting the variation does not solely come from compaction or expansion of the chain. The all-atom force field refines residue-level interactions through a finer description of atomic interactions and therefore is expected to provide a more accurate description of molecular interactions stabilizing the condensed protein-rich phase. Closer examination of the differences between coarse-grained and all-atom models indicates that the same residue pairs in each protein have similar shifts, suggesting that they represent small, but significant differences between the models.
To dive deeper into the atomic interactions responsible for the observed role of the amino acids identified above, we determine the interaction modes present when two residues form a vdW contact. Based on the previous literature,21,22,62 the most important modes are sp2/π, hydrogen bonding, cation-π, and salt bridge. Here, we separate these interactions into contacts between backbone atoms (bb-bb), sidechain atoms (sc-sc), or backbone and sidechain (bb-sc) atoms (see supporting methods for definition of these interaction modes). The amino acid pairs are sorted by the number of vdW contacts formed (Fig. S11) and the top 20 amino acid pair types for each group and each protein are shown in Fig. 5 with the full version in Fig. S12. The interaction modes from intramolecular interactions (Figs. S13 and S14) are highly similar to those from intermolecular interactions, so we only discuss the intermolecular version here.
Figure 5:
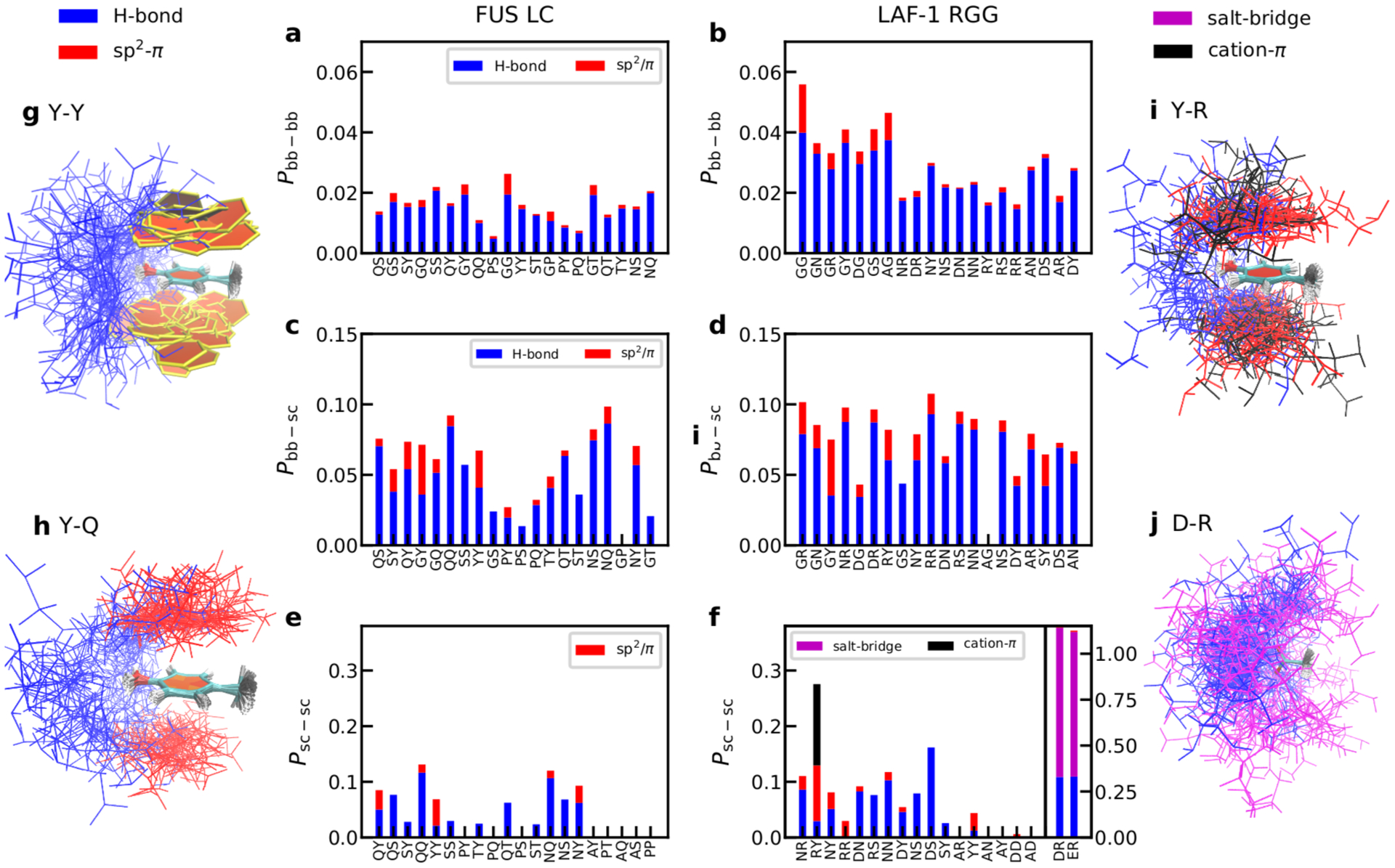
Interaction modes contributing to the intermolecular contacts separated into contributions between backbone atoms (bb-bb, a and b), between backbone and sidechain atoms (bb-sc, c and d) and between sidechain atoms (sc-sc, e and f). The amino acid pairs are sorted by the number of contacts formed between these pairs in each group as shown in Fig. S11. Some configurations of representative interacting amino acids are shown in g for FUS LC Tyr:Tyr, h for FUS LC Tyr:Gln, i for LAF-1 RGG Tyr:Arg and j for LAF-1 RGG Asp:Arg. The configurations are aligned to Tyr in g, h and i and to Asp in j. The color code is the same as the interaction mode shown in the legend. Rings are shown in paperchain representation.66
For both FUS LC and LAF-1 RGG, we first note that most of the vdW contacts are non-specific and thus only a small fraction can be classified into any of the aforementioned specific interaction modes (Figs. 5a–f). This emphasizes the importance of non-specific interaction modes, including the hydrophobic interactions, in promoting LLPS. Within the context of interaction modes in FUS LC, all pairs except for those involving Tyr are primarily stabilized by hydrogen bonds (Figs. 5a,c and e). Interactions involving sp2/π groups are a relatively small fraction of the contacts, except for residue pairs involving Tyr, with contributions from the sp2/π mode higher than from hydrogen bonds. The configurations of representative amino acid interactions are also shown in Figs. 5g and h. For both Tyr and Gln interactions, sp2/π interaction modes tend to form on top or bottom of the sidechain whereas hydrogen bonds are around the side. This suggests for aromatic amino acids like Tyr, hydrogen bonds might not directly compete with forming sp2/π interactions and can still be a major contribution to stabilizing the condensates.
For the LAF-1 RGG, we include two additional interaction modes, salt bridges and cation-π interactions, involving charged residues (Figs. 5b,d and f). We find that charged amino acids contribute heavily to LAF-1 sidechain interactions, with hydrogen bond and sp2/π interactions from aromatic amino acids playing secondary roles (Fig. 5f). Previously, we have shown that certain pairings of residues can form contacts using different interaction modes, either switching between them, or forming multiple contacts cooperatively,36 particularly cation-π and sp2/π interactions between Arg and Tyr. Here we also find hydrogen bonds and salt bridges between cationic-aromatic pairings and oppositely-charged residues are among the strongest interactions occurring within the LAF-1 condensate (Fig. 5f), and different interaction modes can occur at the same time, e.g. cation-π and sp2/π interactions between Arg and Tyr (Fig. 5i), and salt bridge and hydrogen bonds between Arg and Asp (Fig. 5j). This is also the reason the total probability of interaction modes might exceed 1 for interactions involving charged amino acids (Fig. 5f).
Conclusion
In this work, we present a general methodology for initializing, conducting, and analyzing all-atom explicit-solvent simulations of biomolecular condensates in coexistence with a surrounding aqueous phase. We have optimized the procedure for systems with components of similar size to FUS LC and LAF-1 RGG so that similar simulations should be accessible using even general-purpose computing hardware (Table S1). We have leveraged our earlier work with CG simulations of IDP phase coexistence,5,22,24,30,32,36,41,42,67 and atomistic studies of inter-protein interactions5,22,24,36 to obtain important mechanistic details of the underlying molecular interactions of condensates. We note there are properties that cannot be adequately sampled by all-atom simulations, however we believe there are a number of key insights such as atomic level interactions and diffusion of protein, water and ions in the condensed phase that cannot be obtained in a CG simulation.
We find that the proteins are remarkably dynamic in the condensed phase, having intramolecular correlation times very comparable to those typical of isolated intrinsically disordered proteins. This flexibility is key to the liquid-like properties of the protein-rich phase. While the dense phase is highly viscous, we are also able to measure the protein diffusivity, finding excellent agreement with experimental results where available. Similarly, we show that water and ions are able to rapidly diffuse between phases, with diffusion coefficients within the dense phase reduced.
For both tested proteins, the equilibrium distribution of sodium and chloride ions within the condensed phase is essentially determined by the charge distribution and water content inside the phase-separated proteins. This implies that there is no strong preferential interaction of these ions with protein residues in these systems under the conditions we study. We note, however, that ions exhibiting stronger Hofmeister effects, or higher salt concentrations,68–70 may alter this result, and would be interesting to consider in future work.
Finally, we find many types of residue-residue interactions are responsible for stabilizing the condensed phase, and contacts involving Gly are particularly abundant due to its frequency in the sequence. After normalizing for residue frequency, however, it appears that each Tyr contributes more interactions per residue than any other residue type, explaining its apparent importance in mutagenic approaches. For LAF-1 RGG, in addition to Tyr interactions, we observe that both cation-π interactions (particularly involving Arg) and salt bridges contribute to the condensate’s stability. The approach outlined here can be used to explore the generality of these findings in the context of other protein sequences.
Supplementary Material
Acknowledgement
We acknowledge useful discussions with Dr. Anastasia Murthy. This work was supported in part by the National Institutes of Health (NIH) grants R01GM120537 (J.M.), R01NS116176 (N.L.F. and J.M.), and R01GM118530 (N.L.F.), National Science Foundation grants DMR-2004796 (J.M.) and MCB-2015030 (W.Z.). R.B. was supported by the Intramural Research Program of the National Institute of Diabetes and Digestive and Kidney Diseases of the NIH and Y.C.K by the Office of Naval Research via the U.S. Naval Research Laboratory base program. This research used computational resources of Anton 2, XSEDE (supported by the NSF project no. TG-MCB120014), and the NIH HPC Biowulf cluster (http://hpc.nih.gov). The Anton 2 machine at PSC was generously made available by D.E. Shaw Research and the computer time was provided by the Pittsburgh Supercomputing Center (PSC) through NIH Grant R01GM116961.
Footnotes
Supporting Information Available
Supporting information includes: Detailed description of simulation setup, conversion to atomic resolution, minimization, and production simulation as well as description of modes of contact.
References
- (1).Berry J; Weber SC; Vaidya N; Haataja M; Brangwynne CP RNA transcription modulates phase transition-driven nuclear body assembly. Proc. Natl. Acad. Sci. U.S.A 2015, 112, E5237–E5245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (2).Feric M; Vaidya N; Harmon TS; Mitrea DM; Zhu L; Richardson TM; Kriwacki RW; Pappu RV; Brangwynne CP Coexisting liquid phases underlie nucleolar subcompartments. Cell 2016, 165, 1686–1697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (3).Mitrea DM; Cika JA; Stanley CB; Nourse A; Onuchic PL; Banerjee PR; Phillips AH; Park C-G; Deniz AA; Kriwacki RW Self-interaction of NPM1 modulates multiple mechanisms of liquid–liquid phase separation. Nat. Commun 2018, 9, 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (4).Burke KA; Janke AM; Rhine CL; Fawzi NL Residue-by-residue view of in vitro FUS granules that bind the C-terminal domain of RNA polymerase II. Mol. Cell 2015, 60, 231–241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (5).Ryan VH; Dignon GL; Zerze GH; Chabata CV; Silva R; Conicella AE; Amaya J; Burke KA; Mittal J; Fawzi NL Mechanistic View of hnRNPA2 Low-Complexity Domain Structure, Interactions, and Phase Separation Altered by Mutation and Arginine Methylation. Mol. Cell 2018, [DOI] [PMC free article] [PubMed] [Google Scholar]
- (6).Riback JA; Katanski CD; Kear-Scott JL; Pilipenko EV; Rojek AE; Sosnick TR; Drummond DA Stress-triggered phase separation is an adaptive, evolutionarily tuned response. Cell 2017, 168, 1028–1040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (7).Brangwynne CP; Eckmann CR; Courson DS; Rybarska A; Hoege C; Gharakhani J; Jülicher F; Hyman AA Germline P granules are liquid droplets that localize by controlled dissolution/condensation. Science 2009, 324, 1729–1732. [DOI] [PubMed] [Google Scholar]
- (8).Marzahn MR; Marada S; Lee J; Nourse A; Kenrick S; Zhao H; Ben-Nissan G; Kolaitis R-M; Peters JL; Pounds S et al. Higher-order oligomerization promotes localization of SPOP to liquid nuclear speckles. EMBO J. 2016, e201593169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (9).Sabari BR; Dall’Agnese A; Boija A; Klein IA; Coffey EL; Shrinivas K; Abraham BJ; Hannett NM; Zamudio AV; Manteiga JC et al. Coactivator condensation at super-enhancers links phase separation and gene control. Science 2018, 361, eaar3958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (10).Milovanovic D; Wu Y; Bian X; De Camilli P A liquid phase of synapsin and lipid vesicles. Science 2018, 361, 604–607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (11).Larson AG; Elnatan D; Keenen MM; Trnka MJ; Johnston JB; Burlingame AL; Agard DA; Redding S; Narlikar GJ Liquid droplet formation by HP1α suggests a role for phase separation in heterochromatin. Nature 2017, 547, 236–240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (12).Shin Y; Chang Y-C; Lee DSW; Sanders DW; Ronceray P; Wingreen NS; Haataja MP; Brangwynne CP Liquid nuclear condensates mechanically sense and restructure the genome. Cell 2018, 175, 1481–1491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (13).Sanulli S; Trnka MJ; Dharmarajan V; Tibble RW; Bascal BD; Burlingame AL; Griffin PR; Gross JD; Narlikar GJ HP1 reshapes nucleosome core to promote phase separation of heterochromatin. Nature 2019, 575, 390–394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (14).Gibson BA; Doolittle LK; Schneider MWG; Jensen LE; Gamarra N; Henry L; Gerlich DW; Redding S; Rosen MK Organization of chromatin by intrinsic and regulated phase separation. Cell 2019, 179, 470–484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (15).Patel A; Lee HO; Jawerth L; Maharana S; Jahnel M; Hein MY; Stoynov S; Mahamid J; Saha S; Franzmann TM et al. A liquid-to-solid phase transition of the ALS protein FUS accelerated by disease mutation. Cell 2015, 162, 1066–1077. [DOI] [PubMed] [Google Scholar]
- (16).Gomes E; Shorter J The molecular language of membraneless organelles. J. Biol. Chem 2019, 294, 7115–7127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (17).Simon JR; Carroll NJ; Rubinstein M; Chilkoti A; López GP Programming molecular self-assembly of intrinsically disordered proteins containing sequences of low complexity. Nat. Chem 2017, 9, 509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (18).Lau HK; Paul A; Sidhu I; Li L; Sabanayagam CR; Parekh SH; Kiick KL Microstructured Elastomer-PEG Hydrogels via Kinetic Capture of Aqueous Liquid-Liquid Phase Separation. Adv. Sci 2018, 5, 1701010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (19).Roberts S; Harmon TS; Schaal JL; Miao V; Li KJ; Hunt A; Wen Y; Oas TG; Collier JH; Pappu RV et al. Injectable tissue integrating networks from recombinant polypeptides with tunable order. Nat. Mater 2018, 17, 1154–1163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (20).Nott TJ; Craggs TD; Baldwin AJ Membraneless organelles can melt nucleic acid duplexes and act as biomolecular filters. Nat. Chem 2016, 8, 569–575. [DOI] [PubMed] [Google Scholar]
- (21).Vernon RM; Chong PA; Tsang B; Kim TH; Bah A; Farber P; Lin H; Forman-Kay JD Pi-Pi contacts are an overlooked protein feature relevant to phase separation. Elife 2018, 7, e31486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (22).Murthy AC; Dignon GL; Kan Y; Zerze GH; Parekh SH; Mittal J; Fawzi NL Molecular interactions underlying liquid- liquid phase separation of the FUS low-complexity domain. Nat. Struct. Mol. Biol 2019, 26, 637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).Kim TH; Tsang B; Vernon RM; Sonenberg N; Kay LE; Forman-Kay JD Phospho-dependent phase separation of FMRP and CAPRIN1 recapitulates regulation of translation and deadenylation. Science 2019, 365, 825–829. [DOI] [PubMed] [Google Scholar]
- (24).Conicella AE; Dignon GL; Zerze GH; Schmidt HB; Alexandra M; Kim YC; Rohatgi R; Ayala YM; Mittal J; Fawzi NL TDP-43 α-helical structure tunes liquid-liquid phase separation and function. Proc. Natl. Acad. Sci. U.S.A 2020, 117, 5883–5894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (25).Dignon GL; Best RB; Mittal J Biomolecular Phase Separation: From Molecular Driving Forces to Macroscopic Properties. Annu. Rev. Phys. Chem 2020, 71, 53–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (26).Darling AL; Liu Y; Oldfield CJ; Uversky VN Intrinsically Disordered Proteome of Human Membrane-Less Organelles. Proteomics 2018, 18, 1700193. [DOI] [PubMed] [Google Scholar]
- (27).Asherie N Protein crystallization and phase diagrams. Methods 2004, 34, 266–272. [DOI] [PubMed] [Google Scholar]
- (28).Pak CW; Kosno M; Holehouse AS; Padrick SB; Mittal A; Ali R; Yunus AA; Liu DR; Pappu RV; Rosen MK Sequence determinants of intracellular phase separation by complex coacervation of a disordered protein. Mol. Cell 2016, 63, 72–85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (29).Zerze GH; Zheng W; Best RB; Mittal J Evolution of All-atom Protein Force Fields to Improve Local and Global Properties. J. Phys. Chem. Lett 2019, 10, 2227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (30).Monahan Z; Ryan VH; Janke AM; Burke KA; Zerze GH; O’Meally R; Dignon GL; Conicella AE; Zheng W; Best RB et al. Phosphorylation of FUS low-complexity domain disrupts phase separation, aggregation, and toxicity. EMBO J. 2017, doi, 10.15252/embj.201696394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (31).Hofweber M; Hutten S; Bourgeois B; Spreitzer E; Niedner-Boblenz A; Schifferer M; Ruepp M-D; Simons M; Niessing D; Madl T et al. Phase separation of FUS is suppressed by its nuclear import receptor and arginine methylation. Cell 2018, 173, 706–719. [DOI] [PubMed] [Google Scholar]
- (32).Dignon GL; Zheng W; Best RB; Kim YC; Mittal J Relation between single-molecule properties and phase behavior of intrinsically disordered proteins. Proc. Natl. Acad. Sci. U.S.A 2018, 115, 9929–9934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (33).Lin Y-H; Chan HS Phase Separation and Single-Chain Compactness of Charged Disordered Proteins Are Strongly Correlated. Biophys. J 2017, 112, 2043–2046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (34).Best RB Computational and theoretical advances in studies of intrinsically disordered proteins. Curr. Opin. Struct. Biol 2017, 42, 147–154. [DOI] [PubMed] [Google Scholar]
- (35).Best RB Emerging consensus on the collapse of unfolded and intrinsically disordered proteins in water. Curr. Opin. Struct. Biol 2020, 60, 27–38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (36).Schuster BS; Dignon GL; Tang WS; Kelley FM; Ranganath AK; Jahnke CN; Simpkins AG; Regy RM; Hammer DA; Good MC et al. Identifying sequence perturbations to an intrinsically disordered protein that determine its phase-separation behavior. Proc. Natl. Acad. Sci. U.S.A 2020, 117, 11421–11431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (37).Martin EW; Holehouse AS; Peran I; Farag M; Incicco JJ; Bremer A; Grace CR; Soranno A; Pappu RV; Mittag T Valence and patterning of aromatic residues determine the phase behavior of prion-like domains. Science 2020, 367, 694–699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (38).Karandur D; Wong K-Y; Pettitt BM Solubility and aggregation of Gly5 in water. J. Phys. Chem. B 2014, 118, 9565–9572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (39).Rauscher S; Pomès R The liquid structure of elastin. Elife 2017, 6, e26526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (40).Paloni M; Bailly R; Ciandrini L; Barducci A Unraveling molecular interactions in a phase-separating protein by atomistic simulations. bioRxiv 2020, 10.1101/2020.05.16.099051. [DOI] [PubMed] [Google Scholar]
- (41).Dignon GL; Zheng W; Kim YC; Best RB; Mittal J Sequence determinants of protein phase behavior from a coarse-grained model. PLoS Comput. Biol 2018, 14, e1005941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (42).Dignon GL; Zheng W; Kim YC; Mittal J Temperature-Controlled Liquid-Liquid Phase Separation of Disordered Proteins. ACS Cent. Sci 2019, 5, 821. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (43).Perdikari TM; Jovic N; Dignon GL; Kim YC; Fawzi NL; Mittal J A predictive coarse-grained model for position-specific effects of post-translational modifications on disordered protein phase separation. bioRxiv 2020, 10.1101/2020.06.12.148650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (44).Regy RM; Dignon GL; Zheng W; Kim YC; Mittal J Sequence dependent co-phase separation of RNA-protein mixtures elucidated using molecular simulations. bioRxiv 2020, 10.1101/2020.07.07.192047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (45).Conicella AE; Zerze GH; Mittal J; Fawzi NL ALS mutations disrupt phase separation mediated by α-helical structure in the TDP-43 low-complexity C-terminal domain. Structure 2016, 24, 1537–1549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (46).Elbaum-Garfinkle S; Kim Y; Szczepaniak K; Chen CC-H; Eckmann CR; Myong S; Brangwynne CP The disordered P granule protein LAF-1 drives phase separation into droplets with tunable viscosity and dynamics. Proc. Natl. Acad. Sci. U.S.A 2015, 112, 7189–7194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (47).Shaw DE; Grossman J; Bank JA; Batson B; Butts JA; Chao JC; Deneroff MM; Dror RO; Even A; Fenton CH et al. Anton 2: raising the bar for performance and programmability in a special-purpose molecular dynamics supercomputer. Proceedings of the international conference for high performance computing, networking, storage and analysis. 2014; pp 41–53. [Google Scholar]
- (48).Rotkiewicz P; Skolnick J Fast procedure for reconstruction of full-atom protein models from reduced representations. J. Comput. Chem 2008, 29, 1460–1465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (49).Vitalis A; Pappu RV ABSINTH: A new continuum solvent model for simulations of polypeptides in aqueous solutions. J. Comput. Chem 2008, 30, 673–699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (50).Best RB; Zheng W; Mittal J Balanced protein-water interactions improve properties of disordered proteins and non-specific protein association. J. Chem. Theory Comput 2014, 10, 5113–5124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (51).Abascal JLF; Vega C A general purpose model for the condensed phases of water: TIP4P/2005. J. Chem. Phys 2005, 123, 234505. [DOI] [PubMed] [Google Scholar]
- (52).Luo Y; Roux B Simulation of osmotic pressure in concentrated aqueous salt solutions. J. Phys. Chem. Lett 2010, 1, 183–189. [Google Scholar]
- (53).Brady JP; Farber PJ; Sekhar A; Lin Y-H; Huang R; Bah A; Nott TJ; Chan HS; Baldwin AJ; Forman-Kay JD et al. Structural and hydrodynamic properties of an intrinsically disordered region of a germ cell-specific protein on phase separation. Proc. Natl. Acad. Sci. U.S.A 2017, 114, E8194–E8203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (54).Wei M-T; Elbaum-Garfinkle S; Holehouse AS; Chen CC-H; Feric M; Arnold CB; Priestley RD; Pappu RV; Brangwynne CP Phase behaviour of disordered proteins underlying low density and high permeability of liquid organelles. Nat. Chem 2017, [DOI] [PMC free article] [PubMed] [Google Scholar]
- (55).Bullerjahn JT; von Bülow S; Hummer G Optimal estimates of self-diffusion coefficients from molecular dynamics simulations. J. Chem. Phys 2020, 153, 024116. [DOI] [PubMed] [Google Scholar]
- (56).Mills R Self-diffusion in normal and heavy water in the range 1–45. deg. J. Phys. Chem 1973, 77, 685–688. [Google Scholar]
- (57).Forman-Kay JD; Kriwacki RW; Seydoux G Phase separation in biology and disease. J. Mol. Biol 2018, 430, 4603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (58).Soranno A; Buchli B; Nettels D; Cheng RR; Müller-Späth S; Pfeil SH; Hoffmann A; Lipman EA; Makarov DE; Schuler B Quantifying Internal Friction in Unfolded and Intrinsically Disordered Proteins with Single-molecule Spectroscopy. Proc. Natl. Acad. Sci. U.S.A 2012, 109, 17800–17806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (59).Borgia A; Borgia MB; Bugge K; Kissling VM; Heidarsson PO; Fernandes CB; Sottini A; Buholzer KJ; Nettels D; Kragelund BB et al. Extreme disorder in an ultra-high-affinity protein complex. Nature 2018, 555, 61–66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (60).Kabsch W; Sander C Dictionary of protein secondary structure: pattern recognition of hydrogen-bonded and geometrical features. Biopolymers 1983, 22, 2577–2637. [DOI] [PubMed] [Google Scholar]
- (61).Song J; Ng SC; Tompa P; Lee KAW; Chan HS Polycation-π Interactions Are a Driving Force for Molecular Recognition by an Intrinsically Disordered Oncoprotein Family. PLoS Comput. Biol 2013, 9, e1003239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (62).Wang J; Choi J-M; Holehouse AS; Lee HO; Zhang X; Jahnel M; Maharana S; Lemaitre R; Pozniakovsky A; Drechsel D et al. A molecular grammar governing the driving forces for phase separation of prion-like RNA binding proteins. Cell 2018, 174, 688–699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (63).Fromm SA; Kamenz J; Nöldeke ER; Neu A; Zocher G; Sprangers R In Vitro Reconstitution of a Cellular Phase-Transition Process that Involves the mRNA Decapping Machinery. Angew. Chem. Int. Edit 2014, 53, 7354–7359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (64).Gabryelczyk B; Cai H; Shi X; Sun Y; Swinkels PJ; Salentinig S; Pervushin K; Miserez A Hydrogen bond guidance and aromatic stacking drive liquid-liquid phase separation of intrinsically disordered histidine-rich peptides. Nat. Commun 2019, 10, 1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (65).Lin Y; Currie SL; Rosen MK Intrinsically disordered sequences enable modulation of protein phase separation through distributed tyrosine motifs. J. Biol. Chem 2017, 292, 19110–19120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (66).Cross S; Kuttel MM; Stone JE; Gain JE Visualisation of cyclic and multi-branched molecules with VMD. J. Mol. Graph. Model 2009, 28, 131–139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (67).Dignon GL; Zheng W; Mittal J Simulation methods for liquid–liquid phase separation of disordered proteins. Curr. Opin. Chem. Eng 2019, 23, 92–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (68).Baldwin RL How Hofmeister ion interactions affect protein stability. Biophys. J 1996, 71, 2056–2063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (69).Vancraenenbroeck R; Harel YS; Zheng W; Hofmann H Polymer effects modulate binding affinities in disordered proteins. Proc. Natl. Acad. Sci. U.S.A 2019, 116, 19506–19512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (70).Welsh TJ; Krainer G; Espinosa JR; Joseph JA; Sridhar A; Jahnel M; Arter WE; Saar KL; Alberti S; Collepardo-Guevara R et al. Single particle zeta-potential measurements reveal the role of electrostatics in protein condensate stability. bioRxiv 2020, 10.1101/2020.04.20.047910. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


