Significance
Nonpharmaceutical interventions (NPIs), such as social distancing, reduce not only COVID-19 cases but also other circulating infections such as influenza and RSV. The susceptible population for these infections will increase while NPIs are in place. Using models fit to historic cases of RSV and influenza, we project large future outbreaks of both diseases may occur following a period of extended NPIs. These outbreaks, which may reach peak numbers in the winter, could increase the burden to healthcare systems.
Keywords: COVID-19, RSV, influenza, nonpharmaceutical interventions
Abstract
Nonpharmaceutical interventions (NPIs) have been employed to reduce the transmission of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), yet these measures are already having similar effects on other directly transmitted, endemic diseases. Disruptions to the seasonal transmission patterns of these diseases may have consequences for the timing and severity of future outbreaks. Here we consider the implications of SARS-CoV-2 NPIs for two endemic infections circulating in the United States of America: respiratory syncytial virus (RSV) and seasonal influenza. Using laboratory surveillance data from 2020, we estimate that RSV transmission declined by at least 20% in the United States at the start of the NPI period. We simulate future trajectories of both RSV and influenza, using an epidemic model. As susceptibility increases over the NPI period, we find that substantial outbreaks of RSV may occur in future years, with peak outbreaks likely occurring in the winter of 2021–2022. Longer NPIs, in general, lead to larger future outbreaks although they may display complex interactions with baseline seasonality. Results for influenza broadly echo this picture, but are more uncertain; future outbreaks are likely dependent on the transmissibility and evolutionary dynamics of circulating strains.
Nonpharmaceutical interventions (NPIs) have proven effective in reducing the spread of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) in many contexts (1–5). Policy measures including social distancing, school closures, travel restrictions, and the use of masks in public spaces have been implemented to reduce the transmission of the virus. In addition to SARS-CoV-2, NPIs may also reduce the transmission of other directly transmitted, respiratory infections (6, 7). Understanding the possible influence of a SARS-CoV-2 NPI period on the incidence of these infections remains a key question for the broader public health impact of the pandemic. Furthermore, the implications of relaxing NPIs for future outbreaks of these other infections have not been fully considered.
Many endemic, directly transmitted, respiratory infections exhibit distinct seasonal and longer-term cycles in incidence (8–10). While climate may drive the seasonality of these diseases in some cases (11–14), other directly transmitted infections, such as measles, are driven primarily by seasonal cycles of population aggregation such as the timing of school semesters (15, 16). Secular changes in susceptible recruitment, for instance, due to vaccination campaigns or declines in birth rates, can disrupt long-run patterns of infection dynamics (17, 18). Similarly, human movement via either displacement or migration has also been shown to alter patterns of infection (19). While there has been less work to identify the polymicrobial implications of nonpharmaceutical control measures, evidence from the 1918 influenza pandemic suggests that NPIs may have reduced measles transmission by 38% (20).
Two important directly transmitted, viral respiratory diseases circulating in the US population are seasonal influenza and respiratory syncytial virus (RSV). Seasonal influenza accounts for significant annual mortality, with the ongoing evolution of the virus’ antigenic sites leading to evasion of the host immune system (21, 22). Epidemics of seasonal influenza at higher latitudes are driven largely by variations in climate (12, 13). While there is some evidence of herd immunity, a complex interaction between alternating subtypes and antigenic drift determines year-to-year variation in susceptibility and corresponding outbreak size (10, 23).
RSV causes lower respiratory tract infections in young infants, and contributes to approximately 5% of under-five deaths globally (24), with no vaccine currently available. Previous models show RSV epidemics exhibit limit cycle behavior, tuned by climate-driven seasonality (Materials and Methods) (11, 25). In most regions in the United States, RSV and influenza exhibit peak incidence in the winter months, coinciding with cold, dry climatic conditions (11, 13).
Here we consider the impact of nonpharmaceutical control measures on the incidence of these two respiratory infections. We focus primarily on RSV, with the simpler limit cycle dynamics presenting an opportunity to probe interactions with NPIs. High interannual irregularity in influenza dynamics, driven by variation in circulating strains and subtypes, makes it harder to attribute the impact of NPIs. We first evaluate the influence of control measures targeting SARS-CoV-2 using influenza and RSV surveillance data. Since changes to physician visits for both viruses could be driven by behavioral responses to control measures, we look at the percent positive tests for both viruses as reported from laboratory surveillance data (see Discussion for the limitations of this measure).
Results
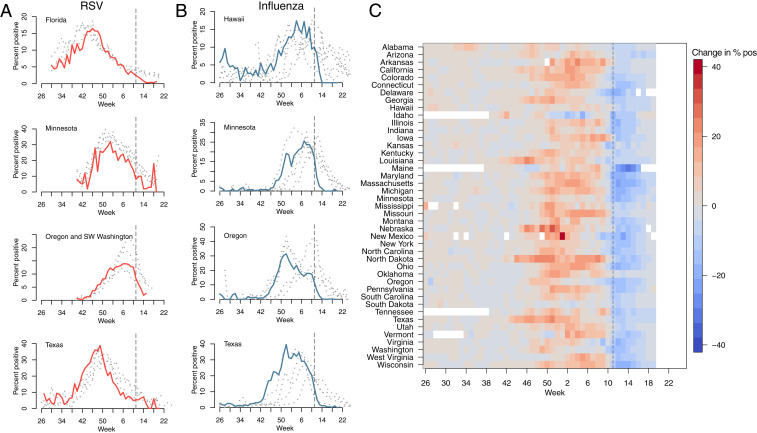
Fig. 1 shows the percent positive tests for RSV (Fig. 1A) and influenza (Fig. 1B) for 2019–2020 (highlighted) and four preceding years, for four states (RSV data with at least 2 y of observations were not available for other states). A national emergency in response to the COVID-19 pandemic was declared on March 13, 2020 in the United States, shown with the dashed line. Following the declaration, many states put in place control measures to limit the spread of SARS-CoV-2. Despite the declaration occurring after the typical seasonal peak in cases, a decline in prevalence is observed beyond mean seasonal levels. In Florida, where RSV cases tend to persist throughout the year (11, 25), observed RSV prevalence is reduced to near zero in March 2020. A similar pattern is visible in Hawaii for influenza, where cases are normally persistent. In Fig. 1C, we show the 2019–2020 change in percentage positive influenza tests relative to weekly mean over the previous four seasons. The 2019–2020 influenza season appears to have been more severe than average, with a relative increase in prevalence prior to March 2020 possibly driven by increased circulation of influenza subtype B (SI Appendix, Figs. S1 and S3). However, following the declaration of emergency, declines to below average levels can be observed across almost all reporting states.
Fig. 1.
Reduction in RSV and Influenza cases since March 2020. The percent positive laboratory tests for (A) RSV and (B) influenza across four US states. Data from 2020 are highlighted in red (RSV) and light blue (influenza). Data from previous seasons (2016–2019) are highlighted in gray. (C) The 2020 change relative to seasonal mean for influenza for all available US states (RSV surveillance data are only available for select states). Dashed line shows timing of the declaration of national emergency.
To explore the possible implications of control (i.e., NPI) periods for the future dynamics of influenza and RSV, we use epidemiological models and consider a range of possible scenarios for the length and intensity of control measures. Given the current uncertainty in the future course of the COVID-19 pandemic, and how responses might change over time, we cannot make precise predictions of future outcomes. For RSV, we use the time series Susceptible–Infected–Recovered (SIR) model (26, 27), fitted to historic US case data described in previous work (11). Specifically, we evaluate how NPI perturbations impact the epidemic limit cycles of RSV. We first consider a range of control period lengths and percent reduction in transmission based on Florida and Texas seasonality. We consider these two states for two reasons. First, the states exhibit distinct dynamics patterns of RSV incidence, with Florida having persistent cycles and an earlier summertime outbreak, and Texas having annual, wintertime outbreaks. Second, in terms of data availability, both these locations have recent surveillance data as well as historic case data, enabling the estimation of possible changes to transmission in 2020. Minnesota was not considered here because the percent positive surveillance data do not accurately reveal the biennial dynamics in this location (11).
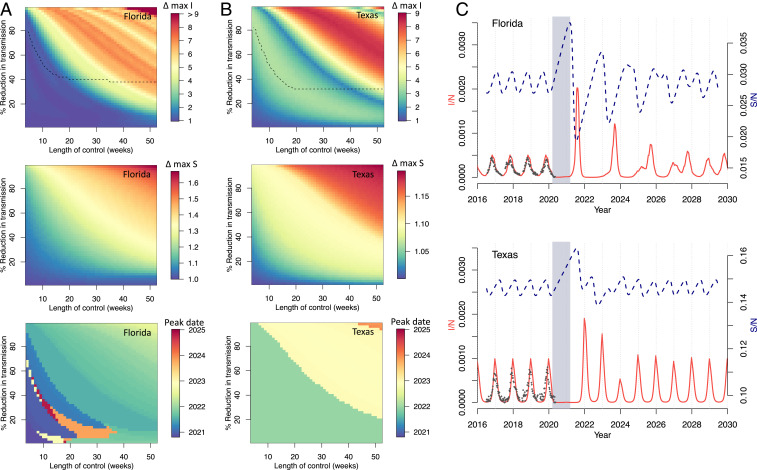
Fig. 2 A and B shows the impact of these varied controls on peak incidence (I/N), peak proportion susceptible (S/N), and timing of peak I/N. Major dynamic effects are caused by a buildup of susceptible individuals as NPIs reduce transmission. Longer controls, with a greater reduction in transmission, generally lead to a greater increase in susceptibility and larger resulting outbreaks. For Florida, these outbreaks tend to occur in the summer months, but can occur throughout the year. For Texas, where seasonal transmission peaks in the winter, peak outbreaks occur only in the winter months, with the earliest outbreak in 2022.
Fig. 2.
RSV simulations for Florida and Texas. (A and B) Surface plots show the change in peak incidence per capita and peak susceptibility per capita, relative to pre-2020 maxima, for varied lengths of control (weeks) and percent reduction in transmission. Black dashed line in the first plot row shows the region above which minimum incidence drops below 1, that is, where local extinction is possible. The lower surface plot shows the timing of peak incidence in this period. Results for (A) Florida and (B) Texas are shown. (C) Simulations of future RSV epidemics, assuming a control period of 1 y and a 20% reduction in transmission, are shown for Florida and Texas. Gray block represents the NPI period, red line is proportion infected (I/N), and blue dashed line is proportion susceptible (S/N).
We use RSV laboratory surveillance data for Florida and Texas to parameterize the actual reduction in transmission caused by SARS-CoV-2 NPIs. We find that a reduction in transmission of 20% is able to conservatively capture the decline in prevalence recently observed in the surveillance data (Fig. 2C and SI Appendix, Fig. S4). Using this model parameterization, we run simulations with a control period of 1 y. Results from Florida and Texas, shown in Fig. 2C, indicate an increased likelihood of severe RSV outbreaks after the control period has ended.
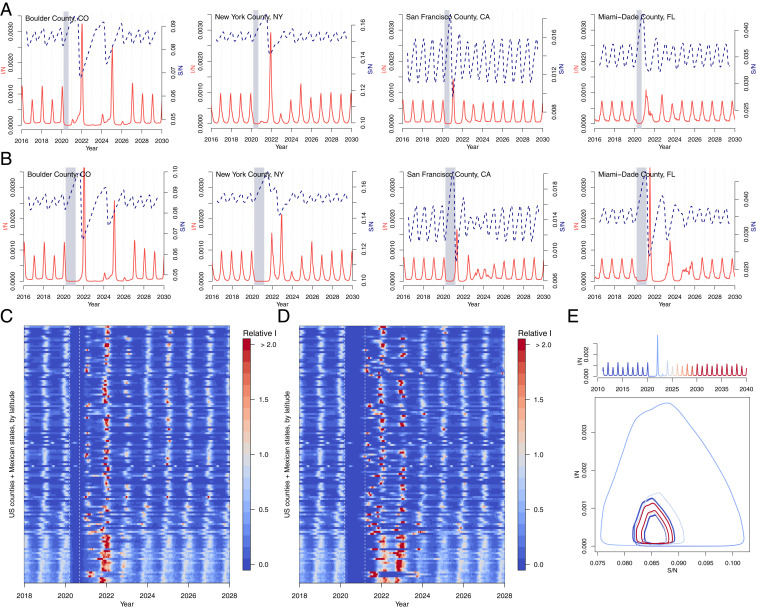
We run simulations to investigate the potential impact of control measures on RSV for over 300 US counties and Mexican states using the time series SIR model fitted to historic county-level case data (Fig. 3) (11). Counties with short time series (less than 5 y of data) and sparse numbers of cases (under 10 at peak) are removed. We compare the impact of two periods of control: lasting 6 mo (Fig. 3 A and C) and lasting 1 y (Fig. 3 B and D). Although the 6-mo control period occurs outside of the peak season of the virus, substantial RSV outbreaks are still projected as a lagged response to the SARS-CoV-2 NPIs. In general, the longer, 1-y control period results in larger RSV outbreaks, yet complex interactions with seasonality arise. For New York County, the shorter control period results in a large outbreak in the following winter (2021–2022), but the longer control period results in a more persistent but less intense outbreak. In contrast, a large RSV outbreak is observed in Miami after a year of control measures. In most cases, simulated dynamics eventually return to the pre-NPI attractor. For Boulder County, by contrast, control periods have complex interactions with the seasonal biennial epidemics of the disease. In these deterministic simulations, a longer control period in Boulder County causes the epidemic trajectory to shift to a separate coexisting attractor (Fig. 3E and SI Appendix, Fig. S8). In general, the timing and size of future outbreaks will depend on the interaction between the dynamics of susceptibility and the seasonality of transmission.
Fig. 3.
RSV simulations for US counties and Mexican states. Simulations for four US counties with either (A) 6 mo or (B) 1 y of controls. Simulations for all US counties (with population 500,000) and Mexican states in data with (C) 6-mo or (D) 1-y control period, where max incidence prior to the control period is set to 1. (E) Susceptible–Infected phase plane plot for Boulder, CO, showing epidemic trajectory with incidence time series above. The epidemic settles on a coexisting attractor postcontrol shown by the distinct precontrol (dark blue) and postcontrol (dark red) stable trajectories.
Compared to RSV, influenza epidemics exhibit a less uniform seasonal pattern. Gradual evolution of the influenza virus’ antigenic sites (antigenic drift) means population susceptibility changes over time (21), and different subtypes may circulate each year with different levels of transmission (28). In our preliminary analysis, we therefore focus on the overall dynamics of susceptibility, ignoring year-to-year differences in circulating strains. We simulate influenza using a Susceptible–Infected–Recovered–Susceptible (SIRS) model, developed in previous analyses to explore influenza seasonality in the United States, where varies between a maximum and minimum value driven by changes in absolute humidity (12, 13). To capture the variability in transmission rates, we consider two scenarios: and , based on the range of prior estimates (13, 28). In both scenarios, . We simulate the model using the climate of New York City.
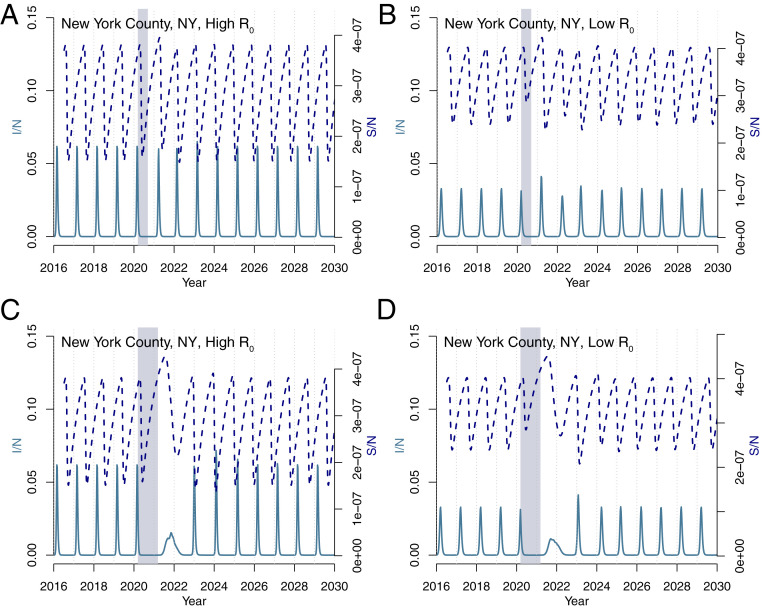
Fig. 4 shows the results using the influenza model under two control scenarios (6 mo and 1 y with a 20% reduction in transmission) and two transmission scenarios (high and low ). The 6-mo controls have relatively little impact on influenza seasonality in New York in the high-transmission scenario. In the equivalent lower-transmission scenario, outbreaks after the NPI period are slightly elevated. In contrast, longer control periods provide more time for the susceptibility to build, resulting in an earlier influenza epidemic starting in the summer months. In the low-transmission scenario, this is followed by a large outbreak in 2021. While these results suggest a more uncertain impact of NPI periods on future influenza outbreaks, dynamics will likely differ in locations with more-persistent influenza cycles, such as the tropics (9).
Fig. 4.
Influenza simulations for New York County. Simulations using a (A and B) 6-mo and (C and D) 1-y control period for both (A and C) high () and (B and D) low () transmission rates.
Discussion
NPIs put in place to limit the spread of SARS-CoV-2 are already beginning to affect the transmission of other directly transmitted, endemic diseases. Our results suggest that a buildup of susceptibility during these control periods may result in large outbreaks in the coming years. Shorter NPIs may occur outside of the peak season of the disease but still lead to elevated future outbreaks. Longer NPIs may overlap with seasonal peak forcing, resulting in larger future outbreaks on average, but with complex transient effects (a more detailed analysis of NPI timing is shown in SI Appendix, Figs. S9 and S10). Results for RSV in the United States suggest that these outbreaks may reach their peak in the winter of 2021–2022. This finding appears robust even when we account for possible imported cases. Following perturbation, RSV generally returns to the endemic attractor, but more complex behavior is possible (Fig. 3E).
Preliminary results for influenza suggest outbreaks may occur outside of the typical season, coinciding with the end of the control period. However, we do not address complex features of the influenza virus such as circulating subtypes or the implications of global NPIs for antigenic drift. The latter may prove significant, for example, if the evolution rate first declines with NPIs, then rebounds (29). More broadly, our results suggest that healthcare systems may need to prepare for future outbreaks of non–COVID-19 infections, as NPIs are relaxed. These outbreaks may occur several years after initial NPIs were put into place.
There are several caveats to these results. First, we are at the early stages of understanding the implications of SARS-CoV-2 NPIs for endemic infections. In our model, we used a fixed reduction in transmission; however, this may not capture heterogeneities in NPIs across locations and over time. As more surveillance data become available, tracking further changes to endemic disease prevalence will be important. Serological surveys, currently used to measure exposure and potential immunity to SARS-CoV-2, could similarly be employed to monitor these polymicrobial responses (30–32).
Second, and importantly, an influx of COVID-19 cases could artificially lower the percent positive test data we use to calibrate reductions in RSV and influenza transmission. For RSV, this seems unlikely, as the mean age of infection is much lower than for COVID-19, and cases are unlikely to overlap. Most individuals are infected with RSV before the age of 2 y (18). In contrast, infants appear less likely to be infected with SARS-CoV-2, and severe respiratory presentations are unusual (33, 34). We also note that total tests for RSV have declined since March (SI Appendix, Fig. S2). For influenza, it is more plausible that an influx of COVID-19 cases could be biasing results; however, the sharp decrease observed across states right after the national emergency declaration suggests that it is unlikely to be primarily driven by this factor. The total influenza specimens collected have also declined (SI Appendix, Fig. S1). As a further check, we create an incidence proxy, following ref. 35, by multiplying percent influenza-like illness by percent positive tests (SI Appendix, Fig. S11). Substantial declines in this measure are still observed following the emergency declaration.
Possible biases could inflate our measure of the percent reduction in transmission due to NPIs (estimated at 20%). However, similarly, the relatively limited time horizon of our data, and the fact that current NPIs are concurrent with the seasonal lower transmission period, could mean we are underestimating this reduction. Recent evidence from Hong Kong estimated a 33 to 44% reduction in influenza transmission due to NPIs (7). We therefore stress that our results are uncertain, and we cannot yet make precise predictions. Unbiased polymicrobial surveillance would enable better attribution of NPI effects and is a crucial area for future development. In addition, interactions between the SARS-CoV-2 virus and endemic viruses may be more complex than described here. Immunological relationships between viruses, both competitive and cooperative, may have broad-scale implications for future infection dynamics (36). The impact of NPIs on strain structure of RSV (37) is an important area for future work.
Finally, although we have primarily focused on the United States, outcomes may be more severe in Southern Hemisphere locations where NPI timing aligns with the peak season for seasonal wintertime diseases. Our results also illustrate the potential for COVID-19 NPI to impact the dynamics and persistence of a much wider range of infections. Increased surveillance, serological surveys, and local modeling efforts will help determine the future dynamics and risk from these circulating infections.
Materials and Methods
Data.
Recent (2016–2020) disease data based on laboratory results from either antigen or PCR tests for RSV are obtained from the corresponding government websites for each state: Florida (unspecified) (38), Minnesota (antigen) (39), Oregon (antigen and PCR) (40), and Texas (antigen) (41). Even though a few other states report RSV surveillance, we do not include them in our analysis, as they do not provide information on RSV circulation from previous years. Some RSV data are extracted from the graphs of the state surveillance reports, as raw values are unavailable. Influenza surveillance data are obtained from Centers for Disease Control and Prevention FluView Interactive (42). Historic RSV data (pre-2010) used to train the RSV model come from hospitalizations data originally obtained from the State Inpatient Databases of the Healthcare Cost and Utilization Project maintained by the Agency for Healthcare Research and Quality (43). Population data for the United States are obtained from publicly available combined files of US Census Bureau data available via the National Bureau of Economic Research (44). US birth data are downloaded from the Centers for Disease Control (45). Transmission in the influenza model relies on specific humidity data taken from NASA’s Modern-Era Retrospective analysis for Research and Applications version 2 dataset (46, 47).
Models.
We first calculate location-specific seasonal transmission rates using the time series Susceptible–Infected–Recovered model (TSIR), a discrete time adaptation of the SIR model (26, 48). County-level transmission rates were calculated for a previous study (11). The TSIR model describes the number of infected and susceptible individuals as a set of difference equations. The number of susceptible individuals is given by
| [1] |
where is the number of susceptible individuals, is the number of infected individuals, is births, and is additive noise, with . The time period is the generation time for RSV, set at 1 wk. The susceptible population can be rewritten as , where is the mean number of susceptible individuals in the population and is the unknown deviation from the mean number of susceptible individuals at each time step. Eq. 1 is rewritten in terms of these deviations and iterated starting at ,
| [2] |
where is the reporting rate which accounts for both underreporting of RSV hospitalizations and infections that did not result in hospitalization, and is the reported incidence.
Using this formulation, it is shown that a linear regression of cumulative births on cumulative cases gives as the residuals, assuming is small. The inverse of the slope of the regression line provides an estimate of the reporting rate . is calculated by defining the expected number of infected cases at each time step, , as
| [3] |
which is log-linearized as
| [4] |
where are biweekly factors that capture the seasonal trend in transmission rate, and is a constant that captures heterogeneities in mixing and the discretization of a continuous time process. We fix at 0.97 to be consistent with prior studies (11, 49). Eq. 4 is fit using a Poisson regression with log link. The mean number of susceptible individuals, , can then be estimated using marginal profile likelihoods from estimating Eq. 4, for a range of candidate values. Following ref. 11, we add one to zero observations in the infected time series which represents continual low-level background transmission, resulting in the lack of epidemic extinction we observe in the data. For fitting the TSIR, we use the tsiR package (50). When fitting to state-level data for Texas and Florida, we use a locally varying spline regression for Eq. 2, which accounts for macroscale changes in reporting over time.
We generate forward simulations using county seasonal transmission rates, , assuming a constant population and birth rate (based on average population and average birth rates from the historic time series). Model results are shown in terms of incidence per capita. The simulations are initially run for 40 y to remove transient dynamics. The control period is introduced to the model by lowering the seasonal transmission rates by a fixed proportion, starting on week 11 of 2020 (the week when a national emergency was declared). For all simulations, we lower the transmission by 20% unless otherwise specified.
The percentage reduction in transmission is estimated by comparing model simulations to laboratory RSV data from 2020 for Texas and Florida. State-level data from Minnesota are not used because the laboratory data does not capture the biennial cycles of incidence that exist in this state (11). Other states do not have multiple years of available data to compare present reductions in prevalence. Laboratory test data are scaled to the model projection using the 2016–2020 mean, that is, , where is the laboratory test data and is the model projections. Simulations are run using reductions in transmission ranging from 0 to 90% in 10% intervals. For Florida, a 20% reduction in transmission, starting in week 11 (when the national emergency was declared), is found to be the best fit (mean absolute error) reduction based on available data (SI Appendix, Fig. S4). For Texas, both 10% reduction and 20% reduction give similarly good fits. Joint error is minimized using the 20% reduction rate.
For influenza we use a climate-driven SIRS model (13, 14, 28). Antigenic drift of the influenza virus results in a seasonal return to susceptibility, meaning TSIR methods are not appropriate for this infection. The model is described by a series of differential equations (51),
| [5] |
| [6] |
As before, is the susceptible population, is the number of infected individuals, and is the total population. , the mean infectious period, is set at 4 d. , the duration of immunity, is fixed at 40 wk, allowing the influenza epidemic to recur each season. is the contact rate at time and is related to the basic reproductive number by . is related to specific humidity using the equation
| [7] |
where , based on earlier findings (12, 13, 28). is minimum reproductive number, fixed at 1.2, following ref. 28. is the maximum reproductive number. In Fig. 4, we use values of and , based on plausible ranges observed in refs. 13 and 28.
Supplementary Material
Acknowledgments
R.E.B. is supported by the Cooperative Institute for Modeling the Earth System. This study is supported by the Princeton Institute for International and Regional Studies and the Princeton Environmental Institute.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2013182117/-/DCSupplemental.
Data Availability.
Data for this study come from publicly available datasets. Code and collated data to recreate the main results are available via GitHub at https://github.com/rebaker64/NPIs.
References
- 1.Pei S., Kandula S., Shaman J., Differential effects of intervention timing on COVID-19 spread in the United States. medRxiv:10.1101/2020.05.15.20103655 (29 May 2020). [DOI] [PMC free article] [PubMed]
- 2.Tian H., et al. , An investigation of transmission control measures during the first 50 days of the COVID-19 epidemic in China. Science 368, 638–642 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lai S., et al. , Effect of non-pharmaceutical interventions to contain COVID-19 in China. Nature 585, 410–413 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Chinazzi M., et al. , The effect of travel restrictions on the spread of the 2019 novel coronavirus (COVID-19) outbreak. Science 368, 395–400 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hsiang S., et al. , The effect of large-scale anti-contagion policies on the COVID-19 pandemic. Nature 584, 262–267. [DOI] [PubMed] [Google Scholar]
- 6.Leung N. H., et al. , Respiratory virus shedding in exhaled breath and efficacy of face masks. Nat. Med. 26, 676–680 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cowling B. J., et al. , Impact assessment of nonpharmaceutical interventions against coronavirus disease 2019 and influenza in Hong Kong: An observational study. Lancet Public Health 5, e279–e288 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Martinez M. E., The calendar of epidemics: Seasonal cycles of infectious diseases. PLoS Pathog. 14, e1007327 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Viboud C., Alonso W. J., Simonsen L., Influenza in tropical regions. PLoS Med. 3, e68 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Viboud C., et al. , Synchrony, waves, and spatial hierarchies in the spread of influenza. Science 312, 447–451 (2006). [DOI] [PubMed] [Google Scholar]
- 11.Baker R. E., et al. , Epidemic dynamics of respiratory syncytial virus in current and future climates. Nat. Commun. 10, 5512 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Shaman J., Kohn M., Absolute humidity modulates influenza survival, transmission, and seasonality. Proc. Natl. Acad. Sci. U.S.A. 106, 3243–3248 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Shaman J., Viboud C., Pitzer V. E., Grenfell B. T., Lipsitch M., Absolute humidity and the seasonal onset of influenza in the continental United States. PLoS Biol. 8, e1000316 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Baker R. E., Yang W., Vecchi G. A., Metcalf C. J. E., Grenfell B. T., Susceptible supply limits the role of climate in the early SARS-CoV-2 pandemic, Science 369, 315–319 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Grenfell B. T., Bjørnstad O. N., Kappey J., Traveling waves and spatial hierarchies in measles epidemics. Nature 414, 716–723 (2001). [DOI] [PubMed] [Google Scholar]
- 16.Ferrari M. J., et al. , The dynamics of measles in sub-Saharan Africa. Nature 451, 679–684 (2008). [DOI] [PubMed] [Google Scholar]
- 17.Bolker B., Grenfell B. T., Impact of vaccination on the spatial correlation and persistence of measles dynamics. Proc. Natl. Acad. Sci. U.S.A. 93, 12648–12653 (1996). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Pitzer V. E., et al. , Demographic variability, vaccination, and the spatiotemporal dynamics of rotavirus epidemics. Science 325, 290–294 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wesolowski A., et al. , Quantifying seasonal population fluxes driving rubella transmission dynamics using mobile phone data. Proc. Natl. Acad. Sci. U.S.A. 112, 11114–11119 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Becker A. D., Wesolowski A., Bjørnstad O. N., Grenfell B. T., Long-term dynamics of measles in London: Titrating the impact of wars, the 1918 pandemic, and vaccination. PLoS Comput. Biol. 15, e1007305 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Webster R., Laver W., Air G., Schild G., Molecular mechanisms of variation in influenza viruses. Nature 296, 115–121 (1982). [DOI] [PubMed] [Google Scholar]
- 22.Petrova V. N., Russell C. A., The evolution of seasonal influenza viruses. Nat. Rev. Microbiol. 16, 47–60 (2018). [DOI] [PubMed] [Google Scholar]
- 23.Smith D. J., et al. , Mapping the antigenic and genetic evolution of influenza virus. Science 305, 371–376 (2004). [DOI] [PubMed] [Google Scholar]
- 24.Wang H., et al. , Global, regional, and national life expectancy, all-cause mortality, and cause-specific mortality for 249 causes of death, 1980–2015: A systematic analysis for the global burden of disease study 2015. Lancet 388, 1459–1544 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Pitzer V. E., et al. , Environmental drivers of the spatiotemporal dynamics of respiratory syncytial virus in the United States. PLoS Pathog. 11, e1004591 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Finkenstädt B. F., Grenfell B. T., Time series modeling of childhood diseases: A dynamical systems approach. J. Roy. Stat. Soc. C Appl. Stat. 49, 187–205 (2000). [Google Scholar]
- 27.Grenfell B. T., Bjørnstad O. N., Finkenstädt B. F., Dynamics of measles epidemics: Scaling noise, determinism, and predictability with the TSIR model. Ecol. Monogr. 72, 185–202 (2002). [Google Scholar]
- 28.Yang W., Lipsitch M., Shaman J., Inference of seasonal and pandemic influenza transmission dynamics. Proc. Natl. Acad. Sci. U.S.A. 112, 2723–2728 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Arinaminpathy N., et al. , Impact of cross-protective vaccines on epidemiological and evolutionary dynamics of influenza. Proc. Natl. Acad. Sci. U.S.A. 109, 3173–3177 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Winter A. K., et al. , Revealing measles outbreak risk with a nested immunoglobulin g serosurvey in Madagascar. Am. J. Epidemiol. 187, 2219–2226 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Mina M. J., et al. , Measles virus infection diminishes preexisting antibodies that offer protection from other pathogens. Science 366, 599–606 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Mina M. J., et al. , A global immunological observatory to meet a time of pandemics. eLife 9, e58989 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Dowd J. B., et al. , Demographic science aids in understanding the spread and fatality rates of COVID-19. Proc. Natl. Acad. Sci. U.S.A. 117, 9696–9698 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hong H., Wang Y., Chung H. T., Chen C. J., Clinical characteristics of novel coronavirus disease 2019 (COVID-19) in newborns, infants and children. Pediatr Neonatol. 61, 131–132 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Goldstein E., Cobey S., Takahashi S., Miller J. C., Lipsitch M., Predicting the epidemic sizes of influenza A/H1N1, A/H3N2, and B: A statistical method. PLoS Med. 8, e1001051 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Nickbakhsh S., et al. , Virus–virus interactions impact the population dynamics of influenza and the common cold. Proc. Natl. Acad. Sci. U.S.A. 116, 27142–27150 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.White L., et al. , Understanding the transmission dynamics of respiratory syncytial virus using multiple time series and nested models. Math. Biosci. 209, 222–239 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Florida Department of Health , RSV surveillance activity summary. http://www.floridahealth.gov/diseases-and-conditions/respiratory-syncytial-virus. Accessed 21 May 2020.
- 39.Minnesota Department of Health, Weekly influenza & respiratory activity: Statistics https://www.health.state.mn.us/diseases/flu/stats/index.html. Accessed 21 May 2020.
- 40.Oregon Health Authority , Oregon’s Weekly RSV surveillance report. https://www.oregon.gov/oha/PH/DISEASESCONDITIONS/Pages/index.aspx. Accessed 21 May 2020).
- 41.Texas Health and Human Services , RSV Data by health service region. https://www.dshs.texas.gov/IDCU/disease/rsv/Data/. Accessed 21 May 2020.
- 42.Centers for Disease Control and Prevention , Flu activity and surveillance, FluView interactive. https://www.cdc.gov/flu/weekly/fluviewinteractive.htm. Accessed 21 May 2020.
- 43.Agency for Healthcare Research and Quality , Healthcare cost and utilization project. https://www.distributor.hcup-us.ahrq.gov/. Accessed 2012. [DOI] [PubMed]
- 44.National Bureau of Economic Research , Census U.S. intercensal county population data. 1970–2014. https://data.nber.org/data/census-intercensal-county-population.html). Accessed 2018.
- 45.Centers for Disease Control and Prevention , Natality information, live births. https://wonder.cdc.gov/natality.html. Accessed 2018.
- 46.Gelaro R., et al. , The modern-era retrospective analysis for research and applications, version 2 (MERRA-2). J. Climate 30, 5419–5454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.National Aeronautics and Space Administration , Global Modeling and Assimilation Office, Modern-Era Retrospective Analysis for Research and Applications (MERRA). https://gmao.gsfc.nasa.gov/reanalysis/MERRA/. Accessed 1 March 2020.
- 48.Bjørnstad O. N., Finkenstädt B. F., Grenfell B. T., Dynamics of measles epidemics: Estimating scaling of transmission rates using a time series SIR model. Ecol. Monogr. 72, 169–184 (2002). [Google Scholar]
- 49.Glass K., Xia Y., Grenfell B. T., Interpreting time-series analyses for continuous-time biological models—Measles as a case study. J. Theor. Biol. 223, 19–25 (2003). [DOI] [PubMed] [Google Scholar]
- 50.Becker A. D., Grenfell B. T., tsiR: An R package for time-series susceptible-infected-recovered models of epidemics. PloS One 12, e0185528 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Dushoff J., Plotkin J. B., Levin S. A., Earn D. J., Dynamical resonance can account for seasonality of influenza epidemics. Proc. Natl. Acad. Sci. U.S.A. 101, 16915–16916 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data for this study come from publicly available datasets. Code and collated data to recreate the main results are available via GitHub at https://github.com/rebaker64/NPIs.