Abstract
The mathematical basis of the hypothesis that type-2 topoisomerases recognize and act at specific DNA juxtapositions has been investigated by coarse-grained lattice polymer models, showing that selective segment passages at hooked juxtapositions can result in dramatic reductions in catenane and knot populations. The lattice modeling approach is here extended to account for the narrowing of variance of linking number (Lk) of DNA circles by type-2 topoisomerases. In general, the steady-state variance of Lk resulting from selective segment passages at a specific juxtaposition geometry j is inversely proportional to the average linking number, 〈Lk〉j, of circles with the given juxtaposition. Based on this formulation, we demonstrate that selective segment passages at hooked juxtapositions reduce the variance of Lk. The dependence of this effect on model DNA circle size is remarkably similar to that observed experimentally for type-2 topoisomerases, which appear to be less capable in narrowing Lk variance for small DNA circles than for larger DNA circles. This behavior is rationalized by a substantial cancellation of writhe in small circles with hook-like juxtapositions. During our simulations, we uncovered a twisted variation of the hooked juxtaposition that has an even more dramatic effect on Lk variance narrowing than the hooked juxtaposition. For an extended set of juxtapositions, we detected a significant correlation between the Lk narrowing potential and the logarithmic decatenating and unknotting potentials for a given juxtaposition, a trend reminiscent of scaling relations observed with experimental measurements on type-2 topoisomerases from a variety of organisms. The consistent agreement between theory and experiment argues for type-2 topoisomerase action at hooked or twisted–hooked DNA juxtapositions.
Keywords: DNA supercoils, writhe, torsional energy, self-avoiding lattice polygons, Madras–Orlitsky–Shepp algorithm
Introduction
DNA topology1,2 is regulated by topoisomerases.3 Topological entanglements can arise in DNA as a natural outcome of replication1 as well as stochastic consequences of conformational fluctuations.4–6 Because the two strands of a double helix are intertwined, its replication results in two catenated, or linked, daughter DNAs that need to be separated.7–11 Because DNA is in a tightly packed, confined environment, DNA knots occur in vivo.12–17 DNA knotting can lead to mutation and replicon dysfunction.18 Thus, efficient resolution of DNA entanglements is essential for cellular function. Type-2 topoisomerases perform this task by enabling the DNA to interconvert among different topoisomers. Topoisomerases are, therefore, crucial in transcription, replication, recombination, and condensation and segregation of chromosomes.19–24
How topoisomerases carry out their essential functions has been studied for nearly 40 years and yet data continue to surprise and new questions continue to arise. For example, Rybenkov et al. discovered that type-2 toposiomerases reduce catenane and knot populations 16- to 90-fold below those in “topological equilibrium”.25 Their findings imply that segment passages catalyzed by type-2 topoisomerases are directed toward removing problematic topological states of DNA and are thus not indiscriminate. How does a type-2 topoisomerase determine the global topological state of the much larger DNA molecule? Several hypotheses have been proposed25–32 (reviewed in Ref. 24). Following our previous approach,33,34 this study evaluates the hooked juxtaposition hypothesis,31 which accommodates that type-2 topoisomerases bind two segments of DNA.35–40 A hooked juxtaposition is one in which the two juxtaposed DNA segments curve toward each other. Unlike other hypotheses that require DNA bending or complicated probing by the topoisomerase, the hooked juxtaposition hypothesis stipulates that the information contained in preexisting DNA juxtapositions yields powerful discrimination. It argues that disentangling can be achieved by performing segment passage selectively when a DNA juxtaposition is hooked. Using lattice models, we have shown that such an operation can indeed result in significantly reduced catenane33 and knot34 populations. A subsequent independent study41 demonstrated that segment passage at hook-like juxtapositions can also result in substantial unknotting in a freely jointed chain model.42 The robustness of these unknotting results has inspired a conjecture41 that the effect might be related to the locations of hooked juxtapositions in ideal knots.43 Using a wormlike DNA chain model,44 we confirmed that selective segment passage at hooked juxtapositions with the geometrical characteristics gleaned from recent x-ray crystal structure of a DNA-bound type-2 topoisomerase45 can achieve high degrees of decatenating and unknotting46 similar to those observed experimentally.25 The only remaining topological aspect that has not been explored is the narrowing of supercoil distribution observed by Rybenkov et al., which is the subject of this study.
DNA supercoiling serves important biological functions and is regulated by both type-1 and type-2 topoisomerases.47 For instance, negative supercoiling—meaning that the DNA is underwound—can facilitate reading of internal nucleotide bases by the cellular machinery (reviewed in Ref. 48). Supercoiling can also affect protein–DNA interactions through its effects on the occurrence and geometric characteristics of DNA juxtapositions49,50 as well as the local concentration of DNA.51 Computational studies52 have underscored an intricate interplay between supercoiling and knotting.6,53 Experiments on topo IV (a type-2 topoisomerase) revealed that supercoiling increases the enzyme’s effectiveness in decatenating54,55 but not in unknotting54,56 (reviewed in Ref. 57). The mechanisms underlying these phenomena are not yet understood.
The main focus of the present study is on supercoil distribution narrowing. Experiments on the effect of type-2 topoisomerases on the DNA linking number, Lk, indicated that these enzymes can reduce the variance of Lk distribution in DNA circles by a factor as much as 1.8 relative to topological equilibrium.25,30,58 What is the physical origin of this behavior and how does it relate to the enzymes’ decatenating and unknotting actions? These questions have not been addressed quantitatively by the active bending model26,27 or by any other model of type-2 topoisomerase actions that treated DNA conformations explicitly. An approximate, non-explicit-chain analytical treatment based upon a kinetic proofreading idea28 predicted a constant supercoil distribution narrowing factor of 2.29 However, more extensive data from subsequent experiments30,58 have shown that the Lk variance reduction factor can be significantly smaller than 2 when DNA circle size is ≲4 kb. To date, no theory has yet addressed this dependence on DNA circle size.
To what extent can the hooked juxtaposition hypothesis rationalize reduction of the Lk variance by type-2 topoisomerases? Building on the success of the hypothesis in accounting for decatenating33 and unknotting,34 we have now extended our explicit-chain approach to tackle lattice-model DNA molecules with twisting energies.44 In this effort, substantial new development in analytical formulation became necessary because narrowing of the Lk distribution entails transitions between multiple Lk states, which is mathematically more complex than the binary transitions between the unknotted and knotted states or between the catenated and decatenated states.33,34 Results below show that segment passages at hook-like juxtapositions in our model can indeed lead to supercoil distribution narrowing with a dependence on DNA circle size similar to that observed experimentally, lending further support to the hooked juxtaposition hypothesis.
Results and Discussion
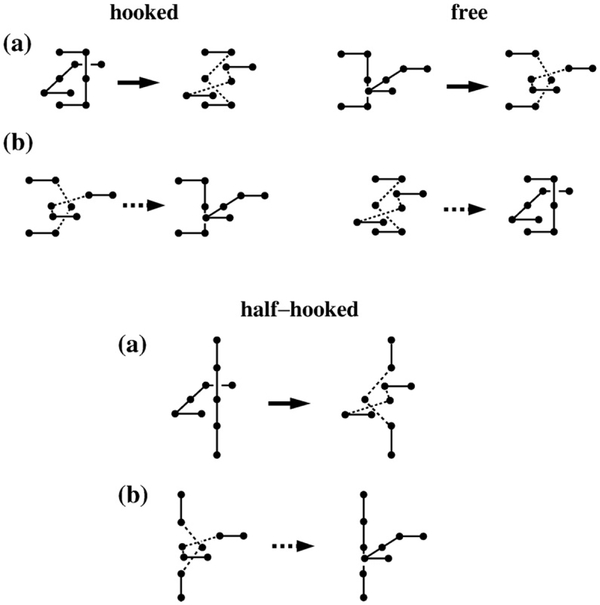
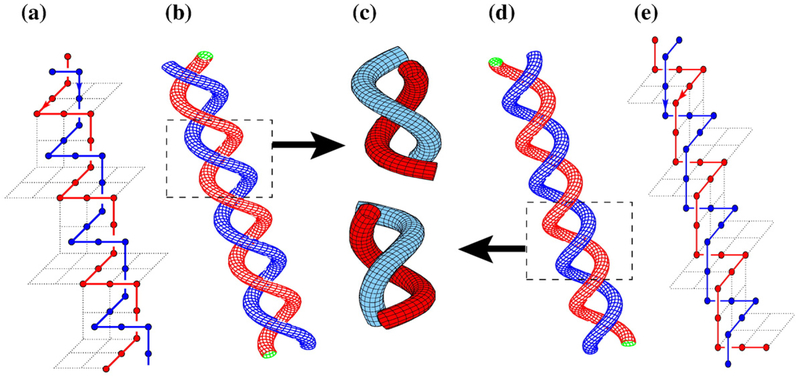
Our lattice model and computational methodology are given in Materials and Methods. As in previous applications of our juxtaposition-centric approach,33,34 we first determined the topological and supercoiling states of conformations with a preformed juxtaposition and then performed virtual segment passages (Fig. 1) to mimic type-2 topoisomerase actions. Our model predictions below were derived using either the original segment-passage operations (Fig. 1a) or an improved procedure that includes j*-symmetrized operations (Fig. 1b). The biophysical rationale of the improved procedure is provided in Materials and Methods. Despite some quantitative differences, the trends obtained using the original and the improved segment-passage operations are similar.
Fig. 1.
Symmetrized virtual segment passages. (a) Examples of virtual segment passages defined originally in Refs. 33 and 34 (operation symbolized by solid arrows). (b) Reverse virtual segment passages (symbolized by dashed arrows) at the juxtaposition j* conjugate to j in (a) defined in Materials and Methods. The hooked and free juxtapositions are conjugate to each other. The conjugate of the half-hooked juxtaposition is the one shown at the bottom right.
Linking number distribution depends on juxtaposition geometry
We began by investigating the distribution of Lk among conformations with a preformed juxtaposition (Fig. 2). The distribution was computed in two steps. We first determined the normalized distribution of writhe subject to the constraint of a preformed juxtaposition j for conformations with zero torsional energy, using the lattice method in Refs. 59 and 60 to calculate writhe. We denote this distribution as P00,j(Wr), wherein the two zeros symbolize that torsional energy = 0 and Lk = 0. Examples are given in Fig. 2a. To simplify notation, here we use Lk to stand for ΔLk, where Δ represents the actual value of a given variable minus the value of the variable for a fully relaxed DNA circle. In other words, an Lk=0 lattice conformation in the present study corresponds to a fully relaxed DNA circle. Similarly, Tw (twist) in the present study stands for ΔTw, and Wr stands for ΔWr. To obtain a distribution of Lk, we applied the Călugăreanu–White–Fuller theorem61–63
| (1) |
that relates Lk to Wr and Tw and introduced a torsional (twisting) energy
| (2) |
for Tw. Here, Kt=0.48 is equivalent to the variable C/l0 in Liu and Chan44 with l0 being the Kuhn statistical length ≈1000 Å. The torsional energy in the present formulation is in units of kBT, where kB is the Boltzmann constant and T is the absolute temperature, and is identical with that in Ref. 44. By incorporating Boltzmann weighting into P00,j(Wr), that is, P00,j(Wr)→P00,j(Wr) exp[−Et(Wr; Lk)], then summing over Wr, and finally introducing an overall normalization factor, we obtained the normalized distribution Pj(Lk), which is subject to the constraint of a preformed j (see examples in Fig. 2b).
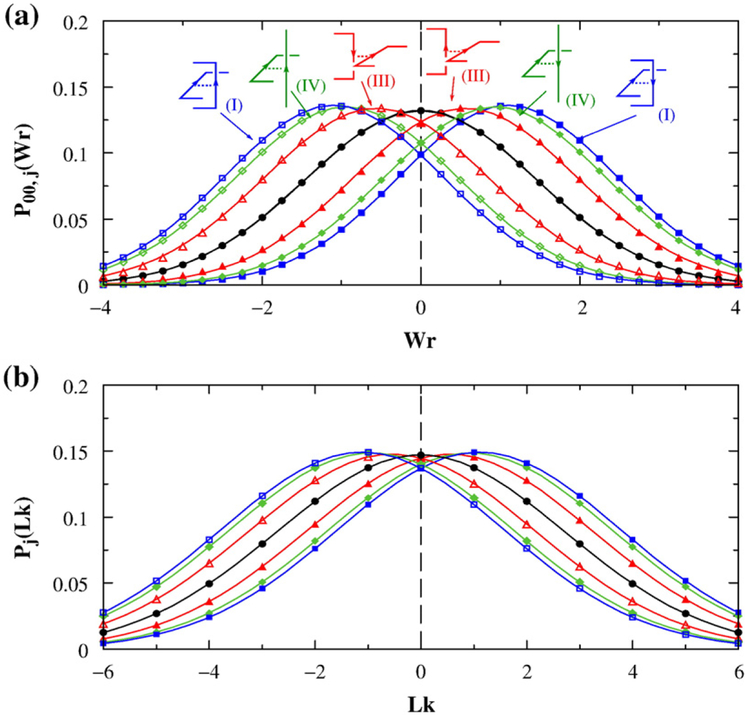
Fig. 2.
Distribution of writhe (Wr) and linking number (Lk). Results are for n=100 circles on the simple-cubic lattice. Continuous curves are Gaussian fits to the simulated data points. (a) Normalized distribution P00,j(Wr) for chains with no torsional energy (Kt=0) but with preformed juxtaposition j. Color curves are for constrained chains with preformed hooked (I), free (III), or half-hooked (IV) juxtapositions. Constrained distributions are shown for preformed juxtapositions with both positive and negative crossings. The black curve is the distribution P00(Wr) for chains without the constraint of a preformed juxtaposition. (b) The corresponding normalized distribution Pj(Lk) and P00(Lk) for chains with torsional energy Kt=0.48 plotted using the same color code as in (a).
Using lattice circles of chain length n=100 as an example, we show in Fig. 2 that preformed juxtapositions shift the mean values of the Wr and Lk distributions. The preformed juxtaposition itself is the main contributor to the shift of the mean Wr or Lk relative to the zero value for circles without the constraint of a preformed juxtaposition (black curves in Fig. 2). Therefore, not surprisingly, the sign of the shift (negative or positive) is the same as the crossing sign of the preformed juxtaposition itself (color curves in Fig. 2). However, a preformed juxtaposition has very little effect on the width of the distribution. For the examples in Fig. 2, the mean value 〈Lk〉j of the Pj(Lk) distribution is substantially different for a preformed hooked, half-hooked, and free juxtaposition, with 〈Lk〉j=±1.10, ±0.93, and ±0.54, respectively (〈…〉 symbolizes conformational averaging, and the subscript j indicates the constraint of a preformed juxtaposition j). In contrast, the corresponding values for the standard deviation of the distribution are essentially the same, with =2.67, 2.68, and 2.70, respectively. All of these values are also practically identical with the standard deviation σLk=2.71 for the P00(Lk) distribution (black curve) in Fig. 2b for circles without the constraint of a preformed juxtaposition.
Our next step is to use the Pj(Lk) distributions to determine the steady-state distribution of Lk maintained by selective segment passages. Type-2 topoisomerases apparently act on juxtapositions of both crossing signs.64 Accordingly, here we performed model segment passages at a given juxtaposition geometry with a positive crossing as well as a juxtaposition with a negative crossing that reverses the direction of one of the given juxtaposition’s segments but is otherwise identical with it (Fig. 3a). In this way, the two juxtapositions acted upon by the topoisomerase in the present model are of the same shape and are merely “one-segment reverse” of each other.
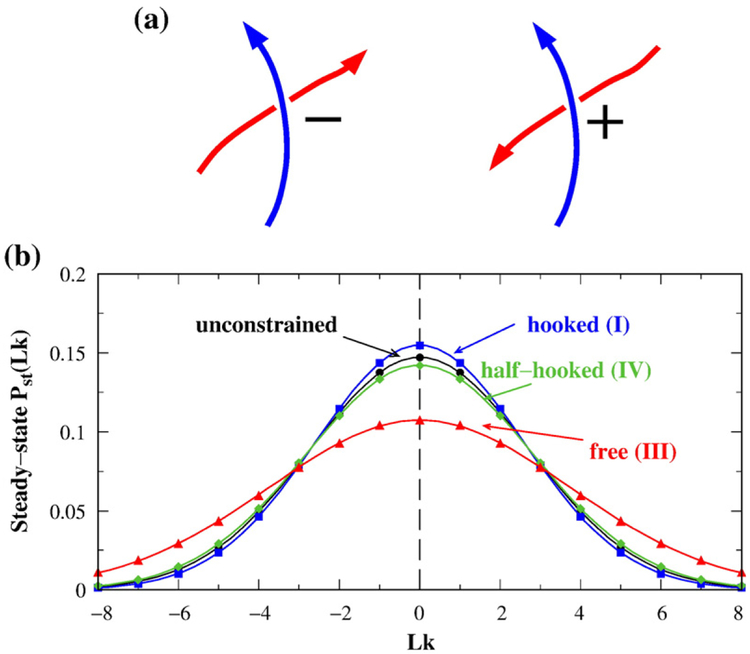
Fig. 3.
Selective segment passages at specific juxtaposition geometries change Lk distribution. (a) Type-2 topoisomerase action is modeled here by selective segment passages at juxtapositions of a given shape; that is, passages are effected at crossings of both signs that share the same shape. (b) Steady-state Pst(Lk) of n=100 lattice circles resulting from selective segment passages at the hooked, free, or half-hooked juxtaposition of both crossing signs (plotted in color); bj(+)ρj(+)=bj(−)ρj(−) for these juxtapositions. Peq(Lk) for unconstrained circles is included for comparison (plotted in black). Continuous curves are Gaussian fits to the simulated data points. j*-symmetrization is not used in this figure or Figs. 4–6.
In general, the steady-state Lk distribution Pst(Lk) for selective segment passages at any juxtaposition j(+) with a positive crossing and any other juxtaposition j(−) with a negative crossing may be computed from the equilibrium Lk distributions Pj(+)(Lk) and Pj(−)(Lk) with j(+) and j(−) preformed, respectively. Because Lk can only change to Lk±2 by one segment passage, the flux exiting an Lk population via segment passage is proportional to bj(+)ρj(+)Pj(+)(Lk)/Peq(Lk) + bj(−)ρj(−)Pj(−)(Lk)/Peq(Lk), where bj(+) and bj(−) are the segment-passage rates and ρj(+) and ρj(−) are the densities, respectively, of juxtapositions j(+) and j(−), following the general definitions for bj and ρj in Materials and Methods, and Peq(Lk) is the equilibrium unconstrained distribution of Lk. In the steady state, the flux exiting an Lk population must equal to the flux entering it. Thus, using the notation
| (3) |
the equality of incoming and outgoing fluxes requires
| (4) |
The only physically viable condition for satisfying this equation is that of detailed balance (i.e., there is no net flux between any pair of states), which entails a recursive relation
| (5) |
that is simpler than that in Eq. (4). It follows that S(Lk) for Lk≠0 can be solved:
| (6) |
where the top or bottom signs in ∓ and ± applies when Lk is, respectively, a positive or negative even number. Hence, by substituting simulated Pj(±)(Lk) values with preformed juxtapositions j(+) and j(−) into Eq. (6), S(Lk) for all Lk may be expressed in terms of S(0). The entire steady-state distribution Pst(Lk) can then be computed using the simulated equilibrium (unconstrained) distribution Peq(Lk) via Eq. (3), with S(0) being the only remaining unknown, which can now be absorbed into the normalization for Pst(Lk).
Applying this formulation to the virtual segment passages in Fig. 1a for the j(+)′s and j(−)′s of the hooked, half-hooked, and free juxtapositions, we show in Fig. 3b that the steady-state Pst(Lk) distribution for the hooked juxtaposition is narrower [(σLk)st=2.58] than the equilibrium Peq(Lk) distribution (σLk=2.71). This result is qualitatively in line with experimentally observed narrowing of Lk distribution by type-2 topoisomerases,25,30,58 although the ratio of the variances [σLk/(σLk)st]2≈(2.71/2.58)2 =1.10 from this model is less than the experimental value25,30,58 of ~1.35–1.8. In contrast, the half-hooked and free juxtaposition geometries widen the steady-state Lk distribution relative to Peq(Lk) in Fig. 3b.
Chain length dependence of supercoil distribution narrowing
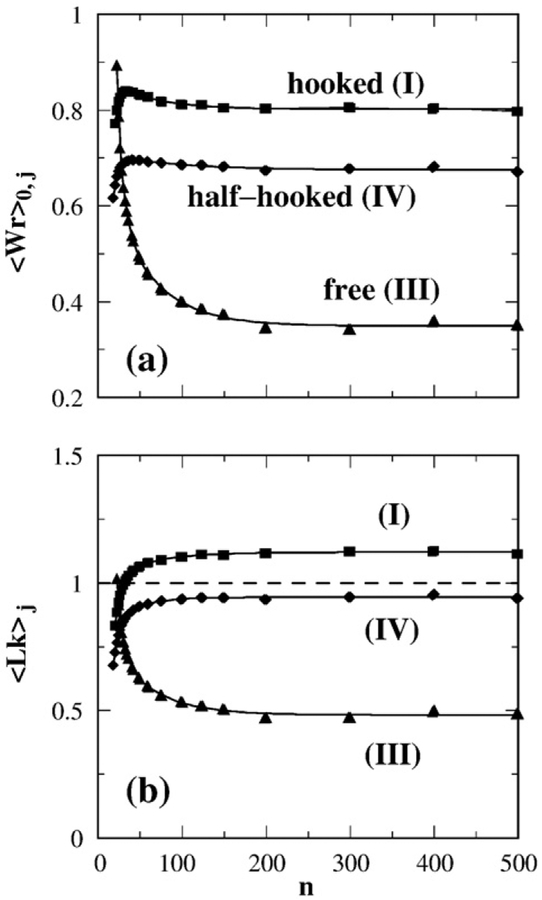
Figure 4 shows the chain length dependence of the average writhe 〈Wr〉j (among relaxed Lk=0 circles) and average linking number 〈Lk〉j (over circles with all Lk values) in the presence of a preformed hooked, half-hooked, or free juxtaposition. The two averages 〈Wr〉j and 〈Lk〉j level off to an essentially constant value for n>200, suggesting that the effect of the preformed juxtaposition on Wr and Lk is local provided the circles are large. However, for small circles with n≲50, both 〈Wr〉j and 〈Lk〉j vary sharply with n. Furthermore, the roles of the mutually conjugate hooked and free juxtapositions for large n are apparently reversed when n becomes small, namely, the 〈Lk〉j values for the hooked juxtaposition for small n are seen to approach 〈Lk〉j values for the free juxtaposition for large n, and vice versa. As will be elucidated below after the necessary analytical formulation has been developed, this trend is critical in the accounting for how supercoil distribution narrowing by type-2 topoisomerases depends on DNA circle size.
Fig. 4.
Chain length (n) dependence of average Wr and Lk. Averages in (a) and (b) are over lattice model chains with torsional energy (Kt=0.48) and constrained by a preformed juxtaposition j where j is the hooked (I), free (III), or half-hooked (IV) juxtaposition. (a) 〈Wr〉0,j is averaged over conformations with Lk=0. (b) 〈Lk〉j is averaged over all Lk values.
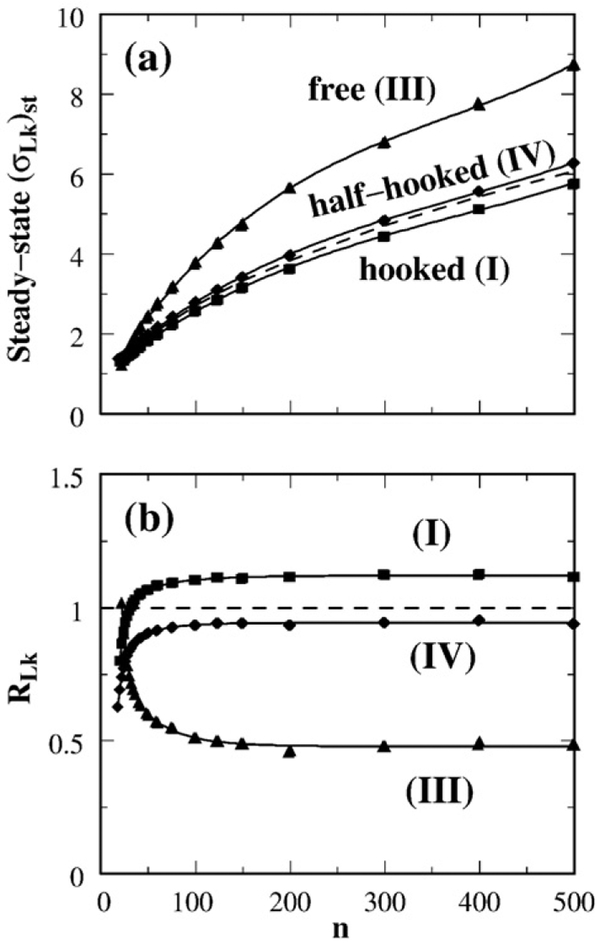
Figure 5a provides the chain length dependence of the standard deviation of steady-state distribution Pst(Lk) maintained by selective segment passages. Naturally, the width of both the equilibrium and steady-state Lk distributions increases with circle size. Irrespective of this overall increase, Fig. 5a shows that for circle sizes larger than n≈50, Pst(Lk) is always significantly wider than the equilibrium Lk distribution Peq(Lk) for the free juxtaposition, but Pst(Lk) is only slightly wider and slightly narrower than Peq(Lk), respectively, for the half-hooked and hooked juxtapositions. Following Rybenkov et al.,25 we define the supercoil distribution narrowing factor (Fig. 5b) as the variance of Peq(Lk) divided by the variance of Pst(Lk):
| (7) |
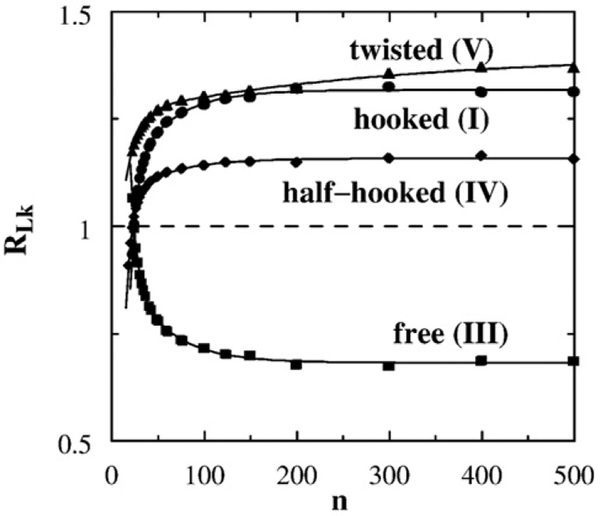
This definition is identical with the R parameter in Stuchinskaya et al.58 and is the reciprocal of the 〈ΔLk2〉S/〈ΔLk2〉0 factor plotted in Fig. 2D of Trigueros et al.30 Figure 5b shows the chain length dependence of RLk in our model. For the hooked juxtaposition, the narrowing of the Lk distribution (RLk>1 in the model) for circle sizes n≳50 is consistent with experiment. Moreover, the n dependence exhibited by the hooked juxtaposition (I) curve in Fig. 5b is remarkable in that it captures an intriguing, yet unexplained, experimental trend of decreasing RLk for small DNA circles as displayed first in Fig. 2D of Trigueros et al.30 and more recently in Fig. 4a of Stuchinskaya et al.58 This match between theory and experiment should provide important clues to the physics of type-2 topoisomerase action. We return to this point below.
Fig. 5.
Effect of selective segment passage on the width of linking number distribution P(Lk). (a) Continuous curves with symbols show the standard deviation of Pst(Lk) maintained in a steady state by segment passages at the hooked (I), free (III), or half-hooked (IV) juxtapositions; each of these curves gives (σLk)st as a function of chain length n. The dashed curve is σLk of Peq(Lk) for unconstrained circles. (b) Chain length dependence of supercoil distribution narrowing factor RLk.
Analytical treatment relates supercoil distribution narrowing with average Lk in the presence of the selected juxtaposition
Inspection of Figs. 4b and 5b indicates that, for the three juxtapositions considered, the supercoil distribution narrowing factor RLk by selective segment passage at a given juxtaposition j is essentially equal to the mean 〈Lk〉j of the constrained Lk distribution with preformed j. Is this a fundamental relation generalizable to all juxtaposition geometries? We found through the following analytical derivation that RLk≈〈Lk〉j is indeed generally valid and that this relation affords an important mathematical link between the constraint imposed on DNA conformations by the type-2 topoisomerase-preferred juxtaposition geometry on the one hand and type-2 topoisomerase-mediated supercoil distribution narrowing on the other.
Data such as those in Fig. 2a suggest that Wr distributions, independently of the presence or absence of a preformed juxtaposition, are generally well approximated by a Gaussian:
| (8) |
where 〈Wr〉 and σWr are, respectively, the mean and standard deviation of the distribution that depend on chain length and the preformed juxtaposition. We use 〈Wr〉00 and (σWr)00 to denote, respectively, the average writhe and the corresponding standard deviation for the “00” distribution with no torsional energy (Kt=0, black curve in Fig. 2a):
| (9) |
For the case when torsional energy Et is operative (Kt>0), let 〈Wr〉0 and (σWr)0 be, respectively, the mean and standard deviation of the writhe distribution among relaxed, Lk=0, chains, the Gaussian approximation of which is expressed here as
| (10) |
Because Eq. (2) is equal to 2Ktπ2(Wr)2/n for Lk=0, up to an overall normalization,
| (11) |
where
| (12) |
Therefore, it is clear from comparing Eq. (10) with Eqs. (11) and (12) that
| (13) |
In general, for Lk≠0, using Eq. (12) and completing squares for the variables Wr and Lk, and noting the relationship [(σWr)00]2 = B[(σWr)0]2 from Eq. (13),
| (14) |
After averaging the above expression for P(Wr; Lk) over Wr by performing ∫d(Wr), we arrive at the following expression for P(Lk) up to the standard normalization factor for a Gaussian distribution (note that both the first and second terms of the last line of the above equation yielded a constant independent of Lk after integration):
| (15) |
It follows that the average value of Lk over conformations with torsional energy is
| (16) |
where the second equality follows from Eq. (13), and the variance of the P (Lk) distribution
| (17) |
As noted in the starting point of our derivation in Eq. (8), the above relations apply regardless of the presence or absence of a preformed juxtaposition. Hence, more specifically, for the case with a preformed juxtaposition j, Eq. (16) becomes
| (18) |
where 〈Wr〉00,j stands for the average writhe in the presence of preformed juxtaposition j over conformations with no torsional energy. The full Lk distribution with a preformed juxtaposition j may be expressed as
| (19) |
which can be further simplified because our simulation results in Fig. 2a indicate that, to a very good approximation, the standard deviation in Lk is independent of the existence of a preformed juxtaposition; that is, . Making use of this observation and combining Eqs. (6) and (19), we obtain
| (20) |
From the definition in Eq. (3) and the fact that average Lk is zero at topological equilibrium, viz., Peq(Lk) ∝ exp[−(Lk)2/2(σLk)2], we arrive at
| (21) |
Therefore,
| (22) |
and
| (23) |
Thus, by Eq. (23),
| (24) |
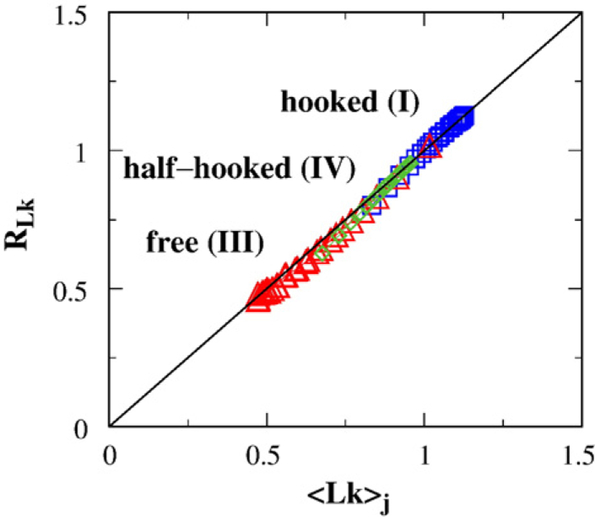
It is noteworthy that the segment-passage rates bj(−), bj(+) and the juxtaposition densities ρj(+), ρj(−) affect the mean [Eq. (22)] but not the standard deviation [Eq. (23)] of the steady-state Lk distribution. For special cases in which the juxtaposition satisfies 〈Lk〉j(+)=−〈Lk〉j(−), Eq. (24) reduces to RLk=〈Lk〉j(+), which we denote simply as 〈Lk〉j. This relation is verified in Fig. 6 for the hooked, free, and half-hooked juxtapositions, all of which satisfy 〈Lk〉j(+)=−〈Lk〉j(−). The result in Fig. 6 shows extremely good agreement between RLk computed via the recurrence relation in Eq. (6) and the analytical expression 〈Lk〉j from Eq. (24).
Fig. 6.
Agreement between computed RLk [using Eq. (6)] and the analytical expression 〈Lk〉j [Eq. (24)]. Results are for a range of chain lengths up to n=500 (as in Fig. 5b) with selective passages at the hooked (I, blue squares), free (III, red triangles), or half-hooked (IV, green diamonds) juxtapositions.
Lk distribution narrowing by selective j*-symmetrized segment passages
The results so far (Figs. 3–6) were computed using our original virtual segment-passage operation (Fig. 1a). We now include the symmetrized operations (Fig. 1b) in the improved procedure to obtain j*-symmetrized Pst(Lk) and RLk values, as for the analysis for knots and catenanes in Materials and Methods. Let j(±)* be the juxtapositions conjugating to j(±). Because a juxtaposition and its conjugate have opposite signs, the process conjugating to that of an Lk flux passing through j(+) to become Lk−2 is that of an Lk−2 flux passing through j(+)* to become Lk. Similarly, the process conjugating to that of an Lk flux passing through j(−) to become Lk+2 is that of an Lk+2 flux passing through j(−)* to become Lk. Therefore, by stipulating that the statistical weights for the j(±) and j(±)* processes are equal, the j*-symmetrized Pst(Lk) may be computed by replacing every Pj(∓) or Pj(±) factor in Eq. (6) by a symmetrized factor, viz.,
| (25) |
where we have used Lk′ to represent any given variable for Pj(∓) or Pj(±) in Eq. (6) to distinguish it from the Lk variable defined by S(Lk) in that equation. Note that the expression in Eq. (25) also provides the replacement for Pj(∓), as may be made explicit by interchanging the “+” and “−” signs in Eq. (25). With all the Pj(±) values modified by Eq. (25), the j*-symmetrized Pst(Lk), and thus the j*-symmetrized RLk, can be determined using Eq. (3) and the recurrence relation Eq. (6) as described above.
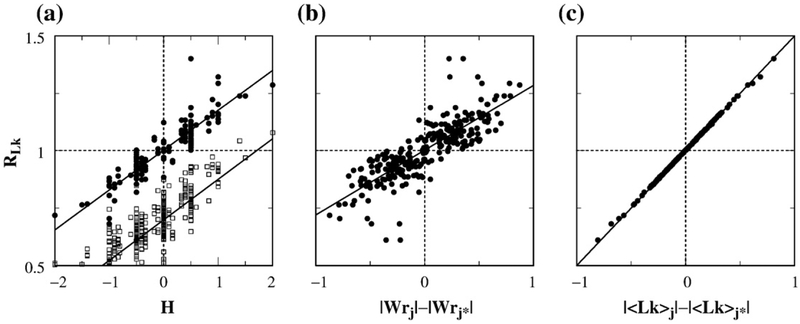
Figure 7a compares the supercoil distribution narrowing factor RLk computed with and without j*-symmetrization. The scatter plot shows that the j*-symmetrized RLk values are higher, with the highest value reaching ≈1.4 instead of the highest RLk value of ≈1.1 in the absence of j*-symmetrization. j*-symmetrization also improves the correlation between RLk and the hookedness parameter H, raising the Pearson correlation coefficient to r=0.88 from r=0.70 for the RLk values obtained without j*-symmetrization. Figure 7b shows the scatter plot of j*-symmetrized RLk versus the difference in absolute values of the writhes of the juxtaposition and its conjugate. The quantity Wrj in Fig. 7b is defined by Wrj = ∑i,i′∊{j} Wr(i, i′), where Wr(i, i′) is the writhe of two bonds i and i′ and the summation is restricted only to the bonds constituting the juxtaposition j. The degree of correlation between j*-symmetrized RLk with |Wrj|−|Wrj*| is similar to that between j*-symmetrized RLk and H.
Fig. 7.
Correlation between RLk and geometric properties of the juxtaposition. Each j*-symmetrized supercoil distribution narrowing factor RLk was computed by considering four juxtapositions, j(+), j(−), j(+)*, and j(−)*, as described in the text. Shown here are scatter plots of RLk with (a) the hookedness parameter H of the juxtapositions, (b) the difference in absolute value between writhe of the juxtapositions and that of the conjugate juxtapositions, and (c) the difference between |〈Lk〉| constrained by the juxtapositions and that constrained by the conjugate juxtapositions. Data are for 425 juxtapositions (each represented by a dot) that permit virtual segment passage as well as j*-symmetrization. Specifically, in (a), H is for j(+), that is, H=Hj(+); by definition,33,34 Hj(+)=Hj(−)=−Hj(+)*=−Hj(−)*. In (b), Wrj and Wrj* denote, respectively, the writhe values Wrj(+) and Wrj(+)* for j(+) and j(+)*. By construction, Wrj(+)=−Wrj(−) and Wrj(+)*=−Wrj(−)*. In (c), |〈Lk〉j| is shorthand for |〈Lk〉j(+)−〈Lk〉j(−)|/2, whereas |〈Lk〉j*| is shorthand for |〈Lk〉j(−)*−〈Lk〉j(+)*|/2. All results shown are for n=100 lattice circles. The upper straight line in (a) and the straight lines in (b) and (c) are least-squares fits to the dots, with correlation coefficients r=0.88, 0.82, and 1.0, respectively. Also shown in (a) is the RLk–H scatter plot and least-squares fit for RLk computed without j*-symmetrization for the set of all 680 juxtapositions that permit virtual segment passages (open squares; r=0.70).
Can we devise an equation with similar accuracy to that of Eq. (24) that relates j*-symmetrized RLk values with mean Lk values of constrained distributions? As illustrated in Fig. 1, j*-symmetrization entails including reverse virtual segment passages through conjugate juxtapositions. Because the initial state of the Lk→Lk+2 reverse virtual segment passages via juxtaposition j(+)* is equivalent to the final state of the Lk+2→Lk virtual segment passages via j(+)*, the mean of the Lk distribution for the initial state of the Lk→Lk+2 reverse virtual segment passages via juxtaposition j(+)* is equal to 〈Lk〉j(+)*+2. Similarly, the mean of the Lk distribution for the initial state of Lk→Lk−2 reverse virtual segment passage via j(−)* is equal to 〈Lk〉j(−)*−2. Heuristically, the selective segment passage under j*-symmetrization involving two original and their conjugate juxtapositions may be viewed as via a pair of effective positive and negative juxtapositions with the means of their respective Lk distributions equal to [〈Lk〉j(+)+〈Lk〉j(+)*+2]/2 and [〈Lk〉j(−)+〈Lk〉j(−)*−2]/2. Treating these expressions as the effective 〈Lk〉 quantities, respectively, for the positive and negative juxtapositions in Eq. (24), we arrive at the following ansatz for the j*-symmetrized supercoil distribution narrowing factor
| (26) |
We test this ansatz in Fig. 7c. The scatter plot in Fig. 7c shows a nearly perfect match between j*-symmetrized RLk values obtained by direct simulations using Eqs. (3), (6), and (25) on the one hand and the right side of Eq. (26) on the other. Consistent with Eq. (26), the horizontal variable in Fig. 7c is in good agreement with 2(RLk−1). Strictly speaking, the derivation of Eqs. (20)–(24) does not apply when segment passage is allowed to proceed via more than one juxtaposition of the same sign (as in the j*-symmetrized operation) because the sum of two Gaussian distributions is not a Gaussian distribution. Nonetheless, the sum of two Gaussian distributions whose difference in mean is small compared to their individual widths may be approximated not too badly by a single Gaussian distribution with a mean that equals to the average of the two original means. This is a likely reason for the success of Eq. (26). For example, for circles with chain length n=100, 〈Lk〉j(+)=1.10 when j(+) is the hooked juxtaposition with a positive crossing, 2+〈Lk〉j(+)*=2−0.54=1.46 when j(+)* is the free juxtaposition with a negative crossing; one can see that the difference 〈Lk〉j(+)−(2+〈Lk〉j(+)*)=1.46−1.10=0.36 is small compared to σLk≈2.7.
Twisted–hooked and hooked juxtapositions have comparable disentangling and supercoil distribution narrowing potentials
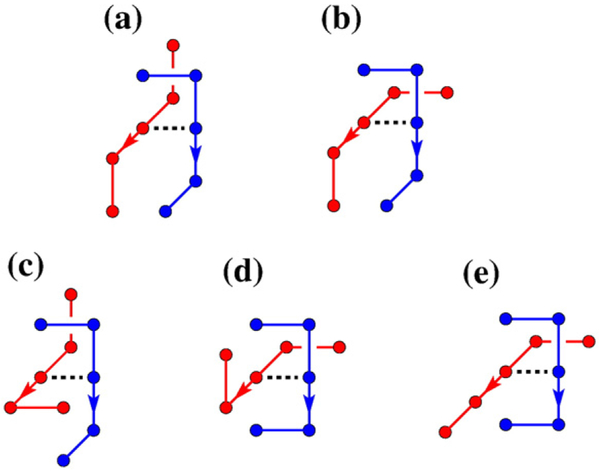
The scatter plot for j*-symmetrized RLk in Fig. 7a (filled circles) shows that three RLk values at H=1/2 and H=1 are higher than that of the hooked juxtaposition at H=2. In other words, the exhaustive scanning of juxtaposition geometries in Fig. 7a has uncovered juxtapositions that can be even more effective in supercoil distribution narrowing than the hooked juxtaposition. Figure 8 shows the five juxtapositions besides the hooked juxtaposition that have the highest j*-symmetrized RLk values. Unexpectedly, not all juxtapositions with high RLk values were effective in unknotting and decatenating. Table 1 shows that juxtapositions (a) and (b) were clearly not effective in decatenating. Comparing the log10 RL and log10 RK values of the juxtapositions in Table 1 with that of log10 RL=1.21 and log10 RK=2.39 for the hooked juxtaposition (for n=100) indicates that juxtaposition (c) has both a higher unknotting potential and a slightly higher supercoil distribution narrowing potential (RLk=1.31) than that of the hooked juxtaposition (RLk=1.28), though the decatenating potential of juxtaposition (c) is somewhat lower than that of the hooked juxtaposition. Juxtapositions (d) and (e) in Fig. 8 should be of interest in future studies because although their RLk values are smaller than those of juxtapositions (a)–(c) and the hooked juxtaposition, their RL and RK values are quite high. We call (c) the twisted–hooked juxtaposition and it may be viewed as a repeating unit in a lattice supercoil (Fig. 9). For circle sizes up to n=500 we tested, the supercoil distribution narrowing of the twisted–hooked juxtaposition was consistently higher than that of the hooked juxtaposition; the difference increases with n for n≳200 (Fig. 10).
Fig. 8.
Juxtapositions with highest supercoil distribution narrowing potentials. Shown here are five of the six juxtapositions with the highest RLk values in our model. The RLk values are listed in Table 1. We refer to (c) as the twisted–hooked juxtaposition (V). The hooked juxtaposition (not shown in this figure) has RLk=1.28, ranking just below that of the twisted–hooked juxtaposition.
Table 1.
Lk variance and topological reduction factors computed using j*-symmetrization for the juxtapositions in Fig. 8 for n=100
| Juxtapositions | RLk | RK | log10 RK | RL | log10 RL |
|---|---|---|---|---|---|
| (a) | 1.40 | 15.1 | 1.18 | 1.30 | 0.11 |
| (b) | 1.34 | 37.3 | 1.57 | 1.37 | 0.14 |
| (c) | 1.31 | 396.6 | 2.60 | 7.04 | 0.85 |
| (d) | 1.24 | 164.8 | 2.22 | 8.30 | 0.92 |
| (e) | 1.24 | 53.4 | 1.73 | 7.29 | 0.86 |
Fig. 9.
Twisted juxtaposition as part of a supercoil. (a) A lattice “supercoil” with negative crossings between two strands (red and blue). The mirror image of (a) is the lattice supercoil in (e) with positive crossings. (b) and (d) are tube representations, respectively, of (a) and (e). Dotted boxes in (b) and (d) enclose parts of the supercoils that correspond, respectively, to the twisted–hooked juxtaposition in Fig. 8c and its mirror image. Tube representations of the twisted–hooked juxtapositions are depicted individually in (c).
Fig. 10.
Chain length dependence of supercoil distribution narrowing factor. RLk values computed using j*-symmetrization for the hooked (I), free (III), half-hooked (IV), and twisted–hooked (V) juxtapositions are shown as functions of n. Note that the j*-symmetrized RLk values for (I), (III), and (IV) here are higher than the corresponding RLk values obtained without j*-symmetrization in Fig. 5b.
Sterics imposed by a hook-like juxtaposition reduce supercoil distribution narrowing in small circles
Figure 10 shows that the supercoil distribution narrowing factors RLk of the twisted–hooked juxtaposition (V) as well as the juxtapositions with one or two hooked segments [hooked (I) and half-hooked (IV)] exhibit a decreasing trend for small circle size n. As in Fig. 5b above, this trend is remarkably similar to that observed in experiments. Measured RLk values from two independent studies30,58 show little dependence of DNA circle size for size ≳4 kb but a clear decreasing trend for DNA circle size ≲4 kb. At first glance, this behavior of RLk is peculiar because it is opposite to the observed experimental trend that type-2 topoisomerases are more effective in unknotting smaller DNA circles.25 Why should the unknotting and supercoil distribution narrowing actions of type-2 topoisomerase show opposite dependence on DNA circle size? This question constitutes a challenge for various proposed models of type-2 topoisomerase action, as Stuchinskaya et al. recognized, commenting that “one might expect the models involving a bent G segment and detection of hooked juxtapositions to predict enhanced effects with small circles and reduced effects with larger ones”.58
Contrary to the assumption of Stuchinskaya et al., our data demonstrate that the experimental RLk dependence on DNA circle size can be rationalized by selective segment passage through the hooked or twisted–hooked juxtaposition geometries (Fig. 10). RLk values for the half-hooked juxtaposition are smaller. Nonetheless, they show a similar n dependence, attesting to the robustness of the trend. However, the model unknotting potential of the half-hooked juxtaposition does not increase with decreasing n (Fig. 6 of Ref. 34). To our knowledge, the hooked juxtaposition hypothesis31 is the only theory that has been demonstrated quantitatively to reproduce both of the opposite experimental trends for an increasing RK (unknotting)24,34 and for a decreasing RLk with decreasing DNA circle size. What physics captured by our model is responsible for this success?
Figure 11 analyzes this question by comparing the constraining effects imposed by a hooked juxtaposition on the writhe of a small circle versus those imposed by a free juxtaposition. For the issue at hand, it suffices to focus on writhe because, by Eq. (24), the supercoil distribution narrowing factor of a juxtaposition is given by the average Lk in the presence of the juxtaposition (note that RLk=|〈Lk〉j| for the hooked and free juxtapositions). In turn, by Eq. (18), 〈Lk〉j is given by the average writhe 〈Wr〉00,j in the presence of the same juxtaposition. Therefore, we may understand why the supercoil distribution narrowing effect of a juxtaposition has a certain dependence on DNA circle size by deciphering how the effect of the given juxtaposition on writhe depends on n. It will be clear from the analysis below that the geometric origin of the small-n behavior of the twisted–hooked juxtaposition should be very similar to that of the hooked juxtaposition, which we now consider.
Fig. 11.
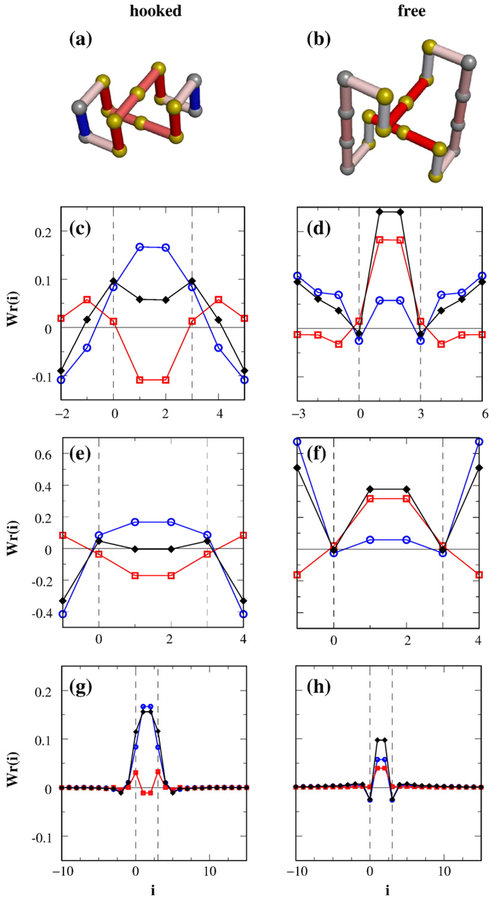
Writhe of small circles with a preformed hooked or free juxtaposition differs significantly from writhe of larger circles with the same constraining preformed juxtaposition. (a) Conformation of the smallest circle on the simple-cubic lattice with a hooked juxtaposition (n=14, Wr=1/2). (b) Conformation of the smallest circle with a free juxtaposition (n=18, Wr=3/2). The Wr(i) profiles for (a) and (b) are provided, respectively, in (c) and (d). The colors of the bonds in (a) and (b) indicate the corresponding variation in Wr(i) ranging from negative (blue) to positive (red) values. The Wr(i) profile in (e) is for a circle with two bonds connecting a hooked juxtaposition; the one in (f) is for a circle with two bonds connecting a free juxtaposition (see text). We found that Wr=−1/2 for (e) and Wr=5/2 for (f). The 〈Wr(i)〉 profile averaged over ensembles of n = 100 circles (no torsional energy) with a preformed hooked juxtaposition is shown in (g). The corresponding 〈Wr(i)〉 for the free juxtaposition is shown in (h). In (c)–(h), black diamonds denote Wr(i) or 〈Wr(i)〉 [summing Wr(i, j) over all j′s], which we resolved into two contributions: (i) from the juxtaposition [blue open circles, summing Wr(i, j) only over j′s for the eight segments in the juxtaposition] and (ii) from the rest of the circle (red open squares). Bonds labeled as i=0, 1, 2, and 3 (region between vertical dashed lines) are those in one segment of the juxtaposition. A position at i<0 is equivalent to position n + i. Because the two segments of either the hooked or the free juxtaposition are equivalent, (c)–(h) only show contributions from one of the segments.
As shown in Fig. 4, the averaged values of Wr and Lk with preformed hooked and free juxtapositions are nearly constant for large n, but show sharp variations for small n. For n≳200, 〈Lk〉j=〈Wr〉00,j≈1.11 and 0.49, respectively, for the hooked and free juxtapositions (Fig. 4b)†. For smaller n, the 〈Lk〉j values, and thus the 〈Wr〉00,j values, of the two juxtapositions show an obvious converging trend. As n decreases, 〈Lk〉j for the hooked juxtaposition remains larger than that for the free juxtaposition until the order reverses at n=22 (for which 〈Lk〉j=0.88 for the hooked juxtaposition and 1.02 for the free juxtaposition). Ultimately, when n decreases further, for the unique smallest circles possible with either a preformed hooked juxtaposition or a preformed free juxtaposition (Fig. 11a and b), the 〈Wr〉00,j=Wr=0.5 value for the hooked juxtaposition becomes significantly smaller than the Wr=1.5 value for the free juxtaposition‡.
Intuitively, it is quite clear from an inspection of Fig. 11a why a hooked juxtaposition would constrain Wr in a small circle. The conformation in Fig. 11a is a limiting case but it serves to illustrate an important principle: A tightly connected small circle places such a severe restriction on conformational freedom that the first bond (pink, see below for color code) and second bond (blue) connected to one end of a segment of a hooked juxtaposition tend to run antiparallel with a nearby bond (red) belonging to the hooked juxtaposition itself. In the case of Fig. 11a, the bonds in such a pair run exactly antiparallel and are separated by the shortest nonzero distance on the simple-cubic lattice. This can be seen by following the contour of the circle in either directions. Mathematically, the contributions to Wr from a pair of antiparallel bonds in close spatial proximity always cancel to a large extent. There are eight such antiparallel bond pairs in Fig. 11a; hence, a small |Wr| ensues. In contrast, for a small circle containing a free juxtaposition, the limiting case in Fig. 11b shows that antiparallel bonds are, on average, farther apart; thus, their contributions to Wr do not cancel as much as antiparallel bond pairs in Fig. 11a. Moreover, in Fig. 11b, contributions to Wr from the bonds outside the free juxtaposition tend to be constructive to (has the same sign as) those from the juxtaposition itself (see below), thus adding to a larger |Wr|.
Considering these findings quantitatively, we label the beads and bonds of our circles by 0, 1, 2, 3, …, n−1, where bond i<n−1 connects beads i and i+1, and bond n−1 connects bead i−1 and bead 0. As in Ref. 44, we express Wr of a circle as
| (27) |
where the summations are over terms involving cross products of pairs of bonds. Note that j here is a bond summation index, not to be confused with the label for juxtapositions. We referred to the set of Wr(i, j) as the two-dimensional writhe map.44 For our purpose of understanding supercoil distribution narrowing, we find it useful to first examine the one-dimensional writhe profile,
| (28) |
which is the contribution from the ith bond to the writhe of a circle.
The Wr(i) profiles for the smallest circles in the lattice model that contain either a hooked or a free juxtaposition (Fig. 11a and b) are plotted in Fig. 11c and d. For the n = 14 circle in Fig. 11a, the contributions to Wr from the hooked juxtaposition (plotted in blue in Fig. 11c) are largely compensated by contributions outside the juxtaposition (plotted in red in Fig. 11c). In contrast, for the n=18 circle in Fig. 11b, Fig. 11d shows that the Wr contributions from inside and outside the free juxtaposition partly reinforce one another. This notable difference, highlighted by the color of the bonds in Fig. 11a and b, elucidates why Wr of a very small circle with a hooked juxtaposition is significantly smaller than a similarly small circle with a free juxtaposition.
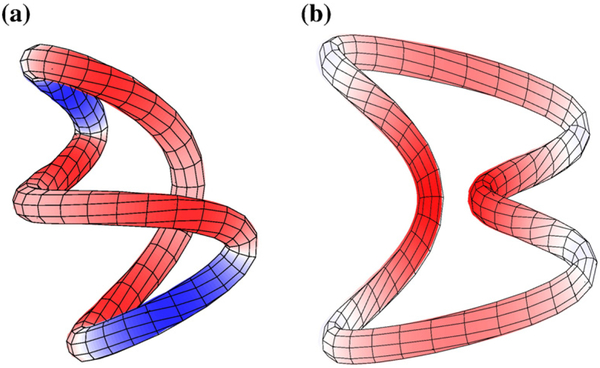
To better understand the influence of juxtaposition geometry on writhe, we further consider two circles constructed by adding two bonds to either a hooked or a free juxtaposition (Fig. 11e and f). In these constructs, each of the added bonds connects the end of one segment to another segment of the juxtaposition directly. The added bonds are longer than the unit lattice spacing, and they do not run along an edge of the simple-cubic lattice. The Wr(i) profiles of these constructs in Fig. 11e and f are similar, respectively, to those in Fig. 11c and d. Taken together, Fig. 11a–f demonstrate consistently that the difference in Wr between small circles containing a hooked juxtaposition and those containing a free juxtaposition is a consequence of writhe compensation and reinforcement (Fig. 12).
Fig. 12.
Cancellation and enhancement of writhe in small circles. Tube representations of the lattice conformations in Fig. 11 show dramatically different consequences of the constraints imposed on the circles by a hooked juxtaposition (a) versus those by a free juxtaposition (b). Similar to the color coding in Fig. 11a and b, red and blue here indicate, respectively, significantly positive and negative Wr(i) values along the chains; white signals Wr(i)≈0.
For a hooked juxtaposition in a larger circle (Fig. 11g), the contributions to Wr from the bonds outside the hooked juxtaposition (plotted in red) are small and cannot subtract much from the large contributions to Wr from the bonds inside the hooked juxtaposition itself (plotted in blue); thus, |Wr| is larger for large circles with a hooked juxtaposition. For a free juxtaposition in a large circle (Fig. 11h), the contributions to Wr from the cross products between the bonds within the juxtaposition and those outside the juxtapositions (plotted in red for i=1, 2) are much lower compared to the corresponding contributions in a small circle (Fig. 11d). Without the tight connectivity of a small circle, directions of the bonds immediately outside the free juxtaposition are more random with little bias to reinforce the contributions to Wr from the juxtaposition itself. Consequently, |Wr| is smaller for large circles with a free juxtaposition. Therefore, the differing effects of the juxtapositions on the writhe of a small circle versus that of a large circle are, in essence, consequences of differing steric effects of adopting these juxtapositions in small and large circles. Analysis of the corresponding Wr(i, j) maps is shown in Fig. S4.
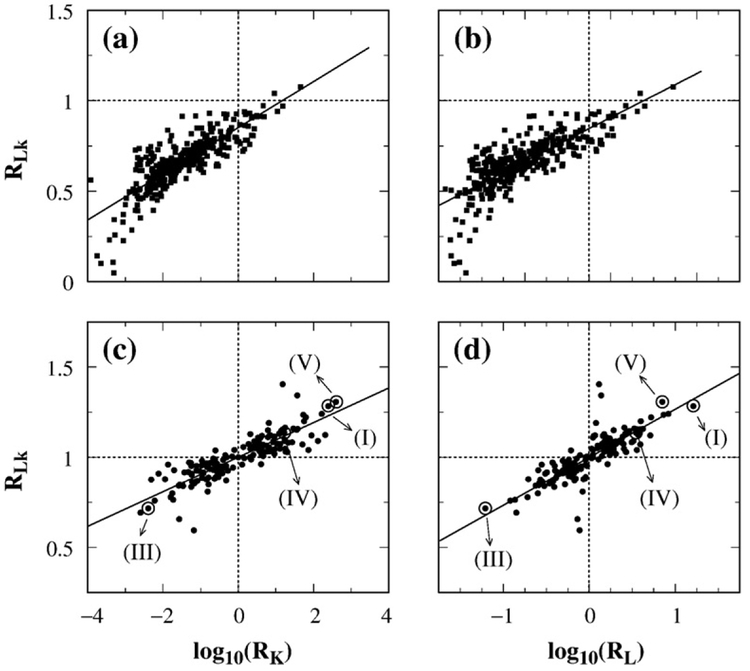
Scaling relations among RLk, RK, and RL reflect experimental observations
Finally, we examine in Fig. 13 the relationship among RLk, RK, and RL. For the juxtapositions we studied, RLk correlates with both log RK and log RL. The data also show that j*-symmetrization led to better correlations (Fig. 13c and d), thus improving the qualitative agreement between our simulation and the experiment of Rybenkov et al.25 In Ref. 25, reductions in knot and link populations were quantified, respectively, by Rkn=(PK)eq/(PK)st and Rcat = (PL)eq/(PL)st. These quantities are slightly different from our RK and RL. The definitions of RK and RL followed naturally from our formulation34 because they do not require separate calculations of (PK)eq and (PL)eq [see Eqs. (38)–(40)], but (PK)eq and (PL)eq were needed to determine Rkn and Rcat. Nonetheless, as we have pointed out,34 because (PK)eq and (PL)eq are small in experiment as well as in simulation, RK≈Rkn and RL≈Rcat. For instance, for the effect of topo IV on the 10 kb P4 DNA in Ref. 25, the experimental (PK)eq = 0.03 and (PL)eq = 0.064 imply that RK=1.03Rkn and RL=1.06Rcat.
Fig. 13.
Scaling relations among topological simplification factors. Scatter plots of the supercoil distribution narrowing factor RLk with the logarithm of knot reduction factor RK (a and c) and the logarithm of link (catenane) reduction factor RL (b and d). Results were obtained by Monte Carlo sampling with no j*-symmetrization for 680 juxtapositions in (a) and (b) and with j*-symmetrization for 425 juxtapositions in (c) and (d). Data points in (c) and (d) for the hooked (I), free (III), half-hooked (IV), and twisted–hooked (V) juxtapositions are indicated by arrows. The straight lines are least-squares fits, with correlation coefficients r equal to (a) 0.81, (b) 0.77, (c) 0.86, and (d) 0.80.
The experimental data of Rybenkov et al.25 on the effect of six type-2 topoisomerases from different organisms on the 7 kb pAB4 DNA are consistent with the scaling34
| (29) |
Remarkably, both our lattice34 and wormlike DNA chain46 models predicted a similar scaling of RK≈(RL)2.0. The different degrees of reduction in Lk variance determined experimentally for the same set of type-2 topoisomerases (Fig. 3B of Ref. 25) are consistent with
| (30) |
which, by virtue of Eq. (29), suggests that
| (31) |
The trend in Fig. 13c and d from our model, viz., RLk≈0.26(log10 RL)+1 and RLk≈0.10(log10 RK)+1, agrees qualitatively with these experimental observations, arguing that our juxtaposition-centric view is capturing an important part of the mechanism underlying real type-2 topoisomerase action. Indeed, the only physical rationalization to date of the experimental scaling behavior has been provided by our models. Nonetheless, the RLk versus log RL and RLk versus log RK slopes estimated in Fig. 13 are less steep than those observed in experiment. The differences in slope are proportionally larger than the ≈0.4 difference between the theoretical and experimental exponents for the RK versus RL scaling. In this comparison, it is also noteworthy that whereas there was little scatter in the RK versus RL plots of our models (r≈0.96 for the lattice model34), there is considerable scatter in the RLk versus log RK or log RL plots in Fig. 13, suggesting that the corresponding slopes can be higher if the correlation were restricted to a subset of the juxtapositions. Elucidation of these issues awaits more extensive experimental data and further theoretical analyses.
Concluding remarks
The work reported above has demonstrated that selective segment passage at the hooked or twisted–hooked juxtaposition can lead to significant reduction in Lk variance, similar to that observed in experiment.25,30,58 The dependence of RLk on DNA circle size n in our model (Fig. 10) is also consistent with experiment.30,58 Thus, our model provides a physical rationalization in terms of chain connectivity constraints on conformational entropy (Figs. 11–13) for the otherwise puzzling experimental trend of decreasing RLk for DNA circle size ≲4 kb observed by Trigueros et al.30 and by Stuchinskaya et al.58 Our model indicates further that RLk b1 is possible for very small circles (e.g., RLk=0.93 for n=22 for the hooked juxtaposition in Fig. 10). In this regard, Trigueros et al. reported a decrease from RLk≈1.8 for 6.8 kb DNA circles to an almost neutral value of RLk≈1.05 for 1.4 kb DNA circles,30 hinting at a likely agreement with our prediction. It will be interesting to test experimentally whether RLk can indeed be decreased below unity for even smaller minicircles.65
Systematic scanning of juxtaposition geometries (Figs. 7–9) has led us to identify the twisted–hooked juxtaposition that is as effective as—and in the instance of supercoil distribution narrowing is even more effective than—the hooked juxtaposition. Because the twisted–hooked juxtaposition is also hook-like, the present finding of its significant disentangling potential represents a generalization of the hooked juxtaposition hypothesis.31 Notably, the twisted–hooked juxtaposition may also be viewed as a unit of DNA writhing (Fig. 9). Unlike a hooked juxtaposition with a crossing angle =90°, the two segments of the twisted juxtaposition are not perpendicular. Effort is underway to study consequences of this feature in light of structural data suggesting that type-2 topoisomerases act on juxtapositions with a crossing angle≠90°66 and that such asymmetry is expected to contribute to the chirality sensing ability of the enzymes.30,48,57,64,67,68
Results here and from previous studies33,34 showed that steady-state reductions in knot, link, and supercoil populations are determined by the geometry of the juxtaposition. In our model, the RK, RL, and RLk reduction factors for the hooked and the twisted–hooked juxtapositions come close to matching the experimental values for real type-2 topoisomerases. In contrast, the corresponding reduction factors for the half-hooked juxtaposition, which is equivalent to those of the “hairpin” or “active bending” model of Vologodskii et al.,26,27 are much too low in comparison with experiment. Using an improved wormlike chain model for DNA, we also found that the half-hooked juxtaposition was quantitatively insufficient to explain the experimental data.46
In view of its simplicity, it is remarkable that simple lattice modeling can capture—at least semi-quantitatively—subtle effects such as scaling relations among different topological reduction factors and their divergent dependence on DNA circle size. Given these successes, we are confident that new challenges emerging from our study, such as the differences between theoretical and experimental scaling exponents noted above, will in time become opportunities for progress. Although the present study has focused on the lattice model, much of the formalism we developed is general. Thus, the stage is set for further in-depth analyses using geometrically and energetically more realistic DNA chain models44,46 in our endeavor to decipher the mathematical and physical basis of how type-2 topoisomerases simplify DNA topology.
Materials and Methods
We describe below several extensions to our modeling methods33,34,44 developed for the present study to provide a more comprehensive account of the decatenating, unknotting, and supercoil distribution narrowing actions of type-2 topoisomerases.
Selective segment passage at multiple juxtaposition geometries
We begin with the master equation for knot and unknot populations undergoing selective segment passages through one specific juxtaposition geometry.34 Although this formulation was introduced for lattice modeling, it is generally applicable to any chain representation.46 We now generalize this formulation to allow for selective segment passages at multiple juxtaposition geometries. There are at least two reasons for this exercise: (i) In off-lattice continuum modeling, the geometrical characteristics selected by a type-2 topoisomerase would likely entail an ensemble of juxtaposition geometries. (ii) The extension is needed for expanding our lattice modeling effort. For example, segment passages can occur at two different juxtapositions when the shape but not the sign of the juxtaposition is selected by the topoisomerase (see Results and Discussion).
We use PU and PK to denote the unknot and knot populations, respectively, whereas and are the corresponding subpopulations in which each conformation has at least one instance of juxtaposition j. Generalizing our previous master equation [Eq. (2) in Ref. 34] to allow for segment passages at multiple juxtaposition geometries, we obtain the equation
| (32) |
where the summation over juxtaposition j is restricted to those through which segment passage can occur, t is time, and bj is the rate of segment passage at j. The weight coefficients bj can be different because segment passage may, a priori, proceed at different rates for different juxtaposition geometries. This feature is useful for treating the possibility that a topoisomerase may recognize and bind different juxtaposition geometries with different affinities or act to pass segments through different juxtaposition geometries at different kinetic rates. The quantities and are, respectively, unknot-to-knot and knot-to-unknot transition probabilities. Following Ref. 34, we use and to symbolize, respectively, the fraction of unknot and knot population that contain juxtaposition j; that is, and . In this notation, Eq. (32) becomes
| (33) |
Now, let (PU)st and (PK)st be, respectively, the steady-state unknot and knot populations. Because they are steady-state populations, d(PU)st/dt = d(PK)st/dt = 0. Therefore, from Eq. (33),
| (34) |
Using the c(j) notation, the transition probabilities
| (35) |
| (36) |
where Nj is the total number of instances of juxtaposition j in all conformations (j can occur more than once in a conformation). Each is the fraction of Nj that entails a specific transition; thus, the quantities satisfy the normalization condition . Our knot reduction factor RK is given by34
| (37) |
Hence, combining Eqs. (34)–(36), and defining ρj≡Nj/Peq as the density of juxtaposition j where Peq=(PU)eq+(PK)eq is the total chain population, we obtain
| (38) |
as the generalized knot reduction factor. Our original formulation in Ref. 34 corresponds to having only one term in each of the summations in Eq. (38). In that case, the bjρj factors cancel and Eq. (38) reduces to our previous equation for RK for a single juxtaposition. Analogously, the generalized expression for the link (catenane) reduction factor is
| (39) |
where “L” symbolizes linked (catenated), “U” symbolizes unlinked, and is the density of juxtaposition j among two-circle configurations. When only one juxtaposition is selected, the factors in Eq. (39) cancel and RL is independent of DNA concentration.
The lattice model
The present effort is based on our lattice DNA model.33,34 As a general approach, lattice modeling has proven since the 1930s69,70 to be a powerful technique in statistical mechanics.71 It has contributed tremendously to polymer physics,72,73 including protein biophysics.74–81 Lattice techniques have been instrumental in developing important mathematical concepts used to elucidate the biophysics of DNA knots and links.4,33,34,82–86 Lattice techniques complement continuum coarse-grained approaches such as the “pearl necklace”,87,88 freely jointed (random flight),14,41,42,89,90 and wormlike6,44,53,91 chain models (reviewed in Ref. 92).
Each conformation in our study consists of n bonds joining n beads to form a closed circuit on the simple-cubic lattice. We refer to these conformations as circles, and n (circle size) as chain length (equivalent to “loop size” in Ref. 34). To ascertain how selective segment passages affect the steady-state distribution of the lattice DNA conformations, we first considered the hooked (I), free (III, referred to as “free nonplanar” in Ref. 34), and half-hooked (IV) juxtapositions (see Fig. 1a). We then broadened our study to all 680 5mer-on-5mer lattice juxtapositions that permit virtual segment passages.34
Our lattice model is for exploring general biophysical principles, not for accurate structural modeling of DNA. One lattice bond is customarily identified with the Kuhn statistical length (l0, ≈300 base pairs) or the persistence length (≈l0/2 for DNA). Thus, a circle of chain length n in our lattice model may correspond approximately to a DNA circle with 150n–300n base pairs. However, because of the coarse-grained nature of the model, this relationship should only be regarded as a rough, order-of-magnitude estimate. For this reason, we focus on general trends of dependence of model properties on n but we do not attempt to match n directly with experimental DNA circle size.
Conformational statistics were computed using exact enumeration34 for small circles (n ≤ 30) and Monte Carlo sampling for larger circles (up to n=500). As before,34 conformational sampling was conducted using a combination of the Madras–Orlitsky–Shepp93 (MOS) and the Berg–Foerster–Aragão de Carvalho–Caracciolo–Fröhlich94,95 (BFACF) algorithms. For the hooked, half-hooked, and free juxtapositions, each n>30 data point was obtained from 8×108 to 3.2×109 simulation time steps. When scanning the comprehensive set of all possible juxtapositions (n=100), we used 3.6×107 simulation time steps for each juxtaposition. Aside from the preformed juxtapositions, conformation freedom was not restricted in our simulations. This modeling situation was chosen to correspond to the conditions of the in vitro experiments we aim to rationalize here. In future studies, it would be interesting to extend the present methodology to investigate how the disentangling actions of type-2 topoisomerases might be affected by the compactness of the DNA conformations in confined spaces.13–17
Symmetrized segment-passage operations in the lattice model likely provide a geometrically more accurate account of type-2 topoisomerase action
We have also developed an improved procedure for the virtual segment-passage operation.33,34 As explained below and in Supplementary Data, the original virtual segment-passage operation likely gave rise to a larger fraction of conformations being entangled than is physically realistic (Figs. S1 and S2). Thus, the original procedure was biased toward underestimating the disentangling power of selective segment passages. Accordingly, although the link and knot reduction factors RL and RK for the hooked juxtaposition we computed previously were already significiant,33,34 the corresponding reduction factors were even larger after the bias was removed (Fig. S3).
The rationale for the new procedure is as follows. Because each bond in a lattice chain corresponds roughly to l0, the separation, d, between two segments of a juxtaposition in our self-avoiding lattice model is d≈l0≈1000 Å. Considering that the width of a type-2 topoisomerase is typically ≈100 Å,45 it is almost certain that d<l0 in reality. In view of a DNA excluded-volume diameter ≈25 Å (0. 025l0), it is instructive to consider an idealized situation in which the DNA chain is infinitely thin so that two segments of a juxtaposition have zero contact distance (d=0) and segment passage changes the crossing sign but leaves the conformation otherwise unchanged. One consequence of this hypothetical d=0 situation is that the passage at a juxtaposition with two straight segments would have no effect on knot population because, by symmetry, the conformational distributions before and after segment passage are exactly identical. Experiments to date do not provide a precise value for d but it is safe to assume that the value lies somewhere between the bounds of d=0–1000 Å. The considerations above suggest that it is closer to d=0 than to d=1000 Å.
In a separate study, we explored d values ranging from 25 to 200 Å (≈0.025–0.2 l0) using a continuum wormlike DNA model and found that the knot reduction factor RK increases with decreasing d for hook-like juxtapositions.46 In an independent study using a random-flight model without excluded volume, passing of segments separated by as far as one Kuhn length was also considered.41 The physical basis of the variation of RK with d may be understood by considering the original virtual segment passage in our lattice model (Fig. 1a), which transforms an on-lattice conformation to one not configured entirely on the lattice (dashed bonds in Fig. 1). As a result of their extra conformational freedom, chains created by virtual segment passages have a higher level of entanglement relative to those restricted strictly to the lattice (see Supplementary Data). Because the deformation caused by segment passage and thus the resulting bias toward relatively more entanglement increases with d, RK decreases with increasing d.
Up to a degree, the bias observed in our lattice models can be a reflection of reality. Because DNA has a finite diameter (d>0) and is elastic, the transient conformational geometries created by local segment passages would be energetically slightly strained around the site of the passage. As a result, these conformational geometries have a slightly higher knotting probability than the conformations created by the corresponding ideal (d=0) segment passages that do not entail such an energetic strain. Indeed, wormlike DNA model studies27,46 indicated that segment passages at a juxtaposition with two straight segments could result in an RK≈0.7–0.8, which is slightly biased toward knotting, rather than the neutral RK=1.0 expected for the d=0 ideal case. However, the corresponding bias in the lattice model was substantially higher, yielding for n=100 an RK=0.18 for a juxtaposition with two straight segments.34
Our new lattice procedure aims to compensate for this large bias so as to achieve results more akin to those for the d = 0 ideal situation. To do so, we augmented the contribution from the original virtual segment passage at a juxtaposition j (as in Fig. 1a) by the contribution from the reverse segment passage at the juxtaposition′s conjugate j* (as in Fig. 1b). We call this procedure j*-symmetrization. Intuitively, the conjugate j* of juxtaposition j is the “relaxed form” of the juxtaposition resulting from segment passage at j. For instance, the hooked and free juxtapositions are conjugate to each other. In general, let the position of any bead i of the two segments (1 and 2) of a juxtaposition j* be and . Then the corresponding positions of its conjugate juxtaposition j* are (unchanged) and , where is the vector from the center bead of segment 2 to the center bead of segment 1; j and j* thus have opposite crossing signs. Because this construction can result in excluded volume violations, some juxtapositions do not have conjugates. Among the 680 5mer-on-5mer juxtapositions that can undergo virtual segment passages,34 425 have conjugates.
We define a j*-symmetrized segment passage as the forward transition via j (solid arrows in Fig. 1) plus the reverse transition via j* (dashed arrows in Fig. 1). This procedure is equivalent to extending the segment-passage operations to include all virtual conformations (those with dashed bonds in Fig. 1) created by forward transitions as well as the original, on-lattice conformations. Using Eq. (38) for a pair of selected juxtapositions and stipulating equal statistical weights for j and j*, we arrive at
| (40) |
as the j*-symmetrized knot reduction factor. The j*-symmetrized link reduction factor RL is obtained by substituting “K” in the above expression with “L” (changing to , etc). As noted above, j*-symmetrization increases RK and RL for all juxtapositions (Fig. S3)§. Thus, our conclusion24,33,34 in support of the hooked juxtaposition hypothesis31 is strengthened by the introduction of the symmetrized segment-passage operation. Further discussion of the procedure is provided in Supplementary Data.
Supplementary Material
Acknowledgements
We thank Dr. Lorenzo Sadun (University of Texas, Austin) and Dr. Dorothy Buck (Imperial College London) for a discussion in 2006 about symmetry of segment passages in lattice models. Support for this research was provided in part by Ministry of Science and Technology of China Grant 2009CB918500 and National Natural Science Foundation of China Grant 20973016 to Z.L., National Institutes of Health (USA) grant RO1 AI054830 to L.Z., and the Natural Sciences and Engineering Research Council of Canada through a Discovery Grant to H.S.C. (216901), who holds a Canada Research Chair in Proteomics, Bioinformatics, and Functional Genomics.
Footnotes
Supplementary Data
Supplementary data associated with this article can be found, in the online version, at doi:10.1016/j.jmb.2010.05.007
As stated, 〈Lk〉j = RLk = 〈Wr〉00,j. Note that 〈Wr〉00,j computed without torsional energy is always larger than the 〈Wr〉j computed with torsional energy for Lk = 0 in Fig. 4a because of Eq. (13) and the fact that B > 1 [Eq. (12)].
Note that the Wr values of the two conformations in Fig. 11a and b are conforming to the theorem that Wr must be equal to an integer/4 for the simple-cubic lattice.59,60
For the juxtaposition with two straight segments, j and j* are equal except for their opposite signs. It follows that for every transition in Eq. (40), and thus, the j*-symmetrized RK = RL = 1 for the lattice juxtaposition with two straight segments, as if the juxtaposition were ideal with d = 0.
References
- 1.Delbrück M (1954). On the replication of deoxyribonucleic acid (DNA). Proc. Natl Acad. Sci. USA, 40, 783–788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Delbrück M (1962). Knotting problems in biology In Mathematical Problems in the Biological Sciences (Proceedings of Symposia in Applied Mathematics, Vol. 14), pp. 55–63, American Mathematical Society, Providence, RI. [Google Scholar]
- 3.Wang JC (1971). Interaction between DNA and an Escherichia coli protein ω. J. Mol. Biol 55, 523–533. [DOI] [PubMed] [Google Scholar]
- 4.Sumners DW & Whittington SG (1988). Knots in self-avoiding walks. J. Phys. A: Math. Gen 21, 1689–1694. [Google Scholar]
- 5.Rybenkov VV, Cozzarelli NR & Vologodskii AV (1993). Probability of DNA knotting and the effective diameter of the DNA double helix. Proc. Natl Acad. Sci. USA, 90, 5307–5311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Podtelezhnikov AA, Cozzarelli NR & Vologodskii AV (1999). Equilibrium distributions of topological states in circular DNA: interplay of supercoiling and knotting. Proc. Natl Acad. Sci. USA, 96, 12974–12979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Sundin O & Varshavsky A (1980). Terminal stages of SV40 DNA replication proceed via multiply intertwined catenated dimers. Cell, 21, 103–114. [DOI] [PubMed] [Google Scholar]
- 8.Sundin O & Varshavsky A (1981). Arrest of segregation leads to accumulation of highly intertwined catenated dimers—dissection of the final states of SV40 DNA replication. Cell, 25, 659–669. [DOI] [PubMed] [Google Scholar]
- 9.Adams DE, Shekhtman EM, Zechiedrich EL, Schmid MB & Cozzarelli NR (1992). The role of topoisomerase IV in partitioning bacterial replicons and the structure of catenated intermediates in DNA replication. Cell, 71, 277–288. [DOI] [PubMed] [Google Scholar]
- 10.Zechiedrich EL & Cozzarelli NR (1995). Roles of topoisomerase IV and DNA gyrase in DNA unlinking during replication in Escherichia coli. Genes Dev. 9, 2859–2869. [DOI] [PubMed] [Google Scholar]
- 11.Schvartzman JB & Stasisak A (2004). A topological view of the replicon. EMBO Rep. 5, 256–261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Shishido K, Komiyama N & Ikawa S (1987). Increased production of a knotted form of plasmid pBR322 DNA in Escherichia coli DNA topoisomerase mutants. J. Mol. Biol 195, 215–218. [DOI] [PubMed] [Google Scholar]
- 13.Arsuaga J, Vazquez M, Trigueros S, Sumners DW & Roca J (2002). Knotting probability of DNA molecules confined in restricted volumes: DNA knotting in phage capsids. Proc. Natl Acad. Sci. USA, 99, 5373–5377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Micheletti C, Marenduzzo D, Orlandini E & Sumners DW (2006). Knotting of random ring polymers in confined spaces. J. Chem. Phys 124, 064903; Correction: 124, 219903 (2006). [DOI] [PubMed] [Google Scholar]
- 15.Arsuaga J, Blackstone T, Diao Y, Hinson K, Karadayi E & Saito M (2007). Sampling large random knots in a confined space. J. Phys. A: Math. Theor 40, 11697–11711. [Google Scholar]
- 16.Micheletti C, Marenduzzo D, Orlandini E & Sumners DW (2008). Simulations of knotting in confined circular DNA. Biophys. J 95, 3591–3599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Marenduzzo D, Orlandini E, Stasiak A, Sumners DW, Tubiana L & Micheletti C (2009). DNA–DNA interactions in bacteriophage capsids are responsible for the observed DNA knotting. Proc. Natl Acad. Sci. USA, 106, 22269–22274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Deibler RW, Mann JK, Sumners DWL & Zechiedrich L (2007). Hin-mediated DNA knotting and recombining promote replicon dysfunction and mutation. BMC Mol. Biol 8, 44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wang JC (1996). DNA topoisomerases. Annu. Rev. Biochem 65, 635–692. [DOI] [PubMed] [Google Scholar]
- 20.Champoux JJ (2001). DNA topoisomerases: structure, function, and mechanism. Annu. Rev. Biochem 70, 369–413. [DOI] [PubMed] [Google Scholar]
- 21.Maxwell A, Costenaro L, Mitelheiser S & Bates AD (2005). Coupling ATP hydrolysis to DNA strand passage in type IIA DNA topoisomerases. Biochem. Soc. Trans 33, 1460–1464. [DOI] [PubMed] [Google Scholar]
- 22.Schoeffler AJ & Berger JM (2005). Recent advances in understanding structure–function relationships in the type II topoisomerase mechanism. Biochem. Soc. Trans 33, 1465–1470. [DOI] [PubMed] [Google Scholar]
- 23.Schoeffler AJ & Berger JM (2008). DNA topoisomerases: harnessing and constraining energy to govern chromosome topology. Q. Rev. Biophys 41, 41–101. [DOI] [PubMed] [Google Scholar]
- 24.Liu Z, Deibler RW, Chan HS & Zechiedrich L (2009). The why and how of DNA unlinking. Nucleic Acids Res. 37, 661–671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Rybenkov VV, Ullsperger C, Vologodskii AV & Cozzarelli NR (1997). Simplification of DNA topology below equilibrium values by type II topoisomerases. Science, 277, 690–693. [DOI] [PubMed] [Google Scholar]
- 26.Vologodskii A (1998). Maxwell demon and topology simplification by type II topoisomerases In RECOMB 98: Proceedings of the Second Annual International Conference on Computational Molecular Biology, pp. 266–269, Association for Computing Machinery, New York, NY. [Google Scholar]
- 27.Vologodskii AV, Zhang W, Rybenkov VV, Podtelezhnikov AA, Subramanian D, Griffith JD & Cozzarelli NR (2001). Mechanism of topology simplification by type II DNA topoisomerases. Proc. Natl Acad. Sci. USA, 98, 3045–3049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Yan J, Magnasco MO & Marko JF (1999). A kinetic proofreading mechanism for disentanglement of DNA by topoisomerases. Nature, 401, 932–935. [DOI] [PubMed] [Google Scholar]
- 29.Yan J, Magnasco MO & Marko JF (2001). Kinetic proofreading can explain the suppression of supercoiling of circular DNA molecules by type-II topoisomerases. Phys. Rev. E, 63, 031909. [DOI] [PubMed] [Google Scholar]
- 30.Trigueros S, Salceda J, Bermúdez I, Fernández X & Roca J (2004). Asymmetric removal of supercoils suggests how topoisomerase II simplifies DNA topology. J. Mol. Biol 335, 723–731. [DOI] [PubMed] [Google Scholar]
- 31.Buck GR & Zechiedrich EL (2004). DNA disentangling by type-2 topoisomerases. J. Mol. Biol 340, 933–939. [DOI] [PubMed] [Google Scholar]
- 32.Vologodskii A (2009). Theoretical models of DNA topology simplification by type IIA DNA topoisomerases. Nucleic Acids Res. 37, 3125–3133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Liu Z, Zechiedrich EL & Chan HS (2006). Inferring global topology from local juxtaposition geometry: interlinking polymer rings and ramifications for topoisomerase action. Biophys. J 90, 2344–2355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Liu Z, Mann JK, Zechiedrich EL & Chan HS (2006). Topological information embodied in local juxtaposition geometry provides a statistical mechanical basis for unknotting by type-2 DNA topoisomerases. J. Mol. Biol 361, 268–285. [DOI] [PubMed] [Google Scholar]
- 35.Zechiedrich EL & Osheroff N (1990). Eukaryotic topoisomerases recognize nucleic acid topology by preferentially interacting with DNA crossovers. EMBO J. 9, 4555–4562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Howard MT, Lee MP, Hsieh T-S & Griffith JD (1991). Drosophila topoisomerase II–DNA interactions are affected by DNA structure. J. Mol. Biol 217, 53–62. [DOI] [PubMed] [Google Scholar]
- 37.Roca J & Wang JC (1992). The capture of a DNA double helix by an ATP-dependent protein clamp: a key step in DNA transport by type II DNA topoisomerases. Cell, 71, 833–840. [DOI] [PubMed] [Google Scholar]
- 38.Corbett AH, Zechiedrich EL & Osheroff N (1992). A role for the passage helix in the DNA cleavage reaction of eukaryotic topoisomerase II. A two-site model for enzyme-mediated DNA cleavage.J. Biol. Chem 267, 683–686. [PubMed] [Google Scholar]
- 39.Timsit Y, Duplantier B, Jannink G & Sikorav J-L (1998). Symmetry and chirality in topoisomerases II–DNA crossover recognition. J. Mol. Biol 284, 1289–1299. [DOI] [PubMed] [Google Scholar]
- 40.Strick TR, Croquette V & Bensimon D (2000). Single-molecule analysis of DNA uncoiling by a type II topoisomerase. Nature, 404, 901–904. [DOI] [PubMed] [Google Scholar]
- 41.Burnier Y, Weber C, Flammini A & Stasiak A (2007). Local selection rules that can determine specific pathways of DNA unknotting by type II DNA topoisomerases. Nucleic Acids Res. 35, 5223–5231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Flammini A, Maritan A & Stasiak A (2004). Simulations of action of DNA topoisomerases to investigate boundaries and shapes of spaces of knots. Biophys. J 87, 2968–2975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Katritch V, Bednar J, Michoud D, Scharein RG, Dubochet J & Stasiak A (1996). Geometry and physics of knots. Nature, 384, 142–145. [DOI] [PubMed] [Google Scholar]
- 44.Liu Z & Chan HS (2008). Efficient chain moves for Monte Carlo simulations of a wormlike DNA model: excluded volume, supercoils, site juxtapositions, knots, and comparisons with random-flight and lattice models. J. Chem. Phys 128, 145104; Erratum: 131, 049902 (2009). [DOI] [PubMed] [Google Scholar]
- 45.Kong KC & Berger JM (2007). Structural basis for gate–DNA recognition and bending by type IIA topoisomerases. Nature, 450, 1201–1205. [DOI] [PubMed] [Google Scholar]
- 46.Liu Z, Zechiedrich L & Chan HS (2010). Local site preference rationalizes disentangling by DNA topoisomerases. Phys. Rev. E, 81, 031902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Wang JC (1985). DNA topoisomerases. Annu. Rev. Biochem 54, 665–697. [DOI] [PubMed] [Google Scholar]
- 48.Fogg JM, Catanese DJ, Randall GL, Swick MC & Zechiedrich L (2008). Differences between positively and negatively supercoiled DNA that topoisomerases may distinguish In Mathematics of DNA Structure, Function and Interactions; The IMA Volumes in Mathematics and its Applications (Benham CJ, Harvey S, Olson WK, Sumners DW & Swigon D, eds), vol. 150, pp. 73–121, Springer, New York, NY. [Google Scholar]
- 49.Vologodskii A & Cozzarelli NR (1996). Effect of supercoiling on the juxtaposition and relative orientation of DNA sites. Biophys. J 70, 2548–2556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Polikanov YS, Bondarenko VA, Tchernaenko V, Jiang Y, Lutter LC, Vologodskii A & Studitsky VM (2007). Probability of the site juxtaposition determines the rate of protein-mediated DNA looping. Biophys. J 93, 2726–2731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Halford SE & Marko JF (2004). How do site-specific DNA-binding proteins find their targets? Nucleic Acids Res. 32, 3040–3052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Vologodskii AV & Cozzarelli NR (1994). Conformational and thermodynamic properties of supercoiled DNA. Annu. Rev. Biophys. Biomol. Struct 23, 609–643. [DOI] [PubMed] [Google Scholar]
- 53.Burnier Y, Dorier J & Stasiak A (2008). DNA supercoiling inhibits DNA knotting. Nucleic Acids Res. 36, 4956–4963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Ullsperger C & Cozzarelli NR (1996). Contrasting enzymatic activities of topoisomerase IV and DNA gyrase from Escherichia coli. J. Biol. Chem 271, 31549–31555. [DOI] [PubMed] [Google Scholar]
- 55.Zechiedrich EL, Khodursky AB & Cozzarelli NR (1997). Topoisomerase IV, not gyrase, decatenates products of site-specific recombination in Escherichia coli. Genes Dev. 11, 2580–2592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Deibler RW, Rahmati S & Zechiedrich EL (2001). Topoisomerase IV, alone, unknots DNA in E. coli. Genes Dev. 15, 748–761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Witz G & Stasiak A (2010). DNA supercoiling and its role in DNA decatenation and unknotting. Nucleic Acids Res. 38, 2119–2133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Stuchinskaya T, Mitchenall LA, Schoeffler AJ, Corbett KD, Berger JM, Bates AD & Maxwell A (2009). How do type II topoisomerases use ATP hydrolysis to simplify DNA topology beyond equilibrium? Investigating the relaxation reaction of nonsupercoiling type II topoisomerases. J. Mol. Biol 385, 1397–1408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Lacher RC & Sumners DW (1991). Data structures and algorithms for computation of topological invariants of entanglememts: link, twist and writhe In Computer Simulation of Polymers (Roe RJ, ed), pp. 365–373, Prentice-Hall, Englewood Cliffs, NJ. [Google Scholar]
- 60.Laing C & Sumners DW (2006). Computing the writhe on lattices. J. Phys. A: Math. Gen 39, 3535–3543. [Google Scholar]
- 61.Călugăreanu G (1959). L′intégral de Gauss et l′analyse des noeuds tridimensionnels. Rev. Math. Pures Appl. 4, 5–20. [Google Scholar]
- 62.White JH (1969). Self-linking and the Gauss integral in higher dimensions. Am. J. Math 91, 693–728. [Google Scholar]
- 63.Fuller FB (1971). The writhing number of a space curve. Proc. Natl Acad. Sci. USA, 68, 815–819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Stone MD, Bryant Z, Crisona NJ, Smith SB, Vologodskii A, Bustamante C & Cozzarelli NR (2003). Chirality sensing by Escherichia coli topoisomerase IV and the mechanism of type II toposiomerases. Proc. Natl Acad. Sci. USA, 100, 8654–8659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Fogg JM, Kolmakova N, Rees I, Magonov S, Hansma H, Perona JJ & Zechiedrich EL (2006). Exploring writhe in supercoiled minicircle DNA. J. Phys. Condens. Matter, 18, S145–S159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Corbett KD, Schoeffler AJ, Thomsen ND & Berger JM (2005). The structural basis for substrate specificity in DNA topoisomerase IV. J. Mol. Biol 351, 545–561. [DOI] [PubMed] [Google Scholar]
- 67.Neuman KC, Charvin G, Bensimon D & Croquette V (2009). Mechanisms of chiral discrimination by topoisomerase IV. Proc. Natl Acad. Sci. USA, 106, 6986–6991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Randall GL, Zechiedrich L & Pettitt BM (2009). In the absence of writhe, DNA relieves torsional stress with localized, sequence-dependent structural failure to preserve B-form. Nucleic Acids Res. 37, 5568–5577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Fowler FH & Rushbrooke GS (1937). An attempt to extend the statistical theory of perfect solutions. Trans. Faraday Soc. 33, 1272–1294. [Google Scholar]
- 70.Chang TS (1939). Statistical theory of the adsorption of double molecules. Proc. R. Soc. London, Ser. A, 169, 512–531. [Google Scholar]
- 71.Onsager L (1944). Crystal statistics. I. A two-dimensional model with an order–disorder transition. Phys. Rev 65, 117–149. [Google Scholar]
- 72.Orr WJC (1947). Statistical treatment of polymer solutions at infinite dilution. Trans. Faraday Soc. 43, 12–27. [Google Scholar]
- 73.Domb C (1969). Self-avoiding walks on lattices. Adv. Chem. Phys 15, 229–259. [Google Scholar]
- 74.Taketomi H, Ueda Y & Gō N (1975). Studies on protein folding, unfolding and fluctuations by computer simulation. 1. The effect of specific amino acid sequence represented by specific inter-unit interactions. Int. J. Pept. Protein Res. 7, 445–459. [PubMed] [Google Scholar]
- 75.Chan HS & Dill KA (1990). The effects of internal constraints on the configurations of chain molecules. J. Chem. Phys 92, 3118–3135; Erratum: 107, 10353 (1997). [Google Scholar]
- 76.Chan HS & Dill KA (1990). Origins of structure in globular proteins. Proc. Natl Acad. Sci. USA, 87, 6388–6392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Shakhnovich EI, Farztdinov G, Gutin AM & Karplus M (1991). Protein folding bottlenecks: a lattice Monte Carlo simulation. Phys. Rev. Lett 67, 1665–1668. [DOI] [PubMed] [Google Scholar]
- 78.Leopold PE, Montal M & Onuchic JN (1992). Protein folding funnels: a kinetic approach to the sequence–structure relationship. Proc. Natl Acad. Sci. USA, 89, 8721–8725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Camacho CJ & Thirumalai D (1993). Kinetics and thermodynamics of folding in model proteins. Proc. Natl Acad. Sci. USA, 90, 6369–6372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Hinds DA & Levitt M (1994). Exploring conformational space with a simple lattice model for protein structure. J. Mol. Biol 243, 668–682. [DOI] [PubMed] [Google Scholar]
- 81.Chan HS, Shimizu S & Kaya H (2004). Cooperativity principles in protein folding. Methods Enzymol. 380, 350–379. [DOI] [PubMed] [Google Scholar]
- 82.Soteros CE, Sumners DW & Whittington SG (1992). Entanglement complexity of graphs in Z3. Math. Proc. Cambridge Philos. Soc 111, 75–91. [Google Scholar]
- 83.Yao A, Matsuda H, Tsukahara H, Shimamura MK & Deguchi T (2001). On the dominance of trivial knots among SAPs on a cubic lattice. J. Phys. A: Math. Gen 34, 7563–7577. [Google Scholar]
- 84.Moore NT, Lua RC & Grosberg AY (2004). Topologically driven swelling of a polymer loop. Proc. Natl Acad. Sci. USA, 101, 13431–13435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Hua X, Nguyen D, Raghavan B, Arsuaga J & Vazquez M (2007). Random state transitions of knots: a first step towards modeling unknotting by type II topoisomerases. Topol. Appl 154, 1381–1397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Baiesi M, Orlandini E & Stella AL (2007). Ranking knots of random, globular polymer rings. Phys. Rev. Lett 99, 058301. [DOI] [PubMed] [Google Scholar]
- 87.Bruns W & Naghizadeh J (1976). Off-lattice Monte Carlo study of ring polymers. J. Chem. Phys 65, 747–751. [Google Scholar]
- 88.Chen Y-D (1981). Monte Carlo study of freely jointed ring polymers. II. The writhing number. J. Chem. Phys 75, 2447–2453. [Google Scholar]
- 89.Dobay A, Dubochet J, Millett K, Sottas PE & Stasiak A (2003). Scaling behavior of random knots. Proc. Natl Acad. Sci. USA, 100, 5611–5615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Rawdon EJ, Kern JC, Piatek M, Plunkett P, Stasiak A & Millett KC (2008). Effect of knotting on the shape of polymers. Macromolecules, 41, 8281–8287. [Google Scholar]
- 91.Vologodskii AV, Levene SD, Klenin KV, Frankkamenetskii M & Cozzarelli NR (1992). Conformational and thermodynamic properties of supercoiled DNA. J. Mol. Biol 227, 1224–1243. [DOI] [PubMed] [Google Scholar]
- 92.Orlandini E & Whittington SG (2007). Statistical topology of closed curves: some applications in polymer physics. Rev. Mod. Phys 79, 611–642. [Google Scholar]
- 93.Madras N, Orlitsky A & Shepp LA (1990). Monte Carlo generation of self-avoiding walks with fixed endpoints and fixed length. J. Stat. Phys 58, 159–183. [Google Scholar]
- 94.Berg B & Foerster D (1981). Random paths and random surfaces on a digital computer. Phys. Lett. B, 106, 323–326. [Google Scholar]
- 95.Aragão de Carvalho C, Caracciolo S & Fröhlich J (1983). Polymers and g|Φ|4 theory in four dimensions. Nucl. Phys. B, 215, 209–248. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.