Skip to main content
PMC home page
UKPMC Funders Author Manuscripts logoLink to UKPMC Funders Author Manuscripts
. Author manuscript; available in PMC: 2018 Oct 18.
Published in final edited form as: Nat Genet. 2014 Feb 23;46(4):405–408. doi: 10.1038/ng.2905

Direct measurement of transcription factor dissociation excludes a simple operator occupancy model for gene regulation

Petter Hammar 1,#, Mats Walldén 1,#, David Fange 1, Fredrik Persson 1, Özden Baltekin 1, Gustaf Ullman 1, Prune Leroy 1, Johan Elf 1,*
PMCID: PMC6193529  EMSID: EMS56750  PMID: 24562187

Abstract

Transcription factors (TFs) mediate gene regulation by site specific binding to chromosomal operators. It is commonly assumed that the level of repression is given by the equilibrium binding of a repressor to its operator alone. However, this assumption has not been possible to test in living cells. Here, we have developed a single molecule chase assay to measure how long an individual transcription factor molecule remains bound at a specific chromosomal operator site. We find that the lac repressor dimer stays bound on average 5 minutes at the native lac operator in Escherichia coli and that a stronger operator results in slower dissociation rate, but similar association rate. Our findings do not support the simple equilibrium model. The discrepancy can for example be accounted for by considering that transcription initiation drives the system out of equilibrium. Such effects need to be considered when predicting gene activity from TF binding strengths.

Transcription factors (TFs) are the major regulators of gene expression. TF based regulation of transcription initiation is often described by a simple operator occupancy model, where in the case of repressors it is assumed that transcription is ‘off’ when the repressor is bound and ‘on’ when the promoter is free 1,2. In this scenario the resulting ratio of expression levels with and without repressor, i.e. the repression ratio RR, becomes

RR=τon+τoffτon, Eq. 1

where τoff is the average time the repressor is bound, and τon is the average time the promoter is free (Supplementary Note 1). The repression ratio is high when the repressor is bound for a long time (large τoff) or when the repressor concentration is high which leads to fast binding (small τon). The simple equation has a central position in quantitative biology since it relates the state of the cell, i.e. transcription factor concentrations, to the change of the state, i.e. gene expression. The equation is therefore used in most synthetic and systems biology studies although the underlying assumptions have not been tested in living cells, where cooperative binding, active transcription, DNA replication, and chromosome dynamics could influence gene regulation.

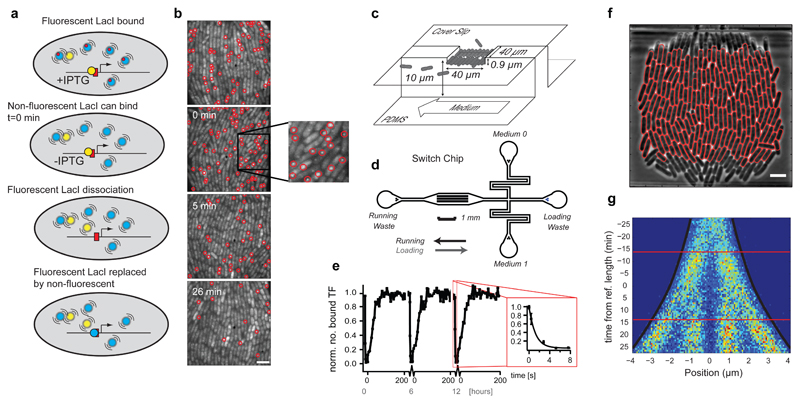
The challenge of testing the operator occupancy model in living cells is to measure the rate of operator association, τon-1, and dissociation, τoff-1, directly in live cells rather than inferring them from reporter expression assays 3,4. Recently, we developed a direct single molecule microscopy assay to measure the rate of binding to a single lac operator site in the bacterial chromosome 5. Here we present an in vivo version of a biochemical chase assay 6, which enables direct measurements of spontaneous dissociation of the lac repressor protein, LacI, from individual chromosomal operator sites (Fig. 1a, b). In our assay operator-bound fluorescent LacI-YFP dimers that spontaneously dissociate are replaced (chased) by non-fluorescent LacI tetramers. The non-fluorescent LacI molecules are present in excess (Supplementary Fig. 1a) and prevent rebinding of fluorescent LacI. The spontaneous dissociation process can thus be followed by counting the average number of bound fluorescent molecules per cell over time. In order to start the experiment with the fluorescent LacI bound, a point mutation has been introduced in the fluorescent LacI such that it cannot bind the inducer isopropyl β-D-1-thiogalactopyranoside (IPTG)7. The presence of IPTG prevents binding of the non-fluorescent LacI until IPTG is removed at the start of the experiment (Supplementary Fig. 1b, c). To ensure that dissociation kinetics is independent of IPTG outflux we show that the intracellular concentration of IPTG within 1 min drops to a level where non-fluorescent LacI binds effectively (Supplementary Fig. 2, Supplementary Note 2) and subsequently analyze dissociation kinetics starting from 1.5 min after removing IPTG. An extended analysis of how the finite concentrations of non-fluorescent LacI influence the result is found in the Online Methods. The model for replication induced LacI dissociation is extended in Supplementary Note 3. The kinetic assays are performed on E. coli cells residing in a microfluidic growth chamber (Fig. 1c, d), which allows the cells to be maintained in a constant state of exponential growth (generation time 26 min) 8 as well as rapid media exchange (2 seconds). Image acquisition and media exchange are automated and synchronized so that the experiment is repeatable with high precision (Fig. 1e). Cell segmentation and detection of fluorescent spots are also automated and enable mapping of individual molecules on an intra-cellular coordinate system for an arbitrary number of cells (Fig. 1f). For example, Figure 1g (and Supplementary Fig. 3) shows the probability distribution of the intracellular location of specifically bound LacI-YFP molecules as a function of position in the cell cycle.

Fig. 1. The single molecule chase assay.

Fig. 1

Open in a new tab

(a) Outline of the single molecule chase assay. When fluorescent LacI dimers (yellow) dissociate they are replaced by non-fluorescent wild type LacI tetramers (blue) present in excess. (b) Examples of fluorescence images (4 s exposure) taken at different time points after removal of IPTG. Scale bar = 4 µm. (c and d) The microfluidic switching chip (d) contains 51 traps as illustrated in (c). Each trap harbors ~250 E. coli cells and allows for sustained exponential growth and fast change of medium. (e) Media switch induced TF dissociation and association. When media is switched from high ONPF (anti-inducer) to high IPTG (inducer) the TFs dissociate in a few seconds (inset). When media is switched back, TFs associate in ~30 s. The graph shows three switching cycles separated by 6 h recovery periods. (f) Automatically segmented cells using a phase contrast image. Scale bar = 4 µm. (g) Intracellular positions of bound LacI-YFP molecules (x-axis) mapped to the cell replication cycle (y-axis). Individual cell replication cycles are synchronized so that the time 0 min always imply a cell length 4.25 µm. Horizontal lines mark the average time for cell divisions.

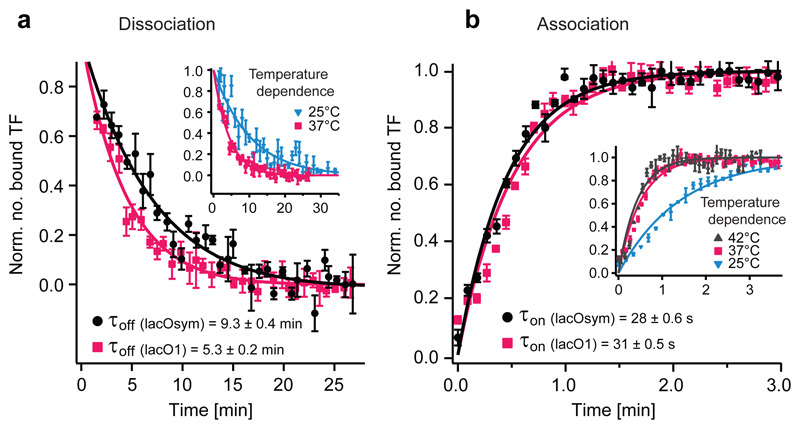
We used the in vivo chase assay to measure the kinetics for two operators of different strength, the natural lacO1 and the stronger symmetric artificial lacOsym operator. Figure 2a displays the dissociation curves for the LacI-YFP dimer from the lacO1 and lacOsym operators respectively at 37°C. The average time LacI stays bound to its operator (τoff) is 5.3±0.2 (s.e.m.) min for lacO1 and 9.3±0.4 (s.e.m.) min for lacOsym. The average time before the operator is bound by a repressor (τon) was measured under identical experimental conditions (Fig. 2b) and gives 30.9±0.5 (s.e.m.) s for lacO1 and 27.6±0.6 (s.e.m.) s for lacOsym. Thus, a stronger operator has a slower dissociation rate but a similar association rate.

Fig. 2. Kinetic measurements for individual lac operators.

Fig. 2

Open in a new tab

(a) Dissociation curves for lacOsym and lacO1. Error bars indicate ± s.e.m.; n≥7. Data are from 3 biological replicates. (Inset) Temperature dependence for dissociation from lacO1. Error bars indicate ± s.e.m.; n≥4. (b) Association curves for lacOsym and lacO1. Error bars indicate ± s.e.m.; n≥5. Data are from 2 and 3 biological replicates respectively. (Inset) Temperature dependence for association to lacO1. Error bars indicate ± s.e.m.; n≥3.

We are now ready to ask if the measured association and dissociation times can be used to predict the repression ratio using the simple operator occupancy model, i.e. Eq. 1 as given by the model in Figure 3a without any cooperative interaction between LacI and RNA polymerase (RNAP) (ω=1). Combining the association and dissociation measurements we calculate that the repression ratio is expected to be 11.2±0.5 (s.e.m.) for lacO1 and 21.2±0.9 (s.e.m.) for lacOsym (Table 1). The corresponding measurements of the repression ratios for the LacI-Venus dimer based on an enzymatic reporter assay are 10.0±1.3 (s.e.m.) for lacO1 and 29.7±3.4 (s.e.m.) for lacOsym (Table 1). We conclude that the operator occupancy model accounts for the repression ratio for lacO1 but not for lacOsym, where the observed repression ratio is higher than expected from association and dissociation rates alone.

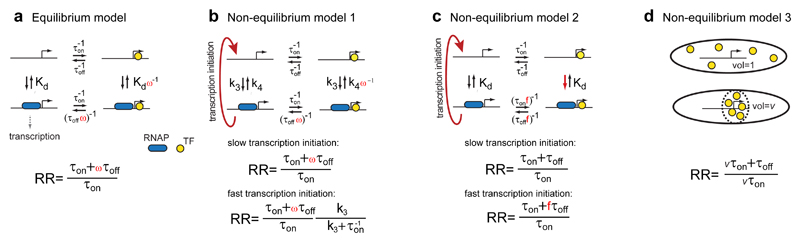
Fig. 3. Models of gene regulation.

Fig. 3

Open in a new tab

(a) At equilibrium the repression ratio only depends on the fraction of time the operator is bound independent of kinetic schemes. Due to cooperative binding (ω>1) the fraction can be modulated by other factors. (b) Transcription initiation can drive the system out of equilibrium such that the repression ratio depends on the rate of transcription initiation. (c) The TF binds and dissociates slower when RNAP is bound. Transcription drives the system out of equilibrium such that the TF associate at naked DNA and dissociate at RNAP-bound DNA. (d) When the TFs are maintained in a reduced volume, v, TF association rates are in the simplest case increased by the corresponding factor.

Table 1. Comparison of repression ratios from reporter expression assays and direct single molecule in vivo measurements.

Repression ratio
 Single molecule kinetics
Operator region Reporter expression assay† τon+τoffτon τon (s) τoff (min)
lacO1 10.0±1.3 11.2±0.5 30.9±0.5 5.3±0.2
lacOsym 29.7±3.4 21.2±0.9 27.6±0.6 9.3±0.4
Open in a new tab

The repression ratio is: †induced (+IPTG) divided by repressed (-IPTG) lacZ expression in terms of Miller units (normalized β-galactosidase activity), and normalized to the lower repressor concentrations in the kinetic experiments (Supplementary Note 4 and Supplementary Fig. 8). ± are s.e.m.; n≥8 (reporter expression), n≥5 (τon) and n≥7 (τoff).

This discrepancy for lacOsym motivates more complex interaction models. One possibility is an equilibrium model where LacI interacts cooperatively with the RNAP or another protein binding near to the operator and where the degree of cooperativity depends on the operator sequence. This model is represented by Figure 3a using ω=1.5 and ω =1 for lacOsym and lacO1 respectively which results in excellent agreement with the measured repression ratio. Such a difference in cooperativity between lacO1 and lacOsym could be due to the markedly different bending of DNA when LacI is bound to the different operators 8,9. Operator sequence specific interactions between LacI and RNAP has previously been suggested when the operator is positioned upstream of the placUV5 promoter 10. Although this equilibrium mechanism is possible also with the operator downstream of the promoter, a model with operator specific cooperativity is not needed to describe our data. Cellular reaction dynamics is commonly out of equilibrium and we therefore also consider more simple non-equilibrium schemes. In Figure 3b-d we outline three such schemes that can increase the repression ratio beyond the simple operator occupancy model. We will discuss them one at a time:

The first non-equilibrium scheme (Fig. 3b) is similar to the scheme with cooperative interaction with RNAP (Fig. 3a), except here active transcription initiation clears the promoter in the absence of LacI. Slow transcription initiation leads to a repression ratio as in the cooperative equilibrium model, whereas fast transcription initiation leads to a reduced repression ratio since it is possible to make transcripts before the repressor has equilibrated with DNA. Interestingly we find that the fully induced lac operon transcription rate is 5.4±0.5 (s.e.m.) times higher in the strain with the lacO1 sequence as compared to the strain with the lacOsym sequence next to the promoter (Supplementary Note 4). This difference in transcription rate, in combination with the measured association and dissociation rates is sufficient to fully account for the measured repression ratios when ω=1.5 for both lacO1 and lacOsym. The reason is that the lacOsym is closer to the equilibrium case (slow transcription) described above, while lacO1 is out of equilibrium (fast transcription) and thus has a lower RR than what is expected from the equilibrium model alone (Fig. 3b). This means that no operator sequence dependent interaction between LacI and RNAP is needed in this case since the sequences are transcribed at different rates.

Also in the second non-equilibrium scheme (Fig. 3c) transcription initiation drives the system out of equilibrium but this time without having any cooperative binding between RNAP and LacI. Here the RNAP binds to one of the alternative lac promoters next to the operator-bound LacI, but does not continue into open complex formation 11. In contrast, when RNAP binds in absence of LacI it proceeds rapidly and irreversibly into transcription, clearing the promoter. Consequently, LacI will most often bind in an RNAP-free promoter region, and dissociate from an RNAP-bound operator region. Thus, if bound RNAP slow down LacI dissociation, this would result in repression beyond the equilibrium model, even if the binding strength for LacI is unaltered by the bound RNAP. The average time for LacI association and dissociation is expected to increase by up to a factor of 2 when a protein is bound next to the lac operator, since sliding on DNA in and out of the operator is blocked from one side 5. To test this hypothesis we positioned the tet repressor protein, TetR, next to the lac operator site and measured the time for LacI dissociation and association. We found that the time for association increased by a factor f=1.35±0.04 (s.e.m.) when TetR was bound next to lacOsym and that the effect on dissociation was similar (Table 2 and Supplementary Fig. 4) as is expected from detailed balance when the steady state binding is not altered. The effect was smaller (f=1.16±0.03 (s.e.m.)) for lacO1, for which the lower binding probability reduces the impact of the diffusion blockade 5. If RNAP binds in a closed complex near LacI and blocks sliding in the same way as TetR, the repression ratios is expected to increase up to 12.8±0.6 (s.e.m.) and 28.2±1.4 (s.e.m.) for lacO1 and lacOsym respectively by this effect alone.

Table 2. Binding kinetics dependence on roadblocks.

τon (s) τoff (min) Repression ratio
Without roadblock 27.6±0.6 9.3±0.4 21.2±0.9
With roadblock 37.1±0.6 11.6±1.4 19.7±1.1
Open in a new tab

Association and dissociation rates measured for LacI-YFP with (lower row) or without (upper row) TetR binding next to one side of the operator lacOsym. ± are s.e.m.; n≥5 (τon) and n≥8 (τoff).

In the final scheme (Fig. 3d) active transport, or a combination of slow diffusion and degradation, maintains a higher concentration of LacI close to the operator sites. This can lead to faster association rates than we report above, since our association process starts from a random position in the cells when IPTG dissociates from LacI. A local gradient effect is expected to be higher for lacOsym than for lacO1 since LacI is more likely to bind lacOsym before escaping to a random position 5. Furthermore, previous studies have reported that the spatial distribution of LacI in the cell under poor growth conditions depend on where in the chromosome the protein is encoded 12,13. However, under our experimental conditions we cannot observe any significant difference in the spatial distributions of non-operator bound LacI expressed from different chromosomal loci with different intracellular location (Supplementary Note 5 and Supplementary Fig. 5). Using single particle tracking, we also do not observe that LacI can get trapped locally in the nucleoid for more than a few seconds. This time is far less than what would be required to maintain a locally higher concentration of LacI close to the point of synthesis (Supplementary Fig. 6). In addition we do not observe a change in repression of the LacI regulated lacZYA operon when the lacI gene is moved to its mirror position on the other chromosome arm (Supplementary Note 5). Together these results make it unlikely that LacI association is faster under steady state growth than in our measurements due to local concentration gradients of the repressor.

The single molecule chase method has allowed us to identify inconsistencies in the simple operator occupancy model of gene regulation in living E. coli cells, a model system where it is possible to make the experiment with sufficient accuracy. The inconsistencies are most easily explained by simple non-equilibrium mechanisms driven by transcription initiation itself. The same mechanisms are expected in eukaryotic cells, where the added complexity of ATP-dependent chromatin remodeling 14 and clearing of the TF binding region by divergent transcription 15 will contribute to keeping operator occupancy out of equilibrium. Overall, non-equilibrium TF kinetics adds a new layer of complexity to the genomics puzzle beyond the steady state mapping of TF concentrations to gene activity.

Online Methods

1. Strain construction

Strains were constructed in a BW25993 background 16 using the λ Red 16 or pKO3 17 protocols. Detailed strain descriptions are found in the Supplementary Note 6 and the Supplementary Figure 7.

2. Growth conditions

Cells were grown in M9 minimal liquid medium supplemented with 0.4% glucose and RPMI amino acids (Sigma). For growth of strains harboring the plasmids pBAD24-(lacI, lacI-Venus, xylR) the medium was supplemented with carbenicillin (Sigma).

For microfluidics experiments, saturated (overnight) cultures were diluted 1:200 in 40 mL medium and grown at 37°C for 4 hours unless otherwise specified. Cells were collected by centrifugation and immediately loaded onto microfluidic chips as previously described 18.

Information about growth conditions in other microscopy experiments and expression assays is found in Supplementary Note 7.

3. Fluorescence microscopy and microfluidics

Microfluidic switching chips – design and preparation

Microfabrication of the templates and construction of the individual devices were performed in accordance with the protocols described previously 18 with the exception that an extra media port was added to allow for rapid exchange of media. Inert 2 µm diameter Polystyrene beads (Sigma-Aldrich) were added to one medium reservoir. The beads allow for the detection of flow rates and flow directions necessary for determining the induction states of the device during operation.

The relative height differences between medium reservoirs were used to control the pressure gradients and thereby flow rates and directions in the device during running and medium exchange. Medium exchange, i.e. anti-correlated elevation/lowering of reservoirs, was automated by using programmable linear actuators (Robocylinder, Intelligent Actuators Inc.), the control of which was synchronized with image acquisition using a custom written Java program.

Optical setup

We used a Nikon Eclipse Ti-E microscope (with Nikon’s Apo TIRF 100x/1.49 oil immersion objective) equipped with a dichroic mirror (Chroma t515.5rdc), an excitation filter (Chroma 514/10), an emission filter (Chroma 550/50) and an EMCCD camera (iXon EM+ DU-897 from Andor) for detection. The camera was cooled to -80°C and the linearized EM gain set to 150. A 2X magnification lens was placed in the emission path before the camera. Fluorescence was excited by a Coherent Innova-304 Ar+-laser at 514 nm. When measuring association and dissociation rates the power was 15W/cm2 using 4 s exposures. For single particle tracking the power was 650W/cm2 and for overnight growth experiments the power was <5W/cm2 (see Supplementary Note 5 for details). A second camera (Scion corp.) was used for external phase contrast imaging. The microscope was enclosed in an OkiLab-cage incubator where the set temperature was maintained at 37°C±0.1°C, 42°C±0.1°C or 25.5±0.3. Image acquisition was controlled by the open source software µManager 19 in combination with custom written acqusition scripts.

Spot detection

We used an á Trous wavelet 3 plane decomposition 20 and detected the spots in the second wavelet plane. The significant wavelet coefficients were determined through scale dependent kσ thresholding where σ is the standard deviation of the second wavelet plane, estimated by the MAD estimate 21, and k = 3 (association experiments) or k = 4 (dissociation experiments).

4. LacI-Venus kinetics using automated switch of medium

Experiments were started when cells had grown to fill the whole microfluidic traps. For a fast and well-defined switch of medium, the media reservoirs were connected to linear actuators (see above) and controlled from the computer in parallel with the µManager-run imaging acquisition.

For the analysis of operator-bound single LacI in fusion with the fluorescent protein, YFP-derived Venus 22 (LacI-Venus), spots were detected as described above. Since the traps of the microfluidic chip is full with densely packed cells we normalize the number of spots per trap with total cell area.

Association to a single operator

The principle of the experiment is essentially as presented previously 5,23, with the exception that it is performed in the microfluidic device to allow for direct comparison with the corresponding dissociation experiment at 37°C. The experiment is started by switching the medium for the induced cells from IPTG to the competitor 2-Nitrophenyl β-D-fucopyranoside (ONPF) at 1 mM. The addition of ONPF at high concentration is used to ensure that the association rate is not limited by the time it takes for IPTG to leave the cell (see below). Cells were imaged with 4 s exposures with a frame rate of ~0.18 s-1. Fluorescent spots were counted as described above and binding curves with data from the same strain were fitted (Igor Pro (v6.12A)) to the single exponential function y=a(1-be-kt), where a, b are independent for each series and k the same for all series. Experiments were repeated to get sufficient statistics to test the hypothesis. For visualization in Figure 2b the a and b-parameters are used to normalize the data points in individual series before calculating the average and s.e.m. for each time point and plotting together with the fitted curve.

In Supplementary Figure 2c the rate of LacI-Venus association is plotted as a function of the added ONPF concentration and it shows that 1 mM is a saturating concentration. It also shows that LacI binds 1 minute faster by the addition of ONPF at saturating concentration, which suggests that it takes up to 1 minute for the intracellular IPTG concentration to drop to a level where LacI can bind the operator. This will be important for the dissociation assay described below.

Chase assay for measuring of dissociation rates

In the in vivo chase experiment, LacI-Venus molecules are first bound to individual, single, operator sites and then, through the competition with a non-fluorescent wild type (wt) LacI in excess, they can be seen to dissociate as the number of fluorescent spots decreases. The chase experiment relies on the possibility to induce binding of non-fluorescent LacI at a well-defined time while LacI-Venus is already bound. To accomplish this a single point substitution was introduced in the lac repressor gene (LacID274N), which causes more than a 1000-fold reduction in IPTG-affinity without changing the operator-binding strength 7. The gene (referred to as lacIs) was expressed in fusion with Venus, resulting in a chromosomally expressed LacIs-Venus which does not dissociate even in the presence of 1 mM IPTG (Supplementary Fig. 1c). Wt-LacI was expressed from an arabinose inducible promoter on the plasmid pBAD24.

The ratio between LacIs-Venus and wt-LacI monomers when the plasmid was un-induced is seen at time 0 in Supplementary Figure 1a. When the plasmid was fully induced for a long time the competitor copy number became so high that either 1 mM IPTG did not saturate LacI to prevent operator-binding; or, the LacIs-Venus/LacI heterodimers, which naturally form (and is dominant when LacI is overexpressed) and bind one IPTG-molecule, did not bind the operator. When instead XylR was expressed from pBAD24, LacIs-Venus was unaffected by IPTG (Supplementary Fig. 1c).

Before the switch, with IPTG present, the LacIs-Venus homodimer bound the operator. When the IPTG was removed at t=0 there was a short (1 min) period of increased binding (Supplementary Fig. 1b). This was probably due to the association of heterodimers (in competition with non-fluorescent wt-LacI) to available operator sites. Because of this initial association and the time-delay required to reduce the intracellular IPTG concentration to a level where non-fluorescent LacI bind (see below and Supplementary Fig. 2) we fit the dissociation process from 1.5 min after switching to media without IPTG to an exponential decay process that takes into account that the TF also is displaced once per generation due to replication. The implications of the approximation are quantified below and in the Supplementary Note 3).

Time dependent excess of non-fluorescent LacI

Since too much non-fluorescent LacI could not be present from the start of the experiment we induced its expression at time 0 (medium containing 1 mM IPTG was switched to medium containing 0.2% arabinose). This result in a time dependent and increasing concentration of the non-fluorescent LacI chase molecules (Supplementary Fig. 1a). This time dependent increase motivates a calculation of how this would influence the measured dissociation kinetics. The equations that describe the probabilities that an operator initially is bound by a fluorescent molecule (PF), that it is empty (PE), or that it is occupied by a non-fluorescent molecule (PN) are:

dPF(t)dt=τon−1PE−τoff−1PFdPE(t)dt=τoff−1(PF+PN)−τon−1(1+q(t))PEdPN(t)dt=q(t)τon−1PE−τoff−1PNdPF(0)dt=1,dPE(0)dt=0,dPN(0)dt=0 Eq. 2

Here q(t) is the fold excess of non-fluorescent TF, which is measured directly by the western blot in Supplementary Figure 1a, and is closely approximated by q(t)=4+t2, where t is the time in minutes after addition of IPTG.

For an infinitely high q, PF will decay as a pure exponential with rate τoff-1 starting from t=0. For a finite q, the observed dissociation process is slightly slower. When fitting a single exponential function to the solution of PF(t), using parameters from Table 1, starting from 1.5 min and ending at 20 min, the dissociation rate is underestimated by up to 11% for lacO1 and 9% for lacOsym due to the finite concentration of non-fluorescent LacI. This would change the predicted repression ratios (based on the simple operator occupancy model) to 10.2 for lacO1 and 19.4 for lacOsym, which do not alter the conclusions drawn when assuming high excess of non-fluorescent LacI.

5. Models

Cooperative LacI binding

Consider the scheme in Figure 3a, b written in some more detail.

O⇄k2=τoff−1k1=τon−1O⋅TFk3↓↑k4k3↓↑ω−1k4O⋅RNAP⇄ω−1k2=ω−1τoff−1k1=τon−1O⋅TF⋅RNAPk6↓ Eq. 3

Here LacI and RNAP bind ω times longer when they are binding at the same time.

The repression ratio in this non-equilibrium scheme is

RR=1+k1(k1+k2+k3+k4+k6)(k3+k4ω−1)k2ω−1(k1+k2+k3+k4)(k3+k4+k6) Eq. 4

If we assume that transcription initiation is slow k6 → 0 (equilibrium case)

RR=1+ωk1(k3+k4ω−1)k2(k3+k4)→k3≫k41+ωk1k2=1+ωτoffτon Eq. 5

If we assume that transcription initiation is fast k6 → ∞ (far from equilibrium case)

RR=1+k1(ωk3+k4)k2(k1+k2+k3+k4)→k3≫k41+ωk1k2k3k1+k2+k3≈1+ωk1k2k3k1+k3 Eq. 6

These are the limiting approximations given in the main text (Fig. 3a, b). To see what we get with specific numbers we use the measured τon and τoff and assume that ω=1.5, k3=1 min-1 and k4=0.1 min-1. This gives RR=10.0 and an induced transcription initiation rate of 0.61 min-1 24, 25 when k6=1.7 min-1 for lacO1, and RR=28.2 and an induced transcription initiation rate of 0.61/5.4 min-1 for lacOsym when k6=0.14 min-1. The value 5.4 is the measured difference in expression between the induced lac operon controlled by lacO1 or lacOsym.

Non-Equilibrium model with roadblock

Consider the scheme in Figure 3c written in some more detail

O⇄k2=τoff−1k1=τon−1O⋅TFk3↓↑k4k3↓↑k4O⋅RNAP⇄f−1k2=f−1τoff−1f−1k1=f−1τon−1O⋅TF⋅RNAPk6↓ Eq. 7

The repression ratio, RR, is here

RR=k1(k3+k4)(k4+k6)k2(k3+k4+k6)+k4+f−1(k1+k2+k3)(k1(k3+k4)k2(k3+k4+k6)+1)f−1(k1+k2+k3)+k4 Eq. 8

Assuming that the system is far from equilibrium, such that k6>>k3+k4 and that the transcription initiation rate is fast enough, such that k1(k3+k4)/(k2k6)<<1 then the repression ratio is

RR=1+k1(k3+k4)k2(k4+f−1(k2+k3+k1)). Eq. 9

Further assuming that the RNAP binding is strong, k3≫k4, that turn-over of RNA polymerase is faster than the turn-over of TF such that k3>>k1+k2 and, that f is not very much smaller than one, then the repression ratio is

RR=1+fk1k2=1+fτoffτon Eq. 10

Supplementary Material

Supplementary Information is linked to the online version of the paper at XXX.

Supplementary information

Acknowledgements

We thank KS Matthews for advice on LacI mutants, G-W Li for helpful comments, XS Xie (Department of Chemistry and Chemical Biology, Harvard University) for the MalI-Venus strain and I Barkefors for critical reading of the manuscript. This work was supported by the European Research Council (ERC), the Knut and Alice Wallenberg Foundation (KAW), Vetenskapsrådet (VR), the Foundation for Strategic research (SSF), and Göran Gustafsson Foundation.

Footnotes

Author Contributions:

J.E. conceived the project, J.E. and P.H. conceived the chase method, M.W. designed the microfluidics chip, P.H. and P.L. made strains, P.H., M.W., O.B., F.P. and P.L. performed experiments, F.P., G.U., D.F. and MW developed and implemented analysis routines, P.H., F.P., M.W., G.U., D.F. and O.B. analyzed the data, J.E., and D.F. developed theoretical models, J.E., P.H., D.F., M.W. and F.P. wrote the manuscript.

Author Information:

The authors declare no competing financial interests.

References

  • 1.Bintu L, et al. Transcriptional regulation by the numbers: applications. Current opinion in genetics & development. 2005;15:125–135. doi: 10.1016/j.gde.2005.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Oehler S, Amouyal M, Kolkhof P, von Wilcken-Bergmann B, Muller-Hill B. Quality and position of the three lac operators of E. coli define efficiency of repression. The EMBO journal. 1994;13:3348–3355. doi: 10.1002/j.1460-2075.1994.tb06637.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Oehler S, Eismann ER, Kramer H, Muller-Hill B. The three operators of the lac operon cooperate in repression. The EMBO journal. 1990;9:973–979. doi: 10.1002/j.1460-2075.1990.tb08199.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Choi PJ, Cai L, Frieda K, Xie XS. A stochastic single-molecule event triggers phenotype switching of a bacterial cell. Science. 2008;322:442–446. doi: 10.1126/science.1161427. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Hammar P, et al. The lac repressor displays facilitated diffusion in living cells. Science. 2012;336:1595–1598. doi: 10.1126/science.1221648. [DOI] [PubMed] [Google Scholar]
  • 6.Riggs AD, Bourgeois S, Cohn M. The lac repressor-operator interaction. 3. Kinetic studies. Journal of molecular biology. 1970;53:401–417. doi: 10.1016/0022-2836(70)90074-4. [DOI] [PubMed] [Google Scholar]
  • 7.Chang WI, Barrera P, Matthews KS. Identification and characterization of aspartate residues that play key roles in the allosteric regulation of a transcription factor: aspartate 274 is essential for inducer binding in lac repressor. Biochemistry. 1994;33:3607–3616. doi: 10.1021/bi00178a018. [DOI] [PubMed] [Google Scholar]
  • 8.Bell CE, Lewis M. A closer view of the conformation of the Lac repressor bound to operator. Nature structural biology. 2000;7:209–214. doi: 10.1038/73317. [DOI] [PubMed] [Google Scholar]
  • 9.Bell CE, Lewis M. Crystallographic analysis of Lac repressor bound to natural operator O1. Journal of molecular biology. 2001;312:921–926. doi: 10.1006/jmbi.2001.5024. [DOI] [PubMed] [Google Scholar]
  • 10.Garcia HG, et al. Operator sequence alters gene expression independently of transcription factor occupancy in bacteria. Cell reports. 2012;2:150–161. doi: 10.1016/j.celrep.2012.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Sanchez A, Osborne ML, Friedman LJ, Kondev J, Gelles J. Mechanism of transcriptional repression at a bacterial promoter by analysis of single molecules. The EMBO journal. 2011;30:3940–3946. doi: 10.1038/emboj.2011.273. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Kuhlman TE, Cox EC. Gene location and DNA density determine transcription factor distributions in Escherichia coli. Molecular systems biology. 2012;8:610. doi: 10.1038/msb.2012.42. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Hermsen R, ten Wolde PR, Teichmann S. Chance and necessity in chromosomal gene distributions. Trends in genetics : TIG. 2008;24:216–219. doi: 10.1016/j.tig.2008.02.004. [DOI] [PubMed] [Google Scholar]
  • 14.Vignali M, Hassan AH, Neely KE, Workman JL. ATP-dependent chromatin-remodeling complexes. Molecular and cellular biology. 2000;20:1899–1910. doi: 10.1128/mcb.20.6.1899-1910.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Seila AC, Core LJ, Lis JT, Sharp PA. Divergent transcription: a new feature of active promoters. Cell cycle. 2009;8:2557–2564. doi: 10.4161/cc.8.16.9305. [DOI] [PubMed] [Google Scholar]
  • 16.Datsenko KA, Wanner BL. One-step inactivation of chromosomal genes in Escherichia coli K-12 using PCR products. Proceedings of the National Academy of Sciences of the United States of America. 2000;97:6640–6645. doi: 10.1073/pnas.120163297. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Link AJ, Phillips D, Church GM. Methods for generating precise deletions and insertions in the genome of wild-type Escherichia coli: application to open reading frame characterization. Journal of bacteriology. 1997;179:6228–6237. doi: 10.1128/jb.179.20.6228-6237.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Ullman G, et al. High-throughput gene expression analysis at the level of single proteins using a microfluidic turbidostat and automated cell tracking. Philosophical transactions of the Royal Society of London. Series B, Biological sciences. 2013;368 doi: 10.1098/rstb.2012.0025. 20120025. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Edelstein A, Amodaj N, Hoover K, Vale R, Stuurman N. Computer control of microscopes using microManager. Current protocols in molecular biology / edited by Frederick M. Ausubel … [et al.] 2010;Chapter 14:Unit14 20. doi: 10.1002/0471142727.mb1420s92. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Olivo-Marin JC. Extraction of spots in biological images using multiscale products. Pattern Recogn. 2002;35:1989–1996. [Google Scholar]
  • 21.Sadler BM, Swami A. Analysis of multiscale products for step detection and estimation. Ieee T Inform Theory. 1999;45:1043–1051. doi: 10.1109/18.761341. [DOI] [Google Scholar]
  • 22.Nagai T, et al. A variant of yellow fluorescent protein with fast and efficient maturation for cell-biological applications. Nature biotechnology. 2002;20:87–90. doi: 10.1038/nbt0102-87. [DOI] [PubMed] [Google Scholar]
  • 23.Elf J, Li GW, Xie XS. Probing transcription factor dynamics at the single-molecule level in a living cell. Science. 2007;316:1191–1194. doi: 10.1126/science.1141967. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Taniguchi Y, et al. Quantifying E. coli proteome and transcriptome with single-molecule sensitivity in single cells. Science. 2010;329:533–538. doi: 10.1126/science.1188308. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Yu J, Xiao J, Ren X, Lao K, Xie XS. Probing gene expression in live cells, one protein molecule at a time. Science. 2006;311:1600–1603. doi: 10.1126/science.1119623. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary information
NIHMS56750-supplement-Supplementary_information_.pdf (3MB, pdf)

RESOURCES