Abstract
Individualized treatment rules (ITR) can improve health outcomes by recognizing that patients may respond differently to treatment and assigning therapy with the most desirable predicted outcome for each individual. Flexible and efficient prediction models are desired as a basis for such ITRs to handle potentially complex interactions between patient factors and treatment. Modern Bayesian semiparametric and nonparametric regression models provide an attractive avenue in this regard as these allow natural posterior uncertainty quantification of patient specific treatment decisions as well as the population wide value of the prediction-based ITR. In addition, via the use of such models, inference is also available for the value of the Optimal ITR. We propose such an approach and implement it using Bayesian Additive Regression Trees (BART) as this model has been shown to perform well in fitting nonparametric regression functions to continuous and binary responses, even with many covariates. It is also computationally efficient for use in practice. With BART we investigate a treatment strategy which utilizes individualized predictions of patient outcomes from BART models. Posterior distributions of patient outcomes under each treatment are used to assign the treatment that maximizes the expected posterior utility. We also describe how to approximate such a treatment policy with a clinically interpretable ITR, and quantify its expected outcome. The proposed method performs very well in extensive simulation studies in comparison with several existing methods. We illustrate the usage of the proposed method to identify an individualized choice of conditioning regimen for patients undergoing hematopoietic cell transplantation and quantify the value of this method of choice in relation to the Optimal ITR as well as non-individualized treatment strategies.
1 Introduction
There is increasing recognition in clinical trials that patients are heterogeneous and may respond differently to treatment. A major goal of precision medicine is to identify which patients respond best to which treatments and tailor the treatment strategy to the individual patient. This personalization of treatment based on patient clinical features, biomarkers, and genetic information is formalized as an individualized treatment rule (ITR) by Qian and Murphy [1]. Individualized treatment rules extend classical subgroup analysis, in which pre-specified subgroups of the population are assessed for differential treatment effects, to the point where the treatment benefit for each individual is used to determine a treatment assignment rule that is, in some sense, optimal.
Several strategies for identifying treatment rules have been proposed in the literature. Many of these utilize a model for the conditional mean function of the outcome given treatment and covariates, and optimize it over available treatments to define an ITR. Qian and Murphy [1] show that good prediction accuracy of the outcome model is sufficient in order to ensure good performance of the associated ITR. As a result a number of strategies for flexible prediction models have been proposed, including a large linear aproximation space with penalization to avoid overfitting ([1, 2]), generalized additive models ([3]), boosting ([4]), random forests ([5]), support vector regression ([6]), kernel ridge regression ([7]), and tree based methods or recursive partitioning ([8, 9, 10, 11, 12, 13]). An alternative strategy is to directly optimize an estimator of the expected outcome of a treatment rule over a class of potential rules ([14, 15, 16, 17]). This has the advantage of not requiring an accurate prediction model, but does require specification of the class of treatment rules allowed. While each method uses its own “optimal” choice, in this article we reserve the phrase “Optimal ITR” for the ITR defined by Qian and Murphy [1] in their Equation 1, and also stated in our Equation 1 below.
The Bayesian framework leads to natural quantification of uncertainty that allows construction of credible and prediction intervals. A major distinguishing feature as described later is that our method provides direct inference on the value of the Optimal ITR while it is not clear how this can be done with other existing methods. The Bayesian nonparametric regression method we have implemented here is Bayesian Additive Regression Trees (BART) ([18]) to model the conditional mean function of the outcome and to inform identification of an ITR. BART has been shown to be efficient and flexible with performance comparable to or better than its non-Bayesian competitors such as boosting, lasso, MARS, neural nets and random forests ([18]). Furthermore, our simulations described later in the article show that BART ITR’s performance was better than or comparable to other existing methods in this setting of identifying an ITR. Because of its tree based structure, BART can effectively address interactions among variables, which is important in this context for identification of treatment interactions leading to differential treatment recommendations. In addition, recent modifications to BART have been proposed that maintain excellent out-of-sample predictive performance even when a large number of additional irrelevant regressors are added ([19]).
We present our work in the following sequence. In the next section we describe the notation for individualized treatment rules. Following that, we review the BART methodology briefly. The next section titled “BART for ITRs and Value Function Estimation” describes our proposed BART based ITR and addresses estimation of its value function as well as that of the Optimal ITR. Subsequently we show excellent performance of the proposed BART ITR in a benchmark simulation comparison to existing methods for ITRs. In the next section we conduct additional simulations to examine the operating characteristics of the BART prediction model and the estimation of the value function. In the section titled “Summarizing the BART ITR” we discuss ways to approximate the BART ITR to get an interpretable clinical rule for treatment assignment, similar to identification of subgroups of patients who would benefit from assignment to particular treatments. The following section illustrates the usage of the proposed method on a medical application in hematopoietic cell transplantation. The article ends with a discussion of our contribution as well as of some planned future developments.
2 Individualized Treatment Rules
Let Y be the outcome of interest, with higher values of Y being more desirable. We focus on a binary outcome in this article, where Y = 1 indicates a favorable outcome and Y = 0 its complement, but the proposed method could easily be used with a continuous outcome as well. Let 𝒜 be the treatment space with 𝒜 = {−1, 1} and let X = (x1, …, xp) be the vector of patient characteristics being used to personalize treatment, with population space ΩX defined so that p(A = 1|X = x) is bounded away from 0 and 1, i.e. ΩX = {X: p(A = a|X = x) ∈ (0, 1), ∀a ∈ 𝒜}. We assume observations represent a random sample (Y, A,X) either from a randomized trial or observational study. For an observational study we make the usual assumptions to allow causal inference that treatment assignment is strongly ignorable, i.e. treatment A is independent of the potential outcomes Y|A = 1 and Y|A = 0 given X. Note that BART models have been proposed for use in observational studies in [20].
A treatment rule g(X) is a mapping from the covariate space Ωx to the treatment space 𝒜 so that patients with covariate value X are assigned to treatment g(X). Let P be the distribution of (Y, A,X) and E(Y) be the expectation with respect to P. Let Pg be the distribution of (Y, A,X) given that A = g(X) and let Eg(Y) be the expectation with respect to Pg. The value function V(g) of a treatment rule g(X) is the expected outcome associated with that treatment rule, i.e., V(g) = Eg(Y). An Optimal ITR g0 is a treatment rule that optimizes the value function,
where G is a collection of possible treatment rules. Since the value function can be written as
Qian and Murphy [1] show that the Optimal ITR satisfies
| (1) |
so that one possible solution is to assign to each patient the treatment which has the higher conditional expectation given their covariate vector X. In practice, this strategy requires modeling of the conditional mean function and use of the estimated conditional mean function in the above expression to determine treatment assignment. Qian and Murphy [1] showed that if the prediction error of such a model is small, then the reduction in value of the associated ITR g compared to the Optimal ITR g0 is also small, pointing to the need for a flexible and accurate prediction model for the conditional mean function.
3 BART methodology
As BART is based on an ensemble of regression tree models, we begin with a simple example of a regression tree model. We then describe how BART uses an ensemble of regression tree models for a numeric outcome. Finally, we describe how the BART model for a numeric outcome is augmented to model a binary outcome.
Suppose yi represents the (numeric) outcome for individual i, and xi is a vector of covariates with the regression relationship yi = h(xi; T,M) + εi. Notationally, h(xi; T,M) is a binary tree function with components T and M that can be described as follows. T denotes the tree structure consisting of two sets of nodes, interior and terminal, and a branch decision rule at each interior node which typically is a binary split based on a single component of the covariate vector. An example is shown in Figure 1 wherein interior nodes appear as circles, and terminal nodes as rectangles. The second tree component M = {μ1, …, μb} is made up of the function values at the terminal nodes.
Figure 1.
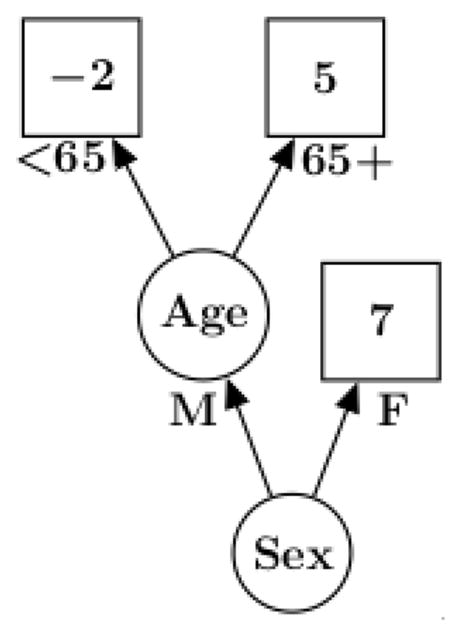
An example of a single tree with branch decision rules and terminal nodes
BART employs an ensemble of such trees in an additive fashion, i.e., it is the sum of m trees where m is typically large such as 200. The model can be represented as:
| (2) |
To proceed with the Bayesian specification we need a prior for f. Notationally, we use
| (3) |
and describe it as made up of two components: a prior on the complexity of each tree, Tj, and a prior on its terminal nodes, Mj|Tj. Using the Smith-Gelfand bracket notation [21] as a shorthand notation for writing a probability density or conditional density, we write [f] = Πj[Tj] [Mj|Tj]. Following [18], we partition [Tj] into 3 components: the tree structure or process by which we build a tree and create interior nodes, the choice of a covariate given an interior node and the choice of decision rule given a covariate for an interior node. The probability of a node being interior is defined by describing the probabilistic process by which a tree is grown. We start with a tree which is a single node and then recursively let a node have children (so that it is not a terminal node) with probability α(1+d)−γ where d represents the branch depth, α ∈ (0, 1) and γ ≥ 0. We assume that the choice of a covariate given an interior node and the choice of decision rule branching value given a covariate for an interior node are both uniform. We then use the prior where bj is the number of terminal nodes for tree j and μjℓ ~ N(0, τ2/m) on the values of the terminal nodes. This gives f(x) ~ N(0, τ2) for any x since the value f(x) will be the sum of m independent N(0, τ2/m). Along with centering of the outcome, these default prior mean and variance are specified such that each tree is a “weak learner” playing only a small part in the ensemble; more details on this can be found in [18].
To apply the BART model to a binary outcome, we use a probit transformation
where Φ is the standard normal cumulative distribution function and f ~ BART. To estimate this model we use the approach of Albert and Chib [22] and augment the model with latent variables Zi:
| (4) |
where IZ≥0 is one if Z ≥ 0 and zero otherwise and εi ~ N(0, 1). The Albert and Chib method then gives inference for f using the Gibbs sampler which draws Z|f and f|Z.
The model just described can be readily estimated using existing software for binary BART. It allows one to estimate the functions f(x) through Markov Chain Monte Carlo draws of f from which draws of the corresponding success probabilities p(x) = Φ(μ0 + f(x)) are readily obtained. Here μ0 is a tuning parameter to be chosen. For example, setting μ0 = 0 centers the prior for p(x) at .5 since the BART prior for f is centered at 0; however, the BART model is fairly robust to different prior values of μ0 given sufficient data. In the binary probit case, we let τ = 3/k, where k is a tuning parameter. With this choice of τ and the default value of k = 2 recommended in [18] and used in the BART R package, there is a 95% prior probability that f(x) is in the interval ±2(1.5) giving a reasonable range of values for p(x). Note that logit transformations could also be used for the binary outcome setting, and a logit implementation is also available in the BART package. However, because we are doing a prediction model and not focusing on parameter estimates like odds ratios, it is unclear whether probit or logit is more useful, so we have proceeded with the simpler probit framework.
4 BART for ITRs and value function estimation
Due to the excellent flexibility in modeling complex interactions and the strong predictive performance, we propose to use individualized predictions of patient outcomes from the BART model to determine an ITR. In addition to constructing an ITR based on BART predictions, we use the BART MCMC to assess uncertainty about various aspects of the treatment decision and resulting value function.
In applying BART to the ITR problem, our “x” of the previous section (in which we reviewed BART) becomes (x, a) where, as in the section introducing ITR’s, a is the decision variable and x is patient information.
The BART model implies p(Y = 1|x, a, f) = Φ(μ0 + f(x, a)) where f is expressed as the sum of trees as in Equation (4). Posterior MCMC draws { } consist of the individual trees j = 1, 2, …, m, for MCMC iterations d = 1, 2, …, D. Using Equation (4), each of these draws results in a draw fd of the function f. In this section, it is helpful to view the function f as the fundamental underlying parameter. BART is viewed as giving us draws from the posterior distribution of f.
4.1 Decision Theoretic Predictive BART ITR
From Equation (1), the Optimal ITR is obtained by choosing the value of a which maximizes E(Y|x, a) = p(Y = 1|x, a) conditional on X = x. In our Bayesian framework, p(Y = 1|x, a) is the predictive probability that Y = 1 which is obtained by integrating p(Y = 1|x, a, f) over the posterior distribution of the parameter f. Given MCMC draws {fd} from the posterior distribution of f, this integral is approximated by averaging over the draws:
| (5) |
Thus, p̄(x, a) is the MCMC estimate of the predictive p(Y = 1|x, a). Illustrations of inference on patient specific predictive probabilities are shown later in the Example Section and in Figure 5.
We can now define the BART based ITR as the one in which the treatment for each individual is given by maximizing the patient specific predictive probability over available treatments:
| (6) |
The construction of gBART follows the basic prescription of Bayesian decision theory in which we pick the action which maximizes expected utility. In this case, our utility is the outcome Y, and because Y is binary, the expected Y is the probability that Y = 1, so we simply pick the action which gives us the highest predictive probability of a successful outcome.
4.2 Posterior Distribution of the Value function of an ITR
For any ITR g(x) it is of interest to assess its value across the patient population so that different ITRs may be compared via this value. With an underlying function f, the value of the ITT g is defined as
which is the average (over x) of the probability of a good outcome. Given MCMC draws we can approximate the marginal distribution of this function of the uncertain f by simply plugging in draws of f:
| (7) |
The posterior samples {Vd(g)}, d = 1, 2, …, D, provide inference for the value function of any ITR g, including the BART ITR in Equation (6), approximating the expectation over X by an average over a representative distribution of x which is often taken to be the observed samples in the covariate space. Illustrations of inference on the value function can be found later in the Example Section and in Figure 5.
4.3 Posterior Distribution of the Value function of the Optimal ITR
It is also possible to estimate and assess uncertainty of the value associated with the optimal ITR as defined in Equation (1). We consider the optimal ITR as a function of f. If we knew f then, given x, the optimal action is given by
with corresponding maximum success probability p*(x, f) = maxa p(Y = 1|x, a, f). Draws of the value of the Optimal ITR, namely V* = EX(p*(x, f)) can be obtained from draws of f as
Again, the expectation over X is typically an average of representative x values, often using the observed samples in the covariate space. We can interpret the draws Vd collectively as representing uncertainty about the value of the Optimal ITR, i.e., the ITR for an agent who acts knowing the true f. Illustration of this is also found later in the Example Section and Figure 5(c) and (d).
5 Comparison with Existing Methods
We conducted extensive simulation studies benchmarking the proposed BART ITR strategy against existing methods for identifying ITRs. In order to avoid any concerns that we are deliberately selecting simulation settings where BART will show good performance, we reproduced simulation settings from two recent papers ([14, 4]) with a binary outcome variable Y and binary treatment A. The first set of simulations from [14] included 5 additional binary covariates XA: XE, 5 ordinal covariates Xa: Xe with 4 categories each, and one or two continuous covariates XCa,XCb. Eight different scenarios for the logit of the probability of response were simulated according to the following:
0.5XC1 + 2(XB1 + Xa3 * XA1) * A
0.5XC1 + 2(XB1 + Xa3 * (Xb2 + Xb3)) * A
0.05(−XA1 + XB1) + [(Xa2 + Xa3) + (Xb2 + Xb3) * XCa] * A
log log[(Xb3 + Xc3) + 5(Xa2 + Xa3 + XA1XB1) * A + 20]2
(XA1 + XB1) + 2 * A
0.5XA1 + 0.5XB1 + 2I(XCa < 5,Xa < 2) * A
0.5XA1 + 0.5XB1 + 2I(XCa < 5,XCb < 2) * A
0.5XCa + 0.5XCb + 2I(XCa < −2,XCb > 2) * A
We also considered a modification of these scenarios (denoted (A2-H2)) in which the treatment interaction term was reduced to 1/4th of the given value, in order to better differentiate among the competing methods. In the second set of simulations from [4], up to 3 independent continuous markers X1,X2,X3 were included in seven different models for the probability of nonresponse according to the following:
-
(K1)
logitp(Y = 0|A,X) = 0.3 + 0.2X1 − 0.2X2 − 0.2X3 + A(−0.1 − 2X1 − 0.7X2 − 0.1X3), Xj ~ N(0, 1)
-
(K2)
logitp(Y = 0|A,X) = 0.3 + 0.2X1 − 0.2X2 − 0.2X3 + A(−0.1 − 2X1 − 0.7X2 − 0.1X3), Xj ~ N(0, 1) except for 2% of high leverage points with X1 ~ Uniform(8, 9).
-
(K3)
log(−log p(Y = 0|A,X)) = −0.7 − 0.2X1 − 0.2X2 + 0.1X3 + A(0.1 + 2X1 − X2 − 0.3X3), Xj ~ N(0, 1)
-
(K4)
, Xj ~ Uniform(−1.5, 1.5)
-
(K5)
, Xj ~ N(0, 1)
-
(K6)
logitp(Y = 0|A,X) = 0.1 − 0.2X1 + 0.2X2 − X1X2 + A(−0.5 − X1 + X2 + 3X1X2), Xj ~ N(0, 1)
-
(K7)
(K7) p(Y = 0|A,X) = I(X1 < 8)(1 + e−η)−1 + I(X1 ≥ 8)(1 − (1 + e−η)−1), where η = 0.3+0.2X1−0.2X2−0.2X3+A(−0.1−2X1−0.7X2−0.1X3) and Xj ~ N(0, 1) except for 2% of high leverage points with X1 ~ Uniform(8, 9).
In all cases, ITRs were generated using a training dataset with n = 500 observations, and then each ITR was applied to a fixed independent test dataset of 2000 observations in order to compute the value function for this ITR from the true model. This process was replicated using 50 training datasets, and the average value function across the 50 training sets was obtained. This average value function for a particular ITR was normalized as a fraction of the true optimal value function to facilitate comparisons across scenarios.
For the BART ITR, we considered both use of the default prior parameters (BARTd), as well as cross-validation to select the number of trees (m=80,200) and the value of k from among values of (0.2, 0.8, 2.0) with default value of 2 (BARTcv). Several competing methods were included for comparison, including regularized outcome weighted subgroup identification (ROWSI) ([14]), Outcome Weighted Learning (OWL) ([16]), use of random forests (RF) for outcome prediction along the lines of virtual twins approach ([5]) with cross validation of number of trees and minimum node size, and boosting with classification tree working model (KANG) ([4]). Ordinal variables were handled as ordinal for BART and other tree based methods, but were otherwise treated as categorical variables.
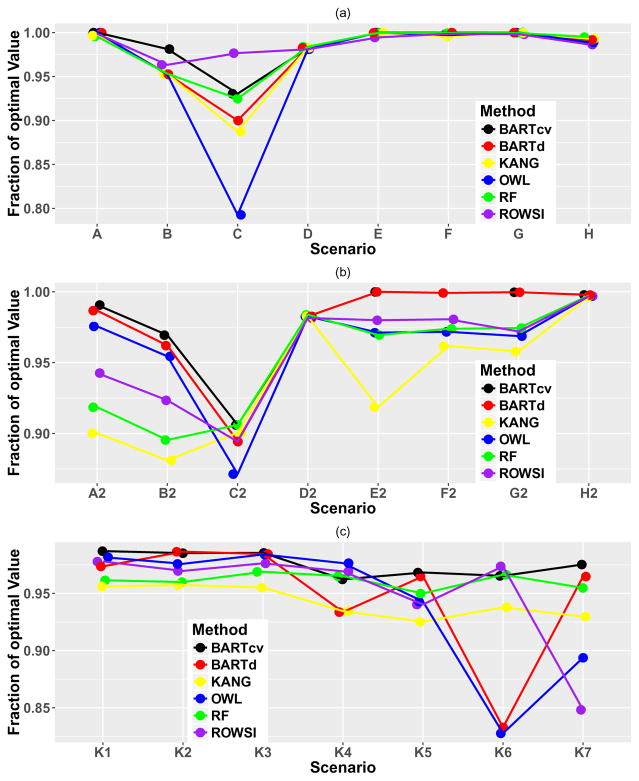
Results are shown in Figure 2. In all cases, the value function of the BART ITR with cross-validation performed at or near the top of the competing methods. BART with the default settings also performed comparably to the other existing methods, with good performance in most situations.
Figure 2.
Value function relative to the optimal value function for simulation settings in (a) scenarios as in [14], (b) same as (a) but with treatment effects cut by 25%, and (c) scenarios as in [4]
6 Illustration of Operating Characteristics of BART prediction models and Estimation of Optimal Value Function
We demonstrate the features of the proposed method using generated data from two settings: a complex treatment interaction setting, and a main effect only setting. In each case, training datasets of either n = 500 or n = 5000 were generated and applied to an independent test dataset of 2000 observations. Logistic regression with a binary outcome and three independent Uniform(−1.5, 1.5) covariates was used to generate the data, with a complex treatment interaction model according to
and a no treatment interaction model according to
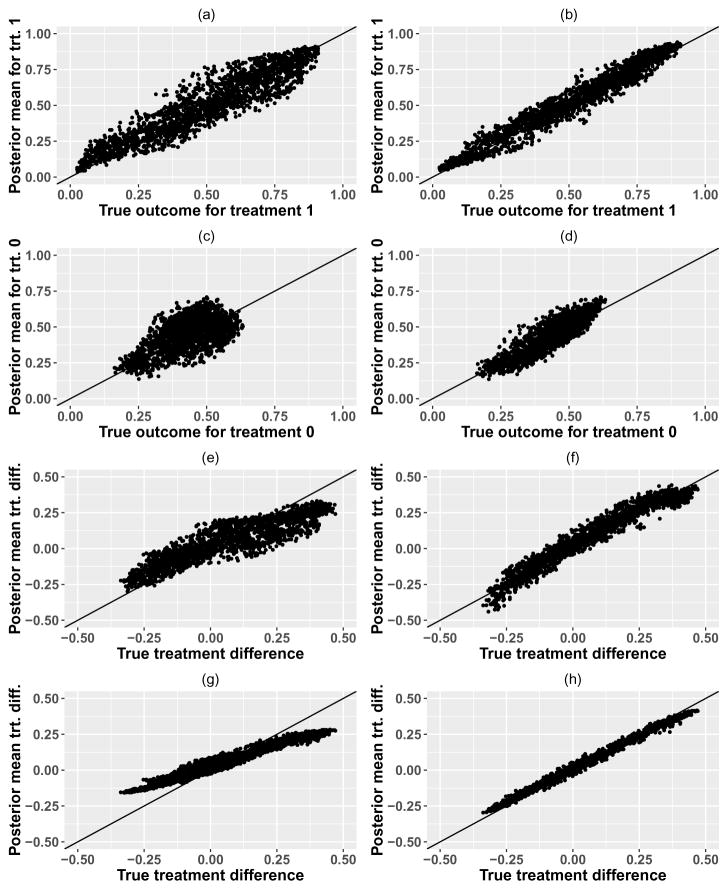
In Figure 3 we plot the BART posterior means vs. the true probabilities of treatment outcome for the test dataset, for each treatment as well as for the treatment difference, for single training datasets of size n = 500 ((a),(c),(e)) and n = 5000 ((b),(d),(f)) using the complex interaction model. The posterior mean prediction from the BART model has excellent accuracy for the large sample size, both for individual treatment outcomes as well as for the treatment difference, despite the complex treatment interaction model which includes linear and quadratic covariate-treatment interactions as well as an interaction term with a thresholded value of a covariate. The larger training dataset shows improved accuracy compared to the smaller training dataset, which has some modest shrinkage of the treatment effects.
Figure 3.
BART posterior means vs. true probabilities for complex interaction model, with n = 500 (left side) and n = 5000 (right side). First two rows show predictions for individual treatment outcomes, while row 3 shows predictions for treatment differences, all using a single training dataset. Row 4 shows the posterior means for the treatment difference averaged over 400 repeated data simulations of the training set.
We also conducted repeated data simulations with 400 replicates to look at the bias of the prediction model as well as coverage of the 95% interval estimates for the value function of the Optimal ITR, using the quantiles of the posterior samples for the value function of the Optimal ITR. Bias over 400 replicates for the treatment difference is shown in Figure 3, panels (g) and (h). As is seen with the single training dataset, there is some small bias and shrinkage of the treatment effects for smaller sample size which disappears with larger sample size. Coverage probabilities of 95% credible intervals for the value of the Optimal ITR are 90% for training dataset of size n = 500 and 95% for training dataset of size n = 5000, indicating that once the sample size is sufficient to reduce the shrinkage of the treatment effects, coverage of the value function for the Optimal ITR is excellent. We also examined coverage of 95% credible intervals for the treatment effect for each individual in the test dataset; median (Inter-Quartile Range) of these coverage probabilities are 96.7% (89.5%–99.0%) for training datasets of size n = 500, and 99.2% (98.5%–99.5%) for training datasets of size n = 5000. Average widths of these 95% credible intervals for the treatment effect for each individual were 0.43 for n = 500 and 0.25 for n = 5000.
Similar results are shown for the model with no treatment-covariate interaction in Figure 4. Note that the true treatment differences show very narrow variability due to the data generating model, and the BART model shows predictions for treatment differences which are also small and which narrow with increasing sample size. These predictions are unbiased in repeated simulation, as indicated by the convergence to the diagonal line in Figure 4 panels (c) and (d). Coverage of the value function and individual treatment effects was similar to the complex interaction setting.
Figure 4.
BART posterior means vs. true probabilities for no interaction model, with n = 500 (left side) and n = 5000 (right side). First row shows predictions for treatment differences using a single training dataset, while row 2 shows the posterior means for the treatment difference averaged over 400 repeated data simulations of the training set.
7 Summarizing the BART ITR
The ITR based on the BART prediction model does not directly yield a simple interpretable rule; this issue in general with flexible models has been discussed in [7], who propose directly optimizing the value function over an interpretable set of rules. In contrast, we separate the modeling of outcome from the determination of an interpretable rule, by trying to develop an approximation to this BART ITR which is interpretable and yields good performance. We propose a “Fit-the-fit” strategy, in which one develops a single tree fit to the posterior mean treatment differences as a function of patient characteristics. Essentially, the posterior mean treatment differences are treated as the “data” and we try and fit an interpretable single tree to this data. The single tree then provides an interpretable way to explain which groups of patients should receive which treatment, as well as the magnitude of the treatment difference for that group of patients. This strategy was originally proposed as a variable selection technique for a BART prediction model, but has been adapted here to focus on summarizing the inference on treatment differences and the BART ITR. A similar strategy of applying a tree to estimated treatment differences was proposed by [5, 23], where they also note that estimation of individual treatment effects using random forests could be improved by expanding the set of predictor variables to explicitly include treatment interactions. Expansion of the set of predictor variables could also be used in BART, though any improvements would likely need inclusion of the correct form of the interactions which may be difficult in practice. Also, there may be a cost to adding a lot of additional terms to be considered in the trees. Further research is needed to investigate the potential benefit of this strategy.
To fit an appropriate tree and also identify the best set of variables to include in that tree, a sequence of trees are fit, where variables are sequentially added to the candidate set of splitting variables in a stepwise manner to improve the fit. Given a current set of variables and a corresponding tree built using those variables, the fit of the current tree is assessed using the R2 between the fitted values from the tree and the posterior mean treatment difference (which is being used as the “data”). Additional variables are considered to be added one at a time yielding new trees built with an increasing set of variables, and their R2 is assessed for each new variable added and corresponding tree. The variable which most increases the R2 is selected at each step. Once the R2 does not improve appreciably with addition of a new variable (we used ΔR2 < 1%), the procedure ends and the current tree is used as the approximation to the BART ITR.
Note that each single tree fit can be implemented very quickly, so this fit the fit postprocessing procedure takes minimal computing time. It may not always be possible to identify such a single tree (this is in fact the benefit of ensemble methods to provide improved prediction), but note that the quality of such an interpretable approximation can be assessed using the R2 between the single tree and the BART prediction model. It is also possible to compute the value function of the single-tree approximation ITR, and compare it with that of the full BART-ITR.
This “fit-the-fit” approach may require a very complicated tree in order to provide a sufficiently accurate approximation to the BART treatment differences, and sometimes it still may be unsuccessful; this is precisely the situation where an ensemble prediction model is most needed. A complicated tree may also lose ease of interpretability. As an alternative, one also could consider growing a classification tree to fit the treatment decision process, rather than the treatment effect itself. This may result in a simpler tree which is accurate for approximating BART based treatment decisions, but doesn’t necessarily differentiate between small and large treatment effects.
8 Example
We illustrate the proposed methodology with a study of 1 year survival outcomes after a hematopoietic cell transplant (HCT) used to treat a variety of hematologic malignancies. We use data on 3802 patients receiving reduced intensity conditioning for their HCT between 2011–2013, with data reported to the Center for International Blood and Marrow Transplant Research (CIBMTR). Follow up to 1 year is complete for all patients so we analyze the outcomes using binary methods as described throughout the paper applied to the patient’s survival status at 1 year. Note that a full survival analysis could also be conducted with BART methods available for survival data([24]), however this requires consideration of the appropriate target outcome to optimize and so we defer this for future research. The primary treatment of interest is the type of conditioning regimen used (Fludarabine/Melphalan, or FluMel for short, vs. Fludarabine/Busulfan, or FluBu for short). A variety of patient, donor, and disease factors were examined for their utility in personalizing the selection of the conditioning regimen, including age, race/ethnicity, performance score, Cytomegalovirus status, disease, remission status, disease subtypes, chemosensitivity, interval from diagnosis to transplant, donor type, Human Leukocyte Antigen (HLA) matching between donor and recipient, prior autologous transplant, gender matching between donor and recipient, comorbidity score, and year of transplant. This observational cohort appears to be well balanced between the regimens across these factors, indicating reasonable equipoise by clinicians on which conditioning regimen is most appropriate for individual patients.
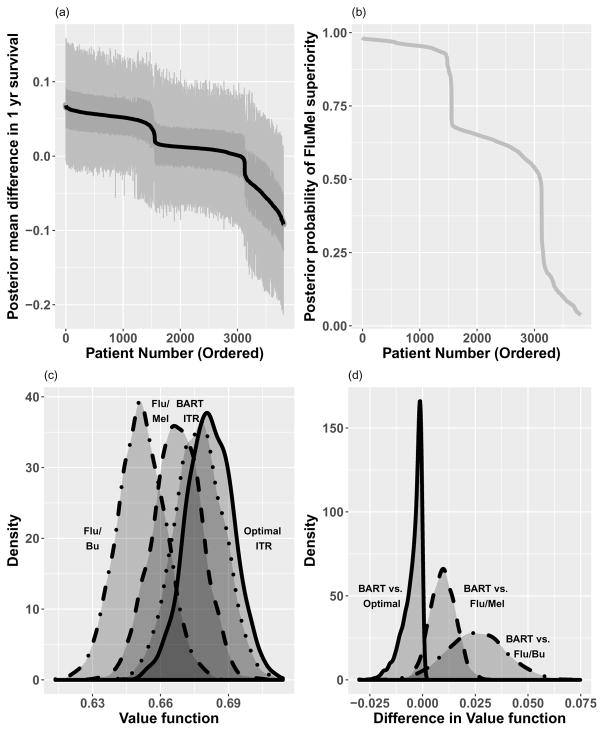
Fitting of the BART model provides samples from p(Y = 1|x, a, fd) for d = 1, …, D. In Figure 5 we show waterfall plots of the differences in 1 year survival between Flu/Mel and Flu/Bu conditioning across patients in two ways. In (a) we use the samples from the patient specific difference in 1 year survival, p(Y = 1|x, a = Flu/Mel, fd) −p(Y = 1|x, a = Flu/Bu, fd), and plot the posterior mean of these differences in 1 year survival for each patient, sorted by the magnitude of the difference. This is equivalent to the difference in predictive probabilities under each treatment condition as described in Equation 5. Inter-quartile ranges and 95% posterior intervals are also shown to indicate the variability of the differences. In (b) we show the waterfall plot of the posterior probabilities that Flu/Mel has a higher 1 year survival than Flu/Bu. This is obtained by computing
Figure 5.
Results of BART ITR for HCT example. (a) Waterfall plot of 1 yr survival differences (FluMel-FluBu) by patient (posterior mean differences, along with inter-quartile ranges and 95% posterior intervals), (b) Waterfall plot of posterior probabilities that survival is higher for Flu/Mel, (c) Density plot of value functions for three treatment strategies (FluMel, FluBu, BART ITR) as well as Optimal ITR, and (d) Density plot of difference in value functions for treatment strategies compared to BART ITR. The posterior mean of the value function distributions for each treatment strategy are: FluBu: 0.651, FluMel: 0.667, BART1I9TR: 0.677, Optimal ITR: 0.682.
These plots indicate some heterogeneity in treatment benefit, where approximately 3000 of the patients seem to benefit from Flu/Mel, albeit with varying degrees of magnitude and/or certainty surrounding that benefit, while the remaining patients seem to benefit from Flu/Bu conditioning.
We implemented BART using the default settings of m = 200 and k = 2. To examine sensitivity of the width of the posterior intervals for the patient specific treatment difference to the choice of tuning parameters, we examined these widths under standard values of m and k. Average widths across patients in the cohort with m = 50 were 0.13,0.13,0.12 for k = 1, 2,3 respectively. Average widths with m = 200 were 0.16,0.14,0.12 for k = 1, 2, 3 respectively. This suggests only mild sensitivity to the tuning parameters, with higher values of k and lower values of m tending to produce slightly narrower intervals, likely due to greater borrowing of information from neighboring observations. Note however that narrower intervals due to larger k or smaller m may also have greater bias due to this same phenomenon, so narrower interval widths are not the best target for choosing m and k. Cross-validation focused on prediction error is useful for this purpose, and for this dataset, cross validation ended up also selecting the default values of k = 2 and m = 200.
Also in Figure 5(c) we show the value functions as described in Equation 7 for the cohort of n = 3802 patients for three treatment rules: all patients receive Flu/Bu, all patients receive Flu/Mel, and patients receive treatment according to the BART based ITR. The BART ITR value function distribution is shifted to the right, indicating improved 1 year survival outcomes over the overall cohort using this individualized strategy. The posterior mean of the value function distributions for each treatment strategy are: FluBu: 0.651, FluMel: 0.667, BART ITR: 0.677, Optimal ITR: 0.682. Figure 5(d) shows the density functions of the difference in value function for the BART ITR compared to the other strategies, indicating high likelihood that the BART ITR is superior to the fixed treatment strategies. On the other hand, it is inferior to the Optimal ITR as expected, but the differences are small.
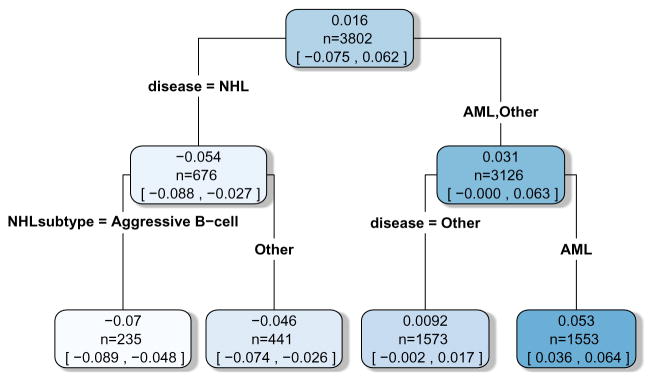
As pointed out earlier, one drawback of the BART based ITR is that it does not lead to a simple interpretable rule. Next we apply the fit the fit technique to approximate the BART based ITR with an interpretable treatment rule which has nearly as good performance. In order to do this, the posterior mean treatment differences in 1 year survival are treated as the “data” and we try and fit an interpretable single tree to this data. In order to do this, a sequence of trees are fit, where variables are added sequentially to the set of potential splitting variables of the tree in a stepwise manner to improve the fit. Once the change in R2 is less than 1% with addition of a new variable, the procedure ends and the current tree is used as the approximation to the BART ITR. The results of the final tree fit are shown in Figure 6; R2 between the tree fit and the posterior mean treatment differences is 97%. The first splitting variable used, Non-Hodgkins Lymphoma (NHL) disease vs. other disease, was sufficient to match the BART ITR exactly in terms of selection of conditioning regimen; Patients with NHL have approximately 5% better 1 year OS with Flu/Bu conditioning, while patients without NHL have approximately 3% better 1 year OS with Flu/Mel conditioning. A second level of splitting variables provided further resolution on the magnitude of the treatment benefit for disease subgroups, but did not affect the directional benefit. The splits in the tree also match up with the drops in the treatment effects seen in the waterfall plot in Figure 5, where the drops from each plateau seem to indicate a subpopulation change. Patients with AML have approximately 5% better 1 year OS with Flu/Mel conditioning, while patients with other diseases have approximately 1% better 1 year OS with Flu/Mel conditioning. Similarly, among patients with NHL disease, those with aggressive B-cell subtype may experience slightly more benefit from Flu/Bu conditioning compared to those with other subtypes (7% vs. 5%). Note that in this case, this simple rule completely matched the BART based ITR, and so the value function associated with this rule also matches the BART ITR value function in the previous figure. This type of approximation to a BART based ITR can greatly facilitate communication with clinicians on how the ITR works and what types of patients benefit from one treatment vs. another.
Figure 6.
Tree fit to the posterior mean treatment differences. Values in each node represent the posterior mean and 95% credible intervals for the average treatment effect of the subgroup of patients represented in that node.
9 Discussion
In this article, we presented a framework for identifying optimal individualized treatment rules using Bayesian Additive Regression Trees. BART is a flexible fully nonparametric prediction model which can handle complex functional forms as well as interactions among variables, and therefore it is well suited for examining treatment interactions which drive ITRs. There are two main advantages to using BART to identify an ITR. First, our proposed method has excellent performance when benchmarked against existing methods, including other flexible prediction methods as well as policy search methods such as outcome weighted learning; overall it performed better than or comparable to other existing methods across a range of ITR simulation settings established in other papers. Second, our method provides direct inference on the value of the BART ITR as well as the Optimal ITR. This requires incorporation of both the uncertainty in the prediction model, as well as uncertainty in the individual patient treatment selection that depends on the prediction model. Both can be handled in a straightforward manner using the posterior samples for the prediction model function in the Bayesian framework. In contrast, it is not clear how to do this for policy search methods which do not provide a direct prediction model for outcome, as well as for other flexible models such as random forests which do not directly provide uncertainty measures.
We observed that the BART model tends to shrink the treatment effect estimates for smaller sample size leading to underestimation of the true value of the Optimal ITR. Larger sample sizes do overcome this shrinkage from the prior. Further consideration of ways to reduce this unidirectional bias could provide better inference on the value function for small sample sizes.
One limitation of our proposed method is that the BART method generates a “black box” prediction model which is difficult to explain to clinicians. However, we showed how the posterior mean differences available from the model can be fed into a tree procedure to yield an interpretable ITR which provides a close approximation to the BART ITR and which can be readily explained to clinicians. A recent article [25] describes the use of BART and utility specifications with the goal of identifying subgroups with elevated treatment effects, in contrast to finding an individualized treatment rule.
Our proposed method uses “off-the-shelf” BART software; minimal processing is needed to obtain posterior inference under each treatment condition for patients in a test dataset. Inference for the value of an ITR is also readily available. While BART can be computationally demanding as a Markov Chain Monte Carlo (MCMC) technique, it can be parallelized to save computational time since the chains do not share information beyond the data itself. An example of code to implement the methods discussed in this manuscript is available in the Web Appendix.
Work of all authors is supported in part by the Advancing a Healthier Wisconsin Endowment at the Medical College of Wisconsin. The authors would like to thank Dr. Menggang Yu from University of Wisconsin for providing software to implement the ROWSI method in the simulation study.
The Web Appendix, referenced in the Discussion section, is available with this paper at the Statistical Methods in Medical Research website.
Supplementary Material
References
- 1.Qian M, Murphy SA. Performance Guarantees for Individualized Treatment Rules. Annals of statistics. 2011;39(2):1180–210. doi: 10.1214/10-AOS864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Imai K, Ratkovic M. Estimating treatment effect heterogeneity in randomized program evaluation. Ann Appl Stat. 2013;7(1):443–470. doi: 10.1214/12-AOAS593. doi: 10.1214/12-AOAS593. URL . [DOI] [Google Scholar]
- 3.Moodie EE, Dean N, Sun YR. Q-learning: Flexible learning about useful utilities. Statistics in Biosciences. 2014;6(2):223–43. [Google Scholar]
- 4.Kang C, Janes H, Huang Y. Combining biomarkers to optimize patient treatment recommendations. Biometrics. 2014;70(3):695–07. doi: 10.1111/biom.12191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Foster JC, Taylor JMG, Ruberg SJ. Subgroup identification from randomized clinical trial data. Statistics in medicine 2011. 2011;30(24):2867–880. doi: 10.1002/sim.4322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Zhao Y, Zeng D, Socinski MA, et al. Reinforcement Learning Strategies for Clinical Trials in Nonsmall Cell Lung Cancer. Biometrics. 2011;67(4):1422–433. doi: 10.1111/j.1541-0420.2011.01572.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Zhang Y, Laber EB, Tsiatis A, et al. Using decision lists to construct interpretable and parsimonious treatment regimes. Biometrics. 2015;71(4):895–04. doi: 10.1111/biom.12354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Dusseldorp E, Conversano C, Os BJV. Combining an additive and tree-based regression model simultaneously: STIMA. Journal of Computational and Graphical Statistics. 2010;19(3):514–30. [Google Scholar]
- 9.Doove LL, Dusseldorp E, Deun KV, et al. A comparison of five recursive partitioning methods to find person subgroups involved in meaningful treatment–subgroup interactions. Advances in Data Analysis and Classification. 2014;8(4):403–25. doi: 10.1007/s11634-013-0159-x. doi: 10.1007/s11634-013-0159-x. URL . [DOI] [Google Scholar]
- 10.Lipkovich I, Dmitrienko A, Denne J, et al. Subgroup identification based on differential effect search–a recursive partitioning method for establishing response to treatment in patient subpopulations. Statistics in medicine. 2011;30(21):2601–621. doi: 10.1002/sim.4289. [DOI] [PubMed] [Google Scholar]
- 11.Su X, Tsai CL, Wang H, et al. Subgroup analysis via recursive partitioning. Journal of Machine Learning Research. 2009 Feb;10:141–58. [Google Scholar]
- 12.Zeileis A, Hothorn T, Hornik K. Model-Based Recursive Partitioning. Journal of Computational and Graphical Statistics. 2008;17(2):492–14. doi: 10.1198/106186008X319331. doi: 10.1198/106186008X319331. URL . [DOI] [Google Scholar]
- 13.Laber E, Zhao Y. Tree-based methods for individualized treatment regimes. Biometrika. 2015:501–14. doi: 10.1093/biomet/asv028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Xu Y, Yu M, Zhao YQ, et al. Regularized outcome weighted subgroup identification for differential treatment effects. Biometrics. 2015;71(3):645–53. doi: 10.1111/biom.12322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Zhang B, Tsiatis AA, Laber EB, et al. A robust method for estimating optimal treatment regimes. Biometrics. 2012;68(4):1010–018. doi: 10.1111/j.1541-0420.2012.01763.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zhao Y, Zeng D, Rush AJ, et al. Estimating Individualized Treatment Rules Using Outcome Weighted Learning. Journal of the American Statistical Association. 2012;107(449):1106–118. doi: 10.1080/01621459.2012.695674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Fu H, Zhou J, Faries DE. Estimating optimal treatment regimes via subgroup identification in randomized control trials and observational studies. Statistics in medicine. 2016;35(19):3285–302. doi: 10.1002/sim.6920. [DOI] [PubMed] [Google Scholar]
- 18.Chipman HA, George EI, McCulloch RE. Bart: Bayesian Additive Regression Trees. The Annals of Applied Statistics. 2010;4(1):266–98. [Google Scholar]
- 19.Linero A. Bayesian regression trees for high dimensional prediction and variable selection. Journal of the American Statistical Association. 2017 doi: 10.1080/01621459.2016.1264957. [DOI]
- 20.Hill JL. Bayesian Nonparametric Modeling for Causal Inference. Journal of Computational and Graphical Statistics. 2011;20(1):217–40. doi: 10.1198/jcgs.2010.08162. [DOI] [Google Scholar]
- 21.Gelfand AE, Smith AF. Sampling-based approaches to calculating marginal densities. Journal of the American statistical association. 1990;85(410):398–09. [Google Scholar]
- 22.Albert J, Chib S. Bayesian Analysis of Binary and Polychotomous Response Data. Journal of the American Statistical Association. 1993;88(422):669–79. [Google Scholar]
- 23.Foster JC, Taylor JM, Kaciroti N, et al. Simple subgroup approximations to optimal treatment regimes from randomized clinical trial data. Biostatistics (Oxford, England) 2015;16(2):368–82. doi: 10.1093/biostatistics/kxu049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Sparapani RA, Logan BR, McCulloch RE, et al. Nonparametric survival analysis using Bayesian Additive Regression Trees (BART) Statistics in medicine. 2016;35:2741–753. doi: 10.1002/sim.6893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Sivaganesan S, Müller P, Huang B. Subgroup finding via Bayesian additive regression trees. Statistics in Medicine. 2017 doi: 10.1002/sim.7276. [DOI] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.