Significance
Seeing a snapshot of individuals at different stages of a dynamic process can reveal what the process would look like for a single individual over time. Biologists apply this principle to infer temporal sequences of gene expression states in cells from measurements made at a single moment in time. However, the sparsity and high dimensionality of single-cell data have made inference difficult using formal approaches. Here, we apply recent innovations in spectral graph theory to devise a simple and asymptotically exact algorithm for inferring the unique dynamic solution under defined approximations and apply it to data from bone marrow stem cells.
Keywords: single cell, hematopoiesis, pseudotime, dynamic inference, spectral graph theory
Abstract
Single-cell expression profiling reveals the molecular states of individual cells with unprecedented detail. Because these methods destroy cells in the process of analysis, they cannot measure how gene expression changes over time. However, some information on dynamics is present in the data: the continuum of molecular states in the population can reflect the trajectory of a typical cell. Many methods for extracting single-cell dynamics from population data have been proposed. However, all such attempts face a common limitation: for any measured distribution of cell states, there are multiple dynamics that could give rise to it, and by extension, multiple possibilities for underlying mechanisms of gene regulation. Here, we describe the aspects of gene expression dynamics that cannot be inferred from a static snapshot alone and identify assumptions necessary to constrain a unique solution for cell dynamics from static snapshots. We translate these constraints into a practical algorithmic approach, population balance analysis (PBA), which makes use of a method from spectral graph theory to solve a class of high-dimensional differential equations. We use simulations to show the strengths and limitations of PBA, and then apply it to single-cell profiles of hematopoietic progenitor cells (HPCs). Cell state predictions from this analysis agree with HPC fate assays reported in several papers over the past two decades. By highlighting the fundamental limits on dynamic inference faced by any method, our framework provides a rigorous basis for dynamic interpretation of a gene expression continuum and clarifies best experimental designs for trajectory reconstruction from static snapshot measurements.
Genome-scale high-dimensional measurements on single cells have transformed our ability to discover the constituent cell states of tissues (1). The most mature of these technologies, single-cell RNA sequencing (scRNA-seq), can be applied at relatively low cost to thousands and even tens of thousands of cells to generate an “atlas” of cell states in tissues, while also revealing transcriptional gene sets that define these states (2, 3). Rapidly maturing technologies are also enabling single-cell measurements of the epigenome (4), the proteome (5, 6), and the spatial organization of chromatin (7).
A more ambitious goal of single-cell analysis is to describe dynamic cell behaviors and, by extension, to reveal dynamic gene regulation. Since high-dimensional single-cell measurements are destructive to cells, they reveal only static snapshots of cell state. However, it has been appreciated that dynamic progressions of cell state can be indirectly inferred from population snapshots by methods that fit a curve or a tree to the continuous distribution of cells in high-dimensional state space. A number of methods address the problem of “trajectory reconstruction” from single-cell data and have been used to order events in cell differentiation (8–12), cell cycle (13), and perturbation response (14). The most advanced algorithms have addressed increasingly complex cell state topologies including branching trajectories (15).
The general challenge, even with perfect data, is that many regulatory mechanisms can generate the same dynamic process, and many dynamic processes can give rise to the same distribution. It is thus doubly impossible to rigorously infer mechanisms from snapshots of cells. However, because the distributions still reflect the underlying mechanisms, it is possible to consider which mechanisms would be inferred if additional biophysical constraints were imposed. In our opinion, the most useful current methods for dynamic inference might be more accurately described as methods for nonlinear dimensionality reduction, or “manifold discovery”: they robustly solve the problem of how to describe a static continuum of cell states using a small number of coordinates but provide minimal guidance on how the observed static continuum should be interpreted with respect to the many redundant dynamic processes that could give rise to it.
Here, we explore whether one can derive a framework for inferring cell state dynamics from static snapshots that explicitly incorporates critical assumptions needed to disambiguate the alternative dynamics associated with a static snapshot of single cells. Our second focus is to develop a practical algorithm for dynamic inference, which we call population balance analysis (PBA). PBA provides a continuum description of cell states, just as existing methods do. However, PBA also formally solves a problem of dynamic inference from biophysical principles and can thus be considered predictive of cell dynamics under clearly stated assumptions. For example, it assigns to each transcriptional state a set of testable fate probabilities. We apply PBA to scRNA-seq data of hematopoietic progenitor cells (HPCs), reconciling these data with fate assays made over the past few decades in this system. Validation of novel PBA predictions in HPCs forms the subject of another study (16).
The biophysical foundation of PBA is embodied by a diffusion-drift equation over high-dimensional space, which, although simple to define, cannot be practically solved using established computational tools. We therefore invoke an asymptotically exact and highly efficient solution to diffusion-drift equations using recent innovations in spectral graph theory. The ubiquity of diffusion-drift equations in fields of quantitative biology (17) and physics (18) suggests that applications of these methods may exist in other fields. Overcoming this computational challenge represents the major technical contribution of this work.
Results
A First-Principles Relationship of Cell Dynamics to Static Observations.
When reconstructing a dynamic process from single-cell snapshot data, cells are typically observed in a continuous spectrum of states owing to asynchrony in their dynamics. The goal is to reconstruct a set of rules governing possible dynamic trajectories in high-dimensional gene expression space that are compatible with the observed distribution of cell states. The inferred rules could represent a single curve or branching process in gene expression space, or they could reflect a more probabilistic view of gene expression dynamics. In some cases, multiple time points can be collected to add clarity to the temporal ordering of events. In other cases, a single time point could capture all stages of a dynamic process, such as in steady-state adult tissue turnover.
To develop a framework for dynamic reconstruction from first principles, we want to identify a general, model-independent, mathematical formulation linking cell dynamics to static observations. One possible starting point is the “population balance equation” [also known as the flux balance law (19)], which has the following form:
| [1] |
Eq. 1 states that, in each small region of gene expression space, the rate of change in the number of cells (left-hand side of the equation) equals the net cell flux into and out of the region (right-hand side) (Fig. 1A). The equation introduces the cell density, c(x,t), which is the distribution of cell states from which we sample a static snapshot of cells in an experiment. This density depends on the net average velocity, v(x), of the cells at point x, a feature of the dynamics that we want to infer. Notably, being an average quantity, v is not necessarily a description of the dynamics of any individual cell, but it alone governs the form of the sampled cell density c. Eq. 1 also introduces a third variable: (x) is a rate of cell accumulation and loss at point x caused by the discrete phenomena of cell proliferation and cell death, and by entrance and exit from the tissue being isolated for analysis. Although Eq. 1 is likely a good starting point for analyzing many biological systems, it nonetheless introduces some specific assumptions about the nature of cell state space. First, it approximates cell state attributes as continuous variables, although they may in fact represent discrete counts of molecules such as mRNAs or proteins. Second, it assumes that changes in cell state attributes are continuous in time. This means, for example, that the sudden appearance or disappearance of many biomolecules at once cannot be described in this framework.
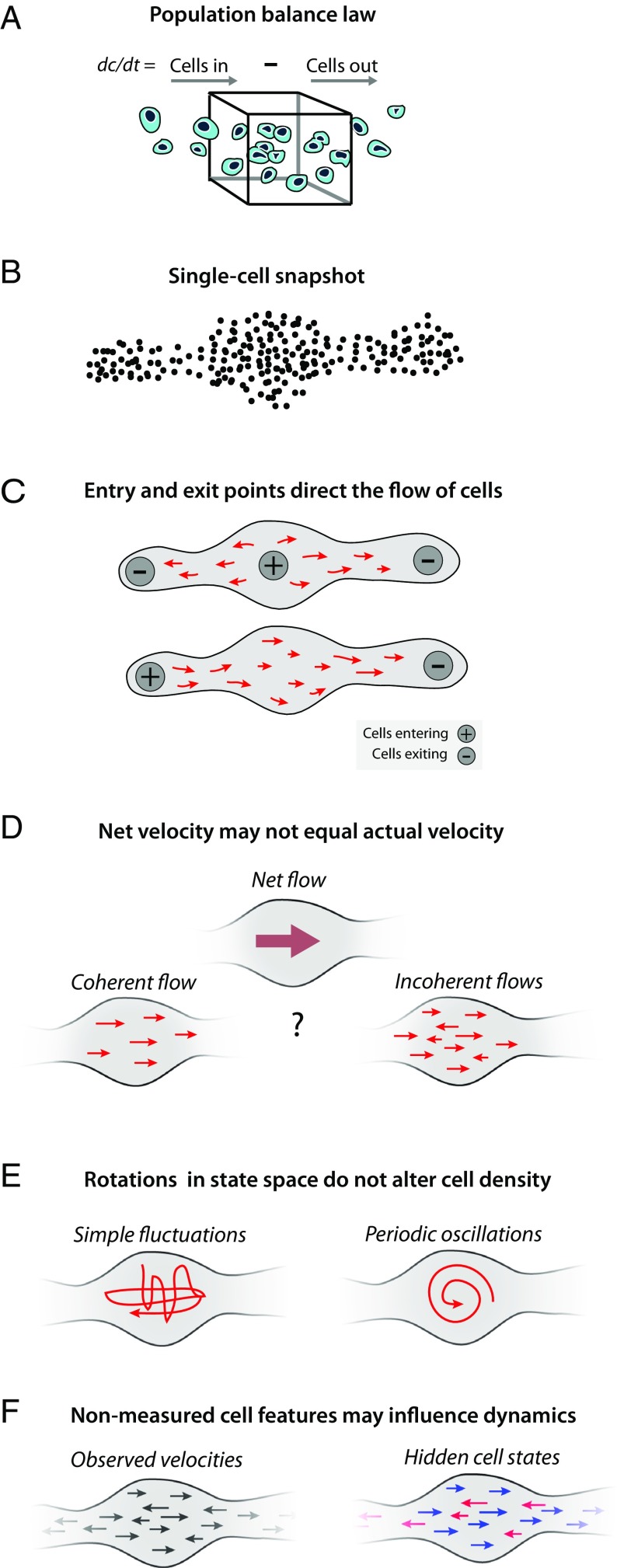
Fig. 1.
Symmetries and inhomogeneities of the population balance law set fundamental limits on dynamic inference. (A) Schematic of the population balance law (Eq. 1), which serves as a starting point for inferring cell dynamics from high-dimensional snapshots. In each small region of gene expression space, the rate of change in cell density equals the net cell flux into and out of the region. Symmetries and unknown variables of the population balance law mean that there is no unique solution for dynamics from a static snapshot (B), shown schematically in C–E. (C) Alternative assumptions on cell entry and exit rates across gene expression space lead to different dynamic solutions. (D) Snapshot data constrain only net cell flows through the population balance law, and not the noise in dynamic trajectories of individual cells. (E) A gauge symmetry of the population balance law means that static snapshots arising from periodic oscillations of cell state can also be explained by simple fluctuations that do not have a consistent direction and periodicity. (F) Hidden but stable properties of a cell—such as epigenetic state—allow for a superposition of cell populations following different dynamic laws. These unknowns are constrained by assumptions in any algorithm inferring dynamics from static snapshot data.
Multiple Dynamic Trajectories Can Generate the Same High-Dimensional Population Snapshots.
Given knowledge of the cell population density, c(x,t), we hope to infer the underlying dynamics of cells by solving for the average velocity field v in Eq. 1. This approach falls short, however, because v is not fully determined by Eq. 1, and even if it were, knowing the average velocity of cells still leaves some ambiguity in the specific trajectories of individual cells. This raises the question: Does there exist a set of reasonable assumptions that constrain the dynamics to a unique solution? To explore this question, we enumerate the causes of nonuniqueness in cell state dynamics.
First, assumed cell entry and exit points strongly influence inferred dynamics: For the same data, different assumptions about the rates and location of cell entry and exit lead to fundamentally different inferences of the direction of cell progression in gene expression space, as illustrated in Fig. 1C. Cells can enter a system by proliferation, by physically migrating into the tissue that is being analyzed, or by up-regulating selection markers used for sample purification (e.g., cell surface marker expression). Similarly, cells exit observation by cell death, physical migration out of the tissue being studied, or by down-regulation of cell selection markers. Referring to Eq. 1, this discussion is formally reflected in the need to assume a particular form for the rate field R(x) when inferring dynamics v from the observed cell density c.
Second, net velocity does not equal actual velocity: A second unknown is the stochasticity in cell state dynamics, reflected in the degree to which cells in the same molecular state will follow different paths going forward. A net flow in gene expression space could result from imbalanced flows in many directions or from a single coherent flow in one direction (Fig. 1D). If the goal of trajectory analysis is to go beyond a description of what states exist and make predictions about the future behavior of cells (e.g., fate biases) given their current state, then it is necessary to account for the degree of such incoherence of dynamics.
Third, rotations and oscillations in state space do not alter cell density: Static snapshot data cannot distinguish periodic oscillations of cell state from simple fluctuations that do not have a consistent direction and periodicity (Fig. 1E). As with incoherent motion above, predictive models may need to explicitly consider oscillatory behaviors. The inability to detect oscillations from snapshot data are formally reflected in Eq. 1 by invariance of the concentration c to the addition to v of arbitrary rotational velocity fields u satisfying .
Fourth, hidden features of cell state can lead to a superposition of different dynamic processes: Stable properties of cell state that are invisible to single-cell expression measurements, such as chromatin state or tissue location, could nonetheless impact cell fate over multiple cell state transitions (Fig. 1F). The existence of such long-term “hidden variables” would clearly compromise attempts to predict the future fate of a cell from its current gene expression state.
Because of these phenomena, no unique solution exists for dynamic inference. However, sensible predictions about dynamics can still be made by making certain assumptions. Our framework for cell trajectory analysis (see below) is based on explicit, reasonable assumptions that together are necessary and sufficient to constrain a unique solution (Fig. 2). These assumptions may nevertheless be inaccurate in certain situations.
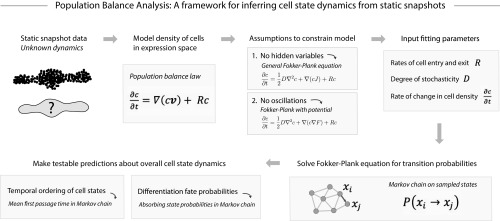
Fig. 2.
Population balance analysis (PBA). Although many dynamics are consistent with a given static snapshot of cell states, testable assumptions can constrain a unique solution. Shown schematically here is PBA, one such approach to dynamic inference under explicit assumptions. PBA constrains the population balance law by assuming a dynamics that is Markovian and described by a potential landscape (see Construction of the PBA Framework for details), and including fitting parameters that incorporate prior knowledge or can be directly measured. The resulting diffusion-drift equation is solved asymptotically exactly in high dimensions on single-cell data through a graph theoretic result (SI Appendix, Theory Supplement and ref. 22). The PBA algorithm outputs transition probabilities for each pair of observed states, which can then be used to compute dynamic properties such as temporal ordering and fate potential.
Construction of the PBA Framework.
To infer cell dynamics from an observed cell density c, we make the following assumptions.
The Fokker–Planck equation models memoryless cell state dynamics.
The first assumption is that the properties of the cell available for measurement (such as its mRNA content) fully encode a probability distribution over its possible future states. This assumption is made implicitly by all current approaches to trajectory analysis and cell fate prediction, and we reflect on its plausibility in the discussion.
An equivalent statement of this first assumption is that cell trajectories are Markovian, or that any form of cellular memory is encoded in their measured properties. If so, the cell trajectories underlying Eq. 1 can be approximated as biased random walks, with a deterministic component that reflects the reproducible aspects of cell state changes such as their differentiation through stereotypical sequences of states, and a stochastic component that reflects random fluctuations in cell state, partly driven by bursty gene expression, fluctuations in cellular environment, and intrinsic noise from low–molecular-number processes. In this approximation, with noise specifically treated as Gaussian in nature, Eq. 1 takes the form of a Fokker–Planck equation.
Fokker–Planck equations have been applied previously to low-dimensional biological processes, such as differentiation with a handful of genes (20) or a one-parameter model of cell cycle progression (13). Here, we apply them to high-dimensional data. Although Fokker–Planck descriptions are necessarily approximations, their emergence from first-principles descriptions of transcriptional dynamics in terms of chemical master equations (21), and their ubiquity in describing chemical reaction systems (22), help justify their use instead of the more general form of Eq. 1. Specifically, the generalized Fokker–Planck approximation takes the form of Eq. 1 with velocity field, , where the first term is a deterministic average velocity field, and the second term is a stochastic component of the velocity that follows Fickian diffusion with a diffusion matrix (Fig. 2). We assume here that is isotropic and invariant across gene expression space. Although more complex forms of diffusion could better reflect reality, we propose that this simplification for is sufficient to gain predictive power from single-cell data in the absence of specific data to constrain it otherwise.
The resulting population balance equation is thus as follows:
| [2] |
Eq. 2 explains the rate of change of cell density () as a sum of three processes: (i) stochastic gene expression, , which causes cells to diffuse out of high-density regions in gene expression space; (ii) convergences (and divergences) of the mean velocity field, , which cause cells to accumulate (or escape) from certain gene expression states over time; and (iii) as before, cell entry and exit rates, , will cause certain cell states to gain or lose cells over time.
Potential landscapes define a minimal model for dynamic inference.
Our second assumption is that there are no rotational (e.g., oscillatory) gene expression dynamics. Although oscillations certainly do exist in reality—for example, the cell cycle—it is impossible to establish their existence from static snapshots alone. One is therefore forced to make an a priori assumption about their existence. In cases where oscillations are orthogonal to the process of interest, they may be safe to ignore. We systematically investigate the cost of ignoring oscillations through several simulations and identify circumstances where it has a large impact. Our analysis of scRNA-seq data in a later section suggests that useful predictions can be made despite this assumption.
In the Fokker–Planck formalism, the presumed absence of oscillations implies that the velocity field is the gradient of a potential function (i.e., . The potential would define a landscape in gene expression space, with cells flowing toward minima in the landscape, akin to energy landscapes in descriptions of physical systems. Applying the potential landscape assumptions to Eq. 2 gives rise to the simplified diffusion-drift equation below, where the potential is represented by a function :
| [3] |
A recipe for dynamic inference from first principles.
Eq. 3 represents our best attempt to relate an observed density of cell states () to an underlying set of dynamical rules, now represented by a potential landscape () rather than the exact velocity field v. Crucially, we have, in these first few sections of Results, explained why the net cell velocity v is inherently unknowable from snapshot data, clarified why the description provided by a potential field F is the best that any method could propose without further knowledge about the system, and identified critical fitting parameters (, , and ), which are not revealed by single-cell snapshot measurements but are required for determining aspects of the dynamics such as temporal ordering of states and fate probabilities during differentiation. By starting from first principles, it becomes clear that these requirements are not limited to any particular algorithm; they affect any method one might develop for trajectory inference.
The challenge now is to develop a practical approach that relates the fitting parameters , , and to dynamic predictions through Eq. 3. In the following, we focus on steady-state systems where , and use prior literature to estimate . We report results for a range of values of . Building on the work here, more elaborate approaches could be taken, for example determining R from direct measurements of cell division and cell loss rates or integrating data from multiple time points to estimate , thus generalizing to non–steady-state systems.
Reducing to Practice: Solving the Population Balance Equation with Spectral Graph Theory.
Equipped with single-cell measurements and estimates for each fitting parameter, we now face two practical problems in using of Eq. 3 to infer cell dynamics: the first is that Eq. 3 is generally high dimensional (reflecting the number of independent gene programs acting in a cell), but numerical solvers cannot solve diffusion equations on more than perhaps 10 dimensions (23). Indeed, until now, studies that used diffusion-drift equations such as Eq. 3 to model trajectories (10, 13, 20) were limited to one or two dimensions, far below the intrinsic dimensionality of typical scRNA-seq data (24). The second practical problem is that we do not in fact measure the cell density c: we only sample a finite number of cells from this density in an experiment.
Overcoming these problems represents the main technical contribution of this paper. We drew on a recent theorem by Ting et al. (25) in spectral graph theory to extend diffusion-drift modeling to arbitrarily high dimension. The core technical insight is that an asymptotically exact solution to Eq. 3 can be calculated on a nearest-neighbor graph constructed with sampled cells as nodes. Our approach, which we call PBA, actually improves in accuracy as dimensionality increases, plateauing at the underlying manifold dimension of the data itself. We thus avoid conclusions based on low-dimensional simplifications of data, which may introduce distortions into the analysis. In practice, some intermediate degree of dimensionality reduction could still be useful (say, to tens or hundreds of dimensions), a point elaborated in Discussion. SI Appendix provides technical proofs and an efficient framework for PBA in any high-dimensional system.
The inputs to PBA are a list of sampled cell states , an estimate for the net rate of cell accumulation or loss at each state , and an estimate for the diffusion parameter . We are assuming steady state, so . The output of PBA is a discrete probabilistic process, that is, a Markov chain that describes the transition probabilities between the states . The analysis is asymptotically exact in the sense that—if a potential exists and the estimates for and are correct—the inferred Markov chain will converge to the underlying continuous dynamical process in the limit of sampling many cells () and high manifold dimension of the data (SI Appendix, Theory Supplement, Theorem 4). We note that the requirement for many cells is to reduce the variance of PBA estimates, and the requirement for high dimension is to reduce the bias.
PBA computes the transition probabilities of the Markov chain using a simple algorithm, which at its core involves a single matrix inversion. Briefly:
-
i)
Construct a k-nearest-neighbor (knn) graph G, with one node at each position extending edges to the k nearest nodes in its local neighborhood. Calculate the graph Laplacian of G, denoted L.
-
ii)
Compute a potential , where is the pseudoinverse of .
-
iii)
To each edge , assign the transition probability
With the Markov chain generating Eq. 3 available, it is possible to calculate the temporal ordering of states, and the fate biases of progenitor cells in a differentiation process, by integrating across many trajectories (Fig. 2). These calculations are simple, generally requiring a single matrix inversion. Temporal orderings can be calculated from mean first-passage times; fate biases can be calculated as absorbing fate probabilities of the Markov chain, starting from each observed state. Specific formulas are provided in SI Appendix, Theory Supplement, section 3. Confidence intervals on inferred mean first-passage times and fate biases, and their sensitivity to parameter choices, can be estimated by bootstrapping. Code for implementing these and other aspects of PBA is available online at https://github.com/AllonKleinLab/PBA.
PBA Accurately Reconstructs Dynamics of Simulated Differentiation Processes.
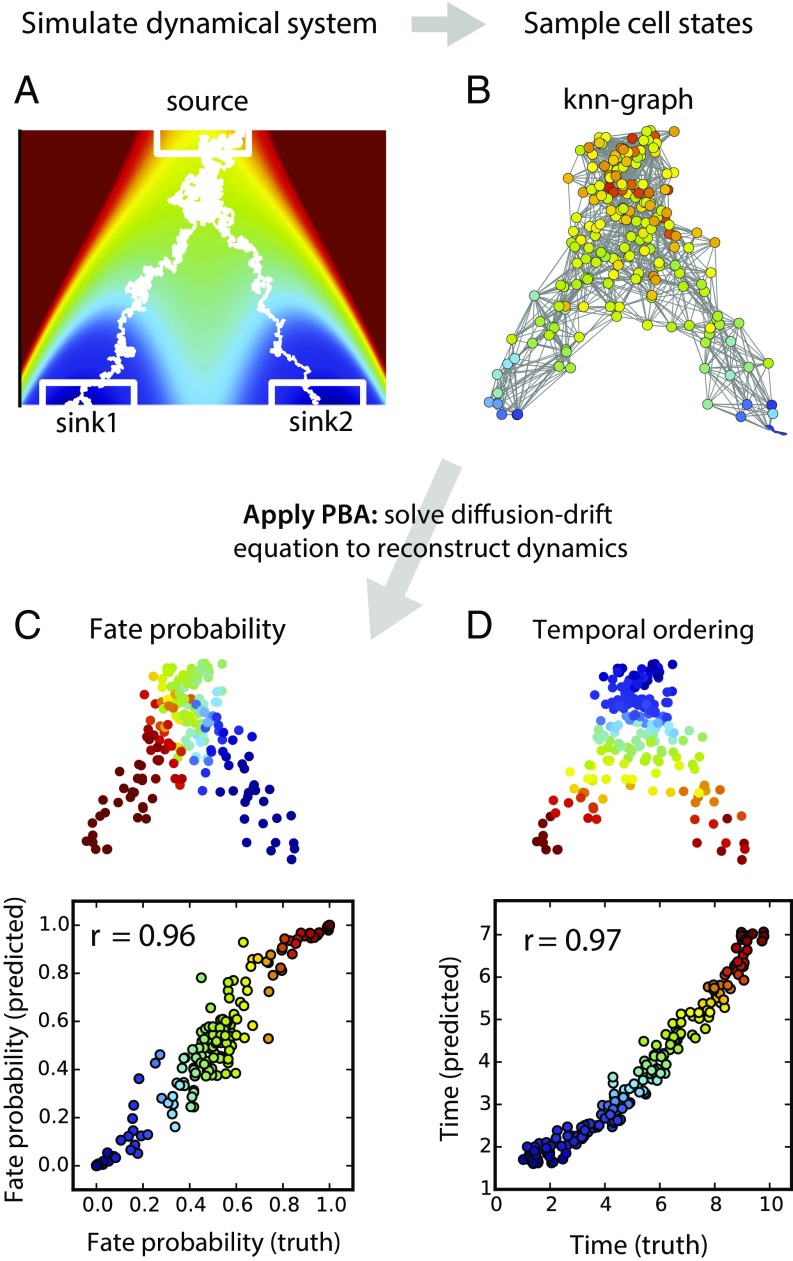
We tested PBA on a sequence of simulations, first using an explicit model of diffusion-drift process, and then moving on to direct simulations of gene regulatory networks (GRNs). In the first simulation (Fig. 3 and SI Appendix, Fig. S1), cells drift down a bifurcating potential landscape into two output lineages, defined formally as absorbing states in the dynamical system. Cell trajectories span a 50-dimensional gene expression space (two of which are shown in Fig. 3A). With 200 cells sampled from this simulated system (Fig. 3B), PBA predicted dynamical properties of the measured cells, including (i) their fate probabilities, defined as the probabilities of reaching either of the absorbing states; and (ii) their temporal ordering, defined as the mean first-passage time to reach them from the simulation starting point. PBA made very accurate predictions (Pearson correlation, ρ > 0.96; Fig. 1 C and D) if provided with correct estimates of proliferation, loss, and stochasticity (parameters R and D). Estimates of temporal ordering remained accurate with even fivefold error in these parameters (ρ > 0.93), but predictions of fate bias degraded (ρ > 0.77; SI Appendix, Fig. S2 A–D). Thus, even very rough knowledge of the entry and exit points in gene expression space is sufficient to generate a reasonable and quantitative description of the dynamics. Interestingly, PBA also remained predictive in the presence of implanted oscillations (SI Appendix, Fig. S3; fate probability ρ > 0.9; temporal ordering ρ > 0.8). In addition, the simulations confirmed the theoretical prediction that inference quality improves as the number of noisy genes (dimensions) increases, and as more cells are sampled: maximum accuracy in this simple case was reached after ∼100 cells and 20 dimensions (SI Appendix, Fig. S2 E–G). These simulations showcase the ability of PBA not just to describe continuum trajectories, but additionally to predict cell dynamics and by extension cell fate. At the same time, they show the fragility of dynamic inference to information not available from static snapshots alone.
Fig. 3.
Demonstration of PBA on a simulated high-dimensional differentiation process. (A) Cells emerge from a proliferating bipotent state (source) and differentiate into one of two fates (sinks 1 and 2) in a high-dimensional gene expression space, with two dimensions shown. Heat map colors show a potential field containing the cell trajectories. Example trajectories are shown in white. (B) Static expression profiles sampled asynchronously through differentiation serve as the input to PBA, which reconstructs trajectories and accurately predicts future fate probabilities (C) and timing (D) of each cell.
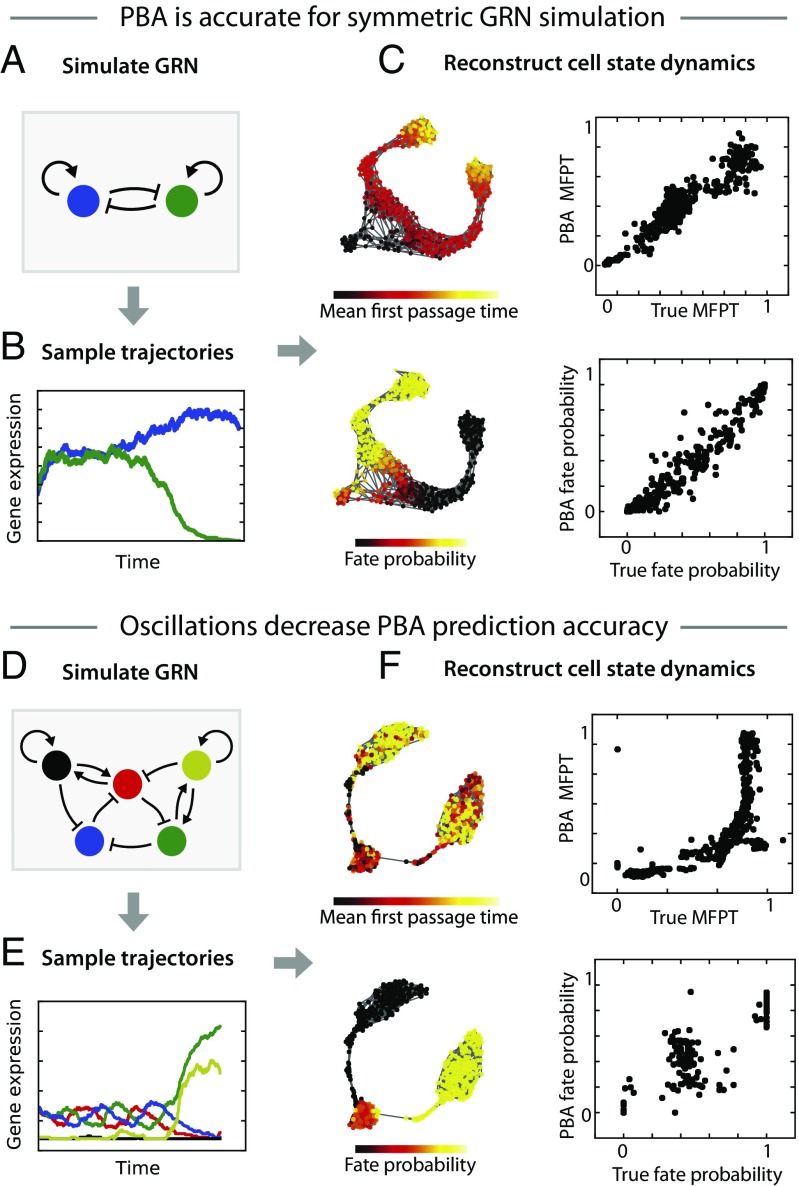
Having demonstrated the accuracy of PBA on an explicit model of a diffusion-drift process, we next tested its performance on gene expression dynamics arising from GRNs (Fig. 4). As before, we simulated cell trajectories, obtained a static snapshot of cell states, and supplied PBA with this static snapshot as well as the parameter encoding the location of entry and exit points. We began with a simple GRN representing a bistable switch, in which two genes repress each other and activate themselves (Fig. 4A). Simulated trajectories from this GRN begin with both genes at an intermediate expression level, but quickly progress to a state where one gene dominates the other (Fig. 4B). In addition to the two genes of the GRN, we included 48 uncorrelated noisy dimensions. With 500 cells sampled from this process, PBA predicted cell fate bias (absorbing state probabilities) and temporal ordering (mean first passage time from the start point) very well (r > 0.98 for fate bias and r > 0.89 for ordering; Fig. 4C), although the precise accuracy depended on the assumed level of diffusion (SI Appendix, Fig. S4; the values that gave the best results were used for Fig. 4).
Fig. 4.
Test of PBA on cell states from a simulated gene regulatory network (GRN). (A) We tested PBA on cell states sampled from a GRN composed of two genes that repress each other and activate themselves. (B) Trajectories from this GRN begin in an unstable state with both genes at an intermediate level and progress to a stable state with one gene dominating. (C) PBA was applied to a steady-state snapshot of cells from this process (shown on Left using a force-directed layout generated by SPRING). The resulting predictions for temporal ordering (Top) and fate probability (Bottom) are compared with ground truth. (D) To challenge PBA, we defined a GRN with two stable states that compete with semistable limit cycle. (E) Trajectories from the GRN begin with all genes oscillating and then progress to stable state where one pair of genes dominates. (F) PBA was applied to a steady-state snapshot of cells from this process, with predictions for ordering (Top) and fate probability (Bottom) compared with ground truth. In C and F, the mean first-passage time (MFPT) is defined as the mean simulation time taken to enter the neighborhood of each sampled state; the “fate probability” equals the fraction of simulations starting from each sampled state that reach one of the two absorbing states.
PBA assumes the absence of oscillations in gene expression space. Therefore, it is unclear how well PBA can infer cell trajectories that result from GRNs with oscillatory dynamics. We simulated an oscillatory GRN in the form of a “repressilator” circuit (26) with the addition of positive-feedback loops that create two “escape routes” leading to alternative stable fixed points of the dynamics (Fig. 4D). Simulated trajectories from this GRN begin with all genes oscillating, followed by a stochastic exit from the oscillation when one of the genes surpasses a threshold level (Fig. 4E). With 500 cells sampled from this process, PBA was significantly less accurate than for the previous simulations (Fig. 4F). Although PBA correctly identified which cells were fully committed to the two “escape routes,” it was entirely unable to resolve the fate biases of cells in the uncommitted oscillatory state. PBA also made poor predictions of mean first-passage time, underestimating the amount of time that cells spent in the oscillatory state. Unsurprisingly, when the assumptions of PBA are strongly violated, its prediction accuracy suffers.
PBA Predictions of Fate Bias in Hematopoiesis Reconcile Past Experiments.
To test PBA on experimental data from real biological systems, we made use of single-cell gene expression measurements of 3,803 adult mouse HPCs from another study by our groups (ref. 16; data at Gene Expression Omnibus, accession no. GSE89754).
HPCs reside in the bone marrow and participate in the steady-state production of blood and immune cells through a balance of self-renewal and multilineage differentiation. Descriptions of HPC differentiation invoke a tree structure, with gradual lineage-restriction at branch points. However, the precise tree remains controversial (27, 28), since existing measurements of fate potential reflect a patchwork of defined HPC subsets that may have internal heterogeneity (29) and provide only incomplete coverage of the full HPC pool. We asked whether PBA applied to single-cell RNA profiling of HPCs could generate predictions consistent with experimental data, and possibly help resolve these controversies by providing a global map of approximate cell fate biases of HPCs.
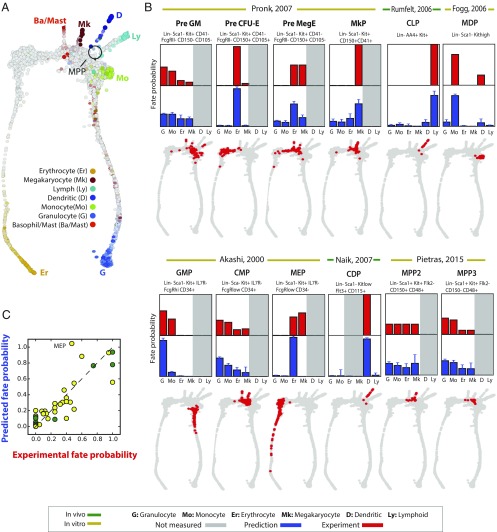
The single-cell expression measurements—derived from mouse bone marrow cells expressing the progenitor marker Kit—represent a mixture of multipotent progenitors as well as cells expressing lineage commitment markers at various stages of maturity. Since PBA depends on analyzing a k-nearest-neighbor (knn) graph of the cells, we developed an interactive knn visualization tool for single-cell data exploration, called SPRING (https://kleintools.hms.harvard.edu/tools/spring.html; ref. 30). The SPRING plot (Fig. 5A) revealed a continuum of gene expression states that pinches off at different points to form several downstream lineages. Known marker genes (SI Appendix, Table S1) identified the graph endpoints as monocytic (Mo), granulocytic (G), dendritic (D), lymphoid (Ly), megakaryocytic (Mk), erythroid (Er), and basophil or mast (Ba/Mast) cell progenitors (SI Appendix, Fig. S5); we also identified cells in the graph expressing hematopoietic stem cell markers. The lengths of the branches reflect the timing of Kit down-regulation and the abundance of each lineage.
Fig. 5.
Population balance analysis reproduces known fate probabilities of hematopoietic progenitor cell (HPC) subpopulations from single-cell data. (A) Single-cell profiles of 3,803 Kit+ HPCs reveal a continuum of gene expression states that pinches off at different points to form seven downstream lineages. Cells in this map are colored by marker gene expression and are laid out as a k-nearest-neighbor (knn) graph using SPRING, an interactive force-directed layout software. (B) PBA is applied to HPCs, and the predicted fate probabilities (blue bars) are compared with those observed experimentally (red bars) for reported HPC subpopulations (red dots on gray HPC map; identified using transcriptional similarity to existing microarray profiles for each reported subpopulation). Cell fates predicted by PBA but not measured experimentally are shaded gray. Error bars represent 90% confidence intervals across 120 parameter combinations for the PBA pipeline. (C) Summary of comparisons made in B; green points, in vivo measurements; yellow points, in vitro measurements.
For steady-state systems, PBA requires as fitting parameters an estimate of the diffusion strength and the net rates of cell entry and exit at each gene expression state (. We estimated R using prior literature (Materials and Methods) and tested a range of values of D, with the range chosen to ensure that the number of cells predicted to be multipotent by PBA would lie within bounds established in the literature. All results that follow hold over the physiological range of PBA parameter values (SI Appendix, Fig. S6).
Applied to single-cell measurements, for the range of fitting parameters, PBA estimated seven fate probabilities for each cell, defined formally as the probabilities that a trajectory initiated at each cell would terminate among the most mature cells in each of the seven lineages (Materials and Methods). We compared PBA results to fate probabilities reported for subsets of the HPC hierarchy, which have been previously defined by cell surface marker expression, and transcriptionally profiled using microarrays. To carry out the comparison, we identified the cells in our data that were most similar to each subset using their published microarray profiles (Fig. 5B, red dots), and we then computed the average PBA-predicted fate probabilities across cells in each subset. Remarkably, for a panel of 12 progenitor cell populations from six previous papers (31–36) (SI Appendix, Table S2) the PBA-predicted fate outcomes (Fig. 5B, bar charts) closely matched fate probabilities measured in functional assays (defined as the proportion of clonogenic colonies containing a given terminal cell type; SI Appendix, Fig. S5). The main qualitative disagreement between PBA predictions and experiment was in the behavior of Lin−Sca1−Kit+IL7R−FcgRlowCD34− HPCs, previously defined as megakaryocyte-erythroid precursors (31). Our prediction was that these cells should lack megakaryocyte potential, which is indeed consistent with recent studies (27, 29, 37). Excluding these cells, our predicted fate probabilities matched experimental data with correlation ρ = 0.91 (Fig. 5C). In another study (16), we test several novel predictions in hematopoiesis emerging from PBA.
Discussion
In developing PBA, we hoped that an algorithm with clear assumptions would help to clarify the ways in which data analysis might mislead us about the underlying biology. More practically, we hoped that the algorithm would suggest how to best design experiments to extract dynamic information from static measurements, and how to visualize single-cell data to preserve aspects of the true dynamics. We discuss a number of points that follow from our analysis, along with a note about the technical underpinnings of PBA.
Experimental Design for Trajectory Reconstruction from Static Snapshot Measurements.
We have shown that accurate dynamic inference requires knowledge of the density of cells in high-dimensional state space, as well as the rates of cell entry and exit across the density. These requirements immediately suggest a set of principles for experimental design to optimize dynamic inference. First, to minimize distortions in the cell density in gene expression space, it is useful to profile a single, broad population, and to avoid merging data from multiple subpopulations fractionated in advance. Where possible, one should consider testing for uniform cell-sampling probability across states. Second, if cells of interest are sorted before analysis, it is best to minimize the number of sorting gates and enrichment steps, since each introduces an additional term to the entry/exit rates and subsequently a risk of distortion to the inferred dynamics. The HPC dataset analyzed in this paper was well suited for trajectory reconstruction because it consisted of a single population, enriched using a single marker (Kit). This contrasts with previous scRNA-seq datasets of hematopoietic progenitors that included a composite of many subpopulations (38) or used complex FACS gates to exclude early progenitors (29).
How PBA Could Go Wrong.
To constrain a unique solution for trajectory reconstruction, PBA makes several strong assumptions, such as memoryless dynamics with respect to measured states, the absence of oscillations in gene expression space, and an adequately “large” number of sampled cells.
Oscillations.
In SI Appendix, Fig. S3, we show that implanting oscillations into the bistable dynamical system shown in Fig. 3 does not significantly affect prediction accuracy. On the other hand, when we tested PBA on a GRN whose main fate decision-making circuit is driven by oscillations (shown in Fig. 4), accuracy declined. In cases where oscillatory dynamics strongly influence cell fate (e.g., refs. 39 and 40), single-cell snapshot data could therefore be misleading, and methods that infer dynamics from continua of cell states, such as PBA, may be ill suited. However, the simulation results suggest that oscillations may be somewhat benign unless they are the primary driver of cell fate decision making. The agreement of prediction to fate commitment assays when we applied PBA to single-cell profiles of HPCs suggests that, despite some sensitivity to assumptions, accurate inference is possible for complex differentiation systems.
Memory.
In general, the extent to which cell trajectories are defined by the current state of each cell (i.e., Markovian) is unclear. Non-Markovian dynamics could arise from “hidden variables,” defined as stable properties of cell state that are not observed by scRNA-seq but still impact a cell’s behavior over time. Hidden variables could include chromatin state, posttranslational modifications, cellular localization of proteins, metabolic state, and cellular microenvironment. It is also possible that these properties percolate to some aspect of cell state that is observed, for example, effecting a change in the expression of at least one gene measured by RNA-seq. By altering the observed state, such variables would thus not be hidden. For example, chromatin state exists in constant dialogue with transcriptional state and could be well reflected in mRNA content.
Statistical error.
The exact convergence of PBA is proved in the limit of high dimension and many cells, but it may be difficult to discern whether it is statistically well powered for any given dataset. Calculating statistical power is hampered by a lack of formal convergence results for the graph operator at the heart of PBA (25) and by the fact that the actual outputs of PBA (e.g., fate probabilities) are complex functions of this operator. Since a knn graph is not the only possible construction that could be considered, it is possible that other graph-construction approaches may converge faster and would be preferred for particular densities c(x). In practice, statistical power can be estimated through bootstrapping, for example, by repeating the analysis for down-sampled datasets or scanning over in parameters, including the number of neighbors, k.
Normalization, Principal-Components Analysis, and Other Coordinate Transformations.
In this study, we described a framework for modeling the movement of cells in a space of gene expression, the units of which might be considered to be (dimensionless) counts of individual molecules. How then should one think about routine transformations of gene expression coordinates performed during practical low-level processing of single-cell expression data, such as transformation into logarithmic space, or dimensionality reduction by principal-components analysis? Here, the asymptotic analysis of PBA makes clear that coordinate transformations may not be important when cells are densely sampled, as they should leave the empirical single-cell graph topology unchanged. The equations of PBA are indeed invariant to coordinate transformations, with the exception of the diffusion operator, which is isotropic and spatially homogeneous but may not remain so upon coordinate system transformation. Since our assumption of isotropic and invariant diffusion is already an approximation, it does not support a priori one coordinate system over another. For small and noisy datasets, the choice of coordinate system could affect conclusions, however, and it is probably best to use the coordinate system that provides the richest view of single-cell population structure, or that agrees most with known biology.
A related question is whether technical noise in gene expression measurements can be distinguished from biological effects. For scRNA-seq methods that use techniques such as linear amplification and unique molecular identifiers, technical noise can mostly be attributed to undersampling of the mRNAs in a cell, and therefore follows a predictable Poisson distribution determined by the underlying gene expression and technical sampling rate. Distinguishing technical noise using known features of this distribution would be an area for improvement.
Fundamental Limits on the Inference of Gene Regulatory Networks.
One promise of single-cell expression measurements is their possible use for reconstructing GRNs (2, 11). However, since any GRN model entails specific hypotheses about the gene expression trajectories of cells, efforts to infer GRNs from single-cell data must also confront the limits of knowledge identified in our framework. In particular, GRN inference may benefit from an explicit consideration of cell entry and exit rates (embodied by R) and the rate of change in the cell density (), as well as acknowledging the inability to distinguish oscillations from fluctuations.
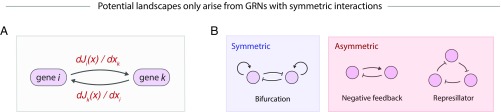
Indeed, the inability to detect oscillations in single-cell data, embodied in our framework by the use of a potential landscape, suggests severe limits on the types of underlying gene regulatory relationships that can be modeled. In fact, potential landscapes can only emerge from GRNs with strictly symmetric interactions, meaning every “arrow” between genes has an equal and opposite partner. This result follows from observing that the arrows in a GRN describe the influence of gene on gene , which is given by (Fig. 6A), where is the deterministic component of average cell velocities (Eq. 2). The assumption of a potential landscape (i.e., then imposes symmetry on the GRN because = . Although a few well-known GRN motifs follow this symmetry rule—such as the “bistable switch” resulting from the mutual inhibition of two genes—many others do not, such as negative-feedback loops and oscillators (Fig. 6B). Potential landscapes are frequently invoked to explain gene expression dynamics (10, 41, 42), and we have shown them to be useful for predicting HPC fate outcomes in the context of PBA. It seems paradoxical that a tool that provides realistic phenomenological descriptions of gene expression dynamics reflects an entirely unrealistic picture for the underlying gene regulatory mechanisms. Resolving this paradox is an interesting direction for future work.
Fig. 6.
Potential landscapes arise from symmetric GRNs. (A) Inferences about the deterministic component of average cell velocities, J(x), can be interpreted as statements about an underlying gene regulatory network (GRN), with dJi/dxj giving the sensitivity of the dynamics of gene i to the expression level of gene j. (B) The existence of a potential landscape-driven dynamics implies that the underlying GRN has strictly symmetric interactions, which allows for some common gene regulatory motifs but rules out many others.
How Should We Visualize Single-Cell Data?
At its core, the PBA algorithm performs dynamic inference by solving a diffusion-drift equation in high dimensions. This computation relies on a 2011 result in spectral graph theory by Ting et al. (25) that describes the limiting behavior of k-nearest-neighbor graph Laplacians on sampled point clouds. Interestingly, several recent studies (8, 15, 43) have developed k-nearest neighbor graph-based representations of single-cell data, and others have suggested embedding cells in diffusion maps (24, 44) on the basis of other similarity kernels. It has been unclear, until now, how to evaluate which of these different methods provides the most useful description of cell dynamics. Our technical results (SI Appendix, Theorems 1–4 in SI Appendix, Theory Supplement) confirm that certain graph representations provide an asymptotically exact description of the cell state manifold on which dynamics unfold, suggesting them to be useful techniques for visualizing single-cell datasets. Therefore, PBA formally links dynamical modeling to choices of single-cell data visualization.
Materials and Methods
A formal derivation of PBA is provided with PBA pseudocode in SI Appendix, Theory Supplement. A PBA implementation in Python is made available at https://github.com/AllonKleinLab/PBA and was implemented as described in SI Appendix, SI Methods, section 1. PBA was then applied to simulated diffusion-drift processes, simulated GRNs, and to empirical data on HPCs: numerical simulations of diffusion-drift processes are detailed in SI Appendix, SI Methods, section 2; PBA application to these simulations in SI Appendix, SI Methods, section 3; the effect of gene oscillations on PBA predictions in SI Appendix, SI Methods, section 4. GRN simulations and corresponding applications of PBA are detailed in SI Appendix, SI Methods, section 5. For application to bone marrow data, data processing and normalization of scRNA-seq data were carried out as described in SI Appendix, SI Methods, section 5; and determination of the PBA parameters R and D for empirical PBA was carried out as described in SI Appendix, SI Methods, sections 7 and 8. Comparisons of PBA-predicted fate probabilities to published datasets were carried out as described in SI Appendix, SI Methods, section 9.
Supplementary Material
Acknowledgments
We thank Kyogo Kawaguchi, Andreas Hilfinger, Jeremy Gunawardena, Johan Paulsson, and Rebecca Ward for their helpful feedback and comments. This work was funded by a Burroughs Wellcome Fund Career Awards at the Scientific Interface award and an Edward J. Mallinckrodt Foundation grant (to A.M.K.), and by Leukemia and Lymphoma Society Scholar Award 1728-13 and Grants R01DK100915 and R01099281 (to M.S.). S.W. and C.W. are supported by NIH Training Grant 5T32GM080177-07.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1714723115/-/DCSupplemental.
References
- 1.Linnarsson S, Teichmann SA. Single-cell genomics: Coming of age. Genome Biol. 2016;17:97. doi: 10.1186/s13059-016-0960-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Klein AM, et al. Droplet barcoding for single-cell transcriptomics applied to embryonic stem cells. Cell. 2015;161:1187–1201. doi: 10.1016/j.cell.2015.04.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Macosko EZ, et al. Highly parallel genome-wide expression profiling of individual cells using nanoliter droplets. Cell. 2015;161:1202–1214. doi: 10.1016/j.cell.2015.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Buenrostro JD, et al. Single-cell chromatin accessibility reveals principles of regulatory variation. Nature. 2015;523:486–490. doi: 10.1038/nature14590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lombard-Banek C, Moody SA, Nemes P. Single-cell mass spectrometry for discovery proteomics: Quantifying translational cell heterogeneity in the 16-cell frog (Xenopus) embryo. Angew Chem Int Ed Engl. 2016;55:2454–2458. doi: 10.1002/anie.201510411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bendall SC, et al. Single-cell mass cytometry of differential immune and drug responses across a human hematopoietic continuum. Science. 2011;332:687–696. doi: 10.1126/science.1198704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Stevens TJ, et al. 3D structures of individual mammalian genomes studied by single-cell Hi-C. Nature. 2017;544:59–64. doi: 10.1038/nature21429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bendall SC, et al. Single-cell trajectory detection uncovers progression and regulatory coordination in human B cell development. Cell. 2014;157:714–725. doi: 10.1016/j.cell.2014.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Macaulay IC, et al. Single-cell RNA-sequencing reveals a continuous spectrum of differentiation in hematopoietic cells. Cell Rep. 2016;14:966–977. doi: 10.1016/j.celrep.2015.12.082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Marco E, et al. Bifurcation analysis of single-cell gene expression data reveals epigenetic landscape. Proc Natl Acad Sci USA. 2014;111:E5643–E5650. doi: 10.1073/pnas.1408993111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Moignard V, et al. Decoding the regulatory network of early blood development from single-cell gene expression measurements. Nat Biotechnol. 2015;33:269–276. doi: 10.1038/nbt.3154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Shin J, et al. Single-cell RNA-seq with waterfall reveals molecular cascades underlying adult neurogenesis. Cell Stem Cell. 2015;17:360–372. doi: 10.1016/j.stem.2015.07.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kafri R, et al. Dynamics extracted from fixed cells reveal feedback linking cell growth to cell cycle. Nature. 2013;494:480–483. doi: 10.1038/nature11897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gaublomme JT, et al. Single-cell genomics unveils critical regulators of Th17 cell pathogenicity. Cell. 2015;163:1400–1412. doi: 10.1016/j.cell.2015.11.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Setty M, et al. Wishbone identifies bifurcating developmental trajectories from single-cell data. Nat Biotechnol. 2016;34:637–645. doi: 10.1038/nbt.3569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Tusi BK, et al. Population snapshots predict early haematopoietic and erythroid hierarchies. Nature. doi: 10.1038/nature25741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Andrews SS, Dinh T, Arkin AP. Stochastic models of biological processes. In: Meyers RA, editor. Encyclopedia of Complexity and Systems Science. Springer; New York: 2009. pp. 8730–8749. [Google Scholar]
- 18.Chandrasekhar S. Stochastic problems in physics and astronomy. Rev Mod Phys. 1943;15:1–89. [Google Scholar]
- 19.Ramkrishna D. Population Balances. Academic; San Diego: 2000. Introduction; pp. 1–6. [Google Scholar]
- 20.Morris R, Sancho-Martinez I, Sharpee TO, Izpisua Belmonte JC. Mathematical approaches to modeling development and reprogramming. Proc Natl Acad Sci USA. 2014;111:5076–5082. doi: 10.1073/pnas.1317150111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gillespie DT. Stochastic simulation of chemical kinetics. Annu Rev Phys Chem. 2007;58:35–55. doi: 10.1146/annurev.physchem.58.032806.104637. [DOI] [PubMed] [Google Scholar]
- 22.Grima R, Thomas P, Straube AV. How accurate are the nonlinear chemical Fokker–Planck and chemical Langevin equations? J Chem Phys. 2011;135:084103. doi: 10.1063/1.3625958. [DOI] [PubMed] [Google Scholar]
- 23.Sun Y, Kumar M. Numerical solution of high dimensional stationary Fokker–Planck equations via tensor decomposition and Chebyshev spectral differentiation. Comput Math Appl. 2014;67:1960–1977. [Google Scholar]
- 24.Angerer P, et al. destiny: Diffusion maps for large-scale single-cell data in R. Bioinformatics. 2015;32:1241–1243. doi: 10.1093/bioinformatics/btv715. [DOI] [PubMed] [Google Scholar]
- 25.Ting D, Huang L, Jordan M. 2011. An analysis of the convergence of graph Laplacians. arXiv:1101.5435v1.
- 26.Elowitz MB, Leibler S. A synthetic oscillatory network of transcriptional regulators. Nature. 2000;403:335–338. doi: 10.1038/35002125. [DOI] [PubMed] [Google Scholar]
- 27.Notta F, et al. Distinct routes of lineage development reshape the human blood hierarchy across ontogeny. Science. 2016;351:aab2116. doi: 10.1126/science.aab2116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ema H, Morita Y, Suda T. Heterogeneity and hierarchy of hematopoietic stem cells. Exp Hematol. 2014;42:74–82.e2. doi: 10.1016/j.exphem.2013.11.004. [DOI] [PubMed] [Google Scholar]
- 29.Paul F, et al. Transcriptional heterogeneity and lineage commitment in myeloid progenitors. Cell. 2015;163:1663–1677. doi: 10.1016/j.cell.2015.11.013. [DOI] [PubMed] [Google Scholar]
- 30.Weinreb C, Wolock S, Klein A. SPRING: A kinetic interface for visualizing high dimensional single-cell expression data. Bioinformatics. 2017 doi: 10.1093/bioinformatics/btx792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Akashi K, Traver D, Miyamoto T, Weissman IL. A clonogenic common myeloid progenitor that gives rise to all myeloid lineages. Nature. 2000;404:193–197. doi: 10.1038/35004599. [DOI] [PubMed] [Google Scholar]
- 32.Fogg DK, et al. A clonogenic bone marrow progenitor specific for macrophages and dendritic cells. Science. 2006;311:83–87. doi: 10.1126/science.1117729. [DOI] [PubMed] [Google Scholar]
- 33.Naik SH, et al. Development of plasmacytoid and conventional dendritic cell subtypes from single precursor cells derived in vitro and in vivo. Nat Immunol. 2007;8:1217–1226. doi: 10.1038/ni1522. [DOI] [PubMed] [Google Scholar]
- 34.Pietras EM, et al. Functionally distinct subsets of lineage-biased multipotent progenitors control blood production in normal and regenerative conditions. Cell Stem Cell. 2015;17:35–46. doi: 10.1016/j.stem.2015.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Pronk CJ, et al. Elucidation of the phenotypic, functional, and molecular topography of a myeloerythroid progenitor cell hierarchy. Cell Stem Cell. 2007;1:428–442. doi: 10.1016/j.stem.2007.07.005. [DOI] [PubMed] [Google Scholar]
- 36.Rumfelt LL, Zhou Y, Rowley BM, Shinton SA, Hardy RR. Lineage specification and plasticity in CD19− early B cell precursors. J Exp Med. 2006;203:675–687. doi: 10.1084/jem.20052444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Psaila B, et al. Single-cell profiling of human megakaryocyte-erythroid progenitors identifies distinct megakaryocyte and erythroid differentiation pathways. Genome Biol. 2016;17:83. doi: 10.1186/s13059-016-0939-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Nestorowa S, et al. A single-cell resolution map of mouse hematopoietic stem and progenitor cell differentiation. Blood. 2016;128:e20–e31. doi: 10.1182/blood-2016-05-716480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Kueh HY, Champhekar A, Nutt SL, Elowitz MB, Rothenberg EV. Positive feedback between PU.1 and the cell cycle controls myeloid differentiation. Science. 2013;341:670–673, and erratum (2013) 342:311. doi: 10.1126/science.1240831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Pauklin S, Vallier L. The cell-cycle state of stem cells determines cell fate propensity. Cell. 2014;156:1338. doi: 10.1016/j.cell.2014.02.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Wang J, Xu L, Wang E, Huang S. The potential landscape of genetic circuits imposes the arrow of time in stem cell differentiation. Biophys J. 2010;99:29–39. doi: 10.1016/j.bpj.2010.03.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Moris N, Pina C, Arias AM. Transition states and cell fate decisions in epigenetic landscapes. Nat Rev Genet. 2016;17:693–703. doi: 10.1038/nrg.2016.98. [DOI] [PubMed] [Google Scholar]
- 43.Samusik N, Good Z, Spitzer MH, Davis KL, Nolan GP. Automated mapping of phenotype space with single-cell data. Nat Methods. 2016;13:493–496. doi: 10.1038/nmeth.3863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Coifman RR, et al. Geometric diffusions as a tool for harmonic analysis and structure definition of data: Diffusion maps. Proc Natl Acad Sci USA. 2005;102:7426–7431. doi: 10.1073/pnas.0500334102. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.