Significance
This paper considers the experimental evidence for and against the two major current models for protein folding, the theoretically hypothesized many-pathway model, and the experiment-based defined-pathway model. The questions of how proteins fold, why they fold in that way, and how the folding pathway of each protein is encoded in its sequence and structure have fundamental significance for protein structure and design, folding and misfolding, regulation and function, clinical problems, and industrial applications. The present analysis attempts to distinguish the models and answer these questions.
Keywords: protein folding, foldons, energy landscape theory
Abstract
We consider the differences between the many-pathway protein folding model derived from theoretical energy landscape considerations and the defined-pathway model derived from experiment. A basic tenet of the energy landscape model is that proteins fold through many heterogeneous pathways by way of amino acid-level dynamics biased toward selecting native-like interactions. The many pathways imagined in the model are not observed in the structure-formation stage of folding by experiments that would have found them, but they have now been detected and characterized for one protein in the initial prenucleation stage. Analysis presented here shows that these many microscopic trajectories are not distinct in any functionally significant way, and they have neither the structural information nor the biased energetics needed to select native vs. nonnative interactions during folding. The opposed defined-pathway model stems from experimental results that show that proteins are assemblies of small cooperative units called foldons and that a number of proteins fold in a reproducible pathway one foldon unit at a time. Thus, the same foldon interactions that encode the native structure of any given protein also naturally encode its particular foldon-based folding pathway, and they collectively sum to produce the energy bias toward native interactions that is necessary for efficient folding. Available information suggests that quantized native structure and stepwise folding coevolved in ancient repeat proteins and were retained as a functional pair due to their utility for solving the difficult protein folding problem.
Protein folding is among the most important reactions in all of biology. However, 50 y after C. B. Anfinsen showed that proteins can fold spontaneously without outside help (1, 2), and despite the intensive work of thousands of researchers leading to more than five publications per day in the current literature, there is still no general agreement on the most primary questions (3–5). How do proteins fold? Why do they fold in that way? How is the course of folding encoded in a 1D amino acid sequence? These questions have fundamental significance for protein science and its numerous applications. Over the years these questions have generated a large literature leading to different models for the folding process.
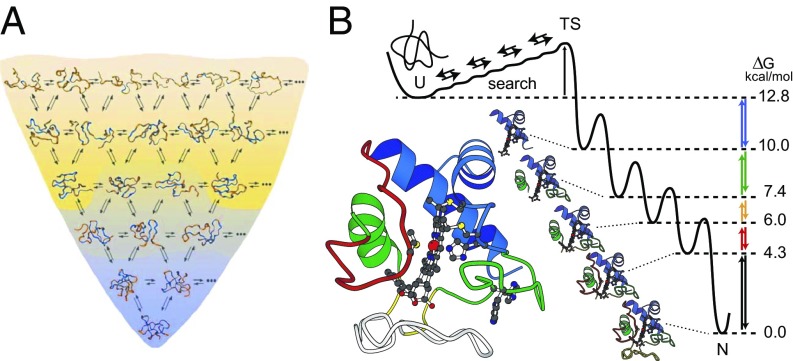
The “new view” folding model, derived from hypothetical energy landscape and statistical mechanical considerations (6–12), proposes that folding proteins navigate to their native state through very many independent pathways. The many trajectories in Fig. 1A imply an unfolded protein conformationally searching for its lowest-energy native state by way of dynamic bond rotations in a way that is guided by its energy landscape, as for any chemical reaction. For effective performance, folding proteins must “know” how to select native as opposed to nonnative interactions. This information is said to be contained in the shape of the energy landscape, but how it is implemented in the physical chemistry of any given protein, or proteins in general, is unknown. The funnel-shaped energy landscape simply expresses some general thermodynamic constraints equally applicable to the folding of any protein, or even RNA or any other polymer. Folding proceeds energetically downhill (the z axis), losing conformational entropy (the generalized XY plane) as it goes. To adapt the funnel picture to suggest pertinent folding information it is often embellished by notional features such as frictional roughness that slows folding and modified slope to alter energetic drive, some qualitative equations are often cited to codify some general constraints, and the whole picture has come to take on the name energy landscape theory (ELT) (13, 14).
Fig. 1.
Alternative protein folding models. (A) ELT proposes that proteins fold to their native state by energetically downhill conformational searching through innumerable pathways at the level of residue-level dynamics. The selection of native as opposed to nonnative interactions during folding is directed by a funnel-shaped energy landscape (80). (B) Experiment shows that, under equilibrium native conditions, cyt c unfolds by stepping energetically uphill through a ladder of forms that differ one from the next by the unfolding of one more native-like foldon (far right) (16, 17). HX MS experiments during kinetic folding demonstrate a pathway that steps sequentially downhill through the same intermediates (40). These results are able to specify the stepwise pathway in close to 3D structural detail (rather than as a 1D projection onto some reaction coordinate) because the downhill kinetic folding units and the uphill equilibrium unfolding units are very similar to the foldons that compose the native structure.
The discovery and study of protein foldons (15–17) point to a different folding mechanism, illustrated in Fig. 1B. Experiment shows that many proteins are built in a modular format composed of cooperative unfolding–refolding units called foldons, perhaps 15–35 residues in size. Several proteins have been shown to fold in macroscopic foldon formation steps, building the native protein by forming and assembling native-like foldon-based intermediates in a more or less sequential pathway. The structural units that assemble kinetic intermediates are much the same as the cooperative building blocks of the native protein. This strategy separates the kinetic folding puzzle into a sequence of smaller puzzles, forming pieces of the native structure and putting them into place in a stepwise pathway (Fig. 1B). This is the defined-pathway model.
Much work has provided valuable information. The numerous trajectories envisioned in the many-pathway model have been detected and characterized (18–20) and so can be considered on their merits rather than by abstract inference. Continued methods development (21, 22) has enhanced the search for foldons and the investigation of their role in both equilibrium and kinetic folding (16, 17). Advances in computational methods add a new vantage point (23–26). Other pertinent considerations include the size of the energetic interactions that are necessary to guide protein folding pathways and recent progress in evolutionary science.
The purpose of this paper is to consider the present status of these quite different models and relate them to the central questions of protein folding—how, why, and the encoding problem. We propose to rely on the solid ground of experiment rather than the countless less-definitive suggestions and inferences that have been so often used in this difficult field.
Results and Considerations
Foldons and Defined Pathways.
To investigate protein folding mechanisms, experimentalists have exploited every available methodology to define intermediate forms between the unfolded and native states. The major problem is that kinetic folding intermediates have short lifetimes and cannot be isolated for structural studies. Widely used methods that can follow the folding process in real time, mostly spectroscopic in nature, provide kinetic but little structural information.
Hydrogen exchange (HX) and related methods (21, 27) have made it possible to obtain informative structural information on intermediate states and their formation and progression in folding and unfolding pathways. Early HX work found that cytochrome c (cyt c) (28) and other proteins (29) reversibly unfold and refold at a low level under native conditions. HX-NMR studies were able to divide the equilibrium unfolding of cyt c into an energy ladder of reversible partially unfolded forms (PUFs; Fig. 1B) (15). Mutational and stability modification experiments in both kinetic (30) and equilibrium (31–34) modes established the identity of the high-energy PUFs, as shown in the ribbon diagrams in Fig. 1B. Reading upward in free energy from the native state in Fig. 1B, the identity of the cyt c PUFs is infrared alone unfolded (large bottom loop), then infrared + red unfolded, then those two + yellow unfolded, then those three + green, and finally the additional unfolding of blue, producing the fully unfolded protein (cyt c color coding as in Fig. 1B). Each energetically upward step unfolds one more foldon unit of the native protein. In light of microscopic reversibility, the sequential unfolding ladder defined under native conditions suggested that cyt c might normally fold in a similar stepwise sequence in reverse order down the free energy ladder (Fig. 1B).
A recently advanced HX mass spectrometry experiment (HX MS) (35–38) is uniquely able to define the structure of populated intermediates during kinetic folding. In this experiment a denaturant-unfolded protein is diluted into folding conditions. Folding synchronously commences. After various test folding times the sample is subjected to a brief D-to-H HX pulse to label, in a structure-sensitive way, partially folded transient intermediates that may be present (39). The protein sample is quenched (low pH, cold) to halt further exchange, proteolytically fragmented into many peptides, and the many peptides are roughly separated by HPLC and then further separated and analyzed at high resolution by MS. One result is that the same sequence of cyt c foldon-dependent intermediate forms seen in the equilibrium-uphill unfolding experiments form in reverse order as on-pathway intermediates in downhill kinetic folding, as illustrated in Fig. 1B (40).
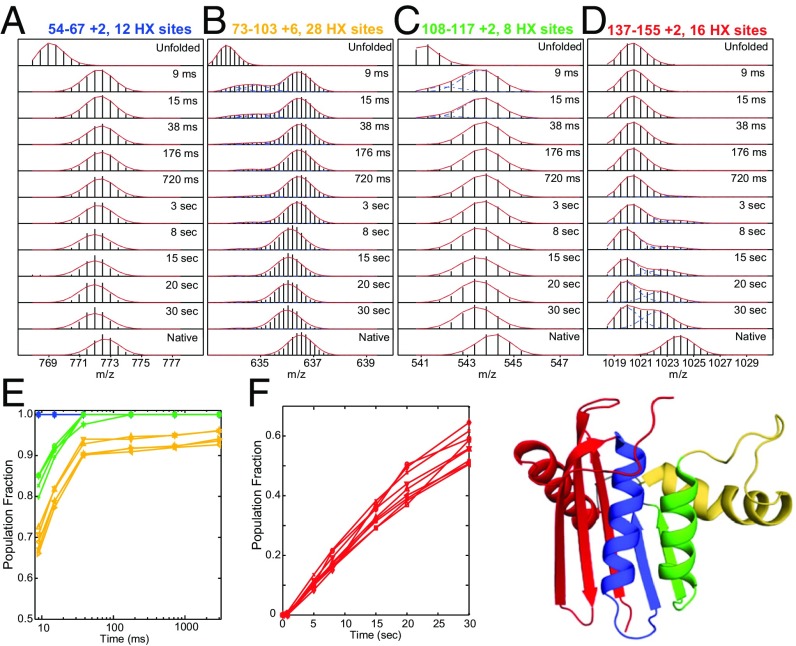
The example in Fig. 2 shows that RNase H similarly folds through an ordered sequence of native-like foldon units (41). Each of the 156 overlapping peptides obtained in the HX MS experiment provides a time- and structure-resolved series of snapshots of the fraction of the protein population that is already protected (folded) against the D-to-H labeling pulse (heavier) and not yet protected (lighter) at each segmental position at the time of the HX labeling pulse. Fig. 2 A–D show time-dependent HX MS data for the folding of four peptides that represent known protein segments within four distinct RNase H foldon units. The bimodal MS envelopes for each peptide show that the protein segment that it represents transits from an unfolded (unprotected) to a folded (protected) condition in a concerted reaction. The same behavior is seen throughout the protein. The entire protein population folds energetically downhill by forming a first structural unit (blue) in much less than 9 ms, then a second (green) with ∼5-ms lifetime, and so on for yellow and red (Fig. 2 E and F). Each segment once folded remains folded as later foldons add on, tracing a sequential folding process.
Fig. 2.
The stepwise folding of RNase H. Reprinted from ref. 41. The HX MS experiment together with HX pulse labeling monitors kinetic folding in real time, resolved to the level of short protein segments. (A–D) MS isotopic envelopes for four segments representative of the four color-coded foldon units in RNase H. In a series of folding experiments, a brief D-to-H labeling pulse (10 ms) was imposed after the folding times noted. The bimodal MS envelopes show that each segment folds in a concerted step (unprotected to protected) and persists through later folding steps elsewhere in the protein. (E and F) The time sequence for the folding of many high signal-to-noise peptides.
As for cyt c, these results document a well-defined, linear, stepwise folding pathway. In the case of heterogeneous pathways expected for many-pathway behavior, different molecules would fold any given segment in different orders at different rates. Rather, these experiments reveal concerted population-wide intermediate formation in a given sequence, each at the same given rate. The entire protein population folds the same segment first, all at the same rate, and all experience the same subsequent steps in the same order at the same rate, as suggested in Fig. 1B and detailed in Fig. 2 A–D.
Much experimental work using HX and other methods indicates that other proteins all share the same behavior. Maltose binding protein first forms a native-like on-pathway intermediate that brings together sequentially distant segments from its two domains and then more slowly folds the rest of the protein (42). Bai and coworkers (43) used HX-NMR and mutational methods to define a foldon-dependent sequential folding pathway for apocytochrome b562. Georgescauld et al. (44) used HX MS to determine a structurally defined folding pathway for a TIM barrel protein (DapA) when it is encapsulated inside the GroEL chaperonin. Similar results have been found for other proteins including apomyoglobin (45, 46), apoflavodoxin (47), OspA from Borrelia burgdorferi (48), staphylococcal nuclease (49), and a β-sandwich FHA domain (50). Silverman and Harbury used a sulfhydryl reactivity method to demonstrate foldons and their role in the sequential equilibrium unfolding of triose phosphate isomerase (51). Kay used relaxation dispersion NMR to define foldons in several small proteins and infer their on-pathway nature (52).
In summary, a quantity of direct experimental evidence for different proteins using various methods authenticates the reality and the ubiquity of cooperative foldon units as building blocks of native proteins and the stepwise formation of the same foldons in fairly well-defined folding pathways. These and other experiments would have detected multiple structure-formation pathways if they existed.
The Many-Pathway Model.
Although various observations have been thought to be consistent with the many-pathway model, there has been no clear experimental demonstration that characterizes or even detects the many trajectories. The one case to do so is analyzed here.
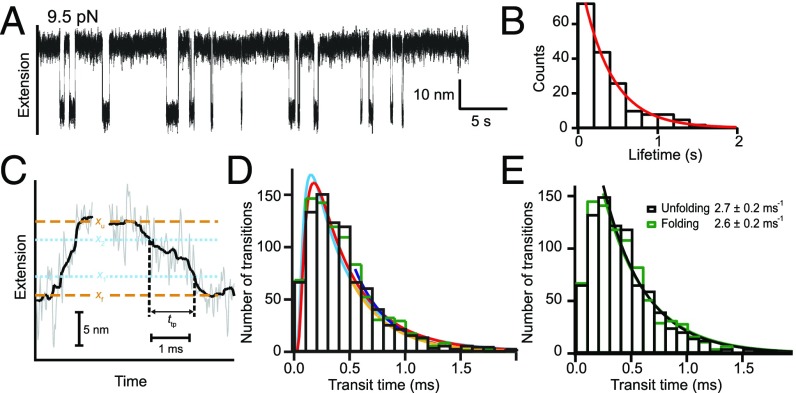
Ritchie and Woodside (18) and Woodside and Block (53), using high time-resolution single-molecule force spectroscopy, were able to detect many transitions between the unfolded and folded states of a monomeric prion (54) and also between the unfolded state and the first folded state on the (mis)folding pathway of a dimerized prion (19, 20). The prion protein was held in a dual-trap optical tweezers instrument under a constant pulling force, poised at the midpoint of a folding–unfolding transition so that many dynamic transitions in both directions could be observed. The experiment was able to time-resolve not only unfolding and refolding rates (Fig. 3 A and B) but also the more fleeting transition paths as individual molecules climb the transition barrier (Fig. 3 C and D). Fig. 3A is a recording of dwell times in the unfolded and folded states of the monomeric prion (54), which folds in a fast two-state manner rate-limited by an initial barrier-crossing event. The initial pathway step is rate-limiting because subsequent steps on the folding pathway are even faster. As expected, folding times are stochastically distributed, some faster and some slower, and the number distribution of dwell times fits a single exponential decay (Fig. 3B), indicating the two-state folding rate constant.
Fig. 3.
Many trajectories by single-molecule dual-trap optical tweezers experiments. (A) Dwell times in the fast folding and unfolding of a monomeric prion (19). (B) The exponential distribution of folding times (19). (C) Transit time between the unfolded and first folded state of a covalently dimeric prion (20), measured between the two blue lines for one successful unfolding step and one folding step. (D) The up-and-down distribution of folding and unfolding transit times matches the shape expected when successful transitions require the crossing of two positions (the blue lines) (55). (E) The entire downsweep part of the distribution is well fit by a single exponential indicating a common homogeneous population rate constant rather than the diverse heterogeneous trajectories expected for the many-pathway model.
The tethered dimer prion protein folds more slowly to some nonnative state through a distinct pathway with three detectable intermediates (19). Apparently, the two adjacent prion molecules are easily entangled, perhaps by domain swapping, and new kinetic barriers for structure formation are inserted. Neupane et al. (20) focused on the first step in this pathway and were able to measure the transition path time (i.e., the time spent in mounting the initial free energy barrier). Fig. 3C illustrates one unfolding transit and one folding transit. The transition path time is the time required to jump between the two blue dashed lines, which mark the dual trap extensions taken to represent the unfolded condition of the dimeric prion and its first partially folded state. The time for many such transits was measured. As before, some are faster and some slower. Their time distribution is in Fig. 3D. Other details are not distinguishable.
In Fig. 3D, the absence of measured transits at zero transit time and the subsequent upsweep of the distribution curve are due to instrument response time, the finite time needed to accomplish even the fastest start-to-end crossing between the two positions marked in Fig. 3C, and other factors. The later time bins (downsweep) capture the distribution of transition path times that are not limited by the exigencies of measurement and the initial built-in delay function. Calculation predicts this kind of up-and-down transit-time distribution (55). The entire measurable downsweep is well fit by a single exponential (Fig. 3E), indicating a given population rate constant rather than the heterogeneous population expected for the many-pathway model. The same experiment performed with a short DNA hairpin found multiple transition path trajectories with a time distribution like Fig. 3D and a single population rate constant (20).
In a commentary, P. G. Wolynes (56) equates the varied transition paths and path times with the many disparate folding pathways proposed in ELT and supplies a figure to emphasize the concept of pathway heterogeneity. He states that the multiplicity and heterogeneity of the trajectories confirms some of the most basic notions of ELT, and that there is no evidence for an obligate single folding pathway. This view ignores that the trajectories observed proceed only to formation of an initial distinct intermediate on a reproducible stepwise pathway through later distinct intermediates (19).
Further, the variability that does exist among the many trajectories seems to have no functional impact. For heterogeneity of the kind that is integral to meaningful ELT considerations (Fig. 1A), one expects a range of distinguishable folding rates and transition times as if for a mixture of different proteins, as implied in the commentary. In fact, the distribution of transit times measured for the dimeric prion, as for the folding times of the monomeric prion, shows a simple stochastic distribution as expected for a homogeneous population. All molecules reach the same target structure within the maximally narrow time distribution expected for a given population rate constant. Their different trajectories undoubtedly explore many different bond rotational configurations in different time order, but these differences have no physically meaningful effect in respect to rate constants, pathways, or intermediate states.
In summary, the single-molecule experiments of Ritchie and Woodside (18) and Woodside and Block (53) were finally able to measure the multiple parallel trajectories that anchor energy landscape considerations. The results show that trajectory multiplicity and variability do exist but the distribution of folding rates (Fig. 3B) and transition path rates (Fig. 3E) is as expected for a kinetically homogeneous population. Especially interesting, the multiple trajectories carry all of the dimer prion molecules only to an initial distinct intermediate state, all with the same homogeneous population rate constant, which is then followed by other distinct intermediates in a distinct pathway (19). These results do not match the basic characteristics expected for the heterogeneous many-pathway model but are fully consistent with the defined-pathway model.
Energy Considerations.
A critical feature of the funneled ELT model is that the many-pathway residue-level conformational search must be biased toward native-like interactions. Otherwise, as noted by Levinthal (57), an unguided random search would require a very long time. How this bias might be implemented in terms of real protein interactions has never been discovered. One simply asserts that natural evolution has made it so, formulates this view as a so-called principle of minimal frustration, and attributes it to the shape of the funneled energy landscape. Proteins in some unknown way “know” how to make the correct choices.
A calculation by Zwanzig et al. (58) at the most primary level quantifies the energy bias that would be required. In order for proteins to fold on a reasonable time scale, the free energy bias toward correct as opposed to incorrect interactions, whatever the folding units might be, must reach 2 kT (1.2 kcal/mol). The enthalpic bias between correct and incorrect interactions must be even greater, well over 2 kcal/mol, because competition with the large entropic sea of incorrect options is so unfavorable. Known amino acid interaction energies, less than 1 kcal/mol (59), seem to make this degree of selectivity impossible at the residue–residue level.
In contrast, the foldon hypothesis is able to satisfy the requirement for a large energetic bias toward native-like interactions (58) because it operates at a more macroscopic level that naturally adds the energies of many native interactions at each important step. Each foldon formation step is definitively demarcated not by individual weak residue-level interactions but by the concerted sum of the energies of multiple cooperatively organized stereochemically native-like intrafoldon interactions. Each sequential pathway step is determined by collectively summed stereochemically native-like interfoldon interactions.
The natural tendency of partially folded forms toward energy minimization seems likely to additionally entrain not-yet-folded residues in stabilizing nonnative ways. For example, in cyt c folding, the first-formed PUF (blue foldon folded, Fig. 1B) is more stable than the unfolded state by almost 3 kcal/mol in free energy (60), even though the isolated blue foldon is much less stable (61, 62). In RNase H folding the first two foldons seem unlikely to be stable in isolation (see model in Fig. 2).
In summary, many microscopic-level folding trajectories undoubtedly exist, especially at the earliest stage of folding, but conformational searching at this level seems unable to account for the energy bias or the structural selectivity that is needed to support native-directed choices, either at this stage or in subsequent structure formation. The more macroscopic foldon-dependent model combines cooperative sets of interactions that are stereochemically native-like. They naturally recognize native choices and can account for the degree of energy bias required to choose them.
Foldon Evolution.
Experiment shows that proteins unfold and refold by stepping through the cooperative subglobal units that compose them. This behavior seems definitive and widespread. How can one rationalize this situation? One general possibility is that folding in steps is an unavoidable consequence of protein structural cooperativity, a manifestation of the same kind of cooperative interactions that give rise to secondary structure. Another is that this folding strategy is such an effective way to overcome the difficulties of the folding process that biological evolution has over time discovered and widely incorporated it.
A more specific suggestion comes from recent work on repeat proteins. Over the last 15 y, one has become aware of families of repeat proteins that make up as much as 5% of the global proteome. These proteins have a nonglobular body plan made of small repeated motifs in the 20–40 residue range that are assembled in a linear array (63–65). The repeat units are individually cooperative, have low stability, and are further stabilized by their interfacial interactions. Repeat proteins have been found to fold in repeat-sized steps, one or several units at a time, in a distinct pathway order (66, 67). Thus, the repeat units look like and act like known foldons in contemporary globular proteins.
The different families of repeat proteins are very different in detailed structure but within each family the repeats are topologically nearly identical. These observations suggest that repeat proteins arose through repeated duplication at an early stage in the evolution of larger proteins from smaller fragments (68–70). Available examples show that globular organization can arise from continued repetitive growth that closes the linear geometry, and by the fusion of nonidentical units (69, 71), and so would carry forward their foldon-like properties.
The utility of foldons for the efficient folding of proteins might be seen as a dominant cause for the development and retention of a foldon-based body plan through protein evolution. In this view, contemporary proteins came so consistently to their modular foldon-based design and their foldon-based folding strategy because these linked characteristics coevolved. However, the fact that many known foldons bring together sequentially remote segments requires, at the least, some additional mechanism.
Computer Simulations.
One has long looked forward to the time when computer simulations would illuminate the intimate details of protein folding processes. The effort has been obstructed by the lack of formal equations that can capture the delicate balance of multiple interlocking structural interactions and by the immense computer power needed to simulate protein folding in atomistic detail (72). Much of the theoretical folding literature describes efforts to overcome these limitations. Crucial advances have been accomplished with the design of the Anton generation of computers (23), and massively parallel computing (26), and other promising strategies (73). Microlevel dynamics continue to be seen but they do not energetically drive or conformationally direct the course of folding. A key finding is that proteins fold by putting their structural elements into place over and over again in the same reproducible sequence (24, 74). Whether or not these elements formally qualify as typical foldons, the very same physical chemical principles that govern the defined stepwise folding model seem to be in play.
Theoretical efforts to search for foldons have been few. Soon after their discovery, Panchenko et al. (75) scanned the sequence database to search for putative foldons using a criterion of uncertain provenance (ratio of a contiguous segment’s energetic stability gap to the energy variance of that segment’s molten globule states). It may be useful to note that half of known foldons incorporate different segments that are not contiguous. A partially successful effort used a course-grained Gō model simulation with no side chains to compute some of the known foldons in cyt c (76). These approaches have not been revisited.
Discussion
The present survey assesses the two current general models for the protein folding process and its determinants.
The Energy Landscape Model.
When the many-pathway model was formulated in the period 1988–1995, the accepted view was that conformational searching for native structure occurs at the microscopic amino acid level. Levinthal (57, 77) had contributed the seminal observation that a random search could not account for known folding rates. The funneled landscape proposal accepted the microscopic search view and so was forced to adopt the suggestion that the conformational search is not random. The search must be biased to select correct native-like interactions in a way that, it was expected, would soon be explained. However, how this propensity might be encoded in the physical chemistry of protein structure has never been discovered. One simply asserts the general proposition that it is encoded in the shape of the landscape and to an ad hoc principle named minimal frustration imposed by natural evolution (78).
Energy landscapes are commonly drawn to illustrate the physical chemistry and quantum mechanics that are built into molecules and govern their reaction rates and behaviors (79). Atypically, the funneled landscape emblematic of energy landscape theory does not deal with molecular properties that would serve to guide interactions. It portrays some external thermodynamic constraints that are valid for the folding of proteins, RNA, or any other polymer. It contains in itself no molecular information or molecule-based constraints or predictions.
One does not doubt that the different proteins in a refolding population will explore many microscopically different configurations. This is characteristic for any thermally driven diffusional process when viewed at a sufficiently microscopic level. The experimental measurement of microscopic trajectories early in folding, now achieved in single-molecule studies (20), displays their reality but shows that the initial folding step exhibits a single homogeneous population rate constant. The trajectory diversity has no influence. Further, residue-level searching does not account for the subsequent structure-formation pathway. The HX MS experiment applied to several proteins (e.g., Fig. 2) would have detected the presence of many alternative pathways during structure formation, as would other folding studies, but they have not. An analogous situation seems to hold even for small apparently two-state folding proteins (24, 52). (Suggestions in the experimental literature for two or so alternative pathways do not constitute a great multiplicity and seem to require some other interpretation.) Quantitative evaluation described above shows that individual residue–residue interaction energies are inadequate for selecting native-like interactions in competition with the large number of competing nonnative alternatives. The assertion that the needed degree of energetic bias is supplied by the shape of an indefinite energy landscape because nature has made it so is—plainly said—not a useful physical–chemical explanation.
These considerations indicate the lack of an influential role for the heterogeneous microscopic search imagined in Fig. 1A. The question is what kind of conformational searching can explain the processes and pathways that carry unfolded proteins to their native state. The foldon-dependent defined-pathway model directly answers each of these challenges.
The Defined-Pathway Model.
Experimental results described before provide clear evidence for the existence and ubiquity of protein foldons and their determining role in constructing well-defined protein folding pathways. Cooperative foldons have been identified as integral structural units in over a dozen proteins of different sizes and topologies. They have been shown to determine intermediates and pathways in experiments on equilibrium unfolding, on kinetic folding, under varied conditions, and using varied methodologies. The selection of native vs. nonnative interactions as folding proceeds, and thus the construction and order of formation of pathway intermediates, is determined by cooperative intra- and interfoldon interactions that are encoded in the collective energies and stereochemistry of the same sets of interactions that cooperatively stabilize the native protein.
The defined-pathway model requires no new physical chemistry but uses familiar cooperativity principles to solve a demanding problem in a previously unsuspected way. Whole-molecule cooperativity is subdivided into smaller but still cooperative units, and kinetic folding recapitulates this foldon-based construction. The same stereochemical information and collective energetics that determine the equilibrium native structure of any given protein also specify the kinetic folding pathway for getting there. These are the factors that make fast definitive protein folding possible. Evolutionary considerations credibly tie together the early codevelopment of foldon-based equilibrium structure and foldon-based kinetic folding.
Does the defined-pathway model guarantee an absolutely single pathway? The MS envelopes in Fig. 2 A–D and other proteins so far determined in this way rule out the presence of a minor pathway that would carry as much as 5% of the folding flux. However, because protein structure and folding pathways are energetically determined, they can be manipulated in obvious ways (mutation, solution conditions, etc.), foldon structures must be somewhat malleable, on-pathway foldon formation may adopt an alternative order, and more than one pathway order may coexist depending on relative stabilities and kinetic barriers.
It has been suggested that the different pathway views discussed here might dominate at different stages in folding. Microscopic many-trajectory behavior is most likely at the earliest prenucleation stage. It may also contribute to subsequent structure-formation steps, although assisted folding guided by prior structure, so-called sequential stabilization (32), must play a dominant role.
Acknowledgments
We thank Y. Bai, R. L. Baldwin, D. Barrick, S. Marqusee, G. D. Rose, S. Piana, D. E. Shaw, T. R. Sosnick, A. Szabo, and M. T. Woodside for helpful discussions. This work was supported by NIH Grant GM031846, NSF Grant MCB1020649, and the G. Harold and Leila Y. Mathers Charitable Foundation.
Footnotes
The authors declare no conflict of interest.
References
- 1.Anfinsen CB, Haber E, Sela M, White FH., Jr The kinetics of formation of native ribonuclease during oxidation of the reduced polypeptide chain. Proc Natl Acad Sci USA. 1961;47:1309–1314. doi: 10.1073/pnas.47.9.1309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Anfinsen CB. Principles that govern the folding of protein chains. Science. 1973;181:223–230. doi: 10.1126/science.181.4096.223. [DOI] [PubMed] [Google Scholar]
- 3.Dill KA, MacCallum JL. The protein-folding problem, 50 years on. Science. 2012;338:1042–1046. doi: 10.1126/science.1219021. [DOI] [PubMed] [Google Scholar]
- 4.Sosnick TR, Barrick D. The folding of single domain proteins–have we reached a consensus? Curr Opin Struct Biol. 2011;21:12–24. doi: 10.1016/j.sbi.2010.11.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Abaskharon RM, Gai F. Meandering down the energy landscape of protein folding: Are we there yet? Biophys J. 2016;110:1924–1932. doi: 10.1016/j.bpj.2016.03.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bryngelson JD, Wolynes PG. Spin glasses and the statistical mechanics of protein folding. Proc Natl Acad Sci USA. 1987;84:7524–7528. doi: 10.1073/pnas.84.21.7524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Leopold PE, Montal M, Onuchic JN. Protein folding funnels: A kinetic approach to the sequence-structure relationship. Proc Natl Acad Sci USA. 1992;89:8721–8725. doi: 10.1073/pnas.89.18.8721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bryngelson JD, Onuchic JN, Socci ND, Wolynes PG. Funnels, pathways, and the energy landscape of protein folding: A synthesis. Proteins. 1995;21:167–195. doi: 10.1002/prot.340210302. [DOI] [PubMed] [Google Scholar]
- 9.Wolynes PG, Onuchic JN, Thirumalai D. Navigating the folding routes. Science. 1995;267:1619–1620. doi: 10.1126/science.7886447. [DOI] [PubMed] [Google Scholar]
- 10.Dill KA, Chan HS. From Levinthal to pathways to funnels. Nat Struct Biol. 1997;4:10–19. doi: 10.1038/nsb0197-10. [DOI] [PubMed] [Google Scholar]
- 11.Plotkin SS, Onuchic JN. Understanding protein folding with energy landscape theory. Part I: Basic concepts. Q Rev Biophys. 2002;35:111–167. doi: 10.1017/s0033583502003761. [DOI] [PubMed] [Google Scholar]
- 12.Sali A, Shakhnovich E, Karplus M. Kinetics of protein folding. A lattice model study of the requirements for folding to the native state. J Mol Biol. 1994;235:1614–1636. doi: 10.1006/jmbi.1994.1110. [DOI] [PubMed] [Google Scholar]
- 13.Glasstone S, Laidler KEH. The Theory of Rate Processes: The Kinetics of Chemical Reactions, Viscosity, Diffusion and Electrochemical Phenomena. McGraw-Hill; New York: 1941. [Google Scholar]
- 14.Johnson FH, Eyring H, Stover BJ. The Theory of Rate Processes in Biology and Medicine. Wiley; New York: 1974. [Google Scholar]
- 15.Bai Y, Sosnick TR, Mayne L, Englander SW. Protein folding intermediates: Native-state hydrogen exchange. Science. 1995;269:192–197. doi: 10.1126/science.7618079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Englander SW, Mayne L. The nature of protein folding pathways. Proc Natl Acad Sci USA. 2014;111:15873–15880. doi: 10.1073/pnas.1411798111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Englander SW, Mayne L, Kan ZY, Hu W. Protein folding-how and why: By hydrogen exchange, fragment separation, and mass spectrometry. Annu Rev Biophys. 2016;45:135–152. doi: 10.1146/annurev-biophys-062215-011121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ritchie DB, Woodside MT. Probing the structural dynamics of proteins and nucleic acids with optical tweezers. Curr Opin Struct Biol. 2015;34:43–51. doi: 10.1016/j.sbi.2015.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Yu H, et al. Protein misfolding occurs by slow diffusion across multiple barriers in a rough energy landscape. Proc Natl Acad Sci USA. 2015;112:8308–8313. doi: 10.1073/pnas.1419197112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Neupane K, et al. Direct observation of transition paths during the folding of proteins and nucleic acids. Science. 2016;352:239–242. doi: 10.1126/science.aad0637. [DOI] [PubMed] [Google Scholar]
- 21.Mayne L. Hydrogen exchange mass spectrometry. Methods Enzymol. 2016;566:335–356. doi: 10.1016/bs.mie.2015.06.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gallagher ES, Hudgens JW. Mapping protein-ligand interactions with proteolytic fragmentation, hydrogen/deuterium exchange-mass spectrometry. Methods Enzymol. 2016;566:357–404. doi: 10.1016/bs.mie.2015.08.010. [DOI] [PubMed] [Google Scholar]
- 23.Shaw DE, et al. Proceedings of the 2009 ACM/IEEE Conference on Supercomputing (SC09) ACM; New York: 2009. Millisecond-scale molecular dynamics simulations on Anton. [Google Scholar]
- 24.Lindorff-Larsen K, Piana S, Dror RO, Shaw DE. How fast-folding proteins fold. Science. 2011;334:517–520. doi: 10.1126/science.1208351. [DOI] [PubMed] [Google Scholar]
- 25.Adhikari AN, Freed KF, Sosnick TR. Simplified protein models: Predicting folding pathways and structure using amino acid sequences. Phys Rev Lett. 2013;111:028103. doi: 10.1103/PhysRevLett.111.028103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Lane TJ, Shukla D, Beauchamp KA, Pande VS. To milliseconds and beyond: Challenges in the simulation of protein folding. Curr Opin Struct Biol. 2013;23:58–65. doi: 10.1016/j.sbi.2012.11.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Krishna MMG, Hoang L, Lin Y, Englander SW. Hydrogen exchange methods to study protein folding. Methods. 2004;34:51–64. doi: 10.1016/j.ymeth.2004.03.005. [DOI] [PubMed] [Google Scholar]
- 28.Bai Y, Milne JS, Mayne L, Englander SW. Protein stability parameters measured by hydrogen exchange. Proteins. 1994;20:4–14. doi: 10.1002/prot.340200103. [DOI] [PubMed] [Google Scholar]
- 29.Huyghues-Despointes BM, Pace CN, Englander SW, Scholtz JM. Measuring the conformational stability of a protein by hydrogen exchange. Methods Mol Biol. 2001;168:69–92. doi: 10.1385/1-59259-193-0:069. [DOI] [PubMed] [Google Scholar]
- 30.Hoang L, Bédard S, Krishna MMG, Lin Y, Englander SW. Cytochrome c folding pathway: Kinetic native-state hydrogen exchange. Proc Natl Acad Sci USA. 2002;99:12173–12178. doi: 10.1073/pnas.152439199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Krishna MMG, Maity H, Rumbley JN, Lin Y, Englander SW. Order of steps in the cytochrome C folding pathway: Evidence for a sequential stabilization mechanism. J Mol Biol. 2006;359:1410–1419. doi: 10.1016/j.jmb.2006.04.035. [DOI] [PubMed] [Google Scholar]
- 32.Maity H, Maity M, Englander SW. How cytochrome c folds, and why: Submolecular foldon units and their stepwise sequential stabilization. J Mol Biol. 2004;343:223–233. doi: 10.1016/j.jmb.2004.08.005. [DOI] [PubMed] [Google Scholar]
- 33.Maity H, Maity M, Krishna MM, Mayne L, Englander SW. Protein folding: The stepwise assembly of foldon units. Proc Natl Acad Sci USA. 2005;102:4741–4746. doi: 10.1073/pnas.0501043102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Maity H, Englander SW. Stability labeling studies demonstrate a sequential folding/unfolding pathway in cytochrome c. Biophys J. 2005;88:40A–41A. [Google Scholar]
- 35.Kan ZY, Walters BT, Mayne L, Englander SW. Protein hydrogen exchange at residue resolution by proteolytic fragmentation mass spectrometry analysis. Proc Natl Acad Sci USA. 2013;110:16438–16443. doi: 10.1073/pnas.1315532110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Walters BT, Ricciuti A, Mayne L, Englander SW. Minimizing back exchange in the hydrogen exchange-mass spectrometry experiment. J Am Soc Mass Spectrom. 2012;23:2132–2139. doi: 10.1007/s13361-012-0476-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Mayne L, et al. Many overlapping peptides for protein hydrogen exchange experiments by the fragment separation-mass spectrometry method. J Am Soc Mass Spectrom. 2011;22:1898–1905. doi: 10.1007/s13361-011-0235-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Kan ZY, Mayne L, Chetty PS, Englander SW. ExMS: Data analysis for HX-MS experiments. J Am Soc Mass Spectrom. 2011;22:1906–1915. doi: 10.1007/s13361-011-0236-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Roder H, Elöve GA, Englander SW. Structural characterization of folding intermediates in cytochrome c by H-exchange labelling and proton NMR. Nature. 1988;335:700–704. doi: 10.1038/335700a0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Hu W, Kan ZY, Mayne L, Englander SW. Cytochrome c folds through foldon-dependent native-like intermediates in an ordered pathway. Proc Natl Acad Sci USA. 2016;113:3809–3814. doi: 10.1073/pnas.1522674113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Hu W, et al. Stepwise protein folding at near amino acid resolution by hydrogen exchange and mass spectrometry. Proc Natl Acad Sci USA. 2013;110:7684–7689. doi: 10.1073/pnas.1305887110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Walters BT, Mayne L, Hinshaw JR, Sosnick TR, Englander SW. Folding of a large protein at high structural resolution. Proc Natl Acad Sci USA. 2013;110:18898–18903. doi: 10.1073/pnas.1319482110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Feng H, Zhou Z, Bai Y. A protein folding pathway with multiple folding intermediates at atomic resolution. Proc Natl Acad Sci USA. 2005;102:5026–5031. doi: 10.1073/pnas.0501372102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Georgescauld F, et al. GroEL/ES chaperonin modulates the mechanism and accelerates the rate of TIM-barrel domain folding. Cell. 2014;157:922–934. doi: 10.1016/j.cell.2014.03.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Jamin M, Baldwin RL. Two forms of the pH 4 folding intermediate of apomyoglobin. J Mol Biol. 1998;276:491–504. doi: 10.1006/jmbi.1997.1543. [DOI] [PubMed] [Google Scholar]
- 46.Uzawa T, et al. Hierarchical folding mechanism of apomyoglobin revealed by ultra-fast H/D exchange coupled with 2D NMR. Proc Natl Acad Sci USA. 2008;105:13859–13864. doi: 10.1073/pnas.0804033105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Bollen YJM, Kamphuis MB, van Mierlo CPM. The folding energy landscape of apoflavodoxin is rugged: Hydrogen exchange reveals nonproductive misfolded intermediates. Proc Natl Acad Sci USA. 2006;103:4095–4100. doi: 10.1073/pnas.0509133103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Yan S, Kennedy SD, Koide S. Thermodynamic and kinetic exploration of the energy landscape of Borrelia burgdorferi OspA by native-state hydrogen exchange. J Mol Biol. 2002;323:363–375. doi: 10.1016/s0022-2836(02)00882-3. [DOI] [PubMed] [Google Scholar]
- 49.Bédard S, Mayne LC, Peterson RW, Wand AJ, Englander SW. The foldon substructure of staphylococcal nuclease. J Mol Biol. 2008;376:1142–1154. doi: 10.1016/j.jmb.2007.12.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Liang X, Lee GI, Van Doren SR. Partially unfolded forms and non-two-state folding of a beta-sandwich: FHA domain from Arabidopsis receptor kinase-associated protein phosphatase. J Mol Biol. 2006;364:225–240. doi: 10.1016/j.jmb.2006.08.090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Silverman JA, Harbury PB. The equilibrium unfolding pathway of a (beta/alpha)8 barrel. J Mol Biol. 2002;324:1031–1040. doi: 10.1016/s0022-2836(02)01100-2. [DOI] [PubMed] [Google Scholar]
- 52.Kay LE. New views of functionally dynamic proteins by solution NMR spectroscopy. J Mol Biol. 2016;428:323–331. doi: 10.1016/j.jmb.2015.11.028. [DOI] [PubMed] [Google Scholar]
- 53.Woodside MT, Block SM. Reconstructing folding energy landscapes by single-molecule force spectroscopy. Annu Rev Biophys. 2014;43:19–39. doi: 10.1146/annurev-biophys-051013-022754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Yu H, et al. Energy landscape analysis of native folding of the prion protein yields the diffusion constant, transition path time, and rates. Proc Natl Acad Sci USA. 2012;109:14452–14457. doi: 10.1073/pnas.1206190109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Chaudhury S, Makarov DE. A harmonic transition state approximation for the duration of reactive events in complex molecular rearrangements. J Chem Phys. 2010;133:034118. doi: 10.1063/1.3459058. [DOI] [PubMed] [Google Scholar]
- 56.Wolynes P. Biomolecular folding. Moments of excitement. Science. 2016;352:150–151. doi: 10.1126/science.aaf6626. [DOI] [PubMed] [Google Scholar]
- 57.Levinthal C. Are there pathways for protein folding? J Chim Phys. 1968;65:44–45. [Google Scholar]
- 58.Zwanzig R, Szabo A, Bagchi B. Levinthal’s paradox. Proc Natl Acad Sci USA. 1992;89:20–22. doi: 10.1073/pnas.89.1.20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Fersht A. Structure and Mechanism in Protein Science. Freeman; New York: 1999. [Google Scholar]
- 60.Krishna MMG, Lin Y, Mayne L, Englander SW. Intimate view of a kinetic protein folding intermediate: Residue-resolved structure, interactions, stability, folding and unfolding rates, homogeneity. J Mol Biol. 2003;334:501–513. doi: 10.1016/j.jmb.2003.09.070. [DOI] [PubMed] [Google Scholar]
- 61.Kuroda Y. Residual helical structure in the C-terminal fragment of cytochrome c. Biochemistry. 1993;32:1219–1224. doi: 10.1021/bi00056a004. [DOI] [PubMed] [Google Scholar]
- 62.Wu LC, Laub PB, Elöve GA, Carey J, Roder H. A noncovalent peptide complex as a model for an early folding intermediate of cytochrome c. Biochemistry. 1993;32:10271–10276. doi: 10.1021/bi00089a050. [DOI] [PubMed] [Google Scholar]
- 63.Main ER, Jackson SE, Regan L. The folding and design of repeat proteins: Reaching a consensus. Curr Opin Struct Biol. 2003;13:482–489. doi: 10.1016/s0959-440x(03)00105-2. [DOI] [PubMed] [Google Scholar]
- 64.Kajander T, Cortajarena AL, Main ERG, Mochrie SGJ, Regan L. A new folding paradigm for repeat proteins. J Am Chem Soc. 2005;127:10188–10190. doi: 10.1021/ja0524494. [DOI] [PubMed] [Google Scholar]
- 65.Javadi Y, Itzhaki LS. Tandem-repeat proteins: Regularity plus modularity equals design-ability. Curr Opin Struct Biol. 2013;23:622–631. doi: 10.1016/j.sbi.2013.06.011. [DOI] [PubMed] [Google Scholar]
- 66.Bradley CM, Barrick D. The notch ankyrin domain folds via a discrete, centralized pathway. Structure. 2006;14:1303–1312. doi: 10.1016/j.str.2006.06.013. [DOI] [PubMed] [Google Scholar]
- 67.Dao TP, Majumdar A, Barrick D. Highly polarized C-terminal transition state of the leucine-rich repeat domain of PP32 is governed by local stability. Proc Natl Acad Sci USA. 2015;112:E2298–E2306. doi: 10.1073/pnas.1412165112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Zhu H, et al. Origin of a folded repeat protein from an intrinsically disordered ancestor. Elife. 2016;5:e16761. doi: 10.7554/eLife.16761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Smock RG, Yadid I, Dym O, Clarke J, Tawfik DS. De novo evolutionary emergence of a symmetrical protein is shaped by folding constraints. Cell. 2016;164:476–486. doi: 10.1016/j.cell.2015.12.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Balaji S. Internal symmetry in protein structures: Prevalence, functional relevance and evolution. Curr Opin Struct Biol. 2015;32:156–166. doi: 10.1016/j.sbi.2015.05.004. [DOI] [PubMed] [Google Scholar]
- 71.Wilson CG, Kajander T, Regan L. The crystal structure of NlpI. A prokaryotic tetratricopeptide repeat protein with a globular fold. FEBS J. 2005;272:166–179. doi: 10.1111/j.1432-1033.2004.04397.x. [DOI] [PubMed] [Google Scholar]
- 72.Perez A, Morrone JA, Simmerling C, Dill KA. Advances in free-energy-based simulations of protein folding and ligand binding. Curr Opin Struct Biol. 2016;36:25–31. doi: 10.1016/j.sbi.2015.12.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Adhikari AN, Freed KF, Sosnick TR. De novo prediction of protein folding pathways and structure using the principle of sequential stabilization. Proc Natl Acad Sci USA. 2012;109:17442–17447. doi: 10.1073/pnas.1209000109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Piana S, Lindorff-Larsen K, Shaw DE. Atomic-level description of ubiquitin folding. Proc Natl Acad Sci USA. 2013;110:5915–5920. doi: 10.1073/pnas.1218321110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Panchenko AR, Luthey-Schulten Z, Wolynes PG. Foldons, protein structural modules, and exons. Proc Natl Acad Sci USA. 1996;93:2008–2013. doi: 10.1073/pnas.93.5.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Weinkam P, Zong C, Wolynes PG. A funneled energy landscape for cytochrome c directly predicts the sequential folding route inferred from hydrogen exchange experiments. Proc Natl Acad Sci USA. 2005;102:12401–12406. doi: 10.1073/pnas.0505274102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Levinthal C. 1969. How to fold graciously. Mossbauer Spectroscopy in Biological Systems Proceedings, University of Illinois Bulletin (Univ of Illinois Press, Urbana, IL), pp 22–24.
- 78.Ferreiro DU, Komives EA, Wolynes PG. Frustration in biomolecules. Q Rev Biophys. 2014;47:285–363. doi: 10.1017/S0033583514000092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Wales DJ. Energy Landscapes. Cambridge Univ Press; Cambridge, UK: 2003. [Google Scholar]
- 80.Oliveberg M, Wolynes PG. The experimental survey of protein-folding energy landscapes. Q Rev Biophys. 2005;38:245–288. doi: 10.1017/S0033583506004185. [DOI] [PubMed] [Google Scholar]