Abstract
We measure dynamic traction forces exerted by epithelial cells on a substrate. The force sensor is a high-density array of elastomeric microfabricated pillars that support the cells. Traction forces induced by cell migration are deduced from the measurement of the bending of these pillars and are correlated with actin localization by fluorescence microscopy. We use a multiple-particle tracking method to estimate the mechanical activity of cells in real time with a high-spatial resolution (down to 2 μm) imposed by the periodicity of the post array. For these experiments, we use differentiated Madin-Darby canine kidney (MDCK) epithelial cells. Our data provide definite information on mechanical forces exerted by a cellular assembly. The maximum intensity of the forces is localized on the edge of the epithelia. Hepatocyte growth factor promotes cell motility and induces strong scattering activity of MDCK cells. Thus, we compare forces generated by MDCK cells in subconfluent epithelia versus isolated cells after hepatocyte growth factor treatment. Maximal-traction stresses at the edge of a monolayer correspond to higher values than those measured for a single cell and may be due to a collective behavior.
Keywords: cell mechanics, microfabrication, traction forces, multiple particle tracking
Mechanical stress exerted at cell-substrate and cell-cell interfacial boundaries is involved in the regulation of a variety of physiological processes. In the case of epithelial cells such as Madin-Darby canine kidney (MDCK), it is becoming increasingly apparent that epithelial cell movement and changes in morphology are central to both development and regeneration of epithelial organs. This finding has implications for many pathological processes such as transformation of epithelia to carcinoma and metastasis (1, 2). Epithelial cells contain apical and basolateral plasma membrane domains that are separated by distinct junctional complexes. Epithelial cell-cell junctions are mediated by E-cadherin, a transmembrane receptor that joins interacting cell plasma membranes to actin filaments through catenins. During epithelial-to-mesenchymal transitions, the stability of the adherent cell-cell junctions is compromised (3). In particular, hepatocyte growth factor (HGF) stimulates the disassembly of epithelial cell-cell junctions and promotes cell motility. In addition, epithelial cells expressing the HGF receptor (c-met) exhibit strong scattering activity. These responses are accompanied by the modification of the actin cytoskeleton, including increased membrane ruffling and lamellipodium extension (4, 5).
Understanding this phenotypic change implies a comprehension of the dynamics of cell adhesion on their substrate. The mechanisms underlying the dynamic rearrangement of cell-cell adhesion and traction forces during the HGF-induced scattering remain unclear. When cells begin to migrate, they exert forces against the substrate to move forward. During these processes of adhesion and migration, forces are generated by the action of myosin II on the cytoskeleton through integrin-extracellular matrix linkages to create tractions on the substrate (6–8).
Most of the previous work on stresses at the cell-to-substrate interface uses deformations within elastic materials such as thin polymer films or thick polymer gels (9–14). In the latter case, displacements of beads embedded randomly throughout the elastomer are correlated to deformations generated by cells (15). These methods have provided important quantitative information on force distributions and have led to significant improvements in our understanding of spatial and temporal traction response in cells (14–17). Nevertheless, such techniques present limitations, mostly because, as deformations propagate on continuous surfaces, the relation between bead displacements and forces is difficult to compute. Moreover, beads form a discrete network in the surface, and these methods cannot provide force measurements between these markers (18, 19). An alternative strategy has been to use an array of discrete microfabricated force sensors (cantilevers), an elegant but technologically challenging method limited also by the density of sensors on the surface (10). Along the same line, another technique has been recently developed to surmount these limitations. It consists of a discrete array of vertical microneedles of silicone elastomer used as cantilevers on which cells attach and exert forces (20). The deflection of the posts caused by the attached cells is a direct measurement of the local forces. However, in these previous experiments, because of the route used for the fabrication of the microposts, the density of micropillars under the cells was kept low, leading to a spatial resolution limited to 9 μm. Moreover, this low pillar density seem to affect cell adhesion and cell locomotion compared with a flat and continuous surface.
To circumvent some of these limitations, this paper describes an approach by using a considerably higher density of microfabricated pillars to measure traction forces exerted by MDCK cells. In the present study, we have focused our analysis on the comparison of the mechanical activity of subconfluent monolayers versus isolated single cells obtained by the addition of HGF. The microdimensional force sensor array (μFSA) is made of elastomeric pillars with known physical and surface chemical properties (21). We use arrays of closely spaced posts (from 2 to 4 μm center-to-center) (Fig. 1A). Such large pillar densities improves the spatial force resolution and behaves as at continuous interface so as not to interfere with cell spreading and locomotion. By using this dense and discrete array of posts rather than a continuous substrate, we directly measure and quantify the space and time dependence of the forces exerted by the cell on its underlying substrate. In the linear regime of small deformations, the deflection of the micropillars is directly proportional to the force. The linear elastic theory of a cylinder of radius, r, and length, L, bent by the application of a lateral force F at its extremity then gives the following relation (Eq. 1):
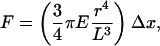 |
[1] |
where E, and Δx, are the Young's modulus and the deflection of the post, respectively (see Fig. 1) (22).
Fig. 1.
Scanning electron micrographs. (A) Closely spaced microfabricated posts after PDMS molding. (B) Individual cells lying on μFSA (1 μm diameter and 2 μm distance center-to-center). (C) A cell monolayer (2 μm diameter and 3 μm distance center-to-center). (C Inset) Magnified view of the area delimited by the black square. Cells spread only on the top of pillars (B and C).
Materials and Methods
Pattern Formation and Chemical Preparation of Poly(dimethylsiloxane) (PDMS) Micropillars for μFSA. Using conventional photolithography followed by a deep etching process (“Bosch Process”), silicon wafers are patterned with an array of cylindrical pits. Briefly, the desired pattern is replicated in positive photoresist by photolithography. Bare parts of the wafers are then etched by the deep Si etching process down to the desired depth to obtain the negative pattern of the array. After cleaning, the wafers are silanized with tridecafluoro-trichlorosilane in vapor phase to facilitate the release of the elastomer from the wafers after curing. A liquid silicone prepolymer, PDMS (Sylgard 184, Dow-Corning), is then poured over the silicon template, cured at 65°C for 12 h, and then peeled off from it. After release from the mold, the replica is oxidized and sterilized in an air plasma (Harrick) for 2 min. This process makes the PDMS surface hydrophilic, which facilitates adsorption of fibronectin (incubated for 1 h in 20 μg/ml fibronectin (Sigma-Aldrich) in PBS buffer).
For some of the experiments, the top of the pillars is fluorescently labeled. The arrays are then prepared by a reverse microcontact printing method (23, 24). A flat PDMS stamp is oxidized by plasma treatment and incubated with fluorescently labeled fibronectin for 1 h (Alexa 488 coupled, Molecular Probes). The stamp is then dried with a stream of nitrogen and gently placed in contact with the μFSA surface. The entire surface is then coated with nonfluorescent fibronectin to achieve a constant concentration of extracellular matrix protein over the substrate.
Cell Culture. MDCK cells are maintained at 37°C in a humidified atmosphere of 5% CO2 and 95% air in DMEM containing 10% bovine calf serum, 100 units/ml penicillin, 100 μg/ml streptomycin, and 100 μg/ml glutamine. Dense cell monolayers are obtained after 3 days of culture with media exchange every 1–2 days. Nonconfluent cells are used for microscopy observations 24 h after deposition on the substrates.
MDCK cells are stimulated with HGF (Calbiochem), introduced at a concentration of 10 ng/ml in the DMEM.
Phase-Contrast, Bright-Field Microscopy. Living cells are observed by using either phase-contrast microscopy or bright-field microscopy through a 10× or 60× (NA 0.8) air objectives on an inverted Olympus IX71 microscope. Images are acquired by using an intensified charge-coupled device camera (Roper Scientific, Princeton, NJ) by using a 100-msec exposure time and a 10-sec interval between acquisitions.
Cell Videomicroscopy Observation. To maintain a 37°C temperature in the sample, the microscope is equipped with a heated stage (Linkam, Tadworth, U.K.). Hepes (10 mM, pH 7.4) (Sigma) is added to the medium, and the chamber is sealed on top with a layer of paraffin.
Immunofluorescence Labeling. For filamentous actin visualization, cells are fixed with 4% paraformaldehyde in PBS for 10 min at room temperature, rinsed three times with PBS and permeabilized (50 mM NH4Cl for 10 min and 0.1% Triton X-100 in PBS for 4 min). After rinsing with PBS, the cells are stained with tetramethylrhodamine-conjugated phalloidin (Molecular Probes). All images are acquired with a Olympus 100×, NA 1.4 objective.
Scanning Electron Micrograph (SEM) Observation. SEM is first used to visualize the pillar surfaces and, at a later time, to observe the adhesive MDCK cells on this substrate. In this latter case, cells are cultured on a μFSA for 1 day after their previous resuspension, fixed with 4% paraformaldehyde in PBS for 1 h, and then further rinsed three times with PBS buffer. Dehydration is performed by rinsing the samples through graded ethanol/water mixtures (50%, 70%, 80%, 90%, and finally 100%, each step for 10 min at 4°C). Ethanol is slowly exchanged successively by amyl acetate and liquid CO2. Finally, samples are dried by using the critical point method and then sputter-coated by a thin layer of gold.
Characterization of the Substrate. To evaluate the Young's modulus of the PDMS, we use dimensionally calibrated macroscopic cylinders of this material (l = 4 cm in height and 2 cm in diameter) and measure their compressions under a fixed normal strain, σ. The Young's modulus, E, is calculated according to the equation: E = σ(Δl/l), where, Δl is the change in length. We find that E depends on the PDMS cure time from 1.5 MPa after curing for 4 h at 65°C up to 2.5 MPa after a week at 65°C. Consequently, we have used a consistent cure time of 12 ± 2 h at 65°C corresponding to a Young's modulus of 2 ± 0.1 MPa. Using SEM observation, we have measured the dimensions of the pillars and calculated the spring constant according to Eq. 1.
Calibrated glass microplates obtained as described in ref. 25 are also used to directly evaluate this spring constant. These plates are mounted onto a piezoelectric manipulator fixed on the microscope stage. The top of an individual pillar is placed in contact with the microplate displaced by the piezomanipulator, and the deflection of the post is measured by videomicroscopy.
Image Analysis and Calculation of Traction Forces. We measure the local deformation of the pillars by using a homemade multiparticle tracking software. In bright-field microscopy, the local contrast between the top of the posts that act as waveguides and the background is high enough to allow for a good determination of each post position by using a simple Gaussian fit. The first step of this tracking process consists of a manual assignment of the hexagonal lattice while the posts are at rest (not covered by cells). Each post is then digitally labeled with its corresponding position on the lattice (the number of posts in each image is of the order of 1,000). The second step takes the entire image stack and determines the actual position of the posts compared with their rest position (δx, δy). For long experiments, corresponding to a total time of about a few hours, the drift (mechanically or thermally induced) of the microscope stage is taken into account. The time resolution, corresponding to the calculation of the overall stress pattern for one image, is <1 sec. The resolution of the displacements is of the order of 50 nm, and as previously mentioned, the principal source of noise depends mainly on the local contrast between the top of the posts and the background (26). To calculate the local force, the deflection of the posts is multiplied by the spring constant. Depending on the spring constant (between 1 nN/μm and 20 nN/μm), the force resolution varies from 50 pN to 1 nN. The contribution of the thermal noise to the fluctuations of micropillars, which corresponds to ≈1 nm, is negligible.
The spatial force resolution, determined by the periodicity of the μFSA, is 3 or 4 μm in the present study, comparable with the estimated spatial resolution obtained on continuous polyacrylamide substrates (15–17).
The forces are classically represented by drawing a vector on each pillar whose length is proportional to the force intensity. We have also used an alternative way to represent the spatial distribution of the intensity of the forces by attributing a gray level to each pillar from white (low activity) to black (high activity).
Traction stresses are calculated by assuming that forces are only transmitted through the pillars. The effective surface area corresponds to the cross section of these posts.
Results
Cell Behavior and Calibration of PDMS Substrates. First, we compare the kinetics of MDCK cell adhesion, locomotion, and division on μFSA versus PDMS flat substrate by using the same fibronectin coating. Basic cellular functions, including adhesion, locomotion, and proliferation, are not affected by the array of closely spaced pillars (see Fig. 7, which is published as supporting information on the PNAS web site). The ability to reform a cell epithelial monolayer after resuspension is not altered by the presence of the micropillars and takes the same time as under standard cell culture conditions (Fig. 7).
The order of magnitude of forces generated by cells is about a few nN (27). Therefore, the stiffness of microfabricated pillars is chosen to be in a regime relevant for studying MDCK cell traction forces. We have varied the dimensions of the posts from 1 to 2 μm in diameter and 3 to 8 μm in height. As the spring constant of the posts is proportional to the 4th power of the diameter and inversely proportional to the cube of the length according to Eq. 1, we can easily vary the mechanical stiffness of the pillars over three orders of magnitude (from 0.47 to 174 nN/μm). These values are in good agreement with spring constants directly obtained with calibrated glass micropipettes. In this work, we have used posts of 1 or 2 μm in diameter and either 5.2 or 6 μm in height, corresponding to a range of spring constants from 1.3 to 21.8 nN/μm (see Fig. 1 A). In that case, we ensure that the deflection of the post caused by the cells is small enough to stay in the linear regime of deformation (Eq. 1).
Cell-to-Substrate Observations. We used SEM analysis to ensure that the cells were actually growing on the posts and not between them. Cells are fixed at low density on the surface to facilitate SEM observations after 1 day in standard cell culture conditions (instead of the 3 days necessary to reconstitute a complete cell monolayer). Because of the high density of pillars from 2 to 4 μm center-to-center, cells only spread on the top of the posts (Fig. 1 B and C). Therefore, the cell–surface interactions take place only at the top of the micropillars. Hence, cell tractions on the substrate are directly proportional to the deflection of the posts; no contribution can be attributed to elastomer compliances between the pillars (20).
The observations in optical microscopy are performed by using both phase-contrast microscopy and bright-field microscopy to follow cell movements on the substrates. To ensure a good focusing of the microscope and therefore a proper determination of the forces, we have focused on the fluorescently labeled tops of the micropillars. Movements of the top of the underlying posts are tracked in bright-field microscopy by using the multiple-particle tracking software described in Materials and Methods.
Distribution of Mechanical Forces Under MDCK Cells. We have first examined the overall pattern of deformation exerted by established MDCK cell monolayers. MDCK cells were cultured for 3 days on the μFSA and grown to confluency. The cell monolayer in a nonmotile state is observed for 4 h at 37°C with time-lapse videomicroscopy. Under such conditions, we do not observe any significant deflections of the micropillars as a function of time, even for the softest pillars used in this study. Deviations from the standard undeflected positions of the pillars in a confluent MDCK cell monolayer are <50 nm, corresponding to our limiting sensitivity in detection.
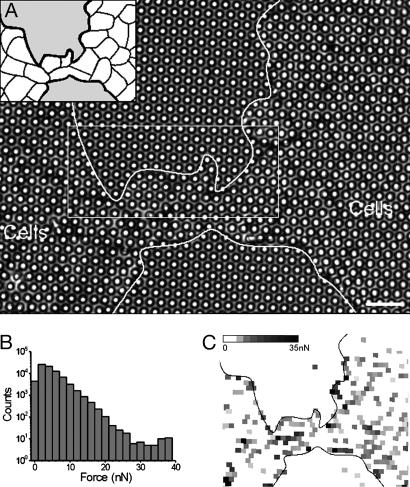
Consequently, MDCK cells are plated at subconfluent density. Movie 1, which is published as supporting information on the PNAS web site, shows the growth of a patch of monolayer on a μFSA of 1-μm pillar diameter. As the leading edge approaches a post, rearward movements of micropillars are clearly seen. Fig. 2 analyzes the stress pattern in the same culture conditions on a μFSA with a 21.8 nN/μm spring constant. Posts not covered by cells show no significant deflections. Forces are found to depend on their relative position in the monolayer: the strongest deformations are always localized at the edge of the islands of cells in the active areas of cell protrusions (Fig. 2 A and Movie 1). Traction forces at the edge are distributed with an average value of ≈5 nN and the largest forces, >20 nN, are mostly due to the mechanical activity of the edge (Fig. 2B). These results are confirmed by the grayscale mapping representation of the deformations (Fig. 2C). Moreover, the analysis of the deformations at the edge demonstrates that forces present a broad distribution both in magnitude and direction. Nevertheless, they are on average oriented normally to the monolayer edges (Fig. 3A) in the opposite direction of the advancing front of the cells.
Fig. 2.
Magnitude of forces applied in and at the edge of a monolayer. (A) Transmission image of a monolayer grown onμFSA for 2 days (2μm diameter and 4 μm distance center-to-center). (Inset) Drawing of the adherent cell-cell junctions. (Scale bar: 12 μm.) (B) Histogram of magnitude of forces measured on the whole film. The stack contains 72 images and corresponds to 2 h. (C) Reconstructed image: each post is associated with a gray square localized at the undeflected position of the post in the image. Grayscaled mapping depends on the magnitude of the force from white (for low forces) to black (for high forces).
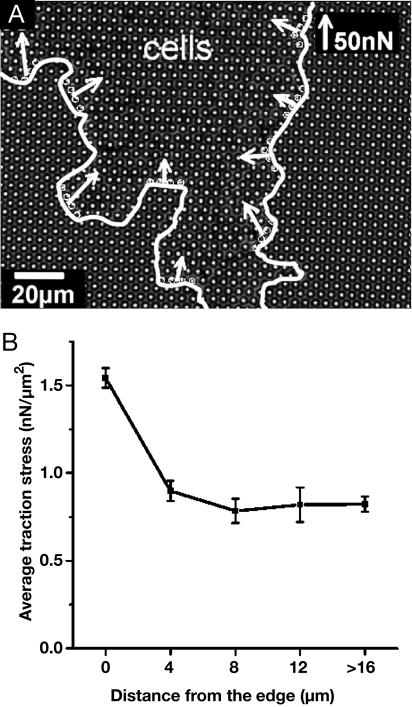
Fig. 3.
Magnitude and orientation of traction stress along the edge of a monolayer. (A) A growing cell monolayer on μFSA (2 μm diameter, 4 μm center to center) observed by transmission microscopy (60× air objective). The edge of the monolayer is outlined by the white line. The white arrows indicate the resulting force applied on four consecutive posts along the edge (indicated by circles). The magnitude of these traction stresses is not uniform, but the orientation remains centripetal all along the edge. (B) Average traction stress versus distance from the edge. Equidistant posts from the edge are pooled together to calculate for each distance the corresponding average traction stress. Posts used to calculate the last point are further than 16 μm toward the interior of the monolayer of A.
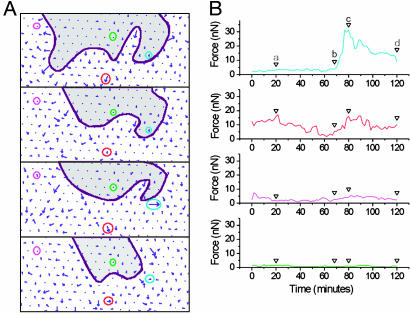
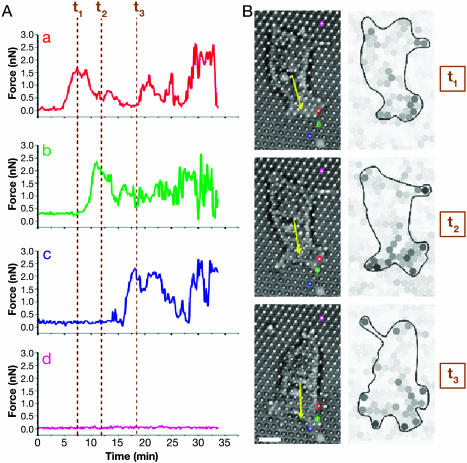
On Fig. 4, we have plotted the time variations of the force on four chosen posts. First, it shows the existence of a “residual” activity under a subconfluent monolayer with a broad range of intensity (magenta and red curves, Fig. 4B). The corresponding values remain smaller than ≈15 nN, whereas instantaneous forces often reach ≈30 nN at the edge (blue curve, Fig. 4B). As the edge of the monolayer reaches and covers a post, the force increases with a characteristic time of ≈10 min to its maximum value.
Fig. 4.
Temporal evolution of forces applied by cells on individual posts. The time-lapse sequence analyzed here corresponds to the area boxed in Fig. 2 A. (A) Force cartographies at different times. The edge of the cell monolayer is figured by the purple line; the cells are located in the white part of the image. Center-to-center spacing between pillars is 4 μM. An arrow of such a length corresponds to a 30-nN force. The origin of each arrow is the undeflected position of the corresponding post. Four differently located posts have been labeled with colored circles. (B) Forces applied by cells on these four posts as a function of time. Vertical arrows indicate the time of the image sequence (a–d). The blue curve illustrates the increase (≈10 min) and release (≈30 min) of the force as the leading edge passes over the post. The middle curves (magenta and red) reflect the residual activity further from the edge than the blue one. The green curve corresponds to an uncovered post.
As a comparison, the average distribution of the stress inside a growing monolayer is plotted in Fig. 3B. The average traction stress rapidly decreases within the size of less than one cell from its maximum value at the edge (1.6 nN/μm2) to half this value. This result also demonstrates that within the monolayer, the activity inside a growing epithelium depends on its size because it is higher in this case than within a confluent monolayer. Furthermore, traction is found to be mostly localized at the cell-to-cell junctions than underneath the nucleus (Fig. 2C and Movie 1).
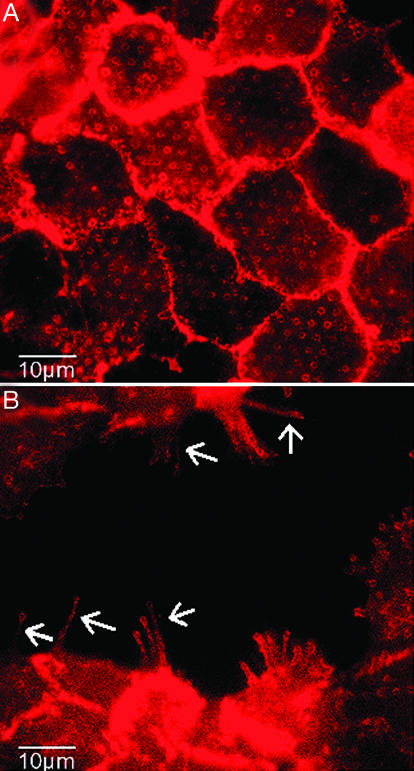
Immunofluorescence microscopy allows us to correlate traction stresses with spatial localization of proteins. Fig. 5 shows that F-actin partly colocalizes with the tips of the posts in both the absence (Fig. 5A) and the presence (Fig. 5B) of HGF. When cells are treated with HGF, we observe the formation of thin actin protrusions with ends localized at the top of the microposts (Fig. 5B). These results suggest that the organization of actin is directly related to local traction stresses. In contrast, E-cadherins are localized at the cell-cell junctions and not accumulated in the plasma membrane at the contact sites with the pillars (data not shown).
Fig. 5.
Immunofluorescence labeling of actin. Repartition of actin in the interior of a normal monolayer (A) and for a monolayer treated with HGF (B) for 6 h (100× oil objective). White arrows indicate actin-rich fibrillar structures due to dissociation of the epithelium.
We have also investigated the migratory dynamics of individual epithelial cells by treating cells with HGF/scatter factor. MDCK cells are grown on μFSA as illustrated in Fig. 8, which is published as supporting information on the PNAS web site, under subconfluent density conditions, leading to HGF-induced cell scattering (28). The disruption of cell-cell adhesion leading to scattering of individual cells on the substrate takes a few hours. Dissociation of the epithelium also induces cellular protrusions that seem to be actin-driven (Fig. 5B and ref. 5).
After dissociation, individual cells with a fibroblastoid morphology migrate on μFSA at a velocity of ≈1 μm/min (Fig. 6). Cell-to-substrate interactions show a deformation pattern where most forces near the leading edge of the cell are directed rearward and those of the posterior region are directed forward. Fig. 6 represents the force as a function of time for several posts under an individual cell. Maximal forces between 2 and 3 nN were detected at the leading edge. Such forces corresponding to traction stress values between 2.5 and 3.8 nN/μm2 are consistent with previous studies (14, 29).
Fig. 6.
Forces applied by a single motile cell during migration. (A) Temporal variation of the magnitude of forces exerted on four posts (a–d) during a 30-min-long experiment. Posts positions are shown on B; the colors of the circles drawn around each post correspond to the ones of the curves on A. (B) Cell position toward the chosen posts and corresponding intensity pictures at three different times. The yellow arrow represents the direction of migration. Intensity pictures are presented in grayscale (white, low forces; black, high forces). Cell border is figured by a black line. Times corresponding to the three pictures in B are reported on A by vertical brown dotted lines. Post d, chosen as control, is not covered by the cell. The dimensions of the posts used here are 5.2 μm in height and 1 μm in diameter. (Scale bar: 10 μm.)
Discussion
We have mapped the mechanical forces exerted by epithelial cells before and after the epithelial-mesenchymal transition by using an approach that combines microfabrication of flexible substrates and multiple-particle tracking microscopy. With this method, we could obtain a dynamic cartography of the developed forces with high spatial and temporal resolutions. As the fabrication process described here is quite simple, there is hope that this method might become a general tool for studying cell mechanics. The analysis of micropillar deflection directly gives rise to the mapping of exerted forces and so could be used to follow mechanical activity in real time, in contrast with computationally intensive techniques (14–17, 29, 30). Moreover, because each pillar is independent of its neighbors, the measured traction stresses under the cells are directly and unambiguously determined (18, 29).
Prior studies have analyzed the migration of individual cells. We have reported here the mechanical activity of an epithelial monolayer, showing that the highest average traction stress (≈1.6 nN/μm2) is localized at the edge and centripetally oriented. The scattering activity of epithelial cells induced by HGF allowed us to compare the force distribution under an established monolayer and under a moving single cell.
First, for a single migrating cell, the analysis of the traction pattern leads to an average value of 0.6 nN/μm2, taking into account the contributions of all of the underlying posts. Nevertheless, maximal stresses exerted by an isolated cell on a single post are found to be much larger than this average value, of the order of 3.8 ± 0.1 nN/μm2. Previous analyses (14, 29) have indicated a 5.5 nN/μm2 value relating force and contact area. Our experiments thus give comparable results, and the smaller value we obtained may be attributed to the different cell type we used or to an overestimated evaluation of the stress area in our experiments. Indeed, SEM observations indicate that adhesive contacts between cells and the pillars do not cover the entire surface (see arrows in Fig. 1C Inset).
We found also that it is feasible to compare single cell movements with a subconfluent epithelium. In this case, we have measured maximal traction stresses inside the epithelium of the order of 12.7 ± 0.3 nN/μm2. This significantly higher value hints that the stresses developed at the epithelium edges may be the result of a collective behavior.
Interestingly, we have also observed that the residual mechanical activity within a subconfluent epithelium is much larger than in a confluent monolayer. Indeed, the average value of forces, mostly localized at the cell-to-cell junctions inside islands of MDCK cells (meaning far from the edges), is of the order of 2 nN. In contrast, we observe no deformation of the pillars at confluent density in the same conditions of cell culture and on the same substrate.
We have demonstrated that microfabricated substrates can precisely detect mechanical activity in correlation with the presence of proteins involved in cell-to-cell or cell-to-substrate adhesions. Our further goal is to perform measurements on cells expressing GFP derivatives of focal adhesion proteins and molecules regulating cell-cell junctions.
The μFSA substrates made in PDMS present the advantage that they may easily be modified by changing their chemical or physical properties. Cell morphology can be controlled by surface chemistry (31, 32). Moreover, surface rigidity modifies cell adhesion and the forces exerted by cells on the substrate (12, 33). This method provides a way to easily measure forces from ≈50 pN to 150 nN.
μFSA substrates with a small spatial periodicity have make it possible to grow cells under standard culture conditions and to visualize their mechanical interactions with the surface. Here, we have used a 4 μm spatial resolution that is compatible with the observed deformations. Indeed, larger deflections of the posts would lead to interactions between successive pillars and then to nonresolved traction stress patterns. Nevertheless, we can still decrease the periodicity of the arrays by both increasing the spring constant of the pillars and improving the spatial resolution of the multiple particle tracking method down to 10 nm (34).
Supplementary Material
Acknowledgments
We thank P.-G. de Gennes, O. Cardoso, P. S. Doyle, J.-M. di Méglio, and T. Savin for helpful discussions concerning force calculations; N. Desprat and S. Warlus for calibration of the micropillars; A. Richert for cell culture; P. S. Doyle and T. Senden for critical readings of the manuscript; H. Boulekbache and D. Montero in Centre Interuniversitaire de Microscopie Electronique/Jussieu in Paris for SEM observations. This work was supported in part by grants from the “Ministère de la Recherche” (A.C.I. Jeunes chercheurs), the Association pour la Recherche contre le Cancer, the program “Dynamique et Réactivité des Assemblages Biologiques” from the Centre National de la Recherche Scientifique, and by Fondation de France postdoctoral grants (to O.d.R.). This work was performed in part at the Cornell Nano-Scale Science and Technology Facility (a member of the National Nanofabrication Users Network), which is supported by the National Science Foundation under Grant ECS-9731293, its users, Cornell University, and industrial affiliates.
Abbreviations: HGF, hepatocyte growth factor; MDCK, Madin-Darby canine kidney; μFSA, microdimensional force sensor array; PDMS, poly(dimethylsiloxane); SEM, scanning electron micrograph.
References
- 1.Adams, C. & Nelson, W. J. (1998) Curr. Opin. Cell Biol. 10, 572-577. [DOI] [PubMed] [Google Scholar]
- 2.Gumbiner, B. M. (1996) Cell 84, 345-357. [DOI] [PubMed] [Google Scholar]
- 3.Stoker, M., Gherardi, E., Perryman, M. & Gray, J. (1987) Nature 327, 239-242. [DOI] [PubMed] [Google Scholar]
- 4.Weidner, K. M., Sachs, M. & Birchmeier, W. (1993) J. Cell Biol. 121, 145-154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ridley, A. J., Comoglio, P. M. & Hall, A. (1995) Mol. Cell. Biol. 15, 1110-1122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Sheetz, M. P., Felsenfeld, D. P. & Galbraith, C. G. (1998) Trends Cell Biol. 8, 51-54. [DOI] [PubMed] [Google Scholar]
- 7.Burridge, K. & Chrzanowska-Wodnicka, M. (1996) Annu. Rev. Cell. Dev. Biol. 12, 463-518. [DOI] [PubMed] [Google Scholar]
- 8.Ingber, D. (1991) Curr. Opin. Cell Biol. 3, 841-848. [DOI] [PubMed] [Google Scholar]
- 9.Harris, A. K., Wild, P. & Stopak, D. (1980) Science 208, 177-179. [DOI] [PubMed] [Google Scholar]
- 10.Galbraith, C. G. & Sheetz, M. P. (1997) Proc. Natl. Acad. Sci. USA 94, 9114-9118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Lee, J., Leonard, M., Oliver, T., Ishihara, A. & Jacobson, K. (1994) J. Cell Biol. 127, 1957-1964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Pelham, R. J., Jr., & Wang, Y.-I. (1997) Proc. Natl. Acad. Sci. USA 94, 13661-13665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Burton, K. & Taylor, D. L. (1997) Nature 385, 450-454. [DOI] [PubMed] [Google Scholar]
- 14.Balaban, N. Q., Schwarz, U. S., Riveline, D., Goichberg, P., Tzur, G., Sabanay, I., Mahalu, D., Safran, S., Bershadsky, A., Addadi, L. & Geiger, B. (2001) Nat. Cell Biol. 3, 466-472. [DOI] [PubMed] [Google Scholar]
- 15.Dembo, M., Oliver, T., Ishihara, A. & Jacobson, K. (1996) Biophys. J. 70, 2008-2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Tolic-Norrelykke, I. M., Butler, J. P., Chen, J. & Wang, N. (2002) Am. J. Physiol. 283, C1254-C1266. [DOI] [PubMed] [Google Scholar]
- 17.Munevar, S., Wang, Y-L. & Dembo, M. (2001) Biophys. J. 80, 1744-1757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Schwarz, U. S., Balaban, N. Q., Riveline, D., Bershadsky, A., Geiger, B. & Safran, S. A. (2002) Biophys. J. 83, 1380-1394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Pelham, R. J., Jr., & Wang, Y. (1999) Mol. Biol. Cell 10, 935-945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Tan, J. L., Tien, J., Pirone, D. M., Gray, D. S., Bhadriraju, K. & Chen, C. S. (2003) Proc. Natl. Acad. Sci. USA 100, 1484-1489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.du Roure, O., Dequidt, C., Richert, A., Austin, R. H., Buguin, A., Chavrier, P., Silberzan, P. & Ladoux, B. (2004) Proc. SPIE Int. Soc. Opt. Eng. 5345, 26-34. [Google Scholar]
- 22.Landau, L. & Lifchitz, E. (1990) in Théorie de l'Élasticité (M.I.R., Moscow) 2nd Ed., pp. 107-126.
- 23.Singhvi, R., Kumar, A., Lopez, G. P., Stephanopoulos, G. N., Wang, D. I., Whitesides, G. M. & Ingber, D.E. (1994) Science 264, 696-698. [DOI] [PubMed] [Google Scholar]
- 24.Tien, J. & Chen, C. S. (2001) in Methods of Tissue Engineering, ed. Lanza, R. (Academic, San Diego), pp. 113-120.
- 25.Thoumine, O. & Ott, A. (1997) J. Cell Sci. 110, 2109-2116. [DOI] [PubMed] [Google Scholar]
- 26.Cheezum, M. K., Walker, W. F. & Guilford, W. H. (2001) Biophys. J. 81, 2378-2388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Choquet, D., Felsenfeld, D. P. & Sheetz, M. P. (1997) Cell 88, 39-48. [DOI] [PubMed] [Google Scholar]
- 28.Balkovetz, D. F. (1999) Life Sciences 64, 1393-1401. [DOI] [PubMed] [Google Scholar]
- 29.Dembo, M. & Wang, Y. L. (1999) Biophys. J. 76, 2307-2316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Beningo, K. A., Dembo, M., Kaverina, I., Small, J. V. & Wang, Y. L. (2001) J. Cell Biol. 153, 881-887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Brock, A., Chang, E., Ho, C.-C., LeDuc, P., Jiang, X., Whitesides, G. M. & Ingber D. E. (2003) Langmuir 19, 1611-1617. [DOI] [PubMed] [Google Scholar]
- 32.Gallant, N. D., Capadona, J. R., Frazier A. B., Collard D. M. & Garcia A. J. (2002) Langmuir 18, 5579-5584. [Google Scholar]
- 33.Yeung, T., Georges, P. C., Flanagan, L. A., Marg, B., Ortiz, M., Funaki, M., Zahir, N., Ming, W., Weaver, V., & Janmey, P. A. (2005) Cell Motil. Cytoskeleton 60, 24-34. [DOI] [PubMed] [Google Scholar]
- 34.Savin, T. & Doyle, P. S. (2005) Biophys. J. 88, 623-638. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.