Summary
To facilitate comparative treatment selection when there is substantial heterogeneity of treatment effectiveness, it is important to identify subgroups that exhibit differential treatment effects. Existing approaches model outcomes directly and then define subgroups according to interactions between treatment and covariates. Because outcomes are affected by both the covariate–treatment interactions and covariate main effects, direct modeling outcomes can be hard due to model misspecification, especially in presence of many covariates. Alternatively one can directly work with differential treatment effect estimation. We propose such a method that approximates a target function whose value directly reflects correct treatment assignment for patients. The function uses patient outcomes as weights rather than modeling targets. Consequently, our method can deal with binary, continuous, time-to-event, and possibly contaminated outcomes in the same fashion. We first focus on identifying only directional estimates from linear rules that characterize important subgroups. We further consider estimation of comparative treatment effects for identified subgroups. We demonstrate the advantages of our method in simulation studies and in analyses of two real data sets.
Keywords: Comparative effectiveness, Heterogeneity of treatment effectiveness, Regularization, Subgroup, Variable selection
1. Introduction
Subgroup identification for differential outcomes is becoming an increasingly important methodological research topic in this era of personalized medicine and high medical costs (Ruberg, Chen, and Wang, 2010). Identification of subgroups via valid predictive markers can facilitate tailored intervention to maximize effectiveness. The controversy and challenges of subgroup identification have been well documented (Brookes et al., 2004; Lagakos, 2006; Ruberg et al., 2010). Yet there are still great needs for descriptive and exploratory subgroup identification using existing data to develop new hypothesis, to facilitate study population selection for further investigation, and to generate new evidence for medical decision making (Varadhan et al., 2013).
The classical approach to identify subgroups involves fitting of a parametric outcome model which includes covariate main effects as well as interactions between covariates and treatment. Subgroups are identified based on significance of specific interaction terms (Kehl and Ulm, 2006). Besides the multiplicity issue, misspecification of the main effects in the presence of many covariates interferes with the covariate–treatment interaction estimation and thus impedes valid subgroup identification. Nonparametric approaches based on the classification and regression tree methodology (Breiman et al., 1984) were attempted to separate the main effects from the covariate–treatment interaction effects, either through multiple testing strategies (Su et al., 2008, 2009; Lipkovich et al., 2011; He, 2012) or prediction (Foster, Taylor, and Ruberg, 2011). For example, Su et al. (2009) developed an interaction tree method by building splitting rules based on covariate– treatment interaction tests. Foster et al. (2011) developed the virtual twins method by first estimating treatment differences based on random forests and then applying tree to those estimates to form subgroups. Alternatively, Cai et al. (2011) built in calibration steps to alleviate the model misspecification problem when using parametric or semiparametric models.
In this article, we propose an approach that works directly with differential treatment effect estimation. Instead of modeling the outcome, we use a causal inference formulation (Zhao et al., 2012) that leads to a target function directly reflecting the covariate–treatment interaction effect. This spares the need to model the covariate main effects. The function uses patient outcomes as weights rather than modeling targets. Consequently, our method can deal with binary, continuous, time-to-event, and possibly contaminated outcomes in the same fashion, and can be implemented using existing packages. Foster et al. (2011) pointed out that instead of focusing on finding the optimal or largest subgroup with enhanced treatment effects, it may be more desirable to determine a sub-optimal subgroup from simple and interpretable predictive variables. Similar to Imai and Ratkovic (in press), we focus on linear rules and build in smoothness constraints that allow the resulting subgroup to be more interpretable. Recent applications often involve a large number of covariates. Considering covariate–treatment interaction terms also increases the dimension of the covariate matrix. Thus, we add a regularization step in the subgroup identification process. The framework and details of our methodology are given in Section 2. We note that such regularization has been used in dynamic treatment regimens (Song et al., in press).
Our motivating example is a mammography screening randomized trial that tested the efficacy of interventions to promote mammography screening among eligible women who were 51 years or older (Champion et al., 2007). Data were collected from 09/01/96 to 11/30/02. Different from the usual drug trial, this study intended to change health behavior of the study subjects, which was more complicated and challenging. Besides establishing an overall efficacy, it was also highly desirable to determine whether the interventions were more effective for certain subgroups determined by their social and behavioral variables. For this reason, in addition to demographics and social economic variables, the study collected many health behavioral variables such as self-efficacy, susceptibility, knowledge, fear, fatalism, benefits, and barriers based on the well-established Health Belief Model (Janz and Becker, 1984). These variables intended to capture corresponding behavioral constructs. If interventions benefit subjects differently according to their characteristics, then they can be applied more cost-effectively. In addition, newer interventions can be designed to target relevant behavioral constructs and other modifiable characteristics. It is therefore highly desirable that the resulting treatment assignment rules are interpretable and simple. For this purpose, we focus on finding one-way and two-way interactions among the covariates and interventions. Nevertheless, a large number of variables still need to be investigated due to the many levels of the behavioral variables, prompting us to focus on parsimonious and interpretable models.
In Section 2, we argue that for many popular models, it suffices to find the optimal linear rule. The linearity allows regularization that can lead to sparse solutions, in contrast with Zhao et al. (2012). In Section 3, we develop an inference procedure on the enhanced treatment effects to further evaluate the benefit of the identified subgroup. Such a step is important to aid practical decision making. Our method is compared with some other recent subgroup identification methods, including a sparse version of Zhao et al. (2012), through simulation studies in Section 4, and is applied to two real life examples in Section 5. We conclude with a discussion of our findings and future work in Section 6.
2. Subgroup Identification
Assume data are collected from a randomized trial with a binary treatment T ∈ {−1, 1 being according to P(T = 1) = π a clinical outcome Y, and a p-dimensional covariates vector X = (X1,…, Xp)′. We allow X to contain derived covariates such as interaction terms as well as dummy variables for categorical covariates. Let be an assignment rule based on X, P the distribution of (Y, T, X) in the data and the distribution of (Y, T, X) given that . Then, the expected outcome under the rule is given by (Qian and Murphy, 2011; Zhao et al., 2012; Zhang et al., 2012)
where I(·) is the indicator function. Our main goal is to assign each individual to an appropriate treatment based on X to optimize the clinical outcome. Assuming larger Y is preferable, we want to find the optimal rule that maximizes , or equivalently
| (1) |
In general, the optimal rule could be a very complicated function of X. However, we show in the following proposition that, under mild conditions, the optimal rule only depends on the sign of a linear function of X.
Proposition 1
Suppose E(Y|T, X) = h(X, T X′ β†), where for any real number a ∈ R, the bivariate function h(a, b) satisfies h(a, b) ≥ h(a, −b) for b ≥ 0 and h(a, b) < h(a, −b) for b < 0. Then, for almost surely any fixed x, sign = (x′ β†), where sign(x) = 1 if x ≥ 0 and sign(x) 1= − 1 otherwise.
Indeed, many popular statistical models satisfy the requirements of Proposition 1, including the following two classes of models.
Example 1
The response Y follows a single index model, E(Y|T, X) = h{l(X) + g(T X′ β†)}, where h(x) and g(x) are increasing functions. This example satisfies the assumptions in Proposition 1 and includes the logistic model as a special case. The optimal rule is unrelated to l(X), the main effects of X, which may not be linear in X.
Example 2
The response Y is a time-to-event variable and follows the Aalen-Cox model λY(y|X, T) = λ0(y, X) exp(−TX′β†). In right-censored data, Y is censored by another variable C where C is independent of (Y, T) given X. That is we only observe Y ∧ C = min(Y, C). Then , where G(u|X) is the conditional survival distribution of C given X. Therefore, by considering Y ∧ C as the outcome, we have and h satisfies the conditions in Proposition 1.
Obviously, one way to find the optimal rule is to estimate β† by modeling E(Y|T, X) = h(X, T X′β†) directly. However, unless the form of h is simple and the dimension of X is low, this outcome modeling based approach may not be preferable as model misspecification can be severe. On the other hand, as implied by Proposition 1, correct treatment selection may not depend so much on the outcome model. Important variables for predicting the outcome also may not be relevant for treatment selection (Janes et al., 2011; Sargent and Mandrekar, 2013). Even if h is a complicated function, the resulting treatment assignment rule can still be very simple and interpretable. For this reason, in the rest of this article we focus on finding a linear rule with
| (2) |
Under the assumptions of Proposition 1, β† is one solution. If β∗ is a solution, so is kβ∗ for any positive constant k, since for any k > 0.
The 0–1 loss in (2) is not only non-convex but also non-continuous. In practice, it is computationally hard to solve (2). Similar to the common practice in classification algorithms (Bartlett, Jordan, and McAuliffe, 2006), we propose to replace the 0–1 loss with a convex and continuous surrogate loss ϕ(·) and solve the following optimization problem:
| (3) |
Since (3) is a convex optimization problem, is its unique solution. We approximate the optimal rule . In general, can differ from β* due to the surrogate loss ϕ(·). In some cases, and β† differ only by a multiplier and, hence, . One example is when E(Y|T, X) = h(T X′β†) for some function h and when the conditional expectation E(X′b|X′β†) is linear in X′β† for any b ∈ Rp. This latter condition is satisfied when the distribution of X is elliptically symmetric, for example the normal distribution (Li, 1991). Even if the distribution of X is not exactly elliptically symmetric, Li (1991) argued that for most directions b, E(X′b|X′β†) is approximately linear in X′β†. Hence is expected to be approximately parallel to β†, which makes a good approximation of sign(X′β†).
In applications, we solve (3) with expectation being replaced by the sample average based on independent samples (Yi, Ti, Xi), i = 1,…, n, identically distributed as (Y, T, X). The dimension of β in (3) could be very high, especially when we include interactions between covariates. Hence, we propose to add two sparsity induced penalties and solve
| (4) |
where ‖β‖1 is the L1 norm of β. The second penalty η(β) is optional and is imposed on the effects of ordinal variables with more than two levels. It could combine adjacent levels of such ordinal variables to result in simpler interpretation. In particular, we use a fused LASSO penalty (Tibshirani et al., 2004). For example, if one ordinal variable has Cj levels, then the corresponding penalty term is where If there are no ordinal variables or if there is no strong evidence that adjacent levels of an ordinal variable can have similar effects, we can also remove the corresponding fused LASSO penalty. As discussed in Section 1, the solution directly reflects the covariate-treatment effects. Subgroups of patients that receive different treatment effects could be identified according to the non-zero elements of . Finally, our empirical rule is defined as .
Since β̃ and β∗ may be different, in Section 3 we propose an inference procedure to characterize the treatment effects for the identified subgroup. The validity of the inference procedure hinges on the stability of . We therefore prove a theoretical property of to ensure the validity of the proposed procedure. We show in the Web Appendix A the consistency of to as both n and p diverge to infinity with n−1 log p → 0. The results are shown for the case of bounded Y under the logistic loss: ϕ(x) = log(1 + e−x), but can be easily extended to other types of outcomes. We also assume that X contains both categorical and continuous covariates as well as their pairwise interactions. In particular, we show that possesses the weak oracle property (Fan and Lv, 2011), namely with large probability, identifies all zero components of and gives consistent estimates to non-zero components of in a rate slower than .
3. Inference on Enhanced Comparative Treatment Effects
To evaluate the effect of subgroup identification, we consider the following quantity measuring the improvement of response when assigning subgroups of subjects to appropriate treatments:
| (5) |
The actual comparative treatment effect for the subgroup identified for T = 1 via is reflected by , and the mean effect is for the identified subgroup. The expectation EX is with respect to X and we treat βˆ as “fixed” for future studies, similar to Foster et al. (2011). Correspondingly, the actual comparative treatment effect for the subjects identified for T = −1 is reflected by , and the mean effect is. Ideally, both and should be as large as possible. However it is also likely that one of them is small, for example when T = –1 is an inactive control. Inference about both and is important and can aid practical decision making regarding the identified subgroups.
In the following, we propose a bootstrap method to construct confidence intervals (CIs) for and . If such intervals only contain positive numbers, we conclude that subgroup identification is indeed beneficial for treatment enhancement. We consider cases when P(X′β† = 0) = 0 and when P(X′β† = 0) > 0. The first case is regular and we can use the usual bootstrap. The second case is irregular (Shao, 1994; Laber and Murphy, 2011) due to a non-negligible probability concentrated at the discontinuous points of as a function of . In this case, we adopt the m-out-of-n bootstrap (Shao, 1994; Bickel, Götze, and van Zwet, 1997; Chakraborty, Laber, and Zhao, 2013). The method uses the bootstrap sample size m smaller than n to asymptotically avoid the non-negligible probability concentrated at the discontinuous points. Usually m is chosen as nα for some α < 1. Chakraborty et al. (2013) used α = 0.8. We also adopt this choice in our simulation and data analysis. Some preliminary sensitivity analysis on different choices of α is presented in the Web Appendix D. In practice, if many covariates are continuous, we can use the ordinary bootstrap (Moodie and Richardson, 2010). If many covariates are categorical, we propose to use m-out-of-n bootstrap.
Let {(Yi, Ti, Xi), i = 1,…, n} be the original dataset. The m-out-of-n bootstrap algorithm comprises the following two steps.
Step 1: Generate a bootstrap sample with size , from the original dataset. Obtain the corresponding estimates . Let , , , and |Aj| be the size of the set Aj for j = 1, 2, 3, and 4. Calculate and .
Step 2: Repeat Step 1 B times. Let and be the α/2 and 1−α/2 quantiles of , and and corresponding quantiles of respectively. Then, the (1 − α) CI of is given by and the (1 − α) CI of is given by .
4. Numerical Results
In this section, we consider binary outcomes. Some of our simulation studies for time-to-event outcomes are presented in the Web Appendix B. We numerically compare our proposed regularized outcome weighted subgroup identification (ROWSi) method with some other recent subgrouping methods: (1) the FindIt by Imai and Ratkovic (in press), (2) the virtual twins (VT) by Foster et al. (2011), (3) the interaction tree (IT) by Su et al. (2009), (4) the logistic regression with LASSO penalty (logLASSO) by Qian and Murphy (2011), 5) the L1-penalized support vector machine (L1-SVM) method adapted from Zhao et al. (2012).
To implement the FindIt, we used the R package FindIt developed by Imai and Ratkovic with optimal tuning parameters chosen by their algorithm. We only considered two-way or three-way interactions among the treatment and covariates. To implement the VT, we first used the R function<monospace>randomForest</monospace>to estimate individual treatment effect for subject i, and the average treatment effect Then, we assigned subjects to treatment T = 1 if their individual treatment effects were greater than the average effect plus a constant, 0.05, as in Foster et al.(2011). We also followed Foster et al.(2011) for the choices of the terminal node size and complexity parameter. For the IT method, we first grew a large regression tree, where each split was induced by a threshold on some selected covariates. We then pruned the tree and selected the best-sized subtree based on an interaction-complexity measurement and an additional penalty on the total number of internal nodes (Su et al., 2009).
In presence of a large number of interaction terms especially when many categorical variables exist, we adopted two options in our method. For the first option, we used a screening step similar to the sure independence screening method (Fan and Lv, 2008) to ease the computational burden of solving (4). In particular, we used a group LASSO procedure (Yuan and Lin, 2005) to pre-screen the interaction terms at the variable level in (4). For example, for the interaction between one variable with Cj levels and one variable with Ck levels, we treated the total Cj × Ck levels of interactions as a group and imposed a group LASSO penalty on it. For the second option, we abandoned this interaction screening step and directly solved (4). We chose tuning parameters λ1n and λ2n by the Akaike Information Criterion (AIC). We labeled our method using the latter option as “ROWSi–onestep” which allows us to investigate the advantage from the “screening step.”
All of our simulated data sets contained five binary covariates XA, XB, XC, XD, XE, five ordinal covariates Xa, Xb, Xc, Xd, Xe and one continuous covariate XCa. Here we use capital letters in the subscript for binary variables, small letters for ordinal variables, and Ca for the continuous variable. For binary covariates, we use, for example XA1, to denote the case level of XA. For ordinal covariates, we use, for example Xa3 to denote the third level of Xa. All binary covariates were simulated from the Bernoulli distribution with success probability of 1/2. All ordinal covariates had four uniformly distributed levels. The continuous covariate was simulated from the standard normal distribution. The treatment T was independent of the aforementioned covariates and took values of −1 and 1 with equal probabilities. We examined three different sample sizes: n = 500, 1000, and 2000 for each simulated data set and ran 200 simulations in each setting.
We considered a variety of models for logit P(Y = 1) as follows.
0.5XC1 + 2(XB1 + Xa3∗XA1)∗T;
0.5XC1 + 2{XB1 + Xa3∗(Xb2 + Xb3)}∗T
0.05(−XA1+XB1)+{(Xa2 +Xa3)+(Xb2 +Xb3)∗XCa}∗T;
log log{(Xb3 + Xc3) + 5(Xa2 + Xa3+XA1XB1)∗T + 20}2;
(XA1 + XB1) + 2∗;
0.5XA1 + 0.5XB1 + 2I{XCa < 5, Xa < 2}∗T
0.5XA1 + 0.5XB1 + 2I{XCa < 5, XCb < 2}∗T
0.5XCa + 0.5XCb + 2I{XCa < −2, XCb > 2}∗T
Models (A)–(C) are logistic models with various interaction structures. In particular, Model (A) has one main effect (XC1), one first-order interactions (XB1 ∗ T), and one second-order interaction (Xa3 *XA1*T). Model (B) is similar to (A) but has different second-order interactions. Model (C) has more complicated structure of main effects and interaction effects. Model (D) is not a logistic model and can be used to compare the robustness of different methods in case of link function misspecification. Model (E) is a logistic model without covariate–treatment interactions. Models (F)–(H) take treelike forms which are not linear in terms of covariates.
We evaluated the performance of each method by four criteria: sensitivity, specificity, prediction accuracy, and the expected outcome under the resulting rules (a.k.a the value function, Zhao et al. (2012)). Sensitivity is the proportion of true non-zero interactions (including both first-order and second-order interactions) being estimated as non-zero. Specificity is the proportion of true zero interactions being estimated as zero. Prediction accuracy is the proportion of empirical treatment assignments, , that are consistent to the “oracle” assignments sign(X′β†). Finally, interaction term selection accuracy is the proportion of a particular interaction term being selected.
To evaluate the sensitivity and specificity, Figure 1 plots the product of sensitivity and specificity for each method. Our method appears to outperform the competitors notably. Figure 2 plots prediction accuracy. Again, our method seemingly surpasses all other methods in almost all settings except under Model (H), where the true assignment rule is not linear. We present comparison of the value function in the Web Appendix C.
Figure 1.
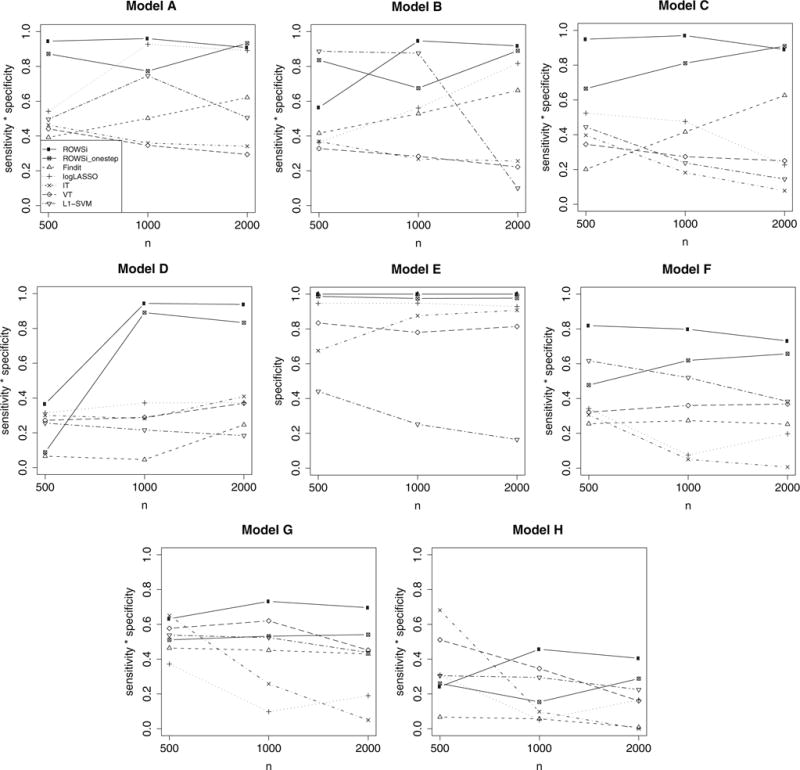
Comparison of the product of sensitivity and specificity by seven methods, represented by various types of points and lines as in the legend of Model A (number of simulations = 200).
Figure 2.
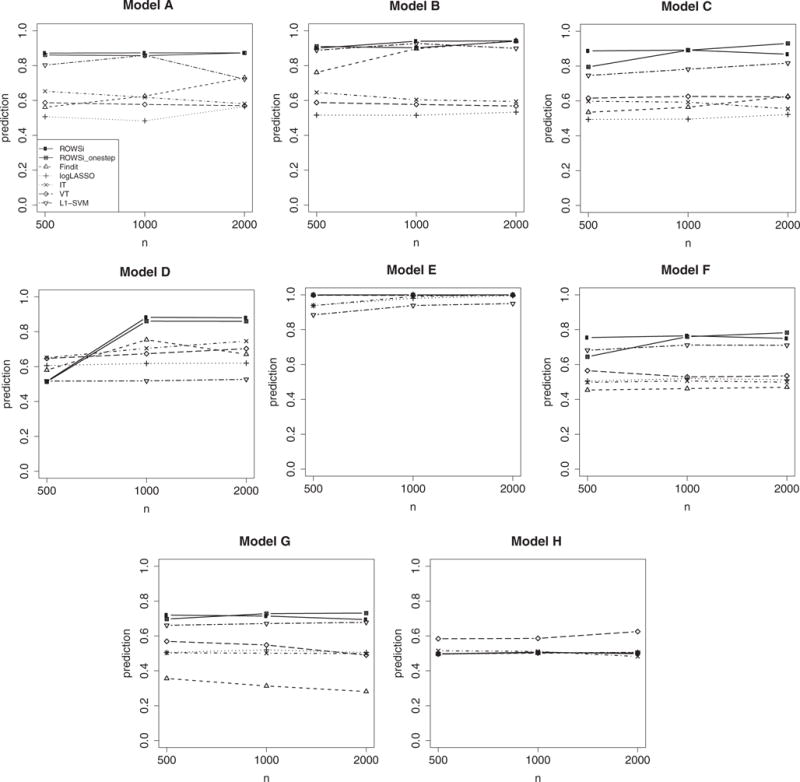
Comparison of prediction accuracy by seven methods, represented by various types of points and lines as in the legend of Model A (number of simulations = 200).
We used Models (A) and (C) to illustrate the construction of CI for enhanced comparative treatment effects. Model (A) does not satisfy the property that P(X′β† = 0) = 0 whereas Model (C) does. Hence, we used the m-out-of- n bootstrap for Model (A) and the regular bootstrap for Model (C). The bootstrap resampling was repeated for 1000 runs, from which a CI was obtained. We ran the above procedures for 1000 repetitions and report the mean length of CIs in Table 1. The length of CIs decreases as n increases. We also see that all CIs only include positive numbers, which indicates that treatment effects are enhanced in the subgroups identified by our method. In addition, we also report the coverage probabilities of the CIs for and . Both of the two expectations were evaluated from a large independent testing data set with a sample size of 100,000. The performance seems satisfactory when the same size is 2000. There is some over-coverage when n = 1000. We noted that the performance depended on the choice of α in the m-out-of-n bootstrap. For this reason, we also investigated the sensitivity of this choice in Web Appendix D. Instead of a subjective choice, a double bootstrap procedure (Davison and Hinkley, 1997; Chakraborty et al., 2013) can be used for choosing α in a data-driven manner. Due to its computational intensity, we do not pursue here.
Table 1.
Confidence intervals of enhanced comparative treatment effects in Models (A) and (C). Reported values are the means from 1000 repetitions, each of which uses 1000 subsamples for the bootstrap. For notational simplicity, we denote and .
|
n = 500
|
n = 1000
|
n = 2000
|
||||
|---|---|---|---|---|---|---|
| d+ | d− | d+ | d− | d+ | d− | |
| Model (A) | ||||||
| CI length MEAN coverage |
0.55 | 0.57 | 0.41 | 0.34 | 0.24 | 0.24 |
| 0.93 | 0.98 | 0.97 | 0.99 | 0.96 | 0.96 | |
| Model (C) | ||||||
| CI length MEAN coverage |
0.17 | 0.19 | 0.13 | 0.14 | 0.09 | 0.10 |
| 0.93 | 0.94 | 0.97 | 0.97 | 0.95 | 0.96 | |
5. Data Analysis
In this section, we apply our proposed method to two real studies and compare it with the FindIt, VT and IT methods. The first is the National Supported Work (NSW) study (LaLonde, 1986) that appeared in Imai and Ratkovic (in press) and the FindIt package. The second is the mammography screening study discussed in the introduction section.
5.1. National Supported Work Study
In the NSW study, a training program was administered to a heterogeneous group of workers. The treatment is randomly assigned to each subject. It is of interest to investigate whether the treatment effect varies as a function of individual characteristics. The treatment and control groups consist of 297 and 425 individuals, respectively. There are seven pre-analysis covariates including age, years of education, logarithm of annual earnings, race, marriage status, college degree status, and employment status. Including first and second order interactions, there are 45 covariates in total. The response is whether there is an increase on earnings from the year of 1975–1978.
Our method indicated that being married, having no high school degree and lower earnings had positive effects from the program; being Hispanics, employed, and having older age with higher earnings had negative effects. The FindIt method found that black people, people having lower education were positively affected by the program, but Hispanics who had higher earnings were negatively affected. The VT method found that the youth with lower earnings tended to get benefits. The IT method found that the white youth with lower earnings, or the youth with lower earnings and lower education tended to get benefits. The detailed resulting rules for subgroup identification from these methods are included in Web Appendix E.
To compare the performance of various methods, we randomly used 4/5 of samples (rounded to integers) as training sets to tune penalty parameters and the rest as test sets to evaluate the enhanced comparative treatment effects. The procedures were repeated for 200 random splits and the mean enhanced treatment effects are reported in Table 2. The estimated comparative treatment effects of each training set were estimated from the following formula:
where nT is the sample size of the corresponding test set and t = 1 or −1. The assignment rules were determined from the comparison methods and the training set. Results are shown in Table 2, including average subgroup sizes from the 200 random training sets. We see that our method led to higher increments of response rate than the other methods. Based on the whole data, we further calculated the 95% CIs for and using the m-out-of-n bootstrap, which were (6.92%, 23.90%) and (3.03%, 21.41%), respectively. Since 0 is not contained in the above two intervals, we conclude that the treatment effects were likely enhanced in the subgroups identified by our method.
Table 2.
NSW study: the average estimated enhanced comparative treatment effects and subgroup sizes based on cross-validation. The cross-validation used 200 random splits and reported values are the means from these random splits. For notational simplicity, we denote and
| Enhanced treatment effect (subgroup size)
|
|||||
|---|---|---|---|---|---|
| ROWSi | FindIt | VT | IT | ||
|
|
18.9% (121) | 5.61% (74) | 3.53% (97) | 3.66% (106) | |
|
|
4.5% (23) | −2.34% (70) | −3.84% (47) | −5.66% (38) | |
5.2. Mammography Screening Study
This is a randomized study that included female subjects who were non-adherent to mammography screening guidelines at baseline (i.e., no mammogram in the year prior to baseline) (Champion et al., 2007). One primary interest of the study was to compare the intervention effects of phone counseling on mammography screening (phone intervention) versus usual care at 21 months post-baseline. The outcome is whether the subject took mammography screening during this time period. There are 530 subjects with 259 in the phone intervention group and 271 in the usual care group. There are 16 binary variables, including socio-demographics, health belief variables, and stage of readiness to undertake mammography screening, and 1 categorical variable, number of years had a mammogram in past 2 to 5 years, in the study. Considering the covariates’ main effects and the first and second order interactions with T, there are 409 covariates in total.
Our method found that people having more past mammograms or with higher self efficacy score benefited from the phone intervention. On the other hand, people with low household income or higher barriers scale score were negatively affected by the phone intervention. The FindIt method did not find any covariate–treatment interaction. The VT method found that people having more past mammograms and at the ready stage with higher household income, or married people with fewer past mammograms and at the ready stage benefited from the phone intervention. The IT method found that people having more past mammograms, or people who were at the ready stage with higher household income benefited from the phone intervention. The resulting rules from these methods are included in Web Appendix E.
Similar to the cross-validation procedure we used for Table 2, we report the average estimated enhanced treatment effects and subgroup sizes in Table 3. Due to the smaller sample size, we used half-half random splits. Our identified subgroups again have higher increments of response rate than the other methods on average. We were not able to obtain for FindIt because it did not find any covariate-treatment interaction in many training sets. We further calculated the 95% CIs for and for our method using the m-out-of-n bootstrap, which were (5.88%, 11.21%) and (4.39%, 10.91%) respectively. The CIs do not include 0, indicating plausible identifications for subgroups.
Table 3.
Mammography screening study: the average estimated enhanced comparative treatment effects and subgroup sizes based on cross-validation. The cross-validation used 200 random splits and reported values are the means from these random splits. For notational simplicity, we denote and
| Enhanced treatment effect (subgroup size)
|
|||||
|---|---|---|---|---|---|
| ROWSi | FindIt | VT | IT | ||
|
|
7.88% (149) | 2.83% (265) | 3.58% (135) | 3.42% (126) | |
|
|
6.89% (116) | NA | 0.38% (130) | 3.10% (139) | |
6. Conclusion and Discussion
In this article, we proposed a regularized outcome weighted method for subgroup identification. The method differs from many existing methods for subgroup identification in that it is based on a target function that directly relates to covariate-treatment interaction. Such separation from the covariate main effects is important as these main effects usually affect the estimation of interactions. Because the clinical outcomes are used as weights instead of as modeling targets, our method can be extended to deal with continuous, time-to-event, and possibly contaminated outcomes. Another advantage of our method is that it could be easily implemented by using standard packages. In fact, under the logistic surrogate loss ϕ (x) = log(1 + e−x), if the regularization part of (4) is ignored, we can essentially solve
based on a logistic regression model for T weighted by outcomes. This can be conveniently fitted using standard packages such as the SAS LOGISTIC procedure by using subject-specific weights. For more general settings, we have presented some codes in the Web Appendix F. To keep it easier for the readers to implement, we have only presented codes that use LASSO as the penalty. We are developing an R package that will also incorporate the fused LASSO penalty.
We demonstrated the impressive performance of our method compared with other methods in various settings. Moreover, we not only identified the subgroups, but also carried out an additional inference procedure to assess how much benefit such a subgroup identification procedure could bring. Our approach for subgroup identification is mainly used to determine the rules for treatment assignment. This should be distinguished from other approaches for “subgroup identification” that focus on identifying some natural regions in the covariate space with enhanced treatment effects with no implication that the complement of that region constitutes another subgroup with a negative treatment effect (Kehl and Ulm, 2006; Lipkovich et al., 2011; Dusseldorp and Van Mechelen, 2014). This distinction is important as it may lead to different strategies in personalized medicine: one is to find the right drugs for patients and the other to find right patients for drugs.
For simplicity of presentation, we have assumed a complete randomization scheme from clinical trial data, that is P(T = 1) = π. Our method also works when the treatment assignment depends on X, that is, P(T = 1|X) = π(X) by replacing Tπ + (1 − T)/2 in (1)–(4) with Tπ(X) + (1–T)/2. The approach can also be extended to multiple interval treatments. The framework will be similar to dynamic treatment regimes, which are customized sequential decision rules for individual patients that can adapt over time to an evolving illness (Murphy, 2003; Zhao et al., in press). We can generalize the proposed method based on dynamic programming, which identifies the best rule at each interval backwards and recursively.
Zhang et al. (2012) showed that the optimal treatment regime could be regarded as the solution of the classification problem that , in which C (X) = E(Y|T = 1, X) − E(Y|T = −1, X) is the treatment contrast. Our formulation in (1) can be generalized by using C(X) based subject-specific weight. However, C(X) is unknown and needs to be estimated. Zhang et al. (2012) proposed a doubly robust estimator of C(X), which protects the estimation against model misspecification, especially when treatment assignment probabilities are known as in a randomized clinical trial. It will be of great interest to further investigate such a procedure as well as its theoretical properties.
Supplementary Material
Acknowledgments
The research efforts were partly supported by the University of Wisconsin Carbone Cancer Center support grant, NIH/NIA P30 CA014520 (for Drs. Menggang Yu and Yaoyao Xu), a development fund from the University of Wisconsin Carbone Cancer Center (for Dr. Menggang Yu), and NIH 5 R01 HG007377-02 (for Dr. Sijian Wang).
Footnotes
Supplementary Materials
Web Appendices and program codes, referenced in Sections 2–5, are available with this paper at the Biometrics website on Wiley Online Library.
References
- Bartlett PL, Jordan MI, McAuliffe JD. Convexity, classification, and risk bounds. Journal of the American Statistical Association. 2006;101:138–156. [Google Scholar]
- Bickel PJ, Götze F, van Zwet WR. Resampling fewer than n observations: Gains, losses, and remedies for losses. Statistica Sinica. 1997;7:1–31. [Google Scholar]
- Breiman L, Friedman JR, Stone CJ, Olshen R. Classification and Regression Trees. Wadsmith: Chapman and Hall; 1984. [Google Scholar]
- Brookes ST, Whitely E, Egger M, Smith GD, Mulheran PA, Peters TJ, et al. Subgroup analyses in randomized trials: Risks of subgroup-specific analyses; power and sample size for the interaction test. Journal of Clinical Epidemiology. 2004;57:229. doi: 10.1016/j.jclinepi.2003.08.009. [DOI] [PubMed] [Google Scholar]
- Cai T, Tian L, Wong PH, Wei L. Analysis of randomized comparative clinical trial data for personalized treatment selections. Biostatistics. 2011;12:270–282. doi: 10.1093/biostatistics/kxq060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chakraborty B, Laber EB, Zhao Y. Inference for optimal dynamic treatment regimes using an adaptive m-out-of-n bootstrap scheme. Biometrics. 2013;69:714–23. doi: 10.1111/biom.12052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Champion V, Skinner CS, Hui S, Monahan P, Juliar B, Daggy J, Menon U. The effect of telephone v. print tailoring for mammography adherence. Patient Education and Counseling. 2007;65:416. doi: 10.1016/j.pec.2006.09.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davison AC, Hinkley DV. Bootstrap Methods and Their Applications. Cambridge: Cambridge University Press; 1997. [Google Scholar]
- Dusseldorp E, Van Mechelen I. Qualitative interaction trees: A tool to identify qualitative treatment Subgroup interactions. Statistics in Medicine. 2014;33:219–237. doi: 10.1002/sim.5933. [DOI] [PubMed] [Google Scholar]
- Fan J, Lv J. Sure independence screening for ultrahigh dimensional feature space. Journal of the Royal Statistical Society, Series B. 2008;70:849–911. doi: 10.1111/j.1467-9868.2008.00674.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan J, Lv J. Nonconcave penalized likelihood with npdimensionality. IEEE Transactions on Information Theory. 2011;57:5467–5484. doi: 10.1109/TIT.2011.2158486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foster JC, Taylor JM, Ruberg SJ. Subgroup identification from randomized clinical trial data. Statistics in Medicine. 2011;30:2867–2880. doi: 10.1002/sim.4322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He X. PhD thesis. University of Wisconsin-Madison; 2012. Identification of subgroups with large differential treatment effects in genome-wide association studies. [Google Scholar]
- Imai K, Ratkovic M. Estimating treatment effect heterogeneity in randomized program evaluation. Annals of Applied Statistics. 2013;7:443–470. [Google Scholar]
- Janes H, Pepe M, Bossuyt P, Barlow W. Measuring the performance of markers for guiding treatment decisions. Annals of Internal Medicine. 2011;154:253–9. doi: 10.1059/0003-4819-154-4-201102150-00006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janz N, Becker M. The health belief model: A decade later. Health Education Quarterly. 1984;11:1–47. doi: 10.1177/109019818401100101. [DOI] [PubMed] [Google Scholar]
- Kehl V, Ulm K. Responder identification in clinical trials with censored data. Computational Statistics & Data Analysis. 2006;50:1338–1355. [Google Scholar]
- Laber EB, Murphy SA. Adaptive confidence intervals for the test error in classification. Journal of the American Statistical Association. 2011;106:904–13. doi: 10.1198/jasa.2010.tm10053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lagakos SW. The challenge of subgroup analyses – Reporting without distorting. New England Journal of Medicine. 2006;354:1667–1669. doi: 10.1056/NEJMp068070. [DOI] [PubMed] [Google Scholar]
- LaLonde R. Evaluating the econometric evaluations of training programs with experimental data. American Economic Review. 1986;76:604–20. [Google Scholar]
- Li KC. Sliced inverse regression for dimension reduction. Journal of American Statistical Association. 1991;86:316–27. [Google Scholar]
- Lipkovich I, Dmitrienko A, Denne J, Enas G. Subgroup identification based on differential effect searchA recursive partitioning method for establishing response to treatment in patient subpopulations. Statistics in Medicine. 2011;30:2601–2621. doi: 10.1002/sim.4289. [DOI] [PubMed] [Google Scholar]
- Moodie EE, Richardson TS. Bias correction in non-differentiable estimating equations for optimal dynamic regimes. Scandinavian Journal of Statistics. 2010;37:126–146. doi: 10.1111/j.1467-9469.2009.00661.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy S. Optimal dynamic treatment regimes (with discussion) Journal of the Royal Statistical Society, Series B. 2003;65:331–66. [Google Scholar]
- Qian M, Murphy SA. Performance guarantees for individualized treatment rules. Annals of Statistics. 2011;39:1180. doi: 10.1214/10-AOS864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruberg SJ, Chen L, Wang Y. The mean does not mean as much anymore: Finding sub-groups for tailored therapeutics. Clinical Trials. 2010;7:574–583. doi: 10.1177/1740774510369350. [DOI] [PubMed] [Google Scholar]
- Sargent D, Mandrekar S. Statistical issues in the validation of prognostic, predictive, and surrogate biomarkers. Clinical Trials. 2013;10:647–52. doi: 10.1177/1740774513497125. [DOI] [PubMed] [Google Scholar]
- Shao J. Bootstrap sample size in nonregular cases. Proceedings of the American Mathematical Society. 1994;122:1251–1262. [Google Scholar]
- Song R, Wang W, Zeng D, Kosorok M. Penalized q-learning for dynamic treatment regimens. Statistica Sinica. 2015;25 doi: 10.5705/ss.2012.364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Su X, Tsai CL, Wang H, Nickerson DM, Li B. Subgroup analysis via recursive partitioning. The Journal of Machine Learning Research. 2009;10:141–158. [Google Scholar]
- Su X, Zhou T, Yan X, Fan J, Yang S. Interaction trees with censored survival data. The International Journal of Biostatistics. 2008;4:1–26. doi: 10.2202/1557-4679.1071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tibshirani R, Saunders M, Rosset S, Zhu J, Knight K. Sparsity and smoothness via the fused lasso. Journal of the Royal Statistical Society, Series B. 2004;67:91–108. [Google Scholar]
- Varadhan R, Segal JB, Boyd CM, Wu AW, Weiss CO. A framework for the analysis of heterogeneity of treatment effect in patient-centered outcomes research. Journal of Clinical Epidemiology. 2013;66:818–825. doi: 10.1016/j.jclinepi.2013.02.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan M, Lin Y. Model selection and estimation in regression with grouped variables. Journal of the Royal Statistical Society, Series B. 2005;68:49–67. [Google Scholar]
- Zhang B, Tsiatis A, Davidian M, Zhang M, Laber E. Estimating optimal treatment regimes from a classification perspective. Stat. 2012;1:103–114. doi: 10.1002/sta.411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Y, Zeng D, Laber E, Kosorok M. New statistical learning methods for estimating optimal dynamic treatment regimes. Journal of the American Statistical Association. doi: 10.1080/01621459.2014.937488. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Y, Zeng D, Rush A, Kosorok M. Estimating individualized treatment rules using outcome weighted learning. Journal of the American Statistical Association. 2012;107:1106–1118. doi: 10.1080/01621459.2012.695674. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


