Abstract
Previous studies have shown that synchronized beta frequency (14-30 Hz) oscillations in the primary motor cortex are involved in maintaining steady contractions of contralateral arm and hand muscles. However, little is known about the role of postcentral cortical areas in motor maintenance and their patterns of interaction with motor cortex. We investigated the functional relations of beta-synchronized neuronal assemblies in pre- and postcentral areas of two monkeys as they pressed a hand lever during the wait period of a visual discrimination task. By using power and coherence spectral analysis, we identified a beta-synchronized large-scale network linking pre- and postcentral areas. We then used Granger causality spectra to measure directional influences among recording sites. In both monkeys, strong Granger causal influences were observed from primary somatosensory cortex to both motor cortex and inferior posterior parietal cortex, with the latter area also exerting Granger causal influences on motor cortex. Granger causal influences from motor cortex to postcentral sites, however, were weak in one monkey and not observed in the other. These results are the first, to our knowledge, to demonstrate in awake monkeys that synchronized beta oscillations bind multiple sensorimotor areas into a large-scale network during motor maintenance behavior and carry Granger causal influences from primary somatosensory and inferior posterior parietal cortices to motor cortex.
Keywords: cerebral cortex, motor maintenance, parietal, local field potential, coherence
Oscillatory activity in the beta frequency range (14-30 Hz) is widely observed in sensorimotor cortex in relation to motor behavior in both humans (1, 2) and nonhuman primates (3-6). Specifically, beta oscillations in monkeys appear in local field potential (LFP) and spiking activity during tactile exploratory forelimb movements (4, 7, 8), movement preparation (5, 6, 9), and steady-state isometric contractions (10). Beta oscillatory activity is often observed to be synchronized between different parts of sensorimotor cortex (4, 5, 7, 9-11), between motor cortical LFPs and descending pyramidal tract neuron discharge (10, 12), between single motor units (13, 14), and between motor cortical activity and muscle activity (1, 4, 10, 12, 15, 16).
Although the role of beta oscillations in the outflow of activity from motor cortex to muscles is relatively well characterized for certain types of behavior, the relation of beta oscillations in postcentral areas and motor cortex remains poorly understood. This article addresses the functional relations between beta oscillations in pre- and postcentral cortical areas in premovement motor maintenance behavior. It has long been proposed that behavior of this type depends on a corticoperipheral cortical sensorimotor loop (17, 18), and more recently that this loop is supported by oscillatory neuronal activity (19). Reports of beta oscillations in both somatosensory and motor cortices during premovement maintenance behavior (3, 5, 6, 9), taken together with recent studies proposing that beta rhythms are uniquely suited for synchronization over long conduction delays (20, 21), thus suggest the hypothesis that beta oscillations provide a mechanism that binds sensory and motor cortical areas into a functioning loop.
Here, we test this hypothesis and investigate related issues using LFP recordings from distributed neuronal assemblies in somatosensory and motor cortices of macaque monkeys as they maintained steady motor output while pressing a hand lever in a visual discrimination task. Power and coherence spectral analyses of cortical LFPs were used to identify beta-synchronized large-scale networks (22), and Granger causality spectral analysis to evaluate the patterning of directional influence in those networks. Granger (23) defined causal influence in terms of stochastic processes: one stochastic process is causal to a second if the autoregressive predictability of the second process at a given time point is improved by including measurements from the immediate past of the first. Granger causality has been shown to be suitable for the study of directionality in neuronal interactions by assessment on neurophysiological data in both the frequency and time domains (24-26), as well as on simulated simple systems where the direction and relative strength of Granger causal influence could be reliably established (26-28).
The combined use of power and coherence spectral analysis in this study provides evidence that primary somatosensory cortex, inferior posterior parietal cortex, and primary motor cortex are bound together in a beta-synchronized large-scale cortical network subserving premovement maintenance behavior. The further use of Granger causality spectral analysis indicates that motor cortical activity in this network is modulated by input from primary somatosensory and inferior posterior parietal areas.
Methods
LFP Recording and Behavioral Paradigm. Bipolar Teflon-coated platinum microelectrodes (51-μm diameter) were used to record surface-to-depth LFPs (2.5-mm tip separation) from up to 15 distributed sites located in the hemisphere contralateral to the dominant hand of two adult male rhesus macaque monkeys (right hemisphere in monkey GE and left hemisphere in monkey LU). Experiments were performed at the Laboratory of Neuropsychology at the National Institute of Mental Health, and animal care was in accordance with institution guidelines at the time. The monkeys were highly trained to perform a GO/NO-GO visual pattern discrimination task in experimental sessions of ≈1,000 trials. Although results from the same monkeys have been reported (29), the sessions used in the present study were not previously published. On each trial they depressed a hand lever, and kept it pressed during a random interval ranging from 0.12 to 2.2 s (wait period) while waiting for stimulus appearance. On GO trials, a water reward was provided if the monkey released the lever within 500 ms after stimulus onset. LFPs were amplified by Grass P511J amplifiers (-6 dB at 1 and 100 Hz, 6 dB/octave falloff), digitized at 200 Hz, and collected from 90 ms before to 500 ms after stimulus onset.
Data Preprocessing. This study was aimed at testing for the presence of a beta oscillatory network in sensorimotor cortex. Therefore, the recording sites located in pre- and postcentral cortical areas of each monkey (six in GE and four in LU) were selected for analysis. Trials contaminated with artifacts, or for which the behavioral response was incorrect, were removed. Power line contamination at 60 Hz was reduced in the remaining trials by a multitapering method (30). For each single-trial LFP time series, each amplitude value was divided by the temporal standard deviation to give equal weight to the data from each recording site and trial. For each monkey, three experimental sessions having similar response time histograms were selected. Although preliminary analysis of correct GO and NO-GO trials in the wait period gave similar results, only the results from correct GO trials are presented here because only this trial type could be used to determine the similarity of response time histograms. Combining the correct GO-trial LFP recordings from these sessions resulted in a pooled ensemble of ≈900 trials for each monkey. Finally, the ensemble mean time series from each site was subtracted pointwise from each of its single-trial time series. This procedure allowed the ensemble of single-trial time series to be treated as coming from a zero-mean stochastic process, as is required for the autoregressive modeling method described in the next section.
Multivariate Autoregressive (MVAR) Spectral Analysis. After data preprocessing, spectral analysis was performed on the MVAR model (refs. 31 and 45 and Appendix) that was estimated from the LFP time series in a 110-ms (22 point) analysis window extending from 90 ms prior until 20 ms after stimulus onset (wait window). We sought to determine an optimal order for the MVAR model by locating the minimum of the Akaike Information Criterion (AIC) (32) as a function of model order. However, the AIC dropped monotonically with increasing model order up to a value of 15. We therefore compared spectra produced by using model orders of 5, 10, and 15, and found the overall results to be consistent. A model order of 10 (50 ms) was selected as a tradeoff between sufficient spectral resolution and overparameterization. The analyzed LFP data from all trials were treated as realizations of a common stochastic process, and thus were used to estimate the model coefficients for that process.
Power, coherence, and relative phase spectral estimates were derived from the MVAR spectral matrix for all sites and site pairs (see Appendix). The frequency range was from 9 to 100 Hz. The lower end corresponds to one full cycle of oscillation in the 110-ms analysis window. Power spectra from all sites were examined to identify beta oscillatory activity by the presence of a power spectral maximum (peak) in the beta range (14-30 Hz). The peak frequencies of those sites showing beta oscillatory activity are tabulated in Tables 1 and 2. Coherence spectra for all pairwise combinations of sites were examined for synchronized beta oscillatory activity. Beta coherence peaks were identified and then tested for significance by a permutation procedure (33). The procedure involved creating 1,000 permuted versions of the LFP data set, in which trial order was independently permuted for each site. Permutation of the trial order had the effect of disrupting task-related coherences and yielding coherence values that were due to chance. Beta coherence estimates were obtained from each permuted data set by MVAR spectral analysis, and used to create a permutation distribution. Statistical significance was determined for each original peak beta coherence value by comparison to the permutation distribution, thus testing the null hypothesis that these values occurred by chance. Significance values were corrected for multiple comparisons (over site pairs) by Dunn's multiple comparison procedure. Tables 1 and 2 list the peak coherence value and its frequency for each pair having a corrected significance level of P < 0.005. Relative phase spectra were calculated for site pairs having significant beta coherence peaks. Values of phase at the frequencies of significant coherence peaks were converted to time delays for standardized comparison across different frequencies. These time delays are also listed in Tables 1 and 2.
Table 1. Peak power and coherence values for monkey GE.
| Coherence
|
|||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Electrode site
|
Power
|
2
|
3
|
4
|
5
|
6
|
|||||||||||
| Peak | f, Hz | Peak | f, Hz | lag, ms | Peak | f, Hz | lag, ms | Peak | f, Hz | lag, ms | Peak | f, Hz | lag, ms | Peak | f, Hz | lag, ms | |
| 1 | NP | 0.203 | 22 | 10 | 0.140 | 22 | −6 | 0.080 | 22 | 1 | 0.072 | 22 | −7 | 0.029 | 16 | 3 | |
| 2 | 6.75 | 22 | — | 0.304 | 23 | −17 | 0.144 | 23 | −13 | 0.053 | 22 | −19 | NS | ||||
| 3 | 8.80 | 22 | — | — | 0.517 | 23 | 3 | 0.086 | 23 | −3 | NS | ||||||
| 4 | 5.37 | 21 | — | — | — | 0.060 | 23 | −6 | NS | ||||||||
| 5 | NP | — | — | — | — | NS | |||||||||||
| 6 | NP | — | — | — | — | — | |||||||||||
Electrode site numbers correspond to the numbered locations in Fig. 2. The primary motor site is numbered 1, and the postcentral sites are numbered 2, 3, and 4. The two additional precentral sites are numbered 5 and 6. The columns under Power show the power (normalized by the mean power) of the largest spectral peak and its frequency in Hz. NP, no peak. In the columns under Coherence are shown the peak coherence value, peak frequency in Hz, and phase difference converted to time lag in milliseconds for each pair of sites. Values are shown only for coherence spectra determined to be significant by the permutation procedure described in Methods. NS, not significant.—, a redundant pairing or the pairing of a site with itself, because coherence is a pairwise measure between different sites. A positive number for the time lag indicates that the electrode site at the left leads the site at the top, and a negative number indicates that it lags.
Table 2. Peak power and coherence values for monkey LU.
| Coherence
|
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Electrode site
|
Power
|
2
|
3
|
4
|
|||||||
| Peak | f, Hz | Peak | f, Hz | lag, ms | Peak | f, Hz | lag, ms | Peak | f, Hz | lag, ms | |
| 1 | 2.32 | 23 | 0.115 | 21 | −4 | 0.300 | 29 | −1 | 0.026 | 20 | −20 |
| 2 | 5.48 | 21 | — | 0.260 | 20 | 3 | 0.052 | 20 | −21 | ||
| 3 | 3.69 | 22 | — | — | 0.124 | 17 | 26 | ||||
| 4 | 4.09 | 18 | — | — | — | ||||||
Electrode site numbers correspond to the numbered locations in Fig. 2. The primary motor site is numbered 1, and the postcentral sites are numbered 2, 3, and 4. The two columns under Power show the power (normalized by the mean power) of the largest power spectral peak and its frequency in Hz. In the columns under Coherence are shown the peak coherence value, peak frequency in Hz, and phase difference converted to time lag in milliseconds for each pair of sites. Values are shown only for coherence spectra determined to be significant by the permutation procedure described in Methods.—, a redundant pairing or the pairing of a site within itself, because coherence is a pairwise measure between different sites. A positive number for the time lag indicates that the electrode site at the left leads the site at the top, and a negative number indicates that it lags.
Granger Causality Spectral Analysis. Coherence analysis alone does not address the question of the predictability of activity at one cortical site from that at another. Therefore, Granger causality spectra (34) were computed to evaluate the relative strengths of influence, in the Granger sense of predictability, between two sites in both directions and at different frequencies (see Appendix). Geweke (34) showed that, for the data from a given site, the power at a specific frequency can be decomposed into an intrinsic part and a part predicted by the data from another site. The Granger causality at each frequency is thus defined by the ratio of predicted power to total power, and the Granger causality spectrum can be viewed in terms of the fraction of the variance in one time series that can be attributed to another (see Appendix). Granger spectral peaks were identified and were then tested for significance by the same permutation procedure described above. Tables 3 and 4 list the peak value and frequency for each Granger causality spectrum that was significant at P < 0.005.
Table 3. Peak Granger causality values for monkey GE.
| Granger causality | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Electrode site
|
1
|
2
|
3
|
4
|
5
|
6
|
||||||
| Peak | f, Hz | Peak | f, Hz | Peak | f, Hz | Peak | f, Hz | Peak | f, Hz | Peak | f, Hz | |
| 1 | — | NS | NS | NS | NS | NS | ||||||
| 2 | 0.150 | 23 | — | 0.117 | 24 | 0.074 | 23 | 0.025 | 22 | NS | ||
| 3 | 0.113 | 22 | 0.046 | 24 | — | 0.271 | 23 | 0.030 | 23 | NS | ||
| 4 | 0.022 | 21 | 0.016 | 28 | 0.025 | 32 | — | NS | NS | |||
| 5 | 0.038 | 20 | NS | NS | NS | — | NS | |||||
| 6 | NS | NS | NS | NS | NS | — | ||||||
Direction of influence is from the electrode site at the left to the site at the top. Values of peak Granger causality are displayed together with the peak frequency in Hz. Values are only shown for spectra determined to be significant by the permutation procedure described in Methods. NS, not significant; —, the pairing of a site with itself, because the Granger causality is measured only between different sites.
Table 4. Peak Granger causality values for monkey LU.
| Granger causality
|
||||||||
|---|---|---|---|---|---|---|---|---|
| Electrode site
|
1
|
2
|
3
|
4
|
||||
| Peak | f, Hz | Peak | f, Hz | Peak | f, Hz | Peak | f, Hz | |
| 1 | — | 0.030 | 25 | NS | 0.018 | 26 | ||
| 2 | 0.106 | 21 | — | 0.118 | 21 | NS | ||
| 3 | 0.091 | 30 | 0.013 | 18 | — | 0.020 | 23 | |
| 4 | NS | NS | 0.041 | 16 | — | |||
Direction of influence is from the electrode site at the left to the site at the top. Values of peak Granger causality are displayed together with the peak frequency in Hz. Values are shown only for spectra determined to be significant by the permutation procedure described in Methods. NS, not significant; —, the pairing of a site with itself, because the Granger causality is measured only between different sites.
Results
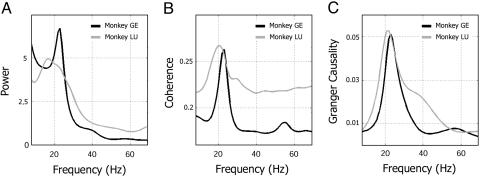
Identification of Synchronized Beta Oscillations. Power spectra were computed for all pre- and postcentral recording sites of each monkey in the wait window. Coherence spectra and Granger causality spectra were computed for all pairwise combinations of sites. Fig. 1 shows the mean power spectra computed over all sites (A), and the mean coherence spectra (B) and Granger causality (C) spectra computed over all site pairs. The mean power spectra (A) show beta oscillatory activity as prominent peaks near 20 Hz, and the mean coherence spectra (B) illustrate that these oscillations were often synchronized. The mean Granger causality spectra (C) show pronounced peaks near 20 Hz, indicating that the Granger causal influences between sites were mediated by beta range oscillations.
Fig. 1.
Mean power spectra computed over all sites, and mean coherence and mean Granger causality spectra computed over all significant site pairs. Results are from monkeys GE (black curves) and LU (gray curves) during the wait period of the task (Methods). The overall dominance of activity near 20 Hz in the power (A), coherence (B), and Granger causality (C) spectra indicates that a beta-synchronized network of neuronal assemblies supported directionally specific Granger causal influences in the sensorimotor cortex.
Individual power spectra were examined to determine which recording sites had oscillatory LFP activity in the beta frequency range. In monkey GE, the three postcentral sites had prominent beta range power spectral peaks, all ≈22 Hz, whereas the precentral sites did not (Table 1). In monkey LU, all of the sites had prominent beta power peaks, with peak frequencies ranging from 18 to 23 Hz (mean = 21 ± 2.1 Hz; Table 2).
Coherence spectra from all pairwise site combinations were tested to identify those site pairs having significant beta peaks, which is indicative of synchronized beta LFP oscillations. (The threshold coherence level for significance at P < 0.005 was determined by the permutation procedure to be 0.016 for LU and 0.020 for GE). LFPs from multiple cortical sites were found to be significantly coherent in the beta range in both monkeys, with coherence spectral peak frequencies similar to those of the power spectra (Tables 1 and 2). All of the sites in both monkeys showed significant beta coherence with at least one other site. All of the six possible pairwise combinations of sites in LU, and 11 of 15 in GE, showed significant beta coherence peaks. Significant beta coherence peaks were observed for site pairs within postcentral cortex and precentral cortex, as well as between post- and precentral sites (see coherence graphs in Fig. 2 A and B Left). Overall, the largest coherence values in both monkeys linked sites in three areas: the areas immediately anterior (primary motor cortex) and posterior (primary somatosensory cortex) to the central sulcus, and a third area inferior to the intraparietal sulcus.
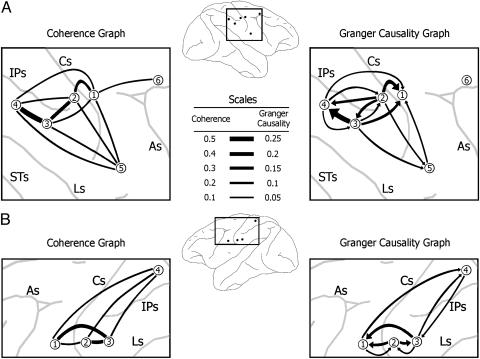
Fig. 2.
Beta oscillatory networks in monkey sensorimotor cortex. Coherence (Left) and Granger causality graphs (Right) are depicted in monkeys GE (A) and LU (B). The coherence and Granger causality values are coded by the thickness of the lines between recording sites (Center). The lines in the Granger causality graphs have arrowheads, indicating the direction of Granger causal influence. Lines between site pairs not reaching significance in the coherence and Granger causality measures are not shown. Cs, central sulcus; IPs, intraparietal sulcus; STs, superior temporal sulcus; Ls, lateral sulcus; As, arcuate sulcus.
A synchronized network was demonstrated in monkey GE by the fact that all coherence peaks but one were at either 22 or 23 Hz (Table 1). The one exception (site 1 with site 6) was low both in magnitude and frequency, and because this coherence peak marked site 6's only involvement in the network, this involvement appeared marginal. It is interesting that, although site 1 had no beta power spectral peak, it did have significant beta coherence with every other site (Table 1 and Fig. 2A Left). This finding suggests that LFP oscillatory activity may be synchronized between cortical sites even when it is too weak to produce prominent power spectral peaks.
A synchronized network was also found in monkey LU, where four of six coherence peaks were either at 20 or 21 Hz (Table 2). One pair (sites 1 and 3) deviated from the group with a higher peak coherence frequency (29 Hz), but closer inspection of the coherence spectrum revealed a shoulder peak at 22 Hz, corresponding in frequency to the power spectra of these two sites. Thus, it appeared that the coherence spectrum for this pair had two peaks in close proximity, one at 22 Hz, corresponding to the main concentration of power in the individual power spectra, and a second at 29 Hz, which did not correspond to any observable concentration of power. A second pair (sites 3 and 4) deviated from the group with a lower peak coherence frequency (17 Hz), suggesting that one of the sites (site 4) in this pair dominated their synchronization because this peak coherence frequency was close to that site's peak power frequency (18 Hz).
Granger Causal Relations Within the Beta Oscillatory Network. Granger causality spectra were computed in both directions for all site pairs, and spectra having significant beta peaks were identified. (The threshold level for significance at P < 0.005 was determined by the permutation procedure to be 0.011 for LU and 0.012 for GE). In monkey GE, six of the 11 coherent pairs only had significant Granger causality in one direction, three pairs showed significant Granger causality in both directions (but with different magnitudes), and two were not significant in either direction (Table 3). In monkey LU, two of the six coherent pairs were significant only in one direction, three pairs showed significant bidirectional influences, and one pair did not show any significant influence (Table 4). Significant Granger causal relations are plotted as Granger causality graphs in Fig. 2 A (GE) and B (LU) Right.
In general, there was a close correspondence between the characteristics of the Granger causality spectra and the coherence, as suggested by visual comparison of Fig. 1 B and C. All pairs having significant Granger causality beta-range peaks also had significant coherence beta-range peaks. However, Granger causality relations (Tables 3 and 4) were generally inconsistent with time delay values derived from phase spectra (Tables 1 and 2), because the sign of the time delay did not predict the direction of unidirectional Granger causality.
Ten of the 12 Granger causality spectra in GE having significant beta peaks had peak frequencies that were within 2 Hz of their corresponding coherence peak frequency, with the mean difference between Granger causality and coherence peak frequencies equal to 0.6 ± 0.7 Hz. The peaks in the two other Granger causality spectra (from site 4 to 2 and from site 4 to 3) had frequencies that were higher, by 5 and 9 Hz, respectively, than the corresponding coherence spectra and Granger causality spectra in the other direction. These discrepancies may be related to the small magnitude of these peaks (0.016 and 0.025).
In LU, five of the eight Granger causality spectra having significant beta peaks had peak frequencies that were within 2 Hz of their corresponding coherence peak frequency. The mean difference between Granger causality and coherence peak frequencies for these five spectra was 1.0 ± 0.7 Hz. The peaks in the other three Granger causality spectra had frequencies that were 4 Hz (from site 1 to 2), 6 Hz (from site 1 to 4), and 6 Hz (from site 3 to 4) higher than their corresponding coherence spectra. These three peaks were all low in magnitude (0.030, 0.018, and 0.020, respectively).
The anterior postcentral (primary somatosensory cortex) sites (site 2 in both GE and LU) appeared to play a clear role as a driver in both monkeys, exerting a far greater influence on other network sites than it received. The summed peak Granger causality exerted by site 2 on other sites was 5.9 (0.366/0.062) times that which other sites exerted on it in GE, and 5.2 (0.224/0.043) times in LU. An opposite pattern was observed in both monkeys for the corresponding precentral sites (site 1 in both GE and LU). These sites appeared to play a clear receiving role within the observed network. For GE, no significant outgoing influence was observed from site 1, whereas the total incoming peak Granger causality was 0.32. For LU, the summed incoming influence to site 1 was 4.1 (0.197/0.048) times the total outgoing. Finally, both monkeys had sites in the area inferior to the intraparietal sulcus that played both driving and receiving roles. However, although this area had relatively balanced output and input influences, its input was mainly from the primary somatosensory cortex, whereas its output was mainly to the motor cortex. In fact, these inferior posterior parietal sites exerted significant Granger causal influences on the primary motor sites (site 1 in both GE and LU), but in no case did they receive a direct return influence.
Discussion
We observed that neuronal assemblies at distributed sites in the sensorimotor cortex of two macaque monkeys were joined in large-scale networks oscillating near 20 Hz during maintenance of a sustained contralateral hand lever press. This result is consistent with previous findings of widespread, high-amplitude LFP oscillations transiently synchronized in sensorimotor areas during sensorimotor tasks (4, 11), and with models indicating that beta oscillations are particularly well suited to support interactions between widespread cortical areas (20, 21). By distinguishing between large-scale network synchrony due to driving and that due to mutual interactions, Granger causality analysis provided a deeper understanding of cortical interaction patterns than could be obtained from correlation or coherence measures. This distinction had two important consequences: (i) it allowed more definitive hypotheses to be made about the functional involvement of sensorimotor cortical areas in motor maintenance, and (ii) it suggested that unidirectional driving was an important aspect of that involvement.
Three consistent features of the proposed unidirectional driving were discerned in both monkeys. First, a somatosensory site was observed to drive both inferior posterior parietal and motor sites (Tables 3 and 4 and Fig. 2). Second, a motor site received Granger causal influences from postcentral sites while returning either no influence or only a very weak influence. Third, inferior posterior parietal sites received Granger causal influences from the somatosensory cortex and also exerted influences on the motor cortex.
These results support the idea that somatosensory feedback provides information to the sensorimotor system that is used to control motor output. It is well known that the maintenance of sustained motor output is severely impaired when somatosensory input is lacking (35-37). Thus, it seems reasonable that the modulation of motor cortex by primary somatosensory cortex reported here depends on ongoing input from the periphery, an explanation that is compatible with the existence of a sensorimotor loop through the periphery (19, 38). The results further suggest that the cortical portion of this loop is part of a more extensive network that includes the inferior posterior parietal cortex (Fig. 2). The observed patterns of casual influence of inferior posterior parietal sites (site 3 and 4 in GE, and site 3 in LU) support the role that some have proposed for this region in the transformation of tactile and proprioceptive to motor information and the organization of nonvisually guided motor behaviors (39).
Although various elements of the large-scale network reported here have previously been implicated in sensorimotor processing, the present study points to synchronized beta oscillations as a mechanism for binding distributed somatosensory and motor cortical areas into a functioning network. Maxima in the LFP power spectra were found near 20 Hz at all postcentral sites in monkey GE and at all post- and precentral sites in monkey LU. These peaks indicate that the neuronal assemblies at these sites had a strong tendency to oscillate in a relatively narrow mid-beta frequency range (see Fig. 1A). This oscillatory activity was synchronized across distributed neuronal assemblies within and between post- and precentral areas. However, a significant coherence between two sites did not depend on there being peaks in their power spectra. It was found, for instance, that site 1 in GE, which had no power spectral peak, was significantly coherent with all of the other sites, even with sites 5 and 6, which also had no power spectral peaks.
It is unlikely that the patterns of beta-range peak power, coherence, and Granger causality observed in this study were due simply to a uniformly transmitted signal or to volume conduction from a common generator. First, the differential bipolar recording technique was designed to suppress LFPs from nonlocal assemblies. Evidence for the effectiveness of this design was found in the averaged evoked potentials at neighboring electrode sites, such as sites 2 and 3 in monkey LU, which had very different waveforms. Also arguing for independently oscillating local cortical generators were the differences observed in the peak beta frequencies of power, coherence, and Granger causality spectra for some site pairs. Such variations seem incompatible with a unitary imposed rhythm.
The significant coherence levels observed in this study indicate that sensorimotor LFPs showed a consistent trial-to-trial relative phase relation during the wait window. In this way, our results are consistent with previous studies (40-43) showing the functional relevance of relative phase coupling of LFPs across cortical areas. However, no clear relation was found between the time delay derived from the mean phase difference and the Granger causality, thus suggesting that the mean relative phase is not indicative of the directionality of causal relations between cortical assemblies.
The final issue to be addressed is the nature of the relations revealed by Granger causality analysis. It should be emphasized that the concept of Granger causality is statistical in nature, and thus the observation of a Granger causal influence in the cortex does not in itself constitute proof that one neuronal assembly activates another over a direct axonal pathway. The influence could be mediated by either direct or indirect pathways, through the cortex or subcortical structures. Nonetheless, given the strong anatomical interconnectivity known to link the areas examined in this study (44), it is highly likely that the observed patterns of Granger causality reflect the functional interactions of neurons in those areas in support of motor maintenance behavior.
As an approach to large-scale cortical network analysis, the combined application of power, coherence, and Granger causality measures appears to provide a valuable tool for in-depth investigation of the nature of functional coupling of distributed neuronal assemblies. With well designed experimental paradigms, we expect that it should be possible to track the dynamic evolution of Granger causal influences in large-scale coherent networks with changing cognitive state in a wide variety of behavioral tasks.
Acknowledgments
We thank the Charles E. Schmidt College of Science at Florida Atlantic University for providing computing facilities and Dr. M. Rosenblum for helpful discussions on the application of directionality measures to biological signals. This work was supported by National Science Foundation Grant IBN0090717, National Institute of Mental Health Grants MH64204 and MH42900, and Office of Naval Research Grant N00014-99-1.
Appendix
Denoting the p channels of LFP recordings at time t by Xt = (x1t, x2t,..., xpt)T, where T stands for matrix transposition, the MVAR model of order m describes the data as:
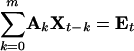 |
where Et is a temporally uncorrelated residual error with covariance matrix σ, and Ak are p × p coefficient matrices (45). In the present study, p was 6 for monkey GE and 4 for monkey LU. We obtain estimates of the coefficient matrices by solving the multivariate Yule-Walker equations (of size mp2) by using the Levinson, Wiggins, and Robinson algorithm (31). Estimation of the model coefficients is based on the assumption that the repeated trials are realizations of a stationary stochastic process.
Once the model coefficients Ak and σ are estimated, the spectral matrix can be written as
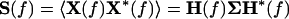 |
where the asterisk denotes matrix transposition and complex conjugation, and 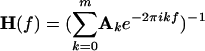 is the transfer function of the system. The power spectrum of channel l is given by Sll(f), which is the lth diagonal element of the spectral matrix S(f). The (squared) coherence spectrum between channel l and channel k is given by:
is the transfer function of the system. The power spectrum of channel l is given by Sll(f), which is the lth diagonal element of the spectral matrix S(f). The (squared) coherence spectrum between channel l and channel k is given by:
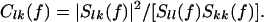 |
The value of coherence can range from 1, indicating maximum interdependence between channel l and channel k at frequency f, down to 0, indicating no interdependence. The phase of the cross spectrum Slk(f) plotted as a function of f gives the phase spectrum.
To compute the Granger causality spectrum, we first obtain the bivariate autoregressive model for two LFP time series x1t and x2t according to the procedure above. According to Geweke's (34) formulation of Granger causality in the spectral domain, the Granger causality spectrum from x2t to x1t is computed according to
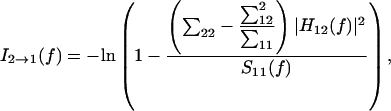 |
where σ11, σ22, and σ12 are elements of σ, and S11(f) is the power spectrum of channel 1 at frequency f. Similarly, the Granger causality spectrum from x1t to x2t is given by
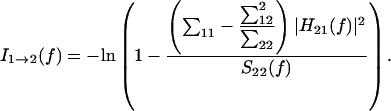 |
The time-domain Granger causality from x2t to x1t can be interpreted (34) as the reduction in the unexplained variance of x1t, as computed solely from the past values of x1t, that comes from subsequent inclusion of past values of x2t. The size of this reduction can be viewed as the “amount of variance” of x1t explained by the history of x2t. Geweke's frequency decomposition of the Granger causality can also be given this interpretation (46, 47). The variance ratio is obtained from the Granger causality value at a given frequency as 1 - e-I(f), where I(f) denotes the Granger causality value at frequency f.
This paper was submitted directly (Track II) to the PNAS office.
Abbreviations: LFP, local field potential; MVAR, multivariate autoregressive.
References
- 1.Salenius, S. & Hari, R. (2003) Curr. Opinion Neurobiol. 13, 678-684. [DOI] [PubMed] [Google Scholar]
- 2.Pfurtscheller, G. & Lopes da Silva, F. H. (1999) Clin. Neurophysiol. 110, 1842-1857. [DOI] [PubMed] [Google Scholar]
- 3.Rougeul, A., Bouyer, J. J., Dedet, L. & Debray, O. (1979) Electroencephalogr. Clin. Neurophysiol. 46, 310-319. [DOI] [PubMed] [Google Scholar]
- 4.Murthy, V. N. & Fetz, E. E. (1992) Proc. Natl. Acad. Sci. USA 89, 5670-5674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Sanes, J. N. & Donoghue, J. P. (1993) Proc. Natl. Acad. Sci. USA 90, 4470-4474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.MacKay, W. A. & Mendonca, A. J. (1995) Brain Res. 704, 167-174. [DOI] [PubMed] [Google Scholar]
- 7.Murthy, V. N. & Fetz, E. E. (1996) J. Neurophysiol. 76, 3949-3967. [DOI] [PubMed] [Google Scholar]
- 8.Lebedev, M. A. & Wise, S. P. (2000) Exp. Brain Res. 130, 195-215. [DOI] [PubMed] [Google Scholar]
- 9.Donoghue, J. P., Sanes, J. N., Hatsopoulos, N. G. & Gaal, G. (1998) J. Neurophysiol. 79, 159-173. [DOI] [PubMed] [Google Scholar]
- 10.Baker, S. N., Olivier, E. & Lemon, R. N. (1997) J. Physiol. (London) 501, 225-241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Murthy, V. N. & Fetz, E. E. (1996) J. Neurophysiol. 76, 3968-3982. [DOI] [PubMed] [Google Scholar]
- 12.Baker, S. N., Kilner, J. M., Pinches, E. M. & Lemon, R. N. (1999) Exp. Brain Res. 128, 109-117. [DOI] [PubMed] [Google Scholar]
- 13.Farmer, S. F., Bremner, F. D., Halliday, D. M., Rosenberg, J. R. & Stephens J. A. (1993) J. Physiol. (London) 470, 127-155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kilner, J. M., Alonso-Alonso, M., Fisher, R. & Lemon, R. N. (2002) J. Physiol. (London) 541, 937-948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Feige, B., Aertsen, A. & Kristeva-Feige, R. (2000) J. Neurophysiol. 84, 2622-2629. [DOI] [PubMed] [Google Scholar]
- 16.Mima, T., Matsuoka, T. & Hallet, M. (2001) Clin. Neurophysiol. 112, 122-126. [DOI] [PubMed] [Google Scholar]
- 17.Asanuma, H. (1989) The Motor Cortex (Raven, New York).
- 18.Favorov, O., Sakamoto, T. & Asanuma, H. (1988) J. Neurosci. 8, 3266-3277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Mackay, W. A. (1997) Trends Cogn. Sci. 1, 176-183. [DOI] [PubMed] [Google Scholar]
- 20.Kopell, N., Ermentrout, G. B., Whittington, M. A. & Traub, R. D. (2000) Proc. Natl. Acad. Sci. USA 97, 1867-1872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Bibbig, A., Traub, R. D. & Whittington, M. A. (2002) J. Neurophysiol. 88, 1634-1654. [DOI] [PubMed] [Google Scholar]
- 22.Bressler, S. L. (1995) Brain Res. Rev. 20, 288-304. [DOI] [PubMed] [Google Scholar]
- 23.Granger, C. W. J. (1969) Econometrica 37, 424-438. [Google Scholar]
- 24.Bernasconi, C. & König, P. (1999) Biol. Cybern. 81, 199-210. [DOI] [PubMed] [Google Scholar]
- 25.Bernasconi, C., von Stein, A., Chiang, C. & König, P. (2000) NeuroReport 11, 1-4. [DOI] [PubMed] [Google Scholar]
- 26.Hesse, W., Moller, E., Arnold, M. & Schack, B. (2003) J. Neurosci. Methods 124, 27-44. [DOI] [PubMed] [Google Scholar]
- 27.Kamiñski, M., Ding, M., Truccolo, W. A. & Bressler, S. L. (2001) Biol. Cybern. 85, 145-157. [DOI] [PubMed] [Google Scholar]
- 28.Baccala, L. A. & Sameshima, K. (2001) Biol. Cybern. 84, 463-474. [DOI] [PubMed] [Google Scholar]
- 29.Bressler, S. L., Coppola, R. & Nakamura, R. (1993) Nature 366, 153-156. [DOI] [PubMed] [Google Scholar]
- 30.Mitra, P. P. & Pesaran, B. (1999) Biophys. J. 76, 691-708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Ding, M., Bressler, S. L., Yang, W. & Liang, H. (2000) Biol. Cybern. 83, 35-45. [DOI] [PubMed] [Google Scholar]
- 32.Akaike, H. (1974) IEEE Trans. Autom. Control 19, 716-723. [Google Scholar]
- 33.Edgington, E. S. (1980) Randomization Tests (Dekker, New York).
- 34.Geweke, J. (1982) J. Am. Stat. Assoc. 77, 304-313. [Google Scholar]
- 35.Knapp, H. D., Taub, E. & Berman, A. J. (1963) Exp. Neurol. 7, 305-315. [DOI] [PubMed] [Google Scholar]
- 36.Merton, P. A. (1964) Symp. Soc. Exp. Biol. 18, 387-400. [PubMed] [Google Scholar]
- 37.Rothwell, J. C., Traub, M. M., Day, B. L., Obeso, J. A., Thomas, P. K. & Marsden, C. D. (1982) Brain 105, 515-542. [DOI] [PubMed] [Google Scholar]
- 38.Phillips, C. G. (1969) Proc. R. Soc. London Ser. B 173, 141-174. [DOI] [PubMed] [Google Scholar]
- 39.Rushworth, M. F., Nixon, P. D. & Passingham, R. E. (1997) Exp. Brain Res. 117, 292-310. [DOI] [PubMed] [Google Scholar]
- 40.Roelfsema, P. R., Engel, A. K., Konig, P. & Singer, W. (1997) Nature 385, 157-161. [DOI] [PubMed] [Google Scholar]
- 41.Rodriguez, E., George, N., Lachaux, J. P., Martinerie, J., Renault, B. & Varela, F. J. (1999) Nature 397, 430-433. [DOI] [PubMed] [Google Scholar]
- 42.Bressler, S. L. & Kelso, J. A. S. (2001) Trends Cogn. Sci. 5, 26-36. [DOI] [PubMed] [Google Scholar]
- 43.Varela, F., Lachaux, J. P., Rodriguez, E. & Martinerie, J. (2001) Nat. Rev. Neurosci. 2, 229-239. [DOI] [PubMed] [Google Scholar]
- 44.Felleman, D. J. & Van Essen, D. C. (1991) Cereb. Cortex 1, 1-47. [DOI] [PubMed] [Google Scholar]
- 45.Lütkepohl, H. (1993) Introduction to Multiple Time Series Analysis (Springer, Berlin).
- 46.Pierce, D. A. (1979) J. Am. Stat. Assoc. 74, 901-910. [Google Scholar]
- 47.Pierce, D. A. (1982) J. Am. Stat. Assoc. 77, 315-316. [Google Scholar]