Summary
Generation of potent antibodies by a mutation-selection process called affinity maturation is a key component of effective immune responses. Antibodies that protect against highly mutable pathogens must neutralize diverse strains. Developing effective immunization strategies to drive their evolution requires understanding how affinity maturation happens in an enviroment where variants of the same antigen are present. We present an in silico model of affinity maturation driven by antigen variants which reveals that induction of cross-reactive antibodies often occurs with low probability because conflicting selection forces, imposed by different antigen variants, can frustrate affinity maturation. We describe how variables such as temporal pattern of antigen administration influence the outcome of this frustrated evolutionary process. Our calculations predict, and experiments in mice with variant gp120 constructs of the HIV envelope protein confirm, that sequential immunization with antigen variants is preferred over a cocktail for induction of cross-reactive antibodies focused on the shared CD4 binding site epitope.
INTRODUCTION
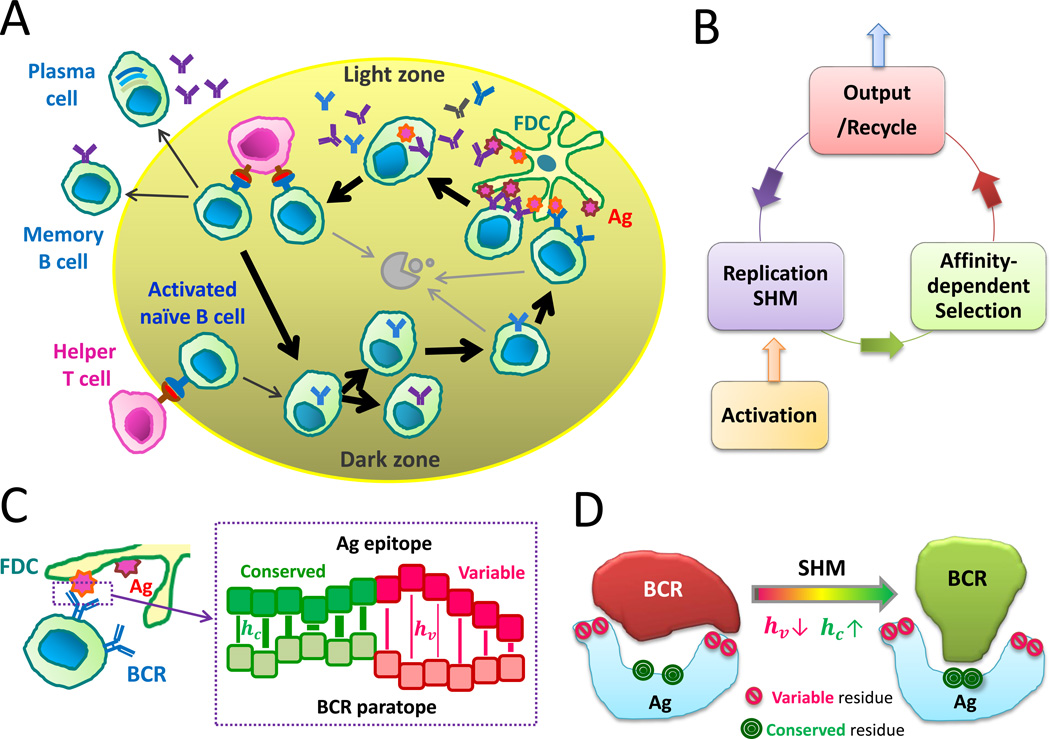
Antibodies (Abs) with high affinity for antigen are produced by the process of affinity maturation (AM), which takes place in germinal centers (GCs). GCs are dynamic structures within secondary lymphoid tissues that arise in response to antigen stimulation (Shlomchik and Weisel, 2012; Victora and Nussenzweig, 2012). GCs house B cells, antigen-specific T helper cells that develop in concert with GC B cells (Baumjohann et al., 2013; Kelsoe, 1996), and antigens presented on follicular dendritic cells (FDCs) (Figure 1A). GC B cells enhance the antigen affinity of their receptors by 10—1000 fold through cycles of mutation and selection against antigens presented on FDCs, a Darwinian evolutionary process that occurs on a very short time scale. Soluble forms of the high affinity receptors are potent Abs. AM has been studied extensively using diverse experimental methods (Batista and Neuberger, 1998; Berek and Milstein, 1987; Berek et al., 1991; Eisen and Siskind, 1964; Jacob et al., 1991; Kocks and Rajewsky, 1988), mathematical models (Deem and Lee, 2003; Kepler and Perelson, 1993; Meyer-Hermann, 2002, Meyer-Hermann et al., 2006; Oprea and Perelson, 1997; Zhang and Shakhnovich, 2010), and computer simulations (Kesmir and de Boer, 2003; Shlomchik et al., 1998; Swerdlin et al., 2008). Recent experiments have uncovered new aspects of GC dynamics (Allen et al., 2007; Shulman et al., 2013; Victora et al., 2010).
Figure 1. Schematic depiction of in silico model.
(A) Players and processes in the GCR. (B) Major steps in our in silico model of the GCR. (C) Model for BCR-Ag interactions. (Left) An FDC-held Ag interacting with a BCR. (Right) A zoom-in view of interactions (bars) between the residues on the Ag epitope and those on the BCR paratope. An affinity-affecting mutation on a paratope residue will change its interaction strength h with the corresponding paratope residue, denoted by hc (hv) if the latter is conserved (variable). (D) Conformational coupling between non-adjacent residues on the BCR is incorporated via correlated changes in hc and hv; weakening interaction with the variable residues and the residues that shield the conserved residues of the epitope (red), i.e., hv↓, would facilitate access to the conserved residues (green), i.e., hc↑. See also Supplementary Figure S1.
Effective Ab responses are likely to be required for a protective prophylactic vaccine against highly mutable pathogens. For HIV, a quintessential example of such a pathogen, despite extensive efforts, there has been no definitive success in designing such a vaccine (Burton et al., 2012; Klein et al., 2013; Kwong et al., 2013; Mascola and Haynes, 2013). This is in large part due to the variability of HIV (Burton et al., 2012; Mascola and Haynes, 2013).
The protective effects of an Ab are predicated on its ability to bind to a set of residues (the epitope) on the surface of virions. For example, the HIV-1 envelope glycoprotein trimer (Env) is the sole target of known HIV-1 neutralizing Abs (Burton et al., 2012; Kwong et al., 2013; Mascola and Haynes, 2013; West et al., 2014). During the first few months of infection, the induced neutralizing Abs are primarily strain-specific and target variable regions of Env. As the concentrations of such strain specific Abs increase, neutralization escape variants with mutations in the variable epitopes are selected. A pathogen’s molecular surfaces that interact with host receptors (e.g. the CD4 binding site) provide epitopes that contain a relatively conserved set of residues. They can serve as targets for Abs that are able to neutralize a greater diversity of HIV strains. A shield of glycans and immunodominant variable loops can restrict antibody access to these relatively conserved epitopes (Julien et al., 2013; Kwong et al., 2002; Lyumkis et al., 2013; Pancera et al., 2014; Wei et al., 2003; Wyatt et al., 1998). Yet, some HIV-1 infected individuals do develop Abs that focus on such epitopes and neutralize a broad cross section of HIV strains in vitro (Kwong et al., 2013). However, these broadly neutralizing antibodies (bnAbs) are produced only beginning around 2 years after infection, and in only a limited fraction of chronically infected patients. Nonetheless, the emergence of bnAbs in some patients is proof that AM can result in bnAbs. This suggests the tantalizing possibility that appropriately designed immunogens and immunization protocols may be able to elicit bnAbs rapidly in a large fraction of individuals, thus resulting in an effective vaccine.
Recent longitudinal tracking of a developing HIV-1 bnAb lineage and the co-evolving virus in a patient showed that extensive, and even specifically directed, viral diversification occurred prior to the development of breadth (cross-reactive Abs) (Gao et al., 2014; Liao et al., 2013), supporting the idea that escape mutants of the virus drive bnAb evolution. More importantly, this observation highlights that induction of bnAbs will likely require immunization with multiple variants of the antigen.
When multiple complex antigen variants are used as immunogens, several new questions become important, for example: 1] Which antigen variants should be used as immunogens? 2] What should be the concentrations and temporal order in which they are administered (e.g., cocktails versus sequential)? The answers to these questions are drawn from a huge number of possibilities, and random selection from a large number of combinations of options may not allow sufficient sampling to find efficacious strategies. Intuition is unlikely to guide choices correctly because a mechanistic understanding of how AM occurs in the face of variant or mutating antigens is not available, as past studies have focused on AM in response to single model antigens. This gap in basic immunobiology needs to be addressed. A fundamental understanding of AM induced by several antigen variants that mimic the complexity of how conserved epitopes are shielded on the intact viral spike could be harnessed to design optimal immunogens and immunization protocols for the development of universal vaccines against highly mutable pathogens (e.g. HIV-1, influenza).
To take steps toward these goals, we developed an in silico model of AM induced by variant antigens. This stochastic dynamic model enables examination of the key mechanisms and factors that influence AM in the face of variant antigens, and the development of bnAbs. Our calculations predict markedly distinct outcomes if designed antigen (Ag) variants are presented in different concentrations and temporal patterns during immunization. Experiments in mice using model HIV antigens are consistent with these predictions. Thus, our complementary computational and experimental results provide broadly applicable fundamental insights, and a guide for further studies aimed at overcoming roadblocks to the induction of bnAbs against HIV-1 by vaccination.
RESULTS
In silico model
The purpose of our in silico modeling is not quantitative recapitulation of existing experiments, but to provide fundamental mechanistic insights into AM induced by multiple Ag variants and to compare the predicted relative efficacy of different immunization schemes in inducing cross-reactive broadly neutralizing Abs (bnAbs). Two key features not considered before must be incorporated explicitly in such studies; viz., the presence of multiple Ag variants during GC reactions and the molecular complexity of the Ags. To mimic interactions of B cell receptors with complex immunogens such as the HIV-1 trimeric spike, we account for the fact that the conserved protein epitope of desired Abs are partially shielded, and that insertions and deletions in the variable loops can hinder the formation of strong interactions with the conserved residues of the epitopes (e.g. those in the CD4bs).
We computationally simulate the dynamics of a typical GC (Figure 1A). The GC reaction (GCR) starts on day 3 (Nieuwenhuis and Opstelten, 1984) after Ag injection, with three B cell blasts (Jacob et al., 1991; Kroese et al., 1987) that barely meet a relatively low affinity threshold, Ea. The qualitative results we report do not depend on the particular value of Ea since all other affinities are scaled relative to it. The B cells expand without mutation, reaching a population size of about 1500 cells around day 7(Jacob, 1991).
Hypermutation in the Dark Zone of the GC
At day 7, AID-mediated somatic hypermutation (SHM) in the immunogloblin (Ig) genes turns on (Källberg et al., 1996) with a rate of 10−3 per base pair per division (Berek and Milstein, 1987). Variations in the time at which SHM begins do not affect our results as we start timing AM processes after this point. Each B cell in the dark zone of the GC (the region where this replication/mutation occurs) replicates twice, and we assume that mutation occurs uniformly, neglecting preferential replacements or hypermutation hotspots (Wagner et al., 1995). We assume that the activated B cells are from an appropriate germline (Kepler et al., 2014). The probability of a functionally silent mutation (no change in affinity) is pS=0.5, the probability that a mutation is lethal (e.g., non-folding) is pL=0.3, and the rest are affinity-affecting mutations (probability pA=0.2) (Shlomchik et al., 1998). For affinity-affecting mutations, the affinity of a BCR (i) with a particular type of antigen (j), Eij, is changed. The extent of the change is chosen from a probability distribution characterized by a long tail of deleterious mutations that reduce affinity, as experimental data suggests that favorable mutations are less likely than deleterious ones (Figure S1A). Our BCR-Ag affinity model is defined in a later sub-section.
Selection in the Light Zone of the GC
B cells whose re-expressed surface Ig genes do not carry lethal mutations then go through affinity-dependent selection. Two survival signals are required for a B cell to be positively selected. First, the BCR on a B cell must bind to the Ag (immunogen) displayed on the FDC sufficiently strongly to enable internalization. Since processes occur stochastically, in our simulations, B cells internalize Ag with a probability related to the binding affinity of its BCR for the Ag. The greater the difference between the affinity (Eij) of a B cell (i) for its epitope on Ag j and a threshold (Ea) required for Ag internalization, the greater the probability of Ag internalization. This probability is described mathematically in analogy with a Langmuir isotherm (Equation 1 in Methods).
B cells that internalize Ag display antigenic peptides (p) bound to major histocompatibility complex (MHC) molecules on their surface. T cell receptors expressed on T helper cells can bind to these pMHCs to deliver a key survival signal. B cells compete with each other for the limited availability of T cell help (Victora et al., 2010). T helper cells are specific for peptides derived from the Ag, but they are responsive to diverse pMHCs, not just those derived from the epitope targeted by the BCR. Thus, we assume that the probability of a B cell receiving T cell help is dictated by the amount of internalized Ag, regardless of the identity of its targeted epitope. A B cell that successfully internalizes Ag receives T cell help with a probability that depends upon its probability of internalizing Ag relative to the average probability of internalizing Ag of all the other B cells present in the GC (Equation 2 in Methods). A B cell with a high affinity for its target epitope competes better for T cell help.
To study AM against Ag variants that may be present simultaneously, we have to confront an issue for which no experimental information exists: when a GC B cell encounters a FDC, with how many types of Ag variants can it simultaneously interact? We consider two scenarios: 1] Each GC B cell interacts with one type of Ag variant during an encounter. 2] Each GC B cell interacts simultaneously with all Ag variants held on the FDCs. We find that which of these scenarios describes the heterogeneity of Ag display on FDCs strongly influences the outcome of AM, indicating the importance of experimental interrogation of this issue.
We study two extreme cases of competition for T cell help: 1] GC B cells compete only with contemporary GC B cells (“peers only”). 2] In addition to current GC B cells, all antibodies generated in previous rounds of mutation/selection also participate in the competition (“Ab feedback”). Reality should be bounded by these scenarios.
Recycling, differentiation, and termination of the GCR
From seminal studies (Oprea and Perelson, 1997), 90% of the selected cells are recirculated to the dark zone. The rest differentiate into equal numbers of Ab-secreting plasma cells and memory cells that can re-expand upon future activation. Ab feedback is provided by objects in our agent-based model with affinities representing these past GC emigrants. As AM proceeds, at first, the number of B cells in the GC decreases. In some cases, all B cells apoptose and the GC extinguishes. In others, upon reaching a population bottleneck, favorable clones emerge, and the number of B cells rises (Zhang and Shakhnovich, 2010). We terminate the GCR once the GC population recovers to the initial size (i.e.~1500 cells), or when an assumed maximum duration of 120 d (or 240 GCR cycles) is reached, whichever comes first. The first condition reflects the fact that an abundance of GC B cells will internalize all the Ag on FDCs. The second condition may reflect antigen decay over time which we do not model explicitly.
Model for BCR-Ag affinity
In classic computational studies focused on GCR stimulated by a single model Ag, B cells were binned into different affinity classes for the Ag (e.g. Kepler and Perelson, 1993). The correlated affinities for different Ag variants require a more detailed description. Other studies have considered mathematical models (such as NK-models) for BCR properties and their Ag affinity which present rugged landscapes for affinity evolution (Deem and Lee, 2003). To unambiguously define affinity to different Ag variants and to consider complex immunogens that reflect features on viral spikes, we developed a coarse-grained model with “residue-level” resolution for key BCR-Ag interactions (Figure 1C). Our model was inspired by the CD4bs on the trimeric HIV-1 viral spike, which is targeted by many monoclonal bnAbs for HIV-1 (Burton et al., 2012). But, it applies to other epitopes which contain highly conserved residues, and can easily be modified to consider other pathogens. We ignore distracting epitopes that do not contain conserved residues because they are less likely to elicit bnAbs.
BCRs can potentially make contacts with three types of residues on the viral spike: (1) Highly conserved residues of the epitope (18 such residues in model). (2) Residues representing motifs, such as glycan attachment sites, which, when occupied, can be associated with sterically blocking access to the conserved residues (6 such residues in model). (3) Variable residues, which upon mutation (includes insertions/deletions), can further mask the conserved residues of the epitope. We include 22 such residues from the variable loops of Env which mimic the most mutable sites in the Seaman neutralization test panel (Seaman et al., 2010; Walker et al., 2011) sequences and publicly available Env sequences.
Each epitope residue is described in a coarse grained manner, such that it is either the wild type (WT) amino acid or a mutant. The strength of interaction of a residue (k) on BCR (i) with a residue on the epitope is denoted by . The binding affinity, Eij, between a B cell clone h⃗i and a viral strain s⃗f is modeled as
| (1) |
The first M interactions (i.e. k≤M) are with variable contact residues on the viral spike, where sk can be either 1 (WT) or −1 (mutated). The other (N−M) sites (i.e. k>M) are conserved residues on the epitope with sk=1. The interaction strength hk is drawn from a continuous and uniform distribution within a bounded range (details in Supplemental Simulation Methods).
Equation 1 is, however, just a starting point for the affinity between a particular BCR and Ag, as BCRs do not interact with peptide chains in a linear fashion, and interactions between residues are not independent, as Equation 1 may imply. Epitope-paratope interactions are distinctly 3-dimensional, and structural aspects of CD4bs bnAbs also point to the importance of how interactions with some residues on the viral spike might influence interactions with other epitope residues (Zhou et al., 2010). For instance, most CD4bs bnAbs avoid contact with almost the entire V1/V2 loop except for a few conserved residues near the stem, and the very potent VRC01 Ab avoids the V5 loop. This suggests that avoiding interactions with some residues can allow better access and stronger interactions with the conserved residues of the epitope. Furthermore, affinity enhancement of bnAbs (such as VRC01) is influenced by alteration of non-contact residues (Klein et al., 2013). We account for these effects as described below (mathematical details in Supplemental Simulation Methods).
BCR mutations that strengthen (weaken) interactions with the residues that shield the conserved residues could result in a decreased (increased) binding strength (value of h in Equation 1) for a randomly chosen paratope residue that can potentially interact with a conserved residue on the epitope. This feature reflects the fact that BCRs that decrease contacts with shielding residues are more likely to be able to access and make contacts with the protected conserved residues.
Current knowledge on Env structures (Julien et al., 2013; Lyumkis et al., 2013; Pancera et al., 2014) indicates that V1 is likely to be a dynamic, unfolded and disordered flexible loop, and mutations in V2, especially insertions/deletions, can hide the conserved residues of a neutralizing epitope. So, paratope alterations that weaken interaction with a mutated variable loop residue result in an increased binding strength (value of h in Equation 1) for a randomly chosen paratope residue that can potentially interact with a conserved residue on the epitope (Figure 1D), and vice versa.
Choice of Immunogens and immunization schemes
In silico, we study three Ag variants, the WT Ag (only unmutated residues) and two mutants. Of the 22 most mutable residues in the variable loops, 20 residues are mutated in the majority of the 141 Seaman test panel sequences (Figure S1B). As these highly mutated strains are viable, to maximize the number of non-overlapping mutated residues on the Ag variants, we studied two mutant strains with 11 non-overlapping mutations in the variable sites. We also studied variants with 4 and 8 such mutations.
We investigate three immunization schemes in silico: 1] Scheme I (WT+v1+v2): WT Ag and two variants administered as a cocktail. 2] Scheme II (WT|v1+v2): Immunization with WT Ag first, followed by administration of the two variants simultaneously. 3] Scheme III (WT|v1|v2): Immunization with WT Ag first, followed by sequential administration of the two variants. In our murine experiments we studied schemes I and III.
For each immunization protocol, we simulate many GC reactions. When all steps of immunization and AM are completed, we check whether the affinity of each Ab produced by a GC exceeds a threshold value against each strain in the Seaman panel. The breadth of coverage is defined as the fraction of test panel sequences to which an Ab binds with an above-threshold affinity. We collect statistics from many Abs and simulations, and report results as histograms or probabilities of obtaining Abs with a certain breadth. As many GCs are induced in each vaccinated person, these results reflect the probability of obtaining Abs that exhibit particular breadths of coverage in a typical individual.
Model reproduces known features of affinity maturation with a single antigen
Immunization with only the WT Ag leads to affinity enhancement on conserved and variable residues alike (Figure S1E). The number of accumulated mutations (7 affinity-affecting mutations in 2 weeks, Figure S1D) and the incremental changes in interaction strength (Figure S1E) are consistent with experiment (Berek et al., 1991; Kocks and Rajewsky, 1988; Wedemayer et al., 1997). Higher affinity clones continuously emerge, producing potent Abs (Figure S2 C and F).
The effect of antigen concentration
For a single Ag, if Ag dose is too low (Figure S2 A–B and D–E, lowest Cwt), B cells are unlikely to be selected during GC reactions, the GC collapses, and there is no Ab production. If Ag dose is too high (Figure S2 A–B and D–E, highest Cwt), selection is easy, there is little competition between B cells, and GCs are rapidly filled with low affinity clones (Eisen and Siskind, 1964; Goidl et al., 1968). Our agent-based stochastic approach naturally reproduces the inverse correlation between Ag concentration and heterogeneity in Ab affinities (Figure S2 G–H) observed in early experiments (Eisen and Siskind, 1964).
For the three immunization schemes with antigen variants, Ag concentration is again a very important variable (Figure 2). If the Ag concentration is too low most GCs collapse as expected. However, there is a curious decline in GC survival and Ab breadth if the Ag concentration is too high for immunization schemes II and III. During AM after immunizing with a high dose of WT Ag, many B cells survive easily and the GC reaction draws to an end quickly. Therefore, these B cells are largely low affinity clones that have not accumulated mutations that enhance contacts with the conserved residues of the epitope. So, upon administering either a cocktail of the two Ag variants or just one variant, these B cells have a small chance of binding sufficiently strongly with the mutants and surviving, and so GCs collapse despite the abundance of Ag. The few Abs produced do not develop breadth as the large number of mutations required to confer breadth do not evolve (see examples in Figure S3).
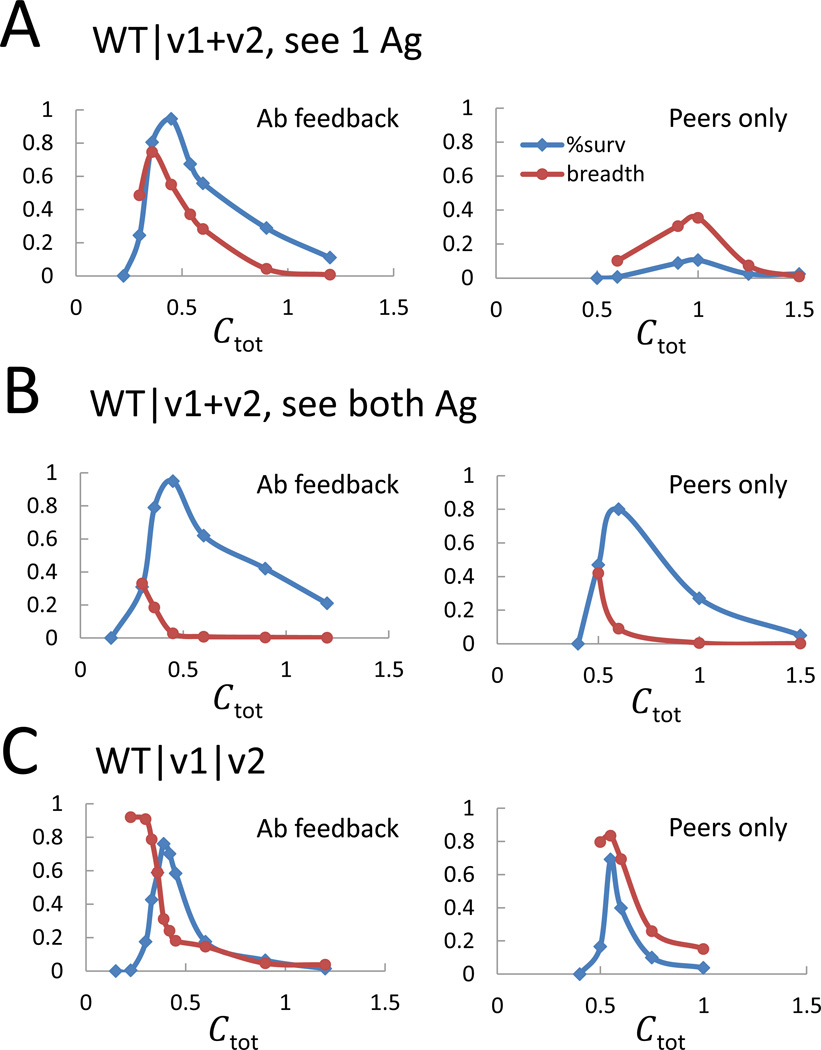
Figure 2. Concentration dependence of GC survival and antibody breadth in “WT first” schemes.
For a relevant range of Ag concentrations (Ctot), the fraction of surviving GCs (%surv, blue) and their Ab breadth (red) are shown for (A) Scheme II (see 1 Ag), (B) Scheme II (see both Ag) and (C) Scheme III, with full (left column) or none (right column) Ab feedback. See also Supplementary Figures S2 and S3.
Hereon, for each immunization scheme, we show results for the Ag concentration (listed in Table 1) that yields Abs with a near optimal breadth (peak of red curves in Figure 2). In Scheme III, the chosen concentration is slightly higher to ensure high Ab production.
Table 1.
Properties of antibody responses produced by various immunization schemes.
| Scheme | %surv | Breadth | hc | hv | Ctot |
|---|---|---|---|---|---|
| WT only (tmax = 80) | |||||
| Ab feedback | 54% | 0.6% | 0.45 | 0.39 | 0.3 |
| peers only | 79% | 0.7% | 0.49 | 0.43 | 0.5 |
| (I) WT+v1+v2 (tmax = 240) | |||||
| See 1 Ag; Ab feedback | 1% | 11% | 0.72 | 0.29 | 0.6 |
| peers only | 1% | 2% | 0.52 | 0.22 | 1.0 |
| See all Ag; Ab feedback | 1% | 5% | 0.84 | 0.70 | 0.3 |
| peers only | 3% | 3% | 0.89 | 0.83 | 0.5 |
| (II) WT|v1+v2 (tmax = 80 + 160 = 240) | |||||
| See 1 Ag; Ab feedback | 80% | 75% | 1.21 | 0.16 | 0.36 |
| peers only | 10% | 35% | 0.73 | 0.16 | 1.0 |
| See both Ag; Ab feedback | 31% | 33% | 1.07 | 0.37 | 0.3 |
| peers only | 47% | 42% | 1.22 | 0.41 | 0.5 |
| (II) WT|v1|v2 (tmax = 80 × 3 = 240) | |||||
| Ab feedback | 43% | 79% | 1.38 | 0.22 | 0.33 |
| peers only | 69% | 83% | 1.64 | 0.24 | 0.55 |
%surv: percentage of seeded GCs that produce antibodies efficiently; Breadth: defined in text; hc (hv): the average strength of interactions with conserved (variable) residues of the epitope—large values of hc indicate focusing on the conserved residues of the epitope; Ctot: antigen concentration.
Immunizing with a cocktail of WT Ag and two variants fails to elicit an effective response
Figure 3A shows in silico results for the distribution of the breadth of coverage (for the Seeman panel) of Abs produced using immunization Scheme I (cocktail of WT+v1+v2). Ag concentration is fixed to yield the greatest breadth, but two more variables could be important: during selection in the light zone, does a B cell-FDC encounter involve one or all Ag variants? Is “Ab feedback” important during AM? For this immunization scheme, in most scenarios, just a few percent of GCs survive (Table 1); i.e., Ab titers are predicted to be low. To see why, consider first the situation where B cells interact with only one Ag variant during each encounter with FDCs. B cells that bind moderately strongly to one of the three variants seed the GC, and they do not have any strong interactions with the conserved residues of the epitope yet. Now consider a B cell that is selected by a particular Ag variant in an early round, then mutates, and returns to the light zone to encounter a different variant. Without even moderately strong contact with the conserved residues, the probability that such a B cell is cross-reactive to the new variant is small. Thus, apoptosis is the most likely outcome, leading to collapse of the GC. For the rare GCs that do survive, there is evolution of interactions with the conserved residues and dimunition of interactions with variable loops during AM, and this confers some breadth (relative to immunization with WT Ag alone, see Table 1).
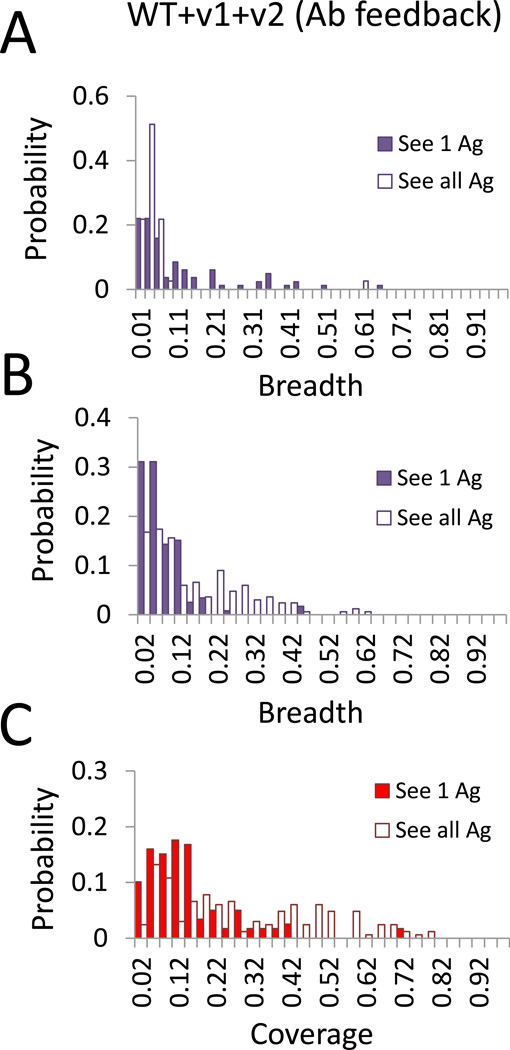
Figure 3. Distribution of breadth of individual antibodies and their total coverage for surviving GCs in scheme I—WT+v1+v2.
(A and B) Histograms of breadth for having 11 (A) or 4 (B) non-overlapping mutations in the two variants. Histograms are obtained as a distribution for all the surviving GCs. (C) Histograms of coverage for surviving GCs under the same conditions as in (B). The coverage is defined as a sum of non-overlapping specificities. Results are shown for the cases of “see 1 Ag” (filled bars) and “see all Ag” (unfilled bars), with Ab feedback. See also Supplementary Figure S4.
If B cells interact with all Ag variants during each encounter with FDCs, and the Ag concentration is chosen to be the one that confers optimal breadth, the percentage of surviving GCs and the distribution of breadth is not very different compared to the case where only one Ag variant is encountered at a time (Figure 3A). However, importantly, the optimal concentration is lower when B cells can interact with all Ag variants. If the Ag concentrations were made the same as when B cells interact with one Ag at a time, then most GCs would survive when all Ag variants are simultaneously encountered (Figure S4B). This is because, in this case, B cells that bind sufficiently strongly to any one Ag variant can progress through AM. As a consequence, the generated Abs are likely to be strain specific. Thus, if Ag is displayed homogeneously on FDCs, for immunization scheme I, optimal conditions for inducing Abs efficiently at high titers would not induce bnAbs. The lower Ag concentration required for optimal breadth results in the survival of only a relatively low fraction of GCs (Figure 3A).
We also carried out calculations where the Ag variants differ from each other by only four non-overlapping mutations. When all variants are simultaneously encountered in each interaction with FDCs and Ab feedback is turned on, comparing results for this case (Figure 3B) with that when the variants differ by eleven mutations (Figure 3A), we find that a much higher fraction (10% vs 1%) of GCs succeed in producing Abs (Figure S4D). This is because the Ags vary less from each other, and so the chance of a B cell being cross-reactive to variants in early stages of AM is higher, thus increasing the probability of it being positively selected. The breadth of the Abs produced is not large because many variable residues that are unmutated in the Ag variants are mutated in the test panel sequences, and strain specific Abs are likely to be produced as all Ag variants on FDCs are simultaneously encountered. This is why the total coverage (Figure 3C), defined as the breadth of coverage offered by the polyclonal response from all the Abs, is higher than the average breadth of coverage of individual Abs (Figure 3B). Results for the case where only one Ag variant is encountered at a time on FDCs are shown in Figures 3B and 3C (filled bars), and for no Ab feedback see Table 1.
In our in silico studies of this immunization scheme, we did not find any conditions that result in bnAbs with high probability (Figures S7 and S8). This is because B cell evolution during AM is made difficult by the potentially conflicting selective pressures imposed by Ag variants simultaneously displayed on FDCs. We term this phenomenon, frustrated AM. The degree to which AM is frustrated is controlled by a complex interplay between Ag concentration, heterogeneity of Ag display on the FDCs, the number of mutations that separate the Ag variants, and the extent to which Ab feedback is important.
Immunizing with WT Ag first and then a cocktail of the two variants yields Abs with significant breadth in special circumstances
Consider first the situation in which there is no Ab feedback and only one Ag variant is encountered at a time on FDCs (Figure 4B filled bars). In the first period of AM induced by the WT Ag, moderately strong contacts with the conserved residues of the epitope can evolve. During AM following immunization with the cocktail, individual B cells have equal chance of encountering either Ag variant during selection. Since the two variants have non-overlapping mutated residues, beneficial BCR mutations for one strain are deleterious for the other. Maturing B cell lineages are frustrated in satisfying these conflicting requirements for selection in successive rounds, but less so than in Scheme I because moderately strong interactions with the conserved residues have evolved during AM driven by the WT Ag prime, resulting in some cross-reactivity. Therefore, a greater fraction (~ 10 %) of GCs survive compared to scheme I. Since a relatively high Ag concentration is required for GC survival in this case (Figure 2A right panel blue curve), B cells can expand readily and GCRs terminate quickly. Short maturation times limit the average breadth (~35%, Figure 2A right panel red curve), but Abs with large breadth do evolve with low probability.
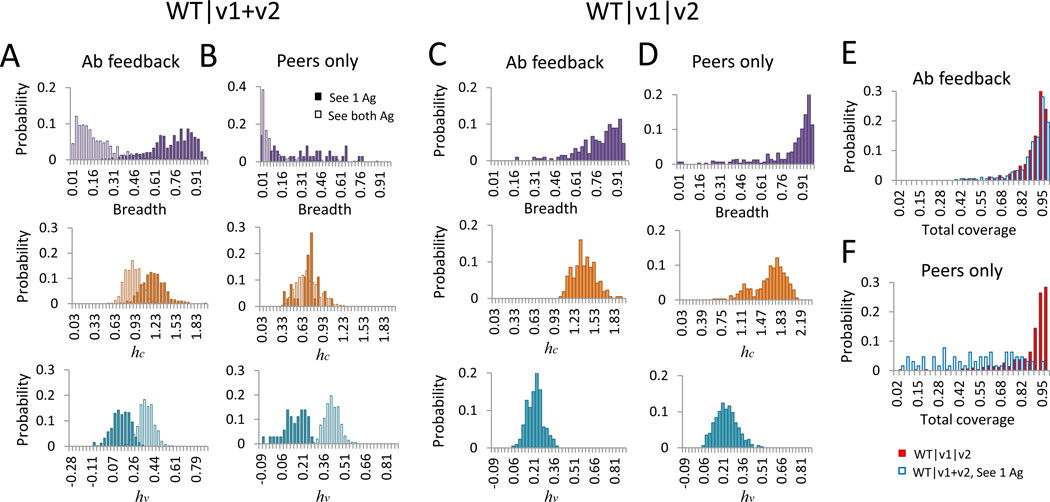
Figure 4. Comparison of statistics for surviving GCs in Scheme II—WT|v1+v2 and Scheme III—WT|v1|v2.
Shown are histograms for breadth, mean interaction strength with conserved residues (hc) and with variable residues (hv) (A–D), and for total coverage (E and F) via a polyclonal response. Results are shown for “Ab feedback” (A, C, E) and “peers only” (B, D, F) scenarios. For Scheme II (A and B), cases of “see 1 Ag” (filled bars) and “see both Ag” (unfilled bars) are shown. Total coverage (E and F) is presented for Scheme III (WT|v1|v2) by red filled bars and for Scheme II (WT|v1+v2, see 1 Ag) by blue unfilled bars. See also Supplementary Figure S5.
If there is Ab feedback, lower Ag concentrations still allow GCs to mature successfully. This is because Abs produced in previous rounds of AM often have lower affinities for the encountered Ag than the best clones produced during the current round of mutation and selection. This confers a competitive advantage to these best B cell clones because they are not just competing with each other, but also with the weaker affinity Abs (Supplemental Simulation Methods). Also, the Abs compete effectively with unfavorable mutant cells that may emerge and be stochastically selected only to be extinguished in a future round of mutation-selection. Lowering Ag concentration diminishes the probability of selection in each round, thus allowing AM to proceed for a longer time before all the Ag on FDCs is internalized. This allows mutations that confer breadth to accumulate. This balance of lowering frustration through Ab feedback and increasing frustration by reducing Ag concentration results in a very high survival rate for GCs and considerable breadth in the Ab response (Figure 2A left, Figure 4A filled bars).
If multiple Ags are encountered during each interaction with FDCs, the outcome is different (Figures 4A and 4B, unfilled bars). Since a choice of being selected by the same variant (rather than a randomly chosen one of the two) is always available in successive rounds of AM, the frustration is low. In most cases, we find that B cells are selected by one of the variants repeatedly, and so strain-specific Abs are likely to evolve (Table 1). Furthermore, access to both Ag variants allows B cells to multiply successfully in the GC and quickly consume all the Ag on FDCs. The duration of AM is short, so mutations that confer breadth evolve rarely, and the average breadth is no more than 40%, regardless of the extent of Ab feedback (Table 1). For this optimal breadth to develop, the antigen concentrations must be much lower than when only one Ag variant is seen during each B cell-FDC encounter (Figure 2B vs 2A).
Our results suggest that this immunization scheme has the potential to produce bnAbs (~ 75 % breadth) with high probability if B cells encounter one Ag variant at a time on FDCs and all Abs produced in previous rounds migrate through ongoing GCs. Rather than the extreme situations of full Ab feedback or none at all, there is some middle ground, and also most likely, B cells encounter one FDC Ag variant in some rounds of selection and all variants during others. Thus, our results suggest that, depending upon circumstances, this immunization scheme produces Abs efficiently with a probability between 10%–80%, and with average breadths ranging from 30 % to 80 % (Table 1). This scheme may be analogous to what ensues in patients who develop bnAbs upon natural infection as they are first exposed to the infecting strain, which then diversifies. However, the sensitivity of our results to varying conditions suggest that it may be quite difficult to induce bnAbs consistently in diverse patients using this immunization scheme. This is because the conditions noted above are likely to vary between and within individuals.
Sequential immunization with antigen variants leads to efficient induction of an antibody response with broad specificity
Sequential immunization with the the three Ag variants temporally separates the mutually conflicting selective driving forces imposed by multiple variants. Confounding effects associated with whether one or multiple types of Ags participate in each B cell-FDC encounter in the GC are also obviated.
Consider first the situation where there is no Ab feedback (Figure 4D). Maturation against the WT Ag results in some strong interactions with the conserved residues. When AM ensues with the first variant, two main types of lineages evolve in the simulations (Figure S5). Both types of lineages tend to reduce interactions with the residues that are mutated in the first variant Ag. But, in one type of lineage, interactions with the unmutated variable residues in the first variant (which are mutated in the second variant) are enhanced; in the other type of lineage, these interactions do not change very much. When the second variant with non-overlapping mutations is introduced, the latter lineages have a good chance of outcompeting the former ones during AM. This is because clones that did not increase their footprint on the variable residues that are now mutated in the second variant can simply reduce interactions with these residues, and focus strongly only on the conserved residues of the epitope. This is why Abs produced in Scheme III exhibit a narrow distribution of very large breadth (Figure 4D top panel) rather than a broad distribution of Abs with moderate breadth seen in the analogous situation using Scheme II (Figure 4B top panel, filled bars). In scheme II, lineages specific for one or the other variant strain have a higher chance of survival. In scheme III, Abs that focus contacts with the conserved residues of the epitope and minimize interactions with all the variable residues are more likely to emerge (Figures 4B and 4D, middle panels).
Comparing “Ab feedback” (Figure 4C) and “peers only” scenarios (Figure 4D) in Scheme III, we see that Ab feedback leads to narrower distributions of Abs with large breadth, due to the same effects of Ab feedback noted for Scheme II. As shown in Figures 4E and 4F, the distributions of total coverage for Abs produced by Schemes II and III are very close when there is Ab feedback (Figure 4E), and the average values are both as high as 90%. If there is no Ab feedback (Figure 4F), however, Scheme III gives a similar broad coverage (89%) whereas Scheme II yields a moderate coverage (51%) even with polyclonal responses. So, scheme III is predicted to be more robust to many varying conditions.
Experiments in mice with a model sytem show that antibodies that focus on the conserved residues emerge upon sequential immunization, but not upon immunization with a cocktail
Our calculations predict that, compared to the other immunization schemes we studied, truly cross-reactive Abs that focus contacts on the conserved residues of the epiope with a small footprint outside are most likely to emerge robustly upon sequential immunization with Ag variants. Immunization with a cocktail of Ags is predicted to result in a significantly worse outcome compared to sequential immunization. We note previous immunization studies that have suggested the advantages of sequential immunization of HIV Env in generating cross-reactive Abs, in further agreement with our computational results (Malherbe et al., 2011; Pissani et al., 2012). Here we tested our predictions comparing sequential immunization and cocktails in mouse studies using precisely engineered Ag variants. It is important to note that the variant Ags we have engineered are gp120 monomers of Env, not trimers. Thus, they cannot be expected to produce bnAbs that neutralize virus particles with intact trimeric spikes. The goal of our experiments was to precisely test whether cross-reactive Abs that focus on the conserved residues of an epitope (CD4bs) are more likely to develop upon sequential immunization, compared to administration of a cocktail of the same immunogens, as per our in silico predictions.
As described in Extended Experimental Procedures, we engineered variants of a minimized gp120 core protein immunogen (the “stripped core”) that incorporate diversification at 43 surface residues outside the CD4bs, while retaining binding affinity to the VRC01 bnAb (Table S1, Figure S6). These immunogens are designed to present biochemically novel residues outside the CD4bs such that only the desired CD4bs epitope is conserved across all the immunogens. We used four engineered variants (including stripped core) that fit these criteria. Our in silico results should hold irrespective of whether three or four variants are used.
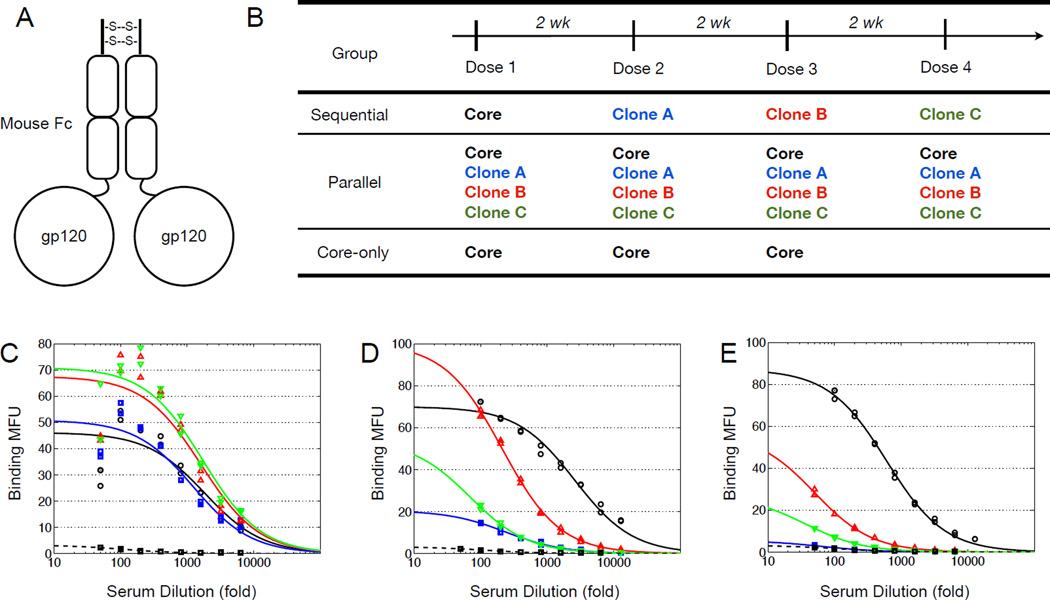
BALB/c mice were immunized intranasally with HEK 293-produced immunogens fused to mouse Fc (Figure 5A) with a CpG oligonucleotide adjuvant, following protocols described elsewhere (Ye et al., 2011). Immunogens were administered every two weeks at a total protein dose of 50 pmol. Animals were divided into three groups (Figure 5B). The “Sequential” group of four mice was immunized sequentially with each of the four Ag variants. The “Parallel” group of four mice received a cocktail of all four variants at each administration. The “Core-only” group of two mice was given three doses of the same stripped core immunogen. Serum was collected every week.
Figure 5. Immunization of mice with variant immunogens.
(A) Schematic of an Fc-gp120 immunogen. (B) Immunization groups and dosing schedule for mouse experiment. (C–E) Serum titrations (day 48) of a representative mouse from each group—(C) sequential, (D) parallel, (E) core-only—on yeast displaying stripped core (black), clone A (blue), clone B (red), or clone C (green). Each plot also includes serum from an unimmunized mouse binding to yeast displaying clone C (black dashed). Binding data is fit to a monovalent binding isotherm of the form where “dil” is the serum dilution and y is the binding signal in MFU. Discussion of the fitted parameters can be found in the supplemental material. See also Supplementary Figure S6 and Table S1.
Serum binding to the Ag variants was assayed by flow cytometry of yeast displaying each of the four variants. Representative curves for each of the three immunization groups are shown in Figures 5C–E. Sequentially-immunized mice exhibit similar binding to each of the four Ag variants, consistent with serum that recognizes and focuses contacts with a shared epitope presented on all variants (Figure 5C). Mice immunized with a cocktail of four variants show a broader spread of binding affinities, consistent with dominant serum specificities for some variants but not others (Figure 5D). In the mouse represented, for example, it appears that the serum recognizes the epitope on stripped core that is not present on Clones A or C. Serum from mice immunized only with stripped core bind strongly to stripped core but not to the other immunogens, consistent with our immunogen design objective that the four variants not share common surface residues outside the CD4bs (Figure 5E), like the non-overlapping mutations in Ag variants in our calculations.
Serum specificity for the CD4bs was determined in two ways. First, we measured the binding of serum to the stripped core mutant D368R, which is known to disrupt the binding of several CD4bs-directed Abs (Thali et al., 1992). Serum samples collected after the third and fourth immunizations were incubated at a 1:100 dilution with yeast displaying either stripped core or the D368R mutant (Figure 6A). For mice from the sequential immunization group, the fractional binding of serum to D368R was similar to that of VRC01 at saturating concentrations. Of the mice that were immunized with a cocktail of all four immunogens, three are very sensitive to D368R after three immunizations but appear to lose this specificity by the fourth administration.
Figure 6. Determination of serum specificity for the CD4 binding site.
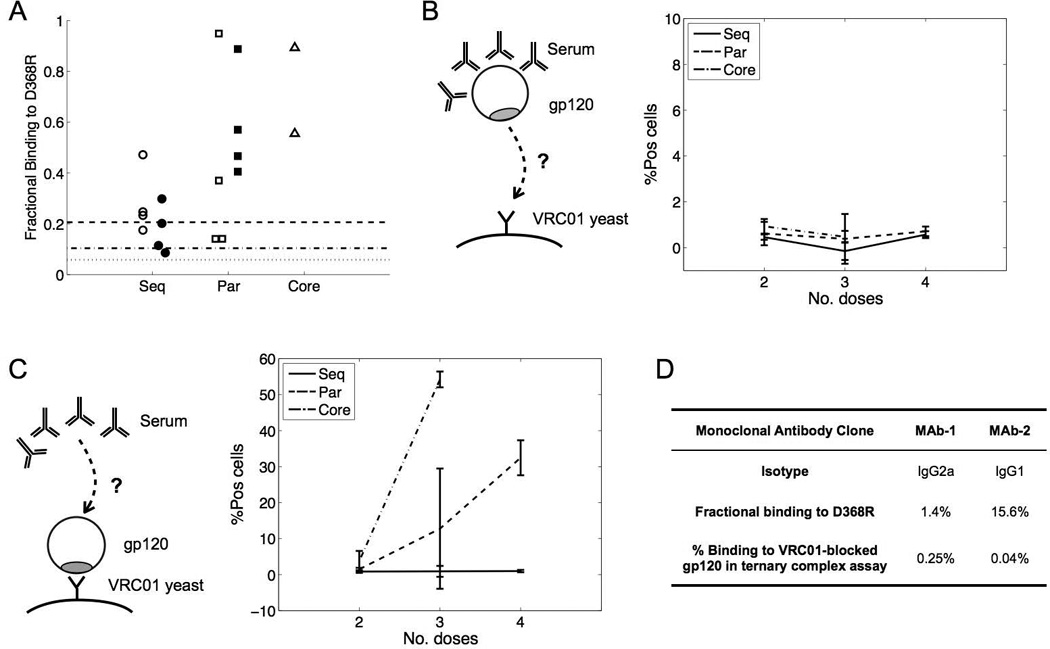
(A) Fractional binding to D368R mutant vs stripped core of serum from each group after three (open markers) and four (filled markers) immunizations. The fractional binding to D368R for antibody VRC01 at various concentrations is shown as lines: 0.21 at 93 nM (dashed line), 0.10 at 75 nM (dash-dotted line), and 0.06 at 8.2 nM (dotted line). (B) Schematic and data from ternary complex assay in which gp120 (CD4bs shown in gray) is pre-incubated with serum then added to VRC01 yeast. The formation of a ternary comlex is only possible if VRC01 is able to bind to its epitope on gp120 after serum has bound. The figure shows the percentage of yeast cells positive for mouse serum from each immunization group—sequential (solid line), parallel (dashed line), core-only (dash-dotted line)—for various time points. (C) Schematic and data from ternary complex assay in which gp120 is pre-loaded onto VRC01 yeast then incubated with serum. The formation of a ternary complex is only possible if serum antibodies are able to bind to their epitope(s) after VRC01 has bound. The figure shows the percentage of yeast cells positive for mouse serum from each immunization group as above. (D) Analysis of two monoclonal antibodies from a sequentially-immunized mouse: fractional binding to D368R vs. stripped core gp120 was assayed with 10 nM monoclonal antibody (analogous to 6A); percentage binding in the ternary complex assay (analogous to 6C), in which gp120 is pre-bound to VRC01 yeast.
A second assay used to determine specificity was to evaluate the simultaneous binding of VRC01 and serum antibodies to gp120 (Methods). The assay was performed first by pre-incubating the gp120 with mouse serum before introducing VRC01-displaying yeast (Figure 6B). If serum antibodies compete with VRC01 for its binding site, the gp120-serum complex will not bind to the yeast. No binding signal was observed for any of the serum samples, suggesting that all contained some fraction of VRC01-competitive antibodies. This result is consistent with the D368R gp120 binding results discussed above.
The same assay was then performed by pre-incubating gp120 with VRC01 yeast before introducing the serum (Figure 6C) to determine whether the serum contains any specificity other than to the CD4bs. Note that due to plasmid loss in yeast during culture, ~60% positive cells is the maximum observable signal in the assay. Mice immunized with just stripped core (53%, 56%) or with a cocktail of four Ags (mean = 32% ± 5%) developed antibodies that bind to other epitopes on gp120. However, mice immunized sequentially did not (mean = 1.0% ± 0.3%). These experiments suggest that sequential immunization with Ag variants elicited a serum response that was VRC01-competitive and entirely focused on the conserved residues targeted by the VRC01 Ab. Mice that were exposed to a cocktail of the variants generated some VRC01-competitive antibodies, but also Abs that targeted non-conserved residues on a single immunogen, i.e. were not cross-reactive. In other words, only sequential immunization robustly elicited a response that is focused on the conserved residues of the desired epitope. These findings are in harmony with our in silico results.
To establish that individual CD4bs-competitive antibodies were generated by sequential immunization, hybridomas were generated by splenotypic fusion from a mouse immunized using this protocol. Two distinct gp120-binding monoclonal antibodies were isolated (for sequences, see Extended Experimental Procedures). The antibodies both targeted the CD4bs epitope, as both were disrupted by the D368R mutation (at 10 nM antibody, fractional binding to D368R vs. stripped core gp120 of 1.4% and 15.6%) and neither was able to bind to stripped core that had been pre-blocked with VRC01 (Figure 6D). These data make clear that the monoclonal antibodies are indeed focused on the CD4bs upon sequential immunization with the variant antigens.
DISCUSSION
The induction of bnAbs against highly mutable pathogens, such as HIV and influenza, will require immunization with Ag variants. Rational design of immunogens and efficient immunization protocols that elicit bnAbs requires mechanistic understanding of a basic problem in immunobiology: viz., how AM occurs in the presence of variant Ags. Our studies of AM in this setting have revealed new concepts, suggested new avenues for experimental and theoretical research, and have practical value. An important concept that emerges is that, when multiple Ag variants are used as immunogens, they can present conflicting selection forces during AM which frustrates the evolution of Abs. This phenomenon is most acutely manifested upon immunization with a cocktail of Ag variants. In this case, a B cell of a particular lineage that is selected in one round by a particular Ag variant is likely, after the next round of mutation, to encounter a different Ag variant on FDCs. This B cell is unlikely to be positively selected in this encounter, thus ending the evolution of a potentially favorable B cell lineage. The degree to which AM is frustrated is determined by a complex interplay of effects dependent on Ag concentration, how heterogeneously Ag variants are displayed on FDCs, the number of mutations that separate the Ag variants, and the extent to which previously generated Abs migrate through ongoing GCs. Our results provide empirical evidence that these parameters can be tuned to achieve an optimal level of frustration. Too much frustration prevents GC reactions from evolving favorable mutations that confer breadth. Too low a level of frustration (the extreme case being immunization with one Ag) results in the development of strain-specific antibodies. An avenue for future theoretical research is to define a quantitative metric of frustration that describes precisely how the degree of frustration depends on the pertinent variables. The metric of frustration could then be optimized to design effective immunization protocols.
Our in silico results suggest that if one primes with the WT Ag, and then boosts with a cocktail of variants, bnAbs can emerge, but only if some special conditions hold. Such a scenario may have been the driver of bnAb production in naturally infected patients because this immunization strategy mimics natural infection with one strain and subsequent viral diversification. However, our results show that deviations from these special conditions make the evolution of bnAbs unlikely in this setting (Table 1). This suggests that potent bnAbs evolve during natural infection only when special conditions are met, which happens rarely and thus take a long time to emerge by chance. Controlling immunization protocols precisely to satisfy special conditions in every vaccinated individual seems difficult. Furthermore, even if the conditions were set to perfectly mimic a situation that resulted in the evolution of bnAbs upon natural infection, the outcome may not be favorable because Darwinian evolution is inherently stochastic and cannot be replicated exactly. So, although it is important to understand how bnAbs are produced during natural infection, mimicking these conditions may not be an efficient way to induce bnAbs by vaccination.
We find that when Ag variants are administered sequentially, bnAbs can develop with relatively high probability over a wider range of conditions than if other strategies are deployed (Table 1, and Figures 2—4). In this case, the conflicting selection forces due to the variant Ags are temporally separated. This can lead to successful evolution of multiple B cell lineages that first develop moderate interactions with the conserved residues of the epitope, and then progressively acquire mutations that evade contacts with one set of variable residues, and then another. Evolution of a set of possible clones which have a chance at maturing into bnAbs after AM against the first variant makes success more likely as all of them are unlikely to go extinct during stochastic mutation and selection upon immunizing with the second variant. Our in silico results predict that this immunization strategy is superior to immunization with a cocktail of the same set of variants, and our model experiments in mice support this prediction.
Sequential immunization with Ag variants that share a single epitope to induce B cells specific for the common epitope has been tried with linear peptide epitopes derived from HIV gp41, though the resulting Abs were non-neutralizing (Guenaga et al., 2011; Correia et al., 2010). Past work also emphasizes the importance of masking irrelevant epitopes, but by itself, this strategy is insufficient for succesful vaccination (Pantophlet et al., 2003; Selvarajah et al., 2005). Our in silico and in vivo studies suggest that precisely engineered variant intact virus spike immunogens administered in a sequential fashion under appropriate conditions may offer the best opportunities for induction of bnAbs against HIV-1 and other highly mutable pathogens.
METHODS
In silico model
The probability of a B cell internalizing antigen is given by:
| (1) |
Here Cj is the concentration of Ag of type j presented on the FDCs. The sum over the Ag index j runs through nA distinct types of Ags that B cell i could potentially interact with simultaneously during an encounter with a FDC bearing multiple Ag variants.
The proability of a B cell to succeed in receiving T cell help is given by:
| (2) |
where is the average probability of internalizing Ag of all the other B cells present in the GC. is the total Ag concentration, and the dependence on this variable accounts for the observation that the number of activated T helper cells increases with Ag dose, thus making it more likely that B cells receive T cell help.
Binding assay to determine competitiveness with VRCO1
Yeast displaying the scFv of VRC01 was incubated with soluble stripped core gp120 and an excess of mouse antiserum. The formation of a ternary complex—a sandwich of VRC01, gp120, and mouse serum—was detected as the presence of mouse antibodies on yeast by flow cytometry (% positive cells).
The experiment was done in two ways as described in text.
See Extended Supplement Methods for additional information
Supplementary Material
ACKNOWLEDGMENTS
Financial support provided by the Ragon Institute of MGH, MIT, & Harvard (AKC, SW, MK, KDW, JMF) and the International AIDS Vaccine Initiative (IAVI) through the Neutralizing Antibody Consortium SFP1849 (DRB); NIH grants R01 AI033292 (DRB), and Center for HIV/AIDS Vaccine Immunology and Immunogen Discovery grant UM1AI100663 (DRB, AKC). We are grateful to Kevin Kaczorowski and Dariusz Murakowski for helpful discussions and comments.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
AUTHOR CONTRIBUTIONS
SW, AKC, MK, and DRB conceived and designed in silico studies; SW, AKC, MK analyzed in silico data; SW performed in silico studies; JMF, DJI, MH, KDW designed experiments and JMF, KDW analyzed data; JMF performed experiments; BK helped engineer Ag variants; AKC, SW, MK, JMF, KDW, DRB, HNE wrote paper.
REFERENCES
- Allen CDC, Okada T, Tang HL, Cyster JG. Imaging of germinal center selection events during affinity maturation. Science. 2007;315:528–531. doi: 10.1126/science.1136736. [DOI] [PubMed] [Google Scholar]
- Batista FD, Neuberger MS. Affinity dependence of the B cell response to antigen: a threshold, a ceiling, and the importance of off-rate. Immunity. 1998;8:751–759. doi: 10.1016/s1074-7613(00)80580-4. [DOI] [PubMed] [Google Scholar]
- Baumjohann D, Preite S, Reboldi A, Ronchi F, Ansel KM, Lanzavecchia A, Sallusto F. Persistent antigen and germinal center B cells sustain T follicular helper cell responses and phenotype. Immunity. 2013;38:596–605. doi: 10.1016/j.immuni.2012.11.020. [DOI] [PubMed] [Google Scholar]
- Berek C, Milstein C. Mutation drift and repertoire shift in the maturation of the immune response. Immunol. Rev. 1987;96:23–41. doi: 10.1111/j.1600-065x.1987.tb00507.x. [DOI] [PubMed] [Google Scholar]
- Berek C, Berger A, Apel M. Maturation of the immune response in germinal centers. Cell. 1991;67:1121–1129. doi: 10.1016/0092-8674(91)90289-b. [DOI] [PubMed] [Google Scholar]
- Burton DR, Ahmed R, Barouch DH, Butera ST, Crotty S, Godzik A, Kaufmann DE, McElrath MJ, Nussenzweig MC, Pulendran B, et al. A blueprint for HIV vaccine discovery. Cell Host Microbe. 2012;12:396–407. doi: 10.1016/j.chom.2012.09.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Correia BE, Ban YE, Holmes MA, Xu H, Ellingson K, Kraft Z, Carrico C, Boni E, Sather DN, Zenobia C, et al. Computational design of epitope-scaffolds allows induction of antibodies specific for a poorly immunogenic HIV vaccine epitope. Structure. 2010;18:1116–1126. doi: 10.1016/j.str.2010.06.010. [DOI] [PubMed] [Google Scholar]
- Deem MW, Lee HY. Sequence space localization in the immune system response to vaccination and disease. Phys. Rev. Lett. 2003;91:068101. doi: 10.1103/PhysRevLett.91.068101. [DOI] [PubMed] [Google Scholar]
- Eisen HN, Siskind GW. Variations in affinities of antibodies during the immune response. Biochem. 1964;3:996–1008. doi: 10.1021/bi00895a027. [DOI] [PubMed] [Google Scholar]
- Gao F, Bonsignori M, Liao HX, Kumar A, Xia SM, Lu X, Cai F, Hwang KK, Song H, Zhou T, et al. Cooperation of B cell lineages in induction of HIV-1-broadly neutralizing antibodies. Cell. 2014;158:481–491. doi: 10.1016/j.cell.2014.06.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goidl EA, Paul WE, Siskind GW, Benacerraf B. The effect of antigen dose and time after immunization on the amount and affinity of anti-hapten antibody. J. Immunol. 1968;100:371–375. [PubMed] [Google Scholar]
- Guenaga J, Dosenovic P, Ofek G, Baker D, Schief WR, Kwong PD, Karlsson Hedestam GB, Wyatt RT. Heterologous epitope-scaffold prime: boosting immuno-focuses B cell responses to the HIV-1 gp41 2F5 neutralization determinant. PLoS One. 2011;6:e16074. doi: 10.1371/journal.pone.0016074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacob J, Kassir R, Kelsoe G. In situ studies of the primary immune response to (4-hydroxy-3-nitrophenyl)acetyl. I. The architecture and dynamics of responding cell populations. J. Exp. Med. 1991;173:1165–1175. doi: 10.1084/jem.173.5.1165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Julien J-P, Cupo A, Sok D, Stanfield RL, Lyumkis D, Deller MC, Klasse PJ, Burton DR, Sanders RW, Moore JP, et al. Crystal structure of a soluble cleaved HIV-1 envelope trimer. Science. 2013;342:1477–1483. doi: 10.1126/science.1245625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Källberg E, Jainandunsing S, Gray D, Leanderson T. Somatic mutation in immunoglobulin V genes in vitro. Science. 1996;271:1285–1289. doi: 10.1126/science.271.5253.1285. [DOI] [PubMed] [Google Scholar]
- Kelsoe G. The germinal center: a crucible for lymphocyte selection. Semin. Immunol. 1996;8:179–184. doi: 10.1006/smim.1996.0022. [DOI] [PubMed] [Google Scholar]
- Kepler TB, Munshaw S, Wiehe K, Zhang R, Yu JS, Woods CW, Denny TN, Tomaras GD, Alam SM, Moody MA, et al. Reconstructing a B-cell clonal lineage. II. mutation, selection, and affinity maturation. Front. Immunol. 2014;5:170. doi: 10.3389/fimmu.2014.00170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kepler TB, Perelson AS. Somatic hypermutation in B cells: an optimal control treatment. J. Theor. Biol. 1993;164:37–64. doi: 10.1006/jtbi.1993.1139. [DOI] [PubMed] [Google Scholar]
- Kesmir C, de Boer RJ. A spatial model of germinal center reactions: cellular adhesion based sorting of B cells results in efficient affinity maturation. J. Theor. Biol. 2003;222:9–22. doi: 10.1016/s0022-5193(03)00010-9. [DOI] [PubMed] [Google Scholar]
- Klein F, Diskin R, Schied JF, Gaebler C, Mouquet H, Georgiev IS, Pancera M, Zhou T, Incesu R-B, Fu BZ, et al. Somatic mutation of the immunoglobulin framework are generally required for broad and potent HIV-1 neutralization. Cell. 2013;153:126–138. doi: 10.1016/j.cell.2013.03.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kocks C, Rajewsky K. Stepwise intraclonal maturation of antibody affinity through somatic hypermutation. Proc. Nat. Acad. Sci. USA. 1988;85:8206–8210. doi: 10.1073/pnas.85.21.8206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kroese FGM, Wubbena AS, Hendrik GS, Nieuwenhuis P. Germinal centers develop oligoclonally. Eur. J. Immunol. 1987;17:1069–1072. doi: 10.1002/eji.1830170726. [DOI] [PubMed] [Google Scholar]
- Kwong PD, Doyle ML, Casper DJ, Cicala C, Leavitt SA, Majeed S, Steenbeke TD, Venturi M, Chaiken I, Fung M, et al. HIV-1 evades antibody-mediated neutralization through conformational masking of receptor-binding sites. Nature. 2002;420:678–682. doi: 10.1038/nature01188. [DOI] [PubMed] [Google Scholar]
- Kwong PD, Mascola JR, Nabel GJ. Broadly neutralizing antibodies and the search for an HIV-1 vaccine: the end of the beginning. Nat. Rev. Immunol. 2013;13:693–701. doi: 10.1038/nri3516. [DOI] [PubMed] [Google Scholar]
- Liao H-X, Lynch R, Zhou T, Gao F, Alam SM, Boyd SD, Fire AZ, Roskin KM, Schramm CA, Zhang Z, et al. Co-evolution of a broadly neutralizing HIV-1 antibody and founder virus. Nature. 2013;496:469–476. doi: 10.1038/nature12053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyumkis D, Julien JP, de Val N, Cupo A, Potter CS, Klasse PJ, Burton DR, Sanders RW, Moore JP, Carragher B, et al. Cryo-EM structure of a fully glycosylated soluble cleaved HIV-1 envelope trimer. Science. 2013;342:1484–1490. doi: 10.1126/science.1245627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malherbe DC, Doria-Rose NA, Misher L, Beckett T, Puryear WB, Schuman JT, Kraft Z, O'Malley J, Mori M, Srivastava I, et al. Sequential immunization with a subtype B HIV-1 envelope quasispecies partially mimics the in vivo development of neutralizing antibodies. J. Virol. 2011;85:5262–5274. doi: 10.1128/JVI.02419-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mascola JR, Haynes BF. HIV-1 neutralizing antibodies: understanding nature's pathways. Immunol. Rev. 2013;254:225–244. doi: 10.1111/imr.12075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer-Hermann ME. A mathematical model for the germinal center morphology and affinity maturation. J. Theor. Biol. 2002;216:273–300. doi: 10.1006/jtbi.2002.2550. [DOI] [PubMed] [Google Scholar]
- Meyer-Hermann ME, Maini PK, Iber D. An analysis of B cell selection mechanisms in germinal centres. Math. Med. Biol. 2006;23:255–277. doi: 10.1093/imammb/dql012. [DOI] [PubMed] [Google Scholar]
- Nieuwenhuis P, Opstelten D. Functional anatomy of germinal centers. Am. J. Anatomy. 1984;170:421–435. doi: 10.1002/aja.1001700315. [DOI] [PubMed] [Google Scholar]
- Oprea M, Perelson AS. Somatic mutation leads to efficient affinity maturation when centrocyctes recycle back to centroblasts. J. Immunol. 1997;158:5155–5162. [PubMed] [Google Scholar]
- Pancera M, Zhou T, Druz A, Georgiev IS, Soto C, Gorman J, Huang J, Acharya P, Chuang GY, Ofek G, et al. Structure and immune recognition of trimeric pre-fusion HIV-1 Env. Nature. 2014;514:455–461. doi: 10.1038/nature13808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pantophlet R, Wilson IA, Burton DR. Hyperglycosylated mutants of human immunodeficiency virus (HIV) type 1 monomeric gp120 as novel antigens for HIV vaccine design. J. Virol. 2003;77:5889–5901. doi: 10.1128/JVI.77.10.5889-5901.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pissani F, Malherbe DC, Robins H, DeFilippis VR, Park B, Sellhorn G, Stamatatos L, Overbaugh J, Haigwood NL. Motif-optimized subtype A HIV envelope-based DNA vaccines rapidly elicit neutralizing antibodies when delivered sequentially. Vaccine. 2012;30:5519–5526. doi: 10.1016/j.vaccine.2012.06.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seaman MS, Janes H, Hawkins N, Grandpre LE, Devoy C, Giri A, Coffey RT, Harris L, Wood B, Daniels MG, et al. Tiered categorization of a diverse panel of HIV-1 Env pseudoviruses for assessment of neutralizing antibodies. J. Virol. 2010;84:1439–1452. doi: 10.1128/JVI.02108-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Selvarajah S, Puffer B, Pantophlet R, Law M, Doms RW, Burton DR. Comparing antigenicity and immunogenicity of engineered gp120. J. Virol. 2005;79:12148–12163. doi: 10.1128/JVI.79.19.12148-12163.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shlomchik MJ, Weisel F. Germinal centers. Immunol. Rev. 2012;247:5–10. doi: 10.1111/j.1600-065X.2012.01125.x. [DOI] [PubMed] [Google Scholar]
- Shlomchik MJ, Watts P, Weigert MG, Litwin S. Clone: a Monte-Carlo computer simulation of B cell clonal expansion, somatic mutation, and antigen-driven selection. Curr. Top. Microbiol. Immunol. 1998;229:173–197. doi: 10.1007/978-3-642-71984-4_13. [DOI] [PubMed] [Google Scholar]
- Shulman Z, Gitlin AD, Targ S, Jankovic M, Pasqual G, Nussenzweig MC, Victora GD. T follicular helper cell dynamics in germinal centers. Science. 2013;341:673–677. doi: 10.1126/science.1241680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swerdlin N, Cohen IR, Harel D. The lymph node B cell immune response: dynamic analysis in-silico. Proc. IEEE. 2008;96:1421–1443. [Google Scholar]
- Thali M, Furman C, Ho DD, Robinson J, Tilley S, Pinter A, Sodroski J. Discontinuous, conserved neutralization epitopes overlapping the CD4-binding region of human immunodeficiency virus type 1 gp120 envelope glycoprotein. J. Virol. 1992;66:5635–5641. doi: 10.1128/jvi.66.9.5635-5641.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Victora GD, Nussenzweig MC. Germinal centers. Annu. Rev. Immunol. 2012;30:429–457. doi: 10.1146/annurev-immunol-020711-075032. [DOI] [PubMed] [Google Scholar]
- Victora GD, Schwickert TA, Fooksman DR, Kamphorst AO, Meyer-Hermann ME, Dustin ML, Nussenzweig MC. Germinal center dynamics revealed by multiphoton microscopy with a photoactivatable fluorescent reporter. Cell. 2010;143:592–605. doi: 10.1016/j.cell.2010.10.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner SD, Milstein C, Neuberger MS. Codon bias targets mutation. Nature. 1995;376:732. doi: 10.1038/376732a0. [DOI] [PubMed] [Google Scholar]
- Walker LM, Huber M, Doores KJ, Falkowska E, Pejchal R, et al. Broad neutralization coverage of HIV by multiple highly potent antibodies. Nature. 2011;477:466–470. doi: 10.1038/nature10373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wedemayer GJ, Patten PA, Wang LH, Schultz PG, Stevens RC. Structural insights into the evolution of an antibody combining site. Science. 1997;276:1665–1669. doi: 10.1126/science.276.5319.1665. [DOI] [PubMed] [Google Scholar]
- Wei X, Decker JM, Wang S, Hui H, Kappes JC, Wu X, Salazar-Gonzalez JF, Salazar MG, Kilby JM, Saag MS, et al. Antibody neutralization and escape by HIV-1. Nature. 2003;422:307–312. doi: 10.1038/nature01470. [DOI] [PubMed] [Google Scholar]
- West AP, Scharf L, Scheid JF, Klein F, Bjorkman PJ, Nussenzweig MC. Structural insights on the role of antibodies in HIV-1 vaccine and therapy. Cell. 2014;156:633–648. doi: 10.1016/j.cell.2014.01.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wyatt R, Kwong PD, Desjardins E, Sweet RW, Robinson J, Hendrickson WA, Sodroski JG. The antigenic structure of the human immunodeficiency virus gp120 envelope glycoprotein. Nature. 1998;393:705–711. doi: 10.1038/31514. [DOI] [PubMed] [Google Scholar]
- Ye L, Zeng R, Bai Y, Roopenian DC, Zhu X. Efficient mucosal vaccination mediated by the neonatal Fc receptor. Nat. Biotechnol. 2011;29:158–163. doi: 10.1038/nbt.1742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang J, Shakhnovich EI. Optimality of mutation and selection in germinal centers. PLoS Comput. Biol. 2010;6:e1000800. doi: 10.1371/journal.pcbi.1000800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou T, Georgiev I, Wu X, Yang ZY, Dai K, Finzi A, Kwon YD, Scheid JF, Shi W, Xu L, et al. Structural basis for broad and potent neutralization of HIV-1 by antibody VRC01. Science. 2010;329:811–817. doi: 10.1126/science.1192819. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.