Abstract
We consider a setting in which we have a treatment and a potentially large number of covariates for a set of observations, and wish to model their relationship with an outcome of interest. We propose a simple method for modeling interactions between the treatment and covariates. The idea is to modify the covariate in a simple way, and then fit a standard model using the modified covariates and no main effects. We show that coupled with an efficiency augmentation procedure, this method produces clinically meaningful estimators in a variety of settings. It can be useful for practicing personalized medicine: determining from a large set of biomarkers the subset of patients that can potentially benefit from a treatment. We apply the method to both simulated datasets and real trial data. The modified covariates idea can be used for other purposes, for example, large scale hypothesis testing for determining which of a set of covariates interact with a treatment variable.
1 Introduction
To develop strategies for personalized medicine, it is important to identify the treatment and covariate interactions in the setting of randomized clinical trials [Royston and Sauerbrei, 2008]. To confirm and quantify the treatment effect is often the primary objective of a randomized clinical trial. Although important, the final result (positive or negative) of a randomized trial is a conclusion with respect to the average treatment effect on the entire study population. For example, a treatment may not be different from the placebo in the overall study population, but it may still be better for a subset of patients. Identifying the treatment and covariate interactions may provide valuable information for determining this subgroup of patients.
In practice, there are two commonly used approaches to characterize the potential treatment and covariate interactions. First, a panel of simple patient subgroup analyses, where the treatment and control arms are compared in different subgroups defined a priori, such as male, female, diabetic and non-diabetic patients, may be performed following the main comparison. Such an exploratory approach is mainly focusing on simple interactions between treatment and a dichotomized covariate. However it often suffers from false positive findings due to multiple testings and can not find complicated treatment-covariates interaction.
In a more rigorous analytic approach, the treatment-covariates interactions can be examined in a multivariate regression analysis where the product of the binary treatment indicator and a set of baseline covariates are included in the regression model. Recent breakthroughs in biotechnology make a vast amount of data available for exploring potential interaction effects with the treatment and assisting in the optimal treatment selection for individual patients. However, it is very difficult to detect the interactions between treatment and high dimensional covariates via the direct multivariate regression. Appropriate variable selection methods such as Lasso are needed to reduce the number of covariates interacting with the treatment. The presence of the main effect, which often have a bigger effect on the outcome than interactions, further compounds the difficulty in dimension reduction since a subset of variables need to be selected for modeling the main effect as well.
Recently, Bonetti and Gelber [2004] formalized the subpopulation treatment effect pattern plot (STEPP) for characterizing interactions between the treatment and continuous covariates. Sauerbrei et al. [2007] proposed an efficient algorithm for multivariate model-building with flexible fractional polynomials interactions (MFPI) and compared the empirical performance of MFPI with STEPP. Su et al. [2008] modified the CART to explore the covariates and treatment interactions in survival analysis. Tian and Tibshirani [2011] proposed a simple way to construct an index score, the sum of selected dichotomized covariates, to stratify the patient population according to the treatment effect. In a more recent work, Zhao et al. [2012] proposed a novel approach to directly estimate the optimal treatment selection rule via maximizing the expected utility. There are also rich Bayesian literatures for flexible modeling nonlinear, nonadditive or interaction covariate effects [Chipman et al., 1998, Gustafson, 2000, Chen et al., 2012]. However, most of these existing methods except for the one by Zhao et al. [2012], are not designed for analyzing high-dimensional covariates.
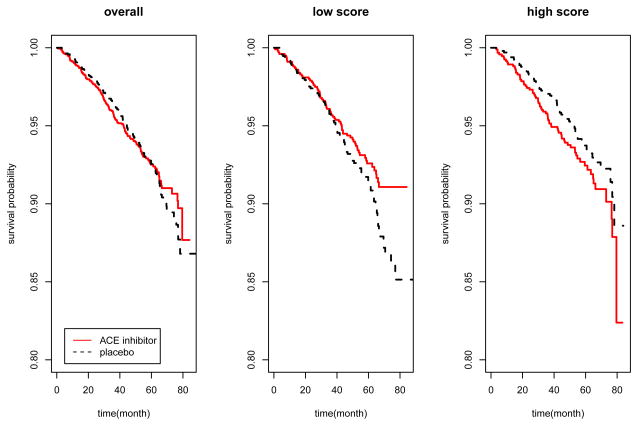
In this paper, we propose a simple approach to estimate the covariates and treatment interactions without the need for modeling the main effects in analyzing data from a randomized clinical trial. The idea is simple, and in a sense, obvious. We simply code the treatment variable as ±1 and then include the products of this variable with each covariate in an appropriate regression model. Figure 1 gives a preview of the results of our method. The data consist of baseline covariates including various biomarker measurements and medical history for patients with stable coronary artery disease and normal or slightly reduced left ventricular function, who were randomized to either the angiotensin converting enzyme(ACE) inhibitor or placebo arm. Our proposed method constructs a numerical score using baseline information on a training set to reveal covariates-treatment interactions. The panels show the estimated survival curves for patients in a separate validation set, overall and stratified by the score. Although there is no significant survival difference between two arms in the overall comparison (p = 0.67), we see that patients with low scores have better survival with the ACE inhibitor treatment than with the placebo (hazard ratio=0.74, p = 0.06). This type of information after appropriate validation could be very useful in clinical practice.
Figure 1.
Example of the modified covariate approach, applied to patients with stable coronary artery disease and normal or slightly reduced left ventricular function, who were randomly given ACE inhibitor or placebo in a randomized trial. Our procedure constructed a score based on baseline covariates to detect covariates-treatment interactions. The numerical score was constructed on a training set, and then categorized into low and high. The panels show the survival curves in a separate validation set, overall and stratified by the score.
In section 2, we describe the methods for the continuous, binary as well as survival type of outcomes. In section 3, the finite sample performance of the proposed method has been investigated via extensive numerical studies. In section 4, we apply the proposed method to two real data examples. Finally, limitation and potential extensions of the method are discussed in section 5.
2 Method
In the following, we let T = ±1 be the binary treatment indicator and Y(1) and Y(−1) be the potential outcome if the patient received treatment T = 1 and −1, respectively. We only observe Y = Y(T), T and Z, a q–dimensional baseline covariate vector. Here we assume that the treatment is randomly assigned to a patient, i.e., T and Z are independent. The observed data consist of N independent and identically distributed copies of (Y, T, Z), {(Yi, Ti, Zi), i = 1, ···, N}. Furthermore, we let W(·) : Rq → Rp be a p dimensional functions of baseline covariates Z and always include an intercept. In practice, W(·) may include spline basis functions and interactions selected by the users. We denote W(Zi) by Wi in the rest of the paper. Here the dimension of Wi could be large relative to the sample size N. For simplicity, we assume that P(T = 1) = P(T = −1) = 1/2.
2.1 Continuous Response Model
When Y is a continuous response, a simple multivariate linear regression model for characterizing the interactions between the treatment and covariates is
| (1) |
where ε is the mean zero random error. In this simple model, the interaction term models the heterogeneous treatment effect across the population and the linear combination of can be used for identifying the subgroup of patients who may or may not benefit from the treatment. Note that since the vector W(Z) contains an intercept, the main effect for treatment is always included in the model. Specifically, under model (1), we have
i.e., measures the causal treatment effect for patients with the baseline covariate z. With observed data, γ0 can be estimated via the ordinary least squares (OLS) method.
On the other hand, noting the relationship that
one may estimate γ0 by directly minimizing
| (2) |
We call this the modified outcome method, where 2YT can be viewed as the modified outcome, which has been first proposed in the Ph.D thesis of James Sinovitch, Harvard University.
Under the simple linear model (1), estimators from both methods are consistent for γ0, and the full least squares approach in general is more efficient. In practice, the simple multivariate linear regression model is often just a working model approximating the complicated underlying probabilistic relationship among the treatment, baseline covariates and outcome variables. It comes as a surprise that even when model (1) is mis-specified, the multivariate linear regression and modified outcome estimators still converge to the same non-random limit γ* determined by the joint distribution of (Y(1), Y(−1), Z). Furthermore, the score W(z)′γ* is a sensible estimator for the interaction effect in the sense that it seeks the “best” function of z in a functional space
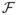 to approximate Δ(z) by minimizing
to approximate Δ(z) by minimizing
where the expectation is with respect to Z.
2.2 The Modified Covariate Method
The modified outcomes estimator defined above is useful for the Gaussian case, but does not generalize easily to more complicated models. Hence we propose a new estimator which is equivalent to the modified outcomes approach in the Gaussian case and extends easily to other models. This is the main proposal of this paper.
We consider the simple working model
| (3) |
where ε is the random error. Based on model (3), we propose the modified covariate estimator γ̂ as the minimizer of
| (4) |
That is, we simply multiply each component of Wi by one-half the treatment assignment indicator (= ±1) and perform a regular linear regression. Now since
the modified outcome and modified covariate estimates are identical and share the same causal interpretations. Operationally, we can perform a simple linear regression with the modified covariates without intercept. We summarize the general proposal below.
|
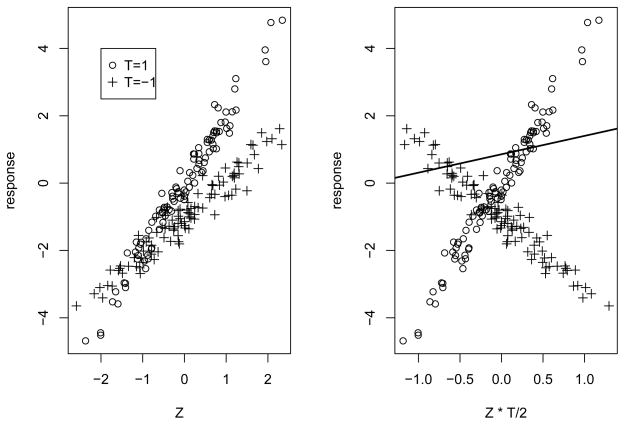
Figure 2 illustrates how the modified covariate method works for a single covariate Z. The raw data are shown on the left and the data with modified covariate are shown on the right. The regression line in the right panel estimates the personalized treatment Δ(z).
Figure 2.
Example of the modified covariate approach. The raw data is generated from the regression model Y = 2ZI(T = 1) + (Z − 1)I(T = −1) + N(0, 1/9) consisting of a single covariate Z and a treatment T = 1 or −1 and shown on the left. On the right panel, we have plotted the response against the modified Z · T/2. The regression line computed in the right panel estimates the personalized treatment effect for each given value of covariate Z = z, Δ(z) = z + 1.
The advantage of this new approach is twofold: it avoids having to directly model the main effects and it has a causal interpretation for the resulting estimator regardless of the adequacy of the assumed working model (3). Furthermore, unlike the modified outcome method, it is straightforward to generalize the new approach to other types of outcome.
2.3 Binary Responses
When Y is a binary response, in the same spirit as the continuous outcome case, we propose to fit a logistic regression model with modified covariates W* = W(Z) · T/2 :
| (7) |
If model (7) is correctly specified, then
and thus has an appropriate causal interpretation. However, even when model (7) is not correctly specified, we still can estimate γ0 by treating (7) as a working model. In general, the maximum likelihood estimator (MLE) of the working model converges to a deterministic limit γ* and W(z)′γ*/2 can be viewed as the solution to the following optimization problem
where the expectation is with respect to (Y, T, Z). Therefore, if W(z) forms a “rich” set of basis functions, W(z)′γ*/2 is an approximation to the minimizer of E{Yf(Z)T − log(1 + ef(Z)T)}. In the Appendix, we show that the latter can be represented as
under very general assumptions. Therefore,
may serve as an estimate for the covariate-specific treatment effect and used to stratify the patient population, regardless of the validity of the working model assumptions.
As described above, the MLE from the working model (7) can always be used to construct a surrogate to the personalized treatment effect measured by the “risk difference”
On the other hand, different measures for individualized treatment effects may also be of interest. In supplementary materials we have provided an alternative approach to approximate the personalized treatment effect using the “relative risk” rather than “risk difference”.
2.4 Survival Responses
When the outcome variable is survival time, we often do not observe the exact outcome for every subject in a clinical study due to incomplete follow-up. In this case, we assume that the outcome Y is a pair of random variables (X, δ) = {X˜ ∧ C, I(X˜ < C)}, where X˜ is the survival time of primary interest, C is the censoring time and δ is the censoring indicator.
Firstly, we propose to fit a Cox regression model with modified covariates
| (8) |
where λ(t|·) is the hazard function for survival time X˜ and λ0(·) is a baseline hazard function free of Z and T. When model (8) is correctly specified,
and can be used to stratify the patient population according to Δ(z), where is a monotone increasing function. Under the proportional hazards assumption, the maximum partial likelihood estimator γ̂ is a consistent estimator for γ0 and semiparametric efficient. Moreover, even when model (8) is mis-specified, we still can “estimate” γ0 by maximizing the partial likelihood function. In general, the resulting estimator, γ̂, converges to a deterministic limit γ*, which is the root of a limiting score equation [Lin and Wei, 1989]. More generally, W(z)′γ*/2 can be viewed as the solution of the optimization problem
where N(t) = I(X˜ ≤ t)δ, τ is a fixed time point such that P(X ≥ τ) > 0, and the expectations are with respect to (Y, T, Z). Therefore, W(z)′γ*/2 can be viewed as an approximation to
In Appendix, we show that if the censoring time does not depend on (Z, T), then the minimizer f* satisfies
for a monotone increasing function Λ*(u). Thus, when censoring rates are balanced between the two arms, e.g., the hazard rate is low and most of the censoring is due to administrative reasons,
can be used to characterize the covariate-specific treatment effect and stratify the patient population even when the working model (8) is mis-specified.
2.5 Regularization for the High Dimensional Data
When the dimension of W*, p, is high, we can easily apply appropriate variable selection procedures based on the corresponding working model. For example, L1 penalized (Lasso) estimators proposed by Tibshirani [1996] can be directly applied to the modified data (6). In general, one may estimate γ by minimizing
| (9) |
where and
The resulting Lasso regularized estimator may share the appealing finite sample oracle properties [Van De Geer, 2008, Zhang and Huang, 2008, Van De Geer and Buhlmann, 2009, Negahban et al., 2012]. For example, for continuous outcomes, if we select the penalty parameter λn = O({log(p)/N}1/2) and the covariates W(Zi)Ti/2, i = 1, ···, N satisfy the restricted eigenvalue condition, then
where , γ̂λN is the corresponding Lasso regularized estimator, #γ* is the number of non-zero components in the vector γ*, and ci, i = 1, 2, 3 are positive constants depending on the joint distribution of (Y, W(Z), T) [Negahban et al., 2012]. Therefore, although the dimension p may be big, γ* can always be approximated by the Lasso estimator with an approximation error proportional to only the number of its non-zero components, which is small if γ* is sparse. Following the Corollary 3 of Negahban et al. [2012], similar results hold when γ* is not exactly sparse but can be approximated by a sparse vector. One consequence is that if W(·) is adequately rich such that |W(z)′γ* − f*(z)| is small and γ* is either exact or approximately sparse, then is a good approximation of f*(z) with a high probability, where f*(z) is a monotone transformation of the individualized treatment effect Δ(z). This property holds for any pair of finite N and p with a sufficiently small ratio log(p)/N and does not depend on the correct specification of the working model. A similar result for the expected utility in the patient population with the estimated optimal treatment assignment rule has been established in Qian and Murphy [2011]. This result can be extended to the binary case, with appropriate regularity condition on the covariates W(Zi)Ti/2 to ensure that the negative log-likelihood function satisfies a form of restricted strong convexity [Negahban et al., 2012]. For the survival case, parallel results have been established for Lasso-regularized maximum partial likelihood estimator under the assumption that the multiplicative Cox model is correctly specified [Kong and Nan, 2013, Huang et al., 2013]. The finite sample properties of the Lasso estimator for mis-specified Cox model are still unknown and warrants further study.
Note that the Lasso regularization method may not be able to consistently recover all the nonzero components of γ* [Zhao and Yu, 2006, Zou, 2006]. However, since our focus is on approximating the personalized treatment effect under a potentially misspecified working model, where the regression coefficients γ* may not have a clinically meaningful interpretation, this limitation is not necessarily a severe drawback of the proposed method.
Regularization methods other than Lasso especially those with nonconvex penalties such as SCAD and MCP may also be used [Fan and Li, 2001, Zhang, 2010]. The composite gradient descend algorithm and the adaption thereof developed recently can be used to compute the corresponding regularized optimizer efficiently [Loh and Wainwright, 2012]. In addition, in contrast to Lasso, some nonconvex regularization methods may provide consistent estimates for the support of γ* under suitable regularity conditions if the working model is correctly specified. [Zou, 2006, Huang and Xie, 2007, Huang et al., 2008, Zhang and Zhang, 2012].
2.6 Efficiency Augmentation
When the models (5, 7 and 8) with modified covariates are correctly specified, the MLE estimator for γ* is the most efficient estimator asymptotically. However, when models are treated as working models subject to mis-specification, a more efficient estimator can be obtained for estimating the same γ*. To this end, note that in general γ̂ is defined as the minimizer of an objective function motivated from a working model:
| (10) |
Since for any function a(z) : Rq → Rp, E{Tia(Zi)} = 0 due to the randomization, the minimizer of the augmented objective function
converges to the same limit as γ̂. Furthermore, by selecting an optimal augmentation term a(·), the minimizer of the augmented objective function may have smaller variance than that of the original estimator. In supplementary materials, we show that
are optimal choices for continuous and binary responses, respectively. Therefore, we propose the following two-step procedures for estimating γ* :
-
Estimate the optimal a0(z) :
- For continuous responses, fit the linear regression model E(Y|Z) = ξ′B(Z) for the appropriate function B(Z). Let
- For binary response, fit the logistic regression model logit{P(Y = 1|Z)} = ξ′B(Z) for the appropriate function B(Z). Let
Here as W(z), B(z) is a transformation of z selected by users.
-
Estimate γ*
- For continuous responses, we minimize (appropriately regularized)
- For binary responses, we minimize (appropriately regularized)
For survival outcome, the log-partial likelihood function is not a simple sum of i.i.d terms. However, in supplementary materials, we show that the optimal choice of a(z) is
where G1(u; z) = E{M(u)|Z = z, T = 1}, G2(u; z) = E{M(u)|Z = z, T = −1},
Unfortunately, a0(z) depends on the unknown parameter γ*. On the other hand, for the high-dimensional case, the interaction effect is usually small and it is not unreasonable to assume that γ* ≈ 0. Furthermore, if the censoring patterns are similar in both arms, we have G1(u, z) ≈ G2(u, z). Using these two approximations, we can simplify the optimal augmentation term as
where
Therefore, we propose to employ the following approach to implement the efficiency augmentation procedure:
-
Calculateand fit the linear regression model E(M̂(τ)|Z) = ξ′B(Z). Let
- Estimate γ* by minimizing (appropriately regularized)
Remark 1
When the response is continuous, the augmented estimator minimizes
This equivalence implies that this efficiency augmentation procedures is asymptotically equivalent to that based on a simple multivariate regression with main effect “ξ̂′B(Z)” and interaction “γ′W(Z) · T”. This is not a surprise: the specification of the main effect in the linear regression does not affect the asymptotical consistency of estimating the interactions. On the other hand, a good choice of the main effect model can help estimate the interaction, i.e., personalized treatment effect, more accurately. Another consequence is that one may directly use the same standard algorithm to compute the augmented estimator when the Lasso penalty is used. For binary or survival responses, the augmented estimator under the Lasso regularization also can be computed with an efficient algorithm, which is given in the supplementary materials.
Remark 2
For nonlinear models such as logistic and Cox regressions, the augmentation method is NOT equivalent to the full regression approach including both the main effect and interaction terms. In those cases, different specifications of the main effects in the full regression model result in asymptotically different estimates for the interaction terms, which, unlike the proposed modified covariate estimators, in general can not be interpreted as good surrogates for the personalized treatment effects.
Remarks 3
The similar technique can also be used for improving other estimators such as that proposed by Zhao et al. [2012], where the surrogate objective function for the weighted mis-classification error can be written in the form of (2.6) as well. The optimal function a0(z) needs to be derived case by case.
3 Numerical Studies
In this section, we performed extensive numerical studies to investigate the finite sample performance of the proposed method in various settings: the treatment may or may not have the marginal main effect; the personalized treatment effect may depend on complicated functions of covariates such as interactions among covariates; the regression model for detecting the interactions may or may not be correctly specified. Due to the limitation of the space, we only presented simulation results from the selected representative cases.
3.1 Continuous Responses
For continuous responses, we generated N independent Gaussian samples from the regression model
| (11) |
where the covariates (Z1, ···, Zp) follow a mean zero multivariate normal distribution with a compound symmetric variance-covariance matrix, (1 − ρ)Ip + ρ1′1, and ε ~ N(0, 1). We let (γ0, γ1, γ2, γ3, γ4, γ5, ···, γp) = (0.4, 0.8, −0.8, 0.8, −0.8, 0, ···, 0), αij = 0.8I(i = 1, j = 2), , N = 100, and p = 50 and 1000 representing low and high dimensional cases, respectively. The treatment T was generated as ±1 with equal probability at random. We consider four sets of simulations:
, j = 3, 4, ···, 10 and ρ = 0;
, j = 3, 4, ···, 10 and ρ = 1/3;
, j = 3, 4, ···, 10 and ρ = 0;
, j = 3, 4, ···, 10 and ρ = 1/3.
Settings 1 and 2 represented cases with relatively small main effects, where the variations in responses contributable to the main effect, interaction and random error were about 37.5%, 37.5% and 25%, respectively, when the covariates were correlated. Settings 3 and 4 represented cases with relatively big main effects, where the variations in responses contributable to the main effect, interaction and random error were about 75%, 15% and 10%, respectively, when the covariates were correlated. For each of the simulated data set, we implemented three methods:
full regression: Fit a multivariate linear regression with complete main effects and covariate/treatment interaction terms, i.e., the dimension of the covariate matrix was 2(p + 1). The Lasso was used to select the variables.
new: Fit a multivariate linear regression with the modified covariate W* = (1, Z)′ · T/2. The dimension of the covariate matrix was p + 1. Again, the Lasso was used.
new/augmented: The proposed method with efficiency augmentation, where E(Y|Z) was estimated with Lasso-regularized ordinary least squared method and B(z) = z.
The selection of W(z) = B(z) = z mimicked the realistic situation where the knowledge of the true functional forms for interaction and main effects were often lacking. For all three methods, we selected the Lasso penalty parameter via 10-fold cross-validation. The outputs of all three methods are estimated scores, which are linear combinations of W(z) approximating the personalized treatment effect Δ(z) or a transformation thereof. Specifically, the score is γ̂′W(z), where γ̂ is simply the estimated coefficients for the covariate-treatment interaction terms in the full regression approach and the estimated coefficients for modified covariates in our proposal. The estimated scores can be used to rank patients according to their personalized treatment effects and select a subgroup of patients who may benefit from the treatment. Therefore, to evaluate the performance of the resulting score, we estimated the Spearman’s rank correlation coefficient between the estimated score and the “true” treatment effect
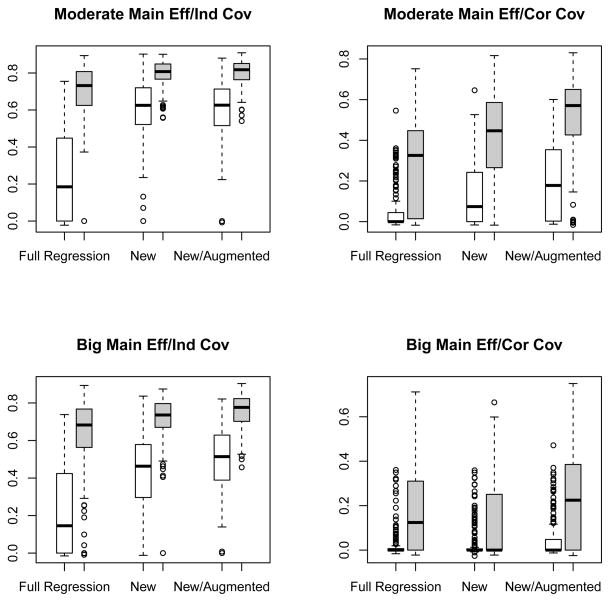
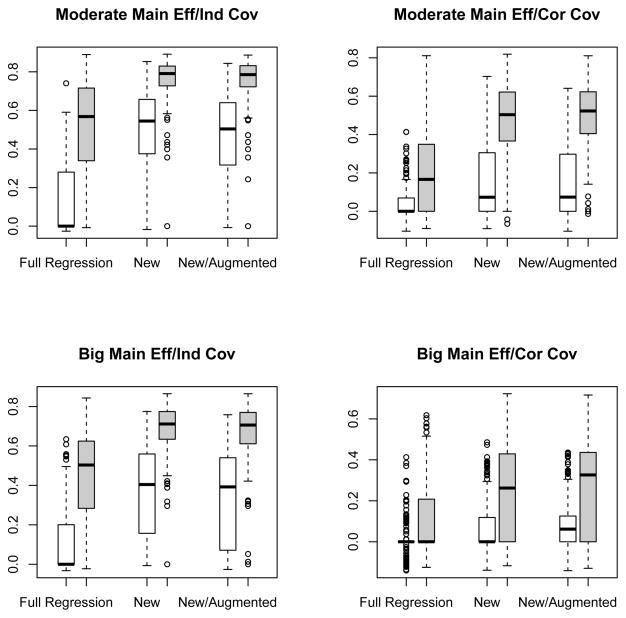
in an independently generated set with a sample size of 10000. Based on 500 sets of simulations, we plotted the boxplots of the rank correlation coefficients between the estimated scores γ̂′W(Z) and Δ(Z) under simulation settings (1), (2), (3) and (4) in the top left, top right, bottom left and bottom right panels of Figure 3, respectively. For all settings, the performance of the modified covariates method was better than that of the full regression approach with further boosting from the efficiency augmentation. The superiority of the new method was fairly obvious especially when p = 1000. For example, in the setting 3, where all the covariates were independent and the main effect was relatively big, the median correlation coefficients were 0.15, 0.46 and 0.51 for the full regression, new and new/augmented methods, respectively. Furthermore, the results on identifying covariates interacting with the treatment are reported at Tables 1 and 2 for p = 50 and 1000, respectively. The new method was also superior in terms of selecting the right covariates. For example, in the setting 3 with p = 1000, while the new method with augmentation on average selected 25.2 covariates with 2.9 true positives, i.e. covariates from Zi, 1 ≤ i ≤ 4, the full regression method only selected 4.9 covariates with 0.9 true positive.
Figure 3.
Boxplots for the correlation coefficients between the estimated score and true treatment effect with three different methods applied to continuous outcomes. The empty and filled boxes represent high and low dimensional (p = 1000 and p = 50) cases, respectively. Left upper panel: moderate main effect and independent covariates; right upper panel: moderate main effect and correlated covariates; left lower panel: big main effect and independent covariates; right lower panel: big main effect and correlated covariates.
Table 1.
Simulation Results for Moderate Dimensional Covariates (p = 50): Full Reg. is the multivariate regression analysis with both main effect and covariate/treatment interaction; New is the regression analysis with the modified covariate; New/Aug. is the efficiency augmented regression analysis with modified covariates.
| Response | Cor+ | Main Eff. | Average Number of Nonzero Coefficients
|
||||||
|---|---|---|---|---|---|---|---|---|---|
| True | Correct
|
Incorrect
|
|||||||
| Full Reg. | New | New/Aug. | Full Reg. | New | New/Aug. | ||||
| Continuous | 0 | Moderate | 4 | 3.4 | 4.0 | 4.0 | 8.2 | 11.3 | 10.8 |
| 0.5 | Moderate | 4 | 1.8 | 2.4 | 3.1 | 5.1 | 6.6 | 9.2 | |
| 0 | Big | 4 | 3.1 | 3.7 | 3.9 | 8.4 | 9.8 | 10.0 | |
| 0.5 | Big | 4 | 1.1 | 0.8 | 1.4 | 3.6 | 2.9 | 4.6 | |
|
| |||||||||
| Binary | 0 | Moderate | 4 | 2.0 | 3.6 | 3.6 | 2.9 | 7.6 | 8.5 |
| 0.5 | Moderate | 4 | 1.0 | 2.4 | 2.7 | 1.9 | 6.4 | 7.2 | |
| 0 | Big | 4 | 1.7 | 3.1 | 3.3 | 2.6 | 6.7 | 7.5 | |
| 0.5 | Big | 4 | 0.7 | 1.5 | 1.6 | 1.5 | 4.1 | 3.6 | |
|
| |||||||||
| Survival | 0.5 | Moderate | 4 | 1.1 | 2.7 | 2.8 | 1.4 | 5.3 | 5.3 |
| 0 | Moderate | 4 | 2.3 | 3.8 | 3.8 | 2.6 | 7.0 | 7.1 | |
| 0 | Big | 4 | 2.0 | 3.5 | 3.5 | 2.2 | 5.6 | 5.4 | |
| 0.5 | Big | 4 | 0.7 | 1.4 | 1.6 | 1.1 | 3.1 | 3.2 | |
The common correlation coefficient between covariates Zi and Zj, 1 ≤ i < j ≤ p.
Table 2.
Simulation Results for High Dimensional Covariates (p = 1000): Full Reg. is the multivariate regression analysis with both main effect and covariate/treatment interaction; New is the regression analysis with the modified covariate; New/Aug. is the efficiency augmented regression analysis with modified covariates.
| Response | Cor+ | Main Eff. | True | Average Number of Nonzero Coefficients
|
|||||
|---|---|---|---|---|---|---|---|---|---|
| Correct
|
Incorrect
|
||||||||
| Full Reg | New | New/Aug | Full Reg | New | New/Aug | ||||
| Continuous | 0 | Moderate | 4 | 1.0 | 3.4 | 3.4 | 3.3 | 23.2 | 24.9 |
| 0.5 | Moderate | 4 | 0.4 | 1.1 | 1.5 | 5.0 | 11.0 | 16.3 | |
| 0 | Big | 4 | 0.9 | 2.5 | 2.9 | 4.0 | 16.0 | 22.3 | |
| 0.5 | Big | 4 | 0.2 | 0.2 | 0.4 | 6.5 | 3.6 | 10.8 | |
|
| |||||||||
| Binary | 0 | Moderate | 4 | 0.4 | 1.9 | 2.0 | 1.9 | 12.8 | 14.3 |
| 0.5 | Moderate | 4 | 0.1 | 0.7 | 0.8 | 1.6 | 8.1 | 7.2 | |
| 0 | Big | 4 | 0.3 | 1.4 | 1.5 | 1.7 | 11.6 | 11.7 | |
| 0.5 | Big | 4 | 0.1 | 0.4 | 0.5 | 1.3 | 7.4 | 6.9 | |
|
| |||||||||
| Survival | 0 | Moderate | 4 | 0.5 | 2.5 | 2.4 | 1.8 | 9.2 | 8.8 |
| 0.5 | Moderate | 4 | 0.2 | 0.9 | 0.9 | 1.4 | 5.1 | 5.1 | |
| 0 | Big | 4 | 0.5 | 2.0 | 1.8 | 1.8 | 7.5 | 6.8 | |
| 0.5 | Big | 4 | 0.1 | 0.4 | 0.4 | 1.5 | 4.3 | 4.4 | |
The common correlation coefficient between covariates Zi and Zj, 1 ≤ i < j ≤ p.
3.2 Binary Responses
For binary responses, we used the same simulation design as that for the continuous response. Specifically, we generated N independent binary samples from the regression model
| (12) |
where all the model parameters were the same as those in the case of continuous responses. Noting that the logistic regression model was mis-specified under the chosen simulation design. We also considered the same four settings with different combinations of βj and ρ. For each of the simulated data set, we implemented three methods as those for the continuous outcome: full regression, new and new/augmented. The logistic regression working model is used for all three approaches. In the efficiency augmentation, E(Y|Z) was estimated with the Lasso-penalized logistic regression.
To evaluate the performance of the resulting score measuring the individualized treatment effect, we estimated the Spearman’s rank correlation coefficient between the estimated score and the “true” treatment effect
Although the scores measuring the interaction from the first and second/third methods were different even when the sample size goes to infinity, the rank correlation coefficients put them on the same footing in comparing performances.
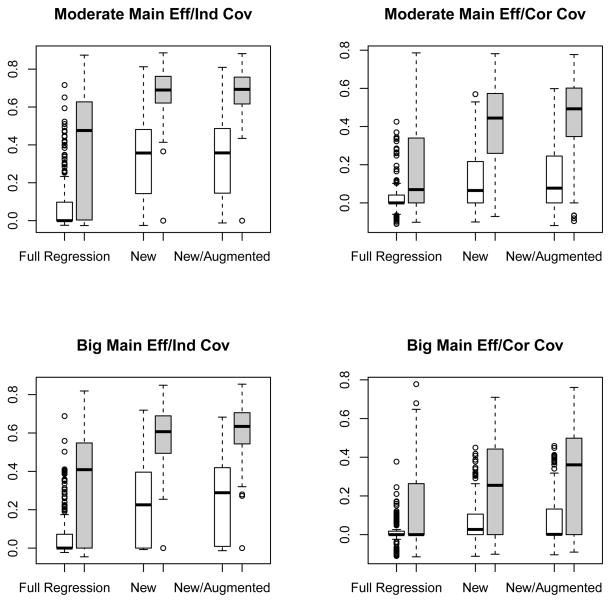
In the top left, top right, bottom left and bottom right panels of Figure 4, we plotted the boxplots of the correlation coefficients between the estimated scores γ̂′W(Z) and Δ(Z) under simulation settings (1), (2), (3) and (4), respectively. The patterns were similar to those for the continuous response and confirmed our findings that the “efficiency-augmented method” performed the best or close to the best in all four settings. For example, in the setting 3, the median correlation coefficients were 0, 0.23 and 0.29 for the full regression, new and new/augmented methods, respectively, when p = 1000. In addition, while the proposed method with augmentation on average selected 13.2 covariates with 1.5 true positives, the full regression method only selected 2.0 covariates with 0.3 true positive in the same setting. Here the true positive covariates of interest are again Zi, 1 ≤ i ≤ 4. The detailed results on covairates identification were given at Tables 1 and 2.
Figure 4.
Boxplots for the correlation coefficients between the estimated score and true treatment effect with three different methods applied to binary outcomes. The empty and filled boxes represent high and low dimensional (p = 1000 and p = 50) cases, respectively. Left upper panel: moderate main effect and independent covariates; right upper panel: moderate main effect and correlated covariates; left lower panel: big main effect and independent covariates; right lower panel: big main effect and correlated covariates.
3.3 Survival Responses
For survival responses, we used the same simulation design as that for the continuous and binary responses. Specifically, we generated N independent survival times from the regression model
| (13) |
where all the model parameters were the same as those in the previous subsections. The censoring time was generated from the uniform distribution U(0, ξ0), where ξ0 was selected to induce a censoring rate of 25%. For each simulated data set, we implemented the following three methods as above: full regression, new and new/augmented. The Cox regression working model is used for all three methods. In the efficiency augmentation, E{M(τ)|Z} is estimated with the Lasso-regularized linear regression.
To evaluate the performance of the resulting score measuring the individualized treatment effect, we estimated the Spearman’s rank correlation coefficient between the estimated score and the “true” treatment effect based on survival probability at t0 = 20
In the top left, top right, bottom left and bottom right panels of Figure 5, we plotted the boxplots of the correlation coefficients between the estimated scores γ̂′W(Z) and Δ(Z) under simulation settings, (1), (2), (3) and (4), respectively. The patterns were similar to those for the continuous and binary responses. For example, when p = 1000, the median correlation coefficients were 0.00, 0.40 and 0.39 in the setting 3 for the full regression, new and new/augmented methods, respectively.
Figure 5.
Boxplots for the correlation coefficients between the estimated score and true treatment effect with three different methods applied to survival outcomes. The empty and filled boxes represent high and low dimensional (p = 1000 and p = 50) cases, respectively. Left upper panel: moderate main effect and independent covariates; right upper panel: moderate main effect and correlated covariates; left lower panel: big main effect and independent covariates; right lower panel: big main effect and correlated covariates.
Lastly, we also repeated the aforementioned numerical studies for continuous, binary and survival outcomes with the Lasso replaced by adaptive Lasso, whose empirical performance is often similar to that of nonconvex regularization such as SCAD and MCP. The simulation results (not shown here) are very similar to those presented above, demonstrating that the modified covariate approach can be coupled with regularization methods other than Lasso for the purpose of dimension reduction in practice.
4 Examples
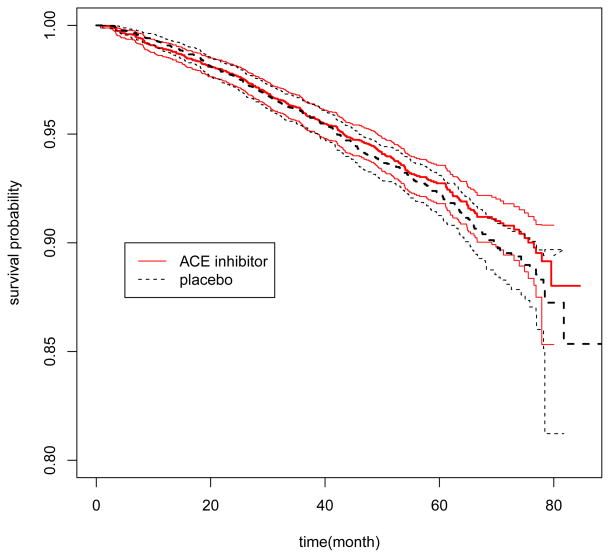
In this section, we applied the proposed method to analyze two real data examples. In the first example, we considered a recent clinical trial “Preventive of Events with Angiotensin Converting Enzyme Inhibition” (PEACE) to study if the ACE inhibitors are effective for lowering cardiovascular risk for patients with stable coronary artery disease and normal or slightly reduced left ventricular function [Braunwald et al., 2004]. In this study, 8290 patients were randomly assigned to treatment and control arms with 633 deaths occurred by the end of the study. The estimated hazard ratio is 0.95 with an insignificant p-value of 0.13. However, in a secondary analysis, Solomon et al. [2006] reported that ACE inhibitors might significantly reduce the mortality for patients whose kidney function was abnormal at the baseline. Although this result needs to be interpreted cautiously, it suggests the possibility of existence of a subgroup of patients who may benefit from the treatment. For this example, we considered the survival time as the primary endpoint and the objective was to use seven baseline covariates: age, gender, left ventricular ejection fraction (LVEF), renal function measured by EGFR, hypertension, diabetic status and history of myocardial infarction to build a scoring system capturing the individualized treatment effect. Those covariates were selected for their known association with the cardiovascular risk. The continuous covariates, age, LVEF and EGFR are log-transformed. In addition to the seven covariates, we also included all the two-way interactions among them in the model. In summary, Z was a 7 dimensional vector and W(Z) was a 7 + 7 × 6/2 = 28 dimensional vector. We included all patients with complete information on these seven covariates. The final data set consisted of 3947 patients in the treatment arm and 3918 patients in the placebo arm. The outcome of interest was the survival time and there were 292 and 315 deaths in the treatment and placebo arms, respectively. The estimated survival curves by arms were plotted in Figure 6. The goal of the analysis was to construct a score using baseline covariates to identify subgroups of patients who may or may not be benefited from the ACE inhibition treatment. To this end, we selected the first 2000 patients in the treatment arm and placebo arm to form the training set and reserved the rest 3865 patients as an independent validation set. In selecting the training and validation sets, we used the original order of the observations in the data set without additional sorting to ensure the objectivity.
Figure 6.
Survival functions of the ACE inhibitor and placebo arms (7865 patients): solid line, the ACE inhibitor arm; dashed line, the placebo arm; thin line, the point-wise 95% confidence limits.
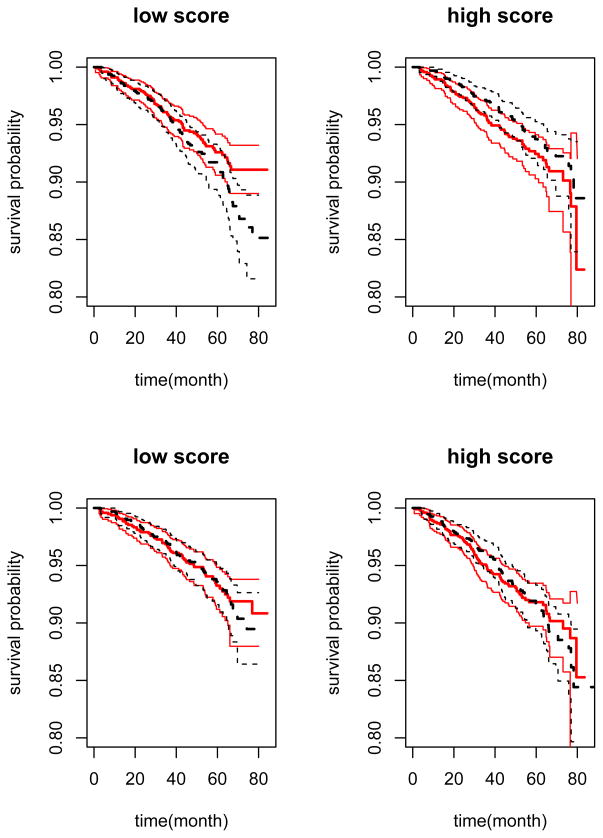
First we maximized the partial likelihood function with modified covariates to construct a score aiming for capturing the individualized treatment effect. The resulting score was a linear combination of selected covariates and their two-way interactions. Here, a low score favored ACE inhibition treatment. We then applied the score to classify the patients in the validation set into the high and low score groups depending on whether the patient’s score was greater than the median level. In the high score group, the survival time in the ACE inhibition arm was slightly shorter than that in the placebo arm with an estimated hazard ratio of 1.27 for ACE inhibitor versus placebo (p = 0.163). In the low score group, the survival time in the ACE inhibition arm was longer than that in the placebo arm with an estimated hazard ratio of 0.74 (p = 0.061). The estimated survival functions of both treatment arms were plotted in the upper panels of Figure 7. The interaction between the constructed score and treatment was statistically significant in the multivariate Cox regression based on the validation set (p = 0.022).
Figure 7.
Survival functions of the ACE inhibitor and placebo arms stratified by the estimated score in the validation set: solid line, the ACE inhibitor arm; dashed line, the placebo arm; thin line, the point-wise 95% confidence limits. Upper panels: the score is based on the “new” method; lower panel: the score is based on the “full regression” method.
Furthermore, we implemented the efficiency augmentation method and obtained a new score. Again, we classified the patients in the validation set into the high and low score groups based on the constructed gene score. The results were very similar and the interaction between the constructed score and treatment was also statistically significant (p = 0.025).
For comparison purposes, we also fitted a multivariate Cox regression model with treatment, W(Z), and their interactions as the covariates. In this model, we had 57 different covariates. The resulting score failed to stratify the population according to the treatment effect in the validation set. The results were shown in the lower panel of Figure 7. The interaction between the constructed score and treatment was not statistically significant (p = 0.980).
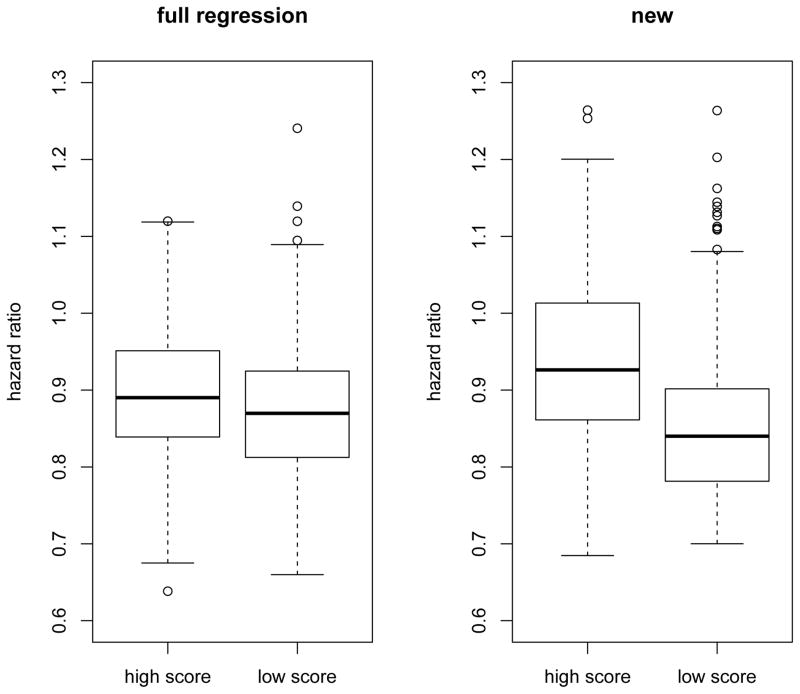
To further objectively examine the performance of the proposal in this data set, we randomly split the data into a training set of 2000 patients and a validation set of 5865 patients. We then estimated the score measuring individualized treatment effect in the training set with the modified covariates and full regression approaches. The Lasso method coupled with BIC criterion was used in the full regression approach due to the large number of covariates relative to the number of deaths in the training set. Patients in the validation set were then stratified into the high and low score groups. We calculated the hazard ratios of the ACE inhibition arm versus the placebo arm in high and low score groups, respectively. In Figure 8, we plotted the boxplots of the hazard ratios in the high and low risk groups of the validation set based on 500 random splits. The results indicated that the proposed method tended to perform better than the commonly used full regression method in separating patients according to the treatment effect measured by the hazard ratio, which was consistent with our previous findings from the simulation studies. Furthermore, the empirical probability of obtaining an interaction significant at the one-sided 0.05 level in the validation set was 27.0% for the new method and 13.6% for the full regression method. This observation supported that our previous significant findings for the detected interaction was likely not due to the random chance.
Figure 8.
Boxplots for hazard ratios in high and low risk groups based on 500 random splits of the PEACE data. A big difference between the two groups represents high quality of the constructed score in stratifying patients according to the individualized treatment effect.
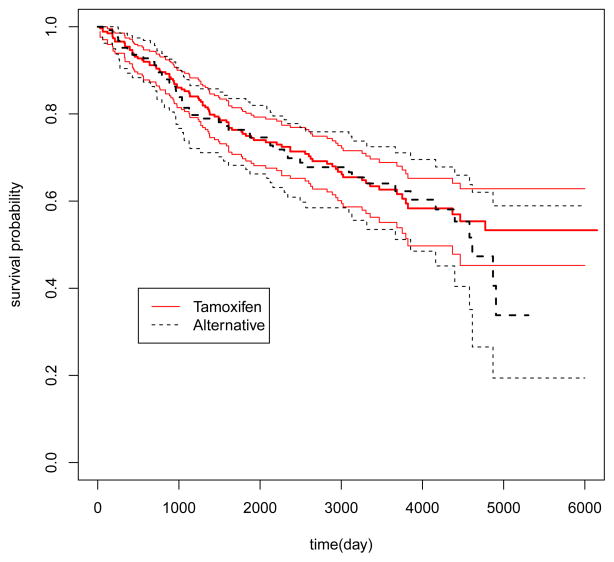
It has been known that the breast cancer can be classified into different subtypes using gene expression profile and the effective treatment may be different for different subtypes of the disease [Loi et al., 2007]. In the second example, we applied the proposed method to study the potential interactions between gene expression levels and Tamoxifen treatment in breast cancer patients. The data set consisted of 414 patients in the cohort GSE6532 collected by Loi et al. [2007] for the purpose of characterizing ER-positive subtypes with gene expression profiles. The data set can be downloaded from the web-site www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE6532. Excluding patients with incomplete information, there were 268 and 125 patients receiving Tamoxifen and alternative treatments, respectively. In addition to the routine demographic information, we had 44, 928 gene expression measurements for each of the 393 patients. The outcome of the primary interest here was the distant metastasis free survival (MFS) time, which could be right censored due to incomplete follow-up. The MFS times were not statistically different between the two groups with a two-sided p value of 0.59 (Figure 9). The goal of the analysis was to construct a gene score using gene expression levels to identify a subgroup of patients who may benefit from the Tamoxifen treatment. We selected the first 90 patients from each group to form the training set and reserved the rest 213 patients as the independent validation set.
Figure 9.
Survival functions of the Tamoxifen and alternative treatment groups: solid line, the Tamoxifen group; dashed line, the alternative treatment arm; thin line, the point-wise 95% confidence limits.
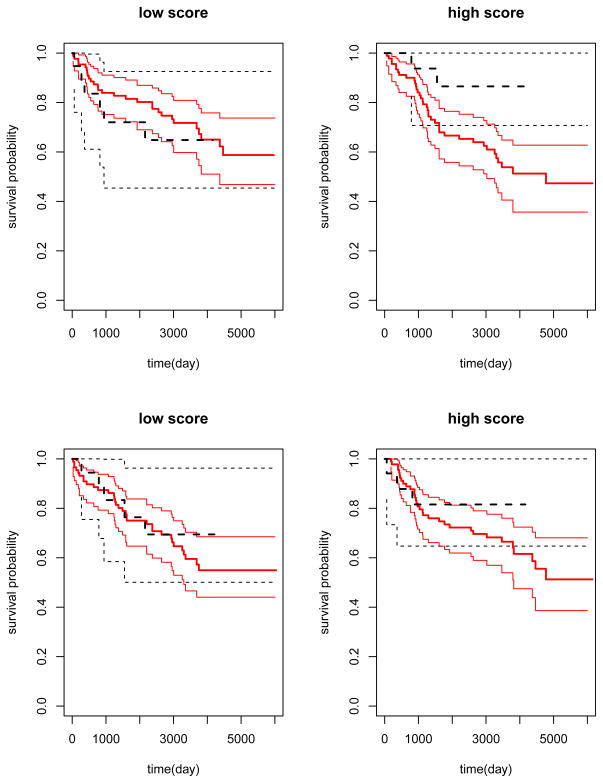
We identified 5,000 genes with the highest empirical variances and then constructed a gene score by fitting the Lasso-penalized Cox regression model with modified covariates in the training set. The Lasso penalty parameter was selected via cross-validation. The resulting gene score was a linear combination of expression levels of seven genes. We applied the gene score to classify the patients in the validation set into the high and low score groups according to the median. In the high score group, the MFS time in the Tamoxifen group was shorter than that in the alternative group with an estimated hazard ratio of 3.52 (p = 0.064). In the low score group, the MFS time in the Tamoxifen group was longer than that in the alternative group with an estimated hazard ratio of 0.694 (p = 0.421). The estimated survival curves for both groups were plotted in the upper panels of Figure 10. The interaction between constructed score and treatment was statistically significant in the validation set (p = 0.004).
Figure 10.
Survival functions of the Tamoxifen and alternative treatment groups stratified by the estimated score in the validation set: solid line, the Tamoxifen treatment group; dashed line, the alternative treatment group; thin line, the point-wise 95% confidence limits. Upper panels: the score is based on the “new” method; lower panel: the score is based on “full regression” method.
We implemented the efficiency augmentation method to obtain a new gene score, which was based on the expression level of eight genes. Again, we classified the patients in the validation set into the high and low score groups using the constructed score. The results were very similar to that from the gene score constructed without augmentation.
When we fitted a multivariate Cox regression model with treatment, the gene expression levels, and all treatment-gene interactions as the covariates, only one gene interacting with the treatment was selected by Lasso. However, the interaction could not be reproduced in the validation set (lower panel of Figure 10). Furthermore, the computational speed was substantially slower due to the high-dimensional covariates matrix in this case.
The second example was chosen for demonstrating the potential use of the proposed method in the high-dimensional setting. An important limitation of this example is that the treatment was not randomly assigned to patients as in PEACE trial and the gene expression levels were measured at the study baseline, which may be different from the treatment initiation time. Therefore, the results need to be interpreted with caution and further verification based on data from a randomized clinical trial is desired.
5 Discussion
In this paper, we have proposed a simple method to explore the potential interactions between treatment and a set of high dimensional covariates. The general idea is to use W(Z)·T/2 as new covariates in a regression model to predict the outcome. This provides a convenient approach for constructing a proper objective function whose optimizer can be used to estimate the individualized treatment effect as a function of given covariates. Once the objective function is constructed, one may employ one’s favorite algorithms such as boosting to optimize the empirical version of the objective function and the resulting estimator can be used to stratify the patient population according to the treatment benefit. Therefore, the proposed method can be used in a much broader way than those already described in the paper. For example, after creating the modified covariates W(Z) · T/2, data mining techniques such as nearest shrunken centroid classification, PAM and support vector machines can also be used to link the new covariates with the outcomes [Friedman, 1991, Tibshirani et al., 2002, Hastie and Zhu, 2006]. For univariate analysis, we also may perform large scale hypothesis testing on the modified data, to identify a list of covariates having interaction with the treatment; one could for example directly use the Significance Analysis of Microarrays (SAM) method for this purpose [Tusher et al., 2001].
When the randomization is not one-to-one, i.e., P(T = 1) = π ≠ 1/2, one may weight the observations in the T = 1 arm by 1 − π and observations in the T = −1 arm by π and perform the weighted regression analysis with modified covariates. The theoretical justification is given at the end of the Appendix.
As a limitation, the proposed method is primarily designed for analyzing data from randomized clinical trials. When applied to an observational study, where the covariates and treatment assignment are correlated, the constructed score may lose its causal interpretation. On the other hand, if a reasonable propensity score model is available, then we can still implement the modified covariate approach on matched or reweighted data so that the resulted score may retain the appropriate causal interpretations [Rosenbaum and Rubin, 1983].
Lastly, we want to emphasize that although the proposed method aims to estimate the individualized treatment effect with casual interpretation, the method is not immune to the common problems encountered in high dimensional data analysis such as multiple testing, false discovery, over-fitting et al., as the numerical studies demonstrated. Therefore the proposed method is just an exploratory tool and it is crucial to withhold an independent validation set, which can be used to verify the estimated interaction. In the validation set, one may make valid statistical inference on various parameters of interest. For example, one may estimate and test the treatment effect in subgroup of patients selected from the estimated covaraite-treatment interactions.
Supplementary Material
Acknowledgments
This research was partially supported by NIH grants R01-HL089778, U54-CA149145 and N01-HV28183, NSF grant DMS-9971405 and Doris Duke Foundation. The authors also thank the editor, the associate editor and two referees for their constructive comments.
Appendix: Justification for the Model-Based Loss
Under the linear working model for continuous responses, we have
where mt(z) = E(Y(t)|Z = z) for t = 1 and −1. Therefore
The minimizer of this objective function is f*(z) = {m1(z) − m−1(z)}/2 = Δ(z)/2 for all z ∈ Support of Z.
Under the logistic working model for binary responses, we have
Therefore
which implies that the minimizer of
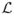 (f) is
(f) is
for all z ∈ Support of Z.
Under the Cox working model for survival outcomes, we have
where λt(u; Z) is the hazard function for X˜(t) given Z for t = 1/− 1. Thus
where X(j) = X˜(j) ∧ C(j), C(j) is the censoring time if the patient is assigned to the group j,
Setting the derivative at zero, the minimizer f*(z) satisfies
for all z ∈ Support of Z, where is an increasing function of v. Here, we assume that C and (Z, T) are independent and fC(·) is the density function of C. Furthermore, when censoring rates in two arms are close to each other for all given z, i.e., P(δ = 1|T = 1, Z = z) ≈ P(δ = 1|T = −1, Z = z),
If P(T = 1) = π ≠ 1/2, we perform the modified covariate analysis with observations in T = 1 and −1 arms weighted by (1 − π) and π, respectively. All the justifications above still hold. For example, for the continuous outcome, the weighted loss function is
whose minimizer is still f*(z) = Δ(z)/2.
Contributor Information
Lu Tian, Email: lutian@stanford.edu, Associate Professor, Department of Health Research and Policy, Stanford University, Palo Alto, CA 94305.
Ash A Alizadeh, Email: arasha@stanford.edu, Assistant Professor, Department of Medicine, Stanford University, Palo Alto, CA 94305.
Andrew J Gentles, Email: andrewg@stanford.edu, Senior Research Scientist, Integrative Cancer Biology Program, Stanford University, Palo Alto, CA 94305.
Robert Tibshirani, Email: tibs@stanford.edu, Professor, Department of Health Research and Policy and Department of Statistics, Stanford University, Palo Alto, CA 94305.
References
- Bonetti M, Gelber R. Patterns of treatment effects in subsets of patients in clinical trials. Biostatistics. 2004;5(3):465–81. doi: 10.1093/biostatistics/5.3.465. [DOI] [PubMed] [Google Scholar]
- Braunwald E, Domanski M, Fowler S, Geller N, Gersh B, Hsia J, Pfeffer M, Rice M, Rosenberg Y, Rouleau J PEACE trial investigators. Angiotension-coverting-enzyme inhibition in stable coronary artery disease. New England Journal of Medicine. 2004;351:2058–2068. doi: 10.1056/NEJMoa042739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen W, Ghosh D, Raghunathan T, Norkin M, Sargent D, Bepler G. On bayesian methods of exploring qualitative interactions for targeted treatment. Statistics in Medicine. 2012;31 doi: 10.1002/sim.5429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chipman H, George E, McCulloch R. Bayesian CART model search. Journal of the American Statistical Association. 1998;93 [Google Scholar]
- Fan J, Li R. Variable selection via nonconcave penalized likelihood and its oracle properties. Journal of American Statistical Association. 2001;96:1348–1361. [Google Scholar]
- Friedman J. Multivariate adaptive regression splines (with discussion) Annals of Statistics. 1991;19(1):1–141. [Google Scholar]
- Gustafson P. Bayesian regression modeling with interactions and smooth effects. Journal of the American Statistical Association. 2000;95(451):795–806. [Google Scholar]
- Hastie T, Zhu J. Discussion of “Support Vector Machines with Applications” by Javier Moguerza and Alberto Munoz. Statistical Science. 2006;21(3):352–357. [Google Scholar]
- Huang J, Xie H. Asymptotic oracle properties of SCAD-penalized least squares estimators. Asymptotics: Partices, Processes and Inverse Problems (IMS Lecture Notes-Monograph Series) 2007;55:149–166. [Google Scholar]
- Huang J, Ma S, Zhang C. Adaptive lasso for sparse high-dimensional regression models. Statistica Sinica. 2008;18:1603–1608. [Google Scholar]
- Huang J, Sun T, Ying Z, Zhang C. Oracle inequalities for the lasso in the Cox model. Annals of Statistics. 2013;41:1055–1692. doi: 10.1214/13-AOS1098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kong S, Nan B. Non-asymptotic oracle inequalities for the high-dimensional Cox regression via lasso. The Annals of Statistics. 2013;41(3):1142–1165. doi: 10.5705/ss.2012.240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin D, Wei LJ. Robust inference for the Cox proportional hazards model. Journal of the American Statistical Association. 1989;84(107):1074–1078. [Google Scholar]
- Loh P, Wainwright MJ. Technical Report. 2012. Regularized M-estimators with nonconvexity: Statistical and algorithmic theory for local optima. arXiv:1305.2436. [Google Scholar]
- Loi S, Haibe-kains B, Desmedt C, et al. Definition of clinically distinct molecular subtypes in estrogen rceptor-positive breast carcinomas through genomic grade. Journal of Clinical Oncology. 2007;25(10):1239–1246. doi: 10.1200/JCO.2006.07.1522. [DOI] [PubMed] [Google Scholar]
- Negahban S, Ravikumar P, Wainwright M, Yu B. A unified framework for high dimensional analysis of M-estimators with decomposable regularizers. Statistical Science. 2012;27:1214/12–STS400. [Google Scholar]
- Qian M, Murphy S. Performance guarantees for individualized treatment rules. Annals of Statistics. 2011;39:1180–1210. doi: 10.1214/10-AOS864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenbaum P, Rubin D. The central role of the propensity score in observational studies for causal effects. Biometrika. 1983;70:41–55. [Google Scholar]
- Royston P, Sauerbrei W. Interactions between treatment and continuous covariates: A step toward individualizing therapy. Journal of Clinical Oncology. 2008;26(9):1397–99. doi: 10.1200/JCO.2007.14.8981. [DOI] [PubMed] [Google Scholar]
- Sauerbrei W, Royston P, Zapien K. Detecting an interaction between treatment and a continuous covariate: A comparison of two approaches. Computational Statistics and Data Analysis. 2007;51(8):4054–63. [Google Scholar]
- Solomon S, Rice M, Jablonski K, Jose J, Domanski M, Sabatine M, Gersh B, Rouleau J, Pfeffer M, Braunwald E (PEACE) Investigators . Renal function and effectiveness of angiotensin-converting enzyme inhibitor therapy in patients with chronic stable coronary disease in the prevention of events with ace inhibition (PEACE) trial. Circulation. 2006;114:26–31. doi: 10.1161/CIRCULATIONAHA.105.592733. [DOI] [PubMed] [Google Scholar]
- Su X, Zhou T, Yan X, Fan F, Yang S. Interaction trees with censored survival data. The International Journal of Biostatistics. 2008;4(1):Article 2. doi: 10.2202/1557-4679.1071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tian L, Tibshirani R. Adaptive index models for marker-based risk stratification. Biostatistics. 2011;12(1):68–86. doi: 10.1093/biostatistics/kxq047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tibshirani R. Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society, Series B. 1996;58:267–288. [Google Scholar]
- Tibshirani R, Hastie T, Narasimhan B, Gilbert C. Diagnosis of multiple cancer types by shrunken centroids of gene expression. Proceedings of the National Academy of Sciences. 2002;99(10) doi: 10.1073/pnas.082099299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tusher V, Tibshirani R, Gilbert C. Significance analysis of microarrays applied to the ionizing radiation response. Proceedings of the National Academy of Sciences. 2001;98(9):5116–5121. doi: 10.1073/pnas.091062498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van De Geer S. High-dimensional gneralized linear models and lasso. Annals of Statistics. 2008;36:614–645. [Google Scholar]
- Van De Geer S, Buhlmann P. On the conditions used to prove oracle results for lasso. Electronic Journal of Statistics. 2009;3:1360–1392. [Google Scholar]
- Zhang C. Nearly unbiased variable selection under minimax concave penalty. Annals of Statistics. 2010;38:894–942. [Google Scholar]
- Zhang C, Huang J. The sparsity and bias of the lasso selection in high-dimensional linear regression. Annals of Statistics. 2008;36:1567–1594. [Google Scholar]
- Zhang C, Zhang T. A general theory of concave regularization for high-dimensional sparse estimation problems. Statistical Science. 2012;27:576–593. [Google Scholar]
- Zhao P, Yu B. On model selection consistency of lasso. Journal of Machine Learning Research. 2006;7:2541–2563. [Google Scholar]
- Zhao Y, Zeng D, Rush A, Kosorok M. Estimating individualized treatement rules using outcome weighted learning. Journal of the American Statistical Association. 2012;107(499):1106–1118. doi: 10.1080/01621459.2012.695674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zou H. The adaptive lasso and its oracle properties. Journal of the American Statistical Association. 2006;101:1418–1429. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.