Abstract
Kinases perform phosphoryl-transfer reactions in milliseconds; without enzymes, these reactions would take about 8000 years under physiological conditions. Despite extensive studies, a comprehensive understanding of kinase energy landscapes, including both chemical and conformational steps, is lacking. Here we scrutinize the microscopic steps in the catalytic cycle of adenylate kinase, through a combination of NMR measurements during catalysis, pre-steady-state kinetics, MD simulations, and crystallography of active complexes. We find that the Mg2+ cofactor activates two distinct molecular events, phosphoryl transfer (>105-fold) and lid-opening (103-fold). In contrast, mutation of an essential active-site arginine decelerates phosphoryl transfer 103-fold without substantially affecting lid-opening. Our results highlight the importance of the entire energy landscape in catalysis and suggest that adenylate kinases have evolved to activate key processes simultaneously by precise placement of a single, charged and very abundant cofactor in a pre-organized active site.
INTRODUCTION
Phosphate esters and anhydrides are high-energy linkages that are extremely resistant to nucleophilic attack and are therefore fundamental to genomic stability, long signaling state lifetimes, and storage of biochemical energy1-4. While stability is critical, organisms must respond rapidly and effectively to their environment and have therefore evolved enzymes that catalyze transfer of phosphoryl groups with exquisite specificity and enormous rate accelerations relative to the uncatalyzed reaction in solution5-10. Impressive progress has been made in understanding protein phosphorylation in cellular processes11,12 and fundamental work on non-enzymatic phosphoryl transfer (P-transfer) has delivered a deep mechanistic understanding of P-transfer in solution5-10; however, a comprehensive understanding of kinase catalyzed phosphorylation is still lacking despite the wealth of literature on many different P-transfer enzymes5,13. This includes crystal structures that reveal conservation in the active site and accompanying domain architecture14; kinetic studies that establish the rate-limiting steps and the order of events13; and NMR that links local fluctuations to global protein dynamics15,16.
However, catalysis is typically composed of multiple microscopic steps spanning a hierarchy of time and space, which often obscures underlying molecular mechanisms. This has led to persistent controversies, for example about the role of the Mg2+ cofactor in kinase catalysis. While some kinases are activated by a single Mg2+ ion, additional Mg2+ binding may either be required for full activation, result in inhibition, or be involved in structural stabilization13,17,18. The variety of different mechanisms attributed to the Mg2+ cofactor has resulted in arguments about the kinetic schemes to account for the role of Mg2+ in catalysis19. Other heated debates focus on the role of conformational changes in the enzymatic reaction20-25. Quantitative descriptions of the entire energy landscape of catalysis are necessary to reconcile these different mechanisms including the canonical role of Mg2+ in kinase catalysis.
Here we have performed a comprehensive investigation of the adenylate kinase (Adk) energy landscape and have quantified multiple kinetic states along the reaction pathway at atomic resolution. Adk is a ubiquitous and essential phosphoryl-transfer enzyme found in all cells. Adks reversibly transfer a phosphoryl group from ATP to AMP thereby maintaining the equilibrium between cytoplasmic nucleotides (Fig. 1a). During the enzymatic cycle, Adk undergoes large conformational changes by opening/closing of the ATP- and AMP-lid (defined as the protein fragments that close over the Mg-ATP and AMP binding sites, respectively), as visualized in Fig. 1a. Unlike many protein kinases that are activated by protein–protein interactions or covalent modifications14, Adk is fully active in the presence of its nucleotide substrates and catalyzes a reversible reaction. This provides a tractable framework for a quantitative analysis of the reaction-energy landscape. Using complementary techniques to examine the enzyme during catalysis across many orders of temporal and spatial resolution, we separated the microscopic steps of phosphoryl transfer and conformational motions with pre-steady-state kinetics and NMR dynamics experiments, investigated the mechanism of transition-state stabilization by crystallography and explored the active-site dynamics by molecular dynamics simulation. Combined, these results reveal the major players responsible for the overall rate acceleration and address the key question of how the enzyme dramatically lowers the energy barrier of P-transfer and accelerates conformational changes essential for both efficient catalysis and suppression of detrimental hydrolysis.
Figure 1. Adk free-energy landscape of catalysis and exploration of the phosphoryl-transfer step by X-ray crystallography.
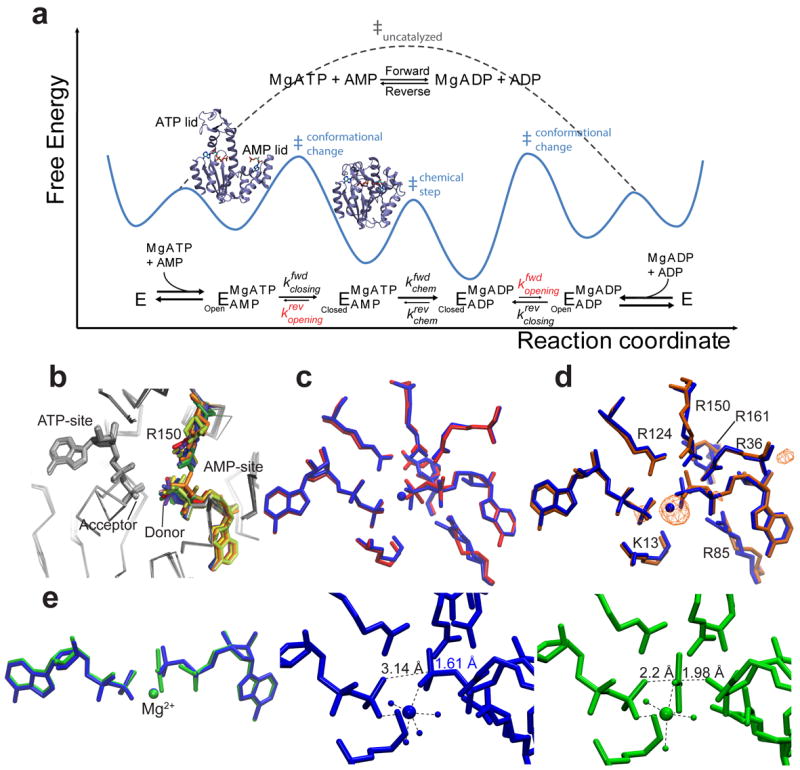
(a) Overall Adk reaction, minimal reaction scheme, and corresponding schematic of the catalytic energy landscape based on the measured enzyme kinetics (Table 2). Rate-limiting lid-opening (kopening) is shown in red and visualized by the open and closed structures. (b) The superposition of AAdk structures with ADPs bound. Conformational heterogeneity of the donor phosphate group and R150 are highlighted in color. (c) Superposition of AAdk structures with bound ADPs in the presence (PDB 4CF7, blue) and absence (PDB 4JL5, red) of Mg2+. (d) Superposition of AAdk complexed with Mg2+–ADP–ADP (blue) and Co2+–ADP–ADP (PDB 4JKY, orange). The anomalous scattering of the electron density at the Co-edge (λ=1.609 Å) is shown as anomalous difference map contoured at 5.5 σ (orange). (e) Superposition of Mg2+–ADP–AMP–AlF4– (PDB 3SR0, green) with Mg2+–ADP–ADP (blue). Detailed structures of the active site of both the substrate–enzyme complex (blue) and transition-state analogue (green) showing metal coordination and relevant O–P or O–Al distances (dashed lines) and the covalent O–P bond (blue).
RESULTS
Mg2+ as electrostatic “pivot” for phosphoryl transfer
Expanding on previous structural studies and to set the stage for experiments to characterize the free-energy landscape, we obtained a number of Adk crystal structures in multiple biochemical states (e.g., with substrates, with and without metals, and with a transition-state mimic). Many structures of Adks are available that reveal in atomistic detail the conformational cycle between ligand-free and ligand-bound states26-29. However, few have been solved with natural substrates in an active quaternary complex, making it difficult to dissect how the enzyme activates P-transfer16. Here we present a number of Aquifex aeolicus Adk (AAdk) structures bound to natural substrates that have provided mechanistic insight into the catalysis of P-transfer (Table 1). An overlay of many high-resolution snapshots of the AAdk–ADP–ADP ternary complex (AAdk1–4,6) revealed that the transferable phosphoryl group of the donor ADP and its active-site partner R150 show conformational heterogeneity while the acceptor ADP was held rigidly (Fig. 1b). This hinted to movement of only the phosphoryl group of the donor ADP and not the nucleotide acceptor during P-transfer. We note that presenting multiple redundant structures of crystal isoforms is unusual; however, a single structure even with partial occupancy refinement would not illustrate this observed conformational sampling in the active site.
Table 1.
Data collection and refinement statistics
| AAdk1 ADP–ADP |
AAdk2 ADP–ADP |
AAdk3 ADP–ADP |
AAdk4 ADP–ADP |
AAdk5 AMPPN– AMPPN |
AAdk6 ADP–ADP |
|
|---|---|---|---|---|---|---|
| Data collection | ||||||
| Space group | P212121 | P212121 | P212121 | P212121 | P212121 | P212121 |
| Cell dimensions | ||||||
| a, b, c (Å) | 66.17,69.56, 85.39 | 66.64,70.54, 85.88 | 67.00,73.73, 87.52 | 67.00,74.72, 88.15 | 66.47, 71.56, 86.30 | 66.94, 73.89, 87.80 |
| α, β, γ (°) | 90, 90, 90 | 90, 90, 90 | 90, 90, 90 | 90, 90, 90 | 90, 90, 90 | 90, 90, 90 |
| Resolution (Å) | 29.0–1.24 (1.31–1.24) | 42.9–1.55 (1.64–1.55) | 37.6–1.53 (1.61–1.53) | 38.0–1.79 (1.88–1.79) | 43.2–1.65 (1.74–1.65) | 43.9–2.12 (2.23–2.12) |
| Rmerge | 0.062 (0.427) | 0.139 (1.287) | 0.072 (1.342) | 0.105 (0.566) | 0.065 (0.653) | 0.174 (1.698) |
| I / σI | 22.1 (5.7) | 8.1 (1.4) | 18.8 (1.9) | 14.5 (3.2) | 11.9 (2.0) | 7.8 (1.8) |
| Completeness (%) | 99.4 (96.2) | 97.6 (93.5) | 100.0 (99.8) | 100.0 (100.0) | 99.1 (98.0) | 91.1 (99.9) |
| Redundancy | 14.0 (12.1) | 11.5 (9.4) | 14.0 (13.3) | 12.0 (9.3) | 6.8 (6.2) | 6.5 (6.8) |
| Refinement | ||||||
| Resolution (Å) | 29.0–1.24 | 36.1–1.55 | 36.6–1.53 | 38.0–1.79 | 42.4–1.65 | 43.9–2.12 |
| No. reflections | 111278 | 57161 | 62870 | 42421 | 49227 | 22909 |
| Rwork / Rfree | 0.130/0.159 | 0.185/0.229 | 0.173/0.232 | 0.180/0.232 | 0.208/0.241 | 0.186/0.256 |
| No. atoms | ||||||
| Protein | 7181 | 3360 | 3306 | 3386 | 3365 | 3256 |
| Ligand/ion | 195 | 108 | 108 | 108 | 108 | 108 |
| Water | 797 | 471 | 510 | 644 | 361 | 227 |
| B-factors | ||||||
| Protein | 16.1 | 24.6 | 28.1 | 21.5 | 33.5 | 39.2 |
| Ligand/ion | 9.7 | 18.7 | 21.2 | 16.7 | 26.0 | 31.4 |
| Water | 26.7 | 37.6 | 38.2 | 31.8 | 40.6 | 37.8 |
| r.m.s. deviations | ||||||
| Bond lengths (Å) | 1.501 | 1.215 | 1.204 | 1.234 | 1.237 | 1.234 |
| Bond angles (°) | 0.010 | 0.006 | 0.005 | 0.007 | 0.007 | 0.008 |
| AAdk7 Co2+–ADP– ADP |
AAdk8 Mg2+–ADP– AMP–AlF4– |
AAdk9 R150K |
AAdk10 R150K |
AAdk11 Mg2+–ADP– ADP |
|
|---|---|---|---|---|---|
| Data collection | |||||
| Space group | P212121 | P212121 | P212121 | P212121 | P212121 |
| Cell dimensions | |||||
| a, b, c (Å) | 67.55, 73.53, 87.47 | 65.95, 69.58, 85.67 | 67.17, 71.01, 85.83 | 67.01, 70.46, 85.58 | 64.09, 64.70,86.26 |
| α, β, γ (°) | 90, 90, 90 | 90, 90, 90 | 90, 90, 90 | 90, 90, 90 | 90, 90, 90 |
| Resolution (Å) | 56.3–2.37 (2.50–2.37) | 41.8–1.57 (1.65–1.57) | 48.8–1.73 (1.82–1.73) | 36.6–1.43 (1.51–1.43) | 64.7–1.59 (1.64–1.59) |
| Rmerge | 0.062 (0.198) | 0.085 (0.310) | 0.054 (0.123) | 0.053 (0.268) | 0.088 (0.622) |
| I / σI | 25.6 (9.8) | 11.9 (3.7) | 18.1 (6.5) | 17.5 (4.3) | 12.2 (3.1) |
| Completeness (%) | 99.7 (97.9) | 99.7 (98.3) | 99.9 (100.0) | 99.9 (99.8) | 100.0 (100.0) |
| Redundancy | 13.5 (12.7) | 6.4 (4.8) | 6.4 (5.0) | 6.7 (5.1) | 6.5 (6.7) |
| Refinement | |||||
| Resolution (Å) | 53.5–2.37 | 41.8–1.57 | 42.4–1.73 | 36.1–1.43 | 40.3–1.59 |
| No. reflections | 17150 | 56016 | 43855 | 74937 | 48566 |
| Rwork / Rfree | 0.199/0.267 | 0.148/0.189 | 0.161/0.210 | 0.153/0.195 | 0.182/0.216 |
| No. atoms | |||||
| Protein | 3245 | 6995 | 3367 | 3365 | 3300 |
| Ligand/ion | 110 | 160 | 108 | 108 | 159 |
| Water | 144 | 759 | 518 | 703 | 335 |
| B-factors | |||||
| Protein | 42.0 | 16.0 | 21.1 | 20.0 | 20.5 |
| Ligand/ion | 34.0 | 10.6 | 15.6 | 14.8 | 14.0 |
| Water | 37.4 | 28.1 | 32.7 | 33.6 | 28.0 |
| r.m.s. deviations | |||||
| Bond lengths (Å) | 1.276 | 1.515 | 1.222 | 1.253 | 1.328 |
| Bond angles (°) | 0.008 | 0.014 | 0.006 | 0.005 | 0.007 |
The number of crystals for each structure is one.
One of the most important components of enzyme-catalyzed P-transfer, the Mg2+ cofactor, was not detected in the X-ray structures of the AAdk–ADP–ADP ternary complex despite being present in the mother liquor (Fig. 1b). To obtain a high-resolution structure of AAdk–ADP–ADP with magnesium in the active site, we soaked crystals in the crystallization solution containing 20 mM Mg2+ at an elevated pH of 9. A comparison between the structures with and without Mg2+ bound showed that they are very similar (Fig. 1c) except for the extra electron density of the Mg2+ and its coordination to the six ligands. It is notoriously difficult to distinguish Mg2+ from structural water by electron density alone and therefore the position of the Mg2+ in the presence of natural substrates is ambiguous in many cases30. Consequently, in order to unequivocally determine the position of the metal cofactor in the active site of the enzyme–substrate complex, we also obtained a structure of the ternary AAdk–ADP–ADP complex in the presence of Co2+ (AAdk7, Fig. 1d). The position of the cobalt atom derived from anomalous signal collected with the X-ray source at the Co2+ edge together with the electron density, was confirmed to be identical to that of Mg2+ (AAdk11, Fig. 1d)31. Based on these structures, we propose that the metal cofactor helps anchor the flexible donor phosphoryl group for a more favorable attack by the oxygen nucleophile of the acceptor nucleotide.
What happens to the active-site players in the transition state (TS) of the P-transfer reaction? A structure of the AAdk–Mg2+–ADP–AMP quaternary complex with aluminum fluoride as transition-state analogue revealed first that a square planar tetrafluoroaluminate (AlF4−) and not a neutral AlF3 was in the active site (AAdk8)32-34. This agrees with the fundamental work by Baxter and colleagues on the importance of balancing charge in active sites, a general principle that has been demonstrated for many phosphoryl-transfer enzymes, including β-phosphoglucomutase, phosphoglycerate kinase, protein kinase A, and UMP–CMP kinase2,35-37. Second, the AlF4− was positioned equidistant between acceptor and donor phosphates due to a 1 Å movement of the latter (Fig. 1e and Supplementary Fig. 1a, b). Third, the Mg2+ cofactor was clearly present and maintained its position and coordination partners relative to the AAdk–Mg2+–ADP–ADP quaternary complex (Fig. 1e and Supplementary Fig. 1a,b). The position of the divalent ion (Fig. 1d,e and Supplementary Fig. 1a-c) was identical while the phosphoryl group was transferred between the donor and acceptor sites, suggesting that the Mg2+ cofactor acted as an “electrostatic pivot” during P-transfer. In contrast, the active-site R150 shifted in concert with the movement of the phosphoryl group.
Active-site dynamics probed by molecular dynamics simulation
To test our hypothesis that Mg2+ helps organize the Adk active-site architecture by positioning the donor and acceptor phosphates in close proximity, we performed 200 ns molecular dynamics (MD) simulations on the closed AAdk–ADP–ADP ternary complex with and without Mg2+.
Simulations with Mg2+ showed a stable active-site configuration where both nucleotides experience limited fluctuations (Fig. 2a). Water molecule ligands to the metal ion were also stable and remain coordinated during the simulation (Supplementary Fig. 1c,d). In contrast, simulations in the absence of Mg2+ revealed that the active site, and in particular the donor phosphoryl group, samples a much larger distribution of states, (Fig. 2b). These simulations indicate a substantially reduced probability of sampling productive conformations without Mg2+, suggesting an appreciable stabilization of pre-catalytic states by the cofactor 38.
Figure 2. Role of active-site dynamics in efficient phosphoryl transfer versus unproductive hydrolysis.

(a,b)Superposition of representative snapshots of 200 ns MD simulations of the ADP–ADP ternary complex of AAdk (a) with (yellow) and (b) without Mg2+. (c) Unproductive ATP hydrolysis by 100 μM of EAdk. Fit of the time dependence of nucleotide concentrations yielded a hydrolysis rate of ~2°10–6 s–1. (d) Overlay of the active site of the crystal structure of AAdk bound to Mg2+–ADP–AMP–AlF4– (green) including bound water molecules (green spheres) and a typical snapshot from a 200 ns MD simulation of the AAdk–Mg2+–ADP–ADP complex (yellow). The transparent yellow spheres represent the isosurface of value 0.75 for the fractional occupancy of the water oxygen atoms during the MD simulation. A cavity excluded from access to bulk solvent (transparent green) is solvated by a number of water molecules.
A major challenge for kinases is catalyzing P-transfer efficiently while suppressing the more favorable hydrolysis side reaction. For Adk we measured an extremely slow hydrolysis rate of about 2·10−6 s−1 (Fig. 2c) relative to the productive rate of phosphoryl transfer of about 2·102 s−1. In comparison to other members of the kinase family with hydrolysis rates in the range of 10−2 to 10 s−1 39,40, Adk’s ability to execute P-transfer efficiently and avoid unproductive hydrolysis is impressive. From an evolutionary perspective, this striking difference in hydrolysis rates can be rationalized because Adks are abundant proteins that are always active to maintain nucleotide homeostasis whereas many protein kinases are only transiently activated while participating in signaling cascades11,12.
What possible mechanisms does Adk employ for such efficient suppression of destructive hydrolysis? An obvious way to prevent hydrolysis would be to exclude water from the active site; however, X-ray structures showed that about 20 water molecules were trapped in the AAdk active-site cavity (Fig. 2d). It is likely that these waters helped reduce the energetic penalty associated with de-solvating the highly-charged nucleotide substrates when binding to the active site. Rather than exclude water from the active site to minimize hydrolysis, Adk tightly coordinates these water molecules thereby sequestering them from the phosphoryl groups. The stability of water molecules, present at the same positions in the active site of all crystal structures (AAdk1–11), was investigated in long MD simulations (Supplementary Figs. 1d and 2 and Movie 1). While the average positions occupied by these water molecules inside the pocket agreed well with those identified in the crystal structures (Fig. 2d), the dynamic behavior of these waters was very different in the presence and absence of Mg2+. Without Mg2+, the waters that are initially present inside the active site exchange with bulk solvent on a timescale of 100 ns. However, in the presence of the metal cofactor the water molecules inside the active-site pocket are prevented from exchanging with bulk solvent throughout the simulations (Supplementary Fig. 2 and Movie 1). The terminal phosphates of the substrates, Mg2+, and the four water molecules coordinating the metal ion form a very stable complex (Supplementary Fig. 1d), serving as a cap to block water exchange. In all simulations we performed (with a combined run time of several microseconds) the water molecules remained tightly coordinated at positions incapable of nucleophilic attack. We note that the discussed points are merely a hypothesis, since hydrolysis happens on the timescale of hours, well beyond the timescales of lid-opening/closing and the MD regime41,42.
Dissecting microscopic steps by rapid kinetics experiments
Although Mg2+ has minimal impact on the Adk structure (Fig. 1c), it is generally known that Mg2+ has an enormous effect on the turnover rate of P-transfer enzymes5,6,8,13. To determine the energetic contribution of Mg2+ to the overall rate acceleration of P-transfer, we measured turnover rates in the absence of Mg2+.
For all kinetic and NMR experiments described below, we used Escherichia coli Adk (EAdk), which has an identical active-site architecture, catalytic mechanism, and rate-limiting steps as AAdk (cf. Fig. 3 and Supplementary Fig. 3a-c)43,44, and higher catalytic efficiency at room temperature. This choice was rooted in the inability to measure conformational dynamics for AAdk by NMR, as explained in the next paragraph. To eliminate traces of divalent metals from solution we included ethylenediaminetetraacetic acid (EDTA) in excess in all metal-free reactions performed (Supplementary Fig. 3d). For EAdk, Mg2+ accelerated overall turnover by about five orders of magnitude, in agreement with the general notion that Mg2+ is essential for enzyme-catalyzed P-transfer reactions. However, since lid-opening and not P-transfer is rate limiting in the presence of Mg2+ 44, the actual rate acceleration of the chemical step by Mg2+ must be even greater.
Figure 3. Catalytic effect of the Mg2+ cofactor.
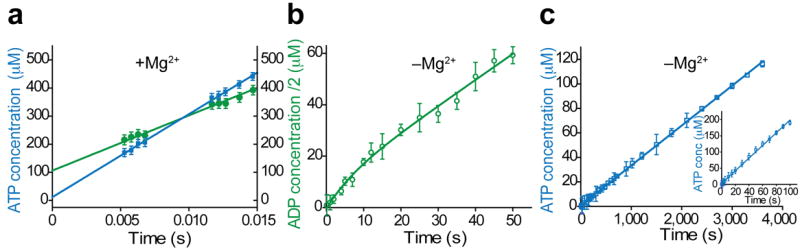
Pre-steady-state kinetics of EAdk at 25 °C measured by quench-flow (a) with and (b,c) without Mg2+ (n = 3 experiments; mean ± s.e.m.). (a) 113 μM EAdk, 4 mM ATP, 4 mM AMP and 8 mM MgCl2 in the forward direction (green) and 4 mM ADP and MgCl2 in the reverse direction (blue) were used. (b) A resolved burst phase is seen in the forward direction with 20 μM EAdk and 4 mM ATP and AMP, providing the rates of both the P-transfer and lid-opening, while in the reverse reaction (c) No burst phase is seen with 20 μM or 500 μM EAdk (inset) and 4 mM ADP.
To catch the chemical step directly, we measured the pre-steady-state rate of product formation by quench-flow13 (Fig. 3 and Supplementary Fig. 3e). With Mg2+, P-transfer on the enzyme was faster than lid-opening, which resulted in an initial burst of product formation as the enzyme completed its first turnover, followed by a linear product increase that was identical to the rate of lid-opening (Fig. 3a). Remarkably, P-transfer was faster than ~500 s−1 since the burst phase was completed within the dead time of the instrument (~5 ms). The ratio of the pre-steady-state burst amplitudes reports directly on the on-enzyme equilibrium [EAdk–Mg2+–ADP–ADP]/[EAdk–Mg2+–ATP–AMP] of about 10, with the sum of the two burst amplitudes equal to the total enzyme concentration (Fig. 3a). This is in contrast to the free nucleotide equilibrium of about 1. The values for the on-enzyme nucleotide equilibrium were confirmed by nucleotide saturation experiments (Supplementary Fig. 3f,g). We note that an on-enzyme equilibrium of 10:1 is equivalent to a small difference in free energy (~1.3 kcal/mol) between the states, which is fully consistent with the idea that optimal enzyme catalytic efficiency is achieved when the free energies of reaction intermediates are balanced8.
In the absence of Mg2+, P-transfer is severely impaired. In the reverse reaction, no burst phase was observed and the turnover rates were identical between the pre- and steady-state regimes, indicating that P-transfer was rate limiting (Fig. 3c). Unexpectedly, in the forward direction a resolved burst followed by a second phase seemed to imply that a step following P-transfer was also drastically slowed down to about 0.05 s−1 without Mg2+ (Fig. 3b and Supplementary Fig. 3e).
Mg2+ greatly accelerates lid-opening
Could this other slow step in the absence of Mg2+ be the lid-opening? 15N-CPMG NMR relaxation dispersion experiments have previously been used to quantify the millisecond lid-opening rates during catalysis in the presence of Mg2+ 44. Strikingly, when we measured EAdk during catalysis without Mg2+, the dispersion profiles were flat (Fig. 4a and Suppl. Note 1), indicating that the rate of lid-opening could be shifted into the slow-exchange regime and thus too slow to be detected. Such NMR relaxation behavior of the enzyme agrees with the rate of lid-opening of 0.05 s−1 as determined by pre-steady-state kinetics (Table 2). We note that in the slow-exchange regime, one would expect to see signals for both states in the HSQC spectrum, which we did not observe here for EAdk (Fig. 4b). A plausible explanation for this phenomenon is a small population of the minor, open state that would give rise to weak signals. In addition, the line broadening of signals corresponding to the open state is proportional to the closing rate, which is considerably faster than the opening rate, and could broaden the already weak signals beyond detection. However, the absence of NMR dispersion could also be caused by a lack of motions. To differentiate between these scenarios, we measured the temperature dependence of the NMR relaxation dispersion profiles45. For an exchange process that is slow on the NMR timescale, the exchange contribution (Rex) is equal to the lid-opening rate whereas for a fast-exchange process it is inversely proportional to the sum of the lid-opening/closing rate.
Figure 4. EAdk structure and dynamics during catalysis with and without Mg2+ studied by NMR.
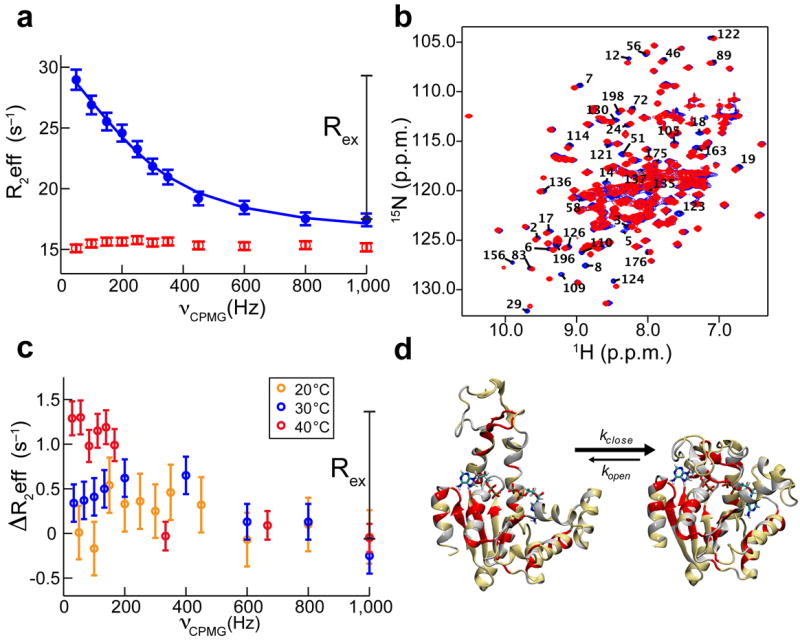
(a) 15N-TROSY CPMG relaxation dispersion NMR experiments at 25 °C on WT EAdk saturated with 20 mM nucleotides. Representative dispersion profile for residues sensitive to lid-opening/closing in the presence of Mg2+ (blue) are fully suppressed in its absence (red). (b) Overlay of [1H-15N]-TROSY-HSQC spectra of WT EAdk during turnover with (blue) and without (red) Mg2+. (c) Temperature dependence of normalized 15N-TROSY CPMG relaxation dispersion profiles of WT EAdk. (d) Residues with dispersion curves at 40 °C without Mg2+ are plotted on the EAdk–ADP–ADP open and closed structures (red); residues with no data due to overlap or missing signals are shown in grey and nucleotides are shown in stick representation. Uncertainties (s.d.) in R2eff (a,c) were estimated from the variance for a number of non-exchanging peaks (n = 7).
Table 2.
Microscopic rate constants for EAdk catalysis
| metal | Rate constant (s–1) | ||||
|---|---|---|---|---|---|
| P-transfer | Lid-opening | ||||
| forward | reverse | forward | reverse | ||
| WT | none | 0.14 ± 0.1 (a) | 0.005 ± 0.003 (a) | 0.05 ± 0.01 (a),(*) | 0.09 ± 0.05 (a) |
| Mg2+ | >5000 (c) | >500 (b) | 190 ± 30 (d),(**) | 2800 ± 200 (d) | |
| Ca2+ | >500 (b) | 24 ± 4 (e) | 260 ± 30 (d),(***) | >2600 (f) | |
| Co2+ | >500 (b) | 150 ± 15 (e) | 190 ± 20 (d) | >1900 (f) | |
| R150K | none | (4.6 ± 0.2)°10–5 (e) | (6.5 ± 1.2)°10–6 (e) | <1 (g) | <1 (g) |
| Mg2+ | 0.7 ± 0.2 (e) | 0.5 ± 0.1 (e) | 300 ± 75 (g) | ||
from the observed forward and reversed rates from quench-flow data and on-enzyme equilibrium.
lower limit determined from the burst within the dead time of the quench-flow instrument (~5 ms).
lower limit from the quench-flow dead time and on-enzyme equilibrium
from the steady-state (linear) phase of the quench-flow experiment and on-enzyme equilibrium.
from the linear phase of the quench-flow experiment.
calculated from kcat,obs and probability to be in the corresponding states.
from NMR relaxation dispersion data.
in good agreement with upper limit established by NMR (<1 s–1).
in good agreement with NMR value of 210 ± 80 s–1.
in good agreement with NMR value of 370 ± 140 s–1.
We observed an increase in Rex by raising the temperature from 20 to 40 °C, with a uniform amplitude of ~1 s−1 for all residues that experience the exchange process (Fig. 4c). When plotted on the structures (Fig. 4d), these residues are very similar to the ones that report on the lid-opening/closing in the presence of magnesium44. These results confirm that the lid-opening in the absence of magnesium is indeed slow on the NMR timescale. Consequently, Rex reflects the rate of lid-opening; however, the dispersion data do not provide its accurate value nor information about the closing rate and the relative population of the states. Therefore, we conclude that a second, unexpected role for the Mg2+ cofactor is to dramatically accelerate lid-opening by about three orders of magnitude (Table 2).
How can Mg2+ lower the activation barriers of the two major steps in the catalytic cycle? We envision that Mg2+ simultaneously helps shield the strong electrostatic interactions between active-site arginines and substrates to facilitate lid-opening and correctly orients the active-site players for efficient P-transfer. This suggests that substituting other divalent metals for Mg2+ should activate lid-opening similarly while P-transfer might be more specifically tuned to the charge density of Mg2+. Indeed, we found that P-transfer for all divalent cations other than Mg2+ was much slower and, in fact, rate limiting, indicating that the active-site chemistry is optimized for Mg2+ (Fig. 5a, Supplementary Fig. 4, Table 2, and Supplementary Table 1). In contrast, the rates of lid-opening/closing measured in the presence of Mg2+ and Ca2+ were similar (Fig. 5b, Table 2, Supplementary Table 2, and Suppl. Note 2), implying electrostatics as the predominant cause for this strong acceleration of lid-opening. Simple electrostatic potential and interaction energy calculations reveal that the coordination of a divalent cation to the nucleotides opposite to the coordinating arginine side chains weakens the strong electrostatic interactions between the phosphates of the nucleotides and the arginine residues from the lids (Fig. 5c,d). Since these interactions need to be broken for the lids to open, the placement of Mg2+ in Adk indeed accelerates lid-opening via electrostatics.
Figure 5. The nature of the divalent cation drastically affects phosphoryl transfer but not Adk conformational dynamics.
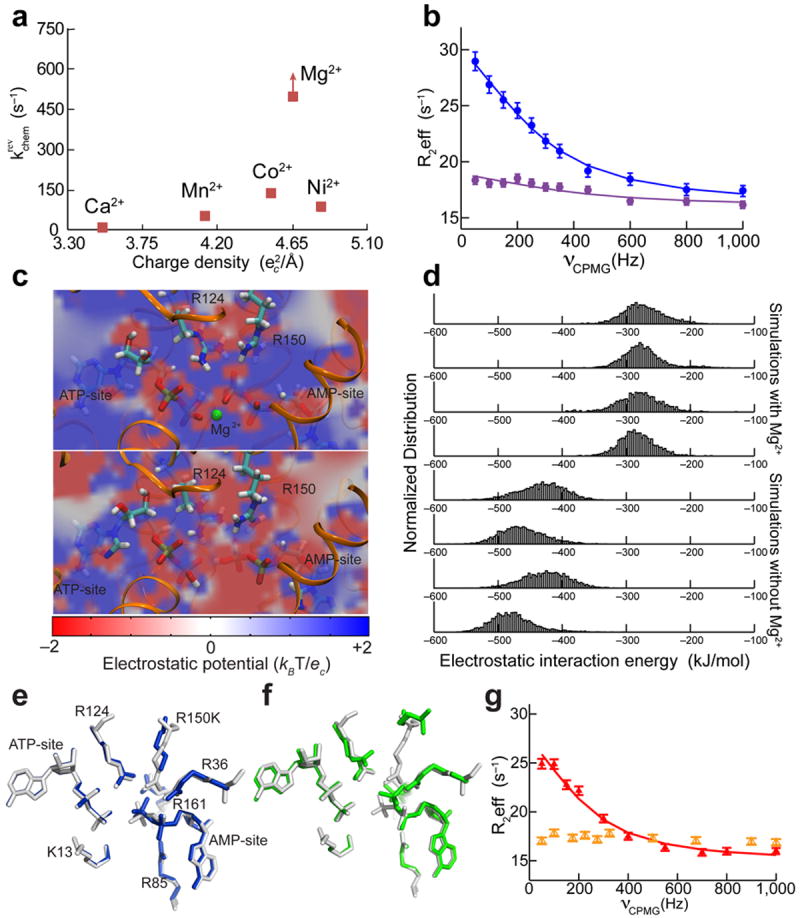
(a) The P-transfer step of EAdk in the reverse reaction measured as a function of different divalent metals. The rate constant shown for Mg2+ is a lower limit. (b) 15N-TROSY CPMG relaxation dispersion profiles of EAdk with Mg2+ (blue) or Ca2+ (purple). (c) Active-site electrostatic potential computed from representative structures extracted from the MD simulations with (top) or without (bottom) Mg2+, plotted on a plane cutting through the active site. (d) The distribution of the electrostatic interaction energy between the ADP molecules and R124 and R150 is plotted for four MD simulations with and without Mg2+. The histograms show the electrostatic interaction energies computed for configurations evenly distributed in time along the trajectories. (e,f) The two molecules in the asymmetric unit of AAdk R150K with ADP bound (blue and green) are superimposed with WT AAdk (gray). (g) 15N-TROSY CPMG relaxation dispersion at 25 °C on the EAdk R150K mutant saturated with 20 mM nucleotides. Dispersion curves for residues sensitive to lid-opening/closing in the presence of Mg2+ (red) are fully suppressed in the absence of Mg2+ (orange). Uncertainties (s.d.) in R2eff (b,g) were estimated from the variance for a number of non-exchanging peaks (n = 7).
We note that the lid-opening rates of AAdk without Mg2+ were too slow to be measured by 15N-CPMG relaxation dispersion experiments45; therefore, EAdk was used for all kinetic and NMR experiments.
A conserved arginine accelerates P-transfer 103-fold
In an effort to inventory the contribution of other players in lowering the energy barrier of catalysis, we focused our attention on the conserved active-site R150. We have already seen that this residue is flexible and mirrors the donor phosphoryl group position (Fig. 1b). Mutation of R150 has previously been shown to drastically inhibit the rate of enzyme turnover46. A comparison between the X-ray crystal structures of wild-type (WT) AAdk (AAdk1) and R150K mutant (AAdk9–10) shows that this mutation disrupts the hydrogen bonding between R150 and the donor β-phosphate. This implies that a specific coordination of the bidentate guanidinium group of the arginine side chain to the transferring phosphoryl group, rather than a positive charge, is needed to position the reactants for catalysis (Fig. 5e,f). By quantifying the change in the P-transfer and lid-opening rates for the EAdk R150K mutant (numbering refers to AAdk, see Supplementary Fig. 3a) we found that this arginine residue has a 103-fold effect on P-transfer but negligible effect on lid-opening (Fig. 5g, Supplementary Fig. 5, Table 2, Supplementary Table 2, and Suppl. Notes 3 and 4). The total acceleration from Mg2+ and R150 together was therefore larger than 108-fold on the rate of P-transfer (Table 2).
DISCUSSION
Our results reveal how Adks accelerate the rate of P-transfer (kchem >500 s−1) by more than 14 orders of magnitude relative to the uncatalyzed reaction (3.9·10−12 s−1)6 while minimizing the hydrolysis side reaction. We find that Mg2+ specifically accelerates P-transfer (>105-fold) by reducing non-productive active-site fluctuations (Fig. 2a,b), stabilizing an architecture resembling the TS, and serving as an anchor to the phosphoryl group pivoting between donor and acceptor nucleotides (Fig. 1e). In addition, the Mg2+ cofactor accelerated lid-opening (103-fold) by weakening the strong electrostatic interactions of the closed quaternary complex (Fig. 5c,d). The multiple catalytic roles for Mg2+ is remarkable considering that P-transfer and lid-opening are very different molecular events: one involves a subtle, 2 Å transfer of a phosphoryl group and the other a large-scale, coordinated motion of domains. In contrast, non-enzymatic P-transfer was only accelerated 10-fold by Mg2+ 6, highlighting the evolutionary impact of this highly charged and abundant cation on the enzyme’s energy landscape. R150 contributed an additional 103-fold acceleration to the phosphoryl-transfer step (Table 2) on top of the large acceleration provided by converting a bimolecular reaction in solution to a unimolecular one with a preferred active-site geometry47. Our results rule out a previously proposed mechanism of activation of Adk by direct binding of a second Mg2+ 19; their data can be fully explained by our model and the well-known KD of Mg2+ to nucleotides.
We note that there is extensive literature on Adks, and kinases in general, that can be confusing and contradictory because enzyme catalysis is often reduced to an observed rate constant (kcat/KM) that is a convolution of multiple reaction steps. This has contributed to mechanistic misinterpretations because critical conformational motions are often hidden and therefore ignored. The importance of characterizing kinase catalysis in molecular detail has been emphasized many times5,16,46, but has unfortunately lagged far behind our understanding of non-enzymatic P-transfer5. Here we have quantified the microscopic states along the Adk energy landscape (Fig. 1a and Table 2) by analyzing the enzyme during catalysis which sheds light onto long-standing controversies and provides a general framework for understanding the role of divalent metals and conformational changes in kinase function13. However, we prefer to avoid speculation about associative versus dissociative transition states in enzymatic phosphoryl transfer.
We have characterized the free-energy landscape of catalysis and quantified the energetic contributions of individual players to each microscopic step. Our experiments reveal the catalytic strategies Adks use to both pre-organize the active site for P-transfer and destabilize the quaternary complex for efficient product release. As was elegantly demonstrated by Mayo and collaborators, the principles of reducing unproductive active-site fluctuations and minimizing solvent accessibility is essential to improve the design of enzymes48. However, despite remarkable progress48-51, nature’s enzymes remain far superior highlighting the urgent need to understand the entire energy landscape of enzymatic catalysis.
A complete description of the tremendous rate acceleration achieved by biological catalysts continues to be a captivating topic in biology38,52-55. A large number of X-ray structures of active complexes, detailed kinetic characterizations, and computational studies on kinases have been reported and may lead to the assumption that little is left to be discovered about kinase function. However, the understanding of free-energy landscapes underlying the impressive acceleration of P-transfer by kinases has been limited. For hydrogen-transfer enzymes, the role of active-site pre-organization and conformational sampling in catalysis has been extensively investigated38,53-56. It has been 27 years since Fierke and coworkers quantified the microscopic steps of the dihydrofolate reductase (DHFR) energy landscape57, and the exquisite distance sensitivity of hydride transfer continues to make this and similar systems attractive for studies of enzyme catalysis54. We hope that the comprehensive catalytic framework described here for Adk will provide a similar foundation for understanding the catalytic power of one of the most important classes of enzymes, kinases.
ONLINE METHODS
X-ray crystallography structure determination
For crystallization, Aquifex aeolicus adenylate kinase (AAdk1–8,11) and its R150K mutant (AAdk9–10) were expressed and purified as described before 44.
AAdk crystals were grown at 18 or 22 °C with 20–50 mg/mL protein in the following conditions: 20 mM MgCl2, 20 mM ADP, and 25 mM in citric acid at pH 4.6 (AAdk1); 25 mM MgCl2, 25 mM ATP, 25 mM AMP, and 20 mM Tris-HCl at pH 7.4 (AAdk2); 35 mM ADP and 20 mM citric acid at pH 4.6 (AAdk3); 38 mM MgCl2, 38 mM ADP, and 20 mM MES at pH 5.0 (AAdk4); 22 mM AMPPNP and 20 mM MES at pH 5.0 (AAdk5); 15 mM MgCl2, 15 mM ADP, and 20 mM Tris-HCl at pH 7.0 (AAdk6); 17.3 mM ADP, 41.2 mM CoCl2, and 20 mM Tris-HCl at pH 7.4 (AAdk7); 25 mM ADP, 20 mM MgSO4, and 20 mM AlFx (AAdk8); 20 mM ADP, 20 mM MgCl2, and 20 mM Tris-HCl at pH 7.0 (AAdk9–11). All complexes were mixed with the crystallization solution that contains 0.1 M sodium acetate trihydrate (pH 4.6), 0.2 M ammonium acetate, and 30% (w/v) polyethylene glycol 4000 in a 1:1 (v/v) ratio.
During the growth of AAdk5 crystals with AMPPNP, the AMPPNP analogue hydrolyzed to AMPPN. Since the electron density of AMPPN’s nitrogen is indistinguishable from the density of ADP’s oxygen, we used ADP for modeling. For AAdk8 crystals, AAdk was premixed with ADP and incubated for one week before addition of 20 mM MgSO4 and AlFx [from the mixture of Al(NO3) · 9 H2O and NaF]. After another day of incubation, crystal trays were set up with aforementioned conditions and crystals were grown for another week. We note that this structure has a minor occupancy of ADP–ADP in the active site, but due to low occupancy we did not refine it further and only Mg2+–ADP–AMP–AlF4− was used for modeling. For AAdk11, crystals were soaked in crystallization solution where the pH had been raised to pH 9 after the addition of 20 mM Mg2+. We note that for AAdk11 there is ~25% AMP occupancy in the AMP lid.
Diffraction data were collected at 100 K at the Advanced Light Source (Lawrence Berkeley National Laboratory) beamline 8.2.1 for AAdk2–3,5, 8–11 and beamline 8.2.2 for AAdk4,6–7. Diffraction data for AAdk1 were collected at 100 K at and the Advanced Photon Source beamline 23ID-B. The details of the data collection are listed in Table 1.
Data were processed, scaled, phased, and refined using iMOSFLM 58, Scala 59, Phaser 60, and REFMAC5 61 in CCP4 62. The space groups were determined by Pointless59 and are identical for all data sets: P212121. The AAdk structure (PDB 2RGX43) without ligand was used as the search model for molecular replacement. Initial refinement was carried out, followed by manual rebuilding in Coot 63,64, and further iterative refinements were carried out using PHENIX 65 (except for AAdk11 where REFMAC5 was used). Hydrogen atoms were added and refined as isotropic for the AAdk1 and AAdk8 models while other models do not include protons. For data sets with an atomic resolution better than 1.7 Å (except for AAdk11), the individual anisotropic ADP refinement method was applied. The final structural models of each data set were validated using the tools available in PHENIX (phenix.model_vs_data) 66 or CCP4. The collection wavelengths for AAdk1–6,8–11 were between 0.973900 and 1.00001 Å.
For AAdk1–6 and AAdk8–11, there were no residues in the disallowed regions of the Ramachandran plot while the lowest percentage of favorable Ramachandran angles was 98.76% for AAdk6. The highest percentage of rotamer outlier for these data sets was also for AAdk6 with 2.26% of residues.
For AAdk7 crystals, the diffraction data were collected at the Cobalt absorption edge (λ=1.608600 Å). The anomalous scattering was identified by running Phaser-EP in PHENIX. In MR-SAD phasing mode, a refined protein model from Phaser and REFMAC5 was used as partial model for detecting the anomalous peak positions. The anomalous difference map confirms the location of cobalt in the active site. Not only Co2+ atoms, but also the location of the P and S atoms could be confirmed and are consistent with anomalous scattering at this wavelength. While fixing the Co2+ atom based on the anomalous peak position, further refinements were carried out. The occupancy of cobalt was not full, albeit cobalt in the active site of chain A displayed anomalous scattering up to 17 sigma level. The anomalous multiplicity for the AAdk7 refinement was 7.2 (6.7) and the anomalous completeness was 99.4% (96.4%). For this data set, 0.74% and 96.03% of residues were in the disallowed and favorable regions of the Ramachandran plot, respectively. In addition, 4.53% of AAdk7 residues were in rotamer outlier configurations.
For AAdk11 crystals, the presence of Mg2+ in the active site of chain B was established from the electron density and in addition from the perfect six-fold coordination of nearby water molecules and the nucleotides. Moreover, the Mg2+ position is in agreement with the position in the AAdk8 structure and the anomalous density in the Aadk7 Co2+-structure. We note that there is partial occupancy of ~25% AMP in the donor site in chain B. In chain A, we did not model a Mg2+ as little electron density is seen in this site and the coordination to the nearby water molecules is not perfect, very similar to what is observed in the crystal structures AAdk1–8 where no Mg2+ is present.
Structural alignments were done using maximum likelihood algorithms implemented in the program “theseus”, which produces more accurate results compared to conventional least-square criteria67.
Molecular Dynamics Simulations
The A molecule of the AAdk1 crystal structure (see Table 1) in complex with two ADP molecules was used as an initial model for all atom classical molecular dynamics (MD) simulations. Parameterization was performed with the CHARMM 22-protein all-atom force field with the CMAP backbone energy correction included 68,69 using the program CHARMM 70. The parameters for the bound ADP molecules, singly protonated on the terminal phosphates, were derived by combining parameters for a fully charged ADP and for inorganic phosphate PO4H2− included in the standard force field 71. The system was solvated in a truncated octahedral TIP3P 72 water box using the software Solvate (http://www.mpibpc.mpg.de/home/grubmueller/downloads/solvate/index.html) and CHARMM 70.
Note on the choice of a classical treatment for the active site: a complete quantitative understanding of the impact of the magnesium ion on the catalyzed reaction may require an accurate quantum-mechanical description of the active site region 73-76. However, the size of the system, the timescale of the dynamical properties under study, and the difficulties in the characterization of precise structural and geometrical properties of the active site in terms of the magnesium ion positioning and protonation states of the ADP nucleotides, make a direct quantum-mechanical approach infeasible without a previous mechanistic exploration at classical level 77,78. Furthermore, even though the classical nonpolarizable force-fields with fixed atom charges have limited accuracy, they have been successfully applied to similar metal ion and/or nucleotide dependent problems 79-81. A quantitative QM investigation of the catalyzed chemical step of the phosphoryl-transfer reaction is currently underway, but it is beyond the scope of the present study.
The simulation boxes for both systems, with and without the Mg2+ ion in the active site, were neutralized and then 50 mM NaCl was added using CHARMM 70. The solvated structures were minimized with the Conjugate Gradient method as implemented in NAMD 2.7b2 82, and then gradually heated to 300 K with a time step of 1 fs while gradually releasing positional restraints in a MD simulation of 2 ns. Periodic boundary conditions were applied to the simulation cell. Electrostatics were treated with the Particle Mesh Ewald scheme 83. The bonds of all hydrogens were constrained with the SHAKE algorithm 84. The structures were equilibrated for an additional 20 ns in the NPT ensemble (T = 300 K, P = 1.01325 bar) with the software NAMD 2.7b2. The temperature was controlled with the Langevin dynamics method 85 while keeping the pressure constant using the combined Langevin piston Nose-Hoover method 86,87 as implemented in NAMD 2.7b2.
Equilibrated structures were then converted to GROMACS 4.5.3 88 using a set of in-house scripts. For each of the two setups, with and without the Mg2+ ion bound to the active site, four independent replicas of 100 ns each were simulated in the NPT ensemble (T = 300 K,P = 1.01325 bar), constraining the hydrogen bond lengths with LINCS 89 and constraining the TIP3P waters with SETTLE90. The temperature was controlled with the Nose-Hoover thermostat 91,92 and pressure was controlled with the Parrinello-Rahman pressure coupling 93,94, as implemented in GROMACS 4.5.3. Four of the trajectories were further extended to 200 ns.
To define the protein cavities during the analysis of the water dynamics (see Fig. 2d and Supplementary Fig. 2) we used an algorithm based on the clustering of the alpha spheres 95 implemented in Fpocket 96. Fpocket relies on the Voronoi tassellation of space implemented in the software Qvoronoi (http://www.qhull.org/). The volume of the cavity and the water molecules present inside those cavities were determined using a set of scripts that can partition a complex geometry by defining a convex hull based on atomic positions (kindly provided by Dr. Patrick Varilly 97).
The calculations of the electrostatic potential (see Fig. 5c) have been performed using the software APBS 98 using the interface built into VMD 1.9 99. The linearized form of the Poisson-Boltzmann equation (LPBE) at 298.15 K was solved, placing the protein in a cubic box of size 80 Å and 129 grid points in each dimension. The solvent dielectric constant was set to 78.54. To account for the solution buffer, 50 mM monovalent positive and negative mobile ions were included in the calculation.
All trajectories were analyzed with the software VMD 1.9 99. The software Grace (http://plasma-gate.weizmann.ac.il/Grace) was used for the plots and Tachyon ray tracer (built into VMD 1.9, http://jedi.ks.uiuc.edu/~johns/raytracer) for the molecular renderings.
Pre-steady-state kinetics measurements
Pre-steady-state kinetics was measured using a 3-syringe rapid quench-flow apparatus RQF-3 (KinTek Corp). Protein solution was loaded into one of the syringes, nucleotides (ADP or AMP+ATP mixture with or without divalent ions) into the second syringe and quench solution (30% TCA + 6 M HCl mixture) was loaded into the third syringe. The reaction was initiated by a simultaneous push of all 3 syringes by a high-precision servo-motor. Required delay between the initial mixing of the regent and the following quench with acid was achieved by selecting aging loops of different length (which increases the path length for the acid component thus delaying the quench). The forward and reverse reactions were initiated by mixing ADK with AMP and ATP or ADP, respectively. The protein concentration in the syringe (before mixing) was varied between 40 and 1000 μM while the nucleotide concentration (in the syringe) was 8–32 mM, depending on the experiment. The buffer contained 100 mM Tris (pH 7.0), 80 mM KCl, and equimolar (with total concentration of nucleotides) concentration of Mg2+ or 50 mM EDTA. The temperature was controlled with a circulating water bath Isotemp 2150 Nano (Fisher Scientific) set to 25 °C unless specified otherwise.
The amount of product was quantified using high-pressure liquid chromatography (HPLC). Protein precipitated by quench was separated using Spin-X centrifugal tube filters (Costar), filtered supernatant was diluted to avoid HPLC detector saturation, and pH was brought to 6.0 to achieve optimal separation. The samples were analyzed on an HPLC system (Agilent Infinity 1260) with a high precision autosampler (injection error <0.1 μL), analytical HPLC column ACE (i.d. 2.4 mm, length 250 mm, C18-AR, 5 Å pore-size) and separated using isocratic elution with potassium phosphate mobile phase (100 μM, pH 6.0). Control experiments were performed to determine residual contamination in the commercially purchased ADP, ATP, and AMP stocks.
The rate constants of the phosphoryl transfer in the forward and reversed direction (kT.M.→D.D. and kD.D→T.M., respectively) reported in Table 2 were calculated considering a) the exponential phase of the forward reaction EATP.AMP → EADP.ADP, which is determined by the sum of the constants kT.M.→D.D. + kD.D.→T.M. and b) the on-enzyme equilibrium which gives the ratio between two the constants (kT.M.→D.D.) / (kD.D.→T.M.).
Lid-opening in the forward direction (opening out of the EADP.ADP state) can be determined directly from the slope of the linear phase in Fig. 3b, since the equilibrium is highly skewed towards EADP.ADP state.
Lid-opening in the reverse direction (opening out of the EATP.AMP state) cannot be directly read from the slope in Fig. 3c, since in this direction phosphoryl transfer is rate-limiting. Instead, one can calculate the lid-opening rate constant from the observed rate of phosphoryl transfer after accounting for the probabilities of opening and going back into EADP.ADP state. The rate constant can be calculated from the observed rate constant according to the following equation:
Time-correction procedure for very fast kinetics in the quench-flow experiments
Data obtained in the presence of Mg2+, Ca2+, or Co2+ (very fast kinetics) displayed unphysical amplitudes of the burst phase. The apparent amplitude was greater than the enzyme concentration, which indicated a discrepancy between the real quench delay and the delay value specified in the instrument. To take into account this apparent dead time of the instrument, data were corrected, using quenched-flow experiments performed in the forward and reverse directions. Instrumental delay calculations were based on the fact that the sum of the pre-steady-state bursts for forward and reversed reactions must be equal to the total enzyme concentration.
Experimental bursts can be found as:
where A′± are experimentally measured bursts in the forward and reverse direction, k± are kinetic rates in the forward and reverse direction, and A ± are «true» bursts in the forward and reverse direction.
Thus the delay time td is
Finally, the true experimental delay in the experimental data can be calculated as
where t′ is a delay without the dead-time correction.
All values reported in Table 2 were obtained from individual fits. Consistent results are also obtained through global fitting using KinTek Explorer, linking the values of all rate constants among the data sets including the values from in-solution and on-enzyme nucleotide equilibrium.
NMR Dynamics
15N-TROSY CPMG relaxation dispersion experiments 100 were collected on either Varian Inova 500 or 600 MHz or Bruker Avance 800 MHz (cryo-probe) spectrometers. Adk concentrations were usually 2 mM. Substrate saturation of Adk was achieved with 20 mM ADP in 100 mM HEPES, 50 mM NaCl (pH 7.0) and 5 mM TCEP. The concentration of divalent metal used in CPMG dispersion experiments was kept equimolar with the concentration of ADP. Sample measured in the absence of divalent metals were conducted in the presence of 5 mM EDTA.
Typical parameters for 15N-TROSY CPMG relaxation dispersion experiments were a 40 millisecond constant-time period; 2 second delay between transients; 12 different refocusing field strengths from 50 – 1000 Hz collected interleaved; with 1024 and 128 direct and indirect points, respectively; and 25 °C. For experiments conducted at 30 °C and 40 °C, the constant-time period was increased to 60 and 72 milliseconds, respectively.
Standard [1H-15N]-TROSY-HSQCs were always collected before and after the CPMG experiment to check sample stability. CPMG experiments usually took 2.5 days to complete. 15N-CPMG dispersions collected on the Avance 800 MHz were collected as downfield and upfield pairs to minimize off-resonance effects for the larger sweep-width and for lower 15N pulse powers required on cryoprobes.
Data was processed using the NMRPipe software suite 101 and visualized by either CCPN or NMRViewJ 102,103. Relaxation-dispersion profiles were calculated from peak intensities and analyzed with the general Carver-Richards equation for two-site exchange with in-house scripts 104-107. Uncertainties were estimated from the average variation in dispersion for residues not experiencing exchange together with the signal-to-noise ratio of each resonance to be analyzed. Global fit uncertainties were estimated by a jackknife method.
Steady-State Kinetics Measurements
Steady-state kinetics measurements were collected with 4 mM ADP and equimolar (with nucleotide) concentrations of divalent metal. The enzyme concentration was varied between 0.5 nM to 25 nM; buffer was 100 mM HEPES (pH 7.0) and 80 mM KCl; measurements were collected at room temperature. The amount of product produced over 16 min was quantified using high-pressure liquid chromatography (HPLC) as described above for pre-steady-state kinetics.
Supplementary Material
Acknowledgments
We are grateful to the staff at ALS/BCSB and APS for support, Y. Xiong, T. Lang, P. Afonine, R. Read, and mentors from the CCP4 School at APS (2011) for advice in the refinement of X-ray data, members of the C. Miller lab for handling crystals, the staff at the National Energy Research Scientific Computing Center, and K. A. Johnson for assistance with the KinTek Explorer software and fitting kinetic data.
We dedicate this manuscript to Tom Alber, a truly amazing and inspiring scientist and close friend who will live in our hearts forever. His creativity, joy and generosity deeply influenced the field of structural biology and several generations of scientists.
This work was supported by the Howard Hughes Medical Institute (HHMI), the Office of Basic Energy Sciences, Catalysis Science Program, US Department of Energy (award DE-FG02-05ER15699), the US National Institute of Health (RO1-GM100966), and by the Teragrid (XSEDE) allocation TG-MCB090166 (D.K.). R.O. is supported as a HHMI Fellow of the Damon Runyon Cancer Research Foundation (DRG-2114-12).
Footnotes
AUTHOR CONTRIBUTIONS
S.J.K, R.V.A, Y.J.C, D.V.P., F.P, M.F.H., and D.K. designed experiments; S.J.K., R.V.A., Y.J.C., F.P., R.O., D.V.P., L.A.P., and P.N.M. performed experiments; S.J.K, R.V.A, Y.J.C, F.P, R.O., D.V.P., S.K., L.A.P., P.N.M., V.T., T.A., and D.K. analyzed data; S.J.K., R.V.A., F.P., R.O., and D.K. wrote the manuscript.
ACCESSION CODES
BMRB (http://www.bmrb.wisc.edu): 19089, 19090, 19091, 19092, and 19093
PDB: 4JL5 (AAdk1), 4JLD (AAdk2), 4JLB (AAdk3), 4JL8 (AAdk4), 4JL6 (AAdk5), 4JLA (AAdk6), 4JKY (AAdk7), 3SR0 (AAdk8), 4JLO (AAdk9), 4JLP (AAdk10), 4CF7 (AAdk11)
REFERENCES FOR MAIN TEXT
- 1.Westheimer FH. Why nature chose phosphates. Science. 1987;235:1173–1178. doi: 10.1126/science.2434996. [DOI] [PubMed] [Google Scholar]
- 2.Bowler MW, Cliff MJ, Waltho JP, Blackburn GM. Why did Nature select phosphate for its dominant roles in biology? New Journal of Chemistry. 2010;34:784–794. [Google Scholar]
- 3.Schroeder GK, Lad C, Wyman P, Williams NH, Wolfenden R. The time required for water attack at the phosphorus atom of simple phosphodiesters and of DNA. Proceedings of the National Academy of Sciences of the United States of America. 2006;103:4052–4055. doi: 10.1073/pnas.0510879103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kamerlin SC, Sharma PK, Prasad RB, Warshel A. Why nature really chose phosphate. Q Rev Biophys. 2013;46:1–132. doi: 10.1017/S0033583512000157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lassila JK, Zalatan JG, Herschlag D. Biological phosphoryl-transfer reactions: understanding mechanism and catalysis. Annu Rev Biochem. 2011;80:669–702. doi: 10.1146/annurev-biochem-060409-092741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Stockbridge RB, Wolfenden R. The Intrinsic Reactivity of ATP and the Catalytic Proficiencies of Kinases Acting on Glucose, N-Acetylgalactosamine, and Homoserine A THERMODYNAMIC ANALYSIS. Journal of Biological Chemistry. 2009;284:22747–22757. doi: 10.1074/jbc.M109.017806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Jencks WP. Catalysis in chemistry and enzymology. Dover, New York: 1987. pp. xvi–836. [Google Scholar]
- 8.Knowles JR. Enzyme-catalyzed phosphoryl transfer reactions. Annual Review of Biochemistry. 1980;49:877–919. doi: 10.1146/annurev.bi.49.070180.004305. [DOI] [PubMed] [Google Scholar]
- 9.Cleland WW, Hengge AC. Enzymatic mechanisms of phosphate and sulfate transfer. Chemical Reviews. 2006;106:3252–3278. doi: 10.1021/cr050287o. [DOI] [PubMed] [Google Scholar]
- 10.Thatcher GRJ, Kluger R. Mechanism and Catalysis of Nucleophilic-Substitution in Phosphate-Esters. Advances in Physical Organic Chemistry. 1989;25:99–265. [Google Scholar]
- 11.Hunter T. Tyrosine phosphorylation: thirty years and counting. Curr Opin Cell Biol. 2009;21:140–146. doi: 10.1016/j.ceb.2009.01.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Jura N, et al. Catalytic control in the EGF receptor and its connection to general kinase regulatory mechanisms. Mol Cell. 2011;42:9–22. doi: 10.1016/j.molcel.2011.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Adams JA. Kinetic and catalytic mechanisms of protein kinases. Chemical Reviews. 2001;101:2271–90. doi: 10.1021/cr000230w. [DOI] [PubMed] [Google Scholar]
- 14.Endicott JA, Noble ME, Johnson LN. The structural basis for control of eukaryotic protein kinases. Annu Rev Biochem. 2012;81:587–613. doi: 10.1146/annurev-biochem-052410-090317. [DOI] [PubMed] [Google Scholar]
- 15.Henzler-Wildman K, Lei M, Thai V, Karplus M, Kern D. A hierarchy of timescales in protein dynamics linked to enzyme catalysis. 2007 doi: 10.1038/nature06407. [DOI] [PubMed] [Google Scholar]
- 16.Masterson LR, et al. Dynamics connect substrate recognition to catalysis in protein kinase A. Nat Chem Biol. 2010;6:821–8. doi: 10.1038/nchembio.452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Mukherjee K, Sharma M, Jahn R, Wahl MC, Sudhof TC. Evolution of CASK into a Mg2+-Sensitive Kinase. Science Signaling. 2010;3 doi: 10.1126/scisignal.2000800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bao ZQ, Jacobsen DM, Young MA. Briefly Bound to Activate: Transient Binding of a Second Catalytic Magnesium Activates the Structure and Dynamics of CDK2 Kinase for Catalysis. Structure. 2011;19:675–690. doi: 10.1016/j.str.2011.02.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Tan YW, Hanson JA, Yang H. Direct Mg2+ binding activates adenylate kinase from Escherichia coli. J Biol Chem. 2009;284:3306–13. doi: 10.1074/jbc.M803658200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Bhabha G, et al. Divergent evolution of protein conformational dynamics in dihydrofolate reductase. Nat Struct Mol Biol. 2013;20:1243–9. doi: 10.1038/nsmb.2676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Bhabha G, et al. A dynamic knockout reveals that conformational fluctuations influence the chemical step of enzyme catalysis. Science. 2011;332:234–8. doi: 10.1126/science.1198542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kamerlin SCL, Warshel A. At the dawn of the 21st century: Is dynamics the missing link for understanding enzyme catalysis? Proteins: Structure, Function, and Bioinformatics. 2009;9999 doi: 10.1002/prot.22654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Adamczyk AJ, Cao J, Kamerlin SC, Warshel A. Catalysis by dihydrofolate reductase and other enzymes arises from electrostatic preorganization, not conformational motions. Proc Natl Acad Sci U S A. 2011;108:14115–20. doi: 10.1073/pnas.1111252108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Nagel ZD, Klinman JP. A 21st century revisionist’s view at a turning point in enzymology. Nature Chemical Biology. 2009;5:543–550. doi: 10.1038/nchembio.204. [DOI] [PubMed] [Google Scholar]
- 25.Klinman JP, Kohen A. Hydrogen tunneling links protein dynamics to enzyme catalysis. Annu Rev Biochem. 2013;82:471–96. doi: 10.1146/annurev-biochem-051710-133623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Muller CW, Schlauderer GJ, Reinstein J, Schulz GE. Adenylate kinase motions during catalysis: An energetic counterweight balancing substrate binding. Structure. 1996;4:147–156. doi: 10.1016/s0969-2126(96)00018-4. [DOI] [PubMed] [Google Scholar]
- 27.Muller CW, Schulz GE. Structure of the Complex between Adenylate Kinase from Escherichia-Coli and the Inhibitor Ap5a Refined at 1.9 Å Resolution - a Model for a Catalytic Transition-State. Journal of Molecular Biology. 1992;224:159–177. doi: 10.1016/0022-2836(92)90582-5. [DOI] [PubMed] [Google Scholar]
- 28.Berry MB, Bae EY, Bilderback TR, Glaser M, Phillips GN. Crystal structure of ADP/AMP complex of Escherichia coli adenylate kinase. Proteins-Structure Function and Bioinformatics. 2006;62:555–556. doi: 10.1002/prot.20699. [DOI] [PubMed] [Google Scholar]
- 29.Berry MB, et al. The Closed Conformation of a Highly Flexible Protein - the Structure of Escherichia-Coli Adenylate Kinase with Bound AMP and AMPPNP. Proteins-Structure Function and Genetics. 1994;19:183–198. doi: 10.1002/prot.340190304. [DOI] [PubMed] [Google Scholar]
- 30.Cowan JA. Metal Activation of Enzymes in Nucleic Acid Biochemistry. Chemical Reviews. 1998;98:1067–1088. doi: 10.1021/cr960436q. [DOI] [PubMed] [Google Scholar]
- 31.Kladova AV, et al. Cobalt-, zinc- and iron-bound forms of adenylate kinase (AK) from the sulfate-reducing bacterium Desulfovibrio gigas: purification, crystallization and preliminary X-ray diffraction analysis. Acta Crystallogr Sect F Struct Biol Cryst Commun. 2009;65:926–9. doi: 10.1107/S1744309109029157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Wittinghofer A. Signaling mechanistics: aluminum fluoride for molecule of the year. Curr Biol. 1997;7:R682–5. doi: 10.1016/s0960-9822(06)00355-1. [DOI] [PubMed] [Google Scholar]
- 33.Coleman DE, et al. Structures of active conformations of Gi alpha 1 and the mechanism of GTP hydrolysis. Science. 1994;265:1405–12. doi: 10.1126/science.8073283. [DOI] [PubMed] [Google Scholar]
- 34.Sondek J, Lambright DG, Noel JP, Hamm HE, Sigler PB. GTPase mechanism of Gproteins from the 1.7-Å crystal structure of transducin alpha-GDP-AIF-4. Nature. 1994;372:276–9. doi: 10.1038/372276a0. [DOI] [PubMed] [Google Scholar]
- 35.Cliff MJ, et al. Transition state analogue structures of human phosphoglycerate kinase establish the importance of charge balance in catalysis. J Am Chem Soc. 2010;132:6507–16. doi: 10.1021/ja100974t. [DOI] [PubMed] [Google Scholar]
- 36.Baxter NJ, et al. Atomic details of near-transition state conformers for enzyme phosphoryl transfer revealed by rather than by phosphoranes. Proceedings of the National Academy of Sciences. 2010;107:4555. doi: 10.1073/pnas.0910333106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Baxter NJ, et al. Anionic charge is prioritized over geometry in aluminum and magnesium fluoride transition state analogs of phosphoryl transfer enzymes. J Am Chem Soc. 2008;130:3952–8. doi: 10.1021/ja078000n. [DOI] [PubMed] [Google Scholar]
- 38.Warshel A, et al. Electrostatic basis for enzyme catalysis. Chemical Reviews. 2006;106:3210–35. doi: 10.1021/cr0503106. [DOI] [PubMed] [Google Scholar]
- 39.Armstrong RN, Kondo H, Kaiser ET. Cyclic AMP-dependent ATPase activity of bovine heart protein kinase. Proc Natl Acad Sci U S A. 1979;76:722–5. doi: 10.1073/pnas.76.2.722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Prowse CN, Lew J. Mechanism of activation of ERK2 by dual phosphorylation. Journal of Biological Chemistry. 2001;276:99–103. doi: 10.1074/jbc.M008137200. [DOI] [PubMed] [Google Scholar]
- 41.Wang Y, Gan L, Wang E, Wang J. Exploring the dynamic functional landscape of adenylate kinase modulated by substrates. J Chem Theory Comput. 2012;9:84–95. doi: 10.1021/ct300720s. [DOI] [PubMed] [Google Scholar]
- 42.Gur M, Madura JD, Bahar I. Global transitions of proteins explored by a multiscale hybrid methodology: application to adenylate kinase. Biophys J. 2013;105:1643–52. doi: 10.1016/j.bpj.2013.07.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Henzler-Wildman KA, et al. Intrinsic motions along an enzymatic reaction trajectory. Nature. 2007;450:838–44. doi: 10.1038/nature06410. [DOI] [PubMed] [Google Scholar]
- 44.Wolf-Watz M, et al. Linkage between dynamics and catalysis in a thermophilic-mesophilic enzyme pair. Nature Structural & Molecular Biology. 2004;11:945–949. doi: 10.1038/nsmb821. [DOI] [PubMed] [Google Scholar]
- 45.Palmer AG. NMR characterization of the dynamics of biomacromolecules. Chemical Reviews. 2004;104:3623–3640. doi: 10.1021/cr030413t. [DOI] [PubMed] [Google Scholar]
- 46.Yan HG, Tsai MD. Nucleoside monophosphate kinases: Structure, mechanism, and substrate specificity. Advances in Enzymology. 1999;73:103. doi: 10.1002/9780470123195.ch4. [DOI] [PubMed] [Google Scholar]
- 47.Page MI, Jencks WP. Entropic contributions to rate accelerations in enzymic and intramolecular reactions and the chelate effect. Proc Natl Acad Sci U S A. 1971;68:1678–83. doi: 10.1073/pnas.68.8.1678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Privett HK, et al. Iterative approach to computational enzyme design. Proc Natl Acad Sci U S A. 2012;109:3790–5. doi: 10.1073/pnas.1118082108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Rothlisberger D, et al. Kemp elimination catalysts by computational enzyme design. Nature. 2008;453:190–5. doi: 10.1038/nature06879. [DOI] [PubMed] [Google Scholar]
- 50.Kiss G, Celebi-Olcum N, Moretti R, Baker D, Houk KN. Computational enzyme design. Angew Chem Int Ed Engl. 2013;52:5700–25. doi: 10.1002/anie.201204077. [DOI] [PubMed] [Google Scholar]
- 51.Blomberg R, et al. Precision is essential for efficient catalysis in an evolved Kemp eliminase. Nature. 2013;503:418–21. doi: 10.1038/nature12623. [DOI] [PubMed] [Google Scholar]
- 52.Schwartz SD, Schramm VL. Enzymatic transition states and dynamic motion in barrier crossing. Nat Chem Biol. 2009;5:551–8. doi: 10.1038/nchembio.202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Benkovic SJ, Hammes-Schiffer S. A perspective on enzyme catalysis. Science. 2003;301:1196–202. doi: 10.1126/science.1085515. [DOI] [PubMed] [Google Scholar]
- 54.Klinman JP. An integrated model for enzyme catalysis emerges from studies of hydrogen tunneling. Chem Phys Lett. 2009;471:179–193. doi: 10.1016/j.cplett.2009.01.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Boehr DD, Dyson HJ, Wright PE. An NMR perspective on enzyme dynamics. Chemical Reviews. 2006;106:3055–79. doi: 10.1021/cr050312q. [DOI] [PubMed] [Google Scholar]
- 56.Rozovsky S, McDermott AE. The time scale of the catalytic loop motion in triosephosphate isomerase. Journal of Molecular Biology. 2001;310:259–70. doi: 10.1006/jmbi.2001.4672. [DOI] [PubMed] [Google Scholar]
- 57.Fierke CA, Johnson KA, Benkovic SJ. Construction and evaluation of the kinetic scheme associated with dihydrofolate reductase from Escherichia coli. Biochemistry. 1987;26:4085–92. doi: 10.1021/bi00387a052. [DOI] [PubMed] [Google Scholar]
- 58.Battye TG, Kontogiannis L, Johnson O, Powell HR, Leslie AG. iMOSFLM: a new graphical interface for diffraction-image processing with MOSFLM. Acta Crystallogr D Biol Crystallogr. 2011;67:271–81. doi: 10.1107/S0907444910048675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Evans P. Scaling and assessment of data quality. Acta Crystallogr D Biol Crystallogr. 2006;62:72–82. doi: 10.1107/S0907444905036693. [DOI] [PubMed] [Google Scholar]
- 60.McCoy AJ, et al. Phaser crystallographic software. J Appl Crystallogr. 2007;40:658–674. doi: 10.1107/S0021889807021206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Murshudov GN, et al. REFMAC5 for the refinement of macromolecular crystal structures. Acta Crystallogr D Biol Crystallogr. 2011;67:355–67. doi: 10.1107/S0907444911001314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Winn MD, et al. Overview of the CCP4 suite and current developments. Acta Crystallogr D Biol Crystallogr. 2011;67:235–42. doi: 10.1107/S0907444910045749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Emsley P, Cowtan K. Coot: model-building tools for molecular graphics. Acta Crystallogr D Biol Crystallogr. 2004;60:2126–32. doi: 10.1107/S0907444904019158. [DOI] [PubMed] [Google Scholar]
- 64.Emsley P, Lohkamp B, Scott WG, Cowtan K. Features and development of Coot. Acta Crystallogr D Biol Crystallogr. 2010;66:486–501. doi: 10.1107/S0907444910007493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Adams PD, et al. PHENIX: a comprehensive Python-based system for macromolecular structure solution. Acta Crystallogr D Biol Crystallogr. 2010;66:213–21. doi: 10.1107/S0907444909052925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Afonine PV, et al. phenix.model_vs_data: a high-level tool for the calculation of crystallographic model and data statistics. J Appl Crystallogr. 2010;43:669–676. doi: 10.1107/S0021889810015608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Theobald DL, Steindel PA. Optimal simultaneous superpositioning of multiple structures with missing data. Bioinformatics. 2012;28:1972–1979. doi: 10.1093/bioinformatics/bts243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.MacKerell AD, et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. Journal of Physical Chemistry B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 69.MacKerell A, Banavali N, Foloppe N. Development and current status of the CHARMM force field for nucleic acids. Biopolymers. 2000;56:257–265. doi: 10.1002/1097-0282(2000)56:4<257::AID-BIP10029>3.0.CO;2-W. [DOI] [PubMed] [Google Scholar]
- 70.Brooks BR, et al. Charmm - a Program for Macromolecular Energy, Minimization, and Dynamics Calculations. Journal of Computational Chemistry. 1983;4:187–217. [Google Scholar]
- 71.Pavelites J, Gao J, Bash PA, Mackerell AD. A molecular mechanics force field for NAD(+), NADH, and the pyrophosphate groups of nucleotides. Journal of Computational Chemistry. 1997;18:221–239. [Google Scholar]
- 72.Price DJ, Brooks CL. A modified TIP3P water potential for simulation with Ewald summation. Journal of Chemical Physics. 2004;121:10096–10103. doi: 10.1063/1.1808117. [DOI] [PubMed] [Google Scholar]
- 73.Gresh N, et al. Analysis of the Interactions Taking Place in the Recognition Site of a Bimetallic Mg(II)-Zn(II) Enzyme, Isopentenyl Diphosphate Isomerase. A Parallel Quantum-Chemical and Polarizable Molecular Mechanics Study. Journal of Physical Chemistry B. 2010;114:4884–4895. doi: 10.1021/jp907629k. [DOI] [PubMed] [Google Scholar]
- 74.Pontikis G, Borden J, Martinek V, Florian J. Linear Energy Relationships for the Octahedral Preference of Mg, Ca and Transition Metal Ions. Journal of Physical Chemistry A. 2009;113:3588–3593. doi: 10.1021/jp808928f. [DOI] [PubMed] [Google Scholar]
- 75.Yang SY, et al. Whether proton transition to the triphosphate tail of ATP occurs at protein kinase environment: A car-parrinello ab initio molecular dynamics study. International Journal of Quantum Chemistry. 2008;108:1239–1245. [Google Scholar]
- 76.Peters MB, et al. Structural Survey of Zinc Containing Proteins and the Development of the Zinc AMBER Force Field (ZAFF) J Chem Theory Comput. 2010;6:2935–2947. doi: 10.1021/ct1002626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Ditzler M, Otyepka M, Sponer J, Walter NG. Molecular Dynamics and Quantum Mechanics of RNA: Conformational and Chemical Change We Can Believe In. Accounts of Chemical Research. 2010;43:40–47. doi: 10.1021/ar900093g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Banas P, Jurecka P, Walter N, Sponer J, Otyepka M. Theoretical studies of RNA catalysis: Hybrid QM/MM methods and their comparison with MD and QM. Methods. 2009;49:202–216. doi: 10.1016/j.ymeth.2009.04.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Venkatramani R, Radhakrishnan R. Computational study of the force dependence of phosphoryl transfer during DNA synthesis by a high fidelity polymerase. Physical Review Letters. 2008;100 doi: 10.1103/PhysRevLett.100.088102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Banas P, Walter N, Sponer J, Otyepka M. Protonation States of the Key Active Site Residues and Structural Dynamics of the glmS Riboswitch As Revealed by Molecular Dynamics. Journal of Physical Chemistry B. 2010;114:8701–8712. doi: 10.1021/jp9109699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Khavrutskii I, Grant B, Taylor SS, McCammon JA. A Transition Path Ensemble Study Reveals a Linchpin Role for Mg2+ during Rate-Limiting ADP Release from Protein Kinase A. Biochemistry. 2009;48:11532–11545. doi: 10.1021/bi901475g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Schulten K, et al. Scalable molecular dynamics with NAMD. Journal of Computational Chemistry. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Darden T, York D, Pedersen L. Particle Mesh Ewald - an N.Log(N) Method for Ewald Sums in Large Systems. Journal of Chemical Physics. 1993;98:10089–10092. [Google Scholar]
- 84.Ryckaert J, Ciccotti G, Berendsen HJC. Numerical-Integration of Cartesian Equations of Motion of a System with Constraints - Molecular-Dynamics of N-Alkanes. Journal of Computational Physics. 1977;23:327–341. [Google Scholar]
- 85.Brünger AT. X-PLOR, Version 3.1 : a system for X-ray crystallography and NMR. Yale University Press; New Haven: 1992. pp. xvii–382. [Google Scholar]
- 86.Feller S, Zhang Y, Pastor RW, Brooks BR. Constant-Pressure Molecular-Dynamics Simulation - the Langevin Piston Method. Journal of Chemical Physics. 1995;103:4613–4621. [Google Scholar]
- 87.Martyna G, Tobias DJ, Klein ML. Constant-Pressure Molecular-Dynamics Algorithms. Journal of Chemical Physics. 1994;101:4177–4189. [Google Scholar]
- 88.Hess B, Kutzner C, van der Spoel D, Lindahl E. GROMACS 4: Algorithms for highly efficient, load-balanced, and scalable molecular simulation. Journal of Chemical Theory and Computation. 2008;4:435–447. doi: 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
- 89.Hess B, Bekker H, Berendsen HJC, Fraaije JGEM. LINCS: A linear constraint solver for molecular simulations. Journal of Computational Chemistry. 1997;18:1463–1472. [Google Scholar]
- 90.Miyamoto S, Kollman PA. Settle - an Analytical Version of the Shake and Rattle Algorithm for Rigid Water Models. Journal of Computational Chemistry. 1992;13:952–962. [Google Scholar]
- 91.Nose S. A Molecular-Dynamics Method for Simulations in the Canonical Ensemble. Molecular Physics. 1984;52:255–268. [Google Scholar]
- 92.Hoover WG. Canonical Dynamics - Equilibrium Phase-Space Distributions. Physical Review A. 1985;31:1695–1697. doi: 10.1103/physreva.31.1695. [DOI] [PubMed] [Google Scholar]
- 93.Parrinello M, Rahman A. Polymorphic Transitions in Single-Crystals - a New Molecular-Dynamics Method. Journal of Applied Physics. 1981;52:7182–7190. [Google Scholar]
- 94.Nose S, Klein ML. Constant Pressure Molecular-Dynamics for Molecular-Systems. Molecular Physics. 1983;50:1055–1076. [Google Scholar]
- 95.Liang J, Edelsbrunner H, Woodward C. Anatomy of protein pockets and cavities: Measurement of binding site geometry and implications for ligand design. Protein Science. 1998;7:1884–1897. doi: 10.1002/pro.5560070905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Le Guilloux V, Schmidtke P, Tuffery P. Fpocket: An open source platform for ligand pocket detection. Bmc Bioinformatics. 2009;10 doi: 10.1186/1471-2105-10-168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Patel A, Varilly P, Chandler D, Garde S. Quantifying Density Fluctuations in Volumes of All Shapes and Sizes Using Indirect Umbrella Sampling. Journal of Statistical Physics. 2011;145:265–275. doi: 10.1007/s10955-011-0269-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Baker N, Sept D, Joseph S, Holst MJ, McCammon JA. Electrostatics of nanosystems: Application to microtubules and the ribosome. Proceedings of the National Academy of Sciences of the United States of America. 2001;98:10037–10041. doi: 10.1073/pnas.181342398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Humphrey W, Dalke A, Schulten K. VMD: visual molecular dynamics. Journal of Molecular Graphics. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 100.Loria J, Rance M, Palmer AG. A TROSY CPMG sequence for characterizing chemical exchange in large proteins. Journal of Biomolecular NMR. 1999;15:151–155. doi: 10.1023/a:1008355631073. [DOI] [PubMed] [Google Scholar]
- 101.Delaglio F, et al. NMRPipe: a multidimensional spectral processing system based on UNIX pipes. J Biomol NMR. 1995;6:277–93. doi: 10.1007/BF00197809. [DOI] [PubMed] [Google Scholar]
- 102.Johnson BA, Blevins RA. NMR View: A computer program for the visualization and analysis of NMR data. Journal of Biomolecular NMR. 1994;4:603–614. doi: 10.1007/BF00404272. [DOI] [PubMed] [Google Scholar]
- 103.Vranken WF, et al. The CCPN data model for NMR spectroscopy: development of a software pipeline. Proteins: Structure, Function, and Bioinformatics. 2005;59:687–696. doi: 10.1002/prot.20449. [DOI] [PubMed] [Google Scholar]
- 104.Davis D, Perlman ME, London RE. Direct measurements of the dissociation-rate constant for inhibitor-enzyme complexes via the T1 rho and T2 (CPMG) methods. J Magn Reson B. 1994;104:266–75. doi: 10.1006/jmrb.1994.1084. [DOI] [PubMed] [Google Scholar]
- 105.Carver J, Richards R. A general two-site solution for the chemical exchange produced dependence of T2 upon the Carr-Purcell pulse separation. Journal of Magnetic Resonance (1969) 1972;6:89–105. [Google Scholar]
- 106.Jen J. Chemical exchange and NMR T2 relaxation—The multisite case. Journal of Magnetic Resonance (1969) 1978;30:111–128. [Google Scholar]
- 107.Millet O, Loria J, Kroenke C, Pons M, Palmer AG., III The static magnetic field dependence of chemical exchange linebroadening defines the NMR chemical shift time scale. Journal of the American Chemical Society. 2000;122:2867–2877. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


