Significance
Single-cell measurement technologies such as flow cytometry permit the investigation of specific cellular subpopulations. Mass cytometry currently measures >40 parameters per cell and produces phenotypically rich datasets that may be retrospectively interrogated for relevant biological signal. There are few methods that identify experimentally relevant subpopulations within these datasets, and most do not scale well to higher-dimensional measurements. To address this bottleneck, we present a data-driven method termed Citrus that identifies cell subsets associated with an experimental endpoint of interest. Citrus can test diverse experimental hypotheses and is demonstrated through the systematic identification of (i) blood cells that signal in response to experimental stimuli and (ii) T-cell subsets whose abundance is predictive of AIDS-free survival risk in patients with HIV.
Keywords: informatics, biomarker discovery
Abstract
Elucidation and examination of cellular subpopulations that display condition-specific behavior can play a critical contributory role in understanding disease mechanism, as well as provide a focal point for development of diagnostic criteria linking such a mechanism to clinical prognosis. Despite recent advancements in single-cell measurement technologies, the identification of relevant cell subsets through manual efforts remains standard practice. As new technologies such as mass cytometry increase the parameterization of single-cell measurements, the scalability and subjectivity inherent in manual analyses slows both analysis and progress. We therefore developed Citrus (cluster identification, characterization, and regression), a data-driven approach for the identification of stratifying subpopulations in multidimensional cytometry datasets. The methodology of Citrus is demonstrated through the identification of known and unexpected pathway responses in a dataset of stimulated peripheral blood mononuclear cells measured by mass cytometry. Additionally, the performance of Citrus is compared with that of existing methods through the analysis of several publicly available datasets. As the complexity of flow cytometry datasets continues to increase, methods such as Citrus will be needed to aid investigators in the performance of unbiased—and potentially more thorough—correlation-based mining and inspection of cell subsets nested within high-dimensional datasets.
Single-cell measurements have enabled the detailed investigation of cellular function, intracellular signaling networks, immune state, and the role of specific cellular subsets in disease. Specifically, the behavior of specific cellular subpopulations (i.e., subpopulation abundance or functional activity) has been shown to serve as a surrogate marker of disease status or to predict clinical outcome in many studies (1–5). Such subpopulations may be of interest for follow-up studies that aim to improve disease diagnosis or prognosis or to enable a better understanding of disease mechanism. Currently, fluorescence-based flow cytometers permit the concurrent measurement of 12–17 parameters per cell, whereas the next generation of mass cytometry platforms (CyTOF) has increased this number to >40 (6). Additionally, multiplexing techniques such as fluorescent and mass tag cell barcoding have enabled the concurrent robust measurement of samples subjected to dozens of experimental conditions (7).
With a continual increase in the number of simultaneously measurable parameters by flow cytometry, experimental complexity, and number of samples measured in disease studies, there is an urgent need for methods that enable intersample-group analyses, multivariate effects, and identification of rare cell subsets with novel behaviors. For instance, many flow cytometry experiments seek “stratifying” subpopulations of cells whose abundance or behavior is correlated with a known endpoint of interest (e.g., subpopulations whose behavior is predictive of sample disease state, sensitivity to drug therapy, or patient outcome). However, there are currently few methods for automatically identifying such relevant populations in datasets of the complexity and size that can be produced with CyTOF and related high-parameter platforms. Where—and how—in high-dimensional space does one begin to search for changes induced by experimental perturbations?
Historically, approaches to identifying stratifying cellular subpopulations have relied on manual identification (gating) of cell subsets within each sample. Gating is typically followed by domain knowledge-driven quantitation and comparison of various population properties between sample groups (for instance, response to therapy or nonresponsiveness). However, manual examination is labor-intensive and has been shown to be subjective (8), resulting in a nonexhaustive analysis that does not scale in circumstances with a large number of patient samples or experimental conditions.
Many methods have been developed that attempt to automate various stages of the manual analysis pipeline. For instance, a variety of automated gating approaches were developed to ease the bottleneck of manual gating. Methods use various strategies for identifying cell subsets, including nonparametric clustering (9–11), model-based approaches (12–14), density-based methods (15–17), and combinations thereof (18). However, estimating the true number of clusters in a dataset remains a challenge for these methods (SI Appendix, Fig. S10), and many (i.e., binning and model-based approaches) do not scale well to higher-dimensional data. Another class of methods, such as those featured in the Flow Cytometry: Critical Assessment of Population Identification Methods II (FlowCAP-II) competition, automate the task of predicting the disease state of an unanalyzed flow cytometry sample by using classification models trained on previously annotated samples (19). Many of these approaches rely on nonregularized classification models such as support vector machines that are difficult to interpret. Consequently, formulation of biological hypotheses from the constructed model can be challenging. Most recently, Aghaeepour et al. described a method—termed “flowType”—that automatically identifies subsets of cells correlated with patient outcome (20). In their work, Aghaeepour et al. use flowType with flowMeans clustering to identify many cellular subsets in a cohort of HIV-infected patients. A Cox proportional-hazards model was then used to identify which cell subsets’ abundance was correlated with patient AIDS-free survival time. For cells measured by using a panel of n markers, flowType examines all 3n permutations of cell subsets defined by positive, negative, or neutral combinations of measured markers, making it infeasible for use with higher-dimensional datasets (i.e., 30 parameters).
To address issues of scalability, subjectivity, sensitivity, and model cell subset correlations with outcome, we developed an automated, data-driven method for identifying stratifying cell subsets (termed here as Citrus). Given cytometry data from many samples and an endpoint of interest for each sample (e.g., good or poor patient outcome, patient survival time), Citrus identifies clusters of phenotypically similar cells in an unsupervised manner, characterizes the behavior of identified clusters by using biologically interpretable metrics, and leverages regularized supervised learning algorithms to identify the subset of clusters whose behavior is predictive of a sample’s endpoint. While requiring minimal expertise and input to operate, Citrus produces a list of stratifying clusters and behaviors, plots conventional biaxial or other data representations describing the phenotype of each cluster, and provides a predictive model that can be used to analyze newly acquired or validation samples.
Herein, Citrus is described in the context of its application to a synthetic dataset, used to detect known biological responses in stimulated healthy blood samples after stimulation compared with control, evaluated on publicly available datasets, and compared with existing methods.
Results
Summary of Citrus.
Citrus begins by identifying clusters of phenotypically similar cells in all samples in an unsupervised manner. To facilitate equal representation of samples and decrease compute time, Citrus randomly selects a user-specified number of cells from all sample files and combines them into a single representative dataset (Fig. 1, i). Clusters of cells in the aggregate data are identified by hierarchically clustering cell events based on marker similarity (Fig. 1, ii). Citrus is predicated on an assumption that physiologically or clinically relevant cell populations that are representative of a given phenotype will be seen as robustly recurring events in the aggregate data. Citrus by default conservatively specifies that clusters of interest must contain at least 5% of measured events. All cell clusters identified in the clustering hierarchy larger than this minimum cluster-size threshold (MCST) are marked for subsequent analysis, thus permitting cells to be assigned to multiple clusters that are part of a given hierarchy (SI Appendix, section S1.2). The MCST may be changed based on prior knowledge of cellular abundances (stem cell abundance, for instance).
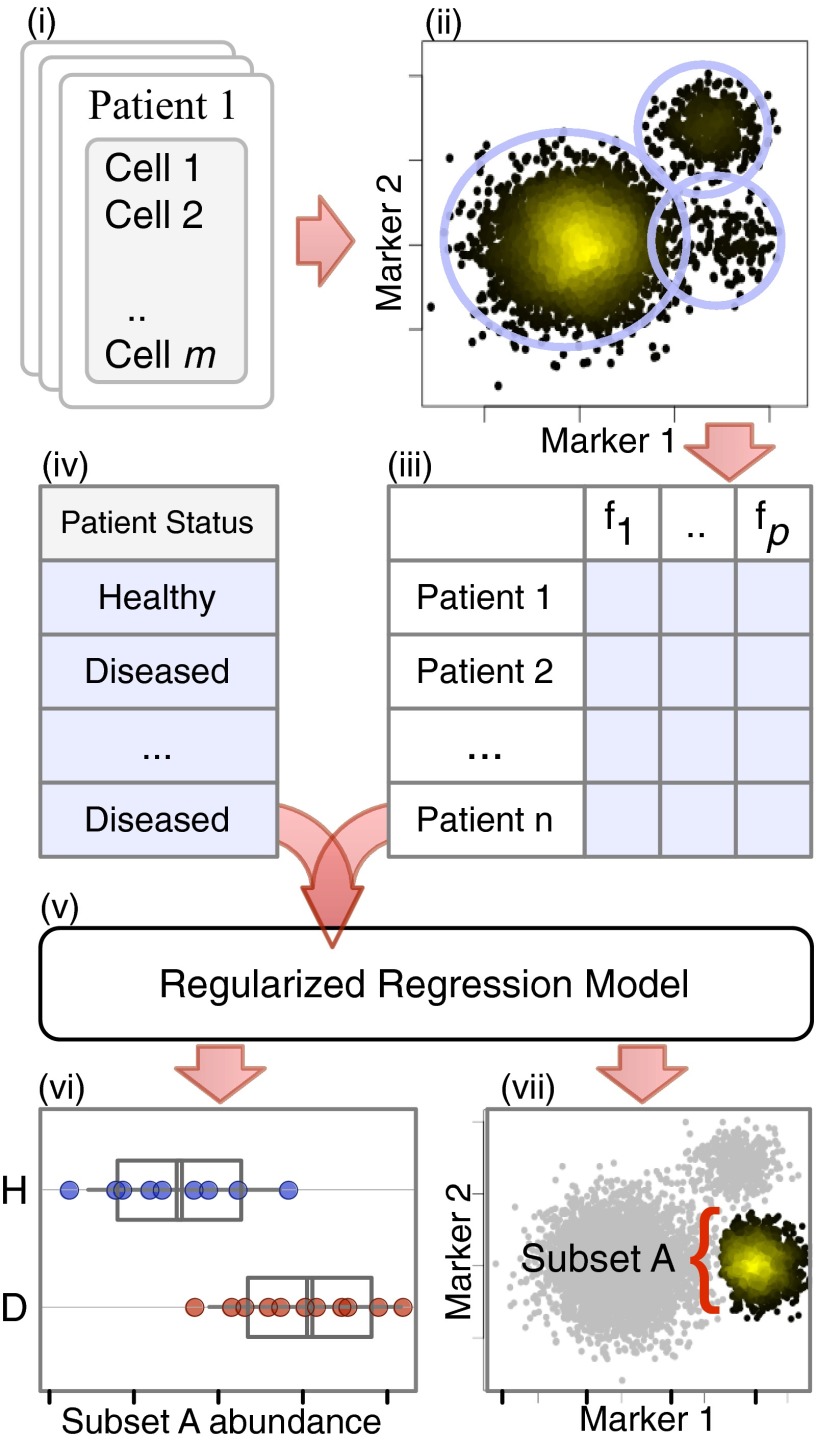
Fig. 1.
Overview of Citrus. Cells from all samples (i) are combined and clustered by using hierarchical clustering (ii). Descriptive features of identified cell subsets are calculated on a per-sample basis (iii) and used in conjunction with additional experimental metadata (iv) to train a regularized regression model predictive of the experimental endpoint (v). Predictive subset features are plotted as a function of experimental endpoint (vi), along with scatter or density plots of the corresponding informative subset (vii). In this example, the abundance of cells in subset A was found to differ between healthy and diseased samples (vi; H, subset A abundance in healthy patients; D, subset A abundance in diseased patients). Scatter plots show that cells in subset A have high expression of marker 1 and low expression of marker 2 relative to all measured cells (shown in gray).
Citrus next splits the combined clustered data back into individual sample components and calculates features that describe each cluster on a per-sample basis. These features include the proportion of a sample’s cells in each cluster, the median level of each functional marker in a cluster of cells, and the difference in these values across multiple experimental conditions (if measured) (Fig. 1, iii).
Citrus uses regularized supervised learning algorithms to identify stratifying clusters and cell response features that are the best predictors of a known experimental endpoint of interest (Fig. 1, iv and v). For intergroup analyses, a regularized classification model is trained to predict the known experimental group of each sample (e.g., healthy patients or diseased patients). By definition, the regularized model automatically identifies the subset of cluster features that best predict a sample’s group—thus revealing clusters of cells with stratifying behaviors within the dataset. Citrus estimates, and then plots, the accuracy of the classification model via cross-validation, thus enabling the investigator to assess the quality of the results (SI Appendix, section S1.2 and Fig. S7). The values of stratifying features are then plotted on a per-group basis (Fig. 1, vi). The marker expression phenotype of each relevant cell cluster is then plotted (Fig. 1, vii).
Prior knowledge suggests that most cluster-calculated features will not be good predictors of a sample’s group. Accordingly, Citrus constructs classification models using the lasso-regularized logistic regression and nearest shrunken centroid methods (21, 22). In general, both of these methods construct classification models from automatically selected subsets of informative features and restrict the number of model regressors by applying a regularization penalty, λ, for each feature included in the model. In practice, the number of predictive features selected by a model is inversely proportional to the regularization threshold. Because the true number of informative features in the data is unknown to the user a priori, a series of models with increasing complexity is constructed by using a range of regularization thresholds, and the error rates of these models are estimated by using K-fold cross-validation. After cross-validation, Citrus generates a plot showing the fit of all models as a function of the regularization threshold, allowing the investigator to readily identify models having a low and/or acceptable error rate.
Validation of Citrus by Analysis of BCR/FCR Cross-Linked Peripheral Blood Mononuclear Cells.
To demonstrate analytical capabilities, Citrus was applied to laboratory data from Bodenmiller et al. (7). Specifically, Citrus was used to identify subsets of peripheral blood mononuclear cells (PBMCs) that responded to B-cell receptor (BCR)/Fc receptor (FCR) cross-linking compared with PBMCs without treatment. Data consisted of 16 samples of PBMCs from eight healthy donors, 8 of which were unstimulated and 8 of which were stimulated with BCR/FCR cross-linker for 30 min before measurement (SI Appendix, section S1.1) (7). Each sample was analyzed by quantifying a panel of 10 cell-type (lineage) and 14 intracellular functional markers (Table 1). Based on maps of signaling pathways downstream of the BCR/FCR, we hypothesized that, relative to unstimulated samples, stimulated samples would contain subsets of B cells with activated BCR pathway proteins, such as Bruton's tyrosine kinase (BTK), extracellular signal-regulated kinase (ERK), phospholipase C isoform 2 (PLCγ2), and ribosomal protein S6 (S6), as well as subsets of activated FCR-expressing monocytes (23).
Table 1.
Summary of markers measured in healthy PBMCs
| Marker type | Measured marker |
| Lineage | CD45, CD4, CD20, CD33, CD123, CD14, IgM, HLA-DR, CD7, CD3 |
| Functional | pNF-κB (pS529), pp38 (pT180/pY182), pSTAT5 (pY694), pAKT (pT308), pSTAT1 (pY701), pSHP2 (pY580), pZAP70/pSYK (pY319/pY352), pSTAT3 (pY705), pSLP76/pBLNK (pY128/pY72), pBTK/pITK (pY551/pY511), pPLCγ2 (pY759), pERK1/2 (pT202/pY204), pLAT (pY226), pS6 (pS235/pS236) |
Citrus randomly selected up to 5,000 cell events from each sample based on data availability, combined them, and clustered the aggregate data based on lineage marker similarity, resulting in the identification of 75,576 cellular clusters. For this proof-of-concept analysis, a MCST of 5% was specified, meaning that that subsets of interest must contain a minimum of 5% of measured events. This conservative threshold was selected to constrain output to a small set of results. A total of 31 clusters, each containing at least 3,700 cells (5% of the number of events in the aggregated dataset) were retained by Citrus for further analysis. Citrus characterized the behavior of each cluster by calculating cluster functional marker medians on a per-sample basis, resulting in a total of 465 descriptive cluster features for each sample.
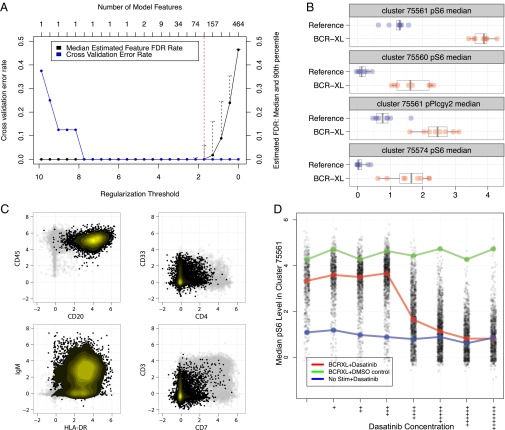
Cluster features were used to train a nearest shrunken centroid classifier of the sample’s simulation group (stimulated or unstimulated) at a range of regularization thresholds. Cross-validation and permutation tests were used to estimate and plot the classification error rates and feature false discovery rates (FDRs) of each model, respectively (Fig. 2A).
Fig. 2.
Identification of stratifying cell subsets between unstimulated and BCR/FCR cross-linked PBMCs. (A) Estimated model accuracy and feature FDRs as a function of model regularization threshold. The regularization threshold selected to constrain the final model is shown by the dotted red line. (B) The first 4 of 117 identified stratifying features between the unstimulated and stimulated samples. Levels of phosphorylated S6 in cluster 75561 were found to be the best predictor of sample stimulation group. All stratifying features and corresponding clusters are shown in SI Appendix, Figs. S1 and S2. (C) Scatter plots showing lineage marker values from cells in cluster 75561. Expression of the same lineage markers in all other cells is shown in gray. High expression of CD45, CD20, and HLA-DR combined with low expression of CD7 and CD3 indicate that cluster 75561 comprises B cells. (D) S6 phosphorylation levels as a function of dasatinib concentration in cluster 75561. S6 phosphorylation induced by BCR/FCR cross-linking was reduced to baseline levels by dasatinib in a dose-dependent manner.
To determine all cluster features that differed between stimulated and unstimulated samples, error plots produced by Citrus were used to identify the smallest regularization threshold that produced a model with perfect cross-validation accuracy and an estimated feature FDR of <1%. Citrus used this regularization threshold to constrain a final classification model constructed from all samples. From an original set of 465 cluster features, the final regularized model identified a subset of 117 that differed between the two stimulation conditions (SI Appendix, Figs. S1 and S2).
Stratifying cell subsets in PBMCs.
Of the 117 identified stratifying features, the median level of phosphorylated S6 in cluster 75561 was the best predictor of the sample stimulation group (Fig. 2B). Cluster 75561 was found to be enriched for markers CD20, CD45, and HLA-DR, but not CD3, CD7, or CD4 (Fig. 2C). This result conforms to expectations for a cell subset comprising primarily B cells; this observation was further confirmed by manual gating. As expected, activation of proteins downstream of the BCR in a population of B cells is a consequence of BCR cross-linking, thus confirming the ability of Citrus to reidentify known stratifying signals in a canonical cellular population. Compared with the expert-driven efforts of manual population identification and inspection used by Bodenmiller et al. (7), Citrus was able to identify this relevant population and stratifying response among hundreds of potentially informative signals without prior knowledge of B-cell biology.
Further inspection of additional stratifying subsets revealed phosphorylation of S6, ERK, and PLCγ2 in B cells, as well as S6 in HLA-DR+ monocytes (cluster 75560). Results were consistent with existing knowledge of intracellular signaling networks and were also reported by Bodenmiller et al. (7). Additionally, Citrus detected an unexpected but systematic change in levels of phosphorylated NF-κB p65 in all cells and subtle but consistent differences in phosphorylated BTK and SLP76 levels in many cell populations that would not normally be expected to respond to BCR cross-linking (SI Appendix, Figs. S1 and S2). Although responses to cross-linking in BCR/FCR-expressing populations would be expected and likely identified by an investigator performing a manual analysis, the unexpected and sometimes subtle changes of phosphorylated NF-κB p65, BTK, and SLP76 levels in off-target populations could potentially go unnoticed when manually inspecting data.
Validation of stratifying responses.
Stratifying signals identified using Citrus were validated by measuring the effect of dasatinib, a tyrosine kinase inhibitor, on putative cross-linker–induced phosphorylation events. Additional experimental data from Bodenmiller et al., including measurements from stimulated and unstimulated samples in the presence of dimethyl-sulfoxide or dasatinib, were mapped to stratifying cell subsets identified by Citrus (SI Appendix, section S1.2). Median phosphoprotein levels in each cell subset were calculated in the presence of increasing concentrations of dasatinib (Fig. 2D).
Dasatinib reduced levels of phosphorylated pS6, pERK, pAKT, and pPLCγ2 in B-cells (cluster 75561) and pS6 in HLA-DR+ monocytes (cluster 75560) in a dose-dependent manner, confirming that phosphorylation events in these cell subsets were induced by BCR/FCR cross-linking (SI Appendix, Fig. S15). Levels of phosphorylated BTK, SLP76, and NF-κB p65 in off-target populations were found to be experimental artifacts introduced by multiplexing protocols and were not affected by dasatinib. Thus, an unbiased identification of stratifying signals across all cell subsets revealed both expected biological and unexpected experimental effects. These stratifying signals could enable investigators to develop biological hypotheses for follow-up studies and, in this circumstance, allow the user to improve experimental protocols accordingly.
Evaluation of Citrus vs. Existing Methods.
The performance of Citrus was compared with existing computational methods by way of three analyses. First, the ability of hierarchical clustering to reidentify manually gated populations was quantified in five datasets from the FlowCAP-I competition. Second, the capacity of Citrus to identify prognostic cell subsets in HIV-infected patients was compared with that of an existing analytical method, flowType. Finally, the ability of Citrus to perform binary classification of flow cytometry samples was measured in two datasets from the FlowCAP-II competition.
Evaluation of hierarchical clustering performance.
The capacity of Citrus to reidentify manually gated populations was quantified in five datasets from the FlowCAP-I competition (SI Appendix, Table S2) (19). Populations of cells in each FlowCAP-I dataset were identified by an expert using manual gating and may be used as a reference against which to evaluate the performance of a given clustering algorithm. In contrast to most existing population-finding algorithms, Citrus does not attempt to define the exact number of populations in a dataset at the time of clustering. Rather, Citrus identifies many overlapping candidate subsets that may contain informative signal and then uses regularized regression to identify those with stratifying behavior after clustering. Because all clusters in the clustering hierarchy are examined for stratifying signal, the clustering sensitivity of Citrus was quantified based on its ability to identify a manually gated population at any point in the clustering hierarchy.
The F1 measure was used to quantify the similarity between an algorithmically defined cluster and a manually gated population of cells as described in Aghaeepour et al. (19, 24). F1 measures were calculated between every manually gated population and computationally identified cluster within a sample and were used to identify the cluster that best “matched” each manually gated population. The clustering’s sensitivity measure was defined to be the average of F1 measures from clusters that best matched manually gated populations (SI Appendix, section S1.4).
Hierarchical clustering was used to identify cell subsets in all FlowCAP-I dataset samples, and clustering sensitivity measures were computed for each dataset. For comparison, the same clustering sensitivity measures were computed for FlowCAP-I competition methods (Fig. 3A and SI Appendix, Fig. S9). Notably, the stated objective for FlowCAP-I methods was to identify the single best cluster for each cell. Conversely, hierarchical clustering has many opportunities to identify a manually gated population in a dataset. Therefore, these results are only intended to illustrate that by identifying many overlapping cell subsets, Citrus is better able to reidentify manually gated populations than methods that identify a fixed partition of the data. Additionally, plots of clustering sensitivity as a function of number of identified clusters showed that hierarchical clustering is able to achieve a majority of its sensitivity with a minimum cluster size cutoff of 1% or 0.5% in most datasets (Fig. 3B).
Fig. 3.
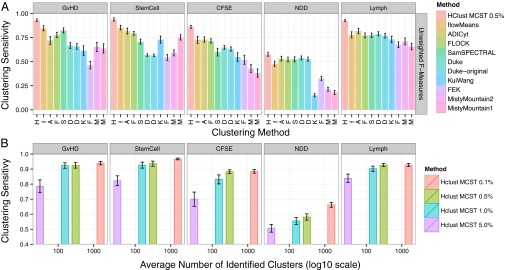
Clustering sensitivity of hierarchical clustering in FlowCAP-I datasets. (A) Clustering sensitivity measures from hierarchical clustering and other FlowCAP-I methods in FlowCAP-I datasets. Methods are ordered by their sensitivity across all datasets. For hierarchical clustering, the MCST was set to be 0.5% of the clustered dataset size. The number of manually gated populations used to calculate clustering sensitivity is reported in SI Appendix, Table S2. (B) Clustering sensitivity as a function of number of identified clusters for hierarchical clustering. Smaller minimum-cluster-size thresholds for hierarchical clustering increases clustering sensitivity but identifies more clusters (hclust MCST 0.01–5.0%).
Citrus trades clustering specificity for improved sensitivity by treating every identified cluster in the clustering dendrogram as an independent cell subset, rather than attempting to find a fixed height at which to cut the clustering dendrogram. In other words, Citrus increases its chances of finding informative cell subsets by deriving many overlapping cell subsets, including some that will be uninformative with respect to the experimental endpoint of interest. Although sensitivity gains at the expense of clustering specificity may not be acceptable for some analyses (i.e., when automating the reidentification of a manually defined population), data-driven exploratory analyses benefit from this tradeoff so long as relevant signal is not obscured by noise from identified, but noninformative, clusters. The relationship between clustering specificity and the power of Citrus to detect stratifying signal is discussed further in Method Sensitivity in Relationship to Analysis Parameters.
Identification of prognostic cell subsets in HIV-infected patients.
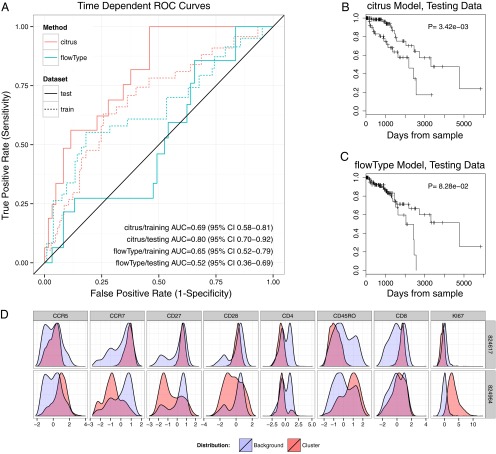
The impact of clustering sensitivity in practice was assessed by comparing the ability of Citrus to identify prognostic cell subsets with that of flowType. More specifically, both methods were used to identify cell subsets associated with increased risk of AIDS onset in HIV-infected patients from the U.S. Military HIV Natural History Study (25). Data were first divided into training and testing sets (two-thirds and one-third of data, respectively). Each method was used to identify cell subsets in the training dataset, and subset abundances were quantified on a per-patient basis. AIDS-free survival risk was modeled as a function of each method’s feature set by using a multivariate L1-penalized Cox proportional-hazards model. Training data were further split into 10 groups, and cross-validated time-dependent receiver operating characteristic (ROC) curves were used to estimate each method’s training model accuracy (Fig. 4A) (26, 27). For each method, a regularization threshold having the minimum average partial likelihood deviance across 10 cross-validation runs was used to constrain a final model built from method features. Each method’s Cox model was used to predict the relative risk of AIDS-free survival in testing set patients, and prognostic performance was assessed by using time-dependent ROC curves and Kaplan–Meier plots (Fig. 4 A–C).
Fig. 4.
Prognostic performance of Citrus and flowType Cox models. (A) Time-dependent ROC curves for Citrus and flowType models. Curves were evaluated at the mean patient survival time of 1,025 d. (B and C) Kaplan–Meier curves of AIDS-free survival time in testing patients. Each model (Citrus, B; and flowType, C) was used to estimate the relative risk for each patient, and average patient risk was calculated across all testing-cohort patients. Patients with higher- and lower-than-average risk were assigned to high- and low-risk groups, respectively. Differences in survival time between groups in testing patients were calculated by using the log-rank test. (D) Phenotype plots of clusters that were selected in all 10 cross-validation models. Both naive CD8+ T-Cells and Ki-67+ cells were identified as having prognostic utility in previous analyses.
Time-dependent ROC curves and Kaplan–Meier plots of testing cohort patients show the model constructed from the features of Citrus to be a more accurate predictor of AIDS-free survival risk. Further details of factors contributing to discrepancies in model performance are provided in Discussion. During the Citrus analysis, five cell subsets were identified as prognostic in two-thirds of cross-validation runs and were plotted to determine phenotype (Table 2 and SI Appendix, Fig. S3). Two clusters, 824617 and 824984, were selected by models in all 10 cross-validation runs (Fig. 4D). The proportion of a patient’s cells found in cluster 824617 was inversely correlated with AIDS-free survival risk. Cells in this cluster expressed high levels of CD8, CD28, CD27, and CCR7 and low levels of CD4 and CD45RO, a phenotype of naive CD8+ T cells. This association was also detected and reported in the flowType manuscript and by Ganesan et al., who first analyzed these data by hand (4, 20). Additionally the abundance of Ki-67+ cells (cluster 824964) was found to be positively correlated with risk of AIDS onset. This association was also reported by Ganesan et al. and Aghaeepour et al. Of the remaining clusters frequently selected during cross-validation, two (clusters 824715 and 824971) had a phenotype of CCR7+ naive CD4+ T-cells (28), whereas the third (cluster 824823) had a similar phenotype to the Ki-67+ cluster. Although depletion of naive CD4+ T cells is known to be associated with HIV progression (29), the relationship between cells in cluster 824823 and HIV is not well characterized. However, these cell types may now be considered candidates for follow-up studies that assess their biological relevance to disease progression.
Table 2.
Summary of clusters frequently selected during cross-validation
| Cluster ID | CV selection frequency, % | Coefficient average | Abundance average, % |
| 824823 | 70 | 7.24 | 0.85 |
| 824971 | 70 | −0.79 | 7.64 |
| 824715 | 80 | −9.30 | 0.61 |
| 824617 | 100 | −17.36 | 0.61 |
| 824964 | 100 | 15.79 | 1.49 |
Classification of samples in FlowCAP-II datasets.
Lastly, the ability of Citrus to perform binary classification of samples was evaluated by using two datasets from the FlowCAP-II competition. Each FlowCAP-II dataset comprises samples from two classes of patients (i.e., healthy and diseased patients). The analysis objective within each dataset is to build a model that can be used to predict the class of a new, unlabeled sample. Each dataset is divided into a training and a testing set of samples that are used to construct and evaluate predictive models, respectively.
Citrus was used to analyze datasets from the Acute Myeloid Leukemia (AML) and HIV Vaccine Trials Network (HVTN) FlowCAP-II challenges. By using AML training data, Citrus was used to construct a classifier of AML presence. In the HVTN dataset, Citrus was used to construct a classifier of antigen-stimulation groups in post-HIV vaccination T cells (SI Appendix, section S1.1). Dataset models were used to predict testing sample labels in a blinded fashion, and results were compared with true labels of test-set samples. SI Appendix, Table S3 summarizes the classification performance of Citrus in each dataset. Citrus correctly predicted 22 of 22 test-set labels in the HVTN dataset and 179 of 180 test-set labels in the AML dataset. Performance was similar to other top-performing methods in the FlowCAP-II competition, although many of those methods did not provide interpretable results (SI Appendix, Fig. S5). Notably, the single incorrect prediction made by Citrus in the AML dataset was in patient 340, a sample that was frequently misclassified by other algorithms in the FlowCAP-II competition. One explanation for this trend discussed by the competition organizers is that patient 340 may have had a preleukemic condition rather than AML (19).
Method Sensitivity in Relationship to Analysis Parameters.
A Citrus analysis requires that investigators specify the number of cells that are selected from each sample, markers on which to perform clustering, and a MCST. To evaluate the relationship between clustering sensitivity and events selected per sample, a varying number of cells were selected per sample, the selected data were clustered, and the clustering’s sensitivity measure was calculated (SI Appendix, section S1.7). Results showed that the number of events selected per sample did not have a large effect on clustering sensitivity in these datasets (SI Appendix, Fig. S11). However, an adequate number of cells must be clustered to ensure that subsets contain enough events to accurately estimate subset abundances and median phosphoprotein levels. By default, this parameter may be set so that that the smallest cluster included in the regression analysis contains an average of 50 cells per sample.
The MCST parameter dictates the smallest cell subset included in the endpoint regression analysis. A smaller MCST will increase the number of clusters included in the regression analysis but decrease the model’s power to detect more subtle effects. To assess the relationship between the MCST and the power of Citrus to detect differences between groups, iterations of the Bodenmiller PBMC analysis were run by using differing MCSTs (SI Appendix, section S1.7). Analyses that used smaller MCSTs identified signal in more rare cell subsets but had less power to resolve subsets whose behavior subtly differed between groups (SI Appendix, Table S4). SI Appendix, note S4.1 outlines several ways to maintain statistical power when searching for stratifying signal in rare cell subsets and offers a further discussion of how to set all parameters in a Citrus analysis.
Discussion
We present a method (Citrus) for unsupervised identification of subsets of cells in multidimensional flow cytometry whose behavior correlates with sample endpoints of interest. Citrus automates this process by applying hierarchical clustering to identify clusters of cells within a dataset, calculating descriptive features of each cluster, and then applying regularized supervised learning methods to determine which cell subsets’ behavior are correlated with a sample’s endpoint. The methodology of Citrus was demonstrated through the analysis of several cytometry datasets. The first dataset was PBMCs from which Citrus recovered known biological and experimentally induced responses. In HIV-infected patients, Citrus identified subsets of cells associated with AIDS-free survival risk. Finally, the clustering sensitivity and binary classification power of Citrus were evaluated with datasets from the FlowCAP competition.
Within the PBMC dataset, Citrus identified multiple subsets of cells that responded to BCR/FCR cross-linking. B cells, the primary target of the cross-linking agent, showed the strongest response to stimuli with multiple phosphoproteins in the signaling pathways downstream of the BCRs responding. Smaller but consistent responses in FCR-pathway proteins were also detected in monocytes. These phosphoprotein responses were validated by using additional kinase inhibitor experimental data from Bodenmiller et al. Activation of AKT in B cells, although detected by Citrus, was not reported by Bodenmiller et al. Conversely, subtle inductions of ERK and PLCγ2 phosphorylation in dendritic cells were identified by Bodenmiller et al. but were not detected by Citrus. Both discrepancies are the due to the fact that Bodenmiller et al. identified protein responses based on repeated measurements from a single patient, whereas our analysis identified responses occurring across all eight PBMC samples. For instance, AKT activation in B cells, although minimal in their single patient, was seen in the seven additionally analyzed patients. Likewise, ERK and PLCγ2 responses in dendritic cells, although likely responding in their single patient, did not systematically differ across all eight samples (SI Appendix, note S4.2).
Analysis of FlowCAP-I datasets shows the hierarchical clustering used by Citrus to be at least as sensitive as existing methods when reidentifying manually gated populations. In practice, this clustering enabled Citrus to identify several cell subsets associated with AIDS-free survival in HIV-infected patients. The predictive model constructed from cell subsets identified using Citrus was found to have better performance on testing-set patients than the model constructed using subsets identified by flowType. Discrepancies in model performance are likely attributable to several factors. First, the multivariate clustering used by Citrus was able to automatically identify a rare subset of prognostically relevant Ki-67+ cells. However, this subset proved difficult for flowType’s univariate clustering to identify (20). In turn, Aghaeepour et al. used manual gating to define boundaries for this cell subset in their analysis. Because these boundaries were not provided to flowType during our evaluation, the ability of Citrus to automatically detect this prognostic cell subset partially accounts for differences in the performance of each method’s predictive model. Second, Citrus identified and used fewer cell subsets for modeling than flowType (316 vs. 177,147), making it easier for the penalized Cox model to detect informative signal. Because the number of cell subsets identified by Citrus is a function of minimum cluster size rather than the dimensionality of measured data, our approach will scale well to data produced by high-dimensional cytometry platforms such as CyTOF, whereas methods such as flowType will identify fewer clusters on lower-dimensionality data (SI Appendix, Fig. S8).
Perhaps the biggest difference between the hierarchical clustering used by Citrus and existing population-finding algorithms such as those entered in the FlowCAP-I competition is that Citrus identifies many overlapping clusters rather than defining fixed partition of the data. This approach is motivated by the fact that estimating the true number of clusters in a dataset remains a challenging issue for clustering algorithms. Indeed, the sensitivity of FlowCAP-I algorithms is higher when the number of manually gated populations is explicitly provided rather than estimated (SI Appendix, Fig. S10). Predictably, descriptive features derived from related cell subsets (e.g., parents and children in the clustering hierarchy) are often correlated. The regression models used by Citrus deal with these correlated features differently. The multivariate L1-regularized regression model selects the most predictive feature from a set of correlated features and ignores the others, because they cannot explain any additional variance in the endpoint variable. Conversely, the nearest shrunken centroid’s univariate approach evaluates the prognostic utility of each feature independently. Thus, sets of correlated features may be selected for model construction so long as they are informative by themselves. Sets of correlated features identified by either model may be visualized in the context of the clustering hierarchy to identify cell subsets with similar behavior (SI Appendix, note S4.3 and Figs. S12–S14).
Moving forward, a variety of methodological enhancements could improve the ability of Citrus to identify stratifying signals. Although Citrus currently analyzes all cell subsets in the clustering hierarchy larger than a specified size, information-theoretic approaches could be used to intelligently prune cell subsets containing redundant information before endpoint regression. The removal of such redundant features would improve the sensitivity of Citrus to subtle associations between subset behavior and experimental endpoints. Alternatively, sparse regression models such as the group lasso (30) that explicitly account for correlated features could be incorporated into the Citrus workflow, thus eliminating a need to reconcile related cell subsets after regression.
Citrus scales well to high-dimensional data and enables efficient identification of correlations between subpopulation behavior and diverse categorical or continuous sample attributes, such as copy number variation, genomic mutations, or other sample data found in the patient’s clinical record. Because many candidate subsets are evaluated for stratifying signal, numerous samples are needed to differentiate stratifying signal from normal interpatient variability. Therefore, Citrus is not well suited for identifying stratifying signals in experiments having a limited number of patients in each experimental group and is not suitable for identifying differences between two patient samples. Additionally, evaluations show the hierarchical clustering used by Citrus to be a sensitive identifier of manually gated populations. However, because Citrus requires that clusters have a minimum number of cells in them to be included in an analysis, it may not be appropriate for identifying signatures in extremely rare subsets such as antigen-specific T cells.
As flow cytometry experiments become increasingly complex and the amount of metadata available for each sample grows (e.g., other experimental measures or rich patient history), automated methods will greatly aid investigators in the identification of informative populations of cells whose behavior is predictive of experimental or clinical endpoints. Although this work demonstrates Citrus through analysis of mass and fluorescence-based cytometry data, it is also generally applicable to many data types, including multiparameter image cytometry data. Although results always rely on the presence of discerning markers within samples, an unbiased, but more comprehensive, approach to data analysis should aid investigators in the exploration of increasingly complex flow cytometry datasets.
Materials and Methods
SI Appendix, section S1.1 lists analyzed datasets and data preprocessing steps. SI Appendix, section S1.2 details analytical steps of Citrus. Supporting figures and tables for presented analyses along with additional analysis details are found in SI Appendix, sections S2, S3, and S4, respectively. Code, documentation, and examples for running Citrus are available at https://zenodo.org/record/10310.
Supplementary Material
Acknowledgments
We thank the two manuscript referees for their many helpful comments and feedback. We also wish to thank N. Kotecha for additional feedback on the manuscript, R. Finck for insight during method development, and M. Linderman for his work on the Rclusterpp R package. R.V.B. is supported by National Library of Medicine Training Grant T15 LM007033. B.B. is supported by grants from the Swiss National Science Foundation, the European Molecular Biology Organization, and a Marie Curie International Outgoing Fellowship. D.L.D. is supported by National Cancer Institute Grant U54CA149145. R.J.T. is supported by National Science Foundation Grant DMS-9971405 and National Institutes of Health (NIH) Grant N01-HV-28183. G.P.N. is supported by NIH Grants UL1RR025744, 0158 G KB065, 1R01CA130826, 5U54CA143907, HHSN272200700038C, N01-HV-00242, 41000411217, 5 24927, P01 CA034233-22A1, P01 CA034233-22A1, PN2EY018228, RFA CA 09-009, RFA CA 09 011, U19 AI057229, and U54CA149145; California Institute for Regenerative Medicine Grants DR1-01477 and RB2-01592; European Commission Grant HEALTH.2010.1.2-1; U.S. Food and Drug Administration Grant HHSF223201210194C: BAA-12-00118; and U.S. Department of Defense Grant W81XWH-12-1-0591 OCRP-TIA NWC.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1408792111/-/DCSupplemental.
References
- 1.Kotecha N, et al. Single-cell profiling identifies aberrant STAT5 activation in myeloid malignancies with specific clinical and biologic correlates. Cancer Cell. 2008;14(4):335–343. doi: 10.1016/j.ccr.2008.08.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Basso G, et al. Risk of relapse of childhood acute lymphoblastic leukemia is predicted by flow cytometric measurement of residual disease on day 15 bone marrow. J Clin Oncol. 2009;27(31):5168–5174. doi: 10.1200/JCO.2008.20.8934. [DOI] [PubMed] [Google Scholar]
- 3.Irish JM, et al. B-cell signaling networks reveal a negative prognostic human lymphoma cell subset that emerges during tumor progression. Proc Natl Acad Sci USA. 2010;107(29):12747–12754. doi: 10.1073/pnas.1002057107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ganesan A, et al. Infectious Disease Clinical Research Program HIV Working Group Immunologic and virologic events in early HIV infection predict subsequent rate of progression. J Infect Dis. 2010;201(2):272–284. doi: 10.1086/649430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Freeman SD, et al. Prognostic relevance of treatment response measured by flow cytometric residual disease detection in older patients with acute myeloid leukemia. J Clin Oncol. 2013;31(32):4123–4131. doi: 10.1200/JCO.2013.49.1753. [DOI] [PubMed] [Google Scholar]
- 6.Bendall SC, et al. Single-cell mass cytometry of differential immune and drug responses across a human hematopoietic continuum. Science. 2011;332(6030):687–696. doi: 10.1126/science.1198704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bodenmiller B, et al. Multiplexed mass cytometry profiling of cellular states perturbed by small-molecule regulators. Nat Biotechnol. 2012;30(9):858–867. doi: 10.1038/nbt.2317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Maecker HT, et al. Standardization of cytokine flow cytometry assays. BMC Immunol. 2005;6:13. doi: 10.1186/1471-2172-6-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Murphy RF. Automated identification of subpopulations in flow cytometric list mode data using cluster analysis. Cytometry. 1985;6(4):302–309. doi: 10.1002/cyto.990060405. [DOI] [PubMed] [Google Scholar]
- 10.Aghaeepour N, Nikolic R, Hoos HH, Brinkman RR. Rapid cell population identification in flow cytometry data. Cytometry A. 2011;79(1):6–13. doi: 10.1002/cyto.a.21007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Zare H, Shooshtari P, Gupta A, Brinkman RR. Data reduction for spectral clustering to analyze high throughput flow cytometry data. BMC Bioinformatics. 2010;11:403. doi: 10.1186/1471-2105-11-403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lo K, Brinkman RR, Gottardo R. Automated gating of flow cytometry data via robust model-based clustering. Cytometry A. 2008;73(4):321–332. doi: 10.1002/cyto.a.20531. [DOI] [PubMed] [Google Scholar]
- 13.Pyne S, et al. Automated high-dimensional flow cytometric data analysis. Proc Natl Acad Sci USA. 2009;106(21):8519–8524. doi: 10.1073/pnas.0903028106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Finak G, Bashashati A, Brinkman R, Gottardo R. Merging mixture components for cell population identification in flow cytometry. Adv Bioinforma. 2009;2009:247646. doi: 10.1155/2009/247646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Walther G, et al. Automatic clustering of flow cytometry data with density-based merging. Adv Bioinforma. 2009;2009:686759. doi: 10.1155/2009/686759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Sugár IP, Sealfon SC. Misty Mountain clustering: Application to fast unsupervised flow cytometry gating. BMC Bioinformatics. 2010;11:502. doi: 10.1186/1471-2105-11-502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Qian Y, et al. Elucidation of seventeen human peripheral blood B-cell subsets and quantification of the tetanus response using a density-based method for the automated identification of cell populations in multidimensional flow cytometry data. Cytometry B Clin Cytom. 2010;78(Suppl 1):S69–S82. doi: 10.1002/cyto.b.20554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ge Y, Sealfon SC. flowPeaks: A fast unsupervised clustering for flow cytometry data via K-means and density peak finding. Bioinformatics. 2012;28(15):2052–2058. doi: 10.1093/bioinformatics/bts300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Aghaeepour N, et al. FlowCAP Consortium DREAM Consortium Critical assessment of automated flow cytometry data analysis techniques. Nat Methods. 2013;10(3):228–238. doi: 10.1038/nmeth.2365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Aghaeepour N, et al. Early immunologic correlates of HIV protection can be identified from computational analysis of complex multivariate T-cell flow cytometry assays. Bioinformatics. 2012;28(7):1009–1016. doi: 10.1093/bioinformatics/bts082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Tibshirani R. Regression shrinkage and selection via the lasso. J R Stat Soc B. 1996;58(1):267–288. [Google Scholar]
- 22.Tibshirani R, Hastie T, Narasimhan B, Chu G. Diagnosis of multiple cancer types by shrunken centroids of gene expression. Proc Natl Acad Sci USA. 2002;99(10):6567–6572. doi: 10.1073/pnas.082099299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kanehisa M, Goto S, Sato Y, Furumichi M, Tanabe M. KEGG for integration and interpretation of large-scale molecular data sets. Nucleic Acids Res. 2012;40(Database issue):D109–D114. doi: 10.1093/nar/gkr988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Van Rijsbergen CJ. Information retrieval. London: Butterworths; 1979. [Google Scholar]
- 25.Weintrob AC, et al. Increasing age at HIV seroconversion from 18 to 40 years is associated with favorable virologic and immunologic responses to HAART. J Acquired Immune Deficiency Syndromes. 2008;49(1):40–47. doi: 10.1097/QAI.0b013e31817bec05. [DOI] [PubMed] [Google Scholar]
- 26.Simon RM, Subramanian J, Li MC, Menezes S. Using cross-validation to evaluate predictive accuracy of survival risk classifiers based on high-dimensional data. Brief Bioinform. 2011;12(3):203–214. doi: 10.1093/bib/bbr001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Heagerty PJ, Lumley T, Pepe MS. Time-dependent ROC curves for censored survival data and a diagnostic marker. Biometrics. 2000;56(2):337–344. doi: 10.1111/j.0006-341x.2000.00337.x. [DOI] [PubMed] [Google Scholar]
- 28.Appay V, van Lier RAW, Sallusto F, Roederer M. Phenotype and function of human T lymphocyte subsets: Consensus and issues. Cytometry A. 2008;73(11):975–983. doi: 10.1002/cyto.a.20643. [DOI] [PubMed] [Google Scholar]
- 29.Roederer M, et al. CD8 naive T cell counts decrease progressively in HIV-infected adults. J Clin Invest. 1995;95(5):2061–2066. doi: 10.1172/JCI117892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Yuan M, Lin Y. Model selection and estimation in regression with grouped variables. J R Stat Soc B. 2006;68(1):49–67. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.