During chemotactic movement, D. discoideum exhibits step-wise amoeboid motility driven by both contractile axial forces and lateral forces.
Abstract
Chemotaxing Dictyostelium discoideum cells adapt their morphology and migration speed in response to intrinsic and extrinsic cues. Using Fourier traction force microscopy, we measured the spatiotemporal evolution of shape and traction stresses and constructed traction tension kymographs to analyze cell motility as a function of the dynamics of the cell’s mechanically active traction adhesions. We show that wild-type cells migrate in a step-wise fashion, mainly forming stationary traction adhesions along their anterior–posterior axes and exerting strong contractile axial forces. We demonstrate that lateral forces are also important for motility, especially for migration on highly adhesive substrates. Analysis of two mutant strains lacking distinct actin cross-linkers (mhcA− and abp120− cells) on normal and highly adhesive substrates supports a key role for lateral contractions in amoeboid cell motility, whereas the differences in their traction adhesion dynamics suggest that these two strains use distinct mechanisms to achieve migration. Finally, we provide evidence that the above patterns of migration may be conserved in mammalian amoeboid cells.
Introduction
Directional cell migration toward a chemical cue (chemotaxis) is required for a variety of physiological and pathological processes including cancer metastasis, immune system response, and food scavenging and multicellular development in the model system Dictyostelium discoideum (Bagorda et al., 2006; Grabher et al., 2007).
Chemotaxing amoeboid cells migrate on flat, 2D surfaces by using a repetitive sequence of shape changes involving the protrusion of frontal pseudopodia and the retraction of the back of the cell (Webb et al., 2002; Uchida and Yumura, 2004). When these cells are placed on elastic substrates embedded with fluorescent beads, one can measure the cell-induced gel deformation by tracking the displacements of the beads and subsequently calculate the stresses exerted by the cells on the substrate. The time variation of the length of the cells and the mechanical work they impart on their substrate (strain energy) exhibit strikingly simple spatiotemporal dynamics (Alonso-Latorre et al., 2011), including a well-defined periodicity (Uchida and Yumura, 2004; del Álamo et al., 2007). These periodic fluctuations are coordinated into four broadly defined phases: protrusion of the cell’s front (cell length, strain energy, and level of frontal F-actin increase), contraction of the cell’s body (all three time records reach a maximum), retraction of the rear (decrease in all three time records), and relaxation (all three time records reach a minimum; Meili et al., 2010; Bastounis et al., 2011). Essential to the implementation of these phases are: the dynamics of the actin cytoskeleton and its associated cross-linking proteins, the regulation of the actin-myosin contraction, and the dynamics of the substrate adhesion sites (Huttenlocher et al., 1995; Jay et al., 1995).
In amoeboid-type locomotion, the directional dendritic polymerization of F-actin at the front creates a pseudopod that propels the edge of the cell forward (Pollard and Borisy, 2003; Lämmermann and Sixt, 2009). As the pseudopod advances, new substrate adhesions are formed that, on maturation, allow the cell to generate traction forces. Unlike less motile cells that adhere to their substrate through stable integrin-containing protein assemblies (focal adhesions), neutrophils and D. discoideum do not (Friedl et al., 2001; Fey et al., 2002). Adhesion sites in D. discoideum (focal contacts) are more diffuse and transient (Uchida and Yumura, 2004), making studying them relatively more challenging compared with slower moving cells such as fibroblasts (Balaban et al., 2001; Gov, 2006). Mechanically, these sites connect the cell to its substrate and mediate the contractile traction forces that drive cell movement. Although it has long been established that these contractile forces are a prominent feature of amoeboid motility (del Álamo et al., 2007), the precise mechanisms that control migration efficiency via the spatiotemporal coordination of the cellular traction forces are still unknown.
In this study, we investigate the fundamental questions of how amoeboid cells move by analyzing the dynamics of the active traction adhesions (TAs). “Mechanically active traction adhesions” or short “traction adhesions” are defined as the locations where the cell transmits traction forces to the substrate. We use Fourier traction force microscopy (FTFM) to quantify the dynamics of the traction stresses of chemotaxing cells with high spatiotemporal resolution. Stacking these measurements jointly in space and time, we constructed kymographs and examined the dynamics of amoeboid motility with an unprecedented level of detail. We demonstrate that D. discoideum wild-type cells achieve efficient migration by forming stationary TAs at their front and back halves while contracting inward axially (along the anterior–posterior [AP] axis) as well as laterally. When implementing this motility mode, the cell moves forward by periodically stepping from old to newly formed front TAs, whereas front TAs transition to back TAs as the cell moves over them. We show that this mode is prevalent during chemotaxis or when cells move persistently in the absence of a chemoattractant. We demonstrate, for the first time, that apart from the axial forces, lateral forces are important in cell motility and may not be associated with the periodic polymerization of F-actin at the leading edge and Myosin II (MyoII) contraction at the posterior. We found that cells migrating on adhesive substrates increase their lateral contractility in order to break adhesions and move, whereas cells with reduced actin cross-linking are unable to move on such substrates because they cannot increase their contractility substantially. On regular substrates, these less polarized mutant strains rely more on lateral contractions for their movement because their axial contractility is reduced and disorganized. Finally, we observed that neutrophil-like cells exhibit traction stress dynamics similar to those of D. discoideum, which suggests that the pattern of migration of amoeboid cells may be highly conserved.
Results
Analysis of traction stress dynamics during cell motility
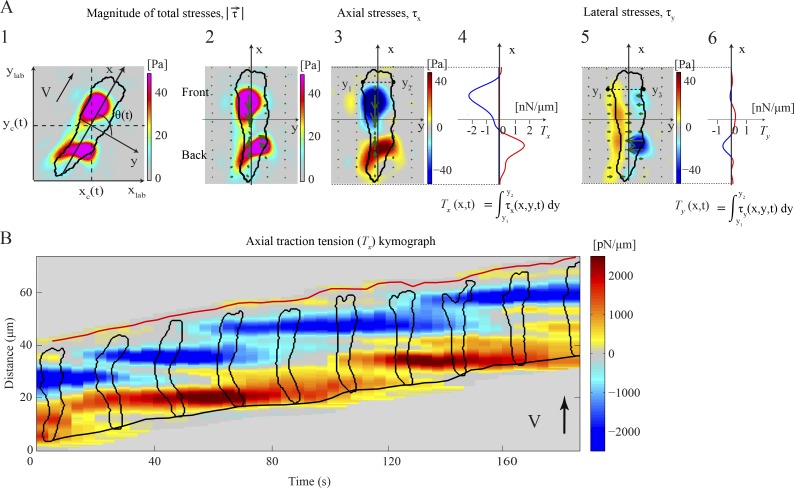
When migrating on elastic 2D substrates up a chemoattractant gradient, wild-type cells move by exhibiting periodic elongations and contractions (Video 1; Wessels et al., 1988; del Álamo et al., 2007). Moving cells exert traction forces on the substrate that localize, on average, to two or three diffuse areas, located along the cell’s AP axis and are directed inward toward the cell’s center (Fig. 1 A, 1; and Video 2). Hereafter, we refer to these areas as TAs because they are the location where the cell exerts traction stresses on the substrate.
Figure 1.
Characterization of the dynamics of amoeboid motility with high spatiotemporal resolution. (A) Traction stresses (force/area) and tension (force/length) for a representative cell at a given instant of time. Color bars at the right side of each traction stress map indicate stress values in [Pa]. (1) Color contours mapping the instantaneous magnitude of the traction stresses, , in the laboratory reference frame (xlab, ylab). The black contour shows the cell outline. The axes (x, y) are aligned with the cell’s principal axes and their origin is located at the cell’s center of mass (xc, yc). V indicates the cell’s velocity and the black arrow shows the direction of motion. (2) in a reference frame rotated to coincide with (x, y). Green arrows show the intensity and direction of the stresses. (3) Axial traction stresses, τx. Stresses pointing toward the cell’s front are considered positive and are shown in red while negative stresses are shown in blue. (4) Integral of τx across the width of the cell (axial tension, Tx) as a function of the position along its length. The horizontal axis displays the Tx values in [nN/µm]. Positive and negative values are shown in red and blue, respectively. (5) Lateral traction stresses, τy. Stresses pointing toward the right of the cell are considered positive and are shown in red, whereas negative stresses are shown in blue. (6) Integral of τy across the width of the cell (lateral tension, Ty) as a function of the position along its length. (B) Spatiotemporal kymograph of Tx(x, t) as a function of the position along the cell trajectory, x, and time, t. At any given instant of time the centroid of the cell is displaced vertically according to its motion so that the cell is moving upward. The inclined red and black lines indicate the instantaneous position of the front and back cell edges. The black contours are cell outlines, shown every 20 s. The color map represents Tx in [pN/µm], plotted every 4 s. Red or blue patches represent positive or negative values of Tx and correspond to tensions aligned with the direction of cell motion or pointing in the opposite direction.
The traction stresses can be plotted in a reference frame where the horizontal and vertical axes (x, y) coincide with the minor and major axes of the cell, respectively (Fig. 1 A, 2), allowing the axial (along the cell’s major axis) and lateral (perpendicular to the cell’s major axis) components of the traction stresses to be examined separately (Fig. 1 A, 3 and 5). In this representation, the axial stresses are negative at the front TA (pointing in the negative y direction and directed inward toward the back of the cell) and positive at the back (directed inward toward the front; Fig. 1 A, 3). Similarly, because the cell is always contracting inward, the lateral stresses at the right and left sides of the cell are of opposite signs (Fig. 1 A, 5). Integrating the axial stresses across the cell width yields the axial traction tension along the cell’s major axis (Fig. 1 A, 4). The integrated axial tension values are negative at the front half of the cell (blue, pointing toward the rear) and positive at the back half (red, pointing toward the front). Similar integration of the lateral stresses across the cell width does not add information because opposite lateral stresses balance out due to mechanical equilibrium (Fig. 1 A, 6).
Jointly stacking the measurements of the instantaneous axial tension (Fig. 1 B) in space (vertical) and time (horizontal) produces high-resolution 2D representations (kymographs) that depict the spatiotemporal patterns of the cell’s TAs in the direction of movement. Using these kymographs, one can examine the time variation of the location and magnitude of the TAs along the AP axis of the cell (represented in the tension kymograph by the blue and red patches; Fig. 1 B). This graphical representation allows the easy identification of the different motility modes implemented by the chemotaxing cell, thus providing insight into the underlying mechanical regulatory mechanisms (Fig. S1, A–D). For example, if a front or back TA remains stationary as the cell body moves forward, then the corresponding blue or red patch will be horizontal (parallel to the time axis; Fig. 2 A).
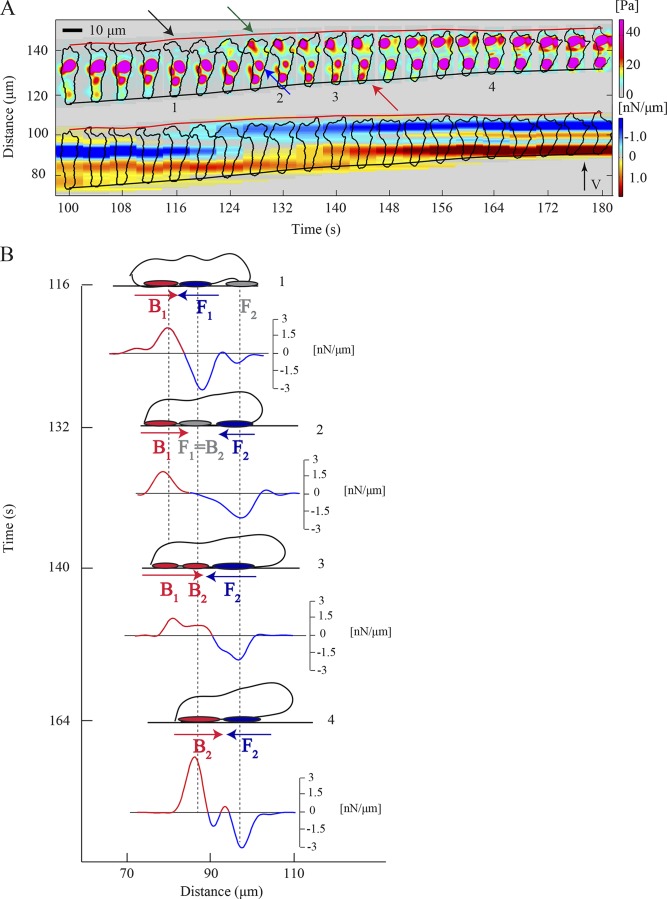
Figure 2.
S-S motility mode. (A) Kymograph of the instantaneous magnitude of the traction stresses, (upper part), and traction tension, Tx (lower part), for a representative wild-type cell. The black arrow indicates pseudopod protrusion, followed by front TA formation (green arrow). The blue arrow shows the transition of the front TA to back and the red arrow points to the TA loss. The inclined red and black lines indicate the instantaneous position of the front and back cell edges. (B) Schematic representation of the time evolution of the magnitude and location of the TAs, illustrating the implementation of the S-S mode. A side view of the cell is shown as a cartoon for four instants of time and refers to the cell shown in A. The vertical axis indicates time and the horizontal axis depicts the cell location in the direction of motion. Front and back TAs are shown as blue and red ovals underneath the cell. Gray ovals represent weak, newly formed TAs or front TAs undergoing a transition in mechanical load and becoming back TAs. Blue and red arrows illustrate the direction of Tx at the cell’s front and back, respectively. Underneath each cartoon the corresponding Tx(x, t) is plotted. The vertical axis of each plot indicates the scale for Tx values [nN/µm]. Red or blue color indicates positive or negative Tx.
Wild-type motility is characterized by stable, stationary front and back TAs
We analyzed the spatiotemporal regulation of the stresses and dynamics of the TAs of wild-type cells using traction stress and tension kymographs. We observed that more than two thirds of the time wild-type cells implement one specific mode of TA dynamics (Fig. S1, A–D). In this mode, the blue (front TAs) and red (back TAs) patches remain horizontal, which indicates that both TAs remain stationary in space as the cell moves forward. Fig. 2 A shows that shortly after a new pseudopod forms (black arrow), the cell establishes a new TA under the nascent front pseudopod (green arrow). The “old” front TA now becomes the “new” back TA (blue arrow), while the “old” back TA is lost once the cell passes its position (red arrow). This switching of the front TA to a back (from blue to red) can be observed by following a blue patch horizontally and seeing how it fades gradually, and later on turns to a red horizontal patch in the kymographs in Figs. 1 B and 2 A.
This quasiperiodic process is schematically illustrated in the diagram shown in Fig. 2 B, which depicts the cell’s shape and the corresponding axial traction tension (Tx) during a period of ∼80 s: the cell adheres actively in two regions, one at the front (F1) and one at its back (B1), while protruding a pseudopod (Fig. 2 B, 1). This pseudopod actively attaches to the substrate forming a new front TA F2, while the previous “stationary” front TA F1 now becomes the new back TA B2 and the previous back TA B1 weakens (Fig. 2 B, 2 and 3). At this point, the cell is attached at three TAs. As the cell continues to translocate forward, it moves over and through the B1 TA, the B1 site disappears at the posterior of the cell, and the cell actively attaches at only two TAs (Fig. 2 B, 4). This cycle repeats itself when the cell (with attachments at B2 and F2) starts protruding a new pseudopod at the leading edge (Fig. 2 B, 4). We named this mechanical mode of cell movement “stable-stable” (S-S) because the cell moves in a step-wise fashion, forming sequential TAs that remain stationary in space and stable in time (Fig. 2, A and B; and Fig. 3 A).
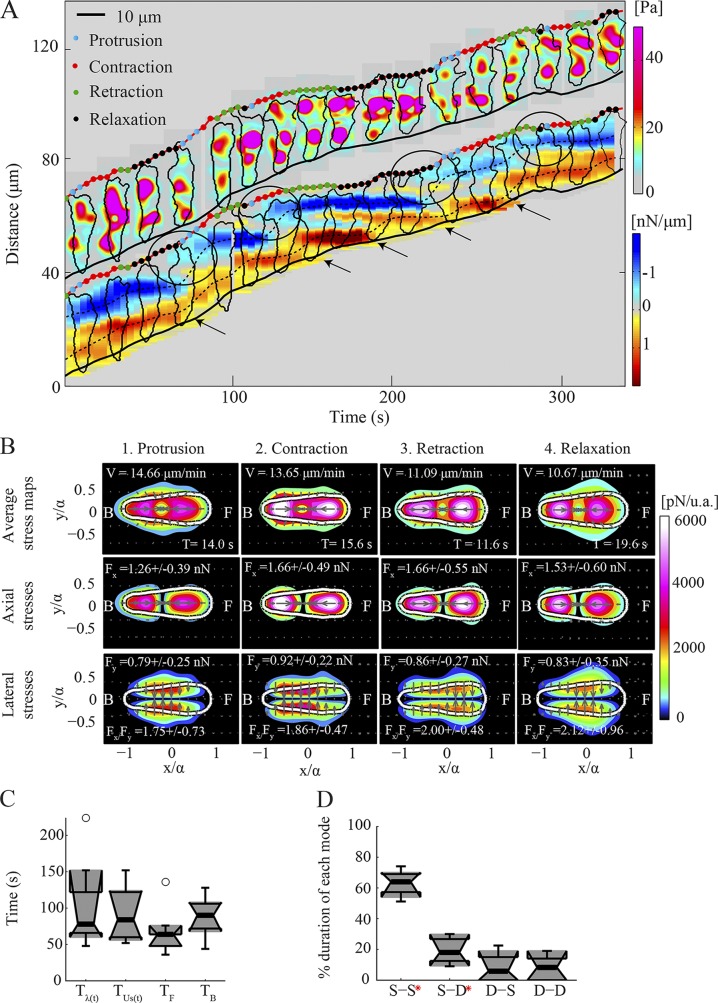
Figure 3.
Wild-type cells implement the S-S mode periodically. (A) Kymograph of the instantaneous magnitude of the traction stresses, (upper part), and axial tension, Tx (lower part), for a representative wild-type cell (the cell shown in Fig. 2 corresponds to t = 100 s until t = 180 s). and cell contours are displayed every 20 s. The dots superimposed on the front cell edge indicate the phases of the cycle. Black circles show pseudopod protrusion and front TA formation. Black arrows show TA loss and back cell edge retraction. The inclined red and black lines indicate the instantaneous position of the front and back cell edges. (B) Phase-average traction stress maps in the cell-based reference frame for the cell shown in A. Each column corresponds to a different phase. The first, second, and third rows show the magnitude of the total, axial, and lateral traction stresses, respectively, for each phase. The color patches indicate the magnitude of the traction stresses, and the arrows denote their direction. The white contours depict the average cell shape. The cell’s front (F) and back (B) are indicated. For each phase, the mean duration (T), speed (V), axial and lateral force (Fx and Fy), and ratio of axial to lateral force (Fx/Fy) are displayed. (C) Box plots of the period of the oscillations of: the cell length, Tλ(t); strain energy, ; and the position of the minimum and maximum Tx at the cell’s front and back with respect to its centroid, TF and TB (n = 8). Circles represent outliers, and the box plots’ notched sections show the 95% confidence interval around the median. (D) Box plots of the relative time duration of each mode implemented by wild-type cells (n = 8). Red asterisks denote a distribution whose median is not 0 (P < 0.05).
For short periods of time, the front and, more frequently, back TAs are more dynamic and less localized in space (Fig. S2, A and B). During these transient events, two or more diffuse TAs often coexist in close spatial proximity, which results occasionally in their merging. In the tension kymographs, this dynamic behavior is captured when the slope of the broken lines that track the TAs becomes positive. By measuring the speed of the TAs (the slope of the broken lines) normalized by the speed of migration of the whole cell as a quantitative indicator (Fig. S1, A–D; see the Materials and methods section), we found that, on average, wild-type cells implement a well-defined S-S mode 63% of the time (Fig. 3 D).
To assess if the S-S mode is specific to chemotaxing cells undergoing a directional migration, we calculated the traction stresses of cells migrating randomly (without chemoattractant source). Because these cells move less persistently, forming new and multiple protrusions in different directions, it was not useful to analyze their dynamics using kymographs, which are most appropriate for polarized cells with TAs aligned with their AP axis (and thus the direction of movement). Nevertheless, by inspecting the instantaneous traction stress maps, we found that randomly migrating cells establish multiple TAs during their movement that are more dynamic, and weaker than those of chemotaxing cells (Video 3). However, when a TA is stronger, it appears to be more stable (Video 3, black arrows), and the cell temporarily polarizes, increasing the otherwise low ratio of axial to lateral forces (Video 3, inset). These findings suggest that the cell’s potential to contract strongly axially and implement the S-S mode is associated with its ability to adopt a polarized shape and follow persistent movement.
The coordination of the front and back TAs is synchronized with the motility cycle
Fig. 3 A and Video 1 show that wild-type chemotaxing cells modulate their length and strain energy periodically, implementing a motility cycle coupled to the turnover of the TAs that is comprised of four phases with distinct mechanical characteristics. Using previously described algorithms (Meili et al., 2010), we analyzed our traction measurements by identifying these phases in each recording. We then plotted our measurements in a dimensionless cell-based coordinate system by calculating the major and minor moments of inertia of the cells and by rotating each cell to align its major axis with the horizontal axis with the cell’s front in the positive direction (Fig. 1 A, 1 and 2). A dimensionless cell-based representation was then obtained by rescaling the coordinates with the length of the major cell semiaxis. This representation allows us to compute phase-average stress maps including data from many cells and different instants of time (Figs. 3 B and S2 D), which provide an average snapshot of the organization of the cell’s traction stresses in each phase of the cycle.
To resolve the dynamics of the TAs during each phase of the motility cycle, we superimposed information about the phases on the kymographs using different colored dots at the front edge of each cell. The results show that the protrusion phase of the cycle is most often associated with the formation of a new front TA (Fig. 3 A, black circles). As shown in Fig. 3 A, while actively adhering at two TAs, the cell initiates protrusion of a new pseudopod during the relaxation phase (black dots; Soll, 1999). The pseudopod then adheres actively during the protrusion phase (cyan dots), and during the following contraction phase (red dots), the mechanical stress increases on the new front TA as the cell reaches its maximum length and speed (Fig. 3 A). Concurrently, the previously front TA progressively unloads as the cell moves forward and the middle of the cell nears it. This stationary TA becomes the new back TA in the forthcoming retraction phase (green dots) while the back cell edge nears the site of the previous back TA, which eventually breaks with the back edge of the cell retracting forward (black arrows). The cell then becomes less elongated and its speed decreases (relaxation phase), and the first signs of the formation of a new protrusion and the reinitiation of a cycle appear. Consistent with previous descriptions, we found that the time records of the cell length (λ), strain energy (Us), and the position of the front and back TAs relative to the cell’s centroid oscillate with roughly similar periods (Fig. 3 C), which suggests that all four time records are closely interrelated.
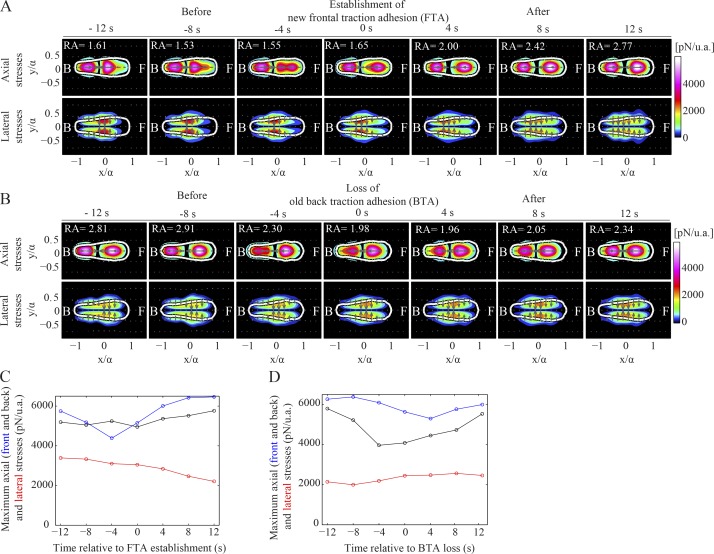
To determine what happens just before and after a TA is established or lost at the front or back half of the cell, we compiled average maps of the axial and lateral stress components for several wild-type cells, during these instants of time as well as 4, 8, and 12 s before and after (Fig. 4, A and B). Before the establishment of a new TA, we observed a local increase of the lateral traction stresses at the front half of the cells (Fig. 4, A and C). In marked contrast to the high front lateral stresses observed before the establishment of a new TA, we did not observe anything similar before the loss of a back TA (Fig. 4, B and D). This finding suggests that for the loss of the back TA, lateral stresses are not as important, and the cell’s ability to contract axially probably facilitates the back TA loss.
Figure 4.
Axial and lateral traction stresses during the establishment (and loss) of a TA. (A and B) Average stress maps during the establishment (A) and loss (B) of a TA (n = 8 cells). Top and bottom rows display the color contours of the magnitude of the axial and lateral traction stresses, respectively. Columns 1–7 show the average stress maps in a time interval of 12 s before and after the TA establishment or loss, and RA denotes the mean ratio of peak axial to lateral stress. (C and D) Average peak front axial (blue), back axial (black), and lateral stresses (red) during the establishment of a front TA (C) and the loss of a back TA (D). Average values refer to the cells shown in A and B. u.a., unit area.
Migration on highly adhesive substrates identifies a role for lateral contractions
The localized increase in the lateral stresses exerted at the front half of wild-type cells before the establishment of a new front TA suggests that lateral forces could play a role in frontal pseudopod formation and forward movement. To investigate the importance of lateral stresses and to assess the role that the dynamics of the TAs play in migration, we analyzed the dynamics of the movement of cells on highly adhesive substrates coated with collagen and the polycation poly-l-Lys (Jay et al., 1995; Videos 4 and 5).
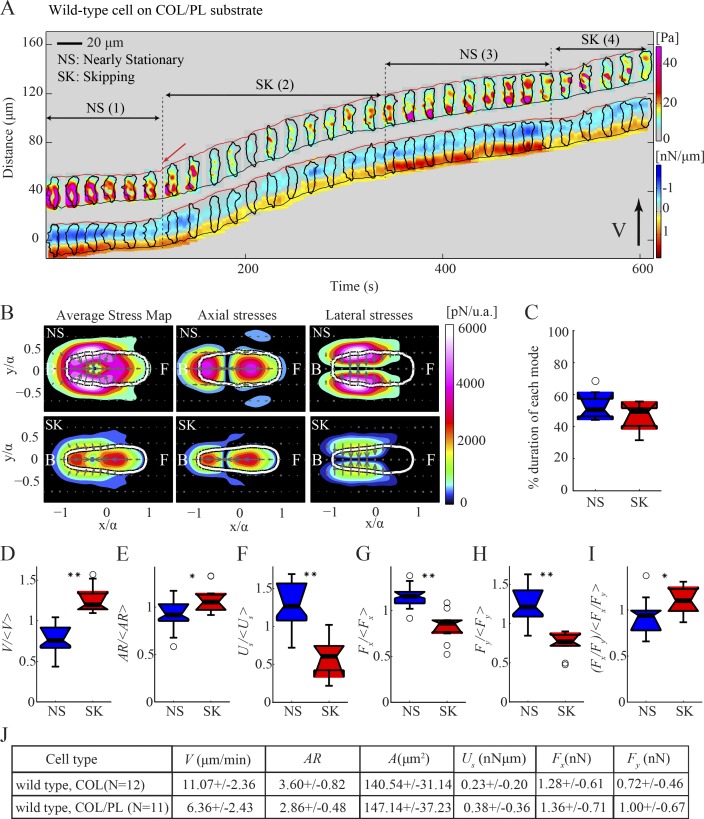
While chemotaxing on highly adhesive substrates, the cells exhibit two motility modes, distinct from the S-S mode implemented on regular substrates (Figs. 5 A and S3, A and B). When plated on this surface, the cells are less polarized and contract strongly inward (Fig. 5 A). They then initiate slow movement that we named nearly stationary (NS) by producing strong lateral contractions equal to or larger than the axial ones (Fig. 5 B). The increase in the lateral contractility leads to an elongation of the cell’s body and the protrusion of a pseudopod (Fig. 5 A, red arrow). Once the cell starts to move, it implements a mode we named “skipping” (SK), in which the cell becomes more polarized and does not form stationary front nor back TAs but instead forms numerous, weak, transient, and diffuse TAs along the cell’s length, as if it is skipping along the substrate (Fig. 5, A and D–I). Cells sporadically slow down as they adhere more tightly to the substrate, whereupon they start to increase their strain energy (Us) until the adhesions are broken and the cells start to move again (Fig. 5 A, see NS (3) and SK (4)). Cells spend approximately half of their time strongly adhering and squeezing and half their time skipping (Fig. 5 C). Although the overall mean migration speed (V) of wild-type cells on adhesive substrates is considerably lower than on collagen alone, there are no major differences between the mean speed during the SK compared with the S-S mode (Fig. S3, C and L). However, unlike the S-S mode, we found that cells migrate on adhesive surfaces without undergoing major changes in their length (λ) nor their strain energy (Us; Fig. S3, I and J), as can be observed by the trajectories of the cell’s front and back, which are parallel to the trajectory of the cell centroid (Fig. 5 A).
Figure 5.
Traction force dynamics in wild-type cells migrating on adhesive substrates. (A) Kymograph of the instantaneous magnitude of the traction stresses and axial tension for a wild-type cell chemotaxing on a highly adhesive substrate, showing that the cell alternates between the NS and SK modes. The inclined red and black lines indicate the instantaneous position of the front and back cell edges. (B) Left, middle, and right columns show the mean magnitude of the total, axial, and lateral stresses, respectively, in cell-based coordinates for the cell depicted in A during the NS (top) and SK (bottom) modes. (C) Box plots of the time duration of the NS (blue) and SK (red) modes (n = 9 cells). (D–I) Box plots of motility parameters corresponding to the NS and SK modes (n = 9 cells). Each parameter is normalized with its mean value for each cell. (D) Migration speed, V/V〉. (E) Aspect ratio, AR/AR〉. (F) Strain energy, Us/Us〉. (G) Axial force, Fx/Fx〉. (H) Lateral force, Fy/Fy〉. (I) Ratio of axial to lateral force, (Fx/Fy)/Fx/Fy〉. One or two asterisks denote statistically significant differences between medians (<0.05 or <0.01, respectively). (J) Table showing mean migration speed (V), aspect ratio (AR), cell area (A), strain energy (Us), axial and lateral force (Fx and Fy) for n = 11 cells on poly-L-Lys–coated substrate versus control (collagen only, n = 12).
We found that the increase in lateral forces in the NS mode is approximately twice as high as the corresponding increase in axial forces, compared with the SK mode (Fig. 5, B and G–J). This increase in lateral forces appears to be important for the release of nonspecific cell–substrate adhesions. Overall, our findings are consistent with lateral stresses being important for migration under conditions of increased adhesiveness, and suggest that amoeboid cells sense their environment and respond by modulating the strength and organization of their traction stresses.
Defects in actin cross-linking result in improper distribution of traction stresses and TAs as well as a failure to move on adhesive substrates
F-actin cross-linkers are essential for maintaining the mechanical integrity of the actin cytoskeleton. They stabilize the leading edge F-actin network and contribute to maintaining cortical tension, functions that are required for chemotaxis (Cox et al., 1995; Schindl et al., 1995). To understand their role in regulating the dynamics of axial and lateral contractions, we examined two strains with distinct defects in cytoskeletal F-actin cross-linking: myosin (MyoII) heavy chain null cells (mhcA−) and filamin (Abp120) null cells (abp120−). Assembled MyoII localizes to the lateral sides and posterior of cells and acts as both an F-actin cross-linker and a motor, which is important for the posterior contraction of the trailing edge (Fukui and Yumura, 1986; Uchida et al., 2003). Filamin localizes to the leading edge F-actin and is required for stabilization of the pseudopod F-actin network (Cox et al., 1996; Kicka et al., 2011).
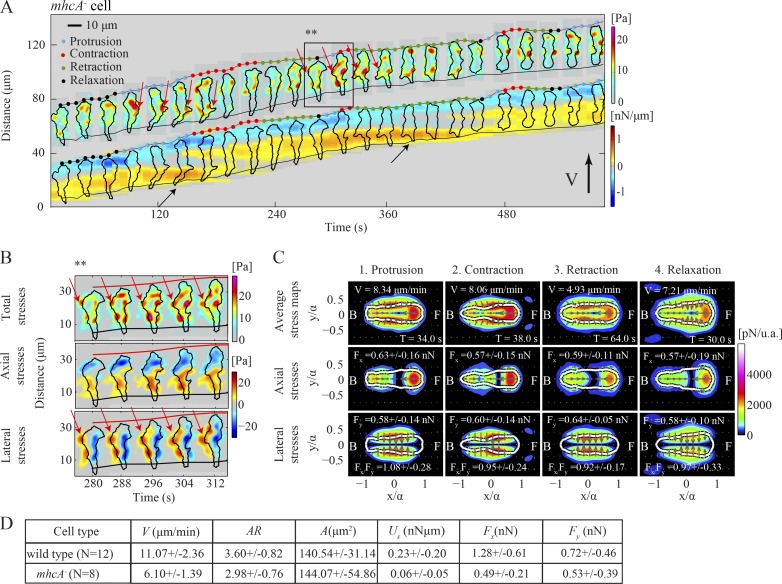
In agreement with previous studies, we find that mhcA− cells move slower than wild type, and both their strain energy (Us) and axial forces (Fx) are decreased compared with those of wild type, whereas their lateral forces (Fy) are comparable (Figs. 6 D and S4 A; Meili et al., 2010). The decrease in axial contractility is illustrated in the phase-average stress maps of mhcA− cells (Figs. 6 C and S4 A), which also show that the stresses lack a clear front-to-back polarity but instead are exerted inward toward the cell’s center from all around the cell’s perimeter. The axial stresses are localized and are stronger at the front half of the cell, while they are weaker and spread over a larger area at the back half. These stress maps can be better understood through inspection of the tension kymographs, which show that mhcA− cells form multiple TAs located along the cell’s periphery (Fig. 6 A and Video 6). These peripheral TAs often colocalize with lateral pseudopodia (Fig. 6 A, red arrows) and have a strong lateral stress component (Fig. 6 B). The exact nature of these TAs cannot be easily assessed quantitatively, as they are multiple and not localized along the cell’s AP axis, which is one of the limitations of the kymographic method. However, it is evident that the TAs (Fig. 6 A, black arrow) are occasionally stationary while the back cell edge is barely moving. This observation, together with the slower migration speed during their prolonged retraction phase, is consistent with the role of MyoII in promoting the contraction of the cell’s posterior (Fig. 6 A and Video 7; Jay et al., 1995; Lombardi et al., 2007). Therefore, we conclude that MyoII cross-linking and motor activities are essential for the cell to contract axially and develop a polarized shape. In the absence of MyoII, cells are less polarized but can still migrate, in part, by actively adhering at multiple mostly stationary TAs and contracting relatively more laterally (Fukui et al., 1989; Salbreux et al., 2012).
Figure 6.
Traction force dynamics in mhcA− cells. (A and B) Kymograph of the instantaneous magnitude of the traction stresses and axial tension for a mhcA− cell. Black and red arrows in A indicate stationary back and lateral TAs, respectively. A detailed view of the dynamics of the lateral TAs is shown in B, corresponding to the time interval indicated by the black box in A. Top, middle, and bottom rows show the magnitude of the total, axial, and lateral stresses, respectively. The inclined red and black lines indicate the instantaneous position of the front and back cell edges. (C) Same as Fig. 3 B but now corresponding to the mhcA− cell shown in A. (D) Same as Fig. 5 J for n = 8 mhcA− and n = 12 wild-type cells.
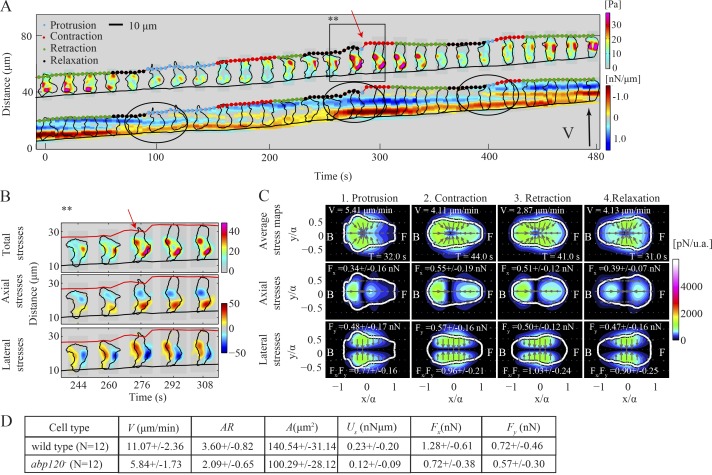
We used abp120− cells to investigate the role of proper F-actin cross-linking at the leading edge in the dynamics of traction forces and the potential role of lateral traction in cells’ motility. Similar to mhcA− cells, abp120− cells are less polarized and exhibit reduced axial forces (Fx) compared with wild type (Figs. 7 D and S4, K and L). The stress maps of a representative abp120− cell shown in Fig. 7 A demonstrate that on average these cells migrate by adhering actively on two sites that can be localized either along the cell’s AP axis or along the lateral sides (Fig. 7, A and B; and Video 8). We found that the mean ratio of axial to lateral forces is lowest in the relaxation and protrusion phases (Figs. 7 C and S4 G). In accordance with this, the cell shown in Fig. 7 A is less polarized during relaxation (black dots), during which it initiates lateral squeezing through two TAs located along the periphery (Fig. 7, A and B). In protrusion (Fig. 7, A and B, cyan dots), the cell continues squeezing laterally while effectively protruding a pseudopod forward (black circles). Once the cell attaches its pseudopod to the substrate, it enters the contraction phase (red dots) and initiates back-to-front contraction that enables the cell to pull its back forward (retraction phase, green dots). We found that abp120− cells lack localization of the Lifeact marker for F-actin near the cell’s leading edge (Fig. S5 A). Overall, these findings support a model in which abp120− cells may use lateral squeezing to propel cytoplasmic material at the front and achieve forward movement, and that leading edge F-actin polymerization plays a reduced role.
Figure 7.
Traction force dynamics in abp120− cells. (A and B) Kymograph of the instantaneous magnitude of the traction stresses and axial tension for an abp120− cell. The black circles in A denote protrusion events. A detailed view of the pseudopod protrusion resulting from sideways squeezing is shown in B, corresponding to the time interval indicated by the black box in A. Top, middle, and bottom rows show the magnitude of the total, axial, and lateral stresses, respectively. The inclined red and black lines indicate the instantaneous position of the front and back cell edges. (C) Same as Fig. 3 B but corresponding to the abp120− cell shown in A. (D) Same as Fig. 5 J for n = 12 abp120− and n = 12 wild-type cells.
Unlike wild-type cells, when both mutant cells are plated on an adhesive substrate, they attach firmly to it, generating contractile traction stresses all around the cell periphery, and move much slower than on a regular substrate (Fig. S5, B, C, F, and G; Jay et al., 1995). Contrary to wild-type cells that can increase their lateral contractility when migrating on an adhesive substrate, we found no difference in the mean axial and lateral forces (Fx and Fy) that the mutants exert on adhesive substrates compared with the control (Fig. S5, D, E, H, and I). This finding suggests that the extremely low velocity of the abp120− and mhcA− cells on highly adhesive substrates originates from their inability to modulate their traction stresses and generate sufficient lateral contractions to break the nonspecific adhesions with the substrate and initiate movement. The mutants generally adopt a rounder shape over time and eventually pop, possibly due to reduced tension needed to stabilize their cortex (Cox et al., 1995; Laevsky and Knecht, 2003).
Stable front TAs in chemotaxing neutrophil-like cells
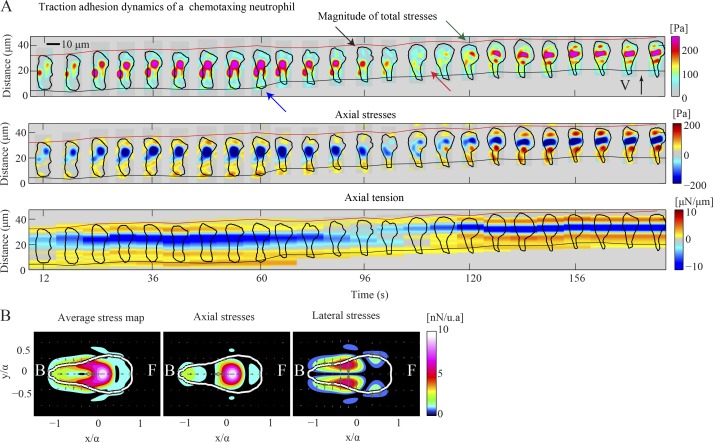
To test whether the S-S mode we found in D. discoideum amoebae is a conserved mechanism of amoeboid chemotactic migration, we performed experiments on chemotaxing dHL60 cells. The traction stresses of these cells and of human neutrophils were documented previously (Oakes et al., 2009; Jannat et al., 2010; Shin et al., 2010), but this is the first study that focuses on their dynamics. In accordance with previous work and similar to D. discoideum, neutrophils exert inward directed traction stresses (Fig. 8, A and B). Fig. 8 A shows the traction stress and tension kymographs for a chemotaxing dHL60 cell. Similar to D. discoideum cells, this neutrophil-like cell develops a stationary front TA and protrudes a pseudopod (black arrow). When the pseudopod actively attaches to the substrate (green arrow), a new front stationary TA is created (green arrow) while the previous front TA becomes the new back TA (red arrow). Our findings suggest that neutrophil traction stress dynamics share many similarities to those of D. discoideum and confirm that the kymographic representation can be a valuable tool for studying the migration of other amoeboid-type moving cell types.
Figure 8.
Traction force dynamics in a dHL60 cell. (A) Kymograph of the instantaneous magnitude of the traction stresses (top), axial stresses (middle), and axial traction tension (bottom) shown every 6 s for a chemotaxing dHL60 cell. The black arrow indicates pseudopod protrusion, followed by front TA formation (green arrow). The red arrow shows the transition of the front TA to the back. The blue arrow points to the back TA loss. The inclined red and black lines indicate the instantaneous position of the front and back cell edges. (B) Average maps of the magnitude of total (left), axial (middle), and lateral (right) traction stresses in cell-based coordinates for the cell shown in A.
Discussion
Stationary TAs are turned over in concert with the amoeboid motility cycle
During chemotaxis, cells translate the spatial information of the chemoattractant gradient into a series of spatiotemporally controlled intracellular signals (Weiner, 2002; Van Haastert and Devreotes, 2004). These, in turn, regulate the periodic generation of mechanical forces that mediate the movement of the cell up the chemical gradient, a process we and others have described as a motility cycle (Weber et al., 1995; Lauffenburger and Horwitz, 1996; del Álamo et al., 2007). This cycle can be broadly divided into four phases during which wild-type D. discoideum cells exhibit periodic oscillations in cell length, axial contractility, and turnover of their TAs (Meili et al., 2010). Previous studies suggested that amoeboid motility uses traction stresses caused by protrusion of the leading edge by F-actin polymerization and by retraction of the trailing edge by MyoII/F-actin contraction (Fukui et al., 1991; Zigmond, 1996). Increased cytosolic pressure due to MyoII-mediated contractions has been proposed to play a role in amoeboid motility (Langridge and Kay, 2006). However, none of these observations alone can fully explain the mechanical processes underlying the cell’s movement.
Using high-resolution stress maps obtained using FTFM techniques, we analyzed the dynamics of traction stresses of chemotaxing D. discoideum cells on flat 2D elastic substrates. We examined how wild-type cells regulate the formation and disassembly of their TAs in concert with the generation of axial and lateral contractility. By quantitatively analyzing and comparing wild-type to mutant cells with either F-actin cross-linking defects or those placed on adhesive substrates, we obtained new insights into how amoeboid cells move. Our findings in neutrophil-like cells suggest that the dynamics of the TAs found in D. discoideum may be conserved in a range of chemotaxing amoeboid-type cells.
We find that D. discoideum wild-type cells regulate their TAs in a step-wise fashion (S-S mode) in which the turnover of the TAs is tightly coordinated with the implementation of the motility cycle. When we juxtapose the phases of the motility cycle with the temporal dynamics of TAs during the S-S mode, we provide strong evidence that both processes are coregulated.
During persistent chemotactic migration of wild-type cells, the S-S mode is dominant 63% of the time. During the remaining 37%, the TAs are more dynamic and spatially dispersed, particularly at the back half of the cell. The resolution of our stress maps (∼1 µm in space and 4 s in time) makes it difficult to assess whether these multiple/diffuse TAs remain stationary while disassembling and reassembling at a high temporal rate, or if they continuously slide. Sliding of adhesions was proposed previously for other cell types whose cell–substrate adhesions were recorded using a fluorescent marker (Ballestrem et al., 2001; Jacobelli et al., 2009). The predominantly stationary nature of the TAs that we describe is consistent with previous studies visualizing the localization of ventral F-actin or the cell–substrate contacts (Weber et al., 1995; Yumura et al., 2013).
We further investigated whether the S-S mode is specific for persistent movement in a chemotactic gradient or whether it also applies to randomly moving cells. We found that during random motility, cells are not polarized and establish multiple weak and dynamic TAs. This finding suggests that the implementation of the S-S mode is associated with the cells’ ability to adopt a highly polarized shape and move directionally. It is possible that during random migration, the more dynamic, weaker TAs allow cells to readily change direction.
Evidence that lateral contractions are important for cell movement
Present and previous findings show that cells move at a fairly constant speed throughout all stages of the motility cycle, with cells moving only 20% faster during protrusion compared with relaxation (Meili et al., 2010). Our studies using mutants with defects in F-actin cross-linking or MyoII contractility reveal that the ability of cells to strongly contract axially is linked to proper leading-edge F-actin polymerization and MyoII contraction, whereas lateral contractility is not affected. These findings suggest that leading edge F-actin polymerization and MyoII are not fully responsible for generating the forces for cell movement. Our observations of wild-type D. discoideum chemotaxing cells demonstrate that lateral forces squeezing inward (perpendicular to the AP axis) are approximately half the magnitude of the axial forces. The presence of lateral forces was documented previously for non-amoeboid cells such as keratocytes and fibroblasts (Lee et al., 1994; Burton et al., 1999; Fournier et al., 2010). They contribute to the detachment of adhesions and the retraction of the back of the cell while their emergence is explained by the action of the transverse actin-myosin fibers that terminate at the lateral flanks of the cell (Burton et al., 1999). However, in our studies we observed a local increase of the lateral traction stresses immediately before the establishment of a new TA, which supports a role for lateral contractility in extending the pseudopod forward. Therefore, we suggest that these lateral forces may facilitate the development of pressure-driven protrusions that, along with anterior dendritic F-actin polymerization, are proposed to drive pseudopod protrusion and cell motility (Langridge and Kay, 2006; Charras, 2008).
Further evidence of the importance of lateral contractility in cell motility is provided by our analysis of cells migrating on adhesive substrates. In this case, wild-type cells exhibit a bimodal chemotaxis behavior distinct from the S-S mode observed on regular substrates. Cells sporadically get “stuck” or move very slowly, developing lateral contractions that are often stronger than the axial. We hypothesize that there may be a mechanosensing positive feedback loop, whereby a cell increases the lateral stresses until the assumed buildup of internal pressure is released by the cell protruding a pseudopod as it releases the nonspecific TAs between the plasma membrane and the substratum. Consistent with this model, Luo et al. (2013) showed that in micropipette-aspirated cells, the greater the applied pressure, the higher the local accumulation of MyoII. It is possible that the increase in lateral stresses is due to the enhanced action of MyoII in response to the increased buildup of internal pressure. Once the adhesions are broken, the cell moves rapidly, appearing to “skip” along the surface while forming multiple, weaker TAs, thereby minimizing the interaction with the sticky substrate. Different motility modes characterized by varying speed or adhesion dynamics have been observed in other cell types (Sahai and Marshall, 2003; Jacobelli et al., 2009). However, no previous studies have investigated the dynamics of traction stresses to identify and categorize how cells mechanistically move.
Cytoskeletal integrity is essential for efficient motility on normal and adhesive substrates
Our analysis of mutant strains that lack distinct F-actin cross-linking proteins suggests the involvement of lateral contractions in amoeboid cell motility. Consistent with previous studies, we determined that, compared with wild-type cells, mhcA− cells (which lack both MyoII cross-linking and motor activity) impart reduced strain energy to their substrate, and are incapable of applying strong axial contractions (Bosgraaf and van Haastert, 2006; Meili et al., 2010). The decrease in axial forces may be partially caused by defects in the architecture of the F-actin polymer network that result in cells with reduced cytoskeletal integrity and an increased number of lateral pseudopodia (Wessels et al., 1988). mhcA− cells move by forming numerous, generally stationary TAs all along the cell’s periphery, which often colocalize with the lateral pseudopodia. This is consistent with previous observations showing that convex extensions of the cell surface remain stationary as cells migrate (Van Haastert, 2011; Driscoll et al., 2012). It is possible that the decreased axial versus lateral contractility observed in mhcA− cells may, in part, originate from the presence of lateral pseudopodia that exert higher lateral stresses through the action of other contractile proteins (Salbreux et al., 2012).
We also found that cells lacking Filamin A (abp120−), an orthogonal F-actin cross-linker that localizes at the leading edge F-actin network and is important for cortical integrity, also have reduced axial contractility (Cox et al., 1995; Reichl et al., 2008). Our analysis of the stress dynamics of abp120− cells yielded findings consistent with a model in which pseudopod protrusion can occur, in part, through lateral contractions that generate sufficient turgor pressure to help push cytoplasmic material forward (Condeelis, 1992; Cox et al., 1992). It appears logical that abp120− cells require a higher level of lateral contraction for the protrusion of the pseudopod than do the wild-type cells because they cannot effectively form an F-actin–driven pseudopod.
We find that disrupting MyoII contractility or the F-actin cross-linker Filamin A inhibits the ability of the cells to modulate their lateral contractility to break up attachments to the substrate and initiate forward motion on substrates of increased adhesiveness. This observation suggests that the ability of cells to contract strongly must rely in part on activity of contractile proteins and on the cytoskeletal integrity of the cells (Jay et al., 1995). We have limited our study to mhcA− and abp120− cells but, given our observations, other proteins involved in contractility (Levayer and Lecuit, 2012; Salbreux et al., 2012) and cytoskeletal cross-linking (Kee et al., 2012; Luo et al., 2012) must also contribute to the generation of axial and lateral contractility.
Amoeboid motility modes may be a highly conserved mechanism
Through experiments on chemotaxing neutrophil-like cells, we demonstrate that their traction stress dynamics are similar to those of wild-type D. discoideum cells. Our findings suggest there may be a common mode of amoeboid cell movement, or one that is used by cells as evolutionarily distinct as D. discoideum and neutrophil-like cells. It is plausible that we have uncovered a highly conserved mechanism that works in a similar fashion in a range of amoeboid cells, such as neutrophils, as well as other forms of cell motility.
Materials and methods
D. discoideum culture, preparation of aggregation competent cells, and microscopy
D. discoideum cells were grown under axenic conditions in HL5 growth medium on tissue culture plates. We used wild-type cells (Ax2 and Ax3), abp120− cells (generated from Ax2), and mhcA− cells (generated from Ax3) obtained from the Dicty Stock Center. We transformed all cell lines to generate lines expressing Lifeact (Abp140-GFP; Riedl et al., 2008), a 17-amino-acid peptide that binds F-actin. For all chemotaxis applications, cells were taken from axenic exponentially growing or “log-phase” cultures. These can be obtained by shaking cells in nutrient medium, in an autoclaved Erlenmeyer flask at 150 rpm, at 22°C overnight. The next morning the cells were counted using a hemocytometer to determine cell density. Aggregation-competent cells were prepared by pulsing a 5 × 106 cells/ml suspension in Na/K phosphate starvation buffer (9.6 mM KH2PO4 and 2.4 mM Na2HPO4, pH 6.3) with cAMP to a concentration of 30 nM every 6 min for 6 h (Meili et al., 1999). Cells were then diluted in Na/K phosphate buffer at low density (105 cells/ml), and 200 µl of cells were seeded onto a flat elastic collagen-coated polyacrylamide substrate and allowed to adhere. A drawn glass capillary mounted on a micromanipulator served as the source of chemoattractant (150 µM cAMP in an Eppendorf femtotip).
We acquired images using an inverted microscope (TE300; Nikon) with a Plan Fluor 40× 0.6 NA air objective lens and a cooled charge-coupled device camera (HQ CoolSNAP; Roper Scientific). A PC running MetaMorph software (Molecular Devices) controlled the entire setup including filter wheels. For the image acquisition of the cells expressing the Lifeact marker, we used a spinning disk confocal microscope (DMIRE2 [Leica]; CSU10 [Yokogawa Corporation of America]) with a Plan Apochromat 40× 1.4 NA oil objective lens and a PC running Slidebook software (3I) to control the entire setup. The microscope was equipped with a piezo-Z actuator (ASI).
Culture of HL60 cells, preparation of DMSO differentiation of HL60 cells, and microscopy
Culture and DMSO differentiation of HL60 cells were performed as described previously (Millius and Weiner, 2010). In brief, undifferentiated HL60 cells were cultured in RPMI 1640 medium plus 1-glutamine and 25 mM Hepes cell culture medium supplemented with 10% antibiotics/ antimycotics (Invitrogen) and 15% heat-inactivated fetal bovine serum (Invitrogen).
For differentiation, 1.3% DMSO was added to the supplemented RPMI 1640 described previously, and 1.5 × 104 cells were suspended in the medium. Cells were incubated with DMSO-containing medium for 5 d. On the fifth day, 2.6 × 104 DMSO-differentiated HL60 cells (dHL60) suspended in 200 µl of RPMI 1640 cell culture medium were seeded onto a flat elastic fibronectin-coated polyacrylamide substrate and allowed to attach for ∼1 h. Before seeding with cells, we incubated the gels in cell culture medium for a minimum of 1 h at 37°C. A drawn glass capillary mounted on a micromanipulator served as the source of chemoattractant (1 µM fMLP in an Eppendorf femtotip).
For the image acquisition of the dHL60 cells, we used an inverted microscope (DMI3000 B; Leica) with a Plan Fluor 40× 0.7 NA air objective lens and a PC running Openlab software (PerkinElmer) to control the entire setup. The experiments were conducted at 37°C and the pH of the medium was stabilized by the 25 mM Hepes, pH 7.4, contained in the culture medium.
Polyacrylamide gel fabrication
12-mm-diameter and ∼40-µm-thick polyacrylamide hydrogels were prepared using 5% acrylamide and 0.06% bis-acrylamide (Young’s modulus ∼1,200 Pa) on a glass carrier and were coated with 0.25 mg/ml collagen I and used as substrates for our cells (Wang and Pelham, 1998; Engler et al., 2004). The gels consist of two layers: the bottom layer contains no beads, and the top contains 0.04% (by volume) carboxylate-modified red latex beads 0.1 µm in diameter (FluoSpheres; Molecular Probes). To improve the signal-to-noise ratio, the polyacrylamide gel was fabricated as two sequential layers, with the first containing no beads and the second containing 0.03% carboxylate modified yellow latex beads with a 0.1-µm diameter (FluoSpheres). The exact protocol we followed consisted of three steps described below.
Lower glass coverslip treatment.
25-mm glass coverslips were placed on a hot plate and 500 µl of 0.1 M NaOH was added to cover the entire surface of the coverslips. Once the liquid evaporated, leaving a uniform, thin, white film of NaOH on the surface, the coverslips were removed from the plate and placed in a fume hood. The coverslips were covered with 100 µl of 3-aminopropyltriethoxysilane (APES) for 5 min and then rinsed thoroughly with distilled water. The coverslips were dried, and 100 µl of a premixed solution of 0.5% glutaraldehyde in PBS buffer was added to them and let stand for 30 min. The coverslips were then rinsed and dried to ready them for gel attachment.
Preparation of the two gel layers.
The polyacrylamide gel consisted of two layers: the bottom containing no beads and the top containing 4 µl of 2% carboxylate modified yellow latex beads. Two solutions of 5% acrylamide and 0.06% bis-acrylamide were prepared using 12 mM Na/K phosphate starvation buffer, pH 6.3, as a solvent, and one contained 0.03% carboxylate modified red latex beads (Fluospheres). The solutions were placed on ice in a vacuum for 15 min to reduce dissolved oxygen. 0.8 µl of TEMED (cross-linker) and 1.2 µl of 10% APS (catalyst) were added to the solution containing no beads, and then 3.6 µl of the mixture was placed at the center of circular glass coverslips, which were positioned on top of the treated square coverslips to “sandwich” the polyacrylamide gel. When the gel polymerized (10–30 min), the second layer containing the tracker beads was added in a similar manner and some weight was placed on the top coverslip to make the bead-containing layer slightly thinner. The square coverslips with the two layers on top of them were then mounted into Petri dishes filled with 50 mM Hepes buffer, pH 8.5, using silicon grease (Dow Corning).
Inspection of the gel and activation with Sulfo-SANPAH.
Gels were examined under the microscope to verify that the distribution of beads was uniform and that the layer of beads was confined in one focal plane (the uppermost). Otherwise they were discarded. We then cross-linked collagen I to the surface of the gels using Sulfo-SANPAH (Thermo Fisher Scientific; 1 mM in Hepes buffer, pH 8.5). After UV activation and washing thoroughly, 0.25 mg/ml collagen protein in Hepes was added and the gels were incubated overnight at room temperature. After washing the gels were stored with buffer (50 mM Hepes buffer, pH 8.5) and antibiotic (40 mM ampicillin) for use within a week. Substratum thickness was measured by locating the top and bottom planes of the gel and subtracting their z positions. The gels were stored in 4°C and could be used within one week.
To study the mechanics of cell motility on highly adhesive substrates, we used poly-l-Lys (20 mg/ml, mol wt 30,000–70,000; Sigma-Aldrich) mixed together with the collagen solution, while the rest of the steps in the protocol remained the same. The optimal concentration of poly-l-Lys that still allowed the cells to chemotax with decreased migration speed was determined empirically.
We slightly modified fabrication for seeding differentiated HL60 cells. Polyacrylamide hydrogels were prepared with 4% acrylamide and 0.15% bis-acrylamide (Young’s modulus = ∼3,500 Pa) on a glass carrier. The upper layer in this case contained 0.04% carboxylate-modified green latex beads 0.2 µm in diameter (FluoSpheres), and the substrates were coated with 10 µg/ml bovine fibronectin (Sigma-Aldrich) overnight. Gels were prepared and coated with fibronectin the day before the experiment.
Cell identification
We acquired differential interference contrast (DIC) images using a 40× air objective lens at 4-s intervals for D. discoideum cells and 6-s time intervals for HL60 cells. Time-lapse fluorescent confocal images were acquired using a 40× oil immersion lens at 12-s intervals. For each time point, z stacks along the cell height were also acquired with a z spacing of 1 µm (typically 15 images). We used a custom algorithm using MATLAB (MathWorks) to automatically identify the contour of the cells from the DIC images and the fluorescent confocal images (del Álamo et al., 2007). In brief, in the case of the DIC images, imperfections were removed from the individual images using the average of the image series. A threshold was then applied to the resulting images to extract the most intense features, which were refined using two consecutive image dilations and erosions with structuring elements of increasing size. Details of the exact contour identification method can be found elsewhere (del Álamo et al., 2007). For the fluorescent confocal images, the contour of the cell was found by setting a predefined, constant threshold. In the case of the fluorescent confocal images, we performed the 3D reconstruction (rendering) of the cell using IMARIS software (Bitplane).
The location of the centroid (center of mass; xc, yc), and the orientation of the major and minor moments of inertia (longitudinal and transverse axes) of each cell were calculated using standard MATLAB functions. We determined the front and back as the two parts in which the minor axis of inertia splits each cell, with the front pointing toward the direction of motion (del Álamo et al., 2007).
Measurements of the substrate deformation
As the cells apply traction forces, they induce deformations on the elastic substrate on which they attach. We measured the deformation of the substrate from the displacements of the fiduciary fluorescent beads embedded in the upper layer of the substrate. In brief, at each time interval we measured the 2D deformation of the substrate at each point using a technique similar to particle image velocimetry (Willert and Gharib, 1991; Gui and Wereley, 2002). We calculated the local deformation vector by performing an image correlation between each image and the unstretched reference image. We used interrogation windows of 16 × 16 pixels with a 50% overlap. Further details of this technique can be found in del Álamo et al. (2007) and in the supplemental image analysis workflow.
Calculation of the traction stresses, strain energy, and construction of the axial tension kymograph
The traction stress (traction force per unit area) field exerted by the cells on the surface of the substrate was calculated from the measured deformation using in-house FTFM methods (del Álamo et al., 2007; DynaCyte 1.0). These methods consist of solving analytically the elastostatic equation of equilibrium for a linear, homogeneous, isotropic, 3D body using a Fourier series and taking into account the finite thickness of the substrate (h), thus improving the accuracy of previous methods based on unconstrained FTFM (Butler et al., 2002). The thickness of the substrate h was on average 40 µm, the measured Young’s modulus E of the substrate was 1.2 kPa (Bastounis et al., 2011), and the Poisson’s ratio σ was assumed to be ∼0.45, as reported in previous studies (Li et al., 1993; Engler et al., 2004; Frey et al., 2007).
The boundary conditions used were as follows: no slip at the base of the substrate (, where ), the displacements at h0 are and and the vertical stress is τzz (z = h) = 0, since the density of the cells and the surrounding buffer are similar and the contractile fibers of the cytoskeleton tend to predominantly orient horizontally. We assumed periodicity in the horizontal directions. Thus the equations governing the displacement field for a linear, homogeneous, isotropic, 3D body of finite thickness are:
We find the solution of the elastostatic equation using Fourier series:
where α and β are the wavenumbers for the x, y directions and and are the complex Fourier coefficients for and , which are functions of the vertical coordinate and are linearly related to the Fourier coefficients of the horizontal displacements measured at z = h0. A mathematical derivation of the solution is provided in del Álamo et al. (2007).
Once the cell contour was determined from the DIC images, we identified the location of the major and minor second moments of inertia and the orientation of their axes. The traction stress field was then calculated (Fig. 1 A, 1) and rotated to make the cell’s major axis parallel to the vertical direction at each instant of time. Fig. 1 A (2) shows the magnitude of the instantaneous traction stresses, . In this new coordinate system, we calculated at each instant of time the axial traction tension by integrating the x component of the traction stresses across the cell width (minor axis, y direction), as shown in Fig. 1 A (3):
The axial traction tension Tx(x, t) defined this way has the dimension of force per unit length and typically is of the order of pN/µm. The tension kymograph was then constructed by stacking different temporal measurements and plotting Tx(x, t) in two dimensions, with t in the horizontal axis and the position in the vertical axis (Fig. 1 B). This representation allows for a detailed quantitative analysis of the coupled evolution of shape changes and the location and magnitude of the traction forces during migration with high temporal resolution.
To investigate how directed contractility contributes to the cell motility, we decomposed the traction force vector exerted by the cell on the substrate into its axial and lateral components Fx and Fy. We then define the axial and lateral contractility Fx and Fy as:
where Ff and Fb are the surface integrals of the axial traction stresses exerted by the cell in its front and back halves, respectively, while Fl and Fr are the surface integrals of the lateral traction stresses that the cell exerts at its right and left halves (relative to the cell’s major axis):
Note that Ff = −Fb and Fl = −Fr, as the inertia of the cell is negligible and the cell is always in static equilibrium. We calculate at each instant of time the strain energy (Us) as the mechanical work per unit area done by the cell to deform its substrate:
where is the measured displacement vector field on the free surface of the substrate and represents a surface integral. Further details of the calculation of the traction stresses have been provided previously (del Álamo et al., 2007; Alonso-Latorre, 2010).
Cell-based reference system, average traction stress maps, and phase-average splitting
The shape and the orientation of the cells constantly change in the laboratory reference. Thus, to perform statistical analysis over long periods of time and over many different cells, we represent the instantaneous traction stress fields in a cell-based, dimensionless coordinate system (x/a, y/α). The cell-based representation involves aligning the longitudinal major axis of the cell with the horizontal axis, with the cell’s front always pointing in the positive direction (Fig. 1 A, 1 and 2), and rescaling all the length dimensions with the half cell length α. The centroid of each cell (xc, yc) is positioned at the origin of the cell-based coordinate system. Details of the cell-based coordinate system can be found elsewhere (del Álamo et al., 2007; Alonso-Latorre, 2010; Figs. 3 B and S2 D).
We used conditional statistics to characterize the mean traction stresses exerted by the different cell lines during the four phases of their motility cycle. The phase-average stress maps were calculated from instantaneous maps of traction stresses after arranging the experimental time-lapse data series by phases. The sorting procedure is based on conditional statistics applied to the time record of the length of the cell, λ(t). First, we manually selected the peaks and valleys of each cell length time record. Then, a computer algorithm automatically divided each cycle of λ(t) into four phases: phase 1, protrusion (when the length is increasing); phase 2, contraction (when the length is maximal); phase 3, retraction (when the length is decreasing); and phase 4, relaxation (when the length is at a local minimum). This previously described algorithm (Meili et al., 2010) worked by applying the following adaptive threshold on λ(t):
where tmin and tmax are the instants of time associated with the nearest local minimum and maximum of λ(t), λmin = λ(tmin), and λmax = λ(tmax). Once a phase had been assigned to each time point of our time-lapse experiments, we calculated the average maps of traction stresses based on the conditions that Phase(t) = 1, … 4. The threshold needs to be 0 < α < 0.5 to avoid overlap of adjacent phases and was set to α = 0.2. The selection of a threshold for separating the motility cycle into stages was shown to have a negligible effect on the phase-averaged traction maps (Meili et al., 2010).
Analysis of the different cell motility modes
At each time point, we estimated the position of minima and maxima of the axial traction tension Tx at the front (blue indicates negative traction tension) and at the back (red indicates positive traction tension) of the cell by calculating the centers of gravity of the fourth power of the positive and negative axial traction tensions. The resulting time records of the positions represent the trajectories of the front and back TAs of the cell. These trajectories were smoothed out using a triangular convolution kernel, and their time derivatives were calculated using a second-order finite difference scheme. These time derivatives represent the speeds of the front (VF) and rear (VB) TAs of the cell. The mean speed of the cell centroid was obtained (VCM〉) using the same numerical procedures, and we normalized VF and VB with VCM〉. The magnitude of the normalized speeds VF/VCM〉 and VB/VCM〉 was used to determine the dynamics of the TAs. When VF or VB are near zero, it means that the corresponding TA remains stationary (fixed in space). The spikes in these signals are associated with discontinuities in the trajectories of the front and back TAs and thus indicate the establishment or loss of a new TA at the front or back half of the cell, respectively (for further explanation see Fig. S1, A–D).
Using the axial tension kymographs and the calculated values of the normalized speeds of TAs, we established a semiautomatic criterion to identify the distinct motility modes. We assumed that normalized TA speeds <0.5 suggest stationary TA sites (Fig. S1 D, open circles). Intermediate normalized speeds between 0.5 and 1 (Fig. S1 D, asterisks) are associated with more diffused, occasionally multiple and temporally dynamic TAs. Finally, normalized speeds >1 are associated with spikes in the signals caused by the appearance or disappearance of TAs. Points between spikes are counted and if the majority have normalized speeds <0.5, the corresponding TA is considered stationary, whereas if the majority have normalized speeds between 0.5 and 1 the corresponding TA is classified as dynamic. Thus, four different modes can arise from this classification: (1) S-S, when both front and rear TAs are clearly stable and stationary, (2) stable-dynamic (S-D), when the frontal TA is clearly stable but the rear is more diffused and is either continuously sliding or stationary but has a turnover rate comparable with the experimental time resolution (4 s); (3) dynamic–stable (D-S), and (4) dynamic–dynamic (D-D).
In the case of wild-type cells migrating on highly adhesive substrates coated with poly-L-Lys, we followed a similar method to identify the motility modes. In this condition, cells were observed rapidly creating and destroying TAs, resulting in spikes at the normalized TA speeds (Fig. S3 B). When that occurs, the specific mode is characterized as SK. Asterisks or circles between spikes are counted. If the majority are asterisks the TA is classified as SK, and if not, it is considered stable. We noticed that the vast majority of time the cell barely moves but the TAs are stable. Thus, we named this second case of S-S mode NS.
Average stress maps during the establishment or loss of TAs
To gain insight into what happens just before a TA is established at the front half of wild-type cells, we identified these events by tracking the spikes in the speed of the location of maximum tension at the front half of the cells (VF). Because wild-type cells predominantly move using the S-S motility mode, each spike corresponds to the establishment of a new TA at the front of the cells. We then compiled average maps of the axial and lateral components of the stresses for several wild-type cells 4, 8, and 12 s before and after these spikes. In a similar manner, to elucidate what happens on average just before a TA is lost at the back half of the cells, we identified these events by tracking the spikes in the speed of the location of maximum tension at the back half of the cells (VB). We then compiled average maps of the axial and lateral components of the stresses for several wild-type cells 4, 8, and 12 s before and after these spikes.
Online supplemental material
Fig. S1, related to Fig. 2, illustrates how the motility modes of chemotaxing wild-type D. discoideum cells on regular collagen-coated substrates are identified. Fig. S2, related to Fig. 3, shows the traction stress and tension kymographs of a representative wild-type cell that is not implementing the S-S mode as well as the phase-average traction stresses during the motility cycle of Ax2 wild-type cells. Fig. S3, related to Fig. 5, illustrates the dynamics and statistics of motility modes in wild-type cells migrating on highly adhesive substrata. Fig. S4, related to Figs. 6 and 7, depicts the phase-average stress maps and motility statistics of mhcA− cells and abp120− cells compared with wild type. Fig. S5 illustrates that abp120− cells show no F-actin localization on regular collagen-coated substrates and that both abp120− and mhcA− cells are unable to migrate on substrates additionally coated with poly-L-Lys. Video 1, related to Fig. 3 A, shows the time evolution of the traction stresses and the corresponding progressive emergence of a tension kymograph for a chemotaxing wild-type D. discoideum cell. Video 2, related to Fig. 3, illustrates the 3D shape changes and traction stresses of a chemotaxing wild-type cell. Video 3 shows the time evolution of the traction stresses in the laboratory reference frame during wild-type random migration. Video 4 refers to Fig. 5 A, and indicates the traction stresses and the emergence of the tension kymograph for a chemotaxing wild-type cell migrating on a highly adhesive substratum. Video 5 refers to Fig. 5, and shows the 3D shape changes and traction stresses of a chemotaxing wild-type cell on a highly adhesive substratum. Videos 6 and 7 refer to Fig. 6, and depict the traction stresses and corresponding tension kymograph for a representative chemotaxing apb120− cell, and the 3D shape changes and traction stresses of another representative chemotaxing apb120− cell, respectively. Videos 8 and 9 refer to Fig. 7, and demonstrate the traction stresses and corresponding tension kymograph for a representative chemotaxing mhcA− cell, and the 3D shape changes and traction stresses of another representative chemotaxing apb120− cell, respectively. The image analysis workflow and associated original data in the JCB DataViewer document the image processing steps used to derive the data shown in Fig. 2 A, Fig. 3 A, and Video 1. Online supplemental material is available at http://www.jcb.org/cgi/content/full/jcb.201307106/DC1. Additional data are available in the JCB DataViewer at http://dx.doi.org/10.1083/jcb.201307106.dv.
Supplementary Material
Acknowledgments
We would like to thank Susan Lee for her assistance.
E. Bastounis and J. Francois were funded, in part, by a training grant (5T32 HL105373) from the U.S. Public Health Service (USPHS). This work was funded by USPHS grants R01 GM084227 and R01 GM037830.
The authors declare no competing financial interests.
Footnotes
Abbreviations used in this paper:
- AP
- anterior–posterior
- DIC
- differential interference contrast
- FTFM
- Fourier traction force microscopy
- MyoII
- Myosin II
- NS
- nearly stationary
- SK
- skipping
- S-S
- stable-stable
- TA
- traction adhesion
References
- Alonso-Latorre B. 2010. Force and shape coordination in amoeboid cell motility. PhD thesis University of California, San Diego: 152 pp [Google Scholar]
- Alonso-Latorre B., Del Álamo J.C., Meili R., Firtel R.A., Lasheras J.C. 2011. An oscillatory contractile pole-force component dominates the traction forces exerted by migrating amoeboid cells. Cell. Mol. Bioeng. 4:603–615 10.1007/s12195-011-0184-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bagorda A., Mihaylov V.A., Parent C.A. 2006. Chemotaxis: moving forward and holding on to the past. Thromb. Haemost. 95:12–21 [PubMed] [Google Scholar]
- Balaban N.Q., Schwarz U.S., Riveline D., Goichberg P., Tzur G., Sabanay I., Mahalu D., Safran S., Bershadsky A.D., Addadi L., Geiger B. 2001. Force and focal adhesion assembly: a close relationship studied using elastic micropatterned substrates. Nat. Cell Biol. 3:466–472 10.1038/35074532 [DOI] [PubMed] [Google Scholar]
- Ballestrem C., Hinz B., Imhof B.A., Wehrle-Haller B. 2001. Marching at the front and dragging behind: differential alphaVbeta3-integrin turnover regulates focal adhesion behavior. J. Cell Biol. 155:1319–1332 10.1083/jcb.200107107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bastounis E., Meili R., Alonso-Latorre B., del Álamo J.C., Lasheras J.C., Firtel R.A. 2011. The SCAR/WAVE complex is necessary for proper regulation of traction stresses during amoeboid motility. Mol. Biol. Cell. 22:3995–4003 10.1091/mbc.E11-03-0278 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bosgraaf L., van Haastert P.J. 2006. The regulation of myosin II in Dictyostelium. Eur. J. Cell Biol. 85:969–979 10.1016/j.ejcb.2006.04.004 [DOI] [PubMed] [Google Scholar]
- Burton K., Park J.H., Taylor D.L. 1999. Keratocytes generate traction forces in two phases. Mol. Biol. Cell. 10:3745–3769 10.1091/mbc.10.11.3745 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butler J.P., Tolić-Nørrelykke I.M., Fabry B., Fredberg J.J. 2002. Traction fields, moments, and strain energy that cells exert on their surroundings. Am. J. Physiol. Cell Physiol. 282:C595–C605 10.1152/ajpcell.00270.2001 [DOI] [PubMed] [Google Scholar]
- Charras G.T. 2008. A short history of blebbing. J. Microsc. 231:466–478 10.1111/j.1365-2818.2008.02059.x [DOI] [PubMed] [Google Scholar]
- Condeelis J. 1992. Are all pseudopods created equal? Cell Motil. Cytoskeleton. 22:1–6 10.1002/cm.970220102 [DOI] [PubMed] [Google Scholar]
- Cox D., Condeelis J.S., Wessels D., Soll D.R., Kern H., Knecht D.A. 1992. Targeted disruption of the ABP-120 gene leads to cells with altered motility. J. Cell Biol. 116:943–955 10.1083/jcb.116.4.943 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox D., Ridsdale J.A., Condeelis J.S., Hartwig J. 1995. Genetic deletion of ABP-120 alters the three-dimensional organization of actin filaments in Dictyostelium pseudopods. J. Cell Biol. 128:819–835 10.1083/jcb.128.5.819 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox D., Wessels D., Soll D.R., Hartwig J., Condeelis J. 1996. Re-expression of ABP-120 rescues cytoskeletal, motility, and phagocytosis defects of ABP-120− Dictyostelium mutants. Mol. Biol. Cell. 7:803–823 10.1091/mbc.7.5.803 [DOI] [PMC free article] [PubMed] [Google Scholar]
- del Álamo J.C., Meili R., Alonso-Latorre B., Rodríguez-Rodríguez J., Aliseda A., Firtel R.A., Lasheras J.C. 2007. Spatio-temporal analysis of eukaryotic cell motility by improved force cytometry. Proc. Natl. Acad. Sci. USA. 104:13343–13348 10.1073/pnas.0705815104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Driscoll M.K., McCann C., Kopace R., Homan T., Fourkas J.T., Parent C., Losert W. 2012. Cell shape dynamics: from waves to migration. PLOS Comput. Biol. 8:e1002392 10.1371/journal.pcbi.1002392 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engler A., Bacakova L., Newman C., Hategan A., Griffin M., Discher D. 2004. Substrate compliance versus ligand density in cell on gel responses. Biophys. J. 86:617–628 10.1016/S0006-3495(04)74140-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fey P., Stephens S., Titus M.A., Chisholm R.L. 2002. SadA, a novel adhesion receptor in Dictyostelium. J. Cell Biol. 159:1109–1119 10.1083/jcb.200206067 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fournier M.F., Sauser R., Ambrosi D., Meister J.J., Verkhovsky A.B. 2010. Force transmission in migrating cells. J. Cell Biol. 188:287–297 10.1083/jcb.200906139 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frey M.T., Engler A.J., Discher D.E., Lee J., Wang Y.L. 2007. Microscopic methods for measuring the elasticity of gel substrates for cell culture: microspheres, microindenters, and atomic force microscopy. Methods Cell Biol. 83:47–65 10.1016/S0091-679X(07)83003-2 [DOI] [PubMed] [Google Scholar]
- Friedl P., Borgmann S., Bröcker E.B. 2001. Amoeboid leukocyte crawling through extracellular matrix: lessons from the Dictyostelium paradigm of cell movement. J. Leukoc. Biol. 70:491–509 [PubMed] [Google Scholar]
- Fukui Y., Yumura S. 1986. Actomyosin dynamics in chemotactic amoeboid movement of Dictyostelium. Cell Motil. Cytoskeleton. 6:662–673 10.1002/cm.970060614 [DOI] [Google Scholar]
- Fukui Y., Lynch T.J., Brzeska H., Korn E.D. 1989. Myosin I is located at the leading edges of locomoting Dictyostelium amoebae. Nature. 341:328–331 10.1038/341328a0 [DOI] [PubMed] [Google Scholar]
- Fukui Y., Murray J., Riddelle K.S., Soll D.R. 1991. Cell behavior and actomyosin organization in Dictyostelium during substrate exploration. Cell Struct. Funct. 16:289–301 10.1247/csf.16.289 [DOI] [PubMed] [Google Scholar]
- Gov N.S. 2006. Modeling the size distribution of focal adhesions. Biophys. J. 91:2844–2847 10.1529/biophysj.106.088484 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grabher C., Cliffe A., Miura K., Hayflick J., Pepperkok R., Rørth P., Wittbrodt J. 2007. Birth and life of tissue macrophages and their migration in embryogenesis and inflammation in medaka. J. Leukoc. Biol. 81:263–271 10.1189/jlb.0806526 [DOI] [PubMed] [Google Scholar]
- Gui L., Wereley S.T. 2002. A correlation-based continuous window-shift technique to reduce the peak-locking effect in digital PIV image evaluation. Exp. Fluids. 32:506–517 10.1007/s00348-001-0396-1 [DOI] [Google Scholar]
- Huttenlocher A., Sandborg R.R., Horwitz A.F. 1995. Adhesion in cell migration. Curr. Opin. Cell Biol. 7:697–706 10.1016/0955-0674(95)80112-X [DOI] [PubMed] [Google Scholar]
- Jacobelli J., Bennett F.C., Pandurangi P., Tooley A.J., Krummel M.F. 2009. Myosin-IIA and ICAM-1 regulate the interchange between two distinct modes of T cell migration. J. Immunol. 182:2041–2050 10.4049/jimmunol.0803267 [DOI] [PubMed] [Google Scholar]
- Jannat R.A., Robbins G.P., Ricart B.G., Dembo M., Hammer D.A. 2010. Neutrophil adhesion and chemotaxis depend on substrate mechanics. J. Phys. Condens. Matter. 22:194117 10.1088/0953-8984/22/19/194117 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jay P.Y., Pham P.A., Wong S.A., Elson E.L. 1995. A mechanical function of myosin II in cell motility. J. Cell Sci. 108:387–393 [DOI] [PubMed] [Google Scholar]
- Kee Y.S., Ren Y., Dorfman D., Iijima M., Firtel R., Iglesias P.A., Robinson D.N. 2012. A mechanosensory system governs myosin II accumulation in dividing cells. Mol. Biol. Cell. 23:1510–1523 10.1091/mbc.E11-07-0601 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kicka S., Shen Z., Annesley S.J., Fisher P.R., Lee S., Briggs S., Firtel R.A. 2011. The LRRK2-related Roco kinase Roco2 is regulated by Rab1A and controls the actin cytoskeleton. Mol. Biol. Cell. 22:2198–2211 10.1091/mbc.E10-12-0937 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laevsky G., Knecht D.A. 2003. Cross-linking of actin filaments by myosin II is a major contributor to cortical integrity and cell motility in restrictive environments. J. Cell Sci. 116:3761–3770 10.1242/jcs.00684 [DOI] [PubMed] [Google Scholar]
- Lämmermann T., Sixt M. 2009. Mechanical modes of ‘amoeboid’ cell migration. Curr. Opin. Cell Biol. 21:636–644 10.1016/j.ceb.2009.05.003 [DOI] [PubMed] [Google Scholar]
- Langridge P.D., Kay R.R. 2006. Blebbing of Dictyostelium cells in response to chemoattractant. Exp. Cell Res. 312:2009–2017 10.1016/j.yexcr.2006.03.007 [DOI] [PubMed] [Google Scholar]
- Lauffenburger D.A., Horwitz A.F. 1996. Cell migration: a physically integrated molecular process. Cell. 84:359–369 10.1016/S0092-8674(00)81280-5 [DOI] [PubMed] [Google Scholar]
- Lee J., Leonard M., Oliver T., Ishihara A., Jacobson K. 1994. Traction forces generated by locomoting keratocytes. J. Cell Biol. 127:1957–1964 10.1083/jcb.127.6.1957 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levayer R., Lecuit T. 2012. Biomechanical regulation of contractility: spatial control and dynamics. Trends Cell Biol. 22:61–81 10.1016/j.tcb.2011.10.001 [DOI] [PubMed] [Google Scholar]
- Li Y., Hu Z., Li C. 1993. New method for measuring Poisson’s ratio in polymer gels. J. Appl. Polym. Sci. 50:1107–1111 10.1002/app.1993.070500619 [DOI] [Google Scholar]
- Lombardi M.L., Knecht D.A., Dembo M., Lee J. 2007. Traction force microscopy in Dictyostelium reveals distinct roles for myosin II motor and actin-crosslinking activity in polarized cell movement. J. Cell Sci. 120:1624–1634 10.1242/jcs.002527 [DOI] [PubMed] [Google Scholar]
- Luo T., Mohan K., Srivastava V., Ren Y., Iglesias P.A., Robinson D.N. 2012. Understanding the cooperative interaction between myosin II and actin cross-linkers mediated by actin filaments during mechanosensation. Biophys. J. 102:238–247 10.1016/j.bpj.2011.12.020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo T., Mohan K., Iglesias P.A., Robinson D.N. 2013. Molecular mechanisms of cellular mechanosensing. Nat. Mater. 12:1064–1071 10.1038/nmat3772 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meili R., Ellsworth C., Lee S., Reddy T.B., Ma H., Firtel R.A. 1999. Chemoattractant-mediated transient activation and membrane localization of Akt/PKB is required for efficient chemotaxis to cAMP in Dictyostelium. EMBO J. 18:2092–2105 10.1093/emboj/18.8.2092 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meili R., Alonso-Latorre B., del Alamo J.C., Firtel R.A., Lasheras J.C. 2010. Myosin II is essential for the spatiotemporal organization of traction forces during cell motility. Mol. Biol. Cell. 21:405–417 10.1091/mbc.E09-08-0703 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Millius A., Weiner O.D. 2010. Manipulation of neutrophil-like HL-60 cells for the study of directed cell migration. Methods Mol. Biol. 591:147–158 10.1007/978-1-60761-404-3_9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oakes P.W., Patel D.C., Morin N.A., Zitterbart D.P., Fabry B., Reichner J.S., Tang J.X. 2009. Neutrophil morphology and migration are affected by substrate elasticity. Blood. 114:1387–1395 10.1182/blood-2008-11-191445 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pollard T.D., Borisy G.G. 2003. Cellular motility driven by assembly and disassembly of actin filaments. Cell. 112:453–465 10.1016/S0092-8674(03)00120-X [DOI] [PubMed] [Google Scholar]
- Reichl E.M., Ren Y., Morphew M.K., Delannoy M., Effler J.C., Girard K.D., Divi S., Iglesias P.A., Kuo S.C., Robinson D.N. 2008. Interactions between myosin and actin crosslinkers control cytokinesis contractility dynamics and mechanics. Curr. Biol. 18:471–480 10.1016/j.cub.2008.02.056 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riedl J., Crevenna A.H., Kessenbrock K., Yu J.H., Neukirchen D., Bista M., Bradke F., Jenne D., Holak T.A., Werb Z., et al. 2008. Lifeact: a versatile marker to visualize F-actin. Nat. Methods. 5:605–607 10.1038/nmeth.1220 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sahai E., Marshall C.J. 2003. Differing modes of tumour cell invasion have distinct requirements for Rho/ROCK signalling and extracellular proteolysis. Nat. Cell Biol. 5:711–719 10.1038/ncb1019 [DOI] [PubMed] [Google Scholar]
- Salbreux G., Charras G., Paluch E. 2012. Actin cortex mechanics and cellular morphogenesis. Trends Cell Biol. 22:536–545 10.1016/j.tcb.2012.07.001 [DOI] [PubMed] [Google Scholar]
- Schindl M., Wallraff E., Deubzer B., Witke W., Gerisch G., Sackmann E. 1995. Cell-substrate interactions and locomotion of Dictyostelium wild-type and mutants defective in three cytoskeletal proteins: a study using quantitative reflection interference contrast microscopy. Biophys. J. 68:1177–1190 10.1016/S0006-3495(95)80294-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shin M.E., He Y., Li D., Na S., Chowdhury F., Poh Y.C., Collin O., Su P., de Lanerolle P., Schwartz M.A., et al. 2010. Spatiotemporal organization, regulation, and functions of tractions during neutrophil chemotaxis. Blood. 116:3297–3310 10.1182/blood-2009-12-260851 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soll D.R. 1999. Computer-assisted three-dimensional reconstruction and motion analysis of living, crawling cells. Comput. Med. Imaging Graph. 23:3–14 10.1016/S0895-6111(98)00058-5 [DOI] [PubMed] [Google Scholar]
- Uchida K.S., Yumura S. 2004. Dynamics of novel feet of Dictyostelium cells during migration. J. Cell Sci. 117:1443–1455 10.1242/jcs.01015 [DOI] [PubMed] [Google Scholar]
- Uchida K.S., Kitanishi-Yumura T., Yumura S. 2003. Myosin II contributes to the posterior contraction and the anterior extension during the retraction phase in migrating Dictyostelium cells. J. Cell Sci. 116:51–60 10.1242/jcs.00195 [DOI] [PubMed] [Google Scholar]
- Van Haastert P.J.M. 2011. Amoeboid cells use protrusions for walking, gliding and swimming. PLoS ONE. 6:e27532 10.1371/journal.pone.0027532 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Haastert P.J., Devreotes P.N. 2004. Chemotaxis: signalling the way forward. Nat. Rev. Mol. Cell Biol. 5:626–634 10.1038/nrm1435 [DOI] [PubMed] [Google Scholar]
- Wang Y.L., Pelham R.J., Jr 1998. Preparation of a flexible, porous polyacrylamide substrate for mechanical studies of cultured cells. Methods Enzymol. 298:489–496 10.1016/S0076-6879(98)98041-7 [DOI] [PubMed] [Google Scholar]
- Webb D.J., Parsons J.T., Horwitz A.F. 2002. Adhesion assembly, disassembly and turnover in migrating cells — over and over and over again. Nat. Cell Biol. 4:E97–E100 10.1038/ncb0402-e97 [DOI] [PubMed] [Google Scholar]
- Weber I., Wallraff E., Albrecht R., Gerisch G. 1995. Motility and substratum adhesion of Dictyostelium wild-type and cytoskeletal mutant cells: a study by RICM/bright-field double-view image analysis. J. Cell Sci. 108:1519–1530 [DOI] [PubMed] [Google Scholar]
- Weiner O.D. 2002. Regulation of cell polarity during eukaryotic chemotaxis: the chemotactic compass. Curr. Opin. Cell Biol. 14:196–202 10.1016/S0955-0674(02)00310-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wessels D., Soll D.R., Knecht D., Loomis W.F., De Lozanne A., Spudich J. 1988. Cell motility and chemotaxis in Dictyostelium amebae lacking myosin heavy chain. Dev. Biol. 128:164–177 10.1016/0012-1606(88)90279-5 [DOI] [PubMed] [Google Scholar]
- Willert C.E., Gharib M. 1991. Digital particle image velocimetry. Exp. Fluids. 10:181–193 10.1007/BF00190388 [DOI] [Google Scholar]
- Yumura S., Itoh G., Kikuta Y., Kikuchi T., Kitanishi-Yumura T., Tsujioka M. 2013. Cell-scale dynamic recycling and cortical flow of the actin-myosin cytoskeleton for rapid cell migration. Biol. Open. 2:200–209 10.1242/bio.20122899 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zigmond S.H. 1996. Signal transduction and actin filament organization. Curr. Opin. Cell Biol. 8:66–73 10.1016/S0955-0674(96)80050-0 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.