Abstract
Motivation: Advancements in high-throughput technology have allowed researchers to examine the genetic etiology of complex human traits in a robust fashion. Although genome-wide association studies have identified many novel variants associated with hundreds of traits, a large proportion of the estimated trait heritability remains unexplained. One hypothesis is that the commonly used statistical techniques and study designs are not robust to the complex etiology that may underlie these human traits. This etiology could include non-linear gene × gene or gene × environment interactions. Additionally, other levels of biological regulation may play a large role in trait variability.
Results: To address the need for computational tools that can explore enormous datasets to detect complex susceptibility models, we have developed a software package called the Analysis Tool for Heritable and Environmental Network Associations (ATHENA). ATHENA combines various variable filtering methods with machine learning techniques to analyze high-throughput categorical (i.e. single nucleotide polymorphisms) and quantitative (i.e. gene expression levels) predictor variables to generate multivariable models that predict either a categorical (i.e. disease status) or quantitative (i.e. cholesterol levels) outcomes. The goal of this article is to demonstrate the utility of ATHENA using simulated and biological datasets that consist of both single nucleotide polymorphisms and gene expression variables to identify complex prediction models. Importantly, this method is flexible and can be expanded to include other types of high-throughput data (i.e. RNA-seq data and biomarker measurements).
Availability: ATHENA is freely available for download. The software, user manual and tutorial can be downloaded from http://ritchielab.psu.edu/ritchielab/software.
Contact: marylyn.ritchie@psu.edu
Supplementary information: Supplementary data are available at Bioinformatics online.
1 INTRODUCTION
The sequencing of the human genome and significant advancements in high-throughput technology allow for exploratory analyses, which have the goal of interrogating variation at different levels of biological regulation (Ideker et al., 2001; Reif et al., 2004). These technologies generate a massive amount of various types of data and are steadily becoming less expensive and more efficient (Pareek et al., 2011). One major bottleneck in making full use of these data is the analysis strategy. First, because of the massive amount of data being generated, analysts must have access to computers with adequate resources. Second, computational techniques must be used that can analyze datasets with hundreds of thousands to millions of predictor variables in a feasible amount of time. Finally, to incorporate the potential complexity of these predictor variables, statistical methods must be used that can detect non-linear interactions and handle various types of data appropriately. Thus far, the most commonly used analytical techniques have focused on the first two requirements. For example, genome-wide association studies (GWAS) calculate the association of each individual single nucleotide polymorphism (SNP) from a high-throughput genotyping platform with the trait of interest. The P-value is then corrected for all of the statistical tests that were done (Watanabe, 2011). Inherently, this type of analysis is only going to find associations with strong enough main effects to pass the significance threshold. Therefore, GWAS will not find SNPs with phenotypic effects that rely on variation at another predictor variable (gene × gene or gene × environment interactions). This could be a factor in one of the major criticisms of GWAS—much of the trait variability estimated to be due to genetic factors remains unexplained by the thousands of novel variants identified by these studies (Visscher et al., 2012).
To address this criticism, various statistical methods have been developed that allow for the discovery of gene–gene and gene–environment interactions (Cordell, 2009). For example, multifactor dimensionality reduction performs an exhaustive analysis of all n-wise interacting loci to generate multilocus predictor models (Ritchie et al., 2001). Here, we assess several methods that have capacity to perform a meta-dimensional analysis. A meta-dimensional study is defined as one that integrates different types of data that represent different levels of biological regulation to predict a given outcome (Holzinger and Ritchie, 2012). The Analysis Tool for Heritable and Environmental Network Associations, or ATHENA, is a software package that combines various statistical methods as a filtering-modeling pipeline to identify complex prediction models (Holzinger et al., 2010, 2011, 2012; Turner et al., 2010). The overall goal of ATHENA is to provide the user with a platform to flexibly apply the statistical techniques to identify models that may be missed by other methods or any single method alone. The statistical methods in ATHENA are selected based on a number of criteria, including robustness to non-linear interactions, which will allow us to assess the role of these types of genetic effects on phenotypic variation in complex human traits. Figure 1 shows a schematic of the ATHENA methodology. ATHENA includes filtering and modeling components to generate the complex prediction models. In this analysis, we assess the modeling methods’ abilities to identify complex genetic models using simulated data. Owing to the substantial increase in noise that is inherent to high-throughput data, we apply the ATHENA filtering method Random Jungle (RJ) to the biological dataset before generating the prediction models. The filtering and modeling methods have been previously tested with various inputs, including SNPs and expression data. Future work will assess other components of ATHENA, such as the inclusion of environmental factors and the impact of certain characteristics of genetic data such as sample size, missing data points and minor allele frequency.
Fig. 1.

ATHENA filtering and modeling components
2 MATERIALS AND METHODS
2.1 Data simulation
To test our approach, we simulated data that consisted of SNP genotypes with two functional SNPs that predicted a binary outcome. These datasets were generated using genomeSIMLA, which has been previously described in detail (Dudek et al., 2006). Several genetic models were simulated with different effect types, effect sizes and variable counts for a total of 12 models. Two null models (where no genetic effect was simulated) were also generated to get a false-positive estimate. The data were simulated with patterns of correlation between the SNPs to represent linkage disequilibrium. Details of the model parameters are show in Table 1. The penetrance functions used to generate the models can be found in Supplementary Table S1.
Table 1.
SNP-only simulation details
| Parameter | Values |
|---|---|
| Genetic effect model | No main effects; main and interaction effects |
| Effect sizea | 0.01; 0.05; 0.15 |
| Variable count | 100; 1000 |
| Individuals | 2000 cases/2000 controls |
| Datasets per model | 100 |
aCalculated as broad sense heritability or the proportion of outcome variation due to all genetic effects.
For the meta-dimensional data simulation, we modified a previously developed technique to generate SNP genotype and expression variables (EVs) that predict a quantitative outcome (Chalise and Fridley, 2012). This method has previously been described in detail (Holzinger et al., 2012). We generated datasets with genetic effect models that consisted of two or three function variables with various effect types, effect sizes and variable counts for a total of 12 models. The descriptions of these models are shown in Table 2. We also simulated two null models for this analysis. More details about the genetic effects of the models can be found in Supplementary Table S2. Figure 2 shows a schematic of each of the three genetic effect models as described in Table 2. For each model, an indirect effect SNP was generated by forcing correlation between this SNP and the functional EV with an R2 value of ∼0.3.
Table 2.
Meta-dimensional data simulation details
| Parameter | Values |
|---|---|
| Genetic effect model | All main effects (main); SNP × SNP interaction effect + EV main effect (S × S + E); SNP × EV interaction effect (S × E) |
| Effect sizea | 0.05; 0.15 |
| Variable count | 100 SNPs/50 EVs; 1000 SNPs/500 EVs |
| Individuals | 4000 with quantitative outcome |
| Datasets per model | 100 |
aCalculated as the adjusted R2 value from the linear regression model that included all of the main and interaction effects listed.
Fig. 2.

Schematic of the three meta-dimensional genetic effect models. From left to right: main effect model, SNP × SNP + EV (S × S + E), SNP × EV (S × E). SNP.IND had an indirect effect on the phenotype via its correlation with the EV
2.2 Biological dataset
For this analysis, we used a publicly available dataset that consists of genome-wide SNPs, EVs and a cytotoxicity measurement generated from 172 HapMap lymphoblastoid cell lines (LCLs). Details of this dataset can be found from a previous study that used these data (Huang et al., 2007). Briefly, cytotoxcity of etoposide, a chemotherapeutic agent, was calculated as IC50, or the concentration of drug at which 50% of the cells remain viable. IC50 values were log-transformed. This quantitative outcome was adjusted to account for relatedness, ethnicity and gender using the residuals from a mixed model regression analysis in genABEL in the R software package (Aulchenko et al., 2007). We reduced the initial number of SNPs downloaded from the HapMap Web site from ∼3 to ∼1.3 million by removing SNPs with minor allele frequency <0.05 and genotyping call rate of <100% (i.e. no missing data). The EV data consisted of ∼18 000 transformed and normalized baseline expression levels from the LCLs using the Affymetrix GeneChip Human Exon 1.0ST Array. These expression levels were downloaded from Gene Expression Omnibus, accession id: GSE7792.
2.3 ATHENA filtering: RJ
For the biological dataset analysis, we applied a variable filtering method before modeling to reduce the noise in the dataset. We used RJ (Schwarz et al., 2010), which is a parallelized and faster implementation of Random Forests (RF) (Breiman, 2001). Briefly, RFs use a bootstrap sample of the data to grow a collection of decision or regression trees without pruning. The importance of each of the variables is then tested using the out-of-bag individuals not included the bootstrap sample and then ranked according to an importance score. The importance score is calculated as the percent increase in mean squared error after permuting the variable values. Specifically, we used a modified version of the importance score, which takes into account correlated predictor variable (i.e. linkage disequilibrium in SNPs) (Meng et al., 2009).
2.4 ATHENA modeling: GENN and GESR
Two different analysis methods are available in ATHENA: grammatical evolution neural networks (GENN) and grammatical evolution symbolic regression (GESR) (Motsinger et al., 2006, submitted for publication; Turner et al., 2010; Holzinger et al., 2011). Both use computational evolution to optimize an initial random population of solutions to generate a final best model. Specifically, grammatical evolution (O’Neill and Ryan, 2001), a more computationally efficient variation of genetic programing (Koza, 1992) is used to optimize artificial neural networks (ANNs) or symbolic regression formulas (SRs) in GENN and GESR, respectively. ANNs are a collection of analog processors that operate in parallel to model the relationship between a set of input variables (i.e. SNPs) and the output variable (i.e. case or control status) (Bishop, 1995). SRs are mathematical functions that map input variables to an output variable and are traditionally optimized using a form of genetic programing (Moore et al., 2007). The details of the grammatical evolution (GE) algorithm for both GENN and GESR are given below:
The dataset is divided into five equal parts for 5-fold cross-validation (4/5 for training and 1/5 for testing).
Training begins by generating a random population of binary strings initialized to be functional ANNs or SRs. Both the model structure and the variables included are randomly generated. The population is divided into demes across a user-defined number of CPUs for parallelization.
The ANNs or SRs in the population are evaluated using the training data and the fitness (balanced classification accuracy for binary outcomes or R2 for quantitative outcomes) for each model is recorded. The solutions with the highest fitness are selected for crossover and reproduction, and a new population is generated.
Step 3 is repeated for a predefined number of generations. Migration of best solutions occurs between CPUs every n-number of generations, as specified by the user.
The overall best solution across generations is tested using the remaining 1/5 data and fitness is recorded.
Steps 2–5 are repeated four more times, each time using a different 4/5 of the data for training and 1/5 for testing. The best model is defined as the model identified the most over all five cross-validations. Ties are broken using the fitness metrics described later in the text.
For this analysis, fitness is calculated using R2 for quantitative outcomes, where, for each individual i, y is the observed value, y-hat is the predicted value and y-bar is the mean of the observed values (Equation 1). Balanced accuracy is used for binary outcomes, where TP are the true positives, FN are the false negatives and TN are the true negatives (Equation 2). This is the average of the sensitivity and specificity of the solution.
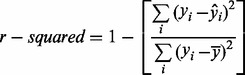 |
(1) |
| (2) |
2.5 Lasso
We compare GENN and GESR with Lasso, a regression-based variable selection method that minimizes the sum of squared errors using a tuning parameter (Tibshirani, 1996). The resulting coefficient shrinkage allows for the generation of a parsimonious prediction model. For this study, we implemented Lasso using the R package penalized (Goeman, 2010). For each of the genetic models, we optimized the lambda value (or coefficient shrinkage tuning parameter) as suggested by the authors. We also used 5-fold cross-validation so that R2 values would be comparable with those in GENN and GESR.
3 IMPLEMENTATION
3.1 ATHENA
ATHENA is implemented in C++ and uses the libGE (version 0.2.6) grammatical evolution library and the GAlib (version 2.4.7) genetic algorithms library for both GENN and GESR. The application can run in parallel with multiple populations and uses the Message Passing Interface (MPI) for communication. In cases where no parallel infrastructure exists, a serial version can be compiled to run with a single population. Dummy configuration files showing specific parameters for the simulated and biological dataset analyses are shown in Supplementary Table S3. These parameter settings were chosen based on a series of previous optimization tests that were done to identify the settings that performed best across various genetic models (Holzinger et al., 2010, 2011).
3.2 RJ
The Linux 64 Bit MPI version of RJ (Build 1.3.0) was downloaded precompiled from http://imbs-luebeck.de/imbs/de/node/227. For this analysis, we used the parallel implementation of RJ (rjunglep). The specific parameter settings for each of the runs are shown in Supplementary Table S4.
4 RESULTS
4.1 Simulated data
For the simulation studies, we applied GENN, GESR and Lasso directly to the datasets with no variable filtering. We simulated the data to have variable counts similar to what is expected for the post-filtering number in biological data. For both the SNP-only and the SNP + gene expression (or meta-dimensional) data, we compare the detection power (number of times the correct variables were identified in the best model), modeling accuracy and parsimony of the three modeling methods.
4.1.1 SNP-only data
We ran GENN, GESR and Lasso on all 100 datasets and calculated various detection powers. We also compare the average balanced accuracy of the best models in the testing set and the average number of variables in the best models as a metric of deviation from the expected value of two SNPs.
Figure 3 shows the results for each of the 14 genetic effect models for the SNP-only simulations (Pendergrass et al., 2010). For each model, the average fitness (balanced accuracy), average model size (number of variables in the best model) and various detection powers are shown.
Fig. 3.
Results from the SNP-only simulation analyses. Description of the 14 genetic effect models is shown in the first three columns. Detection power is defined as the number of times out of 100 datasets the indicated variable(s) is identified. Avg. Fitness is defined as balanced accuracy. Avg. Model Size is defined as the average number of variables in the best model
For GENN (squares) and GESR (triangles), detection power is summarized as the number of times out of the 100 datasets that SNP1, SNP2, both SNPs (full model) or both SNPs with no false positives (full model specific) are identified in the final best model. Because the Lasso models (circles) were much less parsimonious, full model detection was calculated as the number of times SNP1, SNP2 or both SNPs appeared in the top four variables as determined by the absolute value of the regression coefficient. This value was chosen because it was the average size of the GENN and GESR models across all models. The full model specific detection power was calculated as the number of times both SNPs were identified in the top two variables as determined by the absolute value of the regression coefficient.
For the models with main and interaction effects (1–6), all three methods identify both SNPs in the best model at least 50/100 datasets (green bars). GENN adds additional loci in the best model as indicated by a lower full model specific detection power (yellow bars). However, the average model size is <2.5 for each of the GENN analyses, so the method is adding few additional ‘false positive’ loci to the model and is still relatively parsimonious. Overall, GENN also has slightly better average fitness than GESR for these models.
GENN has better detection power and is more parsimonious than GESR and Lasso for all of the models with no main effects (7–12). Importantly, Lasso had essentially no power to identify the model with no main effects, as shown by the circles. Lasso was also much less parsimonious as shown by the model size. Additionally, for model 12, none of the methods identified the model. This appears to be an effect size/variable count threshold at which the parameters of GENN and GESR (i.e. number of generations and population size) would need to be adjusted to allow for model detection.
4.1.2 Meta-dimensional simulated data
For each of the meta-dimensional data simulations models, we ran the three methods on 100 datasets per model. Figure 4 shows the results from this analysis. The detection power results are summarized slightly differently than the SNP-only simulation results. SNP detection power is the average number of times either SNP was identified in the best model for the genetic effects that include two SNPs (main and S × S + E). EV detection power is the number of times the EV was identified in the best model. Two var. detection power is the number of times at least two of the variables from the genetic effect model were identified. Full model detection power is the number of times all of the direct effect variables were identified. The detection power for Lasso was calculated so that full model indicates that the functional variables were in the top five and full model specific indicates they were in the top two or three as determined by the absolute value of the coefficient. We standardized the coefficients so that they would be comparable for SNPs and EVs. Note that because the S × E model only has two direct effect variables, the two var. and full model detection powers will be identical.
Fig. 4.
Results from the meta-dimensional simulation analyses. Description of the 14 genetic effect models is shown in the first three columns. Detection power is defined as the number of times out of 100 datasets the indicated variable(s) is identified. Avg. Fitness is defined as R2. Avg. Model Size is defined as the average number of variables in the best model
For most of the genetic effect models, Lasso has highest power to detect the functional variables. This could be, in part, due to the manner in which the meta-dimensional data were simulated. The effect of each variant on the outcome is determined by a linear function as described previously (Holzinger et al., 2012). Because Lasso is generating a linear prediction model, it may have an advantage over GENN and GESR for this specific type of simulation not seen in the SNP-only data. For GENN and GESR, GENN had higher detection power for identifying two variables (green bars) and the SNP (blue bars), whereas GESR has overall higher EV detection power (red bars). Additionally, GESR is too parsimonious as shown by the average model size which is ∼1 for each of the genetic effect models where the correct model has either three (main and S × S + E) or two (S × E) direct effect variables. Again, Lasso is the least parsimonious with up to 73 variables in the final model.
Notably, neither GENN nor GESR was able to identify all three variables in the model for the main and S × S + E genetic effects >2/100 times. This could be due to the restrictions on parameter settings that improve detection power but also result in longer run times and increased memory consumption. To test this, we ran 5/100 datasets from the 3-variable genetic effect models (150 variables and an effect size of 0.15) with a larger population size, maximum depth and longer number of generations in GENN and GESR. Table 3 shows the results from these analyses. For GENN, 3/5 best models included all three direct effects for the main effects datasets. One of the other models included the two direct effect SNPs and the indirect effect SNP, which is correlated with the EV. For the S × S + E model, 5/5 best models included all three direct effect variables. These analyses took ∼10 h per dataset to run (∼50 h for the entire analysis). Comparatively, the analysis for all 100 datasets took 0.8 h per dataset (80 h for the entire analysis). These parameter settings would have been a large computation burden because it would take 1000 h to run all 100 datasets. GESR did not identify >2 of the direct effect variables in any of the models, but computation time was shorter at ∼2.2 h per dataset.
Table 3.
GENN and GESR results from meta-dimensional simulated data from analyses with longer runtime
| Method-model | Best model variables | Testing R2 | Time |
|---|---|---|---|
| GENN-Main | SNP1 SNP2 EV FP1 FP2 FP3 | 0.16 | 10 h |
| SNP1 SNP2 SNP.IND | 0.13 | ||
| SNP1 SNP2 EV FP1 FP2 | 0.18 | ||
| SNP1 SNP2 EV SNP.IND FP1 | 0.13 | ||
| SNP1 SNP2 FP1 | 0.15 | ||
| GENN-S × S + E | SNP1 SNP2 EV SNP.IND FP1 FP2 FP3 | 0.14 | 10 h |
| SNP1 SNP2 EV | 0.15 | ||
| SNP1 SNP2 EV FP1 FP2 | 0.14 | ||
| SNP1 SNP2 EV FP1 FP2 | 0.13 | ||
| SNP1 SNP2 EV FP1 | 0.16 | ||
| GESR-main | SNP1 FP1 FP2 | 0.05 | 2.2 h |
| SNP2 | 0.05 | ||
| SNP1 FP1 | 0.09 | ||
| SNP2 | 0.08 | ||
| SNP1 EV | 0.12 | ||
| GESR-S × S + E | EV | 0.06 | 2.2 h |
| SNP2 EV | 0.09 | ||
| EV | 0.06 | ||
| EV | 0.07 | ||
| EV | 0.09 |
Note: The correct variables are shown in bold. The direct effect variables are SNP1, SNP2 and EV. The indirect effect variable is SNP.IND. The false-positive variables are shown as FP-number. Fitness is the R2 value of the model in the testing set. Time is computation hours per dataset.
Owing to the ability to model more complex effects, and the generally higher detection power, we chose to use GENN for the biological dataset analysis. Also, because Lasso had the highest detection power for all of the simulated meta-dimensional models, we assessed its performance on the biological data, as well.
4.2 Biological dataset
The biological dataset consisted of 172 individuals with genome-wide SNPs, EVs and etoposide cytotoxicity, which was measured as the concentration of drug at which 50% of the cells in the LCL survived, or IC50. We used RJ to filter the SNPs and EVs to achieve a variable count similar the simulated datasets. The filtered variables were analyzed using GENN and Lasso based on the results from the simulated data. Figure 5 is a schematic of the biological dataset analysis design.
Fig. 5.
Schematic of the filtering-modeling pipeline for the biological dataset analysis
We ran RJ on the SNPs and EVs separately and performed parameter tuning as suggested by the RF authors (Step 1). Supplementary Tables S5 and S6 show the results from this parameter tuning. Next, we took the top 10% of the variables with non-zero importance scores in the final iteration of the optimized RJ runs and ran them in GENN and Lasso. The filtered datasets consisted of 428 SNPs and 39 EVs. We ran both methods the following ways: only SNPs (Step 2.1), only EVs (Step 2.3) and SNPs + EVs (Step 2.2). Finally, we assessed only the SNPs and EVs from the best GENN and Lasso models (Step 3). The results are shown in Table 4. Strikingly, GENN is much more parsimonious than Lasso when selecting variables for the final model. Additionally, even with far fewer variables, the R2 values are larger in the GENN model in every analysis except Step 2.2. Many of the same variables appear in both the Lasso and GENN models, whereas several are unique to the analysis type. For example, the EVs HIST1H4A-1 and HIST1H4A-2 only appear in the GENN models. This could indicate that they were identified because of non-linear interaction effects that Lasso would not be able to identify.
Table 4.
Results from modeling analyses of the RJ filtered data
| Analysis | Best GENN model | Best Lasso model | Testing R2 (GENN/ Lasso) | |
|---|---|---|---|---|
| SNPs (step 2.1) | rs1014390 | rs1600172 | rs12327115 | 0.18/0.15 |
| rs883834 | rs7283476 | rs158 | ||
| rs1600172 | rs883834 | rs951340 | ||
| rs1014390 | rs4788961 | |||
| rs6726177 | rs4483064 | |||
| rs10889205 | rs947939 | |||
| rs9355434 | rs735155 | |||
| rs7867860 | rs17675487 | |||
| rs1025926 | rs4783018 | |||
| rs17119606 | rs35335364 | |||
| EVs (step 2.3) | HIST1H4A-1 | FAM3A | TECPR2 | 0.42/0.27 |
| ACER2 | TLL2 | ARMCX2 | ||
| EDARADD | TRIM3 | LMNA | ||
| GDI2 | EDARADD | LARP6 | ||
| ACER2 | MREG | |||
| SNPs + EVs (step 2.2) | rs1600172 | rs883834 | rs735155 | 0.21/0.44 |
| HIST1H4A-1 | rs7283476 | rs10497812 | ||
| HIST1H4A-2 | rs1600172 | rs12453548 | ||
| rs1014390 | rs12113766 | |||
| rs6726177 | rs158 | |||
| rs7867860 | rs12327115 | |||
| rs10889205 | rs2709984 | |||
| rs17119606 | rs17675487 | |||
| rs4783018 | EDARADD | |||
| rs11964461 | ACER2 | |||
| rs16964544 | FAM3A | |||
| rs12189541 | TRIM3 | |||
| rs9355434 | MVP | |||
| rs4788961 | ARMCX2 | |||
| rs11681616 | LMNA | |||
| Top SNPs + EVs (step 3) | rs883834 | rs7283476 | rs12327115 | 0.57/0.55 |
| rs1014390 | rs883834 | rs947939 | ||
| rs1600172 | rs17119606 | rs4483064 | ||
| HIST1H4A-1 | rs1014390 | rs17675487 | ||
| HIST1H4A-2 | rs6726177 | rs1025926 | ||
| EDARADD | rs1600172 | FAM3A | ||
| rs7867860 | EDARADD | |||
| rs10889205 | TRIM3 | |||
| rs4788961 | ACER2 | |||
| rs4783018 | ARMCX2 | |||
| rs9355434 | LMNA | |||
| rs735155 | HPN | |||
| rs158 | LARP6 | |||
| rs951340 | ||||
Furthermore, we compared the R2 value from the best GENN model with the adjusted R2 value from a linear regression model that included the same three SNPs and five EVs using the R software package (R Development Core Team, 2011). The adjusted R2 value for this model was 0.47 and the model P-value was 2.2 × 10−16. The larger R2 suggests that the GENN best model (0.57) is capturing the non-linear relationships between the variables that explain a portion of the phenotype variation that the linear regression model would not detect. Supplementary Figure S1 shows the most predictive ANN model from the GENN analysis described in Step 3. Taken together these results suggest that using >1 variable type is more informative than either of the variable types alone (Step 3). However, the number of input variables has a large impact on the modeling performance of GENN, as shown by comparing the best models from Step 2.2 and Step 3. Although they contain many of the same variables, the testing R2 is substantially greater when the number of variables is reduced in Step 3
5 DISCUSSION
ATHENA is a software package that incorporates various existing statistical methods that have specific strengths (i.e. variable selection or variable modeling) to allow the user to perform a powerful meta-dimensional study. ATHENA can be used to analyze one or more data types, while allowing for interactions between variables to generate meta-dimensional models that predict either a binary or quantitative phenotypes. For this analysis, we used simulated datasets to assess the performance of the ATHENA modeling methods GENN and GESR and compared them with Lasso. Overall, our results suggest that GENN is better at correctly and accurately detecting genetic models with no main effects (Fig. 3). In the simulated meta-dimensional data, Lasso had higher detection power for the full model than both GENN and GESR. However, when we used more powerful parameter settings, GENN was also able to identify the full model consistently. The amount of noise in the data has an increasingly detrimental effect on GENN and GESR, as shown by the substantial decrease in detection power from 100 to 1000 SNPs in the simulated data (Figs 3 and 4). To address this, we used RJ as a variable selection method because it allows for the identification of non-linear interactions and the output from the analysis is a ranked list of variables, which can be seamlessly filtered into a more powerful and parsimonious modeling technique, like GENN.
Another important consideration when selecting analysis methods is the computation time. Supplementary Table S7 shows the CPU time for GENN, GESR and Lasso for each of the different analyses. Lasso is considerably faster than either GENN or GESR, so if computational resources are a major limitation, this may be the optimal method. However, Lasso is not robust to models with no main effects, so the overall benefit of a faster analysis would need to be weighted accordingly.
The filtering-modeling pipeline used here does have certain limitations. First, none of the modeling techniques specifically identify conditional relationships, which are likely to be ubiquitous in meta-dimensional data. For example, if a SNP-affected gene expression level, which, in turn, affected the phenotype, methods such as GENN are more likely to identify either the SNP or the EV, but not both. One method, which could model these types of relationships in a more informative manner are Bayesian networks (Jiang et al., 2010; Carniak, 1991). Future improvement to ATHENA will include incorporating Bayesian networks into the software package to allow for the generation of more interpretable meta-dimensional models.
Another limitation of our analysis is the selection of the threshold in the RJ results for filtering variables into GENN. There is no direct correlation between the RJ importance scores and a more interpretable metric such as a P-value. Therefore, the significance level that best distinguishes signal from noise for different types of data is difficult to determine. One threshold selection technique may involve running RJ x-number of times with a different random seed each time and selecting the variables that appear in the top spots across the analyses. One issue with this process, however, is the computational burden of running RJ many times as one single analysis can take hours or days to complete. Alternatively, there are other variable selection methods that do not rely on computationally intense data-driven analyses. Biofilter (Bush et al., 2009), which is currently a part of the ATHENA package, is a method that uses information from databases such as Kyoto Encyclopedia of Genes and Genomes (KEGG) and Gene Ontology (GO) to select SNPs that are more likely to be a part of the same pathway or interacting with one another based on known biological functions. Other filtering techniques will be explored in future work.
In our best model, there were three SNPs and three EVs, which explained ∼57% of the adjusted trait variation in our dataset. This model was more predictive than a linear regression model that included the same variables. One limitation in our biological analysis, however, is the small sample size (n = 172). This issue is somewhat ameliorated by the relatively large heritability estimates of chemotherapeutic agent cytotoxicity in LCLs (Watters, 2004). With this sample size, we should still be able to identify valid models with larger effects; however, an ideal dataset would be larger to allow for the identification of smaller effects. The next step in validating this model is to show that it predicts etoposide cytotoxicity in independent datasets. For a single SNP, there are factors that make replication less than trivial. Briefly, the most significant SNP is likely correlated with, or tagging, the true causal SNP. If the correlation patterns between the discovery and replication datasets are different, the effect sizes and significance levels will also be different, making exact replication difficult. This effect is amplified when trying to replicate SNP–SNP interactions or, in our case, meta-dimensional models. One option for expanding the idea of replication to meta-dimensional model discovery is to determine whether sets of SNPs or genes that are correlated with the originally identified variables are predictive in independent datasets. Additionally, functional studies could be done to determine if perturbing the identified genetic regions results in a phenotypic change. For this analysis, an in vitro experiment could be done using the available LCLs to determine if the IC50 values change when the genes in the predictive model are knocked down.
The ultimate goal of ATHENA is to identify biological pathways or sets of genes that are a part of the genetic etiology of various complex phenotypes. These models could then be used to identify potential drug targets or to identify genes that predict drug response. By developing a method that incorporates data from different levels of biological regulation and captures non-linear relationships between variables, we may be able to explain more of the trait variability, as was observed in this analysis.
Funding: Funding for this work was provided by NIH grants from the National Library of Medicine: LM010040, National Heart, Lung, and Blood via the Pharmacogenomics Research Network, specifically HL065962 which funds the PGRN Statistical Analysis Resource (P-STAR), and E.R.H. was funded by an NIGMS training grant 5T32GM080178.
Conflict of Interest: None declared.
Supplementary Material
REFERENCES
- Aulchenko YS, et al. GenABEL: an R library for genome-wide association analysis. Bioinformatics. 2007;23:1294–1296. doi: 10.1093/bioinformatics/btm108. [DOI] [PubMed] [Google Scholar]
- Bishop CM. Neural Networks for Pattern Recognition. London: Oxford University Press; 1995. [Google Scholar]
- Breiman L. Random Forests. Machine Learning. 2001;45:5–32. [Google Scholar]
- Bush WS, et al. Biofilter: a knowledge-integration system for the multi-locus analysis of genome-wide association studies. Pac. Symp. Biocomput. 2009:368–379. [PMC free article] [PubMed] [Google Scholar]
- Carniak E. Bayesian networks without tears. AI Magazine. 1991:50–63. [Google Scholar]
- Chalise P, Fridley BL. Comparison of penalty functions for sparse canonical correlation analysis. Comput. Stat. Data Anal. 2012;56:245–254. doi: 10.1016/j.csda.2011.07.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cordell HJ. Genome-wide association studies: detecting gene-gene interactions that underlie human diseases. Nat. Rev. Genet. 2009;10:392–404. doi: 10.1038/nrg2579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dudek SM, et al. Data simulation software for whole-genome association and other studies in human genetics. Pac. Symp. Biocomput. 2006;11:499–510. [PubMed] [Google Scholar]
- Goeman JJ. L1 penalized estimation in the Cox proportional hazards model. Biom. J. 2010;52:70–84. doi: 10.1002/bimj.200900028. [DOI] [PubMed] [Google Scholar]
- Holzinger ER, Ritchie MD. Integrating heterogeneous high-throughput data for meta-dimensional pharmacogenomics and disease-related studies. Pharmacogenomics. 2012;13:213–222. doi: 10.2217/pgs.11.145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holzinger ER, et al. ATHENA optimization: the effect of initial parameter settings across different genetic models. In: Pizzuti C, et al., editors. Evolutionary Computation, Machine Learning and Data Mining in Bioinformatics. Berlin, Heidelberg: Springer Berlin Heidelberg; 2011. pp. 48–58. [Google Scholar]
- Holzinger ER, et al. Comparison of methods for meta-dimensional data analysis using in silico and biological data sets. In: Giacobini M, et al., editors. Evolutionary Computation, Machine Learning and Data Mining in Bioinformatics. Berlin, Heidelberg: Springer Berlin Heidelberg; 2012. pp. 134–143. [Google Scholar]
- Holzinger ER, et al. Initialization parameter sweep in ATHENA: optimizing neural networks for detecting gene-gene interactions in the presence of small main effects. Genet. Evol. Comput. Conf. 2010;12:203–210. doi: 10.1145/1830483.1830519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang RS, et al. A genome-wide approach to identify genetic variants that contribute to etoposide-induced cytotoxicity. Proc. Natl Acad. Sci. USA. 2007;104:9758–9763. doi: 10.1073/pnas.0703736104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ideker T, et al. A new approach to decoding life: systems biology. Annu. Rev. Genomics Hum. Genet. 2001;2:343–372. doi: 10.1146/annurev.genom.2.1.343. [DOI] [PubMed] [Google Scholar]
- Jiang X, et al. Identifying genetic interactions in genome-wide data using Bayesian networks. Genet. Epidemiol. 2010;34:575–581. doi: 10.1002/gepi.20514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koza JR. Genetic Programming: On the Programming of Computers by Means of Natural Selection. Cambridge, MA: MIT Press; 1992. [Google Scholar]
- Meng YA, et al. Performance of random forest when SNPs are in linkage disequilibrium. BMC Bioinformatics. 2009;10:78. doi: 10.1186/1471-2105-10-78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moore JH, et al. Symbolic modeling of epistasis. Hum. Hered. 2007;63:120–133. doi: 10.1159/000099184. [DOI] [PubMed] [Google Scholar]
- O’Neill M, Ryan C. Grammatical evolution. IEEE Trans. Evol. Comput. 2001;5:349–358. [Google Scholar]
- Pareek CS, et al. Sequencing technologies and genome sequencing. J. Appl. Genet. 2011;52:413–435. doi: 10.1007/s13353-011-0057-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pendergrass SA, et al. Synthesis-View: visualization and interpretation of SNP association results for multi-cohort, multi-phenotype data and meta-analysis. BioData Min. 2010;3:10. doi: 10.1186/1756-0381-3-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Development Core Team. R: a language and environment for statistical computing. 2011 ISBN 3900051070. R Foundation for Statistical Computing, Vienna, Austria. http://www.R-project.org (22 October 2013, date last accessed) [Google Scholar]
- Reif DM, et al. Integrated analysis of genetic, genomic and proteomic data. Expert Rev. Proteomics. 2004;1:67–75. doi: 10.1586/14789450.1.1.67. [DOI] [PubMed] [Google Scholar]
- Ritchie MD, et al. Multifactor-dimensionality reduction reveals high-order interactions among estrogen-metabolism genes in sporadic breast cancer. Am. J. Hum. Genet. 2001;69:138–147. doi: 10.1086/321276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwarz DF, et al. On safari to Random Jungle: a fast implementation of Random Forests for high-dimensional data. Bioinformatics. 2010;26:1752–1758. doi: 10.1093/bioinformatics/btq257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tibshirani R. Regression shrinkage and selection via the Lasso. J. R Stat. Soc. B. 1996;58:267–288. [Google Scholar]
- Turner SD, et al. Grammatical evolution of neural networks for discovering epistasis among quantitative trait Loci. Lect. Notes Comput. Sci. 2010;6023:86–97. doi: 10.1186/1756-0381-3-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Visscher PM, et al. Five years of GWAS discovery. Am. J. Hum. Genet. 2012;90:7–24. doi: 10.1016/j.ajhg.2011.11.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watanabe RM. Statistical issues in gene association studies. In: DiStefano JK, editor. Disease Gene Identification. Totowa, NJ: Humana Press; 2011. pp. 17–36. [DOI] [PubMed] [Google Scholar]
- Watters JW. Genome-wide discovery of loci influencing chemotherapy cytotoxicity. Proc. Natl Acad. Sci. USA. 2004;101:11809–11814. doi: 10.1073/pnas.0404580101. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.





