Abstract
This study evaluates the economic consequences of the successful eradication of hookworm disease from the American South. The hookworm-eradication campaign (c. 1910) began soon after (i) the discovery that a variety of health problems among Southerners could be attributed to the disease and (ii) the donation by John D. Rockefeller of a substantial sum to the effort. The Rockefeller Sanitary Commission (RSC) surveyed infection rates in the affected areas (eleven southern states) and found that an average of forty percent of school-aged children were infected with hookworm. The RSC then sponsored treatment and education campaigns across the region. Follow-up studies indicate that this campaign substantially reduced hookworm disease almost immediately. The sudden introduction of this treatment combines with the cross-area differences in pre-treatment infection rates to form the basis of the identification strategy. Areas with higher levels of hookworm infection prior to the RSC experienced greater increases in school enrollment, attendance, and literacy after the intervention. This result is robust to controlling for a variety of alternative factors, including differential trends across areas, changing crop prices, shifts in certain educational and health policies, and the effect of malaria eradication. No significant contemporaneous results are found for adults, who should have benefited less from the intervention owing to their substantially lower (prior) infection rates. A long-term follow-up of affected cohorts indicates a substantial gain in income that coincided with exposure to hookworm eradication. I also find evidence that eradication increased the return to schooling.
Keywords: tropical disease, hookworm, Rockefeller Sanitary Commission, American South
1 Introduction
The importance of the burden of tropical disease in impeding economic development has received considerable attention in recent years. The establishment and maintenance of an environment free of infectious disease is an important public good. The very nature of the transmission mechanism of such diseases implies a manifest externality. This might serve as a rationale for collective action to reduce the incidence of infectious disease. However, little is known about the long-term benefits of such actions, and therefore there is nothing to compare with the short-term costs.
Unfortunately, simple correlations of public health and economic outcomes are unlikely to measure the causal effect since public health is endogenous. Indeed, it is likely a normal good: rich areas purchase more of it. To measure the contribution of a disease-free environment, we need to analyze plausibly exogenous improvements in public health. Targeted public-health interventions are a possible source of such variation.
The present study focuses on one specific intervention targeted toward hookworm disease in the American South. The hookworm-eradication campaign (circa 1910–1915) began soon after (i) the discovery that a variety of health problems among Southerners could be attributed to the disease and (ii) the donation by John D. Rockefeller of a substantial sum to the campaign. The Rockefeller Sanitary Commission (RSC) surveyed infection rates in the affected areas, and found that an average of forty percent of school-aged children in the American South suffered from hookworm infection. The RSC then sponsored treatment dispensaries that traveled these areas providing deworming medications and educating local physicians and the public about prevention. Follow-up studies indicate that the campaign brought about a substantial immediate reduction in hookworm disease and, furthermore, that the seeds were sown for preventing its return.
The introduction of this treatment (broadly defined) combines with the cross-area differences in pre-treatment infection rates to form the basis of my identification strategy. As the RSC surveys demonstrated, different areas of the country had distinct incidences of the hookworm disease. Areas with high infection rates had more to gain from the newly available treatments, whereas areas with little hookworm disease did not. This heterogeneity allows for a treatment/control strategy.
Moreover, the eradication campaign began — and was ultimately successful — because of critical innovations to knowledge. I argue that such innovations were not related to or somehow in anticipation of the future growth prospects of the affected areas, and therefore should not be thought of as endogenous in this context. For example, the discovery of the transmission mechanism for hookworm was made by a European doctor whose initial experimental evidence consisted of accidentally infecting himself while diagnosing a patient. At that time, hookworm infection in the American South was not even recognized as a problem.
Hookworm disease, while rarely fatal, has potentially severe chronic symptoms. The hookworm is a parasite that lodges itself in the victim’s digestive system, and burrows into the intestinal wall and tapping into the host’s bloodstream. Listlessness, anemia, and stunting of growth are common symptoms among infected children. Because schoolwork is an energy-intensive activity for children, it is plausible that hookworm disease would depress the returns to human-capital investment.
After hookworm eradication, school enrollment, regular school attendance, and literacy increased markedly in counties that had previously suffered from high rates of hookworm infection. This is true in absolute terms as well as relative to comparison counties that had lower levels of hookworm infection. I find this result using either a two-period double difference or a multi-period setup that allows for differential trends across areas. Furthermore, the conclusion is robust to controlling for a variety of other alternative hypotheses, including crop-specific shocks, demographic shifts, the near-simultaneous reduction in malaria, parental socioeconomic status, and certain policy changes. Estimates using Indirect Least Squares imply that a child infected with hookworm had a twenty percent lower probability of school enrollment, although it is impossible to completely rule out that the intervention had effects through channels besides measured hookworm infection. Replicating this design using state-of-birth-level variation in hookworm infection yields similar estimates for these variables, although the results for enrollment are imprecise.
Next, I present analogous results for adults as a specification check. A priori we would expect that adults would be substantially less affected by the hookworm-eradication campaign because adults were substantially less likely to have hookworm [RSC, 1911; Smillie and Augustine, 1925]. Moreover, human-capital investments not made in childhood due to hookworm would be water under the bridge once the disease environment improved. On the other hand, if the results for children were due to changes in income or migration patterns, we would see changes in adult outcomes as well. Instead, I find evidence that there was little contemporaneous impact on adults, measured along several important dimensions: literacy, labor-force participation, and occupation.
I also follow up on the cohorts that potentially benefited from hookworm eradication during childhood. Here I contrast individuals based on (i) the pre-eradication hookworm burden in their state of birth and (ii) their year of birth relative to the RSC. Cohorts more exposed to the eradication efforts went on to earn substantially higher incomes as adults. This pattern is seen using data on wage and salary incomes from the 1940 Census. Again using Indirect Least Squares (and subject to the same caveat lector as above), I estimate that being infected with hookworm through one’s childhood lead to a reduction in adult wages of approximately forty percent. I also consider occupational proxies of income, which are defined over a broad range of Census years, and show that the shift in the hookworm-income relationship coincides with childhood exposure to the eradication campaign, rather than with some pre-existing trend or autoregressive process. No statistically significant long-term effect of hookworm is found on the years of schooling (in accordance with the imprecise result for enrollment using state variation), but both literacy and returns to schooling increased with exposure to hookworm eradication.
The rest of this study is organized as follows. Section 2 describes the symptoms and history of the disease. Section 2.4 discusses in particular how the circumstances of the discovery of the hookworm problem in the South and the subsequent anti-hookworm campaign lend themselves to a strategy for identifying the effect of hookworm. Section 3 describes the data employed. The contemporaneous results using sequential cross sections are presented in Sections 4 and 5. The long-term follow-up is found in Section 6. I conclude the study in Section 7.
2 Hookworm and the Rockefeller Sanitary Commission
2.1 Hookworm Disease
Hookworm is an intestinal parasite that lodges itself in the human intestine and absorbs nutrients from the victim’s bloodstream. The symptoms of hookworm infection (or uncinaria) are lethargy and anemia. In rare cases, the anemia can become so severe as to cause death. The life cycle of the hookworm is dependent on unsanitary conditions. The nematodes lay their eggs in the intestine, but the larvae are passed out of the digestive system in feces. Hookworm is therefore transmitted through skin contact with infected fecal matter. The larvae then burrow their way in through the skin. The lifespan of a hookworm is much shorter than that of a human, and so continuous reinfection is required to generate any sustained worm load.
There are two angles for managing hookworm: treatment and prevention. The treatment consists of simply taking a deworming medicine. Preventative measures include limiting skin contact with polluted soil (through the use of shoes, for example) and dealing with excrement in ways that minimize soil pollution in the first place (e.g., the use of sanitary latrines).
2.2 The Eradication Campaign
The Rockefeller Sanitary Commission for the Eradication of Hookworm Disease was formed in 1910 with the donation of one million dollars by John D. Rockefeller. Some years before, an American doctor (Charles W. Stiles) had recognized hookworm symptoms in Southerners. Through intermediaries, Dr. Stiles had convinced Rockefeller that taking on hookworm was a good foray into large-scale charity. The Commission began by conducting surveys of hookworm-infection rates among children across the region. The RSC surveyed over six hundred counties in the South and found hookworm infection to be over forty percent among children.
Soon after, the treatment campaign began. First, the RSC sent teams of health-care workers to counties to administer and dispense deworming treatments free of charge. RSC dispensaries visited a large and mostly contiguous fraction of the South and the campaign treated over 400,000 individuals with deworming medication.1 Second, the RSC sought to educate doctors, teachers, and the general public on how to recognize the symptoms of hookworm disease so that fewer cases would go untreated. Another part of this publicity campaign included education about the importance of hygiene, especially with regard to the use of sanitary privies. In this period, oftentimes even public buildings such as schools and churches did not have such hygienic facilities. Follow-up surveys conducted afterward showed a substantial decline in hookworm infection [RSC, 1915]. Although the stated goal of eradication was not achieved, the hookworm-infection rate of the region did drop by more than half, and fewer extreme cases of the disease went unnoticed and untreated.
Because the deworming treatments are short-term solutions, eradication requires (a) sustained monitoring (and treatment as needed) and (b) a reduction in the probability of reinfection. Follow-up efforts by private and governmental actors likely played a key role in consolidating the gains from the RSC and continuing the progress toward complete eradication.2 Even after the RSC formally disbanded, the effort to eradicate hookworm infection continued. State governments ramped up their funding of anti-hookworm campaigns as the RSC was winding down. Local and state governments eventually took over some of its activities. The successor to the RSC, the Rockefeller Foundation’s International Health Board (IHB), continued to be involved at a lower level of funding. The IHB sponsored a handful of demonstration projects of the “intensive method,” which combined the deworming treatments and publicity campaigns of the RSC with technical assistance in building latrines at homes and public buildings. The state boards of health largely adopted this method and applied it to a degree throughout their jurisdictions. Harder to measure, but of considerable importance, the hookworm problem had entered into the public consciousness.
2.3 Testimonials Following the Campaign
Anecdotal evidence suggests that the RSC had an impact on human capital. Periodically educators would write the Commission thanking it for its efforts and describing the improvements following hookworm treatment. The following letter is from the school board of Varnado, La. [RSC, 1912].
As a result of your treatment for hookworm in our school, we find that children who were ranking fifth and sixth in their classes now rank second and third. Their lessons are not so hard for them; they pay better attention in class and they have more energy. […] In short, we have here in our school-rooms today about 120 bright, rosy-faced children, whereas had you not been sent here to treat them we would have had that many pale-faced, stupid children.
Farmer [1970] relates the following testimonials from the same period:
Teachers, school officials, and editors continued to be amazed at the difference in children after treatment for hookworm disease. A. J. Caldwell, Principal of Hammond High School in Louisiana, wrote that there was a decided improvement in the students in his school. One girl, who was in the fifth grade and did not attend school regularly because she was so pale and weak, started regaining her color and strength after treatment and finished the school term at the top of her class. C. C. Wright, Superintendent of Schools in Wilkes County, North Carolina, was an ardent supporter of the eradication program after examination of the pupils in his district revealed over 50 percent infection. Treatment cured the majority of these cases and the quality of performance in the county schools was raised considerably.
Typical of school officials’ attitude was that of W. H. Smith, State Supervisor of Rural Schools in Mississippi, who was thoroughly convinced that the economic prosperity of the people and the progress of educational development of the state depended largely on the successful eradication of the hookworm. The mental and physical growth of hundreds of children was evident. Smith asked for expansion of the program so that the thousands of children who were still suffering from mental and physical retardation might be saved. An editorial in a county newspaper of Hardin County, Texas, congratulated the County Commissioners for appropriating $300 toward the expense of operating five dispensaries throughout the county. According to the editorial, “300 dollars was never spent for a better purpose.”
And a report [RSC, 1915] describes the experience of one community in Virginia (in the sandy-soil Tidewater area of the state):
Henry Thrift, of Village, Va., [the school’s headmaster] told me in simple words an appealing story of how the treatment of these children had transformed the school. Children who were listless and dull are now active and alert; children who could not study a year ago are not only studying now, but are finding joy in learning. These children were born of anemic parents; were themselves infected in infancy; for the first time in their lives their cheeks show the glow of health. With this has come a new light to the eye, a new spring to the step, a new outlook on life. All this shows itself in a new spirit in the school. […] Some of the 45 children who had never attended school, having been treated, have come in during the year. Others have declared their intention to enter in the fall.
2.4 Identification Strategy
The first factor for identifying the effect of the hookworm-eradication campaign is that different areas of the South had distinct incidences of the disease. Hookworm larvae were better equipped to survive in areas with sandy soil and a warm climate. Broadly, this meant that the residents of the coastal plain of the South were much more vulnerable to infection than were those from the piedmont or mountain regions. Populations in areas with high (pre-existing) infection rates were in a position to benefit from the newly available treatments, whereas areas with low prevalence were not. This heterogeneity allows for a treatment-control strategy.
Second, the initiation of the campaign by the RSC was largely a function of factors external to the Southern states;3 The eradication campaign was made possible by critical innovations to knowledge: understanding how the disease worked and more importantly recognizing its presence. This contrasts with explanations that might have troublesome endogeneity problems, such as changes in government spending or positive income shocks in the infected areas. But even with the knowledge of the hookworm problem, there would have been formidable obstacles to taking action. The public-health infrastructure of this period was extremely limited. Rockefeller’s donation was an important precondition for attacking the problem.
Thirdly, the anti-hookworm campaign achieved considerable progress against the disease in less than a decade. This is a sudden change on historical time scales. Moreover, I examine outcomes over a fifty-year time span, which is unquestionably long relative to the five-year RSC intervention.
These factors combine to form the central variable in the present study:
More compactly, call this variable ( ), where j indexes the geographic area and t indicates j the year. The variable denotes the level of hookworm infection among school-aged children j in area j at the time of the RSC’s initial survey, and Postt is a dummy variable indicating whether year t is later than the active years of the RSC campaign (1910–1915).
I compare the evolution of outcomes (e.g., investment in human capital) across counties with distinct hookworm-infection rates, in order to assess the contribution of the eradication campaign to the observed changes. Estimating4 equation (1) measures the reduced-form differences by pre-eradication hookworm for some outcome Yijt for person i in area j at time t.
| (1) |
in which Yijt is the outcome of interest, the δt are time dummies, the δj are geographic fixed effects, and Xijt is some vector of individual-level controls.5
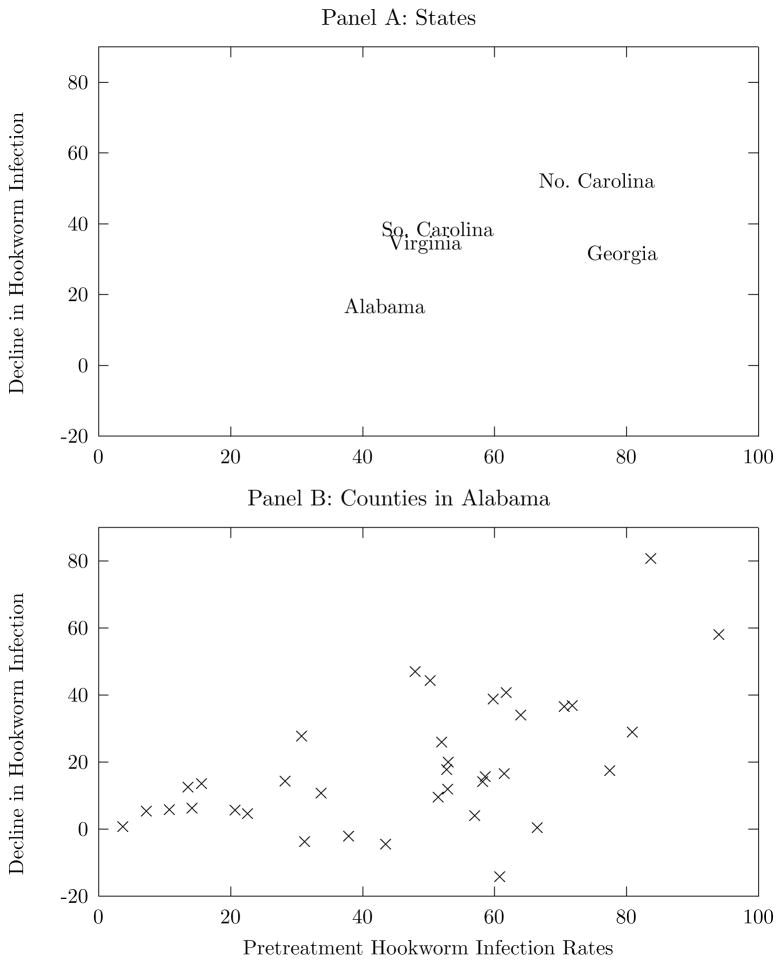
How realistic is the assumption that areas with high infection rates benefited more from the eradication campaign? Resurveys found a decrease in hookworm infection of thirty percentage points across the infected areas of the South. Such a dramatic drop in the region’s average infection rate, barring a drastic reversal in the pattern of hookworm incidence across the region, would have had the supposed effect of reducing infection rates more in highly infected areas than in areas with moderate infection rates. Figure I presents data on this issue.6 The basic assumption of this section — that areas where hookworm was highly endemic saw a greater drop in infection than areas with low infection rates — is born out across states and across counties.
Figure I.
Highly Infected Areas Saw Greater Declines in Hookworm
Notes: The y axis displays the decrease in hookworm infection post-intervention, as measured by follow-up surveys. The x axis is the pre-treatment hookworm infection rate, as measured by the Rockefeller Sanitary Commission. Panel A displays data at the state level, as reported by Jacocks (1924). Panel B contains data from counties in Alabama, as reported by Havens and Castles (1930). Both resurveys are from the early 1920s. The average number of children examined per county exceeds 450 in both studies.
2.5 Related Studies
Several pieces of contemporaneous evidence also complement the results from the present study. Summarizing evidence from randomized trials in developing countries, Dickson et al. [2000] find mixed evidence of the effect of hookworm infection on schooling, whereas Miguel and Kremer [2004] estimate the impact to be strong and positive using an experiment in Kenya. Miguel and Kremer argue that infection spillovers contaminated the earlier mixed results. Specifically, previous studies often randomized within schools, but fail to deal with the reinfection problem. As a result, they argue, follow-up surveys often found limited effects; no increase in school attendance is observed because there is little persistent difference in infection rates between control and treatment groups. (Philipson [2000] also discusses this evaluation issue in a general context.) Small-scale interventions that do not manage reinfection are therefore less likely to succeed. The RSC intervention, on the other hand, was of such a scale that it brought about large reductions in hookworm disease in entire areas, and these gains were further consolidated through improvements in sanitation. In the context of economic development, it is precisely such a large and persistent reduction in disease burden that we would wish to consider. This is a further advantage of examining the RSC campaign: enough time has passed since its inception that we can assess its long-term consequences.
There are several other recent studies that consider the early-twentieth-century reduction in tropical diseases in the American South. While childhood effects are the focus of this study, Brinkley [1994] examines the role hookworm played in agricultural productivity. He finds a negative conditional correlation between hookworm infection and agricultural income per capita, although he does not specifically use the RSC intervention to identify this relationship. Bleakley [2002a] examines the interaction between malaria and hookworm. Bleakley and Lange [2004] consider the hookworm-related increase in returns to schooling in a quantity-quality model, and examine the fertility behavior of households in response to hookworm eradication. Additionally, an earlier version of the present study was found in the first chapter of Bleakley [2002b], and those results were partially summarized by Bleakley [2003]. The latter, summary piece discussed results for schooling and income, but did not treat literacy or regular school attendance nor did it consider whether hookworm-related changes in adult income were an artifact of some alternative time-series process, nor did it report results considering possible omitted variables.
3 Data and Descriptive Statistics
This study links aggregate data on hookworm infection with individual-level data on human capital and work. The aggregated data show a region with high levels of infection and substantial increases in school attendance in the Census year following the anti-hookworm campaign. Table I contains summary statistics of various aggregate outcomes. Since county boundaries change during my sample, I use aggregated county groupings, the so-called “State Economic Areas” (SEA) as the geographic unit, and so the j in equation (1) indexes SEAs.
Table I.
Summary Statistics
| Whole Sample
|
By Hookworm Infection
|
Source
|
||
|---|---|---|---|---|
| > 40 %
|
< 40 %
|
|||
| Hookworm-Infection Rate | 0.320 (0.230) | 0.554 (0.137) | 0.164 (0.117) | RSC Annual Reports |
| Individuals Treated At Least Once by the RSC, Per School-Age Child | 0.206 (0.205) | 0.342 (0.199) | 0.109 (0.147) | RSC Annual Reports |
| School Enrollment, 1910 | 0.721 (0.104) | 0.711 (0.099) | 0.729 (0.108) | IPUMS; author’s calculations |
| Change in School Enrollment, 1910–20 | 0.089 (0.080) | 0.103 (0.090) | 0.078 (0.072) | IPUMS; author’s calculations |
| Full-time School Attendance, 1910 | 0.517 (0.140) | 0.469 (0.123) | 0.551 (0.141) | IPUMS; author’s calculations |
| Change in Full-time School Attendance, 1910–20 | 0.203 (0.097) | 0.246 (0.093) | 0.172 (0.089) | IPUMS; author’s calculations |
| Literacy, 1910 | 0.853 (0.104) | 0.824 (0.101) | 0.875 (0.102) | IPUMS; author’s calculations |
| Change in Literacy, 1910–20 | 0.060 (0.067) | 0.081 (0.075) | 0.045 (0.057) | IPUMS; author’s calculations |
| Population Black, 1910 | 0.357 (0.221) | 0.41 (0.208) | 0.318 (0.223) | IPUMS; author’s calculations |
| Fraction Population Urban, 1910 | 0.174 (0.200) | 0.167 (0.214) | 0.180 (0.190) | ICPSR (1984) |
| School Term, in Months, c. 1910 | 5.251 (1.066) | 5.055 (1.042) | 5.391 (1.068) | State annual reports |
| Schools per Square Mile, c. 1910 | 0.195 (0.358) | 0.142 (0.053) | 0.233 (0.465) | State annual reports; ICPSR |
| Value of School Property, per Pupil, Current Dollars, c. 1910 | 5.518 (4.037) | 4.699 (3.159) | 6.104 (4.496) | State annual reports |
| Teacher-to-School Ratio, c. 1910 | 1.336 (0.545) | 1.397 (0.505) | 1.293 (0.572) | State annual reports |
| Sample Size | 115 | 48 | 67 | n/a |
Notes: Variable means displayed to the right of variable name. Standard deviations displayed in parentheses below the mean. Sample selection: native-born whites and blacks in the IPUMS, in the RSC-surveyed geographic units, for the indicated years. The school enrollment and attendance data are constructed from children aged 8–16; literacy data are for children 10–16, and the RSC reported infection rates for children aged 8–16. See the Data Appendix for further information on sources and variable construction.
The hookworm-infection rates were computed by the Rockefeller Sanitary Commission for more than 550 counties across the South. The RSC collected these data as a prelude to mounting a widespread treatment campaign. The data collection took place between 1910 and 1914 (at a single point in time for each county), and the summary statistics were constructed from samples of school-aged children in each county.7 The RSC surveys measured an average infection rate across SEAs of 32%.
The RSC also reported county-specific details of their subsequent treatment campaign. For example, I include data on the number of treatments issued by the RSC. These numbers (scaled by 1910 SEA youth population) are also reported in Table I. The second and third columns display the means by subsamples that are separated based on the severity of their hookworm problem. Because of the policy of treating any infected person who presented himself at a Commission dispensary, the RSC directed more resources towards the areas with greater hookworm infection.
Over four hundred thousand individuals were treated for hookworm through the RSC dispensaries up through the end of 1915. This is about 64% of the population aged 6–17 in the affected counties. Comparing these measures at the SEA level in a regression (N = 113 and R2 = .495) yields the following estimates:
where Trj is the number of individuals treated at least once by the RSC, divided by the school-aged population (ages six to seventeen, inclusive). This indicates that, on the margin, about 62% of sufferers were treated.8 Note, however, that I do not present the results below literally as effects of the campaign’s free medicines. The RSC had a multi-pronged approach to fighting hookworm disease. Deworming was a central part, to be sure, but mounting publicity campaigns for sanitation and educating doctors to recognize the symptoms were other strategies of note.
The micro-level data employed in the present study come from the Integrated Public Use Mi-cro Sample (IPUMS), the output of a project to harmonize the coding of historical U.S. Census microdata (Ruggles and Sobek (1997)). The RSC’s activities took place in the first of the 1910s, therefore the core component of the data come from the censuses that bracket the intervention: 1910 and 1920. For sensitivity analysis, I include census micro data from 1900–1950, and for the long-term followup comprises census samples from 1880–1990.
Three binary indicators of human capital are used in the present study: school enrollment, regular or “full-time” school attendance, and literacy. The enrollment variable measures whether the child had gone to school for at least one day in the months preceding the Census.9 I proxy for regular or “full time” school attendance by combining the enrollment variable with occupational information. Children were coded as attending school full time if they were both enrolled in school and did not report a gainful occupation. The literacy variable indicates whether the child can read and write.
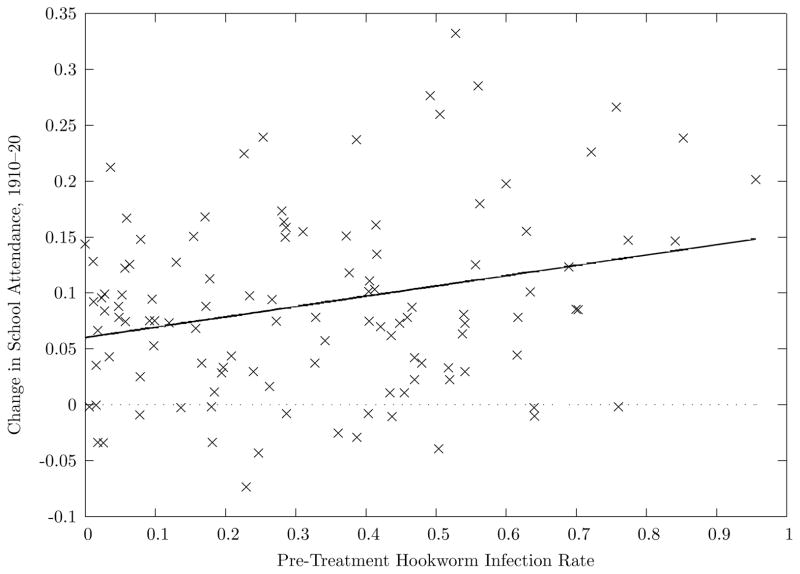
The data show faster increases from 1910 to 1920 in the enrollment, attendance, and literacy rates in areas with high hookworm infection, coupled with lower average levels of these measures in 1910. The fact that this period coincides with the hookworm-eradication campaign is prima facie evidence that the increase in school attendance was caused by the reduction in hookworm disease. The numbers suggest a substantial effect of hookworm: the increase in school post-RSC is over thirty percent higher in the areas with higher infection rates prior to the RSC. Figure II shows this in greater disaggregation: the 1910–20 change in school attendance by SEA versus its pre-treatment hookworm infection rate. The upward-sloping relationship shown in the graph is statistically significant at conventional confidence levels.
Figure II.
Highly Infected Areas Saw Greater Increases in School Attendance
Notes: The y axis displays the 1910–20 change in school-attendance rates, based on author’s calculations from the IPUMS microdata. The x axis is the pre-treatment hookworm infection rate, as measured by the Rockefeller Sanitary Commission. The unit of observation is the State Economic Area (SEA), an aggregation that contains on average six counties. The school data are averages from a sample consisting of all native-born white and black children in the IPUMS between the ages of 8 and 16 in the RSC-surveyed geographic units for 1910 and 1920. Each SEA’s change is marked with a × symbol. The solid line plots the fitted values from a bivariate regression (weighted by cell size), which has an R̄2 of 0.083 and a coefficient (standard error) of Δ school attendance on infection of 0.092 (0.029).
Areas with greater hookworm burdens were different along other margins as well, as shown in Table I. For one, they were more rural, and had higher proportions of black residents. Additionally, the hookworm-infested areas shorter school terms, had fewer schools per square mile, and a lower capital stock invested in primary education. There were also more teachers per school in these areas, in part because of prevalence of one-room common schools. These variables and others will be important controls in the sensitivity analysis below.
Finally, I examine the spatial correlations between hookworm and several other categories of sickness in Table II. Since the registration area for mortality was not fully developed until much later, I am constrained to use data from various, disparate sources. Data compiled by Maxcy (1923) was used to measure the relationship between hookworm infection and malaria mortality. Even though no simple correlation is present, I do find a significant relationship once I condition on the racial makeup and population density of the county. Malaria rates will therefore be included as a control variable below. Pellagra, a condition caused by nutrition deficiency, was prevalent in the Deep South in this period, but receded gradually as diets improved with income and with the vitamin fortification of cereals. I use data from a survey of pellagra morbidity in Mississippi. In Column 2, I show that, although hookworm and pellagra were correlated in the cross section of Mississippi counties, this result was due to the racial composition of those areas. For this and many other reasons, controls for race will be an integral component of the analysis below. Mortality from typhoid fever, a disease related to poor sanitation, was measured in Kentucky by that state’s Board of Health for 1911–1915. In the subsample of Kentucky counties, I find no significant correlation between hookworm and typhoid. Data on child mortality are computed using the Preston-Haines (1984) methodology from the 1900 and 1910 Census microdata from the IPUMS project. As noted above, hookworm infection very rarely resulted in death. Consistent with this, no significant relationship between child mortality and hookworm infection is evident in Column 4.
Table II.
Correlations with Other Diseases
| (1) | (2) | (3) | (4) | |
|---|---|---|---|---|
| Health Indicator: | Malaria mortality /10K pop | Pellagra morbidity per 100 pop | Typhoid mortality per 100 pop | Child mortality |
| Dependent Variable Mean: | 1.6316 | 0.5518 | 0.1921 | 0.1248 |
| Independent Variables:
|
||||
| Panel A: Bivariate Regressions | ||||
| Hookworm Infection Rate | −0.0029 (0.0040) | −0.0039 * (0.0020) | −0.0011 (0.0010) | 0.0000 (0.0002) |
| No. of observations | 594 | 74 | 53 | 115 |
| Panel B: Regressions with Additional Controls | ||||
| Hookworm Infection Rate | −0.0079 ** (0.0038) | 0.0197 (0.0209) | −0.0012 (0.0010) | −0.0001 (0.0002) |
| Fraction of county black, 1910 | 5.1161 *** (0.4494) | 1.0675 *** (0.4191) | 0.2098 (0.3131) | 0.0496 *** (0.0129) |
| Population density of county, 1910 | −0.6115 ** (0.2542) | 0.2228 (0.2238) | −0.1471 ** (0.0563) | 0.0061 * (0.0035) |
| No. of observations | 575 | 70 | 53 | 115 |
Notes: The dependent variable for each column is the health indicator noted above. The unit of observation is the county (except for the child-mortality data, which is at the State-Economic-Area (SEA) level to manage changing county boundaries). Panel A displays the results of bivariate regressions with the RSC measure of hookworm as the independent variable. The regressions in Panel B also contain the listed control variables. Huber-White standard errors are in parentheses below the point estimates. Single asterisk denotes statistical significance at the 90% level of confidence; double, 95%; triple, 99%. Reporting of the constant term is suppressed. County-level malaria data are from Maxcy (1923) and cover the whole South for the year 1919. Pellagra-morbidity data are taken from the Mississippi Board of Health (1917), and cover all counties in that state in 1914. Typhoid information is from the Kentucky Board of Health (1917) and measures mortality from the disease in Kentucky counties for the years 1911–15. Child mortality is constructed from IPUMS data using the Preston-Haines methodology (1984) and covers the South (by SEA) for 1900 and 1910.
4 Contemporaneous Effects on Children
The dramatic reduction in hookworm infection in the South brought about a substantial increase in human-capital investment. To support this conclusion, I use and extend the methodology outlined above and present several pieces of evidence in this section:
A regression analysis of changes in literacy, school enrollment, and school attendance between the 1910 and 1920 Censuses (i.e., pre- and post-RSC) shows that schooling attendance rose substantially in areas with higher rates of pre-period hookworm infection. This increase was both in absolute terms and relative to areas with lower levels of hookworm infection in 1910.
Further analysis of a longer panel of Censuses indicates that this result is not due to differential trends between the high-infection and low-infection areas.
The results also are robust to a “horse race” against a variety of alternative hypotheses, including controls for health and health policy, educational resources, mean reversion, race and race relations, urbanization and land use, and parental background.
Overall, I argue that the evidence weighs in favor of a substantial increase in human capital as a result of the reduction in the burden of hookworm disease.
4.1 Main Results
In this subsection, I estimate the effect of the hookworm-eradication campaign using equation (1) above. This involves comparing the census microdata on human capital before and after the RSC. As described above, the variable of interest ( ) is the interaction of pre-period hookworm infection, , with a dummy, Postt, indicating whether the year comes after the RSC.
Using the two-period comparison, I find a substantial increase in school enrollment among children living in areas that had high levels of hookworm infection in 1910. This is true in absolute terms and also relative to areas with lower levels of infection. Specifically, the coefficient on ( ) implies that a county with a 1910 infection rate of 50% would experience an increase in schooling enrollment of five percentage points, relative to a county with no infection problem. In 1910, the mean of school enrollment in the sample was 0.78 and the standard deviation across SEAs was 0.11. Moreover, the standard deviation of hookworm infection rates across SEAs in 1910 was 0.23; so a one-standard-deviation increase in lagged hookworm infection is associated with a post-RSC increase in schooling enrollment of one quarter of a standard deviation.
These empirical results are presented in Table III. Estimates of the variable of interest, pre-period hookworm × post, are displayed for various outcomes and specifications. Panel A presents the estimates using the 1910 and 1920 censuses, which bracket the RSC intervention. In addition to the results on school enrollment mentioned in the previous paragraph, I estimate positive effects of hookworm eradication on full-time school attendance and literacy as well. Panel B contains similar estimates using the Census microdata from 1900–1950. (The literacy variable is not available in the later Censuses, so Column 3 is blank in Panels B-D; literacy results in Panels E-G use the 1910–20 Censuses.)
Table III.
Hookworm and Human Capital: Basic Results
| School Enrollment
|
Full-time School Attendance
|
Literacy
|
|---|---|---|
| Panel A: Results from 1910–1920 Censuses | ||
| 0.0883 *** (0.0225) | 0.1591 *** (0.0252) | 0.0587 *** (0.0186) |
| Panel B: Results from 1900–1950 Censuses | ||
| 0.0608 ** (0.0261) | 0.1247 *** (0.0286) | |
| Panel C: Add Hookworm × Trend | ||
| 0.0929 ** (0.0414) | 0.1454 *** (0.0488) | |
| Panel D: Allow for SEA-Specific Trends | ||
| 0.0954 *** (0.0233) | 0.1471 *** (0.0287) | |
| Panel E: Include State × Post Dummies | ||
| 0.1313 *** (0.0245) | 0.2144 *** (0.0290) | 0.0417 ** (0.0207) |
| Panel F: Allow for State-Specific Mean Reversion | ||
| 0.1148 *** (0.0265) | 0.1813 *** (0.0312) | 0.0408 ** (0.0206) |
| Panel G: Use Infection Rate in State of Birth Instead | ||
| 0.0489 (0.0504) | 0.2057 *** (0.0765) | 0.0907 ** (0.0451) |
Notes: This table reports estimates of the interaction of pre-treatment hookworm and a post-RSC dummy in equation 1. The dependent variables are the binary indicators denoted in the column headings. Robust standard errors in parentheses (clustering on area times Postt). Single asterisk denotes statistical significance at the 90% level of confidence; double 95%; triple, 99%. The base sample consists of all native-born white and black children in the IPUMS between the ages of 8 and 16 for 1900 and 1950. In Panels A–F, the sample is drawn from the RSC-surveyed county groups (State Economic Areas or SEAs). In Panel G, the sample consists of individuals in the 48 states and territories for which Kofoid and Tucker (1921) reports hookworm infection rates. All regressions include fixed effects for area and time; controls for age, female, female×age, black, and black×age; and the interactions of the demographic controls with Postt. The average school enrollment in 1910 (× Postt) is used to control for mean reversion in Panels F and G. In Panel F, this variable is interacted with state dummies to control for state-specific mean reversion. Reporting of additional coefficient estimates is suppressed. Because literacy is not available in the later Censuses, no estimates are available for literacy in Panels B–D.
The surge in schooling attendance in high-hookworm counties coincided with the campaign for hookworm eradication. This is reassuring because it indicates that the differences estimated above were not due to pre-existing differential trends across the region. Such trends — coming from a number of possible factors — might have caused differential movements in school attendance even in the absence of the anti-hookworm campaign. However, my estimates of the effect of the reduced hookworm infection are robust to allowing for these trends.
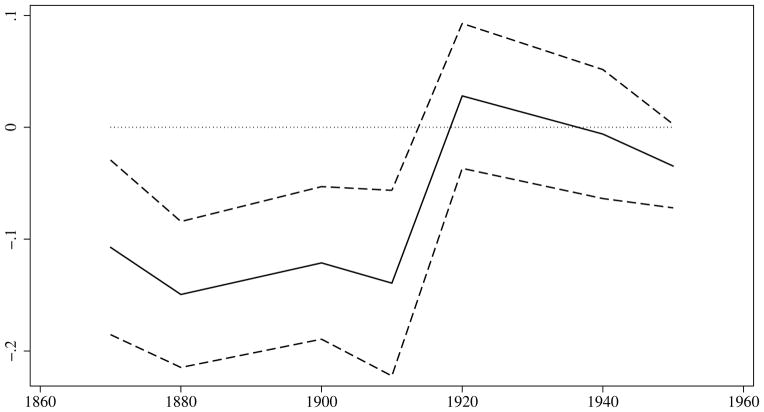
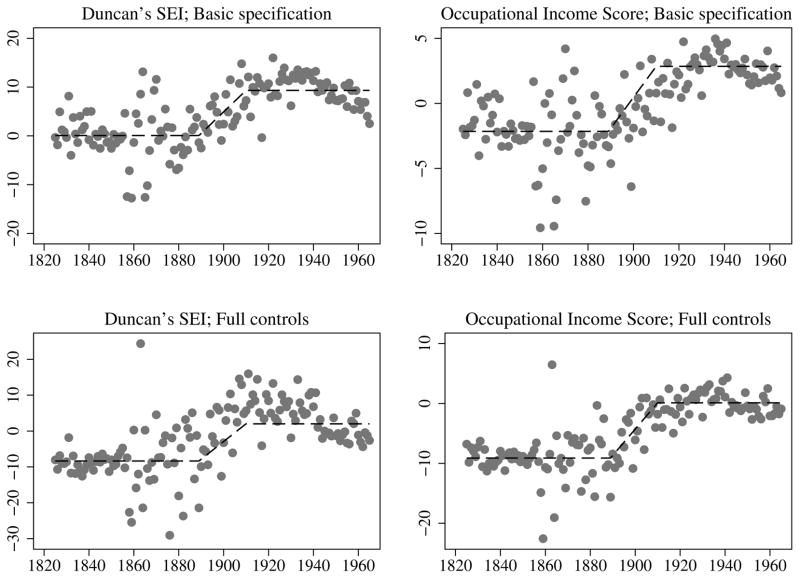
The surge in school attendance in high-hookworm counties coincided with the campaign for hookworm eradication. This can be seen in Figure III.10 As shown in the graph, areas with more hookworm infection had lower levels of school attendance prior to the RSC, but these groups converge markedly thereafter. This lends credence to the view that this separation was caused by the anti-hookworm intervention.
Figure III.
Hookworm Eradication and School Attendance, 1870–1950
Notes: The y axis plots the year-specific coefficients on the circa 1913 hookworm-infection rate (solid line), plus the 95%-confidence intervals (dashed lines). The x axis is the Census year. The sample consists of all native-born white and black children in the IPUMS between the ages of 8 and 16 in the RSC-surveyed geographic units for 1870, 1880, 1900, 1910, 1920, 1940, and 1950. For each year, the coefficients are estimated in a regression of a school-attendance dummy on pre-intervention hookworm infection and demographic controls. Confidence intervals are constructed using standard errors that are clustered on SEA.
The “timing” hypotheses can be further investigated by augmenting the regression specification in equation 1. Specifically, we can add an addition term to capture these possible pre-existing trends. I construct this term by interacting with t, the time variable. The resulting equation is as follows:
| (2) |
in which the δt are time dummies, the δj are geographic fixed effects, and ( ) is the interaction of with Postt, as above. Differences between the areas that arise due to pre-existing trends will load onto γ, whereas differences that coincide with the anti-hookworm campaign will load onto β.
This comparison of “sudden shift” versus “trend” continues to attribute the increase in schooling among high-hookworm counties to the period following the RSC intervention. These results are seen in Panel C of Table III. Allowing for a differential trend by SEAs with different preexisting infection rates does not alter the main conclusion: the higher-hookworm counties saw relative increases in school attendance immediately following the RSC. This result is also robust to allowing the trends to be SEA-specific (Panel D).
The specification in Panel E contains controls for state-level shocks and policy changes, most notably the compulsory-schooling and child-labor laws that were imposed in the first half of the twentieth century. Since these shifts were at the level of state × year, this specification implements a simple fix to purge the estimates of this effect: including (state × year) fixed effects. Throwing out all of the cross-state variation yields estimated effects that are essentially unchanged.
Another concern is mean reversion across areas: if some counties had high hookworm infection and low schooling because of some (temporary) income shock, we might expect rises in school attendance in the following period even if hookworm had not affected the schooling decision. In Panel F of Table III, I incorporate the interaction of Postt with 1910 average school attendance by SEA into the specification. Differential incidence of state policies (by average school-attendance rates) are also absorbed by the interaction of state × year dummies with lagged school attendance. There is evidence of mean reversion in schooling, but this mechanism does not account for the rise in schooling in higher-hookworm areas.
In Panel G, I re-estimate equation 2 using only state-level variation in the anti-hookworm campaign. Because the RSC did not attempt a systematic survey of hookworm across the whole country, I employ a measure of hookworm infection by state from Kofoid and Tucker (1921), who surveyed infection rates among army recruits. I match individuals to this variable using their state of birth. Because the full set of states is a much more heterogeneous sample, I also control for mean reversion as above.
Restricting the analysis to the state level excludes a substantial fraction of the useful variation: in all cases, the standard error on the estimate of ( ) is approximately twice those found above in the SEA-level analysis. There are two likely reasons for this: (i) I am reducing the number of geographic units and adjusting the standard errors to account for intraclass correlation; (ii) the standard deviation of infection rates across states is substantially smaller that the standard deviation across county groups.
On the other hand, point estimates of the effect of hookworm eradication are approximately the same magnitude as those in the county-level results. The result for enrollment is smaller than the estimates above, and we can reject neither zero nor the estimates from the county-group-level variation. On the other hand, attendance and literacy do show statistically significant responses to hookworm, with magnitudes that are larger than previous estimates.
The results indicate that, at the state level, the effect of hookworm eradication worked principally through the intensive margin of human-capital formation (literacy and full-time school attendance). This suggests that, if we examine these cohorts as adults, we will see increases in human capital, but the estimates (of years of schooling especially) may well be statistically insignificant. These results provide a natural benchmark for the cohort-based analysis in Section 6 below, since the retrospective-cohort analysis employs precisely the state-of-birth variation in hookworm.
4.2 Sensitivity Analysis
The finding that highly infected counties experienced surges in school attendance is not sensitive to controlling for a variety of alternative hypotheses. These include allowing for changes in health and health policy, educational resources, race and race relations, urbanization and land use, and parental background. I contrast these hypotheses with the effect of hookworm and the RSC by starting with equations 1 and 2 and adding plausible proxies for the supposed confounds. These results are found in Table IV. The baseline results from above are shown in Panel A, and the subsequent panels present specifications with additional controls. In every case, the added control variables are jointly significant at conventional confidence levels. (The aggregate control variables enter into the specification interacted with Postt. All aggregate main effects are absorbed by the area fixed effects.)
Table IV.
Sensitivity Analysis
| Dependent Variables: | School Enrollment
|
Full-time School Attendance
|
Literate
|
||
|---|---|---|---|---|---|
| Sample: | 1900–50 | 1910–20 | 1900–50 | 1910–20 | 1910–20 |
| Independent Variables (× Post):
|
|||||
| Panel A: Baseline Results | |||||
| Pre-treatment Hookworm | 0.0954 *** (0.0233) | 0.0883 *** (0.0225) | 0.1471 *** (0.0287) | 0.1591 *** (0.0252) | 0.0587 *** (0.0186) |
| Panel B: Health and Health Policy Controls | |||||
| Pre-treatment Hookworm | 0.1200 *** (0.0291) | 0.1187 *** (0.0262) | 0.1628 *** (0.0355) | 0.1646 *** (0.0294) | 0.0724 *** (0.0233) |
| Examined by the RSC, per capita | −0.0108 (0.1078) | −0.2757 *** (0.1007) | 0.1859 (0.1446) | −0.1626 (0.1175) | 0.0144 (0.0716) |
| RSC Sanitary Index | 0.0005 (0.0008) | −0.0008 (0.0008) | 0.0003 (0.0013) | −0.0021 ** (0.0010) | −0.0012 ** (0.0006) |
| Change in County Spending on Health and Sanitation, 1902–32 | −0.0657 (0.0494) | −0.0373 (0.0523) | 0.0064 (0.0554) | 0.0174 (0.0609) | −0.0620 * (0.0320) |
| Full-time Health Officer, per capita | −0.0011 (0.0344) | −0.0241 (0.0317) | −0.0650 (0.0539) | −0.1033 * (0.0544) | −0.0363 (0.0273) |
| Malaria mortality, c. 1917 | −0.0003 (0.0002) | 0.0000 (0.0002) | −0.0004 (0.0003) | 0.0001 (0.0002) | 0.0000 (0.0001) |
| WWI Camp Size, per capita, c. 1918 | 0.0839 (0.0609) | 0.0217 (0.0721) | 0.1034 * (0.0614) | 0.0625 (0.0704) | 0.0266 (0.0704) |
| Decline in Fertility, 1900–10 | 1.7780 * (0.9889) | 1.0634 (1.0666) | 2.9758 *** (1.0867) | 2.2841 ** (1.0192) | −1.2503 * (0.6468) |
| Panel C: Education and Race Controls | |||||
| Pre-treatment Hookworm | 0.1235 *** (0.0208) | 0.0793 *** (0.0208) | 0.1851 *** (0.0247) | 0.1581 *** (0.0250) | 0.0556 *** (0.0171) |
| Change in School Term, c. 1910–20 | 0.0076 (0.0087) | 0.0115 (0.0082) | 0.0195 ** (0.0092) | 0.0248 ** (0.0103) | 0.0033 (0.0051) |
| Change in Average Monthly Teacher Salary, c. 1910–20 | −0.0423 ** (0.0176) | 0.0103 (0.0150) | −0.0411 * (0.0214) | 0.0110 (0.0208) | −0.0152 (0.0120) |
| Change in Teachers per School, c. 1910–20 | 0.0384 * (0.0210) | −0.0159 (0.0209) | 0.0107 (0.0255) | −0.0389 (0.0288) | 0.0096 (0.0139) |
| Change in Number of Schools per Square Mile, c. 1910–20 | 0.0420 ** (0.0203) | 0.0194 (0.0187) | −0.0166 (0.0222) | −0.0405 * (0.0245) | −0.0226 * (0.0136) |
| Change in Pupil/Teacher Ratio, c. 1910–20 | 0.0267 (0.0203) | 0.0321 * (0.0170) | −0.0445 * (0.0232) | −0.0321 (0.0217) | −0.0276 ** (0.0135) |
| Change in Value of School Plant and Equipment, c. 1910–20 | −0.0085 (0.0069) | −0.0022 (0.0061) | 0.0004 (0.0077) | 0.0035 (0.0081) | 0.0068 (0.0051) |
| Change in Returns to Literacy for Adults, c. 1910–20 | −0.0035 (0.0033) | −0.0066 ** (0.0031) | −0.0018 (0.0040) | −0.0042 (0.0038) | −0.0002 (0.0029) |
| Change in County Educational Spending, per child, 1902–32 | −0.0011 (0.0033) | −0.0012 (0.0031) | 0.0029 (0.0046) | 0.0037 (0.0049) | 0.0019 (0.0024) |
| Child Literacy Rate, 1910 | −0.7746 *** (0.2374) | −1.3063 *** (0.1940) | −0.5695 ** (0.2687) | −0.9434 *** (0.2386) | −0.9583 *** (0.1701) |
| Adult Literacy Rate, 1910 | 0.6119 *** (0.2195) | 0.9468 *** (0.1764) | 0.3860 (0.2619) | 0.6271 *** (0.2278) | 0.4145 ** (0.1631) |
| Rosenwald-funded Classrooms, per capita, 1930 | 0.0056 *** (0.0013) | 0.0030 *** (0.0010) | 0.0075 *** (0.0018) | 0.0044 *** (0.0016) | 0.0013 (0.0008) |
| Lynchings per capita, 1900–30 | −0.0008 (0.0011) | 0.0001 (0.0008) | 0.0010 (0.0013) | 0.0016 (0.0011) | 0.0007 (0.0008) |
| Fraction Black, 1910 | −0.0473 (0.0470) | 0.0443 (0.0384) | −0.1148 ** (0.0557) | 0.0194 (0.0475) | −0.0851 ** (0.0350) |
| Panel C: Agricultural Controls | |||||
| Pre-treatment Hookworm | 0.0982 *** (0.0249) | 0.0954 *** (0.0283) | 0.1331 *** (0.0275) | 0.1198 *** (0.0293) | 0.0480 ** (0.0207) |
| Fraction in Urban Area, 1910 | −0.0528 (0.0401) | −0.1091 ** (0.0434) | −0.1337 ** (0.0569) | −0.2398 *** (0.0530) | −0.1371 *** (0.0272) |
| Change in Fraction Urban, 1900–10 | 0.2267 *** (0.0649) | 0.2382 *** (0.0654) | 0.2178 *** (0.0753) | 0.1300 * (0.0764) | 0.1171 ** (0.0497) |
| Farm Acreage, per capita, 1910 | 0.0075 *** (0.0023) | 0.0012 (0.0022) | 0.0098 *** (0.0030) | 0.0035 (0.0027) | −0.0012 (0.0017) |
| Farm value per capita, 1910 | 0.0309 ** (0.0134) | 0.0329 ** (0.0138) | 0.0150 (0.0147) | −0.0077 (0.0149) | 0.0036 (0.0091) |
| Sharecropped Acreage, per capita, 1910 | −0.0399 *** (0.0080) | −0.0288 *** (0.0069) | −0.0385 *** (0.0094) | −0.0219 *** (0.0084) | −0.0144 ** (0.0069) |
| Cotton Acreage per capita, 1910 | 0.0205 ** (0.0086) | 0.0209 ** (0.0084) | 0.0148 (0.0109) | 0.0298 *** (0.0101) | 0.0099 (0.0071) |
| Tobacco Acreage, 1910 | −0.0105 (0.0503) | −0.0663 (0.0438) | 0.0757 (0.0661) | 0.0633 (0.0607) | −0.0260 (0.0415) |
| Panel D: Parental-Background Controls | |||||
| Pre-treatment Hookworm | 0.1130 *** (0.0291) | 0.0905 *** (0.0224) | 0.1417 *** (0.0383) | 0.1527 *** (0.0238) | 0.0585 *** (0.0186) |
| Father’s Occupational Income Score | 0.0032 *** (0.0002) | 0.0032 *** (0.0002) | 0.0053 *** (0.0002) | 0.0070 *** (0.0003) | 0.0019 *** (0.0002) |
| Father Missing | −0.3159 *** (0.0220) | −0.3116 *** (0.0277) | −0.5804 *** (0.0259) | −0.7963 *** (0.0381) | −0.1998 *** (0.0215) |
| Mother’s Occupational Income Score | 0.0001 (0.0002) | 0.0001 (0.0005) | −0.0019 *** (0.0003) | −0.0064 *** (0.0007) | −0.0009 ** (0.0004) |
| Mother Missing | −0.0670 *** (0.0224) | −0.0571 (0.0540) | −0.2629 *** (0.0295) | −0.7136 *** (0.0714) | −0.1193 *** (0.0456) |
| Panel E: Include Above Controls Simultaneously | |||||
| Pre-treatment Hookworm | 0.1014 *** (0.0349) | 0.0850 *** (0.0224) | 0.1408 *** (0.0421) | 0.1026 *** (0.0325) | 0.0513 ** (0.0213) |
Notes: This table reports estimates of the interaction of pre-treatment hookworm and a post-RSC dummy equation 1 and 2. The dependent variables are the binary indicators denoted in the column headings. Robust standard errors in parentheses (clustering on SEA times post). Single asterisk denotes statistical significance at the 90% level of confidence; double, 95%; triple, 99%. Sample consists of native-born black and white children in the IPUMS between the ages of 8 and 16 in the RSC-surveyed geographic units for the indicated years. Number of clusters = 230. All regressions include fixed effects for area and time; controls for age, female, female×age, black, and black×age; and the interactions of the demographic controls with Postt. Reporting of additional coefficient estimates is suppressed.
These results are not sensitive to controlling for various health-related measures, as seen in Panel B of Table IV. First, I include the number of individuals examined by the RSC, per capita, to consider direct effects of the RSC campaign of dispensaries, which, in addition to hookworm treatments, provided hookworm exams. The stated purpose of the examinations was to determine if children had hookworm disease, but it seems unlikely that trained doctors and nurses would do absolutely nothing if they recognized some other disease. I also use data on sanitation collected by the RSC concurrently with its hookworm survey of Southern counties. Part of the Rockefeller campaign was a campaign of sanitation education for the whole region. It is therefore a reasonable alternative hypothesis that improvements in sanitation had benefits above and beyond simply reducing hookworm. Additionally, I include three variables measuring increased governmental involvement in public health: (i) the number of full-time health officers per capita; (ii) changes in health and sanitation spending by county governments over various intervals11; and, because the federal government involved itself in sanitation efforts in the areas surrounding troop cantonments during World War I, (iii) WWI camp size per capita. Next, I account for the presence of malaria, the other major tropical disease in the South at the turn of the century. Finally, I incorporate the 1900–10 changes in total fertility rates, which might reflect a latent shift in parental attitudes towards the quantity-quality tradeoff.
In Panel C, I control for a number variables related to education and race, and obtain essentially similar estimates on the hookworm variable. If the results that I ascribe to hookworm eradication were instead due to some shift in local educational policy, the school-resources variables should correct for that. Consequently, I include logarithmic changes in the school term, teachers per school, schools per square mile, pupil/teacher ratio, value of school property, and educational spending. I use average literacy rates among children and adults to proxy for mean reversion. Additionally, I control for the estimated 1910–20 change in returns to literacy among adults, by SEA, as a measure of demand-side factors that influence the decision about human-capital investment. Another particular policy shift was the (partial) correction of the resource imbalance between white and black schools, as documented by Margo (1990) and Donohue et al. (2002). While much of this increase took place well after the decade of the 1910s, it is nonetheless useful to consider whether the earlier phases of this transition affect the estimates of the impact of hookworm eradication. The first thing to note is that the above estimates already incorporate (black × year) effects. However, since these extra funds were presumably directed towards with areas with larger black populations, I also allow for effects at the aggregate level. In particular, I interact the percentage black of the SEAs 1910 population with Postt. I also control directly for the schools built through the philanthropy of Julius Rosenwald (see Donohue et al. (2002) for more on this program), which appear to have affected enrollment and attendance. Finally, I proxy for poor race relations using a measure of lynchings per capita. Adding these controls makes little difference for the estimated effect of hookworm eradication.
Hookworm was a relatively rural disease, but changes in school attendance for urban versus rural children are not responsible for the results presented above. In Panel C of Table IV, I allow the human-capital outcomes to change across counties differentially by the fraction of that area’s population living in an urban area, by changes in urbanization in the decade prior to the intervention, and by farm acreage and value per capita. Additionally, the high-hookworm counties tended to be in the coastal plain where crop mixes were different, so I control for the acreages per capita sharecropped and planted with cotton or tobacco.
In Panel D, I include controls for parental background, but these do not materially affect the estimated hookworm coefficient. I proxy for each parent’s income with the occupational income score, and include a binary indicator for whether that parent is present (missing parents getting an imputed income of zero). While these parental SES variables are generally highly statistically significant, their inclusion results in changes of the hookworm coefficient that are less than a standard error. Similar results are obtained when using literacy or Duncan’s socioeconomic indicator as the measures of parental background, as well as if allowing these parental variables to vary across year.
Finally, Panel E of Table IV presents the estimated coefficient on hookworm × Postt when all of the above controls are included in the specification. The estimates are similar to the baseline.
4.3 Demographic Decompositions
The estimated relationship between hookworm and human capital was not simply concentrated on one particular demographic group, although there are noteworthy differences as well. These results are seen in Table V. For preteens and adolescents, the estimates for enrollment and attendance are close in magnitude, which suggests a balancing of two offsetting effects: younger children were more likely to be infected, but adolescents were closer to the margin of enrolling and/or attending regularly. The literacy results are different by age group but, because literacy is a stock variable, the larger coefficient for preteens means that children, following the eradication campaign, became literate earlier in life. Males and females were similarly affected by the intervention (results not shown).
Table V.
Results for Subgroups
| (1) | (2) | (3) | (4) | (5) |
|---|---|---|---|---|
| School Enrollment
|
Full-time School Attendance
|
Literate
|
||
| 1900–50 | 1910–20 | 1900–50 | 1910–20 | 1910–20 |
| Panel A: Baseline Results | ||||
| 0.0954 *** (0.0233) | 0.0883 *** (0.0225) | 0.1471 *** (0.0287) | 0.1591 *** (0.0252) | 0.0587 *** (0.0186) |
| Panel B: Preteens | ||||
| 0.0932 *** (0.0255) | 0.0890 *** (0.0242) | 0.1416 *** (0.0302) | 0.1549 *** (0.0266) | 0.0912 *** (0.0253) |
| Panel C: Adolescents | ||||
| 0.0986 *** (0.0280) | 0.0877 *** (0.0282) | 0.1573 *** (0.0336) | 0.1682 *** (0.0295) | 0.0323 * (0.0165) |
| Panel D: Blacks | ||||
| 0.2299 *** (0.0399) | 0.1838 *** (0.0337) | 0.2601 *** (0.0399) | 0.2205 *** (0.0320) | 0.1078 *** (0.0374) |
| Panel E: Whites | ||||
| 0.0378 (0.0237) | 0.0270 (0.0267) | 0.1103 *** (0.0294) | 0.1169 *** (0.0294) | 0.0264 * (0.0139) |
| Panel F: Preteen Whites | ||||
| 0.0238 (0.0245) | 0.0183 (0.0268) | 0.0741 *** (0.0278) | 0.0811 *** (0.0284) | 0.0454 ** (0.0201) |
| Panel G: Adolescent Whites | ||||
| 0.0679 ** (0.0316) | 0.0474 (0.0345) | 0.1708 *** (0.0394) | 0.1749 *** (0.0373) | 0.0121 (0.0129) |
Notes: This table reports estimates of the variable pre-treatment hookworm × Postt in equation 1 and 2, for the indicated subsamples. The dependent variables are the binary indicators denoted in the column headings. Robust standard errors in parentheses (clustering on SEA times post). Single asterisk denotes statistical significance at the 90% level of confidence; double, 95%; triple, 99%. Base sample consists of native-born black and white children in the IPUMS between the ages of 8 and 16 in the RSC-surveyed geographic units for the indicated years. Number of clusters = 230. All regressions include fixed effects for area and time; controls for age, female, female×age, black, and black×age; and the interactions of the demographic controls with Postt. Reporting of additional coefficient estimates is suppressed.
There was also an important difference between how blacks and whites responded to the anti-hookworm campaign. Whites appeared to have positive responses to hookworm eradication by all three measures of human capital but, for blacks, the estimated effects of hookworm were uniformly larger. There are several candidate explanations for this result. One is that the general health of blacks was more sensitive to a given level of (own) hookworm infection. However, this explanation is inconsistent with existing medical evidence (Vance, 1932; Brinkley, 1994). The other possibility is that whites, because of higher average incomes and therefore better sanitary conditions, had lower rates of infection. Unfortunately, there is no direct published evidence on this hypothesis. Racial decompositions of infection data were apparently intentionally concealed by the RSC in the hopes of not generating controversy in what was already a racially charged climate (Ettling, 1981). A third explanation is that whites, who were more likely than blacks to go to school and be literate, simply had less scope to increase much along these measures of human-capital investment.12
The long-term consequence of these racial differences is less clear because, as noted by Margo (1990), the return to schooling was lower for blacks than whites during this period. Therefore, I revisit this issue in Section 6 when measuring the effect of childhood exposure to hookworm on adult income.
4.4 Interpretation
The estimates presented above imply plausible numbers for the effect of hookworm infection on school attendance. We can compare the reduced-form effect of ( ) (about 0.09) to the estimated decline in infection as a function of the same variable (0.44).13 Dividing the first number by the second gives us the Indirect Least Squares (ILS) estimate of infection on schooling: 0.20. This indicates that a child infected with hookworm is 20% (i.e., percentage points) less likely to be attending school. Similarly, ILS estimates imply a 0.13 lower probability of being literate and 0.33 reduction in the probability of attending school full time.14
These estimates indicate that hookworm played a major role in the South’s lagging behind the rest of the country, as shown in Table VI. In computing the depressing effect of hookworm on the region’s human-capital accumulation, I multiply the ILS estimates from above with an estimate of the area’s hookworm burden. I assume a 40% regional hookworm-infection rate, as reported by the RSC. The resulting numbers account for around half of the human-capital gap.
Table VI.
Regional Comparisons
| (1) | (2) | (3) | |
|---|---|---|---|
| Dependent Variables: | School Enrollment | Literacy | Full-time School Attendance |
| Sample statistics:
|
|||
| Panel A: Means and Mean Differences, 1910 | |||
| Mean, RSC Area | 0.72 | 0.89 | 0.52 |
| Mean, Balance of Country | 0.86 | 0.99 | 0.81 |
| Gap | 0.14 | 0.10 | 0.30 |
| Panel B: Regression Estimates | |||
| ILS Estimates of Hookworm Infection | 0.20 | 0.13 | 0.33 |
| Panel C: Extrapolations | |||
| Effect of hookworm on RSC Area (−) | 0.08 | 0.05 | 0.13 |
| Fraction of regional gap explained | 57% | 52% | 44% |
Notes: The dependent variables, indicated in the column headings, are dummy variables. The sample consists of all native-born white and black children in the 1910 IPUMS between the ages of 8 and 16 (except for literacy, which is only available for ages 10 and up). The RSC area refers to those states visited by the Rockefeller Sanitary Commission. Florida is excluded from the analysis because the state ran its own hookworm campaign concurrently with, but without help from, the RSC. The ILS estimates are the Indirect Least Squares estimates described in the text. The regional impact of hookworm assumes a 40% regional infection rate, as reported by the RSC.
Finally, a simple calculation shows that being hookworm free in childhood would have translated into substantial gains in income as an adult. I perform this calculation by accumulating the flow of school attendance over the sample ages. This is done simply by multiplying the ILS estimate times the age range of the sample (9 years). The estimates from above imply an increase of 2.1 years of school attended and 3.2 years of school attended full time. For the 10% return to schooling estimated in 1940, the 2.1 extra years of schooling would translate into a 21% wage gain. This number would presumably be a lower bound because the more intensive school attendance should increase the return to the inframarginal schooling as well. These extrapolations are confirmed with direct evidence in Section 6 below.
5 Contemporaneous Effects on Adults
Next I examine how adult outcomes in the same time periods respond to the anti-hookworm campaign. This analysis serves as a specification check because adults were much less likely to be directly affected by this particular improvement in public health. As an empirical matter, adults had much lower infection rates.15 Whether this is because adults are more able to resist the parasites or simply because they are more likely to wear shoes is unclear. Nevertheless, since infection rates are lower for adults, we would expect lower responses on their part to the treatment campaign. On the other hand, if the results in Section 4 above are due to changes in income or migration patterns, we would see changes in adult outcomes as well. Finding large effects (especially if they are larger than the effects on children) would be cause for concern.
There was little impact on adults, as measured along several important dimensions: literacy, labor-force participation, an occupation-based measure of income, occupational mix (white collar or not), urban residence, and in-migration. These results are displayed in Table VII, which contains estimates of equation 1 for the whole sample of adults and for certain demographic subgroups. Adult literacy was not significantly affected by the treatment campaign, as seen in Panel A. This result is reassuring given that they were well past schooling years by the time of the hookworm-eradication campaign. Labor-force participation (LFP) was similarly unaffected by the RSC intervention. These estimates are found in Panel B of Table VII. I cannot reject the null hypothesis that there was no differential change across counties with different hookworm-infection rates. In Panel C, I consider the effect of hookworm on the occupational income score, an IPUMS variable that proxies income by occupation using data from later Censuses. Again, there is no statistically significant evidence of a shift in this measure following the hookworm-eradication campaign. I also show that there is no evidence that adults were more likely to take white-collar jobs (Panel D) or live in urban areas (Panel E).
Table VII.
Contemporaneous Effect on Adult Outcomes
| (1) | (2) | (3) | (4) | (5) | (6) | (7) |
|---|---|---|---|---|---|---|
| Samples: | ||||||
| Whole | Male | Female | White | Black | Age < 35 | Age 35–55 |
| Parameter estimates: | ||||||
| Panel A: Literacy | ||||||
| 0.0062 (0.0095) | −0.0107 (0.0108) | 0.0203 (0.0127) | 0.0107 (0.0112) | −0.0014 (0.0229) | 0.0101 (0.0137) | 0.0055 (0.0130) |
| Panel B: Labor-Force Participation | ||||||
| −0.0069 (0.0134) | −0.0069 (0.0065) | −0.0056 (0.0284) | −0.0212 (0.0124) | 0.0036 (0.0249) | 0.0069 (0.0184) | −0.0203 (0.0142) |
| Panel C: Occupational Income Score | ||||||
| 0.0526 (0.2836) | −0.0186 (0.4912) | 0.0581 (0.4163) | 0.0855 (0.3903) | 0.0224 (0.3861) | 0.5341 (0.4043) | −0.3132 (0.3456) |
| Panel D: White-Collar Occupation | ||||||
| 0.0032 (0.0081) | 0.0049 (0.0151) | −0.0010 (0.0077) | 0.0017 (0.0123) | −0.0017 (0.0068) | 0.0014 (0.0080) | 0.0054 (0.0163) |
| Panel E: Lives in Urban Area | ||||||
| 0.0157 (0.0172) | 0.0030 (0.0190) | 0.0280 (0.0177) | 0.0199 (0.0226) | 0.0132 (0.0245) | 0.0165 (0.0185) | 0.0085 (0.0248) |
| Panel F: Born out of State | ||||||
| 0.0142 (0.0172) | 0.0266 (0.0209) | 0.0018 (0.0189) | 0.0119 (0.0223) | 0.0042 (0.0272) | 0.0075 (0.0183) | 0.0327 (0.0240) |
Notes: Each cell reports the coefficient estimate on Hookworm × Post for the indicated sample and dependent variable. Dependent variables are as listed for each Panel. Robust standard errors in parentheses (clustering on SEA times post, number of clusters = 230). None of the reported coefficients is statistically significant at conventional confidence intervals. The sample consists of all native-born white and black adults in the 1910–20 IPUMS between the ages of 25 and 55 (inclusive) in the RSC-surveyed geographic units. Reporting of additional coefficient estimates is suppressed. Specifications also include dummy variables for SEA, age, black, female, and year, as well as interactions of the demographic variables with Postt.
Furthermore, I find no direct evidence of differential migration by hookworm infection. Hook-worm × Postt does not predict whether adults residing in the county were born out of state, the best micro-level indicator of migration available from these Censuses (results shown Panel F of Table VII). Nor is there evidence of changes in the adult population following eradication, as seen in Table VIII. This is shown either in the aggregate, or by demographic or nativity categories.
Table VIII.
Hookworm and the 1910–20 Change in Population
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
| Subgroup: | Total
|
Whites
|
Blacks
|
Natives
|
Native Whites
|
Foreign-Born Whites
|
| Additional Controls:
|
||||||
| Panel A: Population Data for 10 Years and Over | ||||||
| None | 0.0239 (0.0636) | 0.0018 (0.0436) | 0.0219 (0.0266) | 0.0258 (0.0609) | 0.0039 (0.0408) | −0.0020 (0.0043) |
| Fraction Black, 1910 | 0.0284 (0.0668) | 0.0096 (0.0447) | 0.0188 (0.0293) | 0.0306 (0.0642) | 0.0118 (0.0420) | −0.0022 (0.0043) |
| Population Density, 1910 | 0.0556 (0.0607) | 0.0244 (0.0415) | 0.0311 (0.0266) | 0.0585 (0.0580) | 0.0275 (0.0385) | −0.0031 (0.0042) |
| State Dummies | 0.0660 (0.0780) | 0.0264 (0.0536) | 0.0394 (0.0350) | 0.0672 (0.0754) | 0.0278 (0.0508) | −0.0014 (0.0044) |
| All of Above Controls Simultaneously | 0.1126 (0.0759) | 0.0562 (0.0511) | 0.0560 (0.0338) | 0.1142 (0.0732) | 0.0582 (0.0481) | −0.0020 (0.0043) |
| Panel B: Population Data for Males, 21 Years and Over | ||||||
| None | 0.0248 (0.0636) | 0.0102 (0.0433) | 0.0146 (0.0268) | 0.0322 (0.0993) | 0.0088 (0.0402) | 0.0014 (0.0049) |
| Fraction Black, 1910 | 0.0315 (0.0663) | 0.0197 (0.0443) | 0.0120 (0.0290) | 0.0489 (0.1029) | 0.0185 (0.0412) | 0.0011 (0.0049) |
| Population Density, 1910 | 0.0684 (0.0590) | 0.0415 (0.0400) | 0.0269 (0.0263) | 0.1087 (0.0907) | 0.0409 (0.0366) | 0.0006 (0.0048) |
| State Dummies | 0.0625 (0.0784) | 0.0284 (0.0544) | 0.0340 (0.0339) | 0.0879 (0.1229) | 0.0269 (0.0504) | 0.0015 (0.0060) |
| All of Above Controls Simultaneously | 0.1170 (0.0756) | 0.0642 (0.0515) | 0.0526 (0.0328) | 0.1788 (0.1171) | 0.0630 (0.0472) | 0.0012 (0.0058) |
Notes: Each cell reports the coefficient estimate on pre-eradication hookworm from a regression with the population change for the indicated demographic group on the left-hand side. The 1910–20 population change for each subgroup is normalized by the total SEA population in 1910. Robust standard errors in parentheses. None of the reported coefficients is statistically significant at conventional confidence intervals. Reporting of additional coefficient estimates is suppressed.
6 Long-Term Follow-Up of Cohorts Exposed as Children
In this section, I follow up on the subsequent outcomes of the cohorts that, as children, were exposed to the Rockefeller hookworm-eradication campaign. This analysis therefore represents a very different approach to the question: instead of looking at the behavior of fixed age groups at different points in time, I analyze various year- and state-of-birth cohorts in a single cross section. The comparisons are both across areas, based on different preexisting infection rates, and across cohorts, with older cohorts serving as a comparison group because they were not exposed to the RSC during childhood.
The geographic units employed in this analysis are place of birth rather than current residence. Matching individuals with hookworm-infection rates of the area where they end up as adults would then be difficult to interpret because of migration. Instead, I use the information on hookworm prevalence in an individual’s state of birth to conduct the analysis (county of birth is not available in the Census). The central problem with using states instead of counties is that there are fewer of them. As seen above, in Table III, this reduces the precision and as a result the effects estimated above are less likely to be significant using state-level variation.
The effects of the reduction in hookworm infection among children appeared to extend into adulthood for the affected cohorts. This section contains several empirical results supporting this conclusion:
Estimates of the cohort-specific effects of anti-hookworm treatment show marked contrasts in outcomes depending on whether the cohort was exposed to the treatment during childhood. Contrasts are especially evident for literacy and labor earnings. On the other hand, results for years of schooling are less precisely determined.
The results are robust to controlling for possible “mean reversion” across states, as well as to the inclusion of a variety of health and educational controls.
I estimate that the return to schooling increased for those cohorts poised to benefit from the hookworm-eradication campaign, and this appeared to play a central role in the increase in labor earnings.
When considered over a very long horizon (the 1825–1965 birth cohorts), the shift in the hookworm-income relationship coincides with childhood exposure to the eradication campaign, rather than some pre-existing trend or autoregressive process. (For this analysis, I focus on the occupational proxies of income that are defined over a broad range of Census years.)
Combining these results with the estimated reduction in hookworm infection across states, I compute the benefit of a hookworm-free childhood to be approximately 45% of adult wages.
6.1 Results for Earnings, Schooling and Literacy
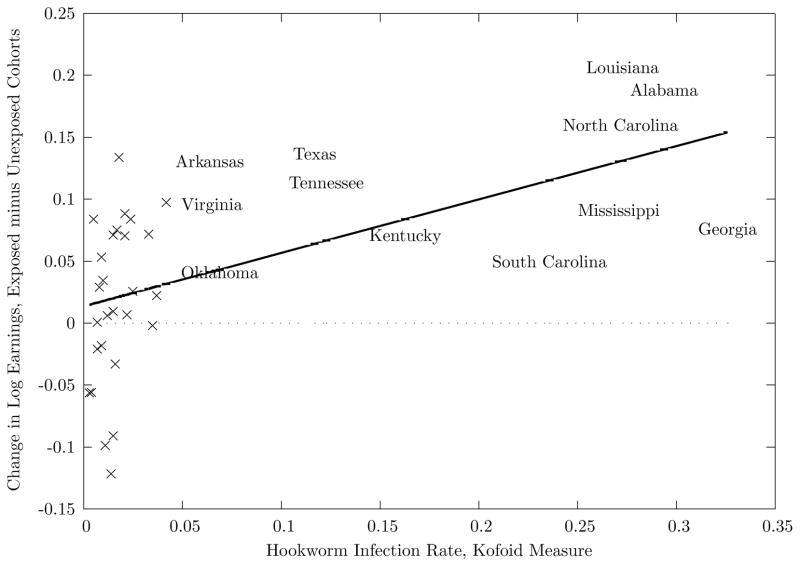
I start with graphical comparisons of the outcomes of different cohorts. First, I compare the 1939 wages among cohorts with different degrees of exposure to the hookworm-eradication campaign. Cohorts older than age twenty in 1910 were too old to have benefited directly from the RSC’s activities, and therefore I define them as unexposed. In contrast, I define fully exposed cohorts to be those born after 1910. Figure IV displays the difference in the log earnings between these two cohorts for each state of birth. I graph this wage difference against the state’s hookworm infection rate. As is evident from the graph, states with higher hookworm burdens saw larger increases in wages saw on average larger increases in wages.
Figure IV.
Comparison of Fully Exposed versus Unexposed Cohorts, by State of Birth
Notes: The x axis is the state’s hookworm-infection rate, as measured by Kofoid and Tucker (1921). The y axis is the state-level change in the natural log of 1939 wage and salary earnings across cohorts fully exposed and unexposed to the RSC. Unexposed cohorts are those older than age 20 in 1913, while fully exposed cohorts are those born after 1913. The earnings data are averages by state of birth and by cohort and were constructed using a base sample consisting of native-born blacks and whites in the age range [25,60] and in the 1940 IPUMS database. States with cell sizes of less than 20 are excluded from the graph. Each state’s change is marked with a × symbol, except for the states specifically labeled. The mean difference among low-hookworm states (infection< .01) is subtracted from the wage data before plotting. The solid line plots the fitted values from a bivariate regression, which has an R̄2 of 0.297.
Next, I focus on a simple parameterization of the cross-cohort comparison: the number of childhood years potentially exposed to the anti-hookworm campaign, times the hookworm intensity in the state of birth. Exposure to the RSC, Expik, will be zero for older cohorts, rise linearly for those born in the nineteen years prior to 1910, and stop at 19 for younger cohorts.16 Nineteen is chosen because most individuals in this period would have completed their schooling investments by that age, and Smilie and Augustine (1926) found that hookworm infection was negligible at older ages. This regression equation is therefore
| (3) |
for which it should be noted that the main effects of Hj (hookworm in state of birth j) and Expik (childhood temporal exposure of cohort k to the RSC) are absorbed by the cohort and state fixed effects. The additional demographic controls consist of indicator variables for age × black × female cell, as well as interactions of state-of-birth dummies with age, black, and female.
Children with more exposure to the campaign, by being born either later and in a state with greater treatment intensity, are more likely to be literate and earn higher incomes as adults. Results are mixed for years of schooling, but this is well within the range of normal statistical variation. Table IX contains these results. Panel A presents the estimates from the basic specification of equation 3.
Table IX.
Long-Term Followup Based on Intensity of Exposure to the Treatment Campaign
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
| Dependent Variables: | Log Earnings, 1939
|
Years of Schooling, 1940
|
Literacy Status, 1920
|
|||
| Independent Variables:
|
||||||
| Panel A: Baseline Results | ||||||
| Hookworm Infection Rate × Years of Exposure | 0.0286 *** (0.0066) | 0.0234 ** (0.0093) | −0.0243 (0.0328) | 0.0037 (0.0357) | 0.0158 *** (0.0019) | 0.0115 *** (0.0020) |
| State Average Wage (1899) × Age | 0.0011 (0.0013) | −0.0058 * (0.0032) | 0.0009 *** (0.0002) | |||
| Panel B: Add Controls | ||||||
| Hookworm Infection Rate × Years of Exposure | 0.0214 *** (0.0064) | 0.0187 *** (0.0056) | 0.0313 (0.0290) | 0.0208 (0.0269) | 0.0159 *** (0.0029) | 0.0159 *** (0.0029) |
| Fraction State Population in Urban Areas, 1900, × Age | 0.0083 ** (0.0034) | 0.0089 *** (0.0030) | 0.0180 (0.0213) | 0.0206 (0.0197) | 0.0011 * (0.0006) | 0.0011 * (0.0006) |
| State Literacy Rate, 1910, × Age | −0.0059 (0.0090) | −0.0033 (0.0082) | 0.0433 (0.0677) | 0.0541 (0.0631) | 0.0016 (0.0013) | 0.0015 (0.0013) |
| Fraction State Population Black, 1910, × Age | 0.0001 (0.0003) | −0.0003 (0.0004) | 0.0002 (0.0022) | −0.0016 (0.0026) | 0.0000 (0.0001) | 0.0000 (0.0001) |
| State Doctors per capita, 1898, × Age | 0.0031 ** (0.0013) | 0.0028 ** (0.0012) | 0.0052 (0.0060) | 0.0042 (0.0058) | 0.0006 *** (0.0002) | 0.0006 *** (0.0002) |
| WWI Recruits Found “Defective” at Draft Physical (c. 1918) × Age | −0.0006 (0.0010) | −0.0003 (0.0010) | 0.0142 *** (0.0053) | 0.0155 *** (0.0056) | −0.0001 (0.0002) | −0.0001 (0.0002) |
| Log State Public Health Spending per capita, 1899, × Age | 0.0004 (0.0003) | 0.0006 ** (0.0003) | 0.0002 (0.0013) | 0.0008 (0.0013) | 0.0000 (0.0001) | 0.0000 (0.0001) |
| Change in Child Mortality Rate, (1899–1932) × Age | −0.0001 (0.0000) | −0.0001 (0.0000) | −0.0002 (0.0002) | −0.0002 (0.0002) | 0.0000 (0.0001) | 0.0000 (0.0001) |
| State Child Mortality Rate, (1890) × Age | 0.0000 (0.0001) | 0.0000 (0.0001) | 0.0002 (0.0002) | 0.0001 (0.0003) | 0.0000 (0.0001) | 0.0000 (0.0001) |
| State Fertility Rate, 1900, × Age | −0.0008 (0.0041) | 0.0002 (0.0039) | −0.0303 * (0.0183) | −0.0258 (0.0179) | −0.0016 *** (0.0006) | −0.0017 *** (0.0006) |
| Malaria Mortality per 10K Population (1890) × Age | −0.0477 *** (0.0162) | −0.0541 *** (0.0143) | 0.1746 * (0.0928) | 0.1471 (0.0918) | 0.0038 (0.0040) | 0.0039 (0.0040) |
| Log Change in Average Monthly Teacher Salaries (1907–25) × Age | −0.0013 (0.0018) | −0.0029 (0.0018) | 0.0117 (0.0105) | 0.0053 (0.0123) | −0.0004 (0.0004) | −0.0003 (0.0004) |
| Change in School Term (1907–25) × Age | −0.0095 *** (0.0036) | −0.0117 *** (0.0040) | 0.0173 (0.0226) | 0.0080 (0.0256) | −0.0017 ** (0.0007) | −0.0016 ** (0.0008) |
| Change in Expenditures per Pupil, (1907–1925) × Age | −0.0016 (0.0011) | −0.0022 ** (0.0011) | −0.0102 * (0.0054) | −0.0128 ** (0.0052) | −0.0003 *** (0.0001) | −0.0003 (0.0002) |
| Change in Pupil/Teacher Ratio (1907–1925) × Age | 0.0021 ** (0.0009) | 0.0023 ** (0.0009) | 0.0126 ** (0.0051) | 0.0137 *** (0.0050) | −0.0004 ** (0.0002) | −0.0004 ** (0.0002) |
| State Unemployment Rate (1930) × Age | −0.0004 ** (0.0002) | −0.0003 (0.0002) | −0.0044 ** (0.0021) | −0.0039 * (0.0020) | 0.0001 *** (0.0000) | 0.0001 *** (0.0000) |
| State Average Wage (1899) × Age | −0.0032 ** (0.0016) | −0.0136 (0.0097) | 0.0001 (0.0003) | |||
| Panel C: Predict Missing Data on LHS | ||||||
| Hookworm Infection Rate × Years of Exposure | 0.0033 (0.0029) | 0.0029 (0.0037) | n.a. | n.a. | ||
| State Average Wage (1899) × Age | 0.0001 (0.0004) | |||||
| Panel D: Changing Returns to Schooling | ||||||
| Hookworm Infection Rate × Years of Exposure | 0.0254 *** (0.0044) | 0.0219 *** (0.0063) | n.a. | n.a. | ||
| Infection × Years of Exposure × Years of Schooling | 0.0023 *** (0.0009) | 0.0022 ** (0.0009) | ||||
| State Average Wage (1899) × Age | 0.0008 (0.0010) | |||||
| Panel E: Males | ||||||
| Hookworm Infection Rate × Years of Exposure | 0.0265 *** (0.0056) | 0.0253 *** (0.0080) | −0.0690 ** (0.0326) | −0.0376 (0.0347) | 0.0108 *** (0.0018) | 0.0083 *** (0.0019) |
| State Average Wage (1899) × Age | 0.0003 (0.0013) | −0.0066 ** (0.0032) | 0.0005 *** (0.0001) | |||
| Panel F: Females | ||||||
| Hookworm Infection Rate × Years of Exposure | 0.0322 *** (0.0115) | 0.0157 (0.0165) | 0.0200 (0.0338) | 0.0444 (0.0385) | 0.0209 *** (0.0027) | 0.0148 *** (0.0030) |
| State Average Wage (1899) × Age | 0.0037 * (0.0019) | −0.0050 (0.0037) | 0.0012 *** (0.0003) | |||
| Panel G: Whites | ||||||
| Hookworm Infection Rate × Years of Exposure | 0.0293 *** (0.0071) | 0.0232 ** (0.0103) | −0.0110 (0.0345) | 0.0164 (0.0378) | 0.0131 *** (0.0022) | 0.0086 *** (0.0020) |
| State Average Wage (1899) × Age | 0.0012 (0.0013) | −0.0054 (0.0033) | 0.0008 *** (0.0002) | |||
| Panel H: Blacks | ||||||
| Hookworm Infection Rate × Years of Exposure | 0.0220 *** (0.0072) | 0.0253 ** (0.0103) | 0.1013 *** (0.0387) | 0.0133 (0.0461) | 0.0314 *** (0.0065) | 0.0262 *** (0.0063) |
| State Average Wage (1899) × Age | −0.0013 (0.0025) | −0.0415 *** (0.0104) | 0.0019 * (0.0011) | |||
Notes: Each panel/column reports reports a separate regression for the indicated samples and dependent variables. State-average data are matched to individuals based on their state of birth. The measure of hookworm is from Kofoid and Tucker (1921). Unskilled-wage data from 1899, reported by Lebergott (1964), are used to control for mean reversion. The full sample consists of native-born blacks and whites in the age range [25,60] and in the 1940 IPUMS database (except the literacy regressions, which include ages [16,60] from the 1920 IPUMS data). Robust standard errors in parentheses (clustering on state of birth). Single asterisk denotes statistical significance at the 90% level of confidence; double, 95%, triple 99%. Reporting of additional coefficient estimates is suppressed.
The estimates do not appear to be an an artifact of mean reversion. The Southern states had markedly lower income before the Rockefeller campaign, and the hookworm problem was undoubtedly made worse by the low productivity of the region. If the oldest cohorts had high hookworm infection and low productivity because of some mean-reverting shock, we might expect income gains for the subsequent cohorts even in the absence of a direct effect of hookworm on productivity. I use data on labor earnings by state in 1899 from Lebergott (1964). I interact the natural logarithm of this wage measure with age and include the interaction in the even-numbered columns of Table IX. This analysis yields mixed evidence of mean reversion in the data, but the inclusion of these controls does not affect the main result: labor income and literacy is still estimated to be substantially higher as a result of the anti-hookworm campaign.17 In the analysis that follows, I estimate the hookworm coefficient both with and without this correction for mean reversion.
I estimate effects of hookworm eradication that are similar to the baseline when I incorporating a series of health, demographic, and educational variables into the analysis. These results are seen in Panel B of Table IX. Health controls (all measured prior to 1910 except as noted) include doctors per capita, the natural logarithm of spending by state boards of health, the fraction of WWI recruits rejected for health reasons (c. 1918), the child mortality rate, and the 1890–1932 change in the child mortality rate. Demographic controls include 1910 state-level rates for fertility, literacy, racial composition, urbanization, and unemployment (from 1930). I also control for changes in educational policy with the c. 1905–1925 changes in school term, (log) expenditures per pupil, pupil/teacher ratio, and (log) teacher salaries.
I argue that the earnings results are not contaminated by hookworm-induced changes in the probability of self-employment. The major difficulty in using the earnings data from the 1940 Census is that it was incomplete: labor income from self-employment was excluded. This would complicate the interpretation of the coefficient on earnings if the hookworm also induced changes in choice to be self-employed. I show in Panel C that the hookworm × exposure variable does not predict missing data on earnings. In results not reported here, I also estimate regression equations identical to those used for Panel B of Table IX, but with two new dependent variables: binary indicators for (i) self employment and (ii) non-wage/salary income being greater that fifty dollars. In doing so, I find no statistically significant relationship between the hookworm measure and self employment.18 Finally, I find evidence of hookworm-related increase in the total time worked (either for wage/salary or not), although, once mean reversion controls are included, the increased labor supply does not account for a large fraction of the earnings effect.
I also consider the role played by the quantity of and returns to of schooling in the wage results. Recall that the results for years of schooling were insignificantly different from zero. Consistent with this, controlling directly for education does not significantly change the estimated effect of hookworm treatment. We can nevertheless easily reject, for conventional returns to schooling, the hypothesis that the wage effect is due entirely due to a rise in education.19 However, the fact that I estimate increases in literacy without concomitant rises in the quantity of schooling suggests an alternative hypothesis: changes in quality. In particular, it may be that students spend the same number of years in school, but the time is better spent. For example, there might be less absenteeism, or students might be better equipped to absorb the material while in school. As was shown above, students were less likely to work while in school and were more more likely to be literate, as a consequence of hookworm eradication. This suggests that the return to schooling might have been raised by the hookworm intervention.
There is indeed evidence of an increase in the return to schooling as a result of the intervention. This can be seen in Panel D of Table IX. The crucial interaction is the triple: between years of schooling and the treatment-intensity variable (Hj × Expik). (The additional second-order interactions are absorbed with a series of dummies for birth state × education and birth year × education. The first-order effects of education, state of birth, and year of birth are also absorbed with indicator variables.) The triple interaction is positive and statistically significant for labor earnings.
This hookworm-related change in the return to schooling can potentially explain a large fraction of the increase in earnings described above. This regression, by comparing individuals with different terminal levels of attainment, estimates the average marginal effect of schooling in the sample (and how it changes following hookworm eradication). If the intervention had similar effects on the return to inframarginal schooling, we can compute the overall contribution through this channel. Multiplying the triple interaction (0.0022) by the average years of schooling in the South (7.72) yields 0.0170, almost eighty percent of the coefficient on (Hj × Expik) in the first row of Panel D. (Because the education variable was de-meaned before interaction, the second-order term is evaluated at the mean of education.) Moreover, I cannot reject the hypothesis that all of the earnings effects worked through the rising return to schooling.
These disparate results for human capital are consistent with the evidence from the sequential cross sections above. In Table III, I show that the effect of hookworm eradication in the cross-state evidence played out primarily on the intensive rather than extensive margin of education. Consequently, we would expect relatively little change in years of schooling reported. While years of schooling is an important input measure, the intervention had the effect that children attended school more intensively. It not surprising, then, to find an effect on an output measure like literacy.
Several differences emerge among demographic groups. Results estimated from subsamples of males, females, whites, and blacks are contained in Table IX, Panels E–H, respectively. For no subgroup is there a robustly significant relationship between years of schooling and (Hj × Expik). Estimates for literacy, on the other hand, are positive and significantly different from zero for all demographic groups. Literacy responses are larger for females than for males, as well as for blacks than for whites, possibly because females and blacks had lower pre-existing literacy rates. The estimate of (Hj × Expik) in the earnings equation yields a positive and significant number for males, while the result for females is not sensitive to the inclusion of a mean-reversion control. Whites and blacks show similar earnings responses, on the other hand. This may be because blacks, while gaining more on measured human capital, faced lower returns to skill in the labor market.
As a further check, I assemble information on states’ laws covering compulsory schooling and child labor for various years. These data are based on the work of Acemoglu and Angrist (2000), and I copy their variables verbatim for the years 1914 and forward. Then, using similar methodology, I extend the coverage back to 1894, where possible. (Details on the extension to earlier periods are found in the Data Appendix.) These data consist of two sets of variables: CA and CL. The CA variables refer to laws on compulsory school attendance and the CL variables to laws on child labor restrictions. The base indices are constructed to be in units of implicitly required years of school attended. The dummies used in the regressions are coded as follows:
Compulsory-schooling data are then assigned according to the laws in force in the state of birth of the individual when he/she was 14 years old.20
Controlling for measures of compulsory-schooling laws does not significantly affect the estimates of the effect of hookworm eradication. These results are seen in Table X. In Panel A, there are controls for compulsory-attendance and child-labor laws. The CA dummies show generally positive effects of compulsory-attendance laws on the income and human-capital variables. The CL, however, are mixed in sign. The CL11 variable is excluded from the literacy regressions for lack of within-state variance in that sample. Because I judged the early CA data to be of higher quality, in Panel B I include only the CA dummies as controls for compulsory-schooling laws. In neither Panel do the estimates of the effect of hookworm change substantially from those found above in Table IX.
Table X.
Controls for Compulsory Schooling
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
| Dependent Variables: | Log Earnings, 1939
|
Years of Schooling, 1940
|
Literacy Status, 1920
|
|||
| Independent Variables:
|
||||||
| Panel A: Baseline Coding of Child-Labor Laws | ||||||
| Hookworm Infection Rate × Years of Exposure | 0.0267 *** (0.0061) | 0.0193 ** (0.0087) | −0.0206 (0.0304) | −0.0003 (0.0322) | 0.0115 *** (0.0040) | 0.0114 *** (0.0041) |
| CA9 | 0.0161 (0.0124) | 0.0130 (0.0133) | −0.0268 (0.0514) | −0.0216 (0.0519) | 0.0001 (0.0008) | 0.0001 (0.0008) |
| CA10 | 0.0187 (0.0181) | 0.0240 (0.0185) | 0.0847 (0.1332) | 0.0717 (0.1324) | 0.0004 (0.0011) | 0.0005 (0.0011) |
| CA11 | 0.0140 (0.0181) | 0.0124 (0.0196) | 0.1944 ** (0.0765) | 0.1950 ** (0.0767) | ||
| CL7 | 0.0052 (0.0106) | 0.0079 (0.0107) | 0.0916 (0.0503) | 0.0848 (0.0517) | −0.0015 (0.0010) | −0.0015 (0.0010) |
| CL8 | −0.0168 (0.0154) | −0.0092 (0.0154) | 0.1108 (0.0567) | 0.0901 (0.0598) | 0.0011 * (0.0007) | 0.0012 * (0.0007) |
| CL9 | −0.0083 (0.0175) | −0.0060 (0.0174) | 0.0383 (0.0465) | 0.0349 (0.0467) | −0.0023 * (0.0014) | −0.0023 (0.0014) |
| CL missing | −0.0512 ** (0.0230) | −0.0533 ** (0.0235) | −0.1635 ** (0.0651) | −0.1538 ** (0.0684) | 0.0050 (0.0032) | 0.0050 (0.0033) |
| State Average Wage (1899) × Age | 0.0017 (0.0011) | −0.0045 (0.0032) | 0.0000 (0.0002) | |||
| Panel B: Controls for Compulsory Attendance Only | ||||||
| Hookworm Infection Rate × Years of Exposure | 0.0303 *** (0.0063) | 0.0219 ** (0.0091) | −0.0243 (0.0339) | 0.0055 (0.0365) | 0.0129 *** (0.0040) | 0.0126 *** (0.0042) |
| CA9 | 0.0172 (0.0127) | 0.0153 (0.0137) | 0.0105 (0.0468) | 0.0129 (0.0446) | −0.0006 (0.0007) | −0.0005 (0.0006) |
| CA10 | 0.0180 (0.0178) | 0.0247 (0.0184) | 0.1087 (0.1293) | 0.0869 (0.1279) | 0.0002 (0.0010) | 0.0004 (0.0010) |
| CA11 | 0.0060 (0.0095) | 0.0038 (0.0119) | 0.1710 *** (0.0456) | 0.1758 *** (0.0477) | ||
| State Average Wage (1899) × Age | 0.0018 (0.0013) | −0.0062 (0.0032) | 0.0000 (0.0002) | |||
| Panel C: Alternative Coding of Child-Labor Laws. | ||||||
| Hookworm Infection Rate × Years of Exposure | 0.0272 *** (0.0058) | 0.0193 ** (0.0080) | −0.0208 (0.0302) | 0.0012 (0.0313) | 0.0130 *** (0.0041) | 0.0127 *** (0.0043) |
| CA9 | 0.0095 (0.0118) | 0.0061 (0.0123) | −0.0431 (0.0489) | −0.0368 (0.0492) | −0.0006 (0.0007) | −0.0006 (0.0007) |
| CA10 | 0.0184 (0.0168) | 0.0239 (0.0173) | 0.0859 (0.1353) | 0.0721 (0.1346) | 0.0002 (0.0010) | 0.0004 (0.0009) |
| CA11 | 0.0277 (0.0209) | 0.0307 (0.0236) | 0.0209 (0.0489) | 0.0118 (0.0458) | ||
| CL7 | 0.0202 (0.0105) | 0.0234 ** (0.0113) | 0.1156 *** (0.0441) | 0.1066 ** (0.0435) | 0.0002 (0.0014) | 0.0002 (0.0014) |
| CL8 | −0.0054 (0.0181) | 0.0028 (0.0188) | 0.1400 ** (0.0602) | 0.1164 (0.0611) | −0.0002 (0.0010) | 0.0001 (0.0014) |
| CL9 | −0.0177 (0.0237) | −0.0205 (0.0270) | 0.2817 *** (0.0638) | 0.2888 *** (0.0603) | ||
| State Average Wage (1899) × Age | 0.0018 (0.0011) | −0.0049 (0.0031) | 0.0000 (0.0002) | |||
Notes: Each panel/column reports reports a separate regression for the indicated dependent variables. The measure of hookworm is from Kofoid and Tucker (1921), and the wage data are from Lebergott (1964). State-average data are matched to individuals based on their state of birth. Compulsory-schooling data were assigned according to the laws in force when he/she was 14 years old, except as indicated. The CA and CL variables are year- and state-specific dummies based on state laws for compulsory attendance and child labor, respectively. The full sample consists consists of native-born blacks and whites in the age range [25,60] and in the 1940 IPUMS database (except the literacy regressions, which include ages [16,60] from the 1920 IPUMS data). Robust standard errors in parentheses (clustering on state of birth). Single asterisk denotes statistical significance at the 90% level of confidence; double, 95%; triple, 99%. Reporting of additional coefficient estimates is suppressed. Specifications also include dummy variables for age, black, female, and state of birth, as well as interactions of the black and female with age and state-of-birth dummies.
Similar results are obtained after recoding the early child-labor laws to include only those laws with broad sectoral coverage. These new estimates are shown in Panel C of Table X. Before 1914, many of the Southern states had in force laws restricting youth employment in mines and manufacturing. But these industries represented, at the time, small fractions of state employment. There is therefore the nontrivial concern that such laws provided little to no constraint on the behavior of children desiring to work in the agriculture. Consequently, I also created an alternate coding of the CL variable that indicated the presence of child-labor restrictions across all sectors of the economy.
6.2 Cohort-Specific Relationship Between Income and Pre-Eradication Hookworm
In this subsection, I show that the shift in the hookworm-income relationship coincides with childhood exposure to the eradication efforts. This can be seen graphically, and I also provide statistical tests that indicate that the shift is indeed coincident with exposure to eradication rather than with some pre-existing trend or autoregressive process.
I use two proxies for labor productivity that are available for a large number of Censuses. The occupational income score and Duncan socioeconomic index are both average indicators by disaggregated occupational categories that were calibrated using data from the 1950 Census. The former variable is the average by occupation of all reported labor earnings. The measure due to Duncan (1961) is instead a weighted average of earnings and education among males within each occupation. Both variables can therefore measure shifts in income that take place between occupations. The Duncan measure has the added benefit of picking up between-occupation shifts in skill requirements for jobs. Occupation has been measured by the Census for more than a century, and so these income proxies are available for a substantial stretch of cohorts.
I combine microdata from ten Censuses to construct a panel of average income by cohort. The base sample consists of native-born males in the IPUMS and North Atlantic Population Project (NAPP, 2004) datasets between the ages of 25 and 55, inclusive, for the census years 1880–1990, which results in year-of-birth cohorts from 1825 to 1965. The individual income proxies are projected on to dummies for year-of-birth × Census year (cohorts can appear in multiple Censuses in this design). I then take the average residual from this procedure for each cell defined by year of birth and state of birth.
For each year of birth, OLS regression coefficients are estimated on the resulting cross section of states of birth. Consider a simple regression model of an average outcome, Yjk, for a cohort with state of birth j and year of birth k:
| (4) |
in which βk is year-of-birth-specific coefficient on hookworm, Xj is a vector of other state-of-birth controls, and δk and Γk are cohort-specific intercept and slope coefficients. I estimate this equation using OLS for each year of birth k. This specification allows us to examine how the relationship between income and pre-eradication hookworm (β̂ k) differs across cohorts.
I start with a simple graphical analysis using this flexible specification for cross-cohort comparison. Figure V displays a plot of the estimated βk. The x axis is cohort’s year of birth. The y axis for each graphic plots the estimated cohort-specific coefficients on the state-level hookworm measure. Each cohort’s point estimate is marked with a dot. The top row of graphs contain estimates from the basic specification, in which this state-of-birth average residual is regressed on to hookworm infection, Lebergott’s measure of 1899 wage levels, and a dummy for the Southern region. The bottom row displays estimates from the “full controls” specification, which, in addition to the basic variables, contains the various control variables from Table IX, Panel B.21
Figure V.
Cohort-Specific Relationship Between Income and Pre-Eradication Hookworm
Notes: These graphics summarize regressions of income proxies on pre-eradication hookworm-infection rates (measured by Kofoid and Tucker, 1921). The y axis for each graphic plots the estimated cohort-specific coefficients on the state-level hookworm measure. The x axis is the cohort’s year of birth. Each cohort’s point estimate is marked with a dot. The dashed lines measure the number of years of potential childhood exposure to the Rockefeller Sanitary Commision’s activities. For the underlying regressions, the dependent variables are constructed from the indicated income proxies (the Duncan Socioeconomic Indicator and the Occupational Income Score). The base sample consists of native-born males in the IPUMS and NAPP datasets between the ages of 25 and 55, inclusive, for the census years 1880–1990, which results in year-of-birth cohorts from 1825 to 1965. The individual income proxies are projected on to dummies for year-of-birth × Census year observed (cohorts can appear up to four times in this design), and the residuals are averaged by year of birth and state of birth. For each year-of-birth cohort, OLS regressions coefficients are estimated on the resulting cross section of states of birth. In the basic specification, this state-of-birth average residual is regressed on to hookworm infection, Lebergott’s measure of 1899 wage levels, and a dummy for the Southern region. The“full controls” specification contains, in addition, the various control variables from Table IX, Panel B.
Because hookworm was principally a childhood disease, cohorts that were already adults in 1910 were too old to have benefited from the reduction in hookworm. On the other hand, later cohorts experienced reduced hookworm infection during their childhood. This benefit increased with younger cohorts who were exposed to the RSC’s efforts for a greater fraction of their childhood. The dashed lines therefore measure the number of years of potential childhood exposure (defined above) to the Rockefeller Sanitary Commission’s activities. (The line is rescaled such that pre-1880 and post-1930 levels match those of the β̂k. The exposure line is not rescaled in the x dimension.) Cohorts born late enough to have been exposed to the campaign during childhood generally have higher income than earlier cohorts, and this shift correlates with higher potential exposure to the RSC.
Formal statistical tests confirm that the shift in the income/pre-period hookworm relationship coincided with exposure to hookworm eradication, rather than with some trend or autoregressive process. This can be seen by treating the estimated βk as a time series and estimating the following regression equation:
| (5) |
in which Expk is exposure to hookworm eradication (defined above), the kn terms are nth-order trends, and Φ (L) is a distributed lag operator. To account for the changing precision with which the generated observations are estimated, observations are weighted by the inverse of the standard error for β̂k. Table XI reports estimates of equation 5 under a variety of order assumptions about trends and autoregression. The dependent variables are the cohort-specific regression estimates of income proxies on hookworm that are shown in Figure V for the specifications with broad sets of controls. Panel A contains estimates using the occupational income score as a proxy for income. The estimates on the exposure term are broadly similar across specifications, and there is no statistically significant evidence of trends or autoregression in these βk. When the Duncan SEI is used instead (Panel B), there is evidence of a downward trend, but estimates of the exposure coefficient are stable once this is accounted for.
Table XI.
Exposure to RSC versus Alternative Time-Series Relationships
| (1) | (2) | (3) | (4) | (5) | |
|---|---|---|---|---|---|
| Independent Variables:
|
|||||
| Panel A: Occupational Income Score | |||||
| Fraction of Childhood Exposed to Eradication | 0.3507 *** (0.0289) | 0.3525 *** (0.0888) | 0.3846 *** (0.0536) | 0.3814 *** (0.0997) | 0.3441 *** (0.0986) |
| Year of Birth | 0.0000 (0.0160) | 0.0010 (0.0160) | 0.6770 (0.6400) | ||
| Year of Birth Squared / 1,000 | −0.1790 (0.1660) | ||||
| Lagged Dependent Variable | −0.0970 (0.1200) | −0.0970 (0.1200) | −0.0880 (0.1210) | ||
| Twice Lagged Dependent Variable | 0.1170 (0.0750) | ||||
| Panel B: Duncan’s Socioeconomic Indicator | |||||
| Fraction of Childhood Exposed to Eradication | 0.6112 *** (0.0520) | 0.8966 *** (0.1620) | 0.6415 *** (0.0811) | 0.9698 *** (0.1918) | 1.0510 *** (0.2002) |
| Year of Birth | −0.0670 ** (0.0300) | −0.0730 ** (0.0320) | 4.6840 *** (1.1160) | ||
| Year of Birth Squared / 1,000 | −1.2600 *** (0.2940) | ||||
| Lagged Dependent Variable | −0.0500 (0.0940) | −0.0820 (0.0940) | −0.1500 (0.0920) | ||
| Twice Lagged Dependent Variable | 0.0650 (0.0850) | ||||
Notes: This table reports estimates of equation 5. The dependent variables are the cohort-specific regression estimates of income proxies on hookworm that are shown in Figure V. Robust standard errors are given in parentheses. Single asterisk denotes statistical significance at the 90% level of confidence; double 95%; triple, 99%. Reporting of the constant term is suppressed. Observations are weighted by the inverse of the standard error for β̂ k. For the underlying cohort-specific regressions, the dependent variables are constructed from the indicated income proxies (the Duncan Socioeconomic Indicator and the Occupational Income Score). The base sample consists of native-born males in the IPUMS and NAPP datasets between the ages of 25 and 55, inclusive, for the census years 1880–1990, which results in year-of-birth cohorts from 1825 to 1965. The individual income proxies are projected on to dummies for year-of-birth × Census year observed (cohorts can appear up to four times in this design), and the residuals are averaged by year of birth and state of birth. For each year-of-birth cohort, OLS regressions coefficients are estimated on the resulting cross section of states of birth. The baseline specification corresponds to the “full controls” version in Figure V, in which the state-of-birth average residual is regressed on to hookworm infection, Lebergott’s measure of 1899 wage levels, a dummy for the Southern region, and the various control variables from Table IX, Panel B.
Table XII reports estimates of equation 5 for alternative specifications and constructions of the underlying sample. Panel A repeats the result from above. For Panel B, I restrict the base sample of Census data to a narrower age range, when individuals are more likely to be working and in a job that reflects their permanent income. Coefficients rise for both income proxies. Major revisions to the coding of occupations occurred with the 1980 and 2000 Censuses, but results are not sensitive to including data from after these breakpoints, as seen in Panels C and D. Panels E and F zoom in to narrower ranges of year of birth. Restricting the analysis to one hundred and then forty years of birth cohorts yields similar estimates on exposure, albeit with larger standard errors. Casual inspection of Figure V suggests why: it becomes more difficult to distinguish between exposure and trend when viewing a narrower set of birth years. Indeed, estimates using the occupational income score are not significantly different from zero for the narrowest range.22
Table XII.
Sensitivity Analysis of Retrospective-Cohort Results
| (1) | (2) |
|---|---|
| Occupational Income Score
|
Duncan Socio- Economic Indicator
|
| Panel A: Baseline Specification | |
| 0.3441 *** (0.0986) | 1.0510 *** (0.2002) |
| Panel B: Restrict Ages to [35,50] in Base Sample | |
| 0.4915 *** (0.0956) | 1.0851 *** (0.2018) |
| Panel C: Exclude 1980 and 1990 Censuses | |
| 0.4852 *** (0.1049) | 1.3135 *** (0.2581) |
| Panel D: Include 2000 Census | |
| 0.5530 *** (0.0992) | 1.2291 *** (0.2046) |
| Panel E: Restrict Year of Birth to [1850,1950] | |
| 0.4262 *** (0.1016) | 1.1729 *** (0.2485) |
| Panel F: Restrict Year of Birth to [1880 [1920] | |
| 0.6967 (0.4433) | 1.4494 * (0.7868) |
Notes: This table reports estimates of equation 5 for alternative specifications. The dependent variables are the cohort-specific regression estimates of income proxies on hookworm that are shown in the “full controls” panels of Figure V. Robust standard errors are given in parentheses. Single asterisk denotes statistical significance at the 90% level of confidence; double 95%; triple, 99%. Reporting of the additional coefficient estimates is suppressed. Observations are weighted by the inverse of the standard error for β̂k. For the underlying cohort-specific regressions, the dependent variables are constructed from the indicated income proxies (the Duncan Socioeconomic Indicator and the Occupational Income Score). Except as indicated in the Panel headings, the base sample consists of native-born males in the IPUMS and NAPP datasets between the ages of 25 and 55, inclusive, for the census years 1880–1990, which results in year-of-birth cohorts from 1825 to 1965. The individual income proxies are projected on to dummies for year-of-birth × Census year observed (cohorts can appear up to four times in this design), and the residuals are averaged by year of birth and state of birth. For each year-of-birth cohort, OLS regressions coefficients are estimated on the resulting cross section of states of birth. The baseline specification corresponds to the “full controls” version in Figure V, in which the state-of-birth average residual is regressed on to hookworm infection, Lebergott’s measure of 1899 wage levels, a dummy for the Southern region, and the various control variables from Table IX, Panel B.
6.3 Interpretation
In this section, I characterize the magnitude of the effect of the hookworm reduction in more easily interpretable units, and contrast the estimates with cross-areas differences in income per capita. For ease of the analysis that follows, I focus on the contrast between the cohort with zero childhood exposure to the RSC and the cohort with full exposure. For example, comparing these cohorts in two areas that were one standard deviation (within the RSC-targeted area) apart in hookworm-infection rates, we would expect wages to have increased 11% more in the area with the higher pre-period infection rate.
Using Indirect Least Squares (ILS), I estimate the approximate effect of childhood hookworm infection on adult wages to be around forty-three percent. Again, I compare the fully exposed and non-exposed cohorts to construct the estimate. The increase in wages as a function of the Kofoid measure of is 0.32, when comparing zero to full RSC exposure. Since hookworm was largely eradicated in the time span considered, I regress the pre-RSC hookworm (reported by Jacocks at the state level for certain states) on the Kofoid measure and estimate that the decrease in infection rates as a function of to be 0.748.23 This yields an ILS estimate of −0.43 in natural-log terms. That is, I estimate that hookworm infection during childhood caused a drop of approximately 0.43 in log adult wages.
The ILS estimates using the occupational proxies for income bracket the wage result. The estimated shift in income related to RSC exposure was estimated in Table XI. I compare these estimated changes with their respective averages for men born in the South between 1875 and 1895, and then construct the ILS coefficient as above. For the occupational income score, I estimate that the proportional change in income related to childhood hookworm infection is −0.32. The same estimate for the Duncan SEI is −0.5.
These results point to changes in the returns to schooling as well. I compute the drop in returns to years of schooling due to hookworm to be approximately 0.047 = 0.0022 × 16/0.748, the ILS estimate for the changing returns to a year of education. This represents a substantial drop due to hookworm—around fifty percent of the estimated return to schooling in this period.
The estimated impact is large enough that it bears consideration in a macroeconomic context, although is clearly not so large that it unreasonably explains “everything.” The log-income gap between the North and the South at 1900 was approximately 0.75. For a 40% infection rate in the South and an effect of hookworm on wages of 0.43, we would expect a reduction in Southern incomes of approximately 17 log percentage points. In other words, some 22% of this income gap could be attributed to hookworm infection in the South. On the other hand, if we turn to contemporaneous evidence from developing countries, Miguel and Kremer estimate that the prevalence of intestinal-parasitic infection in the Busia region of Kenya is around 90% among school-aged children. Applying our estimates to this area of Kenya, we would expect a log-income gain of approximately 0.38 from a complete eradication of intestinal worms from the country. This would be enough to raise income per capita to match the level of Zimbabwe, but obviously well short of the 200–300 log percentage points needed to reach OECD levels.24
7 Conclusion
This study evaluates the economic consequences of the successful eradication of hookworm in the American South. The advantages of evaluating this intervention are that (i) its timing was relatively short and well defined, (ii) geographical differences in infection permit a treatment/control design, and (iii) sufficient time has passed that we can evaluate its long-term consequences.
I find that areas with higher levels of hookworm infection prior to the RSC experienced greater increases in school attendance and literacy after the intervention. This result is robust to controlling for a variety of alternative hypotheses, including differential trends across areas, changing crop prices, and shifts in certain education policies. No significant results are found for the sample of adults, who should have benefited less from the intervention owing to their substantially lower (prior) infection rates. Moreover, a long-term follow-up of affected cohorts indicates a substantial income gain as a result of the reduction in hookworm infection. This follow-up also shows a marked increase in the quality rather than the quantity of education.
This study contributes to two important questions in the literature. One is historical: did the reduction in the relative disease burden play a role in the subsequent convergence between the American North and South? Above I show that the hookworm infection rate could account for around half of the literacy gap and about twenty percent of income differences, and so eradication would have closed it by a similar amount. Another question is contemporary: How much does disease contribute to underdevelopment in the tropics?25 The present study suggests potentially large benefits of public-health interventions in developing countries, where hookworm is still endemic today. Nevertheless, I show using a simple calculation that, while reducing hookworm infection could bring substantial income gains to some countries, the estimated effect is approximately an order of magnitude too small to be useful in explaining the global income distribution.
While this broad decomposition of income per capita into institutions versus geography is interesting, one might argue that social scientists should instead focus on the efficacy of specific interventions. Changing the geography or the colonial history of a country is impossible, and unfortunately the institutions literature has little to say about the complicated mess of intermediate variables that determine productivity. The present study quantifies the benefits of one such intervention and finds them to be substantial.
Nevertheless, it remains an open question whether the long-term gains from hookworm eradication estimated for the American South can be realized for developing countries in the present day. As noted above, there have been other episodes in which externally supported eradication efforts failed because of a lack of local followup. Moreover, even if eradication could be achieved in less-developed areas, presumably a whole range of institutional infrastructure (functioning schools not least among them) needs to be in place to take advantage of the improvement in health. Investigating these interactions between health and institutions is therefore an important avenue of future study.
Appendix I. Data Sources and Contruction
There are two major empirical components of the present study, both of which involve combining micro and aggregate data. The first component is an analysis of sequential cross sections (SCS) from different points in time. That is, I compare a particular age group in one year to that same age group later on, and analyze changes over time differentially by area on the basis of each area’s pre-treatment-campaign infection level. The second component is a comparison of outcomes across cohorts. This retrospective cohort (RC) analysis is similarly combined with cross-area comparisons based on pre-treatment disease burden. In this appendix, I discuss the micro data employed in first the SCS and then the RC analyses. I later describe the construction of the aggregate data on hookworm and the additional control variables that factor into the SCS and RC analysis.
I.A Sources and Definitions for the Micro Data
I.A.1 Sequential Cross Sections
The micro data for the SCS component are samples drawn from the Censuses of 1900, 1910, 1920, 1940, and 1950, accessed through the IPUMS project [Ruggles and Sobek, 1997; Accessed May 30, 2003]. The sample consists of native-born whites and blacks in the age range [8,16] in the case of children, and in the age range [25,55] in the case of adults. The age criteria for children serves to select children of school age who are likely not yet old enough to have migrated on their own. The lower age cutoff for adults removes those whose school-years were likely impacted by the RSC in 1920. The outcome variables are defined as follows:
-
School enrollment. This is an indicator variable for whether the child has attended school at any time during a specified interval preceding the day of the Census. The length of this interval varies across the Censuses as follows:
1900: within the past year;
1910 and 1920: since September 1st;
1940: since March 1;
1950: since February 1.
See http://www.ipums.umn.edu/usa/peducation/schoola.html for more detail.
Full-time school attendance. This is an indicator variable that is switched on if the child is attending and not working. I consider a child to be working if the census recorded an occupation for him/her, which corresponds to a nonmissing “occ1950” code less than or equal to 970.
Literacy. This variable is an indicator for the ability to read and/or write. Census questions contained categories for being able to read but not write, vice versa, both or neither. I coded the first three as literate. (The first two responses were relatively rare.) These data were not collected from 1940 on.
Labor-force participation. A binary variable indicating whether the individual is working. Prior to 1940, this variable is based on whether the individual’s reported occupation was classified as a “gainful” one. From 1940 on, the question corresponds more closely to the modern definition.
Occupational income score. See below.
Urban residence. The variable equals one if the IPUMS “metro” variable greater than one, zero otherwise. This ignores central city versus suburban distinctions, and focuses on the urban/rural differences.
White-collar occupation. Defined as “occ1950” less than 100 or between 200 and 499 (inclusive).
I.A.2 Retrospective/Cohort
The micro data for the RC analysis is drawn from the IPUMS data. The sample definitions and data construction for Sections 6.1 and 6.2 are distinct and thus discussed separately.
Construction of the sample for Table IX
The sample used in Section 6.1 consists of native-born whites and blacks in the age range [25,60] in the 1940 Census microdata, except for the literacy sample, which contains native-born whites and blacks with ages [15,45] from the 1920. (The data were accessed February 5, 2003.) The outcome variables are defined as follows:
Earnings. The Census earnings variable from 1940 measures the individual’s wage and salary income from 1939. This measure excludes earnings from self-employment.
-
Years of schooling. I recode the IPUMS “higrade” variable to correspond to years of schooling as follows:
value of higrade recoded to…
n = 0 missing n < 4 0 n ≥4 n − 3 This has the effect of mapping (i) kindergarten or below to zero years of schooling and (ii) the remaining values to be the number of years starting with first grade.
Literacy. Defined above.
Construction of the sample for Figure V
The underlying sample used in Section 6.2 consists of native-born whites in the age range [25,60] in the 1900–1990 IPUMS microdata and the 1880 microdata from the North Atlantic Population Project [NAPP, 2004]. (These data were last accessed November 14, 2005.) This results in a data set with year-of-birth cohorts from 1825 to 1965. The original micro-level variables are defined as follows:
Occupational income score. The occupational income score is an indicator of income by disaggre-gated occupational categories. It was calibrated using data from the 1950 Census, and is the average by occupation of all reported labor earnings. See Ruggles and Sobek [1997] for further details.
Duncan socio-economic index. This measure is a weighted average of earnings and education among males within each occupation. The weights are based on analysis by Duncan [1961] who regressed a measure of perceived prestige of several occupations on its average income and education. This measure serves to proxy for both the income and skill requirements in each occupation. It was similarly calibrated using data from the 1950 Census.
These data are used to construct a panel of income by year and state of birth. The cohort-level outcomes are constructed as follows.
The microdata from 1880–1990 are first pooled together.
-
The individual income proxies are projected on to dummies for year-of-birth × Census year, i.e. I run the following regression:
for individual i in cohort k when observed in census year t. This regression absorbs all cohort, age, and period effects that are common for the whole country.
I then define cells for each combination of year of birth and state of birth. Within each cell, I compute the average of the estimated income residuals (the ε̂itk). Because these averages are constructed with differing degrees of precision, I also compute the square root of the cell sizes to use as weights when estimating equation 4.
I do this separately for both the occupational income score and the Duncan socio-economic index.
These average income proxies by cohort form the dependent variables in Section 6.2 and specifically Figure V.
For the majority of the years of birth, I can compute average income proxies for all of the 51 states plus the District of Columbia. The availability of state-level hookworm data and the control variables restricts the sample further to 46 states of birth. Hawaii is excluded because of missing data on hookworm. Alaska, Colorado, the District of Colombia and Oklahoma are excluded because of missing data for at least one of the other dependent variables. This leaves 46 states of birth in the base sample.
There are a number of cohorts born before 1885 for which as few as 37 states of birth are represented. (See Panel B of Appendix Figure III.) For those born between 1855 and 1885, this appears to be due to small samples, because, while the NAPP data are a 100% sample for 1880, there are no microdata for 1890 and 1900 IPUMS data are only a 1% sample. On the other hand, for the 1843–1855 birth cohorts, all but two of the years have all 46 states represented. Nevertheless, even with the 100% sample from 1880, there are as many as six states per year missing for those cohorts born before 1843. A number of the territories (all of which would later become states) were being first settled by people of European descent during the first half of the XIXth century, and it is quite possible that, in certain years, no one eligible to be enumerated was born in some territories. (Untaxed Indians were not counted in the censuses.) Note that I use the term state above to refer to states or territories. Territories were valid areas of birth in the earlier censuses, and are coded in the same way as if they had been states.
While this procedure generates an unbalanced panel, results are similar when using a balanced panel with only those states of birth with the maximum of 141 valid observations. A comparison of the cohort-specific estimates from the balanced and unbalanced panels shows high correlation (over 0.96, for example, in the case of the full-controls specification for the occupational income score).
I.B Sources and Definitions for the Aggregate Data
I.B.1 Variables used in the SCS Analysis
Because county boundaries change over time and because county of residence is not available in the later Censuses, I use the state economic area (SEA) as the aggregate unit for the sequential-cross-section analysis, such as in Section 4. The SEAs are aggregations of counties, with an average number of 8.5 counties per SEA. SEA boundaries tend to be more stable, in part because they were often defined by a state boundary or significant natural feature (river or mountain range, e.g.). (See Bogue [1951] for more detail.)
The area-level data come from a variety of county-level sources, but principally from the RSC annual reports and the ICPSR’s study #3, the latter of which is a collection of historical Census tabulations. When relevant, the formulae for constructing the variable are presented below. (Variable names are those of the ICPSR study.) Data refer to 1910 unless otherwise noted. To construct SEA-level data, I sum the constituent counties or construct population-weighted averaged, as appropriate. “Per capita” normalizations come from the ICPSR study #3. The following is a list (in thematic groupings) of the aggregate variables with information on sources and definitions. The method of aggregation is noted if different from above. The source is indicated in brackets at the end of each item.
Data on Hookworm and RSC Treatments
Hookworm infection rate. The source data are at the county level and from the period 1911–1915. The infection numbers in most cases are from surveys conducted by the Rockefeller Sanitary Commission (RSC) as prelude to (or simultaneously with) dispensing treatments. In a few instances, the RSC dispensaries had already visited the county before making the survey. For this latter case, I use the examinations conducted by the dispensaries to construct the hookworm infection rate, rather than using surveys collected after the administration of the RSC treatments. (The hookworm-infection rates constructed from survey and examination have a correlation coefficient greater than 0.95 for those cases in which the survey was done first.) [RSC Annual Reports, 1910–1915.]
Individuals treated at least once by the RSC, per capita. The source data are at the county level and from the period 1911–1915. The RSC dispensaries tracked how many individuals received de-worming treatments. If an RSC dispensary visited a county twice, I sum the individuals treated from each visit. While it is possible that some children were double counted in this procedure, generally multiple visits by dispensaries were to cover different territory. [RSC Annual Reports, 1910–1915.]
Health and Health Policy
Examined by RSC per capita. The source data are at the county level and from the period 1911–1915. The RSC tracked how many individuals were examined by the dispensaries’ medical staff. [RSC Annual Reports, 1910–1915.]
Sanitary Index. The RSC conducted independent surveys of the condition of sanitation infrastructure, including whether buildings had proper latrines, clean water sources, etc. Several measures of sanitation were combined by the RSC to form an index. [RSC Annual Reports, 1910–1915.]
Full-time health officer. These data were compiled at the county level, and include information on the first year each county employed a full time health officer. I coded this variable as one if such an office was created between 1910 and 1920 (inclusive). Only one county (Jefferson county in Kentucky) had created such a post before 1910, and the results above are not sensitive to its reclassification. [Ferrell et al. 1932.]
County spending. Data were input at the county level on county-government spending on education and health/sanitation for the years 1902 and 1932. (The 1922 publication in the series did not include these categories of spending, and the 1913 publication did not include earmarked transfers from the state government.) The health spending is normalized by total population, while the education expenditure is normalized by school-age population. [U.S. Bureau of the Census, 1915b and 1935.]
WWI Cantonment size per capita. I collected data on the troop numbers that were mustered and trained at the major Army cantonments of mobilization/embarkation for the First World War. Of the 32 cantonments, there were 19 camps in the South. These were “camps and cantonments that were used for mobilizing and training combat divisions,” but this excludes “miscellaneous groups” which comprised the “special camps, usually of semipermanent construction that were intended for mobilizing and training special troops, such as the Quartermaster Department Camp, Camp Joseph E. Johnston, Jacksonville, Florida.” I input the highest value given for the number of soldiers within a camp during 1918–20. [Bowen, 1928.]
Malaria mortality, 1919–1921. These data were compiled at the county level and refer to the period 1919–1921. [Maxcy, 1923.]
Change in fertility, 1900–10. The fertility rate for 1910 is measured from Census tabulations under the fraction of the population under six years of age, defined as 1 − (v41 + v53)/(v20 + v21). For 1900, the tabulations permit calculating the fraction of the population under five for 1900, or 1−(v22+v37+v39+v41+v43)/(v8+v10). When computing the approximate difference, I up-weight the 1900 number by 5/4. [ICPSR #3.]
Education
Log Change in School Term Length, c. 1905–1925. Average length of school term, in weeks. Kentucky county data are imputed from cross-tabulated data on number of schools by months. The imputation is calibrated using Alabama data, which contain a continuous measure and a cross-tabulation. [Annual and biennial reports of the various state departments of education, 1905–1930.]
Log Change in Average Monthly Salaries for Teachers, c. 1905–1925. Generally these data were reported directly, but in a few cases, I had to construct the variable using annual salaries and term length. No adjustment for full-time equivalence was available from the source data. [Annual and biennial reports of the various state departments of education, 1905–1930.]
Log Change in School density, c. 1905–1925. Number of schoolhouse operating in the county, divided by land area in square miles. [Annual and biennial reports of the various state departments of education, 1905–1930; ICPSR #3.]
Log Change in Number of Teachers per School, c. 1905–1925. [Annual and biennial reports of the various state departments of education, 1905–1930.]
Log Change in Pupil/Teacher Ratio, c. 1905–1925. Average attendance divided by number of teachers. [Annual and biennial reports of the various state departments of education, 1905–1930.]
Log Change in Value of School Plant and Equipment, c. 1905–1925. [Annual and biennial reports of the various state departments of education, 1905–1930.]
Log Change in County spending, c. 1905–1925. See description above with the health controls.
Change in Returns to Literacy for Adults, c. 1910–1920. Measured from a regression of the occupational income score on literacy status, by SEA, for the 1910 and 1920 census samples of adults. (Author’s calculations using the 1910 and 1920 IPUMS data.)
Literacy rates. These data were compiled at the county level and come from the 1910 Census. Child literacy refers to ages 10–20 and is constructed as follows: 1 −(v50/v49). Adult literacy refers to males of voting age, defined as 1 −(v37/v26). [ICPSR #3.]
Race and Race Relations
Fraction black. These data come from the 1910 Census. Defined as the fraction of the areas males who are black, out of the total population of blacks and whites. Specifically this is defined as (v24 + v25)/(v24 + v25 + v22 + v23). [ICPSR #3.]
Rosenwald schools per capita. This measures the number of classrooms per capita built by the Julius Rosenwald Fund as of 1930. The denominator normalizes the number of classrooms by the population of blacks aged 5–19 in 1930. [Johnson, 1941.]
Lynchings per capita, 1900–30. The base data are the number of lynchings per 100,000 population by county in the years 1900–30. The denominator is the county population in 1930. [Johnson, 1941.]
Agricultural/Rural Controls
Population urban, 1900 and 1910. From Census tabulations measuring the population residing in metro areas. For 1910, the urban population is contained in variable v9 in the ICPSR data, which I scale by the total population as defined above. The 1900 fraction urban is also defined in the 1910 data as v13/(v13 + v14). I construct the change in urbanization using the difference between the two variables. [ICPSR #3]
Crop acreage per capita. The base data measures the total farmed acreage at the county level, regardless of tenancy. This is constructed with the formula (v155 + v164 + v175) and scaled by total population. [ICPSR #3]
Sharecropped areas per capita. The base data are a county-level measure of total acreage share-cropped (v164 using the ICPSR variable scheme). I scale this by total population. [ICPSR #3]
Farm value per capita. The base data are a county-level measure of the value of farm land and buildings, regardless of tenancy. This is defined as (v177 + v166 + v157). [ICPSR #3]
Cotton acreage per capita. The base data are cotton acreage in 1910 by county. [Census, 1915.]
Tobacco acreage per capita. The base data are tobacco acreage in 1910 by county. [Census, 1915.]
Parental-Background Controls
The mother’s and father’s Occupational Income Score are used as indicators for socioeconomic status. These data are matched to children using the “momloc” and “poploc” variables in the IPUMS. I also construct dummies for parent is missing, and assigned then incomes of zero. These variables are interacted with census year in the regressions.
I.B.2 Variables Used in the RC Analysis
For the retrospective-cohort analysis, I focus on state on birth as birthplace is not available at further disaggregation. (The District of Columbia is included, where data are available.)
Hookworm Infection. Computed from examinations of army recruits. [Kofoid and Tucker, 1921]
Average wage, 1899. I input the average monthly earnings (with board) for farm laborers by state in 1899. Various other wage measures are summarized by the same source, but are generally not available for a complete set of states. [Lebergott, 1964, Table A–24]
Region of birth. These dummy variables correspond to the Census definition of regions: Northeast, South, Midwest, and West.
Doctors per capita, 1898. Number of physicians per 1,000 inhabitants of each state. The primary source is listed as Polk’s Register of Physicians, 1898. [Abbott, 1900.]
State public-health spending, 1898. Per capita appropriations, by state, for state boards of health in 1898. Primary sources include the annual reports of state boards of health, state appropriations laws, and correspondence with the secretaries of the boards of health. [Abbott, 1900.]
Child mortality, 1890. The estimates of child mortality are constructed from published tabulations. Table 3 in Part III contains enumerated deaths of children under one year. I scale this number by the estimated birth rate (Part I, page 482) times the female population (Part I, Table 2). The rate from 1890 was used because child-mortality data are not available comprehensively for the years 1900–1932, during which time the death-registration system was established. The 1890 mortality data were collected by Census enumerators. [Census, 1894.]
Recruits for World War I found rejected for military service because of health “defects,” 1917–1919. [Love and Davenport, 1920.]
Fertility rate, 1890. The estimated birth rate (from Part I, page 482). [Census, 1894.]
Log change in School Term Length, c. 1902–1932. Average length of school term, in weeks. [Annual reports of the federal Commissioner of Education, 1905–1932.]
Log change in Average Monthly Salaries for Teachers, c. 1902–1932. [Annual reports of the federal Commissioner of Education, 1905–1932.]
Log change in Pupil/Teacher Ratio, c. 1902–1932. Average attendance divided by number of teachers. [Annual reports of the federal Commissioner of Education, 1905–1932.]
Log change in School Expenditure, c. 1902–1932. [Annual reports of the federal Commissioner of Education, 1905–1932.]
Adult literacy rate. Defined as above.
Population urban. Defined as above.
Fraction black. Defined as above.
Male unemployment rate, 1930. [ICSPR #3.]
Compulsory Schooling
The data on compulsory schooling are based on the work of Acemoglu and Angrist (2000). For the year 1914 and forward, I make use of their dataset. For the years prior to 1914, I follow their methodology in coding the state laws on compulsory attendance and child labor. Details on the coding are as follows:
-
Compulsory Attendance. Data were collected for the years 1895–1911 from the US Office of Education’s “Annual Report of the Commissioner Education for the Year…” The Annual Report gave the ages in which students were mandated by state law to attend school. The lowest age was entered as “min,” while the “max” variable took on the value of the highest age.
The Annual Report stopped reporting compulsory school laws in a simple chart form in 1911. In the period 1912–13, it only listed changes in compulsory-attendance laws. If a state was not listed as having a change in their laws, the “min” and “max” variables were simply extended through 1913 with their 1911 values. States with no laws in place were coded “NR.”
The “min” and “max” variables were used in the algorithm described by Acemoglu and Angrist to create the CA variable and the CA dummies: -
Child Labor. I coded the variable “minawork” by taking the youngest age restriction in a major industry in each state. Thus, e.g., if State X disallowed 14 year olds from mining and 16 year olds from manufacturing, then that state would take on a value of 14 for “minawork” that year. States with no laws in place were coded “NR.” Data were collected for the years 1902–1911 from the US Office of Education’s “Annual Report of the Commissioner Education for the Year…” The Annual Report had data on age restrictions in various industries per state. The only time data was extended backwards from 1902 was when “minawork” was coded as NR in 1902. In this case, I extended the “NR” coding back until 1894.
The Annual Report stopped reporting child labor laws in a simple chart form in 1911. In the period 1912–13, it only listed changes in child labor laws. If a state was not listed as having a change in their laws, I just extended the “minawork” value up through 1913 by repeating the 1911 value.
The “minawork” and “min” variables were used in the algorithm (taken from Acemoglu and Angrist) to create the CL variable and the CL dummies: I also created an alternate coding of the CL variable that represented the presence of all-sector child-labor restrictions. For prior to 1914, this variable was coded 0 for all states, with the exception of Wisconsin, which was coded as 5 for the period 1902–1913. From 1914 forward, this recode was equal to the original CL. Additional dummies are generated for this variant of CL in a like manner to that above. I create an additional dummy variables for those state-year cells with missing data for the CL variable.
Finally, these variables are matched to individual based on the laws that were prevailing when he was fourteen years old. (Acemoglu and Angrist, 2000; Joshua Angrist, personal communication, 2003; Bureau of Education, various years.)
References for Data Appendix
- Bogue Donald J. State economic areas; a description of the procedure used in making a functional grouping of the counties of the United States. Washington, DC: U.S. Government Printing Office; 1951. [Google Scholar]
- Bowen Albert S. Activities Concerning Mobilization Camps and Ports of Embarkation. IV. Washington, DC: U.S. Government Printing Office; 1928. Prepared under the direction of The Surgeon General, M. W. Ireland. [Google Scholar]
- Department of Education of the State of Alabama. Annual Report. Montgomery, AL: State of Alabama; 1905–1925. [Google Scholar]
- Department of Education of the State of Georgia. . Annual Report. Atlanta, GA: State of Georgia; 1905–1925. [Google Scholar]
- Inter-university Consortium for Political and Social Research. Computer file. Ann Arbor, MI: Inter-university Consortium for Political and Social Research (ICPSR); 1984. [Accessed Sept. 20, 2002]. Historical, Demographic, Economic, and Social Data: the United States, 1790–1970. http://www.icpsr.org/ [Google Scholar]
- Johnson Charles S. Statistical Atlas of Southern Counties: Listing and Analysis of Socio-Economic Indices of 1104 Southern Counties. Chapel Hill, NC: The University of North Carolina Press; 1941. [Google Scholar]
- Love Albert G, Davenport Charles B. Defects Found in Drafted Men: Statistical Information Compiled from the Draft Records Showing the Physical Condition of the Men Registered and Examined in Pursuance of the Requirement of the Selective Service Act. Washington, DC: U.S. Government Printing Office; 1920. Prepared under the direction of The Surgeon General, M.W. Ireland. [Google Scholar]
- Maxcy Kenneth F. The Distribution of Malaria in the United States as Indicated by Mortality Reports. Public Health Reports. 1923;38:1125–38. [Google Scholar]
- Preston Samuel H, Haines Michael R. New Estimates of Child Mortality in the United States at the Turn of the Century. Journal of the American Statistical Association. 1984;79:272–281. doi: 10.1080/01621459.1984.10478041. [DOI] [PubMed] [Google Scholar]
- Superintendent of Education of the State of South Carolina. Annual Report. Columbia, SC: State of South Carolina; 1905–1925. [Google Scholar]
- Superintendent of Public Education of the State of Louisiana. . Biennial Report. Baton Rouge, LA: State of Louisiana; 1905–1925. [Google Scholar]
- Superintendent of Public Education of the State of Mississippi. . Biennial Report. Jackson, MS: State of Mississippi; 1905–1925. [Google Scholar]
- Superintendent of Public Instruction of the Commonwealth of Kentucky. . Biennial Report. Frankfort, KY: Commonwealth of Kentucky; 1905–1925. [Google Scholar]
- Superintendent of Public Instruction of the Commonwealth of Virginia. . Annual Report. Richmond, VA: Superintendent of Public Printing; 1905–1925. [Google Scholar]
- Superintendent of Public Instruction of the State of Arkansas. . Biennial Report. Little Rock, AR: State of Arkansas; 1905–1925. [Google Scholar]
- Superintendent of Public Instruction of the State of North Carolina. . Biennial Report. Raleigh, NC: State of North Carolina; 1905–1925. [Google Scholar]
- Superintendent of Public Instruction of the State of Tennessee. . Biennial Report. Nashville, TN: State of Tennessee; 1905–1925. [Google Scholar]
- Superintendent of Public Instruction of the State of Texas. . Biennial Report. Austin, TX: State of Texas; 1905–1925. [Google Scholar]
- United States Bureau of the Census. Compendium of the Eleventh Census, 1890. II. Washington, DC: U.S. Government Printing Office; 1894. Vital and Social Statistics. [Google Scholar]
- United States Bureau of the Census. Thirteenth Decennial Census of the United States, 1910. VI & VII. Washington, DC: United States Government Printing Office; 1915a. Report on the Statistics of Agriculture in the United States. [Google Scholar]
- United States Bureau of the Census. . Financial Statistics of State and Local Governments: 1932. Washington, DC: United States Government Printing Office; 1935. [Google Scholar]
- United States Bureau of the Census. . Wealth, Debt and Taxation. II. Washington, DC: United States Government Printing Office; 1915b. [Google Scholar]
- United States Office [Bureau] of Education. . Annual Report of the Commissioner Education. Washington, DC: Government Printing Office; 1894–1913. [Google Scholar]
Appendix II: Geographic Distribution of Hookworm Infection Rates, c. 1910
Notes: This map displays the rate of hookworm infection among children by county groups across the Southern United States. Darker shades of gray indicate higher infection rates. Diagonal hatching indicates that no data are available for those areas. The infection rates are drawn from various annual reports of the Rockefeller Sanitary Commission, and the map/boundary data are from Earle, Otterstrom and Heppen (1999). The county groups, known as State Economic Areas (SEAs), are described in Bogue (1951).
Appendix III: Sample Statistics for the Cohort-Specific Analysis
These graphs report additional summary statistics by year of birth for the β̂t reported in Figure V in the subplot labelled “Occupational Income Score; Full controls”.
Appendix IV: Alternative Computations of Standard Errors for School-Enrollment Regressions
| (1) | (2) | |
|---|---|---|
| Sample period: | 1910–20 | 1900–50 |
| Point estimate on Infection × Post: | 0.0883 | 0.0954 |
| Computations of Standard Errors:
|
||
| Cluster on county group × post | 0.0225 | 0.0233 |
| Cluster on county group × year | 0.0225 | 0.0256 |
| Cluster on county group | 0.0288 | 0.0321 |
| Standard OLS | 0.0153 | 0.0159 |
| Huber-White | 0.0165 | 0.0175 |
Note: The dependent variable is a binary indicator for school enrollment. Columns 1 and 2 of the this table employ the same regression specifications of equation 1 and 2, respectively. Standard errors using alternative assumptions about the error structure are presented in the bottom five rows.
Footnotes
This is a revised version of the first chapter of my doctoral dissertation. I owe thanks to Daron Acemoglu, Joshua Angrist, David Autor, Gary Becker, Eli Berman, Patrick Buckley, Garland Brinkley, Dora Costa, Mark Duggan, Michael Greenstone, Jonathan Guryan, Christian Hansen, Gordon Hanson, Lakshmi Iyer, Simon Johnson, Lawrence Katz, Fabian Lange, Mark Lewis, Robin McKnight, Derek Neal, John Strauss, Robert Triest, Burton Weis-brod, Jonathan Zinman, several anonymous referees, and seminar participants at Boston University, the University of Chicago, Harvard University, Illinois State University, the Massachusetts Institute of Technology, Northwestern University, Princeton University, the University of California at Berkeley, University of California at San Diego, the University of Southern California, and Yale University for useful comments, and to Michael Pisa, Tareq Rashidi, and Elizabeth Stone for excellent research assistance.
Thymol, taken orally, was the recommended treatment of the time.
An interesting episode for comparison comes from Puerto Rico. Around the same time as the RSC, a commission from the U.S. Army sponsored treatment and education campaigns throughout that Caribbean island. Large gains against hookworm were realized immediately after the campaign. Unfortunately, the colonial government provided very little follow-up support, and these gains had almost completely disappeared a decade later. Moreover, recent work in Kenya by Kremer and Miguel [2004] suggests that the initial impulse provided by short-term injections of medication and publicity may have little long-term benefits. The present study is not a guide to how to design a deworming program, and thus I do not take a stand on the relative merits of medications versus publicity versus sanitation. Rather, I take the reduction in hookworm as given and evaluate the socioeconomic consequences.
The historical presentation in this section draws heavily on the work of Ettling [1981].
All of the estimates of this equation below are calculated using ordinary least squares (OLS) regressions.
The infection rates were based on microscopic examination of stool samples. (Several microscopists were generally part of the survey and dispensary teams.) The following quote is from the Second Annual Report of the RSC (1911):
The survey is made by counties: it is based on a microscopic examination of foecal specimens from at least 200 children between the ages of 6 and 18, taken at random—that is, without reference to clinical symptoms—from rural districts distributed over the county.
These numbers are over-estimates because some of the treated were outside of this age range. But, on the other hand, this bias is likely small because there were few people infected at other ages.
The underlying Census question used the word “attendance” rather than “enrollment,” but I call the variable “enrollment” nonetheless. The rather low standard of attending at least one day maps more closely onto enrollment, as the word is used in the contemporary literature.
To construct this figure, I run a regression of school attendance on SEA-level hookworm, separately by Census year from 1900 to 1950. Micro-level controls for age, female, female×age, black, and black×age are also included. The year-specific estimates on are plotted against year.
See Troesken (2004) for a description of the impact of some of these local investments.
Using logit and probit estimators rather a linear probability model, I find that the hookworm effect is sometimes larger for whites, sometimes not, depending on the specification. This bolsters the hypothesis that the two groups are experiencing similar increases in some latent measure (human-capital investment), but that binary nature of the census variables obscures this to some degree.
The latter number comes from the cross-state evidence discussed in Section 2.4, and shown in Figure I. The reduced-form estimate using cross-state variation is similar to the results presented for SEAs. Some of this relationship may be due to “Galton’s fallacy” since it is a comparison of Δxt and xt−1. This resulting upward bias in the first-stage relationship will cause a downward bias in the Indirect-Least-Squares estimates below. (The mean-reversion bias on the reduced-form coefficients was shown to be negligible in Section 4.1, so there is no mean reversion bias in the ILS numerator.) On the other hand, the intervention may have reduced the rate of severe infections more than the overall rate, which would likely cause an upward bias in this estimator.
To the extent that these numbers are comparable, they suggest a somewhat larger effect than those obtained by Miguel and Kremer (2004). Their study reports an IV estimate of −0.203 for the effect of intestinal-parasite infection on school participation. The school-participation variable is based on spot checks of school attendance following the intervention, and therefore is probably most comparable to the full-time school attendance variable in the present study. However, the estimated coefficients are not directly comparable since Miguel and Kremer measure a combined infection rate that includes hookworm, roundworm, schistosomiasis, and whipworm.
Smillie and Augustine (1925) show that hookworm-infection rates among adults were very low in the Southern United States. As they note, this contrasts with the experience of other countries, where hookworm might infect people across a broader range of ages.
Specifically, the formula is Expik = max(min(19, 49 – age i), 0) where age is measured in 1940.
Similar results are obtained by interacting the 1899 wage measure with the exposure variable instead of age and/or including the square of the average wage (× age) as well.
Using controls for mean reversion, the coefficient on Hj × Expik for the first variable is estimated to be −0.003 with a standard error of 0.003, and the estimate for the second variable is −0.001 with a standard error of 0.004.
Similarly, I do not find evidence that the mechanism is migration out of the South, migration into an urban area, shifting to white-collar occupations, or movement out of agriculture. I consider these potential channels by conditioning on the variables in the regressions above, and find that their inclusion makes little difference for the estimate of Hj × Expik. Such variables are themselves endogenous, and therefore these results should be considered a decomposition of the hookworm effect, taking the OLS coefficients on the added variables as correct.
Results for hookworm are not sensitive to matching to the legal variables based on any age between zero and 16.
These consist of the following state-of-birth-level variables: 1910 fraction black, fraction literate (among adults), fraction of population living in urban areas; 1899 infant-mortality rate, the 1899–1932 change in infant mortality rates, 1910 fertility rates, 1890 malaria mortality, 1930 unemployment rate, doctors per capita in 1898, state public health spending per capita in 1898, WWI recruits found “defective” at draft physical; and 1902–32 logarithmic changes in average monthly teacher salaries, school term length, school expenditures per capita, and pupil/teacher ratios.
This is consistent with previous versions of this study, which used the 1940 Census (and concomitantly narrow age range) and found significant effects of exposure on Duncan SEI but not on the occupational income score.
This is a departure from the methodology in Section 4.4 in that I scale the reduced-form coefficient by the pre-existing hookworm infection rate, rather than the change. For the ILS calculation in Section 4, I used follow-up data on infection rates several years after the RSC to gauge the first-stage relationship between pre-RSC hookworm and the decline. In contrast, I consider in this section the effect of the intervention over a span of many more years, by which time hookworm had been mostly eradicated. Because eradication was slightly less than complete, this will likely result in a slight downward bias of the ILS estimate. On the other hand, as in the previous ILS calculation, if the intervention the severity of infections more than the overall rate, it would cause an upward bias in this estimator.
The approximate income figures cited in this paragraph are from Barro and Sala-i-Martin, 1992 and 1999.
This possibility has been advanced recently by Jeffrey Sachs (2001) as part of an agenda highlighting the importance of geographic factors in development. This view has been challenged by Acemoglu, Johnson, and Robinson (2001) who argue in favor of the importance of institutions over geographic determinism.
References
- Acemoglu Daron, Angrist Joshua. How Large Are Human-Capital Externalities? Evidence from Compulsory Schooling Laws. In: Bernanke BS, Rogoff K, editors. NBER Macroeconomics Annual. Cambridge, MA: NBER MIT Press; 2000. p. 958. [Google Scholar]
- Acemoglu Daron, Johnson Simon, Robinson James A. The Colonial Origins of Comparative Development: An Empirical Investigation. American Economic Review. 2001;91:1369–401. [Google Scholar]
- Augustine Donald L, Smillie Wilson G. The Relation of the Type of Soils of Alabama to the Distribution of Hookworm Disease. American Journal of Hygiene. 1926;6:36–62. [Google Scholar]
- Barro Robert J, Sala-i-Martin Xavier. Economic Growth. Cambridge, MA: The MIT Press; 1999. [Google Scholar]
- Bleakley C Hoyt. Mimeo. Massachusetts Institute of Technology; May, 2002. Malaria and Human Capital: Evidence from the American South. [Google Scholar]
- Bleakley C Hoyt. Disease and Development: Evidence from the American South. Journal of the European Economic Association. 2003;1:376–386. [Google Scholar]
- Bleakley C Hoyt. PhD dissertation. Massachusetts Institute of Technology; 2002. Three Empirical Essays on Investment in Physical and Human Capital. [Google Scholar]
- Bleakley C Hoyt, Lange Fabian. Chronic Disease Burden and the Interaction of Education, Fertility and Growth. Yale University; Mimeo: 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brinkley Garland L. The Decline in Southern Agricultural Output, 1860–1880. Journal of Economic History. 1997;57:116–38. [Google Scholar]
- Brinkley Garland L. PhD dissertation. University of California; Davis: 1994. The Economic Impact of Disease in the American South, 1860–1940. [Google Scholar]
- Caselli Franceso, Coleman Wilbur J., II The U.S. Structural Transformation and Regional Convergence: A Reinterpretation. Journal of Political Economy. 2001;109:584–616. [Google Scholar]
- Connolly Michelle P. Human Capital and Growth in the Post-Bellum South: A Separate but Unequal Story. Duke University Mimeo; 2001. [Google Scholar]
- Dickson Rumona, Awasthi Shally, Williamson Paula, Demellweek Colin, Garner Paul. Effects of Treatment for Intestinal Helminth Infection on Growth and Cognitive Performance in Children: Systematic Review of Randomised Trials. British Medical Journal. 2000;320:1697–701. doi: 10.1136/bmj.320.7251.1697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donohue John J, III, Heckman James J, Todd Petra E. The Schooling of Southern Blacks: The Roles of Legal Activism and Private Philanthropy 1910–1960. Quarterly Journal of Economics. 2002;CXVII:225–68. [Google Scholar]
- Duncan Otis D. A Socioeconomic Index for All Occupations. In: Reiss AJ, editor. Occupations and Social Status. New York: The Free Press; 1961. pp. 109–138. [Google Scholar]
- Ettling John. The Germ of Laziness: Rockefeller Philanthropy and Public Health in the New South. Cambridge, MA: Harvard University Press; 1981. [Google Scholar]
- Farmer Henry F., Jr . PhD dissertation. University of Georgia; 1970. The Hookworm Eradication Program in the South, 1909–1925. [Google Scholar]
- Havens Leon C, Castles Ruth. The Evaluation of the Hookworm Problem of Alabama by Counties. Journal of Preventive Medicine. 1930;4:109–114. [Google Scholar]
- Jacocks WP. Hookworm Infection Rates in Eleven Southern States as Revealed by Resurveys in 1920–1923. Journal of the American Medical Association. 1924;82:1601–2. [Google Scholar]
- Kofoid Charles A, Tucker John P. On the Relationship of Infection by Hookworm to the Incidence of Morbidity and Mortality in 22,842 Men of the United States Army. American Journal of Hygiene. 1921;1:79–117. [Google Scholar]
- Kremer Michael, Miguel Edward. Working Paper 10324. Cambridge, MA: National Bureau of Economic Research; 2004. The Illusion of Sustainability. [Google Scholar]
- Lebergott Stanley. Manpower in Economic Growth: the American Record since 1800. New York, NY: McGraw-Hill Inc; 1964. [Google Scholar]
- Margo Robert A. Race and Schooling in the South, 1880–1950: An Economic History. Chicago, IL: University of Chicago Press; 1990. [Google Scholar]
- Maxcy Kenneth F. The Distribution of Malaria in the United States as Indicated by Mortality Reports. Public Health Reports. 1923;38:1125–38. [Google Scholar]
- Miguel Edward, Kremer Michael. Worms: Identifying Impacts on Education and Health in the Presence of Treatment Externalities. Econometrica. 2004;72:159–217. [Google Scholar]
- Mitchener Kris J, McLean Ian W. U.S. Regional Growth and Convergence, 1880–1980. Journal of Economic History. 1999;59:1016–42. [Google Scholar]
- North Atlantic Population Project. Computer file. Minneapolis, MN: Minnesota Population Center; 2004. [Accessed November 12, 2005]. NAPP: Complete Count Microdata, Preliminary Version 0.2. http://www.nappdata.org/ [Google Scholar]
- Philipson Tomas J. Working Paper T0250. Cambridge, MA: National Bureau of Economic Research; 2000. External Treatment Effects and Program Implementation Bias. [Google Scholar]
- Rockefeller Sanitary Commission. Annual Reports. New York, N.Y: Rockefeller Foundation; 1910–1915. [Google Scholar]
- Ruggles Steven, Sobek Matthew. Integrated Public Use Microdata Series: Version 2.0. Minneapolis, MN: Historical Census Projects, University of Minnesota; 1997. http://www.ipums.umn.edu/ [Google Scholar]
- Sachs Jeffrey D. Working Paper 8119. Cambridge, MA: National Bureau of Economic Research; 2001. Tropical Underdevelopment. [Google Scholar]
- Smillie Wilson G, Augustine Donald L. Intensity of Hookworm Infection in Alabama: Its Relationship to Residence, Occupation, Age, Sex, and Race. Journal of the American Medical Association. 1925;85:1958–1963. [Google Scholar]
- Troesken Werner. Water, Race, and Disease. Cambridge, MA: MIT Press; 2004. [Google Scholar]