Abstract
The study of chromatin 3D structure has recently gained much focus owing to novel techniques for detecting genome-wide chromatin contacts using next-generation sequencing. A deeper understanding of the architecture of the DNA inside the nucleus is crucial for gaining insight into fundamental processes such as transcriptional regulation, genome dynamics and genome stability. Chromatin conformation capture-based methods, such as Hi-C and ChIA-PET, are now paving the way for routine genome-wide studies of chromatin 3D structure in a range of organisms and tissues. However, appropriate methods for analyzing such data are lacking. Here, we propose a hypothesis test and an enrichment score of 3D co-localization of genomic elements that handles intra- or interchromosomal interactions, both separately and jointly, and that adjusts for biases caused by structural dependencies in the 3D data. We show that maintaining structural properties during resampling is essential to obtain valid estimation of P-values. We apply the method on chromatin states and a set of mutated regions in leukemia cells, and find significant co-localization of these elements, with varying enrichment scores, supporting the role of chromatin 3D structure in shaping the landscape of somatic mutations in cancer.
INTRODUCTION
The spatial organization of chromatin is of major importance to key processes in the cell. Recently, several studies have shown that, in addition to regulatory functions (1,2), long-range DNA interactions are associated with the mutational landscape and chromosomal alterations in cancer genomes (3–5). Therefore, understanding how DNA is organized in the nucleus is crucial.
One recently published technique called Hi-C (6), has been shown to successfully map genome-wide 3D interactions in several species (7–9). Briefly, the Hi-C method uses formaldehyde to cross-link the DNA, which is subsequently digested using a restriction enzyme, and then paired-end next-generation sequencing determines the frequency of interactions between all pairs of restriction fragments. Other techniques based on chromosome conformation capture (10) include 5C (11) and ChIA-PET (12).
Despite these recent breakthroughs in experimental techniques for mapping chromatin 3D interactions, few tools have been developed to handle the large amounts of data that are produced in a statistically sound way.
We are interested in evaluating whether a set of regions in the genome (our ‘query set of interest’) are spatially closer to each other than what would be expected by chance. The Hi-C data will typically consist of restriction fragments that can be concatenated into bins of a certain constant size, which we will call genomic elements. We wish to evaluate whether a predefined subset of these elements has significantly higher interaction frequencies than what would be expected by chance. As is obvious, both the choice of query set and what we mean by chance is crucial to this question.
One of the first computational methods to handle this question was proposed by Botta et al. (13). In this study, they assumed a null hypothesis where interactions were considered as independent and could therefore be randomized independently, using uniform resampling. They then compared the number of observed interactions with the average number of interactions in the randomized samples. Similarly, Duan et al. (7) and Dai and Dai (14) suggested that the number of interchromosomal interactions within a set of genes is hypergeometrically distributed, based on the assumption that the interactions are independent. However, as the 3D structure implies both transitive relations (if i is close to j and k, then j and k are also close) and correlation between certain pairs of interactions, these independence properties are not valid.
The dependency between interactions was recently pointed out in an article by Witten and Noble (15). In the same article, the authors proposed a simple resampling-based method for evaluating the overrepresentation of interchromosomal interactions in a set of genomic elements. They considered interaction frequencies in binary form, where true interactions were defined as interchromosomal interactions at a false discovery rate <0.01. Letting the size of the query set be n, they uniformly drew n new elements from the total population, and compared the number of interactions in the randomly chosen set with the number of interactions in the original set, keeping the number of elements on each chromosome constant. In this way, they obtained an estimate of the P-value according to the null hypothesis that the set of interest shows no more co-localization than a randomly chosen set of elements. Using this resampling approach, the global 3D structure is maintained, and therefore also the transitive properties. However, the dependency between interactions close in sequence is not preserved.
The Witten and Noble (15) method is designed to work only for interchromosomal interactions, and therefore abundant cis-acting interactions cannot be assessed. Additional properties will have to be considered when taking into account intrachromosomal interactions. Random close contacts in the DNA molecule cause systematically higher numbers of interactions for regions close in sequence compared with more distant regions. Such effects need to be adjusted for when testing on interaction frequencies within a chromosome.
There are several properties of the query set of interest that can be important to preserve in a hypothesis test setting when considering the total data set. Examples of such properties are the proportion of genomic elements close to centromeres and telomeres, or the GC content in the query set of interest. We show in this article that ignoring such features may cause skewness in the P-value distribution under the null model. This is because the interaction frequencies have varying distributions throughout the genome.
Imakaev et al. (16) showed that the three first eigenvectors of the bias corrected Hi-C data capture global patterns of chromatin interactions. The authors showed enrichments of contacts between genomic regions with similar corresponding elements in the first eigenvector. Because this eigenvector is strongly correlated with GC content, it implies that regions with similar GC content have a higher chance of interacting than regions with different GC content. In addition, they showed that the second and third eigenvectors pick up patterns relating to the relative positioning along the chromosome arms, where centromeric and telomeric regions are enriched for contacts within these regions more than between. The first eigenvector is related to the two-compartment model, where chromatin is divided into open and closed compartments, proposed in (6). Here, they also reported higher correlations between interaction frequencies within compartments compared with between compartments.
In this article, we present a genome-wide hypothesis test for inter- and intrachromosomal interactions, either separately or jointly, that can take into account structural properties due to both sequence-based distance and varying compartmental structure defined as domains along the chromosomes. We evaluate the method on both simulated and real data, and find that it performs well in all circumstances. Software for these tests is available online.
MATERIALS AND METHODS
A genome-wide hypothesis test of 3D co-localization of genomic elements
Based on knowledge about the spatial organization of a genome, there are some distinct and important properties to be considered in a hypothesis test context.
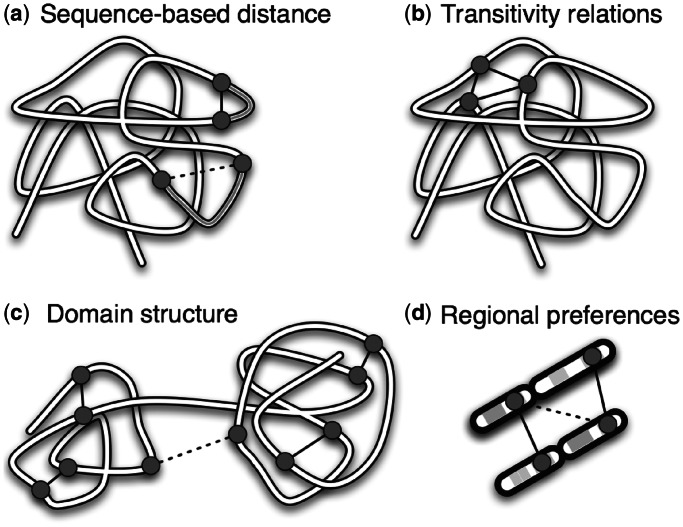
We are more likely to observe intrachromosomal interactions between elements with low sequence-based distance along a chromosome compared with high sequence-based distance (see Figure 1a), as shown in Lieberman-Aiden et al. (6). Consequently, the expectation and variance of the interaction frequencies depend on the sequence-based distance. For interchromosomal interactions, the sequence-based distance is undefined, and therefore the expectation and variance are constant in this case. In the calculation of the test statistics, we adjust for the different expectations and variances of inter- and intrachromosomal interactions given their sequence-based distance.
Figure 1.
An overview of important structural features in chromatin 3D data, and how they are accounted for in the method. High and low interaction frequencies are shown as solid and dotted lines respectively, between selected genomic elements (circles). (a) Relationship between sequence-based distance (grey lines) and 3D contact frequency is corrected for using Equation 1. (b) All transitivity relations are preserved by randomizing the genomic elements only, and not the 3D interactions. (c) Interactions within domains are more prevalent than between domains. (d) Two genomic elements in the same relative position on the chromosome are more likely to interact than genomic elements on different positions. Both (c) and (d) are taken into account by using the domain randomization procedure. All these structural features lead to correlation between interactions with low sequence-based distance, which we take into account by using the CCD randomization procedure.
To maintain the transitive properties (see Figure 1b), we will randomize the query region of interest instead of the 3D structure. Still, in such a randomization, we need to consider the dependency between the interaction frequencies.
We want to test if a set of genomic elements (our ‘query set of interest’) has a higher 3D co-localization than what would be expected by chance. Our hypotheses are as follows:
H0 : The query set of interest has the same 3D co-localization as a random set,
H1 : The query set of interest has more 3D co-localization than a random set.
What we mean by ‘random set’ can vary according to what structural properties of the query set we want to preserve, and will be specified later.
We will now describe a test statistic that measures the amount of 3D co-localization in the query set of interest. Let genomic element ai be the element that starts on base pair i on chromosome a. Let 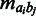 be the interaction frequency between genomic elements ai and bj. We calculate the sequence-based distance corresponding to an interaction as
be the interaction frequency between genomic elements ai and bj. We calculate the sequence-based distance corresponding to an interaction as
If 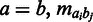 corresponds to an intrachromosomal interaction,
corresponds to an intrachromosomal interaction, 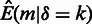 is the empirical mean of all intrachromosomal interaction frequencies with sequence-based distance
is the empirical mean of all intrachromosomal interaction frequencies with sequence-based distance 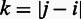 and
and 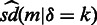 is the sample standard deviation. When
is the sample standard deviation. When 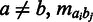 corresponds to an interchromosomal interaction,
corresponds to an interchromosomal interaction, 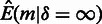 is the empirical mean of all interchromosomal interaction frequencies and
is the empirical mean of all interchromosomal interaction frequencies and 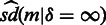 is the sample standard deviation. If the number of observed interactions is low for certain high
is the sample standard deviation. If the number of observed interactions is low for certain high  , it is advisable to assemble these into larger groups such that the estimation will be more accurate. Let
, it is advisable to assemble these into larger groups such that the estimation will be more accurate. Let 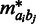 be the corrected interaction frequencies, which are adjusted for the expectation and standard deviation given
be the corrected interaction frequencies, which are adjusted for the expectation and standard deviation given  like the following:
like the following:
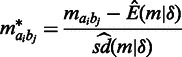 |
(1) |
Let 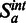 be the set of base pairs corresponding to the genomic elements of interest on chromosome a, and let
be the set of base pairs corresponding to the genomic elements of interest on chromosome a, and let  be our query set of interest over all chromosomes. The corresponding test statistic becomes the sum over all possible inter- and/or intrachromosomal corrected interaction frequencies
be our query set of interest over all chromosomes. The corresponding test statistic becomes the sum over all possible inter- and/or intrachromosomal corrected interaction frequencies 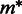 from Equation 1 in our query set Q:
from Equation 1 in our query set Q:
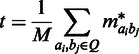 |
(2) |
where M is the number of terms in the sum. Under the null hypothesis, the expected value of the numerator of Equation 1 will be close to zero, and therefore the test statistic in Equation 2 will be close to zero. We know that the variance of the test statistic is the sum over the variance for each corrected interaction frequency, plus the sum over the covariances between all pairs of corrected interaction frequencies. It follows that when the genomic elements in Q are close in sequence, the covariance between interaction frequencies increases, along with the variance of the test statistic.
We estimate the P-value using a permutation test, and resample R random sets. In the permutation of genomic elements, it is important to maintain the query set configuration, meaning the sequence-based distance between the genomic elements of interest. We choose to sample new positions by randomizing the order of the consecutive distances between the genomic elements in the query set. Thereby, the set of all successive distances between the elements in the query set are conserved (see Supplementary Figure S1). This leads us to the following Monte Carlo (MC) randomization strategy, which we name Conserved Consecutive Distances (CCD):
Calculate
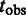 , the test statistic from Equation 2 based on the query set of interest Q.
, the test statistic from Equation 2 based on the query set of interest Q.Calculate sequence-based distance da between all pairs of consecutive genomic elements in
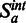 for all a.
for all a.- Repeat the following procedure for
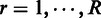 .
.
-
–For each chromosome a, let
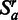 be a random set, where the order of the sequence-based distance da is randomized. It follows that
be a random set, where the order of the sequence-based distance da is randomized. It follows that 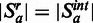 .
. -
–Let tr be the test statistic from Equation 2 based on the random set
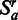 for all a.
for all a.
-
–
We calculate the exact Monte Carlo P-value, described in (17)
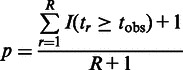 |
(3) |
Testing for alternative hypotheses with lower co-localization, or testing for either lower or higher co-localization, is done in exactly the same way, but with a trivially modified P-value calculation.
We quantify the 3D co-localization of elements in the query set by calculating an enrichment score S. This is given as the ratio of the average observed over average expected co-localization. In the Supplementary methods, we provide a detailed description of the calculations. When presented in percentage, we give the enrichment as 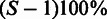 .
.
The domain randomization procedure
It has recently become clear that the structural properties of mammalian chromatin are not constant throughout the entire genome, but varies locally depending on both GC-content and on relative positioning along the chromosome arms [see (16)]. The GC-dependent variation is related to the two-compartment model proposed in (6), where the nucleus is compartmentalized into open and closed chromatin. Therefore, in addition to conserving the consecutive distances within the query set during the randomization, it is often necessary to conserve these additional structural features as well (i.e. being more strict in the definition of a random set). In other words, we compare our query set with random sets with similar properties as the query set (see Figure 1c and d).
To conserve the structural features in the hypothesis test, we divide the genome into domains such that all genomic elements within the same domain have the same desired properties. We then use the CCD randomization strategy separately within each domain. Note that this strategy will not necessarily conserve the consecutive distances between adjacent domains. This, however, is not critical, as interactions are much more prevalent within than between domains.
For comparison, a ‘global’ randomization is performed in the form of using the CCD randomization strategy on the entire chromosome arm.
To evaluate the difference between the presented randomizations, we used two publicly available data sets and looked at two important properties to define the domains. First, we looked at the amount of genomic elements in open and closed compartments, we then considered the relative position of the genomic elements along the chromosome arm. We classified the genomic elements into open and closed compartments using the same method as Lieberman-Aiden et al. (6) (by looking at the sign of the first principal component). To categorize the position of the genomic elements on the chromosome, we divided the chromosome arms into six equally sized groups. To investigate the influence of the domain randomization, we chose 1000 query sets of size 50 at random (with the same domain properties), and compared the resulting P-values to the P-values when using the global randomization procedure. By definition, the P-values are uniform when using the domain randomization, but this does not need to be the case when using the global randomization.
Simulated data and method evaluation
To validate the CCD randomization strategy, we simulated 3D structures where H0 was true by definition, and inspected the distribution of P-values for a large set of such structures. The P-values should be uniformly distributed if the resampling procedure is valid.
The 3D structures were simulated using random walks of size 500 inside a reflecting sphere. Two independent sequences (chromosomes) were simulated using the following algorithm 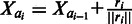 for
for  , where
, where 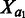 was, for simulated chromosome a, a random starting 3D position sampled within a sphere with a diameter of
was, for simulated chromosome a, a random starting 3D position sampled within a sphere with a diameter of 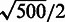 . ri was sampled from a 3D Gaussian distribution with
. ri was sampled from a 3D Gaussian distribution with 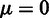 and
and 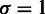 . Each step
. Each step 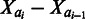 had length one and a random direction in the 3D space. The simulated interaction frequency was defined as
had length one and a random direction in the 3D space. The simulated interaction frequency was defined as 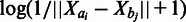 for all possible paired genomic elements between and within the simulated chromosomes. We simulated 5000 such 3D structures containing two chromosomes each.
for all possible paired genomic elements between and within the simulated chromosomes. We simulated 5000 such 3D structures containing two chromosomes each.
We compared our test statistic with an uncorrected version defined in the same way as Equation 2, except that we summed over ‘uncorrected’ interaction frequencies 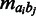 . We compared our Monte Carlo randomization strategy CCD with a simpler strategy where we resampled random sets
. We compared our Monte Carlo randomization strategy CCD with a simpler strategy where we resampled random sets 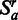 on each chromosome a, by sampling the same number of genomic elements uniformly distributed along the chromosome. We call this MC-strategy ‘UNI’. In total, we compared four different approaches with increasing degree of sophistication: UNI with uncorrected test statistic, UNI with corrected test statistic, CCD with uncorrected test statistic and CCD with corrected test statistic. The distribution of interaction frequencies was similar over the entire simulated genome, so we did not need to use the domain randomization procedure in this particular test.
on each chromosome a, by sampling the same number of genomic elements uniformly distributed along the chromosome. We call this MC-strategy ‘UNI’. In total, we compared four different approaches with increasing degree of sophistication: UNI with uncorrected test statistic, UNI with corrected test statistic, CCD with uncorrected test statistic and CCD with corrected test statistic. The distribution of interaction frequencies was similar over the entire simulated genome, so we did not need to use the domain randomization procedure in this particular test.
To show the effect of variations in the configuration of  , we evaluated all four approaches on three different types of
, we evaluated all four approaches on three different types of 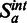 that were meant to represent a wide range of cases. The first type of query region consisted of 10 genomic elements uniformly sampled on each chromosome. In this case, we considered an ensemble of 150 query regions to see the distribution of the P-values in the average case. The second type of query region had 10 unique positions with high dispersion on each chromosome. Here, the positions were sampled using regularly spaced positions with added noise from a uniform distribution between 0 and 10. The last type was a set of 10 genomic elements heavily clustered on each chromosome. The positions for the genomic elements were sampled using ten unique positions from a Gaussian distribution with
that were meant to represent a wide range of cases. The first type of query region consisted of 10 genomic elements uniformly sampled on each chromosome. In this case, we considered an ensemble of 150 query regions to see the distribution of the P-values in the average case. The second type of query region had 10 unique positions with high dispersion on each chromosome. Here, the positions were sampled using regularly spaced positions with added noise from a uniform distribution between 0 and 10. The last type was a set of 10 genomic elements heavily clustered on each chromosome. The positions for the genomic elements were sampled using ten unique positions from a Gaussian distribution with 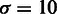 centered on the middle of the chromosome.
centered on the middle of the chromosome.
Specific versus regional co-localization
In analysis of real data, it is of interest to know whether a set of elements is co-localized simply because they are found in larger regions with general closeness, or if the query set itself is specifically co-localized compared with its near neighbors. Precise enrichment could potentially have a different interpretation than a more regional co-localization. To evaluate the specificity of the co-localization, we first perform a hypothesis test on the query set Q and calculate the P-value, and then subsequently perform hypothesis tests on neighboring query sets Qk, where each genomic element is shifted k elements in a random direction from the original position in Q. We let 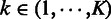 and look at how fast the enrichment scores and the P-values change, according to k.
and look at how fast the enrichment scores and the P-values change, according to k.
Software
All algorithms have been implemented in a publicly available statistical web toolkit called the Genomic Hyperbrowser, at http://hyperbrowser.uio.no/3d-coloc/ (18).
Publicly available data sets used
We used three different publicly available data sets with bin sizes varying from 100 kb to 1 Mb to evaluate inherent properties of chromatin 3D data and for hypothesis testing. All data sets used are adjusted for technical bias using the method of Imakaev et al. (16). For evaluating the domain randomization procedure, we used IMR90 and human embryonic stem cell (hESC) Hi-C data from (9). To test for co-localization of elements marked by somatic mutations, we used K562 Hi-C data from (6), and somatic mutations in leukemia patients from (19). We masked out centromeric, telomeric and gap regions, and performed the randomization within each chromosome arm separately.
RESULTS
In this section, we show how the dependency between interaction frequencies changes according to the sequence-based distance between the interactions, and use simulated data to validate the CCD randomization, which takes this dependency into account. With the publicly available data, we compare global and domain randomization, and use these methods to analyze the hypothesis that chromatin states are co-localized, and the hypothesis that mutated regions in leukemia patients are co-localized.
Interaction frequencies depend on sequence-based distance
A major motivation for the choice of randomization procedure is the occurrence of correlations between the interaction frequencies also after correcting for different sequence-based distances. We are strengthening this statement by showing that pairs of interactions with low sequence-based distance have similar corrected interaction frequencies. Specifically, we calculate the absolute difference 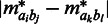 between all pairs of contacts. For each intrachromosomal pair, we find their sequence-based distances defined according to the smallest distance
between all pairs of contacts. For each intrachromosomal pair, we find their sequence-based distances defined according to the smallest distance 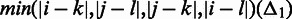 and the distance between the remaining two genomic elements (
and the distance between the remaining two genomic elements (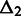 ). For instance, if
). For instance, if 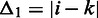 , then
, then 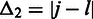 , or if
, or if 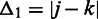 , then
, then 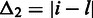 . For each interchromosomal interaction,
. For each interchromosomal interaction, 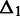 is defined as
is defined as 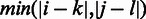 and
and 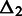 to be
to be 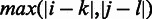 . When
. When 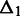 is small, one genomic element from each of the two interactions has low sequence-based distance. When, in addition,
is small, one genomic element from each of the two interactions has low sequence-based distance. When, in addition, 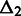 is small, the other two genomic elements from each of the two interactions also have low sequence-based distance.
is small, the other two genomic elements from each of the two interactions also have low sequence-based distance.
In Figure 2, we show the dependency between intrachromosomal interaction frequencies in hESC Hi-C data (9), measured by the average absolute difference, as explained above. As the figure shows, the corrected interaction frequencies tend to be more similar when both 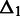 and
and 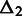 are low, i.e. the interactions have low sequence-based distance. The interaction frequencies seem to be particularly similar for interactions that are separated by <5 bins on either end. This emphasizes the need to maintain the structure in the randomization for interactions with low sequence-based distance. We see the same trends for the IMR90 cell line (9) in Supplementary Figure S2. There does not seem to be a large difference between bin sizes, although the interaction frequencies are more similar when the bin size is large compared with when the bin size is small. This could be because the interaction distribution is smoother for higher bin sizes. We see similar trends for corrected interchromosomal interaction frequencies (data not shown). To maintain this structure, we have chosen to conserve consecutive distances during the randomization (i.e. using the CCD method). Figure 2 also shows that the dependency structure is similar for the random walk structures, even though these interaction frequencies are more similar overall owing to the lack of noise in these structures.
are low, i.e. the interactions have low sequence-based distance. The interaction frequencies seem to be particularly similar for interactions that are separated by <5 bins on either end. This emphasizes the need to maintain the structure in the randomization for interactions with low sequence-based distance. We see the same trends for the IMR90 cell line (9) in Supplementary Figure S2. There does not seem to be a large difference between bin sizes, although the interaction frequencies are more similar when the bin size is large compared with when the bin size is small. This could be because the interaction distribution is smoother for higher bin sizes. We see similar trends for corrected interchromosomal interaction frequencies (data not shown). To maintain this structure, we have chosen to conserve consecutive distances during the randomization (i.e. using the CCD method). Figure 2 also shows that the dependency structure is similar for the random walk structures, even though these interaction frequencies are more similar overall owing to the lack of noise in these structures.
Figure 2.
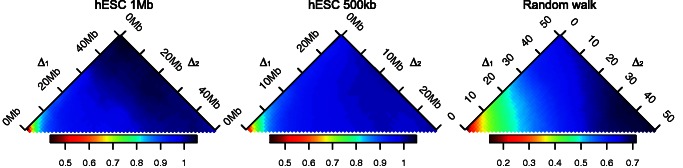
The average absolute difference  between all pairs of corrected intrachromosomal interaction frequencies, given the two distances
between all pairs of corrected intrachromosomal interaction frequencies, given the two distances  and
and 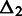 equal to the distance between the remaining two genomic elements. When
equal to the distance between the remaining two genomic elements. When 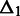 is small, one genomic element from each of the two interactions have low sequence-based distance. When, in addition,
is small, one genomic element from each of the two interactions have low sequence-based distance. When, in addition, 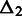 is small, the other two genomic elements from each of the two interactions also have low sequence-based distance. The two sequence-based distances are given in million base pairs (Mb) along the genome. On the left, we see the result using hESC data (9) with bin size 1 Mb, in the middle, using a bin size of 500 kb and to the right, the simulated random walk structures.
is small, the other two genomic elements from each of the two interactions also have low sequence-based distance. The two sequence-based distances are given in million base pairs (Mb) along the genome. On the left, we see the result using hESC data (9) with bin size 1 Mb, in the middle, using a bin size of 500 kb and to the right, the simulated random walk structures.
The resampling produces valid P-values
To validate the CCD resampling procedure, we looked at the distribution of the P-values in simulated data where H0 was true. A valid procedure for P-value estimation should produce a uniform distribution of P-values under H0. We simulate 5000 structures of two chromosomes under H0 (see ‘Materials and Methods’ section). The distribution of the simulated interactions in the random walk structures are similar across the structure, so we use global randomization on the entire chromosomes.
Figure 3 shows the resulting P-value distributions for both simulated intra- and interchromosomal interactions considered jointly. As expected, both the corrected and uncorrected test statistics give uniformly distributed P-values when the genomic elements were in fact generated uniformly. In the middle panels, we see the distribution of the P-values in a more intricate case, i.e. when the query sets are spread out over each chromosome. With spread genomic elements, we observe small uncorrelated interaction frequencies. Using the uncorrected test statistic in combination with UNI, we obtain P-values shifted toward 1, as the true distribution of the uncorrected test statistic has lower expectation and variance than the UNI approximation. Choosing a clustered query set gives P-values that are biased in the other direction, as here, the true distribution of the uncorrelated test statistic has higher expectation and variance than the UNI approximation. The only satisfactory estimation of the P-value for all types of query sets is given by CCD in combination with the corrected test statistic, as we in this situation correct for both the expectation and the variance of the test statistic.
Figure 3.
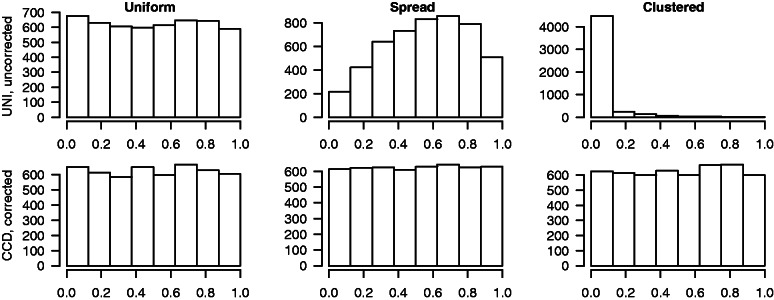
Each plot shows the histogram of 5000 P-values found by performing hypothesis testing on simulated 3D structures (based on a random walk procedure as explained in ‘Materials and Methods’ section) where our null hypothesis is true. The tests are performed on both intra- and interchromosomal interactions simultaneously. The upper row display the least complex approach, using the Monte Carlo resampling strategy UNI and the uncorrected test statistic. The bottom row shows the results from the Monte Carlo resampling strategy CCD and corrected test statistic from Equation 2. The three columns represent the three different configurations in the query sets of interest, uniformly distributed (left column), spread (middle column) and clustered (right column).
In Supplementary Figure S5, we see the resulting P-values for all combination of methods, namely UNI and CCD with both uncorrected and corrected test statistics. The same validations were also performed on simulated intra- and interchromosomal data separately (see, respectively, Supplementary Figures S3 and S4). The overall conclusion is the same: the only method that always gives uniformly distributed P-values for every considered query set when H0 is true, is the corrected test statistic in combination with CCD. For the remainder of the analysis, we will exclusively use the CCD in combination with the corrected test statistic in Equation 2.
Taking into account domain structure is necessary for biologically meaningful P-values
As proposed earlier, it is also possible to use a more strict null hypothesis where we randomize within predefined domains. In this section, we use two Hi-C data sets from (9) to evaluate the domain randomization procedure. We conserve two important properties, first the amount of genomic elements within each open and closed compartment, second the relative positioning of the genomic elements along the chromosome arm, as explained in ‘Materials and Methods’ section. If the P-values are the same using both global and domain randomizations, then the interactions are equally distributed within the domains compared with the entire genome.
In Figure 4, we see, in the left panel, the P-values for query sets from the closed compartments, and in the right panel, query sets from the open compartments. In both cases, the P-values, when using the global randomization, tend to be close to zero. In other words, all the query sets in either open or closed compartments have larger 3D co-localization if we compare them with random sets from the entire genome. These results correspond with the findings in Lieberman-Aiden et al. (6) where they show that there are higher 3D contacts when the genomic elements are in the same compartments compared with when they are distributed between compartments.
Figure 4.
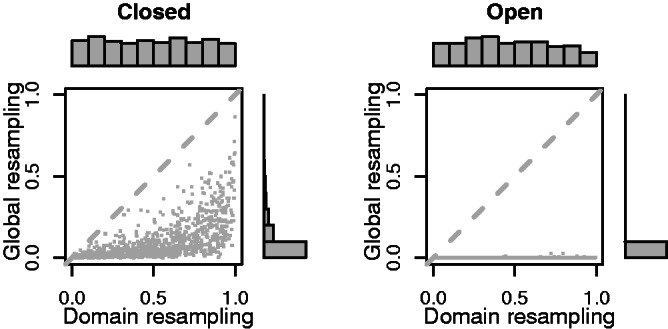
Evaluating random query sets with genomic elements in the closed (left panel) or open compartments (right panel). On the x-axis we see the P-values using the domain randomization, and on the y-axis we see the P-values using the global randomization. The results are based on both inter- and intrachromosomal interactions using the hESC data (9) with bin size 1 Mb.
In Figure 5, we see the P-values for query sets close to the telomeres (left panel), close to the center of the chromosome arms (middle panel) and close to the centromeres (right panel). Query sets in either end of the chromosome arm give P-values close to zero when using the global randomization, meaning they have larger 3D co-localization than if we compared them with random sets from the entire genome. In contrast, if we choose genomic elements in the middle of the chromosome arms, we find that they have lower 3D interaction, than if we compared them with random sets from the entire genome. This is similar to the results reported in Imakaev et al. (16).
Figure 5.
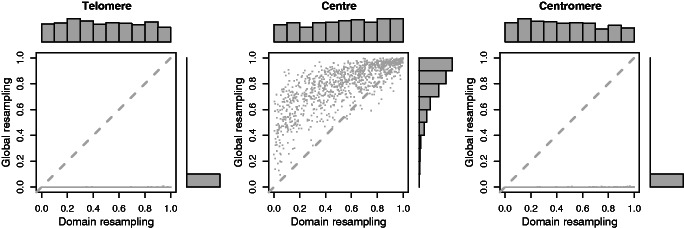
Evaluating random query sets with genomic elements close to the telomeres (left panel), close to the center of the chromosome arms (middle panel) or close to the centromeres (right panel). On the x-axis we see the P-values using the domain randomization, and the y-axis shows the P-values using the global randomization. The results are based on both inter- and intrachromosomal interactions using the hESC data (9) with bin size 1 Mb.
When analyzing genomic elements all located in telomere, centromere or open compartments, one should avoid using the global randomization, as this hypothesis test will always give significance, as seen in the right plot in Figure 4.
In Supplementary Figures S6–S8 we see the results of the same test, using bin sizes 1 Mb, 500 kb and 200 kb, respectively. The analyses are performed on interactions from intrachromosomal, interchromosomal and both combined. In Supplementary Figures S9–S11, we see the results of the same analyses on cell line IMR90. In some of the cases, for example, when the genomic elements in the query set are close to the centromere, there are different results when comparing intra- and interchromosomal interactions. This is reasonable because intra- and interchromosomal interactions potentially represent very different features.
3D co-localization correlates with chromatin state activity
We have demonstrated that our method is capable of producing uniformly distributed P-values under H0 (see Figure 3). However, it is also of interest to confirm that the method produces significant P-values when H0 is not true. We performed a genome-wide test of co-localization for three different sets of genomic elements defined according to chromatin state activity in human embryonic stem cells [using the chromatin states as defined in Ernst et al. (20)]. We therefore classified the 100 kb Hi-C bins in human embryonic stem cells (9) into three categories: All bins covered by ‘active promoter’, all bins covered by ‘strong enhancer’ and all bins covered by >50% ‘polycomb repressed’ regions. For each of these three sets of genomic elements, we performed a hypothesis test using the global randomization and the domain randomization methods with two different domain classifications (open and closed compartments, and chromosome arm positions divided into six groups). All tests were performed on intra- and interchromosomal interactions separately, in addition to jointly. In Figure 6, we see the P-values and enrichment scores (see Supplementary Figures S12–S14 for test statistic distributions). As expected, the regions marked by promoter or enhancer are significantly co-localized ( ), even after taking the domain properties of the query set into account. The enrichment scores represent average changes over the entire query set, thus for large query sets (like these) the values are generally low, and must not be confused with the traditional fold change in gene expression, where genes are analyzed individually. For both query sets, we see a decrease in enrichment score when comparing the global with the domain randomizations. Both enhancers and promoters are highly present in open compartments, making a global randomization problematic. This illustrates the importance of maintaining domain properties during randomization. Regions marked by Polycomb repressed states do not give significant co-localization, despite suggestions that Polycomb group proteins create silencing hubs (21). This could be due to the fact that relatively few Hi-C bins in this data set are spanned largely by Polycomb repressed regions, or that the regions are repressed in other ways than through chromatin interactions.
), even after taking the domain properties of the query set into account. The enrichment scores represent average changes over the entire query set, thus for large query sets (like these) the values are generally low, and must not be confused with the traditional fold change in gene expression, where genes are analyzed individually. For both query sets, we see a decrease in enrichment score when comparing the global with the domain randomizations. Both enhancers and promoters are highly present in open compartments, making a global randomization problematic. This illustrates the importance of maintaining domain properties during randomization. Regions marked by Polycomb repressed states do not give significant co-localization, despite suggestions that Polycomb group proteins create silencing hubs (21). This could be due to the fact that relatively few Hi-C bins in this data set are spanned largely by Polycomb repressed regions, or that the regions are repressed in other ways than through chromatin interactions.
Figure 6.
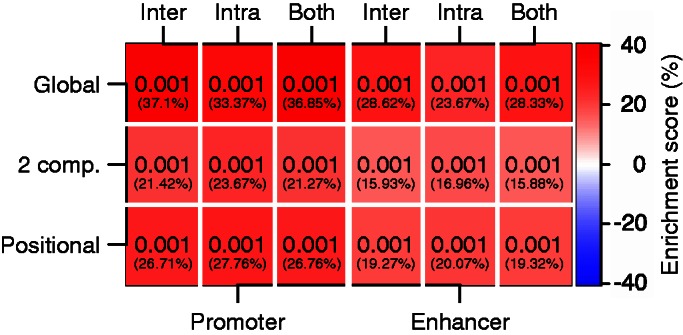
P-values and enrichment scores (in parenthesis) after testing on regions containing promoters (left) and enhancers (right) in hESC cells using 100 kb bins where we randomize globally (Global), within open and closed compartments (2 comp.), and within regions by dividing chromosome arms into six groups (Positional). Analysis was done on intra- and/or interchromosomal contacts.
Mutated regions in leukemia cells show statistically significant co-localization within chromosomes
Chromatin architecture increasingly appears to be of fundamental importance in many cancer-related processes. A recent study has suggested that somatic cancer mutation rates are largely influenced by chromatin organization (5). In that article, the authors showed that several heterochromatin-related epigenetic marks correlate positively with the frequency of somatic mutations in several cancers.
To gain further insight into the overall spatial patterns of mutated regions, we performed a genome-wide test of 3D co-localization of somatic mutations in leukemia samples (19) using a Hi-C data set from a human leukemia cell line (6), with bin sizes ranging from 100 kb to 1 Mb. For bin sizes 100 kb/200 kb, 500 kb and 1 Mb, bins were classified as mutated if they had at least one, two or three mutations within them, respectively. We then used the global randomization and the domain randomization methods with two different domain classifications (two compartments, and chromosome arm position based on six groups). All tests were performed both on intra- and interchromosomal interactions separately, and jointly.
In Figure 7, we see the P-value and enrichment score, and in Supplementary Figures S15–S18, we see the distribution of the test statistics under H0. The top enrichment scores accompany the lower P-values, as expected. For intrachromosomal interactions, we have significant P-values, together with enrichment scores 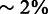 . Such low enrichment scores, accompanied by significant P-values, indicate that either a small subset of the interactions have a large contribution, or that all interactions contribute slightly to the significance. To get a better insight into the individual contributions of interactions in the query set, it is possible to look at a heat map over all individual test statistic terms for each interaction (see Supplementary Figures S15–S18). In our case, it seems that only a subset of interactions contribute to the enrichment.
. Such low enrichment scores, accompanied by significant P-values, indicate that either a small subset of the interactions have a large contribution, or that all interactions contribute slightly to the significance. To get a better insight into the individual contributions of interactions in the query set, it is possible to look at a heat map over all individual test statistic terms for each interaction (see Supplementary Figures S15–S18). In our case, it seems that only a subset of interactions contribute to the enrichment.
Figure 7.
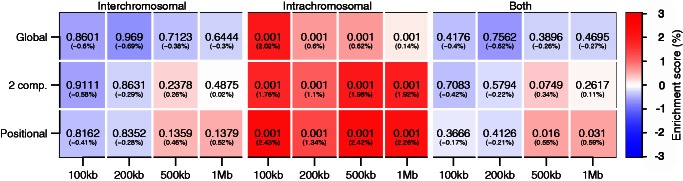
P-values resulting from hypothesis tests on the 3D co-localization of regions containing somatic mutations in leukemia cells. The colors and numbers in parentheses indicate the enrichment scores. Three different randomization strategies are used: the global randomization strategy (Global), domain randomization maintaining open and closed compartments (2 comp.) and domain randomization maintaining regional preferences by dividing chromosome arms into six groups. Analysis was done on intra- and interchromosomal contacts separately, and also jointly (Both). In addition, all tests were done on four different bin sizes (100 kb, 200 kb, 500 kb and 1 Mb) indicated at the bottom.
It is interesting to note the difference in enrichment score when taking the domain structure of the query set into account in the randomization. We know that the query set initially is enriched in heterochromatin regions [as shown in (5)], which has lower co-localization compared with non-heterochromatin regions. As a result of this, the global randomization will place elements into open regions with generally higher co-localization. The domain randomization procedure will maintain the structural properties of the original query set, and will result in a more realistic enrichment score.
The reason why intrachromosomal interactions show a statistically significant enrichment could be owing to replication timing-related processes, as recently shown in (22). Here, they showed that the mutational landscape differ in early and late replication regions, with higher mutation frequencies in late replication regions. They also found that regions with similar mutational frequencies were close in 3D inside the nucleus. We also note that the observed co-localization could arise owing to reduced access of the repair machinery at inaccessible heterochromatic regions (23), or the increased exposure of mutagens in peripheral parts of the nucleus, causing mutations to cluster in specific regions of chromatin (24). If such clusterings of mutations are numerous and spatially separated in the nucleus, the 3D co-localization would mainly be enriched intrachromosomally, as the distance between clusters could be much larger than the distance within clusters. A consequence of this is low enrichment scores because interaction frequencies within clusters would typically be larger than its expected value, and interaction frequencies between clusters would typically be lower than its expected value.
The results emphasize the need for running tests at different resolutions, as P-values and enrichment scores can be radically different depending on the resolution chosen. We observe a trend toward lower P-values at lower resolutions, which probably can be attributed to reduced noise. The point at which the P-values stabilize could be the appropriate choice of bin size. We also note that any statistical test of 3D co-localization should be run on intra- and interchromosomal interactions both separately and jointly, as these could have different interpretations.
The specificity of 3D co-localization
To determine how specific the co-localization is, we performed a series of hypothesis tests where we shifted the elements in the query set away from their original positions. We did this by shifting each element in the query set in a random direction in steps varying from 1 up to 5 bins. In cases where a new position was invalid (typically for large k), we chose their position at random. Figure 8 shows the result of this analysis. The somatic mutations have low, but significant 3D co-localization, and we find significance in some of the query sets in the neighboring bins k = 1, but when moving further away from the original query set, we lose both statistical significance and the quantified enrichment. A similar trend is seen for promoter-centered elements selected from (25), except for a steep drop in enrichment when shifting one bin, probably owing to the high specificity of promoter-centered interactions.
Figure 8.
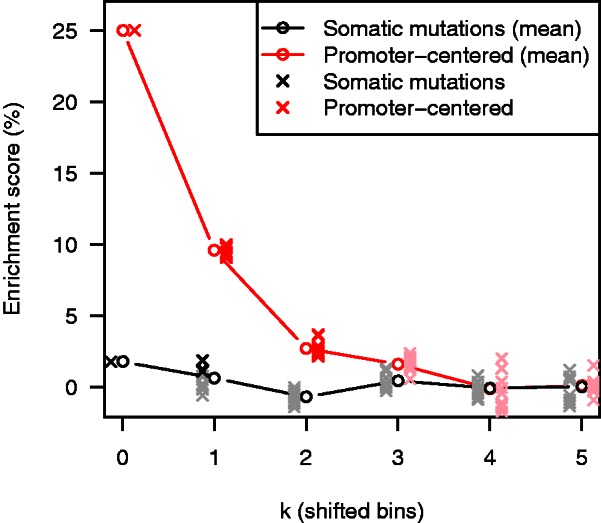
Estimated enrichment score after shifting each element in the original query set k bins in a random direction. The black solid line shows the average enrichment score of 10 independent runs on query sets defined by somatic mutations with a bin size of 100 kb, each indicated by a gray point (black point if the query set becomes significant at 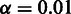 ). The red line shows a comparison with 10 independent runs on query sets defined by the promoter-centered elements (25) inside bins of size 100 kb in the same cell line (K562), where each run is either red (significant at
). The red line shows a comparison with 10 independent runs on query sets defined by the promoter-centered elements (25) inside bins of size 100 kb in the same cell line (K562), where each run is either red (significant at 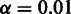 ) or pink (non-significant).
) or pink (non-significant).
DISCUSSION
We have in this article addressed the important issue of dependencies between interaction frequencies in 3D data sets when estimating P-values in a hypothesis test context. We find strong dependency of interaction frequencies between contacts with low sequence-based distance (Figure 2), and show that such structures strongly affect the P-value estimation (Figure 3). We resolve such dependencies by using the CCD randomization strategy. We show that maintaining additional structural properties during randomization is necessary for biologically meaningful P-value estimation if the structures are not globally homogeneous. In mammalian genomes, for example, it was recently shown that interaction frequencies were highly dependent on GC-content and relative positioning along chromosome arms. We maintain such structure by randomizing within predefined domains, while simultaneously using the CCD randomization strategy. This article also presents methods for analyzing both intra- and intrerchromosomal interactons, separately and jointly. The results are presented with P-values and enrichment scores.
We have shown the importance of looking at both statistical significance and quantified contact enrichment, as significant P-values may be associated with different enrichments scores. Factors like sample size can modulate the P-value, meaning that larger query sets are more likely to be significant, given a signal. Given the low, yet significant, enrichments for intrachromosomal interactions between mutated elements in the leukemia cells, it is difficult to establish the biological meaningfulness of this result. Regardless, significance is found for all choices of bin size, and randomization methods. It can also be problematic to directly compare enrichment scores of functional interactions involving promoters and enhancers with 3D proximity of elements peripheral in the nucleus, as these can have different biological functions.
We have used a Monte Carlo strategy in the estimation of the P-value, as there is no adequate choice for the distribution of the test statistic. The main problem is to find a convincing distribution for all types of interaction frequencies that covers all the different aspects of the biological 3D structure. It is therefore highly important to critically evaluate the underlying null models and their relevant Monte Carlo options when using resampling methods in hypothesis testing to take into account the relevant structural properties. To do so, it is essential to know the data and their properties.
In principle, it could also be possible to randomize the 3D structure itself given that one could produce 3D structures from a valid null model universe. This, however, appears to be challenging, as a complete definition of a random chromatin structure needs to be established. We therefore emphasize that randomization in the query set, and not randomization of the 3D structure, is the natural resampling choice.
Our CCD randomization strategy only conserves the distance between successive genomic elements along the genome. This means that sequence-based distances between all possible pairs of genomic elements in the query set are not necessarily the same in the resampled set. It is, in theory, possible to maintain the entire structure in the query set with other choices of randomization procedures, for example, by randomly shifting the entire query set configuration along the genome. However, this leads to fewer resampling outcomes, and the resampling can rapidly become too constrained for useful analyses. We show that the relatively simple strategy of maintaining consecutive distances in the query set is sufficient to give correct P-values, at least in the query set configurations tested here. We also note that if we maintain the entire structure of our query set of interest in every Monte Carlo resampling, there would be no use of including the correction terms in the test statistic in Equation 2, as these would be constant across resamplings. However, we also show that this term is highly necessary when only consecutive distances are conserved.
In this article, we have looked at the question of co-localization between a set of genomic elements. Such co-localization is caused by spatial clustering of genomic elements in 3D, and is of interest in many settings. However, other interesting questions are not covered by this co-localization term, such as the 3D closeness between certain pairs of elements, or the comparison of 3D structures across treatments. We foresee that some of the same strategies as presented here probably will be valid in these settings as well. In practice, significant co-localization of a query set of interest is often resulting from a subset of the interaction frequencies. To visualize the query set consisting of mutated regions in K562, we clustered all elements according to intrachromosomal interaction frequency and visualized the resulting matrix as a heat map (see Supplementary Figures S19–S41). As the figures clearly show, only a subset of the elements seem to show enrichment of contacts. Therefore, a more specific test, such as co-localization of pairs of elements, would be able to find more detailed co-localizations. However, such a test would require more knowledge before running the test.
To evaluate the power of our method under various resampling constraints, we tested whether active parts of the genome were co-localized. We showed that active regions of the genome, such as promoters and enhancers, show significant and strong 3D co-localization, in contrast to polycomb repressed regions, which show no such enrichment. This holds true regardless of the resampling strategy used, which emphasizes the strong connection between genome function and structure.
While large consortia such as ENCODE (26) and the NIH Roadmap Epigenomics Program (27) have given a detailed annotation of epigenetic marks across several tissues and cell lines, the spatial interactions of these elements are not well understood. We believe rigorous statistical and computational methods, such as the one presented here, are needed to fill this gap.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online: Supplementary Figures 1–41 and Supplementary Methods.
FUNDING
National Programme for Research in Functional Genomics (FUGE), and Statistics for Innovation (sfi2), a centre for research-based innovation funded by the Norwegian Research Council. Funding for open access charge: The Norwegian Radium Hospital.
Conflict of interest statement. None declared.
Supplementary Material
ACKNOWLEDGEMENTS
We thank Sveinung Gundersen, Kai Trengereid and Tobias Gulbrandsen Waaler for helpful discussions in the initial phase of the project, and for help with the software implementation.
REFERENCES
- 1.Kleinjan DA, van Heyningen V. Long-range control of gene expression: emerging mechanisms and disruption in disease. Am. J. Hum. Genet. 2005;76:8–32. doi: 10.1086/426833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.West AG, Fraser P. Remote control of gene transcription. Hum. Mol. Genet. 2005;14:R101–R111. doi: 10.1093/hmg/ddi104. [DOI] [PubMed] [Google Scholar]
- 3.De S, Michor F. DNA replication timing and long-range DNA interactions predict mutational landscapes of cancer genomes. Nat. Biotechnol. 2011;29:1103–1108. doi: 10.1038/nbt.2030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Fudenberg G, Getz G, Meyerson M, Mirny LA. High order chromatin architecture shapes the landscape of chromosomal alterations in cancer. Nat. Biotechnol. 2011;29:1109–1113. doi: 10.1038/nbt.2049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Schuster-Böckler B, Lehner B. Chromatin organization is a major influence on regional mutation rates in human cancer cells. Nature. 2012;488:504–507. doi: 10.1038/nature11273. [DOI] [PubMed] [Google Scholar]
- 6.Lieberman-Aiden E, van Berkum NL, Williams L, Imakaev M, Ragoczy T, Telling A, Amit I, Lajoie BR, Sabo PJ, Dorschner MO, et al. Comprehensive mapping of long-range interactions reveals folding principles of the human genome. Science. 2009;326:289–293. doi: 10.1126/science.1181369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Duan Z, Andronescu M, Schutz K, McIlwain S, Kim YJ, Lee C, Shendure J, Fields S, Blau CA, Noble WS. A three-dimensional model of the yeast genome. Nature. 2010;465:363–367. doi: 10.1038/nature08973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sexton T, Yaffe E, Kenigsberg E, Bantignies F, Lebland B, Hoichman M, Parrinello H, Tanay A, Cavalli G. Three-Dimensional folding and functional organization principles of the Drosophila genome. Cell. 2012;148:458–472. doi: 10.1016/j.cell.2012.01.010. [DOI] [PubMed] [Google Scholar]
- 9.Dixon JR, Selvaraj S, Yue F, Kim A, Li Y, Shen Y, Hu M, Liu JS, Ren B. Topological domains in mammalian genomes identified by analysis of chromatin interactions. Nature. 2012;485:376–380. doi: 10.1038/nature11082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Dekker J, Rippe K, Dekker M, Kleckner N. Capturing chromosome conformation. Science. 2002;295:1306–1311. doi: 10.1126/science.1067799. [DOI] [PubMed] [Google Scholar]
- 11.Dostie J, Richmond TA, Arnaout RA, Selzer RR, Lee WL, Honan TA, Rubio ED, Krumm A, Lamb J, Nusbaum C, et al. Chromosome conformation capture carbon copy (5C): a massively parallel solution for mapping interactions between genomic elements. Genome Res. 2006;16:1299–1309. doi: 10.1101/gr.5571506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Fullwood MJ, Liu MH, Pan YF, Liu J, Xu H, Mohamed YB, Orlov YL, Velkov S, Ho A, Mei PH, et al. An oestrogen-receptor-alpha-bound human chromatin interactome. Nature. 2009;462:58–64. doi: 10.1038/nature08497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Botta M, Haider S, Leung IX, Lio P, Mozziconacci J. Intra- and inter-chromosomal interactions correlate with CTCF binding genome wide. Mol. Syst. Biol. 2010;6:426. doi: 10.1038/msb.2010.79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Dai Z, Dai X. Nuclear colocalization of transcription factor target genes strengthens coregulation in yeast. Nucleic Acids Res. 2012;40:27–36. doi: 10.1093/nar/gkr689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Witten DM, Noble WS. On the assessment of statistical significance of three-dimensional colocalization of sets of genomic elements. Nucleic Acids Res. 2012;40:3849–3855. doi: 10.1093/nar/gks012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Imakaev M, Fudenberg G, McCord RP, Naumova N, Goloborodko A, Lajoie BR, Dekker J, Mirny LA. Iterative correction of Hi-C data reveals hallmarks of chromosome organization. Nat. Methods. 2012;9:999–1003. doi: 10.1038/nmeth.2148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Phipson B, Smyth GK. Permutation P-values should never be zero: calculating exact P-values when permutations are randomly drawn. Stat. Appl. Genet. Mol. Biol. 2010;9 doi: 10.2202/1544-6115.1585. Article 39. [DOI] [PubMed] [Google Scholar]
- 18.Sandve G, Gundersen S, Rydbeck H, Glad I, Holden L, Holden M, Liestøl K, Clancy T, Ferkingstad E, Johansen M, et al. The Genomic HyperBrowser: inferential genomics at the sequence level. Genome biol. 2010;11:R121. doi: 10.1186/gb-2010-11-12-r121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Puente XS, Pinyol M, Quesada V, Conde L, Ordóñez GR, Villamor N, Escaramis G, Jares P, Beá S, González-Díaz M, et al. Whole-genome sequencing identifies recurrent mutations in chronic lymphocytic leukaemia. Nature. 2011;475:101–105. doi: 10.1038/nature10113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ernst J, Kheradpour P, Mikkelsen TS, Shoresh N, Ward LD, Epstein CB, Zhang X, Wang L, Issner R, Coyne M, et al. Mapping and analysis of chromatin state dynamics in nine human cell types. Nature. 2011;473:43–49. doi: 10.1038/nature09906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Lanzuolo C, Orlando V. Memories from the polycomb group proteins. Annu. Rev. Genet. 2012;46:561–589. doi: 10.1146/annurev-genet-110711-155603. [DOI] [PubMed] [Google Scholar]
- 22.Liu L, De S, Michor F. DNA replication timing and higher-order nuclear organization determine single-nucleotide substitution patterns in cancer genomes. Nat. Commun. 2013;4:1–9. doi: 10.1038/ncomms2502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Peterson CL, Cote J. Cellular machineries for chromosomal DNA repair. Genes Dev. 2004;18:602–616. doi: 10.1101/gad.1182704. [DOI] [PubMed] [Google Scholar]
- 24.Misteli T. Beyond the sequence: cellular organization of genome function. Cell. 2007;128:787–800. doi: 10.1016/j.cell.2007.01.028. [DOI] [PubMed] [Google Scholar]
- 25.Li G, Ruan X, Auerbach RK, Sandhu KS, Zheng M, Wang P, Poh HM, Goh Y, Lim J, Zhang J, et al. Extensive promoter-centered chromatin interactions provide a topological basis for transcription regulation. Cell. 2012;148:84–98. doi: 10.1016/j.cell.2011.12.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.ENCODE Project Consortium. The ENCODE (ENCyclopedia Of DNA Elements) project. Science. 2004;306:636–640. doi: 10.1126/science.1105136. [DOI] [PubMed] [Google Scholar]
- 27.Bernstein BE, Stamatoyannopoulos JA, Costello JF, Ren B, Milosavljevic A, Meissner A, Kellis M, Marra MA, Beaudet AL, Ecker JR, et al. The NIH roadmap epigenomics mapping consortium. Nat. Biotechnol. 2010;28:1045–1048. doi: 10.1038/nbt1010-1045. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.