Estimating the additive genetic effect of the X chromosome

Jack W Kent, Jr; Thomas D Dyer; John Blangero

doi:10.1002/gepi.20093

. Author manuscript; available in PMC: 2013 Apr 5.

Published in final edited form as: Genet Epidemiol. 2005 Dec;29(4):377–388. doi: 10.1002/gepi.20093

Estimating the additive genetic effect of the X chromosome

Jack W Kent Jr ^1,^*, Thomas D Dyer ¹, John Blangero ¹

PMCID: PMC3617965 NIHMSID: NIHMS76484 PMID: 16294301

Abstract

We propose a method for efficient estimation of the additive genetic effect of the X chromosome with explicit modeling of eutherian-type dosage compensation. The theoretical derivation of the variance-components model for X-linked loci is reviewed in detail. We develop a model of dosage compensation that allows for both incomplete and heterogeneous lyonization, the existence of which is suggested by recent expression studies. Modeling this relationship, especially in the limit cases of complete or absent compensation, allows estimation of the X effect as a single parameter for ease of comparison to other sources of variance. We present simulation studies to estimate the power and computational efficiency of our proposed method.

Keywords: sex linkage, X-chromosome, dosage compensation, variance components, quantitative trait, statistical genetics

INTRODUCTION

Because segregation of the sex chromosomes is directly associated with a readily observed phenotype (sex), X-linked genes were among the first to be localized during the first century of modern genetics. In spite of this, analysis of the X chromosome has not been fully integrated into variance-components-based genetic software, due to the difficulty of analyzing male/female asymmetries in the transmission and dosage of X-linked genes. Because of these analytical complexities, investigators may give lower priority to genotyping X-chromosomal markers in large studies, thereby compounding the obstacles to gene discovery in this part of the genome.

This situation is beginning to change. Ekstrøm [2004] proposed an algorithm for multipoint linkage analysis on the X chromosome. In part to avoid making assumptions about the effects of gene dosage, Ekstrøm’s method estimates separate variance components for male-male, female-female, and male-female relative pairs, with separate identity-by-descent (IBD) matrices for each class of paired individuals. This pattern is applied both to the linkage parameters at a given locus and to the residual additive genetic variance due to other X-linked loci.

We propose a modified method that explicitly parameterizes the effect of dosage compensation in terms of lyonization coefficients (named for Mary Lyon, an early proponent of the X-inactivation hypothesis [Lyon 1961]). Our derivation of these coefficients is general enough to allow for incomplete inactivation, suggested by recent expression studies [Carrel & Willard 2005]. However, we also consider a more parsimonious approach that builds on Bulmer’s [1985] observations on the linear relationship between male and female variances in the complete presence or absence of dosage compensation, as occurs in the majority of X-linked loci in eutherian females. Bulmer’s simple alternate models for these cases allow us to estimate the additive genetic effect of the X chromosome as a single parameter, drawing information from all classes of paired individuals in the pedigree, in a way that should be appropriate for most mammalian systems (and many other organisms as well). We anticipate that any loss of generality in our proposed model may be compensated by the efficiency of estimating a minimal number of new parameters. We report simulation studies designed to estimate the power of our proposed method, including the cost in power when we have misjudged the presence or absence of dosage compensation in a particular case.

Our emphasis in this paper is on estimation of the aggregate additive genetic effect of X-linked loci, for three reasons. (1) The estimation of this effect is necessary for complete specification of the linkage model, and the derivation of expected allele-sharing will inform the calculation of locus-specific IBDs. (2) Inclusion of the X effect may improve model specification even when the focus is on autosomal linkages. (3) Finally and importantly, we wish to give the investigator a rapid estimate of the magnitude of the X-chromosomal contribution to a phenotype of interest, using pedigree data alone, to determine the priority of a more detailed analysis of this chromosome.

THEORETICAL BACKGROUND

The additive effect of X-linked genes is a function of two distinct processes: the transmission of alleles from parent to offspring, and the expression of those alleles. For variance-component analysis in general pedigrees, the decomposition of the phenotypic covariance between relatives should include an X-chromosome-specific variance term (in general, separate variances for each sex) weighted by factors representing the effects of allele-sharing and dosage compensation. Briefly, these factors are:

an X-linkage analog of the autosomal matrix Φ of probabilities that an allele drawn from a locus in one individual is identical by descent (IBD) with that drawn from another individual (or drawn with replacement from the same individual). Following the notation in [Ekstrøm 2004], we call this matrix Ψ. The elements of Ψ can be calculated recursively from pedigree data, as by the algorithm in MINX (“MERLIN in X”) [Abecasis 2005];
IBD weighting coefficients that reflect the unequal copy number of the X in males and females;
weighting coefficients, which we call lyonization coefficients, that account for the dosage-compensation state of the locus or loci under analysis.

The derivation of Ψ and the IBD weights is well-established in the literature [Bulmer 1985, Grossman & Eisen 1989, Cordell et al. 1995, Lynch & Walsh 1998], although there is some disagreement on the weighting for male-female pairs (see below). Because of this disagreement (and some obscurity!) in the literature, we review the derivation below.

The effects of dosage compensation usually have been modeled assuming either complete inactivation (lyonization) of one copy of the X in females or the complete absence of inactivation [Bulmer 1985, Pérez-Enciso et al. 2002]. This assumption is reasonable for most loci in eutherian females, but recent evidence suggests that inactivation may be incomplete at some loci [Carrel & Willard 2005]. Based on expression profiling in human fibroblast cell lines, these authors estimate that ~75% of X-linked loci are liable to inactivation, while ~15% escape inactivation (although inactivation may be incomplete). Unexpectedly, ~10% exhibit rates of inactivation that vary widely among individual females. Consequently, we present a model of dosage compensation that is general enough to allow for incomplete inactivation (below), and can be generalized further to include heterogeneous inactivation (see Appendix). Explicit modeling of dosage compensation establishes a simple mathematical relationship between the male and female variances due to the X, allowing expression of the additive genetic effect of the X in all individuals in terms of the variance in one sex [Bulmer 1985], i.e., as a single additional parameter. We present simulation studies that test the power, accuracy, and computational efficiency of this strategy.

ALLELE SHARING

Allele sharing: female-female pairs

Both individuals i, j are diploid for the X, so the derivation is the same as the autosomal case. The following derivation mirrors that for autosomal loci as presented in a standard text [Lynch & Walsh 1998, p. 143]. For a given locus q, and assuming no dosage compensation,

{cov}_{q} (i, j) = E [(α_{q 1, i} + α_{q 2, i} - μ_{i}) (α_{q 1, j} + α_{q 2, j} - μ_{j})]

where each α is the phenotypic deviation due to the additive effect of an allele at the locus. Because μ_i = μ_j = 0 for deviations from the phenotypic mean,

{cov}_{q} (i, j) = E [(α_{q 1, i} + α_{q 2, i}) (α_{q 1, j} + α_{q 2, j})] = \sum_{k} \sum_{m} E [α_{qk, i} α_{qm, j}], k \in {1, 2}; m \in {1, 2} .

Each of the four elements in the summation is E(α_q²) with probability ψ_ij if the alleles are IBD (where ψ_ij is the X-linked analog of φ_ij), or [E(α_q)]² = 0 otherwise. Therefore,

{cov}_{q} (i, j) = 4 ψ_{ij} E ({α_{q}}^{2}) .

Summing over loci, E(α_q²) = σ²_AX,ff/2, or one-half the additive genetic variance due to X-linked loci in female-female pairs (each α_i accounts for the per-locus contribution of one of the two copies of the X chromosome in each individual). Thus,

{cov}_{X} (i, j) = 2 Ψ_{ff} {σ^{2}}_{AX, ff} .

(1)

As in the autosomal case, the elements of Ψ_ff are P₁/4 + P₂/2, where P₁ and P₂ are the respective probabilities of sharing one or two alleles IBD.

Allele sharing: male-male pairs

Both individuals are haploid for the X chromosome. For a given locus q,

\begin{array}{l} {cov}_{q} (i, j) = E [(α_{q, i}) (α_{q, j})] \\ = ψ_{ij} E ({α_{q}}^{2}) . \end{array}

Summing over loci, E(α_q²) = σ²_AX,mm (only one chromosome provides all of the X-linked additive genetic variance in each individual), and

{cov}_{X} (i, j) = Ψ_{mm} {σ^{2}}_{AX, mm} .

(2)

The elements of Ψ_mm are simply P₁.

Allele sharing: male-female pairs

Note that the male is haploid for the X while the female is diploid. For a given locus q,

\begin{array}{l} {cov}_{q} (i, j) = E [(α_{q, i}) (α_{q 1, j} + α_{q 2, j})] = \sum_{k} E [α_{q, i} α_{qk, j}], k \in {1, 2} \\ = 2 ψ_{ij} E ({α_{q}}^{2}) . \end{array}

Summing over loci, E(α_q²) = σ²_AX,ff/2 for the female relative but σ²_AX,mm for the male relative. Therefore the covariance becomes,

{cov}_{X} (i, j) = 2 Ψ_{mf} {[{σ^{2}}_{AX, mm} ({σ^{2}}_{AX, ff} / 2)]}^{0.5} ρ_{Xg, mf}

(3a)

= (\sqrt 2) Ψ_{mf} σ_{AX, mm} σ_{AX, ff} ρ_{Xg, mf} .

(3b)

ρ_Xg,mf, the correlation of the values of specific genotypes in males and females, can differ from 1 due to X-linked-genotype × sex interactions (or heterogeneous inactivation: see Appendix). The elements of Ψ_mf are P₁/2. If ρ _Xg,mf = 1, Equation 3b can be written as,

{cov}_{X} (i, j) = (1 / \sqrt 2) P_{1} σ_{AX, mm} σ_{AX, ff} .

(3c)

Equation 3c is the “general case” for male-female covariance for X-linked loci as presented (without derivation) by Bulmer [1985].

Equation 3b has a coefficient of √2 because, in the absence of dosage compensation, an X-linked allele accounts for a different proportion of the trait variance in males and females. This is in agreement with some presentations [Bulmer 1985, Grossman & Eisen 1989, Cordell et al. 1995] but not others [Lynch & Walsh 1998, Ekstrøm 2004], where a coefficient of 2 is used. Our notation also differs from that of [Ekstrøm 2004] by explicitly stating the covariance term as σ_AX,mm σ_AX,ff ρ_Xg,mf.

DOSAGE

Now we must deal with possible differences in the expression of X-linked alleles due to their different copy number in males and females. Many species have mechanisms for equalizing the dosage of X-linked genes. In some invertebrates, for example, both copies of the X may be downregulated in homogametic individuals (C. elegans), or the single X in the heterogametic sex may be upregulated (Drosophila spp.) [Amrein 2000]. In female eutherian mammals, a majority of loci on one copy of the X chromosome are downregulated through X-inactivation (lyonization). As presently understood, this inactivation is random with respect to the maternal or paternal copy of the X in different cell lineages, and also random with respect to the timing of inactivation during development; thus a female is a mosaic of patches of cells expressing one or the other X-haplotype.

A general model of eutherian X-inactivation (which can also be applied to any system in which compensation is mosaic and random with respect to the parental origin of the X-homologs) is as follows: Let there be two alleles for an X-linked locus q, with additive effects scaled such that allele A1 contributes 1 to a trait, while A2 contributes 0. Let p = frequency of A1. In males, the single allele is expressed with probability 1. In females, one allele in each cell lineage is fully expressed, while the other is expressed with probability λ_q (or, equivalently, expressed at a fraction λ_q of its maximum possible value: 0 ≤ λ_q ≤ 1). If λ_q is a constant, and because each female is mosaic with each allele equally liable to inactivation in different cell lineages, the mean expressivity due to lyonization of each genotype at q is (1 + λ_q)/2. The resulting phenotypes and their means and variances are shown in Table 1. The Appendix addresses the more complex case where λ_q is a random variable (i.e., where inactivation is heterogeneous).

Table 1.

Phenotypes, means, and variances of a trait influenced by a diallelic X-linked locus with constant inactivation

Male genotype	Phenotype	Frequency
A1	1	p
A2	0	1−p
Mean = p(1) + (1−p)(0) = p
Variance = p(1−p)² + (1−p)(0−p)² = p(1−p)
General case:
Female genotype	Phenotype	Frequency

A1A1	[(1 + λ)/2](2) = 1 + λ	p²
A1A2	[(1 + λ)/2](1) = (1 + λ)/2	2p(1−p)
A2A2	[(1 + λ)/2](0) = 0	(1−p)²
Mean = p²(1 + λ) + 2p(1−p)(1 + λ)/2 + (1−p)²(0) = (1 + λ)p
Variance = p²[(1 + λ) − (1 + λ)p]² + 2p(1−p)[(1 + λ)/2 − (1 + λ)p]² + (1−p)²[0 − (1 + λ)p]²
= p(1−p)(1 + λ)²/2
Limit case: no dosage compensation (λ = 1 at all loci)
Female mean = 2p (i.e., twice the male mean)
Female variance = 2p(1−p) (i.e., twice the male variance)
Limit case: with dosage compensation (λ = 0 at all loci)
Female mean = p (i.e., equal to the male mean)
Female variance = p(1−p)/2 (i.e., half the male variance)

Open in a new tab

See text for explanation. The subscript of λ_q is omitted for clarity.

Classical models of dosage compensation or its absence, such as those of Bulmer [1985], are equivalent to the limit cases of our model where λ_q is either 0 or 1. As these cases are relatively simple (and good alternate hypotheses for most X-linked loci), we have employed them in the simulations that follow. The male and female X-linked additive genetic variances are linearly related ([Bulmer 1985] and Table 1). This allows us to express the additive effect of the X in the population in terms of its effect in one or the other sex – say, for example, the female (the following discussion assumes that females are the homogametic sex):

{cov}_{X} (x, y) = Ψ ⊙ X {σ^{2}}_{AX, ff},

(4)

where ⊙ represents the Hadamard matrix product operator (yielding the elementwise product ψ_i,j × X_i,j for each pair of individuals i and j). Thus, the structuring element is the Hadamard product of a combined Ψ matrix and a coefficient matrix X, each element of which is itself a product of coefficients I_i,jL_iL_j. Each I_i,j is the coefficient of Ψ required by allele-sharing for two individuals i and j, appropriate to their respective sexes (these coefficients were derived in the preceding section). L_i and L_j are lyonization coefficients that allow the single variance parameter σ²_AX,ff to account for the additive effect of the X chromosome in both sexes: L_f = σ_AX,ff/σ_AX,ff (= 1) for females and L_m = σ_AX,mm/σ_AX,ff for males.

No dosage compensation

Without dosage compensation, μ_AX,f = 2μ_AX,m and σ²_AX,ff = 2σ²_AX,mm; consequently, L_m = 1/√2. Then,

\begin{matrix} {cov}_{X} (female, female) = Ψ_{ff} (2) {(1)}^{2} {σ^{2}}_{AX, ff} = 2 Ψ_{ff} {σ^{2}}_{AX, ff}, \\ {cov}_{X} (male, male) = Ψ_{mm} {(1 / \sqrt 2)}^{2} {σ^{2}}_{AX, ff} = (1, 2) Ψ_{mm} {σ^{2}}_{AX, ff}, \\ {cov}_{X} (male, female) = Ψ_{mf} (\sqrt 2) (1 / \sqrt 2) (1) {σ^{2}}_{AX, ff} = Ψ_{mf} {σ^{2}}_{AX, ff} \\ (taking ρ_{Xg, mf} = 1) . \end{matrix}

Inclusion of sex as a covariate is necessary for analyses using this model, since we expect different means in males and females [Bulmer 1985, Ekstrøm 2004].

Dosage compensation

With dosage compensation, the mean additive genetic effect of X-linked loci is the same in both sexes, but σ²_AX,ff is half of σ²_AX,mm; L_m = √2. Then,

\begin{matrix} {cov}_{X} (female, female) = Ψ_{ff} (2) {(1)}^{2} {σ^{2}}_{AX, ff} = 2 Ψ_{ff} {σ^{2}}_{AX, ff}, \\ {cov}_{X} (male, male) = Ψ_{mm} {(\sqrt 2)}^{2} {σ^{2}}_{AX, ff} = 2 Ψ_{mm} {σ^{2}}_{AX, ff}, \\ {cov}_{X} (male, female) = Ψ_{mm} {(\sqrt 2)}^{2} (1) {σ^{2}}_{AX, ff} = 2 Ψ_{mf} {σ^{2}}_{AX, ff} . \end{matrix}

All coefficients in X are equal to 2, so Equation 4 simplifies to

{cov}_{X} (i, j) = 2 Ψ {σ^{2}}_{AX, ff} .

(5)

These results are summarized in Table 2.

Table 2.

Structuring elements and variance components for X-linked additive genetic covariances

			General case:		Dosage compensation:		No dosage compensation:

	ψ_i,j:	I_i,j:	L_i,j:	Variance:	L_i,j:	Variance:	L_i,j:	Variance:
Female-female	P₁/4 + P₂/2	2	1	σ²_AX,ff	1	σ²_AX,ff	1	σ²_AX,ff
Male-male	P₁	1	1	σ²_AX,mm	2	σ²_AX,ff	1/2	σ²_AX,ff
Male-female	P₁/2	√2ρ_Xg,mf^*	1	σ_AX,mmσ_AX,ff	√2	σ²_AX,ff	1/√2	σ²_AX,ff

Open in a new tab

In the absence of X-genotype by sex interactions (or variable lyonization, see Appendix), ρ_Xg,mf = 1.

SIMULATION EXPERIMENTS

POWER AND ACCURACY

All simulations and analyses were carried out using the genetic analysis software SOLAR [Almasy & Blangero 1998]. For initial calculations of power and accuracy, we simulated a normally distributed trait whose sole source of additive genetic variance was an X-linked QTL with two alleles at equal frequencies. Hardy-Weinberg equilibrium was assumed. The underlying pedigree structure, based on a subset of the San Antonio Family Heart Study [Mitchell et al. 1996], is representative of many large family studies. It has a slightly female-biased sex ratio (658 females: 622 males).

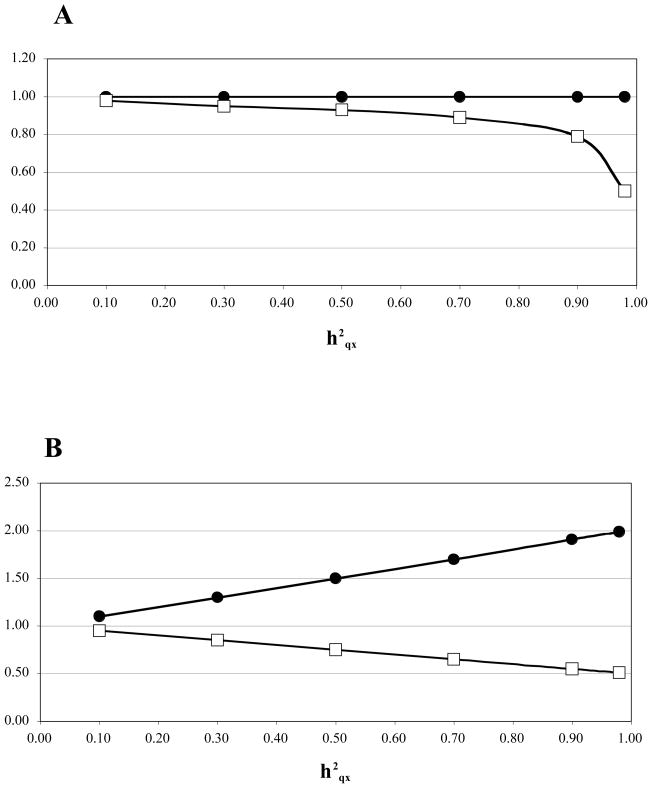
We modified the autosomal QTL simulation routine within SOLAR as follows: Female phenotypic means associated with the QTL genotypes were calculated as for an autosomal QTL across a range of heritabilities (0–70%). Males were required to inherit two copies of the same QTL allele. For a trait modeled assuming dosage compensation, the phenotypic mean associated with each male “homozygote” was set equal to the corresponding female homozygote. For a trait modeled assuming the absence of dosage compensation, the male genotype producing the lower value of the trait was given a phenotypic value equal to that of the corresponding female homozygote, while the other was set equal to the female heterozygote (Table 3). The male/female ratios of phenotypic means and variances in these simulations approached the predictions of Bulmer [1985] as the proportion of total variance due to the QTL approached unity (Figure 1).

Table 3.

Genotype-specific phenotypic means for simulated traits

	With dosage compensation			Without dosage compensation
Females:
genotype:	aa	ab	bb	aa	ab	bb
phenotype:	100-d	100	100+d	100-d	100	100+d

Males:
genotype:	a		b	a	b
phenotype:	100-d		100+d	100-d	100

Open in a new tab

Mean phenotypic effect (arbitrary units) of specified genotypes for an X-linked QTL simulated with or without dosage compensation. The deviation d was calculated for each given QTL heritability assuming a normally distributed trait, within-genotype standard deviation = 10 units, and Hardy-Weinberg equilibrium.

Panel A, male/female ratio of phenotypic means, and panel B, ratio of phenotypic variances, for a trait simulated across a range (0.1 – 0.98) of heritabilities due to an X-linked QTL and h²_r = 0. The trait was simulated either with dosage compensation for the X (closed circles) or without dosage compensation (open squares).

We ran a series of simulations (1000 replicates per experiment) to compare the power and accuracy of estimation of the effect of an X-linked QTL simulated either with or without dosage compensation. We analyzed the simulated data in two ways: assuming dosage compensation (DC; Equation 5) or assuming no dosage compensation (NDC; Equation 4, using the L coefficients from Table 2). In each replicate, the null hypothesis was a polygenic model (all additive genetic effect attributed to autosomes), estimated with separate environmental variance terms for males and females; these components were retained in the X-effect model. (Consequently, in Fig. 1 and subsequent usage, “heritability” refers to ratios of female variance components, since our covariance models use σ²_AX,ff as the point of reference. Thus, h²_x = σ²_AX,ff/(σ²_AX,ff + σ²_A + σ²_Ef), where σ²_Ef is the female environmental variance and σ²_A is the non-sex-specific autosomal additive genetic component. Similarly, h²_r is the residual (autosomal) additive genetic variance, σ²_A/(σ²_AX,ff + σ²_A + σ²_Ef)) Inclusion of sex-specific random environmental variances is desirable to accommodate possible autosomal-genotype × sex interactions, and may increase the sensitivity to detect a significant X-effect (Kent et al., in press).

Significance was tested as twice the difference in log-likelihoods of the X-effect and null model (2lnΔ); this statistic is distributed as a 1/2:1/2 mixture of χ²(df = 1) and a point mass at zero [Self & Liang 1987].

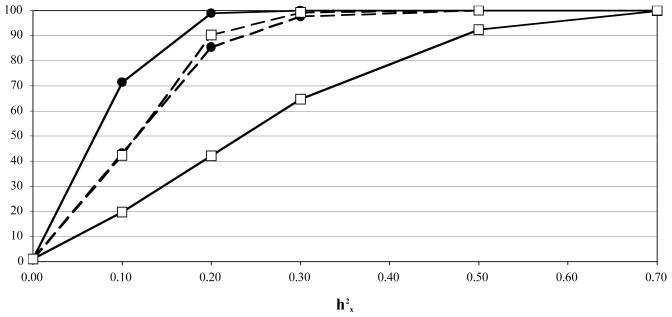
Power to detect an X effect in each scenario is summarized in Figure 2. All scenarios had very low false-positive rates (~0.3%) when the true X effect was zero. This low Type I error rate probably reflects the fact that h²_r was simulated = 0 in these experiments; in the simulations described in the next section, where h²_r was simulated = 0.2, the Type I error rate for the test of h²_x = 0 was about 4.4%. The test that assumed dosage compensation had the greatest power to detect the effect of a trait simulated with dosage compensation (model DC); however, this same method performed poorly when the trait was simulated without dosage compensation. Except for the latter case, all methods had >90% power to detect an X effect when the heritability was 50% or greater.

Power to detect an X effect estimated as percent rejection of the null hypothesis (no additive genetic effect of the X) for a trait simulated over a range (0 – 0.7) of heritabilities due to an X-linked QTL and h²_r = 0. N = 1000 replicates/experiment. Trait was simulated with dosage compensation (closed circles) or without dosage compensation (open squares). X effect was tested assuming dosage compensation (solid lines) or assuming no dosage compensation (broken lines).

Good estimates of the heritability due to the X-linked QTL were obtained when the method of analysis matched the dosage compensation state of the simulated trait (Table 4). In these cases, there was also minimal false attribution of variance to autosomal loci; that is, h²_r was close to zero. However, misspecification of the model resulted in substantial overestimation of h²_r.

Table 4.

Heritability estimates for simulated traits

Simulated with dosage compensation
Simulated h²_x:	DC estimates		NDC estimates
Simulated h²_x:	h²_x	h²_r	h²_x	h²_r
0.00	0.00	0.01	0.00	0.01
0.10	0.08	0.03	0.10	0.05
0.20	0.18	0.03	0.23	0.08
0.30	0.28	0.03	0.33	0.11
0.50	0.48	0.03	0.51	0.18
0.70	0.68	0.04	0.65	0.25

Simulated without dosage compensation
Simulated h²_x:	DC estimates		NDC estimates
Simulated h²_x:	fh²_x	h²_r	h²_x	h²_r
0.00	0.00	0.00	0.01	0.01
0.10	0.03	0.04	0.08	0.02
0.20	0.05	0.08	0.19	0.02
0.30	0.08	0.13	0.29	0.02
0.50	0.11	0.24	0.50	0.02
0.70	0.14	0.38	0.70	0.02

Open in a new tab

Point estimates are given for the h²_x and [spurious] h²_r for an X-linked trait simulated with and without dosage compensation (standard errors for all estimates are < 0.005). Heritabilities were estimated from models that used lyonization coefficients appropriate for dosage compensation (DC) or no dosage compensation (NDC). N = 1000 replicates/experiment.

A combined approach

Given the apparent utility of matching the analytical model to the dosage compensation state of the loci in question (but also acknowledging uncertainty about the extent of lyonization across the X chromosome), one possible approach is to apply DC first (since most loci are subject to lyonization), and then apply NDC if DC does not reject the null. While appealing, this approach runs the risk of increasing Type I error. We performed replicate simulations (N = at least 1000 replicates/experiment), as follows: A dataset was simulated over a range (0 – 0.5) of heritabilities due to an X-linked QTL, with a residual [autosomal] additive genetic heritability = 0.20. If DC did not reject the null, NDC was applied to the same data, and rejection of the null was recorded if rejected by either model. In preliminary experiments, this combined method had an elevated Type I error rate (~7% rejection of null) when the true X effect was zero. Consequently, the rejection threshold was lowered to a Bonferroni-corrected p < 0.025. At each replicate, the same data were then tested with a 3-parameter model (3P) that estimated the male and female X-linked variances and their correlation ρ _Xg,mf; the latter parameter was constrained to the interval {−1,1}. Lyonization coefficients were fixed = 1 (Table 2).

The covariance component for male-female relative pairs was estimated explicitly as σ_AX,ffσ_AX,mmρ _Xg,mf. This re-parameterization of the covariance term of Ekstrøm [2004] is consistent with our derivation of the lyonization coefficients above and in the Appendix (and, for technical reasons, is more conveniently estimated by SOLAR). However, as noted by Amos et al. [2001] in the context of bivariate polygenic analysis, the appropriate asymptotic distribution of the test statistic for this case is somewhat uncertain: the correlation term is undefined (and the corresponding covariance term of [Ekstrøm 2004] is necessarily zero) if either variance term is 0, leaving the precise number of degrees of freedom in doubt. We used an empirical distribution of the test statistic when the trait was simulated under the null hypothesis (i.e., no X-linked additive genetic contribution) to establish the P_0.05 critical value of the test statistic for this comparison (see Appendix).

We recorded the rate of rejection of the null hypothesis and analysis time for the two methods (DC+NDC vs. 3P). When the trait was simulated with dosage compensation, the combined DC+NDC model had comparable power even at the Bonferroni-corrected significance threshold of p < 0.025 (Table 5). When the trait was simulated without dosage compensation, the two models had comparable power at higher values of h²_x; at lower values of h²_x, the 3P model was somewhat more powerful. It should be noted, however, that the relative power of the 3P model is sensitive to the use of the empirically-derived P_0.05 critical value. As discussed in the Appendix, the distribution of the test statistic derived in [Ekstrøm 2004] is probably too conservative; if that theoretical distribution is used, the 3P model has substantially lower power than DC+NDC (data not shown). In addition, there is evidently a cost in computation time for estimating additional parameters. DC+NDC had a shorter analysis time than 3P in all cases, even when both DC and NDC were applied in the combined model, and this difference increased with increasing h²_x. Interestingly, as the magnitude of h²_x increased, a significant X effect due to the NDC trait was identified increasingly often by the DC test, with a consequent reduction in analysis time.

Table 5.

Comparison of combined 1-parameter test vs. 3-parameter test

	Test: DC+NDC				Test: 3P

Simulated h²_x	% rejection of null	% times rej. by DC	runtime, s mean (SD)	% rejection of null	runtime, s mean (SD)
0.00	4.6	54.4	32.4 (8.4)	11.3	37.3(10.1)

DC trait
0.10	60.8	94.7	23.3 (12.7)	62.2	39.3 (8.2)
0.20	96.5	98.9	14.3 (7.2)	93.5	43.1 (9.4)
0.30	100.0	100.0	11.8 (3.2)	98.5	40.4 (7.4)
0.50	100.0	100.0	11.2 (3.0)	99.7	43.4 (9.7)

NDC trait
0.10	31.8	32.1	36.5 (10.7)	57.2	42.4 (10.4)
0.20	81.6	32.3	30.3 (11.7)	92.8	39.1 (8.8)
0.30	98.3	42.9	25.9 (13.4)	100.0	39.9 (7.3)
0.50	100.0	83.6	14.3 (9.6)	100.0	38.1 (5.9)

Open in a new tab

Power to detect an X effect estimated as percent rejection of the null hypothesis (no additive genetic effect of the X) for a trait simulated over a range (0 – 0.5) of heritabilities due to an X-linked QTL and h²_r = 0.2. N = at least 1000 replicates/experiment. Trait was simulated with dosage compensation (DC) or without dosage compensation (NDC). For each replicate, X effect was estimated by a combined 1-parameter test (DC+NDC) and subsequently by a 3-parameter test (3P).

EFFECT ON DETECTION OF AN AUTOSOMAL QTL

In principle, if a phenotype is influenced by both autosomal and X-linked loci, accurate specification of the effect of the X chromosome should improve the ability to detect autosomal linkages by improving the variance-components model. A negative alternative result could be that estimation of an additional parameter could reduce the efficiency of detection. To test these alternatives, we simulated a trait (N = 1000 replicates/experiment) with residual [autosomal] heritability h²_r = 0.2, heritability due to an autosomal QTL (h²_q) over a range of 0 – 0.3, and residual X-linked heritability (h²_x) over a range of 0.1 – 0.3. The residual additive genetic deviations due to the X were simulated assuming dosage compensation in the same way as the residual autosomal effect (except that the deviations were computed as the Cholesky matrix of 2Ψ rather than 2Φ). The autosomal QTL was simulated with two alleles at equal frequencies, and a perfectly linked marker (θ = 0) was simulated with three alleles at frequencies of 0.2, 0.3, and 0.5. In each replicate, the logarithm-of-odds score (LOD) for the QTL was estimated with and without estimation (assuming dosage compensation) of h²_x. Estimation of the X effect did not reduce the evidence for the autosomal locus, and at higher values of h²_q slightly increased the mean LOD score (Table 6).

Table 6.

Effect of estimating X effect on detection of an autosomal QTL

Simulated		Observed

h²_q	h²_x	LOD mean (SE), h²_x not est.	LOD mean (SE), h²_x est.	% rej. of null, h²_x not est.	% rej. of null, h²_x est.
0.0	0.3	0.112 (0.007)	0.108 (0.007)	5.5	4.8
0.1	0.1	0.798 (0.024)	0.800 (0.024)	49.6	50.2
0.1	0.2	0.886 (0.027)	0.899 (0.027)	53.4	54.7
0.1	0.3	0.970 (0.029)	0.999 (0.030)	57.1	58.8
0.2	0.1	2.539 (0.050)	2.541 (0.050)	92.8	92.6
0.2	0.2	2.745 (0.051)	2.782 (0.051)	94.1	94.4
0.2	0.3	3.007 (0.054)	3.094 (0.054)	95.8	96.0
0.3	0.1	5.334 (0.071)	5.338 (0.071)	99.8	99.8
0.3	0.2	5.713 (0.077)	5.774 (0.077)	99.8	99.8
0.3	0.3	6.219 (0.081)	6.334 (0.082)	99.9	99.8

Open in a new tab

N = 1000 replicates/test; h²_r = 0.2 in all tests.

CONCLUSIONS

We propose an efficient method for estimating the additive genetic contribution of the X chromosome from pedigree and phenotype data alone, even when microsatellite or other marker data are not available for this chromosome. We have expanded on the algorithm of [Ekstrøm 2004] by explicitly modeling the effect of either presence or absence of eutherian-type dosage inactivation. Because both possibilities are tested, our method should be applicable to both lyonizing and nonlyonizing X-linked loci, and can be applied to organisms with alternate forms of dosage compensation. (There is one important exception: any case in which dosage compensation is not random with respect to the parental origins of the sex chromosomes. In marsupials, the paternal copy of the X chromosome is preferentially inactivated; this is a special case of imprinting and beyond the scope of this paper.)

Explicit modeling of the effect of dosage compensation allows us to employ Bulmer’s [1985] observation of a linear relationship between the variances due to the X in males and females. Consequently, we can estimate the X effect as a single parameter, rather than for each sex separately. This has an intuitive appeal as it provides a simple measure of the relative importance of X-linked loci to a trait of interest. It also offers improvements in power when dosage compensation is present – the most common case in humans and other eutherians – as well as improvement in computation time in all cases. Compared with a 3-parameter model comparable to that of [Ekstrøm 2004], computation time in our simulations was reduced, on average, by 33% for non-dosage compensated traits to 63% for dosage-compensated traits (Table 5). This improvement in processing time is negligible for a single analysis but should be quite substantial when multiple analyses are required, as in multipoint whole-genome scans requiring model estimation at hundreds of loci.

Our approach offers an efficient method for estimating the residual X-linked additive genetic variance in linkage analyses, but can also test for evidence of X-linkage even when marker data is unavailable. The magnitude of the X effect will depend on the number of QTLs influencing a trait, and what subset of these resides on the X. Thus, if at least one QTL is present on this chromosome, the power to detect an additive genetic effect of the X should be no different than the power to detect an autosomal QTL – and indeed, the sensitivity of our analysis resembles that of conventional linkage analysis (MC Mahaney, pers. commun.)

Our work incorporates estimation of separate environmental variances for males and females, to allow for autosomal-genotype × sex interaction [Kent et al. in press] – or, potentially, for differences in environment due to gender roles or other cultural factors. If it is deemed preferable to estimate the male-male, female-female, and male-female variance components separately, our work suggests some adjustments to the model of [Ekstrøm 2004]. The coefficient due to allele-sharing should be √2 rather than 2, and the distribution of the test statistic presented by Ekstrøm may be overly conservative.

Our proposed method has been implemented within the genetic analysis software package SOLAR [Almasy & Blangero 1998].

Acknowledgments

This work was supported in part by NIH/NIMH grant MH059490-06 (J. Blangero, principal investigator). We appreciate the thoughtful comments of three anonymous reviewers. Harald H. H. Göring provided helpful advice on the computation of the empirical test statistic distribution for the three-parameter model.

APPENDIX

1. HETEROGENEOUS LYONIZATION

In the case where λ_q is constant, the relationship between male and female variances for the phenotype of q is as developed above (Table 1). However, recent evidence [Carrell & Willard 2005] suggests that lyonization may be variable among human females at ~10% of X-linked loci. In this most general case, two females with the same genotype at q may express the genotype differently, influencing the correlation between their phenotypic values. For the sake of completeness, a generalized model allowing for heterogeneous lyonization is sketched below; appropriate simulation tests of the proposed model will be presented in a future report.

Let {(i,j)_k1, (i,j)_k2, … (i,j)_kn} be the set of all pairs of females in a population who share the same genotype k at q. Let (1 + λ_q,i)/2 be the mean expressivity due to lyonization at q for individual i. Then the covariance between expressed values of the genotypes in pairs of individuals can be calculated as,

{cov}_{Xgq, ff} = \sum_{k} f_{k} \sum_{i, j} ((1 + λ_{q, i}) (0.5) q_{k} - Q) ((1 + λ_{q, j}) (0.5) q_{k} - Q),

where f_k = the frequency of genotype k at q, q_k = the additive genetic contribution of that genotype in the absence of lyonization, and Q is the mean expressed value (across all genotypes) at q. Recognizing that individuals i, j are drawn with replacement from a single population of females, we can write the correlation of expressed values as,

ρ_{Xgq, ff} = [\sum_{k} f_{k} \sum_{i, j} ((1 + λ_{q, i}) (0.5) q_{k} - Q) ((1 + λ_{q, j}) (0.5) q_{k} - Q)] / {σ^{2}}_{AX, ff} .

In practice, locus-specific information (genotype means, allele frequencies, etc.) is usually unavailable. However, the locus-specific correlations may be averaged across all loci on the X-chromosome (the average correlation, of course, being influenced by the number of X-linked QTLs affecting the trait and the lyonization state at each QTL), The average correlation may be estimated as part of the covariance decomposition for female-female pairs:

{cov}_{X} (female, female) = Ψ_{ff} (2) ρ_{Xg, ff} {σ^{2}}_{AX, ff},

where the lyonization coefficients are replaced by the correlation term. Note that when λ_q is constant, ρ_Xg,ff = 1.

For male-female pairs,

ρ_{Xgq, mf} = [\sum_{k} f_{k} \sum_{i, j} ((m_{q, k} q_{k} - Q) ((1 + λ_{q, j}) (0.5) q_{k} - Q)] / {σ^{2}}_{AX, ff} .

This is a weighted correlation, in that the denominator contains σ²_AX,ff rather than σ_AX,mmσ_AX,ff; this is required since the X effect is expressed in terms of σ²_AX,ff. It also contains an X-genotype × sex interaction term m_q,k for the male partner. Unlike λ_q,i, this term can take any nonzero value (null expectation = 1), and it is constant for all males of like genotype. The expression for the correlation becomes singular when m_q,k → 0 or m_q,k → ∞ (or equivalently, when one sex-specific variance is zero while the other has a nonzero value). Thus, the model can handle moderate X-genotype × sex interaction but should not be applied to a case in which an X-linked gene is expressed only in one sex.

The resulting decomposition of the male-female covariance (again averaging across loci) is,

{cov}_{X} (male, female) = Ψ_{ff} (\sqrt 2) ρ_{Xg, mf} {σ^{2}}_{AX, ff},

which expands the interpretation of the male-female correlation term introduced in Equation 3b to include both X-genotype × sex interactions and dosage compensation.

The null models nested within this general model are:

ρ_Xg,mf = (σ_AX,mm/σ_AX,ff)√ρ_Xg,ff (m_q,k = 1 in the absence of X-genotype × sex interaction), and
ρ_Xg,ff = 1 (in the absence of heterogeneous lyonization).

Each null model has one less parameter than its more general model, which can be tested for significance with a 1 d.f. likelihood-ratio test. m_q,k is tested within its range, while ρ_Xg,ff is tested on its upper boundary. Thus the test statistic (twice the difference in loglikelihoods) for m_q,k is distributed as χ² with d.f. =1, while the test statistic for ρ_Xg,ff is distributed as a 1/2:1/2 mixture of χ²₀ and χ²₁ [Self & Liang 1987].

It follows that the male-male covariance is decomposed as,

{cov}_{X} (male, male) = Ψ_{ff} (\sqrt 2) {(ρ_{Xg, mf})}^{2} {σ^{2}}_{AX, ff} .

2. EMPIRICAL DISTRIBUTION OF TEST STATISTIC FOR MODEL 3P

In the case where the male and female X-linked variances and correlation are estimated separately, the experimental and null hypotheses are:

\begin{array}{l} H_{1} : Ω = 2 Φ {σ^{2}}_{A} + I {σ^{2}}_{E} + 2 Ψ_{ff} {σ^{2}}_{AX, ff} + Ψ_{mm} {σ^{2}}_{AX, mm} + \sqrt 2 Ψ_{mf} σ_{AX, ff} σ_{AX, mm} σ_{Xg, mf} \\ H_{0} : Ω = 2 Φ {σ^{2}}_{A} + I {σ^{2}}_{E} \end{array}

H₁ is a re-parameterization of the 3-parameter model of Ekstrøm [2004] (which uses the covariance rather than the correlation). In developing the distribution of the test statistic 2lnΔ under H₀, Ekstrøm notes that the variance terms are constrained to their respective lower boundaries (= 0), while the covariance, constrained to 0, is in the middle of its range. He therefore computes a mixture of chi-squares with 1, 2, and 3 degrees of freedom by the method of [Self & Liang 1987]. However, as noted by Amos et al. [2001] for a similar case (a bivariate polygenic model), the appropriate distribution for this case may be hard to define: the correlation in our model 3P is undefined if either variance term is 0, and the covariance in Ekstrøm’s model is necessarily 0 (and thus not independent) in these cases.

We have chosen to simulate a trait under the null hypothesis of no X-linked additive genetic contribution to obtain an empirical distribution of the test statistic for 3P. A trait with 20% of its variance due to autosomal additive genetic effects was simulated in 21,168 replicates using the same underlying pedigree structure as the other simulations in this study (an additional 12,000 replicates with h²_r = 0.4 yielded similar results, not shown). 2lnΔ was computed versus H₀ for both the 1-parameter dosage compensation model (DC) and the 3-parameter model in each replicate. The 90^th, 95^th, and 99^th percentile values of these empirical distributions, corresponding to α = 0.10, 0.05, and 0.01, are shown in Table A.1. The values for the 1-parameter model agree closely with those from the expected mixed distribution (1/2:1/2 χ²₀: χ²₁) [Self & Liang 1987]. The empirical critical values for 3P, however, are roughly equivalent to those expected from a mixed distribution for two new parameters tested on their boundaries: 1/4:1/2:1/4 χ²₀: χ²₁: χ²₂.

Table A.1.

Empirical and theoretical critical values for 2lnΔ

	1-X-linked parameter model		3-X-linked parameter model

Percentile	Empirical	Theoretical¹	Empirical	Theoretical²
0.90	1.624	1.642	2.952	2.952
0.95	2.670	2.706	4.298	4.230
0.99	5.430	5.412	7.452	7.288

Open in a new tab

1/2:1/2 χ²₀: χ²₁

1/4:1/2:1/4 χ²₀: χ²₁: χ²₂

In the above comparison of the 1- and 3-parameter models, we used the empirical critical value P_0.05 = 4.3 to test the significance of 3P. An additional consequence – since our 3P model and Ekstrøm’s model yield the same likelihoods given the same data – is that the null distribution of [Ekstrøm 2004] may be overly conservative.

References

Abecasis GR. [accessed 1/13/2005];MINX: Chromosome X Analyses. The University of Michigan Center for Statistical Genetics MERLIN Reference Sheet. No date [ http://www.sph.umich.edu/csg/abecasis/Merlin/reference.html]
Almasy L, Blangero J. Multipoint quantitative trait linkage analysis in general pedigrees. Am J Hum Genet. 1998;62:1198–1211. doi: 10.1086/301844. [DOI] [PMC free article] [PubMed] [Google Scholar]
Amos CI, de Andrade M, Zhu DK. Comparison of multivariate tests for genetic linkage. Hum Hered. 2001;51:133–144. doi: 10.1159/000053334. [DOI] [PubMed] [Google Scholar]
Amrein H. Multiple RNA-protein interactions in Drosophila dosage compensation. Genome Biol. 2000;1:reviews1030.1–reviews1030.5. doi: 10.1186/gb-2000-1-6-reviews1030. [DOI] [PMC free article] [PubMed] [Google Scholar]
Bulmer MG. The Mathematical Theory of Quantitative Genetics. New York: Oxford University Press; 1985. [Google Scholar]
Carrel L, Willard HF. X-inactivation profile reveals extensive variability in X-linked gene expression in females. Nature. 2005;434:400–404. doi: 10.1038/nature03479. [DOI] [PubMed] [Google Scholar]
Cordell HJ, Kawaguchi Y, Todd JA, Farrall M. An extension of the Maximum Lod Score method to X-linked loci. Ann Hum Genet. 1995;59:435–449. doi: 10.1111/j.1469-1809.1995.tb00761.x. [DOI] [PubMed] [Google Scholar]
Ekstrøm CT. Multipoint linkage analysis of quantitative traits on sex-chromosomes. Genet Epidemiol. 2004;26:218–230. doi: 10.1002/gepi.10310. [DOI] [PubMed] [Google Scholar]
Kent JW, Jr, Lease LR, Mahaney MC, Dyer TD, Almasy L, Blangero J. X chromosome effects and their interactions with mitochondrial effects. doi: 10.1186/1471-2156-6-S1-S157. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
Grossman M, Eisen EJ. Inbreeding, coancestry, and covariance between relatives for X-chromosomal loci. J Hered. 1989;80:137–142. doi: 10.1093/oxfordjournals.jhered.a110812. [DOI] [PubMed] [Google Scholar]
Lyon MF. Gene action in the X chromosome of the mouse (Mus musculus L.) Nature. 1961;190:372–373. doi: 10.1038/190372a0. [DOI] [PubMed] [Google Scholar]
Lynch M, Walsh B. Genetics and Analysis of Quantitative Traits. Sunderland, MA: Sinauer Associates, Inc; 1998. [Google Scholar]
Mitchell BD, Kammerer CM, Blangero J, Mahaney MC, Rainwater DL, Dyke B, Hixson JE, Henkel RD, Sharp M, Comuzzie AG, VandeBerg JL, Stern MP, MacCluer JW. Genetic and environmental contributions to cardiovascular risk factors in Mexican Americans: the San Antonio Family Heart Study. Circulation. 1996;94:2159–2170. doi: 10.1161/01.cir.94.9.2159. [DOI] [PubMed] [Google Scholar]
Pérez-Enciso M, Clop A, Folch JM, Sánchez A, Oliver MA, Óvilo C, Barragán C, Varona L, Noguerra JL. Exploring alternative models for sex-linked quantitative trait loci in outbred populations: Application to an Iberian × Landrace pig intercross. Genetics. 2002;161:1625–1632. doi: 10.1093/genetics/161.4.1625. [DOI] [PMC free article] [PubMed] [Google Scholar]
Self SG, Liang KY. Asymptotic properties of maximum likelihood estimators and likelihood ratio tests under nonstandard conditions. J Am Stat Assoc. 1987;82:605–610. [Google Scholar]
Stram DO, Lee JW. Variance components testing in the longitudinal effects mixed model. Biometrics. 1994;50:1171–1177. [PubMed] [Google Scholar]

[R1] Abecasis GR. [accessed 1/13/2005];MINX: Chromosome X Analyses. The University of Michigan Center for Statistical Genetics MERLIN Reference Sheet. No date [ http://www.sph.umich.edu/csg/abecasis/Merlin/reference.html]

[R2] Almasy L, Blangero J. Multipoint quantitative trait linkage analysis in general pedigrees. Am J Hum Genet. 1998;62:1198–1211. doi: 10.1086/301844. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R3] Amos CI, de Andrade M, Zhu DK. Comparison of multivariate tests for genetic linkage. Hum Hered. 2001;51:133–144. doi: 10.1159/000053334. [DOI] [PubMed] [Google Scholar]

[R4] Amrein H. Multiple RNA-protein interactions in Drosophila dosage compensation. Genome Biol. 2000;1:reviews1030.1–reviews1030.5. doi: 10.1186/gb-2000-1-6-reviews1030. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R5] Bulmer MG. The Mathematical Theory of Quantitative Genetics. New York: Oxford University Press; 1985. [Google Scholar]

[R6] Carrel L, Willard HF. X-inactivation profile reveals extensive variability in X-linked gene expression in females. Nature. 2005;434:400–404. doi: 10.1038/nature03479. [DOI] [PubMed] [Google Scholar]

[R7] Cordell HJ, Kawaguchi Y, Todd JA, Farrall M. An extension of the Maximum Lod Score method to X-linked loci. Ann Hum Genet. 1995;59:435–449. doi: 10.1111/j.1469-1809.1995.tb00761.x. [DOI] [PubMed] [Google Scholar]

[R8] Ekstrøm CT. Multipoint linkage analysis of quantitative traits on sex-chromosomes. Genet Epidemiol. 2004;26:218–230. doi: 10.1002/gepi.10310. [DOI] [PubMed] [Google Scholar]

[R9] Kent JW, Jr, Lease LR, Mahaney MC, Dyer TD, Almasy L, Blangero J. X chromosome effects and their interactions with mitochondrial effects. doi: 10.1186/1471-2156-6-S1-S157. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R10] Grossman M, Eisen EJ. Inbreeding, coancestry, and covariance between relatives for X-chromosomal loci. J Hered. 1989;80:137–142. doi: 10.1093/oxfordjournals.jhered.a110812. [DOI] [PubMed] [Google Scholar]

[R11] Lyon MF. Gene action in the X chromosome of the mouse (Mus musculus L.) Nature. 1961;190:372–373. doi: 10.1038/190372a0. [DOI] [PubMed] [Google Scholar]

[R12] Lynch M, Walsh B. Genetics and Analysis of Quantitative Traits. Sunderland, MA: Sinauer Associates, Inc; 1998. [Google Scholar]

[R13] Mitchell BD, Kammerer CM, Blangero J, Mahaney MC, Rainwater DL, Dyke B, Hixson JE, Henkel RD, Sharp M, Comuzzie AG, VandeBerg JL, Stern MP, MacCluer JW. Genetic and environmental contributions to cardiovascular risk factors in Mexican Americans: the San Antonio Family Heart Study. Circulation. 1996;94:2159–2170. doi: 10.1161/01.cir.94.9.2159. [DOI] [PubMed] [Google Scholar]

[R14] Pérez-Enciso M, Clop A, Folch JM, Sánchez A, Oliver MA, Óvilo C, Barragán C, Varona L, Noguerra JL. Exploring alternative models for sex-linked quantitative trait loci in outbred populations: Application to an Iberian × Landrace pig intercross. Genetics. 2002;161:1625–1632. doi: 10.1093/genetics/161.4.1625. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R15] Self SG, Liang KY. Asymptotic properties of maximum likelihood estimators and likelihood ratio tests under nonstandard conditions. J Am Stat Assoc. 1987;82:605–610. [Google Scholar]

[R16] Stram DO, Lee JW. Variance components testing in the longitudinal effects mixed model. Biometrics. 1994;50:1171–1177. [PubMed] [Google Scholar]

PERMALINK

Estimating the additive genetic effect of the X chromosome

Jack W Kent Jr

Thomas D Dyer

John Blangero

Abstract

INTRODUCTION

THEORETICAL BACKGROUND

ALLELE SHARING

Allele sharing: female-female pairs

Allele sharing: male-male pairs

Allele sharing: male-female pairs

DOSAGE

Table 1.

No dosage compensation

Dosage compensation

Table 2.

SIMULATION EXPERIMENTS

POWER AND ACCURACY

Table 3.

Figure 1. Male/female ratios of means and variances for a simulated trait.

Figure 2. Power to detect an effect of the X chromosome.

Table 4.

A combined approach

Table 5.

EFFECT ON DETECTION OF AN AUTOSOMAL QTL

Table 6.

CONCLUSIONS

Acknowledgments

APPENDIX

1. HETEROGENEOUS LYONIZATION

2. EMPIRICAL DISTRIBUTION OF TEST STATISTIC FOR MODEL 3P

Table A.1.

References

ACTIONS

PERMALINK

RESOURCES

Cite

Add to Collections

PERMALINK

Estimating the additive genetic effect of the X chromosome

Jack W Kent Jr

Thomas D Dyer

John Blangero

Abstract

INTRODUCTION

THEORETICAL BACKGROUND

ALLELE SHARING

Allele sharing: female-female pairs

Allele sharing: male-male pairs

Allele sharing: male-female pairs

DOSAGE

Table 1.

No dosage compensation

Dosage compensation

Table 2.

SIMULATION EXPERIMENTS

POWER AND ACCURACY

Table 3.

Figure 1. Male/female ratios of means and variances for a simulated trait.

Figure 2. Power to detect an effect of the X chromosome.

Table 4.

A combined approach

Table 5.

EFFECT ON DETECTION OF AN AUTOSOMAL QTL

Table 6.

CONCLUSIONS

Acknowledgments

APPENDIX

1. HETEROGENEOUS LYONIZATION

2. EMPIRICAL DISTRIBUTION OF TEST STATISTIC FOR MODEL 3P

Table A.1.

References

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases