Abstract
Microarray expression studies suffer from the problem of batch effects and other unwanted variation. Many methods have been proposed to adjust microarray data to mitigate the problems of unwanted variation. Several of these methods rely on factor analysis to infer the unwanted variation from the data. A central problem with this approach is the difficulty in discerning the unwanted variation from the biological variation that is of interest to the researcher. We present a new method, intended for use in differential expression studies, that attempts to overcome this problem by restricting the factor analysis to negative control genes. Negative control genes are genes known a priori not to be differentially expressed with respect to the biological factor of interest. Variation in the expression levels of these genes can therefore be assumed to be unwanted variation. We name this method “Remove Unwanted Variation, 2-step” (RUV-2). We discuss various techniques for assessing the performance of an adjustment method and compare the performance of RUV-2 with that of other commonly used adjustment methods such as Combat and Surrogate Variable Analysis (SVA). We present several example studies, each concerning genes differentially expressed with respect to gender in the brain and find that RUV-2 performs as well or better than other methods. Finally, we discuss the possibility of adapting RUV-2 for use in studies not concerned with differential expression and conclude that there may be promise but substantial challenges remain.
Keywords: Batch effect, Control gene, Differential expression, Factor analysis, SVA, Unwanted variation
1. INTRODUCTION
Microarray expression studies are plagued by the problem of unwanted variation. In addition to the biological factor(s) that are of interest to the researcher, other factors, both technical and biological, influence observed gene expression levels. A typical example is a batch effect, which can occur when some samples are processed differently than others. For example, significant batch effects may arise when some samples are processed in a different laboratory, by a different technician, or even just on a different day (Leek and others, 2010), (Scherer, 2009). Though infamous, batch effects are not the only source of unwanted variation. Other sources of unwanted technical variation can occur within batches and be just as problematic. Moreover, unwanted biological variation can be a problem as well.
Several methods have been proposed to adjust microarray data to mitigate the problems of unwanted variation. Despite substantial progress, there is still no “silver bullet” and perhaps never will be. As such, there remains a need for both improved methods and ways to evaluate the relative strengths of existing methods. Our primary goal in this paper is to contribute a new method based on control genes and to encourage the use of control genes more generally. A secondary goal is to review some techniques we have found to be useful for comparing the performance of different adjustment methods. Finally, a less explicit though still important theme of this paper is that we believe that the most appropriate way to deal with unwanted variation depends critically on the final goal of the analysis—for example, differential expression (DE), classification, or clustering.
In what remains of the introduction, we present a brief summary of existing methods to adjust for unwanted variation followed by a brief summary of our own method. In Section 2, we discuss techniques to compare the performance of these methods. In Section 3 and Sections A, B, and C of the supplementary material available at Biostatistics online, we provide examples. Details of our method follow in Section D of the supplementary material available at Biostatistics online.
Methods to adjust for unwanted variation can be divided into 2 broad categories. In the first category are methods that can be used quite generally and provide a global adjustment. An example would be quantile normalization (QN), which is generally regarded as a self-contained step and plays no role in the downstream analysis of the data. In the second category are application specific methods that incorporate the batch adjustment directly into the main analysis of interest. For example, in a DE study, batch effects may be handled by explicitly adding “batch terms” to a linear model. The method we present in this paper falls into this second category, where the application is DE.
Most of the progress that has been made with application-specific methods has been for DE studies and has made use of linear models. Some methods presume the batches to be known; in this case, the effects of the known batches can be directly modeled. Combat is one such successful and well-known method; in particular, Combat has been shown to work well with small data sets (Johnson and others, 2007). While Combat and other similar methods can be quite successful, they also have limitations. One limitation is that the batches must be known; in many situations, this is not the case. Another limitation is that even when batch information is known, it may give only a partial hint of the underlying unwanted variation. This is because it is not batch itself that causes batch effects but rather some other physical variable that is correlated with batch. As a simple example, suppose changes in the temperature of the scanner lead to unwanted variation. Consider a study in which some samples are processed at lab A and the rest at lab B. If the scanner at lab A generally runs cooler than the scanner at lab B, this will lead to a “batch effect”. However, if the temperature at lab A is itself quite variable, this will lead to additional within-batch unwanted variation that is not captured in the simple batch model. Section E of the supplementary material available at Biostatistics online provides a brief example from the Microarray Quality Control study of substantial within-batch unwanted variation.
Other linear model-based methods presume the sources of the unwanted variation to be unknown. These methods attempt to infer the unwanted variation from the data and then adjust for it. Often, this is accomplished via some form of factor analysis; several factors believed to capture the unwanted variation are computed and then incorporated into the model in just the same way known confounders are incorporated. In the simplest approach, factors are computed directly from the observed expression matrix by means of a singular value decomposition (SVD) or some other factor analysis technique. This is often successful in practice but can be dangerous—if the biological effect of interest is large, it too will be picked up by the factor analysis and removed along with the unwanted variation. In other words, if one adjusts for unwanted variation by removing the first several principal components from the data, one may very well throw out the baby with the bathwater. This problem has been acknowledged, and several attempts have been made to avoid it. One of the most well-known methods that directly address this problem is SVA (Leek and Storey, 2007), (Leek and Storey, 2008). Other methods of potential interest include Kang and others (2010), Kang, Ye, and others (2008), Kang, Zaitlen, and others (2008), Listgarten and others (2010), Mecham and others (2010), Price and others (2006), Stegle and others (2008) and Yu and others (2005). Some of the first uses of factor analysis to adjust for unwanted variation can be found in Alter and others (2000) and Nielsen and others (2002), although in these examples, there is no explicit linear model.
Our strategy is to use control genes. Negative control genes are genes whose expression levels are known a priori to be truly unassociated with the biological factor of interest. Conversely, positive control genes are genes whose expression levels are known a priori to be truly associated with the factor of interest. For example, if the factor of interest is the presence or absence of ovarian cancer, CyclinE would be a positive control. Negative control genes are in general harder to identify with certainty. So-called housekeeping (HK) genes are often good candidates but not always. Another example of negative controls are the spike-in controls found on many microarray platforms. Two notes on terminology: (i) In other contexts (e.g., Illumina), the term “negative controls” is used to denote probes that should never be expressed in any sample. This usage of the term “negative controls” is different than ours and should not be confused. (ii) When we refer generally to “negative control genes” or simply “control genes,” we often use the term to include the spike-in control probesets as well, despite the fact they are not genes.
Negative control genes are used routinely to detect the presence of unwanted variation. However, as we will see, they can also be used to adjust for unwanted variation. We are not the first to make this observation. In particular, Lucas and others (2006) have used negative control genes to adjust for unwanted variation. However, we do not believe the importance of control genes in adjusting for unwanted variation is widely recognized. Indeed, we believe the roll of control genes is of central importance.
Our method is to perform factor analysis on just the negative control genes and incorporate the resulting factors into a linear regression model. The idea is that since the negative control genes are known to be unassociated with the factor of interest, there is no danger in picking up any of the relevant biology in the factor analysis step and thus no danger of throwing out the baby with the bathwater. We name this method RUV-2, for “Remove Unwanted Variation, 2-step”—the 2 steps are the factor analysis and the regression.
2. CRITERIA FOR A GOOD ADJUSTMENT
Techniques to evaluate the quality of an adjustment are in many ways as important as the adjustment method itself. The statistical models on which adjustment methods are based are artificial. The models are most useful as sources of inspiration for improved methods; they are substantially less useful in proving the worth of a method. In the end, an adjustment method must prove its value by working in practice.
The question thus arises of how to know whether an adjustment is helping or hurting. This is not trivial. In many cases, evidence that seems to suggest an adjustment method is helping (or hurting) is actually ambiguous. As an example, consider a DE study and consider assessing the quality of the study by counting the number of genes “discovered” at a certain false discovery rate (FDR) threshold. If the unwanted variation is roughly orthogonal to the factor of interest, the unwanted variation will manifest itself as additional “noise” that obscures any true association between the factor of interest and gene expression levels. An effective adjustment method would therefore increase the number of discovered genes. On the other hand, if the unwanted variation is correlated with the factor of interest, this will introduce spurious associations between the factor of interest and gene expression levels. An effective adjustment method would therefore decrease the number of discovered genes. As a second example, consider a classification study in which a researcher wants to classify tumor samples into one of several tumor subtypes. Suppose the researcher wants to test her classification algorithm on a set of tumor samples in which the subtype is known, and she does her test once in combination with a method that adjusts for unwanted variation and once without. Suppose the rate of misclassification is higher when the adjustment method is used. This would seem to suggest that the adjustment method is hurting. However, it is equally possible that the adjustment method is working—if the tumor subtypes were processed in batches, the resulting batch effects could artificially help the classifier.
In the following few sections, we review some techniques that we have found to be useful in evaluating the quality of an adjustment. Only the first technique provides a (nearly) unambiguous assessment of the quality of an adjustment. However, its applicability is limited. The other 2 techniques are also very informative, if not entirely definitive, and can be used in a wider variety of situations.
2.1. Control genes / gene rankings
Positive control genes can be used for quality assessment in DE studies. After computing p-values for each gene, we can rank the genes in order of increasing p-value. Positive controls should be toward the top of this list. We can therefore use the number of positive controls ranked in, for example, the top 50 genes as a quality metric. If an adjustment method substantially increases the number of top-ranked positive controls, we have reason to believe the method is effective.
Note that we use the ranks of the p-values and not the p-values themselves. This is for reasons discussed above; a good adjustment may increase or decrease the positive controls' p-values depending on the nature of the unwanted variation. Ranking helps to resolve the ambiguity.
While ranking p-values is generally preferred, there remain some situations in which it may be better to look at the p-values themselves. An example might be when only a very small number of positive controls are available and their rankings do not change substantially after the adjustment. In this case, one might wish to examine the p-values of both positive and negative controls. If the p-values of the positive controls substantially decrease—and the p-values of the negative controls do not—this would suggest that the adjustment helps. On the other hand, if the p-values of the negative controls decrease as well, this may simply suggest an artifact of the adjustment method. Likewise, if the p-values of the positive and negative controls both increase, the result is ambiguous, but the technique described in Section 2.2 might help clarify matters.
Some caution is required when using negative controls to assess the quality of an adjustment. After all, if the method of adjustment is to fit and remove variation characteristic of a set of negative controls, then observing that the adjustment diminishes the association between the factor of interest and the negative controls is simply to be expected. A better strategy would be to use 2 different sets of negative controls—one to make the adjustment and one to use in assessing the quality of the adjustment. Preferably, the 2 sets of negative controls will be different from each other in some important way. For example, we might use spike-in controls to make an adjustment, and HK genes to assess the quality of the adjustment or vice versa.
2.2. The p-value distribution
Consider a DE study in which the factor of interest is assumed to be associated with the expression level of only a fraction of genes. The distribution of the p-values for the genes that are unassociated with the factor of interest would ideally be uniformly distributed over the unit interval, whereas the p-values for the genes that are associated with the factor of the interest will ideally be nearly zero. Thus, a histogram of the p-values will ideally be nearly uniform, with a spike near zero. In practice, however, this is uncommon, as unwanted variation tends to introduce dependence across measured gene expression levels. Since adjusting for unwanted variation should remove this dependence, we might expect a good adjustment to result in p-value histograms closer to the “ideal.” Note that this observation is not new; in particular, Leek and Storey (2007), Leek and Storey (2008) have shown it to be of considerable value.
2.3. RLE plots
Relative log expression (RLE) plots are boxplots that can be used to determine the overall quality of a data set and, in particular, identify bad chips. Consider a set of m chips, each with n genes and denote the log expression level of the jth gene on the ith chip by . Denote the jth column of the matrix by . For each of the n genes, we can calculate , the median (over the m chips) log expression level. For each gene on each chip, we can then calculate , the deviation from the median gene expression level. For each chip, we can then produce a boxplot of its n deviations. In most cases, if the chip is of good quality, this boxplot will be centered around zero and its width (interquartile range) will be around 0.2 or less. Examples of RLE plots can be found in Figure 1 (discussed more fully later). More information about RLE plots can be found in Bolstad and others (2005) and Brettschneider and others (2008).
Fig 1.
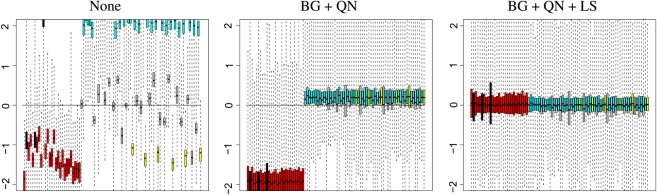
Gender study RLE plots at different stages of preprocessing. From left to right: No preprocessing; BG/QN done separately for each platform type; BG/QN followed by a final LS across all chips. Coloring: red—site A, HG-U95A; yellow—site A, HG-U95Av2; black—site B, HG-U95A; gray—site B, HG-U95Av2; and cyan—site C, HG-U95Av2. Note: The scale on the y-axis is different for these RLE plots than for all other RLE plots in this paper.
3. EXAMPLES
We present 4 examples, 3 of which are in the supplementary material available at Biostatistics online. In 3 of the examples, we discover genes that are differentially expressed in the brain with respect to gender. The final example involves clustering tumors of known types. We chose these examples because “truth” is in some sense known.
We chose DE with respect to gender because it provides us with a clear set of potential positive controls—in this case, genes that are located on the X and Y chromosomes. Treating X and Y genes as positive controls and using our technique of counting the number of top-ranked positive controls (Section 2.1) allows us to compare the performance of various adjustment methods. We chose the brain because of its comparatively complex biology—a very large fraction of genes are expressed in the brain—and the availability of several interesting data sets. Indeed, our lead example is ideal, as the study was originally intended to discover differentially expressed genes in the brain, and the data exhibit profound batch effects.
In all our examples, a few practical issues must be considered. The first is what preprocessing should be done. Microarray data routinely go through 3 stages of preprocessing—background correction (BG), normalization, and summarization. Several algorithms have been proposed for each of these steps. For simplicity, we limit ourselves to the “standard” sequence of algorithms used in Robust Multichip Average (Bolstad and others, 2003), (Irizarry, Bolstad, and others, 2003), (Irizarry, Hobbs, and others, 2003). The preprocessing steps—particularly, the QN—are nonlinear, and it is not clear how they might interact with the adjustment methods. Thus, we repeat many of our analyses omitting one or more stages of preprocessing in order to see what happens.
The second issue to consider is which negative controls to use. To effectively adjust for batch effects, our negative controls must both (i) be uninfluenced by the factor(s) of interest and (ii) be influenced by the unwanted factors. In other words, they must actually be negative controls and their expression levels must accurately reflect the unwanted variation. We focus on 2 classes of possible negative controls—HK genes and spike-in controls. The HK genes we use are those discovered in Eisenberg and Levanon (2003). A good discussion of both spike-in controls and HK genes can be found in Lippa and others (2010).
3.1. Gender study
Vawter and others (2004) conducted a study to find genes differentially expressed in the brain with respect to gender. Samples were taken postmortem from the brains of 10 individuals, 5 men and 5 women. Three samples were taken from each individual—one from the anterior cingulate cortex, one from the dorsolateral prefrontal cortex, and one from cortex of the cerebellar hemisphere. One aliquot of each sample was sent to each of 3 laboratories for analysis. The analyses were done using either Affymetrix HG-U95A or Affymetrix HG-U95Av2. We are unaware of how the decision was made to use which platform for which analysis. One of the laboratories used only HG-U95Av2. Note that there should have been chips total. However, 6 of the combinations were missing, leaving us with 84. Moreover, 3 of the remaining 86 combinations were replicated, so in fact, there is data for 87 chips. We omitted the replicates in our analysis. Data are available on Gene Expression Omnibus (GSE2164).
The HG-U95A platform has 12 626 probesets, and the HGu95Av2 platform has 12 625 probesets. We identified 12 600 probesets that were shared between the 2 platforms. We did not, however, attempt to map individual probes from one platform to the other. Since preprocessing (BG, QN, and summarization) requires probe level data, we did these preprocessing steps for each platform separately. As a result, large differences remained between the different platform types even after the standard preprocessing. The raw HG-U95Av2 expression values are generally larger than their HG-U95A analogs by about a factor of 4, so the expression values for the HG-U95Av2 expression values are generally greater than those of the HG-U95A by about 2. We therefore added an additional preprocessing step after summarization; we performed a location/scale (LS) adjustment in which we linearly rescaled the data so that each chip had the same mean and standard deviation. See Figure 1 for RLE plots at different stages of preprocessing—no preprocessing; BG and QN only (BG + QN); BG, QN, and LS (BG + QN + LS). It is important to note that the vertical scale of the RLE plots in Figure 1 is substantially different than that of all other RLE plots in this paper.
The unwanted variation apparent in Figure 1 is striking. Even ignoring the differences between chip types, observed expression levels differ by up to an order of magnitude between laboratories. There is substantial within-laboratory unwanted variation as well. The average observed expression level varies from chip to chip by roughly a factor of 2 within laboratories. As a result, discovering genes that are differentially expressed with respect to gender is nearly impossible without adjusting for the unwanted variation. On unpreprocessed, unadjusted data, every gene has an FDR-adjusted p-value of approximately 1, and only 7 of the top 60 genes come from the X or Y chromosome. The preprocessing helps; after preprocessing (but no other adjustments), 15 of the top 60 genes are from the X or Y chromosome, and 8 of these have FDR-adjusted p-values that are significant at the 0.05 level. Even after preprocessing, however, substantial unwanted variation persists as can be seen in RLE, p-value, and scree plots.
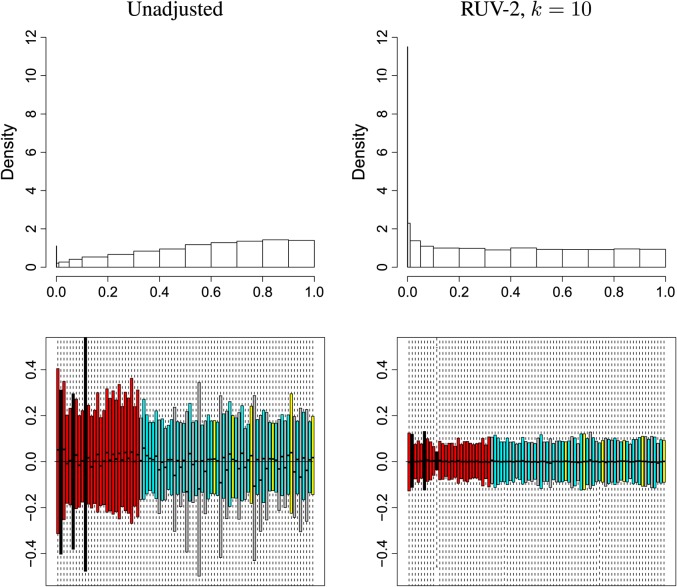
A critical step in RUV-2 is determining the number k of factors to remove. In general, this is difficult, and there is no clear way to determine k. We recommend pursuing several approaches and exercising judgment. We have found RLE plots and p-value histograms to be helpful. In addition, if any positive controls are known, these should be used as well. To make use of RLE plots and p-value plots, it is necessary to complete the analysis for several values of k, and then examine the plots to evaluate the quality of the results. Several such plots can be found in the supplementary material available at Biostatistics online (Figures 11 and 12); based on these plots, we choose a k of 10 (see Figure 2).
Fig 2.
Gender study p-value histograms and RLE plots before and after adjustment. Histogram breakpoints are at 0.001, 0.01, 0.05 and 0.1, 0.2, 0.3, etc. Data were fully preprocessed (BG + QN + LS). The factors were computed by SVD on the HK genes. P-values were computed using Limma.
Several questions remain: Which factor analysis method is best? To what extent does performance depend on k? Does RUV-2 work well in combination with Limma? Do we achieve a better adjustment using HK genes or spike-in controls? How does RUV-2 compare to other adjustment methods such as standard linear regression, Combat, or SVA? How does preprocessing affect performance? We address each of these questions in turn.
Given the central role of factor analysis in RUV-2, one might expect that the choice of factor analysis method is quite important. In our examples, this turns out not to be the case. We repeated our analysis with 3 different factor analysis methods. The first is the SVD. The second is an expectation-maximization (EM) algorithm based on a relatively simple probabilistic model that allows for gene-specific variances in the error term. The model and the algorithm are described in Section 12.2.4 of Bishop (2006). The implementation of the algorithm is our own. The third method is a “robust” method described in Hubert and others (2005) and implemented in the PcaHubert function of the R package rrcov. RLE plots after adjustment looked nearly identical for all 3 factor analysis methods. P-value histograms were also remarkably similar. More convincingly, the number of top-ranked X/Y genes is roughly the same for all 3 methods, as we discuss below.
The choice of k turns out to be critical to the performance of RUV-2. This can be seen in RLE plots and p-value histograms (figures are in the SM) but can be seen most dramatically by counting the number of top-ranked X/Y genes at different values of k. We repeated the analysis for all possible values of k. At first, the number of top-ranked X/Y genes increases with increasing k, as additional unwanted variation is removed. After a certain point, however, increasing k only degrades performance, as adding additional factors to the model simply increases variance (see Figure 3). Note from Figure 3 that although the performance of RUV-2 depends critically on the choice of k, the region over which RUV-2 performs well is fairly large. This is important because it implies, in this example at least, that while RLE plots and p-value histograms may not lead us to the single best choice of k, they can at least lead us to a good one. Finally, note also from Figure 3 that the choice of factor analysis method does not greatly impact the results.
Fig 3.
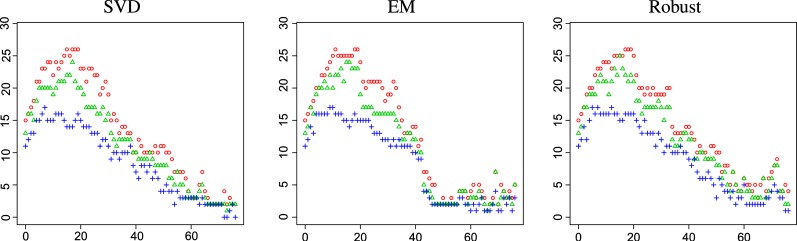
Comparison of performance of different factor analysis methods in the gender study. The number of X/Y genes discovered is plotted as a function of k. Genes were ranked by p-value; results are shown for the number of X/Y genes ranked in the top 20 (plus), top 40 (triangle), and top 60 (circle). corresponds to no adjustment. Data were preprocessed (BG + NM + LS). Principal components were computed using the HK genes. P-values were computed using Limma.
It is common to analyze microarray data using the Limma package in Bioconductor (Smyth, 2004). Limma uses empirical Bayes methods to improve the estimates of the variances of individual genes. Since adjusting with RUV-2 or any other method can substantially affect the general structure of the residuals, we checked to ensure that RUV-2 and Limma work well together. To accomplish this, we completed our analysis once using Limma and once using “ordinary” regression. We did not note any substantial difference in performance (as assessed using RLE plots, p-value histograms, and counts of top-ranked X/Y genes) between the 2 methods. Details can be found in the supplementary material available at Biostatistics online.
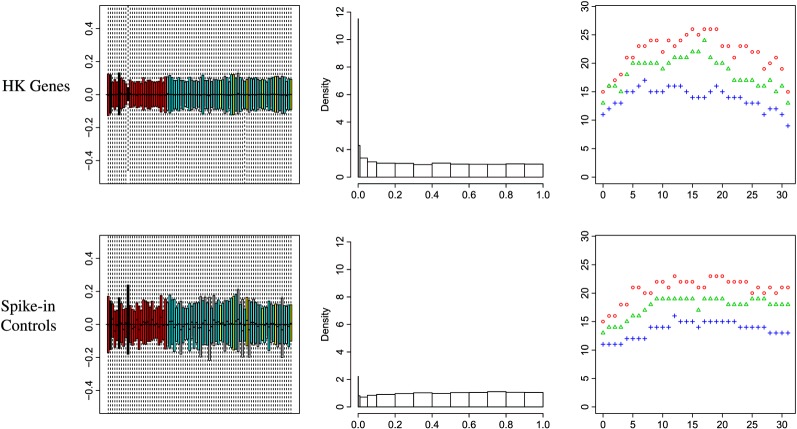
The performance of RUV-2 depends greatly on the choice of negative controls. Adjustments based on both the HK genes and the Affymetrix spike-in controls improved performance relative to unadjusted data, however, the performance increase using HK genes was substantially better (see Figure 4). We believe HK genes may outperform the spike-ins in this example for 3 reasons. Firstly, HK genes may be able to capture unwanted biological variation, whereas spike-in controls can only capture unwanted technical variation. Secondly, even with regards to technical variation, HK genes may be more “representative” than spike-ins. For example, HK genes may capture unwanted variation introduced during sample collection, whereas spike-ins would not. Conversely, spike-ins may exhibit some unique variation related to their own administration. Lastly, there are far more HK genes than there are spike-in controls. There are 799 probesets that correspond to one of the HK genes in Eisenberg and Levanon (2003). However, there are only 33 probesets corresponding to spike-in controls.
Figure 4.
Comparison of results for HK genes and Affymentrix spike-in controls in the gender study. For the RLE plots and p-value histograms, . Factors were computed by SVD. P-values were computed using Limma. Note that there are only 33 spike-in controls, so adjustments with are undefined for the spike-in case. We truncate
Finally, we wish to compare the performance of RUV-2 to that of other adjustment methods and investigate the effects of preprocessing. We use the number of top-ranked X/Y genes as our basis for comparison and present the results in Table 1. Several observations merit mention. RUV-2 outperforms Combat and ordinary regression in all cases, and SVA outperforms them in several cases as well. This is despite the fact that Combat and ordinary regression explicitly model known batches (lab/chip type), whereas RUV-2 and SVA infer the unwanted variation from the data. Moreover, it seems that even when we do explicitly model known batches with RUV-2 by including a “Z” term in the model (see Section D of supplementary material available at Biostatistics online), there is no substantial increase in performance. Another observation is that the level of preprocessing does not seem to matter for the SVD and EM (but not robust) variants of RUV-2, matters slightly for Combat, and matters greatly for the other methods. This seems to suggest that RUV-2 is relatively robust. Moreover, it seems to suggest that, at least in some cases, RUV-2 can obviate the preprocessing. While this is of little immediate value in the current example, it may be useful in situations where there is concern that the nonlinearities introduced by preprocessing are problematic. For example, if a very large number of genes are differentially expressed with respect to the factor of interest, the nonlinearities in the QN may induce an artificial correlation between the negative control genes and the factor of interest. This would violate the assumptions of RUV-2. In such a situation, it may be best to skip the QN. In any case, we regard the fact that RUV-2 performs well even without preprocessing as quite encouraging; after all, the unpreprocessed data are extremely noisy.
Table 1.
Summary of performance of different methods in the gender study. The number of X/Y genes found in the top 20/40/60 is shown for different levels of preprocessing (None; BG, QN; BG, QN, LS), different methods of computing p-values (standard and Limma), and different methods of adjustment (none, standard regression, SVA, Combat, and RUV-2). In the case of RUV-2, results are given for different methods of factor analysis (SVD, EM, robust). Additionally, we present results for models that include an explicit Z term, where Z is a matrix of dummy variables corresponding to site (A, B, or C) and chip type (HGU-95A or HGU-95Av2). For all RUV-2 methods, k = 10 and HK genes were used as negative controls. Results for the two-step variant of SVA are not available in some cases because the function exited with an error. The highest number in each column is shown in bold. A brief comment: Note that more X/Y genes are found when we include a Z term in the “Top 40” and “Top 60” cases. This should be interpreted with caution. Including a Z term results in adjusting for 3 additional factors; similar increases in performance can be seen by dropping the Z term and increasing k to 13 (see Figure 3)
| Top 20 |
Top 40 |
Top 60 |
||||||||||||||||
| No |
No |
No |
||||||||||||||||
| preprocessing |
BG,QN |
BG,QN,LS |
preprocessing |
BG,QN |
BG,QN,LS |
preprocessing |
BG,QN |
BG,QN,LS |
||||||||||
| Std | Lim | Std | Lim | Std | Lim | Std | Lim | Std | Lim | Std | Lim | Std | Lim | Std | Lim | Std | Lim | |
| No adjustment | 7 | 6 | 9 | 9 | 11 | 11 | 7 | 7 | 12 | 12 | 13 | 13 | 7 | 7 | 14 | 13 | 15 | 15 |
| Regression (Z) | 5 | 5 | 14 | 13 | 12 | 12 | 6 | 6 | 15 | 15 | 16 | 15 | 7 | 7 | 16 | 16 | 16 | 17 |
| SVA (IRW) | 5 | 6 | 12 | 11 | 14 | 14 | 6 | 7 | 13 | 14 | 17 | 16 | 7 | 8 | 15 | 14 | 19 | 19 |
| SVA (Two-step) | NA | NA | NA | NA | 16 | 16 | NA | NA | NA | NA | 21 | 20 | NA | NA | NA | NA | 23 | 22 |
| Combat | 11 | 11 | 13 | 13 | 12 | 13 | 14 | 12 | 17 | 17 | 17 | 17 | 16 | 15 | 18 | 18 | 19 | 19 |
| RUV-2–SVD (k = 10) | 15 | 15 | 15 | 15 | 15 | 15 | 22 | 22 | 21 | 19 | 20 | 19 | 24 | 23 | 22 | 21 | 22 | 22 |
| RUV-2–SVD (k = 10), w/Z | 14 | 14 | 15 | 15 | 16 | 15 | 23 | 23 | 22 | 22 | 22 | 22 | 25 | 25 | 24 | 24 | 24 | 25 |
| RUV-2–EM (k = 10) | 17 | 17 | 17 | 17 | 17 | 17 | 22 | 22 | 23 | 22 | 22 | 20 | 24 | 24 | 25 | 25 | 25 | 24 |
| RUV-2–EM (k = 10), w/Z | 16 | 16 | 16 | 16 | 17 | 16 | 22 | 22 | 22 | 22 | 22 | 22 | 24 | 23 | 25 | 24 | 26 | 25 |
| RUV-2–Robust (k = 10) | 8 | 7 | 17 | 16 | 17 | 16 | 11 | 10 | 21 | 21 | 22 | 21 | 12 | 11 | 25 | 25 | 24 | 24 |
3.2. Additional examples
In Sections A (“Alzheimer's Study”) and B (“The Cancer Genome Atlas (TCGA)”) of the supplementary material available at Biostatistics online, we present additional examples in which we discover genes in the brain differentially expressed with respect to gender. Our analysis and conclusions generally parallel those presented here, but there are some interesting exceptions. In Section C (“NCI-60”), we try to adapt RUV-2 to be used in a clustering analysis instead of a DE analysis. We show that this is highly nontrivial, and substantial work remains.
4. DISCUSSION
Methodologically, RUV-2 is extremely simple. Its 2 steps—factor analysis and regression—are well studied and well understood. Despite this simplicity, RUV-2 is highly effective. RUV-2 derives its strength not from any deep new statistical theory but from some powerful biological assumptions. RUV-2 is only as good as these assumptions on which it is based, and it is therefore worthwhile to reiterate these assumptions. The control genes must satisfy 2 key conditions—they must be (i) uninfluenced by the factor of interest and they must be (ii) influenced by the unwanted factors. Different situations will call for different sets of control genes. The choice of an appropriate set of control genes is central to RUV-2.
We have discussed 2 possible sets of control genes—HK genes and spike-in controls. In the DE examples (gender, Alzheimer's, and TCGA), the HK genes are the better choice, presumably because they are more “representative” and because there are more of them. In the NCI-60 example, the spike-in controls are the better choice because the HK genes are not negative controls with respect to tissue type. The NCI-60 example highlights the important fact that HK genes are influenced by biology and cannot be casually assumed to be negative controls in every situation. HK genes are effective negative controls in the first several examples because they are unaffected by gender not because they are unaffected by biology in general. In short, HK genes are a good place to begin a search for negative controls but cannot be relied upon in all cases—the factor of interest matters.
We need not restrict our search for control genes to HK genes and spike-in controls. In other studies, still other sets of genes might be the best choice. For example, a researcher might wish to use genes known to be stably expressed within a particular tissue type (Stamova and others, 2009) or under certain experimental conditions; choosing genes specially suited to the study at hand may improve performance. In other situations, a researcher might wish to include additional control genes with the intent of adjusting for specific types of unwanted variation. For example, if a researcher suspects that the cause of death is an important source of unwanted variation, it might be wise to include control genes that could possibly capture this information—for example, genes associated with cellular stress, apoptosis, etc.
There may be a temptation to “discover” negative control genes. For example, a researcher may wish to find genes whose expression levels are not highly correlated with the factor of interest, label these genes as negative controls, and then adjust via RUV-2. The allure of this approach is clear—finding a set of negative controls would be much easier and could in fact be automated. However, we feel this approach is misguided. If there are unwanted factors that are correlated with the factor of interest, then the expression levels of the true negative controls should in fact be correlated with the factor of interest. Excluding genes correlated with the factor of interest would bias our estimate of the unwanted factors.
Just as the researcher must exercise judgment when choosing a set of control genes, the researcher must also exercise judgment when choosing k. This can be difficult. We have seen that RLE plots and p-value histograms can be quite helpful. Positive controls, when available, can be even more helpful. Some readers may question why we encourage choosing k based on these quality assessments when more “objective” and automated methods exist. For example, it is possible to choose k via a series of hypothesis tests in which one keeps increasing k until no more “statistically significant” factors can be found. This is the approach taken in SVA. However, we feel there are problems with this approach. One reason is that including an additional term in a linear regression model may lead to a decrease in bias, but it can also lead to an increase in variance. Thus, it is possible that we might get a better estimate of β by leaving some of the unwanted factors out of the model. Using hypothesis testing to find k does not account for this bias-variance trade-off; instead the goal is simply to include all factors. A second reason is a bit more philosophical. Whenever a researcher calculates a small p-value, 3 logical possibilities are on the table—the null hypothesis is true and we have observed an unlikely event; the null hypothesis is false; the model is wrong. We know already the model is wrong. We do not know “how wrong” or in precisely which way. Nor do we know exactly how the model misspecification affects the results of any particular hypothesis test. Thus, we feel it is unwise to rely too heavily on a hypothesis test to give us a “good” answer, especially when the choice of k is so important. We feel there is a role here for human judgment and that quality assessments based on positive controls, p-value histograms, etc., are useful tools in guiding this judgment.
The simplicity of RUV-2 makes it relatively flexible, and an excellent starting point for new, more advanced methods. In addition, some of the basic ideas of RUV-2 can be useful in exploratory data analysis. For example, we have used methods similar to RUV-2 to identify the age of a formalin fixed paraffin-embedded tissue sample as an important source of unwanted variation (data not shown). The extended NCI-60 discussion in the supplementary material available at Biostatistics online is another good example.
Finally, we feel it may be possible to apply some of the ideas of RUV-2 to applications other than DE. As we have stated, we feel that unwanted variation is most effectively dealt with when it is considered in the context of the goal of the analysis at hand. RUV-2 deals effectively with unwanted variation in the context of DE studies. However, microarrays are also commonly used for classification and for clustering. We do not yet know how best to handle unwanted variation in these types of studies, but we believe control genes will play an important role.
SUPPLEMENTARY MATERIAL
Supplementary material is available at http://www.biostatistics.oxfordjournals.org.
FUNDING
A National Science Foundation VIGRE Graduate Fellowship (to J. A. G.-B.); National Institutes of Health (5R01 GM083084-03 to T.P.S.); National Cancer Institute (U24 CA126551 to T.P.S.).
Supplementary Material
Acknowledgments
We would like to thank Darya Chudova, Jun Li, Mark Vawter, Hui Shen, Matthew Ritchie, Pierre Neuvial, Juergen von Frese, Sue Wilson, Di Wu, Laurent Jacob, Tim Triche, Dongseok Choi, and Prabhakara Choudary for their helpful comments on a draft version of this paper. We would also like to thank Francois Collin, Moshe Olshansky, Elizabeth Purdom, Pierre Neuvial, Sandrine Dudoit, Jun Li, Mark Vawter, Gordon Smyth, Mark Robinson, Keith Satterley, Leming Shi, Roel Verhaak, Victoria Wang, Ying Xu, and Julia Brettschneider for helpful discussions and logistical support in the course of our research. Finally, we would like to thank Philip Musk and Gene Logic for providing us with their data. Conflict of Interest: None declared.
References
- Alter O, Brown PO, Botstein D. Singular value decomposition for genome-wide expression data processing and modeling. Proceedings of the National Academy of Sciences of the United States of America. 2000;97:10101–10106. doi: 10.1073/pnas.97.18.10101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bishop CM. Pattern Recognition and Machine Learning. New York: Springer; 2006. [Google Scholar]
- Bolstad B, Collin F, Brettschneider J, Simpson K, Cope L, Irizarry R, Speed TP. Quality assessment of Affymetrix GeneChip data. In: Gentleman R, Carey V, Huber W, Irizarry R, Dudoit S, editors. Bioinformatics and Computational Biology Solutions Using R and Bioconductor. New York: Springer; 2005. pp. 33–47. [Google Scholar]
- Bolstad BM, Irizarry RA, Astrand M, Speed TP. A comparison of normalization methods for high density oligonucleotide array data based on variance and bias. Bioinformatics. 2003;19:185–193. doi: 10.1093/bioinformatics/19.2.185. [DOI] [PubMed] [Google Scholar]
- Brettschneider J, Collin F, Bolstad BM, Speed TP. Quality assessment for short oligonucleotide microarray data. Technometrics. 2008;50:241–264. [Google Scholar]
- Eisenberg E, Levanon EY. Human housekeeping genes are compact. Trends in Genetics. 2003;19:362–365. doi: 10.1016/S0168-9525(03)00140-9. [DOI] [PubMed] [Google Scholar]
- Hubert M, Rousseeuw PJ, Vanden Branden K. ROBPCA: a new approach to robust principal component analysis. Technometrics. 2005;47:64–79. [Google Scholar]
- Irizarry RA, Bolstad BM, Collin F, Cope LM, Hobbs B, Speed TP. Summaries of Affymetrix GeneChip probe level data. Nucleic Acids Research. 2003;31:e15. doi: 10.1093/nar/gng015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Irizarry RA, Hobbs B, Collin F, Beazer-Barclay YD, Antonellis KJ, Scherf U, Speed TP. Exploration, normalization, and summaries of high density oligonucleotide array probe level data. Biostatistics. 2003;4:249. doi: 10.1093/biostatistics/4.2.249. [DOI] [PubMed] [Google Scholar]
- Johnson WE, Li C, Rabinovic A. Adjusting batch effects in microarray expression data using empirical Bayes methods. Biostatistics. 2007;8:118–127. doi: 10.1093/biostatistics/kxj037. [DOI] [PubMed] [Google Scholar]
- Kang HM, Sul JH, Service SK, Zaitlen NA, Kong SY, Freimer NB, Sabatti C, Eskin E. Variance component model to account for sample structure in genome-wide association studies. Nature Genetics. 2010;42:348–354. doi: 10.1038/ng.548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kang HM, Ye C, Eskin E. Accurate discovery of expression quantitative trait loci under confounding from spurious and genuine regulatory hotspots. Genetics. 2008;180:1909–1925. doi: 10.1534/genetics.108.094201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kang HM, Zaitlen NA, Wade CM, Kirby A, Heckerman D, Daly MJ, Eskin E. Efficient control of population structure in model organism association mapping. Genetics. 2008;178:1709–1723. doi: 10.1534/genetics.107.080101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leek JT, Scharpf RB, Bravo HC, Simcha D, Langmead B, Johnson WE, Geman D, Baggerly K, Irizarry RA. Tackling the widespread and critical impact of batch effects in high-throughput data. Nature Reviews Genetics. 2010;11:733–739. doi: 10.1038/nrg2825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leek JT, Storey JD. Capturing heterogeneity in gene expression studies by surrogate variable analysis. PLoS Genetics. 2007;3:e161. doi: 10.1371/journal.pgen.0030161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leek JT, Storey JD. A general framework for multiple testing dependence. Proceedings of the National Academy of Sciences of the United State of America. 2008;105:18718–18723. doi: 10.1073/pnas.0808709105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lippa KA, Duewer DL, Salit ML, Game L, Causton HC. Exploring the use of internal and external controls for assessing microarray technical performance. BMC Research Notes. 2010;3:349. doi: 10.1186/1756-0500-3-349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Listgarten J, Kadie C, Schadt EE, Heckerman D. Correction for hidden confounders in the genetic analysis of gene expression. Proceedings of the National Academy of Sciences of the United States of America. 2010;107:16465–16470. doi: 10.1073/pnas.1002425107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lucas J, Carvalho C, Wang Q, Bild A, Nevins J, West M. Sparse statistical modelling in gene expression genomics. In: Do K, Muller P, Vannucci M, editors. Bayesian Inference for Gene Expression and Proteomics. New York: Cambridge University Press; 2006. pp. 155–176. [Google Scholar]
- Mecham BH, Nelson PS, Storey JD. Supervised normalization of microarrays. Bioinformatics. 2010;26:1308–1315. doi: 10.1093/bioinformatics/btq118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen TO, West RB, Linn SC, Alter O, Knowling MA, O'Connell JX, Zhu S, Fero M, Sherlock G, Pollack JR. and others. Molecular characterisation of soft tissue tumours: a gene expression study. The Lancet. 2002;359:1301–1307. doi: 10.1016/S0140-6736(02)08270-3. [DOI] [PubMed] [Google Scholar]
- Price AL, Patterson NJ, Plenge RM, Weinblatt ME, Shadick NA, Reich D. Principal components analysis corrects for stratification in genome-wide association studies. Nature Genetics. 2006;38:904–909. doi: 10.1038/ng1847. [DOI] [PubMed] [Google Scholar]
- Scherer A. Batch Effects and Noise in Microarray Experiments: Sources and Solutions. Chichester, UK: Wiley; 2009. [Google Scholar]
- Smyth GK. Linear models and empirical Bayes methods for assessing differential expression in microarray experiments. Statistical Applications in Genetics and Molecular Biology. 2004;3:3. doi: 10.2202/1544-6115.1027. [DOI] [PubMed] [Google Scholar]
- Stamova BS, Apperson M, Walker WL, Tian Y, Xu H, Adamczy P, Zhan X, Liu DZ, Ander BP, Liao IH and others. Identification and validation of suitable endogenous reference genes for gene expression studies in human peripheral blood. BMC Medical Genomics. 2009;2:49. doi: 10.1186/1755-8794-2-49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stegle O, Kannan A, Durbin R, Winn J. Accounting for non-genetic factors improves the power of eQTL studies. Proceedings of the 12th Annual International Conference on Research in Computational Molecular Biology. 2008;4995:411–422. [Google Scholar]
- Vawter MP, Evans S, Choudary P, Tomita H, Meador-Woodruff J, Molnar M, Li J, Lopez JF, Myers R, Cox D and others. Gender-specific gene expression in post-mortem human brain: localization to sex chromosomes. Neuropsychopharmacology. 2004;29:373–384. doi: 10.1038/sj.npp.1300337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu J, Pressoir G, Briggs WH, Bi IV, Yamasaki M, Doebley JF, McMullen MD, Gaut BS, Nielsen DM, Holland JB and others. A unified mixed-model method for association mapping that accounts for multiple levels of relatedness. Nature Genetics. 2005;38:203–208. doi: 10.1038/ng1702. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.