Abstract
While fast folding of small proteins has been relatively well characterized by experiments and theories, much less is known for slow folding of larger proteins, for which recent experiments suggested quite complex and rich folding behaviors. Here, we address how the energy landscape theory can be applied to these slow folding reactions. Combining the perfect-funnel approximation with a multiscale method, we first extended our previous atomic-interaction based coarse grained (AICG) model to take into account local flexibility of protein molecules. Using this model, we then investigated the energy landscapes and folding routes of two proteins with complex topologies: a multidomain protein adenylate kinase (AKE) and a knotted protein 2ouf-knot. In the AKE folding, consistent with experimental results, the kinetic free energy surface showed several substates between the fully unfolded and native states. We characterized the structural features of these substates and transitions among them, finding temperature-dependent multiroute folding. For protein 2ouf-knot, we found that the improved atomic-interaction based coarse-grained model can spontaneously tie a knot and fold the protein with a probability up to 96%. The computed folding rate of the knotted protein was much slower than that of its unknotted counterpart, in agreement with experimental findings. Similar to the AKE case, the 2ouf-knot folding exhibited several substates and transitions among them. Interestingly, we found a dead-end substate that lacks the knot, thus suggesting backtracking mechanisms.
Keywords: protein folding, molecular dynamics simulations, multiscale simulations, flexible local potential, topological frustrations
In the last two decades, chemico-physical knowledge of protein folding has been greatly deepened primarily focusing on small and fast-folding proteins (1, 2). Many such proteins were identified as two-state folders and their transition state ensembles were experimentally characterized by site-directed mutagenesis via the Φ-value analysis (3, 4). Ultrafast experimental technology enabled direct observation of fast-folding kinetics unambiguously (5–7). Single molecule experiments directly visualized cooperative two-state folding transitions (8–10). In parallel, statistical physics theory clarified that proteins have evolved their sequences to have minimally frustrated and globally funnel-like energy landscapes, providing a general framework of understanding (11, 12). Many simulations inspired by the theory were compared with experimental observations and gave feedback to the theory (13–17). In particular, structure-based models that can concisely realize perfect funnel landscapes of given native topologies showed great promise to capture many essential features for small and fast-folding proteins (13, 14, 18–22). Recently, a specialized computer enabled folding simulations of small proteins with an atomistic model, which were consistent with the two-state folding on funnel-like landscapes (23).
In contrast, much less is understood for slow folding of proteins with medium or large size (e.g., proteins larger than 150 residues.). Generally, the folding of such proteins is much more complex with more than two states. Do such proteins still have globally funnel-like energy landscapes? More specifically, can we use similar perfect funnel models to characterize such complex folding mechanisms of individual proteins? Here, we address these issues focusing on two specific cases: folding of a multidomain protein, adenylate kinase, and that of a designed knotted protein, 2ouf-knot.
Adenylate kinase (AKE) is a medium-sized and slow-folding protein with three domains. Very recently, its folding has been characterized by the high-throughput single molecule fluorescence resonance energy transfer (smFRET) (24). Long time smFRET trajectories were fed into the hidden Markov method to identify approximately six metastable states and state-to-state transition rates. Their analysis revealed that multiple intersecting folding routes coexist in the AKE folding, and denaturant concentration can modulate the probabilities of these folding routes. A somewhat similar combination of single molecule experiments and the learning algorithm were used to obtain a complex multiroute folding networks of calmodulin, a two-domain protein (25). Such complex folding schemes provide us an ideal opportunity to examine the view of funnel-like landscape for multidomain proteins.
The knotted proteins are another class of proteins in which the structures show complexity by making knots. About 10 knotted protein folds have been identified up to now (26, 27). Their folding involves the precise threading of a chain segment through a knotting loop and therefore poses new challenge to the current protein folding theories. Shakhnovich et al. simulated the folding of a pair of related knotted proteins, Yibk and YbeA, using a structure-based Go model (28) and suggested that addition of specific nonnative interactions can greatly facilitate knot formation and thus successful folding, which calls for some alternation in the funnel landscape. Later, Onuchic and coworkers found that the similar Go model, without nonnative interactions, is able to guide the folding of the knotted protein to the native state via slipknot intermediate (29), although the probability of successful folding was very low (≈1–2%) even after selectively strengthening/weakening the native interactions between certain residue pairs. Apparently, further studies are necessary. Recently, by connecting two monomers with a linker or by a disulfide bond, a knotted protein 2ouf-knot and its unknotted counterpart 2ouf-ds were designed (26). The 2ouf-knot and 2ouf-ds have almost identical sequence and tertiary structures and therefore provide ideal model systems to study the role of a knot in the protein folding and to identify the critical energetic factors contributing to the successful folding of the knotted proteins. Here, folding of this pair of proteins, 2ouf-knot and 2ouf-ds, were investigated by computer simulations.
To compare simulations vis-a-vis experiments for the complex folding of larger proteins, we need accurate yet concise simulation methodology. Here, while sticking on the globally funnel-like landscape view, we include sequence-specific and atomic interactions as much as possible. For the purpose, we previously developed an atomic-interaction-based coarse-grained (AICG) model for proteins (30), and here, we extend it to improve description of local flexibility (the extended model designed as AICG2).
In the present work, we first briefly describe the AICG2 model that takes into account sequence-specific local and nonlocal interactions and further optimizes the relative weights of them via a multiscale protocol. Using the AICG2 model, we studied the folding of AKE and a knotted protein 2ouf-knot. We were able to capture all the experimentally found major features in the folding of AKE and further provide structural characterization of and transitions among substates. For the knotted protein, AICG2 realized efficient folding of 2ouf-knot with a probability up to 96%. Thus, the present study suggests that the perfect funnel model can capture essential features of the folding of these proteins with complex topologies once native interactions were carefully tuned and local flexibility was included.
Results and Discussions
Accurate yet Concise Modelling of Folding.
Previously, we developed an AICG using a multiscale protocol (30). AICG uses one-bead-per-residue representation, but its interresidue nonlocal contact energies were derived from atomic interactions. Here, we extended AICG by introducing a flexible local potential (AICG2). The local interactions are described by combination of generic statistical potentials of the residue types and local contact potentials that are based on the native structure. The relative weight and average strength of the local contact potentials were derived by a multiscale protocol, the same as for the nonlocal contact interactions. Incorporating sequence-specificity and the locally flexible nature of chains, AICG2 can reproduce folding energy landscape better than the simple Go model. As an illustration, the asymmetric folding pathways of the topologically symmetric proteins, protein G and protein L, were well reproduced (SI Appendix, Figs. S1 and S2).
High Free Energy Barrier and Substates in the AKE Folding.
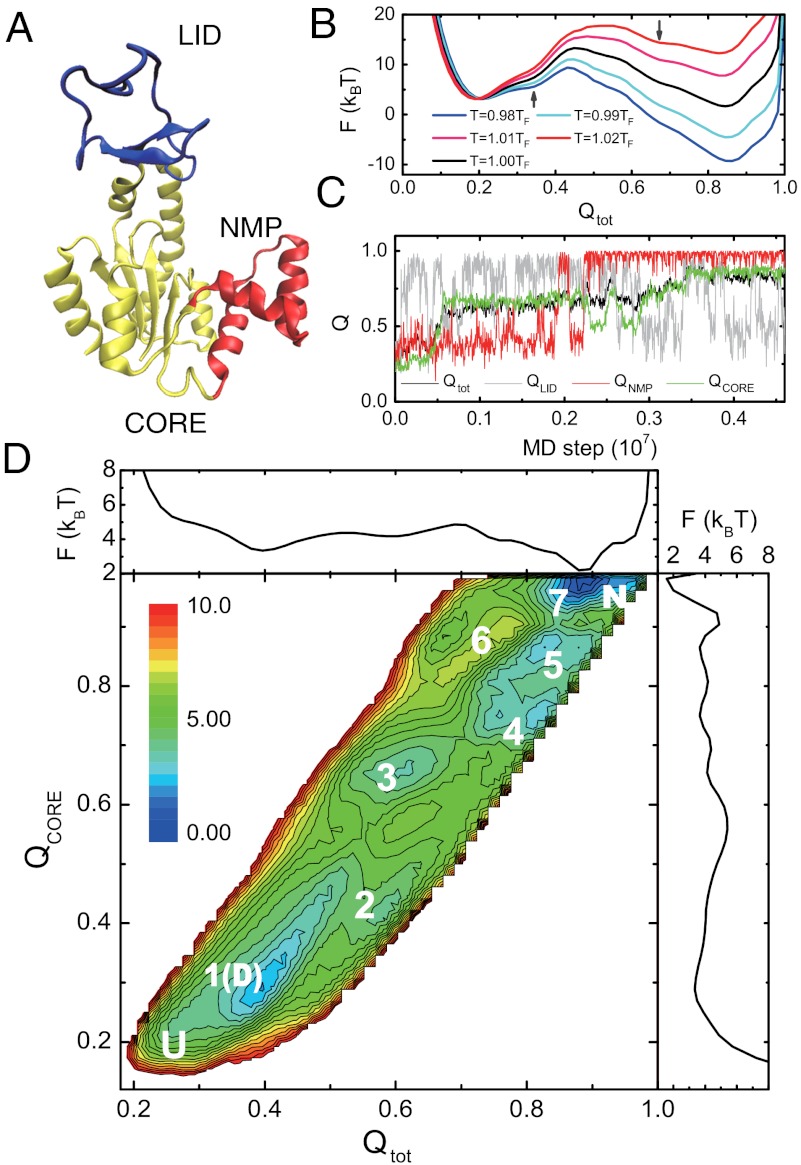
AKE is a 214-residue kinase that plays important roles in maintaining the balance of ATP and ADP in the cell and, more importantly here, it has been used as a model multidomain protein (31). AKE consists of three domains, i.e., LID domain, NMP domain, and CORE domain (31) (Fig. 1A). AKE folds relatively slowly and a recent single molecule experiment revealed complex multiroute folding (24).
Fig. 1.
Free energy surfaces and a representative trajectory of the folding of AKE. (A) Crystal structure of the AKE [Protein Data Bank (PDB): 4ake]. (B) Free energy profiles along Qtot at temperatures T = 0.98TF, 0.99TF, 1.00TF, 1.01TF, and 1.02TF. (C) A representative folding trajectory monitored by Qtot, (black), QLID (gray), QNMP (red), and QCORE (green). (D) Two-dimensional kinetic free energy landscape on the reaction coordinates Qtot and QCORE at 0.90TF, and its one-dimensional projections. The seven substates and completely unfolded (U) and native states (N) are labeled. The substate 1 may correspond to the denatured state (D).
We first tried to realize reversible folding and unfolding transitions using AICG2 model and unbiased molecular dynamics (MD) simulations, which turned out to be difficult due to its intrinsically slow folding. Then, we used the modified multicanonical method (32) for better conformational sampling. The converged one-dimensional free energy profiles near the folding temperature TF (Fig. 1B) show relatively high and broad free energy barrier, consistent with slow folding in vitro (33) and in silico. Albeit no apparent intermediate states in Fig. 1B, the two shoulders labelled by the arrows suggest that the folding/unfolding is not a simple two-state transition (see SI Appendix, Fig. S3). Some substates, virtually hidden in Fig. 1B, may exist between denatured and native states.
Because the high temperature simulations tend to hide the possible substates, we next conducted folding simulations starting from fully unfolded structures at the three temperatures, 0.90TF, 0.92TF, and 0.94TF. A representative time course of formation of native contacts, i.e., so-called Q-score, at 0.90TF (Fig. 1C) shows successive transitions among different substates. Particularly, the CORE domain encounters at least five substates beside the fully unfolded and native states. Such transitions among multiple substates closely resemble smFRET trajectories observed (24), although directly mapping the substates by the experiment with those by the simulation is difficult due to the lack of structural information in the experiment.
To identify these substates robustly and statistically, we plotted the kinetic free energy landscape on the reaction coordinates Qtot and QCORE in Fig. 1D using 200 folding trajectories at 0.90TF. Such a nonequilibrium free energy landscape has been used in characterizing the folding/unfolding pathways of proteins and RNA (34–36). In addition to the fully unfolded and native states, seven other substates can be identified. Qualitatively similar results can be obtained when a different reaction coordinate was used (SI Appendix, Fig. S4). In comparison, the corresponding kinetic free energy landscape obtained by the simple Go model was much smoother (SI Appendix, Fig. S5), suggesting that sequence specificity and realistic local flexibility included in the AICG2 model are responsible for making these substates in AKE.
Structural Features of the Substates in the AKE Folding.
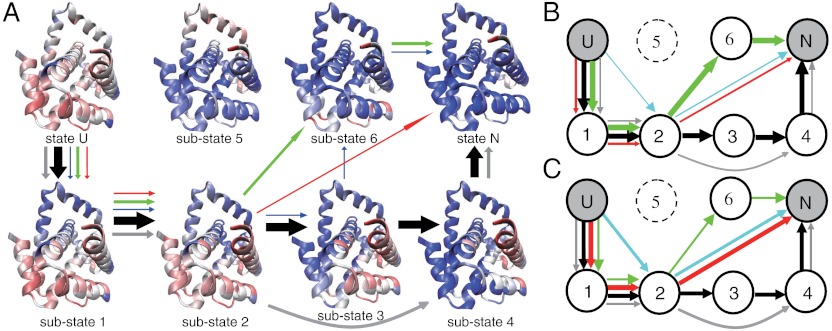
An advantage of the MD simulation is the ability to provide detailed structural information for each of the substates. Fig. 2A shows, for each substate, the average contact scores at every residue by color; continuously from blue (native-like) to red (unfolded). The corresponding contact probability maps are shown in SI Appendix, Fig. S6. Each substate has a well-defined structural feature, which further rationalizes the identified substates. For example, in substates 1, 2, 3, and 4, the LID domain is folded. These substates differ in the order of the CORE domain or the NMP domain. Because of its depth, the state 1 corresponds to the denatured state. Whereas, in substates 5, 6, and 7, the LID domain is unfolded. Interestingly, among the seven substates, the CORE domain has five distinct structural features, consistent with the observations in Fig. 1D. We note that the number of the substates found is less than the product of the number of states of individual domains, suggesting coupling between domains. We also calculated the distributions of the distance between residues 73 and 203, which correspond to the label sites in the single molecule experiment, for each of the substates. Both the peak positions and the distribution widths largely vary among the substates, and resemble the results of the single molecule experiment (SI Appendix, Fig. S7).
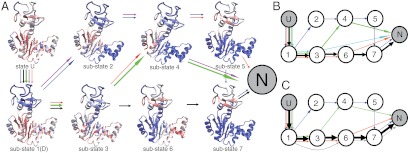
Fig. 2.
Folding routes and structural features of the substates of AKE. (A) Folding routes and residue-resolved contact scores of every substate at T = 0.90TF. Color code: red, unstructured; blue: fully structured. The five most probable folding routes that reach the native state are represented by colored arrows with the line widths representing the abundance of each folding route. Different colors represent different folding routes. (B, C) Same as A but at T = 0.92TF (B) and 0.94TF (C) with the substates represented by circled numbers.
Multiroute Folding of AKE and Its Modulation by Temperature.
To characterize folding routes, we analyzed the transitions among the above defined substates, identifying five most probable folding routes (arrows of each color in Fig. 2 represent one route). In the figure, the breadth of the arrows represents the probabilities of the routes. (see also SI Appendix, Table S2 and Fig. S8 for more details). At 0.90TF (Fig. 2A), the dominant folding route is U → 1(D) → 3 → 4 → N (green arrows). In this route, the LID domain folds first (or it is folded in the denatured state). Then the central β sheet of the CORE domain folds (substate 3), which is followed by folding of the NMP domain (substate 4). At last, N- and C-terminal α helices of the CORE domain dock to make the native state. There was a slightly less probable alternative route, U → 1(D) → 3 → 6 → 7 → N (black arrows), where the LID domain, which was folded in 1(D) and substate 3, transiently unfolded in substate 6, and 7.
This second route became dominant at higher temperatures, 0.92TF and 0.94TF (Fig. 2 B and C). Thus, the AKE folding took heterogeneous routes, and the populations of the folding routes are sensitive to temperatures. These results are in agreement with the single molecule observations in which a few folding routes were identified and were found sensitive to the denaturant concentration. We note that although we can approximately model the effect of denaturant by high temperatures, the actual temperature dependence of folding can be very complicated as shown in a theoretical work (37). Both the equilibrium simulations around the folding temperature and the folding simulations at low temperatures showed that the LID domain frequently transits between the folded and unfolded states during the whole folding trajectory (Fig. 1C, SI Appendix, Fig. S9). As higher temperature tends to destabilize the LID domain (SI Appendix, Fig. S10), increasing the temperature promotes the folding route U → 1(D) → 3 → 6 → 7 → N as observed in Fig. 2. Interestingly, such multiroute folding was also observed in some simple proteins (38), and has been generally linked to topological complexity of the folded state and the structure symmetry (39).
Slow Folding of Knotted Protein 2ouf-knot.
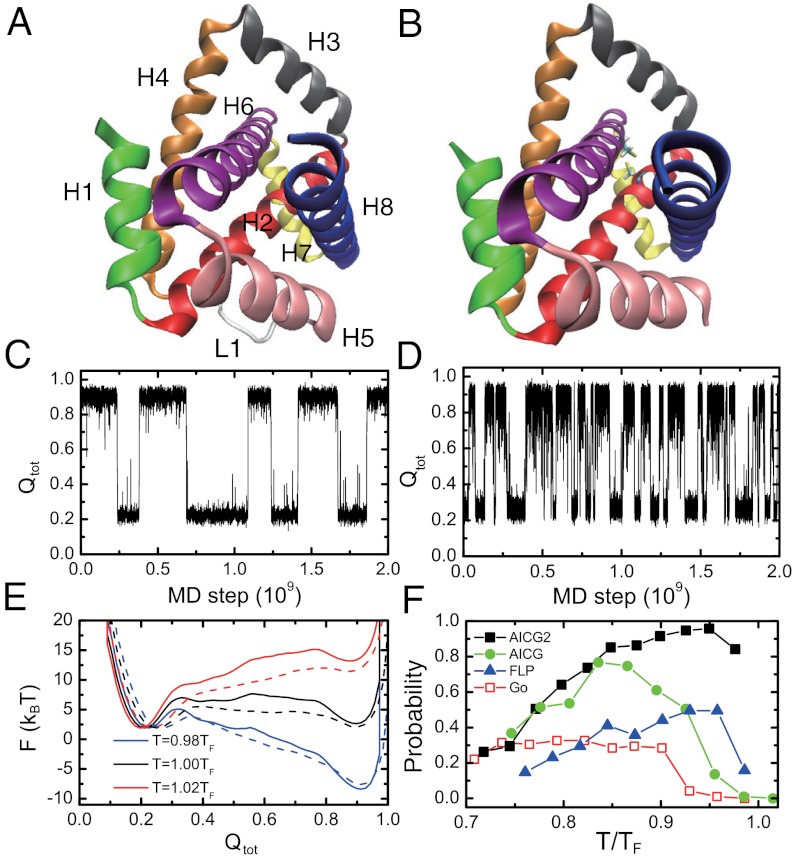
We move to a protein with another type of topological complexity, namely, knot formation. Here we focus on a designed knotted protein, 2ouf-knot, and its unknotted counterpart, 2ouf-ds, which have almost identical sequences and tertiary structures, thus being ideal model systems to study the role of a knot in folding (Fig. 3 A and B). These proteins were designed based on a natural dimeric protein, in which each subunit has four helices. Connecting two subunits with a nine-residue loop (L1 in Fig. 3A) led to 2ouf-knot, with left-handed trefoil knot of 28-residue depth in N terminus and 57-residue depth in C terminus. In contrast, the two subunits were connected with a disulfide bond to make 2ouf-ds that lacks a knot. Experimentally, both proteins reversibly folded, but 2ouf-knot folded an order of magnitude slower than 2ouf-ds (26).
Fig. 3.
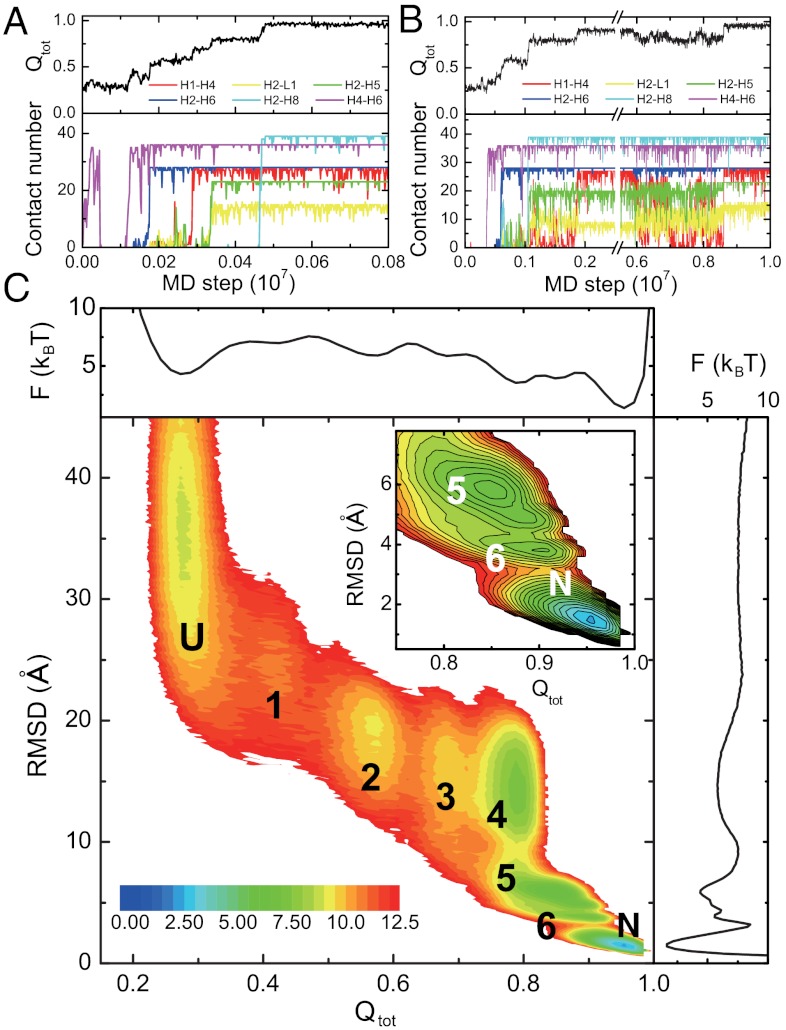
Folding of a designed knotted protein 2ouf-knot and its unknotted counterpart 2ouf-ds. (A, B). Crystal structures of 2ouf-knot (PDB: 3 mlg) (A) and 2ouf-ds (PDB: 3mli) (B). The eight helices are labeled by H1, H2, …, H8, and the loop is labeled by L1. Two cysteines forming the disulfide bond in 2ouf-ds are explicitly shown. (C, D) Time courses of the Q score of the entire protein for the knotted protein (C) and the unknotted protein (D) at the folding temperature T = TF. (E) One-dimensional free energy profiles for the knotted (solid line) and unknotted (dashed line) proteins at T = 0.98TF, 1.00TF, and 1.02TF. (F) The ratios of the successful folding with four different models when started from fully unfolded structures.
Here, using AICG2, we conducted extensive unbiased MD simulations at a wide temperature range for both 2ouf-knot and 2ouf-ds. In simulations, both proteins exhibited reversible folding and unfolding transitions (Fig. 3 C and D) and we confirmed that the knot is indeed formed for 2ouf-knot. Consistent with the experiment, the folding of the knotted one was much slower than the unknotted counterpart (Its folding rate is nearly seven times slower than that of the 2ouf-ds). The higher free energy barrier of 2ouf-knot in the one-dimensional free energy profile (Fig. 3E) also indicates slower folding of the knotted protein than that of 2ouf-ds. Apparently, such slowing of 2ouf-knot folding purely results from the knot because it is the only major difference between 2ouf-knot and 2ouf-ds.
Interaction Heterogeneity and Chain Flexibility Promote the Knot Formation.
The reversible folding/unfolding transitions in Fig. 3C surprised us because previous folding simulations of another knotted protein with a Go model showed quite a low ratio of successful knot formation (29). To quantify the ratio of successful folding, we conducted extensive independent folding simulations in a range of temperatures below TF. The successful folding ratio as a function of temperature showed a bell-like shape with the peak of 96% near 0.95TF (Fig. 3F). In comparison with the previous study, is this high ratio due to interaction features in AICG2 or due to difference in topology? To this end, we conducted additional folding simulations with three different models, namely, a simple Go model and two intermediate models (Fig. 3F; see SI Appendix for the details of each model). Consistent with the previous study (29), the simple Go model led to quite low successful folding ratios (approximately 30%). For majority of the unsuccessful events, the protein stayed at highly trapped structures (SI Appendix, Fig. S11), in which the segment H6-H7 is misplaced around the H3, without forming the knot. Apparently, knotting from this trapped structure requires the detachment of H8 from the H2 and H5, and the threading of the longer C-terminal segment H7-H8 through the H2-H3-H4-L1 loop, which is difficult. On the contrary, for all the successful folding events by simple Go model and AICG2, the protein formed a knot by threading the segment H1 through the H4-L1-H5-H6 loop, which is much easier due to the short length of H1. A chimera model where local interactions are simple Go and nonlocal interactions are AICG (designated AICG) gave an intermediate ratio of successful folding. Similarly, another chimera model where local interactions are of AICG2 type but with homogeneous strength and nonlocal interactions are from simple Go model (designated FLP) also showed intermediate ratio. Thus, we can conclude that both the sequence specificity of contact interactions and the local flexibility in AICG2 contributed to the ability of avoiding the highly trapped structure during folding, although it is not easy to trace such ability to certain specific contacts (SI Appendix, Fig. S12). Actually, a previous study by Onuchic et al. showed that by selectively enhancing certain contact interactions, the successful ratio can be improved to a large extent (29), indicating the importance of the sequence specific interactions. Yet, it is of some surprise because 2ouf-knot is a designed protein and has not evolved to achieve folding ability.
Folding of the 2ouf-knot Is More Topologically Frustrated Than Its Unknotted Counterpart.
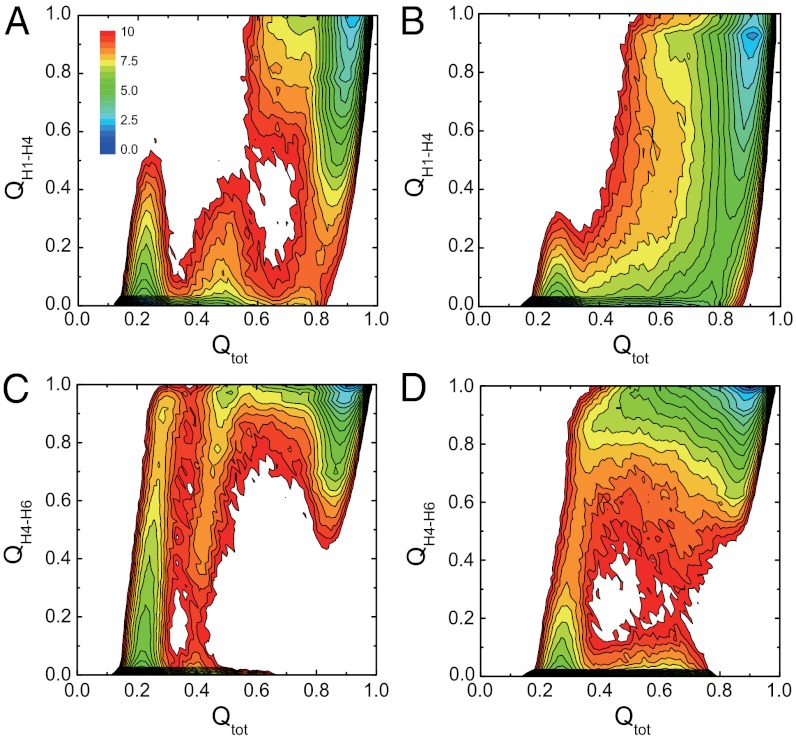
To compare folding mechanisms of knotted and unknotted proteins, we next drew a number of two-dimensional free energy surfaces (Fig. 4, SI Appendix, Figs. S13 and S14). In Fig. 4, although the overall shapes of the free energy surfaces of two proteins show some similarity, the knotted one possesses some unique features. In early stages of folding (Qtot ∼ 0.2 and Qtot ∼ 0.5), the H1-H4 contacts can be formed partly (Fig. 4A). However, because the formation of such H1-H4 contacts hinders the knot formation, they need to be transiently broken up (Qtot ∼ 0.35 and Qtot ∼ 0.6). Thus, the knot formation introduces topological frustrations, which was also observed in the folding of other proteins with complex topology (32). In contrast, the free energy landscape of 2ouf-ds is much smoother (Fig. 4B). The folding order of the H4-H6 contacts also has large differences. For the 2ouf-knot, the H4-H6 contacts are predominantly formed early on (Fig. 4C), whereas for the 2ouf-ds, the H4-H6 contacts can be formed in a later stage with certain probability (Fig. 4D). In addition, for the 2ouf-ds, the folding of the two halves is symmetric due to the symmetry in sequences and the tertiary structures (SI Appendix, Fig. S14). In comparison, for the 2ouf-knot, the pathway with the H1-H4 contacts form before the H5-H8 contact formation is much more probable. Such asymmetry in folding routes is crucial for the efficient folding of the knot, which will be discussed in more detail below.
Fig. 4.
Two-dimensional free energy surfaces of knotted (A, C) and unknotted (B, D) proteins on the reaction coordinates Qtot and QH1–H4 (A, B) and on coordinates Qtot and QH4–H6 (C, D) at TF. The unit of the free energy is kBT.
Structural Features of the Substates in 2ouf-knot Folding.
Similar to the case of AKE, we conducted extensive folding simulations of 2ouf-knot starting from fully unfolded structures at the three temperatures, 0.90TF, 0.925TF, and 0.95TF. Fig. 5 A and B shows two representative trajectories. The stepwise folding of different parts of the 2ouf-knot implies the existence of several substates. We plotted the kinetic free energy landscape projected onto the reaction coordinate Qtot and rmsd in Fig. 5C. Six substates besides the unfolded state and the native state were observed clearly. The structural features of these substates are given in Fig. 6A by the average contact scores at every residue. See SI Appendix, Fig. S15 for more details. In substate 1, the knotting loop consisting of H4, L1, H5, and H6 is formed by H4-H6 or H3-H6 contacts. In substate 2, the contacts between H2 and H6 are also formed. From substate 2, H1 may pack with H4 without correctly threading the knotting loop, leading to the substate 3 (the knot not yet formed completely). The knot formation is complete at substate 4 when H1 correctly threads the knotting loop, as featured by the high contact probability between H2 and L1. In this substate, H7 and H8 are not yet packed to the final positions. Opposite to substate 4, in the substate 6, H7 and H8 are well packed, while H1 is not correctly threaded through L1. The substate 5 corresponds to the highly trapped structure shown in SI Appendix, Fig. S11 C and D.
Fig. 5.
Results of kinetic simulations for the knotted protein. (A, B) Two representative folding trajectories monitored by the Q scores of the entire protein (black), and the number of native contacts between the H1 and H4 (red), H2 and L1 (yellow), H2 and H5 (green), H2 and H6 (blue), H2 and H8 (cyan), and H4 and H6 (purple). Note that the two trajectories have different time scales. The knot formed by concerted threading mechanism (A) or by slipknot intermediate mechanism (B). (C) Two-dimensional kinetic free energy surface at T = 0.90TF on the reaction coordinates Qtot and rmsd and its one-dimensional projections. The six substates are labeled by numbers.
Fig. 6.
Folding routes and structural features of the substates of the knotted protein, 2ouf-knot.
Multiroute Folding of 2ouf-knot.
In the same way as in AKE, we analyzed the folding routes of 2ouf-knot at 0.90TF (Fig. 6A), 0.925TF (Fig. 6B), and 0.95TF (Fig. 6C). More detailed analysis is given in SI Appendix, Table S3 and Fig. S16. Not surprisingly, multiple routes can populate with high probabilities, suggesting the heterogeneity of the 2ouf-knot folding routes. At 0.90TF, the dominant folding route U → 1 → 2 → 3 → 4 → N is the most sequential one. The major feature of this route is that the knot forms before the packing of the H8 to the H2 and H5 (Fig. 5A, Movie S1). In this case, the L1 and H5, parts of the knotting loop, can have high flexibility during the knot formation. Such high flexibility of the L1 and H5 tends to expand and tilt the knotting loop, which could make the threading of H1 much easier. Thus, the knot formation is not just the threading of H1 itself, but it is accompanied with high flexibility of L1 and H5. We thus call it “concerted threading.” Detailed analysis shows that in all the trajectories with this folding route at the temperature of 0.90TF, the knot forms by the concerted threading mechanism. In comparison, if the pathway involves the substate 6, the knot mostly forms via a slipknot intermediate (Fig. 5B, Movie S2). For example, among the trajectories with the folding route U → 1 → 2 → 6 → N, which is the most probable route via substate 6, approximately 80% of the trajectories follow the “slipknot intermediate” knotting mechanism. In this case, the H8 is well packed to H5 before the knot formation (substate 6), which makes the L1 and H5 well fixed. The rigid knotting loop makes the direct threading of H1 difficult. Consequently, the formation of the knot by the slipknot intermediate is preferred (Fig. 5B, Movie S2). Such results suggest that the knotting mechanism depends on the folding order of other parts of the protein. Notably, no route leading to the folded state via the substate 5, which requires the threading of the much longer C terminus (H8 and H9) through a different knotting loop (H2-H3-H4-L1), is observed. We found that most routes involving substate 5 terminate at the substate 5, which is a dead-end trap.
In Fig. 6, we also observe some shortcuts of the folding routes, e.g., U → 1 → 2 → N in which the placements of the N-terminal segment (H1) and the C-terminal segments (H7 and H8) are cooperative. These shortcut routes become more probable at higher temperatures, perhaps because higher temperature usually tends to make the folding transition more cooperative.
Folding of Two Other Knotted Proteins.
Because folding mechanisms of natural proteins and designed proteins could be very different as clarified in ref. 40, we also conducted the folding simulations for two natural proteins with trefoil knot, i.e., MJ0366 and YibK (28, 29, 41), which we briefly describe here. The trefoil knot of YibK is much deeper than those of the 2ouf-knot and MJ0366 (SI Appendix, Figs. S17–S19). For the MJ0366, we found that the maximal ratio of successful folding with AICG2 was 99%, a much higher ratio than that with the simple Go model (50%). However, the maximal ratios of successful folding for YibK by both simple Go model and AICG2 were very low (0.1–0.2%), which may suggest that in addition to the interaction ingredients included in the current AICG2, more realistic interaction features, e.g., nonnative interactions (28, 40), need to be considered in order to achieve efficient folding of YibK.
Material and Methods
Reaction Coordinates and Data Analysis.
In describing the folding of AKE, the Qtot, QCORE, QLID, and QNMP, defined as the fraction of native contacts for the full-length protein, the CORE domain, the LID domain, and the NMP domain, respectively, were used as reaction coordinates. Similarly, in describing the folding of 2ouf-knot and its unknotted counterpart, besides Qtot, we used QH1-H4, QH2-L1, QH2-H6, QH2-H8, QH3-H6, and QH4-H6, defined as the fraction of native contacts between the corresponding segments. We also used the rmsd of Cα atoms. The Koniaris–Muthukumar–Taylor algorithm was used in detecting the knot (42). In constructing the folding routes, the snapshots of the folding trajectories were assigned to the substates according to the values of the reaction coordinates. See SI Appendix for details.
Simulation Details.
We used CafeMol (43) developed in our laboratory for general CG simulations (44). The all-atom MD simulations were conducted by AMBER 11 (45). The protein structures were visualized by VMD software (46). See SI Appendix for details.
Supplementary Material
ACKNOWLEDGMENTS.
This work was based on a joint project between the Japan Society for the Promotion of Science and the National Natural Science Foundation of China, partly supported by Grant-in-Aid for Scientific Research on Innovative Areas “Molecular Science of Fluctuations Toward Biological Functions,” by Research and Development of the Next-Generation Integrated Simulation of Living Matter of the Ministry of Education, Culture, Sports, Science, and Technology, by the National Natural Science Foundation of China (Grants Nos. 11111140012, 11174134, 91127026, and 10834002), and by a project funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1201807109/-/DCSupplemental.
References
- 1.Fersht AR. From the first protein structures to our current knowledge of protein folding: Delights and scepticisms. Nat Rev Mol Cell Biol. 2008;9:650–654. doi: 10.1038/nrm2446. [DOI] [PubMed] [Google Scholar]
- 2.Eaton WA, et al. Fast kinetics and mechanisms in protein folding. Annu Rev Biophys Biomol Struct. 2000;29:327–359. doi: 10.1146/annurev.biophys.29.1.327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Matouschek A, Kellis JT, Jr, Serrano L, Fersht AR. Mapping the transition state and pathway of protein folding by protein engineering. Nature. 1989;340:122–126. doi: 10.1038/340122a0. [DOI] [PubMed] [Google Scholar]
- 4.Fersht AR, Sato S. Phi-value analysis and the nature of protein-folding transition states. Proc Natl Acad Sci USA. 2004;101:7976–7981. doi: 10.1073/pnas.0402684101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Eaton WA, Munoz V, Thompson PA, Chan CK, Hofrichter J. Submillisecond kinetics of protein folding. Curr Opin Struct Biol. 1997;7:10–14. doi: 10.1016/s0959-440x(97)80003-6. [DOI] [PubMed] [Google Scholar]
- 6.Chan CK, et al. Submillisecond protein folding kinetics studied by ultrarapid mixing. Proc Natl Acad Sci USA. 1997;94:1779–1784. doi: 10.1073/pnas.94.5.1779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Gruebele M. The fast protein folding problem. Annu Rev Phys Chem. 1999;50:485–516. doi: 10.1146/annurev.physchem.50.1.485. [DOI] [PubMed] [Google Scholar]
- 8.Schuler B, Lipman EA, Eaton WA. Probing the free-energy surface for protein folding with single-molecule fluorescence spectroscopy. Nature. 2002;419:743–747. doi: 10.1038/nature01060. [DOI] [PubMed] [Google Scholar]
- 9.Rhoades E, Cohen M, Schuler B, Haran G. Two-state folding observed in individual protein molecules. J Am Chem Soc. 2004;126:14686–14687. doi: 10.1021/ja046209k. [DOI] [PubMed] [Google Scholar]
- 10.Chung HS, McHale K, Louis JM, Eaton WA. Single-molecule fluorescence experiments determine protein folding transition path times. Science. 2012;335:981–984. doi: 10.1126/science.1215768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bryngelson JD, Onuchic JN, Socci ND, Wolynes PG. Funnels, pathways, and the energy landscape of protein folding: A synthesis. Proteins. 1995;21:167–195. doi: 10.1002/prot.340210302. [DOI] [PubMed] [Google Scholar]
- 12.Onuchic JN, Luthey-Schulten Z, Wolynes PG. Theory of protein folding: The energy landscape perspective. Annu Rev Phys Chem. 1997;48:545–600. doi: 10.1146/annurev.physchem.48.1.545. [DOI] [PubMed] [Google Scholar]
- 13.Clementi C, Nymeyer H, Onuchic JN. Topological and energetic factors: What determines the structural details of the transition state ensemble and “en-route” intermediates for protein folding? An investigation for small globular proteins. J Mol Biol. 2000;298:937–953. doi: 10.1006/jmbi.2000.3693. [DOI] [PubMed] [Google Scholar]
- 14.Koga N, Takada S. Roles of native topology and chain-length scaling in protein folding: A simulation study with a Go-like model. J Mol Biol. 2001;313:171–180. doi: 10.1006/jmbi.2001.5037. [DOI] [PubMed] [Google Scholar]
- 15.Sali A, Shakhnovich E, Karplus M. Kinetics of protein folding. A lattice model study of the requirements for folding to the native state. J Mol Biol. 1994;235:1614–1636. doi: 10.1006/jmbi.1994.1110. [DOI] [PubMed] [Google Scholar]
- 16.Thirumalai D, Guo ZY. Nucleation mechanism for protein-folding and theoretical predictions for hydrogen-exchange labeling experiments. Biopolymers. 1995;35:137–140. [Google Scholar]
- 17.Cho SS, Levy Y, Wolynes PG. Quantitative criteria for native energetic heterogeneity influences in the prediction of protein folding kinetics. Proc Natl Acad Sci USA. 2009;106:434–439. doi: 10.1073/pnas.0810218105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Munoz V, Eaton WA. A simple model for calculating the kinetics of protein folding from three-dimensional structures. Proc Natl Acad Sci USA. 1999;96:11311–11316. doi: 10.1073/pnas.96.20.11311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Alm E, Baker D. Prediction of protein-folding mechanisms from free-energy landscapes derived from native structures. Proc Natl Acad Sci USA. 1999;96:11305–11310. doi: 10.1073/pnas.96.20.11305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Galzitskaya OV, Finkelstein AV. A theoretical search for folding/unfolding nuclei in three-dimensional protein structures. Proc Natl Acad Sci USA. 1999;96:11299–11304. doi: 10.1073/pnas.96.20.11299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Karanicolas J, Brooks CLR. The origins of asymmetry in the folding transition states of protein L and protein G. Protein Sci. 2002;11:2351–2361. doi: 10.1110/ps.0205402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Chan HS, Zhang Z, Wallin S, Liu Z. Cooperativity, local-nonlocal coupling, and nonnative interactions: Principles of protein folding from coarse-grained models. Annu Rev Phys Chem. 2011;62:301–326. doi: 10.1146/annurev-physchem-032210-103405. [DOI] [PubMed] [Google Scholar]
- 23.Lindorff-Larsen K, Piana S, Dror RO, Shaw DE. How fast-folding proteins fold. Science. 2011;334:517–520. doi: 10.1126/science.1208351. [DOI] [PubMed] [Google Scholar]
- 24.Pirchi M, et al. Single-molecule fluorescence spectroscopy maps the folding landscape of a large protein. Nat Commun. 2011;2:493. doi: 10.1038/ncomms1504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Stigler J, Ziegler F, Gieseke A, Gebhardt JC, Rief M. The complex folding network of single calmodulin molecules. Science. 2011;334:512–516. doi: 10.1126/science.1207598. [DOI] [PubMed] [Google Scholar]
- 26.King NP, Jacobitz AW, Sawaya MR, Goldschmidt L, Yeates TO. Structure and folding of a designed knotted protein. Proc Natl Acad Sci USA. 2010;107:20732–20737. doi: 10.1073/pnas.1007602107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bolinger D, et al. A Stevedore’s protein knot. PLoS Comput Biol. 2010;6:e1000731. doi: 10.1371/journal.pcbi.1000731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Wallin S, Zeldovich KB, Shakhnovich EI. The folding mechanics of a knotted protein. J Mol Biol. 2007;368:884–893. doi: 10.1016/j.jmb.2007.02.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Sulkowska JI, Sulkowski P, Onuchic J. Dodging the crisis of folding proteins with knots. Proc Natl Acad Sci USA. 2009;106:3119–3124. doi: 10.1073/pnas.0811147106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Li W, Wolynes PG, Takada S. Frustration, specific sequence dependence, and nonlinearity in large-amplitude fluctuations of allosteric proteins. Proc Natl Acad Sci USA. 2011;108:3504–3509. doi: 10.1073/pnas.1018983108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Muller CW, Schlauderer GJ, Reinstein J, Schulz GE. Adenylate kinase motions during catalysis: An energetic counterweight balancing substrate binding. Structure. 1996;4:147–156. doi: 10.1016/s0969-2126(96)00018-4. [DOI] [PubMed] [Google Scholar]
- 32.Gosavi S, Chavez LL, Jennings PA, Onuchic JN. Topological frustration and the folding of interleukin-1 beta. J Mol Biol. 2006;357:986–996. doi: 10.1016/j.jmb.2005.11.074. [DOI] [PubMed] [Google Scholar]
- 33.Ratner V, Kahana E, Haas E. The natively helical chain segment 169–188 of Escherichia coli adenylate kinase is formed in the latest phase of the refolding transition. J Mol Biol. 2002;320:1135–1145. doi: 10.1016/s0022-2836(02)00520-x. [DOI] [PubMed] [Google Scholar]
- 34.Zhang Y, Zhang J, Wang W. Atomistic analysis of pseudoknotted RNA unfolding. J Am Chem Soc. 2011;133:6882–6885. doi: 10.1021/ja1109425. [DOI] [PubMed] [Google Scholar]
- 35.Pande VS, Rokhsar DS. Molecular dynamics simulations of unfolding and refolding of a beta-hairpin fragment of protein G. Proc Natl Acad Sci USA. 1999;96:9062–9067. doi: 10.1073/pnas.96.16.9062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Ferrara P, Caflisch A. Folding simulations of a three-stranded antiparallel beta -sheet peptide. Proc Natl Acad Sci USA. 2000;97:10780–10785. doi: 10.1073/pnas.190324897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Liu Z, Chan HS. Desolvation is a likely origin of robust enthalpic barriers to protein folding. J Mol Biol. 2005;349:872–889. doi: 10.1016/j.jmb.2005.03.084. [DOI] [PubMed] [Google Scholar]
- 38.Noe F, Schutte C, Vanden-Eijnden E, Reich L, Weikl TR. Constructing the equilibrium ensemble of folding pathways from short off-equilibrium simulations. Proc Natl Acad Sci USA. 2009;106:19011–19016. doi: 10.1073/pnas.0905466106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Klimov DK, Thirumalai D. Symmetric connectivity of secondary structure elements enhances the diversity of folding pathways. J Mol Biol. 2005;353:1171–1186. doi: 10.1016/j.jmb.2005.09.029. [DOI] [PubMed] [Google Scholar]
- 40.Zhang Z, Chan HS. Competition between native topology and nonnative interactions in simple and complex folding kinetics of natural and designed proteins. Proc Natl Acad Sci USA. 2010;107:2920–2925. doi: 10.1073/pnas.0911844107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Noel JK, Sulkowska JI, Onuchic JN. Slipknotting upon native-like loop formation in a trefoil knot protein. Proc Natl Acad Sci USA. 2010;107:15403–15408. doi: 10.1073/pnas.1009522107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Virnau P, Kantor Y, Kardar M. Knots in globule and coil phases of a model polyethylene. J Am Chem Soc. 2005;127:15102–15106. doi: 10.1021/ja052438a. [DOI] [PubMed] [Google Scholar]
- 43.Kenzaki H, et al. CafeMol: A coarse-grained biomolecular simulator for simulating proteins at work. J Chem Theory Comput. 2011;7:1979–1989. doi: 10.1021/ct2001045. [DOI] [PubMed] [Google Scholar]
- 44.Takada S. Coarse-grained molecular simulations of large biomolecules. Curr Opin Struct Biol. 2012;22:1–8. doi: 10.1016/j.sbi.2012.01.010. [DOI] [PubMed] [Google Scholar]
- 45.Case DA, et al. AMBER 11. San Francisco: University of California; 2010. [Google Scholar]
- 46.Humphrey W, Dalke A, Schulten K. VMD: Visual molecular dynamics. J Mol Graphics. 2010;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.