Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2012 Oct 3;103(7):1566–1575. doi: 10.1016/j.bpj.2012.08.046

Dynamics of Protein and its Hydration Water: Neutron Scattering Studies on Fully Deuterated GFP

Jonathan D Nickels †,‡, Hugh O’Neill §,∗∗, Liang Hong ‖,∗∗, Madhusudan Tyagi ††,‡‡, Georg Ehlers , Kevin L Weiss §, Qiu Zhang §, Zheng Yi ‖,∗∗, Eugene Mamontov , Jeremy C Smith ‖,∗∗, Alexei P Sokolov †,‡,∗
PMCID: PMC3471459  PMID: 23062349

Abstract

We present a detailed analysis of the picosecond-to-nanosecond motions of green fluorescent protein (GFP) and its hydration water using neutron scattering spectroscopy and hydrogen/deuterium contrast. The analysis reveals that hydration water suppresses protein motions at lower temperatures (<∼200 K), and facilitates protein dynamics at high temperatures. Experimental data demonstrate that the hydration water is harmonic at temperatures <∼180–190 K and is not affected by the proteins’ methyl group rotations. The dynamics of the hydration water exhibits changes at ∼180–190 K that we ascribe to the glass transition in the hydrated protein. Our results confirm significant differences in the dynamics of protein and its hydration water at high temperatures: on the picosecond-to-nanosecond timescale, the hydration water exhibits diffusive dynamics, while the protein motions are localized to <∼3 Å. The diffusion of the GFP hydration water is similar to the behavior of hydration water previously observed for other proteins. Comparison with other globular proteins (e.g., lysozyme) reveals that on the timescale of 1 ns and at equivalent hydration level, GFP dynamics (mean-square displacements and quasielastic intensity) are of much smaller amplitude. Moreover, the suppression of the protein dynamics by the hydration water at low temperatures appears to be stronger in GFP than in other globular proteins. We ascribe this observation to the barrellike structure of GFP.

Introduction

Molecular motions in proteins span an extremely broad frequency (time) range from small subpicosecond fluctuations to large conformational changes that occur on timescales of milliseconds (1–4). It has long been recognized that hydration water and other solvents strongly influence the dynamics and activity of proteins (5–7). The concept of slaved-dynamics proposed several decades ago (5), suggests that motions of biomolecules are controlled by, or “slaved to,” the solvent motions. Indeed, detailed simulations demonstrate that translational motions of hydration water and its hydrogen bonding to the protein surface control the internal dynamics of the biomolecule (8,9). However, recent experiments have also revealed significant differences in dynamics of lysozyme, t-RNA, and DNA, and also in the dynamics of their hydration water (10–12). These results suggest that the simple picture of slaved-dynamics is incomplete, and that considerable further study is needed to understand the relationship between the structure and intrinsic dynamics of biomolecules and the dynamics of their hydration water.

It has been recognized that not all components of protein dynamics are controlled by the solvent. Fenimore et al. (13) and Frauenfelder et al. (14) suggested three classes of relaxation processes in proteins: 1), processes that are strongly coupled to the solvent dynamics, 2), ones that are influenced by the solvent dynamics, and 3), those that are decoupled from the solvent dynamics. Methyl group rotation in proteins is an example of the decoupled dynamics (15–18). Methyl group rotations in proteins appear in the nanosecond time window probed by neutron scattering at temperatures from ∼100–150 K. Recent simulations suggested that hydration water also shows some changes in the dynamics at the same temperature range (19). These simulations raise the question of whether the methyl group dynamics can influence dynamics of hydration water.

Direct comparison of protein dynamics and its hydration water will be very helpful in understanding their mutual influence and interplay. There have been many attempts using simulation that have investigated the role of translational motions of water and the importance of hydrogen-bond lifetimes in protein dynamics (8,9). In particular, recent simulations of hydrated lysozyme revealed (20) that whereas hydration water has diffusive-like (translational) motions, proteins exhibit only localized atomic fluctuations on the picosecond-to-nanosecond timescale. However, direct experimental comparisons of protein and hydration water dynamics are very limited. Neutron scattering provides unique opportunity for these kinds of studies due to the significant (∼40 times) difference in incoherent scattering cross-section between hydrogen and deuterium.

In most cases, hydrogenated protein is measured in H2O and in D2O, and then by subtraction the dynamics of the hydration water is estimated. However, the most straightforward way would be to use fully deuterated protein in H2O and fully hydrogenated protein in D2O to measure separately the protein dynamics and the dynamics of its hydration water. These measurements are rare due to the difficulties in synthesis of completely deuterated samples and only a few such proteins (phycocyanin (21,22), purple membrane (bacteriorhodopsin) (23), maltose binding protein (24,25), myoglobin (26), and recently the disordered protein tau (27)), have so far been studied. Contemporary research focuses on studies of green fluorescent protein (GFP). Not only is GFP widely used as a tool in molecular and cell biology, but it has significantly different structure compared to traditionally studied globular proteins, consisting of a β-barrel structure (28) with a central α-helix.

In this article, we present neutron scattering studies of the dynamics of GFP and its hydration water. We measured normal (hydrogenated) protein dry and in D2O and fully deuterated protein in H2O. This allows the separation of protein and hydration water dynamics. The obtained results clearly show the difference in the dynamics between the protein and its hydration water: the former is strongly localized whereas the latter has diffusive character. The experimental data clearly demonstrate that methyl group rotation is decoupled from the dynamics of hydration water. Overall, the dynamics of GFP appear to be qualitatively similar to dynamics of other globular proteins. However, remarkably, the dynamics of hydrated GFP are of much smaller amplitude than, for example, lysozyme at the same hydration level, and is more strongly suppressed by hydration water at low temperatures. The possible influence of the specific barrellike structure on dynamics of GFP is discussed.

Methods

Sample preparation

Green fluorescent protein is a protein consisting of 238 amino acids with a mass of 27 kDa. The crystal structure of GFP (Fig. 1) has been solved and consists of a central helix inside an 11-stranded β-barrel, with a length of ∼4.2 nm and a diameter of ∼2.4 nm (28,29). This protein structure differs significantly from the structures of traditional-type model proteins, such as lysozyme, myoglobin, and RNase A. Recombinant GFP was overexpressed in Escherichia coli BL21 (DE3) transformed with pET28a_AvGFP (30). This GFP analog is identical to the GFPMut3 variant with the mutations F64L, G65T, A72S, F99S, M153T, and V163A (31). Enfors minimal medium, with 0.5% (w/v) D8-glycerol as the carbon source, was used for production of deuterated protein by previously described procedures (32).

Figure 1.

Figure 1

Open in a new tab

Structure of GFP, from PDB:1GFL (29).

In brief, the recombinant protein was purified using a combination of salting-out using ammonium sulfate, anion exchange chromatography, and gel-filtration chromatography (30). The protein was extensively dialyzed against H2O to remove buffer salts before lyophilization. Overexpression and purification of the hydrogenated protein was carried out in an identical manner to deuterated protein except that all media and buffer solutions were prepared in H2O. The purity of the protein was determined by sodium dodecyl sulfate polyacrylamide gel electrophoresis and UV-visible spectrophotometry.

All protein samples were equilibrated in the solvent of opposite isotope (h-GFP in D2O and d-GFP in H2O) to allow for full hydrogen/deuterium exchange of all exchangeable atoms, and then lyophilized. The lyophilized h-GFP sample was used as a dry sample. Other samples were hydrated to a ratio of 0.4 (mass solvent/mass protein) of the appropriate solvent by placing the sample in a hydration chamber under nitrogen and subsequently sealed in aluminum sample holders. Neutron scattering measurements were performed using 100–200 mg of protein samples (dry weight) to have transmission >90% and avoid significant multiple scattering. We point out that the h-GFP/D2O sample has hydrogen atoms only on protein (nonexchangeable hydrogens), whereas d-GFP/H2O sample still has ∼22% of total hydrogen on the protein (exchangeable hydrogen atoms are 24% of all H-atoms in the protein). Thus the neutron scattering data of the latter reflect not only hydration water, but also a minor contribution of GFP’s exchangeable hydrogen atoms. Thus ∼22% of the scattering signal in d-GFP/H2O sample comes from the protein. Details of the scattering cross-section for each component of the samples are included in Table S1 of the Supporting Material.

Neutron scattering

Neutron scattering measurements at several temperatures were performed on three spectrometers. The High Flux Back-scattering Spectrometer (HFBS) NG2 at the National Institute of Standards and Technology was used for elastic scans and quasielastic (QENS) measurements in the energy range ± 17 μeV (corresponding time ∼60 ps) at a resolution of ∼1 μeV (∼1 ns) and the scattering wave-vector range Q = 0.25–1.75 Å−1. Elastic scans were performed at a heating rate of 1 K/min starting from T = 10 K. The Backscattering Spectrometer (BASIS) at the Oak Ridge National Laboratory Spallation Neutron Source was used for QENS measurements in a broader energy range of ± 120 μeV (∼8 ps) with a resolution of 3.5 μeV (∼300 ps) and a Q-range of 0.2–2.0 Å−1 (33). The Cold Neutron Chopper Spectrometer (CNCS) at the Spallation Neutron Source was used for measurements in the energy range up to ∼20 meV (∼0.05 ps) with the resolution ∼50 μeV (∼20 ps) in the Q-range from 0.5 to 4 Å−1 (34). Combination of these three spectrometers covers a broad energy range sufficient for studies dynamics from faster than ps up to ∼1-ns time range. All spectra were corrected for a background and sample holder, and were normalized to the number of hydrogen atoms in each sample (the masses of the samples are presented in Table S2 of the Supporting Material). No multiple scattering corrections have been used.

Results

The mean-square atomic displacements (MSD) 〈r2〉 were calculated from the elastic scan data using the Gaussian approximation,

〈r2〉=−3Q2ln[Iel(Q,T)Iel(Q,10K)], (1)

and a Q-range from 0.65 to 1.75 Å−1 (we excluded four lowest Q detectors, because these have slightly different resolutions than the other detectors). Here Iel(Q,T) is the elastic intensity measured at particular Q and temperature. The 〈r2〉 values reflect contributions from all hydrogen atom motions on timescales faster than ∼1 ns (the resolution of the HFBS spectrometer). As has been emphasized previously (35,36), the factor 3 in Eq. 1 actually corresponds to the mean-squared fluctuations, whereas estimates of the mean-squared displacement for a diffusive-like motion should have the factor 6. In our analysis, however, we will keep the factor 3 to be consistent with 〈r2〉 calculated for other proteins (e.g., lysozyme in Roh et al. (15,37)). A non-Gaussian approximation, that includes the Q4 term, describes the Q-dependence of the elastic intensity better (36). However, our analysis (see the Supporting Material) shows no significant difference between Gaussian and non-Gaussian approximations and we therefore used the Eq. 1 in our analysis for direct comparison to earlier literature data (which were all performed using Gaussian approximation).

Fig. 2 shows the obtained 〈r2〉 as a function of temperature for the three samples. It is interesting that temperature dependence of 〈r2〉 in d-GFP/H2O shows no increase in slope up to T ∼ 180–190 K (Fig. 2 a). Above this temperature, 〈r2〉 increases sharply with T, but with no sign of specific changes in the temperature range of the so-called protein dynamic transition TD ∼ 200–230 K (Fig. 2 a). We limited presentation of the MSD data for the d-GFP/H2O sample to T ∼ 250–270 K, because Gaussian approximation becomes inaccurate at such large 〈r2〉.

Figure 2.

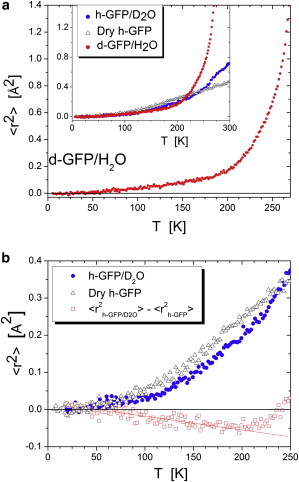
Figure 2

Open in a new tab

Temperature variation of mean-squared displacements. (a) 〈r2〉 in d-GFP/H2O reflects motions of hydration water. (Inset) 〈r2〉 in dry h-GFP, h-GFP/D2O, and d-GFP/H2O. (b) 〈r2〉 in h-GFP/D2O (solid circles) and dry h-GFP (open triangles). The difference (open squares) monotonically decreases with temperature up to T ∼ 200 K.

In contrast to d-GFP/H2O sample, 〈r2〉 of h-GFP in both the dry and hydrated states exhibits a clear change of slope at T ∼ 120 K (Fig. 2 b). This change is ascribed to methyl group rotations that reach the nanosecond time window already at low temperatures (15–17,35,37). In addition, temperature variations of 〈r2〉 in h-GFP/D2O exhibit another change at T ∼ 225 K, the so-called dynamic transition (Fig. 2). It is interesting that 〈r2〉 in dry h-GFP is higher than in h-GFP/D2O in the entire temperature range up to T ∼ 230 K (Fig. 2 b). The difference between mean-squared displacements of h-GFP/D2O and dry h-GFP varies linearly with temperature up to T ∼ 180–190 K, where the difference starts to level off and then decreases above the dynamic transition temperature. This observation suggests that hydration water reduces protein 〈r2〉 at low T, while increasing it at higher T.

Next we compare QENS spectra of h-GFP/D2O and d-GFP/H2O in the μeV energy range (HFBS data, Figs. 3 and 4) summed over all the measured Q. At T = 170 K the h-GFP/D2O sample shows clear broadening, whereas the QENS spectrum of d-GFP/H2O remains within the resolution function (Fig. 3). These observations indicate the presence of some relaxation process in the protein and the absence of any significant relaxation in its hydration water on the nanosecond timescale. The result is consistent with the change in the 〈r2〉 at T ∼ 120 for the protein and a harmonic behavior of 〈r2〉 in its hydration water up to T ∼ 180 K (Fig. 2). Broadening of QENS spectra for both samples is evident at T = 220 K, although it remains stronger for protein than for its hydration water (Fig. 4 a). The situation changes at T = 280 K, where QENS spectrum of hydrated water becomes broader than QENS spectrum of the protein (Fig. 4 b).

Figure 3.

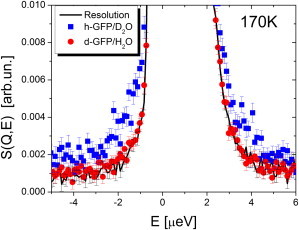
Figure 3

Open in a new tab

Quasielastic neutron scattering spectra of h-GFP/D2O and d-GFP/H2O samples at T = 170 K, summed over all Q. (Line) Spectrum of d-GFP/H2O sample at T = 4 K that presents the resolution function of the HFBS spectrometer.

Figure 4.

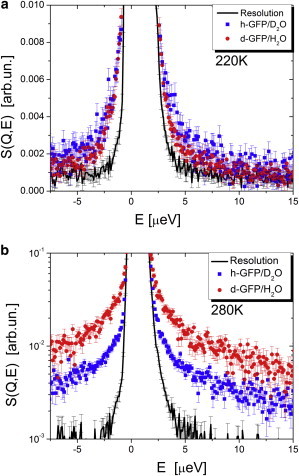
Figure 4

Open in a new tab

QENS spectra measured on HFBS spectrometer and summed over all Q at T = 220 K (a) and at T = 280 K (b) for h-GFP/D2O and d-GFP/H2O. (Lines) Resolution function.

QENS spectra in the broader energy range (BASIS data) are inconclusive at T = 170 K due to the weak broadening and significant spectrometer background, and are not presented here. The spectra at T = 220 K show similar broadening for dry h-GFP and h-GFP/D2O, and slightly lower broadening for d-GFP/H2O (Fig. 5 a). However, at T = 280 K, hydration water shows significantly stronger QENS intensity than the hydrated protein (h-GFP/D2O), and dry protein exhibits the weakest QENS (Fig. 5 b). These results are consistent with the HFBS data (both elastic, Fig. 2, and quasielastic, Figs. 3 and 4).

Figure 5.

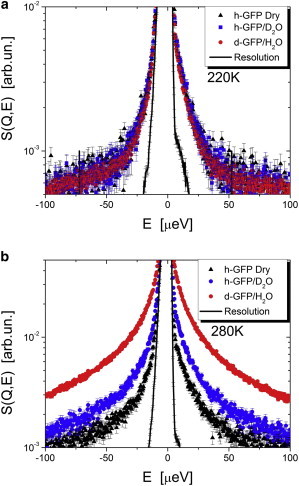
Figure 5

Open in a new tab

QENS spectra in a broader energy range measured on BASIS spectrometer and summed over all Q at T = 220 K (a) and at T = 280 K (b) for dry h-GFP, h-GFP/D2O, and d-GFP/H2O. (Lines) Resolution function.

The neutron scattering data at T = 170 K measured with the spectrometer at the CNCS show QENS spectra at energies <1 meV and an inelastic peak in the range ∼2–5 meV (Fig. 6), the so-called boson peak. The boson peak corresponds to the collective vibrations known for all proteins and glass-forming liquids (38–42). The boson peak in dry protein (dry h-GFP) shifts to higher energy upon hydration (h-GFP/D2O) indicating a more rigid structure (Fig. 6). This shift of the boson peak is consistent with the lower 〈r2〉 of h-GFP/D2O sample at lower temperatures relative to dry h-GFP (Fig. 2). Spectrum of d-GFP/H2O shows a strong peak at E ∼ 6 meV and a shoulder at E ∼ 3–4 meV (Fig. 6). The 3–4 meV peak is in the region of the peak in h-GFP/D2O and can be assigned to the vibrations of protein exchangeable hydrogen atoms, as has been shown for myoglobin in Paciaroni et al. (43). It is interesting that the vibrational spectrum of hydrated protein differs strongly from the spectrum of its hydration water.

Figure 6.

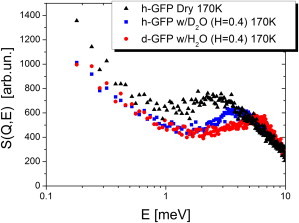
Figure 6

Open in a new tab

Dynamic structure factor from inelastic neutron scattering of d-GFP/H2O (red circles), h-GFP/D2O (blue squares), and dry h-GFP (black triangles) samples at T = 170 K. The spectra are summed over all measured Q (0.5–5 Å−1). Dry h-GFP shows the highest QENS spectrum at E < 1 meV.

Discussion

Dynamics of hydration water

No changes in the temperature dependence of 〈r2〉 of d-GFP/H2O up to T ∼ 180–190 K (Fig. 2 a) and no measurable QENS broadening at T = 170 K (Fig. 3) demonstrate that dynamics of hydration water remains essentially harmonic at these temperatures. No changes are detected around T ∼ 120 K, where methyl group rotations become visible in the protein data (Figs. 2 b and 3). The results provide clear evidence supporting the conclusion that methyl group rotations are decoupled from the dynamics of hydration water, and that the latter does not show any appreciable relaxation in the temperature range below ∼170 K over which protein methyl rotations become visible in the same neutron scattering measurements.

The change in 〈r2〉 of d-GFP/H2O at T ∼ 180–190 K can be ascribed to the glass transition of the system protein and its hydration water. Various measurements of hydrated proteins suggest that their glass transition temperature is in the range T ∼ 160–190 K and the transition is very broad (41,42). A change of the mean-squared displacements at Tg is known for glass-forming systems (44). This change is not related to the main structural relaxation, because the latter is too slow for neutron scattering measurements at temperatures around Tg. The change in the temperature dependence of 〈r2〉 at Tg is usually ascribed to variations in the faster dynamics caused by strong increase of the thermal expansion coefficient upon crossing Tg. The same should be applicable to the protein hydration water.

Structural relaxation in the hydration water is detectable at T ∼ 220 K as a broadening of QENS spectra (Figs. 4 a and 5 a). This broadening becomes more significant at higher T = 280 K. Analysis of the QENS spectra at 280 K shows a strong Q-dependence of the observed broadening. For detailed analysis, the QENS spectra are presented as the imaginary part of the susceptibility (analogous to mechanical or dielectric loss spectra) (Fig.7):

χ″(Q,E)∝S(Q,E)nB(T,E)=S(Q,E)∗[exp(EkT)−1]. (2)

Here, nB(T,E) is the temperature Bose factor. The susceptibility presentation of the neutron scattering spectra has been used in pioneering work (45) demonstrating the existence of fast and slow relaxations in myoglobin. This presentation has several advantages over use of the dynamic structure factor, S(Q,E) (37): 1), characteristic relaxation time can be easily estimated from the maximum of the susceptibility spectrum; 2), any two well-separated relaxation processes appear as two separate peaks in χ″(Q,E); 3), stretching of the relaxation spectrum can be easily estimated from the shape of the peak in χ″(Q,E); and 4), ease of comparison exists with other experimental techniques used to study relaxation phenomena.

Figure 7.

Figure 7

Open in a new tab

Susceptibility spectra of d-GFP/H2O sample at different Q (shown by numbers), measured at T = 280 K. (Lines) Fits to the Cole-Cole function.

The susceptibility spectra of d-GFP/H2O show a clear peak in the μeV range that shifts strongly to higher energy with increase in Q (Fig. 7). The spectrum at each Q is stretched on both sides and can be well fitted by the Cole-Cole distribution function:

χ″(ω)=χ0(ωτ)αSinπα21+2(ωτ)αCosπα2+(ωτ)2α. (3)

Here α ≤ 1 is the stretching exponent, which for a single exponential (Debye) relaxation process is α = 1. A fit to the susceptibility spectra provides estimates of the Q-dependence of characteristic relaxation time τ(Q) (Fig. 8) and of the stretching parameter, α(Q). Although the stretching parameter α(Q) ∼ 0.6 is rather independent of Q, the characteristic relaxation time shows a strong variation with Q characteristic for diffusive motions: τ(Q) ∝ Q−2.5. Regular diffusion has τ(Q) ∝ Q−2 and is observed in bulk water (Fig. 8) (46). The stronger Q-dependence is usually observed in glass-forming systems (47).

Figure 8.

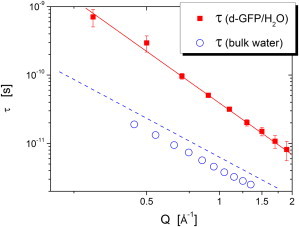
Figure 8

Open in a new tab

Q-dependence of the relaxation time in the d-GFP/H2O spectra (solid squares) at T = 280 K obtained from the fit to the Cole-Cole function (Fig. 7). (Solid line) Fit by a power law. (Open circles) τ of the bulk water from Russo et al. (45) measured at T = 295 K. (Dashed line) Fit of the bulk water data shifted by a factor 1.45 (the ratio of viscosities at T = 280 K and T = 295 K) to take into account the difference in temperature.

The susceptibility spectra of the hydration water of myoglobin and maltose binding protein were analyzed in Wood et al. (24) and Achterhold et al. (26) using time-of-flight spectrometers. Consistent with our results (Fig. 7), the susceptibility spectra did not show a well-resolved peak down to energy ∼0.1 meV, where the significant contribution of the elastic intensity starts to dominate the spectra. The authors of Wood et al. (24) tried to correct the elastic intensity contribution and estimated the relaxation time of hydration water at Q = 1.2 Å−1 and T = 300 K to be ∼15 ps. This value is close to our estimate at the same Q, τ ∼ 25 ps (Fig. 8), taking into account the difference in temperature (our measurements were performed at T = 280 K).

The comparison shown in Fig. 8 illustrates that GFP hydration water is slowed down ∼4 times relative to the bulk water at large Q (Q ∼ 1.8 Å−1), a range probing local-scale motions (L ∼ 2π/Q ∼ 3 Å). This slowdown agrees with dielectric measurements of RNase A (48) and light-scattering measurements of lysozyme (49) that also probe local motions. However, the difference between the dynamics of hydration and bulk water increases with decreasing Q (increase of probe distance) and reaches ∼15 at Q ∼ 0.4 Å−1 (Fig. 8). This stronger Q-dependence of the relaxation time in hydration water can be related to the more tortuous path of molecular diffusion along the surface of proteins in powder samples. Our results for the Q-dependence of the characteristic relaxation time of GFP hydration water agree well with recent simulations of hydration water of lysozyme, τ(Q) ∝ Q−2.5 (20), and with experimental data on the hydration water of deuterated phycocyanin, τ(Q) ∝ Q−2.44 (21). The latter studies also agree with our finding of strong and rather Q-independent stretching of the structural relaxation in phycocyanin’s hydration water. These good quantitative agreements suggest that dynamics of hydration water behaves similarly in different proteins.

Finally we comment on the actively debated topic of the Fragile-to-Strong Crossover in the hydration water of biomolecules, as proposed in Chen et al. (50). Multiple studies using dielectric, neutron scattering, and NMR experiments (22,51–53,55) revealed no cusplike Fragile-to-Strong Crossover in the dynamics of proteins and their hydration water and the authors of these articles ascribed the observed phenomenon to the resolution window of the neutron spectrometers. These results, however, do not provide any additional information for this discussion and this topic is therefore not within the scope of this article.

Dynamics of GFP

Neutron scattering data of h-GFP are dominated by the contribution of the protein’s H-atoms, and can be used to analyze directly the dynamics of GFP. The value 〈r2〉 shows a change in temperature dependence at T ∼ 120 K, similar for both dry h-GFP and h-GFP/D2O (Fig. 2 b). This change is ascribed to rotation of methyl groups that have the relatively low energy barriers for rotation and appear in the nanosecond time range probed by neutron spectroscopy already at T ∼ 100–150 K. There is a suggestion that methyl groups might play a significant role in facilitating the dynamics of proteins (56).

The observation of such a significantly higher 〈r2〉 in dry h-GFP than in the h-GFP/D2O at T below ∼230 K (Fig. 2 b) is unusual. The difference in 〈r2〉 (Fig. 2 b) exhibits smooth temperature dependence up to ∼180–200 K with no sign of any changes at T ∼ 120 K. This observation emphasizes that the difference is not related to methyl groups and that the onset of the methyl groups' contribution to 〈r2〉 appears at a similar T. At the same time, high energy spectra show very clear difference in position of the boson peak at T = 170 K (Fig. 6). This higher energy of the boson peak for hydrated compared to dry proteins at low temperatures has been observed for many other proteins using neutron and light-scattering measurements, including myoglobin (40,44,57–59), lysozyme (38) SNase A (60), azurin (61), and β-lactoglobulin (62). The higher energy of the boson peak suggests higher rigidity of the vibrational modes and leads to smaller 〈r2〉. In addition, the broad QENS spectra in the range ∼0.1–1 meV (Fig. 6) are more intense in dry compared to h-GFP/D2O samples, which also contributes to the increase in 〈r2〉.

Similar behavior of the broad quasielastic spectra has also been observed in DNA using neutron scattering (63) and for lysozyme using light scattering (38). Thus, the observed increase in 〈r2〉 of the dry protein relative to the hydrated protein can be ascribed to the difference in the fast dynamics that appears in the lower energy of the boson peak and the higher intensity of the broad QENS contribution. The latter is usually ascribed to small amplitude conformational fluctuations, i.e., “rattling in a cage” formed by neighbor structural units (64). It is interesting that the spectra of the broad QENS component in GFP and in its hydration water are very similar (Fig. 6). Strong coupling of the fast dynamics in proteins to the fast dynamics of solvents has been emphasized earlier from light-scattering studies (38).

The observed difference in 〈r2〉 between dry h-GFP and h-GFP/D2O suggests that hydration water suppresses dynamics of biomolecules at low temperatures, making them more rigid, and decreasing the amplitude of rattling in cages. The latter indicates that the frozen hydration shell restricts fluctuations of amino-acid residues at lower temperatures. A similar hydration-induced decrease in 〈r2〉 at low temperatures is visible in data for other proteins, e.g., lysozyme (15,65), RNase A (66), myoglobin (7,13), and pig liver esterase (67). However, a suppression of 〈r2〉 with hydration as strong as the present GFP case has not been observed previously. A possible reason for such a pronounced suppression of the MSD at low temperatures is the barrellike structure of GFP that differs significantly from previously studied globular proteins.

Another interesting observation is relatively weak increase in MSD of GFP at ambient temperature upon hydration (inset, Fig. 2 a). To illustrate this point we compare directly the MSD of GFP to that of lysozyme. This requires that the MSD of lysozyme as measured by Roh et al. (37) be recalculated in the same Q-range (0.6–1.7 Å−1) as used in this work for GFP. Although 〈r2〉 ∼ 0.5 Å2 at T ∼ 300 K in h-GFP is slightly higher than 〈r2〉 ∼ 0.45 Å2 in dry lysozyme, h-GFP/D2O has lower 〈r2〉 ∼ 0.7 Å2 than hydrated lysozyme 〈r2〉 ∼ 0.9 Å2 (see Fig. S4 in the Supporting Material). We emphasize that both the GFP and lysozyme data were obtained on the same spectrometer and the data were fit over the same Q-range (0.6–1.7 Å−1). Weaker variations upon hydration are observed also in the QENS spectra: whereas the QENS intensity in h-GFP/D2O increases <2 times relative to the QENS intensity of h-GFP (Fig. 5 b) at T = 280 K, that in hydrated lysozyme at h ∼ 0.4 is ∼3 times higher than in the dry protein (15,68). Taken together, these results suggest that the dynamics of h-GFP/D2O are more depressed than dynamics of lysozyme at a similar hydration level (h ∼ 0.4).

Data for ribonuclease A presented in Wood et al. (66) demonstrate 〈r2〉 in the hydrated protein at T ∼ 300 K is more than twice that of the dry protein, whereas GFP shows only ∼30% increase in 〈r2〉 upon hydration at the same T (Fig. 2). This ratio was also >2 for myoglobin measured on even shorter timescales (using IN13 spectrometer, Fig. 7 of the cited work) (17). Apparently, the barrellike structure of GFP leads to ambient temperature dynamics, which are less affected by the dynamics of hydration water. This may be due to differences in the secondary structures that compose the protein: α-helices are the main structural units of lysozyme and myoglobin, whereas β-sheets dominate the structure of GFP. The β-sheets are usually more rigid than α-helices, and this might explain the observed difference in dynamics of these proteins. Another possibility is the entrance of loop motions and domain motions into the experimental window. Although there are likely to be considerable loop dynamics in GFP at the turns of the β-sheets, there are no intraprotein domain motions expected in GFP. On the other hand, lysozyme, myoglobin, and ribonuclease A have intraprotein domain motions (e.g., hinge-bending) that might be entering the experimental window at near 300 K.

To analyze Q-dependence of the GFP’s QENS spectra we present them as an imaginary part of susceptibility (Fig. 9). The obtained χ″(E,Q) spectra are very broad, suggesting an extremely broad distribution of relaxation times in both dry and hydrated GFP (Fig. 9). However, the statistics of the data are simply not good enough to do any meaningful analysis of the Q-dependence of the spectral shape. The Q-dependence appears only in the intensity of the spectra. This is in strong contrast with the QENS spectra of the hydration water (Fig. 7) and is indicative of localized motions. In the case of dry GFP, the major contribution probably comes from methyl group rotations, which are a local process. Apparently, motions in the hydrated protein are similarly localized on a scale smaller than ∼2π/Qmax∼3 Å.

Figure 9.

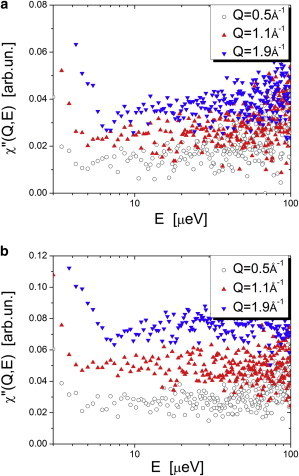
Figure 9

Open in a new tab

Susceptibility spectra of (a) dry h-GFP and (b) h-GFP/D2O measured at different Q at T = 280 K.

This result agrees with earlier experimental (37) and recent simulation (18,20) studies of lysozyme dynamics, which demonstrated that hydration-induced relaxation in a protein is a diffusive-like process confined to a radius of ∼1.5–3 Å. The results presented are consistent with the classification of relaxation processes in proteins proposed in Hong et al. (18): the major contribution to the picosecond-to-nanosecond time window at ambient temperature comes from methyl group rotation and from localized motions of other structural units. This general result can be well understood considering the internal dynamics of folded proteins: In powder samples we can neglect any center-of-mass diffusion and rotation of proteins on the timescale accessible to QENS spectrometers (shorter than ∼2 ns). As long as the protein stays folded, it is difficult to expect that averaged amplitude of motions will exceed ∼3–5 Å when the radius of the entire protein is only ∼20–30 Å.

Conclusions

Detailed analysis of the neutron scattering spectra of d-GFP/H2O and h-GFP/D2O provides a direct comparison of the dynamics of the protein to that of its hydration water. The absence of anharmonic variations in the dynamics of the hydration water up to T ∼ 180 K indicates a complete decoupling of water and methyl group rotations. At ambient temperatures the dynamics of hydration water show clear diffusive character, whereas dynamics of the protein is localized on a scale smaller than 3 Å. This is consistent with expectations for the internal dynamics of folded protein. Our analysis also shows that the dynamics of hydration water on local length scales slows down relative to bulk water by only a factor ∼4. The difference, however, is much larger on longer length scales.

An interesting observation is that hydration water suppresses protein dynamics at lower temperatures (T < ∼200K), while facilitating the dynamics at higher temperatures. Frozen hydration water makes the protein structure more rigid and suppresses fast picosecond fluctuations. Most interestingly, the comparison of the GFP data to earlier studies of other globular proteins, such as lysozyme, myoglobin, and RNase A, indicates a clear influence of the protein structure on its dynamics: The dynamics of h-GFP/D2O at ambient temperature appears with smaller amplitude (smaller MSD and QENS intensity) than that of hydrated lysozyme. We ascribe this observation to the β-barrel structure of GFP. The dynamics of hydration water on the other hand, seem to behave similarly to that of other proteins.

Acknowledgments

Certain commercial materials (and suppliers) are identified in this article to foster understanding. Such identification does not imply recommendation or endorsement by the National Institute of Standards and Technology, nor does it imply that the materials identified are necessarily the best available for the purpose.

J.D.N. and A.P.S. acknowledge Department of Energy support through the Experimental Program to Stimulate Competitive Research program (grant No. DE-FG02-08ER46528) and support from Spallation Neutron Source through UT-Battelle. The research at Oak Ridge National Laboratory's Spallation Neutron Source was sponsored by the Scientific User Facilities Division, Office of Basic Energy Sciences, U.S. Department of Energy. J.C.S. acknowledges support from the National Science Foundation (Molecular Biosystems Cluster). H.O’N., Q.Z., and K.W. acknowledge the support of the Center for Structural Molecular Biology at the Oak Ridge National Laboratory supported by the U.S. Department of Energy, Office of Science, Office of Biological and Environmental Research Project No. ERKP291. This work utilized facilities supported in part by the National Science Foundation under Agreement No. DMR-0944772.

Supporting Material

Document S1. Two tables and four figures
mmc1.pdf (73.7KB, pdf)

References

  • 1.Austin R.H., Beeson K.W., Gunsalus I.C. Dynamics of ligand binding to myoglobin. Biochemistry. 1975;14:5355–5373. doi: 10.1021/bi00695a021. [DOI] [PubMed] [Google Scholar]
  • 2.Frauenfelder H., Sligar S.G., Wolynes P.G. The energy landscapes and motions of proteins. Science. 1991;254:1598–1603. doi: 10.1126/science.1749933. [DOI] [PubMed] [Google Scholar]
  • 3.Henzler-Wildman K., Kern D. Dynamic personalities of proteins. Nature. 2007;450:964–972. doi: 10.1038/nature06522. [DOI] [PubMed] [Google Scholar]
  • 4.Henzler-Wildman K.A., Lei M., Kern D. A hierarchy of timescales in protein dynamics is linked to enzyme catalysis. Nature. 2007;450:913–916. doi: 10.1038/nature06407. [DOI] [PubMed] [Google Scholar]
  • 5.Beece D., Eisenstein L., Yue K.T. Solvent viscosity and protein dynamics. Biochemistry. 1980;19:5147–5157. doi: 10.1021/bi00564a001. [DOI] [PubMed] [Google Scholar]
  • 6.Nienhaus G.U., Frauenfelder H., Parak F. Structural fluctuations in glass-forming liquids: Mössbauer spectroscopy on iron in glycerol. Phys. Rev. B Condens. Matter. 1991;43:3345–3350. doi: 10.1103/physrevb.43.3345. [DOI] [PubMed] [Google Scholar]
  • 7.Fenimore P.W., Frauenfelder H., Parak F.G. Slaving: solvent fluctuations dominate protein dynamics and functions. Proc. Natl. Acad. Sci. USA. 2002;99:16047–16051. doi: 10.1073/pnas.212637899. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Tarek M., Tobias D.J. Role of protein-water hydrogen bond dynamics in the protein dynamical transition. Phys. Rev. Lett. 2002;88:138101–138104. doi: 10.1103/PhysRevLett.88.138101. [DOI] [PubMed] [Google Scholar]
  • 9.Tournier A.L., Xu J., Smith J.C. Translational hydration water dynamics drives the protein glass transition. Biophys. J. 2003;85:1871–1875. doi: 10.1016/S0006-3495(03)74614-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Roh J.H., Briber R.M., Sokolov A.P. Dynamics of tRNA at different levels of hydration. Biophys. J. 2009;96:2755–2762. doi: 10.1016/j.bpj.2008.12.3895. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Khodadadi S., Pawlus S., Sokolov A.P. Influence of hydration on protein dynamics: combining dielectric and neutron scattering spectroscopy data. J. Phys. Chem. B. 2008;112:14273–14280. doi: 10.1021/jp8059807. [DOI] [PubMed] [Google Scholar]
  • 12.Khodadadi S., Roh J.H., Sokolov A.P. Dynamics of biological macromolecules: not a simple slaving by hydration water. Biophys. J. 2010;98:1321–1326. doi: 10.1016/j.bpj.2009.12.4284. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Fenimore P.W., Frauenfelder H., Young R.D. Bulk-solvent and hydration-shell fluctuations, similar to α- and β-fluctuations in glasses, control protein motions and functions. Proc. Natl. Acad. Sci. USA. 2004;101:14408–14413. doi: 10.1073/pnas.0405573101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Frauenfelder H., Chen G., Young R.D. A unified model of protein dynamics. Proc. Natl. Acad. Sci. USA. 2009;106:5129–5134. doi: 10.1073/pnas.0900336106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Roh J.H., Novikov V.N., Sokolov A.P. Onsets of anharmonicity in protein dynamics. Phys. Rev. Lett. 2005;95:038101–038104. doi: 10.1103/PhysRevLett.95.038101. [DOI] [PubMed] [Google Scholar]
  • 16.Wood K., Tobias D.J., Weik M. The low-temperature inflection observed in neutron scattering measurements of proteins is due to methyl rotation: direct evidence using isotope labeling and molecular dynamics simulations. J. Am. Chem. Soc. 2010;132:4990–4991. doi: 10.1021/ja910502g. [DOI] [PubMed] [Google Scholar]
  • 17.Doster W., Settles M. Protein-water displacement distributions. Biochim. Biophys. Acta. 2005;1749:173–186. doi: 10.1016/j.bbapap.2005.03.010. [DOI] [PubMed] [Google Scholar]
  • 18.Hong L., Cheng X., Smith J.C. Surface hydration amplifies single-well protein atom diffusion propagating into the macromolecular core. Phys. Rev. Lett. 2012;108:238102–238106. doi: 10.1103/PhysRevLett.108.238102. [DOI] [PubMed] [Google Scholar]
  • 19.Glass D.C., Krishnan M., Smith J.C. Temperature dependence of protein dynamics simulated with three different water models. J. Chem. Theory Comput. 2010;6:1390–1400. [Google Scholar]
  • 20.Hong L., Smolin N., Smith J.C. Three classes of motion in the dynamic neutron-scattering susceptibility of a globular protein. Phys. Rev. Lett. 2011;107:148102–148105. doi: 10.1103/PhysRevLett.107.148102. [DOI] [PubMed] [Google Scholar]
  • 21.Dellerue S., Bellissent-Funel M.C. Relaxational dynamics of water molecules at protein surface. Chem. Phys. 2000;258:315–325. [Google Scholar]
  • 22.Doster W., Busch S., Scheer H. Dynamical transition of protein-hydration water. Phys. Rev. Lett. 2010;104:098101–098104. doi: 10.1103/PhysRevLett.104.098101. [DOI] [PubMed] [Google Scholar]
  • 23.Wood K., Plazanet M., Weik M. Coupling of protein and hydration-water dynamics in biological membranes. Proc. Natl. Acad. Sci. USA. 2007;104:18049–18054. doi: 10.1073/pnas.0706566104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Wood K., Frölich A., Weik M. Coincidence of dynamical transitions in a soluble protein and its hydration water: direct measurements by neutron scattering and MD simulations. J. Am. Chem. Soc. 2008;130:4586–4587. doi: 10.1021/ja710526r. [DOI] [PubMed] [Google Scholar]
  • 25.Paciaroni A., Cornicchi E., Sacchetti F. Coupled relaxations at the protein-water interface in the picosecond time scale. J. R. Soc. Interface. 2009;6(Suppl 5):S635–S640. doi: 10.1098/rsif.2009.0182.focus. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Achterhold K., Ostermann A., Parak F.G. Dynamical properties of the hydration shell of fully deuterated myoglobin. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2011;84:041930. doi: 10.1103/PhysRevE.84.041930. [DOI] [PubMed] [Google Scholar]
  • 27.Gallat F.-X., Laganowsky A., Weik M. Dynamical coupling of intrinsically disordered proteins and their hydration water: comparison with folded soluble and membrane proteins. Biophys. J. 2012;103:129–136. doi: 10.1016/j.bpj.2012.05.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Ormö M., Cubitt A.B., Remington S.J. Crystal structure of the Aequorea victoria green fluorescent protein. Science. 1996;273:1392–1395. doi: 10.1126/science.273.5280.1392. [DOI] [PubMed] [Google Scholar]
  • 29.Yang F., Moss L.G., Phillips G.N., Jr. The molecular structure of green fluorescent protein. Nat. Biotechnol. 1996;14:1246–1251. doi: 10.1038/nbt1096-1246. [DOI] [PubMed] [Google Scholar]
  • 30.Heller W.T., O’Neill H.M., Baker G.A. Characterization of the influence of the ionic liquid 1-butyl-3-methylimidazolium chloride on the structure and thermal stability of green fluorescent protein. J. Phys. Chem. B. 2010;114:13866–13871. doi: 10.1021/jp105611b. [DOI] [PubMed] [Google Scholar]
  • 31.Cormack B.P., Valdivia R.H., Falkow S. FACS-optimized mutants of the green fluorescent protein (GFP) Gene. 1996;173(1 Spec No):33–38. doi: 10.1016/0378-1119(95)00685-0. [DOI] [PubMed] [Google Scholar]
  • 32.Luo G.M., Zhang Q., O’Neill H. Characterization of sol-gel-encapsulated proteins using small-angle neutron scattering. ACS Appl. Mater. Interfaces. 2009;1:2262–2268. doi: 10.1021/am900430v. [DOI] [PubMed] [Google Scholar]
  • 33.Mamontov E., Herwig K.W. A time-of-flight backscattering spectrometer at the Spallation Neutron Source, BASIS. Rev. Sci. Instrum. 2011;82:085109–085118. doi: 10.1063/1.3626214. [DOI] [PubMed] [Google Scholar]
  • 34.Ehlers G., Podlesnyak A.A., Sokol P.E. The new cold neutron chopper spectrometer at the Spallation Neutron Source: design and performance. Rev. Sci. Instrum. 2011;82:085108–085113. doi: 10.1063/1.3626935. [DOI] [PubMed] [Google Scholar]
  • 35.Schiró G., Caronna C., Cupane A. Direct evidence of the amino acid side chain and backbone contributions to protein anharmonicity. J. Am. Chem. Soc. 2010;132:1371–1376. doi: 10.1021/ja908611p. [DOI] [PubMed] [Google Scholar]
  • 36.Yi Z., Miao Y., Smith J.C. Derivation of mean-square displacements for protein dynamics from elastic incoherent neutron scattering. J. Phys. Chem. B. 2012;116:5028–5036. doi: 10.1021/jp2102868. [DOI] [PubMed] [Google Scholar]
  • 37.Roh J.H., Curtis J.E., Sokolov A.P. Influence of hydration on the dynamics of lysozyme. Biophys. J. 2006;91:2573–2588. doi: 10.1529/biophysj.106.082214. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Caliskan G., Mechtani D., Peral I. Protein and solvent dynamics: how strongly are they coupled? J. Chem. Phys. 2004;121:1978–1983. doi: 10.1063/1.1764491. [DOI] [PubMed] [Google Scholar]
  • 39.Malinovsky V.K., Novikov V.N., Zemlyanov M.G. Universal form of the low-energy (2 to 10 Mev) vibrational-spectrum of glasses. Europhys. Lett. 1990;11:43–47. [Google Scholar]
  • 40.Doster W., Leyser H., Diehl M. Far-infrared emission by boson peak vibrations in a globular protein. Phys. Rev. Lett. 1999;82:2987–2990. [Google Scholar]
  • 41.Doster W. The protein-solvent glass transition. Biochim. Biophys. Acta. 2010;1804:3–14. doi: 10.1016/j.bbapap.2009.06.019. [DOI] [PubMed] [Google Scholar]
  • 42.Khodadadi S., Malkovskiy A., Sokolov A.P. A broad glass transition in hydrated proteins. Biochim. Biophys. Acta. 2010;1804:15–19. doi: 10.1016/j.bbapap.2009.05.006. [DOI] [PubMed] [Google Scholar]
  • 43.Paciaroni A., Orecchini A., Sacchetti F. Fingerprints of amorphous icelike behavior in the vibrational density of states of protein hydration water. Phys. Rev. Lett. 2008;101:148104. doi: 10.1103/PhysRevLett.101.148104. [DOI] [PubMed] [Google Scholar]
  • 44.Buchenau U., Zorn R. A relation between fast and slow motions in glassy and liquid selenium. Europhys. Lett. 1992;18:523–528. [Google Scholar]
  • 45.Doster W., Cusack S., Petry W. Dynamic instability of liquidlike motions in a globular protein observed by inelastic neutron scattering. Phys. Rev. Lett. 1990;65:1080–1083. doi: 10.1103/PhysRevLett.65.1080. [DOI] [PubMed] [Google Scholar]
  • 46.Russo D., Hura G., Head-Gordon T. Hydration dynamics near a model protein surface. Biophys. J. 2004;86:1852–1862. doi: 10.1016/S0006-3495(04)74252-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 47.Richter D., Monkenbusch M., Colmenero J. Neutron spin echo in polymer systems. Adv. Polym. Sci. 2005;174:1–221. [Google Scholar]
  • 48.Oleinikova A., Sasisanker P., Weingartner H. What can really be learned from dielectric spectroscopy of protein solutions? A case study of ribonuclease A. J. Phys. Chem. B. 2004;108:8467–8474. [Google Scholar]
  • 49.Perticaroli S., Comez L., Morresi A. Broadband depolarized light scattering study of diluted protein aqueous solutions. J. Phys. Chem. B. 2010;114:8262–8269. doi: 10.1021/jp101896f. [DOI] [PubMed] [Google Scholar]
  • 50.Chen S.H., Liu L., Mamontov E. Observation of fragile-to-strong dynamic crossover in the protein hydration water. Proc. Natl. Acad. Sci. USA. 2006;103:9012–9016. doi: 10.1073/pnas.0602474103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 51.Khodadadi S., Pawlus S., Sokolov A.P. The origin of the dynamic transition in proteins. J. Chem. Phys. 2008;128:195106–195110. doi: 10.1063/1.2927871. [DOI] [PubMed] [Google Scholar]
  • 52.Pawlus S., Khodadadi S., Sokolov A.P. Conductivity in hydrated proteins: no signs of the fragile-to-strong crossover. Phys. Rev. Lett. 2008;100:108103–108107. doi: 10.1103/PhysRevLett.100.108103. [DOI] [PubMed] [Google Scholar]
  • 53.Vogel M. Origins of apparent fragile-to-strong transitions of protein hydration waters. Phys. Rev. Lett. 2008;101:225701–225704. doi: 10.1103/PhysRevLett.101.225701. [DOI] [PubMed] [Google Scholar]
  • 54.Reference deleted in proof.
  • 55.Rosenstihl M., Vogel M. Static and pulsed field gradient nuclear magnetic resonance studies of water diffusion in protein matrices. J. Chem. Phys. 2011;135:164503–164512. doi: 10.1063/1.3653943. [DOI] [PubMed] [Google Scholar]
  • 56.Nickels J.D., Curtis J.E., Sokolov A.P. Role of methyl groups in dynamics and evolution of biomolecules. J. Biol. Phys. 2012;38:497–505. doi: 10.1007/s10867-012-9268-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 57.Kurkal-Siebert V., Smith J.C. Low-temperature protein dynamics: a simulation analysis of interprotein vibrations and the boson peak at 150 k. J. Am. Chem. Soc. 2006;128:2356–2364. doi: 10.1021/ja055962q. [DOI] [PubMed] [Google Scholar]
  • 58.Tarek M., Tobias D.J. Effects of solvent damping on side chain and backbone contributions to the protein boson peak. J. Chem. Phys. 2001;115:1607–1612. [Google Scholar]
  • 59.Diehl M., Doster W., Schober H. Water-coupled low-frequency modes of myoglobin and lysozyme observed by inelastic neutron scattering. Biophys. J. 1997;73:2726–2732. doi: 10.1016/S0006-3495(97)78301-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 60.Nakagawa H., Kataoka M., Gō N. Hydration-coupled protein boson peak measured by incoherent neutron scattering. Physica B. 2006;385–86:871–873. [Google Scholar]
  • 61.Paciaroni A., Stroppolo M.E., Cannistraro S. Incoherent neutron scattering of copper azurin: a comparison with molecular dynamics simulation results. Eur. Biophys. J. 1999;28:447–456. doi: 10.1007/s002490050227. [DOI] [PubMed] [Google Scholar]
  • 62.Orecchini A., Paciaroni A., Cannistraro S. Low-frequency vibrational anomalies in β-lactoglobulin: contribution of different hydrogen classes revealed by inelastic neutron scattering. J. Phys. Chem. B. 2001;105:12150–12156. [Google Scholar]
  • 63.Sokolov A.P., Grimm H., Dianoux A.J. Slow relaxation process in DNA. J. Biol. Phys. 2001;27:313–327. doi: 10.1023/A:1014228824104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 64.Gotze W., Sjogren L. Relaxation processes in supercooled liquids. Rep. Prog. Phys. 1992;55:241–376. [Google Scholar]
  • 65.Magazù S., Migliardo F., Benedetto A. Puzzle of protein dynamical transition. J. Phys. Chem. B. 2011;115:7736–7743. doi: 10.1021/jp111421m. [DOI] [PubMed] [Google Scholar]
  • 66.Wood K., Caronna C., Zaccai G. A benchmark for protein dynamics: Ribonuclease A measured by neutron scattering in a large wavevector-energy transfer range. Chem. Phys. 2008;345:305–314. [Google Scholar]
  • 67.Kurkal V., Daniel R.M., Smith J.C. Low frequency enzyme dynamics as a function of temperature and hydration: a neutron scattering study. Chem. Phys. 2005;317:267–273. [Google Scholar]
  • 68.Sokolov A.P., Roh J.H., Sakai V.G. Role of hydration water in dynamics of biological macromolecules. Chem. Phys. 2008;345:212–218. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Document S1. Two tables and four figures
mmc1.pdf (73.7KB, pdf)

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES