Abstract
Oxygen-evolving photosynthetic organisms possess nonphotochemical quenching (NPQ) pathways that protect against photo-induced damage. The majority of NPQ in plants is regulated on a rapid timescale by changes in the pH of the thylakoid lumen. In order to quantify the rapidly reversible component of NPQ, called qE, we developed a mathematical model of pH-dependent quenching of chlorophyll excitations in Photosystem II. Our expression for qE depends on the protonation of PsbS and the deepoxidation of violaxanthin by violaxanthin deepoxidase. The model is able to simulate the kinetics of qE at low and high light intensities. The simulations suggest that the pH of the lumen, which activates qE, is not itself affected by qE. Our model provides a framework for testing hypothesized qE mechanisms and for assessing the role of qE in improving plant fitness in variable light intensity.
Keywords: regulation of photosynthesis, nonlinear differential equations, biological feedback, chlorophyll fluorescence, photoprotection
Photosynthetic organisms are highly efficient at absorbing photons and transferring energy to a reaction center, where charge separation takes place. However, when the rate of energy consumption by the reaction center is slower than the rate of energy transfer to the reaction center, long-lived chlorophyll excited states build up in the Photosystem II (PSII) antenna. These long-lived states present a significant hazard to the organism because the energy contained in excited chlorophyll is sufficient to generate singlet oxygen, which is highly reactive and can break bonds in the proteins essential for photosynthesis (1). Because sufficient light harvesting is necessary for fueling growth, but too much is harmful, plants face a challenge in balancing light harvesting and photoprotection, especially when light intensity rapidly fluctuates between levels that limit photosynthesis and levels that exceed the plant’s capacity for photosynthesis (2).
The mechanisms of regulated dissipation of excess absorbed energy in the PSII antenna are collectively known as nonphotochemical quenching (NPQ) (3). NPQ mechanisms dissipate excitation energy harmlessly as heat, reducing the extent of photoinhibition (4). There are multiple mechanisms for NPQ and these mechanisms respond on different timescales (3). The most rapid component of NPQ is called qE, and it responds to fluctuations in light intensity on the timescale of seconds to minutes (5, 6).
The qE quenching pathway is activated by a decrease in the pH of the thylakoid lumen (3). The low pH of the lumen activates qE by protonating the proteins PsbS (7) and violaxanthin deepoxidase (VDE) (8, 9), and possibly other light harvesting complexes (10, 11). VDE goes on to convert the carotenoid violaxanthin to zeaxanthin in the xanthophyll cycle, which includes the intermediate antheraxanthin (12). The presence of zeaxanthin and the xanthophyll lutein, along with PsbS, is necessary for full expression of qE in vivo. In addition to the protonation of PsbS and the formation of zeaxanthin, the PSII antenna undergoes a rearrangement that facilitates quenching of chlorophyll excitations (13, 14). Although many of the essential components of qE are known, the exact sequence of events that lead to quenching remains an area of active research (13–17).
qE is typically observed by pulsed amplitude modulated (PAM) fluorescence, which monitors changes in the chlorophyll fluorescence yield (18). There is a great deal of PAM data showing altered qE dynamics in plants that have been genetically altered or chemically treated with various inhibitors. Interpreting the effects of mutations and chemical treatments on the lumen pH and on the dynamics of qE is difficult because a large number of interrelated processes occur on a large range of timescales (from picoseconds to minutes) in the thylakoid membrane. The ability to quantitatively evaluate and predict the expression of qE in plants would enable the testing of different hypothesized models of the qE mechanism.
Beyond testing hypotheses, a quantitative understanding of qE would provide significant benefits. Numerous experimental studies have shown that qE enhances various metrics of plant vitality in variable light conditions and does not impair the plant’s ability to thrive in constant light conditions (2, 4, 19, 20). Because qE does not seem to negatively affect the performance of plants in natural conditions, the feedback loop that activates qE must be regulated to confer a net benefit to the plant. Understanding the control parameters governing this feedback loop would provide useful information for both optimizing photosynthesis (21–23) and for designing artificial systems that are robust in fluctuating light conditions.
Although there are numerous models of chlorophyll fluorescence kinetics (24–26), the lumen (27), entire thylakoids (28), and zeaxanthin-dependent NPQ (29), we are not aware of any models simulate the kinetics of the appearance and disappearance of qE at low and high light intensities. Simulating qE in both low and high light intensities is necessary for quantifying the benefit that qE confers to plants in fluctuating light conditions. We have developed a mathematical model that describes the kinetics of processes that directly and indirectly affect the lumen pH. The model enables us to simulate measurements of the induction and decay of qE with enough accuracy that it can serve as a starting point for a computational assessment of the role of the components of qE in balancing the organism’s needs for light harvesting and photoprotection.
Mathematical Model
Model Structure.
A general schematic of the model is shown in Fig. 1. Our model consists of 26 nonlinear differential equations describing the evolution of variables involved in photosynthetic light harvesting for a given intensity of actinic light. The equations are of the form
| [1] |
where X is a vector that contains all the variables included in our model, p is a vector containing all the model parameters, and I, the light intensity, is the input. F(X; p) is the set of differential equations that describes how the evolution of the components of X depends on the components themselves, and G(I(t); p) is a function describing how the evolution of the components of X depends on the light intensity. Eq. 1 is given in a more detailed form as Eq. S1 of the SI Text. An illustration of the components of the model is shown in Fig. 2A. We have separated the processes that describe the time-evolution of the components of X into eight modules, labeled F1 through F8, each of which contains a set of differential equations corresponding to a particular process. The modules are (F1) light harvesting, (F2) qE quenching, (F3) electron transfer through the plastoquinone pool, (F4) plastoquinol oxidation at cytochrome b6f, (F5) electron transfer through plastocyanin and Photosystem I (PSI) on to ferredoxin, (F6) reduction of the stroma by ferredoxin, (F7) activation of proton efflux via the ATP synthase enzyme, and (F8) proton and ion dynamics in the lumen and stroma. We consider modules F3–F8 to be the “plant” that converts excitation energy to ATP, F1 to be the regulated input to the plant, and F2 (qE) to be the feedback regulator to F1. A summary of the modules is given in Table S1. The models for light harvesting, qE quenching, and ATP synthesis are described below; further details of the model structure, including a discussion of cyclic electron flow, are given in the SI Text.
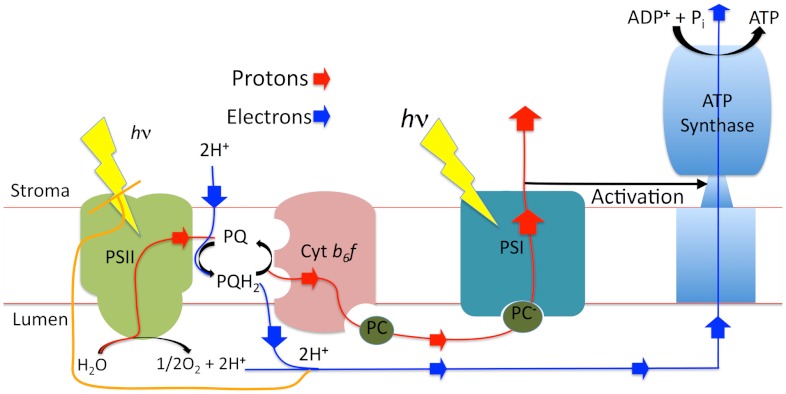
Fig. 1.
Schematic of components described in the model. For more detailed schematics, see ref. 40. Nonphotochemical quenching occurs in PSII.
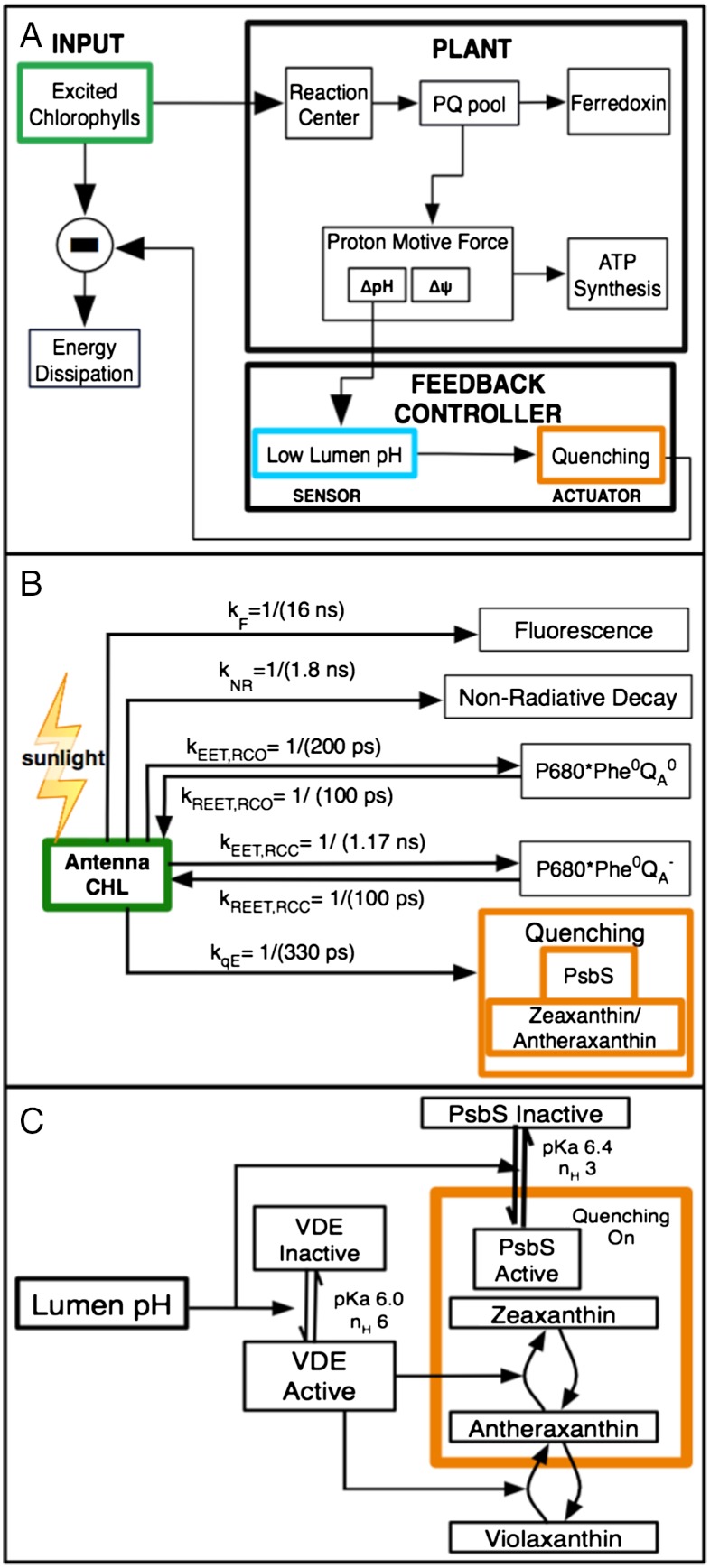
Fig. 2.
(A) Schematic of the system that activates and is affected by qE. qE regulates the concentrations of excited chlorophylls in the PSII antenna, which is directly affected by the light intensity. The ability of the photosynthetic electron transfer (the “plant”) to use the energy contained in the excited chlorophylls (“input”, green box) determines the requirement for qE. We consider qE to be the “controller” (orange box) that is triggered by the lumen pH (light blue box). The lumen pH is a component of the pmf driving ATP synthesis. (B) Modeled pathways and rates for quenching of chlorophyll fluorescence (green box) in PSII. Quenching by qE is shown in orange. (C) Components involved in the activation of qE (orange box) are a protonated PsbS protein and a deepoxodized xanthophyll. Both of these components are triggered by the lumen pH (cyan box). The numerical values of key parameters for qE is given in Table S2.
In total, the model contains 78 parameters, most of which were taken from the literature. The values of parameters in modules F3, F4, F5, and F8, were not modified from literature values. The values of parameters used in the remaining modules were adjusted to some extent (see below). An overall schematic of the model is shown in Fig. 2A, and details of the light harvesting and quenching models are shown in Fig. 2 B and C. The models for light harvesting, qE quenching, and ATP synthesis are described below; the remainder of the model is described in the SI Text.
pH-Regulated Quenching of Excited Chlorophyll.
The evolution of the number of excited chlorophylls in the PSII antenna is given by
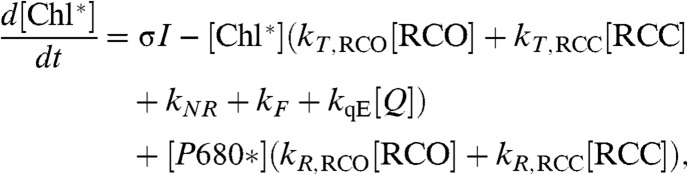 |
[2] |
where [Chl∗] is the number of excited chlorophylls associated with one PSII core; σ is the absorption cross section of one PSII; [RCO] and [RCC] are the fractions of PSII reaction centers that are open (QA oxidized) and closed (QA reduced), respectively; the rates kT,RCO and kT,RCC are the rate constants associated with energy transfer from the light harvesting antenna to P680 when the reaction centers are open and closed, respectively; kR,RCO and kT,RCC are the rate constants associated with energy transfer from excited P680 back to the antenna for open and closed reaction centers (30); kF is the rate constant for spontaneous emission (fluorescence) by an excited chlorophyll; kNR is a rate constant for other nonradiative decay processes such as intersystem crossing and internal conversion; and kqE is the rate constant associated with quenching by a qE quencher. We assume kqE = 1/(330 ps), based on the two PsbS-dependent lifetimes in ref. (4). Eq. 2 contains numerous simplifications that are discussed in the SI Text, Energy transfer within PSII.
The quenching due to qE is modulated in Eq. 2 by the quantity [Q], which is the fraction of quenching sites in the PSII antenna that are able to dissipate excitation energy by qE. We assume that for a quenching site to be present, it is necessary to have an activated PsbS protein and a deepozidized xanthophyll in PSII. We base this assumption on the facts that (1) the npq4 mutant, which lacks PsbS, has no rapidly reversible NPQ in vivo (7) and (2) inhibition of the VDE enzyme, either chemically with dithiothreitol (8) or genetically by removing the gene for it (9), results in decreased levels of rapidly reversible NPQ.
A working model in which both PsbS and a deepoxidized xanthophyll is required for qE in vivo, discussed in ref. (31), assumes that the protonation of VDE and PsbS are uncorrelated with each other, and so the fraction of PSIIs that contain both elements needed for quenching can be written as
| [3] |
where [PsbS]∗ is the fraction of PSIIs with a protonated PsbS and [Z] ([A]) is the fraction of xanthophyll binding sites in PSII that contain zeaxanthin (antheraxanthin) in a site able to perform qE. This expression is a simplification of the exact nature of qE quenching because some VDE-independent NPQ is present in plants (32, 33). Nonetheless, it serves as a reasonable starting point for mechanistically modeling the experimental observations of PsbS-dependent NPQ.
The active forms of PsbS and VDE are both triggered by a low lumen pH, but with different pKas and Hill coefficients. The pKa determines the pH values at which 50% of the proteins are protonated and can be thought of as a “set point” level at which the pH-triggered protein is activated. The Hill coefficient determines the steepness of the pH dependence of the protein in transitioning from the fully active form to the fully inactive form. We assume that PsbS is in equilibrium with the lumen and that the activation of PsbS into a quenching-active state following protonation happens instantaneously, giving the following expression for active PsbS ([PsbS]∗):
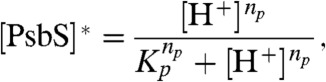 |
[4] |
where Kp and np are the pKa and Hill coefficient of PsbS protonation. To calculate the VDE-dependent component (8), we also assume that the activation of VDE by low lumen pH happens instantaneously. The expression we use for the effective rate constant of VDE (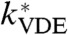 ) is
) is
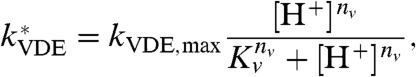 |
[5] |
where kVDE, max is the rate constant of fully protonated VDE activity, and Kv and nv are the pKa and Hill coefficient of VDE protonation. We take the maximum rate of VDE activity to be 4 × 10-2 deepoxidation events per second, which corresponds to a timescale of one deepoxidation event every 20 s if one VDE enzyme is present in each PSII. We assume that, under the conditions used for this work, zeaxanthin epoxidase (ZE) has a fixed concentration and the rate of zeaxanthin epoxidation is constant. This assumption may need to be revised in the future as more information regarding the regulation of ZE emerges (34). The rate of zeaxanthin epoxidase is 10 to 300 times slower than that of violaxanthin deepoxidase (31), so we assumed a rate of 4 × 10-4 epoxidation events per second. With these assumptions, the concentrations of zeaxanthin and antheraxanthin in the PSII antenna are given by
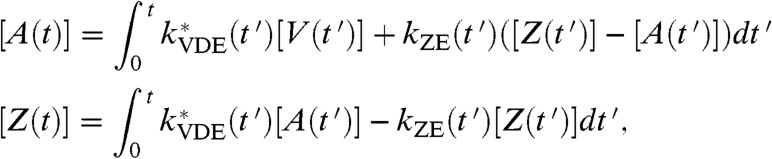 |
[6] |
where [V] = 1 - [Z] - [A] is the fraction of qE-relevant xanthophyll binding sites occupied by violaxanthin.
Plants with elevated levels of PsbS have shown elevated levels of qE (4), indicating that not all possible qE sites are modulated by wild-type levels of PsbS. To account for this effect, we have incorporated an effective PsbS dosage factor, FPsbS, which can be interpreted as the fraction of potential qE sites that are modulated by PsbS (4, 35). For wild type, we set this dose to be 0.6, because that gave the best agreement with experimental data.
For simplicity, we assume that there is only one site of qE in PSII and that it is accessible to all the chlorophylls within PSII, with the probability of quenching being proportional to the rate kqE. We do not incorporate a microscopic model of the quenching process, but rather assume that quenching occurs infinitely fast and therefore that quenching sites are always “open” (in contrast with reaction centers, which are closed when QA is reduced). These assumptions are necessary at this point for simplicity, but it will be important in the future to systematically address the effect of multiple quenching sites and different quenching mechanisms (15–17) on the predictions of the model.
In order to compare the predictions of the model with experimental measurements on intact leaves, the quantum yield of chlorophyll fluorescence was simulated by assuming that the quantum yield is related to variables and parameters in Eq. 3 by
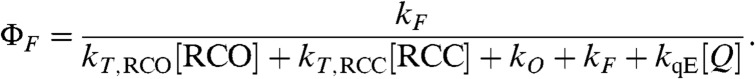 |
[7] |
Quantifying the extent of qE expression in vivo requires knowledge of the lumen pH at each point during the light-adaptation process. To calculate lumen pH, it is necessary to account for the rate of protons entering the lumen, the rate of protons leaving the lumen, and the buffering capacity of the lumen. These processes are interrelated because they all affect and are affected by the proton motive force (pmf) and by the concentration of mobile ions that move across the thylakoid membrane (27). The lumen pH is also affected by the conductivity of ATP synthase, which is activated by linear electron flow through the thioredoxin system (36). Details pertaining to the calculation of lumen pH are given in the SI Text, Lumenal buffering and ion motion. Incorporating a rate for activation of ATP synthase was necessary for simulating qE at low light intensities, and is described in the SI Text, Activation of ATP synthase.
Results and Discussion
Fig. 3 shows an experimental pulse amplitude modulation (PAM) fluorescence (18) trace for Arabidopsis thaliana wild type and npq4 mutant, which lacks PsbS, measured at an actinic light intensity of 1,000 μmol photons m-2 s-1. The amount of total NPQ in each plant, quantified using the formula 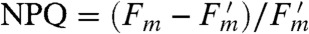 , is shown in Fig. 3B (the formula is explained in the SI Text, Extracting NPQ from PAM measurement). The rapidly reversible component of NPQ (qE) is absent in the npq4 mutant but a substantial slowly reversible NPQ still accumulates that accounts for more than 25% of the total NPQ observed in wild type. Fig. 3C shows the difference in NPQ between the wild type and npq4 mutant. This difference is a measure of the NPQ due to qE and is the experimental observable to which we fit our model. Comparing simulations of models of qE directly to a PAM trace is not appropriate at all light intensities because a substantial fraction of NPQ is not due to qE but is due to other, slowly reversible mechanisms. These mechanisms include qI, which relates to inhibition of PSII; qT, which is quenching due to state transitions between PSII and PSI, (3); and qZ, which is zeaxanthin-dependent but PsbS-independent quenching in the PSII antenna (37). These slower NPQ components are all present in the npq4 mutant, as shown in Fig. 3
A and B, suggesting that the difference in NPQ between npq4 and wild type is a reasonable estimate of qE. A concern is that npq4 would have more qI quenching than wild type due to a reduced ability to protect PSII from photoinhibition (4), but the short duration of illumination presented here (< 15 min) only induces a small (< 0.5) amount of excess NPQ ascribed to qI in npq4 compared to wild type.
, is shown in Fig. 3B (the formula is explained in the SI Text, Extracting NPQ from PAM measurement). The rapidly reversible component of NPQ (qE) is absent in the npq4 mutant but a substantial slowly reversible NPQ still accumulates that accounts for more than 25% of the total NPQ observed in wild type. Fig. 3C shows the difference in NPQ between the wild type and npq4 mutant. This difference is a measure of the NPQ due to qE and is the experimental observable to which we fit our model. Comparing simulations of models of qE directly to a PAM trace is not appropriate at all light intensities because a substantial fraction of NPQ is not due to qE but is due to other, slowly reversible mechanisms. These mechanisms include qI, which relates to inhibition of PSII; qT, which is quenching due to state transitions between PSII and PSI, (3); and qZ, which is zeaxanthin-dependent but PsbS-independent quenching in the PSII antenna (37). These slower NPQ components are all present in the npq4 mutant, as shown in Fig. 3
A and B, suggesting that the difference in NPQ between npq4 and wild type is a reasonable estimate of qE. A concern is that npq4 would have more qI quenching than wild type due to a reduced ability to protect PSII from photoinhibition (4), but the short duration of illumination presented here (< 15 min) only induces a small (< 0.5) amount of excess NPQ ascribed to qI in npq4 compared to wild type.
Fig. 3.
(A) Pulse amplitude modulation (PAM) traces of wild type and npq4
Arabidopsis thaliana leaves at 1,000 μmol photons/m2/s. (B) NPQ in wild type and mutant, calculated using the formula 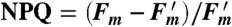 . (C) Difference in NPQ between wild type and npq4, which is a measure of qE. The black bar at the top of each figure indicates times when the plant is darkened, and the white bar indicates actinic light illumination.
. (C) Difference in NPQ between wild type and npq4, which is a measure of qE. The black bar at the top of each figure indicates times when the plant is darkened, and the white bar indicates actinic light illumination.
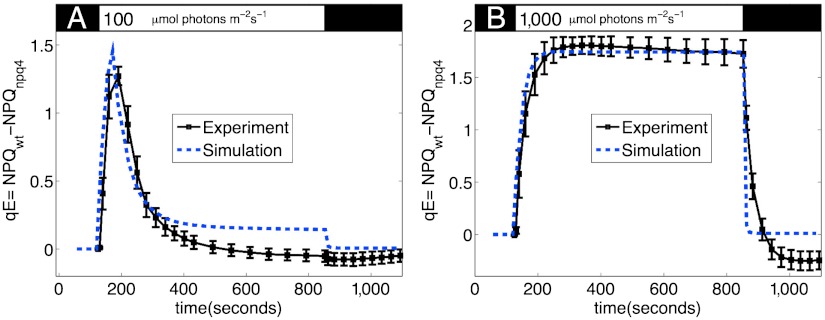
Fig. 4 compares the experimental values of qE with those simulated by the model at light intensities of 100 (Fig. 4A) and 1,000 (Fig. 4B) μmol photons m-2 s-1, for the same set of parameters. At 100 μmol photons m-2 s-1, qE rises to a value of 0.5 within 100 s of illumination, then relaxes to a smaller value within 400 s. When actinic light is turned off, the small steady-state qE rapidly relaxes. The model reproduces the rapid rise of qE, as well as the relaxation of qE to a low steady-state value. The remaining discrepancies between model and experiment are likely due to dynamics of photosynthesis that are not incorporated into the model, particularly the fact that the activation of ATP synthase and the consumption of ATP involve more complicated kinetics than what is currently incorporated into our model.
Fig. 4.
Measured (squares) and simulated (dashed lines) qE for input light intensities of (A) 100 and (B) 1,000 μmol photons/m2s. The experimental trace in B is the same as in Fig. 3C. Other than light intensity, all parameters for the simulation are the same. qE is taken to be the difference in NPQ between the wild type and npq4 mutant in order to subtract the baseline of slowly reversible NPQ. Both measured and simulated NPQ values are determined from the PAM traces shown in Fig. S1. The black bar at the top indicates times when the plant is darkened, and the white bar indicates actinic light illumination.
At higher light intensities, the model gives better agreement with experiment because the rate of proton flux into the lumen is large enough that the ΔpH that activates qE remains large even when ATP synthase is fully activated. As shown in Fig. 4B, at 1,000 μmol photons m-2 s-1, qE increases monotonically to a value of 1.7, with the amount of qE mostly saturating within 300 s. When actinic light is turned off, qE rapidly relaxes back to nearly zero. The model slightly overestimates the rate of qE relaxation, leading to somewhat faster turn-off kinetics than are observed in actual leaves. This discrepancy could be due to two factors: Either the increase in lumen pH is in fact slower than the model predicts, or the transition between a quenched state back to an unquenched state upon the deprotonation of PsbS occurs with a nonnegligible rate. Further comparison between the model and experimental data, including simulations of PAM traces, is given in the SI Text, Fig. S1. Because our model does not incorporate slowly reversible NPQ processes, the simulated qE relaxes to zero but the experimental qE appears to be negative upon relaxation (see above).
The timescale of the appearance and disappearance of qE in Fig. 4 can be understood in terms of the time-dependent concentrations of PsbS and zeaxanthin/antheraxanthin, as shown in Fig. S2. The model indicates that the timescale of the turn on of qE is determined by the timescale of violaxanthin deepoxidation (Fig. S2B), and the rapid turn off of qE is determined by the decrease in protonated PsbS (Fig. S2C). The concentration of both components is determined by the lumen pH, but whereas the fraction of protonated PsbS (Fig. S2A) is determined by the instantaneous pH, the fraction of deepoxidized xanthophyll is determined by the history of the lumen pH and appears more gradually as illustrated in Fig. S2B. It is possible that the reason for the presence of these two components of qE is that the maximal level of qE for a given light intensity is set by the level of zeaxanthin, which persists in PSII, but that the plant retains the ability to rapidly modulate qE between a maximal level and a very low level using only PsbS.
The ability of our model to calculate quantities such as the time-evolution of antheraxanthin and zeaxanthin provides a new opportunity to make testable, quantitative predictions about the qE mechanism. For example, although antheraxanthin, which is a chemical intermediate between violaxanthin and zeaxanthin, is capable of some quenching (33), the relative contribution of antheraxanthin and zeaxanthin to qE-type quenching in vivo is difficult to measure. Our model could easily be modified to include a different rate of quenching by antheraxanthin than by zeaxanthin, which would change the shape of the predicted qE induction curve. By comparing measured qE induction curves with simulations of these curves at a range of parameters and light intensities, it should be possible to clarify the role of antheraxanthin in the appearance and disappearance of qE quenching. As another example, the model could be extended to incorporate a rate of PsbS-induced rearrangement in the PSII antenna that leads to formation of a quenching site once PsbS is protonated and zeaxanthin and antheraxanthin are made. By simulating qE induction curves that can be fit to experimental data for different values of this rearrangement rate, it should be possible to restrict the value of the timescale of qE quenching site formation to a narrower range than is currently known.
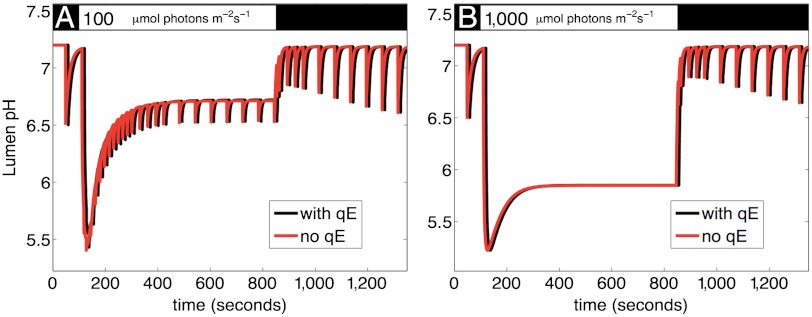
Fig. 5 shows the simulated lumen pH over the course of a PAM measurement with and without qE for input light intensity of 100 and 1,000 μmol photons m-2 s-1. It is notable that the two curves look identical, suggesting that the ΔpH, which triggers qE, is not itself affected by qE. This simulated result is consistent with the experimental finding that in the npq4 mutant ΔpH and xanthophyll cycle pigment levels are the same as those of wild type (4, 7). The fact that qE does not appear to significantly affect the lumen pH indicates that qE does not affect the pmf for driving ATP synthase under steady state conditions; consequently, qE does not dissipate excitons that could be used for driving linear electron flow that generates pmf. This result quantifies and corroborates the interpretation of experimental findings suggesting that, under specific conditions, overexpressing PsbS appears to help plants (19). If qE is a “conservative” feedback loop, overexpressing the capacity for qE provides more photoprotection without excessively quenching useful excitons.
Fig. 5.
Effect of qE on pH of thylakoid lumen at (A) 100 and (B) 1,000 μmol photons/m2/s. For the values for qE activation given in Table S2, the model predicts that qE has minimal effect on the pH of the lumen, suggesting that qE quenching does not lead to a signification reduction in linear electron flow. This result indicates that qE only quenches excitations that do not contribute to pmf and ATP synthesis, suggesting that qE does not waste useful energy. The black bar at the top indicates times when the plant is darkened, and the white bar indicates actinic light illumination.
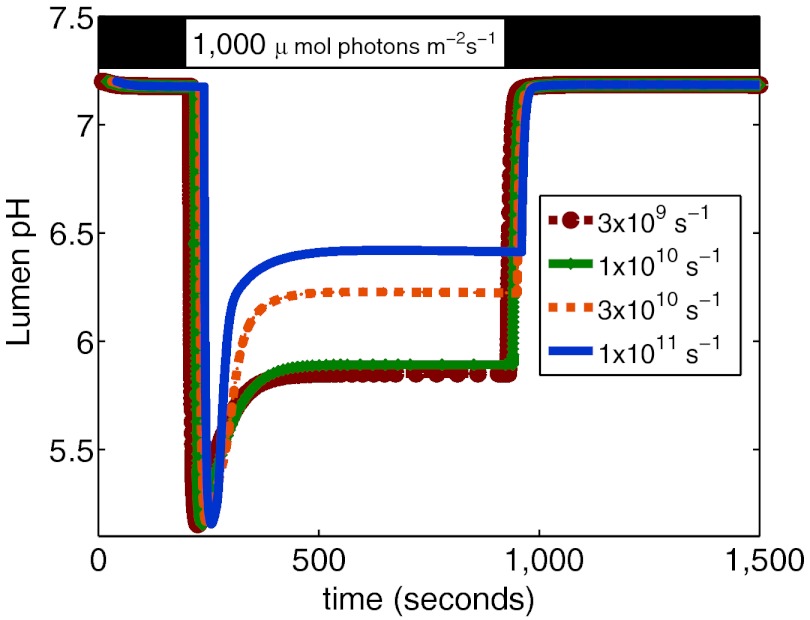
To examine the range of parameters for which the lumen pH is unaffected by qE, we ran the simulation at a range of values of the rate kQ, which modulates the amount of quenching of chlorophyll excitation in the PSII antenna by a quenching site. The lumen pH for values of kQ ranging from 1/300 ps to 1/10 ps is shown in Fig. 6. Physically, this rate is a measure of the probability that a chlorophyll in the PSII antenna will be quenched by a qE site, and, in feedback control terms, can be thought of as the “gain” of the qE quenching feedback loop. Because the lumen pH is a component of the pmf, having too high a gain would reduce the ΔpH and would waste energy that can be used for ATP synthesis; on the other hand, too low of a gain would cause the system to be insufficiently protected by quenching too few excess excited chlorophylls. Fig. 6 suggests that, within the predictions of our current model, quenching rates faster than 1/100 ps would cause the feedback loop to be so aggressive that proton motive force is lost. Additional examples of the way in which the model can be used to asses the effects of parameter varation on qE observables are given in Figs. S3 and S4. We anticipate that this type of analysis, in conjunction with more refined models of qE and of energy transfer in PSII, will provide greater perspective on the role of qE in photosynthesis.
Fig. 6.
Effect of varying the rate kQ on the lumen pH at 1,000 μmol photons/m2/s. For quenching rates of 3 × 109 and 1 × 1010, corresponding to timescales for quenching of 300 ps and 100 ps, the lumen pH is essentially unaffected by qE (see also Fig. 5B). At faster rates of quenching, the feedback quenching of qE is strong enough that it affects the value of the lumen pH, which is the trigger for qE.
Concluding Remarks
We have presented a model of rapidly reversible feedback-activated NPQ in photosynthetic organisms (qE). Our model accurately simulates the changes in the quantum yield of chlorophyll fluorescence that arise from NPQ pathways at low and high light intensities; accurate simulation of the system governing qE at low and high light intensities is an important step towards quantifying the role of qE in protecting PSII in fluctuating light conditions. Currently there is interest in engineering photosynthetic organisms to maximize photosynthetic efficiency, both to increase crop yields and to produce biofuels. Because of the interconnectedness of photosynthetic processes, a systems approach to modeling the properties of photosynthesis is necessary. We have described a model that treats PSII as a system with feedback and that incorporates a mechanistic model of qE. Our model suggests that qE quenching, which is activated by the pH of the thylakoid lumen, does not affect the lumen pH in plants and therefore does not regulate linear electron flow in steady state conditions.
It would be interesting to use the model to explore the range of parameter values for which qE does not affect the lumen pH, the proton motive force and linear electron flow in order to assess the robustness of the qE feedback mechanism to variation in parameter values. Because the model we have presented contains a mechanism for qE that enables an assessment of the effect of physiological parameter values (e.g., pKas of protein residues) on the amount of qE, it can can serve as a tool for assessing how changes in the components of the qE mechanism would affect photosynthetic yield. In the future, it seems likely that this model, in conjunction with systematic measurements of available Arabidopsis mutants at various light intensities, will be valuable for estimating the effect of qE on internal physiological parameters of the thylakoid that are difficult to measure directly in vivo. In particular, examining the NPQ at different light intensities in the npq1 mutant, which lacks VDE; the lut2 mutant, which lacks lutein (38); and the npq1lut2 mutant, which lacks both zeaxanthin and lutein, will provide insight into the contribution to qE from VDE-dependent and VDE-independent components. Lastly, analysis of the robustness of the model to parameter variation, as well as an examination of the structure of the feedback loops that control qE, should inform on the regulatory requirements faced by any light-harvesting systems that exist in conditions where light intensity fluctuates.
Materials and Methods
Measurements of Chlorophyll Fluorescence.
Wild type (ecotype Colombia) and npq4 mutants of Arabidopsis thaliana were grown at 50–100 μmol photons m-2 s-1. Plants were dark-adapted for 30 min before measurements. The fluorescence yield of attached leaves of 6-wk old plants was measured as described previously (39).
Simulations.
The differential equations were solved using the ode15s solver, which is provided with the MATLAB (The Mathworks, Inc) environment for simulating stiff differential equations. Commented code containing the equations used in the model is available online, and the link and instructions are provided with the SI Text.
Supplementary Material
ACKNOWLEDGMENTS.
We thank Tae Kyu Ahn and Yuan-Chung Cheng for helpful discussions, Matthew Brooks for assistance with PAM fluorescence measurements, helpful discussions, and comments on the manuscript, and Eleonora De Re and Saar Kirmayer for comments on the manuscript. This work was supported by the Director, Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy under Contract DE-AC02-05CH11231 and the Division of Chemical Sciences, Geosciences, and Biosciences, Office of Basic Energy Sciences of the U.S. Department of Energy through Grants DE-AC03-76SF000098 and FWP 449B. J.Z. was partially supported by a Chancellor’s Fellowship from University of California, Berkeley. K.A. was supported by a National Science Foundation Graduate Research Fellowship and by the University of California, Berkeley Chemical Biology Graduate Program Training Grant 1 T32 GMO66698. K.K.N is an investigator of the Howard Hughes Medical Institute and the Gordon and Betty Moore Foundation.
Footnotes
The authors declare no conflict of interest.
See Commentary on page 15533.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1211017109/-/DCSupplemental.
References
- 1.Melis A. Photosystem-II damage and repair cycle in chloroplasts: What modulates the rate of photodamage in vivo? Trends Plant Sci. 1999;4:130–135. doi: 10.1016/s1360-1385(99)01387-4. [DOI] [PubMed] [Google Scholar]
- 2.Kulheim C, Agren J, Jansson S. Rapid regulation of light harvesting and plant fitness in the field. Science. 2002;297:91–93. doi: 10.1126/science.1072359. [DOI] [PubMed] [Google Scholar]
- 3.Müller P, Li X-P, Niyogi KK. Non-photochemical quenching. A response to excess light energy. Plant Physiol. 2001;125:1558–1566. doi: 10.1104/pp.125.4.1558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Li X-P, Muller-Moule P, Gilmore AM, Niyogi KK. PsbS-dependent enhancement of feedback de-excitation protects photosystem II from photoinhibition. Proc Natl Acad Sci USA. 2002;99:15222–15227. doi: 10.1073/pnas.232447699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.de Bianchi S, Ballottari M, DallOsto L, Bassi R. Regulation of plant light harvesting by thermal dissipation of excess energy. Biochem Soc Trans. 2010;38:651–660. doi: 10.1042/BST0380651. [DOI] [PubMed] [Google Scholar]
- 6.Ruban AV, Johnson MP, Duffy CDP. The photoprotective molecular switch in the photosystem II antenna. Biochim Biophys Acta. 2012;1817:167–181. doi: 10.1016/j.bbabio.2011.04.007. [DOI] [PubMed] [Google Scholar]
- 7.Li X-P, et al. A pigment-binding protein essential for regulation of photosynthetic light harvesting. Nature. 2000;403:391–395. doi: 10.1038/35000131. [DOI] [PubMed] [Google Scholar]
- 8.Demmig-Adams B. Carotenoids and photoprotection in plants: A role for the xanthophyll zeaxanthin. Biochim Biophys Acta. 1990;1020:1–24. [Google Scholar]
- 9.Niyogi KK, Grossman AR, Björkman O. Arabidopsis mutants define a central role for the xanthophyll cycle in the regulation of photosynthetic energy conversion. Plant Cell. 1998;10:1121–1134. doi: 10.1105/tpc.10.7.1121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Walters R, Ruban AV, Horton P. Identification of proton-active residues in a higher plant light-harvesting complex. Proc Natl Acad Sci USA. 1996;93:14204–14209. doi: 10.1073/pnas.93.24.14204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bassi R, Caffarri S. Lhc proteins and the regulation of photosynthetic light harvesting function by xanthophylls. Photosynth Res. 2000;64:243–256. doi: 10.1023/A:1006409506272. [DOI] [PubMed] [Google Scholar]
- 12.Jahns P, Latowski D, Strzalka K. Mechanism and regulation of the violaxanthin cycle: The role of antenna proteins and membrane lipid. Biochim Biophys Acta. 2009;1787:3–14. doi: 10.1016/j.bbabio.2008.09.013. [DOI] [PubMed] [Google Scholar]
- 13.Johnson MP, Ruban AV. Restoration of rapidly reversible photoprotective energy dissipation in the absence of PsbS protein by enhanced pH. J Biol Chem. 2011;286:19973–19973. doi: 10.1074/jbc.M111.237255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Betterle N, et al. Light-induced dissociation of an antenna hetero-oligomer is needed for non-photochemical quenching induction. J Biol Chem. 2009;284:15255–15266. doi: 10.1074/jbc.M808625200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ruban AV, et al. Identification of a mechanism of photoprotective energy dissipation in higher plants. Nature. 2007;450:575–578. doi: 10.1038/nature06262. [DOI] [PubMed] [Google Scholar]
- 16.Ahn TK, et al. Architecture of a charge-transfer state regulating light harvesting in a plant antenna protein. Science. 2008;320:794–797. doi: 10.1126/science.1154800. [DOI] [PubMed] [Google Scholar]
- 17.Holzwarth AR, Miloslavina Y, Nilkens M, Jahns P. Identification of two quenching sites active in the regulation of photosynthetic light-harvesting studied by time-resolved fluorescence. Chem Phys Lett. 2009;483:262–267. [Google Scholar]
- 18.Baker NR. Chlorophyll fluorescence: A probe of photosynthesis in vivo. Annu Rev Plant Biol. 2008;61:89–113. doi: 10.1146/annurev.arplant.59.032607.092759. [DOI] [PubMed] [Google Scholar]
- 19.Logan BA, Terry SG, Niyogi KK. Arabidopsis genotypes with differing levels of PsbS expression differ in photosystem II quantum yield, xanthophyll cycle pool size, and above ground growth. Int J Plant Sci. 2008;169:597–604. [Google Scholar]
- 20.Graßes T, et al. The role of pH-dependent dissipation of excitation energy in protecting photosystem II against light-induced damage in Arabidopsis thaliana. Plant Physiol Biochem. 2002;40:41–49. [Google Scholar]
- 21.Zhu X-G, Ort DR, Whitmarsh J, Long SP. The slow reversibility of photosystem II thermal energy dissipation on transfer from high to low light may cause large losses in carbon gain by crop canopies: A theoretical analysis. J Exp Bot. 2004;55:1167–1175. doi: 10.1093/jxb/erh141. [DOI] [PubMed] [Google Scholar]
- 22.Murchie EH, Niyogi KK. Manipulation of photoprotection to improve plant photosynthesis. Plant Physiol. 2011;155:86–92. doi: 10.1104/pp.110.168831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Blankenship RE, et al. Comparing photosynthetic and photovoltaic efficiencies and recognizing the potential for improvement. Science. 2011;332:805–809. doi: 10.1126/science.1200165. [DOI] [PubMed] [Google Scholar]
- 24.van Kooten O, Snel J, Vredenberg WJ. Photosynthetic free energy transduction related to the electric potential changes across the thylakoid membrane. Photosynth Res. 1986;9:211–227. doi: 10.1007/BF00029745. [DOI] [PubMed] [Google Scholar]
- 25.Belyaeva NE, et al. PS II model-based simulations of single turnover flash-induced transients of fluorescence yield monitored within the time domain of 100 ns–10 s on dark-adapted Chlorella pyrenoidosa cells. Photosynth Res. 2008;98:105–119. doi: 10.1007/s11120-008-9374-2. [DOI] [PubMed] [Google Scholar]
- 26.Zhu X-G, et al. Chlorophyll a fluorescence induction kinetics in leaves predicted from a model describing each discrete step of excitation energy and electron transfer associatedwith Photosystem II. Planta. 2005;223:114–133. doi: 10.1007/s00425-005-0064-4. [DOI] [PubMed] [Google Scholar]
- 27.Cruz JA, Sacksteder CA, Kanazawa A, Kramer DM. Contribution of electric field (Delta psi) to steady-state transthylakoid proton motive force (pmf) in vitro and in vivo. control of pmf parsing into Delta psi and Delta pH by ionic strength. Biochemistry. 2001;40:1226–1237. doi: 10.1021/bi0018741. [DOI] [PubMed] [Google Scholar]
- 28.Kuvykin IV, Vershubskii AV, Priklonskii VI, Tikhonov AN. Computer simulation study of pH-dependent regulation of electron transport in chloroplasts. Biophysics. 2009;54:455–464. [PubMed] [Google Scholar]
- 29.Ebenhöh O, Houwaart T, Lokstein H, Schlede S, Tirok K. A minimal mathematical model of nonphotochemical quenching of chlorophyll fluorescence. Biosystems. 2011;103:196–204. doi: 10.1016/j.biosystems.2010.10.011. [DOI] [PubMed] [Google Scholar]
- 30.Raszewski G, Renger T. Light harvesting in photosystem II core complexes is limited by the transfer to the trap: Can the core complex turn into a photoprotective mode? J Am Chem Soc. 2008;130:4431–4446. doi: 10.1021/ja7099826. [DOI] [PubMed] [Google Scholar]
- 31.Takizawa K, Cruz JA, Kanazawa A, Kramer DM. The thylakoid proton motive force in vivo. Quantitative, non-invasive probes, energetics, and regulatory consequences of light-induced pmf. Biochim Biophys Acta. 2007;1767:1233–1244. doi: 10.1016/j.bbabio.2007.07.006. [DOI] [PubMed] [Google Scholar]
- 32.Johnson MP, Perez-Bueno ML, Zia A, Horton P, Ruban AV. The zeaxanthin-independent and zeaxanthin-dependent qE components of nonphotochemical quenching involve common conformational changes within the photosystem II antenna in Arabidopsis. Plant Physiol. 2009;149:1061–1075. doi: 10.1104/pp.108.129957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Gilmore AM, Yamamoto H. Linear models relating xanthophylls and lumen acidity to non-photochemical fluorescence quenching. Evidence that antheraxanthin explains zeaxanthin-independent quenching. Photosynth Res. 1993;35:67–78. doi: 10.1007/BF02185412. [DOI] [PubMed] [Google Scholar]
- 34.Zhang R, Kramer DM, Cruz JA, Struck KR, Sharkey TD. The effects of moderately high temperature on zeaxanthin accumulation and decay. Photosynth Res. 2011;108:171–181. doi: 10.1007/s11120-011-9672-y. [DOI] [PubMed] [Google Scholar]
- 35.Niyogi KK, Li X-P, Rosenberg V, Jung H-S. Is PsbS the site of non-photochemical quenching in photosynthesis? J Exp Bot. 2004;56:375–382. doi: 10.1093/jxb/eri056. [DOI] [PubMed] [Google Scholar]
- 36.Buchanan BB. Role of light in the regulation of chloroplast enzymes. Annu Rev Plant Physiol. 1980;31:341–374. [Google Scholar]
- 37.Nilkens M, et al. Identification of a slowly inducible zeaxanthin-dependent component of non-photochemical quenching of chlorophyll fluorescence generated under steady-state conditions in Arabidopsis. Biochim Biophys Acta. 2010;1797:466–475. doi: 10.1016/j.bbabio.2010.01.001. [DOI] [PubMed] [Google Scholar]
- 38.Pogson BJ, Niyogi KK, Bjorkman O, Della Penna D. Altered xanthophyll compositions adversely affect chlorophyll accumulation and nonphotochemical quenching in Arabidopsis mutants. Proc Natl Acad Sci USA. 1998;95:13324–13329. doi: 10.1073/pnas.95.22.13324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Brooks MD, Niyogi KK. In: Chloroplast Research in Arabidopsis: Methods and Protocols. Jarvis RP, editor. Vol II. Heidelberg: Springer; 2011. pp. 299–310. [Google Scholar]
- 40.Avenson TJ, et al. Integrating the proton circuit into photosynthesis: Progress and challenges. Plant Cell Environ. 2005;28:97–109. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.