Abstract
We investigated the wavelength dependence of imaging depth and clearness of structure in ultrahigh-resolution optical coherence tomography over a wide wavelength range. We quantitatively compared the optical properties of samples using supercontinuum sources at five wavelengths, 800 nm, 1060 nm, 1300 nm, 1550 nm, and 1700 nm, with the same system architecture. For samples of industrially used homogeneous materials with low water absorption, the attenuation coefficients of the samples were fitted using Rayleigh scattering theory. We confirmed that the systems with the longer-wavelength sources had lower scattering coefficients and less dependence on the sample materials. For a biomedical sample, we observed wavelength dependence of the attenuation coefficient, which can be explained by absorption by water and hemoglobin.
OCIS codes: (110.4500) Optical coherence tomography, (170.3880) Medical and biological imaging
1. Introduction
Optical coherence tomography (OCT) is a non-invasive optical imaging technique for micrometer-scale cross-sectional imaging of biological tissue and materials [1–3]. Initially, it was a clinically useful diagnostic technique in ophthalmology [4,5]. Since then, OCT instrumentation has undergone substantial improvement and is now well-positioned for wide adoption in various other clinical and research applications [6]. For instance, this technology has been actively used in other clinical applications, such as cardiology [7–9], oncology [10,11], visualization of dental structure [12–14], and so on. Although OCT provides many advantages in medicine, the low penetration depth is a serious limitation for other applications [2]. Because the optical properties of tissue depend on the wavelength used, it is necessary to choose the proper wavelength to maximize the light penetration and enhance the image contrast at deeper depths. Around the near-infrared wavelength region, the first clinical applications of OCT for ophthalmology normally used 800 nm OCT systems. In other applications, such as observation of turbid biological tissue samples, 1300 nm OCT systems have been shown to have superior penetration depth compared with 800 nm OCT systems [12,15–18]. Recently, the long-wavelength window around 1700 nm has attracted attention for OCT imaging. Enhanced penetration depth at 1700 nm in skin, 10% intralipid solution, and rubber was confirmed by Sharma et al. [19]. On the other hand, the dependence of the scattering coefficient on intralipid concentration in water for 1300 nm and 1600 nm systems was examined by Kodach et al. [20]. The advantages of using this longer wavelength region are enhanced penetration depth due to lower scattering in tissue and enhanced imaging contrast at deeper penetration depths where multiple-scattered photons dominate over ballistic photons. However, there have been no studies comparing the performance of ultrahigh-resolution optical coherence tomography (UHR-OCT) for the same sample over a wide wavelength range.
In this study, we constructed UHR-OCT systems using supercontinuum sources at five wavelengths in the range 800–1700 nm. We investigated the wavelength dependence of the images for several different samples and quantitatively compared their optical properties.
2. Experimental setup
2.1. Supercontinuum sources: Design and output characteristics
We constructed supercontinuum (SC) sources at wavelengths 800 nm, 1060 nm, 1300 nm, 1550 nm, and 1700 nm. For the 800 nm source, we used a Kerr-lens mode-locked Ti:sapphire laser (Spectra Physics Mai-Tai HP). The chirping in the output pulses from the laser was compensated for using a prism pair, and the chirp-compensated pulses were coupled into polarization maintaining fiber (PMF) to generate the SC [21]. For the 1060 nm source, we used a commercially available, compact, diode-pumped soliton mode-locked femtosecond Nd:glass laser (High Q Laser Production). The 100 fs output pulses were coupled into high-numerical-aperture fiber to generate the SC [22]. For the 1300 nm and 1700 nm sources, we used the same laser system, consisting of a passively mode-locked, Er-doped fiber laser (IMRA femtolite B-5) that emitted 100 fs ultrashort pulses at a center wavelength of 1.56 μm as the seed source, an ultrashort-pulse fiber amplifier pumped by three high-power laser diodes at 1480 nm, and a large-mode-area photonic crystal fiber (LMA-PCF:LMA25, Thorlabs) to compensate for the chirping of the output high-power ultrashort pulses [23]. For the 1300 nm source, high-peak-power ultrashort pulses were coupled into normal-dispersion highly nonlinear fiber (ND-HNLF) to generate the SC. A bandpass filter was used at the output of the ND-HNLF to generate a Gaussian-like SC. For the 1700 nm source, high-peak-power ultrashort pulses were coupled into PMF to produce high-power, sech2-shaped soliton pulses with a center wavelength of 1700 nm. The output soliton pulses were then coupled into ND-HNLF to generate the SC [23].
For the 1550 nm source, we used a custom-made Er-doped high-power ultrashort-pulse mode-locked fiber laser, similar to that used in Ref. [24]. The chirping in the output pulses from this laser was compensated for using LMA-PCF (LMA35, Thorlabs), and the chirp-compensated pulses were coupled into ND-HNLF to produce the SC.
Figure 1(a) shows the output spectra of the SC sources together with the spectrum for absorption by water. The SC spectra fit in the valleys or flat regions of the water absorption spectrum, except for the spectrum of the 1550 nm SC. The spectral bandwidths of the SC sources were 121 nm at 800 nm, 101 nm at 1060 nm, 223 nm at 1300 nm, 159 nm at 1550 nm, and 400 nm at 1700 nm. The average output powers were 30.0 mW, 31.0 mW, 12.7 mW, 19.4 mW, and 30.0 mW, respectively. Figure 1(b) shows the theoretical longitudinal resolution at each wavelength, estimated from 2ln 2/π (λc2/Δλ), where λc is the center wavelength, and Δλ is the bandwidth of the light source in the case of a Gaussian-shaped spectrum. The circles in Fig. 1(b) show the estimated longitudinal resolutions in air for the generated supercontinuum spectra.
Fig. 1.
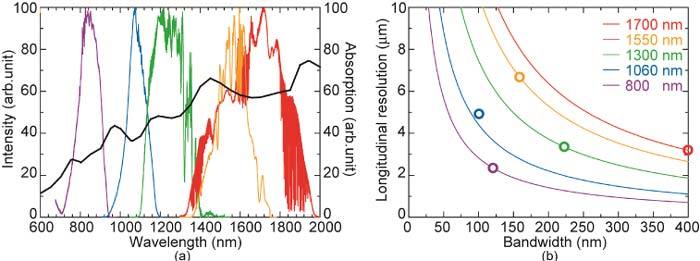
(a) Output spectra of supercontinuum sources together with water absorption spectrum and (b) corresponding theoretical longitudinal resolutions at all wavelengths as a function of bandwidth.
2.2. OCT setup and system characteristics
We constructed a time-domain (TD) OCT system for all wavelengths used in this study. The set-up is depicted schematically in Fig. 2 . The light from each SC source was coupled into a Michelson interferometer based on three broadband optical fiber couplers. The input beam was divided into signal and reference beams at these couplers. The signal beam was introduced into the sample arm containing a two-dimensional scanning system formed of a galvanometer mirror pair. To maintain the longitudinal resolution, the dispersion in the two arms of the interferometer was carefully balanced by using glass plates (BK7, fused silica, and so on) and an achromatic lens. The power of each SC source was 2.1–3.2 mW at the sample. Inline polarization controllers were used to adjust the polarization state of each beam. The reference arm was scanned by using a corner cube prism mounted on a galvanometer. The reference and signal beams were then combined with Coupler 1 in Fig. 2, and the interference signals were detected at a balanced detection system to cancel out the average noise.
Fig. 2.
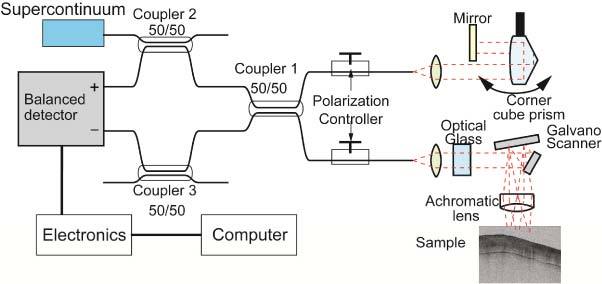
Experimental setup for time-domain optical coherence tomography.
Figure 3 shows the interference signals for all wavelengths. Since the spectral shape was nearly Gaussian, the magnitude of the sidelobes was very small on a linear scale. The observed longitudinal resolutions were 3.3–7.0 μm in air and 2.4–5.0 μm in tissue. The longitudinal resolutions in tissue at all wavelengths were under 5.0 μm, demonstrating that ultrahigh resolution was achieved.
Fig. 3.
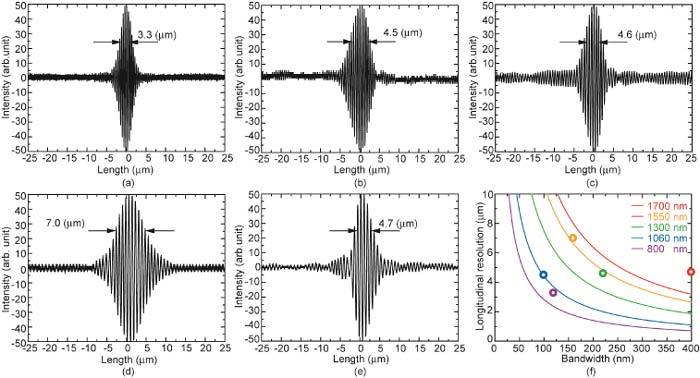
(a–e) Interference signals with mirror as sample at (a) 800 nm, (b) 1060 nm, (c) 1300 nm, (d) 1550 nm, and (e) 1700 nm UHR-OCT in air. (f) Observed longitudinal resolutions (circles) together with theoretical predictions (solid lines).
We used a suitable balanced detector for each wavelength: a Si PIN photodiode-based balanced detector (PDB150A, Thorlabs) for 800 nm, an InGaAs PIN photodiode-based balanced detector (PDB150C, Thorlabs) for 1060 nm, 1300 nm, and 1550 nm, and an extended InGaAs-based balanced detector (PDA10D, Thorlabs) for 1700 nm. The detected interference signal was bandpass filtered, logarithmically demodulated, low-pass filtered, and acquired by a computer. We confirmed higher than 95 dB sensitivity at all wavelengths.
In Figs. 3(c, e), the interference signals have the sidelobes caused by the non-ideal spectral shape of SC sources shown in Fig. 1(a). In the same way, 1500 nm UHR-OCT system has sidelobes in the interference signal at longer distance. They cause the small artifact in OCT images especially at the sample surface.
2.3. Phantom materials
We imaged several phantom and biological samples at all wavelengths. The tested samples were a plastic cover of a semiconductor memory card, made of polycarbonate (PC), an eraser, made of polyvinyl chloride (PVC), a magnet, made of chlorinated polyethylene (CPE) and anisotropic ferrite, a human tooth, and a pig trachea specimen. These samples were chosen to evaluate the dependence of absorption by water in typical industrially used materials and biological samples examined with UHR-OCT. For direct comparison, the OCT systems we constructed had almost the same architecture for all wavelengths. To reduce unwanted errors in estimating the attenuation coefficients, we adjusted the lateral resolution to 20.0 μm for all wavelengths. The focal point was set at the top of the sample. Figure 4 shows the spatial beam profiles at the sample surface for all wavelengths. The lateral resolutions at the sample surface were 17.6 μm at 800 nm, 19.6 μm at 1060 nm, 19.4 μm at 1300 nm, 20.6 μm at 1550 nm, and 21.4 μm at 1700 nm.
Fig. 4.
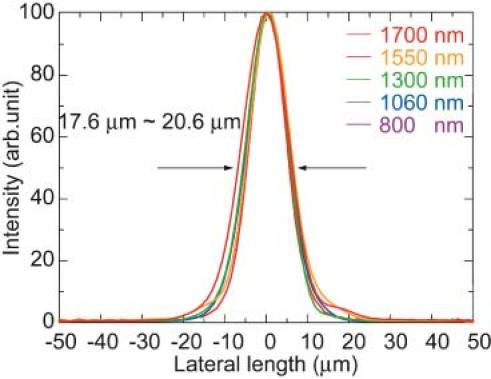
Observed spatial beam profiles at the top of surface of the sample at all wavelengths.
2.4. Numerical analysis and measurement setting
We used the single-backscattering model to determine the total attenuation coefficient μt, which is the sum of the absorption and the scattering coefficient [25]. The principal assumption is that the direction of a wave with power P0 incident upon the sample is reversed only once by a single backscattering event. While the wave travels in the sample, attenuation occurs along the path of the wave before and after it is backscattered. From this model, the backscattered power returning from depth z can be expressed as
| (1) |
where K is a constant that depends on the source coherence function, A(z) is the beam divergence function, and μb is the backscattering coefficient. Because the magnitude of the OCT signal is proportional to the amplitude of the field returning from the sample, the OCT signal on a dB scale is given by
| (2) |
From these equations, we used the maximum likelihood estimation to extract the total attenuation coefficient by finding the condition that minimizes the quantity χ2 given by [26]
| . | (3) |
We repeatedly measured each sample, and extracted the attenuation coefficient from the average of A-line scans to achieve a high degree of precision. In addition, the OCT signals between the surface and several tens of micrometers below the surface were eliminated to avoid the artifact caused by non-ideal spectral shape of light source. In the same way, the OCT signals between the tail or the changing point of slope and several tens of micrometers above there were eliminated.
3. Results
3.1. Plastic cover
Figure 5(a) shows a photograph of a memory card with a plastic cover. From the OCT images at 800 nm in Fig. 5(b) and 1700 nm in Fig. 5(c), we confirmed a deeper penetration depth in the longer wavelength region. Figures 5(d–h) show the results of averaged A-line scans from OCT signals measured at 800 nm, 1060 nm, 1300 nm, 1550 nm, and 1700 nm for quantitative comparison. The total attenuation coefficients were 4.8 mm−1 at 800 nm, 4.6 mm−1 at 1060 nm, 4.8 mm−1 at 1300 nm, 2.6 mm−1 at 1550 nm, and 2.8 mm−1 at 1700 nm. From these results, we confirmed lower attenuation coefficients in longer wavelength regions, demonstrating the usefulness of our system for measuring inside plastic samples. The OCT signal had a peak intensity of almost 20 dB at the surface of the sample, and then the reflected power decreased monotonically in all wavelength regions. The longer the center wavelength was, the lower the slope of the OCT signal intensity versus depth was.
Fig. 5.
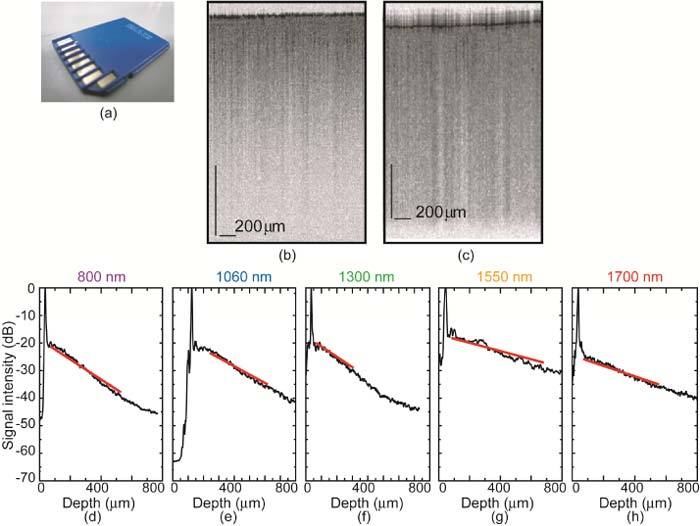
(a) Photograph of semiconductor memory card with plastic cover. (b, c) OCT images obtained at (b) 0.8 μm and (c) 1.7 μm. (d–h) Depth profiles averaged over 250 A-line scans and more than 50 iterative measurements at (d) 800 nm, (e) 1060 nm, (f) 1300 nm, (g) 1550 nm, and (h) 1700 nm. The slopes shown by the red lines were used to determine the total attenuation coefficients.
3.2. Eraser
Figure 6(a) show a photograph of an eraser. Figures 6(b–f) show the results of averaged A-line scans from OCT signals measured at 800 nm, 1060 nm, 1300 nm, 1550 nm, and 1700 nm for quantitative comparison. The total attenuation coefficients were 10.1 mm−1 at 800 nm, 8.0 mm−1 at 1060 nm, 6.6 mm−1 at 1300 nm, 6.7 mm−1 at 1550 nm, and 6.3 mm−1 at 1700 nm. For 1550 nm, we estimated the attenuation coefficient from the slope obtained by disregarding artifacts due to the properties of the light source, as indicate by the dashed line in Fig. 6(e). From these results, similar to the results in Section 3.1, we confirmed lower attenuation coefficient in longer wavelength regions, demonstrating the usefulness of the longer wavelength systems for performing measurement through rubber type materials.
Fig. 6.
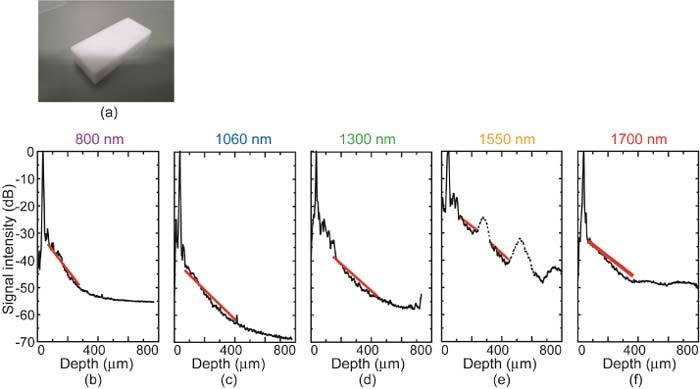
(a) Photograph of eraser. (b–f) Depth profiles averaged over 250 A-lines and more than 50 iterative measurements at (b) 800 nm, (c) 1060 nm, (d) 1300 nm, (e) 1550 nm, and (f) 1700 nm. The slopes shown by the red lines were used to determine the total attenuation coefficients.
3.3. Magnet
Figure 7(a) shows a photograph of the magnet. Figures 7 (b–f) show the results of averaged A-line scans from OCT signals measured at 800 nm, 1060 nm, 1300 nm, 1550 nm, and 1700 nm for quantitative comparison. The total attenuation coefficients were 24.0 mm−1 at 800 nm, 22.3 mm−1 at 1060 nm, 13.9 mm−1 at 1300 nm, 9.6 mm−1 at 1550 nm, and 6.0 mm−1 at 1700 nm. From these results, we confirmed the strong wavelength dependence of the attenuation coefficient, which is different from the other materials in Figs. 5 and 6. For 1550 nm, similar to the results in Section 3.2, we extracted the slope of the OCT signal by disregarding artifacts due to the properties of the light source, as indicated by the dashed line in Fig. 7(e).
Fig. 7.
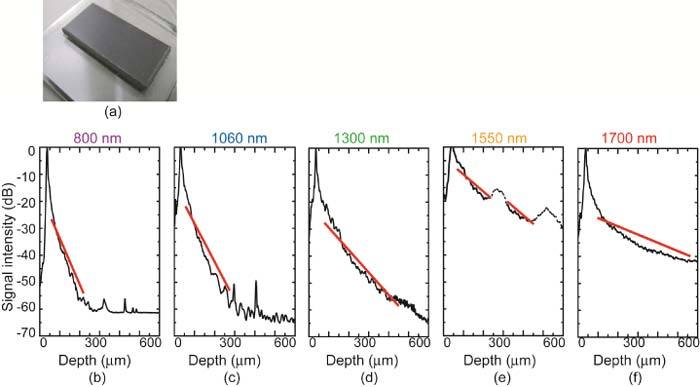
(a) Photograph of magnet. (b–f) Depth profiles averaged over 250 A-lines and more than 50 iterative measurements at (b) 800 nm, (c) 1060 nm, (d) 1300 nm, (e) 1550 nm, and (f) 1700 nm. The slopes shown by the red lines were used to determine the total attenuation coefficients.
3.4 .Total attenuation coefficients of low-water-absorption industrially used materials
Table 1 shows the total attenuation coefficients of the three samples of industrially used materials (plastic cover, eraser, and magnet), which were obtained from the UHR-OCT depth profiles. Figure 8 shows the wavelength dependence of the total attenuation coefficients of these samples. The ranges of variation of the attenuation coefficients over all wavelengths were 2.0 dB/mm for the plastic cover, 3.8 dB/mm for the eraser, and 18.0 dB/mm for the magnet. The magnet showed much larger wavelength dependence.
Table 1. Comparison of total attenuation coefficients of industrially used materials.
| Wavelength | Plastic cover |
Eraser |
Magnet |
Range |
|---|---|---|---|---|
| μt (mm−1) | μt (mm−1) | μt (mm−1) | Max – Min (mm−1) | |
| 800 nm | 4.8 | 10.1 | 24.0 | 19.2 |
| 1060 nm | 4.6 | 8.0 | 22.3 | 17.7 |
| 1300 nm | 4.7 | 6.6 | 13.9 | 9.2 |
| 1550 nm | 2.6 | 6.7 | 9.6 | 7.0 |
| 1700 nm | 2.8 | 6.3 | 6.0 | 3.2 |
| Max – Min | 2.0 | 3.8 | 18.0 |
Fig. 8.
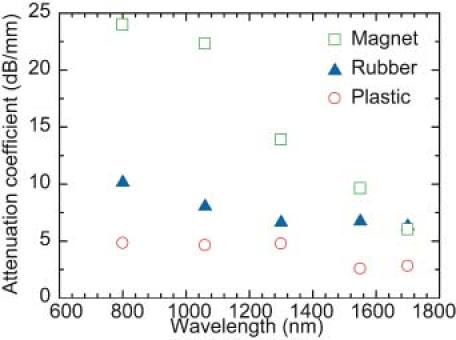
Wavelength dependence of total attenuation coefficient for industrially used materials
The longer the wavelength was, the smaller the range of variation of the total attenuation coefficient was. From Table 1 and Fig. 8, we confirmed the effectiveness of longer-wavelength UHR-OCT for samples showing low absorption by water. Moreover, there was less dependence of the total attenuation coefficient on the sample material at longer wavelengths.
3.5. Human baby tooth
Next, we examined some biological samples. Figure 9(a) shows an image of a human baby tooth. We measured the OCT signal at the red line in Fig. 9(a). Figures 9(b–f) show UHR-OCT images and corresponding A-line scans of the OCT signals at the red dashed line in each OCT image. The OCT signals in Figs. 9(b–f) have more than two slopes. The red line shows the slope at the enamel layer, and the blue line shows the slope at the dentine layer. Figure 9(g) shows the wavelength dependence of the total attenuation coefficients of the enamel and dentine layers. From 800 nm to 1550 nm, the total attenuation coefficient of the enamel layer decreased monotonically. The variation of the total attenuation coefficient of the dentine layer was 0.5 dB/mm, which is much less than that of the enamel layer, namely, 4.6 dB/mm. Thus, the enamel layer had stronger wavelength dependence than the dentine layer. Figures 9(c, d, f) reveal the existence of signals under the dentine layer. The corresponding total attenuation coefficient shown by en2 in Fig. 9(f) was 3.2 dB/mm, which is larger than the total attenuation coefficient of the dentine layer. It is considered that this signal originated from the enamel layer at the bottom side of the thin human baby tooth.
Fig. 9.
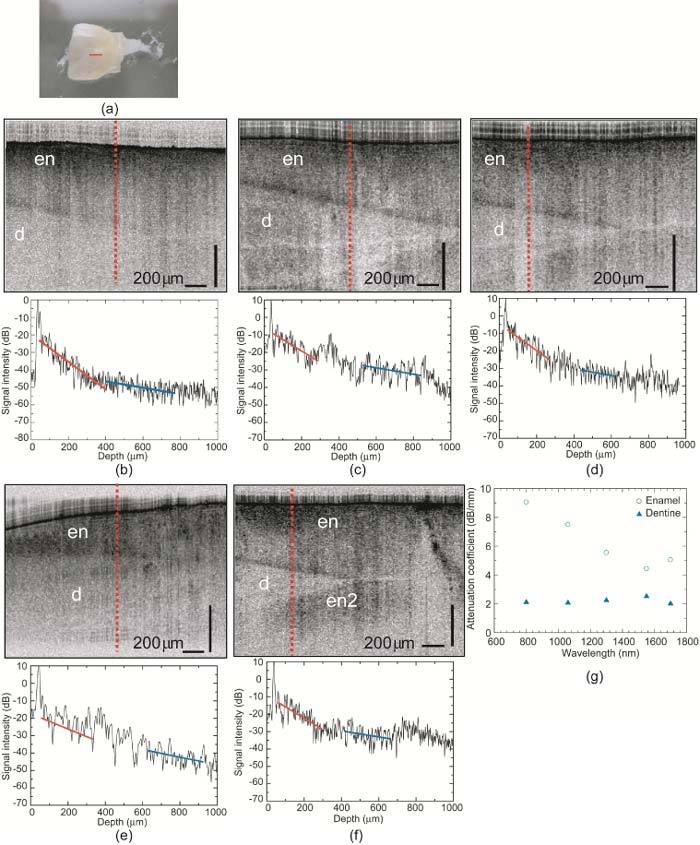
(a) Photograph of human tooth sample. (b–f) OCT images at red line in (a) and depth profiles obtained at red dashed line in each of the OCT images at (b) 800 nm, (c) 1060 nm, (d) 1300 nm, (e) 1550 nm, and (f) 1700 nm. The slopes shown by the red and blue solid lines were used to determine the total attenuation coefficients. (g) Wavelength dependence of total attenuation coefficients of enamel and dentine layers in the sample. Important features inside the sample can be distinguished, such as the enamel layer (en) and the dentin layer (d).
From these results and from comparison with the results of the industrially used materials described above, we confirmed the lower absorption by water in the human tooth sample and greater imaging depth with high contrast at a wavelength of 1700 nm.
3.6. Pig trachea
Figure 10(a) shows a photograph of the pig trachea sample. Figures 10(b–f) show the UHR-OCT images and A-line scans of the OCT signals at the red dashed line in each OCT image used for quantitative comparison. In Figs. 10(b–f), we can distinguish the epithelium, mucosa, and cartilage in the sample. The solid red line shows the slope at the mucosa layer. Figure 10(g) shows the wavelength dependence of the attenuation coefficient of the mucosa in the pig trachea sample. In Fig. 10(g), the total attenuation coefficient is highest at 800 nm, due to absorption by hemoglobin in the mucosa layer. At longer wavelengths, 1060 nm and above, the total attenuation coefficient increased. This was due to the influence of absorption by water around 1400 nm and above 1800 nm.
Fig. 10.
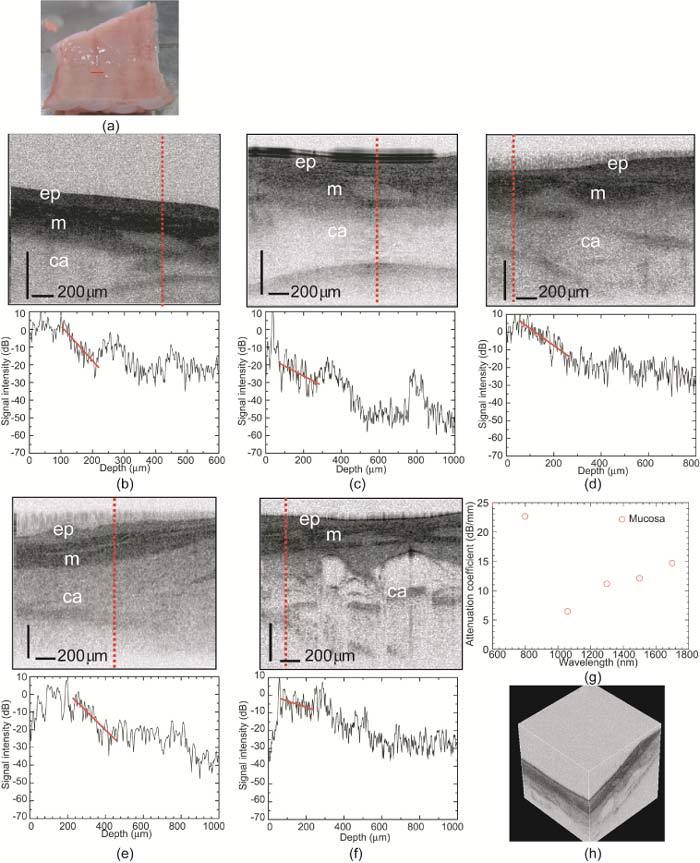
(a) Photograph of pig trachea sample. (b–f) OCT images and depth profiles at the red dashed line in each OCT image at (b) 800 nm, (c) 1060 nm, (d) 1300 nm, (e) 1550 nm and (f) 1700 nm . The slopes shown by the solid red lines were used to determine the total attenuation coefficients. (g) Wavelength dependence of total attenuation coefficients of mucosa in trachea. (h) Three-dimensional (3D) image at 1700 nm (Media 1 (3.1MB, MOV) ). A 3D image at 800 nm is also shown as a movie in Media 2 (3.7MB, MOV) . Important features inside the sample can be distinguished, such as the epithelium layer (ep), the mucosa layer (m), and cartilage (ca).
From these results, we confirmed the influence of absorption by water and hemoglobin on the total attenuation coefficient in the mucosa of the pig trachea sample. The total attenuation coefficient of the mucosa was smallest at 1060 nm. On the other hand, the image contrast between the epithelium, mucosa, and cartilage was much clearer at 1700 nm than at the other wavelengths. Figure 10(h) shows a reconstructed 3D image of the pig trachea at 1700 nm. Reconstructed 3D images at 800 nm and 1700 nm are also shown as movies in Media 1 (3.1MB, MOV) and Media 2 (3.7MB, MOV) . We can see the difference in image contrast and penetration depth in the two movies.
4. Discussion
We observed wavelength dependence of the total attenuation coefficients of various samples in UHR-OCT. Figure 11(a) shows the total attenuation coefficients of the industrially used homogeneous materials. The wavelength dependence of the magnet was much stronger than those of the other samples. The dashed line in Fig. 11(a) shows the fitted curve obtained from Rayleigh scattering theory. The total attenuation coefficients were fitted to this curve by the least-squares method. They were proportional to λ−4, where λ is the center wavelength of the light source. The wavelength dependence of the total attenuation coefficients of the plastic cover and eraser were well-fitted to the λ−4 dependence. It is considered that the slight different behavior of attenuation coefficient of these two materials is caused by the material properties such as hardness, molecular weight, and density. However, the fitness for the magnet was modest. The variation of the total attenuation coefficients at longer wavelengths for the industrially used homogeneous samples was much smaller than the others, in terms of the sample dependence shown in Fig. 11(a). Therefore, it is considered that a longer-wavelength system is useful for examining many kinds of industrially used materials with only a single apparatus. For more precise analysis of optical properties in the materials, it is necessary to compensate the chromatic dispersion inside the material, especially in the shorter wavelength region. In addition, it is expected that the phantoms made of polystyrene sphere in several liquid conditions are also useful to decouple the contribution of the absorption and scattering coefficients. In the human tooth sample, the enamel and dentine layers showed almost the same characteristics as the industrial samples. This is considered to be because of low absorption by water in human teeth. The total attenuation coefficient of the mucosa layer in the pig trachea sample, depicted by the circles in Fig. 11(b), was dependent on the sum of absorption and scattering. The total attenuation coefficient at 800 nm was affected by absorption by hemoglobin, which is described by the red line in Fig. 11(b). On the other hand, the total attenuation coefficient at wavelengths longer than 1060 nm was affected by absorption by water, which resulted in a higher total attenuation coefficient as the wavelength increased. From the imaging results of the pig trachea in Fig. 10(b–f), the OCT images at 800 nm and 1700 nm had clear boundaries between the epithelium, mucosa, and cartilage. On the other hand, the imaging contrast at 1060 nm, 1300 nm, and 1550 nm did not show any dependence on wavelength. From these results, in biomedical measurement, it is considered that there is a trade-off between imaging contrast and total attenuation coefficient, which leads to the greatest possible penetration depth. In addition, it is considered that the evaluation of the wavelength dependence of OCT imaging of skin and blood is effective to investigate the contribution of water and hemoglobin absorptions.
Fig. 11.
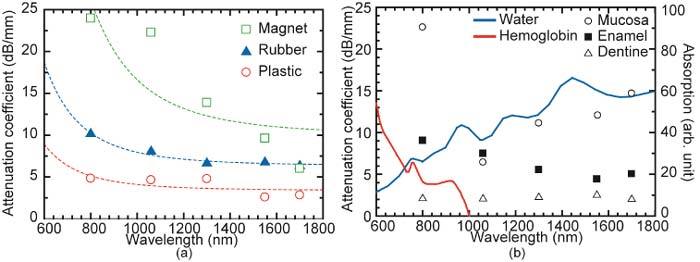
Total attenuation coefficients of (a) industrially used materials and (b) biomedical samples. The absorption coefficients of water [27] and hemoglobin [28] are shown in blue and red lines with arbitrary unit.
5. Conclusion
We investigated the wavelength dependence of the optical properties of samples with ultrahigh resolution optical coherence tomography (UHR-OCT) at wavelengths in the range 0.8–1.7 μm. We constructed supercontinuum sources in five wavelength regions and corresponding optical coherence tomography systems designed to match the broadband characteristics of each supercontinuum source. With these systems, we compared the total attenuation coefficients, which are mainly the sum of the scattering coefficient and absorption of the samples. In the samples of industrially used homogeneous materials showing low absorption by water, the total attenuation coefficients of the samples were fitted by Rayleigh scattering theory. The longer-wavelength systems had low scattering coefficient, leading to high-penetration-depth imaging and less dependence of the total attenuation coefficient on the sample material. One of the biological samples, the human tooth, which had low absorption by water, showed nearly the same total attenuation coefficient and penetration depth behavior. On the other hand, in the pig trachea sample, which showed absorption by water and hemoglobin, the total attenuation coefficient depended on the wavelength, due to absorption and scattering in the mucosa layer, and the imaging contrast at 800 nm and 1700 nm was much higher than at the other wavelengths.
References and links
- 1.Huang D., Swanson E. A., Lin C. P., Schuman J. S., Stinson W. G., Chang W., Hee M. R., Flotte T., Gregory K., Puliafito C. A., Fujimoto J. G., “Optical coherence tomography,” Science 254(5035), 1178–1181 (1991). 10.1126/science.1957169 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Schmitt J. M., “Optical coherence tomography (OCT): a review,” IEEE J. Sel. Top. Quantum Electron. 5(4), 1205–1215 (1999). 10.1109/2944.796348 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Zysk A. M., Nguyen F. T., Oldenburg A. L., Marks D. L., Boppart S. A., “Optical coherence tomography: a review of clinical development from bench to bedside,” J. Biomed. Opt. 12(5), 051403 (2007). 10.1117/1.2793736 [DOI] [PubMed] [Google Scholar]
- 4.Costa R. A., Skaf M., Melo L. A. S., Jr, Calucci D., Cardillo J. A., Castro J. C., Huang D., Wojtkowski M., “Retinal assessment using optical coherence tomography,” Prog. Retin. Eye Res. 25(3), 325–353 (2006). 10.1016/j.preteyeres.2006.03.001 [DOI] [PubMed] [Google Scholar]
- 5.Mujat M., Chan R. C., Cense B., Park B. H., Joo C., Akkin T., Chen T. C., de Boer J. F., “Retinal nerve fiber layer thickness map determined from optical coherence tomography images,” Opt. Express 13(23), 9480–9491 (2005). 10.1364/OPEX.13.009480 [DOI] [PubMed] [Google Scholar]
- 6.B. E. Bouma and G. J. Tearney, Handbook of Optical Coherence Tomography (Informa Healthcare, New York, 2001). [Google Scholar]
- 7.Bouma B. E., Tearney G. J., “Clinical imaging with optical coherence tomography,” Acad. Radiol. 9(8), 942–953 (2002). 10.1016/S1076-6332(03)80465-8 [DOI] [PubMed] [Google Scholar]
- 8.Fujimoto J. G., Boppart S. A., Tearney G. J., Bouma B. E., Pitris C., Brezinski M. E., “High resolution in vivo intra-arterial imaging with optical coherence tomography,” Heart 82(2), 128–133 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Tearney G. J., Yabushita H., Houser S. L., Aretz H. T., Jang I. K., Schlendorf K. H., Kauffman C. R., Shishkov M., Halpern E. F., Bouma B. E., “Quantification of macrophage content in atherosclerotic plaques by optical coherence tomography,” Circulation 107(1), 113–119 (2003). 10.1161/01.CIR.0000044384.41037.43 [DOI] [PubMed] [Google Scholar]
- 10.Boppart S. A., Luo W., Marks D. L., Singletary K. W., “Optical coherence tomography: feasibility for basic research and image-guided surgery of breast cancer,” Breast Cancer Res. Treat. 84(2), 85–97 (2004). 10.1023/B:BREA.0000018401.13609.54 [DOI] [PubMed] [Google Scholar]
- 11.Zuluaga A. F., Follen M., Boiko I., Malpica A., Richards-Kortum R., “Optical coherence tomography: a pilot study of a new imaging technique for noninvasive examination of cervical tissue,” Am. J. Obstet. Gynecol. 193(1), 83–88 (2005). 10.1016/j.ajog.2004.11.054 [DOI] [PubMed] [Google Scholar]
- 12.Colston B. W., Jr, Everett M. J., Da Silva L. B., Otis L. L., Stroeve P., Nathel H., “Imaging of hard- and soft-tissue structure in the oral cavity by optical coherence tomography,” Appl. Opt. 37(16), 3582–3585 (1998). 10.1364/AO.37.003582 [DOI] [PubMed] [Google Scholar]
- 13.Otis L. L., Colston B. W., Jr, Everett M. J., Nathel H., “Dental optical coherence tomography: a comparison of two in vitro systems,” Dentomaxillofac. Radiol. 29(2), 85–89 (2000). 10.1038/sj.dmfr.4600507 [DOI] [PubMed] [Google Scholar]
- 14.Freitas A. Z., Zezell D. M., Vieira N. D., Ribeiro A. C., Gomes A. S. L., “Imaging carious human dental tissue with optical coherence tomography,” J. Appl. Phys. 99(2), 024906 (2006). 10.1063/1.2160716 [DOI] [Google Scholar]
- 15.Schmitt J. M., Knüttel A., Yadlowsky M., Eckhaus M. A., “Optical-coherence tomography of a dense tissue: statistics of attenuation and backscattering,” Phys. Med. Biol. 39(10), 1705–1720 (1994). 10.1088/0031-9155/39/10/013 [DOI] [PubMed] [Google Scholar]
- 16.Pan Y., Farkas D. L., “Nonivasive imaging of living human skin with dual-wavelength optical coherence tomography in two and three dimensions,” J. Biomed. Opt. 3(4), 446–455 (1998). 10.1117/1.429897 [DOI] [PubMed] [Google Scholar]
- 17.Radhakrishnan S., Rollins A. M., Roth J. E., Yazdanfar S., Westphal V., Bardenstein D. S., Izatt J. A., “Real-time optical coherence tomography of the anterior segment at 1310 nm,” Arch. Ophthalmol. 119(8), 1179–1185 (2001). [DOI] [PubMed] [Google Scholar]
- 18.Aguirre A., Nishizawa N., Fujimoto J. G., Seitz W., Lederer M., Kopf D., “Continuum generation in a novel photonic crystal fiber for ultrahigh resolution optical coherence tomography at 800 nm and 1300 nm,” Opt. Express 14(3), 1145–1160 (2006). 10.1364/OE.14.001145 [DOI] [PubMed] [Google Scholar]
- 19.Sharma U., Chang E. W., Yun S. H., “Long-wavelength optical coherence tomography at 1.7 microm for enhanced imaging depth,” Opt. Express 16(24), 19712–19723 (2008). 10.1364/OE.16.019712 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kodach V. M., Kalkman J., Faber D. J., van Leeuwen T. G., “Quantitative comparison of the OCT imaging depth at 1300 nm and 1600 nm,” Biomed. Opt. Express 1(1), 176–185 (2010). 10.1364/BOE.1.000176 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Nishiura M., Kobayashi T., Adachi M., Nakanishi J., Ueno T., Ito Y., Nishizawa N., “In vivo ultrahigh-resolution ophthalmic optical coherence tomography using Gaussian-shaped supercontinuum,” Jpn. J. Appl. Phys. 49(1), 012701 (2010). 10.1143/JJAP.49.012701 [DOI] [Google Scholar]
- 22.Bourquin S., Aguirre A. D., Hartl I., Hsiung P., Ko T. H., Fujimoto J. G., Birks T. A., Wadsworth W. J., Bünting U., Kopf D., “Ultrahigh resolution real time OCT imaging using a compact femtosecond Nd:glass laser and nonlinear fiber,” Opt. Express 11(24), 3290–3297 (2003). 10.1364/OE.11.003290 [DOI] [PubMed] [Google Scholar]
- 23.Ishida S., Nishizawa N., Ohta T., Itoh K., “Ultrahigh-resolution optical coherence tomography in 1.7 μm region with fiber laser supercontinuum in low water absorption samples,” Appl. Phys. Express 4(5), 052501 (2011). 10.1143/APEX.4.052501 [DOI] [Google Scholar]
- 24.Nishizawa N., Chen Y., Hsiung P., Ippen E. P., Fujimoto J. G., “Real-time, ultrahigh-resolution, optical coherence tomography with an all-fiber, femtosecond fiber laser continuum at 1.5 microm,” Opt. Lett. 29(24), 2846–2848 (2004). 10.1364/OL.29.002846 [DOI] [PubMed] [Google Scholar]
- 25.Schmitt J. M., Knüttel A., Bonner R. F., “Measurement of optical properties of biological tissues by low-coherence reflectometry,” Appl. Opt. 32(30), 6032–6042 (1993). 10.1364/AO.32.006032 [DOI] [PubMed] [Google Scholar]
- 26.Faber D. J., van der Meer F. J., Aalders M. C. G., van Leeuwen T., “Quantitative measurement of attenuation coefficients of weakly scattering media using optical coherence tomography,” Opt. Express 12(19), 4353–4365 (2004). 10.1364/OPEX.12.004353 [DOI] [PubMed] [Google Scholar]
- 27.Hale G. M., Querry M. R., “Optical constants of water in the 200 nm to 200 µm wavelength region,” Appl. Opt. 12(3), 555–563 (1973). 10.1364/AO.12.000555 [DOI] [PubMed] [Google Scholar]
- 28.S. Prahl, “Optical absorption of hemoglobin” (Oregon Medical Laser Center, Portland, Oreg., September 22, 2010), http://omlc.ogi.edu/spectra/hemoglobin/


