Skip to main content
PMC home page
Journal of Computational Biology logoLink to Journal of Computational Biology
. 2011 Nov;18(11):1561–1574. doi: 10.1089/cmb.2011.0154

Vavien: An Algorithm for Prioritizing Candidate Disease Genes Based on Topological Similarity of Proteins in Interaction Networks

Sinan Erten 1,✉, Gurkan Bebek 2,,3, Mehmet Koyutürk 1,,2
PMCID: PMC3216100  PMID: 22035267

Abstract

Genome-wide linkage and association studies have demonstrated promise in identifying genetic factors that influence health and disease. An important challenge is to narrow down the set of candidate genes that are implicated by these analyses. Protein-protein interaction (PPI) networks are useful in extracting the functional relationships between known disease and candidate genes, based on the principle that products of genes implicated in similar diseases are likely to exhibit significant connectivity/proximity. Information flow–based methods are shown to be very effective in prioritizing candidate disease genes. In this article, we utilize the topology of PPI networks to infer functional information in the context of disease association. Our approach is based on the assumption that PPI networks are organized into recurrent schemes that underlie the mechanisms of cooperation among different proteins. We hypothesize that proteins associated with similar diseases would exhibit similar topological characteristics in PPI networks. Utilizing the location of a protein in the network with respect to other proteins (i.e., the “topological profile” of the proteins), we develop a novel measure to assess the topological similarity of proteins in a PPI network. We then use this measure to prioritize candidate disease genes based on the topological similarity of their products and the products of known disease genes. We test the resulting algorithm, Vavien, via systematic experimental studies using an integrated human PPI network and the Online Mendelian Inheritance in Man (OMIM) database. Vavien outperforms other network-based prioritization algorithms as shown in the results and is available at www.diseasegenes.org.

Key words: algorithms, computational molecular biology

1. Introduction

Characterization of disease-associated variants in human genome is an important step toward enhancing our understanding of the cellular mechanisms that drive complex diseases, with profound applications in modeling, diagnosis, prognosis, and therapeutic intervention (Brunner and van Driel, 2004). Genome-wide linkage and association studies in healthy and affected populations provide chromosomal regions containing hundreds of polymorphisms that are potentially associated with certain genetic diseases (Glazier et al., 2002). These polymorphisms often implicate up to 300 genes, only a few of which may have a role in the manifestation of the disease. Investigation of that many candidates via sequencing is clearly an expensive task and thus not always a feasible option. Consequently, computational methods are primarily used to prioritize and identify the most likely disease-associated genes by utilizing a variety of data sources such as gene expression (Lage et al., 2007; Nica and Dermitzakis, 2008) and functional annotations (Adie et al., 2006; Chen et al., 2009b; Turner et al., 2003). However, the scope of methods that rely on functional annotations is limited because only a small fraction of genes in the human genome are currently annotated. Moreover, signals inferred from gene expression profiles are not easily utilized especially for diseases caused by multiple genes, where the impact of each contributor gene can be minimal. Protein-protein interactions (PPIs) provide an invaluable resource in this regard, since they provide functional information in a network context and can be obtained at a large scale via high-throughput screening (Ewing et al., 2007).

Despite their differences, all network-based disease gene prioritization algorithms are based on a unique principle: the association between proteins is correlated with their connectivity/proximity in the PPI network. However, recent research also reveals that networks are organized into recurrent network schemes that underlie the interaction patterns among proteins with different function (Pandey et al., 2007; Bebek and Yang, 2007). Based on this observation, we propose a topological similarity-based disease gene prioritization scheme in this article. For this purpose, we develop a measure of topological similarity among pairs of proteins in a PPI network and use the network similarity between seed and candidate proteins to infer the likelihood of disease association for the candidates.

We first discuss existing network-based disease gene prioritization approaches in Section 2. In Section 3, we present the algorithmic details of the proposed methods. Systematic experimental studies using an integrated human PPI network and the Online Mendelian Inheritance in Man (OMIM) database are presented in Section 4. These results show that the proposed algorithm, Vavien,1 clearly outperforms state-of-the-art network-based prioritization algorithms. We conclude our discussion in Section 5.

2. Background

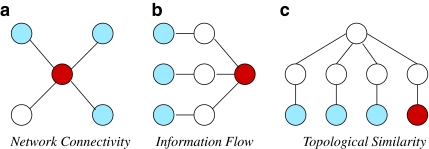
In the last few years, many algorithms have been developed to utilize PPI networks in disease gene prioritization (Navlakha and Kingsford, 2010; Franke et al., 2006; Ideker and Sharan, 2008; Karni et al., 2009; Oti et al., 2006; Chen et al., 2009a; Köhler et al., 2008; Vanunu et al. 2010; Zhang et al., 2010; Wu et al., 2008; Missiuro et al., 2009; Aerts et al., 2006). These algorithms take as input a set of seed proteins (coded by genes known to be associated with the disease of interest or similar diseases), candidate proteins (coded by genes in the linkage interval for the disease of interest), and a network of interactions among human proteins. Subsequently, they use PPIs to infer the relationship between seed and candidate proteins and rank the candidate proteins according to these inferred relationships. The key ideas in network-based prioritization of disease genes are illustrated in Figure 1.

FIG. 1.

FIG. 1.

Open in a new tab

Key principles in network-based disease gene prioritization. Nodes and edges respectively represent proteins and interactions. Seed proteins (proteins known to be associated with the disease of interest) are shown in light blue, proteins that are implicated to be associated with the same disease by the respective principle are shown in dark red, other proteins are shown in white. (a) Network Connectivity infers association of the red protein with the seed proteins because it interacts heavily with them. (b) Information Flow infers association of the red protein with seed proteins because it exhibits crosstalk to them via indirect interactions through other proteins. (c) Topological Similarity, proposed in this article infers association of the red protein with the seed proteins because it (indirectly) interacts with a hub protein in a way topologically similar to them.

Network connectivity is useful in disease gene prioritization

Network-based analyses of diverse phenotypes demonstrate that products of genes that are implicated in similar diseases are clustered together into highly connected subnetworks in PPI networks (Goh et al., 2007; Rhodes and Chinnaiyan, 2005). Motivated by these observations, many studies search the PPI networks for interacting partners of known disease genes to narrow down the set of candidate genes implicated by genome-wide linkage analyses (Franke et al., 2006; Ideker and Sharan, 2008; Karni et al., 2009; Oti et al., 2006) (Fig. 1a). In one of the pioneering studies on network-based disease gene prioritization, Oti et al. (2006) identify potential disease genes by qualitatively investigating the interacting partners of the genes that are known to be associated with the disease of interest. Frank et al. (2006) extend this idea in a quantitative framework to score candidate genes based on the number of interactions between each candidate disease gene and known disease genes. These algorithms are also extended to take into account the information provided by the genes implicated in diseases similar to the disease of interest (Lage et al., 2007). Here, the similarity between diseases refers to the similarity in clinical classification of diseases.

Information flow based methods take into account indirect interactions

Methods that consider direct interactions between seed and candidate proteins do not utilize knowledge of PPIs to their full potential. In particular, they do not consider interactions among proteins that are not among the seed or candidate proteins, which might also indicate indirect functional relationships between candidate and seed proteins. For this reason, connectivity-based (“local”) methods are vulnerable to false negative and positive interactions (Pandey et al., 2010). Information flow–based (“global”) methods ground themselves on the notion that products of genes that have an important role in a disease are expected to exhibit significant network crosstalk to each other in terms of the aggregate strength of paths that connect the corresponding proteins (Fig. 1b). This approach is motivated by the following two observations: (i) multiple alternate paths between functionally associated proteins are often conserved through evolution, owing to their contribution to robustness against perturbations, as well as amplification of signals (Kelley and Ideker, 2005; Li et al., 2006); and (ii) consideration of alternate paths accounts for missing data and noise in PPI networks (Kelley et al., 2003; Koyutürk et al., 2006). Indeed, information flow–based models are also shown to be very effective in network-based functional annotation of proteins (Nabieva et al., 2005) and coexpression-based prioritization of proteomic targets (Bebek et al., 2010). These methods include random walk with restarts (Chen et al., 2009a; Köhler et al., 2008) and network propagation (Vanunu et al., 2010; Zhang et al., 2010), which significantly outperform connectivity-based methods (Navlakha and Kingsford, 2010).

Topological similarity indicates functional association

Recent research reveals that networks are organized into recurrent network schemas that underlie the interaction patterns among proteins with different function (Pandey et al., 2007; Bebek and Yang, 2007). A well-known network schema, for example, is a chain of membrane-bound receptors, protein kinases, and transcription factors, which serves as a high-level description of the backbone of cellular signaling. Dedicated mining algorithms identify more specific network schemes at a higher resolution, indicating that similar principles are used recurrently in interaction networks (Banks et al., 2008; Kirac and Özsoyoglu, 2008). Motivated by these observations, a new generation of network-based functional annotation algorithms exploit the topological similarity among proteins in the PPI network, based on the principle that proteins that interact with proteins of similar function are also likely to have similar functions (Bogdanov and Singh, 2010; Kirac et al., 2006; Kirac and Özsoyoglu, 2008). These algorithms are shown to outperform connectivity and information flow–based algorithms in annotation of biological function (Bogdanov and Singh, 2010; Kirac and Özsoyoglu, 2008). Inspired by these results, in this article, we develop a network-based disease gene prioritization algorithm that uses topological similarity to infer the relationship between seed and candidate proteins (Fig. 1c). Below, we further motivate this approach with an example from the systems biology of cancer.

Motivating example

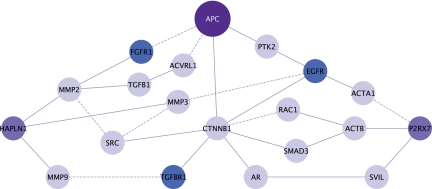
While the APC gene has been identified to be one of the most important genes that play a role in the development of colorectal cancer, there are multiple proteins that work in parallel with Apc to create these cancers (Sjöblom et al., 2006; Wood et al., 2007). Although the actual mechanisms of selection are not clear, it is known that proteins which are not directly interacting with APC, and have similar functions in a cell—such as tumor suppressor genes PTEN (Marsh et al., 2008), TRP53 (Halberg et al., 2008), and p21 (Patel et al., 2010)—when mutated with APC, increase the tumor burden. In a recent study, Bebek et al., (2010) present a pipeline where bimodality of coexpresssion is used to prioritize proteomics targets identified in a mouse model of colorectal cancer. Some of the significant proteins identified are shown in Figure 2 in a PPI network. The identified targets HAPLN1, P2RX7 (colored purple in the figure) are linked to growth factor receptors (GFRs) (EGFR, TGFR1, FGFR1; colored blue in the figure), but not connected to each other. As seen in Figure 2, similarities of these two proteomic targets in their function and role in disease are also reflected in their relative topology with respect to APC and growth factors.

FIG. 2.

FIG. 2.

Open in a new tab

Motivating example for using topological similarity to prioritize candidate disease genes. Two PPI subnetworks connecting key cancer driver genes, APC-HAPLNI (p < 0.0068) and APC-P2RX7 (p < 0.0212), were found significant when bimodality of coexpression with proteomic targets were calculated. Darker nodes represent proteins coded by genes that carry “driver mutations.” Blue nodes represent growth factor receptors (GFRs). Although APC-HAPLNI and APC-P2RX7 do not directly interact or exhibit significant crosstalk with growth factors and products of driver genes, their relative locations with respect to these proteins exhibit similarities.

3. Methods

In this section, we first describe the disease gene prioritization problem within a formal framework. Subsequently, we formulate the concept of topological similarity of pairs of proteins in terms of their proximity to other proteins in the network. Finally, we discuss how topological similarity of proteins is used to prioritize candidate disease genes.

3.1. Disease gene prioritization problem

Let D denote a disease of interest, which is potentially associated with various genetic factors (e.g., sleep apnea, Alzhemier's disease, autism). Assume that a genome-wide association study (GWAS) using samples from control and affected populations is conducted, revealing a linkage interval that is significantly associated with D. Potentially, such a linkage interval will contain multiple genes, which are all candidates for being mechanistically associated with D (i.e., the mutation in a gene in the linkage interval might have a role in the manifestation of disease). This set of candidate genes, denoted 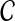Inline graphic, forms the input to the disease gene prioritization problem.

The aim of disease gene prioritization is to rank the genes in 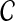Inline graphic based on their potential mechanistic association with D. For this purpose, a set of genes that are already known to be associated with D or diseases similar to D is used (where similarity between diseases is defined phenotypically—e.g., based on the clinical description of diseases). The idea here is that genes in 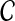Inline graphic that are mechanistically associated with D are likely to exhibit patterns of association with such genes in a network of PPIs. This set of genes is referred to as the seed set and denoted 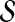Inline graphic. Each gene 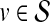Inline graphic is assigned a disease-association score 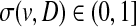Inline graphic, representing the known level of association between v and D. The association score for v and D is set to 1 if it is a known association listed in OMIM database. Otherwise, it is computed as the maximum clinical similarity between D and any other disease associated with v (Erten and Koyutürk, 2010) (a detailed discussion on computation of similarity scores can be found in van Driel et al. [2006]).

In order to capture the association of the genes in 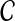Inline graphic with those in 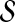Inline graphic, network-based prioritization algorithms utilize a network of known interactions among human proteins. 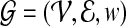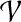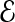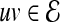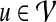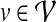The human PPI network Inline graphic consists of a set of proteins Inline graphic and a set of undirected interactions Inline graphic between these proteins, where Inline graphic represents an interaction between Inline graphic and Inline graphic. Since PPI networks are noisy and incomplete (Stumpf et al., 2008), each interaction 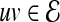Inline graphic is also assigned a confidence score representing the reliability of the interaction between u and v (Sharan et al., 2005; Suthram et al., 2006; Bebek and Yang, 2007). 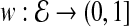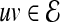Formally, there exists a function Inline graphic, where w(uv) indicates the reliability of interaction Inline graphic.

In this article, the reliability score is derived through a logistic regression model where a positive interaction dataset (MIPS Golden PPI interactions [Mewes et al., 2004]) and a negative interaction dataset (Negatome [Smialowski et al., 2010]) are used to train a model with three variables: (1) co-expression measurements for the corresponding genes derived from multiple sets of tissue microarray experiments (normal human tissues measured in the Human Body Index Transcriptional Profiling [GEO accession no. GSE7307] [Barrett et al., 2009]); (2) the proteins' small world clustering coefficient; and (3) the protein subcellular localization data of interacting partners (Sprenger et al., 2008). Co-expression values are used since co-regulated genes are more likely to interact with each other than are others (Sharan et al., 2005; Bebek and Yang, 2007). Alternatively, the network feature that we are extracting, the small world clustering coefficient, is a measure of connectedness. This coefficient shows how likely the neighbors (interacting peers) of a protein are neighbors of each other (Goldberg and Roth, 2003). We also incorporate the protein subcellular localization data into the logistic model, since this would eliminate interactions among proteins that are not biologically significant (Bebek and Yang, 2007). The logistic regression model is trained on randomly selected 1000 positive and negative training data sets for 100 times, and regression constants are determined to score each PPI.

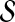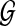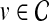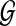Given Inline graphic and Inline graphic, network-based disease gene prioritization aims to compute a score α(v, D) for each Inline graphic, representing the potential association of v with disease D. For this purpose, we develop a novel method,Vavien, to rank candidate genes based on their topological similarity to the seed genes in Inline graphic.

3.2. Topological similarity of proteins in a PPI network

Recent research shows that molecular networks are organized into functional interaction patterns that are used recurrently in different cellular processes (Pandey et al., 2007; Banks et al., 2008). In other words, proteins with similar function often interact with proteins that are also functionally similar to each other (Kirac and Özsoyoglu, 2008). Motivated by this observation, Vavien aims to assess the functional similarity between seed and candidate proteins based on their topological similarity, that is the similarity of their relative location with respect to other proteins in the network. For this purpose, we first define the topological profile of a protein in a PPI network.

Topological profile of a protein

For a given protein 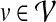Inline graphic and a PPI network 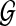Inline graphic, the topological profile βv of v is defined as a 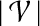Inline graphic-dimensional vector such that for each 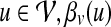Inline graphic represents the proximity of protein v to protein u in 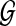Inline graphic. Clearly, the proximity between two proteins can be computed in various ways. A well-known measure of proximity is the shortest path (here, the most reliable path) between the two proteins; however, this method is vulnerable to missing data and noise in PPI networks (Pandey et al., 2010). A reliable measure of network proximity is effective conductance, which is based on a model that represents the network as an electrical circuit. In this model, each edge is represented as a capacitor with capacitance proportional to its reliability score. Effective conductance can be computed using the inverse of the Laplacian matrix of the network; however, this computation is quite costly since it requires computation of the inverse of a sparse matrix (Spielman and Srivastava, 2008). Fortunately, however, computation of effective conductance and random walks in a network are known to be related (Tetali, 1991), and proximity scores based on random walks can be computed efficiently using iterative methods.

Vavien computes the proximity between pairs of proteins using random walk with restarts (Lovász, 1996; Tong et al., 2008). This method is used in a wide range of applications, including identification of functional modules (Macropol et al., 2009) and modeling the evolution of social networks (Tong and Faloutsos, 2006). It is also the first information flow–based method to be applied to disease gene prioritization (Köhler et al., 2008; Chen et al., 2009a) and is shown to clearly outperform connectivity-based methods.

Random walk with restarts computes the proximity between a protein v and all other proteins in the network as follows: A random walk starts at v. At each step, if the random walk is at protein u, it either moves to an interacting partner t of u (i.e., 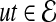Inline graphic) or it restarts the walk at v. The probability P(u, t) of moving to a specific interacting partner t of u is proportional to the reliability of the interaction between u and t, i.e., P(u, t) = w(ut)/W(u) where 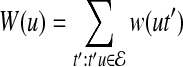Inline graphic is the weighted degree of u in the network. The probability of restarting at a given time step is a fixed parameter denoted r. After a sufficiently long time, the probability of being at node u at a random time step provides a measure of the proximity between v and u, which can be computed iteratively as follows:

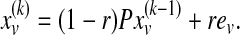graphic file with name M29.gif (1)

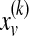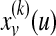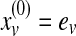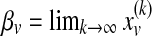Here Inline graphic denotes a probability vector such that Inline graphic equals the probability of being at protein u at the kth iteration of the random walk, Inline graphic, and ev is the restart vector such that ev(u) = 1 if u = v and 0 otherwise. For a given value of r, the topological profile of protein v is defined as Inline graphic.

Note that the concept of topological profile introduced here is not to be confused by the gene closeness profile used by the CIPHER algorithm for disease gene prioritization (Wu et al., 2008). Here, topological profile is constructed using the proximity of a protein of interest to every other protein in the network. It is therefore a global signature of the location of the protein in the PPI network. In contrast, gene closeness profile is based only on the proximity of a protein of interest to proteins coded by known disease genes. Furthermore, the proposed algorithm is different from random walk–based prioritization algorithms in that these algorithms score candidate proteins directly based on random walk proximity to seed proteins (Köhler et al., 2008). In contrast, Vavien uses random walk proximity as a feature to assess the topological similarity between seed and candidate proteins, which in turn is used to score candidate proteins. We now describe this approach in detail.

Topological similarity of two proteins

Let u and 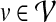Inline graphic denote two proteins in the network. The topological similarity of u and v is defined as

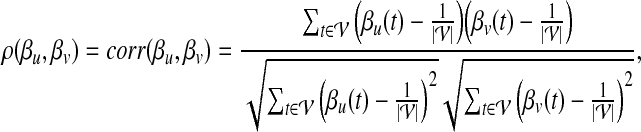graphic file with name M35.gif (2)

where corr(X, Y) denotes the Pearson correlation coefficient of random variables X and Y. The idea behind this approach is that, if two proteins interact with similar proteins, or lay on similar locations with respect to hub proteins in the network, then their topological profiles will be correlated, which will be captured by ρ(βu, βv).

3.3. Using topological similarity to prioritize candidate genes

The core idea behind the proposed algorithm is that candidate genes whose products are topologically similar to the products of seed genes are likely to be associated with D. Based on this idea, we propose three schemes to prioritize candidate genes based on their topological similarity with seed genes. All of these schemes are implemented in Vavien.

Prioritization based on average topological similarity with seed genes (ATS)

For each 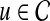Inline graphic, the topological profile vector βu is computed using random walk with restarts. Similarly, topological profile vectors βv of all genes 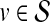Inline graphic are computed separately. Subsequently, for each 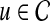Inline graphic, the association score of u with D is computed as the weighted average of the topological similarity of u with the genes in 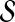Inline graphic, where the contribution of each seed gene is weighted by its association with D, i.e.:

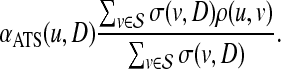graphic file with name M40.gif (3)

Prioritization based on topological similarity with average profile of seed genes (TSA)

Instead of computing the topological similarity for each seed gene separately, this approach first computes an average topological profile that is representative of the seed genes and computes the topological similarity of the candidate gene and this average topological profile. More precisely, the association score of 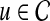Inline graphic with D is computed as:

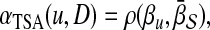graphic file with name M42.gif (4)

where

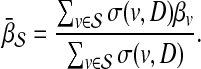graphic file with name M43.gif (5)

Prioritization based on topological similarity with representative profile of seed genes (TSR)

The random walk with restarts model can be easily extended to compute the proximity between a group of proteins and each protein in the network. This can be done by generalizing the random walk to one that makes frequent restarts at any of the proteins in the group. This is indeed the idea of disease gene prioritization using random walk with restarts (Köhler et al., 2008). This method is also useful for directly computing a representative topological profile for 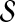Inline graphic, instead of taking the average of the topological profiles of the genes in 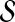Inline graphic. More precisely, for given seed set 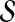Inline graphic and association scores σ for all genes in 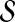Inline graphic, the proximity of the products of genes in 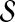Inline graphic to each protein in the network is computed by replacing the restart vector in Equation 1 with vector 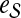Inline graphic where

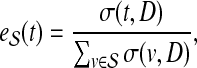graphic file with name M50.gif (6)

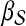if Inline graphic and Inline graphic otherwise. Then, the topological profile Inline graphic of S is computed as 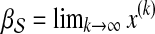Inline graphic. The random walk–based approach to disease gene prioritization estimates the association of each candidate gene with the disease as the proximity between the product of the candidate gene and 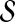Inline graphic under this model (i.e., it directly sets 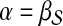Inline graphic. In contrast, we compute the association of 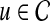Inline graphic with D as

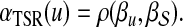graphic file with name M58.gif (7)

Once α is computed using one of (3), (4), or (7), Vavien ranks the candidate genes in decreasing order of α.

4. Results

In this section, we systematically evaluate the performance of Vavien in capturing true disease-gene associations using a comprehensive database of known disease-gene associations. We start by describing the datasets and experimental settings. Next, we analyze the performance of different schemes implemented in Vavien and the effect of parameters. Subsequently, we compare the performance of Vavien with four state-of-the-art network-based prioritization algorithms. Finally, we test the robustness of Vavien against false positive and false negative PPI data by randomly deleting and resampling the network.

4.1. Datasets

We test and compare the proposed methods on a comprehensive set of disease association data, using an integrated human PPI network in which interactions are associated with reliability scores. We describe these datasets in detail below.

Disease association data

The OMIM database provides a publicly accessible and comprehensive database of genotype-phenotype relationship in humans. We acquire disease-gene associations from OMIM and map the gene products known to be associated with disease to our PPI network. The dataset contains 1931 diseases with number of gene associations ranging from 1 to 25, average being only 1.31. Each gene v in the seed set 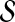Inline graphic is associated with the similarity score σ(v, D), indicating the known degree of association between v and D as mentioned before.

Human PPI network

In our experiments, we use the human PPI data obtained from NCBI Entrez Gene Database (Maglott et al., 2007). This database integrates interaction data from several other databases available, such as HPRD, BioGrid, and BIND. After the removal of nodes with no interactions, the final PPI network contains 8959 proteins and 33,528 interactions among these proteins. We assign reliability scores to these interactions using the methodology described in Section 2.1.

4.2. Experimental setting

In order to evaluate the performance of different methods in prioritizing disease-associated genes, we use leave-one-out cross-validation. For each gene u that is known to be associated with a disease D in our dataset, we conduct the following experiment:

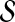  • We remove u from the set of genes known to be associated with D. We call u the target gene for that experiment. The remaining set of genes associated with D becomes the seed set Inline graphic.

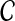  • We generate an artificial linkage interval, containing the target gene u with other 99 genes located nearest in terms of genomic distance. The genes in this artificial linkage interval (including u) compose the candidate set Inline graphic.

  • We apply each prioritization algorithm to obtain a ranking of the genes in Inline graphic.

  • We assess the quality of the ranking provided by each algorithm using the evaluation criteria described below.

Evaluation criteria

We first plot ROC (precision versus recall) curves, by varying the threshold on the rank of a gene to be considered a “predicted disease gene.” Precision is defined as the fraction of true disease genes among all genes ranked above the particular threshold, whereas recall is defined as the fraction of true disease genes identified (ranked above the threshold) among all known disease genes. Note that, this is a conservative measure for this experimental set-up since there exists only one true positive (the target gene) for each experiment. For this reason, we also compare these methods in terms of the average rank of the target gene among 100 candidates, computed across all disease-gene pairs in our experiments. Clearly, lower average rank indicates better performance. Finally, we report the percentage of true disease genes that are ranked as one of the genes in the top 1% (practically, the top gene) and also in the top 5% among all candidates.

4.3. Performance evaluation

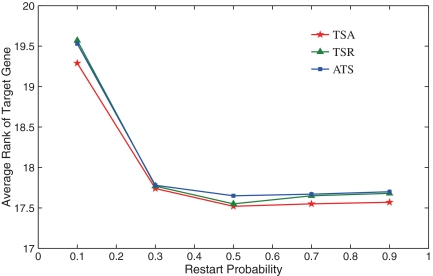
Performance of methods implemented in Vavien and the effect of restart parameter

We compare the three different algorithms (ATS, TSA, and TSR) implemented in Vavien in Figure 3. Since the topological profile of a protein depends on the restart probability (the parameter r) in the random walk with restarts, we also investigate the effect of this parameter on the performance of algorithms. In the figure, the average rank of the target gene among 100 candidate genes is shown for each algorithm as a function of restart probability. As seen in the figure, the three algorithms deliver comparable performance. However, TSA, which makes use of the average profile of seed genes to compute the topological similarity of the candidate gene to seed genes achieves the best performance. Furthermore, the performance of all algorithms implemented in Vavien appears to be robust to the selection of parameter r, as long as it is in the range [0.3–0.9]. In our experiments, we set r = 0.5 and use TSA as the representative algorithm since this combination provides the best performance.

FIG. 3.

FIG. 3.

Open in a new tab

The performance of the three prioritization algorithms implemented in Vavien as a function of the restart probability used in computing proximity via random walk with restarts. The performance here is measured in terms of the average rank of the target gene among 100 candidate genes, a lower value indicating better performance.

Performance of Vavien compared to existing algorithms

We also evaluate the performance of Vavien in comparison to state-of-the-art algorithms for network-based disease gene prioritization. These algorithms are the following:

  • Random walk with restarts: This algorithm prioritizes candidate genes based on their proximity to seed genes, using a random walk with restarts model (i.e., α is set to 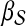Inline graphic) (Köhler et al., 2008).

  • Network propagation: This algorithm is very similar to random walk with restarts, with one key difference. In network propagation, the stochastic matrix in (1) is replaced with a flow matrix in which both the incoming and outgoing flow to a protein is normalized (i.e., 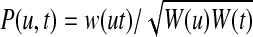Inline graphic in network propagation) (Vanunu et al., 2010).

  • Information flow with statistical correction: Based on the observation that the performance of information flow–based algorithms (including random walk with restarts and network propagation) depend on network degree, this algorithm applies statistical correction to the random walk–based association scores based on a reference model that takes into account the degree distribution of the PPI network (Erten and Koyutürk, 2010).

  • Genomic Data Fusion (Endeavour): Endeavour is a comprehensive and flexible software package, which is freely available. It prioritizes candidate genes based on their similarity to known disease genes by integrating information from multiple data sources such as gene annotations, expression data, sequence information, and PPIs. Endeavour generates separate scores for all candidates based on each heterogeneous data source and obtains a global ranking by applying order statistics on these separate rankings. In this article, we focus on comparing how different approaches utilize network data for the task in hand; thus, we run Endeavour using the PPI data sources only.

While software implementing network propagation (Prince) (Vanunu et al., 2010) and statistical correction (DaDa) (Erten et al., 2011) are available, we here report results based on our implementation of these two algorithms. We run all algorithms using identical settings for data integration and incorporation of disease similarity scores, differing from each other only in how network information is utilized in computing disease association scores. The objective of this approach is to provide a setting in which the algorithmic ideas can be directly compared, by removing the influence of implementation details and datasets used. It should be noted, however, that the performance of these algorithms could be better than the performance reported here if available software and/or different PPI datasets are used.

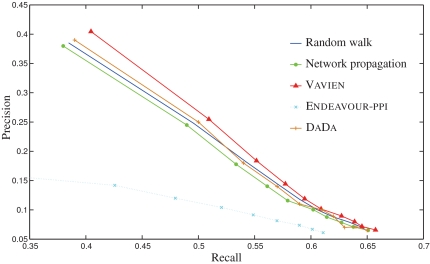
The ROC curves for the four existing methods and Vavien are shown in Figure 4, demonstrating the relationship between precision and recall for each algorithm. Other performance measures for all methods are listed in Table 1. As seen in both the figure and the table, Vavien clearly outperforms all of the existing algorithms in ranking candidate disease genes. In particular, it is able to rank 40% of true disease genes as the top candidate among 100 candidates and it ranks 62% of true disease genes in the top 5% of all candidates.

FIG. 4.

FIG. 4.

Open in a new tab

ROC curves comparing the performance of the proposed method with existing information-flow based algorithms.

Table 1.

Comparison of Vavien with Existing Algorithms for Network-Based Disease Gene Prioritization

Method Average rank Ranked in top 1% Ranked in top 5%
Vavien 17.52 40.48 62.46
Random walk 18.58 38.42 59.01
Network propagation 18.28 37.97 57.96
Random walk with statistical correction 17.86 39.41 59.76
Endeavour (PPI only) 24.05 17.18 52.02
Open in a new tab

Vavien outperforms state-of-the-art information flow–based algorithms with respect to all performance criteria.

Effect of network degree

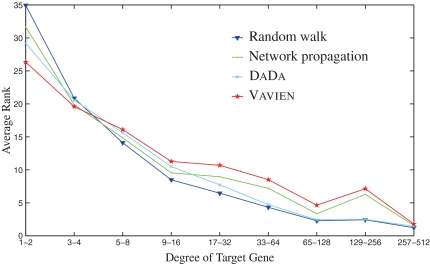
Information flow based algorithms are previously shown to be biased with respect to the degree of the target genes (Erten and Koyutürk, 2010). In other words, these methods work poorly in identifying loosely connected disease genes. Previous efforts reduce this bias to a certain extent by introducing several statistical correction schemes (Erten and Koyutürk, 2010). Motivated by these observations, we here investigate the effect of the bias introduced by degree distribution on the performance of different algorithms. The results of these experiments are shown in Figure 5. In this figure, the change on the performance (average rank of the target gene) of different methods is plotted with respect to the degree of the target gene. As clearly seen, Vavien is the algorithm that is affected least by this bias and it outperforms other methods in identifying loosely connected disease genes. It is particularly impressive that Vavien's performance is less affected by degree distribution as compared to Dada, since DaDa is designed to remove the node degree bias in networks.

FIG. 5.

FIG. 5.

Open in a new tab

Relation between the degree of target disease gene and its corresponding rank among 100 candidates for Vavien and existing algorithms.

Detailed comparison of specific disease genes identified by each algorithm

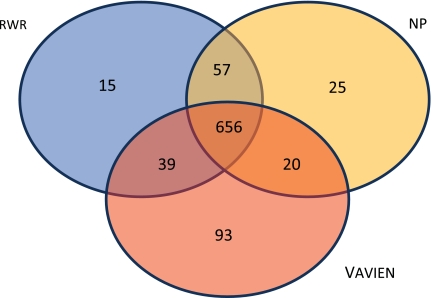
As argued in the previous sections, information flow–based proximity and topological similarity capture different aspects of the relationship between functional association and network topology. Consequently, we expect that the proposed topological similarity and information flow–based algorithms will be successful in identifying different disease-associated genes. In order to investigate whether this is the case, we compare target genes that are correctly identified as the true disease gene by each algorithm. These results are shown by a Venn diagram in Figure 6. In this figure, each value represents the number of true disease genes that are ranked first among 100 candidates by the corresponding algorithm(s). Among 1,996 disease-gene associations, Vavien is able to rank the true candidate first in 808 of the cases. Ninety-three of these genes are not ranked as the top candidate by neither random walk with restarts nor network propagation. On the other hand, the number of true candidates that are uniquely identified by each of the other two algorithms is lower (15 for random walk with restarts, 25 for network propagation), demonstrating that Vavien is quite distinct in its approach, and it is more powerful in extracting information that is missed by other algorithms. Furthermore, the 93 candidates uniquely identified by Vavien mostly code for loosely connected proteins (with 67 of them having ≤5 known interactions). This observation supports our claim that Vavien is indeed less effected by the bias introduced by degree distribution, as compared to information flow–based network proximity.

FIG. 6.

FIG. 6.

Open in a new tab

Venn diagram comparing the true disease genes ranked by each method as the most likely candidate. The sets labeled RWR, NP, and Vavien represent the set of true disease genes that are ranked top by random walk with restarts, network propagation, and topological similarity, respectively. Each number in an area shows the number of true candidates in that se e.g., 20 true disease genes were ranked top by network propagation and Vavien, but not random walk with restarts).

Effect of missing and noisy interaction data on the performance of Vavien

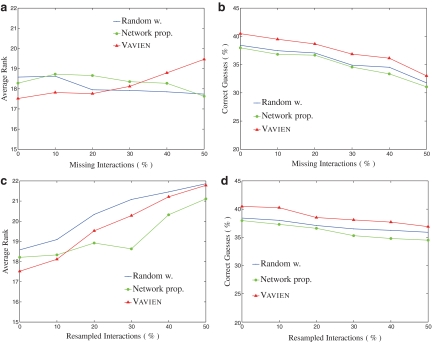
As a final test, we investigate the effect of bias in the interaction data on the performance of Vavien. Here, we conduct two different set of experiments: one by randomly deleting the interactions in the original PPI network and another by resampling the interactions among proteins randomly while conserving the degree distribution of proteins. We gradually increase the amount of noise introduced in the network by both perturbation strategies and plot the change in performance for Vavien, as well as two other information flow algorithms. These results are shown in Figure 7. In Figure 7a,c, the performance criteria is the average rank of the true disease gene among 100 candidates. In Figure 7b,d, we look at the percentage of correctly predicted known disease genes among 1,996 disease-gene association pairs. The results shown are the average of the performance measures obtained by repeating these experiments five times at each noise level for each approaches.

FIG. 7.

FIG. 7.

Open in a new tab

The effect of noise and missing interaction data on the performance of different approaches. In (a,c), the performance criteria is the average rank of the target disease gene among 100 candidates, whereas in (b,d), we investigate the number of top ranked true disease-gene associations among 1996 such pairs. The decrease in the performance for all three methods, are at tolerable levels for up to 50% of noise introduced.

It is evident in the Figure 7 that all three methods are quite robust to false positives and false negatives in interaction data, without a sharp decline in performance for up to 50% of artificial bias introduced. The percentage of correct guesses decreases in all three methods for both of the tests. However, contrary to our expectation, the average rank of target gene does not show significant change for random walk with restarts and network propagation algorithms, as missing interactions are introduced (Fig. 7a). The underlying reason for this behavior might actually be their tendency to favor highly connected genes. Recall that these algorithms rank genes with high-degree very well, while they show relatively poor performance for low-degree genes. Since removal of interactions disconnect the network, low-degree proteins, which are already loosely connected, are affected more by missing interactions. Furthermore, the number of proteins with degree 0 (singletons) goes up as more interactions are removed (since most of the proteins are loosely connected in the original network). Consequently, if the target gene has a higher degree than most of the other candidate genes in the original network, many false candidates have a proximity score of 0 after removal of interactions. On the other hand, if the target gene is loosely connected, the performance of these algorithms is not affected since they also perform less favorably on such genes. Consequently, the average rank of the target gene does not increase as one would expect. However, this is not the case for rewiring experiments. In those experiments, degree distribution is preserved, and disconnected subgraphs are much less likely to be introduced in the network.

5. Conclusion

In this article, we present an algorithm, called Vavien, for harnessing the topological similarity of proteins in a network of interactions to prioritize candidate disease-associated genes. After investigating the performance of the three schemes implemented in Vavien with respect to the restart parameter, we conduct a comprehensive set of experiments on OMIM data and show that Vavien outperforms existing information flow–based models, as well as their statistically adjusted version, in terms of ranking the true disease gene highest among other candidate genes. These results demonstrate that, in addition to the connectivity patterns in PPI networks, topological patterns in these networks are also useful in generating novel insights into systems biology of complex diseases. Vavien is available online at www.diseasegenes.org

Footnotes

1

From va-et-vient (Fr.); an electrical circuit in which multiple switches in different locations perform identical tasks (e.g., control lighting in a stairwell from either end).

Acknowledgments

We would like to thank Vishal Patel, Rob Ewing, and Mark R. Chance (Case Western Reserve University) for many useful discussions. We would also like to note the contribution of anonymous reviewers whose queries and suggestions have helped improve this article significantly. This work was supported, in part, by the NSF (CAREER Award CCF-0953195), the Choose Ohio First Scholarship, and the National Institutes of Health (grants P30-CA043703, UL1-RR024989, and R01- HL106798).

Disclosure Statement

No competing financial interests exist.

References

  1. Adie E. Adams R. Evans K., et al. SUSPECTS: enabling fast and effective prioritization of positional candidates. Bioinformatics. 2006;226:773–774. doi: 10.1093/bioinformatics/btk031. [DOI] [PubMed] [Google Scholar]
  2. Aerts S. Lambrechts D. Maity S., et al. Gene prioritization through genomic data fusion. Nat. Biotech. 2006;24:537–544. doi: 10.1038/nbt1203. [DOI] [PubMed] [Google Scholar]
  3. Banks E. Nabieva E. Peterson R., et al. NETGREP: fast network schema searches in interactomes. Genome Biol. 2008;9:9. doi: 10.1186/gb-2008-9-9-r138. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Barrett T. Troup D.B. Edgar R. NCBI GEO: archive for high-throughput functional genomic data. Nucleic Acids Res. 2009;37:D885–D890. doi: 10.1093/nar/gkn764. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Bebek G. Patel V. Chance M.R. PETALS: Proteomic evaluation and topological analysis of a mutated locus' signaling. BMC Bioinform. 2010;11:596. doi: 10.1186/1471-2105-11-596. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Bebek G. Yang J. Pathfinder: mining signal transduction pathway segments from protein-protein interaction networks. BMC Bioinform. 2007;8:335. doi: 10.1186/1471-2105-8-335. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Bogdanov P. Singh A.K. Molecular function prediction using neighborhood features. IEEE/ACM Trans. Comput. Biol. Bioinform. 2010;7:208–217. doi: 10.1109/TCBB.2009.81. [DOI] [PubMed] [Google Scholar]
  8. Brunner H.G. van Driel M.A. From syndrome families to functional genomics. Nat. Rev. Genet. 2004;5:545–551. doi: 10.1038/nrg1383. [DOI] [PubMed] [Google Scholar]
  9. Chen J. Aronow B. Jegga A. Disease candidate gene identification and prioritization using protein interaction networks. BMC Bioinform. 2009a;10:73. doi: 10.1186/1471-2105-10-73. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Chen J. Bardes E.E. Aronow B.J., et al. TOPP—gene suite for gene list enrichment analysis and candidate gene prioritization. Nucleic Acids Res. 2009b;37:gkp427. doi: 10.1093/nar/gkp427. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Erten S. Bebek G. Ewing R.M., et al. DADA—degree-aware disease gene prioritization. BioData Mining. 2011;4(19) doi: 10.1186/1756-0381-4-19. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Erten S. Koyutürk M. Role of centrality in network-based prioritization of disease genes. Lect. Notes Comput. Sci. 2010;6023:13–25. [Google Scholar]
  13. Ewing R.M. Chu P. Elisma F., et al. Large-scale mapping of human protein-protein interactions by mass spectrometry. Mol. Syst. Biol. 2007;3 doi: 10.1038/msb4100134. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Franke L. Bakel H. Fokkens L., et al. Reconstruction of a functional human gene network, with an application for prioritizing positional candidate genes. Am. J. Hum. Genet. 2006;78:1011–1025. doi: 10.1086/504300. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Glazier A.M. Nadeau J.H. Aitman T.J. Finding genes that underlie complex traits. Science. 2002;298:2345–2349. doi: 10.1126/science.1076641. [DOI] [PubMed] [Google Scholar]
  16. Goh K.-I. Cusick M.E. Valle D., et al. The human disease network. Proc. Natl. Acad. Sci. USA. 2007;104:8685–8690. doi: 10.1073/pnas.0701361104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Goldberg D.S. Roth F.P. Assessing experimentally derived interactions in a small world. Proc. Natl. Acad. Sci. USA. 2003;100:4372–4376. doi: 10.1073/pnas.0735871100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Halberg R.B. Chen X. Amos-Landgraf J.M., et al. The pleiotropic phenotype of apc mutations in the mouse: allele specificity and effects of the genetic background. Genetics. 2008;180:601–609. doi: 10.1534/genetics.108.091967. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Ideker T. Sharan R. Protein networks in disease. Genome Res. 2008;18:644–652. doi: 10.1101/gr.071852.107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Karni S. Soreq H. Sharan R. A network-based method for predicting disease-causing genes. J. Comput. Biol. 2009;16:181–189. doi: 10.1089/cmb.2008.05TT. [DOI] [PubMed] [Google Scholar]
  21. Kelley B.P. Sharan R. Ideker T. Conserved pathways within bacteria and yeast as revealed by global protein network alignment. Proc. Natl. Acad. Sci. USA. 2003;100:11394–11399. doi: 10.1073/pnas.1534710100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Kelley R. Ideker T. Systematic interpretation of genetic interactions using protein networks. Nat. Biotechnol. 2005;23:561–566. doi: 10.1038/nbt1096. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Kirac M. Özsoyoglu G. Yang J. Annotating proteins by mining protein interaction networks. Proc. ISMB. 2006:260–270. doi: 10.1093/bioinformatics/btl221. [DOI] [PubMed] [Google Scholar]
  24. Kirac M. Özsoyoglu G. Protein function prediction based on patterns in biological networks. Proc. RECOMB. 2008:197–213. [Google Scholar]
  25. Köhler S. Bauer S. Horn D., et al. Walking the interactome for prioritization of candidate disease genes. Am. J. Hum. Genet. 2008;82:949–958. doi: 10.1016/j.ajhg.2008.02.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Koyutürk M. Kim Y. Topkara U., et al. Pairwise alignment of protein interaction networks. J. Comput Biol. 2006;13:182–199. doi: 10.1089/cmb.2006.13.182. [DOI] [PubMed] [Google Scholar]
  27. Lage K. Karlberg E. Storling Z., et al. A human phenome-interactome network of protein complexes implicated in genetic disorders. Nat. Biol. 2007;25:309–316. doi: 10.1038/nbt1295. [DOI] [PubMed] [Google Scholar]
  28. Li J. Lee B. Lee A.S. Endoplasmic reticulum stress-induced apoptosis. J. Biol. Chem. 2006;281:7260–7270. doi: 10.1074/jbc.M509868200. [DOI] [PubMed] [Google Scholar]
  29. Lovász L. Random walks on graphs: a survey. Paul Erdos is Eighty. Combinatorics. 1996;2:353–398. [Google Scholar]
  30. Macropol K. Can T. Singh A. RRW: repeated random walks on genome-scale protein networks for local cluster discovery. BMC Bioinform. 2009;10:283. doi: 10.1186/1471-2105-10-283. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Maglott D. Ostell J. Pruitt K.D., et al. ENTREZ GENE: gene-centered information at NCBI. Nucleic Acids Res. 2007;35:D26–D31. doi: 10.1093/nar/gkl993. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Marsh V. Winton D.J. Williams G.T., et al. Epithelial PTEN is dispensable for intestinal homeostasis but suppresses adenoma development and progression after APC mutation. Nat. Genet. 2008;40:1436–1444. doi: 10.1038/ng.256. [DOI] [PubMed] [Google Scholar]
  33. Mewes H.W. Amid C. Arnold R., et al. MIPS: analysis and annotation of proteins from whole genomes. Nucleic Acids Res. 2004;32:D41–D44. doi: 10.1093/nar/gkh092. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Missiuro P.V.V. Liu K. Zou L., et al. Information flow analysis of interactome networks. PLoS comput. Biol. 2009;5:e1000350. doi: 10.1371/journal.pcbi.1000350. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Nabieva E. Jim K. Agarwal A., et al. Whole-proteome prediction of protein function via graph-theoretic analysis of interaction maps. Bioinformatics. 2005;21:i302–i310. doi: 10.1093/bioinformatics/bti1054. [DOI] [PubMed] [Google Scholar]
  36. Navlakha S. Kingsford C. The power of protein interaction networks for associating genes with diseases. Bioinformatics. 2010;26:1057–1063. doi: 10.1093/bioinformatics/btq076. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Nica A.C. Dermitzakis E.T. Using gene expression to investigate the genetic basis of complex disorders. Hum. Mol. Genet. 2008;17:ddn285–134. doi: 10.1093/hmg/ddn285. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Oti M. Snel B. Huynen M.A., et al. Predicting disease genes using protein-protein interactions. J. Med. Genet. jmg. 20062006:041376. doi: 10.1136/jmg.2006.041376. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Pandey J. Koyutürk M. Grama A. Functional characterization and topological modularity of molecular interaction networks. BMC Bioinform. 2010;11:S35. doi: 10.1186/1471-2105-11-S1-S35. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Pandey J. Koyutürk M. Kim Y., et al. Functional annotation of regulatory pathways. Bioinformatics. 2007;23:i377–i386. doi: 10.1093/bioinformatics/btm203. [DOI] [PubMed] [Google Scholar]
  41. Patel V.N. Bebek G. Mariadason J.M., et al. Prediction and testing of biological networks underlying intestinal cancer. PLoS ONE. 2010;5:e12497. doi: 10.1371/journal.pone.0012497. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Rhodes D.R. Chinnaiyan A.M. Integrative analysis of the cancer transcriptome. Nat. Genet. 2005;37(Suppl) doi: 10.1038/ng1570. [DOI] [PubMed] [Google Scholar]
  43. Sharan R. Suthram S. Kelley R.M., et al. Conserved patterns of protein interaction in multiple species. Proc. Natl. Acad. Sci. USA. 2005;102:1974–1979. doi: 10.1073/pnas.0409522102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Sjöblom T. Jones S. Wood L.D., et al. The consensus coding sequences of human breast and colorectal cancers. Science. 2006;314:268–274. doi: 10.1126/science.1133427. [DOI] [PubMed] [Google Scholar]
  45. Smialowski P. Pagel P. Wong P., et al. The Negatome Database: a reference set of non-interacting protein pairs. Nucleic Acids Res. 2010;38:D540–D544. doi: 10.1093/nar/gkp1026. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Spielman D.A. Srivastava N. Graph sparsification by effective resistances. Proc. STOC. 2008:563–568. [Google Scholar]
  47. Sprenger J. Lynn Fink J. Karunaratne S., et al. LOCATE: a mammalian protein subcellular localization database. Nucleic Acids Res. 2008;36:D230–D233. doi: 10.1093/nar/gkm950. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Stumpf M.P.H. Thorne T. de Silva E.A. Estimating the size of the human interactome. Proc. Natl. Acad. Sci. USA. 2008;105:6959–6964. doi: 10.1073/pnas.0708078105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Suthram S. Shlomi T. Ruppin E., et al. A direct comparison of protein interaction confidence assignment schemes. BMC Bioinform. 2006;7:360. doi: 10.1186/1471-2105-7-360. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Tetali P. Random walks and the effective resistance of networks. J. Theor. Probabil. 1991;4:101–109. [Google Scholar]
  51. Tong H. Faloutsos C. Center-piece subgraphs: problem definition and fast solutions. Proc. 12th ACM SIGKDD. 2006:404–413. [Google Scholar]
  52. Tong H. Faloutsos C. Pan J.-Y. Random walk with restart: fast solutions and applications. Knowledge Inform. Syst. 2008;14:327–346. [Google Scholar]
  53. Turner F. Clutterbuck D. Semple C. POCUS: mining genomic sequence annotation to predict disease genes. Genome Biol. 2003;4:R75. doi: 10.1186/gb-2003-4-11-r75. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. van Driel M.A. Bruggeman J. Vriend G., et al. A text-mining analysis of the human phenome. EJHG. 2006;14:535–542. doi: 10.1038/sj.ejhg.5201585. [DOI] [PubMed] [Google Scholar]
  55. Vanunu O. Magger O. Ruppin E., et al. Associating genes and protein complexes with disease via network propagation. PLoS Comput. Biol. 2010;6:e1000641. doi: 10.1371/journal.pcbi.1000641. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Wood L.D. Parsons D.W. Jones S., et al. The genomic landscapes of human breast and colorectal cancers. Science. 2007;318:1108–1113. doi: 10.1126/science.1145720. [DOI] [PubMed] [Google Scholar]
  57. Wu X. Jiang R. Zhang M. Q., et al. Network-based global inference of human disease genes. Mol. Syst. Biol. 2008;4 doi: 10.1038/msb.2008.27. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Zhang L. Hu K. Tang Y. Predicting disease-related genes by topological similarity in human protein-protein interaction network. Central Eur. J. Phys. 2010;8:672–682. [Google Scholar]

Articles from Journal of Computational Biology are provided here courtesy of Mary Ann Liebert, Inc.

RESOURCES