Abstract
We report the addition of two visualisation algorithms, termed PaperChain and Twister, to the freely available Visual Molecular Dynamics (VMD) package. These algorithms produce visualisations of complex cyclic molecules and multi-branched polysaccharides and are a generalization and optimization of those we previously developed in a standalone package for carbohydrates. PaperChain highlights each ring in a molecular structure with a polygon, which is coloured according to the ring pucker. Twister traces glycosidic bonds with a ribbon that twists according to the relative orientation of successive sugar residues. Combination of these novel algorithms and new ring selection statements with the large set of visualisations already available in VMD allows for unprecedented flexibility in the level of detail displayed for glycoconjugate, glycoprotein and carbohydrate-binding protein structures, as well as other cyclic structures. We highlight the efficacy of these algorithms with selected illustrative examples, clearly demonstrating the value of the new visualisations, not only for structure validation, but for facilitating insights into molecular structure and mechanism.
Keywords: carbohydrate, polysaccharide, molecular visualisation, chitinases, chitolectins, oligosaccharides, VMD
1. Introduction
Molecular visualisation aims to highlight the connectivity and important structural features of a molecule and hence facilitate the conceptual understanding necessary for solving structure-function relationships. Abstract representations, such as ribbon[1, 2, 3] or cartoon diagrams[1], have long been preferred over explicit representation of the atomic positions for proteins. However, there are currently few abstract visualisations widely available for other classes of molecules. In particular, aside from DNA, the visualisation of cyclic molecules and multi-branched molecules is largely neglected by current molecular visualisation packages.
Polysaccharides, in particular, are comprised of chains of cyclic sugar residues, often multi-branched. These molecules have an enormous variety of roles to play in biological organisms, from structural molecules to the molecular recognition and cell signalling roles played by many glycoproteins. For example, the elucidation of the mechanisms that govern how oligosaccharides are accommodated in the binding sites of lectins, antibodies and enzymes is currently of major interest. However, the high incidence of incorrect carbohydrate stereochemistry and glycosidic linkages for glycoprotein entries in the PDB database[4, 5, 6] illustrates the difficulty with identifying incorrect structures by researchers less familiar with the intricacies of carbohydrate structure, stereochemistry and favoured ring conformations. For this reason, tools have been developed for general glycan structure verification. The Carbohydrate Structure Suite (CSS)[7] contains the pdb-care program, a verification service for the nomenclature of a saccharide unit that is able to identify and assign carbohydrate structures using only atom types and their 3D atom coordinates[4], The glycoconjugate Data Bank (GDB) can be used to verify N-glycan primary structures.[8] However, even where the stereochemistry and ring structures are correct, the glycan components of glycoproteins can exhibit incorrect ring pucker conformations as a result of the crystal structure refinement process. None of these tools incorporates analysis of the carbohydrate ring pucker parameters, which currently involves separate calculation using available codes.[9] Highlighting altered carbohydrate ring pucker is also useful for analysis of carbohydrate-protein interactions, which often involve a change of ring conformation from low-energy chair conformations, to the higher-energy but relatively stable boat and twist-boat conformations.
In previous work, we developed a standalone application, CarboHydra, to test two novel visualisation algorithms for carbohydrate structures, which we named PaperChain and Twister.[10] These visualisations provide control over the level of detail shown for carbohydrate structures. The PaperChain visualisation highlights the conformation of a ring with a polygon that is coloured according to the ring pucker coordinates. The Twister visualisation is intended to serve the same purpose for carbohydrates as ribbon diagrams do for proteins, tracing the backbone conformation of polysaccharide chains. Here, a curved ribbon highlights the backbone linkages, with the twist of the strand revealing the relative orientation of each successive ring, an important conformational detail in polysaccharides. In addition, Twister is useful in revealing the backbone network of complex multibranched polysaccharides, which are difficult to trace when viewed in typical ball-and-stick representations.
The CarboHydra prototype established the efficacy of the algorithms and initial response from the community of carbohydrate researchers demonstrated a need for these visualisations. However, CarboHydra had limited utility: it did not include any additional molecular visualisations, such as secondary structure or “cartoon” representations for proteins, and was developed solely for Windows platforms. This is an instance of a commonly recognised problem - there is a pressing need to incorporate innovations in visualisation into existing molecular visualisation packages to make them available to a wider community.[11]
We chose the Visual Molecular Dynamics (VMD) package[12] in the first instance for implementation of our algorithms. VMD is widely available and VMD source code is freely accessible available on the web and by remote CVS access. This approach has the added advantage of combining these novel visualisations with those already extant in VMD, thus enabling novel views of glycoproteins and carbohydrate-binding proteins. A further advantage of the incorporation process is that it led to the generalization and improvement of the PaperChain and Twister algorithms. The algorithms were validated on a variety of structures, options for limiting the size of rings were added and the ring-detection procedure was altered so that all cycles are detected, not just those in saccharide residues. In addition, a uniform colour mapping scheme for all rings was implemented: a one-dimensional colour scale based solely on the puckering amplitude as defined by Cremer and Pople.[13] This colour scheme clearly differentiates between planar rings and various degrees of pucker.
Previously, we analysed the value of the Twister and PaperChain visualisations for a selection of carbohydrate structures. The efficacy of the two visualisations is trivial to show in the much more rapid recognition of ring location, ring type and ring pucker for the PaperChain visualisation and relative residue orientation for the Twister visualisation that results. However, the effectiveness of these visualisation techniques is more difficult to quantify where non-quantitative judgements, such as key insights, are involved. Here we focus on visualisations of glycoproteins and lectins, which are made possible by the combination of Twister and PaperChain with the other visualisations implemented into VMD.
In our first example, the ease of locating incorrect structures with our current visualisations is demonstrated on a glycoprotein structure. The second example concerns a chitolectin. Here we visualize this carbohydrate-binding protein to assess whether ring puckering plays a role in carbohydrate binding and to determine whether the use of the PaperChain and Twister visualisations facilitates the development of key insights into the carbohydrate binding mechanism in this class of molecules.
2. Methodology
The VMD package is written in the C++ programming language with the OpenGL graphics library and comprises a large set of classes. Additions were made to the BaseMolecule and DrawMolItem classes to incorporate the PaperChain and Twister visualisations into VMD. In all cases, the visualisations are subject to the powerful VMD selection functions, whereby the visualisation is applied to only the selected atoms in the current molecular structure.
2.1. Identifying Rings
Identification of the rings existing in the current molecular structure is a necessary preprocess for both the PaperChain and Twister visualisation algorithms. However, as this can be relatively time-consuming for large structures, within VMD it is only done on demand: when either of the PaperChain or Twister visualisations is selected. In this way, the addition of these new algorithms does not impact on users who do not require these features. For example, on-demand calculation of rings is particularly beneficial for users working with structures containing millions of atoms, such as synthetic nanodevices, where there might be a huge number of small rings in the interconnected structure that the user would not necessarily wish to highlight.
The ring identification procedure was altered from the original implementation in the CarboHydra package, in order to generalise and optimise the process. Here, we define a ring as a simple loop with no cross-overs. The aim is to locate in the molecular graph all chordless cycles of length less than a defined maximum ring size, M. The ring procedure occurs in two stages: identifying a set of back edges within the molecular graph (i.e. the cycles) and then converting each back edge to a set of rings. The algorithm proceeds as follows.
From the atomic coordinates, we construct an undirected molecular graph, G, where nodes represent atoms and edges represent bonds.
We then construct an (arbitrary) spanning tree of G, keeping a record of all the back edges in the tree. (Every loop in G must, by definition, contain at least one of the back edges, which are therefore used as the starting points for the ring searches.)
- For each back edge in G, we conduct a depth-first search for possible rings, with the following pruning conditions:
- – We exclude back edges previously used as the start of a search - this ensures that each ring is identified only once. Used back edges are recorded in a hash table.
- – We exclude atoms that already exist in the current loop. To eliminate cross-overs, we restrict rings to closed paths in G that visit no atom more than once. Used atoms are recorded in a hash table.
Each ring search halts when either a ring is found or the user-defined maximum ring size, M, is reached.
Once a ring is found for a particular atom, no further searches are made down that path. This ensures that the smallest rings are identified first.
We now consider the time- and space complexity of this algorithm. Generating the spanning tree is O(E + V) in both storage and time complexity, where E and V are, respectively, the number of edges (bonds) and vertices (atoms) in the molecular graph, G. In this process, B <= C, where B is the number of back-edges generated and C is the number of cycles in the graph (there is at least one unique cycle for each back edge).
The next step of the algorithm is a depth-first search from each back edge. Although the search is truncated at depth M, it may still potentially cover the whole graph, so the worst case run time is O(E + V) for each depth-first search. Therefore, the total time for all searches is O(B * (E + V)). For sensible molecular graphs, the portion of the graph that can be reached from a back edge in M steps is independent of the size of the molecule, so that, in practice, the time for each search is O(k), where k is a constant that depends on M. For these graphs, the etire search procedure takes O(B). Noting that B < E, we find that the overall time complexity is:
| (1) |
for the average case and
| (2) |
for the worst case molecular graphs. Therefore, as a safety mechanism, the maximum number of rings identified is prevented from scaling faster than the square root of the number of atoms.
The maximum ring size, M, is adjustable within the VMD graphical user interface. If this is altered, Twister or PaperChain recalculate the rings and their locations. As the implementation of ring finding in VMD is iterative rather than recursive, in practice M can be set to be quite large without a noticeable impact on performance. However, for very large structures, this can be quite slow. As extremely large structures of molecular assemblies are likely to become more frequently investigated in the future, it may become necessary to parallelize the ring finding algorithm. This could proceed as follows. The Bader and Cong algorithm may be used for parallelizing the construction of a spanning tree.[14] If necessary, the back edges could be identified in a second pass, after the spanning tree has been constructed. This would be trivial to parallelize – with each processor examining a subset of the nodes for those edges from the node that are not in the tree G. The subsequent identification of rings would then be embarassingly parallel: each processor being handed a subset of the back-edges to verify.
The ring finding algorithm enhances the already powerful VMD atom selection language, making it possible for rings identified by the algorithm to be fed into analysis scripts, as well as for specifically selected rings to be displayed with particular graphical representations. For example, an atom selection “ringsize 5 from protein” in VMD will select only the 5-membered rings: cycles in proline and the aromatic residues histidine, proline and tryptophan (only the 5-membered ring) from the protein portion of a structure file.
2.2. Orienting Loops
Orientation of each carbohydrate ring is required for the Twister algorithm, which twists a linking ribbon to show the relative position of successive residues. Carbohydrate rings are oriented by searching for an oxygen atom in the loop and then determining whether the carbon immediately after the oxygen in the current ring orientation has the name “C1”. If it is, the ring orientation is reversed. This is consistent with the IUPAC rules for ring orientation.[15]
Our system has the disadvantage that it relies on the carbons being labelled correctly in the molecular structure file. Conversely, an advantage is that this method is predictable and the user can alter the orientation of the rings themselves by changing the atomic labels.
Loops which cannot be orientated using this method are simply marked as unorientated and excluded from the search for paths between rings necessary for the Twister algorithm.
2.3. Identifying Paths Joining Oriented Rings
The Twister algorithm also requires the paths connecting rings to be identified. These may be branched. Paths connecting identified rings are located using a simple depth-first search of the molecular grapgh G from each atom in each oriented ring. The search terminates at a user-defined maximum path length, L, and is restricted in that paths are not allowed to contain loops. Additional pruning conditions used in the search are:
We exclude atoms already in the current path, ensuring that paths do not cross themselves. Used atoms are stored in a hash table.
We exclude atoms which are identified a being part of a ring, except where they occur as the first or last atom in a path.
We exclude atoms which belong to multiple rings. This avoids spurious links between fused rings which share atoms.
A hash table is used to store the mapping from each atom to the ring containing it. Storing the paths encountered is complicated by the fact that each bond may be part of a number of different paths between rings. The storage structure therefore keeps lists of both the paths found and the individual edges which make up these paths. Additionally, to save time, for each edge we store a list of paths where it appears.
2.4. Rendering PaperChain
The PaperChain visualisation depicts the conformation of individual rings by fitting a polyhedron through the participating atoms and the ring centroid. The rings found (both oriented and unoriented rings) are rendered as bipyramids with a user-adjustable height, H. The normal to the ring is calculated using Newell’s method[16] and the tops of the pyramids are located a height H above the centroid in the direction of the ring normal. The base of each pyramid is the (possibly non-planar) closed polygon formed by the ring. Only rings which have all atoms selected are rendered.
2.4.1. Ring colour mapping
In our original CarboHydra implementation, the colour of a hexose ring was defined according to a red, green, blue (RGB) colour scheme, as:
| (3) |
| (4) |
| (5) |
where R is the red component, G is the green component and B is the blue component and θ, ϕ and Q the Cremer-Pople puckering parameters.[13] While this scheme has the advantage of clearly differentiating between the canonical conformations of hexose rings (see Table 1), it is not general for all rings. In addition, the colour of planar rings is arbitrarily defined. Therefore, we implement here a general one dimensional colour scale for all rings with 3 or more atoms. To achieve this, we investigated a variety of colouring schemes, including using the new Hill-Reilly puckering parameters.[9] However, all approaches using puckering angles are problematic, as the puckering angles calculated vary according to the stipulated start point of the ring. For a particular ring type, such as proline rings or glucose rings, common convention has decided the atom order. Unfortunately, implementing this would complicate the ring-finding algorithm with a large number of heuristics. Therefore, we require a universal parameter that is invariant with respect to the starting point of the ring. The Cremer-Pople puckering amplitude has this property.
Table 1.
Comparison of the colouring schemes for 6-membered rings used in the original CarboHydra implementation[10] and this work. The values for the Cremer-Pople puckering parameters for each canonical structure are as listed in Hill at al.[9]. (ϕ and θ in °, Q in Å.) Planar rings, though not listed, appear as black in the old scheme, red in our new scheme.
| Conformer | Cremer-Pople Coordinates |
Original Carbohydra Colours |
Colour | Revised Carbohydra Colours |
Colour | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ϕ | θ | Q | R | G | B | R | G | B | |||
| 1C4 | 0-360 | 180 | 0.57 | 0.0 | 0.57 | 0.0 |
|
0.0 | 1.0 | 0.13 |
|
| 4C1 | 0-360 | 0 | 0.57 | 0.0 | 0.57 | 0.0 |
|
0.0 | 1.0 | 0.13 |
|
| 1,4B | 240 | 90 | 0.76 | 0.76 | 0.0 | 0.0 |
|
0.0 | 0.0 | 1.0 |
|
| B1,4 | 60 | 90 | 0.76 | 0.76 | 0.0 | 0.0 |
|
0.0 | 0.0 | 1.0 |
|
| 2,5B | 120 | 90 | 0.76 | 0.76 | 0.0 | 0.0 |
|
0.0 | 0.0 | 1.0 |
|
| B2,5 | 300 | 90 | 0.76 | 0.76 | 0.0 | 0.0 |
|
0.0 | 0.0 | 1.0 |
|
| 3,6B | 0 | 90 | 0.76 | 0.76 | 0.0 | 0.0 |
|
0.0 | 0.0 | 1.0 |
|
| B3,6 | 180 | 90 | 0.76 | 0.76 | 0.0 | 0.0 |
|
0.0 | 0.0 | 1.0 |
|
| 1H2 | 270 | 129 | 0.42 | 0.33 | 0.26 | 0.33 |
|
0.88 | 1.0 | 0.0 |
|
| 2H1 | 90 | 51 | 0.42 | 0.33 | 0.26 | 0.33 |
|
0.88 | 1.0 | 0.0 |
|
| 2H3 | 150 | 51 | 0.42 | 0.33 | 0.26 | 0.33 |
|
0.88 | 1.0 | 0.0 |
|
| 3H2 | 330 | 129 | 0.42 | 0.33 | 0.26 | 0.33 |
|
0.88 | 1.0 | 0.0 |
|
| 3H4 | 30 | 129 | 0.42 | 0.33 | 0.26 | 0.33 |
|
0.88 | 1.0 | 0.0 |
|
| 4H3 | 210 | 51 | 0.42 | 0.33 | 0.26 | 0.33 |
|
0.88 | 1.0 | 0.0 |
|
| 4H5 | 270 | 51 | 0.42 | 0.33 | 0.26 | 0.33 |
|
0.88 | 1.0 | 0.0 |
|
| 5H4 | 90 | 129 | 0.42 | 0.33 | 0.26 | 0.33 |
|
0.88 | 1.0 | 0.0 |
|
| 5H6 | 150 | 129 | 0.42 | 0.33 | 0.26 | 0.33 |
|
0.88 | 1.0 | 0.0 |
|
| 6H5 | 330 | 51 | 0.42 | 0.33 | 0.26 | 0.33 |
|
0.88 | 1.0 | 0.0 |
|
| 6H1 | 30 | 51 | 0.42 | 0.33 | 0.26 | 0.33 |
|
0.88 | 1.0 | 0.0 |
|
| 1H6 | 210 | 129 | 0.42 | 0.33 | 0.26 | 0.33 |
|
0.88 | 1.0 | 0.0 |
|
| 1S3 | 210 | 88 | 0.62 | 0.62 | 0.02 | 0.62 |
|
0.0 | 1.0 | 0.75 |
|
| 3S1 | 30 | 92 | 0.62 | 0.62 | 0.02 | 0.62 |
|
0.0 | 1.0 | 0.75 |
|
| 5S1 | 90 | 92 | 0.62 | 0.62 | 0.02 | 0.62 |
|
0.0 | 1.0 | 0.75 |
|
| 1S5 | 270 | 88 | 0.62 | 0.62 | 0.02 | 0.62 |
|
0.0 | 1.0 | 0.75 |
|
| 6S2 | 330 | 88 | 0.62 | 0.62 | 0.02 | 0.62 |
|
0.0 | 1.0 | 0.75 |
|
| 2S6 | 150 | 92 | 0.62 | 0.62 | 0.02 | 0.62 |
|
0.0 | 1.0 | 0.75 |
|
| 1E | 240 | 125 | 0.45 | 0.37 | 0.26 | 0.0 |
|
0.69 | 1.0 | 0.0 |
|
| E1 | 60 | 55 | 0.45 | 0.37 | 0.26 | 0.0 |
|
0.69 | 1.0 | 0.0 |
|
| 2E | 120 | 55 | 0.45 | 0.37 | 0.26 | 0.0 |
|
0.69 | 1.0 | 0.0 |
|
| E2 | 300 | 125 | 0.45 | 0.37 | 0.26 | 0.0 |
|
0.69 | 1.0 | 0.0 |
|
| 3E | 360 | 125 | 0.45 | 0.37 | 0.26 | 0.0 |
|
0.69 | 1.0 | 0.0 |
|
| E3 | 180 | 55 | 0.45 | 0.37 | 0.26 | 0.0 |
|
0.69 | 1.0 | 0.0 |
|
| 4E | 240 | 55 | 0.45 | 0.37 | 0.26 | 0.0 |
|
0.69 | 1.0 | 0.0 |
|
| E4 | 60 | 125 | 0.45 | 0.37 | 0.26 | 0.0 |
|
0.69 | 1.0 | 0.0 |
|
| 5E | 120 | 125 | 0.45 | 0.37 | 0.26 | 0.0 |
|
0.69 | 1.0 | 0.0 |
|
| E5 | 300 | 55 | 0.45 | 0.37 | 0.26 | 0.0 |
|
0.69 | 1.0 | 0.0 |
|
| 6E | 360 | 55 | 0.45 | 0.37 | 0.26 | 0.0 |
|
0.69 | 1.0 | 0.0 |
|
| E6 | 180 | 125 | 0.45 | 0.37 | 0.26 | 0.0 |
|
0.69 | 1.0 | 0.0 |
|
Here we colour all rings according to the Cremer-Pople puckering amplitude, which is defined for all rings with size >= 3. The puckering amplitude is mapped to a one-dimensional colour scale, allowing for any three-colour range in one dimension for puckering amplitudes ranging from 0.0 Å to 2.0 Å (any value higher than this is truncated to 2.0). Our default colour range is a “hot-to-cold” scale, ranging from red for planar rings, through yellow, green, cyan and blue. Rings with puckering amplitudes approaching 2.0 Å are mapped to magenta. However, we have set the colouring stationary points to be non-uniform, to suit particularly the most common pentose and hexose rings. The stationary points are set at: 0.0 (red), 0.4 (yellow), 0.56 (green), 0.64 (cyan), 0.76 (blue) and 2.0 (magenta) Å.
A comparison between the original and our new colour mapping schemes for canonical conformations of pyranose rings is shown in Table 1. While puckering amplitude is not unambiguously associated with a particular conformation, this table makes it clear that there is a strong correlation between them. The puckering amplitudes tend to increase from planar rings (red), through half-chairs (yellow), envelopes (yellow-green) , chairs (green), twist-boats (cyan) and boats (blue). Larger rings are associated with higher puckering amplitudes, effectively separating the non-aromatic 5-membered rings such as proline and furanose (which typically map to yellow) from the 6-membered rings. As a further utility for users, we have incorporated the calculated ring puckering amplitude into the VMD atom selection language, giving users the useful ability to apply particular visualisations based on puckering amplitude.
2.5. Rendering Twister
We have dispensed with the disc representation for each ring in the Twister visualisation as implemented in CarboHydra, as this functionality is now provided by the PaperChain visualisation, which can now be effectively combined with Twister. Paths connecting orientated rings are rendered as thin ribbons with adjustable width and thickness.
A user-adjustable option determines whether ribbons start at the centroids of the start and end rings or at the start and end atoms. Newell’s method is again used to calculate the ring normals.
The ribbon is represented as a cubic B-spline, using a similar method to that for protein ribbons. However, Twister ribbons connect rings and thus have an additional constraint: they must have a fixed orientation where they meet up with a ring. This requires the definition of both a starting and ending frame for the ribbon, as follows. The starting frame’s forward vector is the (normalised) tangent at the start of the spline. The right vector is the (normalised) cross-product of the forward vector and the normal to the starting ring. The up vector is the (normalised) cross-product of the forward and right vectors. The ending frame is defined in a similar manner.
The starting frame is then propagated along the spline in a discrete set of steps (the number of steps is configurable in the user interface). At each step, the previous frame is rotated so that its forward vector matches the tangent at the new position on the spline. The final frame will not generally match the ending frame calculated in the step above, so a constant additional rotation is applied at each propagation step to make the final frame match the desired ending frame.
The frames are then used to define small rectangles of width, W, and thickness, T, at each of the discrete points along the spline. The sides of the rectangles are parallel to the right and up frame vectors. The ribbon is finally constructed using flat planes to join the tops, bottoms and sides of adjacent rectangles.
Where the start from ring centroid option is selected by the user, it is necessary that successive ribbons meet exactly to form one smooth ribbon, analogous to protein ribbons. Therefore, in this case, the ribbon starts at a point X which lies on the plane formed by the ring centroid and the ring normal. X is chosen to be as close as possible to the point midway between the centroid and the last atom on the path. This brings the final sections of all ribbons arriving at a single ring into a common plane so that they line-up in a visually pleasing fashion. Any possible gaps where the ribbons meet are filled in by rendering a small circular disk (actually a regular dodecagon).
Finally, only selected paths are rendered (a path is not selected if any of the atoms in the path or any of the atoms in one rings it joins are not currently selected). There is also an option for the user (Hide Shared Links) to not render paths which share bonds with other paths.
2.6. Evaluation
For this work, we eschew controlled user experiments and usability testing of the software because these are difficult to generalise to high-level insights rather than low-level task completion.[17, 18] Instead, we aim to show qualitative rather than quantitative results, in the first instance by demonstrating that the Twister and PaperChain visualisations present information on the conformations of carbohydrate molecules in a manner that is easily recognised and understood by users who are not experts in carbohydrate chemistry. The utility of a visualisation for assisting scientific insight is extremely difficult to establish. To this end, we selected illustrative examples of molecular structures from the Protein Databank where important aspects of the carbohydrate structure were missed by the original authors and show that the use of PaperChain and Twister visualisations could have avoided this situation. We focus on the Simian Immunodeficiency Virus GP120 envelope glycoprotein at 4 Å resolution reported in Chen et al.[19] (PDB code 2BF1) and a chitolectin in complex with chitooligosaccharides: the goat secretory glycoprotein, SPG-40[20] (PDB codes 2DT0, 2DT1, 2DT2 and 2DT3). The molecules were visualized using VMD and the resultant 3D objects were then inspected for key insights.
3. Results and Discussion
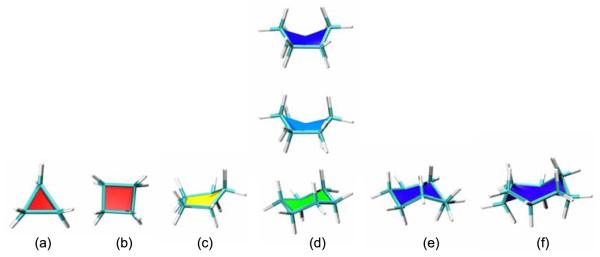
The default hot-to-cold colour scale for PaperChain as applied to representative cycloalkane structures is illustrated in Fig. 1. Here planar (Fig. 1(a)) cyclopropane and (b) cyclobutane are both coloured red, while the characteristic envelope conformation of cyclopentane, (c), is yellow. In cyclohexane, (d), the lowest energy chair structure is green, the twist-boat conformation cyan and the boat conformation blue. The puckered conformations of cycloheptane and cyclooctane (crown conformation) both appear as deep blue. Larger, more dramatically puckered rings are coloured magenta, as for the α-cyclodextrin structure shown in Fig. 6(e).
Fig. 1.
Sample ring structures for cycloalkanes shown with a combination of the VMD Licorice and our new PaperChain visualisation, illustrating the default hot-to-cold colour scale based on the Cremer-Pople ring puckering amplitude.[13] (a) Cyclopropane, (b) cyclobutane, (c) cyclopentane , (d) cyclohexane in boat (top), twist-boat (middle) and chair (bottom) conformations, (e) cycloheptane and (f) cyclooctane in a crown conformation.
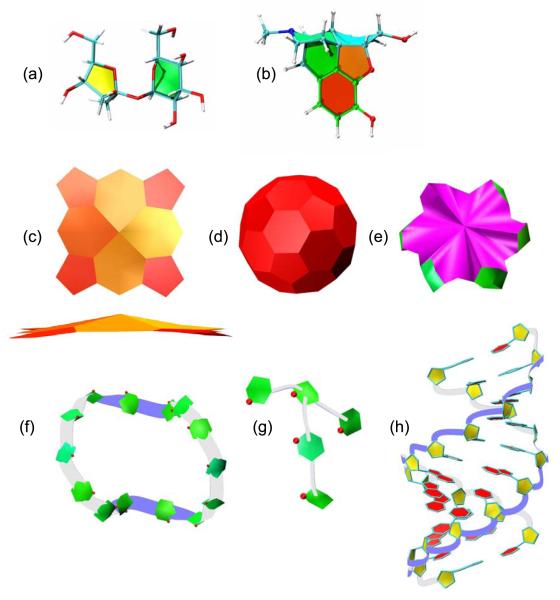
Fig. 6.
A variety of cyclic molecules visualized with PaperChain and Twister, (a) Sucrose shown with PaperChain and the standard VMD Licorice visualisation, (b) Morphine shown with PaperChain and Licorice visualisations, (c) PaperChain visualisation of a haem structure in two orientations. (d) Buckminsterfullerene in the PaperChain visualisation. (e) α-cyclodextrin shown with PaperChain. (f) Cyclotetradecaamylose[33] and (g) amylopectin branch point viewed with both the PaperChain and Twister conformations, and the ring oxygens shown as balls (CPK). Here the top and bottom of the ribbon (defined according to IUPAC convention for saccharides) are coloured white and blue, respectively, (h) A-DNA structure visualized with Twister for the DNA backbone, PaperChain for the rings and Licorice for the bonds connecting the rings.
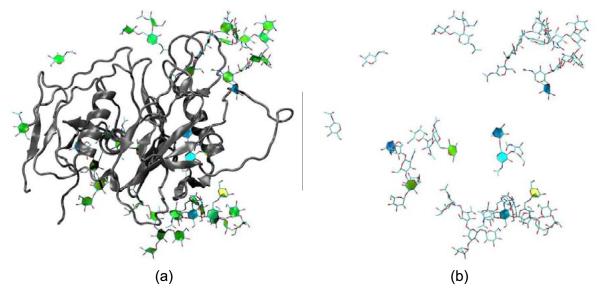
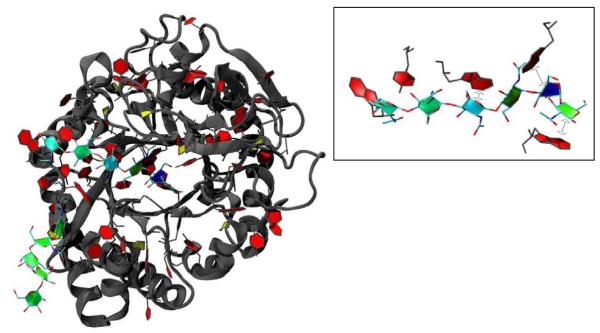
The envelope glycoproteins of HIV and SIV are the molecular agents of cell attachment and membrane fusion and are thus of considerable interest. Fig. 2 shows our visualisation of the crystal structure of an unliganded and fully-glycosylated Simian Immunodeficiency Virus GP120 envelope glycoprotein at 4 Å resolution, as reported in Chen et al.[19] In Fig. 2(a), the SIV the PaperChain visualisation is applied to the glycan components only, using the default colour scale for the ring pucker. In (b), only rings of puckering amplitudes not associated with the low-energy chair conformations of the pyranose rings are highlighted. This was achieved with the new selection statements we added to VMD (i.e “select pucker 0.0 to 0.9 or pucker 0.6 to 1.0” - refer to Table 1 for typical amplitude values). From the yellow and blue colours displayed for the glycan components, it is clear that a number of the saccharide rings exhibit unusual puckering amplitudes and conformations for pyranose rings: biologically unlikely envelope conformations are coloured yellow and yellow-green, while twist-boats are cyan and boats blue. These atypical ring puckering amplitudes are likely a result of the harmonic restraints applied to the glycans during crystal structure refinement inadvertently forcing incorrect ring conformations. Similar errors in ring pucker, including highly puckered proline residues (Q > 0.5, mapping to green rather than yellow in our colour scheme) and non-planar aromatic rings, can be seen for a number of other structures in the PDB database. The PaperChain visualisation thus has broad applicability as a simple check for ring conformations and, therefore, also has utility for molecular model building, where steric clashes during energy minimization procedures can also lead to errors in ring conformation.
Fig. 2.
The SIV GP120 glycoprotein structure determined by Chen et al.[19] (PDB code 2BF1). (a) The protein displayed in the VMD NewCartoon visualisation and the carbohydrate rings displayed with a combination of our PaperChain and the standard VMD Licorice visualisations, (b) The same view of the structure, showing the carbohydrate components only. Only rings with puckering amplitudes less than 0.49 or greater than 0.6 are visualised with PaperChain.
Our second example concerns the lectin family of proteins, which bind sugars with very high specificity. Protein Family 18 chitolectins are homologous to the catalytically active chitinases, but the inactive chitolectins simply bind and do not hydrolyse oligosaccharides, due to a mutation in an active site residue. A series of recent investigations into the X-ray structures and carbohydrate binding properties of SPX-40 family of chitolectins revealed that these proteins bind chitin-like oligosaccharides in a similar mode to the chitinases,[21, 22] within a groove with 9 subsites.[23, 24, 25, 26, 20] A key component of the sugar hydrolysis mechanism for Family 18 chitinases is known to be distortion of the N-acetylglucosamine ring at the binding site from a chair to a boat conformation.[27, 28, 21, 24, 29] However, although a similar distortion of a sugar ring to boat conformation has been seen to occur in the binding of chito-oligosaccharides to human cartilage glycoprotein[23], no commentary on possible ring distortions was made in three recent studies of related chitolectins.[25, 26, 20]
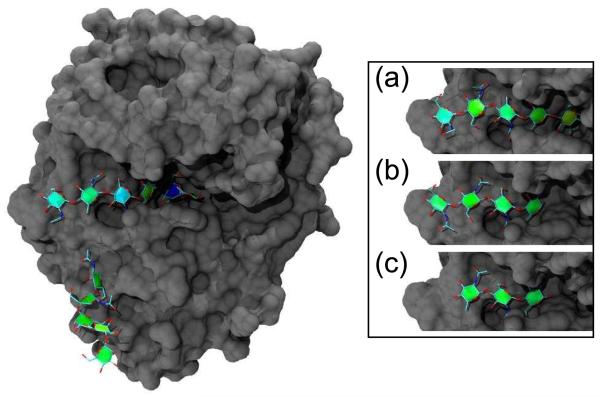
Fig. 3 shows PaperChain visualisations of four N-acetylglucosamine oligosaccharides (GlcNAcn , n=3−6) bound in complex with the SPG-40 goat secretory glycoprotein.[20] This novel combination of visualisations renders the location and conformation of the rings much clearer than the depictions in the original work.[20] The SPG-40 protein is glycosylated: the main image in Fig. 3 shows a pendant oligosaccharide with six residues (6-acetylglucosamine, GlcNAC6). The second residue in this chain, though coloured green, is actually distorted into a boat conformation. This is an example of the puckering amplitude not being unambiguously associated with ring conformation: the ring is coloured green, as for most chairs. Both the bound GlcNAC6 oligosaccharide in the main image and the GlcNAC5 oligosaccharide (inset (a)) show increased puckering amplitudes for the first and third residues, as evinced by green-blue colour. It is also clearly apparent in the PaperChain visualisations that binding alters the pucker of the penultimate (deep blue) residue in the GlcNAC6 chain, deep within the binding pocket at location −2, which is in the boat conformation. This fact was not mentioned in the original work,[20] although a related lectin, human cartilage glycoprotein (HCGP39), has been observed to force a skewed boat conformation for the sugar residue at the −1 binding site. [23, 24] The last residue of GlcNAC5 is in the same location in the binding site and is distorted to a envelope conformation, as is made evident by the yellow colour. The shorter oligosaccharides, GlcNac4 (inset (b)) and GlcNac3 (inset (c)), show puckering amplitudes around 0.56 (green), which are associated with undistorted chair conformations for the rings.
Fig. 3.
A goat secretory glycoprotein (SPG-40) chilotelectin binding a hexasaccharide N-acetylglucosamine, GlcNAc6 (PDB code 2DT3).[20] Inset shows SPG-40 binding (a) pentasaccharide GlcNAc5 (PDB code 2DT2), (b) GlcNAc4 (PDB code 2DT1) and (c) G1CNAC3 (PDB code 2DT0). In each case, the carbohydrate substrate is depicted with a combination of our new PaperChain and the standard VMD Licorice visualisations, while the surface of the protein is shown in gray using the VMD Surf[31] visualisation. The image was rendered with the ambient occlusion lighting feature provided by the Tachyon [32] program included with the VMD distribution.
The SPG-40 protein binds longer oligosaccharides with high affinity, and we suggest that alteration in ring pucker of the saccharide ligand may be necessary for tight binding. The shorter oligosaccharides, GlcNac3 and GlcNac4, which do not show ring distortions, bind with low affinities and do not form stable complexes in solution.[20] We found that a similar situation exists for the binding of N-acetylglucosamine oligosaccharides to the related sheep secretory glycoprotein, SPS-40 (not shown).[26] Again, the shorter oligosaccharides (n=3 and n=4) do not reach location −1 on the binding site and show undistorted ring conformations, while longer oligosaccharides show distorted conformations at position −1. Here ring distortion is also associated with stronger binding: the GlcNac3 and GlcNac4, ligands bind weakly to SPG-40, while GlcNAc5 and GlcNAc6 bind with considerable strength.[20] Thus, we propose that ring distortions are likely to be a key component of the strong binding of oligosaccharides to the chitolectins, a role similar to that played by chair-to-boat ring flips in the sugar hydrolysis mechanism of the related chitinases.[27, 28, 21, 24, 22]
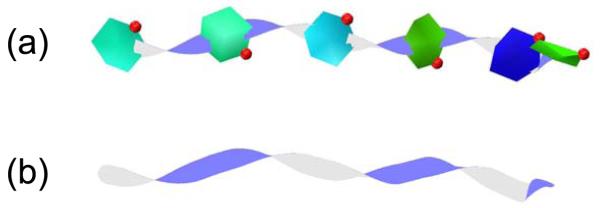
A further advantage of the PaperChain visualisation, is that the cyclic aromatic (red) and proline (yellow to green) residues with proteins are easily located, as shown in an alternative view of the SPG-40 protein in Fig. 4. The inset in this figure shows the interaction of the GlcNac6 substrate with the aromatic tryptophan and tyrosine protein residues located on the floor of the binding groove. The PaperChain representation highlights the stacking orientation of these rings to the carbohydrate residues, which is not clearly apparent in the ball-and-stick representations. This is a common feature of carbohydrate-protein interactions: conserved aromatic amino acid residues are frequently present in carbohydrate-binding sites of proteins, where they are involved in CH-π stacking interactions with the C-H groups of bound sugar rings.[22, 30, 25] Finally, a combination of Twister and PaperChain (Fig. 5(a)) or just Twister (Fig. 5(b)) can be used to show clearly the 180° flip of successive sugar rings for the chito-oligosaccharides. Here, the clear twist in the connecting ribbon between rings highlights the alternating “up” and “down” orientations of the glucose residues - a preferred conformation that is characteristic of both chitin and cellulose polysaccharides.
Fig. 4.
A further visualisation of the goat secretory glycoprotein (SPG-40) chilotelectin binding a hexasaccharide N-acetylglucosamine, GlcNAc6. Here, all cyclic residues are highlighted with both PaperChain and the Licorice visualization. (Cyclic rings in the protein were selected for display in the Licorice representation using “select maxringsize 6 from protein”.) The inset shows interaction of the hexasaccharide substrate with the aromatic residues located in the binding groove, with CH-π stacking interactions between aromatic protein residues and the C-H groups of bound sugar rings indicated by dashed arrows.
Fig. 5.
The six-unit N-acetylglucosamine substrate from Figs. 4 and 5 depicted with (a) PaperChain and Twister and (b) Twister only. Here the relative 180° flip of successive sugar rings is highlighted by the twists in the connecting ribbon.
Thus far, we have considered two illustrative examples of glyoproteins, demonstrating the utility of our new visualisations. To conclude, we present a number of non-protein cyclic molecular structures depicted with the PaperChain and Twister visualisations. In a PaperChain visualisation of sucrose (Fig. 6(a)), the pyranose ring (green, chair conformation) is immediately distinguishable from the furanose ring (yellow, envelope conformation). Visualisation of a morphine molecule (Fig. 6(b)) highlights the very different puckers of the rings in this molecule. These range from planar (red), thorough slight envelope (orange) to chair (green) and twist-boat (cyan). A similar example is the haem group (Fig. 6(c)), where the outermost rings are planar (coloured red), while the rings in the metal coordination centre are in slight envelope conformations (yellow/orange). Macrocyclic rings, such as in α-cyclodextrin (e), can be shown with PaperChain. Nanostructures can also be shown in novel views with PaperChain, an example being Buckminsterfullerene (Fig. 6 (d)). A combination of PaperChain and Twister yields useful depictions of of poly- and oligosaccharides (Fig. 6(f) and (g)) and DNA (h), where both the backbone twist and ring conformation is highlighted. For DNA, the deoxyribose rings are in envelope conformations and hence yellow, while the planar bases are red.
4. Conclusions
The incorporation of the PaperChain and Twister visualisations into the Visual Molecular Dynamics (VMD) package allows for unprecedented flexibility in the visualisation of glycoproteins and carbohydrate-binding proteins. These simplified abstract oligosaccharide representations encapsulate information on the ring conformation and glycosidic linkage orientation in such a way that non-expert users may quickly identify when molecular structure refinement procedures have resulted in deformation of sugar rings. A means for rapid validation of saccharide structures is potentially very useful, considering the large percentage of PDB entries for glycoproteins that have errors in carbohydrate stereochemistry and glycosidic linkage. The PaperChain visualisation reveals that, even where the stereochemistry and ring structures are correct, the glycan components of glycoproteins often exhibit incorrect ring pucker coordinates. Further advantages of the visualisations are depiction of the aromatic rings in amino acid residues and the consequent highlighting of the CH-π ring stacking interactions that are often a feature of protein-carbohydrate binding interactions. Both the Twister and the PaperChain visualisations can, of course, be animated for viewing molecular dynamics trajectories. This fourth dimension of time can thus highlight dynamic changes in the ring pucker (PaperChain) and backbone orientation (Twister).
We have demonstrated the efficacy of the two visualisations in that they assisted in the understanding of the mechanism of binding of oligosaccharides to protein Family 18 chitolectins, where we suggest that strong binding of chito-oligosaccharides by these lectins requires a conformational change of the rings at the −1 and −2 binding sites. However, in some sense the real test of the software will come now that the algorithms are publicly available, as a practical measure of utility is whether the software is widely used in achieving significant biological results.[11] If they do prove useful, the algorithms as described here may be incorporated into other molecular visualisation packages.
Acknowledgements
We thank the South African Centre for High Performance Computing and the National Bioinformatics Network for financial support. Additional support was provided by the USA National Institutes of Health, under grant P41-RR05969
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- [1].Richardson JS. The anatomy and taxonomy of protein structure. Advances in Protein Chemistry. 1981;34:167–218. doi: 10.1016/s0065-3233(08)60520-3. [DOI] [PubMed] [Google Scholar]
- [2].Carson M, Bugg C. Algorithm for ribbon models of proteins. J. Mol. Graph. 1986;4(2):121–122. [Google Scholar]
- [3].Carson M. Ribbon models of macromolecules. J. Mol. Graph. 1987;5(2):103–106. [Google Scholar]
- [4].Lütteke T, von der Lieth C-W. pdb-care (pdb carbohydrate residue check): a program to support annotation of complex carbohydrate structures in pdb files. BMC Bioinformatics. 5 doi: 10.1186/1471-2105-5-69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Crispin M, Stuart DI. Building meaningful models of glycoproteins. Nat. Struct. Mol. Biol. 2007;14:354. doi: 10.1038/nsmb0507-354a. [DOI] [PubMed] [Google Scholar]
- [6].Berman HM, Hendrick K, Nakamura H, Markley J. Reply to: building meaningful models of glycoproteins. Nat. Struct. Mol. Biol. 2007;14:354–355. doi: 10.1038/nsmb0507-354a. [DOI] [PubMed] [Google Scholar]
- [7].Lütteke M. F. Thomas, von der Lieth C-W. Carbohydrate structure suite (CSS): analysis of carbohydrate 3D structures derived from the PDB. Nucleic Acids Res. 2005;33:D242–D246. doi: 10.1093/nar/gki013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Nakahara T, Hashimoto R, Nakagawa H, Monde K, Miura N, Nishimura S-I. Glycoconjugate data bank:structures—an annotated glycan structure database and n-glycan primary structure verification service. Nucleic Acids Research. 2008;36:D368–D371. doi: 10.1093/nar/gkm833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Hill AD, Reilly PJ. Puckering coordinates of monocyclic rings by triangular decomposition. J. Chem. Inf. Model. 2007;47:1031–1035. doi: 10.1021/ci600492e. [DOI] [PubMed] [Google Scholar]
- [10].Kuttel M, Gain J, Burger A, Eborn I. Techniques for visualization of carbohydrate molecules. J. Mol. Graphics Modell. 2006;25:380–388. doi: 10.1016/j.jmgm.2006.02.007. [DOI] [PubMed] [Google Scholar]
- [11].Goddard TD, Ferrin TE. Visualization software for molecular assemblies. Curr. Opin. Struc. Biol. 2007;17:587–595. doi: 10.1016/j.sbi.2007.06.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Humphrey W, Dalke A, Schulten K. VMD – Visual Molecular Dynamics. J. Molec. Graphics. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- [13].Cremer D, Pople JA. A general definition of ring puckering coordinates. J. Am. Chem. Soc. 1975;97(6):1354–1358. [Google Scholar]
- [14].Bader DA, Cong G. A fast, parallel spanning tree algorithm for symmetric multiprocessors (SMPs) J. Parallel Distrib. Comput. 2005;65:994–1006. [Google Scholar]
- [15].McNaught AD. Nomenclature of carbohydrates (recommendations 1996) Adv. Carbohydr. Chem. Biochem. 1997;52:43–177. arbohydr Chem Biochem. [PubMed] [Google Scholar]
- [16].Sutherland IE, Sproull RF, Schumaker RA. A characterization of ten hidden-surface algorithms. ACM Comput. Surv. 1974;6(1):1–55. [Google Scholar]
- [17].Plaisant C. The challenge of information visualization evaluation. AVI ’04: Proceedings of the working conference on Advanced visual interfaces; New York, NY, USA: ACM; 2004. pp. 109–116. [Google Scholar]
- [18].North C. Toward measuring visualization insight. IEEE Comput. Graph. Appl. 2006;26(3):6–9. doi: 10.1109/mcg.2006.70. [DOI] [PubMed] [Google Scholar]
- [19].Chen B, Vogan EM, Gong H, Skehel JJ, Wiley DC, Harrison SC. Structure of an unliganded simian immunodeficiency virus gp120 core. Nature. 2005;433:834–841. doi: 10.1038/nature03327. [DOI] [PubMed] [Google Scholar]
- [20].Kumar J, Ethayathulla AS, Srivastava DB, Singh N, Sharma S, Kaur P, Srinivasan A, Singh TP. Carbohydrate-binding properties of goat secretory glycoprotein (spg-40) and its functional implications: strucutres of the native glycoprotein and its four complexes with chitin-like oligosaccharides. Acta Cryst. 2007;D63:437–446. doi: 10.1107/S0907444907001631. [DOI] [PubMed] [Google Scholar]
- [21].Fusetti F, von Moeller H, Houston D, Rozeboom HJ, Dijkstra BW, Boot RG, Aerts JMFG, van Aalten DMF. Structure of human chitotriosidase. implications for specific inhibitor design and function of mammalian chitinase-like lectins. J. Biol. Chem. 2002;277(28):25537–25544. doi: 10.1074/jbc.M201636200. [DOI] [PubMed] [Google Scholar]
- [22].Aronson NN, Jr., Halloran BA, Alexyev MF, Amable L, Madura JD, Pasupulati L, Worth C, Roey PV. Family 18 chitinase-oligosaccharide substrate interaction: subsite preference and anomer selectivity of serratia marcescens chitinase a. Biochem. J. 2003;376:87–95. doi: 10.1042/BJ20030273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Houston DR, Recklies AD, Krupa JC, van Aalten DMF. Structure and ligand-induced conformational change of the 39-kda glycoprotein from human articular chondrocytes. J. Biol. Chem. 2003;278(32):30206–30212. doi: 10.1074/jbc.M303371200. [DOI] [PubMed] [Google Scholar]
- [24].Fusetti F, Pijning T, Kalk KH, Bos E, Dijkstra B. Crystal structure and carbohydrate-binding properties of the human cartilage glycoprotein-39. J. Biol. Chem. 2003;278(39):37753–37760. doi: 10.1074/jbc.M303137200. [DOI] [PubMed] [Google Scholar]
- [25].Zaheer-ul-Haq, Dalal P, Aronson NN, Jr., Madura JD. Family 18 chitolectins: Comparison of MGP40 and HUMGP39. Biochemical and Biophysical Research Communications. 2007;359(2):221–226. doi: 10.1016/j.bbrc.2007.05.074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Srivastava DB, Ethayathulla AS, Kumar J, Somvanshi RK, Sharma S, Dey S, Singh TP. Carbohydrate binding properties and carbohydrate induced conformational switch in sheep secretory gylcoprotein (SPS-40): Crystal strucutres of four complexes of SPS-40 with chitin-like oligosaccharides. Journal of Strucutral Biology. 2007;158:255–266. doi: 10.1016/j.jsb.2006.11.002. [DOI] [PubMed] [Google Scholar]
- [27].Brameld KA, Ill WAG. Substrate distortion to a boat conformation at subsite −1 is critical in the mechanism of family 18 chitinases. J. Am. Chem. Soc. 1998;120:3571–3580. [Google Scholar]
- [28].Tews I, van Scheltinga ACT, Perrakis A, Wilson KS, Dijkstra BWDW. Substrate-assisted catalysis unifies two families of chitinolytic enzymes. J. Am. Chem. Soc. 1997;119:7954–7959. [Google Scholar]
- [29].Songsiriritthigul C, Pantoom S, Aguda A, Robinson R, Suginta W. Crystal structures of vibrio harveyi chitinase a complexed with chitooligosaccharides: implications for the catalytic mechanism. J. Struct. Biol. 2008;162:491–499. doi: 10.1016/j.jsb.2008.03.008. [DOI] [PubMed] [Google Scholar]
- [30].Fernandez-Alonso M, Canada FJ, Jimenez-Barbero J, Cuevas G. Molecular recognition of saccharides by proteins, insights on the origin of the carbohydrate-aromatic interactions. J. Am. Chem. Soc. 2005;127:7397–7386. doi: 10.1021/ja051020+. [DOI] [PubMed] [Google Scholar]
- [31].Varshney A, Brooks FP, Wright WV. Linearly scalable computation of smooth molecular surfaces. IEEE Computer Graphics and Applications. 1994;14:19–25. [Google Scholar]
- [32].Stone J. Master’s thesis. Computer Science Department, University of Missouri-Rolla; Apr, 1998. An Efficient Library for Parallel Ray Tracing and Animation. [Google Scholar]
- [33].Jacob J, Geßler K, Hoffman D, Sanbe H, Koizumi K, Smith SM, Takaha T, Saenger W. Band-flip and kink as novel structural motifs in α – (1 → 4)-d)glucose oligosaccharides. crystal structures of cyclodeca- and cyclotetradecaamylose. Carbohydr. Res. 1999;322:228–246. [Google Scholar]