Abstract
Sirtuins are protein modifying enzymes distributed throughout all forms of life. These enzymes bind NAD+, a universal metabolite, and react it with acetyllysine residues to effect deacetylation of protein side chains. This NAD+-dependent deacetylation reaction has been observed for sirtuin enzymes derived from archaeal, eubacterial, yeast, metazoan and mammalian species, suggesting conserved chemical mechanisms for these enzymes. The first chemical step of deacetylation is the reaction of NAD+ with an acetyllysine residue which forms an enzyme-bound ADPR-peptidylimidate intermediate and nicotinamide. In this manuscript, the transition state for the ADP-ribosylation of acetyllysine is solved for an Archaeaglobus fulgidus sirtuin (Af2Sir2). Kinetic isotope effects (KIEs) were obtained by the competitive substrate method and were [1N-15N] = 1.024(2), [1′N-14C] = 1.014(4), [1′N-3H] = 1.300(3), [2′N-3H] =1.099(5), [4′N-3H] = 0.997(2), [5′N-3H] = 1.020(5), [4′N-18O] = 0.984(5). KIEs were calculated for candidate transition state structures using computational methods (Gaussian 03 and ISOEFF 98) in order to match computed and experimentally determined KIEs to solve the transition state. The results indicate that the enzyme stabilizes a highly dissociated oxocarbenium ion-like transition state with very low bond orders to the leaving group nicotinamide and the nucleophile acetyllysine. A concerted yet highly asynchronous substitution mechanism forms the ADPR-peptidylimidate intermediate of the sirtuin deacetylation reaction.
1. Introduction
The sirtuins are phylogenetically conserved NAD+ dependent enzymes that regulate diverse signaling processes within cells via protein covalent modification.1, 2 The sirtuins catalyze removal of protein acetyllysines, although in some cases they have been reported to ADP-ribosylate proteins and other substrates as well.3–8 The sirtuins have been implicated in cellular and organism adaptations to stress and nutrient intake,2, 9–11 and regulate lifespan in different organisms including yeast,12 worms,13 flies14 and probably in mammals.15 The mammalian sirtuins regulate adipogenesis,16 adipolysis,16 apoptosis,17–20 insulin secretion,21, 22 gluconeogenesis,23, 24 mitochondrial biogenesis,25, 26 metabolic pathways,25, 26 DNA repair,20, 27–30 senescence30 and proliferation.20, 31, 32 Sirtuins are profound regulators of diverse biological processes and their chemical and enzymatic mechanisms are of heightened interest. In turn, the development of small molecule modulators of sirtuins is an active area of research.33–37
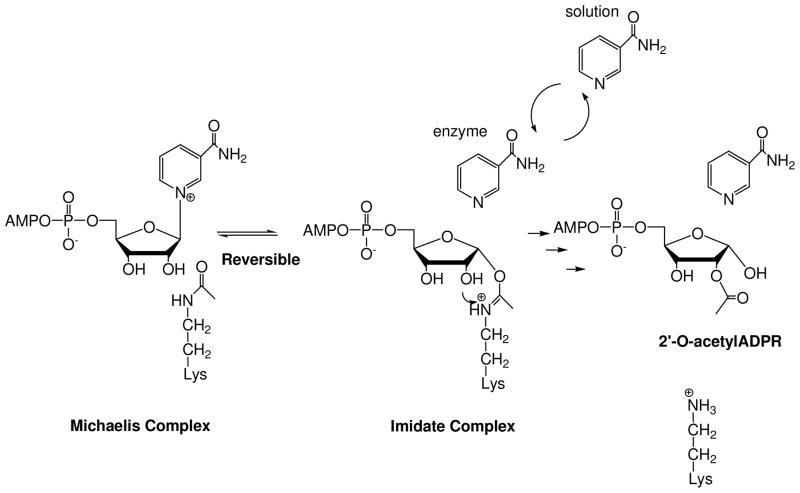
In addition to fascinating biological effects, the sirtuins have unusual chemistry.1 The sirtuins deacetylate proteins using NAD+ as a co-substrate and are sensitive to changes in cellular NAD+ and nicotinamide concentrations.38–40 Sirtuin catalyzed deacetylation generates nicotinamide and the acetyl-transfer product, 2′-O-acetyl-ADPribose (2′-AADPR).41, 42 Sauve et al. proposed that the first step in sirtuin catalysed deacetylation is ADP-ribosyltransfer to the acetyllysine group of a protein or peptide substrate to form an intermediate called an O-alkylamidate,41 also called an ADP-ribosyl-peptidylimidate (Scheme 1).1 The intermediate has versatile properties. For example, NAD+ can be reformed from it when nicotinamide concentrations are elevated in solution (Scheme 1).41 Chemical reversal accounts for the inhibition of sirtuins by metabolic and pharmacologic nicotinamide concentrations.39, 40 Alternatively, the imidate reacts forward via nucleophilic attack of the 2′-OH on the imidate, resulting in deacetylation and enzymatic formation of 2′-AADPR (Scheme 1).41 This mechanistic proposal has explained a variety of chemistries of sirtuins reported by numerous laboratories; however, direct characterizations of mechanistic intermediates or transition states have not been reported.
Scheme 1.
Reaction scheme for Af2Sir2 catalyzed deacetylation.
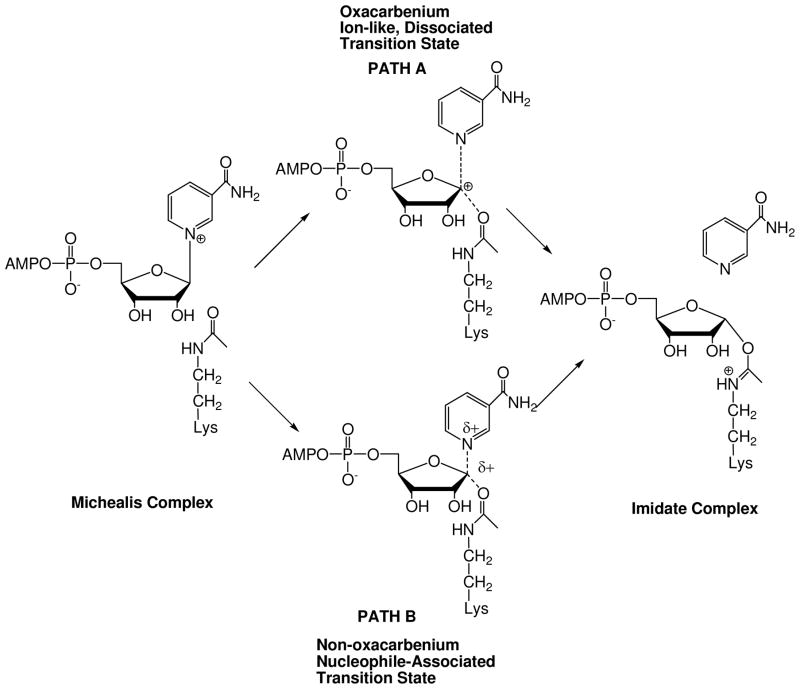
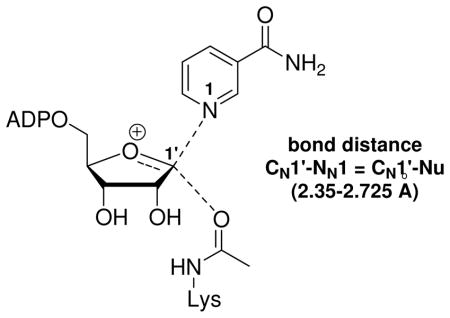
The ADP-ribosylation of the acetyllysine moiety was proposed to involve electrophilic capture of the acetyl-oxygen by an oxacarbenium ion-like transition state, characterized by low bond orders to leaving group and nucleophile (Scheme 2 PATH A).41, 43 Significant mechanistic precedent for this reaction was available from determinations of transition states of both enzymatic and non-enzymatic ADP-ribosylation reactions. For example, kinetic isotope effect (KIE) measurements and computational chemistry had elucidated well-formed oxacarbenium ion-like transition states for ADP-ribosyltransfer reactions of the NAD+-dependent bacterial toxins44–47 and hydrolysis of NAD+ in water (pH = 5).48 Such an electrophilic mechanism overcomes the limitation of the acetyllysine as a poor nucleophile. We disfavored an SN2-type mechanism, distinguished by significant association of the nucleophile at the transition state (Scheme 2, PATH B). Crystallography and mutagenesis also indicated that a proximate base at the active site for nucleophilic activation of the amide was not necessary for the ADP-ribosylation.1, 49
Scheme 2.
Proposed mechanisms for Af2Sir2 catalyzed deacetylation. (A) Oxacarbenium ion, dissociated transition state; (B) non-oxacarbenium ion, nucleophile-associated transition state.
Since the initial mechanistic proposal was published, debate about the mechanism of the ADP-ribosylation step has increased. A provocative study by Smith and Denu generated evidence that the nucleophile has “significant participation” in the ADP-ribosylation step.50 Modified acetyllysine analogues, such as α-monofluoro, difluoro and trifluoro-derivatives provided extremely slow rates of NAD+ turnover leading the authors to conclude that “the rate of nicotinamide-ribosyl bond cleavage [is] consistent with an SN2 like mechanism”50 and inconsistent with a fully dissociated transition state oxacarbenium ion.41, 50 More recently, both high-level computational QM/MM51 and X-ray crystallographic studies52 have supported a largely-dissociated transition state structure, although the computational study concurred that the transition state had some association of the nucleophile.51
The most rigorous experimental determination of transition state structure is from KIEs, which have the advantage of probing the transition state directly without perturbing substrate electronics or sterics. We chose this approach to determine the transition state for the first chemical step of a sirtuin. The transition state for the nicotinamide cleavage/ADP-ribosylation step was solved by the method of matching experimental KIEs to calculated KIEs for candidate transition state structures. These methods have solved a large number of transition state structures of N-ribosyltransferase enzymes,44–47, 53, 54 including thymidine phosphorylase which proceeds via an associative mechanism.55 In this study, we solve the transition state structure of an Archeaoglobus fulgidus sirtuin, Af2Sir2. This enzyme had previously been studied by X-ray crystallography56 and has well characterized deacetylase41 and base-exchange reactions.40 We report here the transition state structure of the ADP-ribosylation step to acetyllysine for this enzyme and conclude that this sirtuin stabilizes an oxacarbenium ion-like transition state with very low bond orders to nicotinamide and acetyl-oxygen.
2. Materials and Methods
General Materials
Archeaoglobus fulgidus Af2Sir2 was expressed from a plasmid as previously described.40 A peptide based on p53 sequence (HLKSKKGQSTSRHK(K-Ac)LMFK), called p53A, was synthesized by the Proteomics Resource Center at Rockefeller University. Enzymes and reagents for NAD+ synthesis are reported in the Supporting Information.
Synthesis of Isotopically Labeled Substrates
[1′N-3H], [4′N-3H], [5′N-3H], [1′N-14C], [2,8A-3H], [8A-14C], [1-15N-5′N-14C]-NAD+s (99 % 1-15N) were prepared enzymatically as described previously.57 [4′N-18O-2,8A-3H]-NAD+ (95% 4′N-18O) was synthesized by modification of methods reported for making isotopically labeled NAD+s46, 57 and this method is included in the Supporting Information. Detailed chemical and enzymatic synthesis of [2′N-3H]-NAD+ is described in the Supporting Information.
Characterization of Steady State [Carbonyl-14C]-Nicotinamide Base Exchange Reactions
Reactions containing 400 μM of NAD+, 250 μM of p53A with varying concentrations of [carbonyl-14C]-nicotinamide were initiated by addition of Af2Sir2 (final concentration, 4.1 μM). Reactions were incubated for 90 min at 37 °C and quenched with 10% TFA to pH 2. After centrifugation, clarified reaction mixtures were injected on HPLC (0.1% TFA eluent) to separate nicotinamide and NAD+. Collected fractions containing nicotinamide and NAD+ were assayed for radioactivity by scintillation counting. Rates were expressed as cpm/s incorporated into NAD+, and converted to a turnover rate (1/s) after adjustment for enzyme concentration and specific radioactivity. Rates were plotted versus nicotinamide concentration and fit to the Michaelis–Menten equation with Kaleidagraph®.
KIE Measurement
A mixture of 3H- and 14C-labeled NAD+ (total 300, 000 cpm each) and peptide was divided into three portions. The first portion (420,000 cpm total) was diluted into 100 mM phosphate buffer (pH 7.5) containing unlabeled NAD+ to a final concentration of 400 μM NAD+ with 250 μM p53A peptide in a volume of 80 μL. Reaction was initiated by addition of Af2Sir2 (final concentration = 4.1 μM). Reaction was stopped when 20% complete (45–60 min), and terminated by addition of 10% TFA to pH 2.0. To convert AADPR to ADP-ribose (ADPR), the quenched reaction was neutralized to pH 7.5 by addition of 3 M NaOH and 1 M phosphate buffer (pH = 9). 1 unit of porcine liver esterase was added, followed by incubation at 37 °C for 2 h. Reaction was quenched by addition of 8 μL of 10% TFA. The second portion (90000 cpm) was incubated at 37 °C for 1 h in the absence of Af2Sir2 as the background control to detect impurity and/or nonspecific hydrolysis of NAD+ and treated similarly with esterase. The third portion (90000 cpm) was used for a 100% hydrolysis reaction using CD38 (prepared as described58) to hydrolyze NAD+ to ADPR. ADPR and remaining NAD+ were separated on a C18 column and fractions containing ADPR were collected, measured to precise 2 mL volumes with 15 mL scintillant and the 3H/14C ratios determined by scintillation counting. The “intrinsic” or experimental KIEs without correction for commitments were determined by equation (1):
| (1) |
where f is the fraction reaction progress and Rf and Ro are the ratios of light to heavy isotope in product at partial and 100 % completion, respectively, corrected for background. The intrinsic KIE was corrected by the factor 1.001 for cases where [2,8A-3H]-NAD+ was used as the remote, except for the [4′N-18O]KIE. In this case the value was divided by 1.001. The remote KIE for [2,8A-3H]-NAD+ was determined to be 1.001(4). Corrections for isotopic purities for 18O and 15N isotope effects were applied.
Forward Commitment to Catalysis
Forward commitment factor was determined by the isotope trapping method previously described.59 A full description of the experimental method is found in the Supporting Information.
Reverse Commitment to Catalysis
Reverse commitment to catalysis was determined by measuring the [1′N-H3]KIE as a function of nicotinamide concentration. Nicotinamide at concentrations 0, 100 μM, 500 μM, 1 mM, 2 mM and 5 mM, was combined in mixtures of [1′N-H3]-, [8A-14C]-NAD+s and p53A. [1′N-H3] KIEs were measured as described above. Forward and reverse commitment factors govern observed KIEs and are predicted by Northrop’s equation (2):
| (2) |
Where KIEobs is the observed KIE, KIEint is the intrinsic KIE for the chemical step in question, Cf and Cr are the forward and reverse commitment factors, respectively, and KIEeq is the equilibrium KIE separating reactants from the products of the reaction step in question. With forward commitment negligible, equation (2) is reduced to (3):
| (3) |
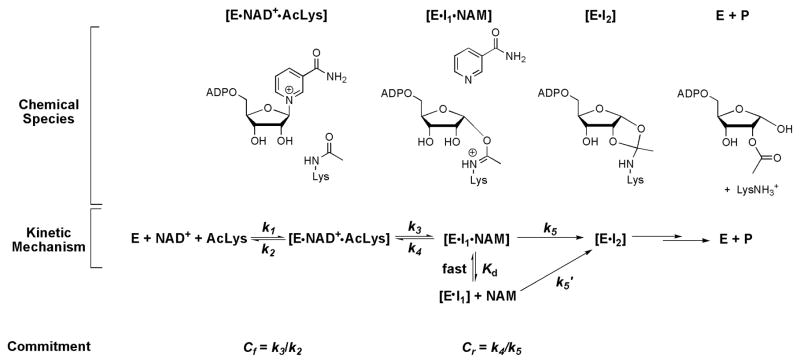
In the case of Af2Sir2 catalyzed reactions, equation (4) was derived from equation (3) to fit the [1′N-H3] KIE data at different nicotinamide (NAM) concentrations. A full derivation based on Scheme 3 is in the Supporting Information.
Scheme 3.
Chemical mechanism for sirtuin catalyzed ADP-ribosylation of acetyllysine and relevant reaction downstream chemistry from imidate. Lower scheme depicts kinetic mechanism, including relevant rate constants and definitions of forward and reverse commitments relevant to the V/K KIE measurement for the ADP-ribosylation of acetyllysine. The base exchange reaction described in text occurs via reaction of NAD+ forward to form the imidate complex (EI1), dissociation of nicotinamide from the EI1·NAM complex, reassociation of radiolabeled nicotinamide to the complex (as shown by fast equilibrium), reformation of NAD+ via step governed by k4, and release of reformed NAD+ back into solution. Commitment equations relevant to observed KIE values are found in Methods and Materials and derivations for this kinetic mechanism are found in Supporting Information.
| (4) |
Kd is defined according to Scheme 3 as the binding constant of NAM to the imidate complex. The observed KIEs are corrected for the reverse commitment according to equation (5) and intrinsic KIEs are listed in Table 1.
Table 1.
Experimental and intrinsic KIEs for Af2Sir2 catalyzed deacetylation
| label of interest | remote label | KIE type | experimental KIEa,b | intrinsic KIEc |
|---|---|---|---|---|
| 1N-15N | 2,8A-3H | primary | 1.024(2) | 1.024(2)d |
| 1′N-14C | 2,8A-3H | primary | 1.014(4) | 1.014(4) |
| 1′N-3H | 8A-14C | α-secondary | 1.289(1) | 1.300(3) |
| 2′N-3H | 8A-14C | β-secondary | 1.095(5) | 1.099(5) |
| 4′N-3H | 8A-14C | γ-secondary | 0.997(2) | 0.997(2) |
| 5′N-3H | 8A-14C | δ-secondary | 1.019(5) | 1.020(5) |
| 4′N-18O | 8A-14C | α-secondary | 0.985(5) | 0.984(5) |
| 2,8A-3H | 8A-14C | remote | 1.001 (4) | 1.001(2) |
KIE determined from at least three experiments and from correction for isotopic depletion.
The number in the parenthesis represents the error in the last digit.
KIE determined from experimental KIE using equation 3 and corrected for commitment factors of Cr = 0.038 and KIEeq = 1.000 except for first entry (See Supporting Information for KIEs calculated for KIEeq = 1.100). Error to the intrinsic KIE value includes variability in the value of Cr (0.036–0.042) due to variability in the 20% conversion to products (±2%).
KIE determined from experimental KIE using equation 3 and corrected for commitment factors of Cr = 0.038 and KIEeq = 1.027 (see reference for the equilibrium isotope effect of 1.027 for full dissociation of nicotinamide). Measurement of [1′N-3H]KIE in the presence of nicotinamidase, which minimizes reverse commitment by degrading nicotinamide, gave an experimental KIE corrected for isotope depletion of but without correction for reverse commitment of 1.307(5) in agreement with the calculated intrinsic in Table 1.
| (5) |
Independently, using the relation Cr = k4/k5, where k4 is the reverse rate of nicotinamide return to NAD+ from the imidate complex (Scheme 3), k5 is the forward rate of reaction from the fully nicotinamide complexed imidate (Scheme 3), the value of Cr was computed using Michaelis parameters for Af2Sir2 using the peptide substrate using the assumption that Kd ≈ Km (nicotinamide) for base exchange and with the assumption that k5 ≈ kdeacetyl and k4 ≈ kB.E as described in the text.
Computational Modeling
The reactant state model of NAD+ was derived from the crystal structure of the lithium salt of NAD+, truncated to nicotinamide riboside (NR) with all hydrogens included.60 The geometry of the NR portion was optimized in vacuo using hybrid density functional methods with B1LYP/6-31G** level of theory implemented in Gaussian 03,61 freezing two dihedral angles to maintain the ribosyl 3′-endo conformation. The transition state was modeled as an oxacarbenium ion-like intermediate, with nicotinamide leaving group and a N-methylacetamide nucleophile placed at different distances to the anomeric carbon. The starting structure for the ribose portion of the transition state was derived from the crystal structure of ribonolactone as described.60,44,48 The carbonyl oxygen was replaced with hydrogen, the orientation of the 5′-hydroxy group was modified according to the crystal structure of Af2Sir2 bound NAD+, and all atoms were minimized at the B1LYP/6-31G** level. The transition state model was adjusted by systematically altering C1′-N1, C1′-nucleophile bond lengths and C1′-C2′, C1′-H1′, C2′-H2′ and C1′-O4′ bond angles and dihedral angles while allowing the rest of the molecule to be optimized as described above. The same level of theory and basis set were used for optimization of substrate as well as for the computation of bond frequencies. KIEs were calculated from the computed frequencies using ISOEFF98.62 The applied geometric constraints were optimized iteratively until the KIEs predicted by the transition state model were a good match to the experimental KIEs. Pauling bond orders were calculated with the equation:
where r1 is the bond length of a single bond, and the corresponding bond distances in the optimized structures were used for the term ri in the equation.
Calculation of Molecular Electrostatic Potential Surface
The CUBE subprogram of Gaussian 03 was used to calculate molecular electrostatic potential (MEP) surfaces. The formatted checkpoint files used in the CUBE subprogram were generated by geometry optimization at the B1LYP/6-31G** level. The MEP surfaces were visualized using Molekel 5.463 at a density of 0.2 electron/Å3.
Calculation of Group Partial Charges
The atomic and group charges for N-methylacetamide, nicotinamide and ribose for both reactant state and transition state were obtained using hybrid density functional methods with B1LYP/6-31G** level of theory implemented in Gaussian 03. These data sets were generated using the Gaussian 03 outputs for Mulliken atomic charges in the initial computational steps for KIE calculation.
Thermochemical Calculations of Transition State Energies
Geometries of the transition states were optimized in vacuo using hybrid density functional methods with B1LYP/6-31G** level of theory implemented in Gaussian 03. The same level of theory and basis set were used for the computation of bond frequencies, from which the free energy change was determined for each molecule calculated. We calculated energies for methylacetamide and nicotinamide riboside (calculated separately), methyl trifluoroacetamide and nicotinamide riboside (calculated separately) and three complexes, methylacetamide-ribosyl-nicotinamide transition state (exo, as described in text with 2.65 Å distance to leaving group and nucleophile) the corresponding iso-structural methyltrifluoroacetamide-ribosyl-nicotinamide complex (exo with 2.65 Å distance to leaving group and nucleophile) and methylacetamide-ribosyl-nicotinamide, the fully dissociated oxacarbenium ion (exo, as described in text with 3.5 Å C1′ distance to leaving group and nucleophile). Energy of complex is relative to the reactant state. Gaussian 03 provides outputs in energy in Hartrees which were converted to kcal/mol by the relation: 1 hartree = 627.5 kcal/mol.
3. Results and Discussion
NAD+ synthesis and assays for determining isotope effects
To measure isotope effects for sirtuin chemistry we chose the competitive radiolabel method.44–47, 53, 54 Isotopically labeled NAD+’s were synthesized according to established procedures57 except for synthesis of the [2′-3H]-NAD+ which required development of new synthetic methodology described in the Supporting Information. Syntheses of the compounds, [1′N-3H], [4′N-3H], [5′N-3H], [1′N-14C], [2,8A-3H], [8A-14C], [4′N-18O-2,8A-3H] and [1-15N-5′N-14C]-NAD+ are described in Materials and Methods and Supporting Information. Each labeled NAD+ was purified to homogeneity by HPLC, and checked for isotopic purity by MALDI-MS in cases where 15N and 18O labels were incorporated.
KIEs were measured by competing two distinctly isotopically labeled substrate NAD+s (one labeled 14C, the other 3H) in a sirtuin reaction. Reactions were permitted to reach 20 % product formation, quenched, neutralized and treated with esterase to convert AADPR to ADPR. The experimental isotope ratio in products was determined by HPLC collection of ADPR followed by scintillation counting. A 100% reaction was generated by converting NAD+ to ADPR by CD38 (See Materials and Methods for complete details). Experimental isotope effects uncorrected for remote and commitment effects were computed according to equation 1 in the Materials and Methods. (Corrections for remote KIEs are described in the Materials and Methods and corrections for commitment factors are more described in a later section).
The competitive method provides the V/K isotope effect, or more plainly, the isotope effect for the first irreversible step(s) occurring on the enzyme. Conditions were identified wherein the nicotinamide cleavage step was the one irreversible step (discussed with section on commitments) using an acetyllysine substrate (HLKSKKGQSTSRHK(K-Ac)LMFK) p53A reacted with Archeaglobus fulgidus Af2Sir2.
Kinetic Isotope Effects
The experimental KIEs corrected for remote effects and for turnover are reported in Table 1. The intrinsic KIEs on nicotinamide cleavage corrected for commitments are also reported in Table 1. The analysis of commitments follows a brief reporting and consideration of the intrinsic KIEs for the reaction. Qualitative descriptions of the chemical and structural influences that affect the values of these KIEs are presented.
[1′N-14C]KIE
The primary KIE at the anomeric carbon is sensitive to the bonding occurring at this atom at the transition state. This KIE was measured by competition of [1′N-14C]-NAD+ against [2,8A-3H]-NAD+. The remote tritium label on adenine has a KIE of 1.001(4). The [1′N-14C]KIE was determined to be 1.014(4) (Table 1). For dissociative N-ribosyltransfer mechanisms the [1′N-14C]KIE is close to unity and in the range 1.0–1.03.44–47, 53, 54 For thymidine phosphorylase the [1′N-14C]KIE is elevated, 1.139(5),55 as expected for an associative, non-oxacarbenium ion transition state.
[1-15N]KIE
The primary leaving group KIE was measured with [1-15N, 5′N-14C]-NAD+ reacted against [2,8A-3H]-NAD+ wherein 15N is used to generate the primary isotope effect, and the 14C acts as the reporter. We demonstrated by mass spectrometry that the 15N is incorporated to 99% (data not shown). The intrinsic value of the KIE was 1.024(2) (Table 1). The theoretical value for this KIE is 1.027 for a fully dissociated transition state.48 A KIE value of 1.025 was computed for a residual 0.0199 bond order remaining between nicotinamide and the ribose ring of NAD+ (Table 2).
Table 2.
Calculated KIEs for symmetric transition state models
| Symmetric Models |
Intrinsic KIEs | ||||||
|---|---|---|---|---|---|---|---|
| Associative → Dissociative | |||||||
| CN1′-NN1 (Å) | 2.300 | 2.500 | 2.650* | 2.675 | 2.725 | 3.55 | |
| CN1′-Nu (Å) | 2.300 | 2.500 | 2.650* | 2.675 | 2.725 | 3.48 | |
| 1N-15N | 1.023 | 1.025 | 1.025* | 1.025 | 1.025 | 1.027 | 1.024(2) |
| 1′N-14C | 1.081 | 1.057 | 1.013* | 1.012 | 1.010 | 0.998 | 1.014(4) |
| 1′N-3H | 1.309 | 1.411 | 1.424* | 1.429 | 1.441 | 1.514 | 1.300(3) |
| 2′N-3H | 1.018 | 1.077 | 1.099* | 1.106 | 1.117 | 1.196 | 1.099(5) |
| 4′N-3H | 0.994 | 1.002 | 1.003* | 1.003 | 1.004 | 1.023 | 0.997(2) |
| 5′N-3H | 1.035 | 1.034 | 1.035* | 1.035 | 1.036 | 1.029 | 1.020(5) |
| 4′N-18O | 0.995 | 0.995 | 0.993* | 0.993 | 0.993 | 0.992 | 0.984(5) |
Intrinsic KIEs are as reported in Table 1. Calculated KIEs are determined as described in experimental. The numbers in the first two rows are bond distances in Å used in the calculation. The ring geometry is 3′-exo, as explained in text. Asterisked represent best fit to experimental KIEs, shown at far right row.
[1′N-3H]KIE
The α-secondary KIE is sensitive to rehybridization occurring at the anomeric carbon, specifically due to changes in steric parameters affecting out-of-plane bending modes at the transition state.44–47, 53, 54 For an associated transition state of N-ribosyltransfer, where nucleophile and leaving group are in a crowded pentacoordinate structure, steric effects limit hydrogen bending and cause this KIE to be near unity or even inverse.55 In cases where steric relief is apparent, as in a dissociative transition state the KIE is well above unity and for many oxacarbenium ion-like transition states for N-ribosyltransfer reactions it has been measured in the range 1.16–1.36.44–47, 53, 54, 59, 64, 65 For Af2Sir2 the [1′N-3H]KIE is 1.300(3) on the very high end of reported values for this KIE (Table 1). The α-secondary and the two primary KIEs indicate an oxacarbenium-type transition state with significant dissociation of the leaving group and nucleophile at the anomeric carbon. The large value for the α-secondary KIE indicates that commitments are not significant and KIEs are nearly fully expressed.
[2′N-3H]KIE
The β-secondary KIE is sensitive to the presence of a transition state orbital valency at the primary carbon 66, 67 In our case, the KIE is dependent upon the degree of hyperconjugative overlap of the C-H bond at the β-position with the orbital at the anomeric carbon at the transition state. Hyperconjugation weakens the β-C-H bond and causes a normal KIE. For solved oxacarbenium ion-like transition states the β-secondary [3H]KIEs have ranged from 1.01–1.12.48, 59, 67, 68 Lower values are indicative of loss of the appropriate dihedral angle for hyperconjugation, reaching the extreme when orthogonality defines the overlap.69 Low values can also result from an associative mechanism where p-orbital development at the primary carbon is less pronounced at the transition state, thus preventing effective hyperconjugation.55, 67 For Af2Sir2 the [2′N-3H]KIE was determined to be 1.099(5), at the high end of this KIE for N-ribosyltransfer oxacarbenium ion-like transition states,48, 67, 69 inconsistent with an associative transition state.55 The value predicts that the β-hydrogen is in substantial overlap with a largely vacant orbital at C1′ at the transition state.
[4′N-18O]KIE
To obtain the value of the [4′N-18O]KIE, we competed [4′N-18O, 2,8A-3H]-NAD+ against [8A-14C]-NAD+. The KIE was 0.984(5) (Table 1), very close to the value obtained for the solution hydrolysis of NAD+ (0.988(7))48 and for hydrolysis of NAD+ catalyzed by diphtheria toxin of (0.988(3)).46 The [4′N-18O]KIE is inverse for oxacarbenium ion-like transition states, because of double bond character at the 4′N-oxygen in a dissociated transition state.48 This effect is closer to unity in associative mechanisms, although the value for the [4′N-18O]KIE for thymidine phosphorylase was not reported.55
[4′N-3H] and [5′N-3H] KIEs
Remote effects typically do not deviate much from unity, and have somewhat limited value for transition state determinations. On occasion, the 5′-position [3H]KIE can be as high as 5%, although it appears the effect is traced to binding isotope effects that propagate into the transition state. In our case we report a modest [4′N-3H]KIE of 0.997(2) and a [5′N-3H]KIE of 1.020(5).
Commitments
In this study, we determined the KIE under conditions where the nicotinamide cleavage step is uniquely the first irreversible enzymatic step. The condition occurs when binding steps are fully reversible (no forward commitment), and if the nicotinamide cleavage step is not reversible (no reverse commitment). The effects of forward and reverse commitments on KIE values are described by equation 2. A forward commitment means that binding is partially irreversible and a reverse commitment means that the nicotinamide cleavage is partially reversible. Commitments typically suppress the KIE and are determined independently of the KIEs.
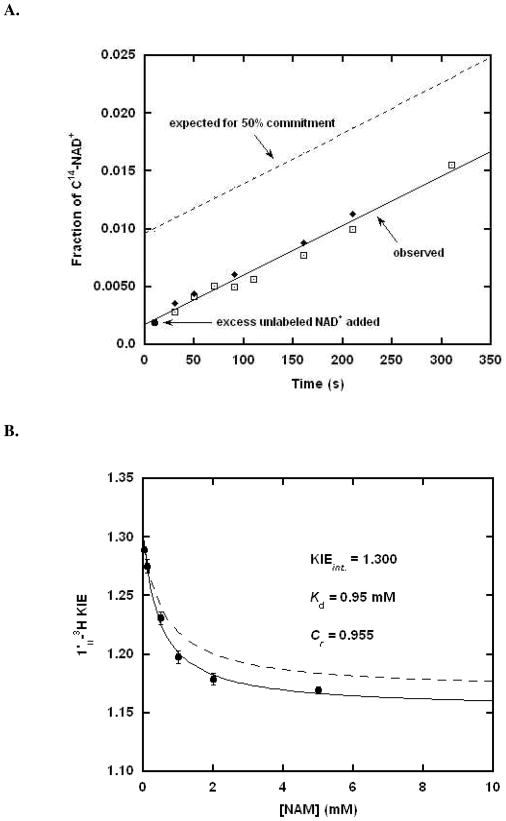
To measure forward commitment, the fraction of Michaelis complexes that go forward irreversibly rather than dissociating substrate (Scheme 3), we used isotope-trapping methods.59 However, Af2Sir2 is so slow as a catalyst (<1 × 10−2 per second), we did not expect an appreciable forward commitment. As shown in Figure 1A, initial incubation with radiolabeled NAD+ followed by treatment with excess unlabeled NAD+ does not lead to trapped counts, and Cf = 0.000. Full details of this experiment are provided in the Supporting Information and in the Figure 1 legend.
Figure 1.
A. Measurement of forward commitment to catalysis for Af2Sir2 by the isotope trapping method. Af2Sir2 was mixed with [8A-14C]-NAD+. After 10s, the reaction was either terminated and analyzed for product formation (circle) or diluted with chase solution containing a large excess (10 mM) of unlabeled NAD+. Aliquots were removed at the indicated time points and analyzed for product formation (square). Controls used the same amount of enzyme added directly to 10 mM NAD+ solution containing [8A-14C]-NAD+, aliquots were removed and quenched at the indicated time points (diamond). The expected results for 50% commitment is shown as dotted line. B. [1′-3H]KIE as a function of nicotinamide concentration (circle). The curve was fitted to the equation 4 in experimental. Values fit for the solid curve are shown in the figure. Independently, the Michaelis parameters of base exchange and deacetylation were used to predict commitment as discussed in the experimental section, and the curve predicting [1′-3H] KIE versus nicotinamide concentration is shown as the dashed curve.
Reverse commitment is a more pertinent because sirtuins are known to reverse the imidate complex back to NAD+ (Scheme 3).39, 40 Af2Sir2 was chosen in light of our prior demonstration of inefficient nicotinamide reversal.40 To obtain the reverse commitment, Cr, (equation 2) we considered the mechanism shown in Scheme 3. The proposed mechanism assumes that nicotinamide is in fast binding equilibrium with the imidate complex and that the forward chemistry terms k5 and k5′ are nearly equal. To determine that nicotinamide is in fast equilibrium compared to chemistry we determined the steady state base exchange rate as a function of solvent viscosity. The base exchange rate is measured with radioactive nicotinamide incubated in solution. Base exchange is caused by release of nicotinamide from the imidate complex followed by rebinding of radioactive nicotinamide. Imidate reversal forms radioactive NAD+ followed by radiolabeled NAD+ release from the enzyme (Scheme 3, See Methods and Materials for experimental). The steady state base-exchange rate is not sensitive to viscosity (Figure S1 Supporting Information), consistent with rapid association and dissociation steps for NAD+, acetyllysine substrate, and nicotinamide to the enzyme compared to chemistry. To provide evidence that complexes E·I1·NAM and E·I1 react forward at similar rates, the enzyme was incubated with elevated concentrations of isonicotinamide and base exchange and deacetylation were assayed. At 20 mM, isonicotinamide inhibited base exchange 18% (Figure S2 Supporting Information), but did not inhibit deacetylation (Figure S3 Supporting Information). Thus, ligand occupancy of the nicotinamide site does not alter the forward reaction parameter i.e. k5 ≈ k5′. Derivation of equation 4, which describes commitments based on Scheme 3 is provided in the Supporting Information.
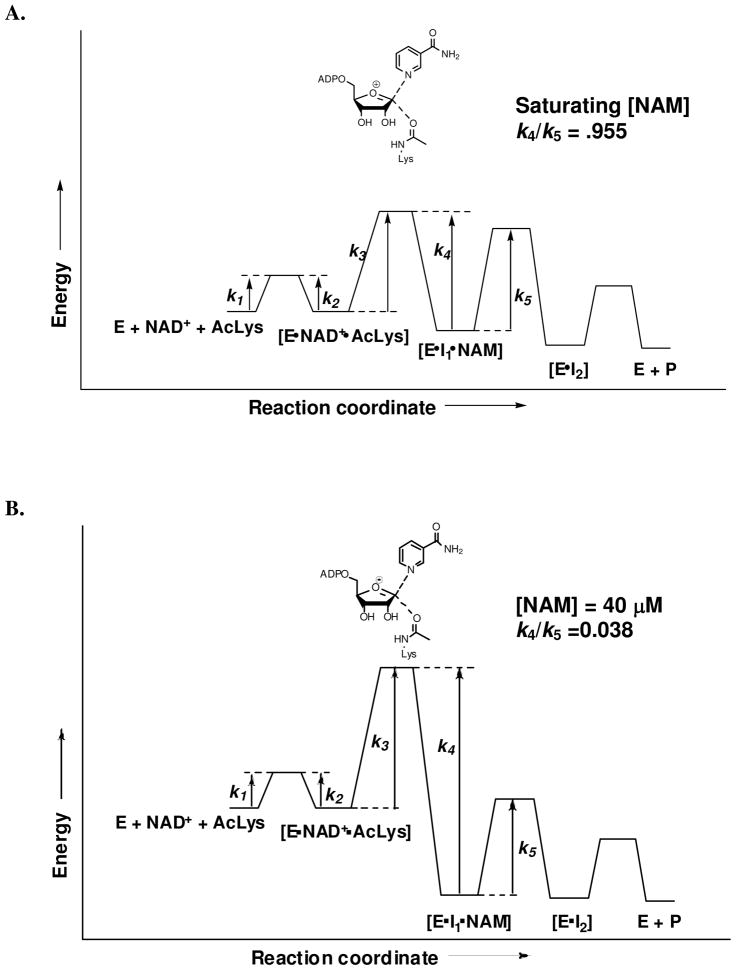
To obtain the value for Cr= k4/k5, we determined the [1′N-3H]KIE as a function of nicotinamide concentrations. Fit of points for the KIE as a function of nicotinamide concentration was obtained using equation 4 (Figure 1B), and provided a value for the intrinsic KIE, the value of Cr (k4/k5) and a value for Kd. The determined intrinsic value for the [1′N-3H]KIE of 1.300 is in fair agreement to the observed experimental value of 1.289(1) uncorrected for reverse commitment, and is in good agreement with the KIE determined in the presence of nicotinamidase 1.307(5) (See Table 1). Nicotinamidase degrades nicotinamide to nicotinic acid and prevents reaction reversal. The value of Cr was found to be 0.955 (at saturating nicotinamide concentrations), and the value of Kd, the nicotinamide binding constant to the imidate complex, was determined to be 0.95 mM.
Reverse commitment could also be estimated from the Michaelis-Menten parameters for base exchange and deacetylation. For base exchange Km was determined to be 1.13 mM, and the kcat was determined to be 1.88 × 10−3 s−1 (See Methods and Materials). For deacetylation, kcat was measured to be 2.58 × 10−3 s−1. Since deacetylation proceeds faster than base exchange, we can infer that k3 > k4 and k4< k5 (Scheme 3). Using the assumptions k4 = kcat (base exchange), k5 = kcat (deacetylation) and Kd = Km, Cr (k4/k5) is 0.729, in fair agreement with the value obtained by curve fit of the KIE values. The curve for dependence of KIE versus nicotinamide from the Michaelis parameters is shown in Figure 1B. For correction of KIEs, we used Cr= 0.955, since it has no assumptions on k4 and k5 or Kd, and was obtained by fit of experimental data. The reaction coordinate relevant for commitment with saturating nicotinamide is shown in Figure 2A.
Figure 2.
Reaction coordinate diagram of Af2Sir2 catalyzed reactions. The irreversible step is nicotinamide-glycosidic bond breaking and making (k3 and k4). A. At saturating nicotinamide concentration, the maximum reverse commitment was found to be 0.955. B. The relevant reaction coordinate during KIE measurements. Under these conditions the average nicotinamide concentration is 40 μM, and the reverse commitment during experiment is 0.038.
To determine the effect of reverse commitment on KIE measurements, consider that 400 μM NAD+ was used with 20% consumption. Under these conditions nicotinamide concentrations average 40 μM, where the reverse commitment is 0.038 (from equation 4), considerably below the maximal value of 0.955. The reaction coordinate relevant to conditions of KIE measurement is shown in Figure 2B. Corrections to the intrinsic KIEs using this commitment value are shown in Table 1. Resulting corrections provide changes to the experimental values that are very small and were used for computational determination of the transition state structure of the nicotinamide cleavage step catalyzed by the enzyme.
Transition state determination by Gaussian and ISOEFF98
The family of KIE data obtained is in good correspondence with values previously determined for many N-ribosyltransferases, and ADP-ribosyltransferases which stabilize oxacarbenium ion-like transition states. To solve a specifically defined transition state for these KIEs, putative transition states were computationally minimized at B1LYP/6-31G** level of theory implemented in Gaussian 03, frequency sets computed, and theoretical KIEs for each putative structure computed via ISOEFF 98. Transition state structures were varied conformationally and in nucleophile and leaving group distances to match calculated and experimentally determined KIEs. Bias was given to matching the primary KIEs and the β-secondary KIEs, since these KIEs were sensitive to nucleophile and leaving group distances and the ribose ring conformation. We did not attempt to match the α-secondary KIE since it did not vary across a variety of models (See Tables 2 and 3) and it is difficult to reliably match computed and experimental α-secondary KIEs for ribosyltransfer transition states.59, 64, 68, 70
Table 3.
Calculated KIEs for asymmetric transition state models
| Asymmetric Models |
Intrinsic KIEs | |||||
|---|---|---|---|---|---|---|
| Early T.S. → Late T.S. | ||||||
| CN1′-NN1 (Å) | 2.500 | 2.650 | 2.675 | 2.600 | 2.800 | |
| CN1′-Nu (Å) | 2.800 | 2.700 | 2.650 | 2.350 | 2.350 | |
| 1N-15N | 1.026 | 1.025 | 1.025 | 1.027 | 1.028 | 1.024(2) |
| 1′N-14C | 1.047 | 1.013 | 1.012 | 1.054 | 1.040 | 1.014(4) |
| 1′N-3H | 1.453 | 1.430 | 1.427 | 1.397 | 1.418 | 1.300(3) |
| 2′N-3H | 1.093 | 1.103 | 1.105 | 1.081 | 1.107 | 1.099(5) |
| 4′N-3H | 1.001 | 1.003 | 1.003 | 0.999 | 1.002 | 0.997(2) |
| 5′N-3H | 1.037 | 1.035 | 1.035 | 1.037 | 1.037 | 1.020(5) |
| 4′N-18O | 0.998 | 0.993 | 0.993 | 0.995 | 0.995 | 0.984(5) |
Intrinsic KIEs are as reported in Table 1. Calculated KIEs are determined as described in experimental. The numbers in the first two rows are bond distances Å used in the calculation. The ring geometry is 3′-exo, as explained in text.
To calculate KIEs, a reactant reference structure and a putative transition state structure were required. We chose the X-ray crystallographically determined Li+ NAD+ structure as the reactant,71 as has been employed in previous studies of this kind. In turn, the transition state starting point was the geometry of ribonolactone72 with subsequent replacement of the anomeric carbonyl oxygen by hydrogen. The 5′-hydroxyl and 5′-carbon were matched to the X-ray crystallographically determined geometry of NAD+ bound on Af2Sir2.73 To improve computational ease, we truncated the NAD+ structure to nicotinamide riboside (NR) as used previously for solution of an ADP-ribosyltransfer transition state,60 and N-methylacetamide was used as the reacting nucleophile. For a demonstration of the reasonableness of the NR truncation, we present calculated KIEs for two isogeometric transition state structures being different only in having a 5′-OH or 5′-phosphate (See Supporting Information, Table S5).
The reactant geometry of NAD+ is 3′-endo (Figure 3 left), but upon binding to a sirtuin, the NAD+ adopts a 3′-exo ring pucker as determined by X-ray crystallography (Figure 3, middle).73 The ring conformation provides maximal hyperconjugative overlap of the 2′-position with a vacant orbital at C1′. The 10% KIE for [2′N-3H]KIE (Figure 3 right) required that the dihedral angle be close to 0 degrees (0.4 degrees) to successfully model the transition state.
Figure 3.
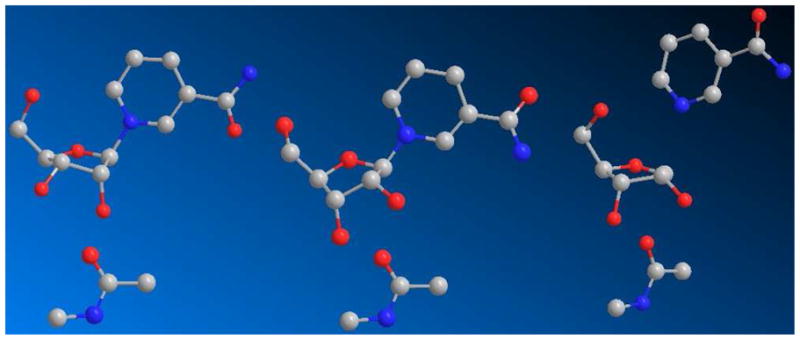
Stick-ball models of reactant (left), Michaelis complex (middle) and solved transition state (right; 2.65 Å leaving group distance, 2.65 Å nucleophile distance).
Nucleophile Associated Transition States
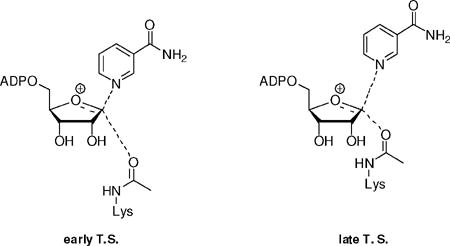
A series of calculations varying symmetrical distances (2.30 to 2.725 Å) of nicotinamide N and acetyllysine carbonyl oxygen to C1′ were performed (Table 2). Two computed KIEs were particularly sensitive to these distances, the [1′N-14C]KIE and the [2′N-3H]KIE. In a 2.3 Å symmetrical 3′-exo-transition state, consistent with a nucleophile associated mechanism, the [1′N-14C]KIE isotope effect was calculated to be 1.081, and the [2′N-3H]KIE was calculated to be 1.018. These values are inconsistent with the experimental values of 1.014(4) and 1.099(5) respectively for these KIEs.
We modeled 3′-exo transition states that were asymmetrical, with early or late character (Table 3). The 2.8 Å (LG), 2.35 Å (NU) transition state model leads to a calculated [1′N-14C]KIE of 1.040 and a calculated [2′N-3H]KIE of 1.107 outside errors for the experimental KIEs. The 2.6 Å (LG), 2.35 Å (NU) model proposed by QM/MM calculations51 provided poor matches for the [1′N-14C] KIE and [2′N-3H]KIE with calculated KIE values of 1.054 and 1.081 respectively. We conclude that transition states with less than 2.6 Å distance to the incoming acetyllysine nucleophile (symmetric or asymmetric) are not supported by our data.
Dissociated Transition States
We considered an early transition state in which dissociation of the leaving group does not occur prior to nucleophile association. This is reported in Table 3 as an asymmetric transition state, with bond distances of 2.5 Å (LG) and 2.8 Å (NU). The calculated [1′N-14C] and [2′N-3H]KIEs were 1.047 and 1.093 respectively. Although the β-secondary KIE is within error, the poor match of [1′N-14C]KIE rules out an early transition state. The fully dissociated oxacarbenium ion-like structure, where bond orders were no greater than 0.001 for both nucleophile and leaving group (3.55 Å (LG), 3.48 Å (NU)) (Table 2) provided calculated [1′-14C] and [2′-3H]KIEs values of 0.998 and 1.196 respectively. The calculated primary KIE is inverse, and the high calculated β-secondary is well above the experimental value. The experimental data set cannot be matched to a fully dissociated oxacarbenium ion.
Weak bonding participation of the nucleophile was required at the transition state to match the primary and β-secondary KIEs. We explored a range of symmetric and asymmetric possibilities as shown in Table 2 and Table 3. Our best values of bond distances were 2.65 Å (LG) and 2.65 Å (NU) at the transition state (Table 2). The slightly more dissociated transition state, 2.65 Å (LG), 2.70 Å (NU) in Table 3 also fit the primary and β-secondary KIEs, but less closely. These transition states both match the intrinsic [1-15N], [1′N-14C] and [2′N-3H]KIEs within error and have reasonable agreement with the [4′N-18O] and [4′N-3H]KIEs. The geometric structures of solution reactant, enzyme bound Michaelis complex and solved enzyme bound transition state (2.65 Å LG, 2.65 Å NU) are depicted in Figure 3.
It is instructive to examine the calculated and experimental KIE values more in detail for the transition state structure that we solved. The calculated values are shown in the asterisked row of Table 2, and the experimental values are shown in the far right row. The primary [1-15N]KIE determined experimentally was found to be 1.024(2), whereas the optimal model was calculated to be 1.025. The agreement is very good, and is consistent with a dissociated transition state structure, with 0.0199 leaving group bond order to the anomeric carbon. The primary [1′N-14C]KIE experimentally determined to be 1.014(4) was calculated to be 1.013. The low KIE for the primary carbon reflects low bond order to leaving group and poor nucleophilic participation at the transition state, with bond order of 0.016 between the anomeric carbon and the acetyl carbonyl oxygen.
The low [1′N-14C]KIE indicates compensatory bond stiffening at this atom, in spite of loss of the C1′-N1 bond, which keeps the observed value near unity. In the optimal transition state the calculated C1′-O4′ bond length is 1.265 Å (1.621 bond order, Table 4) as compared with 1.381 Å (1.101 bond order) in the reactant state. The bond order increases 0.520 at the transition state. Stiffening of the C1′-O4′ bond is also manifested in the inverse [4′N-18O]KIE, calculated to be 0.993, and experimentally determined to be 0.984(5).
Table 4.
Bond order and bond length for NAD+ reactant state and optimal transition state structure and fully dissociated oxacarbenium for reaction catalyzed by Af2Sir2
| Reactant state | Optimal transition state | Oxacarbenium ion | ||||
|---|---|---|---|---|---|---|
| Bond | Bond Length (Å) | Bond Order | Bond Length (Å) | Bond Order | Bond Length (Å) | Bond Order |
| CN1′-NN1 | 1.533 | 0.824 | 2.65 | 0.0199 | 3.550 | 0.001 |
| CN1′-ON4′ | 1.381 | 1.101 | 1.265 | 1.621 | 1.256 | 1.671 |
| CN1′-CN2′ | 1.540 | 0.954 | 1.512 | 1.048 | 1.496 | 1.105 |
| CN1′-HN1′ | 1.092 | 0.993 | 1.084 | 1.020 | 1.089 | 1.003 |
| CN2′-HN2′ | 1.099 | 0.970 | 1.112 | 0.929 | 1.110 | 0.936 |
| CN1′-Nu | 0 | 0 | 2.65 | 0.016 | 3.480 | 0.001 |
Bond lengths and bond orders are determined for optimized structure of symmetric transition state which best matches experimental intrinsic KIEs and calculated KIE values as discussed in text. Bond orders are Pauling bond orders and are calculated by methods in experimental section.
The α and β secondary KIEs are interesting in comparison to the values for the fully dissociated transition state structure. In moving from a 2.65 Å to a 3.5 Å distance for both the leaving and incoming group, the calculated [1′N-3H]KIE increases from 1.424 to 1.514 (Table 2). The calculated value for the oxacarbenium [1′N-3H]KIE is near the theoretical limit for ADPribosyltransfer. The calculated [2′N-3H]KIE for the oxacarbenium ion is 1.196 for a near perfect overlap of the C2′-H2′ bond with the C1′ p-orbital (0.4 degrees) (Table 2), again near the theoretical limit forADP-ribosyltransfer. The [2′N-3H]KIE for the 2.65 Å symmetrical structure was calculated 1.0998 in very good agreement with the experimentally determined value of 1.099(5) (Table 2).
Michaelis Complex to Transition State Progression
An overlay of the geometry of NAD+ bound to Af2Sir273 (truncated to NR) with the determined transition state is shown in Figure 4. This overlay, which assumes nicotinamide N position is virtually unchanged at the transition state is consistent with “nucleophilic displacement by electrophilic migration”, as suggested by recent structural studies.52 The reactant acetyl oxygen at 3.6 Å to the reactant NAD+ C1′, is in fair agreement with the distance of of 3.2 Å reported in the NAD+-acetyllysine termolecular structure of Thermatoga maritime Sir2.74 These superpositions, with the assumption that the leaving group N and acetyl O positions remain largely fixed, as proposed for nucleophilic displacement by electrophilic migration52, 75 indicates that the sugar anomeric carbon progresses 1.1 Å translationally to form the transition state structure. The sugar translates 1.14 Å from the transition state to the imidate complex with a C1′-O bond distance computed to be 1.510 Å.51 The total motion of the sugar ring from reactants to products is 2.24 Å. Interestingly, the 2′-OH migrates 1.8 Å from the NAD+ acetyllysine complex to the thio-imidate on TmSir2.52 The ribose ring movement reduces the bond angle of the nicotinamide N to the ribose ring so that the N1 atom remains in optimal electronic overlap with the developing p-orbital at the transition state.
Figure 4.
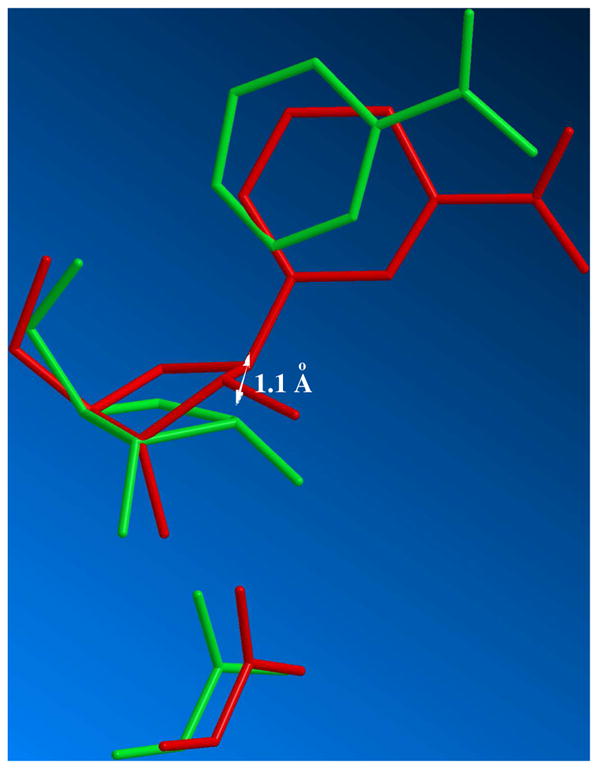
Overlay of structures of Michaelis complex structure determined from crystallography (red) and solved transition state (green; 2.65 Å leaving group distance, 2.65 Å nucleophile distance). The structures are overlaid with pyridine N-position largely unchanged. The proposed displacement of sugar anomeric carbon is determined to be 1.1 Å from the reactant C1′ position. The reactant acetyllysine oxygen was placed 3.6 Å from the anomeric carbon of the reactant.
The sugar translation process causes the C2′-H2′ bond, initially predicted to be −33.8 degrees in dihedral angle to the N1-C1′ bond in the reactant complex, to narrow to 0.4 degrees at the transition state (Figure 5). This provides essentially maximal hyperconjugative overlap of the C2′-H2′ bond with the largely vacant p-orbital at the anomeric carbon in the transition state, and explains the large β-secondary KIE. The initial 3′-exo reactant ring geometry of NAD+ in the reactant complex determined crystallographically73, 74 leads naturally to the solved transition state geometry with ring flattening and anomeric carbon translation.
Figure 5.
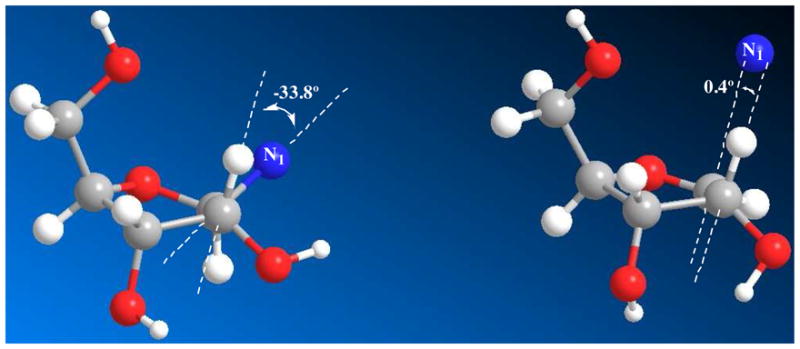
Left: 3′-exo conformation of enzyme-bound reactant state, the N1-C1′-C2′-H2′ dihedral angle is −33.8°; right: 3′-exo conformation of the transition state, the p-orbital-C1′-C2′-H2′ dihedral angle is 0.4°.
Electrostatic Features of the Reactants and Transition State
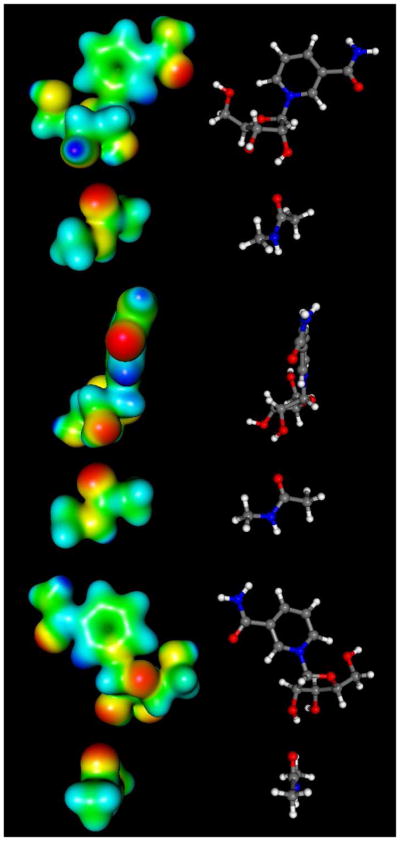
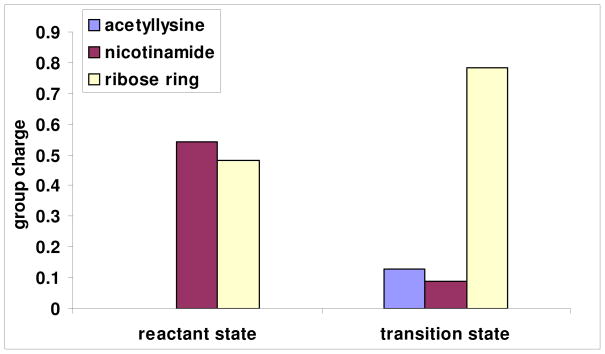
To visualize electronic changes that occur in the reactant as it reaches the transition state we calculated the electrostatic surfaces of reactant and transition state complexes (Figure 6 and 7 respectively) using Gaussian 03. In the reactant, H2, H6 and C2 of the nicotinamide ring bear significant positive charge density prior to reaction. These charges are calculated to be 0.215, 0.218 and 0.189 respectively (See Supporting Information for Table of calculated Mulliken charges for reactant and transition state structures). These charges largely account for the 0.541 charge on the pyridinium ring prior to reaction (Figure 8). The ribose ring also has positive charge density in the reactant state (See Supporting Information), totaling 0.483 charge (Figure 8). The calculations of charge distribution are in agreement with values determined for the pyridinium and ribose ring in a prior computational study.51
Figure 6.
Molecular electrostatic potential surfaces of NAD+ reactant state (front top, side middle and back bottom).
Figure 7.
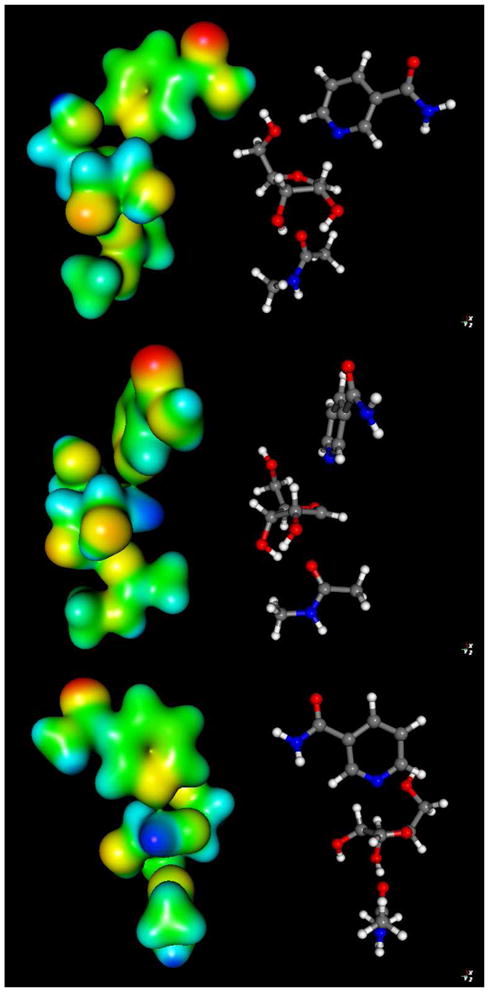
Molecular electrostatic potential surfaces of transition state with 2.65 Å leaving group distance, 2.65 Å nucleophile distance (front top, side middle and back bottom). The transition state was determined in vacuo using the hybrid density functional methods implemented in Gaussian 03 using the B1LYP functional and 6-31G** basis set. The CUBE subprogram of Gaussian 03 was used to generate molecular electrostatic potential (MEP) surfaces, which are visualized using Molekel 5.4.
Figure 8.
Computed group partial charges of acetyllysine, nicotinamide and ribose ring for reactant and transition state.
At the transition state the nicotinamide is nearly neutral (Figure 7). The net charge on the pyridine ring at the transition state is reduced to 0.089 charge (Figure 8), a net charge loss of 0.452. The ribose ring gains charge, so that the total charge is 0.782 charge units at the transition state (Figure 8). The net increase in charge on ribose in going from reactant to transition state is 0.298. The greatest increase of charge occurs on the O4′ atom (increase of 0.168), followed by the H2′, which increases 0.085.
Interestingly, the group charge on the acetyllysine increases from fully neutral at the reactant state to 0.129 at the transition state, even though only 0.016 bond order is calculated for the transition state structure. Inspection of the atomic charges reveals increased negative charge on the carbonyl oxygen (−0.518 in the reactant to −0.599 at the transition state). The charge on the nucleophile indicates a potent effect of the ribose cation on charge distributions on the acetyllysine, even at weak bonding. Increased partial positive charge density on the alpha-hydrogens, amide N, amide H and on N-methyl hydrogens also results (See Supporting Information). A similar charge transfer effect was seen by Hu et al. in the calculation of the 2.6 Å (LG distance), 2.35 Å (NU distance) transition state model, where the bond order was reported to be 0.15 at the transition state, the acetyllysine charge was found to be approximately 0.15.51
Energies and Charge Distributions for Oxacarbenium and Trifluoroacetyl Complexes
The finding that KIEs and calculation determine a weakly bonded oxacarbenium ion-like transition state was very different from interpretations of Smith and Denu,50 where very low rates of turnover with fluorinated acetyllysine derivatives led these authors to propose significant nucleophilic participation in the nicotinamide cleavage transition state. We were interested to understand how a weakly dissociated oxacarbenium-like transition state could be consistent with both data sets. Therefore, we calculated the thermochemical energies in vacuo of the solved transition state structure, a fully dissociated oxacarbenium ion (3.55 Å C1′-LG distance, 3.48 Å C1′-NU distance), and an isogeometric structure to the solved transition state (2.65 Å symmetric) with N-methyltrifluoro-acetamide (See Supporting information Figure S4 for structures). The solved transition state structure relative to reactants was 21.05 kcal/mol, but the fully dissociated oxacarbenium was 25.88 kcal/mol. Thus, calculations confirm that the weakly-bonded transition state is intrinsically stabilized relative to the fully dissociated oxacarbenium.
Mulliken charges for the fully dissociated oxacarbenium ion (See Supporting Information for full charge tables) revealed that the N-methylacetamide nucleophile bears a net charge of 0.094. However, the charge on the fully dissociated ribosyl cation is increased to 0.885 from 0.782 in the oxacarbenium ion-like transition state. The weakly-bonded transition state has increased charge distribution to nicotinamide (Charge on group: Oxacarbenium: 0.0207 TS: 0.0891) and N-methylacetamide (Charge on group: Oxacarbenium: 0.0938, TS:0.129) which could provide some energetic stabilization.
The calculations with the trifluorogroup were consistent with experimental observations showing it reacts very slowly.50 The calculated energy of the trifluoro structure was determined to be 25.17 kcal/mol, destabilized 4.12 kcal/mol versus the isosteric N-methylacetamide structure. The energy accounts for half needed to explain the 670000 fold slower reaction of the trifluoroacetyllysine versus the unsubstituted acetyllysine,50 although our calculations explicitly ignore enzyme and solvent effects. The slow rate could imply poor charge transfer from the weaker nucleophile to the oxacarbenium ion. However, surprisingly, the charge on the N-methyl-trifluoroacetamide was determined to be 0.121 charge units. Moreover the charges on nicotinamide and sugar were 0.0918 and 0.787, very close to the observed charges for the solved transition state with unsubstituted N-methylacetamide. Thus, the charge distribution per se does not define the energy of the complex. We suspect that the interaction of the trifluoro-nucleophile, which the calculation indicates can still redistribute charge, is not stabilizing, since the fully dissociated oxacarbenium ion and the trifluoro-complex are only 0.71 kcal/mol different in energy.
This result sets up the following scenario, proposed by Jencks, for weak nucleophiles.76 He suggested that when a strong nucleophile undergoes a substitution reaction at a reactive sugar anomeric carbon, the reaction is more able to proceed via a concerted mechanism.76 If the nucleophile is sufficiently weakened, the reaction cannot be stabilized through pre-association (even in an “exploded” or highly dissociated transition state), and thereby becomes stepwise. The results here can be interpreted in this manner. For sirtuin chemistry, the acetyllysine nucleophile preassociates in the substitution mechanism to the extent of 0.016 bond order, with the leaving group still associated to the extent of 0.019 bond order. The reaction mechanism, is a concerted one, although highly asynchronous, since the leaving group is largely departed before the nucleophile bond forms. The concerted mechanism of this type is highly energetically favorable relative to the stepwise mechanism, as shown by our energy calculations. However, when the sirtuin nucleophile is switched to trifluoroacetyllysine, the calculations suggest a much higher transition state barrier with little energetic benefit gained from nucleophile pre-association. In fact there is little energy difference between the preassociated structure versus the dissociated oxacarbenium ion as predicted by the Jencks argument. This result implies that the trifluoroacetyllysine nucleophile could react via a stepwise substitution reaction.
A change to a stepwise mechanism opens the reaction coordinate for alternative reaction outcomes. For example, there is a highly conserved Phe residue that sits just over the ribose oxygen, which could intercept the oxacarbenium to form a cation-π complex,52 rather than allowing ribosylation to the trifluoroacetyl nucleophile. Since the nicotinamide is still the best nucleophile in a competitive attack on the oxacarbenium ion, the nicotinamide could rebound onto the oxacarbenium before delivery to the trifluoroacetyllysine ever occurred. Such “internal return” could provide additional rate slowing, which in combination with a much higher barrier to nicotinamide bond cleavage as calculated (in vacuo 4.12 kcal/mol) could account for the majority of the 670000 fold rate decrease observed for trifluoro-substitution. Importantly, almost none of the rate difference is attributable to a mechanism requiring significant preassociation of the nucleophile, as has been suggested.50 There is the additional possibility that a smaller part of the rate difference arises from non-optimal binding of trifluoroacetyllysine to the active site.
Related work has been done in the reactions of β-N-acetylglucosaminidases,77 which process substrates bearing 2-acetamide modifications. Fluorine substitution on the acetyl group causes significant rate deceleration, but not in each case.78, 79 Recent work has suggested that some of the rate deceleration observed for α-fluoro-substitution to the 2-acetamido-group could be attributable to increased positive charge on the pyranose ring at the transition state.79 That does not appear to be the case here. A weaker nucleophile delivers similar charge transfer to the sugar species as compared with a stronger nucleophile in an iso-geometric structure, but with appreciably less overall stabilization.
4. Summary
The transition state structure of Af2Sir2 has been solved by KIE and computational methods and the solved transition state structure shows that Af2Sir2 stabilizes an oxacarbenium ion-like structure in the initial ADP-ribosylation of acetyllysine of proteins with weak bond orders to nucleophile and leaving group. The result is inconsistent with mechanistic proposals invoking significant nucleophilic participation (as measured by bond order) at the transition state. The factors on the enzyme that stabilize an oxacarbenium-like transition state are currently poorly understood.74 Nevertheless the weak acetyllysine and nicotinamide association to the oxacarbenium structure provides a significant energetic stabilization relative to a fully dissociated oxacarbenium ion. Computational studies provided insight into the origins of significant rate decelerations observed for fluoro-substituted acetyllysine nucleophiles. Characterization of other transition states within this family of enzymes is expected to determine how widely conserved the transition state structures are, and how much they can differ on sirtuins from different sources. We suspect, given the high sequence conservation of these enzymes, that sirtuins generally react highly-dissociated oxacarbenium ion-like transition state structures to ribosylate acetyllysine residues to form nicotinamide and the ADP-ribosylpeptidylimidate. It is anticipated that these transition state structures can be used as blueprints for inhibitor design.
Supplementary Material
Acknowledgments
This work was supported by NIH grant R01 DK073466-5 to AAS. The authors thank Piotr Paneth for providing ISOEFF 98 and for a modification to enable the software to work with Gaussian 03 outputs.
Footnotes
Supporting Information Available. Syntheses of materials, calculations of KIEs and Atomic charges of reactants and transitions states. Complete references 35, 36 and 61 are available. This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Sauve AA, Wolberger C, Schramm VL, Boeke JD. Annu Rev Biochem. 2006;75:435–465. doi: 10.1146/annurev.biochem.74.082803.133500. [DOI] [PubMed] [Google Scholar]
- 2.Blander G, Guarente L. Annu Rev Biochem. 2004;73:417–435. doi: 10.1146/annurev.biochem.73.011303.073651. [DOI] [PubMed] [Google Scholar]
- 3.French JB, Cen Y, Sauve AA. Biochemistry. 2008;47:10227–10239. doi: 10.1021/bi800767t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Merrick CJ, Duraisingh MT. Eukaryot Cell. 2007;6:2081–2091. doi: 10.1128/EC.00114-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Du J, Jiang H, Lin H. Biochemistry. 2009;48:2878–2890. doi: 10.1021/bi802093g. [DOI] [PubMed] [Google Scholar]
- 6.Haigis MC, Mostoslavsky R, Haigis KM, Fahie K, Christodoulou DC, Murphy AJ, Valenzuela DM, Yancopoulos GD, Karow M, Blander G, Wolberger C, Prolla TA, Weindruch R, Alt FW, Guarente L. Cell. 2006;126:941–954. doi: 10.1016/j.cell.2006.06.057. [DOI] [PubMed] [Google Scholar]
- 7.Kowieski TM, Lee S, Denu JM. J Biol Chem. 2008;283:5317–5326. doi: 10.1074/jbc.M707613200. [DOI] [PubMed] [Google Scholar]
- 8.Garcia-Salcedo JA, Gijon P, Nolan DP, Tebabi P, Pays E. Embo J. 2003;22:5851–5862. doi: 10.1093/emboj/cdg553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Haigis MC, Guarente LP. Genes Dev. 2006;20:2913–2921. doi: 10.1101/gad.1467506. [DOI] [PubMed] [Google Scholar]
- 10.Guarente L, Picard F. Cell. 2005;120:473–482. doi: 10.1016/j.cell.2005.01.029. [DOI] [PubMed] [Google Scholar]
- 11.Yang T, Fu M, Pestell R, Sauve AA. Trends Endocrinol Metab. 2006;17:186–191. doi: 10.1016/j.tem.2006.04.002. [DOI] [PubMed] [Google Scholar]
- 12.Lin SJ, Defossez PA, Guarente L. Science. 2000;289:2126–2128. doi: 10.1126/science.289.5487.2126. [DOI] [PubMed] [Google Scholar]
- 13.Tissenbaum HA, Guarente L. Nature. 2001;410:227–230. doi: 10.1038/35065638. [DOI] [PubMed] [Google Scholar]
- 14.Rogina B, Helfand SL. Proc Natl Acad Sci U S A. 2004;101:15998–16003. doi: 10.1073/pnas.0404184101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Dali-Youcef N, Lagouge M, Froelich S, Koehl C, Schoonjans K, Auwerx J. Ann Med. 2007;39:335–345. doi: 10.1080/07853890701408194. [DOI] [PubMed] [Google Scholar]
- 16.Picard F, Kurtev M, Chung N, Topark-Ngarm A, Senawong T, Machado De Oliveira R, Leid M, McBurney MW, Guarente L. Nature. 2004;429:771–776. doi: 10.1038/nature02583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Luo J, Nikolaev AY, Imai S, Chen D, Su F, Shiloh A, Guarente L, Gu W. Cell. 2001;107:137–148. doi: 10.1016/s0092-8674(01)00524-4. [DOI] [PubMed] [Google Scholar]
- 18.Vaziri H, Dessain SK, Ng Eaton E, Imai SI, Frye RA, Pandita TK, Guarente L, Weinberg RA. Cell. 2001;107:149–159. doi: 10.1016/s0092-8674(01)00527-x. [DOI] [PubMed] [Google Scholar]
- 19.Yamakuchi M, Ferlito M, Lowenstein CJ. Proc Natl Acad Sci U S A. 2008;105:13421–13426. doi: 10.1073/pnas.0801613105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Firestein R, Blander G, Michan S, Oberdoerffer P, Ogino S, Campbell J, Bhimavarapu A, Luikenhuis S, de Cabo R, Fuchs C, Hahn WC, Guarente LP, Sinclair DA. PLoS ONE. 2008;3:e2020. doi: 10.1371/journal.pone.0002020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Moynihan KA, Grimm AA, Plueger MM, Bernal-Mizrachi E, Ford E, Cras-Meneur C, Permutt MA, Imai S. Cell Metab. 2005;2:105–117. doi: 10.1016/j.cmet.2005.07.001. [DOI] [PubMed] [Google Scholar]
- 22.Bordone L, Motta MC, Picard F, Robinson A, Jhala US, Apfeld J, McDonagh T, Lemieux M, McBurney M, Szilvasi A, Easlon EJ, Lin SJ, Guarente L. PLoS Biol. 2006;4:e31. doi: 10.1371/journal.pbio.0040031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Liu Y, Dentin R, Chen D, Hedrick S, Ravnskjaer K, Schenk S, Milne J, Meyers DJ, Cole P, Yates J, 3rd, Olefsky J, Guarente L, Montminy M. Nature. 2008;456:269–273. doi: 10.1038/nature07349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Rodgers JT, Lerin C, Haas W, Gygi SP, Spiegelman BM, Puigserver P. Nature. 2005;434:113–118. doi: 10.1038/nature03354. [DOI] [PubMed] [Google Scholar]
- 25.Rodgers JT, Lerin C, Gerhart-Hines Z, Puigserver P. FEBS Lett. 2008;582:46–53. doi: 10.1016/j.febslet.2007.11.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Gerhart-Hines Z, Rodgers JT, Bare O, Lerin C, Kim SH, Mostoslavsky R, Alt FW, Wu Z, Puigserver P. Embo J. 2007;26:1913–1923. doi: 10.1038/sj.emboj.7601633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Wang RH, Sengupta K, Li C, Kim HS, Cao L, Xiao C, Kim S, Xu X, Zheng Y, Chilton B, Jia R, Zheng ZM, Appella E, Wang XW, Ried T, Deng CX. Cancer Cell. 2008;14(4):312–323. doi: 10.1016/j.ccr.2008.09.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.O’Hagan HM, Mohammad HP, Baylin SB. PLoS Genet. 2008;4:e1000155. doi: 10.1371/journal.pgen.1000155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Mostoslavsky R. Front Biosci. 2008;13:6966–6990. doi: 10.2741/3203. [DOI] [PubMed] [Google Scholar]
- 30.Chua KF, Mostoslavsky R, Lombard DB, Pang WW, Saito S, Franco S, Kaushal D, Cheng HL, Fischer MR, Stokes N, Murphy MM, Appella E, Alt FW. Cell Metab. 2005;2:67–76. doi: 10.1016/j.cmet.2005.06.007. [DOI] [PubMed] [Google Scholar]
- 31.Mantel C, Broxmeyer HE. Curr Opin Hematol. 2008;15:326–331. doi: 10.1097/MOH.0b013e3283043819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Brooks CL, Gu W. Nat Rev Cancer. 2009;9:123–128. doi: 10.1038/nrc2562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Smith BC, Hallows WC, Denu JM. Chem Biol. 2008;15:1002–1013. doi: 10.1016/j.chembiol.2008.09.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Jiang WJ. Biochem Biophys Res Commun. 2008;373:341–344. doi: 10.1016/j.bbrc.2008.06.048. [DOI] [PubMed] [Google Scholar]
- 35.Milne JC, Lambert PD, Schenk S, Carney DP, Smith JJ, Gagne DJ, Jin L, Boss O, Perni RB, Vu CB, Bemis JE, Xie R, Disch JS, Ng PY, Nunes JJ, Lynch AV, Yang H. Nature. 2007;450:712–716. doi: 10.1038/nature06261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Lara E, Mai A, Calvanese V, Altucci L, Lopez-Nieva P, Martinez-Chantar ML, Varela-Rey M, Rotili D, Nebbioso A, Ropero S, Montoya G, Oyarzabal J, Velasco S, Serrano M, Witt M, Villar-Garea A. Oncogene. 2009;28:781–791. doi: 10.1038/onc.2008.436. [DOI] [PubMed] [Google Scholar]
- 37.Sauve AA. Curr Pharm Des. 2009;15:45–56. doi: 10.2174/138161209787185797. [DOI] [PubMed] [Google Scholar]
- 38.Denu JM. Trends Biochem Sci. 2005;30:479–483. doi: 10.1016/j.tibs.2005.07.004. [DOI] [PubMed] [Google Scholar]
- 39.Jackson MD, Schmidt MT, Oppenheimer NJ, Denu JM. J Biol Chem. 2003;278:50985–50998. doi: 10.1074/jbc.M306552200. [DOI] [PubMed] [Google Scholar]
- 40.Sauve AA, Schramm VL. Biochemistry. 2003;42:9249–9256. doi: 10.1021/bi034959l. [DOI] [PubMed] [Google Scholar]
- 41.Sauve AA, Celic I, Avalos J, Deng H, Boeke JD, Schramm VL. Biochemistry. 2001;40:15456–15463. doi: 10.1021/bi011858j. [DOI] [PubMed] [Google Scholar]
- 42.Jackson MD, Denu JM. J Biol Chem. 2002;277:18535–18544. doi: 10.1074/jbc.M200671200. [DOI] [PubMed] [Google Scholar]
- 43.Sauve AA, Schramm VL. Curr Med Chem. 2004;11:807–826. doi: 10.2174/0929867043455675. [DOI] [PubMed] [Google Scholar]
- 44.Scheuring J, Schramm VL. Biochemistry. 1997;36:8215–8223. doi: 10.1021/bi970379a. [DOI] [PubMed] [Google Scholar]
- 45.Scheuring J, Schramm VL. Biochemistry. 1997;36:4526–4534. doi: 10.1021/bi962841h. [DOI] [PubMed] [Google Scholar]
- 46.Berti PJ, Blanke SR, Schramm VL. J Am Chem Soc. 1997;119:12079–12088. doi: 10.1021/ja971317a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Parikh SL, Schramm VL. Biochemistry. 2004;43:1204–1212. doi: 10.1021/bi035907z. [DOI] [PubMed] [Google Scholar]
- 48.Berti PJ, Schramm VL. J Am Chem Soc. 1997;119:12069–12078. doi: 10.1021/ja971317a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Min J, Landry J, Sternglanz R, Xu RM. Cell. 2001;105:269–279. doi: 10.1016/s0092-8674(01)00317-8. [DOI] [PubMed] [Google Scholar]
- 50.Smith BC, Denu JM. J Am Chem Soc. 2007;129:5802–5803. doi: 10.1021/ja070162w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Hu P, Wang S, Zhang Y. J Am Chem Soc. 2008;130:16721–16728. doi: 10.1021/ja807269j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Hawse WF, Hoff KG, Fatkins DG, Daines A, Zubkova OV, Schramm VL, Zheng W, Wolberger C. Structure. 2008;16:1368–1377. doi: 10.1016/j.str.2008.05.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Schramm VL. J Biol Chem. 2007;282:28297–28300. doi: 10.1074/jbc.R700018200. [DOI] [PubMed] [Google Scholar]
- 54.Schramm VL. Arch Biochem Biophys. 2005;433:13–26. doi: 10.1016/j.abb.2004.08.035. [DOI] [PubMed] [Google Scholar]
- 55.Birck MR, Schramm VL. J Am Chem Soc. 2004;126:2447–2453. doi: 10.1021/ja039260h. [DOI] [PubMed] [Google Scholar]
- 56.Avalos JL, Celic I, Muhammad S, Cosgrove MS, Boeke JD, Wolberger C. Mol Cell. 2002;10:523–535. doi: 10.1016/s1097-2765(02)00628-7. [DOI] [PubMed] [Google Scholar]
- 57.Rising KA, Schramm VL. J Am Chem Soc. 1994;116:6531–6536. [Google Scholar]
- 58.Munshi C, Lee HC. Protein Expr Purif. 1997;11:104–110. doi: 10.1006/prep.1997.0773. [DOI] [PubMed] [Google Scholar]
- 59.Chen XY, Berti PJ, Schramm VL. J Am Chem Soc. 2000;122:1609–1617. [Google Scholar]
- 60.Rising KA, Schramm VL. J Am Chem Soc. 1997;119:27–37. [Google Scholar]
- 61.Frisch MJ. Gaussian 03, Revision E.01. Gaussian, Inc; Wallingford, CT: 2004. [Google Scholar]
- 62.Anisimov V, Paneth P. J Math Chem. 1999;26:75–86. [Google Scholar]
- 63.Varetto U. MOLEKEL Version. Swiss National Supercomputing Centre; Manno (Switzerland): [Google Scholar]
- 64.Singh V, Schramm VL. J Am Chem Soc. 2006;128:14691–14696. doi: 10.1021/ja065419p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Lewandowicz A, Schramm VL. Biochemistry. 2004;43:1458–1468. doi: 10.1021/bi0359123. [DOI] [PubMed] [Google Scholar]
- 66.Sunko DE, Szele I, Hehre WJ. J Am Chem Soc. 1977;99:5000–5005. [Google Scholar]
- 67.Cook PF. Enzyme Mechanisms from Isotope Effects. CRC Press; Boca Raton: 1991. [Google Scholar]
- 68.Singh V, Schramm VL. J Am Chem Soc. 2007;129(10):2783–2795. doi: 10.1021/ja065082r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Defrees DJ, Hehre WJ, Sunko DE. J Am Chem Soc. 1979;101:2323–2327. [Google Scholar]
- 70.Scheuring J, Berti PJ, Schramm VL. Biochemistry. 1998;37:2748–2758. doi: 10.1021/bi972594x. [DOI] [PubMed] [Google Scholar]
- 71.Reddy BS, Saenger W, Muhlegger K, Weimann G. J Am Chem Soc. 1981;103:907–914. [Google Scholar]
- 72.Kinoshita Y, Ruble JR, Jeffrey GA. Carbohydr Res. 1981;92:1–7. [Google Scholar]
- 73.Avalos JL, Bever KM, Wolberger C. Mol Cell. 2005;17:855–868. doi: 10.1016/j.molcel.2005.02.022. [DOI] [PubMed] [Google Scholar]
- 74.Hoff KG, Avalos JL, Sens K, Wolberger C. Structure. 2006;14:1231–1240. doi: 10.1016/j.str.2006.06.006. [DOI] [PubMed] [Google Scholar]
- 75.Fedorov A, Shi W, Kicska G, Fedorov E, Tyler PC, Furneaux RH, Hanson JC, Gainsford GJ, Larese JZ, Schramm VL, Almo SC. Biochemistry. 2001;40:853–860. doi: 10.1021/bi002499f. [DOI] [PubMed] [Google Scholar]
- 76.Banait NS, Jencks WP. J Am Chem Soc. 1991;113:7951–7958. [Google Scholar]
- 77.Lairson LL, Henrissat B, Davies GJ, Withers SG. Annu Rev Biochem. 2008;77:521–555. doi: 10.1146/annurev.biochem.76.061005.092322. [DOI] [PubMed] [Google Scholar]
- 78.Vocadlo DJ, Withers SG. Biochemistry. 2005;44:12809–12818. doi: 10.1021/bi051121k. [DOI] [PubMed] [Google Scholar]
- 79.Greig IA, McCauley MS, Williams IH, Vocadlo DJ. J Am Chem Soc. 2009;131:13415–13422. doi: 10.1021/ja904506u. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.