Abstract
We have built a digital nuclear atlas of the newly hatched, first larval stage (L1) of the wild type hermaphrodite of C. elegans at single cell resolution from confocal image stacks of 15 individuals. The atlas quantifies the stereotypy of the locations and provides for other statistics on the spatial patterns of the 357 nuclei that could be faithfully segmented and annotated of the 558 present at this developmental stage. Given this atlas we then developed an automated approach to assign cell names to each nucleus in a 3D image of an L1 worm. We achieve 86% accuracy in identifying the 357 nuclei automatically. This computational method is essential for high-throughput single cell analyses of the worm at post-embryonic stages, such as determining the expression of every gene in every cell during development from the L1 onward, or ablating or stimulating cells under computer control in a high-throughput functional screen.
INTRODUCTION
Despite the detailed knowledge of the anatomy of the nematode C. elegans1, as well as its determined cell lineage3, the mapped connectivity of its nervous system4–5, and the sequenced genome6–7, we still lack a three dimensional (3D) digital atlas of nuclei positions in any postembryonic stage. Such an atlas has several significant applications. First, it provides us with quantitative knowledge not previously available about the degree of stereotypy of nuclei positions and the details of specific spatial relationships between different cells. Second, the atlas can serve as a standard template so that we can compare any 3D image of a wild-type C. elegans against the atlas and extract the identities of individual nuclei using an automated approach. This is essential for high-throughput analysis of cellular information such as gene expression at single cell resolution. Such an analysis provides much richer information than does analysis of expression data from a DNA microarray experiment8–9, since DNA microarrays reveal average expression from the samples of tissue or entire individual, but not the expression of individual cell.
Prior to this study, the anatomy of C. elegans has been described qualitatively by images with a text description or 2D sketches10. Such sketches and descriptions do not provide a quantitative description of cell nuclei positions nor do they provide statistical information about the variance in cell nuclei positions and spatial relationships between individuals. Early efforts using electron microscopy (EM) have resulted in detailed views of the anatomy10 and even a connectivity graph of the nervous system4–5, but to date an automated or even manual segmentation of the fine structure of such an ultra high-resolution image stack has not taken place. While one might contemplate expending an enormous amount of manual effort to do so on a single individual worm, doing so for enough worms to deliver statistical information on the location of nuclei is effectively impractical.
The method for automatically analyzing individual cells in post-embryonic worms in this paper complements the similar capability developed by Bao et al.11 for the embryo from a single cell to the point where the muscles become enervated after the 350 cell stage. However, the computational problem is completely different. Their method consists of tracking nuclei as they divide in-vivo using the cell lineage information that is already known, whereas our method identifies nuclei in-situ without the help of temporal or lineage information. But while the underlying computations share little overlap, the two capabilities offer the same possibility for medium to high-throughput analysis at single cell resolution at two different phases in a worm’s life cycle. Similar to the proof of concept provided by Murray et al. 12 where they use their embryonic cell tracking technology to measure gene expression, one can immediately see that in principle our method allows for the same capability in the L1. Moreover, the computational method we describe is general and can be applied to a wide range of stereotypic systems, such as other post-embryonic worm stages and the fruit fly embryonic nervous system13.
The paper presents the method of building the atlas first, followed by several analyses of the model that confirm that it is well constructed and recapitulates known biology. Then we describe our automated approach on annotating cell identities in new L1 worm images using the atlas information and demonstrate its accuracy.
RESULTS
Building a 3D digital atlas
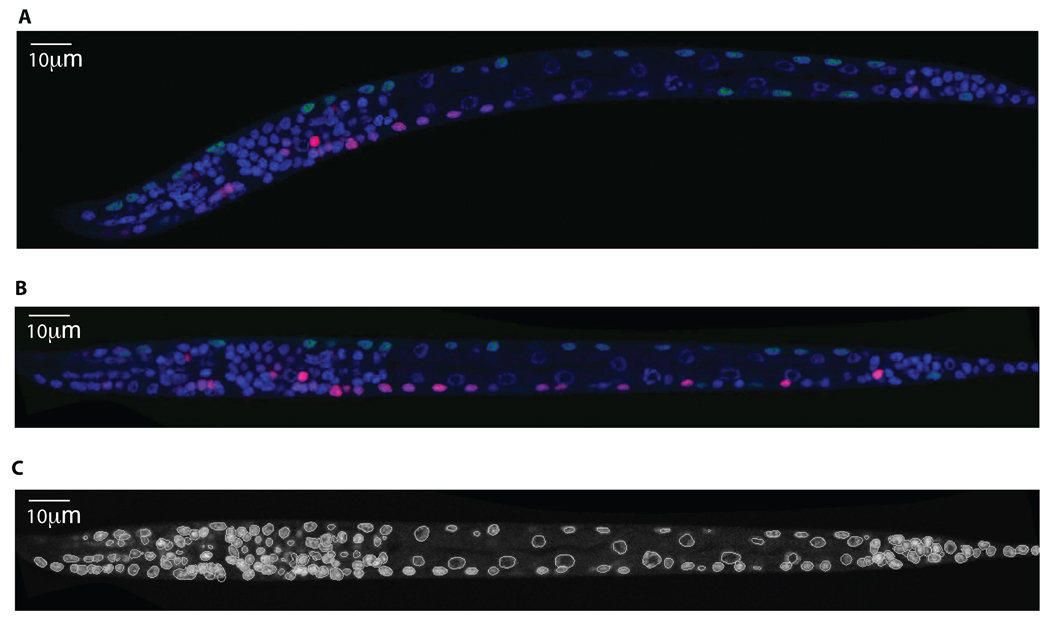
Three-dimensional images of C. elegans at the L1 stage were collected in 3 fluorescent channels. We used DAPI to stain the nuclei of all 558 cells. We used a myo-3:GFP transgene to label the nuclei of the 81 body wall muscle cells and 1 depressor muscle cell. These nuclei serve as fiducial markers that are used by our manual and automated approach to annotate cells. We used mCherry driven by a promoter from a gene of interest to reveal expression in a set of target cells. Three-dimensional images were acquired using a Leica confocal microscope (Fig. 1a) with 63× oil lens and X–Y and Z sampling set at 0.116 µm and 0.122 µm per pixel respectively.
Figure 1.
Automatic processing of a 3D image of C.elegans. (a) A 2D slice of a 3D image. DAPI (blue) is used to stain nuclei of all the 558 cells; Pmyo-3::NLS::GFP (green) is used to stain nuclei of the 81 body wall muscle cells and 1 depressor cell; mCherry (red) is used to stain nuclei of the cells that express gene of interest, in this example, some ventral motor neurons and neurons in the nerve ring. (b) The same 2D slice after worm body straightening. (c) The segmentation result of the DAPI channel of same 3D image, with the same 2D slice shown in A.
As briefly as possible we describe the sequence of computational processes and associated algorithms that are used to produce the atlas. For the reader desiring more details, earlier technical work appearing in the computing algorithms literature is cited below and summarized in Supplementary Methods.
To build a standard digital atlas, we first computationally straightened the curved worm body in the 3D image into a rod shape14 (Fig. 1b, Supplementary Fig. 1 and Video 1). The method first detects the principal curve or “backbone” that represents the anterior/posterior (A/P) line that passes from head to tail through the center of a straightened worm (Supplementary Fig. 1b). It then generates a series of 1-pixel separated planes orthogonal to the backbone and restacks them along a straight A/P line, making them parallel to each other (Supplementary Fig. 1c). Because each local transform is a rigid rotation, the resolution of the straightened image is merely a function of the sub-pixel interpolation error when a straight line is rotated in space. Thus, the overall resolution loss is naturally minimized.
We next developed an automatic approach to segment each individual nucleus in the 3D image of the straightened worm (Fig. 1c and Supplementary Fig. 2). More specifically, our method first applies 3D median filtering (3 × 3 × 3 pixels) followed by Gaussian filtering (σ = 1) to reduce noise so that the intensity distributions within nuclear regions become less variable. It then fills any intensity holes in the nuclei, which are typically nucleoli that are unstained by DAPI (Supplementary Fig. 2b). Next, it uses adaptive thresholding to detect local background levels, generating a location-dependent foreground mask of nuclei or clusters of nuclei. After that, it applies the distance transform which computes the distance of a foreground pixel from the nearest background pixel, converting the binary foreground mask into a gradient image. An initial segmentation of nuclei is then generated from the gradient image using the 3D watershed algorithm15–16 (Supplementary Fig. 2d). Finally, to handle the small number of over- and under-segmented regions, we developed both rule-based and training-based methods to do region merging/splitting. The rule-based method uses the statistical information of the segmented regions to predict regions of wrong segmentation and then uses rules defined on shape, size, and intensity of typical nuclei regions to do region merging/splitting. The training-based method trains an SVM classifier17–18 using the intensity, size, and shape of nuclei to determine if a region should be further split or merged. Splitting and merging of regions are iterated until the classifier predicts that further merging or splitting of a given region is unwarranted (Supplementary Figs. 2e and 2f). Overall, training-based approach produces slightly better results.
The segmented nuclei were then manually validated, corrected, and annotated with cell name conventions of the C. elegans community. For this purpose, we developed a 3D annotation and visualization tool called VANO19 (a Volume-object image ANnOtation system; Supplementary Fig. 3) that permits one to edit any observed errors in the segmentation and to enter a name for every segmented region/nuclei. Our manual annotation is based on the morphology and relative spatial positions of cells (http://www.wormatlas.org)10 (see Methods and Supplementary Methods for details). Since GFP was used to highlight the 81 body wall muscle cells and 1 depressor cell in a separate channel, these nuclei are annotated first. We then used these muscle cells as fiducial markers to identify additional nuclei whose spatial relationships with respect to these markers are stable. The newly annotated nuclei were added to the maker set and we repeated this process. By doing so, we were able to manually annotate approximately 357 nuclei in each image with high confidence.
Individual C. elegans images differ in size and orientation, therefore the final step is to register or map all of the stacks into the same canonical space so that their nuclei positions are comparable. For this purpose, we computed the “median” or “centroid” of the collection of K stacks, say C, for which the sum of the squared differences of the 357 or so nuclei centers between C and every other stack is minimal. We then used it as the reference stack to map every other stack to it via an affine transform. The final atlas is the ensemble of the transformed nuclei positions for each named nuclei in the coordinate system of the reference stack (Supplementary Video 2).
Statistical analysis of the atlas
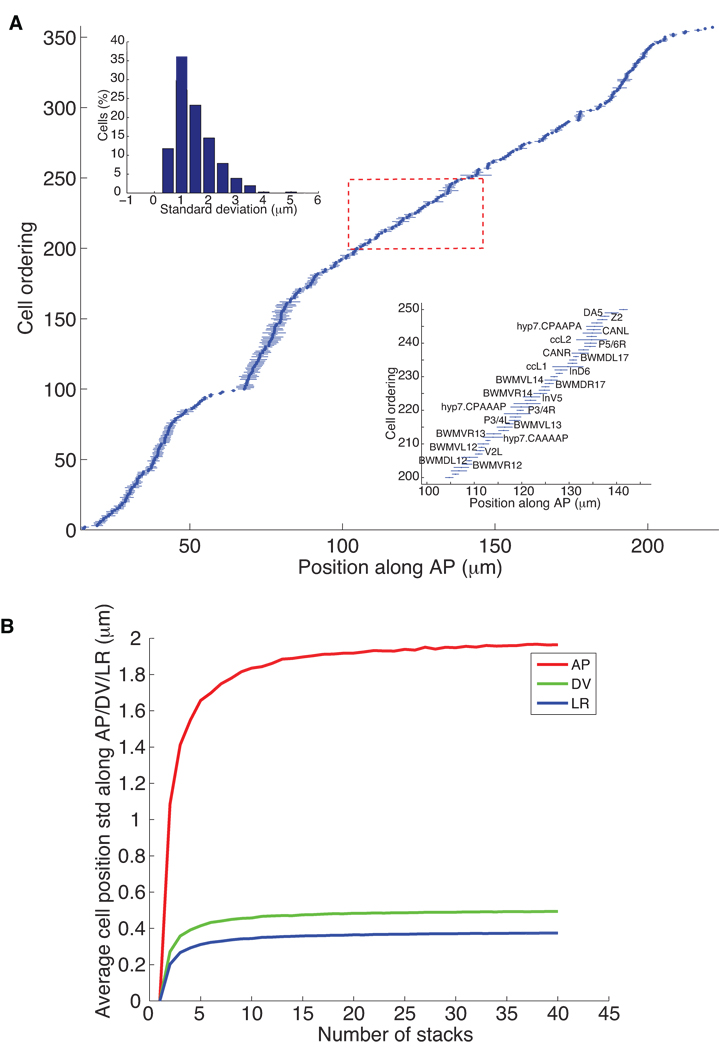
First, we analyzed the mean and standard deviations of the center locations of each cell nucleus along the anterior-posterior (AP; Fig. 2a), dorsal-ventral (DV; Supplementary Fig. 5a), and left-right (LR; Supplementary Fig. 5b) axes (Supplementary Table 1). The standard deviations and their distribution (Fig. 2a) along AP axis show that 77% of the cells vary by less than 2 µm in their location. The average standard deviation of the location of cell nuclei along the AP axis is 1.87 µm, which is about 72% of the average diameter of nuclei. This recapitulates that cell nuclei in the L1 stage have positions that are highly stereotyped and provides a quantitative estimate of the stereotypy of each cell. Note that this estimate is an upper-bound as some of the observed variations may be due to imperfect staging, straightening, registration, and so on.
Figure 2.
Statistics of nuclei positions. (a) The mean and standard deviations of the locations of 357 nuclei along the AP axis computed from 15 randomly selected images of hermaphrodites at the first larval stage. The horizontal axis is the position of nuclei along the AP axis (in µm), the posterior direction being positive. The vertical axis is the ordering of the nuclei sorted according to their mean locations along AP. The dots are the mean locations of the corresponding nuclei and the lines are their standard deviations. The bottom-right inset shows the names of a subset of the 357 nuclei. The up-left inset shows the distribution of the standard deviation of nuclear locations of all the 357 nuclei. (b) The average standard deviation of nuclei positions along AP, DV, and LR dimensions as functions of the number of stacks used to build the atlas.
Several cell nuclei have a standard deviation of their location that is more than twice that of other nuclei along a given axis (see the Supplementary Methods for a complete listing of these cells). These hyper-variable cell nuclei include the nuclei of hypodermal cell hyp7, the intestinal nuclei, and the HSN and coelomocytes (cc) cell nuclei among others. hyp7 is a large syncytium with 23 nuclei that are free to move within the cell relative to each other. The number of intestinal cells varies between individual worms between 19 and 21, and the location of these cells is variable depending on cell number. Finally, the HSN and cc cells start to migrate shortly after hatching. So the results from the atlas agree with known biology suggesting that the positions of these cell nuclei are indeed more variable.
To determine the minimum number of stacks needed to build the atlas, we tested how the statistics of nuclei positions change as the number of stacks increases. For this purpose, we randomly chose K stacks, with K ranging from 5 to 40, and computed the average standard deviations of nuclei positions along AP, DV, and LR for each K. To make the statistics independent of the stacks chosen, we repeated this process 200 times, each time with different subsets of the stacks, and obtained an average curve as shown in Fig. 2b. The average standard deviations of cell positions along AP, DV, and LR tends to increase quickly with K and then taper off with only an inconsequential and asymptotically limited increase after K = 15. This confirms the stability of our computational approach and justifies using 15 stacks for the atlas.
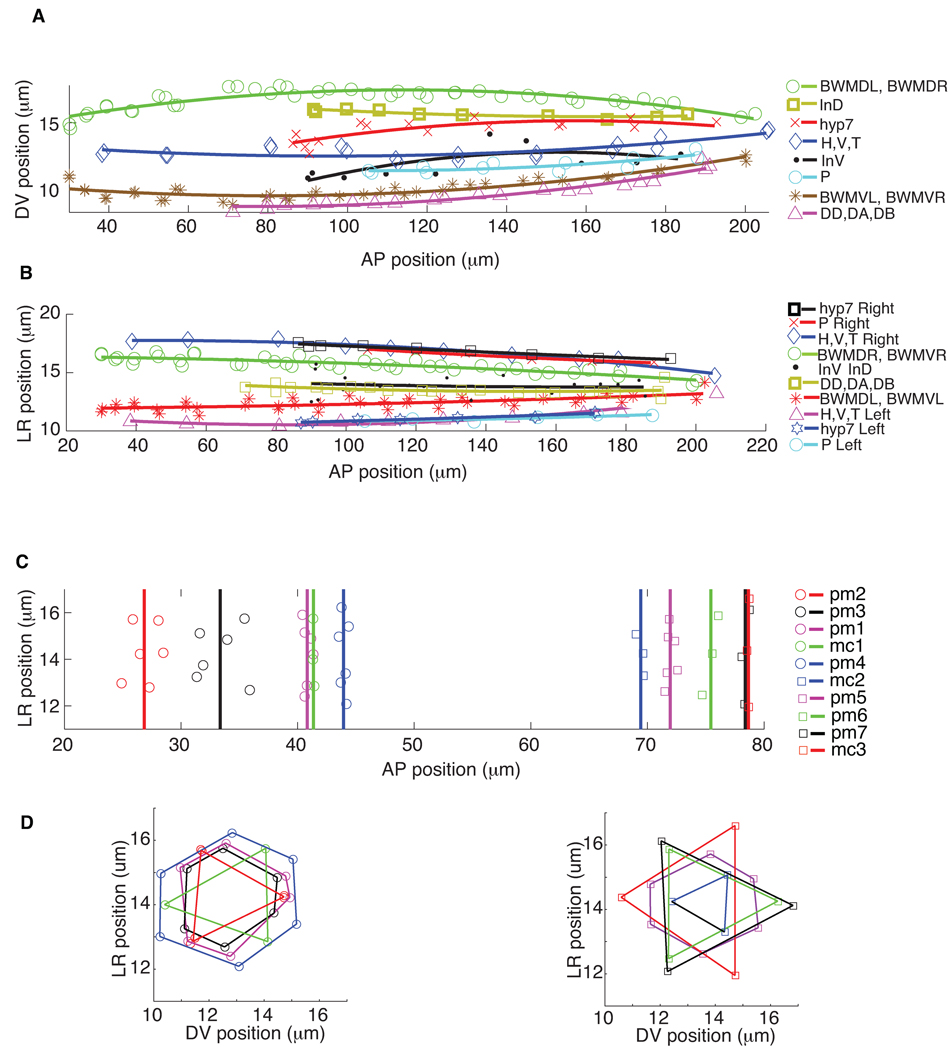
The atlas further permits one to perform more sophisticated analysis on nuclear locations. For instance, we quantitatively modeled and visualized the spatial patterns of nuclei within and across different types of cells, such as the four bundles of body wall muscle cells (BWMVL, BWMVR, BWMDL and BWMDR), the intestinal cells (InD and InV), the hypodermal cell hyp7, the blast cells H, V, and T, the P cells, and the ventral motor neurons DD, DA, and DB, using quadratic polynomial curves through the mean cell nuclei positions (Figs. 3a and 3b). The spatial distributions of pharyngeal muscle (pm) and marginal (mc) nuclei in the head (Figs. 3c and 3d) form 7 rings of pm nuclei and 3 rings of mc nuclei projected onto the AP-LR plane. One immediately sees that the spacing of nuclei within each ring is quite consistent with earlier qualitative descriptions of worm anatomy1,10 (see also http://www.wormatlas.org).
Figure 3.
The nuclei spatial location patterns of different types of cells. (a) and (b) are the nuclei locations of the four bundles of body wall muscle cells (BWMDL, BWMDR, BWMVL, and BWMVR) and most of the trunk cells including dorsal and ventral intestinal cells (InD and InV), trunk hypodermal cells (hyp7), H, V, T, and P cells, as well as ventral motor neurons (DD, DA, DB), projected onto the AP-DV plane and AP-LR plane respectively. For better visualization, we did quadratic polynomial fitting for each type of cells. (c) and (d) are the nuclei locations of the 7 rings of pharyngeal muscle cell nuclei (pm) and the 3 rings of marginal cell nuclei (mc) in the head projected onto AP-DV and AP-LR plane. Vertical lines show the mean locations of each ring along AP dimension. On the AP-LR plane, nuclei of the same ring are connected in lines.
We also analyzed the invariant spatial relationships between nuclei along the AP, DV, and LR dimensions. This information directs the automated cell annotation algorithm to be described below. For this purpose, we built a graph where each nucleus is a vertex and there is a directed edge from u to v if nucleus u is always in front of nucleus v in the dimension under consideration (Fig. 4 and Supplementary Fig. 6). Note that we also applied transitive reduction to the graphs, meaning that if u is always in front of v and v is always in front of w, then the transitively inferable edge from u to w is removed. Fig. 4a shows the AP graph for H, V, T, P, and In (intestinal) cell nuclei that are located mostly in the trunk, and Fig. 4b shows the AP graph of the nuclei of the pharyngeal muscle and marginal cell nuclei in the head. Such graphs showing the statistically verified invariance of the relative positioning of cells, especially among the cells of separate tissues within the body plan, can only be built given an atlas constructed from many worm observations.
Figure 4.
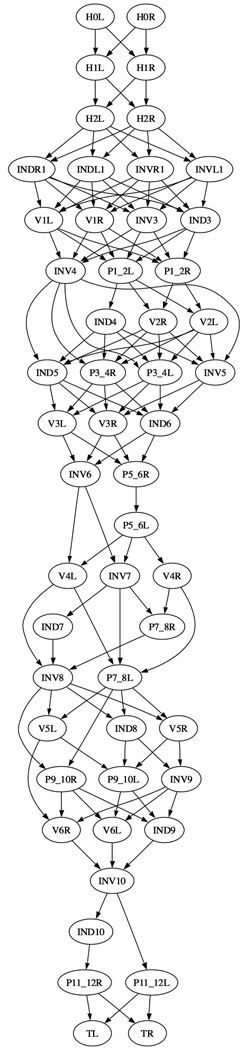
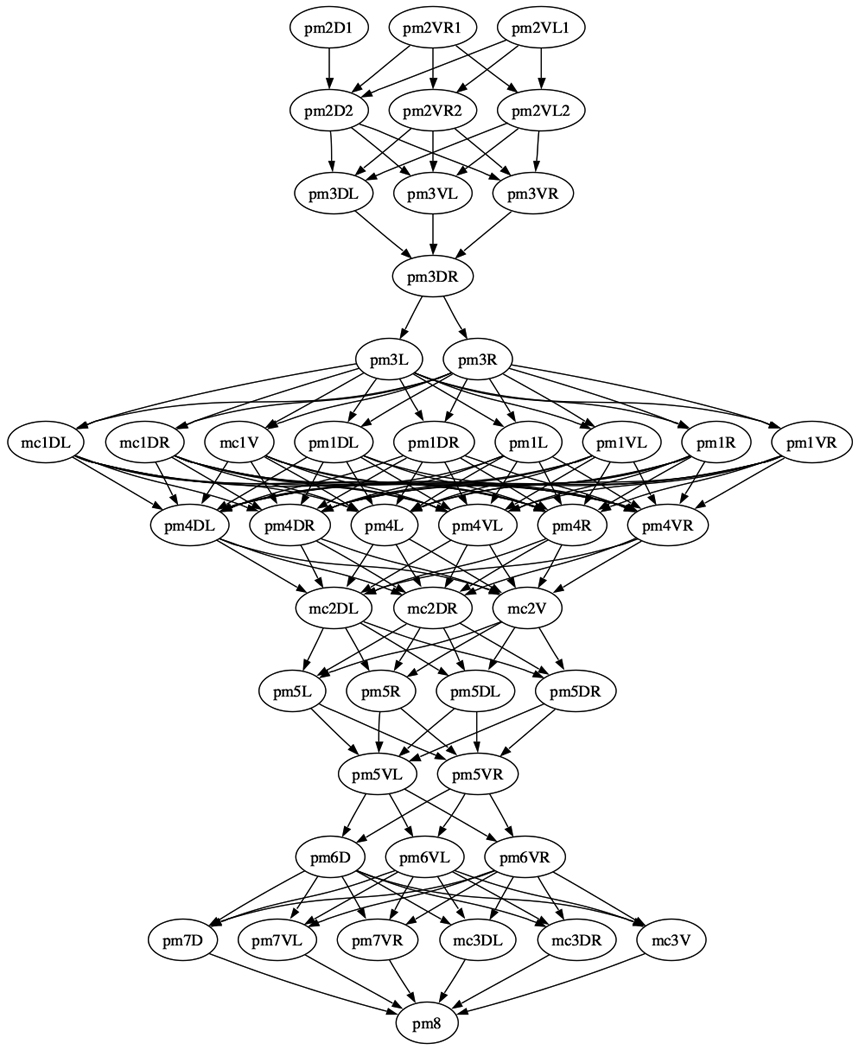
AP graph of (a) the H,V,T,P, and In (intestinal cells) and (b) the pm (pharyngeal muscle) and mc (marginal cells) nuclei derived from the atlas. The graph is displayed after transitive reduction. Thus if there is a directed path from node a to node b, and from node b to node c, then the transitively inferable edge from a to c is removed.
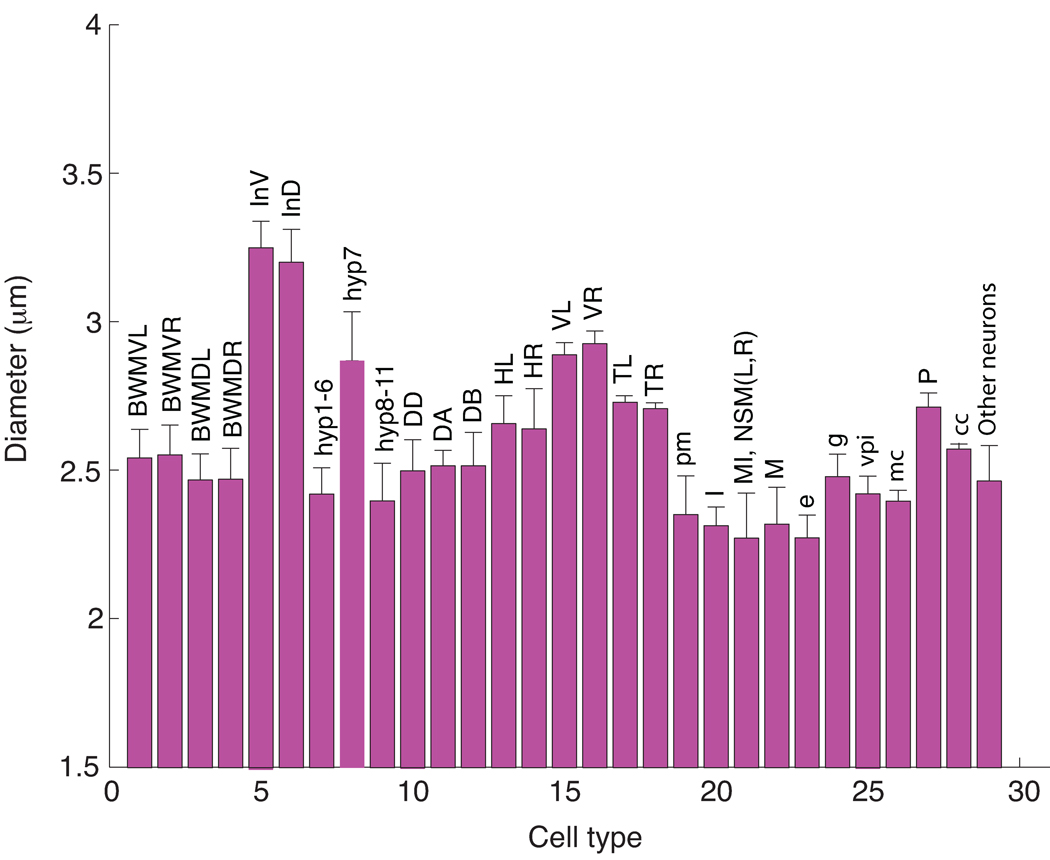
In addition to recording the centers of each nucleus, we also estimated the volume and diameter of every cell in the atlas. Fig. 5 shows the statistics of nuclear sizes for different types of cells. The average diameter of a nucleus at the L1 stage is 2.58 µm, but intestinal cells are much bigger with an average diameter of 3.23 µm. In addition, hypodermal nuclei (hyp7) and V nuclei are also larger with average diameters of 2.88 µm and 2.90 µm respectively. None of the nuclei are considerably smaller than average and the large cells all have a large nucleolus suggesting that there is base-line size for a nucleus that is expanded in proportion to the size of its nucleolus. The unusually large size of the intestinal cell nuclei could be used in their identification.
Figure 5.
Mean and standard deviations of nuclei sizes for different types of cells. BWMVL: body wall muscle ventral left bundle; BWMVR: body wall muscle ventral right bundle; BWMDL: body wall muscle dorsal left bundle; BWMDR: body wall muscle dorsal right bundle; InV and InD: intestine ventral and dorsal cells; hyp: hypodermal cells; DD, DA and DB: ventral motor neurons; HL and HR: H cell left and right bundles; VL and VR: V cell left and right bundle; TL and TR: T cell left and right; pm: pharyngeal muscle; mc: marginal cells in pharynx; vpi: pharyngeal intestinal valve cells; e: pharyngeal epithelial cells; g: pharyngeal gland cells; M: pharyngeal motor neuron; I: pharyngeal motor neurons; cc: coelomocyte; MI, NSM(L,R): pharyngeal motor interneuron, and secretory motor neuron; other neurons include BDU(L,R), ALM(L,R), CAN(L,R), Q(L,R),AVG, SABD, SABV(L,R), RIG(L,R), RIF(L,R), PVT, PVP(L,R), PVQ(L,R), PHA(L,R), PHB(L,R), LUA(L,R), PVC(L,R), ALN(L,R), PHsh(L,R), PLM(L,R), PVR, DVA, and DVC.
Automated annotation of nuclei
With an atlas in hand, we developed an automated approach that replaces the manual annotation of cell identities in the analysis of potentially thousands of stacks of worm lines, each expressing mCherry from a different target gene’s promoter. The motivation is to permit medium- to high-throughput analysis of cellular information at single cell level. In this context, the workflow for a newly acquired image stack is:
Automated straightening
Automated segmentation of the DAPI, GFP, and mCherry channels
Optional manual curation of any or all of the segmentations
Optional manual pre-annotation of “problematic” cell nuclei (see below)
Automated registration and annotation of the atlas cell nuclei
Optional curation of the annotation
Automated extraction of cellular information (e.g. expression levels) of each cell in the mCherry channel.
A Matlab implementation of all the automated steps takes less than 1 hour to process one stack with a 2.3 GHz CPU. A pipeline implemented in C is under development and preliminary timings indicate it will be about 10 times faster. For the manual steps, it takes about 1 hour to curate the segmentation of one stack (i.e. step 3) and another two hours to curate the annotation (i.e. steps 4 and 6). In contrast, it takes about three days to process one stack completely manually.
The computational problem posed by Step 5 is as follows. We are given the K (e.g. K = 15) registered “template” images of the atlas for which 357 nuclei have been annotated, and a “subject” image S in which approximately 558 nuclei have been segmented and yet to be annotated. The problem is to establish a 1-1 correspondence or “matching” between the 357 nuclei in the atlas and a subset of the nuclei in S. We did so in two phases. In the first phase, we annotated the 82 “marker” nuclei stained in the GFP channel. These marker nuclei include 81 body wall muscle cells and 1 depressor cell. They distribute along the entire worm body in 4 bundles (VL, VR, DL, and DR) and can be very accurately segmented. Annotation of these marker cells is achieved by simultaneous registration and matching using a RANSAC-like approach20. More specifically, we registered S to the reference stack C through many trials. In each trial, we selected 4 pairs of non-coplanar corresponding marker nuclei centers and compute an affine transform that map S to C. We then used a bipartite matching algorithm21 to find the best matching between the 82 marker nuclei of C and S under the given transform that minimizes the sum of the Euclidean distance between corresponding nuclei centers. The trial with the smallest distance produces the best annotation of the marker nuclei.
In the second phase, we took the affine transformation TGFP that minimizes the difference between S and C with respect to all 82 GFP-labeled nuclei and used the now-annotated marker nuclei in S to triangulate the remaining cell nuclei in the DAPI channel (see Methods). More specifically, we computed the normalized distance between a non-marker nucleus to be annotated and its nearest marker nuclei (one anterior and one posterior in each of the four muscle bundles) and used this metric to find the best bipartite matching between nuclei in S and a subset of those in the atlas (see Methods). We then examined the AP, DV, and LR relationship in our initial labeling of S to see if there is any assignment that seems to substantially conflict with the invariants of the AP, DV, and LR graphs derived from the atlas22. If so, we assumed the most conflicted assignment is erroneous and rerun the bipartite matching above, but this time prohibiting the conflicting match from being chosen. We iterated this process until the level of conflict cannot be improved.
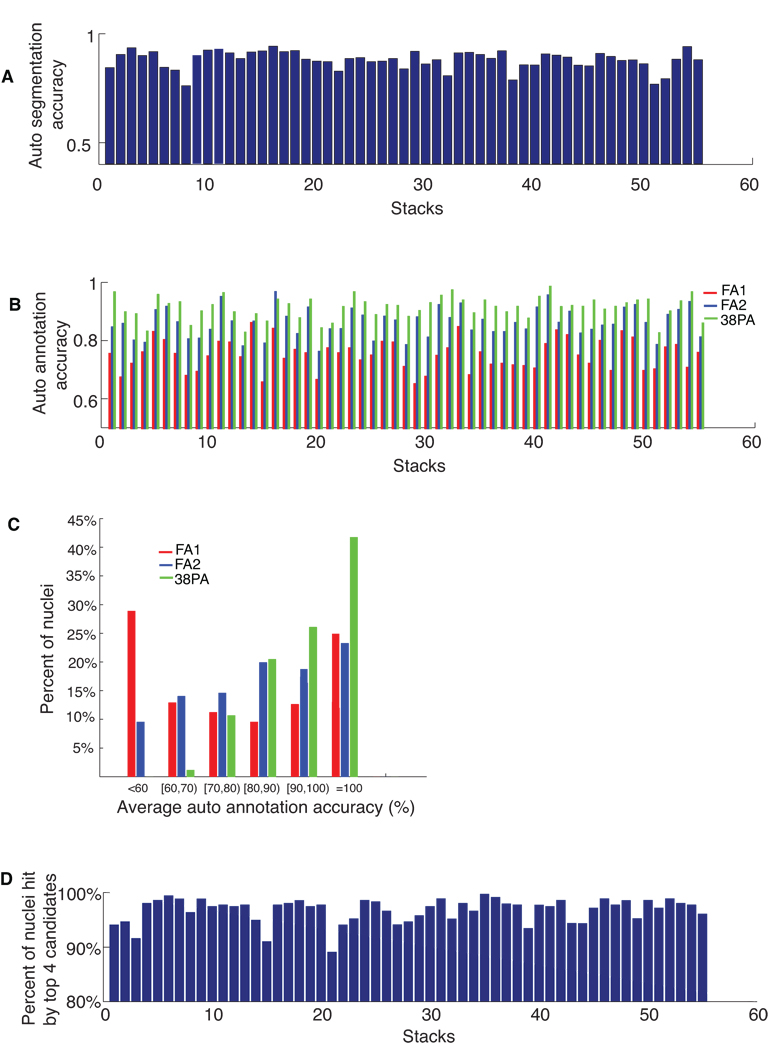
We tested the automated annotation on a new set of 55 confocal image stacks. These 55 stacks were manually annotated as well in order to allow us to assess the accuracy of the automated approach. First, we segmented the ~558 cells in each stack using our automated approach. Fig. 6a shows the accuracy of the automated segmentation. The average accuracy is 89%. Errors mainly occur in the head where nuclei density is very high and the axial resolution is not high enough to resolve the boundary between neighboring nuclei. Among the 55 stacks, 6 of them have notably lower SNR (signal-to-noise-ratio) and segmentation accuracies are lower.
Figure 6.
Accuracies of automated segmentation and annotation of 55 image stacks. (a) The accuracies of automatic segmentation for each stack. (b) The accuracies of automated annotation of the 357 nuclei. Red bars: fully automated segmentation followed by fully automated annotation (FA1). Blue bars: manually curated segmentation followed by fully automated annotation (FA2). Green bars: manually curated segmentation followed by automated annotation of 319 nuclei in each stack. The remaining 38 nuclei with big spatial variations across individuals were pre-annotated (PA) manually. (c) Percentages of nuclei falling into different annotation accuracy ranges for fully automatic annotation of 357 nuclei (FA1; red bars and FA2; blue bars) and for automatic annotation of 319 nuclei (PA; green bars). (d) Percentages of nuclei among 357 whose identities can be hit by the top 4 candidates for each stack.
We then ran automated annotation without any intervening manual curation of the segmentation. Fig. 6b red bars show the annotation accuracy for each of the 55 stacks. The average accuracy is 76% for all 357 cell nuclei in all 55 stacks). In Fig. 6c (red bars), we gave a histogram of the accuracy achieved for individual cells plotted in terms of the percentage of nuclei of all the 357 cells falling into different annotation accuracy ranges.
Since errors in automated segmentation tend to induce errors in the ensuing automated annotation, we also manually corrected the segmentation errors in these stacks using VANO and then applied automated annotation. In Fig. 6b the blue bars show the annotation accuracy of each stack. The average annotation accuracy in this case is 86% for all 357 cells in all 55 stacks. In Fig. 6c the blue bars give the histogram of the accuracy of individual cells. We found that the nuclei of body wall muscle cells (BWM), P cells, H, V, T cells, intestinal cells (In), and most of the ventral motor neurons (D) are annotated with greater than 80% accuracy. There are 38 cell nuclei whose annotation accuracies are lower than 60%. Some are in the pharynx, where cell density is very high, and others have variable positions so they tend not to be in the same location or position the same relative to other nearby cells. If with the help of additional information such as cell morphology and size, one pre-annotates these 38 cell nuclei as suggested in Step 4 of the data flow above, then the automated annotation on the remaining 319 cells in Step 5 becomes more accurate as indicated by the green bars in Fig. 6b. Overall, the average accuracy improves to 92%. The green bars in Fig. 6c shows that the percentages of cells that have higher annotation accuracy also appreciably improves.
Another way to use the automated annotator is to provide for each nucleus s a small list of k candidate identities sorted according to their likelihood for which we use w(s,t) (the score of matching nuclei t in the templates to nuclei s in S, see Methods) as a proxy. That is, we presented to the user the nuclei in the atlas giving the top k scores of w(s,t) for each s in order of score. To understand how good this list is, we considered it to be ‘informative’ if the correct answer was in the list. Fig. 6d shows the percentage of lists that were deemed informative for each of the 55 stacks when k = 4. The average rate was 97%, in other words, the top 4 candidates determined by our approach faithfully cover the right identity of almost every nuclei.
DISCUSSION
By building an atlas of nuclear positions over multiple observations of in situ C. elegans preparations we have quantitatively characterized the stereotypy of nuclear locations and the invariance of their relative locations. While we observed a number of patterns that confirm known biology described qualitatively, there is the potential to query this atlas to confirm or support novel hypotheses about the anatomy of a worm.
For us, the most important application of the atlas is that it allows us to automatically process a novel image stack and identify cells in the lineage of an L1 without human intervention at an accuracy level sufficient to consider high-throughput studies, which cannot be achieved without a digital nuclei atlas and the enabling automated nuclei annotation approach.
We expect the atlas can also be used in many applications. For example, we may use it to measure gene expression patterns at the resolution of single cells and quantitatively characterize the molecular expression signature of each cell. We may also detect mutants at the same developmental stage by observing nuclei locations and gene expression levels of individual cells that differ significantly from those of wild-type C. elegans. Similarly, we may also use it to differentiate hermaphrodites from male worms. We further envision that as our software becomes faster and accuracy further improves with refinement of the methods, that we could place the software on board a microscope and direct the laser ablation or stimulation of channel-rhodophsin or halo-rhodopsin expressing cells automatically. Such automation would, for example, allow high-throughput assays of worm cell function studies.
In our view, an important limitation is that currently the L1 atlas includes only 357 nuclei. The remaining nuclei are mostly neurons in the nerve ring. There are also a small number of hypodermal cells, arcade cells and socket cells in the head that are missing. Unfortunately, the nuclei are very dense in this region of the worm and do not show distinct features from each other in the DAPI channel. This presents difficulty to us in manually annotating their identities. One could consider adding additional fluorescent fiducial markers, analogous to the GFP-labeling of the body-wall muscle cells, to further aid us to resolve nuclei identities in this difficult region and provide training data for automated segmentation and annotation. Another difficulty in resolving nuclei in this region is that standard confocal microscopy doesn’t give quite the resolution needed for annotation. It is our intuitive estimate that a factor of 2 or greater improvement in resolution would be sufficient to resolve these regions and there is some hope that say STED or SPIM microscopy, or some optimally clearing preparation of the worm will give us this factor. Once we are able to resolve the identities of these cells, our computational pipeline can be directly applied to generate the complete atlas.
In the meantime, it is certainly the case that our methodology can be applied directly to other developmental stages and in the future we expect to develop the data to enable this method on a wider range of developmental stages. Indeed, from a purely algorithmic point of view, we have developed a system that can identify objects whose positions are stereotypic given an atlas that is in effect a set of registered and labeled training data. In fact, the pipeline we developed here has also been used to build a nuclei atlas for fruitfly late embryonic stage13. Given that many early developmental body plans or body parts are stereotypic, we expect that the methods herein may be useful in a variety of gene expression studies of development.
METHODS
Manual annotation
To build the atlas, we manually annotated nuclei identities based on the morphology and relative spatial positions of cells in C. elegans qualitatively described in earlier literatures and the WormAtlas website (http://www.wormatlas.org)10 (see Supplementary Methods for details). We assessed the accuracy of our manual annotation and further improved it using three parallel approaches. In the first approach, we manually annotated three stacks, each twice independently. We found that over 98.5% nuclei were assigned the same names in independent trials of annotation in different days. In the second approach, we annotated some worms carrying mCherry reporters whose expression has been well studied, including elt-7, pal-1, cnd-1, die-1 and pha-4. The expression patterns of these reporter based on our annotation were consistent with their cell- and tissue-specific patterns in previous literature. In the third approach, we computed the standard deviations of the positions of nuclei annotated with the same identities across different image stacks. We then pinpointed to those outliers with big standard deviations and corrected potential annotation errors if there were any. Note that position-variable cells were identified using other cues such as their morphology, size, and relative locations to some marker nuclei. This bootstrapping strategy was repeated until we were highly confident that the identities of nuclei were correct. Note that since the atlas was built on the statistical analysis of multiple 3D worm images, it is robust to the potential annotation errors if there were any.
Matching score in automatic annotating nuclei in DAPI channel
For each non-marker nucleus t in DAPI channel, we found the posterior-most marker in each body wall muscle cell bundle that is anterior to t in all templates, and the anterior-most marker that is posterior to t in all templates, if they exist. We called this set Bt the AP-“bracketing markers” for t. For each bracketing marker b we computed the mean µ b.m (t) and standard deviation σ b.m (t) over the K stacks of its distance to t along each dimension m ∈ {AP,DV,LR}. The score of matching nuclei t in the templates to nuclei s in S, w(s,t), is the average number of standard deviations σ b.m (t) that the distance, db.m (s), between s and each bracket marker b (in S) differs from the mean distance µb.m (t) for t, i.e. . This criterion is used to find the best bipartite matching between the nuclei in S and a subset of those in the atlas and serves as an initial annotation of the non-marker nuclei.
Other computational methods
Descriptions of worm body backbone detection, hollow-shaped nuclei pattern filling, adaptive thresholding, watershed algorithm, and region merging/splitting for nuclei segmentation, VANO interface, affine transform in building the atlas, details on computing AP/DV/LR graphs and adding spatial constraints to automatic nuclei annotation are available in Supplementary Methods.
Data and software
The 3D digital atlas of the 357 nuclei is provided in supplementary tables and files. Supplementary Table 1 lists the mean and standard deviation of the position of each nucleus. Supplementary Data 1 FileS1_worm_atlas_L1_357.apo provides a “point-cloud” of the atlas that can be displayed using the software V3D (Peng, et al, unpublished work) we developed for microscopy image data processing and visualization (Supplementary Video 3). Both V3D and the annotation tool VANO are freely downloadable at http://penglab.janelia.org. The Matlab code of this pipeline, called CellExplorer, along with a sample data set, can be downloaded both as the Supplementary Data 2 and from the authors’ websites.
Supplementary Material
ACKNOWLEDGEMENTS
The authors thank Andrew Fire for providing reagents and advice. The work of X.L. and S.K. was funded by the Ellison Medical Foundation and the NIH. X.L. was also funded by the Larry L. Hillblom Foundation. The work of F.L., H.P. and E.M. was funded by Howard Hughes Medical Institute.
Footnotes
AUTHOR CONTRIBUTIONS
F.L., H.P., and E.M. developed the pipeline and related algorithms, built the atlas, performed the statistical analysis, and wrote the manuscript. X.L. and S.K. prepared the worm assays and images, manually annotated the nuclei, and helped in preparing the manuscript.
REFERENCES
- 1.Riddle DL, Blumenthal T, Meyer BJ, Priess JR. C. elegans II. Cold Sprint Harbor Laboratory Press; 1997. [PubMed] [Google Scholar]
- 2.Sulston JE, Schierenberg E, White JG, Thomson JN. The embryonic cell lineage of the nematode Caenorhabditis elegans. Dev Biol. 1983;100:64–119. doi: 10.1016/0012-1606(83)90201-4. [DOI] [PubMed] [Google Scholar]
- 3.Sulston JE, Horvitz HR. Post-embryonic cell lineages of he nematode, Caenorhabditis elegmans. Dev. Biol. 1977;56:110–156. doi: 10.1016/0012-1606(77)90158-0. [DOI] [PubMed] [Google Scholar]
- 4.White JG, Southgate E, Thomson JN, Brenner S. The structure of the nervous system of the nematode C. elegans. Phil. Trans. Royal Soc. London. Series B, Biol Scien. 1986;314:1. doi: 10.1098/rstb.1986.0056. [DOI] [PubMed] [Google Scholar]
- 5.Chen BL, Hall DH, Chklovskii DB. Wiring optimization can relate neuronal structure and function. Proc. Natl. Acad. Sci. USA. 2006;103:4723–4728. doi: 10.1073/pnas.0506806103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Stein LD, et al. The Genome Sequence of Caenorhabditis briggsae: A Platform for Comparative Genomics. PLoS Biol. 2003;1:E45. doi: 10.1371/journal.pbio.0000045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Reece-Hoyes JS, Deplancke B, Shingles J, Grove CA, Hope IA, Walhout AJM. A compendium of Caenorhabditis elegans regulatory transcription factors: a resource for mapping transcription regulatory networks. Genome Biol. 2005;6:R110. doi: 10.1186/gb-2005-6-13-r110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kim S, et al. A gene expression map for C. elegans. Science. 2001;293:2087–2092. doi: 10.1126/science.1061603. [DOI] [PubMed] [Google Scholar]
- 9.Wang J, Kim S. Global analysis of dauer gene expression in Caenorhabditis elegans. Development. 2003;130:1621–1634. doi: 10.1242/dev.00363. [DOI] [PubMed] [Google Scholar]
- 10.Hall DH, Altun ZF. C. elegans atlas. Cold Spring Harbor Laboratory Press; 2007. [Google Scholar]
- 11.Bao Z, Murray JI, Boyle T, Ooi SL, Sandel MJ, Waterston RH. Automated cell lineage tracing in Caenorhabditis elegans. Proc. Natl. Acad. Sci. USA. 2006;103:2707–2712. doi: 10.1073/pnas.0511111103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Murray JI, Bao Z, Boyle TJ, Boeck ME, Mericle BL, Nicholas TJ, Zhao ZY, Sandel MJ, Waterston RH. Automated analysis of embryonic gene expression with cellular resolution in C. elegans. Nature Methods. 2008;5:703–709. doi: 10.1038/nmeth.1228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Layden M, Long F, Hecksher E, Peng H, Myers E, Doe C. Assembling a transcription factor/gal4 neuronal atlas for developmetal analysis of neural circuits. Proceedings of Workshop on Behavioral Neurogenetics of Drosophila Larva; Oct 19–22 2008; Ashburn, VA. [Google Scholar]
- 14.Peng H, Long F, Liu X, Kim S, Myers E. Straightening Caenorhabditis elegans images. Bioinformatics. 2008;24:234–242. doi: 10.1093/bioinformatics/btm569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Vincent L, Soille P. Watersheds in digital spaces: an efficient algorithm based on immersion simulations. IEEE Trans. Pattern Analysis and Machine Intelligence. 1991;13:583–598. [Google Scholar]
- 16.Beucher S, Meyer F. The morphological approach to segmentation: the watershed transformation. In: Dougherty ER, editor. Mathematical Morphology in Image Processing. New York: Marcel Dekker; 1993. pp. 433–482. [Google Scholar]
- 17.Vapnik V. The Nature of Statistical Learning Theory. Springer-Verlag; 1995. [Google Scholar]
- 18.Peng H, Long F, Ding C. Feature selection based on mutual information: criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Pattern Analysis and Machine Intelligence. 2005;27:1226–1238. doi: 10.1109/TPAMI.2005.159. [DOI] [PubMed] [Google Scholar]
- 19.Peng H, Long F, Myers G. VANO: a volume-object image annotation system. Bioinformatics. 2009;25:695–697. doi: 10.1093/bioinformatics/btp046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Fischler MA, Bolles RC. Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM. 1981;24:381–395. [Google Scholar]
- 21.Cormen TH, Leiserson CE, Rivest RL, Stein C. Introduction to algorithms. second edition. MIT Press and McGraw-Hill; 2001. [Google Scholar]
- 22.Long F, Peng H, Liu X, Kim S, Myers E. Automatic recognition of cells (ARC) for 3D images of C. elegans. Lecture Notes in Compute Science. 2008;4955:128–139. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.