Abstract
The origins of the enormous rate accelerations brought about by enzymes are discussed. The focus is on enzymatic C–H activation, which has been shown to take place via tunneling. Four enzyme systems illustrate the impact of site-specific mutagenesis, changes in temperature or changes in protein solvation on the tunneling properties. A model emerges in which conformational sampling is required to access a subset of protein conformers where the H-donor and acceptor undergo a close approach. The evidence for an inverse relationship between protein flexibility and active site compression is likely to extend to all classes of enzyme catalysts.
1. Introduction
Despite more than a half century of detailed investigations of protein structure and function, a generalized theory for the precise physical origins of enzyme catalysis has been lacking. What, in fact, makes this subject such a fascinating one? First and foremost, are the enormous rate accelerations of enzyme reactions in relation to the corresponding uncatalyzed reactions, with rate enhancements in the range of 1010–1020-fold [1]. Second, there is the question of the functional relevance of the small size of enzyme active sites in comparison to the overall large volume occupied by properly folded proteins. Third, and quite compellingly, efforts to generate highly active enzymes from initially inactive precursors have been, thus far, uniformly unsuccessful [2,3]. The ramifications of a comprehensive theory of enzyme catalysis would be enormous, with consequences that could revolutionize the de novo design of new catalysts as well as the paradigms for drug design. As has been recognized from the earliest days of the study of proteins, the ability to predict and design fully functional enzyme catalysts from first principles would represent a stunning advance.
2. Classical view of enzyme catalysis
The dominant theoretical context for the origins of enzyme catalysis was introduced by Linus Pauling. To quote from his 1948 New Scientist article [4], ‘I believe that an enzyme has a structure closely similar to that found for antibodies, but with one important difference, namely that the surface configuration of the enzyme is not so closely contemporary to its specific substrate as is that of an antibody to its homologous antigen, but is instead complementary to an unstable molecule with only transient existence – namely the ‘activated complex’ for the reaction that is catalyzed by the enzyme. The mode of action of an enzyme would then be the following: the enzyme would show a small power of attraction for the substrate molecule or molecules, which would become attached to it in its active surface region. This substrate molecule, or these molecules, would then be strained by the forces of attraction to the enzyme, which would tend to deform it into the configuration of the activated complex, for which the power of attraction of the enzyme is the greatest.’ This statement has been restated using a simple thermodynamic box that interrelates thermodynamic and kinetic processes, Scheme 1. The binding of substrate and transition state is represented by the vertical transitions, defined by Ks and Kts, respectively, whereas kinetic processes are shown in the horizontal regions of the diagram. The ability to combine both kinetic and thermodynamic processes within a single thermodynamic cycle is a result of the formalism of classical transition state theory which relates a measured rate constant to an equilibrium constant for the interconversion of the ground state and the activated complex [5]. In light of the fact that kcat/kuncat = 1010–1020, the expectation has been that Kts/Ks would be of the same order of magnitude. In support of this prediction there have been a few spectacular examples where substrate analogues have been shown to bind with femtomolar affinity to enzymes [6]. For many decades this particular view of enzyme catalysis held sway, with the prevailing interpretation being literal, i.e., that an enzyme in its resting structure will provide many more stabilizing interactions to its substrate at the transition state than in the initially formed ground state complex.
Scheme 1.
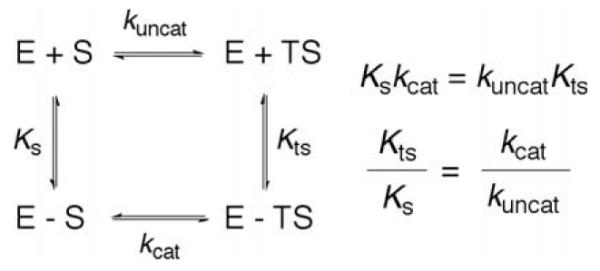
Thermodynamic box comparing the binding constants and rate constants for a non-enzymatic and enzymatic process. KS and KTS are the affinity of the substrate and transition state to enzyme. kuncat and kcat are the uncatalyzed and catalyzed rate constants.
At this juncture the reader is asked to probe more deeply into the significance of Pauling’s hypothesis. One feature that becomes immediately apparent is that the thermodynamic cycle of Scheme 1 will pertain to any catalyzed reaction, whether this occurs in solution or within an enzyme active site. In fact, the illustrated comparison of binding to rate processes is nothing more than a restatement of the fact that a reaction is undergoing catalysis. There is, in principle, nothing incorrect about stating that enzymes give rise to enhanced transition state binding, but this statement completely begs the question of the actual physical processes that provide the ‘enhanced binding’.
To pursue this line of thinking further, let us examine a single enzyme reaction in some detail. The serine proteases provide an excellent example of an extensively studied system [7]. The accepted view of catalysis involves a catalytic triad at the active site, comprised of aspartate (Asp), histidine (His) and serine (Ser), proximal to the peptide substrate undergoing cleavage. The His acts to abstract a proton from the proximal Ser, which is then activated to attack the carbonyl of an internal amide linkage within the bound peptide substrate. This reaction ultimately leads to a covalent complex between the enzyme and substrate and there are a number of successive transition states prior to the release of the cleaved peptide. Scheme 2 illustrates the first transition state in which the active site serine attacks the carbonyl of substrate. There are two dominant features here that are immediately apparent. First, there is the alignment of the His and Ser functional groups close to the bound substrate. Focusing solely on these elements, a comparable reaction in solution would be required to be tri-molecular (involving a His, Ser and peptide), whereas the reaction within the enzyme substrate complex can take place in a unimolecular fashion. This difference in molecularity has formed the basis of the proposed role of entropy reduction in catalysis, elaborated in great depth by Page and Jencks [8]. Proceeding further, close inspection of the reaction indicates that the enzyme provides far more than a simple entropy trap between the active site base (His), nucleophile (Ser) and substrate. The protein also plays an important role in stabilizing the changes in charge that accompany the formation of the transition state, with the Asp of the catalytic triad stabilizing the developing charge on the His as it abstracts a proton from the Ser and the protein backbone stabilizing the negative charge on the carbonyl oxygen of the peptide bone as one of its internal amide groups is converted to the tetrahedral intermediate. This expands the participating components at the transition state to include, at a minimum, five separate reactants making the reaction penta-molecular. And, of course, this description is not complete because the change in charge distribution that takes place within the inner sphere of the reactants will be further stabilized by neighboring regions of protein. It becomes clear that an enormous number of interactions must be optimized simultaneously for the serine proteases as well as other enzymes to proceed with the observed rate accelerations, Scheme 3.
Scheme 2.
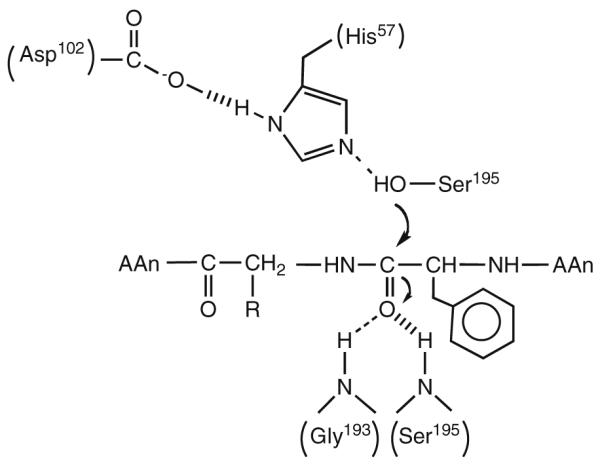
Schematic for the first chemical step in the reaction catalyzed by chymotrypsin. Five residues, Asp102, His57, Ser195, Gly193, and Ser195, are shown participating in the reaction.
Scheme 3.
Schematic of an enzyme active site, where each arrow represents one of the enzyme-substrate interactions that must be achieved simultaneously for effective catalysis to ensue. These interactions will encompass specific hydrogen bonds, electrostatic interactions, pi-stacking, etc.
It is of interest to question the energetic source of the enormous entropic advantage provided by the presentation of such a large number of functional groups within an enzyme active site. This property can, in fact, be easily understood in the context of the cellular machinery for protein synthesis, whereby ATP hydrolysis is linked to peptide bond formation. Since the primary sequence of a protein is sufficient to determine its tertiary structure, the final folded protein will succeed in positioning each of the requisite catalytic residues in close proximity. In other words the cost of reducing the entropic barrier is ‘paid’ at the time of protein synthesis, while the time scale of evolution of life forms on Earth (ca. 3 × 109 years) has provided the ‘laboratory’ for selection of catalysts with the requisite level of function for organismal success.
What does the above analysis mean in the context of Pauling’s original hypothesis? First, it is unlikely that a suitable model reaction can be found to compare directly to the enzyme reaction, because it would require a reaction of such high molecularity that it simply could not take place near room temperature in solution. An alternative, very successful approach, taken by Wolfenden and coworkers, is to compare an enzyme reaction to a reaction in solution in which all of the extra components present on the enzyme are absent [1]. This is an excellent protocol for the estimation of the magnitude of rate acceleration carried out by an enzyme but raises serious questions regarding the application of Scheme 1 to a quantitative description of enzyme reactions since the activated complex that describes the non-enzymatic reaction may be completely different from that for the uncatalyzed reaction [9]. Second, a literal interpretation of Scheme 1, in the context of the extensive 3-dimensional structures now available for a wide range of different enzyme classes, places unrealistic demands upon a static active site with regard to its ability to distinguish between the geometric and charge properties of a substrate and its activated complex.
3. Protein flexibility and its expected impact on catalysis
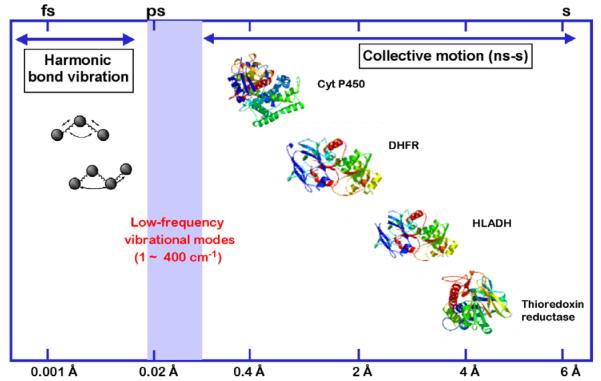
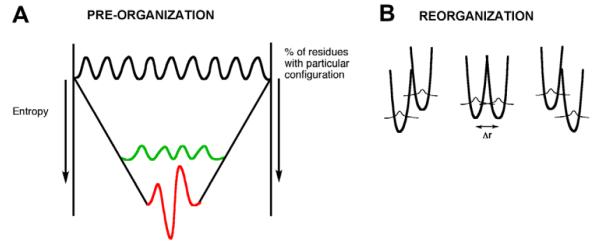
Although many properly folded proteins are known to form well-packed structures with interiors that can be likened to waxes, it is also known that the distribution of thermal energy into a protein will give rise to numerous excursions from its average three-dimensional structure, Scheme 4. The nature of the motions that can be set up within a protein are expected to range from large-scale effects that will alter the inter-relationship of protein subunits or domains, to more structurally localized loop movements or closures, to subtle shifts in protein side chains over distances as small as tenths of angstroms. Both experimental and computational data implicate rate constants for such motions from sec to ns for the more global motions, and ps to fs for the more local changes that are concentrated on atomic positioning (cf. [10]). This property immediately moves us away from a static view of a fully pre-organized enzyme active site that minimizes the tight binding of the substrate while providing exact complimentarity to the activated complex: in the context of a flexible protein, a far more reasonable perspective of catalysis focuses on the degree to which a protein can achieve, via conformational sampling, the precise alignment between bound substrate(s) and a large number of requisite protein associated residues. It is, of course, far easier to demonstrate and characterize motions in an enzyme than it is to demonstrate a direct link between such motions and catalysis. One approach that has yielded important insights has been the study of the time evolution of the rate constant for the conversion of substrate to product within a single protein molecule [11]. Studies of this nature show that a single molecule can access conformational states with different catalytic capabilities in a time-dependent manner. However, a current limitation of single molecule methods is the nature of the experiments, such that only transitions among conformational substates in enzymes that occur more slowly than catalysis, i.e., slower than ms, can be measured. The large number of conformational samplings that are equal to or more rapid than catalysis simply give rise to an averaged property, which is then manifest in an averaged rate constant for each of the conformers in the single molecule experiments. As expanded below, studies of hydrogen tunneling in enzymatic processes offer a means of linking protein motions that occur on a catalytic time scale, ≥ ms, to the bond cleavage event.
Scheme 4.
Different classes of motions that can contribute to catalysis. The collective motions may be quite slow and involve large amplitude changes, as illustrated for experimentally demonstrated domain and loop closures within cytochrome P450 (Cyt P450), dihydrofolate reductase (DHFR), horse liver alcohol dehydrogenase (HLADH), and thioredoxin reductase. The faster motions in the nsec to fs are expected to occur ‘locally’ and over much smaller distances. A major goal has been to understand the contribution of the fast and slow motions to the bond cleavage events catalyzed by enzymes. From Ref. [10].
4. The role of tunneling in enzyme catalysis
The quantum description of electron transfer processes provides an excellent starting point for understanding the behavior of hydrogen transfer in biological systems. The ability to formalize the movement of an electron as a wave is a result of the very small size of the electron and the resulting uncertainty relationship between its momentum and position. It is now generally accepted that an electron may ‘tunnel’ over quite long distances [12]. Classical treatments of electron transfer that are relevant to the temperature range under which most enzymes function can be distinguished by whether the tunneling occurs in a non-adiabatic or adiabatic limit. These two types of behavior reflect the strength of the electronic coupling between the donor and acceptor atoms, designated HAB. In the strongly coupled, adiabatic limit, HAB is large and the electron transfer occurs with high frequency at the transition state, whereas non-adiabatic behavior implies numerous re-crossings at the transition state with an attendant lower efficiency of tunneling. The Marcus Hush Levich expression [13,14], Eq. (1),
| (1) |
shows, in addition to HAB, the impact of environmental reorganization, λ, and reaction driving force, ΔG°, on the reaction barrier. A large number of biological electron transfers occur over long distances and there has been considerable interest in relating the distance dependence of the rate to a constant, β, that determines the extent to which the solvent/protein structure between the electron donor and acceptor modulates the tunneling process; for very long transfer distances, hopping mechanisms have been invoked that provide ‘way stations’ for the electron at specific aromatic residues [15]. From the perspective of Eq. (1), it is possible to incorporate the donor acceptor distance dependence using a second exponential, Eq. (2), for the HAB term [13,14], Eq. (2),
| (2) |
where rAB is the actual distance over which the electron transfer occurs, r defines a distance of closest possible approach between the electron donor and acceptor, and is the electronic coupling within this closest approach. It is generally concluded that the combination of Eqs. (1) and (2) represents a static view of electron tunneling, since the electron transfer between donor and acceptor atoms can be described for a fixed inter-nuclear distance. This follows from the fact that β is fairly small (ca. 1 Å−1) and electron transfer is not expected to be sensitive to small changes in distance between the electron donor and acceptor [16]. (As will be discussed below in the context of hydrogen tunneling, sampling of different donor-acceptor distances may be expected to have a very significant impact on hydrogen tunneling efficiency.) One feature of electron tunneling that may be directly related to protein motions is the environmental reorganization term, λ. It is expected that a range of interactions are present within an enzyme active site that are capable of reducing λ in relation to a comparable electron transfer reaction in solution. The simultaneous realization of all the possible interactions within an enzyme that may play a role in reducing λ is likely to require some type of conformational flexibility/sampling, indicating a contribution of protein motions to the rate expression for electron tunneling.
The progression from a consideration of electron tunneling to hydrogen tunneling is often made in the context of proton coupled electron transfer (PCET) reactions, where different reaction coordinates are used to account for the separate tunneling properties for electrons and hydrogen. Although a number of treatises have emerged to formalize PCET [17], this review focuses on enzymatic systems where the movement of the hydrogen nucleus and its attendant electrons are expected to be tightly coupled. Thus, the discussion herein will be focused on the ‘generic’ behaviors of hydrogen tunneling, with the understanding that this may involve movement of either a proton, a hydrogen atom or a hydride ion.
Some of the earliest evidence of hydrogen tunneling in enzyme catalysis came from an examination of hydride transfer reactions. In early studies of yeast alcohol dehydrogenase the impact of changes in substrate structure (to define changes in charge between the ground state and transition state) was found to yield a transition state structure with properties different from those inferred from secondary deuterium kinetic isotope effects (to define changes in bond hybridization between the ground state and transition state) [18]. A subsequent study of formate dehydrogenase indicated that the experimental kinetic secondary deuterium isotope effect exceeded the semi-classical boundary condition set by the equilibrium isotope effect [19]. Calculations by Schowen and Huskey showed that inflated secondary kinetic isotope effects could arise in the context of a Bell-like hydrogen tunneling model, under conditions where the motions of the primary, transferred hydrogen and the secondary, non-transferred hydrogen were coupled [20]. Experimental support for this model came in 1989, when comparison of secondary kinetic isotope effects for deuterium vs. protium transfer in the yeast alcohol dehydrogenase reaction showed a greatly inflated secondary kinetic isotope effect in the latter case (attributed to more tunneling for the transferred H than D, Scheme 5). The pattern of labeling in Scheme 5 was fortuitous since it allowed for an enhanced sensitivity to tunneling (cf. [21]). A large number of additional measurements of secondary kinetic isotope effects in the alcohol dehydrogenase reaction were collected over a period of ca. 10 years using enzymes from different sources, different substrates within a given enzyme reaction, as well as the modification of enzyme structure via site-specific mutagenesis. Quite recently, global analysis of the aggregate data has indicated that trends in the deviations of the secondary isotope effects arise from the transfer of deuterium rather than protium – opposite to the expectations from a simple tunneling correction model [22]. This initially unexpected result is well integrated into the full tunneling model currently advanced for H-transfer in enzymes (see below).
Scheme 5.
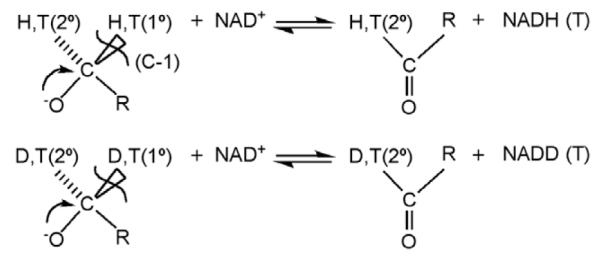
Studies of the oxidation of alcohols catalyzed by alcohol dehydrogenases. Substrate is labeled with either protium and tritium or deuterium and tritium at both the primary (1°) and secondary (2°) positions.
5. Hydrogen tunneling in enzymes and its link to protein motions
A second, major probe of enzymatic tunneling was first investigated in the proton abstraction reaction catalyzed by bovine plasma amine oxidase. Using a substrate where the C–H abstraction step could be shown to be rate-determining from 0 °C to 45 °C, the isotopic ratios, kH/kT and kD/kT, were measured as a function of temperature from which isotope effects on the activation energy and Arrhenius prefactor could be extracted [23]. Prior to this work, the Arrhenius behavior of isotope effects had been characterized in great detail for reactions that adhere to semi-classical behavior, establishing semi-classical limits for the isotopic difference in activation energies, ΔEa = Ea(2) − Ea(1), and the isotopic Arrhenius pre-factors, A(1)/A(2) (where 2 represents the heavy isotope and 1 the light isotope) [24]. The studies of BSAO showed very significant deviation from such semi-classical behavior, with experimental values for AH/AT and AD/AT well below the limits established for non-tunneling H-transfer. These studies generated a great deal of interest within the experimental enzymology community, and numerous similar deviations in A(1)/A(2) were subsequently reported for other enzyme reactions (cf. [25–28] for representative references). In all cases, the direction of the deviations, A(1)/A(2) << 1, could be rationalized by a Bell model, where the light isotope tunnels more than the heavy isotope. With time, this interpretation has proved inadequate, as already noted above for the aberrant enzymatic secondary isotope effects data in the alcohol dehydrogenase reactions.
A new level in the understanding of the tunneling behavior of enzyme reactions emerged following characterization of the hydrogen atom abstraction reaction catalyzed by the enzyme lipoxygenase. The enzyme from plant, soybean lipoxygenase-1 (SLO-1), has now been extensively characterized via both structural and kinetic methods and is often used as a model for the homologous mammalian enzymes [29]. The reaction catalyzed by SLOs involves the removal of a hydrogen atom from a methylene carbon flanked by two alkene functionalities within a long chain fatty acid; ferric hydroxide serves as the activating, H-atom acceptor, Scheme 6. In this manner, SLOs can be categorized as nonheme iron enzymes, with the reactive species being Fe(III)–OH in contrast to the higher valent, Fe(IV)=O, that has been implicated in the large class of 2-His, 1-Asp class enzymes that function to activate less reactive C–H bonds [30]. During the l990s, careful measurements of primary deuterium isotope effects in SLO-1 indicated values that were so far in excess of the semi-classical limit of ca. 7 or the Bell correction model limit of ca. 10–12 as to arouse suspicion. The fact that two laboratories reported the elevated KIEs (kH/kD ~ 80) at the same time was an important validation that the measurements were likely to be correct and unlikely to arise from systematic error [31,32]; further, the initial findings from steady state measurements were subsequently confirmed via stopped flow measurements [33]. Possible interpretations such as a chemical branching mechanism or magnetic isotope effects were examined and ultimately ruled out, with hydrogen tunneling emerging as the explanation for the data. Although elevated KIEs had been reported earlier in a few metal-dependent model systems, once ‘the rock had been lifted’ in the enzyme field, large numbers of biologically based reactions were found to display elevated primary kinetic deuterium isotope effects. The magnitude of the KIE is only one of the kinetic anomalies of SLO-1, which also shows small values for the Arrhenius prefactor and energy of activation, indicating a reaction that is largely entropically driven. In retrospect, however, the single most significant feature to emerge from studies of the SLO-1 reaction is the temperature dependence of the KIE, which varies only slightly in the temperature range studied and yields an isotope effect on the Arrhenius prefactor of AH/AD >> 1 [34,35]. The latter can be rationalized neither by semi-classical theory nor by the Bell tunneling model.
Scheme 6.
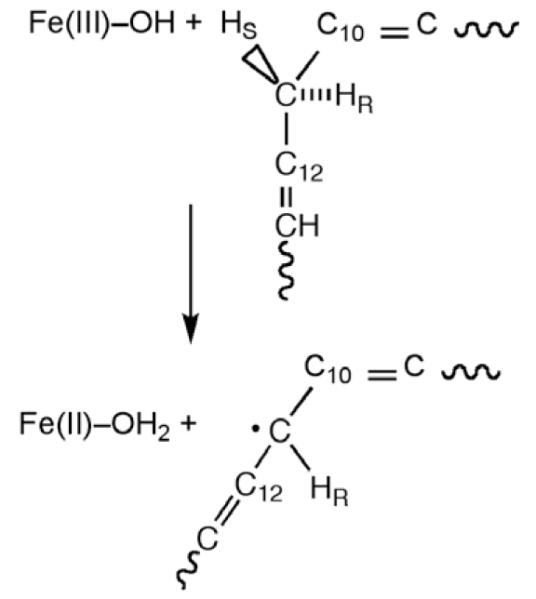
Reaction catalyzed by SLO, in which a hydrogen atom is removed from the C-11 of substrate, transferring an electron to the Fe3+ center and a proton to the hydroxide ion bound to the iron.
In l999, Kuznetsov and Ulstrup presented a full tunneling model that can reproduce weakly temperature-dependent KIEs under the condition that the H-transfer is formulated as a wave function overlap that is mass-dependent but temperature-independent [36]. An additional component of the Kuznetsov–Ulstrup model was the introduction of a distance sampling (or gating) term that integrates the probability of wave function overlap over a range of H-donor and acceptor distances; this is the term that converts largely temperature-independent KIEs as observed for wild-type SLO-1, into KIEs that display a stronger temperature dependence. The idea of distance sampling in an enzyme reaction had, in fact, been put forward earlier in the context of our original studies of isotope effects in the bovine serum amine oxidase reaction. In an important work, Bruno and Bialek showed that distance sampling could reproduce temperature-dependent KIEs (AH/AD << 1) [37]. Using a model where the initial distance between the H-donor and acceptor is too long for tunneling to take place efficiently, a transient reduction in distance between the donor and acceptor atoms becomes a requisite feature. The larger mass and smaller wave length of deuterium compared to protium leads to a greater role for distance sampling in the transfer of deuterium transfer, with a concomitant increase in Ea(D) relative to Ea(H) and reduction of AH/AD to a value that can be much less than unity.
Knapp et al. derived a useful analytical expression that follows from the model proposed by Kuznetsov and Ulstrup and relates, in a fairly simple manner, the dependence of the H-tunneling process on a set of physical parameters [34]:
| (3) |
The rate as shown is a sum over all level specific rates, in which v is the vibrational quantum number for the reactant and w is the vibrational quantum number for products that have been normalized for the thermal populations (Pv). The rate is determined by ∣Vel∣2, the electronic overlap of reactant and product squared, and an environmental energy term relating λ, the reorganization energy to ΔG°, the reaction driving force, cf. Eq. (1); Evib is the vibrational energy difference between product and reactant. The hydrogen stretch is treated quantum mechanically, and its contribution to the rate is due to a vibration level-specific Franck–Condon nuclear overlap tem (F.C. term). Other symbols have their usual meaning: kb is Boltzmann’s constant; h is Max Planck’s constant divided by 2π; and R and T are the gas constant and absolute temperature, respectively.
The isotope dependence within this fully non-adiabatic model arises entirely from the F.C. term, which determines the tunneling probability of hydrogen. Vibration-level Franck–Condon terms for overlap have been described, with the v = 0 → w = 0 transition explicitly shown in Eq. (4a) (Franck–Condon terms for overlap into or out of excited vibrational levels are available in Ref. [34]):
| (4a) |
The parameters in Eq. (4a) are the mass, frequency and distance transferred by the tunneling particle. A small temperature dependence to the isotope effects can arise in Eq. (3) from thermal population of excited hydrogen (or deuterium vibrational levels).
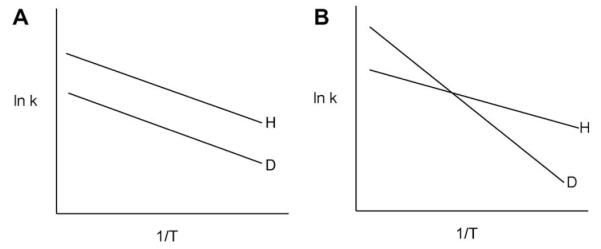
When the placement of the donor and acceptor atoms is optimal for tunneling, the two exponentials in Eq. (3) are adequate to describe the reaction rate. Since the temperature and mass dependencies occur largely in separate, non-interacting expressions, the expectation is a rate discrimination between H- and D-transfer that has a finite, temperature dependent barrier, but little or possibly no trend in the size of the KIE as a function of temperature, Fig. 1A.
Fig. 1.
Isotope effects on Arrhenius plots in which (A) the energy of activation for C–D cleavage is the same as for C–H cleavage; or (B) the energy of activation for C–D cleavage greatly exceeds that for C–H cleavage. Neither behavior in this figure is compatible with the semi-classical theory for hydrogen transfer.
Following the early studies on wild type SLO-1 [33,34], a large number of enzyme reactions have been shown to be characterized by KIEs with little or no sensitivity to temperature (cf. [38–46] for representative references). These observations, upon initial reflection, are both odd and unexpected. First, many of the reactions for which the experimental KIE is temperature-independent involve the movement of charged particles, leading to the expectation of considerable electronic coupling between the donor and acceptor sites. By contrast, Eq. (3) was derived in the electronically non-adiabatic limit. It can be concluded that while the precise analytical form for H-transfer will vary in the adiabatic and non-adiabatic limits, the basic physical picture that describes H-tunneling in condensed phase is independent of the nature of the particle transferred. A second highly surprising feature of the temperature-independent KIES is the implication of H-donor/acceptor distances that are very short, ca. 2.8 Å [47] vs. van der Waals radii on the order of 3.2–3.5 Å. This aspect of H-tunneling at enzyme active sites may be at the heart of enzyme catalysis and will be elaborated upon below in the context of protein conformational sampling and its relationship to C–H bond activation.
Of course, there are many published examples of experimental KIEs in enzyme reactions that are highly temperature-dependent[23,25–28], displaying the behavior of Fig. 1B. This behavior can be easily explained within the context of Eq. (3) via the incorporation of a distance sampling term into the Franck–Condon expression of Eq. (4a):
| (4b) |
This integral expresses the extent to which a distance sampling (or gating) term increases the rate when the initial distance between the transferring atoms is too long to support efficient tunneling. According to Eq. (4b), the final transfer distance is reduced from an initial donor/acceptor separation, r0, by virtue of motions along the H-transfer coordinate. X is a reduced coordinate, which is defined as where mx and ωx are the mass and classically treated frequency of the gating coordinate. Significantly, integration of the Franck–Condon overlap as a function of donor-acceptor distance leads to a function that is both temperature- and mass-dependent, producing the characteristic AH/AD << 1. Though Bruno and Bialek elaborated upon this latter property of H-tunneling in their original article in l992 [37], their derivation was not able to encompass the full range of behaviors observed, where A(1)/A(2) is seen to range anywhere from >>1, to <<1. Hammes–Schiffer and co-workers have derived an analogous expression to Eqs. (3) and (4b) that includes gating, noting the much larger value for β (25 Å−1) in relation to electron transfer [47] (cf. Eq. (2)). Remarkably, when site-specific mutagenesis was performed on SLO-1 to reduce the bulk of a number of active site hydrophobic residues and introduce packing defects, the measured KIEs underwent a progressive increase in their temperature dependence such that the AH/AD >> 1 observed with the wild-type enzyme was converted to AH/AD << 1 [34], actually taking on the semi-classical limit of AH/AD = 1 in one case [65].
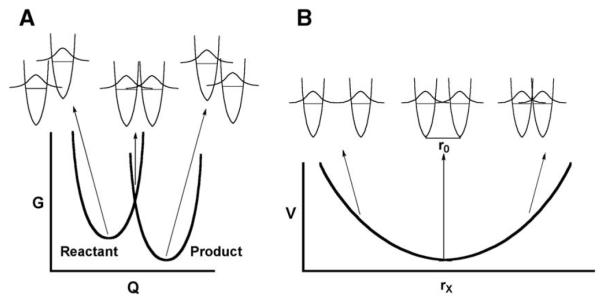
At this juncture, it is appropriate to question the relevance of Eqs. (3) and (4b) to the role of protein motions in catalysis. As described in published research reports [35] and reviews [48,49], two classes of motions appear necessary (at a minimum) to describe the manner in which enzymes catalyze C–H bond cleavage. The motions in Eqs. (3) and (4b) relate to movements within the protein and substrate that function first, to achieve the transient degeneracy between the H-donor and acceptor (referred to as a movement along the vertical axis in Fig. 2A) and second, to bring the H- donor and acceptor closer together (referred to as the horizontal axis in Fig. 2B). Many of these motions are expected to be local and fast, on the ns to fs time scale, and to contribute to what we call the reorganization of the active site. Note that this reorganization is related to the λ term introduced by Marcus in his original description of electron tunneling with the added component of distance sampling. A second type of motion that has been described by a number of investigators is related to the extensive conformational sampling that proteins undergo in solution (cf. [50]). These motions can involve large-scale hinge bending motions, loop closures, etc. and may be expected to take place on anywhere from the ms to ns scale. There has been considerable discussion of this type of motion in the recent literature, primarily in the context of protein conformational changes and the physical motions that describe these changes. The beauty of the enzymatic H-transfer experiment is that they allow this type of conformational sampling, referred to as pre-organization, to be linked directly to the making and breaking of chemical bonds. The reason for this derives from the highly unexpected property of temperature- independent KIEs: Since this phenomenon requires a tunneling-ready configuration that exceeds van der Waals distance between reactants, it cannot be present as the dominant ground state conformation of the protein but must be formed in a transient step via an isotope-independent sampling of a range of protein conformers. In the sections below experimental evidence bearing on these two types of motion will be presented, followed by a more detailed discussion of a generalized model for enzyme catalysis in the context of reorganization and pre-organization.
Fig. 2.
Schematic representation of two coordinates for heavy atom motion that contribute to hydrogen tunneling. The coordinate in (A) represents the energy barrier to bring the H-donor and acceptor into transient degeneracy, while the coordinate in (B) represents the energy barrier to bring H-donor and acceptor to a close enough distance for tunneling to occur.
6. Studies of H-tunneling in SLO-1: insight into the role of ns to ps motions (protein reorganization) in catalysis
The visualization of the active site of SLO-1 comes from high-resolution structures of the enzyme. Despite the absence of a corresponding structure that contains bound substrate or a substrate analog, the substrate linoleic acid has been modeled into the active site using molecular mechanics [34]. The resulting picture of the active site is given in Fig. 3, showing the proximity of the reactive carbon center of substrate (at position 11) to the active site Fe(III)–OH. The three hydrophobic residues that have been the focus of mutagenesis studies, thus far, are Leu546, Leu754 and Ile553, with the two former residues sandwiching the reactive carbon of the bound substrate and the latter residing a helix turn away (with a distance of ca. 13 Å between the peptide backbone at position 553 and the active site iron). The impact of mutagenesis of these three residues is given in Table 1 where it can be seen that the major impact on rate occurs with the Leu546Ala and Ile754Ala mutants. In these two cases the rate is reduced ca. 100- to 1000-fold with corresponding elevations in the energy of activation. This is perhaps not unexpected, since deletion of very local side chains may be expected to alter the environmental term expressed in λ [in the first exponential of Eq. (3)], with an impact on reaction driving force appearing less likely (as ΔG° will be determined to a large extent by the difference in bond dissociation energies between the C–H of reactant and O–H of the active site iron hydroxide). One very clear trend from these two mutants is the preservation of the enormous primary deuterium kinetic isotope effect, together with a change in the temperature dependence of the KIE toward an increased temperature dependence relative to the wild-type SLO-1. This can be understood within the model of Eqs. (3) and (4b), where the exponential terms within the integral determine the dependence of the KIE on temperature. The findings raise the question of why the deletion of hydrophobic side chains has the observed impact. The most likely explanation is that mutagenesis has created packing defects within the active site, such that the bound substrate is farther from the active site Fe(III)–OH within the catalytically relevant conformations of the enzyme. This increase in r0 leads to a greater dependence on distance sampling and, hence, a smaller AH/AD than for wild-type enzyme [34].
Fig. 3.
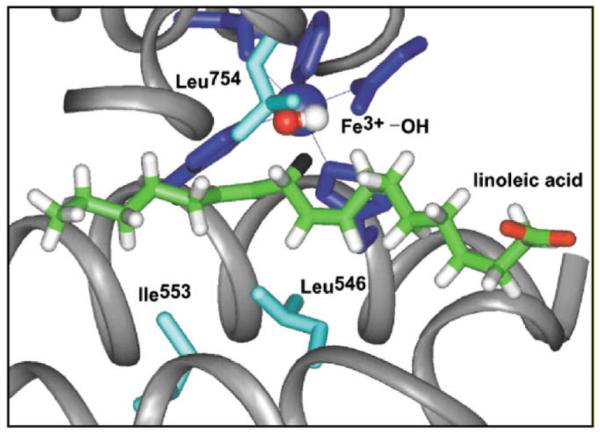
Active site structure for SLO-1 derived from X-ray crystallography [83,84]. The substrate linoleic acid has been modeled into the active site as previously described [34]. The hydrogen at position II of substrate is colored black.
Table 1.
Experimental parameters for Wild-Type (WT) SLO-1 and Alanine Substitution at Positions Leu546, Leu754, and Ile553.a
| kcat (s−1) | KIE | Ea (kcal/mol) | ΔEab (kcal/mol) | AH/AD | |
|---|---|---|---|---|---|
| WT-SLO | 297 (12) | 81 (5) | 2.1 (0.2) | 0.9 (0.2) | 18 (5) |
| Leu546 → Ala | 4.8 (0.6) | 93 (9) | 4.1 (0.4) | 1.9 (0.6) | 4 (4) |
| Leu754 → Ala | 0.31 (0.02) | 112 (11) | 4.1 (0.3) | 2.0 (0.5) | 3 (3) |
| Ile553 → Ala | 280 (10) | 93 (4) | 1.9 (0.2) | 4.0 (0.3) | 0.12 (0.06) |
Ref. [34].
ΔEa = Ea(D) − Ea(H).
Studies of the side chain at position 553 are particularly informative in this regard [35,51]. For this more remote side chain, a series of mutations has been introduced that reduces the bulk in a progressive manner proceeding from Ile to Gly. In no instance does this particular series of changes have a large impact on the kcat for protium cleavage, with the greatest effect being a five-fold reduction for Ile553Gly. At the same time the size of the observed KIE is either maintained (or increased in the case of the glycine mutant). The most significant effect of mutation at this site appears in the AH/AD values that proceed from significantly greater than unity for the wild-type enzyme to significantly less than unity with the Ile553Gly variant, i.e. a progressive increase in Ea(D) − Ea(H), Table 2. High-resolution X-ray structures are available for each of the position 553 mutants, showing two differences that have been concluded to be unrelated to the trends in AH/AD [35]. First, the side chain at position 546 appears to take up a different conformation from wild-type in some of the mutant structures; this is random with regard to the bulk at position 553 and does not correlate with the observed changes in rate and AH/AD. Second, one of the ligands to the active site iron, Gln495, is seen to be in two alternate conformations in the wild-type enzyme but only a single conformation in the mutants. The most important aspect of the mutant structures is the observation that the enzymes do not collapse upon themselves at the position of mutation, nor do they appear to bind water molecules (at least not ordered water molecules that would be detected by the X-ray method). Thus, the origin of the observed kinetic differences cannot be static in nature and has been ascribed to protein dynamical effects. Modeling of the data according to Eqs. (3) and (4b) has been able to reproduce the experimental isotope effects and their temperature dependencies, leading to estimates for the initial distance between the donor and acceptor, r0, and the frequency for the protein gating motion, ωx, Table 2. An important feature in Table 2 is the corresponding decrease in the frequency of protein gating as r0 increases among the active site mutants. This property provides a ready explanation for why mutation at certain positions can lead to a small impact on the rate for protium transfer. As illustrated in Fig. 4, mutations that cause a decrease in the gating frequency result in a reduced energetic cost to reduce the distance between the H-donor and acceptor. With the expectation that the more diffuse wave function for protium will permit effective transfer at a distance somewhat longer in the mutant than for WT-enzyme, the difference between Ea(H),WT and Ea(H),mutant may be quite small. The situation is quite different for deuterium transfer in the mutant proteins, where the two-fold greater mass and accompanying smaller wavelength of the transferred particle introduces a more restrictive distance dependence for tunneling. In fact, the position from which D-transfer occurs in the mutant enzyme may need to be quite similar to that for the WT-enzyme. The accompanying increase in energy required to re-establish this close approach between donor and acceptor for D-transfer is the source of experimental trends of Ea(D) > Ea(H) for the perturbed (mutagenized) protein structure.
Table 2.
Experimental and Calculated Arrhenius Parameters for Wild-Type (WT) SLO-1 and Ile553 Mutantsa.
| Experimental Arrhenius Parameters |
Calculated Arrhenius Parameters |
Input Parameters |
|||||
|---|---|---|---|---|---|---|---|
| SLO-1 | Ea(H) (kcal/mol) | ΔEab (kcal/mol) | AH/AD | Eac (kcal/mol) | AH/ADc | r0, () | ωx (cm−1) |
| Wild-type | 2.1 (0.2) | 0.9 (0.2) | 18 (5) | 1.0 | 15 | 0.66 | 292 |
| Ile553 → Val | 2.4 (0.5) | 2.6 (0.5) | 0.3 (0.2) | 3.1 | 0.4 | 1.24 | 64 |
| Ile553 → Leu | 0.4 (0.7) | 3.4 (0.6) | 0.3 (0.4) | 3.4 | 0.2 | 1.43 | 56 |
| Ile553 → Ala | 1.9 (0.2) | 4.0 (0.3) | 0.12 (0.06) | 4.0 | 0.11 | 1.79 | 47 |
| Ile553 → Gly | 0.03 (0.04) | 5.3 (0.7) | 0.027 (0.034) | 5.2 | 0.027 | 2.55 | 38 |
Fig. 4.
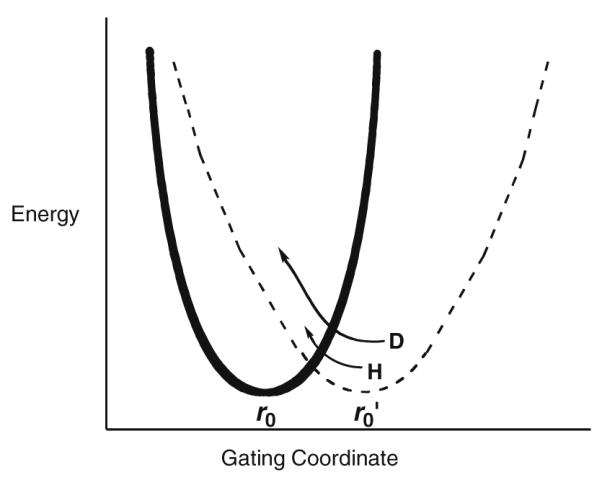
Illustration of the gating coordinate treated as a harmonic oscillator with different values for ωx. The solid line represents the wild-type protein with a crowded active site (small r0) and high frequency for distance sampling. Mutation is expected to lengthen the distance between reactants (larger r0) and to decrease the frequency of the gating coordinate. Note the r0 represents distance within the active site configurations that lead to tunneling, by necessity shorter than the van der Waals distances observed, for example, by X-ray crystallography.
To sum up the data for SLO-1, these show us how the creation of packing defects within the interior of the protein leads to a longer, less optimal binding between the substrate and the Fe(III)–OH center, together with a decrease in the stiffness of the active site that is reflected in the ωx values for gating. The simultaneous increase in ro and decrease in gating frequency leads to a mass-dependent increase in the role for distance sampling and a corresponding decrease in AH/AD. The conversion of the frequency values with units of wave numbers (Table 2) to units of time would indicate that the gating motions are taking place on the time scale of ns to ps. Thus, these experiments with SLO-1 provide one of the most compelling pieces of experimental evidence for a link between fast motions in an enzyme active site and the efficiency of a bond cleavage event.
7. Studies of H-tunneling in a high temperature alcohol dehydrogenase (ADH): insight into the role of pre-organization in catalysis
The prokaryotic alcohol dehydrogenases form a family of homologous proteins that operate across a wide temperature range, with this family comprised of mesophilic, thermophilic and psychrophilic isoforms [52]. Studies from this laboratory on the thermophilic isoform (ht-ADH) have included X-ray studies [53] together with extensive kinetic and protein dynamical measurements. The X-ray structure of the ht-ADH indicates a tetramer in which the cofactor binding domains primarily comprise the oligomerization domains, while the substrate binding domains point outward toward the crystallization solvent. As with the yeast and horse liver ADHs, these proteins contain both a catalytic zinc at the active site and a distal structural zinc that is liganded to four cysteines. The available X-ray structure was obtained with a substrate analog that is seen to bind near the active site zinc ion and defines the substrate-binding domain.
Studies of rate and primary deuterium kinetic isotope effects for benzyl alcohol oxidation, catalyzed by ht-ADH, cf. Scheme 3, have shown that there is a break at ca. 30 °C, below which the enthalpy of activation increases from ca. 15 kcal/mol to 24 kcal/mol [38]. This break in the activity curve is greater using deuterated substrate, leading to a break in the temperature dependence of the KIE as well as the rate. Investigation of the temperature dependence of the KIE has been carried out using either tritium-labeled substrates in competitive measurements or deuterium labeled substrate in non-competitive measurements. Most significantly, the KIEs go from close to temperature-independent above 30 °C to temperature-dependent below 30 °C, Fig. 5. Thus, analogous to the SLO-1 reaction, a trend can be detected in the temperature dependence of the KIE though in the case of the ht-ADH the perturbant is temperature rather than site-specific mutagenesis.
Fig. 5.
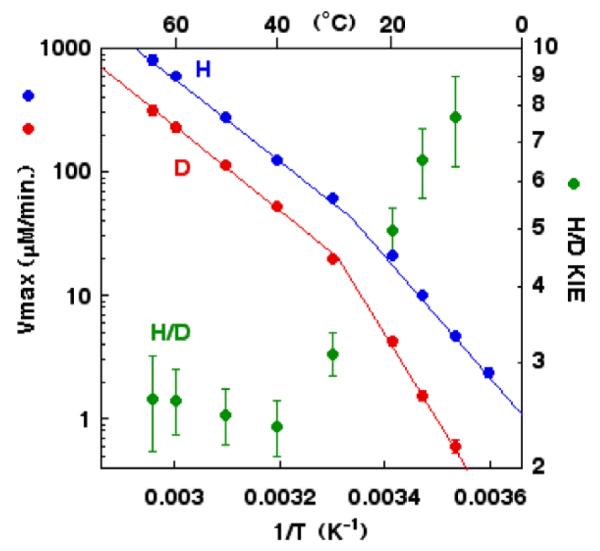
Temperature dependence of the rate of catalysis ( , D and
, D and  , H) and of the H/D KIE (
, H) and of the H/D KIE ( ) for the ht-ADH.
) for the ht-ADH.
A very surprising feature of the kinetic isotopic data for ht-ADH data is the evidence for a more rigid active site at the elevated temperature where the enzyme functions (>30 °C) [54,55] than at the reduced temperature (<30 °C). This follows directly from the values for A(1)/A(2) above and below the break point, with the smaller value for A(1)/A(2) at the elevated, catalytically relevant temperature indicating a more densely packed active site that is characterized by a higher gating frequency. This result appears contradictory to the expectation that, analogous to other thermophilic enzymes, increasing temperature will increase the flexibility of the ht-ADH and that this increase in flexibility is essential for catalysis. Thus, the measurement of the temperature dependence of the KIEs refocused the experimental goals on a physical measurement of the extent of protein motion at the elevated vs. reduced temperatures. While NMR has been used increasingly as a powerful tool to assess protein motions and flexibility, the high mass of the ht-ADH tetramer (160 KDa) made this approach somewhat daunting. As an alternative, H/D exchange linked to mass spectrometry has emerged as a broadly applicable method to assess protein flexibility under a range of experimental conditions [56]. This technique involves H/D exchange into the peptide backbone as a function of time as well as other external factors, followed by quenching of the reaction at different fractional exchanges by going to a combination of low temperatures and pH. Subsequent proteolysis of the target protein into peptide fragments, thus, permits spatial resolution in protein dynamics study. Although the examination of peptides, rather than individual amino acids, provides a coarser grain window into the protein motions, the method is more generally applicable than NMR.
Interrogation of the ht-ADH by this H/D mass spectrometric method has been carried out over the temperature range between 10 °C and 65 °C, allowing an assessment of protein flexibility both below and above the kinetic break point at 30 °C. A total of twenty-one peptides from ht-ADH were analyzed, covering ca. >90% of the protein sequence. Overall, the exchange behavior was found to follow EX-2 behavior in which local equilibrium openings and closings of protein control the time course for deuterium incorporation [56]. Although this technique does not provide kinetic constants for the rate of protein conformational sampling, it does give an assessment of the relative ease with which different regions of a protein can undergo fluctional change and how this varies as a function of external conditions. More than half of the 21 peptides analyzed from ht-ADH were found to display a regular increase in the extent of H/D exchange as a function of increasing temperature [55]. This is the ‘expected’ pattern, as both the unfavorable Keq for protein breathing modes as well as the intrinsic rate constants for exchange of the amide backbone hydrogen with deuterium are predicted to increase with increasing temperature.
By contrast, the remainder of the isolated peptides from the ht-ADH revealed an unusual pattern in which a temperature break was detected for the H/D behavior [55]. In the case of a class of peptides largely located in or near the cofactor binding site, a transition to increased flexibility occurred around 45 °C, with the Kd for cofactor (NAD) binding also found to undergo a modest transition in the same temperature range. Though this observation suggested a catalytically related transition in protein flexibility, a more dramatic pattern of a temperature-dependent transition in flexibility was detected for a series of five peptides in the region of the substrate-binding domain. In this latter case, the temperature above which a change in protein flexibility occurred was 30 °C, the same temperature at which a transition in the kinetic tunneling properties had been earlier detected. The strength of the correlation between the temperature trend in the weighted average rate constant for H/D exchange and the rate constant for catalysis within these five peptides was supported by statistically significant correlation coefficients, r2 > 0.9. The two regions undergoing a temperature-dependent transition in protein flexibility are shown in Fig. 6, illustrating that the flexibility change is selective and focused on regions of the protein that lead from the solvent interface toward the enzyme active site.
Fig. 6.
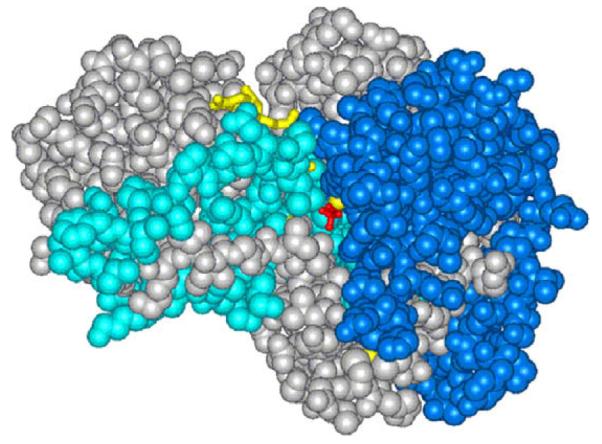
Representation of the structure for ht-ADH, with the regions in cyan indicating the increased flexibility in the cofactor domain above 40 °C and the regions in royal blue representing the increase in flexibility in the substrate domain above 20 °C. Note that these appear as discrete regions of protein that connect the solvent surface to the active site.
The above results indicated that, as had been expected for a thermophilic protein, elevation of the temperature increases the degree of conformational flexibility. How, then, can this property be integrated into the trends in the temperature dependence of the KIE for the ht-ADH? Fundamentally, what these data report is an inverse relationship between local protein flexibility and the rigidity of the enzyme active site. Since conformational sampling is expected to be a direct reflection of local protein flexibility, the results with ht-ADH indicate a need for proteins to sustain a high degree of isotope-independent conformational sampling to minimize the more local motions that contribute to the active site reorganization barrier. This point will be further elaborated below.
8. A mesophilic alcohol dehydrogenase at sub-zero temperatures
While the properties of thermophilic proteins can be examined relatively easily over a wide temperature range, mesophilic proteins generally undergo denaturation at elevated temperatures and require cryosolvents to be studied at reduced temperatures. In the case of horse liver alcohol dehydrogenase (HLADH), Fink and co-workers had shown that this enzyme can tolerate high concentrations of methanol (MeOH), permitting characterization at sub-zero temperatures [57]. In our pursuit of the temperature dependence of KIEs over wide temperature ranges, we corroborated that 50% MeOH permitted study of HLADH down to −50 °C [58], a temperature close to the glass transition of proteins. Given that enzymes undergo a marked restriction in their motions at and below the glass transition [59], HLADH offered an opportunity to investigate whether H-tunneling would persist once protein-breathing modes had been damped or switched off.
Earlier studies of the secondary kinetic isotope effects in wild-type HLADH near room temperature had indicated that kinetic complexity, arising from partially rate-determining substrate binding or release, masked the ability to study the H-transfer step [60]. Thus, an initial approach to the study of HLADH at reduced temperature employed a light sensitive, caged form of the substrate alcohol (either protiated or deuterated at the reactive carbon) that could be pre-bound to enzyme. Though a successful strategy for the synthesis of an HLADH-compatible, caged reagent was developed, laser excitation to produce enzyme-bound substrate was found to be kinetically limited by the photochemically induced rearrangement of the precursor, precluding a direct study of H-tunneling [61]. As an alternative, an active site mutant of HLADH, F93W, that had been previously shown to ‘unmask tunneling’ at elevated temperatures proved amenable to study at temperatures down to −35 °C [61]. Though this temperature falls short of the glass temperature transition, it permits trends in measured KIEs to be pursued between 25 °C and −35 °C.
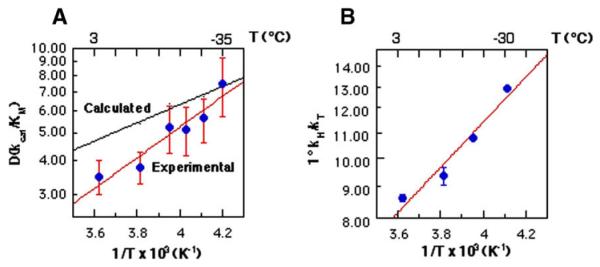
In the course of the characterization of primary KIEs for HLADH, little change in the magnitude of this parameter was observed down to 3 °C, with the size of kH/kD = 3.5 ± 0.5 found to be the same in either water or 40% MeOH at 3 °C, Table 3. However, this temperature-independent KIE was seen to become significantly temperature-dependent between 3 °C and −35 °C (Table 3 and Fig. 7); the resulting values for A(1)/A(2) are AH/AD = 0.015(0.013)) and AH/AT = 0.33(0.16). At the time these measurements were reported, the emerging data on enzymatic H-tunneling were still being discussed in the context of an H-tunneling correction to the semi-classical transition state theory for KIEs. Within such a context, the data for HLADH were interpreted as arising from increased tunneling at sub-zero temperatures, with the implication that any impact of reduced temperature on protein motions had been ‘outweighed’ by a normal tendency for tunneling to become more prominent at reduced temperatures [61].
Table 3.
Temperature dependence of the primary KIE for F93W HLADH at >0 °C and <0 °C.a
| Temperature, 0 °C | D(kcat/Km)b | |
|---|---|---|
| >0 °C | 25 | 4.1c |
| 3 | 3.5 (0.5)d | |
| <0 °C | −10 | 3.8 (0.5) |
| −20 | 5 (1) | |
| −25 | 5 (1) | |
| −30 | 6 (1) | |
| −35 | 7.5 (2) |
Ref. [58].
The KIE is reported for the second order rate constant, kcat/Km, which measures catalysis beginning with free substrate and enzyme; this KIE represents the hydride transfer step, subsequent to formation of the E · S complex. The parameter, kcat/Km, is often used in steady-state enzyme kinetics to isolate the chemical step from other partially rate-determining steps.
From Ref. [85].
The same KIE was obtained at 3 °C with and without the addition of 40% MeOH as cryosolvent.
Fig. 7.
Temperature dependence of the KIE at sub-zero temperatures for F93W HLADH. (A) is a plot of the measured D(kcat/Km) vs. the reciprocal of temperature, with the more shallow (calculated) line representing the expected change in the KIE on the basis of semi-classical considerations. (B) is a plot of the experimental tritium isotope effect, T(kcat/Km) as a function of temperature [58].
It is now possible to re-examine the results for HLADH at reduced temperatures in a new light, within the context of the available data for ht-ADH (see section immediately above) and the model represented in Eqs. (3) and (4b). What has been observed for F93W HLADH is, in fact, identical to the trend in KIEs seen with ht-ADH, however transposed to a lower temperature range. This conforms to the expectation that protein rigidification will occur at a reduced temperature for a mesophilic protein in relation to a thermophilic protein and, further, that such rigidification will alter the properties of tunneling that become manifest in the temperature dependence of the KIE. Using the framework invoked to explain the data for ht-ADH, reduction of the temperature below 0 °C for F93W HLADH leads to a reduced ability of the enzyme to undergo the conformation sampling required to achieve the family of conformations that support efficient H-tunneling. The conformations that are capable of being sampled at reduced temperature are unable to bring the reactants into the precise and fairly rigid geometries achieved under optimal catalysis/tunneling conditions. This leads to an enhanced requirement for distance sampling in order to achieve efficient hydrogenic wave function overlap and, hence, more temperature-dependent KIEs.
9. Impact of the modification of an enzyme surface on H-tunneling
Frauenfelder had suggested a number of years ago that motions within a folded protein motions will be ‘slaved to solvent’, implying a distinct pattern of enzyme solvation that communicates with the active site [62]. While mutations of protein side chains remote from the active site have been shown to affect the properties of enzymatic H-tunneling, the impact derived from alterations at the solvent–protein interface is more difficult to interrogate. The enzyme, glucose oxidase (GO), provides an example of covalent protein surface modification and its impact on H-tunneling.
In the context of studies aimed at commercial use of glucose oxidase as a glucose sensor, researchers at Chiron found that heterologous expression of GO in yeast cells led to enzyme that was very heavily glycosylated on its surface [63]. Two glycoforms of enzyme, with dimer molecular weights of 320 and 205 KDa vs. a dimeric molecular weight of 136 KDa for carbohydrate-free enzyme, have been characterized with regard to H-tunneling. Examination of the X-ray structure for GO shows a distance from the sites of glycosylation sites to the substrate binding pocket of ca. 23 Å, with the additional expectation that the carbohydrate moiety of the protein in solution will be highly hydrated and pointing in the direction of bulk solvent [64]. In this context, the impact of glycosylation shows only a very modest impact on the rate of catalysis using the protio-form of an alternate substrate, 2′-deoxyglucose [64,26]. This is, however, distinct from the impact of protein glycosylation on the oxidation of isotopically labeled substrates discussed below.
A second means of modifying an enzyme surface is via the addition of polyethylene glycol to surface lysine side chains, a procedure that is used industrially to enhance protein stabilization. In GO, the X-ray structure indicates 16 surface accessible amines per monomer (15 lysines and one N-terminus); these have been chemically modified with either PEG350 or PEG5000, leading to dimeric proteins of molecular weights of 146 and 211 kDa, respectively [26]. Once again the oxidation of protio-substrate was found to be only modestly affected by protein pegylation, whereas the rate of turnover with isotopically labeled substrate is altered.
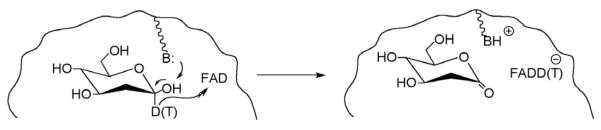
Trends in the impact of the pattern of isotopic labeling of substrate on reactivity can be seen in a straight-forward manner from a comparison of A(1)/A(2) ratios. For the case of GO, these ratios are reported for C–D vs. C–T bond cleavage, Scheme 7; the deuterium vs. tritium protocol was used to ensure that the chemical step was rate-determining and to minimize experimental error [25]. The resulting values for AD/AT are given in Table 4. The data have been sorted according to increasing size of protein, independent of enzyme source or treatment. It can be seen that both native and deglycosylated proteins show values of AD/AT close to unity. Although this observation was originally attributed to semi-classical transition state behavior, it is now clear that values for A(1)/A(2) = 1 can result from full tunneling models in which the active site has properties that reflect a transition between a rigid, optimized state, A(1)/A(2) >> 1 [34] to one in which considerable distance sampling has become a prerequisite for catalysis, A(1)/A(2) << 1. Perhaps the most surprising feature of the data in Table 4 is that all of the tested modifications of the protein surface lead to a decrease in the A(1)/A(2) ratio [26]. From this result it can be concluded that alterations in the solvation pattern at the protein surface, via the addition of varying chain lengths of either polysaccharide or polyethylene glycol, impair the configuration of the reacting pair (2′-deoxyglucose and flavin cofactor) within the active site.
Scheme 7.
Reaction studied in the glucose oxidase reaction, in which the reactive carbon at C-1 of 2′-deoxyglucose has been labeled with deuterium and tritium. The hydride ion from C-1 is transferred to the flavin cofactor (FAD).
Table 4.
Impact of Surface Modification on the Arrhenius Prefactor Values for Glucose Oxidase.a
| Enzyme | AD/ATb | Dimeric MW, KDa |
|---|---|---|
| Wild-Type | 0.98, 0.97, 1.25 | 155 |
| Deglyc320 GO |
|
136 |
| Deglyc205 GO | ||
| Rec205 GO | 0.57, 0.81 | 205 |
| PEG350 GO | 0.55 | 146 |
| Rec320 GO | 0.62 | 320 |
| PEG5000 GO | 0.55 | 211 |
Ref. [26].
Obtained from competitive measurements using C-1 deuterated and tritiated 2′-deoxyglucose.
The temperature-dependent unfolding of protein was measured in an effort to obtain insight into the physical origin of the observed changes in AD/AT [26]. Though the range in experimental Tm values is small, the data were amenable to analysis using a statistical tool that examines individual deviation from the overall mean value of the experimental parameter. Averaging the properties of native protein and comparing this group to the deglycosylated Rec320 and the glycosylated/pegylated variants produces a linear correlation in four out of five cases (the outlier is the PEG350 GO), Fig. 8. A common feature of proteins, that is especially evident when comparing homologous thermophilic and mesophilic proteins, is that increased Tm values arise as protein flexibility decreases [66]. From this perspective, the trend plotted in Fig. 8 indicates a reduction in the value of AD/AT for GO as the protein becomes more rigid. This is directly analogous to the behavior described above for the alcohol dehydrogenases, where a temperature-dependent decrease in protein flexibility leads to smaller values for A(1)/A(2). The fact that the same behavior can be seen by either lowering the temperature using a thermophilic protein or by modifying a protein surface, so as to alter the protein surface solvation, is remarkable. It is concluded that surface modification of GO impairs the protein conformational sampling (pre-organization) that is a prerequisite to the achievement of an optimally efficient active site configuration. A failure to reach such a configuration introduces the need for active site distance sampling and, hence, the reduced values for AD/AT.
Fig. 8.
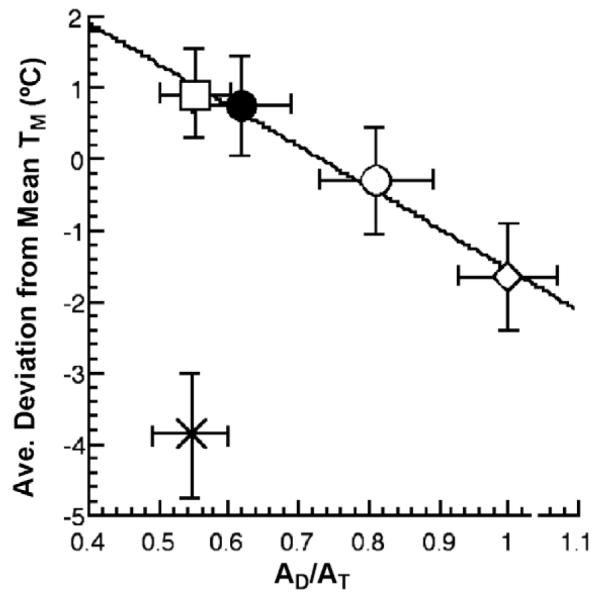
A plot of the average deviation from the mean melting temperature, Tm, of the individual Tm values for □ (PEG5000), ● (Rec320), ○ (Deglycosylated Rec320), ◇ (Wild-type enzyme), and × (PEG350) surface variants of GO [26].
10. An integration of reorganization and pre-organization into a general model for enzyme catalysis
There has been considerable recent focus linking experimental probes of protein dynamics to the conformational changes that control the binding of substrate and release of product from enzymes (cf. [67]) (see below). Although there are many enzyme systems where binding and release steps limit enzyme turnover, this is only possible when the rates for the bond cleavage steps have become extremely efficient. In our view, the central question has been to demonstrate how protein motions contribute to bond cleavage events. With the demonstration of the prevalence of hydrogen tunneling in enzymatic reactions, a new window is opened into the quest to address and answer this question.
A central feature of hydrogen tunneling is that the movement of the transferred atom between donor and acceptor atoms occurs via wave function overlap. Although it is difficult to obtain a precise rate constant for such wave motion it is generally concluded to be instantaneous in the context of the hierarchy of time scales that are important for enzymatic reactions. Thus, all other heavy atom motions can be considered to be contrastingly slow and to constitute the barrier to catalysis. The use of the modified Marcus equation for H-transfer relates protein motion to two dominant coordinates, collectively termed reorganization and represented in Eqs. (3) and (4b) and Fig. 2 above. Recall that the vertical coordinate in Fig. 2 is strictly analogous to electron transfer and describes the motions needed to alter the protein environment in such a way as to bring the energetics of reactant and product into degeneracy. The enthalpies of activation commonly observed in enzymatic C–H activation reactions are expected to arise predominantly from this term. A unique feature of H-tunneling appears in the horizontal coordinate, where the distance between the H-donor and acceptor controls the tunneling efficiency. The property of distance sampling produces a shorter tunneling distance than is present in the initial state, representing a compromise between the more efficient wave function overlap at the shorter distances and the energy input needed to bring the reactants closer than their van der Waals distance. When the initial placement, r0, of the H-donor and acceptor is non-optimal, the barrier for gating is greater for D- than H-transfer, a result of the larger distortion from this value necessitated by the shorter wave length for deuterium, producing values for ΔEa larger than set by the semi-classical limit, cf. Fig. 4 [24,25]. A completely unexpected feature of enzyme reactions is how often ΔEa is seen to be very small, with Ea(H) ~ Ea(D) [34,35,38–46]. The implication of this observation is the absence of a large contribution from the distance sampling term to the tunneling rate expression, as a result of a pre-positioning of the H-donor and acceptor into a tunneling ready distance of ca. 2.7–2.8 Å. The latter, which is ca. 0.4–0.8 Å shorter than equilibrium van der Waals’ distances, requires a driving force that can create reactant states that are much shorter than the resting state of the enzyme.
Pre-organization provides the conceptual basis to understand the source of such ‘ultra-short’ reactant states. In contrast to the fast and local (ns to ps) motions that have been shown to contribute to the distance sampling in SLO-1, pre-organization incorporates larger and slower scale motions (ms–ns) that may be expected to be impacted by residues quite far from the active site. The resulting frequent and varied excursions from an average geometry lead to a highly diverse family of protein conformational substates. In the context of catalytic efficiency, only those substates that achieve, in addition to a close distance, a very large number of catalytically relevant interactions (either between bound substrates or between the bound substrates and enzyme) are capable of proceeding to product with high rate constants. The concept of nearest attack conformation (NAC), which was introduced by Bruice and co-workers, to focus on the precise angular relationship between reactants [68] can be considered as one of the subsets of interactions that is achieved via the pre-organization event. This overall description of catalysis is reminiscent of Pauling’s hypothesis with one critical difference: the multiple interactions required for efficient catalysis are achieved via dynamical events within the protein rather than arising from an initial protein structure that must distinguish upward of 20 orders of magnitude between the charge and structure of the substrate’s ground state vs. its transition state.
Introduction of a pre-organization term into the tunneling rate expression of Eqs. (3) and (4b) modifies the expected rate by the fraction of total enzyme that can achieve a catalytically viable active site configuration. In actuality, the observed catalysis is expected to result from a family of possible conformers, with each conformer, f(i), characterized by a distinct rate constant, k(i) [48]:
| (5) |
Although instances may occur where the requisite pre-organization has a large enthalpic barrier, in general, the energetic features that control pre-organization are expected to result from a compensation of many small enthalpic interactions, both favorable and unfavorable. Recent hydrogen/deuterium exchange studies as a function of temperature on a thermophilic dihydrofolate reductase point toward dominantly small net enthalpic barriers (in the range of kT) for local protein unfolding that reflects the ease of conformational sampling under physiological conditions [69]; a small net enthalpic barrier minimizes the trapping of specific protein conformers into local energy minima, ensuring a large conformational space that can be sampled during catalysis. In the context of small enthalpic changes, the feature controlling the free energy barrier for the pre-organization term becomes the probability of a protein achieving catalytically relevant conformers, i.e., those conformers that generate the very large number of requisite interactions among bound substrates or between substrate and active site side chains. This can be visualized using the funnel presentation in Fig. 9, somewhat analogous to the funnel representation used in the protein-folding field. The frame of reference in Fig. 9 lies at the top of each funnel, which is defined as 100% probability for any protein conformer to achieve one of the many catalytically relevant interactions between substrates with each other and/or protein. The probability of finding conformers with increasing numbers of substrate/protein interactions decreases progressively as we go down the funnel, until we reach the family of conformers with sufficient numbers of interactions for catalysis to proceed. In this manner, progression from the top to the bottom of the funnel represents a decrease in overall entropy [70]. This funnel representation can also take into account the reported behavior of thermophilic proteins at reduced temperature, where TΔS‡ for C–H activation has been found to be appreciably more positive in relation to the magnitude of TΔS‡ for C–H cleavage at the physiologically relevant temperature range [71]. The freezing out of protein flexibility that is found to accompany a reduction in temperature for thermophilic proteins can be represented as a more restrictive conformational space, occurring further down the funnel (shown in red in Fig. 9). For such situations, it becomes necessary to increase protein disorder, such that the protein can move into the range required for optimal catalytic conditions (shown in green in Fig. 9). This is the source of the more positive entropy of activation commonly observed for thermophilic proteins operating at reduced temperatures (cf. [71]).
Fig. 9.
(A) A funnel is used to represent the conformational sampling referred to as pre-organization. The top of the funnel represents 100% of the possible enzyme conformations that lead to one of the requisite interactions for catalysis. The probability of achieving the large number of interactions necessary for efficient catalysis is found further down the funnel with a reduced probability or entropy (green band). Freezing out of conformational sampling, as occurs for thermophilic proteins operating at a reduced temperature, is shown by the red band. In order to function at this reduced temperature, the protein must first increase its flexibility, represented as an increase in TΔS‡. (B) The coordinates designated reorganization (Fig. 2), have been consolidated into a single diagram that allows for protein reorganization to achieve the respective energy levels and inter-nuclear distances needed for tunneling.
Recent findings on the temperature dependence of hydrogen tunneling processes following site-specific mutagenesis provide experimental verification that the above model for reorganization and pre-organization is a useful one for formulating and understanding catalysis. For example in the dihydrofolate reductase reaction, mutation of two distal residues that lie on opposite faces from the active site has been shown to give rise to a greatly impaired rate without any compensating increase in the Eact [72]. The resulting decrease in TΔS‡, which can be attributed to impaired conformational sampling, impacts the tunneling process at the active site; this is accompanied by a decrease in the value for AH/AD from its optimal (>>1) value in wild-type enzyme. In the context of the SLO-1 reaction (cf. Studies of H-tunneling in SLO-1, above), the I553G variant shows a concomitant decrease in both Eact and rate (Table 2), once again implicating a role for an enhanced entropic barrier, analogous to dihydrofolate reductase, that is accompanied by a significant decrease in the magnitude of AH/AD [35]. Recent studies of the ht-ADH indicate that mutations that affect conformational sampling need not be outside of the active site of the protein. In the physiological range for ht-ADH (>30 °C), either the increase in size or deletion of a residue that resides directly behind the reactive nicotinamide ring of cofactor produces a large reduction in rate that is accompanied by a decrease in Eact. The increasing barrier contributed by TΔS‡ is ascribed to impaired conformational sampling that interferes with the precise alignment of the H-donor and acceptor, reflected in values for AH/AD that decrease below that found for the wild-type enzyme [73].
One of the most important features to emerge from studies of the temperature dependence of primary kinetic hydrogen isotope effects in enzyme reactions is the degree to which this indicator of active site geometry is sensitive to subtle changes in structure and dynamics throughout the entire protein. With the growing body of experimental data, patterns have begun to emerge that indicate the manner in which enzymes achieve their enormous catalytic advantage. Perhaps the most unexpected aspect of these studies is the repeated implication of a need for overall protein flexibility to achieve catalytically relevant, closely packed active sites. In three of the systems discussed in this review, overall rigidification of the protein via either a reduction in temperature between 0 °C and 100 °C (ht-ADH), a reduction in temperature below 0 °C (HLADH) or a change in protein surface charge and hydration (GO) leads to an impaired ability of the protein to achieve the optimal active site interactions that permit catalysis to proceed efficiently. This can be manifested in the inter-relationships among secondary kinetic isotope efftects, as well the temperature dependence of the kinetic isotope effects, as shown from the trends in secondary D/T isotope effects in the ADH reactions as a function of protein mutation [22,49,74]. The fact that pre-organization provides the link between protein flexibility and the catalytically optimized active site configuration is, perhaps, not surprising.
The presented model for enzyme catalysis of hydrogen tunneling raises the obvious question of whether a similar model will pertain to the full spectrum of bond cleavage events that are catalyzed at enzyme active sites. Although it is difficult to address this question definitively, one strong hint of an answer comes from the behavior of carbon–deuterium bond cleavage in relation to the corresponding carbon–protium process. It is expected that Nature, while encountering the need to enhance the rate for protium transfer in thousands of different contexts, may have been ‘indifferent’ to the corresponding behavior for the rarer isotope, deuterium. However, as shown repeatedly, the temperature dependence of isotope effects in optimized enzyme systems yields values for AH/AD that reflect a compression within the active site that allows deuterium transfer to occur without any significant increase in its enthalpic barrier, relative to protium, (Ea(H) ~ Ea(D); AH/AD >> 1) (cf. [34,35,38,39,40–46]). Although, the observation of experimental KIEs indicates poorer Franck–Condon overlap for deuterium, the weak temperature dependence of the KIE indicates that a tunneling-appropriate configuration within an optimized enzyme active site is being achieved for both protium and deuterium.
A simple explanation for the above phenomenon is that hydrogen transfer represents a sub-set of a general model for enzyme catalysis. In this context, evolution of flexible proteins gives rise to the property of conformational sampling, which in turn leads to transiently compacted active sites; the latter contain the very large number of catalytically relevant substrate/protein interactions that are a prerequisite for efficient catalysis. According to this scenario, the almost universal detection of tunneling in enzymatic hydrogen transfer reactions becomes a mirror for the uniquely evolved and generic properties of enzyme catalysis.
11. Relationship of the present model to other studies that link protein motions to function
The seminal early work of Frauenfelder and co-workers, on the low temperature rebinding of carbon monoxide to the active site of myoglobin, highlighted the existence of protein conformational substates and their likely link to the mechanism of protein–ligand binding [75]. Much more recent studies, using NMR and single molecule FRET to measure conformational dynamics in the enzyme adenylate kinase, have demonstrated a correspondence between measured rate constants for substrate binding/product release steps and rate constants for protein domain openings and closings [67,76,77]. These studies on adenylate kinase show quite elegantly how protein conformational changes on the time scale of ms can control catalytic turnover in an enzyme for which the rate-limiting step is diffusional rather than chemical in nature.
In the context of understanding the impact of protein motional effects on active site bond cleavage events, the hydride transfer reaction catalyzed by E. coli dihydrofolate reductase has played an important role, implicating a loop closure that occurs in the same time regime (ms) as occurs for the hydride transfer step [78]. If this loop closure is the only relevant motion to the creation of a tunneling-ready configuration, it must be capable of achieving an active site geometry in which the H-donor and acceptor are within 2.7–2.8 Å of each other. The latter is required from the reported temperature independence of the KIE for wild-type DHFR. However, the slow loop closure is unlikely to be the complete story, given the growing support for a hierarchy of motions that are necessary to tune active site interactions as a prerequisite to efficient wave function overlap and the observation of an H-donor/acceptor distance much longer than 2.8 Å from X-ray structures. Additionally, the finding of a double mutant of DHFR with the dual properties of A(1)/A(2) << 1 and a large entropic barrier is in keeping with the parsing of protein motions into two classes [71], Fig. 9. The actual physical link of ns–fs motions to slower processes in proteins continues to be of great interest, and has been discussed quite recently in the context of ms protein conformational changes [67].
The model presented in this review provides a functional reconciliation of slow and fast time scale protein motions, distinguishing the larger time scale/amplitude motions termed pre-organization, from faster motions that control the details of bond cleavage within the active site (reorganization), Fig. 9. The division of motion into two categories of pre-organization and reorganization follows from experimental evidence of a range of temperature-dependent isotope effects for enzymes functioning under a variety of conditions, together with an inverse correlation between overall protein flexibility and the degree of structure within the enzyme active site. Such a conclusion would not have been possible without the non-canonical temperature dependencies of primary hydrogen kinetic isotope effects that have emerged from detailed studies of many different classes of C–H activating enzymes.
12. Future directions
The theory of enzyme catalysis put forth in this review opens up many new directions for experimental testing and verification. The distinctive features of hydrogen tunneling in enzymatic C–H cleavage reactions must be reflective of the nature of enzyme active sites. That is, while H-tunneling can be detected for reaction of many small molecules in bulk solvent at or near room temperature, the properties of the enzymatic tunneling properties indicate an enzyme active site that is well tuned for the promotion of wave function overlap between the H-donor and acceptor. An emerging question regarding the facility with which enzymes promote H-tunneling is whether this is a unique adaptation of proteins to accelerate the rate of cleavage of intrinsically inert C–H bonds or whether it is reflective of a generic feature of enzyme active sites [79]. An important insight into this question comes from the now common observation that enzymatic deuterium transfer mimics protium transfer with regard to the temperature dependence of the rate, indicating that the active site does not impose an additional thermal activation barrier for D-transfer. The fact that an optimized enzyme active site can promote both D- and H- tunneling strongly suggests that tunneling in enzyme reactions reflects an inherent property of the active site. In support of this view, elegant measurements of secondary isotope effects in an enzymatic methyl transfer reaction and comparison of the experimental KIEs to those for the corresponding reaction in solution had led to the early proposal of a more compressed reaction coordinate in the case of the enzymatic reaction [80]. Future examination of secondary KIEs in an enzymatic methyl transfer reaction for both wild-type and α-methyl mutants for which the geometry of the active site has been altered would be of great interest; when coupled with probes of protein flexibility, such studies could begin to address the degree to which a dynamical protein structure is required to generate a compacted active site as a prerequisite for the transfer of a group as large as atomic mass 15, analogous to the behavior seen repeatedly for enzymatic hydrogen transfer.
The issues of barrier width, its alteration via mutagenesis, and the relationship of this alteration to the tunneling properties in an enzyme reaction are amenable to direct measurement via FRET and NMR studies. Although such measurements will, by necessity, reflect the resting state of the enzyme, rather than r0 distances achieved via conformational sampling, the correlation of changes in inter-substrate distances to changes in experimental kinetic parameters would be of considerable relevance to the model for enzyme action put forth in this review. In an early study of the HLADH reaction by X-ray crystallography, mutation at a position in the cofactor domain that resides behind the nicotinamide ring of cofactor had been shown to increase the distance between the reactive C-4 position of cofactor and the C-1 of substrate; these geometric changes were accompanied by a significant change in the inter-relationship of secondary kinetic isotope effects toward a more classical behavior [81], a trend that has been attributed to tunneling within a less crowded active site environment for the mutant protein [22,49,73]. While such results support the premise presented in this review, additional measurements, using physical methods that have greater sensitivity than X-ray crystallography to small distance changes, are timely and important.
There also remains the question of the link between measured activation parameters and the physical processes that determine the H-tunneling efficiency in enzymes. From an experimental standpoint, creation of a series of mutants within a given protein provides a system in which first, changes in tunneling rate can be correlated with changes in activation parameters and second, changes in the experimental activation parameters can be correlated to changes in the overall flexibility of the protein. In this context, mutants that are far from the active site and less likely to impact ns–fs motions proximal to the H-donor and acceptor may show a dominantly entropic impact on rate that goes hand in hand with experimentally detectable changes in protein motions. A trend of this nature has already been seen when comparing H-tunneling in a thermophilic enzyme operating below its functional temperature to the behavior of a homologous psychrophilic protein in the same temperature range [70].
As delineated by other investigators, we still do not understand the manner in which the primary sequence of a protein relates to its functionally critical motions. For example, are there networks of coupled motions that transmit the thermal energy from the solvent surface to the active site [82]? The observation of specific regions of increased protein flexibility at elevated temperatures for the ht-ADH, Fig. 6, that are correlated with changes in tunneling properties [55] supports the idea that energy transmission is specific to a protein fold rather than being uniformly distributed throughout the protein. For the long run, the ability to provide a temporally and spatially defined map of protein motions would go a very long way toward the goal of a ‘road map’ for de novo protein design.
After more than a half century of investigation into the origins of enzyme catalysis, it is gratifying to see the extensive new insights that can be gleaned from the properties of H-tunneling in enzyme catalyzed reactions. The present juncture is an exciting one, providing intellectually provocative models of enzyme catalysis that suggest new avenues for experimental and computational investigations. What is clear is that the conceptual basis for catalysis has moved beyond a straightforward correlation of function to structure to one in which the dominant paradigm is structure → dynamics → function.
Acknowledgements
This work was supported by funds from the National Science Foundation (MCB 0446395) and National Institutes of Health (GM025765). I gratefully acknowledge the talented researchers in my laboratory, present and past, who have made such extensive intellectual and experimental contributions to this work. I also wish to thank Mae Tulfo and Zac Nagel for the execution of the art work on the cover: as drawn, the space filling model repressents the ht-ADH; superimposed on this protein model are energy diagrams representing pre-organization (left) and reorganization (right).
Biography

Judith P. Klinman was born in the city of Philadelphia, PA (USA) in 1941 and educated at the University of Pennsylvania (A.B. 1962 and Ph.D, l966). She spent several years as a postdoctoral fellow at the Weizmann Institute in Israel and at the Fox Chase Cancer Research Center in Philadelphia. After beginning her independent career as a Research Scientist at Fox Chase, she moved to the University of California in l978, where she is now Professor of Chemistry and Professor of Molecular and Cell Biology. Her lifelong fascination with enzymes has led her to investigate a wide range of different enzyme systems, with one particular focus being the study of isotope effects as applied to the properties of enzymatic C–H activation.
References
- [1].Wolfenden R, Snider MJ. Acc. Chem. Res. 2001;34:938. doi: 10.1021/ar000058i. [DOI] [PubMed] [Google Scholar]
- [2].Dwyer MA, Looger LL, Hellinga HW. Science. 2008;319:569. doi: 10.1126/science.319.5863.569b. [DOI] [PubMed] [Google Scholar]
- [3].Jiang L, et al. Science. 2005;309:1868. [Google Scholar]
- [4].Pauling L. Am. Sci. 1948;36:51. [PubMed] [Google Scholar]
- [5].Wolfenden R. In: Transition States of Biochemical Processes. Gandour RD, Schowen RL, editors. Plenum Press; New York and London: 1978. p. 558. [Google Scholar]
- [6].Schramm VL. Ann. Rev. Biochem. 1998;67:693. doi: 10.1146/annurev.biochem.67.1.693. [DOI] [PubMed] [Google Scholar]
- [7].Fersht A. Enzyme Structure and Mechanism. second edn W.H. Freeman & Co.; New York: 2007. p. 405. [Google Scholar]
- [8].Page MI, Jencks WP. Proc. Natl. Acad. Sci. USA. 1971;68:1678. doi: 10.1073/pnas.68.8.1678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Schray K, Klinman JP. Biochim. Biophys. Res. Commun. 1974;57:641. doi: 10.1016/0006-291x(74)90594-4. [DOI] [PubMed] [Google Scholar]
- [10]. <http://www.molmoodb.org>.
- [11].Yang H, et al. Science. 2003;302:262. doi: 10.1126/science.1086911. [DOI] [PubMed] [Google Scholar]
- [12].Marcus RA. Pure Appl. Chem. 1997;69:13. [Google Scholar]
- [13].Marcus RA, Sutin N. Biochim. Biophys. Acta. 1985;811:265. [Google Scholar]
- [14].Sumi H, Marcus RA. J. Chem. Phys. 1986;84:4894. [Google Scholar]
- [15].Giese B, Spochty M, Wessely S. Pure Appl. Chem. 2001;73:449. [Google Scholar]
- [16].Gray HB, Winkler JR. Proc. Natl. Acad. Sci. USA. 2005;102:3534. doi: 10.1073/pnas.0408029102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Mayer JM. Ann. Rev. Phys. Chem. 2004;55:363. doi: 10.1146/annurev.physchem.55.091602.094446. [DOI] [PubMed] [Google Scholar]
- [18].Welsh KM, Creighton DJ, Klinman JP. Biochemistry. 1980;19:2005. doi: 10.1021/bi00551a001. [DOI] [PubMed] [Google Scholar]
- [19].Hermes JD, Morrical SW, O’Leary MH, Cleland WW. Biochemistry. 1984;23:5479. doi: 10.1021/bi00318a016. [DOI] [PubMed] [Google Scholar]
- [20].Huskey WP, Schowen RL. J. Am. Chem. Soc. 1983;105:5704. [Google Scholar]
- [21].Huskey WP. Phys. Org. Chem. 1991;4:361. [Google Scholar]
- [22].Knapp MJ, Meyer M, Klinman JP. Hydrogen Transfer Reactions. Wiley, VCH; Germany: 2007. [Google Scholar]
- [23].Grant KL, Klinman JP. Biochemistry. 1989;28:6597. doi: 10.1021/bi00442a010. [DOI] [PubMed] [Google Scholar]
- [24].Schneider ME, Stern HJ. J. Am. Chem. Soc. 1972;94:1517. The focus on energies of activation rather than enthalpies of activation comes from these early studies using the Arrhenius expression to relate ln k to 1/T. Treatment of the temperature dependence of rate according to transition state theory leads to ΔH‡, which is easily related to the Eact by RT.
- [25].Jonsson T, Edmondson DE, Klinman JP. Biochemistry. 1994;33:1487. doi: 10.1021/bi00253a026. [DOI] [PubMed] [Google Scholar]
- [26].Seymour SL, Klinman JP. Biochemistry. 2002;41:8747. doi: 10.1021/bi020054g. [DOI] [PubMed] [Google Scholar]
- [27].Whittaker MM, Ballou DP, Whittaker JW. Biochemistry. 1998;37:8426. doi: 10.1021/bi980328t. [DOI] [PubMed] [Google Scholar]
- [28].Chowdhury S, Banerjee R. J. Am. Chem. Soc. 2000;122:5417. [Google Scholar]
- [29].Glickman MH, Klinman JP. Biochemistry. 1996;35:12882. doi: 10.1021/bi960985q. [DOI] [PubMed] [Google Scholar]
- [30].Bollinger JM, Jr., Krebs C. J. Inorg. Biochem. 2006;100:586. doi: 10.1016/j.jinorgbio.2006.01.022. [DOI] [PubMed] [Google Scholar]
- [31].Glickman MH, Wiseman J, Klinman JP. J. Am. Chem. Soc. 1994;116:793. [Google Scholar]
- [32].Hwang CC, Grissom CB. J. Am. Chem. Soc. 1994;116:795. [Google Scholar]
- [33].Jonsson T, Glickman MH, Klinman JP. J. Am. Chem. Soc. 1996;118:10319. [Google Scholar]
- [34].Knapp MJ, Rickert K, Klinman JP. J. Am. Chem. Soc. 2002;124:3865. doi: 10.1021/ja012205t. [DOI] [PubMed] [Google Scholar]
- [35].Meyer M, Klinman JP. Proc. Natl. Acad. Sci. USA. 2008;105:1146. doi: 10.1073/pnas.0710643105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Kuznetsov AM, Ulstrup AM. Can. J. Chem. 1999;77:1085. [Google Scholar]
- [37].Bruno WJ, Bialek W. Biophys. J. 1992;63:689. doi: 10.1016/S0006-3495(92)81654-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Kohen A, Cannio R, Bartolucci S, Klinman JP. Nature. 1999;39:496. doi: 10.1038/20981. [DOI] [PubMed] [Google Scholar]
- [39].Wille WAG, Smith AJ, Merkler DJ, Klinman JP. J. Am. Chem. Soc. 2002;124:8194. [Google Scholar]
- [40].Basran J, Sutcliffe MJ, Scrutton NS. Biochemistry. 1999;38:3218. doi: 10.1021/bi982719d. [DOI] [PubMed] [Google Scholar]
- [41].Basran J, Sutcliffe MJ, Scrutton NS. J Biol. Chem. 2001;276:245. doi: 10.1074/jbc.M108296200. [DOI] [PubMed] [Google Scholar]
- [42].Harris RJ, Meskys R, Sutcliffe MJ, Scrutton NS. Biochemistry. 2000;39:1189. doi: 10.1021/bi991941v. [DOI] [PubMed] [Google Scholar]
- [43].Abad JL, Camps F, Fabrias G. Angew. Chem. Int. Ed. 2000;39:3279. doi: 10.1002/1521-3773(20000915)39:18<3279::aid-anie3279>3.0.co;2-g. [DOI] [PubMed] [Google Scholar]
- [44].Sikorski RS, Wang L, Markham KA, Rajagopalan PTR, Benkovic SJ, Kohen A. J. Am. Chem. Soc. 2004;12:4778. doi: 10.1021/ja031683w. [DOI] [PubMed] [Google Scholar]
- [45].Fan F, Gadda G. Biochemistry. 2007;46:6402. doi: 10.1021/bi700255v. [DOI] [PubMed] [Google Scholar]
- [46].Gupta A, Mukherjee A, Matsui K, Roth JP. J. Am. Chem. Soc. 2008;130:11274. doi: 10.1021/ja8042273. [DOI] [PubMed] [Google Scholar]
- [47].Hatcher E, Soudackov V, Hammes-Schiffer S. J. Am. Chem. Soc. 2007;129:187. doi: 10.1021/ja0667211. [DOI] [PubMed] [Google Scholar]
- [48].Nagel Z, Klinman JP. Chem. Rev. 2006;106:3095. doi: 10.1021/cr050301x. [DOI] [PubMed] [Google Scholar]
- [49].Klinman JP. In: Royal Society of Chemistry. Allemann R, Scrutton N, editors. Cambridge: 2009. pp. 132–160. [Google Scholar]
- [50].Benkovic SJ, Hammes-Schiffer S. Science. 2006;312:208. doi: 10.1126/science.1127654. [DOI] [PubMed] [Google Scholar]
- [51].Meyer M, Klinman JP. Chem. Phys. 2005;319:283. doi: 10.1016/j.chemphys.2005.05.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Karlsson A, El-Ahmad M, Johansson K, Shafqat J, Jornvall H, Eklund H, Ramaswamy S. Chem.-Biol. Interact. 2003;143:239. doi: 10.1016/s0009-2797(02)00222-3. [DOI] [PubMed] [Google Scholar]
- [53].Ceccarelli C, Liang Z-X, Strickler M, Prehna G, Goldstein BM, Klinman JP, Bahnson BJ. Biochemistry. 2004;43:5266. doi: 10.1021/bi049736p. [DOI] [PubMed] [Google Scholar]
- [54].Kohen A, Klinman JP. J. Am. Chem. Soc. 2000;122:10738. [Google Scholar]
- [55].Liang Z-X, Lee T, Resing KA, Ahn NG, Klinman JP. Proc. Natl. Acad. Sci. USA. 2004;101:9556. doi: 10.1073/pnas.0403337101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Hoofnagle A, Resing K, Ahn NG. Ann. Rev. Biophys. Biol. Struct. 2003;32:110601. doi: 10.1146/annurev.biophys.32.110601.142417. [DOI] [PubMed] [Google Scholar]
- [57].Geeves MA, Koerber SC, Dunn MF, Fink AL. J. Biol. Chem. 1983;258:12184. [PubMed] [Google Scholar]
- [58].Tsai S, Klinman JP. Biochemistry. 2001;40:2303. doi: 10.1021/bi002075l. [DOI] [PubMed] [Google Scholar]
- [59].Vitkup P, Ringer D, Petsko GA, Karplus M. Nature Struct. Biol. 2000;7:43. doi: 10.1038/71231. [DOI] [PubMed] [Google Scholar]
- [60].Bahnson BJ, Park D-H, Kim K, Plapp BV, Klinman JP. Biochemistry. 1993;31:5503. doi: 10.1021/bi00072a003. [DOI] [PubMed] [Google Scholar]
- [61].Tsai SC, Klinman JP. Bioorg. Chem. 2003;31:170. doi: 10.1016/S0045-2068(03)00018-X. [DOI] [PubMed] [Google Scholar]
- [62].Fenimore PN, Frauenfelder H, McMahon BH, Parak FG. Proc. Natl. Acad. Sci. USA. 2002;99:16047. doi: 10.1073/pnas.212637899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [63].The clones and conditions for expression were kindly provided by Dr. Steve Rosenberg, Chiron.
- [64].Kohen A, Jonsson T, Klinman JP. Biochemistry. 1997;36:2603. doi: 10.1021/bi962492r. [DOI] [PubMed] [Google Scholar]
- [65].Sharma S, Klinman JP. J. Am. Chem. Soc. 2008;130:17632. doi: 10.1021/ja806354w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [66].Tsai AM, Udovic TJ, Neumann DA. Biophys. J. 2001;81:2339. doi: 10.1016/S0006-3495(01)75880-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [67].Henzler-Widman K, Kern D. Nature. 2007;450:964. doi: 10.1038/nature06522. [DOI] [PubMed] [Google Scholar]
- [68].Lightstone FC, Bruice TC. Bioorg. Chem. 1998;26:193. [Google Scholar]
- [69].Oyeyemi O, Sours KM, Lee T, Resing KA, Ahn NG, Klinman JP. in preparation.
- [70].The representation in Fig. 9 contrasts with that used in the protein folding field, where the vertical direction (moving from unfolded to fully folded protein) is plotted as a function of enthalpy
- [71].Liang Z-X, Tsigos I, Bouriotis V, Klinman JP. J. Am. Chem. Soc. 2004;126:9500. doi: 10.1021/ja047087z. [DOI] [PubMed] [Google Scholar]
- [72].Wang L, Goodey MM, Benkovic SJ, Kohen A. Proc. Natl. Acad. Sci. USA. 2006;103:15753. doi: 10.1073/pnas.0606976103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [73].Nagel Z, Klinman JP. in preparation.
- [74].Klinman JP. Philos. Trans. Royal Soc. B. 2006;361:21114. doi: 10.1098/rstb.2006.1870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [75].Frauenfelder H, McMahon BH, Fenimore PW. Proc. Natl. Acad. Sci. USA. 2003;100:8615. doi: 10.1073/pnas.1633688100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [76].Hanson JA, Duclerstacit K, Watkins LP, Bhattacharyya S, Brokaw J, Chu J-W, Yang H. Proc. Natl. Acad. Sci. USA. 2007;104:18055. doi: 10.1073/pnas.0708600104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [77].Henzler-Wildman KA, et al. Nature. 2007:838. doi: 10.1038/nature06522. [DOI] [PubMed] [Google Scholar]
- [78].Schnell JR, Dyson HJ, Wright PE. Ann. Rev. Biophys. Biomol. Struct. 2004;33:119. doi: 10.1146/annurev.biophys.33.110502.133613. [DOI] [PubMed] [Google Scholar]
- [79].Greener M. Scientist. 2005;19:17. [Google Scholar]
- [80].Rodgers J, Femec DA, Schowen RL. J. Am. Chem. Soc. 1982;104:3263. [Google Scholar]
- [81].Bahnson BJ, Colby TD, Chin JK, Goldstein BM, Klinman JP. Proc. Natl. Acad. Sci. USA. 1997;94:12797. doi: 10.1073/pnas.94.24.12797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [82].Lockless AW, Ranganathan R. Science. 1999;286:295. doi: 10.1126/science.286.5438.295. [DOI] [PubMed] [Google Scholar]
- [83].Minor W, Steczko J, Stec B, Otwinowski Z, Bolin JT, Walter R, Axelrod B. Biochemistry. 1996;35:10687. doi: 10.1021/bi960576u. [DOI] [PubMed] [Google Scholar]
- [84].Boyington JC, Gaffney B, Amzel LM. Science. 1993;260:1482. doi: 10.1126/science.8502991. [DOI] [PubMed] [Google Scholar]
- [85].Bahnson BJ, Park D-H, Kim K, Plapp BV, Klinman JK. Biochemistry. 1993;31:5503. doi: 10.1021/bi00072a003. [DOI] [PubMed] [Google Scholar]