Abstract
Epistasis refers to the interaction between genes. Although high-throughput epistasis data from model organisms are being generated and used to construct genetic networks1-3, to what extent genetic epistasis reflects biologically meaningful interactions remains unclear4-6. We address this question by in silico mapping of positive and negative epistatic interactions amongst biochemical reactions within the metabolic networks of E. coli and S. cerevisiae using flux balance analysis. We found that negative epistasis occurs mainly between nonessential reactions with overlapping functions, whereas positive epistasis usually involves essential reactions, is highly abundant, and surprisingly, often occurs between reactions without overlapping functions. We offered mechanistic explanations of these findings and experimentally validated them for 61 S. cerevisiae gene pairs.
Epistasis refers to the phenomenon that the effect of a gene on a trait is masked or enhanced by one or more other genes6,7. Fisher and other population and quantitative geneticists extended the concept to mean non-independent or non-multiplicative effects of genes6,8. The direction, magnitude, and prevalence of epistasis is important for understanding gene function and interaction2,6,9, speciation10, evolution of sex and recombination11,12, evolution of ploidy13, mutation load14, genetic buffering15, human disease4,5, and drug-drug interaction16. Epistasis in fitness between two mutations is commonly defined by ε = WX ȲWXWY, where WX and WY represent the fitness values of two single mutants relative to the wild-type and WXY represents the fitness of the corresponding double mutant. Epistasis is said to be positive when ε > 0, and negative when ε < 0. When deleterious mutations are concerned, positive epistasis lessens the fitness reduction predicted from individual mutational effects, whereas negative epistasis enhances it. The magnitude of epistasis between different pairs of mutations may be compared using scaled epistasis ε̃ 17, which is transformed from and has the same sign as ε, but is normally bounded between -1 and 1. We apply flux balance analysis (FBA) of metabolic networks18 to explore the functional association between biochemical reactions that are epistatic to each other. Assuming a steady state in metabolism, FBA maximizes the rate of biomass production under the stoichiometric matrix of all reactions and a set of flux constraints. The maximized rate in a mutant strain relative to that in the wild-type strain can be regarded as the fitness of the mutant relative to the wild-type17. FBA can be used to investigate the fitness of the cell under various environmental and genetic perturbations19,20 and has been used to generate the epistasis map of yeast metabolic genes17,21,22. We first study the bacterium Escherichia coli, because its reconstructed metabolic network is of high quality and its FBA predictions have been empirically verified20,23.
Using FBA, we identified from the E. coli metabolic network 270 reactions whose removal reduces the fitness under the glucose minimal medium. Removing any of the remaining 661 reactions has no such effect, primarily because the reaction has zero flux under this medium, or occasionally because the network has another reaction that can fully compensate its loss. Among the 270 reactions, 212 are essential, meaning that deleting any one of them results in zero fitness. We considered a genetic perturbation in each reaction that constrains its flux to ≤50% of its wild-type optimal value and then computed the fitness of the mutant by FBA. We similarly computed the fitness values of all possible double mutants and obtained ε and ε̃ for all pairs of the 270 reactions, which reveal the global epistasis pattern within the metabolic network (Supplementary Table 1). Constraining the flux to ≤50% instead of zero17,21,22 allows the investigation of essential reactions. Consequently, the number of pairwise epistasis values obtained here exceeds 25 times that previously obtained17. Constraining the flux to other non-zero levels does not alter our results qualitatively (Supplementary Table 1).
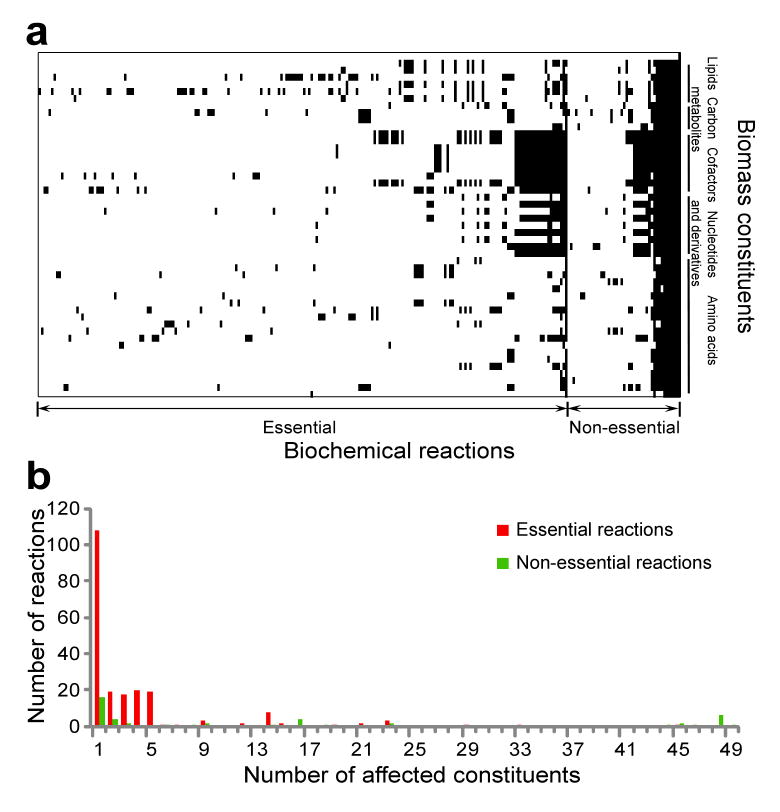
To examine whether metabolic reactions with epistatic relationships are functionally associated, we need to identify the function of each reaction in generating the E. coli biomass, which is composed of 49 constituents. If a reaction is important for producing a set of biomass constituents, the removal of these constituents from the biomass function will recover the biomass reduction caused by the deletion of the reaction. Based on this idea, we designed a removal-recovery method to determine the functions of 255 of the 270 important reactions in generating biomass constituents (Fig. 1a). For the remaining 15 reactions, the functions cannot be unambiguously determined and thus they are excluded from our analysis. The majority of the 255 reactions each contribute to only one biomass constituent, whereas a small number of reactions affect many or even all 49 constituents (Fig. 1b). Note that the glucose minimal medium is again used in determining the function of each reaction, because some reactions have variable functions in different media. Functional assignment by our method is generally consistent with the conventional functional annotation of E. coli reactions24, but our assignment is expected to be more precise in identifying the biomass constituents contributed by each reaction.
Fig. 1.
Functions of E. coli metabolic reactions under the glucose minimal medium. (a) Functions of 255 important reactions in producing 49 biomass constituents. Columns represent reactions and rows represent biomass constituents. (b) Distribution of the number of biomass constituents affected by a reaction.
We found 26 (0.08%) reaction pairs that show apparent negative epistasis (ε̃ ≤ -0.01). Among them, 25 pairs each share functions in producing at least one biomass constituent (Table 1; Fig. 2a, 2b). The remaining pair is between reactions MALS (catalyzed by malate synthase) and PPC (phosphoenolpyruvate carboxylase), anaplerotic reactions feeding the Krebs cycle. The lack of shared biomass constituents between them is due to the incomplete identification of MALS and PPC functions caused by their mutual functional compensation (Supplementary Figure 1). A common interpretation of negative epistasis between two genes is that the two genes can individually perform a common function and thus each of them is able to compensate the loss of the other. Our observation that virtually every pair of reactions with negative epistasis share at least one function strongly support this interpretation (Fig. 2b). While negative epistasis might be expected to occur between two nonessential reactions, this is not absolute. For example, two essential reactions (or one essential reaction and one nonessential reaction) may share a nonessential function in producing a biomass constituent and show negative epistasis by this common function (Table 1).
Table 1.
Numbers of reaction pairs that show epistatic relationships in glucose minimal medium.
| Epistasis in E. coli2 | Epistasis in yeast2 | ||||||
|---|---|---|---|---|---|---|---|
| Reaction pairs1 | Functions | Negative | Zero | Positive | Negative | Zero | Positive |
| E-E | With overlap | 0 | 9 | 4269 | 1 | 2 | 1780 |
| Without overlap | 0 | 0 | 17667 | 0 | 3 | 10617 | |
| Sum | 0 | 9 | 21936 | 1 | 5 | 12397 | |
| E-N | With overlap | 3 | 83 | 3704 | 10 | 67 | 2153 |
| Without overlap | 0 | 34 | 5626 | 0 | 99 | 6203 | |
| Sum | 3 | 117 | 9330 | 10 | 166 | 8356 | |
| N-N | With overlap | 22 | 267 | 288 | 24 | 137 | 402 |
| Without overlap | 1 | 339 | 73 | 7 | 661 | 200 | |
| Sum | 23 | 606 | 361 | 31 | 798 | 602 | |
| All | With overlap | 25 | 359 | 8261 | 35 | 206 | 4335 |
| Without overlap | 1 | 373 | 23366 | 7 | 763 | 17020 | |
| Sum | 26 | 732 | 31627 | 42 | 969 | 21355 | |
Pairwise relationships among 255 important E. coli reactions and among 212 important yeast reactions. E, essential reaction; N, nonessential reaction.
Scaled epistasis of ≥ 0.01 is considered positive, ≤ −0.01 is considered negative, and between -0.01 and 0.01 is considered zero.
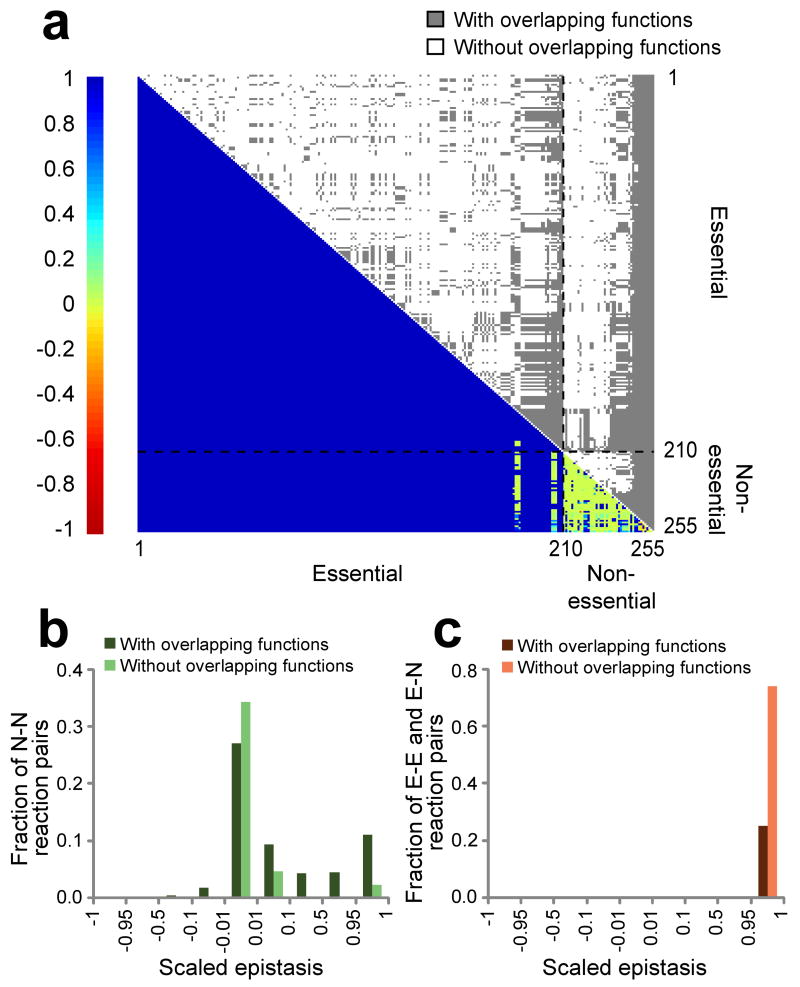
Fig. 2.
Pairwise epistasis and functional association among 255 important reactions in E. coli. (a) An overview of epistasis and functional association among reactions. Both rows and columns represent reactions. Scaled epistasis between reactions is shown in the lower-left triangle by the heat map. Functional association between reactions is presented in the upper-right triangle, where a grey dot is shown when two reactions have overlapping functions. Epistasis and reaction functions are both determined in the glucose minimal medium. (b) Frequency distribution of scaled epistasis between nonessential reactions. (c) Frequency distribution of scaled epistasis between two reactions that include at least one essential reaction. E, essential; N, nonessential. Note the difference in Y-scale between panel b and c.
In contrast to the rare occurrence of negative epistasis, >97% of reaction pairs exhibit apparent positive epistasis (ε̃ ≥ 0.01) (Fig. 2a). However, only ∼26% of them occur between reactions that share at least one biomass constituent (Table 1; Fig. 2c). There is also no significant difference in ε or ε̃ between functionally overlapping and non-overlapping reaction pairs with positive epistasis. It is often observed that a reaction is positively epistatic with a large number of apparently unrelated reactions. Use of ε instead of ε̃ in measuring epistasis does not change this pattern. The lack of functional overlap between most positively epistatic reaction pairs challenges the general interpretation of epistasis as functional association2,9,25.
Why does positive epistasis occur so frequently between functionally unrelated reactions? Fig. 2a shows that virtually every essential reaction exhibits strong positive epistasis (ε̃ ∼ 1) with any other reaction regardless of its function and essentiality. This can be explained by considering that, when an essential reaction is constrained, almost all other reactions in the network do not work in their full capacity such that the composition stoichiometry of the biomass is still maintained (Supplementary Figure 2a, 2b). Consequently, a genetic perturbation in a second reaction that reduces its capacity will have a negligible additional effect, resulting in positive epistasis. Note that positive epistasis sometimes occurs between nonessential genes and in these cases ∼80% (288/361) show functional overlaps (Fig. 2b).
Why is there no such effect between nonessential reactions? There are three requirements for a metabolic reaction to be considered here as important yet nonessential. First, it must function in producing one or more biomass constituents. Second, there must be alternative reactions that can also make its product. Third, compared with the alternative reactions, it must be more efficient in producing at least one constituent. When the flux of a nonessential reaction is constrained, its less efficient alternative reaction will be turned on (Supplementary Figure 2c). Due to the lower efficiency of the alternative reaction, nutrients that previously went through other reactions for making other biomass constituents can be redistributed in such a way that the biomass reduction by the flux constraint is minimized (Supplementary Figure 2c). It can be shown mathematically that when the number of reactions in the network is large, perturbations of two functionally unrelated nonessential reactions will have a nearly multiplicative effect on biomass production and cause negligibly weak positive epistasis15,17 (Supplementary Note).
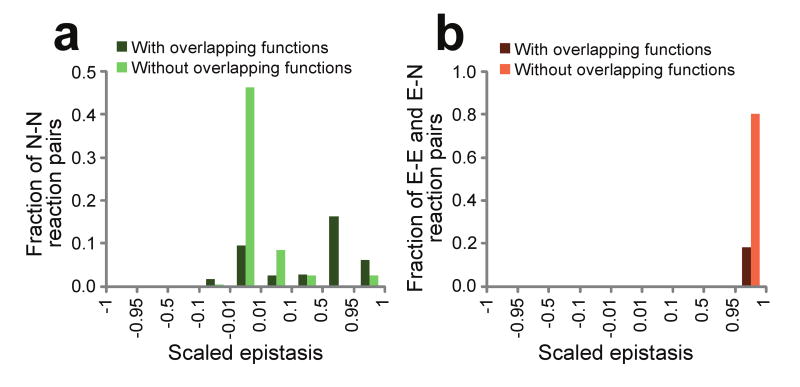
Saccharomyces cerevisiae is another species whose reconstructed high-quality metabolic networks have been extensively validated experimentally19,21. We repeated the above FBA in S. cerevisiae and obtained similar general findings on the frequencies of positive and negative epistasis and the functional relationships of epistatic reactions (Table 1; Fig. 3). Specifically, only 0.2% of reaction pairs show negative epistasis (ε̃ ≤ -0.01), 83% of which have functional overlaps. By contrast, >95% of reaction pairs show positive epistasis (ε̃ ≥ 0.01), but only 20% of which have overlapping functions.
Fig. 3.
Pairwise epistasis and functional association among 212 important reactions in yeast. (a) Frequency distribution of scaled epistasis between nonessential reactions. (b) Frequency distribution of scaled epistasis between two reactions that include at least one essential reaction. E, essential; N, nonessential. Note the difference in Y-scale between panel a and b.
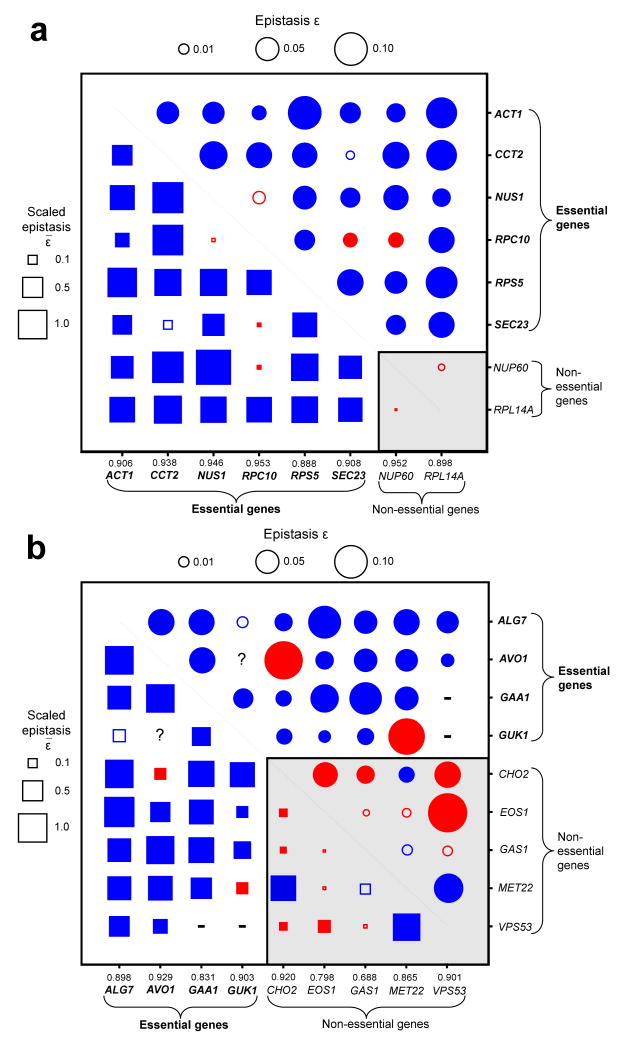
Our computational results appear to be robust against several potential caveats in the computational analysis (Supplementary Note). We further pursued experimental validation of our computational predications in S. cerevisiase, due to the difficulty in conducting partial gene deletion in E. coli. Six essential and two nonessential genes from seven functional categories were examined (Supplementary Tables 2 and 3). We deleted one allele per gene from a diploid S. cerevisiae to achieve partial disruption of a gene. Haploinsufficient genes were used to ensure that partial gene disruption affects fitness. Only non-metabolic genes were examined, because metabolic genes are rarely haploinsufficient26. Non-metabolic genes are expected to behave similarly as metabolic genes in terms of epistasis27, as long as the final product is composed of multiple constituents with a fixed or preferred composition stoichiometry. We then measured the fitness of each strain through a growth competition assay with a reference strain followed by cell counting using fluorescence activated cell sorting (FACS). We then calculated the fitness values of all single-deletion strains and all pairwise double-deletion strains relative to the wild-type, which allowed the estimation of epistasis between genes (Online Methods, Supplementary Note). Among the 27 gene pairs that involve at least one essential gene, 23 (85%) have significantly positive ε (P < 0.05, t test), two have significantly negative ε, and the remaining two do not show significant epistasis (Fig. 4a). The mean ε̃ among the 23 positively epistatic pairs is 0.78, and 11 of them have ε̃ not significantly smaller than 1. The epistasis between the two nonessential genes is not statistically significant. These results strongly support the general findings of our computational predictions that essential genes often show epistasis with functionally unrelated genes.
Fig. 4.
Epistasis (ε) and scaled epistasis (ε̃) among 17 yeast genes. Circles show ε, whereas squares show ε̃. Blue and red colors indicate positive and negative epistasis, respectively, whereas the areas of the circles and squares are proportional to the absolute values of ε and ε̃, respectively, with the scales given on the top and left sides of each panel. Solid symbols indicate statistically significant epistasis (P < 0.05), whereas open symbols indicate insignificant epistasis. The shaded area in the lower-right corner shows relationships between nonessential genes. Fitness values of strains with genes replaced/inserted by LEU2, relative to the wild-types, are presented on the X-axis. (a) Epistasis among 8 haploinsufficient genes, measured in diploid cells after deletion of one allele per gene. All genes belong to different functional categories with the exception of RPS5 and RPL14A, both of which encode ribosomal proteins. (b) Epistasis among 9 haplosufficient genes, measured in haploid cells after reduction of protein expression of essential genes and deletion of nonessential genes. All genes belong to different functional categories with the exception of GAA1 and GAS1. MET22 and CHO2 are metabolic genes, with FBA-predicted scaled epistasis equal to 1. “-”, double-perturbation cells could not be obtained, likely due to unsuccessful experiments or synthetic lethality. “?”, epistasis could not be measured due to the lack of fitness effect of single perturbations. In Supplementary Figure 5, we explain why here negative epistasis between nonessential genes appears more abundant than expected.
Because the above experiment could not examine haplosufficient genes, we employed the newly developed DAmP method28 to mimic partial gene deletion, in which a marker gene is inserted into the 3′ untranslated region of a gene such that its protein expression may be reduced to <50%. We studied 9 haplosufficient genes belonging to 8 functional categories, including 4 essential genes that are knocked down by DAmP and 5 nonessential genes that are knocked out (Supplementary Table 2). We were able to measure the epistasis of 33 of the 36 gene pairs in haploid cells (Fig. 4b; Supplementary Table 4). Of the 23 gene pairs that have epistasis estimates and involve at least one essential gene, 20 (87%) show significantly positive ε (P < 0.05, t test), two show significantly negative ε, and the remaining one does not show significant epistasis (Fig. 4b). These results further support our computational result of abundant positive epistasis involving essential genes, even among functionally unrelated ones. In the Supplementary Note, we discuss possible explanations for why selected previous studies examining the extent of epistasis in E. coli, yeast, and other species did not find a comparably high prevalence of positive epistasis1-3,15,17,29.
In summary, our flux balance analysis of the E. coli and yeast metabolic networks and the subsequent experimental validations for 61 gene pairs in S. cerevisiae reveals a high prevalence of positive epistasis involving essential genes. While negative epistasis was usually found amongst genes involved in reactions with overlapping functions, positive epistasis often occurs amongst genes involved in reactions with unrelated functions. The proportion of essential genes is ∼7% in E. coli, 17% in S. cerevisiae, and 55% in mouse30, and positive epistasis is therefore likely to be even more prevalent in higher eukaryotes than is discovered here. These findings suggest the distinction of genetic interaction from non-multiplicative (or non-additive) gene effects and caution against the use of positive epistasis to infer genetic pathways and gene-gene interactions. While one may argue that, because all metabolic genes share functions in supporting cell growth, their epistasis is not surprising, we suggest that, if epistasis corresponds to such crude functional relationship, it provides little biological insight. Although our results are presented primarily using ε̃, it is clear that positive epistasis is highly abundant and much more prevalent than negative epistasis even when ε is used (Supplementary Figures 3 and 4). This is also the case when the majority of mutations are only slightly deleterious (Supplementary Table 5). These observations also suggest the need for reevaluation of evolutionary theories that depend on overall negative epistasis, such as the mutational deterministic hypothesis of the evolution of sexual reproduction11 and the hypothesis of reduction in mutational load by truncation selection against deleterious mutations14.
Methods
Methods and any associated references are available in the online version of the paper at http://www.nature.com/naturegenetics/.
Supplementary Material
Acknowledgments
We thank Anuj Kumar for yeast strains and plasmids, Nike Bharucha, Gizem Kalay, Anuj Kumar, Jun Ma, and Barry Williams for advice and assistance in yeast experiments, Bernhard Palsson and his group for instruction on FBA, Ben-Yang Liao for drawing Supplementary Figure 2, and Meg Bakewell, Soochin Cho, Wendy Grus, Ben-Yang Liao, and Calum Maclean for valuable comments. This work was supported by research grants from the National Institutes of Health and University of Michigan Center for Computational Medicine and Biology to J.Z.
Footnotes
Author Contributions: X.H. and J.Z. conceived the research. X.H., Z.W., W.Q. and J.Z. designed the experiments. X.H., W.Q., W.Z., Y.L. and J.Z. conducted the experiments. X.H., W.Q., W.Z. and J.Z. analyzed the data. X.H. and J.Z. drafted the manuscript and all authors contributed to the final manuscript writing and its revisions.
We have no competing financial interests.
URLs: Additional analyses related to this publication can be found at http://www.umich.edu/∼zhanglab/download.htm.
References
- 1.Tischler J, Lehner B, Fraser AG. Evolutionary plasticity of genetic interaction networks. Nat Genet. 2008;40:390–1. doi: 10.1038/ng.114. [DOI] [PubMed] [Google Scholar]
- 2.Boone C, Bussey H, Andrews BJ. Exploring genetic interactions and networks with yeast. Nat Rev Genet. 2007;8:437–49. doi: 10.1038/nrg2085. [DOI] [PubMed] [Google Scholar]
- 3.Roguev A, et al. Conservation and rewiring of functional modules revealed by an epistasis map in fission yeast. Science. 2008;322:405–10. doi: 10.1126/science.1162609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Moore JH, Williams SM. Traversing the conceptual divide between biological and statistical epistasis: systems biology and a more modern synthesis. BioEssays. 2005;27:637–46. doi: 10.1002/bies.20236. [DOI] [PubMed] [Google Scholar]
- 5.Cordell HJ. Epistasis: what it means, what it doesn't mean, and statistical methods to detect it in humans. Hum Mol Genet. 2002;11:2463–8. doi: 10.1093/hmg/11.20.2463. [DOI] [PubMed] [Google Scholar]
- 6.Phillips PC. Epistasis--the essential role of gene interactions in the structure and evolution of genetic systems. Nat Rev Genet. 2008;9:855–67. doi: 10.1038/nrg2452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bateson W. Mendel's Principles of Heredity. Cambridge University Press; Cambridge: 1909. [Google Scholar]
- 8.Fisher RA. The correlations between relatives on the supposition of Mendelian inheritance. Trans R Soc Edinburgh. 1918;52:399–433. [Google Scholar]
- 9.Hartman JL, Garvik B, Hartwell L. Principles for the buffering of genetic variation. Science. 2001;291:1001–4. doi: 10.1126/science.291.5506.1001. [DOI] [PubMed] [Google Scholar]
- 10.Coyne JA. Genetics and speciation. Nature. 1992;355:511–5. doi: 10.1038/355511a0. [DOI] [PubMed] [Google Scholar]
- 11.Kondrashov AS. Deleterious mutations and the evolution of sexual reproduction. Nature. 1988;336:435–40. doi: 10.1038/336435a0. [DOI] [PubMed] [Google Scholar]
- 12.Barton NH, Charlesworth B. Why sex and recombination? Science. 1998;281:1986–90. [PubMed] [Google Scholar]
- 13.Kondrashov AS, Crow JF. Haploidy or diploidy: which is better? Nature. 1991;351:314–5. doi: 10.1038/351314a0. [DOI] [PubMed] [Google Scholar]
- 14.Crow JF, Kimura M. Efficiency of truncation selection. Proc Natl Acad Sci U S A. 1979;76:396–399. doi: 10.1073/pnas.76.1.396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Jasnos L, Korona R. Epistatic buffering of fitness loss in yeast double deletion strains. Nat Genet. 2007;39:550–4. doi: 10.1038/ng1986. [DOI] [PubMed] [Google Scholar]
- 16.Yeh P, Tschumi AI, Kishony R. Functional classification of drugs by properties of their pairwise interactions. Nat Genet. 2006;38:489–94. doi: 10.1038/ng1755. [DOI] [PubMed] [Google Scholar]
- 17.Segre D, Deluna A, Church GM, Kishony R. Modular epistasis in yeast metabolism. Nat Genet. 2005;37:77–83. doi: 10.1038/ng1489. [DOI] [PubMed] [Google Scholar]
- 18.Price ND, Reed JL, Palsson BO. Genome-scale models of microbial cells: evaluating the consequences of constraints. Nat Rev Microbiol. 2004;2:886–97. doi: 10.1038/nrmicro1023. [DOI] [PubMed] [Google Scholar]
- 19.Papp B, Pal C, Hurst LD. Metabolic network analysis of the causes and evolution of enzyme dispensability in yeast. Nature. 2004;429:661–4. doi: 10.1038/nature02636. [DOI] [PubMed] [Google Scholar]
- 20.Ibarra RU, Edwards JS, Palsson BO. Escherichia coli K-12 undergoes adaptive evolution to achieve in silico predicted optimal growth. Nature. 2002;420:186–9. doi: 10.1038/nature01149. [DOI] [PubMed] [Google Scholar]
- 21.Harrison R, Papp B, Pal C, Oliver SG, Delneri D. Plasticity of genetic interactions in metabolic networks of yeast. Proc Natl Acad Sci U S A. 2007;104:2307–12. doi: 10.1073/pnas.0607153104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Deutscher D, Meilijson I, Kupiec M, Ruppin E. Multiple knockout analysis of genetic robustness in the yeast metabolic network. Nat Genet. 2006;38:993–8. doi: 10.1038/ng1856. [DOI] [PubMed] [Google Scholar]
- 23.Edwards JS, Ibarra RU, Palsson BO. In silico predictions of Escherichia coli metabolic capabilities are consistent with experimental data. Nat Biotechnol. 2001;19:125–30. doi: 10.1038/84379. [DOI] [PubMed] [Google Scholar]
- 24.Reed JL, Vo TD, Schilling CH, Palsson BO. An expanded genome-scale model of Escherichia coli K-12 (iJR904 GSM/GPR) Genome Biol. 2003;4:R54. doi: 10.1186/gb-2003-4-9-r54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Szathmary E. Do deleterious mutations act synergistically? Metabolic control theory provides a partial answer. Genetics. 1993;133:127–32. doi: 10.1093/genetics/133.1.127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Deutschbauer AM, et al. Mechanisms of haploinsufficiency revealed by genome-wide profiling in yeast. Genetics. 2005;169:1915–25. doi: 10.1534/genetics.104.036871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kishony R, Leibler S. Environmental stresses can alleviate the average deleterious effect of mutations. J Biol. 2003;2:14. doi: 10.1186/1475-4924-2-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Breslow DK, et al. A comprehensive strategy enabling high-resolution functional analysis of the yeast genome. Nat Methods. 2008;5:711–8. doi: 10.1038/nmeth.1234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Elena SF, Lenski RE. Test of synergistic interactions among deleterious mutations in bacteria. Nature. 1997;390:395–8. doi: 10.1038/37108. [DOI] [PubMed] [Google Scholar]
- 30.Liao BY, Zhang J. Mouse duplicate genes are as essential as singletons. Trends Genet. 2007;23:378–81. doi: 10.1016/j.tig.2007.05.006. [DOI] [PubMed] [Google Scholar]
- 31.Segre D, Vitkup D, Church GM. Analysis of optimality in natural and perturbed metabolic networks. Proc Natl Acad Sci U S A. 2002;99:15112–7. doi: 10.1073/pnas.232349399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Mo ML, Palsson BO, Herrgard MJ. Connecting extracellular metabolomic measurements to intracellular flux states in yeast. BMC Syst Biol. 2009;3:37. doi: 10.1186/1752-0509-3-37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Kacser H, Burns JA. The molecular basis of dominance. Genetics. 1981;97:639–66. doi: 10.1093/genetics/97.3-4.639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Brachmann CB, et al. Designer deletion strains derived from Saccharomyces cerevisiae S288C: a useful set of strains and plasmids for PCR-mediated gene disruption and other applications. Yeast. 1998;14:115–32. doi: 10.1002/(SICI)1097-0061(19980130)14:2<115::AID-YEA204>3.0.CO;2-2. [DOI] [PubMed] [Google Scholar]
- 35.Amberg DC, Burke DJ, Strathern JN. Methods in Yeast Genetics, a Cold Spring Harbor Laboratory Course Manual. Cold Spring Harbor Laboratory Press; Cold Spring Harbor: 2005. pp. 59–76. [Google Scholar]
- 36.Tong AH, et al. Systematic genetic analysis with ordered arrays of yeast deletion mutants. Science. 2001;294:2364–8. doi: 10.1126/science.1065810. [DOI] [PubMed] [Google Scholar]
- 37.Nagai T, et al. A variant of yellow fluorescent protein with fast and efficient maturation for cell-biological applications. Nat Biotechnol. 2002;20:87–90. doi: 10.1038/nbt0102-87. [DOI] [PubMed] [Google Scholar]
- 38.Mumberg D, Muller R, Funk M. Yeast vectors for the controlled expression of heterologous proteins in different genetic backgrounds. Gene. 1995;156:119–22. doi: 10.1016/0378-1119(95)00037-7. [DOI] [PubMed] [Google Scholar]
- 39.Steinmetz LM, et al. Systematic screen for human disease genes in yeast. Nat Genet. 2002;31:400–4. doi: 10.1038/ng929. [DOI] [PubMed] [Google Scholar]
- 40.Nagalakshmi U, et al. The transcriptional landscape of the yeast genome defined by RNA sequencing. Science. 2008;320:1344–9. doi: 10.1126/science.1158441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Ekino K, Kwon I, Goto M, Yoshino S, Furukawa K. Functional analysis of HO gene in delayed homothallism in Saccharomyces cerevisiae wy2. Yeast. 1999;15:451–8. doi: 10.1002/(SICI)1097-0061(199904)15:6<451::AID-YEA383>3.0.CO;2-K. [DOI] [PubMed] [Google Scholar]
- 42.Meiron H, Nahon E, Raveh D. Identification of the heterothallic mutation in HO-endonuclease of S. cerevisiae using HO/ho chimeric genes. Curr Genet. 1995;28:367–73. doi: 10.1007/BF00326435. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.