Abstract
We describe Curves+, a new nucleic acid conformational analysis program which is applicable to a wide range of nucleic acid structures, including those with up to four strands and with either canonical or modified bases and backbones. The program is algorithmically simpler and computationally much faster than the earlier Curves approach, although it still provides both helical and backbone parameters, including a curvilinear axis and parameters relating the position of the bases to this axis. It additionally provides a full analysis of groove widths and depths. Curves+ can also be used to analyse molecular dynamics trajectories. With the help of the accompanying program Canal, it is possible to produce a variety of graphical output including parameter variations along a given structure and time series or histograms of parameter variations during dynamics.
INTRODUCTION
Analysing the conformation of nucleic acids has evolved considerably since its beginnings almost 60 years ago. Following Watson and Crick's double-stranded model (1), based on the fibre diffraction patterns of Franklin, the following decade saw a flurry of DNA and RNA fibre studies and the definition of new DNA conformational families beyond the canonical A and B forms (C, D, alternating, etc.) (2–6). All these conformations were derived from the limited data obtainable from fibres and consequently they could not resolve fine structural details. Helical regularity was therefore imposed on the structures, initially with a single nucleotide pair as the repeating symmetry unit, and later with dinucleotide repeats, as in ‘alternating’ DNA. In helically regular structures, it is easy to locate the helical axis by defining vectors between symmetry equivalent pairs of atoms. If these vectors are brought to a common origin, their tips lie in a plane and form a circle. The helical axis of the molecule is perpendicular to this plane and passes through the middle of the circle (7). Starting from this point, it is natural to describe the overall conformation in terms of helical parameters, such as the pitch and diameter of the helix, the rise and twist between successive base pairs and the displacement or inclination of the base pairs from the axis. Supplemented by the calculation of the dihedral angles along the phosphodiester backbone and a pseudorotational description of the sugar ring conformation, it provided a satisfactory way of classifying and comparing regular nucleic acids (6).
The arrival of the first crystal structure of a DNA oligomer in 1981, the so-called Drew–Dickerson dodecamer (8), revealed a new level of conformational detail and showed that both the base sequence and external factors, including crystal packing and drug or protein binding, could lead to significant departures from helical symmetry. The accumulation of single crystal structures also coincided with an increasing number of attempts to simulate the thermal fluctuations of nucleic acids using molecular dynamics. This influx of data clearly required more refined conformational analysis (9). This need was behind the organization of an EMBO workshop in Cambridge in 1988 which brought together many of the crystallographers and modellers interested in structural analysis. The meeting brought to light many of the limitations and inconsistencies in existing analysis methods and set about defining which parameters could be useful in describing helical nucleic acids. In contrast to earlier work, where parameters had been defined as and when the need arose, the Cambridge meeting proposed geometrically complete sets of parameters for describing the relative position of bases and base pairs and their locations with respect to a helical axis (10). A number of necessary criteria were also set out, such as obtaining identical parameters independently of the direction in which a nucleic acid fragment was analysed (with the exception of changes in sign). The results of this meeting laid the foundations for detailed conformational analysis, at least in terms of parameter names and sign conventions; however it did not define how these parameters were to be calculated.
At the time of the Cambridge conventions, a number of groups proposed different analysis approaches (11), but there was no general agreement on how to carry out the calculations. Two principal problems existed. First, what reference systems should be used for obtaining parameters. The choice could be based on specific atoms within the DNA bases or base pairs or reference systems defined in some way with respect to chosen atoms. Although early approaches favoured base pairs, the irregularities seen in high-resolution crystal structures made a system based on individual bases preferable. Since all parameters depend to varying extents on the choice of reference system (12), it was important to come to an agreement on how to define these systems. This was finally achieved at a meeting in Tsukuba in 1999 involving many of the participants of the earlier Cambridge meeting. The corresponding conventions were subsequently published (13).
A second major problem was associated with the fact that a number of DNA oligomers, including the Drew–Dickerson dodecamer, clearly did not have straight helical axes. This problem could be dealt with in a number of ways. The earliest method was to visually define ‘straight’ segments within the oligomer and to calculate the best possible straight helical axes for these segments [using an extension of the Rosenberg–Rich technique described above (7), where the tips of the vectors now form an ellipsoidal cloud rather than a circle, and an eigenvalue approach is used to find the shortest axis of the ellipsoid and thus the closest fit to a helical axis]. This method however involves a subjective choice of segments and is not easily applicable to more strongly curved oligomers.
An alternative was to abandon the notion of a helical axis and to describe the overall structure in terms of parameters linking successive base pairs. This is the approach adopted by 3DNA (14,15), which is now one of the commonly used analysis programs. While this choice makes it possible to have a complete conformational description of a nucleic acid fragment it has some drawbacks. In particular, by dropping the notion of a global (continuous) helical axis it is not well adapted to defining curvature. It also lacks the notion of base pair positioning with respect to the axis, which most directly characterises the difference between the A- and B-families of DNA (although there are other less direct ways of characterising these families). We recall that while rise and twist belong to the set of six parameters relating one base pair position to another, these values are not the same as helical rise and twist unless the base pair reference systems coincide with the overall helical axis of the molecule (16).
The final approach was to try an extend the notion of a helical axis to curved structures. This was the idea behind the original Curves analysis program (16,17), which has also been widely used for nucleic acid analysis. Curves defined a curvilinear helical axis using a least-squares function that distributed conformational irregularities between the positioning of successive bases with respect to local helical axis segments and the positioning of the local axis segments with respect to one another. The local axis positions and orientations were determined by minimising the least-squares function, which was equivalent to distributing the conformational irregularities in a balanced fashion. Conserving the notion of an axis had the advantage of making the definition of curvature straightforward and also maintained the link with earlier descriptions of DNA fibres and the notions of macroscopic helical parameters. It had the disadvantage of creating confusion between parameters defined between successive base pairs (which we termed ‘local’ parameters) and the equivalent parameter defined via the helical axis (which we termed ‘global’ parameters).
Over the last decade, a number of developments have considerably changed the nucleic acid field and have made it worth revisiting the question of conformational analysis. First, the accumulation of crystal and NMR structures of DNA and RNA have made it clear that major deformations within helical segments are very common. This is particularly the case in protein–nucleic acid complexes, and not only in binary complexes, but also in large assemblies such as the nucleosome (18), and RecA/DNA filaments (19). Extreme deformations have also been induced within single nucleic acid molecules by externally applied forces and torques, leading to new conformational families such as S- (20,21) and P-DNA (22). In parallel, algorithmic and computational developments have made molecular dynamics simulations of nucleic acids more reliable and have greatly extended their applicability in terms of the size of systems which can be studied (for example, DNA minicircles or nucleosome core particles), as well as the range of base sequences and the time scales investigated. This work has led to an unprecedented mass of data on conformational dynamics (23,24). Lastly, a wide variety of chemically modified nucleic acids have been synthesised and studied, notably because DNA and RNA are increasingly interesting therapeutic targets.
In the light of these developments, we have taken a fresh look at what a nucleic acid conformational analysis technique should provide and we would like to propose a new version of the Curves algorithm. Curves+ attempts to extend the applicability and ease of use of the old program and, at the same time, overcomes difficulties brought up by users over the last 20 years. The new program is both much faster and more flexible than the old one, while being algorithmically more straightforward. Importantly, it avoids the confusion between local and global helical parameters, while conserving the notion of a helical axis and the advantages that come from this choice. It respects both the Cambridge and Tsukuba conventions and provides a full set of helical and backbone parameters. It also revisits the question of groove geometry and proposes new definitions of width and depth. Lastly, it is adapted to directly analysing the data from molecular dynamics trajectories. After presenting the mathematics behind the new analysis, we illustrate its application to a variety of static and dynamic nucleic acid conformations and discuss the use of the resulting parameters.
METHODOLOGY
Base reference system
The choice of base reference system is that established at the Tsukuba meeting (13). See the work of Lu and Olson (25) for a full discussion of the influence of such a choice. The graphical position of this reference system with respect to standard purines and pyrimidines can be found in the Tsukuba reference. In order to avoid having to give the reference system in Cartesian coordinates for each standard base, we calculate it using chosen base atoms. These are C1', N1(Y)/N9(R) and C2(Y)/C4(R) in standard bases (where Y is a pyrimidine and R is a purine). Users can change these atoms to deal with non-standard cases. For example to deal with the RNA base pseudouridine which is linked to the phosphodiester backbone through C5, the equivalent atoms would be C1', C5 and C4. For completeness, we provide our construction method: this involves the atoms forming the glycosidic bond between each base and the sugar-phosphate backbone, N1–C1' for pyrimidines and N9–C1' for purines and the normal to the mean plane of the base (termed bN below). The direction of the normal is given by the cross product (N1–C1') × (N1–C2) for pyrimidines and (N9–C1') × (N9–C4) for purines. The base reference point (termed bR below) is obtained by rotating a vector of length d (initially aligned with the N–C1' direction) clockwise by an angle τ1 around the normal vector passing through the N atom. The next vector of the reference system, pointing towards the phosphodiester backbone joined to the base (termed bL below) is obtained by a similar rotation, but using a unit vector and the angle τ2. The last vector of the reference system, pointing into the major groove, bD, is obtained from the cross product bL × bN. For the Tsukuba convention, τ1 = 141.47°, τ2 = −54.41° and d = 4.702 Å. The former Curves program used values of 132.19°, −54.51° and 4.503 Å, respectively. The major impact of this change is a movement of the base reference point towards the major groove, which means that Xdisp values (measuring the displacement of bases or base pairs along the pseudodyad with respect to the helical axis) become more positive by 0.77 Å with the new reference system. There is also a change in slide, which is more positive by 0.47 Å with the new reference. For comparisons with earlier results, Curves+ allows the user to optionally select the old reference system.
Since low resolution structures, and also snapshots from MD trajectories, may contain deformed bases, it is advisable to start by least-squares fitting (26) a standard base geometry to the atoms in the input structure before defining the base reference system. Curves+ provides the standard geometries for a number of DNA and RNA bases in a data file (standard_b.lib) that can be modified and extended by the user. Only ring atoms (plus the bound C1') need to be defined in each case. Using this data, Curves+ will automatically perform least-squares fits to the input data, but this fitting can be prevented by the user if desired.
Intra-base pair parameters
The intra-base pair parameters comprise three translations, shear, stretch and stagger, and three rotations, buckle, propeller and opening. Following the Tsukuba convention, zero values of these parameters describe canonical Watson–Crick base pairs and non-zero values describe deformations with respect to the short axis of the base pairs, their long axis and their normal respectively (see Supplementary Figure S1). The parameters are calculated by determining the rigid-body transformation that maps one base reference system onto the other. For the discussion of similar approaches and the underlying mathematics see refs (27–29). However, to account for the pseudodyadic symmetry of Watson–Crick base pairs (involving a 180° rotation around the pseudodyad vector aligned with the short axis of the base pairs and pointing into the DNA grooves), the reference system of the second base is first transformed by inverting the bL and bN vectors before the rigid-body transformation is calculated. In the case of reverse Watson–Crick pairs, the pseudodyad axis corresponds to the base pair normal and the inversion consequently involves the bD and bL vectors.
The rigid-body transformation between the bases of the base pair is defined such that it moves the first base reference system b1 onto the second (dyad inverted) system b2 via a translation vector λA = b2R − b1R combined with a rotation through an angle θA around a unit axis vector UA. It is convenient to express these vectors with respect to components in a mean reference system B associated with the base pair (denoted by the orthogonal vectors BL, BD, BN and the point BR). To do this as symmetrically as possible, we choose an average frame that is obtained by rotation and translation of the first base reference system, but now through the half angle θA/2, about the same axis vector UA, and with the half translation λA/2.
We need to be able to extract the unit rotation axis vector UA and angle θA from knowledge of the two frames b1 and b2 and, conversely, be able to reconstruct one frame from the other given the rotation axis and rotation angle.
With the convention that b1 and b2 are matrices whose rows are the laboratory frame components of the vectors (bD, bL, bN), a rotation matrix Q satisfying b2 = b1 Q can be computed from the two frames as Q = b1Tb2. As Q is itself a proper 3x3 rotation matrix (see Supplementary Material) it has three eigenvalues [(1, exp(iθA), exp(−iθA)]. As the trace of a matrix equals the sum of its eigenvalues, the value of the rotation angle θA can be calculated from the formula:
which yields a unique value for θA in the interval [0,π] radians. The matrix Q is only symmetric in the two extreme cases of θA = 0 and θA = π when its eigenvalues are all real. In the non-symmetric cases, an explicit formula is available for the eigenvector w of Q associated with the eigenvalue 1:
This formula follows from the fact that w is an eigenvector with eigenvalue 1 of both Q and Q−1 = QT, and so w is in the nullspace of the skew-symmetric matrix QT−Q, which is one dimensional and spanned by the given vector. By definition, we take the unit rotation axis vector UA = w/|w|. This formula gives the components of UA in the fixed laboratory frame. The sign convention in our definition of w corresponds to Q being a positive rotation about the direction UA (according to the right hand rule) through the angle θA. See Supplementary Material for the converse operation, generating Q from UA and θA, and for a discussion of special cases of θA.
Using the unit rotation axis vector UA and mid-frame B, we can now define our six intra-bp parameters. We can encode the magnitude of the rotation by considering the vector θA UA (where Curves+ by default measures θA in degrees). Then buckle, propeller and opening are defined as the three components of θA UA in the mid-frame:
In fact, because UA is the rotation axis vector, its components in all three of the frames b1, b2 and B are identical, that is, BUA = b1UA = b2UA so that the mid-frame is not essential for these definitions. Nevertheless, because the definitions are in fact mid-frame components they have particularly simple symmetry properties (see below). Similarly, the three translational parameters shear, stretch and stagger are B λA, or explicitly:
It should be noted that if a base pair MN is analysed from M to N or from N to M (for example, by inverting an entire oligomer before analysis), we will obtain the inverse rigid body transformation, but, because of the definition in terms of components in the mid-frame, the absolute magnitudes for the translational and rotational parameters will be unchanged. However, because of the dyad inversion of the reference systems there will be sign changes in parameters affected by the inversion. Specifically, for Watson–Crick base pairs, inverting the analysis direction will change the signs of shear and buckle.
We caution the reader that in this approach the three rotational parameters, buckle, propeller and opening are components of a vector in a particular frame, and in general, because finite rotations do not commute, this does not correspond to applying successive rotations about the three base vectors in the frame, as in some choices of sets of Euler angles. However, as discussed by Mazur and Jernigan (28), if two parameters are small compared to the third then the error in interpreting the rotational parameters as angles will be small.
Inter-base pair parameters
The inter-base pair parameters comprise three translations, shift, slide and rise, and three rotations, tilt, roll and twist. These parameters describe the relative position of two successive base pairs with respect to their short axes, their long axes and their normals.
This requires defining reference frames for the two base pairs. Each base pair frame is taken to be the mid-frame, as introduced in the previous section, between the two base reference frames. In order to compute inter-base pair parameters (also termed base pair junction parameters) we begin by calculating, as before, the rotation axis corresponding to the transformation between two successive base pair frames. This yields a vector UE, which, when associated with a rotation θE and a translation λE, takes us from the first base pair reference system to the second. We can again generate a mid-frame reference system between the two base pairs using Rodrigues' formula with a half-rotation θE/2 and a half-translation λE/2. As before (see previous sub-section) the translational parameters, shift, slide and rise are the components of the translation vector between the reference points of the base pair frames with respect to the mid-frame and the rotational parameters, tilt, roll and twist are the components of the rotation θE in the same reference system.
Note that, as for the intra-base pair parameters, changing the direction of analysis (for example by inverting an entire oligomer before analysis) modifies the base frames, the base pair frames and the mid-frame. As for the intra-bp parameters, this has no influence on the magnitudes of the inter-base pair parameters, but, will change the signs of shift and tilt.
Defining the helical axis
The overall helical axis of a nucleic acid fragment is defined very simply on the basis of the screw axes which link symmetry equivalent base reference systems. In the simple case of a standard double helix, where all the nucleotides in a given strand are expected to be equivalent, we calculate the screw axes for each successive pair of base reference systems. These axes are the local ‘helical’ axes for the each pair of nucleotides. They are calculated using the standard base reference frames b1 and b2 along a given strand, with origins b1R and b2R, where the indices 1 and 2 now indicate symmetry equivalent nucleotides along a chosen strand. The screw axis is defined by a unit vector which is tangent to a line plus a point on the line. For any two frames we have the displacement between the origins v = b1R − b2R, a unit vector in the direction of the rotation axis U and the rotation angle θ. U and θ are calculated as discussed above. Then the tangent to the helical axis is simply U and elementary geometry in the plane perpendicular to U shows that a point p on the helical axis can be calculated by the formula
where d = [v – (v. U)U]/2, that is, half of the projection of v perpendicular to U.
We associate the axes U with the two bases that generated them. For each base, we generate a new point on U by sliding the point p along U until it satisfies the criteria (bR p). U = 0.
Having treated each strand in this way, the terminal base pairs (or levels for more than two strands) will be associated with U vectors from each strand and the other base pairs with U vectors from each strand and from the screw vectors involving the bases preceding and following the chosen base pair (or base level). These vectors and the points through which they pass are then averaged to yield a single local axis per base pair (or level) UH, passing through point PH, which again obeys the criteria (BR − P). UH = 0. Finally, these axes are smoothed using a polynomial weighting function.
In the case of a regular helical conformation, this procedure finds the true helical axis. In deformed conformations, it generates a smooth curve which is close to the mean screw transformations between successive levels. The procedure described can be applied to any number of strands and can also be used for any chosen symmetry repeat (for example, in Z-DNA a dinucleotide repeat is appropriate). Although this way of generating an overall helical axis is very different from the least-squares function used in the old version of Curves, the results are very similar as we will illustrate in the results section.
Base pair-axis parameters
Once the helical axis UH at a given base pair level is determined, it is necessary to generate a helical reference system in order to calculate base pair-axis parameters. This is done by generating a pseudodyad vector UD, perpendicular to UH and lying on the plane defined by UH and the BD vector of the corresponding base pair. The final vector UL is obtained from the cross product UH × UD. We can now calculate the base pair-axis parameters with the same rigid-body transformation procedure used above for the intra- and inter-base pair parameters. Note that since BR − PH is set perpendicular to UH and that BD is in the plane formed by UH and UD, there are only four base pair-axis parameters, the translations Xdisp (the movement of the bases towards the grooves) and Ydisp (movement perpendicular to the grooves), and the rotations Inclination (around the short axis of the base pairs) and Tip (around the long axis of the base pairs). Once again, due to the pseudodyad symmetry of the base pairs, changing the direction of analysis will leave the magnitude of these parameters unchanged, but will change the signs of Ydisp and Tip.
Backbone parameters
Backbone parameters comprise the single bond torsions along the phosphodiester chain and the conformation of the sugar ring. In a conventional DNA strand, the backbone segment associated with each nucleotide (in the 5′→3′ direction) is described by the torsions α (03′-P-O5′-C5′), β (P-O5′-C5′-C4′), γ (O5′-C5′-C4′-C3′), δ (C5′-C4′-C3′-O3′), ϵ (C4′-C3′-O3′-P) and ζ (C3′-O3′-P-O5′), to which we must add the glycosidic angle χ (O4′-C1′-N1-C2 for pyrimidines and O4′-C1′-N9-C4 for purines) joining the sugar to the base and the ribose OH torsion (C1′-C2′-O2′-H2′) in the case of RNA.
We remark that calculating averages and standard deviations of angular variables is not trivial, unless they cover restricted angular ranges. There is also no simple definition of maximal and minimal values. This problem occurs in many branches of science with broadly distributed angular variables, for example, in analysing wind directions (30). While angular helical variables generally lie within limited ranges, backbone dihedrals can easily span the full range of 360°. In this case, maximal and minimal values in the Curves+ analysis are replaced with the parameter ‘range’ and angular averages and standard deviations are calculated using a vectorial approach. Range is defined as the number of 1° bins visited by a given variable in the interval 0–360°. This gives a good idea of the angular spread of variables. Note that when analysing molecular dynamics trajectories, this value may increase with sampling, giving an indication that more sampling probably needs to be done. However, the details of the angular distribution can be checked using the histogram output option of the supplementary program Canal (see below). For averages, angles are added as vectors in 2D space (with an angle θ having components x = Cos θ and y = Sin θ). The result is converted to a unit vector, whose X and Y components yield the average. Other approaches require assuming that the angles obey a presupposed type of distribution. We have checked our values against one such model (31), and found negligible differences for standard deviations up to roughly 20°. Larger values differ more significantly (5–10°), but in these cases it is the qualitative result that the variables in question fluctuate very strongly that is the most important.
The sugar ring is usefully described using pseudorotation parameters. Although strictly speaking there are four pseudorotation parameters for a five-membered ring (32), only two of these, the so-called phase (Pha) and amplitude (Amp), are generally useful. While the amplitude describes the degree of ring puckering, the phase describes which atoms are most displaced from the mean ring plane. We calculate these parameters using the formulae given below (33), which have the advantage of treating the ring dihedrals ν1 (C1′-C2′-C3′-C4′) to ν5 (O4′-C1′-C2′-C3′) in an equivalent manner. In this approach:
where 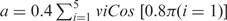 and b =−0.4
and b =−0.4 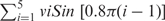 note, if
note, if 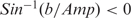 then
then 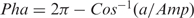 .
.
Conventionally, sugar ring puckers are divided into 10 families described by the atom which is most displaced from the mean ring plane (C1′, C2′, C3′, C4′ or O4′) and the direction of this displacement (endo for displacements on the side of the C5′ atom and exo for displacements on the other side). These pucker families can be easily calculated from the phase angle and are also output by the Curves+ program.
In order to deal with non-standard nucleic acids the backbone parameters are not hard-wired into the program, but are contained in a data file (standard_s.lib) which can be modified or extended by this user. This makes it easy to analyse chemically modified backbones such as those, for example, in PNA (34).
Groove parameters
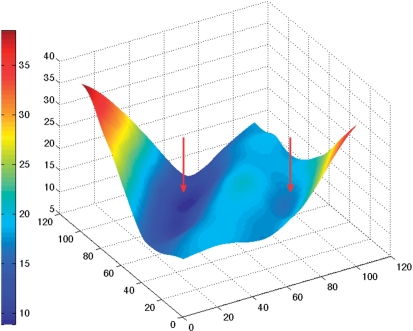
In order to analyse groove widths and depths, we begin by building cubic spline curves along each backbone passing through the phosphorus atoms Pi and tangential to vectors defined as Pi−1 − Pi+1. Vectors on the terminal phosphates, P1 and PN, are obtained by applying the appropriate helical twist rotations to the P2 and PN−1 vectors. Note that Curves+ will not read phosphates (P0 and PN+1 in our notation) ‘outside’ the bases being analysed, whether or not they exist in the input data. We next calculate the distances between two sets of points uniformly spaced along each backbone. These points divide each backbone into a chosen, and common, number of intervals. This yields a two-dimensional distance matrix such as that illustrated in Figure 1 (for the B-DNA dodecamer, pdb code 1bna, discussed in the Results section). The trailing diagonal, TD, of this matrix (vertical and central in Figure 1) corresponds to the distance between points which are equal (fractional) distances along each backbone. The general form of the 3D surface representing this matrix looks like a manta ray, with its raised backbone along TD and its wing tips swept upward at the limits of the leading diagonal. The valleys on either side of TD represent minimal distances between the backbones as we move along the nucleic acid fragment and are a natural way to define groove widths. In the figure, the minor groove falls on the left of TD and the major groove on the right. We find the groove widths by moving along TD and searching for minimal distances along the directions perpendicular to this diagonal. Note that we are only interested in the minima closest to TD, since in distorted or irregular structures secondary minima can occur further from the diagonal. Note also that the valleys defining the grooves cannot extend to the ends of the nucleic acid fragment since they are displaced from TD. In the case of extremely deformed structures, one or both grooves may temporarily disappear in some regions flanking TD because the corresponding valleys cease to exist. (This is more common for the broad major groove than for the narrower minor groove.)
Figure 1.
Two-dimensional surface representing the distance (vertical axis, in Å) between points along the backbones of a double-stranded B-DNA oligomer. The groove widths appear as the valleys (marked by red arrows) on either side of the diagonal (in the centre of the figure). Points which are the same distance along each backbone yield vectors roughly perpendicular to the helical axis of the oligomer. Moving further up the axis pointing left (5′→3′ backbone) rotates the vectors until they span the minor groove, while moving up the axis pointing right (3′→5′ backbone) leads to spanning the major groove. The surface colour shows variations in inter-backbone distance, from 9 Å (dark blue) to 38 Å (dark red). The largest distances naturally occur for vectors which link the two 3'-ends (left-hand corner) or the two 5′-ends (right-hand corner) of the backbones.
Having defined a groove width by a minimal distance at some point along the nucleic acid fragment, we have to calculate the corresponding groove depth. At a base pair level, this is defined as the distance from the centre of the backbone-to-backbone width vector to the mid-point of a vector defining the corresponding base pair. This vector is constructed using the C8 atom of purines and the C6 atom of pyrimidines (these atoms are placed in a specific position in the library file entries used by Curves+, namely, after the three atoms used to define the reference frames and consequently, appropriate atoms can be chosen when building the library entries for non-standard base pairs). For groove depths halfway between base pair levels, we use the average of the corresponding base pair vector mid-points. Note that this choice also works acceptably for both Hoogsteen and reverse Hoogsteen base pairs.
Lastly, to take account of the van der Waals surfaces of the atoms constituting the phosphodiester backbone and the bases, we subtract fixed values from the calculated groove widths and depths. The default values used in Curves+ are 2.9 Å for each backbone (that is, subtracting 5.8 Å from the groove width) and 3.5 Å for the half-width of the base pairs. These values are good approximations, but the user is free to modify them, including the option of setting them to zero.
Non-standard structures
So far we have generally described the analysis of a conventional double-helix, however the same approach can be applied to single-stranded structures and also to 3- or 4-stranded nucleic acids. For single-stranded structures, it is naturally impossible to calculate parameters related to base pairs or helical grooves. In 3- or 4-stranded structures, intra-base pair parameters are calculated between the first strand and all other strands, whereas inter-base pair and base pair-axis parameters are only calculated for the first two strands. In general, the remaining parameters are not helpful in understanding a structure, but they can be obtained if necessary by changing the strand order used for the analysis. All strands are however used in defining the overall helical axis. Grooves are also analysed between all pairs of adjacent strands. Once again, data on ‘virtual’ grooves between non-adjacent strands can be obtained by an appropriate analysis. For example, in a triple helix, the dimensions of the major groove of the Watson–Crick base pairs, which is occupied by the Hoogsteen or reverse-Hoogsteen third strand, can be obtained by repeating the analysis with only the Watson and Crick strands.
Beyond changes in the number of strands, Curves+ can also deal with missing bases (abasic nucleotides), missing nucleotides (strand gaps or bulges) and unpaired terminal nucleotides. Lastly, due to increasing interest in minicircles (35–39), these structures can also be fully analysed taking the ring-closure of the strands into account. This yields a circular, closed helical axis and uninterrupted backbone, helical and groove parameters.
Analysing MD trajectories with Canal
Since MD trajectories now typically produce tens of thousands of conformational snapshots it is necessary to be able to analyse such large datasets quickly. Curves+ can read MD trajectory files directly without the need for creating PDB format files. It currently deals with AMBER format trajectory files. It could be adapted to other formats, but it is also relatively easy to modify trajectory files to the AMBER format (see, for example, Simulaid by M. Mezei http://atlas.physbio.mssm.edu/∼mezei/simulaid/or CatDCD by J. Gullingsrud http://www.ks.uiuc.edu/Development/MDTools/catdcd/).
Curves+ can be used to pick out and analyse a single snapshot or to analyse snapshots at chosen time intervals for the whole trajectory or extract information on a given sequence fragment from an ensemble of trajectories. The present version of Curves+ can analyse roughly 100 conformational snapshots of a 20-bp double-stranded DNA oligomer per second on a 2.5 GHz processor. When multiple snapshots are treated, printed output is suppressed and the program creates an unformatted file which can be treated with a supplementary program named Canal (Curves+ analysis). This program calculates the maxima, minima, mean and standard deviations of any chosen conformational parameters which are output in a list file. It can also generate time series and histograms which are output in flat files that can be used for producing graphics and will optionally calculate linear correlation coefficients between all helical, backbone and groove parameters, which can again be output in files for checking correlations graphically. The simple format of all files output by Canal makes them useable in any common graphic program. We have used both Gnuplot and MatLab (Mathworks Inc.) in preparing the illustrations of Canal data for this article. Canal can lastly be applied to the analysis of files produced by Curves+ from single structures. In this case, it can be used to plot the variation of chosen parameters along an oligomer or, as with trajectories, to look at parameter distributions and correlations. The use of Canal will be further illustrated in an article (manuscript in preparation) concerning the analysis of multiple MD trajectories from the ABC dataset (40,41). A full user guide for Canal is available at the web site cited below.
Availability
Curves+ is freely available for download from http://gbio-pbil.ibcp.fr/Curves_plus. In addition to the Fortran source code and the base and backbone reference files, standard_b.lib and standard_s.lib, Curves+ is accompanied by a user guide, sample analyses, the Canal program with its own user guide and a utility program, Cdif+, which calculates the difference between two structures using the Curves+ output files. We are developing a web-server version of Curves+ which will be available shortly.
RESULTS AND DISCUSSION
We begin by discussing the two standard forms of double helical DNA, the A and B conformations. Table 1, lists the average helical parameters calculated for two DNA oligomers belonging to these families: the B-family ‘Drew–Dickerson’ dodecamer, d(CGCGAATTCGCG) (42) (pdb code 1bna) and the A-family decamer d(ACCGGCCGGT) (43) (pdb code 1d13). The full Curves+ output is provided in the Supplementary Material. Both Table 1, panel A (for A-DNA) and Table 1, panel B (for B-DNA) show a comparison of the average helical parameters calculated with Curves+ and with the old Curves algorithm (Curves version 6.1). It can be seen that the only significant difference due to the change of base reference frame involves an increase in Xdisp which is ∼0.8 Å more positive with the Tsukuba frame and an increase slide which is more positive by ∼0.4 Å (13). (Please refer to Supplementary Figure S1 for the name and sign conventions of the helical parameters.) The new frame also leads to small changes in base pair stretch and opening, but these changes have no practical significance in analysing a structure. The Curves+ helical axis calculation gives an axis which is almost perfectly superposable with the old program, as we will demonstrate for a more irregular conformation below.
Table 1.
Helical, backbone and groove parameters calculated with Curves+ for (panel A) A-DNA and (panel B) B-DNA and (panel C) standard deviations of helical and groove parameters along the oligomers
| Panel A: A-DNA (using PDB file 1d13) | |||||||||
| BP-axis | Xdisp | Ydisp | Incl | Tip | |||||
| A | −3.95 | 0.00 | 16.8 | 0.0 | |||||
| Aold | −4.71 | 0.00 | 16.8 | 0.0 | |||||
| Intra-BP | Shear | Stretch | Stagger | Buckle | Propel | Opening | |||
| A | 0.00 | −0.01 | 0.04 | 0.0 | −15.3 | 4.2 | |||
| Aold | 0.00 | 0.03 | −0.17 | 0.0 | −15.3 | 4.0 | |||
| Inter-BP | Shift | Slide | Rise | Tilt | Roll | Twist | H-Rise | H-Twist | |
| A | 0.00 | −1.23 | 3.26 | 0.0 | 8.4 | 31.7 | 2.72 | 33.1 | |
| Aold | 0.00 | −1.65 | 3.37 | 0.0 | 8.4 | 31.7 | 2.69 | 33.1 | |
| Backbone | α | β | γ | δ | ϵ | ζ | χ | Pha | Amp |
| A | −31.5 | 157.8 | 9.2 | 97.3 | −157.1 | −81.3 | −152.6 | 16.7 | 41.3 |
| Grooves | Min-W | Min-D | Maj-W | Maj-D | |||||
| A | 9.7 | 1.4 | 2.8 | 9.6 | |||||
| Panel B: B-DNA (using PDB file 1bna) | |||||||||
| BP-axis | Xdisp | Ydisp | Incl | Tip | |||||
| B | 0.27 | 0.11 | −0.1 | −1.0 | |||||
| Bold | −0.48 | 0.11 | −0.1 | −1.0 | |||||
| Intra-BP | Shear | Stretch | Stagger | Buckle | Propel | Opening | |||
| B | −0.04 | −0.17 | 0.21 | 0.3 | −13.7 | 1.0 | |||
| Bold | −0.04 | −0.08 | 0.03 | 0.3 | −13.7 | 0.8 | |||
| Inter-BP | Shift | Slide | Rise | Tilt | Roll | Twist | H-Rise | H-Twist | |
| B | −0.02 | 0.14 | 3.36 | −0.2 | −0.3 | 35.8 | 3.35 | 36.0 | |
| Bold | −0.02 | −0.33 | 3.36 | −0.2 | −0.3 | 35.0 | 3.35 | 36.0 | |
| Backbone | α | β | γ | δ | ϵ | ζ | χ | Pha | Amp |
| B | −73.3 | 179.7 | 66.0 | 121.1 | 173.7 | −88.5 | −122.2 | 127.3 | 50.2 |
| Grooves | Min-W | Min-D | Maj-W | Maj-D | |||||
| B | 4.2 | 4.9 | 10.5 | 5.4 | |||||
| Panel C: Standard deviations of parameters along the A-DNA (1d13) and B-DNA (1bna) oligomers | |||||||||
| BP-axis | Xdisp | Ydisp | Incl | Tip | |||||
| A | 0.39 | 0.62 | 1.1 | 5.4 | |||||
| B | 0.56 | 0.23 | 4.7 | 3.1 | |||||
| Intra-BP | Shear | Stretch | Stagger | Buckle | Propel | Opening | |||
| A | 0.18 | 0.08 | 0.25 | 5.3 | 4.5 | 4.6 | |||
| B | 0.27 | 0.08 | 0.19 | 5.9 | 6.9 | 4.3 | |||
| Inter-BP | Shift | Slide | Rise | Tilt | Roll | Twist | H-Rise | H-Twist | |
| A | 0.70 | 0.29 | 0.09 | 3.4 | 0.6 | 4.9 | 0.14 | 4.9 | |
| B | 0.55 | 0.43 | 0.18 | 2.9 | 5.9 | 4.1 | 0.18 | 4.1 | |
| Grooves | Min-W | Min-D | Maj-W | Maj-D | |||||
| A | 0.17 | 0.20 | 0.0 | 0.0 | |||||
| B | 1.29 | 0.30 | 0.71 | 0.96 | |||||
Helical parameters are averages over the oligomers. Backbone parameters refer to G5 in the first strand of 1d13 and to A6 in the first strand of 1bna. Groove parameters refer to the level involving the same central base pairs. Aold and Bold refer to an analysis of 1d13 and 1bna respectively using the old Curves base reference frame. Translational parameters are in Å (shown with two decimal places) and rotational parameters are in degrees (shown with a single decimal place).
Overall, the 1bna analysis (Table 1, panel B) shows the conventional features of B-DNA, with base pairs perpendicular to the helical axis (Incl, Tip ≈ 0), centred on this axis (Xdisp, Ydisp ≈ 0), and more or less planar, with the exception of propeller twisting (Propel ≈ −14°). The rise and twist are 3.4 Å and 36° as expected, whether they are measured from the inter-base pair rotation matrix (Rise and Twist) or from the translation and rotation with respect to the helical axis (H-Rise and H-Twist). Lastly, the groove analysis shows a minor groove that is less than half the width of the major groove and slightly deeper.
The A-DNA conformation (Table 1, panel A), can most easily be distinguished from the B conformation with the bp-axis parameters Xdisp, which shows the base pairs have moved ∼4 Å towards the minor groove and Incl, which shows their significant inclination (17°) with respect to the helical axis. The inter-base pair parameters also show characteristics of the A conformation with negative slide and positive roll angles. Now the base pairs have moved away from the helical axis, there is a visible difference in the two ways of measuring rise and twist, with those based on the inter-bp rotation matrix describing the local displacement between two successive base pairs (Rise 3.26 Å, Twist 31.7°), while using the parameters related to the overall helical axis describes the translation and rotation between the base pairs in this global frame (H-Rise 2.72 Å, H-Twist 33.1°). As would be expected the latter parameters are closer to the values associated with regular (fibre diffraction) models of the A-form. The displacement of the base pairs towards the minor groove is lastly reflected in the groove dimensions, with a broad and shallow minor groove facing a deep and narrow major groove.
Table 1, panels A and B lastly list the backbone parameters for representative nucleotides in the centre of the two oligomers. Note that the sugar puckers in the Curves+ output are given in terms of both phase and amplitude and of pucker, which, for the nucleotides shown, are, C3′-endo (A-DNA) and C1′-exo (B-DNA) respectively.
Although Curves+ lists the helical and backbone parameters for all base pairs within the oligomers (see Supplementary Material), it is also sometimes useful to have a summary of the variability within a given structure. This can be obtained using Canal which lists the mean, minimum, maximum and standard deviation of each parameter. As an example, Table 1, panel C lists the standard deviations of the parameters shown in Table 1, panels A and B for the A- and B-oligomers. It is seen that the most intra-base pair parameters show similar ranges for both oligomers (which have similar percentages of GC pairs, 70–80%). Other helical parameters show more marked differences. For example, A-DNA shows increased fluctuations in Ydisp and roll which could be linked to the displacement of the base pairs towards the periphery of the double helix in this conformation. Note that no fluctuations are shown for the major groove dimensions in A-DNA simply because measurements can only be made at the level of the two central base pairs in this short oligomer, and the dimensions in this region are constant.
We now turn to a much more irregular structure where the graphic output available from Curves+ is particularly useful. We have chosen to analyse the DNA 16-mer d(CTGCTATAAAAGGCTG) bound to the TATA box-binding protein (TBP) (44) (pdb code 1cdw). Once again the full Curves+ analysis is given in the Supplementary Material. TBP binds to this oligomer at the TATAAAA sequence on the minor groove side. This forces the minor groove open and causes the oligomer to bend strongly away from the protein. The helical axis calculated by Curves+ gives an overall bend of 74°. The base pair-axis parameters show strong positive base pair inclination at the protein binding site (up to almost 50°) and negative Xdisp, reflecting the fact that the base pairs have been pulled towards the binding surface of the protein. Coupled with positive roll and decreased twist, this gives the protein binding site an A-like character (45). Note that particularly large roll angles and low twists at T5pA6 and A11pG12 that reflect the partial intercalation of pairs of phenylalanine side chains (F284/F301 and F193/F210, respectively) from the protein.
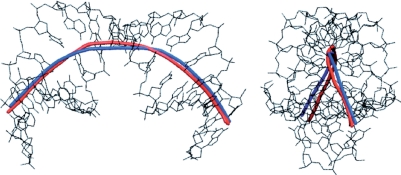
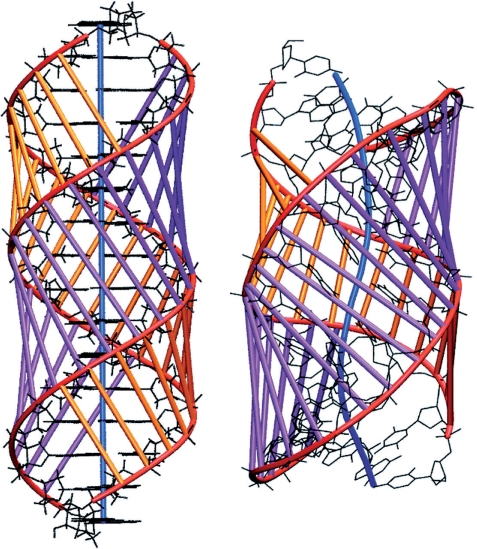
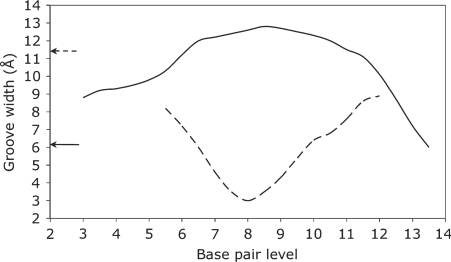
The overall structure of the TBP-bound oligomer is best seen using the graphic output from Curves+. Figure 2 firstly shows the strong, and out-of-plane, curvature resulting from TBP binding. The largest local bends occur at the phenylalanine intercalation sites. It can be seen that, despite the new algorithm used to obtain the overall helical axis, the results of the new and old versions of Curves are very similar. The impact of TBP binding is shown in Figure 3, which illustrates the dramatic opening of the minor groove and the compression of the major groove. These images were obtained using VMD (46) with the PDB format files output by Curves+: name_X.pdb which contains a spline interpolation of the helical axis and name_b.pdb which contains spline interpolated phosphodiester backbones and vectors indicating the grooves widths at base pair and intermediate levels. Since the helical axis, the backbone splines and the groove width vectors in the Curves+ files have different residues names (AXIS, BACA/BACB … and GRVA/GRVB … , respectively), any subset of this data can be selectively coloured and/or displayed, in combination with standard molecular representations, to help clarify the analysis of a nucleic acid structure. The groove dimensions can be represented more quantitatively by plotting width variations along an oligomer, as shown in Figure 4. In the centre of the TBP-binding site, the minor groove has a width of more than 12 Å and a negative depth of −1 → −2 Å (indicating a convex surface with base pairs that protrude beyond the phosphodiester backbones). In contrast, the major groove at the same location has a width of only 3 Å and a depth of 10 → 11 Å.
Figure 2.
The helical axis of the d(CTGCTATAAAAGGCTG) 16-mer bound to TBP calculated with Curves+ (blue) and with Curves 6.0 (red). The side-on (left) and end-on (right) views illustrate the extent of the bending (and its out-of-plane nature) induced by the minor groove-bound protein. Despite the new algorithm, the two analyses give virtually identical results.
Figure 3.
Comparison of the d(CTGCTATAAAAGGCTG) 16-mer in B-DNA (left) and TBP-bound (right) conformations. The backbone spline curves are shown in red, while the vectors defining the minor and major groove widths are shown in purple and orange respectively. The helical axis is shown in blue.
Figure 4.
The variation of the minor (solid line) and major (dotted line) groove widths (Å) along the d(CTGCTATAAAAGGCTG) TBP-bound oligomer (with the protein in positions 5–11). The arrows show the corresponding minor and major groove widths in a canonical B-DNA oligomer and emphasize the localized inversion in groove dimensions induced by protein binding.
We remark that for all the structures we have tested, differences between Curves+ and 3DNA are now very small, as concerns the intra- and inter-base pair parameters. Observed differences are of the order of 0.1 Å for translational parameters and 2° angular parameters. There are more significant differences for base pair-axis parameters, notably with irregular structures such as the TBP-bound oligomer, but this is to be expected since 3DNA calculates these parameters using a vector which approximates a local helical axis (47).
We now consider the use of Canal, a companion program to Curves+, which serves to summarise Curves+ data and also to prepare files for generating graphical output. Canal reads an unformatted file output by Curves+ containing all the helical and backbone parameters from either a single structure or the snapshots generated from a molecular dynamics trajectory. With a single structure, Canal can calculate the minimum, maximum, mean and standard deviation of every parameter and create files containing the values of each parameter along the structure which can be used for plotting (see, for example, the groove widths shown in Figure 4). When used with data from multiple snapshots, Canal can analyse an entire structure or search for a chosen base sequence. In either case, data from many oligomers can be analysed together, provided they have the same lengths. We remark that Canal uses only single-pass algorithms so that results can be accumulated for very large numbers of snapshots without requiring large matrices for storage. It has already been tested on the latest version of the ABC database using a total of almost 108 snapshots.
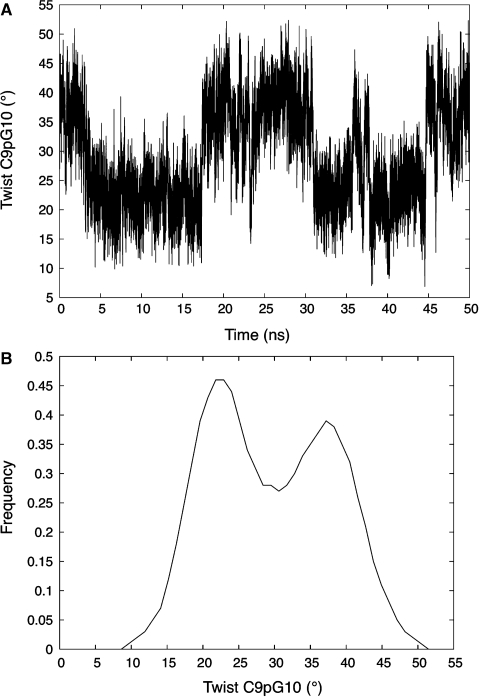
In addition to the printed data, Canal can provide time series and histograms for all variables. We illustrate this using the analysis of a 50 ns molecular dynamics trajectory of the B-DNA 18-mer d(GCCGCGCGCGCGCGCGGC), which belongs to the latest ABC dataset (40,41) presently being analysed. This trajectory consists of 50 000 snapshots (one every ps) stored in 1 ns blocks. Each block of data was analysed with Curves+ and the corresponding output files were concatenated for use in Canal. As an example of the subsequent analysis, we will look at the twist of the central step C9pG10. Canal gives 30° as the mean value of this parameter and indicates a standard deviation of 8°, with minimal and maximal values of 3° and 54°, respectively. These numbers are a good guide to the overall flexibility of this parameter (and of its occasional excursions to very extreme values), but they do not indicate its distribution. This data can be obtained graphically as shown in Figure 5 which contains the 50 ns time series of the CpG twist and provides clear evidence for bistable behaviour. This is further quantified in the histogram obtained from Canal and shown in the lower part of the same figure. The histogram actually corresponds to CpG twists coming from the four most central steps of the oligomer (shown in bold above, and totalling 20 000 data points), each belonging to a GCGC tetranucleotide. This information was obtained with a single query to Canal, asking for sequences corresponding to GCGC, and setting limits to avoid analysing the four base pairs at each end of the oligomer.
Figure 5.
Time series of the C9pG10 twist from a 50 ns molecular dynamics simulation of d(GCCGCGCGCGCGCGCGGC) in explicit water (A) and a histogram of the twist fluctuations derived from the four most central CpG steps of the same oligomer during the trajectory (B).
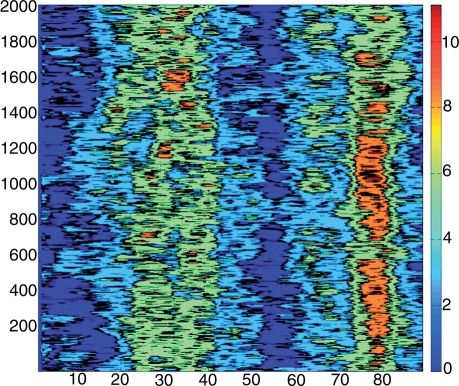
The last example, in Figure 6, shows a two-dimensional time series corresponding to the time evolution (on the vertical axis) of the axis bends (on the horizontal axis) at all dinucleotide steps along an 89 bp DNA minicircle. This single plot gives a good idea of the overall geometry of the minicircle during a 2 ns molecular dynamics trajectory. It clearly shows two regions of more severe bending at base pair positions around 30 and 80, which roughly face one another across the minicircle. It also shows that the bend around position 80 is stronger and more localised than that at 30, although there are periods (around 0.6 ns and after 1.8 ns) when this bend becomes less severe.
Figure 6.
Fluctuations of axis bend for all dinucleotide steps in an 89-bp minicircle during a 2 ns segment of a molecular dynamics trajectory. The base pair positions are given on the horizontal axis and time (ps) increases along the vertical axis. The colour bar shows the variations in bend from 0° (dark blue) to 11° (dark red).
CONCLUSIONS
Since the first version of Curves was produced, some 20 years ago, the variety and the number of available nucleic acid structures have grown enormously. These changes, and the accumulated comments of Curves users, have encouraged us to take a new look at how to make conformational analysis as easy and as informative as possible. The resulting approach, termed Curves+, has been presented in this article, both from an algorithmic and a practical viewpoint.
Curves+ can be used to analyse the helical and backbone conformations of a wide variety of nucleic acid structures with up to four strands and with eventual chemical modifications of the bases or the backbones, arbitrary symmetry repeats and optional ring closure for analysing minicircles. It is algorithmically simpler than earlier versions of Curves, while being both faster and more general. It adopts the generally accepted reference frame for nucleic acid bases and no longer shows any significant difference with analysis programs such as 3DNA for intra- or inter-base pair parameters. Importantly, Curves+ avoids confusion between so-called local and global helical parameters, although, in common with earlier versions, it continues to calculate a well-defined helical axis (which may be straight or curved) and which serves to quantify bending or local kinking.
Curves+ has also been extended in several significant ways, most importantly, by giving the user more control over the parameters to be calculated, by providing continuous measurements of groove width and depth and by being able to directly analyse molecular dynamics trajectories. In conjunction with the companion program Canal, it can analyse parameter fluctuations and correlations along a structure, or over time, generating files for graphical output of a variety of spatial or time series and histograms. The corresponding software, including the source code, is freely available and will shortly be accessible via a web server.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
CNRS and from the ANR grant ALADDIN (to R.L. and K.Z.); Swiss National Science Foundation (to J.H.M.). Funding for open access charge: ANR and SNSF.
Conflict of interest statement. None declared.
Supplementary Material
ACKNOWLEDGEMENTS
We would like to thank our colleagues in the Ascona B-DNA consortium for providing the impetus which led to the development of this new version of Curves.
REFERENCES
- 1.Watson JD, Crick FH. Molecular structure of nucleic acids; a structure for deoxyribose nucleic acid. Nature. 1953;171:737–738. doi: 10.1038/171737a0. [DOI] [PubMed] [Google Scholar]
- 2.Arnott S, Hukins DW. Optimised parameters for A-DNA and B-DNA. Biochem. Biophys. Res. Commun. 1972;47:1504–1509. doi: 10.1016/0006-291X(72)90243-4. [DOI] [PubMed] [Google Scholar]
- 3.Arnott S, Hukins DW, Dover SD. Optimised parameters for RNA double-helices. Biochem. Biophys. Res. Commun. 1972;48:1392–1399. doi: 10.1016/0006-291x(72)90867-4. [DOI] [PubMed] [Google Scholar]
- 4.Arnott S, Chandrasekaran R, Hukins DW, Smith PJ, Watts L. Structural details of double-helix observed for DNAs containing alternating purine and pyrimidine sequences. J. Mol. Biol. 1974;88:523–533. doi: 10.1016/0022-2836(74)90499-9. [DOI] [PubMed] [Google Scholar]
- 5.Leslie AG, Arnott S, Chandrasekaran R, Ratliff RL. Polymorphism of DNA double helices. J. Mol. Biol. 1980;143:49–72. doi: 10.1016/0022-2836(80)90124-2. [DOI] [PubMed] [Google Scholar]
- 6.Saenger W. Principles of Nucleic Acid Structure. New York: Springer; 1984. [Google Scholar]
- 7.Rosenberg JM, Seeman NC, Day RO, Rich A. RNA double helices generated from crystal structures of double helical dinucleoside phosphates. Biochem. Biophys. Res. Commun. 1976;69:979–987. doi: 10.1016/0006-291x(76)90469-1. [DOI] [PubMed] [Google Scholar]
- 8.Dickerson RE, Drew HR. Structure of a B-DNA dodecamer. II. Influence of base sequence on helix structure. J. Mol. Biol. 1981;149:761–786. doi: 10.1016/0022-2836(81)90357-0. [DOI] [PubMed] [Google Scholar]
- 9.Fratini AV, Kopka ML, Drew HR, Dickerson RE. Reversible bending and helix geometry in a B-DNA dodecamer: CGCGAATTBrCGCG. J. Biol. Chem. 1982;257:14686–14707. [PubMed] [Google Scholar]
- 10.Dickerson RE. Definitions and nomenclature of nucleic acid structure components. Nucleic Acids Res. 1989;17:1797–1803. doi: 10.1093/nar/17.5.1797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Lu XJ, Babcock MS, Olson WK. Overview of nucleic acid analysis programs. J. Biomol. Struct. Dyn. 1999;16:833–843. doi: 10.1080/07391102.1999.10508296. [DOI] [PubMed] [Google Scholar]
- 12.Babcock MS, Olson WK. The effect of mathematics and coordinate system on comparability and ‘dependencies’ of nucleic acid structure parameters. J. Mol. Biol. 1994;237:98–124. doi: 10.1006/jmbi.1994.1212. [DOI] [PubMed] [Google Scholar]
- 13.Olson WK, Bansal M, Burley SK, Dickerson RE, Gerstein M, Harvey SC, Heinemann U, Lu XJ, Neidle S, et al. A standard reference frame for the description of nucleic acid base-pair geometry. J. Mol. Biol. 2001;313:229–237. doi: 10.1006/jmbi.2001.4987. [DOI] [PubMed] [Google Scholar]
- 14.Lu XJ, Olson WK. 3DNA: a software package for the analysis, rebuilding and visualization of three-dimensional nucleic acid structures. Nucleic Acids Res. 2003;31:5108–5121. doi: 10.1093/nar/gkg680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lu XJ, Olson WK. 3DNA: a versatile, integrated software system for the analysis, rebuilding and visualization of three-dimensional nucleic-acid structures. Nat. Protocols. 2008;3:1213–1227. doi: 10.1038/nprot.2008.104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Lavery R, Sklenar H. Defining the structure of irregular nucleic acids: conventions and principles. J. Biomol. Struct. Dyn. 1989;6:655–667. doi: 10.1080/07391102.1989.10507728. [DOI] [PubMed] [Google Scholar]
- 17.Lavery R, Sklenar H. The definition of generalized helicoidal parameters and of axis curvature for irregular nucleic acids. J. Biomol. Struct. Dyn. 1988;6:63–91. doi: 10.1080/07391102.1988.10506483. [DOI] [PubMed] [Google Scholar]
- 18.Richmond TJ, Davey CA. The structure of DNA in the nucleosome core. Nature. 2003;423:145–150. doi: 10.1038/nature01595. [DOI] [PubMed] [Google Scholar]
- 19.Chen Z, Yang H, Pavletich NP. Mechanism of homologous recombination from the RecA-ssDNA/dsDNA structures. Nature. 2008;453:489–494. doi: 10.1038/nature06971. [DOI] [PubMed] [Google Scholar]
- 20.Cluzel P, Lebrun A, Heller C, Lavery R, Viovy JL, Chatenay D, Caron F. DNA: an extensible molecule. Science. 1996;271:792–794. doi: 10.1126/science.271.5250.792. [DOI] [PubMed] [Google Scholar]
- 21.Smith SB, Cui Y, Bustamante C. Overstretching B-DNA: the elastic response of individual double-stranded and single-stranded DNA molecules. Science. 1996;271:795–799. doi: 10.1126/science.271.5250.795. [DOI] [PubMed] [Google Scholar]
- 22.Allemand JF, Bensimon D, Lavery R, Croquette V. Stretched and overwound DNA forms a Pauling-like structure with exposed bases. Proc. Natl Acad. Sci. USA. 1998;95:14152–14157. doi: 10.1073/pnas.95.24.14152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Orozco M, Noy A, Pérez A. Recent advances in the study of nucleic acid flexibility by molecular dynamics. Curr. Opin. Struct. Biol. 2008;18:185–193. doi: 10.1016/j.sbi.2008.01.005. [DOI] [PubMed] [Google Scholar]
- 24.Mackerell AD, Nilsson L. Molecular dynamics simulations of nucleic acid-protein complexes. Curr. Opin. Struct. Biol. 2008;18:194–199. doi: 10.1016/j.sbi.2007.12.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lu XJ, Olson WK. Resolving the discrepancies among nucleic acid conformational analyses. J. Mol. Biol. 1999;285:1563–1575. doi: 10.1006/jmbi.1998.2390. [DOI] [PubMed] [Google Scholar]
- 26.McLachlan AD. Gene duplications in the structural evolution of chymotrypsin. J. Mol. Biol. 1979;128:49–79. doi: 10.1016/0022-2836(79)90308-5. [DOI] [PubMed] [Google Scholar]
- 27.Babcock MS, Pednault EP, Olson WK. Nucleic acid structure analysis. Mathematics for local Cartesian and helical structure parameters that are truly comparable between structures. J. Mol. Biol. 1994;237:125–156. doi: 10.1006/jmbi.1994.1213. [DOI] [PubMed] [Google Scholar]
- 28.Mazur J, Jernigan RL. Comparison of rotation models for describing DNA conformations: application to static and polymorphic forms. Biophys. J. 1995;68:1472–1489. doi: 10.1016/S0006-3495(95)80320-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Maddocks JH, Gonzalez O. Extracting parameters for base-pair level models of DNAfrom molecular dynamics simulations. Theor. Chem. Acc. 2001;106:76–82. [Google Scholar]
- 30.Weber RO. Estimators for the standard deviation of horizontal wind direction. J. Appl. Meteorol. 1997;36:1403–1415. [Google Scholar]
- 31.Yamartino RJ. A comparison of several “single-pass” estimators of the standard deviation of wind direction. J. Climate Appl. Meteorol. 1984;23:1362–1366. [Google Scholar]
- 32.Marzec CJ, Day LA. An exact description of five-membered ring configurations. I. Parameterization via an amplitude S, an angle gamma, the pseudorotation amplitude q and phase angle P, and the bond lengths. J. Biomol. Struct. Dyn. 1993;10:1091–1123. doi: 10.1080/07391102.1993.10508697. [DOI] [PubMed] [Google Scholar]
- 33.Westhof E, Sundaralingam M. A method for the analysis of puckering disorder in five-membered rings: the relative mobilities of furanose and proline rings and their effects on polynucleotide and polypeptide backbone flexibility. J. Am. Chem. Soc. 1983;105:970–976. [Google Scholar]
- 34.Egholm M, Buchardt O, Christensen L, Behrens C, Freier SM, Driver DA, Berg RH, Kim SK, Norden B, Nielsen PE. PNA hybridizes to complementary oligonucleotides obeying the Watson-Crick hydrogen-bonding rules. Nature. 1993;365:566–568. doi: 10.1038/365566a0. [DOI] [PubMed] [Google Scholar]
- 35.Cloutier TE, Widom J. Spontaneous sharp bending of double-stranded DNA. Mol. Cell. 2004;14:355–362. doi: 10.1016/s1097-2765(04)00210-2. [DOI] [PubMed] [Google Scholar]
- 36.Lankas F, Lavery R, Maddocks JH. Kinking occurs during molecular dynamics simulations of small DNA minicircles. Structure. 2006;14:1527–1534. doi: 10.1016/j.str.2006.08.004. [DOI] [PubMed] [Google Scholar]
- 37.Du Q, Kotlyar A, Vologodskii A. Kinking the double helix by bending deformation. Nucleic Acids Res. 2008;36:1120–1128. doi: 10.1093/nar/gkm1125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Harris SA, Laughton CA, Liverpool TB. Mapping the phase diagram of the writhe of DNA nanocircles using atomistic molecular dynamics simulations. Nucleic Acids Res. 2008;36:21–29. doi: 10.1093/nar/gkm891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Liverpool TB, Harris SA, Laughton CA. Supercoiling and denaturation of DNA loops. Phys. Rev. Lett. 2008;100:238103. doi: 10.1103/PhysRevLett.100.238103. [DOI] [PubMed] [Google Scholar]
- 40.Beveridge DL, Barreiro G, Byun KS, Case DA, Cheatham TE3, Dixit SB, Giudice E, Lankas F, Lavery R, et al. Molecular dynamics simulations of the 136 unique tetranucleotide sequences of DNA oligonucleotides. I. Research design and results on d(CpG) steps. Biophys. J. 2004;87:3799–3813. doi: 10.1529/biophysj.104.045252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Dixit SB, Beveridge DL, Case DA, Cheatham T.E., III, Giudice E, Lankas F, Lavery R, Maddocks JH, Osman R, et al. Molecular dynamics simulations of the 136 unique tetranucleotide sequences of DNA oligonucleotides. II: sequence context effects on the dynamical structures of the 10 unique dinucleotide steps. Biophys. J. 2005;89:3721–3740. doi: 10.1529/biophysj.105.067397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Wing R, Drew H, Takano T, Broka C, Tanaka S, Itakura K, Dickerson RE. Crystal structure analysis of a complete turn of B-DNA. Nature. 1980;287:755–758. doi: 10.1038/287755a0. [DOI] [PubMed] [Google Scholar]
- 43.Frederick CA, Quigley GJ, Teng MK, Coll M, Van der Marel GA, Van Boom JH, Rich A, Wang AH. Molecular structure of an A-DNA decamer d(ACCGGCCGGT) Eur. J. Biochem. 1989;181:295–307. doi: 10.1111/j.1432-1033.1989.tb14724.x. [DOI] [PubMed] [Google Scholar]
- 44.Nikolov DB, Chen H, Halay ED, Hoffman A, Roeder RG, Burley SK. Crystal structure of a human TATA box-binding protein/TATA element complex. Proc. Natl Acad. Sci. USA. 1996;93:4862–4867. doi: 10.1073/pnas.93.10.4862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Guzikevich-Guerstein G, Shakked Z. A novel form of the DNA double helix imposed on the TATA-box by the TATA-binding protein. Nat. Struct. Biol. 1996;3:32–37. doi: 10.1038/nsb0196-32. [DOI] [PubMed] [Google Scholar]
- 46.Humphrey W, Dalke A, Schulten K. VMD: visual molecular dynamics. J. Mol. Graph. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 47.Bansal M, Bhattacharyya D, Ravi B. NUPARM and NUCGEN: software for analysis and generation of sequence dependent nucleic acid structures. Comput. Appl. Biosci. 1995;11:281–287. doi: 10.1093/bioinformatics/11.3.281. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.