Abstract
Labeling with heavy atom clusters attached to antibody fragments is an attractive technique for determining the 3D distribution of specific proteins in cells using electron tomography. However, the small size of the labels makes them very difficult to detect by conventional bright-field electron tomography. Here we evaluate quantitative scanning transmission electron microscopy (STEM) at a beam voltage of 300 kV for detecting 11-gold atom clusters (Undecagold) and 1.4 nm-diameter nanoparticles (Nanogold) for a variety of specimens and imaging conditions. STEM images as well as tomographic tilt series are simulated by means of the NIST Elastic Scattering Cross-Section Database for gold clusters embedded in carbon. The simulations indicate that the visibility in 2D of Undecagold clusters in a homogeneous matrix is maximized for low inner collection semi-angles of the STEM annular dark-field detector (15–20 mrad). Furthermore, our calculations show that the visibility of Undecagold in 3D reconstructions is significantly higher than in 2D images for an inhomogeneous matrix corresponding to fluctuations in local density. The measurements demonstrate that it is possible to detect Nanogold particles in plastic sections of tissue freeze-substituted in the presence of osmium. STEM tomography has the potential to localize specific proteins in permeabilized cells using antibody fragments tagged with small heavy atom clusters. Our quantitative analysis provides a framework for determining the detection limits and optimal experimental conditions for localizing these small clusters.
Keywords: Scanning transmission electron microscopy, STEM, electron tomography, Nanogold, Undecagold, labeling, protein
1. Introduction
Electron tomography (ET) has become an established technique for determining the 3D ultrastructure of cells (Baumeister, 2005; Baumeister and Steven, 2000; Frank, 2006; Koster et al., 1997; McEwen and Marko, 2001; McIntosh, 2001; McIntosh et al., 2005; Steven and Aebi, 2003). Currently, the spatial resolution in tomographic reconstructions is typically in the range of 5 to 10 nm, which is sufficient to visualize coarse-scale macromolecular organization (McEwen and Marko, 2001; McIntosh et al., 2005). The ultimate goal of ET is to localize specific macromolecules inside the cellular environment. Two approaches are possible, one based on immunolabels consisting of antibody fragments tagged with heavy atom clusters, and the other involving direct visualization of the proteins in a cryotomogram of a frozen-hydrated cell (Baumeister, 2005; Baumeister and Steven, 2000; Cheutin et al., 2002; Cheutin et al., 2003; Grünewald et al., 2003; McIntosh, 2001; McIntosh et al., 2005; Medalia et al., 2002; Nickell et al., 2006; Ziese et al., 2002). Although the idea of locating protein complexes directly from a cryotomogram of a cell frozen in its native state is attractive, at present cryo-electron tomography can only be used to identify larger complexes consistent with the 5–10 nm resolution limit imposed by radiation damage. Locating most macromolecules in a cell would require a resolution of 2 to 3 nm, and even with significant technical improvements in the state-of-the-art of the technique, identification of sparse antigens or very small protein complexes at this resolution would be very difficult to achieve. Currently, labeling with heavy element nanoparticles offers a useful alternative for localizing specific proteins in a cell. Two common labels are clusters of ~67 gold atoms of diameter 1.4 nm (Nanogold) and clusters of 11 gold atoms of diameter 0.8 nm (Undecagold), both of which are available commercially from Nanoprobes Inc. (Hainfeld, 1987; Hainfeld and Furuya, 1992). The small size of these gold clusters provides the advantage of high penetrability into cells, which yields high labeling efficiency (Robinson et al., 2000a; Robinson et al., 2000b). However, because of their small size, imaging these clusters without silver enhancement is difficult by conventional transmission electron microscopy (TEM) (Hainfeld, 1996; Robinson et al., 2000a; Zeuschner et al., 2006).
It is well known that scanning transmission electron microscopy (STEM) is better suited than TEM for imaging clusters of high atomic number elements in a low atomic number matrix (Hainfeld, 1987; Hainfeld, 1996; Wall et al., 1982; Wall, 1999). This is because the signal due to elastic scattering can be collected with very high efficiency in the STEM using an annular dark-field (ADF) detector. The ADF STEM signal has been used extensively for 2D imaging of macromolecules that are labeled with ultrasmall gold clusters (Lipka et al., 1983; Safer et al., 1982; Steinmetz et al., 1998; Yang et al. 1994). However, it is only recently that the technique has been applied to determine the 3D distribution of immunogold labels (Cheutin et al., 2002; Cheutin et al., 2003; Ziese et al., 2002). In one application of STEM tomography, Cheutin et al. (2002) have established the three-dimensional organization of active rRNA genes within the nucleolus by imaging the 3D distribution of fluoronanogold particles enhanced with silver. In another study,Ziese et al. (2002) have shown that STEM tomography offers the capability of imaging ultrasmall gold labels in 3D without the need for silver enhancement. Specifically, these authors have shown that STEM enables the 3D localization of a 15-atom gold cluster deposited onto the surface of a 60 nm stained plastic embedded cell. Detection of heavy-metal clusters in 3D is also of interest in applications to materials science (Arslan et al., 2005; De Jong and Koster, 2002; Midgley et al., 2006; Wikander et al., 2007; Ziese et al. 2004). For example, knowledge of the 3D distribution of metallic nanoparticles within a porous substrate such as silica is important in catalysis because it can govern activity and selectivity (Midgley et al., 2006).
The application of electron microscopy in biology invariably involves maximizing the amount of structural information while avoiding excessive beam damage from the electron irradiation (Glaeser and Taylor, 1978; Grimm et al., 1996; Schroder et al. 1990). For example, in cryoelectron microscopy of frozen-hydrated biological macromolecules, a twofold increase in the signal-to-noise ratio (SNR) is achieved by allowing only elastically scattered electrons to contribute to the image formation (Yonekura et al., 2006). As STEM tomography matures into the technique of choice for locating gold labels inside cells, it becomes important to understand the factors that influence the visibility of the labels in 3D and how to choose the imaging parameters to obtain the maximum visibility for a given electron dose.
Here we investigate the factors influencing the visibility of ultrasmall heavy atom clusters (Undecagold and Nanogold) in biological specimens using STEM tomography. First, we simulate STEM images of Undecagold clusters embedded in carbon by making use of the differential elastic scattering cross sections of gold and carbon atoms. From these simulations, we investigate the influence of the ADF detector collection semi-angle on the visibility of the clusters in 2D and 3D images. We then obtain and analyze experimental STEM tomographic tilt series to test the visibility of Undecagold and Nanogold in a pure carbon matrix as well as in the context of lightly stained, sectioned cells.
2. Experimental
2.1. Specimen preparation
To test the stability of the gold clusters under electron irradiation, ultrathin carbon films were prepared by evaporating approximately 3 nm of carbon onto fresh cleaved mica, floating the ultrathin films in water, and collecting them on 200-mesh grids covered with lacey carbon film. Grids were glow-discharged in air to facilitate adsorption of the gold clusters, and 5-µl droplets of 1:50 diluted Nanogold were deposited onto the surface of some of the grids while 5-µl droplets of 1:20 diluted Undecagold onto the surface of the remaining grids. Both types of nanoparticles were obtained from Nanoprobes (Nanoprobes, Yaphank, NY, USA). After adsorption for 2 minutes, the grids were blotted with filter paper and washed 5 times with 5 µl aliquots of de-ionized water. An additional thin (approximately 1 nm) carbon layer was deposited onto some of the grids to investigate whether this improved the stability of the gold clusters in the electron beam.
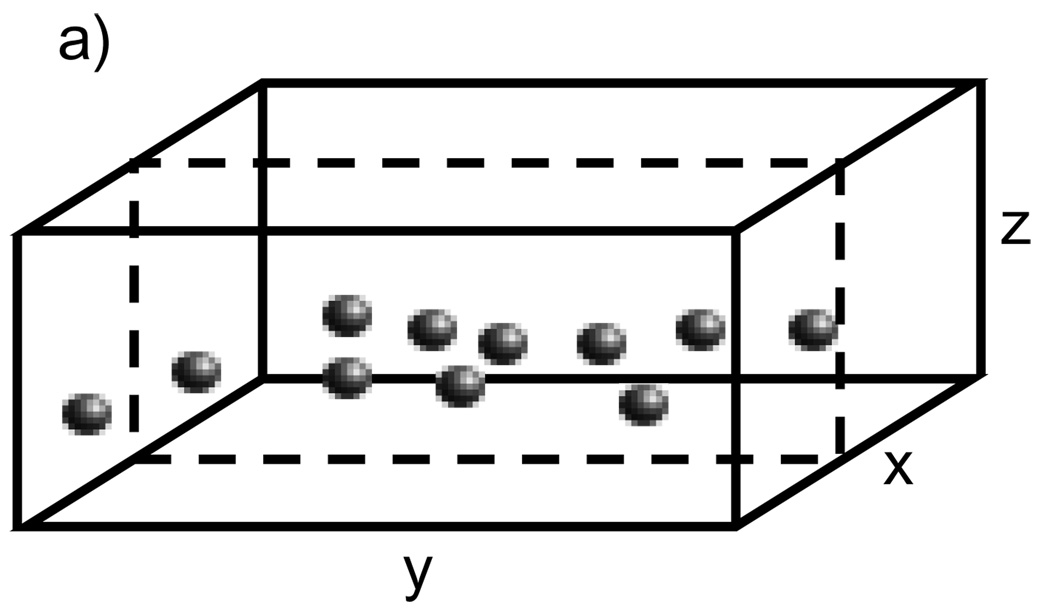
A specimen containing nanoparticles embedded in a 100 nm thick layer of carbon (Fig. 1) was prepared by first depositing Nanogold onto an approximately 35 nm thick evaporated carbon layer supported on a lacey grid. An additional 65 nm layer of carbon was then evaporated onto the specimen on the same side as the deposited Nanogold to give a total specimen thickness of 100 nm with the nanoparticles sandwiched as a layer within a carbon matrix. Larger 10 nm-diameter colloidal gold particles were then deposited onto the top and bottom of the surfaces to serve as fiducials for drift correction during acquisition of the tilt series, as well as for image alignment prior to 3D reconstruction. To prepare a specimen containing Undecagold embedded in a carbon film, the same procedure was followed except that the first layer of evaporated carbon was approximately 15 nm in thickness and the second layer 5 nm, and 3 nm-diameter colloidal gold particles were used as fiducials.
Fig. 1.
Schematic diagram of specimen consisting of Nanogold particles embedded as a layer in a 100 nm thick matrix of carbon. The specimen was used to measure the visibility of gold labels in STEM images.
An 80 nm-thick section of plastic-embedded Caenorhabditis elegans was prepared for assessing the visibility of Nanogold in a lightly stained cell. The C. elegans were placed in a cryopreservative solution of 15% sucrose and frozen in a BAL-TEC HPM-010 high-pressure freezing machine. The frozen blocks were processed at low temperature in a Leica EM-AFS freeze-substitution system using a solution of acetone containing 1.0% osmium tetroxide. After freeze-substitution for 3 days, the specimens were gradually warmed to room temperature and embedded in Epon-Araldite by graded exchange of the acetone. Specimens were polymerized in 100% resin by heating to 60°C for 2 days, sectioned to a nominal thickness of 80 nm with a Leica Ultracut E ultramicrotome, and mounted on 300 mesh EM copper grids. Both Nanogold particles and 10-nm diameter colloidal gold were deposited on top of the sections to test the visibility of the Nanogold in the presence of light stain, with the larger particles serving as fiducials in the alignment of the tilt series.
2.2. Data collection and data processing
Acquisition of tomographic tilt series was performed on a 300 kV field-emission FEI Tecnai microscope (FEI, Hillsboro, OR, USA) with a Fischione HAADF detector (Fischione, Export, PA, USA) situated after the projection-lens system and above the viewing screen. FEI software was used to acquire the tomographic tilt series. STEM tomography of the specimen of Nanogold embedded in carbon was acquired with a tilt range of −60° to +60° in steps of 3°, with an integral dose of 105 e/nm2, and a pixel size in the STEM image of 0.37 nm. The FWHM of the STEM probe was measured on a slow-scan CCD camera and determined to be about 0.6 nm. During data acquisition, the probe was always focused on the surface of the specimen. The inner collection semi-angle of the ADF detector was 16 mrad, the outer semi-angle was 5 times the inner angle (80 mrad), and the convergence semi-angle of the beam on the specimen 10 mrad. For the specimen of Undecagold embedded in carbon, STEM tomography was done with an integral dose of 3.5 × 105 e/nm2, a pixel size of 0.23 nm, and a tilt range from −60° to +60° in steps of 2°. Finally, STEM tomographic tilt series of C. elegans was acquired with a tilt range from −60° to +60° in steps of 2°, with a total dose of 2 × 105 e/nm2, and with a pixel size of 0.3 nm. For all the tomographic series, the images were 2k × 2× pixels in size.
For 3D reconstruction, the images at each tilt increment were aligned in the IMOD software (Kremer et al. 1996) using fiducial markers. For some of the datasets we removed the features corresponding to the gold fiducial markers after alignment of the tilt series and prior to reconstruction in order to eliminate artifactual streaks in the final tomogram caused by the limited tilt range of the dataset (Mastronarde, 2006). The dark-field signal from the gold fiducial markers was typically five times greater than the standard deviation of the pixel intensities for the rest of the image. Therefore it was straightforward to remove the fiducial features by substituting their pixel intensities with the mean pixel intensity of the entire image. Tomographic reconstruction of the aligned tilt series was performed using the simultaneous iterative reconstruction technique (SIRT) algorithm (Gilbert, 1972; Herman, 1980), which we have implemented in our group (Aronova et al., 2007). The specimen of Nanogold embedded in 100 nm of carbon was also reconstructed with weighted back-projection (WBP) (Radermacher, 2006) in IMOD (Kremer, 1996). The tomograms were manipulated in Digital Micrograph (Gatan, Pleasanton, CA, USA) for typical operations such as projecting slices in the z direction, cutting slices, drawing line profiles, etc.
3. Modeling the Cluster Visibility
3.1. Signal Estimation
To assess the visibility of the gold clusters in ADF STEM images, we model the elastic scattering from Undecagold clusters embedded in a thin layer of amorphous carbon. For simplicity, we just consider the 11 gold atoms in the cluster and ignore the organic component. We assume the scattering is incoherent and the specimen is sufficiently thin so that only single elastic scattering events have to be considered. Our calculations are for the same set of experimental conditions used to obtain the measurements that we present later.
For a carbon film of thickness tC illuminated with Iinc incident electrons per pixel, the number of scattered electrons IC accumulated in a single image pixel is given by
| (1) |
where NC is the number of carbon atoms per unit volume, β is the collection semi-angle subtended by the ADF detector, and α is the convergence semi-angle of the incident beam. The scattering cross section σC(β)' is defined as
| (2) |
where is the differential elastic scattering cross section for carbon, , convolved with the angular distribution of the incident electron intensity:
where D(θ) = 1 for θ < α, and D(θ) = 0 for θ ≥ α.
For an Undecagold cluster, the number of scattered electrons IAu that are collected by the ADF detector is given by
| (3) |
where nAu is the number of atoms in the gold cluster, σAu(β)' is the gold elastic scattering cross section, d is the pixel size, and p is the number of pixels over which the signal is integrated.
Determining I(α,β)for carbon and gold from Eq. 1 and Eq. 3, respectively, requires the differential elastic scattering cross sections for carbon and gold atoms. We make use of the National Institute of Standards and Technology (NIST) Electron Elastic-Scattering Cross-Section Database, which provides accurate values for the cross sections at incident electron beam energies up to 300 keV (Jablonski et al., 2003; Jablonski et al., 2004).
3.2. Simulated 2D images and 3D reconstructions
As a first step to assess the visibility of the clusters, we simulate 2D images of Undecagold embedded in a 40 nm-thick carbon film using Eq. 1 and Eq. 3. We consider 300 kV incident electrons, an incident electron dose of 105 e/nm2, a pixel size of 0.2 nm, and a beam convergence semi-angle of 12 mrad. The inner collection semi-angle of the dark-field detector was varied from 12 to 100 mrad with the outer collection angle being 5 times larger than the inner angle. Two sources of noise are considered: shot noise in the incident beam, and specimen-dependent noise due to density fluctuations within the carbon support film.
The second step in the assessment of particle visibility is to reconstruct the 3D distribution of the clusters embedded in the 40 nm carbon film from a tomographic tilt series of simulated STEM images of 2D projected structure. We simulate the tilt series over a range of −69° to +69° with increments of 3° and consider 300 kV incident electrons and an integrated dose of 105 e/nm2. For the carbon support film imaged at tilt angle ϕ, the number of electrons accumulated in a single image pixel in Eq. 1 is modified by an obliquity factor (cos ϕ)−1 to give
| (4) |
For an Undecagold cluster, the number of electrons IAu(α,β) accumulated at a tilt angle ϕ is the same as given in equation 3 because the cluster is assumed to be spherical. Furthermore, the carbon matrix is thin enough for the angular distribution of the scattered electrons from Undecagold not to be broadened appreciably by plural scattering effects.
Tomographic reconstruction of the simulated tilt series was performed using the SIRT algorithm. The results were compared with reconstructions performed with the WBP algorithm implemented in IMOD. In practice, projection images in a tilt series cannot be aligned perfectly, but here the effects of such misalignments on the reconstruction quality were not included.
3.3. Definition of SNR and contrast
Values of SNR and contrast were calculated from the 2D image simulations described above, and they were defined as follows. First, the signal SGC associated with Undecagold clusters plus carbon film was obtained by integrating 1-nm2 regions (i.e., 5×5 pixels) containing Undecagold clusters. The signal within different regions of the background, also for a 1-nm2 window, was then computed and the average SC and standard deviation s of the signal within the various background regions determined. SNR of Undecagold in carbon was then calculated as (SGC – SC)/s while contrast was defined as (SGC –SC)/ SC. The 3D SNR for Undecagold within simulated tomograms was calculated also as (SGC – SC)/s from 1-nm thick slices projected in the z direction.
4. Results and Discussion
4.1. Sensitivity of Nanogold and Undecagold to the incident electron beam
Electron tomography of nanometer size gold labels in biological specimens of moderate thickness can require relatively high electron doses. For example, Ziese et al. (2002) used a total dose of 3.5 × 105 e/nm2 at 200 kV to detect 15-atom gold clusters deposited on the surface of a 60 nm thick stained plastic section. For comparison, electron tomography of frozen-hydrated specimens is performed using doses of the order of 103 to 104 e/nm2 (Hsieh et al., 2002; McIntosh et al., 2005).
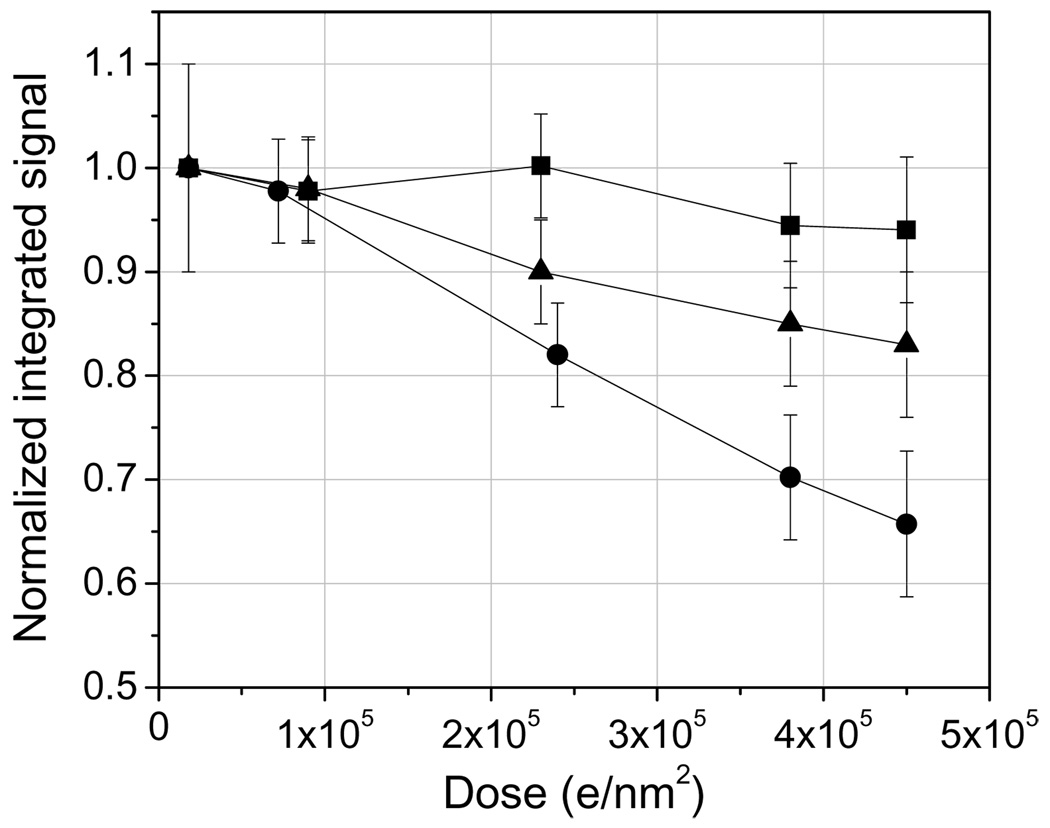
Undecagold has been reported by Wall et al. (1982) to be beam sensitive at 40 kV acceleration voltage, whereas Nanogold has been quoted to be resistant to moderate doses of electron irradiation (Hainfeld and Furuya, 1992). Here we reevaluate the beam damage response of these two labels at an acceleration voltage of 300 kV. Fig. 2 shows the decrease in total integrated signal within Nanogold and Undecagold particles deposited onto ~ 3 nm-thick carbon films as a function of dose. Nanogold loses only 5% of its mass over a dose range of 2.0 × 104 e/nm2 to 4.5 × 105 e/nm2 but Undecagold suffers a 35% mass loss under the same dose conditions. At the lowest dose of 2.0 × 104 e/nm2, Fig. 2 suggests that Undecagold might have already undergone a small 2% mass loss, which would give a total mass loss of around 37% at 4.5 × 105 e/nm2. Fig. 2 also indicates the damage response curve for Undecagold clusters that are coated with approximately 1 nm of carbon. We find that even such thin layers of carbon are enough to decrease the total mass loss of Undecagold from 37% to 19%. These results suggest that despite the sensitivity of Undecagold clusters to the incident electron irradiation when the labels are deposited on the surface, it should be possible to use Undecagold for immunolabeling ET as long as the clusters are contained within a plastic section.
Fig. 2.
Drop in integrated signal for Nanogold (squares) and Undecagold (circles) as a function of electron dose and for 300 kV incident electrons. The gold clusters were located at the surface of a 3 nm-thick carbon film. Addition of an extremely thin additional layer (approximately 1 nm) of carbon on top of the adsorbed Undecagold particles significantly improves its damage response, presumably due to the inability of damage fragments of the Undecagold molecule to be ejected from the specimen (triangles). The dark-field signal intensities were normalized to the one obtained with the smallest dose of 2.0 × 104 e/nm2.
4.2. Comparison of experimental and calculated signals for Nanogold and Undecagold
It is useful to compare the measured image intensities from the Nanogold and Undecagold clusters with calculated signal intensities obtained from the elastic scattering cross section for gold atoms at 300 kV. A reasonable agreement between experiment and calculation gives us confidence about the validity of simulations for a given set of experimental conditions and enables us to assess the detectability of the gold clusters in both 2D and 3D data sets.
The average of the total integrated signal from 50 Nanogold particles is consistent with the calculated value for an ADF detector with an inner collection semi-angle of 16 mrad, the measured values being only 9% lower than the calculation as indicated in Table 1, which also shows a similar agreement for an ADF inner collection semi-angle of 36 mrad. An organic shell surrounds the core of each Nanogold particle and the shell’s constituent atoms are estimated to contribute less than 10% to the total ADF signal from the particle. The measured signal from the Nanogold is therefore up to 20% lower than theoretically predicted but the agreement is still close.
Table 1.
Comparison between experimental and calculated signals for Nanogold and Undecagold. Experimental signals were obtained from a population of 50 particles with an electron dose of 2×104 e/nm2. Theoretical signals were obtained from Eq. 3.
| Inner collection angle of ADF detector |
16 mrad | 36 mrad | ||
|---|---|---|---|---|
| Theory | Experiment* | Theory | Experiment | |
| Nanogold | 414 | 375 ± 13 | 159 | 144 ± 4 |
| Undecagold | 106 | 94 ± 4 | - | - |
± standard error of the mean
We find that the average measured signal from 50 Undecagold clusters is 11% lower than the calculated value. The contribution of the organic constituents of Undecagold cluster to the ADF signal is estimated to be 20%, which would increase the difference between experiment and theory to around 30%. This discrepancy is most likely due to a small uncertainty in the estimation of the experimental parameters and/or to an inability of the differential elastic scattering cross section for an isolated gold atom in predicting the signal obtained from a cluster of atoms.
Recently, we have reported a similar quantification scheme based on scattering theory and on a calibration of the experimental parameters of the microscope to determine in absolute terms the mass of biological macromolecules directly from their STEM signal (Sousa and Leapman, 2007). The present results further support the validity of image simulations based on scattering theory for assessing the accuracy of quantitative dark-field STEM. Below in sections 4.3 and 4.4, we shall make use of simulations to address the detectability of gold labels in 2D and 3D images.
4.3. Effects of inner collection semi-angle on the visibility of Undecagold clusters in simulated 2D images
When a TEM is operated in STEM mode, the collection angle of the ADF detector is variable and depends on the magnification of the convergent beam diffraction pattern in the detector plane. The optimal camera length of the diffraction pattern for detecting Undecagold clusters can be determined by simulating the images of the clusters embedded in a 40 nm film of pure carbon, as well as in a 40 nm film of carbon containing 1 atomic percent osmium.
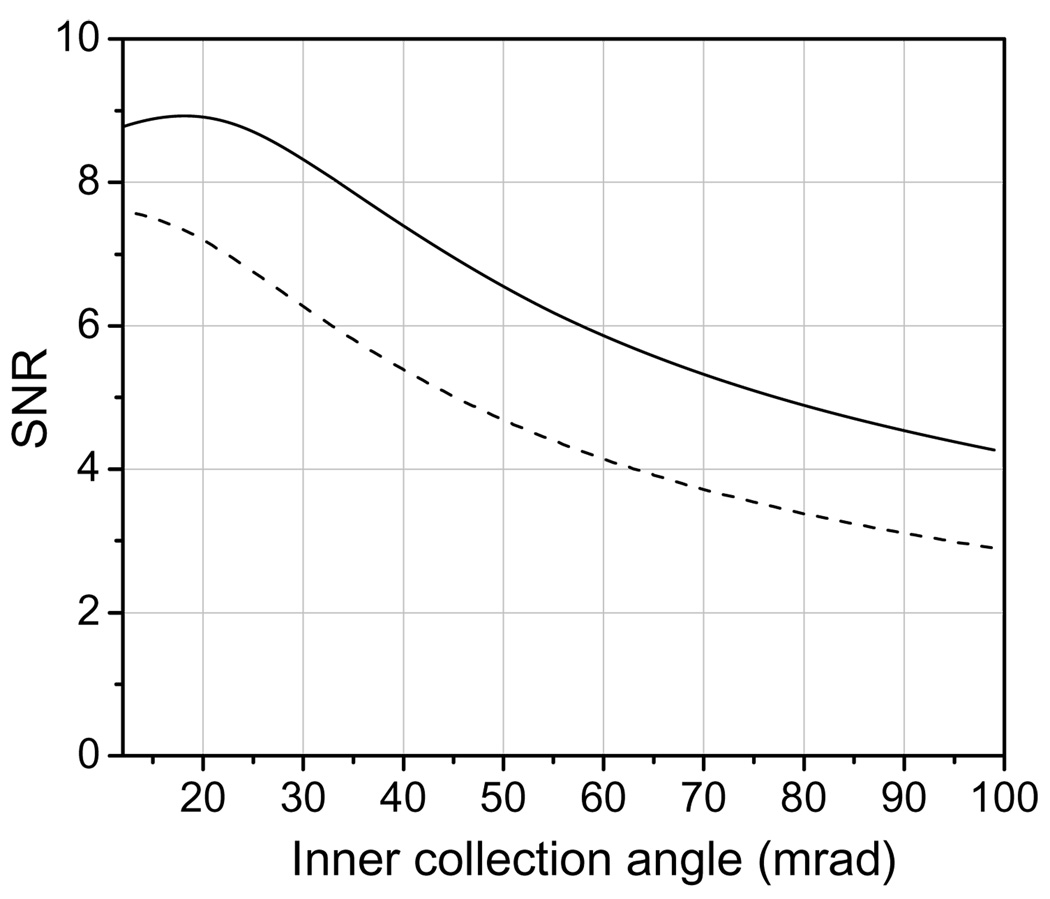
The solid curve in Fig. 3 shows the calculated contrast of an Undecagold cluster as a function of inner collection semi-angle for a 40 nm film of pure carbon. The curve is plotted from 12 mrad, which corresponds to the convergence semi-angle of the incident beam. The dashed curve in Fig. 3 shows the contrast as a function of inner collection angle curve for a carbon film containing 1 atomic percent osmium. The behavior of the SNR as a function of inner collection angle is shown in Fig. 4 for a pure carbon film as well as for a carbon film containing 1 atomic percent osmium. The contrast in Fig. 3 and Fig. 4 were calculated by considering only single elastic scattering events from the Undecagold and carbon. We did test the effects of inelastic scattering from the carbon film but found that this produced negligible effect on the shape of the contrast and SNR curves.
Fig. 3.
Contrast of Undecagold in a 40 nm-thick carbon film as a function of the ADF detector inner collection semi-angle; the outer semi-angle is 5 times larger than the inner angle. The dose used in the calculations was 105 e/nm2. The solid curve is for a pure carbon film, and the dashed curve for a carbon film containing 1 atomic percent osmium. With 1 atomic percent osmium the contrast depends only weakly on the inner semi-angle.
Fig. 4.
SNR for Undecagold in a 40 nm-thick carbon film as a function of ADF detector inner collection semi-angle; the outer semi-angle is 5 times larger than the inner angle. The dose used in the calculations was 105 e/nm2. The solid curve is for a pure carbon film, and the dashed curve for a carbon film containing 1 atomic percent osmium.
For a film of pure carbon, the optimum SNR is obtained for a detector inner semi-angle of 20 mrad (solid curve in Fig. 4), but the SNR only falls by a factor of 1.2 for a 40-mrad inner angle. However, the contrast is 1.7 times higher for a 40-mrad inner angle than for a 20 mrad inner angle (solid curve in Fig. 3). Another factor to be considered is the integrated signal from the Undecagold cluster. At 40 mrad, this signal is as much as 2.4 times smaller than at 20 mrad. As a result (Table 2), it is preferable to work at lower inner semi-angles, e.g., 16 to 20 mrad, for which the integrated signal and the SNR are maximized, even though the contrast is not maximized. In any case it is possible to enhance the contrast digitally post facto.
Table 2.
SNR and contrast for an Undecagold cluster in a 40 nm carbon matrix. SNR at 20 mrad is 1.2 times higher than at 40 mrad, and contrast is 1.7 times higher at 40 mrad.
| Inner collection angle of ADF detector |
20 mrad | 40 mrad |
|---|---|---|
| SNR | 8.91 | 7.40 |
| Contrast | 0.158 | 0.261 |
When we consider a carbon film containing 1 atomic percent osmium, the advantage of working at lower inner semi-angles of the ADF detector becomes very clear: working at lower inner angles optimizes the SNR while incurring only a relatively modest loss in contrast. The advantage of selecting small ADF inner semi-angles for the detection of heavy atom clusters in stained samples is shown in Table 3, which gives the calculated SNR and contrast for inner semi-angles of 20 and 40 mrad. The weak collection angle-dependence of the Undecagold contrast for a matrix containing 1 atomic percent osmium can be explained by the fact that Os and Au have almost identical angular distributions. Thus the addition of only 40 osmium atoms distributed randomly among 3960 atoms of carbon matrix per nm2 area of the specimen is sufficient to decrease significantly the dependence of the Undecagold contrast on the ADF detector inner semi-angle.
Table 3.
SNR and contrast for an Undecagold cluster in a 40 nm carbon matrix containing 1 atomic % osmium. SNR at 20 mrad is 1.3 times higher than at 40 mrad, and contrast is 1.3 times higher at 40 mrad.
| Inner collection angle of ADF detector |
20 mrad | 40 mrad |
|---|---|---|
| SNR | 7.20 | 5.39 |
| Contrast | 0.103 | 0.138 |
So far, we have considered the carbon matrix to be homogeneous and Poisson statistical fluctuations in the incident beam to be the only source of noise (i.e., shot noise). In a real specimen the underlying biological structure makes an additional contribution to the noise, which reduces the visibility of the Undecagold clusters. To test the effect of these specimen-dependent density fluctuations on the cluster visibility in 2D images, we divide the 40 nm-thick carbon matrix into 1 nm3 cubes, each of which contains an average of 100 carbon atoms (assuming a density of 2.0 g/cm3). We simulate two levels of density fluctuations, one in which the standard deviation in the number of carbon atoms within each cube is 20 atoms, and another where it is 50 atoms. When the random fluctuations yielded a negative number of atoms within a cube, then the number of atoms in that cube was set to zero.
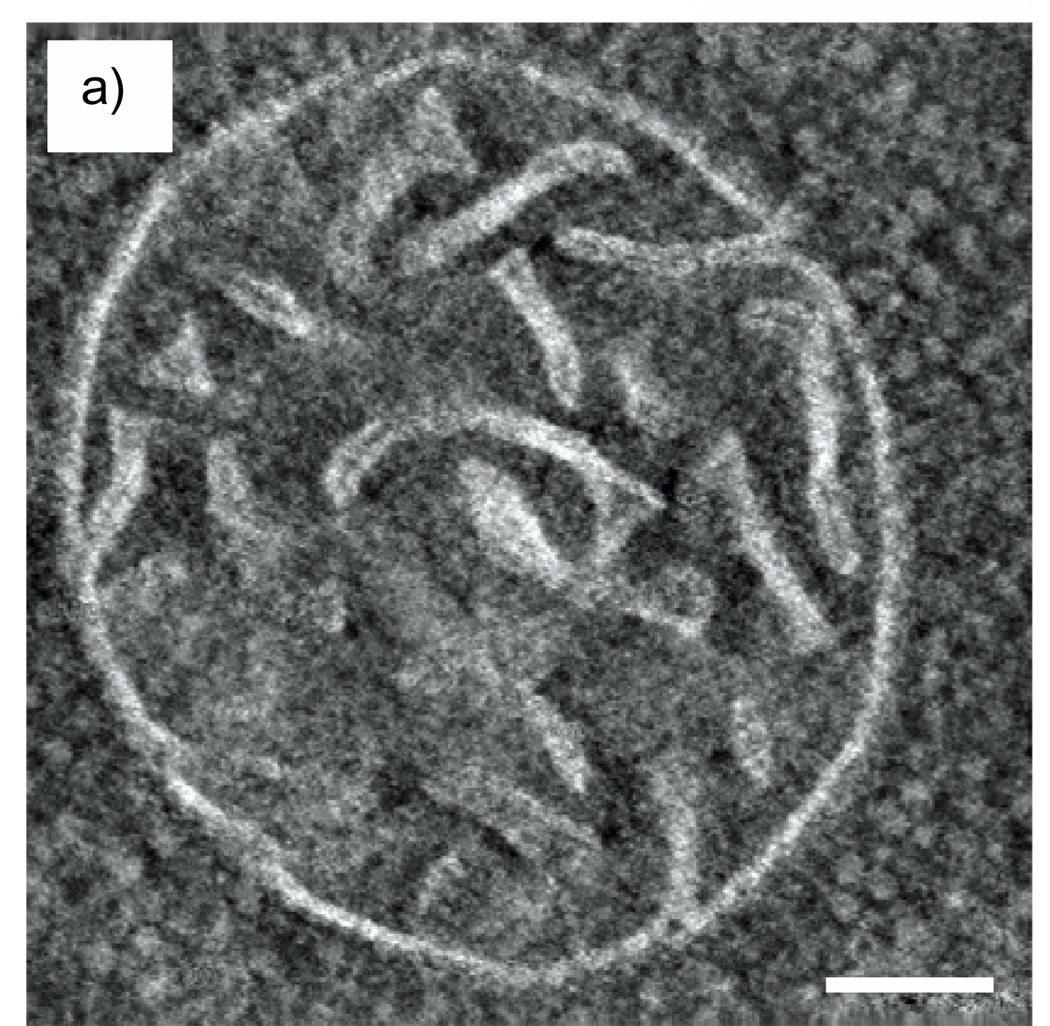
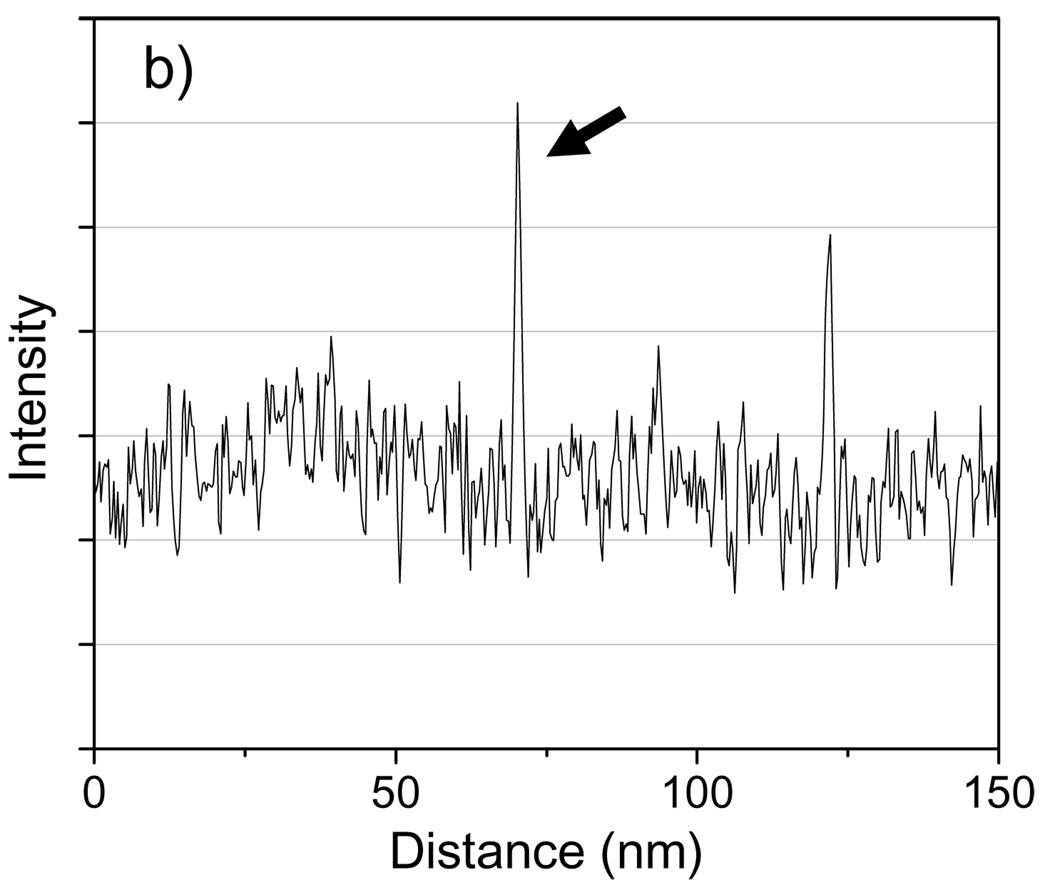
A simulated image of an Undecagold cluster in a carbon film containing 20% density fluctuations on a nanometer scale is shown in Fig. 5a for an ADF inner semi-angle of 16 mrad, and a line profile across the cluster is shown in Fig. 5b. From an average of 20 such particles, the SNR for imaging Undecagold in this model specimen was 4.1, which is significantly smaller than the SNR of 8.9 obtained in the absence of density fluctuations in the matrix.
Fig. 5.
(a) Simulated STEM image of an Undecagold cluster in a 40 nm-thick carbon film containing 20% density fluctuations. The dose was 105 e/nm2 and the ADF detector inner collection semi-angle was 16 mrad. (b) 3-pixel wide line profile across the Undecagold particle indicated with arrow in (a). The SNR of the Undecagold cluster is 4.1 ± 0.3, which is significantly smaller than the SNR of 8.9 (Fig. 4) obtained without including density fluctuations. Scale bar = 2 nm.
Figs. 6a shows a simulated image of an Undecagold cluster in a 40-nm carbon matrix containing 50% density fluctuations for an inner ADF semi-angle of 16 mrad, and Fig. 6b indicates a line profile across the cluster. Figs. 7a and 7b show a similar image and line profile for an inner ADF semi-angle of 50 mrad. For the 16-mrad inner ADF semi-angle, the SNR for detecting an Undecagold cluster averaged over 20 particles is 1.9. This SNR is too low to identify the clusters reliably as evident in Fig. 6. For an inner ADF semi-angle of 50 mrad, the SNR averaged over 20 particles increases to 3.9 so that Undecagold can now be identified with statistical confidence. We point out that the texture seen in Fig. 6a is caused by the large fluctuations of 50% in the number of carbon atoms that we have simulated in subvolumes of 5×5×5 voxels. These fluctuations produce texture in the simulated projected image on a scale of 5×5 pixels.
Fig. 6.
(a) Simulated STEM image of an Undecagold cluster in a 40 nm-thick carbon film containing 50% density fluctuations. The dose was 105 e/nm2 and the ADF detector inner collection semi-angle was 16 mrad. (b) 3-pixel wide line profile across the Undecagold particle indicated with arrow in (a). The SNR of Undecagold is 1.9 ± 0.3, which is too low to identify the cluster. Scale bar = 2 nm.
Fig. 7.
(a) Simulated STEM image of an Undecagold cluster in a 40 nm-thick carbon film containing 50% density fluctuations. The dose was 105 e/nm2 and the ADF detector inner collection semi-angle was 50 mrad. (b) 3-pixel wide line profile across the Undecagold particle in indicated with arrow in (a). The SNR of the Undecagold cluster is 3.9 ± 0.3, which is twice the value of 1.9 ± 0.3 obtained with an inner semi-angle of 16 mrad (Fig. 4). Scale bar = 2 nm.
The results above show that the visibility of ultrasmall gold labels embedded in a light matrix can be seriously compromised if this matrix is not homogeneous but contains density fluctuations throughout. Although the SNR of the gold clusters increases with the use of larger ADF inner semi-angles, the integrated signal of the cluster decreases significantly. In the example above, the integrated signal for an inner semi-angle of 50 mrad would be as much as four times smaller that for a 16 mrad inner semi-angle. Therefore it is predicted that selection of higher inner angles would be inefficient for imaging the structure of a cell stained with heavy elements together with the detection of gold clusters. Selection of higher ADF inner semi-angles makes inefficient use of the incident electron irradiation and adds unnecessary noise to the cellular structure. In marked contrast to the visibility of gold clusters in 2D images, we show next that density fluctuations in the matrix do not strongly affect the visibility of gold clusters in 3D tomographic reconstructions. Importantly, this is true when working with low ADF inner semi-angles, which maximizes the signal collection.
4.4. Visibility of Undecagold clusters in simulated 3D images
Here we investigate through simulations what SNR is achievable based on the principle of electron dose fractionation for 3D imaging of gold clusters in STEM. The principle of dose fractionation was formulated by Hoppe and Hegerl (1976) in the context of bright-field TEM tomography. The principle states that if a voxel is imaged in projection with a dose D at a certain significance level S, then in a tomogram this voxel will be visible with the same significance level S if the integral dose used to collect the tomogram is D. The proof given by Hoppe and Hegerl assumed that a tomogram is collected with complete sampling of the Fourier space and that noise is signal-independent and the same in each projection. In order to evaluate the validity of the dose fractionation principle under more realistic conditions, McEwen et al. (1995) simulated several bright-field TEM tilt series under conditions of limited tilt range, high specimen contrast, and high absorption levels. These authors found that the principle holds true for these more realistic experimental conditions and can therefore be applied in practice.
In the context of dose fractionation, there is one major difference between TEM and STEM tomography. In bright-field TEM tomography, the noise in a projection image from a carbon film or plastic section is approximately the same for each image pixel and is equal to the square root of the number of incident electrons. In STEM, however, the noise of each projection image equals the square root of the number of electrons that are scattered and collected by the annular dark-field detector. Neglecting plural scattering, the number of electrons scattered from a carbon film or plastic section onto the ADF detector is inversely proportional to cos(ϕ), where ϕ is the tilt angle. It is therefore not clear a priori whether Undecagold labels will be visible in 3D with approximately the same significance level as in 2D.
To apply the principle of dose fractionation to a simulated dataset, we first simulate Undecagold clusters in a 40 nm thick carbon matrix. We then calculate a zero-tilt STEM image of the clusters with a dose D and measure the corresponding SNR. Next, we simulate a tomographic tilt series with 47 tilt angles ranging from −69° to +69° in steps of 3°, where the dose at each tilt increment is D/47. After the reconstruction, we take a 1 nm-thick slice centered on the gold particles, measure their 3D SNR, and compare this SNR with the 2D SNR obtained from the zero-tilt image.
Fig. 8 shows the result of applying the principle of electron dose fractionation to the simulated specimen as described above. Fig. 8a shows an Undecagold cluster from a zero-tilt image obtained with a single dose of 105 e/nm2. In a single projection image obtained with the fractionated dose of 1000 / 47 = 2.1×103 e/nm2, the signal from the gold cluster is completely hidden in the background noise (Fig. 8b). After reconstruction with the SIRT algorithm, we observe that the Undecagold particle is easily visible in nanometer thick slices from the tomogram (Figs. 8c–e). Comparing the SNR ratio of Undecagold particles in the zero-tilt image (Fig. 8a) with the SNR of the particles in the 1 nm thick slices (Figs. 8c–e) indicates that the level of significance for detecting Undecagold in 3D images is approximately the same as in 2D images. The 2D SNR was found to be 8.9 compared with a 3D SNR of 6.4 ± 0.3 for an average of 20 particles (all errors are given in terms of the s.e.m.).
Fig. 8.
(a) Simulated STEM image of an Undecagold cluster in a 40 nm-thick carbon film. This image was obtained with a single dose of 105 e/nm2 and an inner collection semi-angle of 16 mrad. (b) Simulated zero-tilt projection image obtained with a fractionated dose of 2.1×103 e/nm2; (c–e) one nanometer thick slices from the STEM tomogram reconstructed with SIRT; (f–h) one nanometer thick slices from the STEM tomogram reconstructed with WBP in IMOD. The gold particles shown in (f), (g), and (h) were extracted from the same locations as those shown in (c), (d), and (e). The 2D SNR of the gold particle in (a) is 8.9, which is comparable with the 3D SNR of 6.4 ± 0.3 and 5.1 ± 0.3 for the SIRT and WBP reconstructions, respectively. As the images and SNR values suggest, gold particles in 3D are better visualized using SIRT for the reconstruction.
Now we apply the principle of dose fractionation for Undecagold embedded in a matrix of carbon containing density fluctuations of 20% and 50% within cubic nanometer sample volumes. Simulated tilt series from these model specimens were reconstructed using the SIRT algorithm. With density fluctuations of 20%, the average SNR for twenty Undecagold particles was 6.2 ± 0.3. This value is almost identical to the SNR of 6.4 ± 0.3, which was obtained for a matrix containing no density fluctuations. Fig. 9a shows a 1-nm slice from the reconstructed tomogram of a gold cluster embedded in a carbon matrix with simulated density fluctuations of 50%, and Fig. 9b shows the line profile across the particle. The average 3D SNR for twenty particles is 4.7 ± 0.3, which is close to the 3D SNR of 6.4 ± 0.3 obtained for a carbon matrix without any density fluctuations.
Fig. 9.
(a) Slice of thickness 1 nm from a simulated STEM tomogram of Undecagold particles embedded in a 40 nm-thick carbon film containing 50% density fluctuations. The integral dose was 105 e/nm2 and the ADF detector inner collection semi-angle was 16 mrad. The reconstruction was performed using SIRT. (b) 3-pixel wide line profile across the Undecagold particle in (a). The SNR of the Undecagold cluster in (a) is 4.7 ± 0.4, which is close to the 3D SNR of 6.4 ± 0.3 obtained without inclusion of density fluctuations (Figs. 8c–e). Scale bar = 2 nm.
Importantly, the simulations were all performed for an ADF detector inner semi-angle of 16 mrad. For 2D images, the SNR for detecting the gold labels decreases drastically in the presence of density fluctuations. However, density fluctuations do not compromise the SNR in the 3D reconstructed volume even at low ADF inner semi-angles. When considering detection of gold labels in a light element matrix that has density fluctuations, the advantage of tomography is really twofold: not only does it enable the localization of the labels in 3D but it also enables their detection with much higher SNR than in a zero-tilt image obtained with a single high dose.
Finally, we compare the SIRT reconstruction algorithm with WBP reconstruction to investigate if the visibility of gold labels in 3D is affected by the reconstruction method. Figs. 8f–h show 1 nm-thick slices from the tomographic reconstruction obtained using the WBP method. The average SNR of twenty gold labels similar to the ones in Figs. 8f–h gives a value of 5.1 ± 0.3, which is somewhat smaller than the SNR of 6.4 ± 0.3 obtained using SIRT for the reconstruction (Figs. 8c–e). This result indicates that the SIRT algorithm provides a better visibility of the gold labels in 3D, which can also be appreciated by direct examination of the images in Figs. 8c–h. Clearly, the Undecagold clusters stand out much more noticeably in Figs. 8c–e obtained with SIRT than in Figs. 8f–h obtained with WBP.
4.5. Measured Visibility of Nanogold and Undecagold clusters embedded in carbon
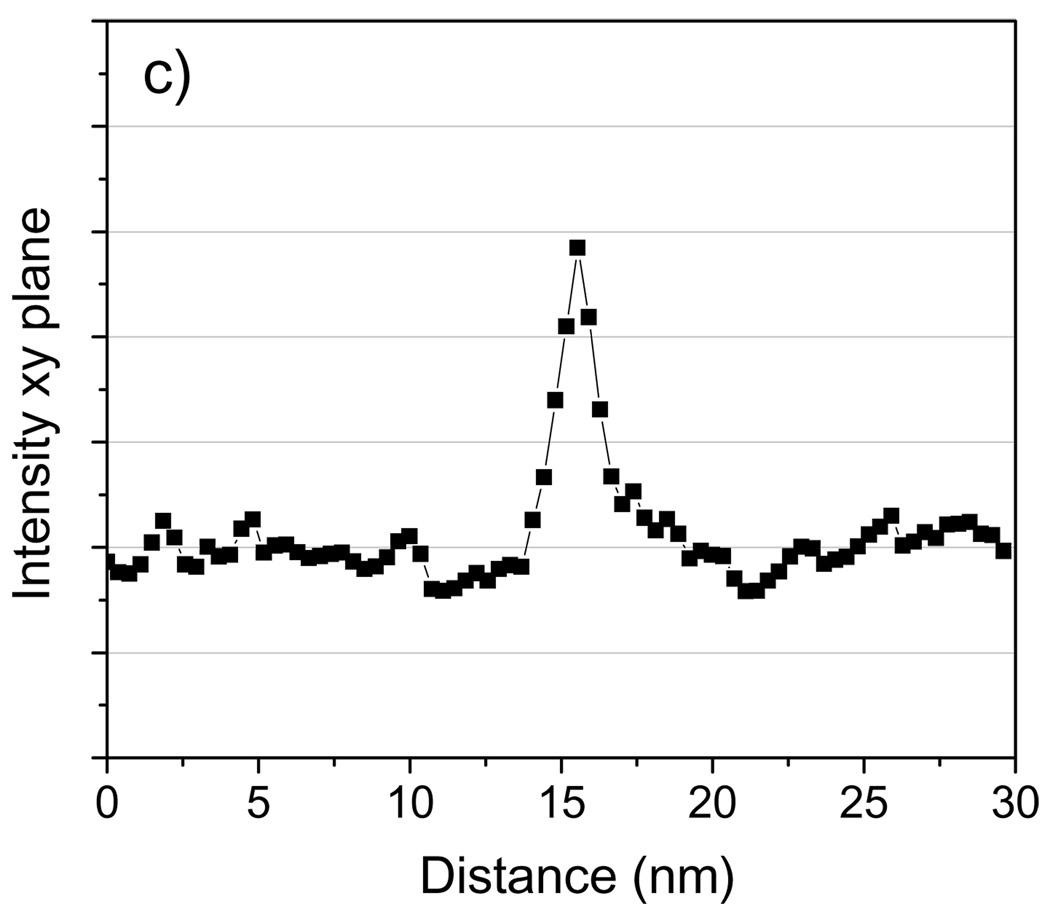
4.5.1. Nanogold
We first assess the capability of STEM tomography to identify Nanogold particles embedded in a 100 nm-thick carbon film. Unless otherwise stated, all reconstructions were performed using the SIRT algorithm. Fig. 10b and Fig. 11b show 2-nm thick slices taken in planes perpendicular and parallel to the z-axis, respectively, across Nanogold particles from a STEM tomogram. Line profiles across the particles indicated by arrows in Fig. 10b and Fig. 11b are displayed in Fig. 10c and Fig. 11c, respectively. As the images and line profiles indicate, Nanogold can be distinguished unambiguously from the carbon matrix. The particles embedded in the 100 nm-thick carbon are located 65 nm below the surface. Since the convergence semi-angle of the incident probe is 10 mrad, at a depth of 65 nm the probe diameter is spread to 1.3 nm by a geometrical divergence factor. In fact, the measured minimum FWHM was ~0.6 nm when the probe was focused on the surface, so the actual probe diameter at a depth of 65 nm is estimated by adding these two terms in quadrature, which gives a value of ~1.4 nm. While a smaller diameter would significantly enhance the visibility of the labels, even with a 1.4 nm-diameter beam Nanogold can still be identified in a carbon matrix of thickness 100 nm with a relatively high SNR. For a 200 nm-thick plastic section, the beam diameter at the bottom of the sample would be 4 nm when the sample was untilted. Labels lying closer to the bottom would be hardly visible under these conditions. A possible solution to this problem would be to decrease significantly the convergence angle of the illumination. With a convergence semi-angle of 5 mrad, for instance, the beam diameter at the bottom of a 200 nm sample would be 2 nm. In our Tecnai TF30, as it is currently configured, it is not possible to achieve a 5 mrad convergence angle by using a smaller condenser aperture. However, it would be possible to obtain smaller convergence angles by using a condenser mini-lens system, which is available in most modern TEMs.
Fig. 10.
(a) Schematic diagram of specimen of Nanogold embedded in 100 nm of carbon. (b) Projection of slice with thickness 2 nm cutting across the particles in the tomogram; the slice was taken perpendicular to the z-axis as shown. (c) 3-pixel wide line profile in the xy plane across the Nanogold particle indicated with an arrow. Tomographic reconstruction was done with SIRT. The presence of two fiducial marker streaks is marked with arrowheads. Scale bar = 10 nm.
Fig. 11.
(a) Schematic diagram of specimen of Nanogold embedded in 100 nm of carbon. (b) Projection of slice with thickness 2 nm cutting across two Nanogold particles in the tomogram. The slice was taken parallel to the z-axis as shown. (c) 3-pixel wide line profile in the yz plane across the Nanogold particle indicated with an arrow. Tomographic reconstruction was done with SIRT. Scale bar = 10 nm.
4.5.2. Undecagold
Next we evaluate the capability of STEM tomography for 3D localization of Undecagold embedded in a 20 nm carbon film. When compared with Nanogold, the smaller number of gold atoms and smaller size of Undecagold evidently poses extra challenges for its 3D localization by STEM tomography. Nevertheless, this technique offers the potential to image ultrasmall labels such as Undecagold in 3D, as demonstrated by Ziese et al. (2002) who have imaged a 15-atom gold cluster deposited on the surface of a 60 nm stained plastic section. A 1 nm-thick slice across Undecagold clusters embedded in 20 nm of carbon from the STEM tomogram, and a line profile across the cluster indicated with an arrow are shown in Fig. 12. We tried identifying Undecagold clusters embedded in 50 nm of carbon but without success. We attribute this result to specimen drift and contamination build-up, which prevented us from focusing the probe accurately on the specimen. In principle, however, it should be possible to identify the clusters in such moderately thick sections. Specifically, the simulations discussed above indicate that it is possible to identify Undecagold in 3D within a 40 nm-thick carbon matrix. Taking into account the difference in density between evaporated carbon (2 g/cm3) and Epon resin (1.25 g/cm3), it should therefore be feasible to detect Undecagold clusters in 64 nm-thick plastic sections, which is a sufficient thickness to yield relevant 3D structural information within sectioned cells. To visualize Undecagold in such sections and in the presence of stain, however, alignment of the tilt series must be carried out very precisely and the electron probe should be as close to focus as possible. Regarding the first condition, specimen drift would have to be reduced to a minimum during the time it takes to acquire a single STEM image (around 30 seconds). An alternative strategy would be to acquire multiple shorter duration images at each tilt, and then align the images and add them. In this case, drift during the acquisition of a single image would be negligible. The second condition that the probe be well focused is more difficult to realize in thicker sections. For example, for a 64 nm-thick plastic section and for a probe convergence semi-angle of the illumination of 10 mrad, the diameter of the beam at the exit surface of the specimen would be 1.3 nm, which is larger than the diameter of Undecagold (0.8 nm). As discussed before, the convergence angle of the beam can be reduced to minimize beam divergence. Further work is necessary to establish detection limits for Undecagold embedded in moderately thick sections as a function of beam divergence.
Fig. 12.
(a) Slice of thickness 1 nm from the STEM tomogram of Undecagold particles embedded in a 20 nm-thick carbon film. Reconstruction was done with SIRT. (b) 3-pixel wide line profile across the cluster indicated with an arrow. Scale bar = 10 nm.
4.5.3. Spatial Resolution
Another important factor to consider is spatial resolution in the final tomogram. The value of spatial resolution determines whether two closely spaced labels can be distinguished from each other. Here we only discuss the issue of resolution briefly; a more in-depth analysis would require additional studies. The STEM tomogram of Nanogold embedded in 100 nm of carbon was obtained with tilt angles ranging from −60° to +60° in steps of 3°. Using the formula of Radermacher (2006) for the resolution of a single-tilt axis reconstruction of an extended slab gives a value of 10 nm for the above imaging parameters. The fact that 1.4 nm gold labels could be clearly visualized in a tomogram that has resolution much worse than 1.4 nm is not surprising. First, Ziese et al. (2002) argues that the resolution of STEM tomograms is better than that given by the formula of Radermacher. Furthermore, for isolated high-contrast nanoparticles the resolution of a tomogram need not be commensurate with the size of the object for it to be visualized in three dimensions. A tomogram with poorer resolution than the diameter of a nanoparticle would cause blurring and reduction in signal-to-noise ratio, yet the nanoparticle should still be identifiable provided that its signal is greater than the noise level of the neighboring voxels. In any case, line profiles across the Nanogold particles in the STEM tomogram (Fig. 10c) give an FWHM of 1.9 ± 0.3 nm. This indicates that two Nanogold particles separated by less than the 2.6-nm resolution, as given by the Radermacher formula, could still be distinguishable from each other. This would be strictly true if the particles were perpendicular to the z axis (on a xy plane) since along the z axis the resolution of a tomogram is degraded due to the missing wedge (Radermacher, 2006).
4.5.4. Influence of fiducial streaks on the visibility of labels
It is known that fiducial markers on the surface of a specimen produce ghost streaks throughout a tomogram (Mastronarde, 2006). The presence of ghost streaks is most often disturbing, and in the context of this work it could have two effects. First, it could compromise detection of gold clusters that lie on their paths, and second, it could produce false positives, i.e., features that appear as gold clusters but are not. To exemplify the influence that ghost streaks can have on a tomogram, we selected a small volume from the tomogram of Nanogold particles embedded in 100 nm of carbon. The volume selected in Fig. 13a shows three distinguishable features, namely two Nanogold particles and one bright feature indicated by an arrow. The bright feature could potentially be a Nanogold particle but it cannot be confidently assigned as one since it lies on the path of a ghost streak. In order to remove ghost streaks from this tomogram, we applied an automatic routine for substituting the fiducial markers of every tilt image by the average intensity of that image. The fiducials were removed prior to reconstruction and after the tilt series had been aligned. Fig. 13b shows the result of this “deghosting” routine. While the two Nanogold clusters in Fig. 13a were unaffected by the deghosting procedure, the bright feature indicated with an arrow disappeared completely indicating that it was an artifact caused by ghost streaks. Aside from removing potential artifacts, overall the deghosting routine produces much cleaner tomograms. In Fig. 10b, for example, two ghost streaks (indicated with arrowheads) contaminating the tomogram can be noticed, one that goes along horizontally through the center of the image and another located nearer the top-right corner. The result of deghosting on this image can be seen in Fig. 14 which is identical to Fig. 10b except that now the ghost streaks are not present.
Fig. 13.
Slices of thickness 2 nm from the STEM tomogram of Nanogold particles embedded in 100 nm of carbon. In (a) three features can be distinguished: two Nanogold particles and one bright feature indicated with arrow. In the image it is not possible to determine whether the bright feature is a Nanogold cluster but closer inspection reveals that the feature lies on the path of a “ghost streak” in the reconstruction. Applying the deghosting routine, in which the fiducial markers are removed from images in the tilt series prior to reconstruction, gives the slice in (b). The bright feature indicated by the arrow in (a) is not present in (b), demonstrating that this feature was not a Nanogold cluster but an artifact produced by ghost streaks. Scale bar = 5 nm.
Fig. 14.
Slice of thickness 2 nm from a STEM tomogram of Nanogold particles that are embedded in a 100-nm thick carbon film. The gold fiducial markers were used for alignment but removed from each tilt image prior to reconstruction. The artifactual ghost streaks present in Fig. 10(b) due to the fiducial markers are not present here. Scale bar = 10 nm.
4.5.5. Influence of the reconstruction method on the visibility of labels
In section 3.4 we reconstructed simulated datasets using both SIRT and WBP, and we showed that gold labels were more visible in tomograms reconstructed with SIRT. Here we compare again these two reconstruction methods to establish for a real dataset whether SIRT performs better than WBP. The same STEM tilt series of Nanogold embedded in 100 nm of carbon reconstructed above with SIRT was reconstructed with WBP in IMOD. We did not try to vary systematically the parameters of the tomographic reconstruction in IMOD to assess the effect on the visibility of the gold clusters. In future, it would be useful to compare the WBP and SIRT methods in more depth, e.g., to determine the effects of the cutoff frequency and width of the Gaussian filter. Fig. 15a shows a 2 nm-thick slice from the STEM tomogram generated with WBP, and Fig. 15b shows a line profile across the particle indicated with an arrow. When comparing Fig. 15 with Fig. 10, we notice that the gold labels are more visible when reconstruction is performed with SIRT (Fig. 10). Specifically, in Fig. 10 gold labels lie on a more “smoothed” background, whereas in Fig. 15 obtained using the WBP method, intensity variations in the background are higher and the visibility of the labels is compromised. We think part of the reason for this behavior is due to the SIRT’s algorithm minimizing the difference between each projection image of a model tomogram with each experimental tilt image. Because the model tomogram does not match all the noise variations in the tilt images, some level of smoothing takes place. In SIRT, the optimum number of iterations towards the best solution depends on the original amount of noise in the images, and this subject is discussed in more details elsewhere (Aronova et al., 2007).
Fig. 15.
(a) Slice of thickness 2 nm from a STEM tomogram of Nanogold particles embedded in a 100 nm-thick carbon film; the reconstruction was done with WBP. (b) 3-pixel wide line profile across the Nanogold particle indicated by arrow. Reconstruction with SIRT (Fig. 10) enables the Nanogold clusters to be visualized with a higher SNR than with WBP. Scale bar = 10 nm.
4.6. 3D localization of Nanogold onto osmium-stained plastic-embedded C. elegans
Next we evaluate the capability of STEM tomography for providing 3D localization of Nanogold particles deposited at the surface of an 80 nm-thick section of osmium-stained plastic-embedded C elegans. A low magnification dark-field STEM image of C. elegans is displayed in Fig. 16a, and the region in the top-right corner is shown at higher magnification in Fig. 16b. The images in Fig. 16, which are contrast-reversed to provide similar contrast to conventional TEM, reveal that treatment with osmium fixative is sufficient to visualize extensive structural detail in C. elegans. Several mitochondria and the Golgi apparatus can be easily recognized, while other structural details are not as straightforward to interpret. A tomographic tilt series was acquired from a mitochondrion such as one seen in Fig. 16, and the 3D volume reconstructed with SIRT.
Fig. 16.
(a) STEM image of an 80 nm-thick section of plastic-embedded osmium-stained C. Elegans. (b) Higher magnification STEM image of the area defined in (a). In both (a) and (b) the contrast was inverted so that more heavily stained regions appear dark. Scale bar in (a) is 1 µm, and in (b) 400 nm.
Fig. 17a shows a 1.8 nm-thick slice within the reconstructed mitochondrion. The inner membrane of this organelle as well as its outer membrane can be seen very distinctly as osmium-stained regions. The features outside the mitochondrion are attributable to ribosomes. A higher magnification region delineated with a square in Fig. 17a is shown again in Fig. 17b with arrows indicating parts of the inner (arrows number 1, 2 and 3) and outer membranes (arrow number 4). Arrows number 2 and 3 point to two parts of the inner membrane lying very close to each other. Fig. 17c shows Nanogold particles deposited on top of the plastic section. Although the Nanogold is located at the surface of the section, it is still possible to address the feasibility of detecting a gold cluster if it were inside the section and surrounded by heavy-metal stain. For this, we make line profiles across image features in Figs. 17b and Fig. 17c. These line profiles are shown in Figs. 18a and 18b, respectively. Fig. 18a indicates variations in intensity in the tomogram as the line profile crosses the inner and outer membranes of the mitochondrion. The numbered arrows in Fig. 18a are derived from the corresponding numbered features in Fig. 17b. The line profile shown in Fig. 18b is taken across the Nanogold particle indicated by the arrow in Fig. 17b. The signal within this particle is well above the signal from less stained regions within the mitochondrion. Furthermore, the integrated signal within the Nanogold particle is significantly higher than the signal within the more heavily stained regions of the mitochondrion associated with its inner and outer membranes.
Fig. 17.
(a) Slice of thickness 1.8 nm from a STEM tomogram of a mitochondrion. The tilt series was acquired from an 80 nm-thick section of plastic-embedded osmium-stained C Elegans. The reconstruction was done with SIRT. (b) Higher magnification of the region in (a) defined by square. (c) Slice of thickness 2 nm from the STEM tomogram of the mitochondrion showing Nanogold particles deposited on top of the section. In (a) the aligned tilt series was binned by 3×3 pixels resulting in a pixel size of 0.9 nm. Scale bar in (a) is 100 nm, in (b) 20 nm, and in (c) 10 nm.
Fig. 18.
(a) Line profile across the dashed line in Fig. 17(b). The slice in Fig. 17b is from a tomogram binned by 3×3 pixels, but the line profile shown here was obtained from an unbinned tomogram. The numbered arrows correspond to the numbered features in Fig. 17(b) that are associated with the mitochondrial membranes. (b) 3-pixel wide line profile across the Nanogold cluster indicated between arrows in Fig. 17(c). The signal from this Nanogold cluster is significantly higher that that obtained from structures within the mitochondrion.
Taken together, Fig. 16 to Fig. 18 suggest that STEM tomography provides an optimized approach for imaging Nanogold labels in 3D without silver enhancement and that the technique can relate the 3D distribution of the labels with cellular structure. Several issues still need to be addressed, however. For instance, it is necessary to determine the minimum amount of heavy-metal stain that is enough to delineate structures of interest in a cell. Too much stain increases the background noise and causes the formation of small stain granules that could be misinterpreted as ultrasmall gold clusters. Also, it is important to consider the effect of beam divergence on the visibility of gold clusters embedded within thicker sections. The possibility of reducing the convergence of the incident beam down to 5 mrad or lower should be considered. Ongoing studies are underway to demonstrate the feasibility of imaging ultrasmall gold labels within heavy-metal stained plastic-embedded cells.
5. Conclusions
We have demonstrated that a quantitative analysis of STEM tomographic data provides a framework for determining the detection limits and optimal experimental conditions for localizing small heavy atom clusters in a cellular context. It is possible to image the 3D distribution of Nanogold clusters while also visualizing the surrounding biological structure in plastic sections of freeze-substituted and osmium-stained cells. Undecagold and Nanogold clusters are generally too small to be detected directly by conventional TEM tomography, which requires the use of larger colloidal gold particles or silver enhancement of the smaller gold clusters. Our results suggest that STEM tomography could be applied to determine the three dimensional distribution of specific Nanogold labeled proteins in lightly stained cells that are sectioned to a thickness of around 100 nm.
Table 4.
SNR in 2D and 3D for detecting Undecagold clusters embedded in a homogeneous 40 nm thick carbon matrix as well as in a matrix containing large density fluctuations.
| 2D SNR | 3D SNR | |
|---|---|---|
| No density fluctuations | 8.9 | 6.4 |
| With density fluctuations | 1.9 | 4.7 |
Acknowledgments
This work was supported by the Intramural Research Program of the National Institutes of Health.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Aronova MA, Kim YC, Harmon R, Sousa AA, Zhang G, Leapman R. Three-dimensional elemental mapping of phosphorus by quantitative electron spectroscopic tomography (QuEST) Accepted by the J. Struct. Biol. 2007 doi: 10.1016/j.jsb.2007.06.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arslan I, Yates TJ, Browning ND, Midgley PA. Embedded nanostructures revealed in three dimensions. Science. 2005;309:2195–2198. doi: 10.1126/science.1116745. [DOI] [PubMed] [Google Scholar]
- Baumeister W. From proteomic inventory to architecture. FEBS Letters. 2005;579:933–937. doi: 10.1016/j.febslet.2004.10.102. [DOI] [PubMed] [Google Scholar]
- Baumeister W, Steven AC. Macromolecular electron microscopy in the era of structural genomics. Trends Biochem. Sci. 2000;25:624–631. doi: 10.1016/s0968-0004(00)01720-5. [DOI] [PubMed] [Google Scholar]
- Cheutin T, O'Donohue MF, Beorchia A, Vandelaer M, Kaplan H, Defever B, Ploton D, Thiry M. Three-dimensional organization of active rRNA genes within the nucleolus. J. Cell. Sci. 2002;115:3297–3307. doi: 10.1242/jcs.115.16.3297. [DOI] [PubMed] [Google Scholar]
- Cheutin T, O'Donohue MF, Beorchia A, Klein C, Kaplan H, Ploton D. Three-dimensional organization of pKi-67: a comparative fluorescence and electron tomography study using FluoroNanogold. J Histochem. Cytochem. 2003;51:1411–1423. doi: 10.1177/002215540305101102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Jong KP, Koster AJ. Three-dimensional electron microscopy of mesoporous materials - Recent strides towards spatial imaging at the nanometer scale. ChemPhysChem. 2002;3:776–780. doi: 10.1002/1439-7641(20020916)3:9<776::AID-CPHC776>3.0.CO;2-E. [DOI] [PubMed] [Google Scholar]
- Frank J, editor. Electron tomography: Three-dimensional imaging with the transmission electron microscope. 2nd ed. New York: Springer; 2006. [Google Scholar]
- Gilbert P. Iterative methods for the three-dimensional reconstruction of an object from projections. J. Theor. Biol. 1972;36:105–117. doi: 10.1016/0022-5193(72)90180-4. [DOI] [PubMed] [Google Scholar]
- Glaeser RM, Taylor KA. Radiation damage relative to transmission electron microscopy of biological specimens at low temperature: a review. J. Microsc. 1978;112:127–138. doi: 10.1111/j.1365-2818.1978.tb01160.x. [DOI] [PubMed] [Google Scholar]
- Grimm R, Koster AJ, Ziese U, Typke D, Baumeister W. Zero-loss energy filtering under low-dose conditions using a post-column energy filter. J. Microsc. 1996;183:60–68. [Google Scholar]
- Grünewald K, Medalia O, Gross A, Steven AC, Baumeister W. Prospects of electron cryotomography to visualize macromolecular complexes inside cellular compartments: Implications of crowding. Biophys. Chem. 2003;100:577–591. doi: 10.1016/s0301-4622(02)00307-1. [DOI] [PubMed] [Google Scholar]
- Hainfeld JF. A small gold-conjugated antibody label: improved resolution for electron microscopy. Science. 1987;236:450–453. doi: 10.1126/science.3563522. [DOI] [PubMed] [Google Scholar]
- Hainfeld JF, Furuya FR. A 1.4-nm gold cluster covalently attached to antibodies improves immunolabeling. J. Histochem. Cytochem. 1992;40:117–184. doi: 10.1177/40.2.1552162. [DOI] [PubMed] [Google Scholar]
- Hainfeld J. Labeling with nanogold and undecagold: techniques and results. Scan. Microsc. 1996;10 Suppl:309–325. [PubMed] [Google Scholar]
- Hegerl R, Hoppe W. Influence of electron noise on three-dimensional image reconstruction. Z. Naturforsch. 1976;31:1717–1721. [Google Scholar]
- Herman GT. Image reconstruction from projections, the fundamentals of computerized tomography. New York: Academic Press; 1980. [Google Scholar]
- Hsieh CE, Marko M, Frank J, Mannella C. Electron tomographic analysis of frozen-hydrated tissue sections. J. Struct. Biol. 2002;138:63–73. doi: 10.1016/s1047-8477(02)00034-5. [DOI] [PubMed] [Google Scholar]
- Jablonski A, Salvat F, Powell CJ. Electron Elastic-scattering Cross-section Database (Version 3.1). SRD 64. Gaithersburg, MD: National Institute of Standards and Technology; 2003. [Google Scholar]
- Jablonski A, Salvat F, Powell CJ. Comparison of electron elastic-scattering cross sections calculated from two commonly used atomic potentials. J. Phys. Chem. Ref. Data. 2004;33:409–451. [Google Scholar]
- Koster AJ, Grimm R, Typke D, Hegerl R, Stoschek A, Walz J, Baumeister W. Perspectives of molecular and cellular electron tomography. J. Struct. Biol. 1997;120:276–308. doi: 10.1006/jsbi.1997.3933. [DOI] [PubMed] [Google Scholar]
- Kremer JR, Mastronarde DN, McIntosh JR. Computer visualization of three-dimensional image data using IMOD. J. Struct. Biol. 1996;116:71–76. doi: 10.1006/jsbi.1996.0013. [DOI] [PubMed] [Google Scholar]
- Lipka JJ, Hainfeld JF, Wall JS. Undecagold labeling of a glycoprotein: STEM visualization of an undecagoldphosphine cluster labeling the carbohydrate sites of human haptoglobin-hemoglobin complex. J. Ultrast. Resear. 1983;84:120–129. doi: 10.1016/s0022-5320(83)90123-5. [DOI] [PubMed] [Google Scholar]
- Mastronarde DN. Fiducial marker alignment and hybrid alignment methods for single and double-axis tomography. In: Frank J, editor. Electron Tomography. 2nd ed. New York: Plenum Press; 2006. pp. 163–185. [Google Scholar]
- McEwen BF, Downing KH, Glaeser RM. The relevance of dose-fractionation in tomography of radiation-sensitive specimens. Ultramicroscopy. 1995;60:357–373. doi: 10.1016/0304-3991(95)00082-8. [DOI] [PubMed] [Google Scholar]
- McEwen BF, Marko M. The emergence of electron tomography as an important tool for investigating cellular ultrastructure. J. Histochem. Cytochem. 2001;49:553–563. doi: 10.1177/002215540104900502. [DOI] [PubMed] [Google Scholar]
- McIntosh JR. Electron microscopy of cells: A new beginning for a new century. J. Cell Biol. 2001;153:F25–F32. doi: 10.1083/jcb.153.6.f25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McIntosh R, Nicastro D, Mastronarde D. New views of cells in 3D: an introduction to electron tomography. Trends Cell Biol. 2005;15:43–51. doi: 10.1016/j.tcb.2004.11.009. [DOI] [PubMed] [Google Scholar]
- Medalia O, Weber I, Frangakis AS, Nicastro D, Gerisch G, Baumeister W. Macromolecular architecture in eukaryotic cells visualized by cryoelectron tomography. Science. 2002;298:1209–1213. doi: 10.1126/science.1076184. [DOI] [PubMed] [Google Scholar]
- Midgley PA, Weyland M, Yates TJ, Arslan I, Dunin-Borkowski RE, Thomas JM. Nanoscale scanning transmission electron tomography. J. Microsc. 2006;223:185–190. doi: 10.1111/j.1365-2818.2006.01616.x. [DOI] [PubMed] [Google Scholar]
- Nickell S, Kofler C, Leis AP, Baumeister W. Innovation: A visual approach to proteomics. Nature Reviews Mol. Cell Biol. 2006;7:225–230. doi: 10.1038/nrm1861. [DOI] [PubMed] [Google Scholar]
- Radermacher M. Weighted back-projection methods. In: Frank J, editor. Electron Tomography. 2nd ed. New York: Plenum Press; 2006. pp. 245–273. [Google Scholar]
- Robinson JM, Takizawa T, Vandre DD. Applications of gold cluster compounds in immunocytochemistry and correlative microscopy: comparison with colloidal gold. J. Microsc. 2000a;199:163–179. doi: 10.1046/j.1365-2818.2000.00734.x. [DOI] [PubMed] [Google Scholar]
- Robinson JM, Takizawa T, Vandre DD. Enhanced labeling efficiency using ultrasmall immunogold probes: immunocytochemistry. J Histochem. Cytochem. 2000b;48:487–492. doi: 10.1177/002215540004800406. [DOI] [PubMed] [Google Scholar]
- Safer D, Hainfeld J, Wall JS, Reardon JE. Biospecific labeling with undecagold: visualization of the biotin-binding site on avidin. Science. 1982;218:290–291. doi: 10.1126/science.7123234. [DOI] [PubMed] [Google Scholar]
- Schroder RR, Hofmann W, Menetret J-F. Zero-loss energy filtering as improved imaging mode in cryoelectronmicroscopy of frozen-hydrated specimens. J. Struct. Biol. 1990;105:28–34. [Google Scholar]
- Sousa AA, Leapman R. Quantitative STEM mass measurement of biological macromolecules in a 300 kV TEM. J. Microsc. 2007 doi: 10.1111/j.1365-2818.2007.01819.x. In press. [DOI] [PubMed] [Google Scholar]
- Steven AC, Aebi U. The next ice age: cryo-electron tomography of intact cells. Trends Cell Biol. 2003;13:107–110. doi: 10.1016/s0962-8924(03)00023-0. [DOI] [PubMed] [Google Scholar]
- Steinmetz MO, Stoffler D, Muller SA, Jahn W, Wolpensinger B, Goldie KN, Engel A, Faulstich H, Aebi U. Evaluating atomic models of F-actin with an undecagold-tagged phalloidin derivative. J. Mol. Biol. 1998;276:1–6. doi: 10.1006/jmbi.1997.1529. [DOI] [PubMed] [Google Scholar]
- Wall JS, Hainfeld JF, Bartlett PA, Singer SJ. Observation of an undecagold cluster compound in the scanning transmission electron microscope. Ultramicroscopy. 1982;8:397–402. [Google Scholar]
- Wall J. Visualizing Greengold clusters in the STEM. J. Struct. Biol. 1999;127:161–168. doi: 10.1006/jsbi.1999.4148. [DOI] [PubMed] [Google Scholar]
- Wikander K, Hungria AB, Midgley PA, Palmqvist AEC, Holmberg K, Thomas JM. Incorporation of platinum nanoparticles in ordered mesoporous carbon. J. Coll. Inter. Sci. 2007;305:204–208. doi: 10.1016/j.jcis.2006.09.077. [DOI] [PubMed] [Google Scholar]
- Yang Y-S, Datta A, Hainfeld JF, Furuya FR, Wall JS, Frey PA. Mapping the lipoyl groups of the pyruvate dehydrogenase complex by use of gold cluster labels and scanning transmission electron microscopy. Biochemistry. 1994;33:9428–9437. doi: 10.1021/bi00198a008. [DOI] [PubMed] [Google Scholar]
- Yonekura K, Braunfeld MB, Maki-Yonekura S, Agard D. Electron energy filtering significantly improves amplitude contrast of frozen-hydrated protein at 300kV. J. Struct. Biol. 2006;156:524–536. doi: 10.1016/j.jsb.2006.07.016. [DOI] [PubMed] [Google Scholar]
- Zeuschner D, Geerts WJC, van Donselaar E, Humbel BM, Slot JW, Koster AJ, Klumperman J. Immuno-electron tomography of ER exit sites reveals the existence of free COPII-coated transport carriers. Nature Cell Biol. 2006;8:377–383. doi: 10.1038/ncb1371. [DOI] [PubMed] [Google Scholar]
- Ziese U, Kübel C, Verkleij AJ, Koster AJ. Three-dimensional localization of ultrasmall immuno-gold labels by HAADF-STEM tomography. J. Struct. Biol. 2002;138:58–62. doi: 10.1016/s1047-8477(02)00018-7. [DOI] [PubMed] [Google Scholar]
- Ziese U, De Jong KP, Koster AJ. Electron tomography: A tool for 3D structural probing of heterogeneous catalysts at the nanometer scale. Appl. Catal. A: General. 2004;260:71–74. [Google Scholar]