Abstract
NMR chemical shifts in proteins depend strongly on local structure. The program TALOS establishes an empirical relation between 13C, 15N and 1H chemical shifts and backbone torsion angles φ and ψ (G. Cornilescu et al. J. Biomol. NMR. 13, 289–302, 1999). Extension of the original 20-protein database to 200 proteins increased the fraction of residues for which backbone angles could be predicted from 65 to 74%, while reducing the error rate from 3 to 2.5 percent. Addition of a two-layer neural network filter to the database fragment selection process forms the basis for a new program, TALOS+, which further enhances the prediction rate to 88.5%, without increasing the error rate. Excluding the 2.5% of residues for which TALOS makes predictions that strongly differ from those observed in the crystalline state, the accuracy of predicted φ and ψ angles, equals ±13°. Large discrepancies between predictions and crystal structures are primarily limited to loop regions, and for the few cases where multiple X-ray structures are available such residues are often found in different states in the different structures. The TALOS+ output includes predictions for individual residues with missing chemical shifts, and the neural network component of the program also predicts secondary structure with good accuracy.
Keywords: heteronuclear chemical shift, secondary structure, order parameter, dynamics, TALOS
Introduction
Chemical shifts are well recognized as important reporters on protein structure. Strong correlations between local structure and chemical shifts have been established by quantum chemistry methods, including both density functional theory (DFT) and Hartree Fock calculations (Xu and Case 2001; Czinki and Csaszar 2007; Moon and Case 2007; Vila et al. 2007; Villegas et al. 2007; Vila et al. 2008), and by alternate computational (Haigh and Mallion 1979; Williamson and Asakura 1993; Case 1995) or fully empirical methods (Wagner et al. 1983; Saito 1986; Spera and Bax 1991; Wishart et al. 1991; Williamson and Asakura 1993; Williamson et al. 1995; Asakura et al. 1997; Ando et al. 1998; Cornilescu et al. 1999; Castellani et al. 2003; Neal et al. 2003; Neal et al. 2006; Shen and Bax 2007). The need for streamlining the protein structure determination process has been well recognized (Billeter et al. 2008), and it is clear that recent chemical shift based approaches offer an attractive route to expedite this process, at least for smaller proteins (Cavalli et al. 2007; Shen et al. 2008; Wishart et al. 2008; Shen et al. 2009). At the same time, conventional structure determination efforts frequently take advantage of the empirical relation between chemical shifts and the backbone torsion angles φ and ψ, most commonly predicted by the program TALOS (Cornilescu et al. 1999), as a complement to conventional NOE distance restraints or to internuclear distances obtained by solid-state NMR.
In its original implementation, the TALOS (Torsion Angle Likeliness Obtained from Shift and Sequence Similarity) program was based on a small, 20-protein database for which complete or nearly complete heteronuclear resonance assignments and high resolution X-ray coordinates were available. In validation trials, the original program reported consistent predictions of φ and ψ for on average 65% of the residues. Subsequent expansion of the database to 78 proteins, implemented in post-2003 releases of the program, yield consistent predictions of φ and ψ for on average 72% of the protein residues, with an error rate decreased to below 3% (unpublished results). Although at a first glance these statistics appear quite encouraging, the vast majority of the predictions pertain to residues located in elements of well-defined secondary structure, where conventional NMR restraints often already define local structure quite well. The 28% of residues for which TALOS obtains ambiguous results are mostly located in regions of irregular structure, including loops and turns. We here report an extension of the original program, named TALOS+, which extends the fraction of consistent predictions to 88%, i.e., which cuts in half the fraction of residues unpredictable by TALOS, while at the same time slightly lowering the error rate to below 2.5 percent.
TALOS+ is largely based on the same concept as the original TALOS program, and now exploits a larger database of 200 proteins originally taken from the BMRB (Markley et al. 2008) for use in the chemical shift prediction program SPARTA (Shen and Bax 2007), but more importantly it includes a neural network component whose output is used as an additional term in the conventional TALOS database search. The neural network component of the program relies on a well established computational framework that optimizes the relation between a large number or input variables, such as amino acid types and chemical shifts, and any given output parameter. The latter, in our application, can be the secondary structure of any given amino acid or the area of the Ramachandran map where the residue resides. Importantly, after training on a database for which the input and output parameters are known, the neural network not only identifies the most likely answer when applied to datasets where the output is unknown, but it also reports a reliable estimate of the likelihood that any of the possible output values is applicable. Neural network algorithms are widely used in information processing, and have found numerous applications in NMR data analysis too. These include work on facilitating resonance assignment (Hare and Prestegard 1994; Huang et al. 1997; Pons and Delsuc 1999), identification of secondary structure in the presence and absence of NMR chemical shift data (Andreassen et al. 1990; Choy et al. 1997; Hung and Samudrala 2003), and approaches that permit prediction of chemical shifts based on known protein structure (Meiler 2003; Moon and Case 2007). Here, the inverse of this latter application is used to identify the approximate region of the Ramachandran map where a given residue resides, based on the chemical shifts and residue type of the residue in question, as well as those of its immediate neighbors in the protein sequence.
In order to expand the program’s ability to predict backbone torsion angles, TALOS+ now also considers the frequently encountered cases where residue assignments are lacking. Although the fraction of such residues for which consistent predictions can be made tends to be significantly lower, the reliability of such predictions remains high. For convenience, and in order to prevent assignment of backbone torsion angles to regions that are dynamically disordered, TALOS+ also reports an estimated backbone order parameter derived from the chemical shifts in a way recently described by (Berjanskii and Wishart 2008).
Methods
Preparation of the NMR database
The original TALOS protein structure database of 20 proteins (Cornilescu et al. 1999) in recent years has been upgraded to include 78 proteins, and this database is used in post-2003 release versions of the program. The current work utilizes the further expanded database of 200 proteins, originally developed for the SPARTA chemical shift prediction program (Shen and Bax 2007). This database, extracted from the BMRB, contains proteins with nearly complete backbone NMR chemical shifts (δ15N, δ13C′, δ13Cα, δ13Cβ, δ1Hα and δ1HN) as well as PDB coordinates from high-resolution X-ray structures. Details regarding the preparation of the database, including calibration of reference frequencies, etc, have been described previously (Shen and Bax 2007). For the current application, if the database entry contains two or less assigned chemical shifts for any given residue, these chemical shift entries are removed. For residues with incomplete sets of chemical shifts (less than six for non-Gly residues, less than five for Gly), a standard TALOS database search (Cornilescu et al. 1999) was performed to find the average (secondary) chemical shifts for the atoms of the center residues of the best 10 matched triplets. These predicted secondary chemical shifts were then assigned to the atom(s) with missing experimental chemical shifts of this residue. Therefore, after this adjustment the database contains residues with either complete 15N, 13C′, 13Cα, 13Cβ, 1Hα and 1HN chemical shifts, or no chemical shift values at all.
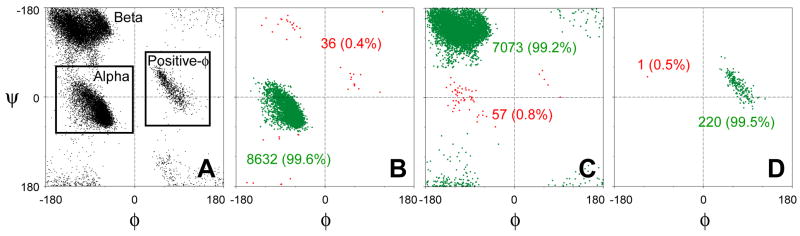
In order to study relations between NMR chemical shifts and backbone torsion angles, a three-state backbone “φ/ψ distribution” code is assigned to each residue: [1 0 0] (Alpha or “A”; −160<φ<0 and −70< ψ<60), [0 0 1] (Left-handed helix, here referred to as positive-φ or “P”; 0<φ<160 and −60< ψ<95), and [0 1 0] (Beta or “B”, comprising all others, including some residues with positive φ angles outside the P region). These regions are depicted in Figure 1A. For each residue in the database, a field was added to indicate the DSSP secondary structure (Kabsch and Sander 1983), determined from the X-ray coordinates, and further regrouped into three states: H (Helix; DSSP classification of H or G), E (Extended strand; E or B) and L (Loop; comprising DSSP classifications I, S, T and C).
Figure 1.
Prediction of the three-state φ/ψ distribution using a neural network with a 3–3 ANN model. (A) φ/ψ distribution of the residues in the 200-protein TALOS database. Boxed areas marking the 3-state φ/ψ regions for Alpha and Positive-φ, with the remainder designated Beta, also shown (see Methods). Note that the Beta region also includes some residues with positive φ angles outside of the left-handed helical region. (B,C,D) φ/ψ distributions of residues with ≥0.9 confidence for their 3-state φ/ψ neural network prediction for (B) “Alpha”, (C) “Beta” and (D) “Positive-φ” predictions. Correct predictions are shown in green, and false predictions in red.
Neural network architecture and training
TALOS+ uses a two-level feed-forward multilayer artificial neural network (ANN) to predict the location in φ/ψ space, or the secondary structure, based on a residue’s NMR chemical shifts and amino acid type, and those of its adjacent residues.
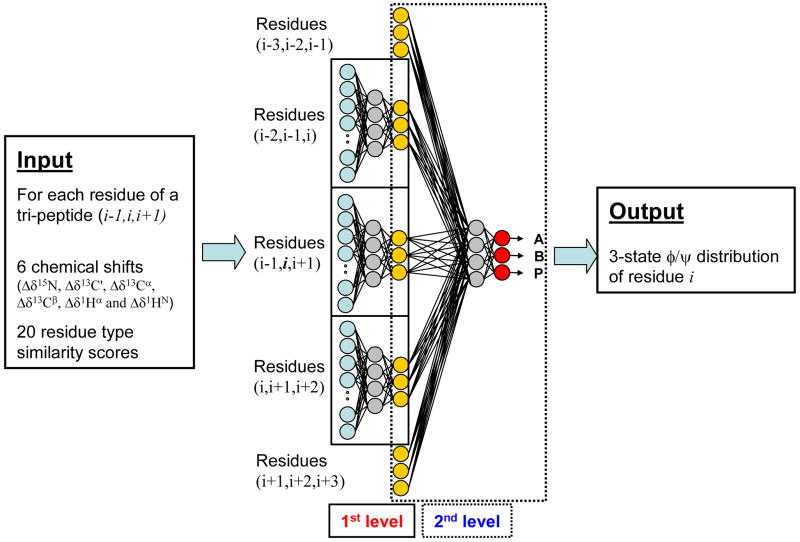
For the first level neural network (Figure 2), the input signals to the first layer consist of tri-peptide parameter sets derived from the above described database. Each tripeptide set has 78 nodes, representing six secondary chemical shift values and twenty amino acid type similarity scores for each residue. In the hidden layer of the network, where each node receives the weighted sum of the input layer nodes as a signal, 20 such nodes (or hidden neurons) are used. The output of a hidden layer node is obtained through a nodal transformation function; here a standard sigmoid function is used (see eq 1).
Figure 2.
Architecture of the two-level feed-forward artificial neural network used to predict the region of the Ramachandran map in which a given residue resides. The ANN calculates the probability for any center residue of a tripeptide fragment to reside in one of the three-state φ/ψ torsion angle regions. The ANN uses as input for the first level feed-forward prediction the known parameters characterizing each of the three residues of the tripeptide and is trained on the 200-protein database to predict the known output φ/ψ state. Besides the six chemical shifts, input parameters for each residue of the tripeptide are represented by a 20-dimensional vector, consisting of the coefficients of its row in the BLOSUM62 matrix, widely used in calculating sequence alignment (see http://www.ncbi.nlm.nih.gov/books/bv.fcgi?rid=sef.figgrp.194). The total of 78 input parameters (aqua) per tripeptide are used to predict the probability for occupation of each of the three φ/ψ states by the center residue of each tripeptide (yellow), used as input for the second level. 20 hidden nodes (grey) are used for the first level of the ANN (Supplementary Figure 1). The ANN output of the first level for 5 sequential residues is used to fine-tune prediction of the φ/ψ state (red), using a hidden level consisting of six nodes (grey). For more details, see main text.
For the purpose of predicting the torsion angle distribution from NMR chemical shifts, the above described three-state φ/ψ torsion angle distribution of the center residue of each tri-peptide in the database is used as the target of the first level network: [1 0 0] for alpha (A), [0 1 0] for beta (B), and [0 0 1] for positive-φ (P). Each output value has one node with a linear activation function (f2(x) = x, eq 1). This procedure is schematically shown in Supplementary Information Figure S1. The empirical relationship between the 3-state φ/ψ torsion angle distribution and NMR chemical shift data received by the first level network is given by
| (1) |
with f1(x) = 1/(1+e−x), and f2(x) = x. X1×78 is the input data vector consisting of 78 elements; W(1) and b(1) are the weight matrix and bias, respectively, for the connection between the nodes in the input and the hidden layer; W(2) and b(2) are the weight matrix and bias, for the connection between the nodes in the hidden and output layer; P1×3 is the training target or the output vector.
The second level of neural network, as implemented here, is used to smoothen the prediction by accounting for commonly observed patterns in proteins, and follows its use in the well-known sequence-based secondary structure prediction programs PHD (Rost and Sander 1993) and PsiPred (Jones 1999). The two-level artificial neural network shown in Figure 1 uses the input information from three sequential residues for the first level, and the input from five sequential residues for the second level, and will be referred to as a 3–5 ANN model. A more detailed discussion of the slightly different ANN models used in this study is presented below.
For all ANN models used, the input layer for the second level uses the parameter set of the three-state φ/ψ torsion angle distribution predicted by the first level of the network for each available tri-peptide in the database, i.e., each set has 15 nodes when the input of five sequential residues is used. The hidden layer contains 6 nodes, and the three-state φ/ψ torsion angle distribution of the center residue of the corresponding pentapeptide in the database is used in the output layer and as the target of the neural network. The empirical formula of the neural network is similar to eq 1:
| [2] |
where X1×15 is the input vector containing the 15 nodes; the definitions of weights, biases, and activation functions are the same as those in eq 1. Eqs 1 and 2 of this two-level network, with the optimized weights and biases obtained from the training dataset, are then used to predict the 3-state φ/ψ torsion angle distribution for residues in any protein of unknown structure. The eq 2 network output vector, P1×3, represents the probabilities for the query residue to be within each of the three states: alpha, beta and positive-φ.
The final “predicted state” of a given residue is assigned to the state with the largest probability. For later analysis of the prediction performance of the network, the confidence of a given prediction is defined as the difference between the probabilities of the two most favored predicted states.
Several slight modifications of the above two-level neural network have been used also, to allow application for cases where missing chemical shift data do not permit use of the above 3–5 ANN model.
3–3 ANN model. Similar to 3–5 ANN model, but the data used in the input layer of the second level neural network are from tripeptides instead of pentapeptides, i.e., 3×3 nodes are used in the input layer, allowing predictions nearer to the protein termini and nearer to segments where two or more sequential residues lack chemical shifts.
3–3 ANN(i−1) model. Similar to the 3–3 ANN model, except that the input layer of the first-level neural network uses tri-peptide parameter sets lacking the six chemical shifts of the first residue, i−1, i.e., each input layer set has 72 nodes.
3–3 ANN(i) model. Similar to the 3–3 ANN(i−1) model, but lacking chemical shifts for the center residue of the triplet.
3–3 ANN(i+1) model. Similar to the 3–3 ANN(i−1) model, but lacking chemical shifts for the last residue of the triplet.
In order to study the relation between the three-state secondary structure (helix or H, extended strand, or E, and loop, L) and NMR chemical shifts, the same two-level neural network architectures are used, in which the three-state secondary structure classification of the center residue of the corresponding penta- or tri-peptide in the database is used in the output layer and as the target for both levels of the neural network.
Neural network training
The weights and bias terms were determined by training of the network, using the chemical shift and sequence information of the 200-protein database, described above. To prevent over-training, a three-fold training and validation procedure was performed for each above mentioned neural network model by dividing the input training dataset into three input subsets followed by separate training of the corresponding neural networks. For each of these three network optimizations, one input subset was excluded from the training dataset but then used to evaluate the performance of the neural network during the training. This subset, referred as the validation dataset, was not used to calculate the weight changes in this network. Training of the network was terminated when the performance of the network on the validation dataset, represented by the mean squared errors (MSE) between the predicted values and targets, began to degrade
Neural network testing and validation
In addition to the above three-fold training and validation, a second validation procedure was performed for a set of 13 additional proteins, which have (1) (nearly) complete chemical shifts, (2) a good quality reference structure, (3) a wide range of folds and (4) no homologous protein (≥30% sequence identity) in the 200-protein database. The neural network prediction used for these 13 proteins was obtained by averaging over the outputs from the three networks separately trained above.
To inspect the network prediction performance of a given state for a protein or dataset, an accuracy score Q is defined (Rost and Sander 1993):
| (3) |
which describes for state i the ratio of residues correctly predicted to be in state i ( ) relative to those experimentally observed to be in state i ( ). The overall network prediction performance for all three states in a protein or dataset can be measured by a Q3 score:
| (4) |
Similarly, the prediction reliability is evaluated by a true-positive ratio:
| (5) |
which describes for state i the ratio of residues correctly predicted to be in state i ( ) relative to those predicted to be in state i ( ). In our TALOS+ application of neural network prediction, the weight assigned to such a prediction depends on the confidence reported by the neural network. We therefore also define the values of eqs 3–5 for results reported at a confidence level >c%, and refer to these as Qc(i), Q3c(i), and TPc(i).
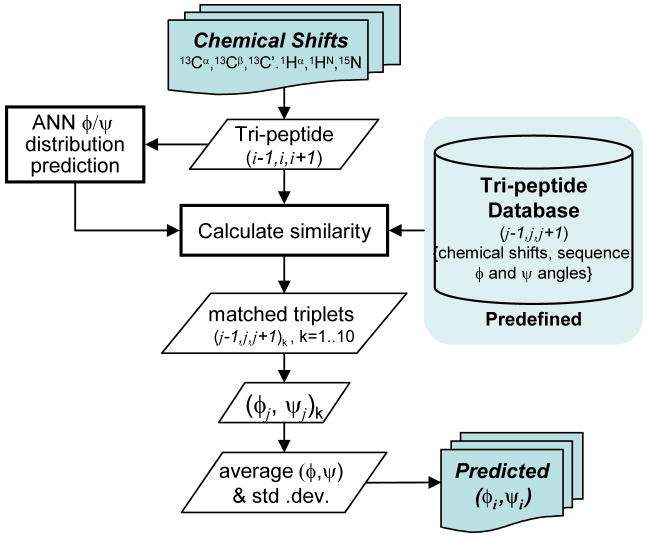
TALOS+ database search approach for predicting backbone φ/ψ angles
The predicted φ/ψ torsion angle classification, obtained by using the above neural network approach, was used as an additional input when carrying out the regular TALOS backbone torsion angle predictions (Cornilescu et al. 1999). This neural network supplemented software package is named TALOS+.
For a given query tri-peptide [i−1, i, i+1], the original TALOS program searches its database for the ten tri-peptides [j−1, j, j+1]k (k=1,…,10) best-matched in terms of backbone chemical shift and residue type. When at least 9 out of the 10 [φj/ψj]k cluster in the same region of the Ramachandran map, the original TALOS program made a φ/ψ prediction for residue i from the average values of the cluster. TALOS+ uses a modified similarity score, accounting for the output of the neural network φ/ψ distribution predictions:
| (6) |
where the terms accounting for the difference in residue type, ΔRestype, and the difference in secondary chemical shift (ΔδXi+n − ΔδXj+n) of nucleus X, including their weighting coefficients kn0 and knX, are identical to those of the standard TALOS similarity score (eq. 1, Cornilescu et al. 1999), X = 15N, 1HN, 1Hα, 13Cα, 13Cβ and 13C′. The new terms account for the difference of the φ/ψ states predicted for query residue i and observed for database residue j:
| (7) |
where Pi (sj) is the predicted probability for query residue i to be in state sj (the observed state of the corresponding residue of the database tri-peptide). The weighting factors for each of the terms are given by kns = 0.2, 1, 0.2 for n=−1,0,1. A confidence threshold value T = 0.8 is used in the default parameterization of the program; when the neural network prediction has a confidence below this value, a less steep weighting factor is used compared to residues whose φ/ψ state is predicted at high confidence, aimed at eliminating residues with φ/ψ states that the neural network deems highly unlikely.
With the addition of the neural network component in eq 7, which tends to narrow the distribution of φ/ψ angles in the top-10 selected triplets considerably, the default setting for accepting a TALOS+ prediction as consistent, or “good” has been changed to cases where the center residues of all 10 selected fragments cluster in the same state, A, B, or P, which requires a confidence level greater than 0.6 by its ANN φ/ψ prediction; otherwise, such a prediction is designated as “ambiguous”. The TALOS+ database search and prediction procedure is shown schematically in Figure 3. Although not indicated in this figure, the neural network component of the program runs by default in the 3–5 ANN mode, but automatically switches to the 3–3 ANN model when chemical shifts are not available for five sequential residues. Moreover, when the first, center, or last residue in the triplet under consideration lacks chemical shifts, the neural network uses the 3–3 ANN(i−1), 3–3 ANN(i), or 3–3 ANN(i+1) model, respectively. These features are implemented in the TALOS+ program in a fully automated manner and therefore do not require user intervention. Predictions for these cases with partially missing chemical shifts extend the fraction of residues for which φ/ψ angles can be predicted at only a small cost in accuracy (vide infra). Additional recommendations regarding the use and interpretation of TALOS+ are available as Supporting Information. The TALOS+ database search procedure is performed by a program largely written in C++, which is several orders of magnitude faster than the original tcl script driving the TALOS search, and thereby far offsets the slowdown caused by the larger database employed by TALOS+. On a PC with a single 2.4 GHz CPU, the TALOS+ database search procedure takes ca 15 seconds for a 100-residue protein.
Figure 3.
Flow diagram for the TALOS+ program.
Results and discussion
φ/ψ distribution from neural network prediction
The neural network analysis used by TALOS+ is trained to predict at the highest possible accuracy the φ/ψ angle state (Alpha, Beta, or Positive-φ) on the basis of the backbone NMR chemical shifts and residue type of the residue itself and its neighbors in the sequence. The 200-protein database used for training the neural network comprised a total of 23,257 residues, and the subset of 19,894 residues with three or more chemical shifts assigned have been used for training of the neural network models. The φ/ψ angle distribution of the full set of database residues is shown in Figure 1A; the number of residues in state Alpha, Beta, and Positive-φ is 11701, 10596 and 960, respectively.
When ignoring the confidence level of the neural network prediction, correct assignment (TP(i); eq 5) of the Alpha, Beta, and Positive-φ regions is found for 96.6 and 96.3% of the database residues for the 3–5 ANN and 3–3 ANN models, respectively (Table S1). These numbers drop to about 94% when one of the residues in the triplet is lacking chemical shifts (Table S1). Importantly, when limiting the evaluation to residues whose φ/ψ region can be predicted at a confidence ≥80%, the success rate TP80(i) is much higher, 98.7%, almost independently of the neural network type used (Table S1). However, as expected, the fraction of residues for which a confidence level ≥80% is obtained drops when fewer data are available, from 89% when the 3–5 ANN model can be used, to 81% when the chemical shifts for the residue in question are missing (but shifts for the adjacent residues are available; model 3–3 ANN(i)). When the confidence level threshold is raised to 0.9, the error rate in the neural network output drops to well below 1% (Figure 1B–D). An average TP80(i) score of 99.0% for 13 test proteins which are not part of the 200-protein database used during neural network training (Table S3) is very similar to what is seen for the database itself and confirms that no over-training of the neural network has taken place.
TALOS+ backbone φ/ψ torsion angle prediction
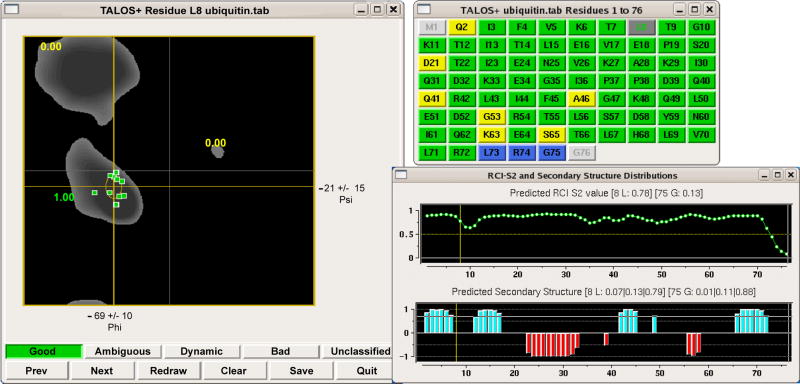
The TALOS+ user interface is very similar to that of the original TALOS program, (Figure 4). New features include a marking on the Ramachandran map of the ANN-predicted probability to find any given residue in the Alpha, Beta, or Positive-φ region, and two graphs displaying the RCI-derived (Berjanskii and Wishart 2005; Berjanskii and Wishart 2008) order parameter, S2, and the ANN-predicted secondary structure. For the latter, the length of the bars corresponds to probability of a residue to be helix or β-strand. In the sequence display, unambiguous predictions are marked in green, ambiguous results in yellow, and residues predicted to be dynamically disordered are colored in blue. As with the original TALOS program, separate output files containing the details of each prediction are also generated.
Figure 4.
TALOS+ graphic user interface, displaying results for residue L8 of query protein ubiquitin. The left panel shows a scatter plot of the φ/ψ angles of the 10 closest database matches, superimposed on a Ramachandran map of the favored conformations of a Leu residue. The ANN Alpha, Beta and Positive-φ scores for L8 are also marked on the plot, in this case 1.00, 0.00, and 0.00, respectively. The top right panel displays the sequence of the protein with residues for which no prediction is obtained marked in light grey, consistent predictions in green, ambiguous predictions in yellow, and dynamic residues (with RCI-S2 <0.5) in blue. The RCI-S2 value is shown as a function of residue number in the bottom right panel, together with the predicted secondary structure (red, helix; aqua, β-sheet). The height of the bars reflects the probability assigned by the neural network secondary structure prediction.
Backbone torsion angles were predicted by both the original TALOS and the new TALOS+ programs for all of the 200 database proteins, using the cross-validation “leave-one-out” manner, i.e., for predicting the backbone angles of any given protein that protein was removed from the database prior to the search. Results are summarized in Table 1. The original TALOS method, on average, makes “unambiguous” predictions for about 74% of the residues when applied to our larger database, with 2.48% of the predicted φ/ψ torsion angles having large errors relative to those observed in the reference X-ray structures. As seen in Table 1, the root-mean-square differences (rmsd) between the predicted and crystallographically observed backbone angles are slightly larger for the angles reported by TALOS+ than by TALOS. However, this small increase results primarily from the fact that TALOS+ includes far more predictions outside regions of regular secondary structure. When restricting the rmsd evaluation to the residues predicted by TALOS, the rmsd obtained by TALOS+ is actually slightly lower (Table 1). With TALOS+, the number of “unambiguous” predictions jumps to 88.5%, while the error rate decreases slightly to 2.46%. More details regarding how well TALOS and TALOS+ compare for different residue types, and for the different proteins in the database is provided in Supplementary Information Figures S2 and S3.
Table 1.
TALOS and TALOS+ predictions for the 200 database proteins database.a
| Consistent | Ambiguous | <sd>b (φ/ψ) | Rmsdc (φ/ψ) | ||
|---|---|---|---|---|---|
| Good | Bad | Warn | |||
| TALOS | 18714 (72.31%d) | 475e (2.48%f) | 6693 (25.86%d) | 12.2/11.4 (12.1/11.3) | 12.9/12.3 (12.8/12.2) |
| TALOS+ | 23030 (86.35%d) | 580e (2.46%f) | 3062 (11.48%d) | 12.6/12.2 (11.7/11.2) | 13.5/12.8 (12.6/12.0) |
TALOS and TALOS+ runs were performed for 200 proteins present in its reference database, with all residues from the protein under investigation excluded from the search.
average standard deviation of φ/ψ torsion angles for the center residues of the 10 best matched tri-peptides for “Good” TALOS/TALOS+ predictions, representing the average precision of the predictions; the statistics over consensus predictions, i.e. residues with unambiguous and good predictions by both TALOS and TALOS+, are given in parentheses.
rmsd values between TALOS or TALOS+ predicted φ/ψ angles (“Good” predictions only) and observed φ/ψ angles in the reference structures, representing the average accuracy of the predictions; values corresponding to the consensus TALOS/TALOS+ “Good” predictions are given in parentheses.
percentage relative to the total number of residues for which predictions are calculated.
based on the criterion {[|φobs − φpred|>60° or |ψobs − ψpred|>60°] and |φobs − φpred + ψobs − ψpred|>60°} or {|φobs − φpred|>90o or |ψobs − ψpred|>90°}
percentage relative to the number of total “consistently” predicted residues (“Good”+”Bad”). If an alternate definition is used for what constitutes a “bad” prediction, namely {|φobs − φpred|>2*sdφ or |ψobs − ψpred|>2*sdψ and |φobs − φpred + ψobs − ψpred|>2*(sdφ + sdψ)}, where sdφ and sdψ are the reported standard deviations for φ and ψ, and using minimum cutoff values for sdφ and sdψ of 10°, very similar fractions of predictions are designated “bad” (2.50% for TALOS, and 2.45% for TALOS+).
The performance of TALOS+ predictions was further validated for 13 proteins with various folds and absent from the TALOS database (Table 2). These include the small proteins GB3 (Ulmer et al. 2003), DinI (Ramirez et al. 2000), BAF (Cai et al. 1998), and TolR (Parsons et al. 2008), determined at high resolution by NMR with the aid of RDCs, and nine proteins whose NMR assignments and X-ray structures have recently become available (Table 2). The statistics for the TALOS+ predictions on these new proteins are very similar to those observed for the 200 protein database, with 90% of the residues predicted as “unambiguous”, and an error rate below 2.0%.
Table 2.
TALOS and TALOS+ results for test proteins which are not included in the database.
| Protein Name | PDB/BMRB | α%/β%b | TALOS | TALOS+ | |||
|---|---|---|---|---|---|---|---|
| Good/Warn/Bad | Rmsdc(φ/ψ) | Good/Warn/Dynd/Bad | Rmsde(φ/ψ) | Rmsdc(φ/ψ) | |||
| gb3a | 2OED | 25/42 | 44/10/0 | 12.9/13.1 | 51/3/0/0 | 13.1/11.7 | 12.9/14.4 |
| DinIa | 1GHH | 44/23 | 64/15/0 | 10.1/7.6 | 75/4/0/0 | 10.9/7.9 | 12.5/9.9 |
| TolRa | 2JWL | 36/28 | 55/13/0 | 14.9/16.1 | 62/7/0/0 | 12.4/11.9 | 14.3/13.3 |
| BAFa | 2EZX/1CI4 | 65/0 | 61/25/1 | 7.8/6.7 | 71/12/3/1 | 8.1/6.7 | 11.1/8.8 |
| HR2106 | 2HZ5/6210 | 30/28 | 77/16/1 | 21.6/18.4 | 87/5/1/2(1f) | 20.2/19.1 | 20.1/19.0 |
| TM1112 | 1O5U/5357 | 9/51 | 71/15/0 | 15.0/11.7 | 81/5/0/1(1f) | 15.0/11.5 | 16.0/11.8 |
| TM1442 | 1VC1/5921 | 38/21 | 85/19/2(1f) | 19.5/19.2 | 96/9/0/2(1f) | 19.6/19.4 | 19.5/19.6 |
| XcR50 | 1TTZ/6363 | 32/18 | 57/14/0 | 12.4/10.1 | 65/6/0/1(1f) | 11.7/9.9 | 13.4/13.3 |
| MrR110 | 3E0E/15849 | 8/58 | 72/24/0 | 13.4/12.9 | 81/11/4/0 | 14.5/12.7 | 14.7/13.0 |
| Spo0F | 1SRR/5899 | 44/19 | 92/22/1 | 12.1/13.5 | 100/15/0/2(1f) | 12.2/13.2 | 12.5/13.5 |
| Paxillin | 2VZC/15760 | 58/0 | 100/26/1 | 11.0/10.7 | 117/9/0/2 | 10.7/10.2 | 13.4/12.4 |
| CtR107 | 3E0H/16097 | 25/37 | 108/39/3(1f) | 18.6/14.5 | 127/18/6/4(3f) | 17.4/13.8 | 17.6/15.5 |
| HR41 | 3EVX/6546 | 36/16 | 112/43/3(1f) | 14.4/17.3 | 137/15/0/5(2f) | 13.7/13.3 | 16.1/14.2 |
|
| |||||||
| Average | 76.1/22.9/1.3g | 14.1/13.2 | 88.8/8.7/1.1/1.7h | 13.8/12.4 | 14.8/13.7 | ||
Protein for which an RDC-refined NMR reference structure is used
percentage of α-helical and β-sheet residues in the protein
rmsd values of the “Good” predictions relative to the reference structure
Dynamic residues identified by RCI S2 <0.5
rmsd values of the consensus (see Table 1, footnote b) TALOS/TALOS+ “Good” predictions relative to the highest resolution reference structure.
number of inconsistent “Bad” predictions when comparing TALOS/TALOS+ predictions relative to multiple reference structures.
percentage of total Good/Warning/Bad predictions; percentage of Bad predictions are calculated relative to the total number of “unambiguously” predicted residues (i.e., residues with “Good” and “Bad” predictions)
percentage of total Good/Warning/Dynamic/Bad predictions; percentage of Bad predictions are calculated relative to the total number of predictable residues (i.e., residues with “Good” and “Bad” predictions)
It is perhaps interesting to note that our reported error rate of the TALOS+ predictions in all likelihood significantly overestimates the true error rate: Many of the “erroneous” predictions occur outside of regions of secondary structure, where the X-ray and solution structures may actually differ from one another. An interesting example in this respect is the protein FluA, for which multiple X-ray structures are available. Comparing the TALOS+ predictions to these structures shows three to seven “errors”, depending on which reference structure is used (Figure S4; Table S4). However, not a single one of these “erroneous” predictions differs consistently with all three X-ray structures, suggesting that the TALOS+ result simply reflects the difference between the solution state of the protein and the various states of these residues observed by X-ray crystallography.
Secondary structure prediction by TALOS+
NMR chemical shifts have been widely used to identify the secondary structure elements in proteins (Wishart et al. 1992; Huang et al. 1997; Wang and Jardetzky 2002; Hung and Samudrala 2003). Here, we also evaluate the prediction performance of our neural network for secondary structure prediction, using the same input data as used above for grouping the backbone torsion angles in three regions, and we include the predicted secondary structure as an additional feature of the TALOS+ program.
By training a 3–3 ANN model, evaluation of TALOS+ secondary structure prediction over the 200 protein database, using the cross validation “leave one out” method, yields Q ratios (eq 4) of 94.3%, 88.3% and 82.4% for helix, extended, and loop residues, respectively. The overall Q3 of 88.9% compares favorably with the 82–89% Q3 range reported by the other NMR-based secondary structure prediction programs, perhaps because TALOS+ uses a larger set of backbone chemical shifts per residue than most of the other programs.
Evaluation of the secondary structure prediction efficiency on the set of 13 proteins whose data are not part of the database yields very similar results, again proving that over-training of our neural network was successfully avoided. Details of the secondary structure prediction efficiency of TALOS+ and the popular CSI (Wishart et al. 1992), PSSI (Wang and Jardetzky 2002), and PsiCSI (Hung and Samudrala 2003) programs are presented in Table S3.
Concluding Remarks
TALOS+ offers a significant extension of our ability to predict protein backbone torsion angles from chemical shifts. Compared to the original TALOS program, the fraction of residues whose backbone angles cannot be predicted unambiguously is reduced by more than 50%. The additional residues whose torsion angles now can be predicted reliably are located outside of regions of secondary structure, where typically such restraints are most needed. Considering that backbone chemical shifts are obtained early on during the NMR study of a protein, these results can guide the further data analysis and may prove particularly important for the study of larger proteins, where typically the number of NOE restraints per residue tends to drop significantly. In this respect it is interesting to note that addition of the unambiguous TALOS+ torsion angle predictions for the protein malate synthase G, the largest single chain protein whose structure has been determined by NMR, falls closer to the X-ray structure (2.6 vs 3.3 Å Cα rmsd) when the new TALOS+ restraints are included instead of the TALOS restraints used originally (Tugarinov et al. 2005; Grishaev et al. 2008).
The improvement in performance of TALOS+ over TALOS is primarily the result of its incorporation of the neural network output into the selection of database fragments that most closely match the residues in the query protein. It is conceivable that with further training and refinement, in combination with an even larger database, small additional improvements may be attainable. On the other hand, a significant fraction of the residues whose backbone torsion angles cannot be predicted unambiguously by TALOS+ exhibit high amplitude backbone motions, as evidenced by their RCI-derived order parameters, and often are found at the termini of the protein or in longer loop regions. For such regions, it is unlikely that further improvements to TALOS+ will provide significant enhancements.
Supplementary Material
Acknowledgments
We thank Alex Grishaev for carrying out the MSG calculation with the new TALOS+ backbone angle restraints. This work was funded by the Intramural Research Program of the NIDDK, NIH.
Footnotes
Software availability
The TALOS+ software package can be downloaded from http://spin.niddk.nih.gov/bax/.
Supplementary Material Available
Four tables with details regarding the performance of the neural network performance and TALOS+ performance; four figures detailing the neural network architecture and the performance of TALOS+; a user guide for the TALOS+ program.
References
- Ando I, Kameda T, Asakawa N, Kuroki S, Kurosu H. Structure of peptides and polypeptides in the solid state as elucidated by NMR chemical shift. J Mol Struct. 1998;441:213–230. [Google Scholar]
- Andreassen H, Bohr H, Bohr J, Brunak S, Bugge T, Cotterill RMJ, Jacobsen C, Kusk PBL, Petersen SB, Saermark T, Ulrich K. Analysis of the Secondary Structure of the Human Immunodeficiency Virus (HIV) Proteins p17, gp120, and gp41 by Computer Modeling Based on Neural Network Methods. J Acquir Immune Defic Syndr. 1990;3:615–622. [PubMed] [Google Scholar]
- Asakura T, Demura M, Date T, Miyashita N, Ogawa K, Williamson MP. NMR study of silk I structure of Bombyx mori silk fibroin with N-15- and C-13-NMR chemical shift contour plots. Biopolymers. 1997;41:193–203. [Google Scholar]
- Berjanskii MV, Wishart DS. A simple method to predict protein flexibility using secondary chemical shifts. J Am Chem Soc. 2005;127:14970–14971. doi: 10.1021/ja054842f. [DOI] [PubMed] [Google Scholar]
- Berjanskii MV, Wishart DS. Application of the random coil index to studying protein flexibility. J Biomol NMR. 2008;40:31–48. doi: 10.1007/s10858-007-9208-0. [DOI] [PubMed] [Google Scholar]
- Billeter M, Wagner G, Wuthrich K. Solution NMR structure determination of proteins revisited. J Biomol NMR. 2008;42:155–158. doi: 10.1007/s10858-008-9277-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cai M, Huang Y, Zheng R, Wei SQ, Ghirlando R, Lee MS, Craigie R, Gronenborn AM, Clore GM. Solution structure of the cellular factor BAF responsible for protecting retroviral DNA from autointegration. Nat Struct Biol. 1998;5:903–909. doi: 10.1038/2345. [DOI] [PubMed] [Google Scholar]
- Case DA. Calibration of ring-current effects in proteins and nucleic acids. J Biomol NMR. 1995;6:341–346. doi: 10.1007/BF00197633. [DOI] [PubMed] [Google Scholar]
- Castellani F, van Rossum BJ, Diehl A, Rehbein K, Oschkinat H. Determination of solid-state NMR structures of proteins by means of three-dimensional N-15-C-13-C-13 dipolar correlation spectroscopy and chemical shift analysis. Biochemistry. 2003;42:11476–11483. doi: 10.1021/bi034903r. [DOI] [PubMed] [Google Scholar]
- Cavalli A, Salvatella X, Dobson CM, Vendruscolo M. Protein structure determination from NMR chemical shifts. Proc Natl Acad Sci U S A. 2007;104:9615–9620. doi: 10.1073/pnas.0610313104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choy WY, Sanctuary BC, Zhu G. Using neural network predicted secondary structure information in automatic protein NMR assignment. J Chem Inf Comput Sci. 1997;37:1086–1094. doi: 10.1021/ci970012c. [DOI] [PubMed] [Google Scholar]
- Cornilescu G, Delaglio F, Bax A. Protein backbone angle restraints from searching a database for chemical shift and sequence homology. J Biomol NMR. 1999;13:289–302. doi: 10.1023/a:1008392405740. [DOI] [PubMed] [Google Scholar]
- Czinki E, Csaszar AG. Empirical isotropic chemical shift surfaces. J Biomol NMR. 2007;38:269–287. doi: 10.1007/s10858-007-9161-y. [DOI] [PubMed] [Google Scholar]
- Grishaev A, Tugarinov V, Kay LE, Trewhella J, Bax A. Refined solution structure of the 82-kDa enzyme malate synthase G from joint NMR and synchrotron SAXS restraints. J Biomol NMR. 2008;40:95–106. doi: 10.1007/s10858-007-9211-5. [DOI] [PubMed] [Google Scholar]
- Haigh CW, Mallion RB. Ring current theories in nuclear magnetic resonance. Prog Nucl Magn Reson Spectrosc. 1979;13:303–344. [Google Scholar]
- Hare BJ, Prestegard JH. Application of neural networks to automated assignment of NMR spectra of proteins. J Biomol NMR. 1994;4:35–46. doi: 10.1007/BF00178334. [DOI] [PubMed] [Google Scholar]
- Huang K, Andrec M, Heald S, Blake P, Prestegard JH. Performance of a neural-network-based determination of amino acid class and secondary structure from H-1-N-15 NMR data. J Biomol NMR. 1997;10:45–52. doi: 10.1023/a:1018340603528. [DOI] [PubMed] [Google Scholar]
- Hung LH, Samudrala R. Accurate and automated classification of protein secondary structure with PsiCSI. Protein Sci. 2003;12:288–295. doi: 10.1110/ps.0222303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones DT. Protein secondary structure prediction based on position-specific scoring matrices. J Mol Biol. 1999;292:195–202. doi: 10.1006/jmbi.1999.3091. [DOI] [PubMed] [Google Scholar]
- Kabsch W, Sander C. Dictionary of protein secondary structure: pattern recognition of hydrogen-bonded and geometrical features. Biopolymers. 1983;22:2577–2637. doi: 10.1002/bip.360221211. [DOI] [PubMed] [Google Scholar]
- Markley JL, Ulrich EL, Berman HM, Henrick K, Nakamura H, Akutsu H. BioMagResBank (BMRB) as a partner in the Worldwide Protein Data Bank (wwPDB): new policies affecting biomolecular NMR depositions. J Biomol NMR. 2008;40:153–155. doi: 10.1007/s10858-008-9221-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meiler J. PROSHIFT: Protein chemical shift prediction using artificial neural networks. J Biomol NMR. 2003;26:25–37. doi: 10.1023/a:1023060720156. [DOI] [PubMed] [Google Scholar]
- Moon S, Case DA. A new model for chemical shifts of amide hydrogens in proteins. J Biomol NMR. 2007;38:139–150. doi: 10.1007/s10858-007-9156-8. [DOI] [PubMed] [Google Scholar]
- Neal S, Berjanskii M, Zhang HY, Wishart DS. Accurate prediction of protein torsion angles using chemical shifts and sequence homology. Magn Reson Chem. 2006;44:S158–S167. doi: 10.1002/mrc.1832. [DOI] [PubMed] [Google Scholar]
- Neal S, Nip AM, Zhang HY, Wishart DS. Rapid and accurate calculation of protein H-1, C-13 and N-15 chemical shifts. J Biomol NMR. 2003;26:215–240. doi: 10.1023/a:1023812930288. [DOI] [PubMed] [Google Scholar]
- Parsons LM, Grishaev A, Bax A. The periplasmic domain of TolR from haemophilus influenzae forms a dimer with a large hydrophobic groove: NMR solution structure and comparison to SAXS data. Biochemistry. 2008;47:3131–3142. doi: 10.1021/bi702283x. [DOI] [PubMed] [Google Scholar]
- Pons JL, Delsuc MA. RESCUE: An artificial neural network tool for the NMR spectral assignment of proteins. J Biomol NMR. 1999;15:15–26. doi: 10.1023/a:1008338605320. [DOI] [PubMed] [Google Scholar]
- Ramirez BE, Voloshin ON, Camerini-Otero RD, Bax A. Solution structure of DinI provides insight into its mode of RecA inactivation. Protein Sci. 2000;9:2161–2169. doi: 10.1110/ps.9.11.2161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rost B, Sander C. Prediction of protein secondary structure at better than 70 percent accuracy. J Mol Biol. 1993;232:584–599. doi: 10.1006/jmbi.1993.1413. [DOI] [PubMed] [Google Scholar]
- Saito H. Conformation-dependent C13 chemical shifts - A new means of conformational characterization as obtained by high resolution solid state C13 NMR. Magn Reson Chem. 1986;24:835–852. [Google Scholar]
- Shen Y, Bax A. Protein backbone chemical shifts predicted from searching a database for torsion angle and sequence homology. J Biomol NMR. 2007;38:289–302. doi: 10.1007/s10858-007-9166-6. [DOI] [PubMed] [Google Scholar]
- Shen Y, Lange O, Delaglio F, Rossi P, Aramini JM, Liu GH, Eletsky A, Wu YB, Singarapu KK, Lemak A, Ignatchenko A, Arrowsmith CH, Szyperski T, Montelione GT, Baker D, Bax A. Consistent blind protein structure generation from NMR chemical shift data. Proc Natl Acad Sci U S A. 2008;105:4685–4690. doi: 10.1073/pnas.0800256105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen Y, Vernon R, Baker D, Bax A. De novo protein structure generation from incomplete chemical shift assignments. J Biomol NMR. 2009;43:63–78. doi: 10.1007/s10858-008-9288-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spera S, Bax A. Empirical correlation between protein backbone conformation and Ca and Cb 13C nuclear magnetic resonance chemical shifts. J Am Chem Soc. 1991;113:5490–5492. [Google Scholar]
- Tugarinov V, Choy WY, Orekhov VY, Kay LE. Solution NMR-derived global fold of a monomeric 82-kDa enzyme. Proc Natl Acad Sci U S A. 2005;102:622–627. doi: 10.1073/pnas.0407792102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ulmer TS, Ramirez BE, Delaglio F, Bax A. Evaluation of backbone proton positions and dynamics in a small protein by liquid crystal NMR spectroscopy. J Am Chem Soc. 2003;125:9179–9191. doi: 10.1021/ja0350684. [DOI] [PubMed] [Google Scholar]
- Vila JA, Aramini JM, Rossi P, Kuzin A, Su M, Seetharaman J, Xiao R, Tong L, Montelione GT, Scheraga HA. Quantum chemical C-13(alpha) chemical shift calculations for protein NMR structure determination, refinement, and validation. Proc Natl Acad Sci U S A. 2008;105:14389–14394. doi: 10.1073/pnas.0807105105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vila JA, Villegas ME, Baldoni HA, Scheraga HA. Predicting C-13(alpha) chemical shifts for validation of protein structures. J Biomol NMR. 2007;38:221–235. doi: 10.1007/s10858-007-9162-x. [DOI] [PubMed] [Google Scholar]
- Villegas ME, Vila JA, Scheraga HA. Effects of side-chain orientation on the C-13 chemical shifts of antiparallel beta-sheet model peptides. J Biomol NMR. 2007;37:137–146. doi: 10.1007/s10858-006-9118-6. [DOI] [PubMed] [Google Scholar]
- Wagner G, Pardi A, Wuthrich K. Hydrogen-Bond Length And H-1-Nmr Chemical-Shifts In Proteins. J Am Chem Soc. 1983;105:5948–5949. [Google Scholar]
- Wang YJ, Jardetzky O. Probability-based protein secondary structure identification using combined NMR chemical-shift data. Protein Sci. 2002;11:852–861. doi: 10.1110/ps.3180102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williamson MP, Asakura T. Empirical Comparisons Of Models For Chemical-Shift Calculation In Proteins. J Magn Reson B. 1993;101:63–71. [Google Scholar]
- Williamson MP, Kikuchi J, Asakura T. Application of H1 NMR chemical shifts to measure the quality of protein structures. J Mol Biol. 1995;247:541–546. doi: 10.1006/jmbi.1995.0160. [DOI] [PubMed] [Google Scholar]
- Wishart DS, Arndt D, Berjanskii M, Tang P, Zhou J, Lin G. CS23D: a web server for rapid protein structure generation using NMR chemical shifts and sequence data. Nucleic Acids Res. 2008;36:496–502. doi: 10.1093/nar/gkn305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wishart DS, Sykes BD, Richards FM. Relationship between nuclear magnetic resonance chemical shift and protein secondary structure. J Mol Biol. 1991;222:311–333. doi: 10.1016/0022-2836(91)90214-q. [DOI] [PubMed] [Google Scholar]
- Wishart DS, Sykes BD, Richards FM. The chemical shift index: A fast and simple method for the assignment of protein secondary structure through NMR spectroscopy. Biochemistry. 1992;31:1647–1651. doi: 10.1021/bi00121a010. [DOI] [PubMed] [Google Scholar]
- Xu XP, Case DA. Automated prediction of N-15, C-13(alpha), C-13(beta) and C-13′ chemical shifts in proteins using a density functional database. J Biomol NMR. 2001;21:321–333. doi: 10.1023/a:1013324104681. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.