Facilitated diffusion with DNA coiling

Model

Previous approaches to facilitated protein diffusion consider bulk exchange for a straight cylindrical chain (21); they invoke scaling properties in different chain configurations (22) without quantitative comparison of the search rates between these; or they reformulate the problem with uncorrelated bulk excursions (23–26). Here, we relate a multiparticle picture to single protein jumps along the DNA contour allowing us to consider DNA as a fluctuating chain.

In our description of the target search process, we use the density per length n(x,t) of proteins on the DNA as the relevant dynamical quantity (x is the distance along the DNA contour). We include 1-dimensional diffusion along the DNA with diffusivity D_1d, protein dissociation with rate k_off^ns and (re)adsorption after diffusion through the bulk fluid with diffusion constant D_3d. The dynamics of n(x,t) is thus governed by

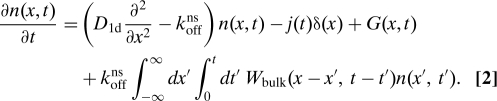Here, j(t) is the flux into the target site located at x = 0, W_bulk(x − x′,t − t′) is the joint probability that a protein returns to the point x at time t after leaving the DNA at x′, t′ for a bulk excursion. G(x,t) is the flux onto the DNA of proteins that have not previously been bound to the DNA (virgin flux). j(t) is determined by imposing the boundary condition n(x = 0,t) = 0 at the target. To consider the transfer kernel W_bulk as homogeneous in space and time we made 2 assumptions that we found to be valid for the system studied in ref. 20: First, that the DNA can be treated as being infinitely long when considering the search rate. In practice this requires that the DNA should be longer than the effective sliding length l_sl^eff introduced in Eq. 14. Note that even in bacteria the DNA length measures several millimeters, whereas DNA's persistence length is of the order of 50 nm. The second assumption is that the coiled DNA conformation fluctuates sufficiently quickly such that subsequent excursion distances x − x′ can be treated as independent.

To proceed, we Laplace and Fourier transform Eq. 2:

where we denote the Fourier and Laplace transform of a function by explicit dependence on the transformed variable. Thus n(q,u) = L[n(q,t)], n(q,t) = F[n(x,t)] and n₀(x) = n(x,t = 0). The Fourier–Laplace transform of W(x,t) is here defined through

We rewrite these equations in the form

where the density

is the solution of the diffusion problem in absence of the target, i.e., when only nonspecific binding between proteins and the DNA occurs. In position space at x = 0 one obtains j(u) = n^nsx(x = 0,u)/W(x = 0,u).

In this study we focus on the long time behavior of j(t) for which the density n^nsx(x,t) will reach an equilibrium value n_eq^ns. Since, by Tauberian theorems, large t correspond to small u we study the u → 0 behavior of j(u), with n^ns(x,u) ∼ n_eq^ns/u. For W₀(x = 0,u) we assume that the limit W(x = 0,u = 0) (time average) is finite and nonzero; this is true when the distance distribution of bulk excursions is sufficiently long tailed, as fulfilled for the transfer kernel W_bulk encountered below. In practice, being interested in the first arrival at the target, we assume that the protein concentration is sufficiently dilute such that this arrival happens after reaching n_eq^ns (“rapid equilibrium”) but still with many searching proteins. Thus j(u) ∼ k_1dn_eq^ns/u, and therefore at long times the stationary current j_stat ∼ k_1dn_eq^ns into the target is reached. Here, we introduce the constant k_1d⁻¹ = W(x = 0,u = 0):

of dimension sec over cm. We also recognize that λ_bulk(x) = W_bulk(x,u = 0) is the distribution of relocation lengths along the DNA after a single 3-dimensional excursion.

We express our results in terms of the association rate

to the target where n_bulk is the density of unbound proteins in the bulk (at nonspecific equilibrium). The nonspecific binding constant per length of DNA is K_ns = n_eq^ns/n_bulk. In terms of the total volume concentration of proteins n_total = n_bulk + l_DNA^totaln_eq^ns, where l_DNA^total is the total length of DNA divided by the volume of the entire system, we have

The rate k_on is related to the mean first arrival time for the steady-state association. Namely, k_onn_bulk is the probability per time for protein association with the target. Thus, the (survival) probability that no protein has arrived at the target yet is P_surv(t) = exp(−k_onn_bulkt), and the average target search time is T = 1/(k_onn_bulk). The flux j(t) being linear in the protein concentration n_total implies that for sufficiently low n_total the steady state is indeed reached well before the first protein actually binds to the specific target (note that in vivo protein concentrations can be as low as nanomolar).

Results

Straight Rod Configuration.

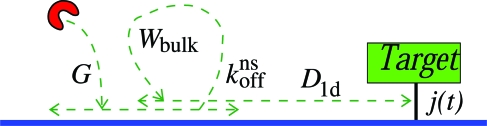
Consider first stretched DNA (see Fig. 1) corresponding to a cylinder of radius r_int (the range of nonspecific interaction), with nonspecific reaction rate k_on^ns at the boundary: the flux of proteins, per length of DNA, onto the DNA is k_on^ns times the bulk concentration next to the DNA. This implies that at equilibrium of nonspecific binding, n_eq^nsk_off^ns = n_bulkk_on^ns such that K_ns = k_on^ns/k_off^ns. (We deviate here from the conventions of ref. 20 by only letting n_bulk count “active enzymes.”)

Fig. 1.

Open in a new tab

To find the distribution W_bulk(x,t) for return to the DNA of a protein released at the DNA at x = 0 and t = 0, we solve the cylindrical diffusion equation for the probability density P(x,r,t) of the protein's position

where r measures the distance to the cylinder axis. The reactive boundary condition for the probability flux out of the cylinder boundary is

The initial distribution outside the cylinder is P(r,t)|_t=0 = 0. From the solution of this problem we obtain W_bulk as k_on^ns P|_r=rint in terms of modified Bessel functions K_ν,

where we abbreviate $\bar{q}=\sqrt{q^2+u/D_{3\text{d}}}$.

With these ingredients one can evaluate numerically the search rate to reach the specific target on a straight DNA, as given by Eq. 7. However, some limits allow for an analytic approximation for the integral in Eq. 7: for k_on^ns ≪ D_3d one may take 1 − λ_bulk(q) ≈ 1, and thus $k_{1\text{d}}^{-1}~{(2\sqrt{D_{1\text{d}}{k}_{\text{off}}^{\text{ns}}})}^{-1}$. One finds the association rate

where $l_{\text{sl}}=\sqrt{D_{1\text{d}}{k}_{\text{off}}^{\text{ns}}}$ is the so-called sliding length of a protein during a single nonspecific binding period. Eq. 13 states that each time a protein, with rate constant k_on^ns, binds to the DNA within a distance l_sl from the target it is able to “slide” onto the target. Note that in this k_on^ns ≪ D_3d limit the search rate k_on is independent of the DNA conformation. When k_on^ns ≪ D_3d the rate of nonspecific binding will limit rebinding such that the protein will relocate by a long distance during a single 3-dimensional excursion. The part of λ_bulk corresponding to such long relocations does not contribute significantly to the integral in Eq. 7, which is the physical reason for the approximation leading to Eq. 13.

In the opposite limit k_on^ns ≫ D_3d one may approximate 1 − λ_bulk(q) ≈ 2πD_3d/[k_on^ns/ln(l_sl^eff/r_int)] where the length

This produces the result

In this limit the protein can rebind quickly after unbinding. This leads to oversampling and a lowered value of k_on compared to Eq. 13. l_sl^eff can be interpreted as an effective sliding length including immediate rebindings (21). Expression 15 generalizes Smoluchowski's result Eq. 1, replacing the naked target size b by the “antenna length” entering Eq. 15. Results 7 and 12 are identical to the classical result for straight, infinitely long DNA (21). However, the approach here allows us to explicitly consider coiled DNA.

Coil with Persistence Length.

To obtain the transfer kernel W_bulk for a random coil DNA configuration (see Fig. 2) we treat the DNA as consisting locally of straight segments. We assume that the local density l_DNA of DNA (length per volume) around a segment is dilute such that the typical distance $1/\sqrt{l_{\text{DNA}}}$ between segments is much larger than r_int. We then apply a superposition technique, where the probability that the protein has reacted with a segment is obtained by treating independently the interaction with each segment, and then choose among these the interaction for which binding happens first. To obtain the dynamics of the interaction of the protein with one segment of DNA we consider a large volume V around the segment of length L. Placing the protein at a uniformly random position in space relative to the DNA segment at t = 0 and denoting the probability that the protein has bound to this DNA before time t by J_single(t), then the probability that it has not bound to any of N pieces of DNA is (with the assumption of independent interactions) P_surv^foreign(t) = [1 − J_single(t)]^N. Taking the limit of V,N,L → ∞ for fixed l_DNA = NL/V we get P_surv^foreign(t) = exp[−J_cap(t)], where

The bulk transfer kernel W_bulk in the coiled conformation then becomes

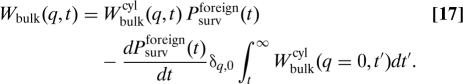Here, the first term on the right-hand side represents proteins that return to the original segment without being captured by foreign segments. Those are represented by the second term, where the factor δ_q,0 is a result of the assumption that a capture by foreign DNA segments leads to a long relocation measured along the DNA contour.* These relocations only contribute close to q = 0 in Fourier space. Exploiting the reasoning behind the approximation that led to Eq. 13 we discard them from W_bulk when the integral in Eq. 7 is calculated. However, even numerically this integral is difficult to handle. A good approximation can be found noting that by Tauberian theorems the Laplace inversion for J_cap(u) can be divided into 3 regimes when k_on^ns ≫ D_3d:

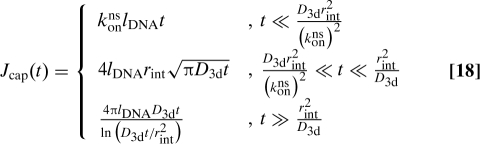The first regime corresponds to reaction limited binding and is very brief for large k_on^ns. We discard this regime and ignore the slowly varying logarithm in the last regime. This allows us to approximate P_surv^foreign by

Numerical analysis shows excellent agreement between P_surv^foreign and P_app. The value of k_cap is fixed self-consistently by the condition that the total amount of proteins returning to the original segment is the same as for P_surv^foreign, i.e.,

We solved this equation numerically. Once a value for k_cap is obtained the choice of P_app in Eq. 19 turns out to be very convenient. In fact, it can be written

where a = $4\sqrt{\pi }{r}_{int}{l}_{\text{DNA}}\sqrt{D_{3\text{d}}}$. When inserted into Eq. 17 in Laplace space we need to evaluate numerically only one integral to obtain W_bulk(q,u), namely

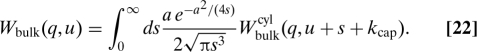The term with δ_q,0 was already discarded here. Eq. 22 generalizes the straight rod result 12. In the limit D_3d ≫ k_on^ns it is consistent with the approximation 1 − λ_bulk(q) ≈ 1 leading to the expected result (13) for that case.

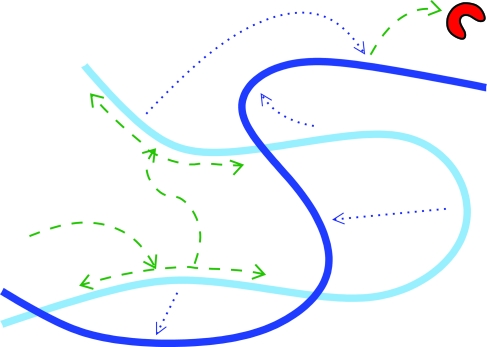
Fig. 2.

Open in a new tab

Discussion

A single stochastic search mechanism is usually not efficient at optimizing a search process. Thus, Brownian motion, whose fractal dimension is d_f = 2, in 1-dimensional and 2-dimensional geometries leads to significant oversampling in the sense that a given site is revisited many times (27, 28). Lévy motion with a jump length distribution λ(x) ≃ |x|^−1−α (0 < α < 2) has fractal dimension d_f = α and thus a comparatively reduced degree of oversampling. However, the first arrival of Lévy motion is hampered by leapovers, i.e., frequent overshoots of the target (29). In 3-dimensional space both Brownian and Lévy motions are inefficient at locating a small target. Whereas typical chemical reactants in a liquid environment have no choice but to passively diffuse until mutual encounter (4) intermittent models combine different search mechanisms (28, 30). An important example of intermittent search models is the facilitated diffusion of transcription factors in gene regulation.

Here, we have developed a theoretical framework analyzing facilitated diffusion in the presence of intersegmental jumps whose relevance depends on the degree of DNA coiling. These results together with the experimental evidence from our single DNA experiments reported in ref. 20 demonstrate that the binding rate of DNA-binding proteins can be significantly enhanced when DNA is allowed to coil freely. This effect would be further amplified when the local density of DNA is increased beyond that of a relaxed coil, for instance, by packaging in a living cell. This is consistent with observations of increased cleavage rate of restriction enzymes in supercoiled over relaxed DNA plasmids (31).

In our derivation of the probability P_surv^foreign we assumed that the density of foreign segments is uniform in space. Although this is not true for a freely fluctuating coil (the density decreases on a scale of the persistence length of the DNA) we argue that this non-uniformity is not important for evaluating the search rate: in fact, if the protein diffuses far away from the original segment it will most likely perform a long relocation measured along the DNA contour. Again it does not matter for the search rate how we bookkeep these long relocations. To estimate the density l_DNA for a random relaxed coil we employ the Worm Like Chain model. A good approximation for the probability density to loop back, for a point on the chain a contour distance s away from another point on the chain, is (32)

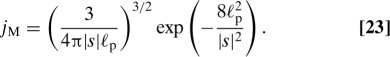For a target in the middle of a chain of length L, this leads to the DNA density ${\int }_{-L/2}^{L/2}ds{j}_{\text{M}}$ around the target.

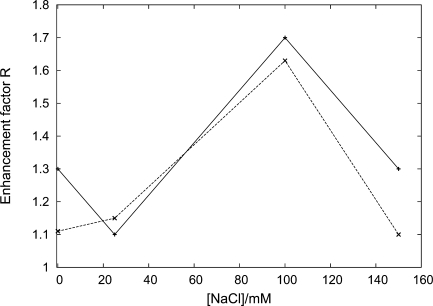
The theory presented here quantitatively describes recent experimental data from an optical tweezers setup reported in ref. 20. In that assay the search rate k_on was measured at various degrees of DNA coiling for a DNA of length L = 6,538 base pairs (approximately 2.24 μ m corresponding to 42 persistence lengths). The relative increase R of k_on in the maximally relaxed DNA configuration compared with k_on in the stretched state is shown in Fig. 3 as a function of the NaCl concentration. R was measured to be ≈ 1.1 – 1.3 in buffers with salt concentrations of 5 mM MgCl₂, and 0–25 mM for NaCl, respectively. This relative increase R compares well with the theory presented here by using estimates of l_DNA based on Eq. 23 giving $1/\sqrt{l_{\text{DNA}}}~500$bp, and a value l_sl^eff ∼ 100 bp based on a quantitative analysis (33) of experiments (34, 35), suggesting effective sliding lengths of this size. Numerical analysis of the theory presented here shows that R depends significantly only on l_DNA and l_sl^eff for realistic ranges of the remaining parameters. At physiological salt (100 mM NaCl) an increase of R ≈ 1.7 is found experimentally (20). This observation agrees well with the increased DNA density expected because of attraction between segments induced by the 5 mM divalent Mg²⁺ ions at this NaCl concentration, see ref. 20 for details. We are not aware of a theory to calculate l_DNA under such attraction. However, the value $1/\sqrt{l_{\text{DNA}}}~l_{\text{sl}}^{\text{eff}}$ needed to obtain R ≈ 1.7 at this salt condition appears reasonable. At even higher salt the ratio R drops again, which is consistent with a reduction in l_sl^eff because of weaker nonspecific binding at high salt (34, 35).

We presented a model for facilitated diffusion that is useful to calculate the search rate of DNA-binding proteins for their specific binding site on a fluctuating DNA coil with variable DNA density. This model represents a convenient way to rephrase the Berg–von Hippel theory with the additional advantage that it interpolates between stretched and coiled DNA configurations. In the development of this theory a number of assumptions were made, in particular, that of sufficiently fast local relaxation of the DNA configuration. This assumption was found to be satisfied for the protein EcoRV used in ref. 20, but it will not hold universally. It would therefore be beneficial to generalize the theory to slowly fluctuating or static (quenched) DNA configurations, potentially leading to effects similar to those found in polymer models (36). Another interesting question for future work concerns the potential effect on in vivo gene regulation of the slow diffusion caused by molecular crowding (37, 38), including interesting consequences for the exchange dynamics of proteins with the DNA (39).