Abstract
Spherical truncations of Coulomb interactions in standard models for water permit efficient molecular simulations and can give remarkably accurate results for the structure of the uniform liquid. However, truncations are known to produce significant errors in nonuniform systems, particularly for electrostatic properties. Local molecular field (LMF) theory corrects such truncations by use of an effective or restructured electrostatic potential that accounts for effects of the remaining long-ranged interactions through a density-weighted mean field average and satisfies a modified Poisson's equation defined with a Gaussian-smoothed charge density. We apply LMF theory to 3 simple molecular systems that exhibit different aspects of the failure of a naïive application of spherical truncations—water confined between hydrophobic walls, water confined between atomically corrugated hydrophilic walls, and water confined between hydrophobic walls with an applied electric field. Spherical truncations of 1/r fail spectacularly for the final system, in particular, and LMF theory corrects the failings for all three. Further, LMF theory provides a more intuitive way to understand the balance between local hydrogen bonding and longer-ranged electrostatics in molecular simulations involving water.
Keywords: effective short-ranged model, spherical truncation, confinement, hydrophobic walls, electric field
An accurate and efficient treatment of Coulomb interactions in molecular simulations represents an important and ongoing challenge. Standard biomolecular simulation packages like CHARMM (1) and AMBER (2), in general, assign effective point charges to interaction sites even in neutral molecules to approximate the charge separation of the electron cloud along polar bonds. Effective point charges are also found in most standard water models such as the extended simple point charge (SPC/E) model (3) shown in Fig. 1A, and water molecules are increasingly being included explicitly in biomolecular simulations.
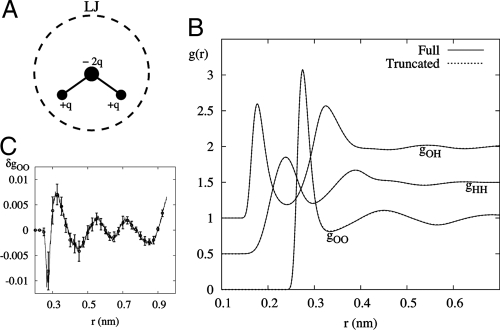
Fig. 1.
Bulk SPC/E water at 300 K and 0.998 g/cm3. (A) Diagram of SPC/E model of water. Point charges are assigned to each atomic site and a Lennard–Jones potential is centered about the oxygen with core diameter σLJ indicated by dashed lines. (B) Various site–site pair correlation functions in bulk SPC/E water are each displaced vertically by 0.5 for clarity. Gaussian-truncated (GT) water using v0(r) with σ = 0.40 nm agrees well with a full treatment of electrostatics. (C) Deviations δgoo, defined as the difference between g(r) for GT water and g(r) using full electrostatics. Simulation error bars are also shown.
To minimize edge effects in necessarily finite simulation cells, these simulations use periodic boundary conditions (4). Researchers have long sought to devise spherical truncations of the Coulomb 1/r potential so that the truncated potential accurately describes the strong Coulomb forces between closely spaced charges that lead to hydrogen bonding in water but then vanish quickly beyond some properly chosen cutoff radius. Then, only the minimum (closest) image of an interacting charge needs to be accounted for and fast and efficient simulations that scale linearly with system size are possible. In bulk-like systems these spherical truncation approaches can be surprisingly accurate, but standard estimates of thermodynamic properties in the bulk liquid are less satisfactory (5–12).
However, it has long been established (13) that when these spherical truncations are employed in nonuniform geometries, such as near a lipid bilayer, there can be pronounced errors in structure, thermodynamics, and particularly electrostatic properties. In those cases, the neglected long-ranged forces (14) compete with the local ordering due to cores and hydrogen bonding captured well by spherical truncations.
These failures have led most researchers to conclude that the success of spherical truncations in bulk was seductive but misleading. Instead, lattice summation techniques—the electrostatic method of choice—give an accurate account of all periodic images. Ewald (15) and Lekner (16) summations have long been used in simulations of charged and dipolar fluids and biomolecules. Much current research is focused on developing more efficient implementations such as particle-mesh Ewald summations (17, 18) and in removing some of the artifacts that may arise from the use of periodic lattice sums in fluid environments (19).
But is it possible to build on the success of spherical truncations of 1/r interactions in uniform environments (5–12) and to understand and correct their failures in nonuniform environments (13, 14)? We show that local molecular field (LMF) theory (20–23) offers exactly that opportunity. LMF theory corrects naive truncation schemes by introducing an effective electrostatic potential VR(r) that accounts for the remaining effects of the long-ranged interactions. LMF theory also suggests a particularly effective smoothed Gaussian-truncation scheme for the charges in SPC/E water and other interaction-site molecular models. Furthermore, the theory provides a general conceptual framework that permits a qualitative as well as quantitative understanding of the effects of long-ranged Coulomb interactions on local water structure—something that is often obscured in black box application of lattice summation techniques.
We will briefly discuss the application of the Gaussian-truncation scheme to bulk SPC/E water. Then we will demonstrate that the inclusion of the effective potential VR(r) given by LMF theory is the sole modification of molecular dynamics simulations of Gaussian-truncated (GT) water required to yield accurate minimum image simulations of water in nonuniform slab environments. Although we focus on systems composed solely of water molecules and simple confinement potentials, we argue below that the LMF approach is relevant for the treatment of electrostatics in general biomolecular simulations.
Bulk Gaussian-Truncated Water
In LMF theory, we split the 1/r potential associated with each∼charge into rapidly varying (v0) and slowly varying (v1) components as
This potential separation isolates strong short-ranged and rapidly varying interactions in v0(r), and the remaining slowly varying long-ranged forces are encompassed by v1(r). This interaction v1(r) is proportional to the electrostatic potential arising from a smooth normalized Gaussian charge distribution with width σ, and is defined via the convolution
Thus, v1(r) is slowly varying in r-space over the smoothing length σ and is simultaneously localized to small wave vectors in reciprocal space, as can be seen from its Fourier transform v̂1(k) = 4πk-2exp[-(kσ)2/4].
Hence, v0(r) ≡ 1/r - v1(r) is the screened potential resulting from a point charge surrounded by a neutralizing Gaussian charge distribution whose width σ also sets the scale for the smooth truncation of v0. For small r < σ, the force due to v0(r) approaches that of the bare point charge. By increasing σ we increase the effective range of essentially unscreened Coulomb interactions included in v0(r).
LMF theory introduces a general mapping from the original system with full Coulomb interactions and an applied electrostatic potential V(r) arising from fixed charges or an applied electric field to a well-chosen “mimic system” with Coulomb interactions replaced by the short-ranged v0(r):
Here, VR(r) is a restructured electrostatic potential in the mimic system that accounts for the averaged effects of the neglected long-ranged forces represented by v1(r), in essence by solving a modified Poisson's equation as explained in a later section.
In this article, we simulate the SPC/E model of water as shown in Fig. 1A. All data are results from molecular dynamics simulations as described in Methods. The point charges in SPC/E water play a dual role, generating both strong short-ranged forces that lead to the local hydrogen-bond network and the longer-ranged dipole–dipole interactions. Neither the point charges nor the Lennard–Jones (LJ) potential describing the molecular cores are perfect representations of actual water interactions, but adjusting the constants makes the total potential quite reasonable for temperatures and densities of interest.
Because the charges generating the local hydrogen-bonding network in water are very strongly coupled, a reasonable first approximation is simply to replace all point–charge interactions by the truncated v0(r) without employing a VR. LMF theory suggests that Coulomb interactions are best truncated on a site–site basis, because it is the basic 1/r potential that we attenuate about each site. Such a site–site scheme has been implemented in other spherical truncations of 1/r interactions as well (10). When the v0(r) truncations are made, we have Gaussian-truncated (GT) water.
Crucial to the success of the Gaussian-truncation scheme is the choice of a σ that will be large enough to accurately describe the nearest-neighbor hydrogen bonds. By using a σ of 0.4 nm or larger, GT water can give a remarkably accurate description of all O and H pair correlation functions in bulk water, as shown in Fig. 1B. The difference between gOO from a full electrostatic treatment (indicated by the labels “Full” in the figures) and gOO from GT water is shown in Fig. 1C to emphasize the good agreement. We expect that certain earlier truncation schemes (10) with very slowly varying v1(r) could give comparably accurate results.
The local hydrogen-bond network is often viewed as the most important qualitative feature of water (24), and GT water captures that feature with a very good description of nearest-neighbor hydrogen-bond energetics and local tetrahedral order, while ignoring the longer-ranged electrostatic effects of the bound charges. As argued elsewhere (Z. Hu, J.M.R., and J.D.W., unpublished data), the accuracy of GT water in bulk arises from a strong cancellation of the long-ranged electrostatic forces exerted by surrounding molecules in the uniform bulk on any given molecular site. These site-based spherical truncations can also yield highly accurate angular correlation functions, a property that is missed with molecule-based truncations that do not neglect only slowly varying forces (8). LMF theory also suggests simple analytic corrections to the energy and pressure such that the thermodynamics of bulk GT water are accurate as well (J.M.R. and J.D.W., unpublished data).
LMF-Corrected GT Water in an Applied Field
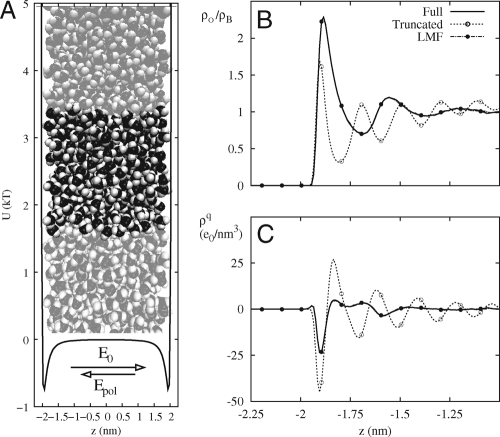
Following previous work (25, 26), we confine SPC/E water between smoothed hydrophobic LJ walls and apply a constant electric field E0 normal to the walls, as sketched in Fig 2A. The confined water should behave like a dielectric slab from introductory electrostatics, resulting in a polarization field Epol opposing the applied electric field (27). The oxygen density profile and charge density profile using only GT water are completely incorrect when we apply an electric field of 10.0 V/nm as shown in Fig. 2B and C.
Fig. 2.
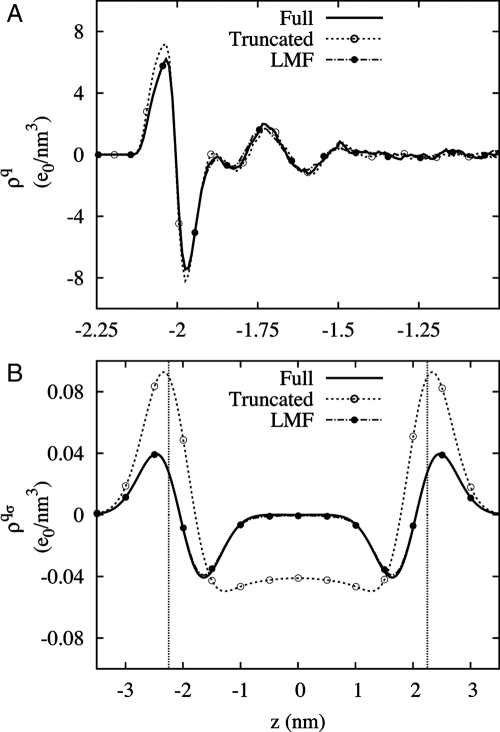
Model hydrophobic wall confinement of SPC/E water with an applied field. GT water with σ = 0.6 nm fails whereas treatment with full LMF theory succeeds. (A) The simulation system and nearest images in the y direction confined by the Lennard–Jones wall potential. (B) The oxygen density profile relative to the bulk density. (C) The charge density profile. Density profiles are only shown for z < −1.0 nm for greater clarity of the atomic level behavior, though these densities are strictly asymmetric about the origin.
Use of spherical truncations alone neglects the long-ranged electrostatic consequences of the local ordering of the water molecules, which act to attenuate and weaken the applied electric field in the central region as suggested by Le Chatelier's principle. Thus, the GT water molecules spectacularly overorder with the unattenuated electric field because the externally applied field induces an incorrect, strongly polarized state throughout the GT water slab that happens to be compatible with an energetically favored arrangement of hydrogen bonding. Inclusion of a self-consistent VR(z) to represent the long-ranged net effect of water molecule polarization makes the density profiles again agree very well with the results for the full system as shown in Fig. 2B and C. With the inclusion of net long-ranged effects, the highly ordered state does not occur because it is entropically disfavored and thus is highly unlikely in the true attenuated field.
The inclusion of a restructured VR(z) also corrects many other properties of confined water when an electric field is applied such as the dielectric constants and details of molecular orientation profiles (J.M.R. and J.D.W., unpublished data). However, the density profile is the simplest and most spectacular example of the failure of GT water in this system, and LMF theory handily corrects that failure.
LMF Theory for Electrostatics
LMF theory has been applied to many different ionic systems, including charge mixtures (23, 28–30). General derivations of the approach are available in the literature (20–22). However, when the LMF truncation is applied to the general 1/r functional form and the same σ is applied to every charge–charge interaction in the system, regardless of identity, we may write a substantially simpler formulation of the LMF mixture equation than previously stated (28). An explanation of these symmetries and the validity of the LMF equation below is given in reference 31 for charge mixtures and can be extended to site-to-site molecular models as well (Z. Hu, J.M.R., and J.D.W., unpublished data).
Provided that the σ chosen is at least large enough for v0(r) to incorporate the nearest-neighbor interactions such as hydrogen bonding in water and for v1(r) to be slowly varying over those nearby correlations, LMF theory predicts that the restructured potential VR is accurately given by
The notation ρRq(r;[VR]) simply indicates that we now use the charge density profile of the mimic system (indicated by R) in the presence of the restructured potential VR. The charge density ρRq encompasses the effect of v0(r) and VR as well as all other nonelectrostatic interactions like the hydrophobic walls and the LJ cores in SPC/E water. We use the constant C to set the zero of our potential. In the systems examined in this article, this formula may be rewritten as a 1-dimensional equation as detailed in ref. 28.
VR can be understood as a mean-field electrostatic potential representing the long-ranged forces that may be reasonably averaged over. Alternatively, harnessing the convolution definition of v1(r) in Eq. 2, we may rewrite the LMF equation as the convolution of a smoothed charge density with the full Coulomb potential. Thus, VR exactly satisfies a modified Poisson's equation
defined with a Gaussian-smoothed charge density
This again emphasizes that all charge interactions in the system must be identically truncated for this modified electrostatics to be valid.
The form of the short-ranged potential v0(r) might suggest an analogy to Ewald summation. However, LMF theory focuses on the short-ranged mimic system and how best to use and correct its properties based on results from equilibrium theory, whereas Ewald summation focuses on the full system with exact periodic boundary conditions. As a result, VR is a static external potential based on equilibrium properties that is determined self-consistently as described in Methods, whereas Ewald summation evaluates fluctuating forces arising from both the short- and long-ranged components of the Coulomb interactions at each time step.
Classical Failure of GT Water Explained
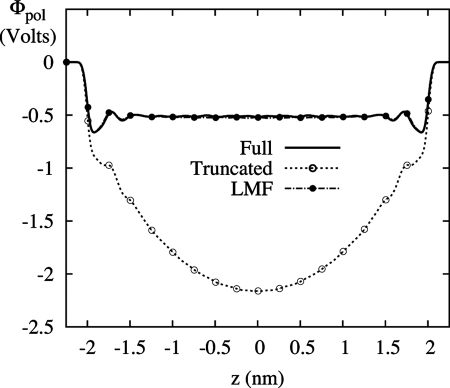
Although we believe that the failure above of GT water alone in an electric field has not been noted before, problems with electrostatic properties of confined truncated water in zero field are well known (13). Shown in Fig. 3 is the classic example of the failure of GT water in nonuniform situations—the incorrect induced potential profile of water molecules. SPC/E water is again confined between the hydrophobic walls, now with no applied electric field. As well-established by Rossky and coworkers (25), water molecules next to the wall tend to point one hydroxyl group into the wall so that one hydrogen bond per molecule on average is broken rather than two. This induces a dipole layer near each hydrophobic surface with the dipole pointing toward the walls. This atomically detailed dipole layer leads to a semidiscrete jump at the surface in the electrostatic potential defined as
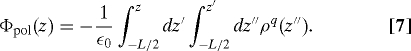 |
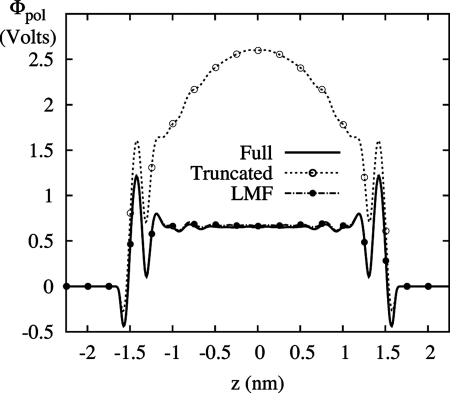
This potential Φpol should plateau in the central bulk region; however, the use of GT water fails dramatically in this respect. Because of the initial overorientation of water molecules at the surface, driven by the maintenance of hydrogen bonds in GT water, the polarization potential never plateaus. This failure is well documented (13, 14) and is attributable to the neglect of net-additive long-ranged forces due to the formation of dipole layers at the surface. As also shown in Fig. 3, LMF theory correctly includes those neglected forces with tremendous success.
Fig. 3.
Polarization potential profile, Φpol(z), between hydrophobic walls with no applied field. GT water does not display the expected plateau in the bulk region. Treatment of the system with LMF theory yields strong agreement with full treatment of the electrostatics.
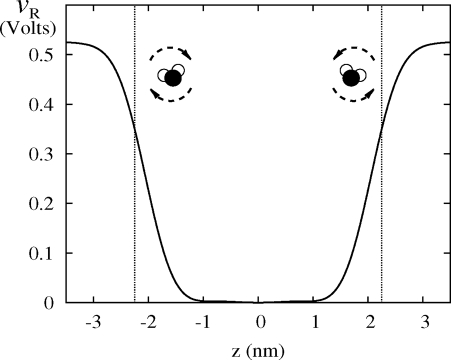
The form of VR(z) shown in Fig. 4 highlights its physical effect on GT water molecules. Without VR, the truncated molecules overorient near the wall. The restructured electrostatic potential VR from LMF theory reflects the net long-ranged forces due to the ordering of water near the surfaces by applying a reorienting torque on surface water molecules. Because VR is defined via a self-consistent equation, it represents a statistical mechanical balance between the favorability of maintaining local hydrogen bonds and the electrostatic penalty for creating an overly severe dipole layer. The potential VR varies smoothly with z because it is determined by averaging over the slowly varying v1(r) in Eq. 4. This suggests that a simple theory yielding this general form may be possible.
Fig. 4.
Form of VR(z) for water confined between hydrophobic walls with no applied electric field. The self-consistent potential applies a reorienting torque on water molecules near the surface, mimicking the effect of the long-ranged dipole layers. Vertical dotted lines indicate positions of LJ walls.
Although the physics of this failure was convincingly established by Spohr (14), its structural roots in the charge density profile remained mysterious. Brooks and coworkers (13) observed an overorientation of molecular dipoles near the walls in spherically truncated water. But as shown in Fig. 5A, the charge density profile for GT water tracks quite closely with the results from full Ewald summation techniques for SPC/E water. A dipole layer near the wall seems quite clear, and there are only slight deviations in the peaks next to the walls. However, the polarization potential Φpol belies the apparent accuracy of the atomic-level charge density profiles for GT water. The polarization potential may be fit accurately by a quadratic function in the central region between the walls. This fit suggests the existence of a constant residual charge density of approximately —0.04 e0/nm3 throughout the “bulk” region neutralizing the overaccumulation of positive charge next to each wall.
Fig. 5.
Charge density profiles for water confined between hydrophobic walls with no applied field. (A) The atomic level charge density ρq for z < 1.0 nm shows only slight discrepancies between GT water and either full or LMF-treated water. This density profile is symmetric about the origin. (B) The Gaussian-smoothed charge density ρqσ shows the failure of GT water to capture the true electrostatic dipole layer much more clearly. The vertical dotted lines indicate the positions of LJ walls. In either instance, the LMF-treated water is in very good agreement with a full treatment of electrostatics.
LMF theory allows us to highlight exactly that relevant structural problem. The writing of the LMF equation as a modified Poisson's equation in Eq. 5 suggests that the charge density that best reflects the long-ranged electrostatics is not ρq, but rather the Gaussian-smoothed charge density ρqσ. The smoothed charge density ρqσ in Fig. 5B clearly shows the dipolar layer at each wall for the water confined with no electric field. Beyond that, GT water alone very obviously spreads the dipole layer into the bulk. The residual negative charge density is approximately the value suggested by the form of Φpol for GT water. Because the smoothed charge density is 2 orders of magnitude smaller than the atomic level charge density, this underlying electrostatics is buried alongside the slight simulation noise in ρq. On Gaussian smoothing, the random simulation noise in ρq cancels, uncovering the smaller but coherent electrostatic features. In a sense, the strong charge layering over 0.2 nm displayed in Fig. 5A is not the long-ranged dipole near the wall. The true dipole layer is due to average behavior over a few molecular layers. Classical electrostatic textbooks often posit some sort of smoothing over such local order (27).
This smoothed charge density allows for a more direct analogy between molecular simulations and classical electrostatics. The LMF approach naturally distinguishes the long-ranged charge–charge interactions representing overall dipolar ordering from the short-ranged charge–charge interactions in simulations that capture hydrogen-bonding and short-ranged polar attraction. Given that any σ greater than some σmin will describe relevant short-ranged interactions like hydrogen bonding and can be used in simulations, too much significance should not be assigned to the particular chosen σ value or the exact magnitudes of the resulting ρqσ. However, we strengthen a previous suggestion (32) that charge density profiles reveal electrostatic effects in a less-biased fashion than molecule-based profiles: perhaps a smoothed profile is even less biased.
LMF Theory Is More Broadly Applicable
We now illustrate the application of LMF theory to moderately more realistic molecular surfaces by replacing the hydrophobic walls with empirical Pt(111) surfaces that order the water molecules at the surface, attracting the oxygen atoms to localized binding sites as shown by Berkowitz and coworkers (33). This surface is meant to represent specific interactions and detailed ordering of water molecules at an atomically corrugated surface, thus mimicking a hydrophilic interaction. The particular wall potential we use does not have explicitly fixed wall charges, but LMF theory can readily handle these as well (31).
Because this surface induces a charge density that is explicitly a function of x, y, and z, one might reasonably conclude that we now must solve the full 3-dimensional LMF equation given in Eq. 4 to obtain a VR that is a function of r. However, the charge smoothing inherent in the LMF equation justifies a much simpler treatment of VR. The lateral variations in charge density are washed out when smoothed with the Gaussian of width σ, leaving only a slowly varying ρqσ(z) in the Poisson-like formulation of the LMF equation given in Eq. 5. This ρqσ(z) again reflects the formation of dipole layers near each wall. Thus, solving a 1-dimensional LMF equation yields remarkably accurate results for the polarization potential profile Φpol(z), as shown in Fig. 6. Such findings give us confidence that the LMF treatment of interesting and more complex simulations, such as water–membrane interfaces and liquid–liquid interfaces, will prove to be just as simple.
Fig. 6.
Polarization potential profile, Φpol(z), between corrugated walls with no applied field. GT water again does not display the expected plateau in the bulk region. Treatment of the system with LMF theory again yields strong agreement with full treatment of the electrostatics.
Conclusions and Outlook
Here, we have demonstrated the utility of the LMF approach both in simulating a molecular system in a slab geometry and also in analyzing the structural properties of this system. The inclusion of a restructured electrostatic potential VR allows for remarkably accurate results in this slab geometry. The spectacular failure of the spherical truncation of 1/r interactions to describe even the density profile of water in an applied field is corrected through the use of LMF theory. Earlier known failures of truncated water models to describe the electrostatic potential for confined water in zero field are also corrected by LMF theory regardless of the specific details of the confining surfaces. Furthermore, the splitting of 1/r into short-ranged and long-ranged components provides a natural way to disentangle the impact of local hydrogen bonding and of long-ranged dipolar interactions in various aqueous systems. In light of LMF theory's success in this slab geometry, we certainly believe that it could be of use in other physically relevant slab-geometry simulations such as biological membranes and liquid–liquid interfaces. Perhaps it also could help resolve a recent dispute over whether or not depletion of water between capacitor plates occurs in the simulation of an open system (34–36). Furthermore, given previous work treating primitive models of ionic solutions with LMF theory (23, 28, 30), the study of aqueous ionic solutions is another natural step forward. Truncating all 1/r interactions via v0(r) with the same σ would lead to a natural mimic system for such ionic solutions.
Examination of either VR or the smoothed charge density ρqσ prescribed by LMF theory also clarifies the underlying electrostatics and the failure of spherical truncations. The Gaussian-smoothed perspective for long-ranged electrostatics greatly elucidates the perceived contradiction between seemingly good charge density profiles but very poor polarization potential profiles for water confined between walls in zero field. Analysis of long-ranged electrostatic properties by using the smoothed charge density seems more plausible because the point charges in classical site–site models approximate the real quantum-mechanical electron cloud, and longer-ranged electrostatic effects should be relatively insensitive to the exact placement and magnitude of point charges in models with the same dipole moment. Thus, in GT water, the short-ranged cores are altered to reflect both hydrogen-bonding and polar attractions represented by v0(r) as well as the LJ cores. Simulation by using GT water without a self-consistent VR will only be reasonable if the resulting ρqσ reflects the underlying electrostatics. Because VR is the solution to a modified Poisson's equation, we should not expect this to be generally true.
Overall, the use of LMF theory for electrostatics in simulations seems very promising, but certainly this approach needs more investigation. Future work should extend the derivation of the simple LMF electrostatic potential given in Eq. 4 to site-to-site molecular models (Z. Hu, J.M.R. and J.D.W., unpublished data) and describe simple analytic corrections for thermodynamics of these mimic systems (J.M.R. and J.D.W., unpublished data). Further investigation into optimizing the solution of the LMF equation is called for, and the slowly varying nature of the smoothed charge density suggests that simple approximations could prove quite useful (30). At present, the LMF mapping is for equilibrium properties only. However, current work has shown that LMF theory used in tandem with with a Born–Oppenheimer-like approximation can describe the slow dynamics and the associated free-energy landscape of charged polymers folding in the presence of mobile salt ions (N.A. Denesyuk and J.D.W., unpublished data). In general, however, a full extension of these ideas to dynamics remains a challenging open question. Its resolution may clarify the relationship between the fluctuations of these short-ranged systems and those in experimental systems.
Although all nonuniform systems examined herein have a slab geometry, LMF theory is valid for general nonuniformity. As such, we view the work presented in this article as a demonstration of the utility of LMF theory to treat and to understand electrostatic interactions in molecular systems far more complex than those studied here.
Methods
For this research, we have used the DLPOLY 2.16 molecular dynamics package (37) modified to include the Lennard–Jones wall potential (25), the Pt(111) wall potential (33), the LMF theory v0(r) potential, and the VR(z) mean field potential, as well as the 3-dimensional corrected Ewald sum for slab systems (EW3DC) (38). SPC/E water (3) was simulated at constant volume and temperature by using the Berendsen thermostat (39) with a time step of 1 fs. For the bulk water pair correlation functions, we simulated 1,728 SPC/E molecules at bulk density for 1.5 ns after 500 ps of equilibration at a temperature of 300 K. For each nonuniform system and electrostatic technique we also have carried out at least 500 ps of equilibration and, subsequently, 1.5 ns of simulation at 298 K. The lateral simulation box size for the smooth Lennard–Jones walls was 2.772 nm × 2.772 nm with 1,024 SPC/E molecules, and the walls were placed at ±2.25 nm to obtain the bulk density of water in the central region. When the electric field of 10.0 V/nm was applied, the walls were moved to 2.153 nm to maintain the bulk density of water. (Therefore, effects of electrostriction were not accounted for.) The Pt(111) wall area was 3.05 nm × 2.88 nm with 1,054 SPC/E molecules, and the zc for the walls (as defined in ref. 33) were placed at ±1.56 nm. In both cases the simulation cell spanned 14.0 nm in the z direction, though this was only crucial for the Ewald summations to maintain sufficient vacuum space between periodically replicated slabs.
The three electrostatic techniques used for the slab geometry were Ewald summation (15), minimum image simulations using a spherically truncated v0(r), and minimum image simulations using a spherically truncated v0(r) and VR(z). The Ewald technique used was the slab-corrected 3-dimensional Ewald scheme of Yeh and Berkowitz (38). We used an α of 3.40 nm-1 and k-vectors spanning (12,12,60) for LJ walls and (13,12,60) for Pt(111) walls. For v0(r) we used a σ of 0.60 nm for slab simulations and 0.40 nm for the bulk simulations. For bulk, the use of a larger σ of 0.60 nm produced equivalent results, though the δg will be slightly different.
The LMF equation must be solved self-consistently so that the ρq determined via simulation by using VR yields the same LMF equation prediction of VR. Self-consistently solving the LMF equation in previous simulation work (29) proved relatively straightforward with a linear mixing parameter λ as VRi+1 = λ · VRLMF + (1-λ) · VRi, where VRLMF is the restructured potential determined by inserting the ρq due to VRi into Eq. 4. However, for these systems, the solution proved more challenging because of the need to distinguish between inherent equilibrium fluctuations in molecular orientations in the short-ranged system and the induced response of the short-ranged system to a variation in the small and slowly varying VR.
We may still solve the LMF equation fairly quickly, given a reasonable initial VR0, by carrying out N simultaneous short-time simulations with distinct starting points during the evolution to a self-consistent solution. The averaged ρq of the N systems simulated in VRi at the ith solution step better revealed the response of the system to the change in VR from VRi-1 to VRi. These short-time simulations each ran for 25 ps of equilibration and 50 ps of accumulation with a larger Δt of 2.5 fs. Then the ρq(z) resulting from each of the N short-time simulations are averaged together and inserted in the LMF equation to yield VRLMF. Just as for the simpler solution schemes, we then used linear mixing with λ ranging from 0.05 to 0.10 to predict the subsequent VRi+1. For σ = 0.60 nm, VR converged within 3 steps of 10 parallel simulations with no applied E0 and within 10 steps of 10 parallel simulations with an applied field of 10.0 V/nm. However, this process was employed simply to demonstrate the utility of a self-consistent LMF treatment of electrostatics in molecular simulations. An optimized approach will likely appear quite different. Currently, by using the interpretation of the LMF equation given in Eq. 5, we are exploring options such as fast Poisson solvers and Car–Parinello techniques in solving the equation adaptively during simulation. Such solutions for VR would still be static in nature once self-consistency was achieved.
Acknowledgments.
We thank Max Berkowitz for a provocative discussion that stimulated our initial interest in water in an electric field and Michael Fisher for very helpful comments on the structure of this article. This work was supported by National Science Foundation Grant CHE-0517818, in part by the University of Maryland, and in part by the National Science Foundation through TeraGrid resources provided by National Center for Supercomputing Applications and Texas Advanced Computing Center. J.M.R. was supported by a University of Maryland Chemical Physics fellowship.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
References
- 1.MacKerell JAD, et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J Phys Chem B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 2.Duan Y, et al. A point-charge force field for molecular mechanics simulations of proteins based on condensed-phase quantum mechanical calculations. J Comp Chem. 2003;24:1999–2012. doi: 10.1002/jcc.10349. [DOI] [PubMed] [Google Scholar]
- 3.Berendsen H, Grigera J, Straatsma T. The missing term in effective pair potentials. J Phys Chem. 1987;91:6269–6271. [Google Scholar]
- 4.Frenkel D, Smit B. Understanding Molecular Simulation: From Algorithms to Applications. 2nd Ed. New York: Academic; 2002. [Google Scholar]
- 5.Zahn D, Schilling B, Kast S. Enhancement of the Wolf damped Coulomb potential: Static, dynamic, and dielectric properties of liquid water from molecular simulation. J Phys Chem B. 2002;106:10725–10732. [Google Scholar]
- 6.Fennell C, Gezelter J. Is the Ewald summation still necessary? Pairwise alternatives to the accepted standard for long-range electrostatics. J Chem Phys. 2006;124:234104. doi: 10.1063/1.2206581. [DOI] [PubMed] [Google Scholar]
- 7.Wolf D, Keblinski P, Phillpot S, Eggebrecht J. Exact method for the simulation of Coulombic systems by spherically truncated, pairwise r-1 summation. J Chem Phys. 1999;110:8254–8282. [Google Scholar]
- 8.Nezbeda I. Towards a unified view of fluids. Mol Phys. 2005;103:59–76. [Google Scholar]
- 9.Hummer G, Pratt L, Garcia A. Free energy of ionic hydration. J Phys Chem. 1996;100:1206–1215. [Google Scholar]
- 10.Hummer G, Soumpasis D, Neumann M. Computer-simulation of aqueous Na-Cl electrolytes. J Phys Condens Matter. 1994;6:A141–A144. [Google Scholar]
- 11.Tironi IG, Sperb R, Smith PE, van Gunsteren WF. A generalized reaction field method for molecular-dynamics simulations. J Chem Phys. 1995;102:5451–5459. [Google Scholar]
- 12.Izvekov S, Swanson JMJ, Voth GA. Coarse-graining in interaction space: A systematic approach for replacing long-range electrostatics with short-range potentials. J Phys Chem B. 2008;112:4711–4724. doi: 10.1021/jp710339n. [DOI] [PubMed] [Google Scholar]
- 13.Feller SE, Pastor RW, Rojnuckarin A, Bogusz S, Brooks BR. Effect of electrostatic force truncation on interfacial and transport properties of water. J Phys Chem. 1996;100:17011–17020. [Google Scholar]
- 14.Spohr E. Effect of electrostatic boundary conditions and system size on the interfacial properties of water and aqueous solutions. J Chem Phys. 1997;107:6342–6348. [Google Scholar]
- 15.Ewald PP. Evaluation of optical and electrostatic lattice potentials. Ann Phys (Leipzig) 1921;64:253. [Google Scholar]
- 16.Lekner J. Summation of Coulomb fields in computer-simulated disorderedsystems. Physica A. 1991;176:485–498. [Google Scholar]
- 17.Darden T, York D, Pederson L. Particle mesh Ewald: An N log(N) method for Ewald sums in large systems. J Chem Phys. 1993;98:10089–10092. [Google Scholar]
- 18.Deserno M, Holm C. How to mesh up Ewald sums. I. A theoretical and numerical comparison of various particle mesh routines. J Chem Phys. 1998;109:7678–7693. [Google Scholar]
- 19.Wu X, Brooks BR. Isotropic periodic sum: A method for the calculation of long-range interactions. J Chem Phys. 2005;122:044107. doi: 10.1063/1.1836733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Weeks JD, Katsov K, Vollmayr K. Roles of repulsive and attractive forces in determining the structure of nonuniform liquids: Generalized mean field theory. Phys Rev Lett. 1998;81:4400–4403. [Google Scholar]
- 21.Weeks JD, Selinger RLB, Broughton JQ. Self-consistent treatment of repulsive and attractive forces in nonuniform liquids. Phys Rev Lett. 1995;75:2694–2697. doi: 10.1103/PhysRevLett.75.2694. [DOI] [PubMed] [Google Scholar]
- 22.Weeks JD. Connecting local structure to interface formation: A molecular scale van der Waals theory of nonuniform liquids. Annu Rev Phys Chem. 2002;53:533–562. doi: 10.1146/annurev.physchem.53.100201.133929. [DOI] [PubMed] [Google Scholar]
- 23.Chen YG, Kaur C, Weeks JD. Connecting systems with short and long ranged interactions: Local molecular field theory for ionic fluids. J Phys Chem B. 2004;108:19874–19884. [Google Scholar]
- 24.Ball P. Water as an active constituent in cell biology. Chem Rev. 2008;108:74–108. doi: 10.1021/cr068037a. [DOI] [PubMed] [Google Scholar]
- 25.Lee CY, McCammon JA, Rossky PJ. The structure of liquid water at an extended hydrophobic surface. J Chem Phys. 1984;80:4448–4455. [Google Scholar]
- 26.Yeh I, Berkowitz M. Dielectric constant of water at high electric fields: Molecular dynamics study. J Chem Phys. 1999;110:7935–7942. [Google Scholar]
- 27.Corson D, Lorrain P. Introduction to Electromagnetic Fields and Waves. San Francisco: Freeman; 1962. [Google Scholar]
- 28.Chen YG, Weeks JD. Local molecular field theory for effective attractions between like charged objects in systems with strong Coulomb interactions. Proc Natl Acad Sci USA. 2006;103:7560–7565. doi: 10.1073/pnas.0600282103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Rodgers JM, Kaur C, Chen YG, Weeks JD. Attraction between like-charged walls: Short-ranged simulations using local molecular field theory. Phys Rev Lett. 2006;97:097801. doi: 10.1103/PhysRevLett.97.097801. [DOI] [PubMed] [Google Scholar]
- 30.Denesyuk NA, Weeks JD. A new approach for efficient simulation of Coulomb interactions in ionic fluids. J Chem Phys. 2008;128:124109. doi: 10.1063/1.2894478. [DOI] [PubMed] [Google Scholar]
- 31.Rodgers JM, Weeks JD. Local molecular field theory for the treatment of electrostatics. J Phys Condens Matter. in press. [Google Scholar]
- 32.Hummer G, Pratt L, Garcia A, Berne B, Rick S. Electrostatic potentials and free energies of solvation of polar and charged molecules. J Phys Chem B. 1997;101:3017–3020. [Google Scholar]
- 33.Raghavan K, Foster K, Motakabbir K, Berkowitz M. Structure and dynamics of water at the Pt(111) interface: Molecular dynamics study. J Chem Phys. 1991;94:2110–2117. [Google Scholar]
- 34.Bratko D, Daub CD, Leung K, Luzar A. Effect of field direction on electrowetting in a nanopore. J Am Chem Soc. 2007;129:2504–2510. doi: 10.1021/ja0659370. [DOI] [PubMed] [Google Scholar]
- 35.Vaitheeswaran S, Yin H, Rasaiah J. Water between plates in the presence of an electric field in an open system. J Phys Chem B. 2005;109:6629–6635. doi: 10.1021/jp045591k. [DOI] [PubMed] [Google Scholar]
- 36.England JL, Park S, Pande VS. Theory for an order-driven disruption of the liquid state in water. J Chem Phys. 2008;128:044503. doi: 10.1063/1.2823129. [DOI] [PubMed] [Google Scholar]
- 37.Smith W, Yong C, Rodger P. DL_POLY: Application to molecular simulation. Mol Simul. 2002;28:385–471. [Google Scholar]
- 38.Yeh I, Berkowitz M. Ewald summation for systems with slab geometry. J Chem Phys. 1999;111:3155–3162. [Google Scholar]
- 39.Berendsen HJC, Postma JPM, van Gunsteren WF, Dinola A, Haak JR. Moleculardynamics with coupling to an external bath. J Chem Phys. 1984;81:3684–3690. [Google Scholar]