Abstract
Diphtheria toxin (DTA) uses NAD+ as an ADP-ribose donor to catalyze the ADP-ribosylation of eukaryotic elongation factor 2. This inhibits protein biosynthesis and ultimately leads to cell death. In the absence of its physiological acceptor, DTA catalyzes the slow hydrolysis of NAD+ to ADP-ribose and nicotinamide, a reaction that can be exploited to measure kinetic isotope effects (KIEs) of isotopically labeled NAD+s. Competitive KIEs were measured by the radiolabel method for NAD+ molecules labeled at the following positions: 1-15N = 1.030 ± 0.004, 1′-14C = 1.034 ± 0.004, (1-15N,1′-14C) = 1.062 ± 0.010, 1′-3H = 1.200 ± 0.005, 2′-3H = 1.142 ± 0.005, 4′-3H = 0.990 ± 0.002, 5′-3H = 1.032 ± 0.004, 4′-18O = 0.986 ± 0.003. The ring oxygen, 4′-18O, KIE was also measured by whole molecule mass spectrometry (0.991 ± 0.003) and found to be within experimental error of that measured by the radiolabel technique, giving an overall average of 0.988 ± 0.003. The transition state structure of NAD+ hydrolysis was determined using a structure interpolation method to generate trial transition state structures and bond-energy/bond-order vibrational analysis to predict the KIEs of the trial structures. The predicted KIEs matched the experimental ones for a concerted, highly oxocarbenium ion-like transition state. The residual bond order to the leaving group was 0.02 (bond length = 2.65 Å), while the bond order to the approaching nucleophile was 0.03 (2.46 Å). This is an ANDN mechanism, with both leaving group and nucleophilic participation in the reaction coordinate. Fitting the transition state structure into the active site cleft of the X-ray crystallographic structure of DTA highlighted the mechanisms of enzymatic stabilization of the transition state. Desolvation of the nicotinamide ring, stabilization of the oxocarbenium ion by apposition of the side chain carboxylate of Glu148 with the anomeric carbon of the ribosyl moiety, and the placement of the substrate phosphate near the positively charged side chain of His21 are all consistent with the transition state features from KIE analysis.
Introduction
Bacteria that use ADP-ribosylating enzymes to exert their toxicity continue to be a major cause of morbidity and mortality around the world. There have been recent, large-scale epidemics of diphtheria in southern Africa,1 eastern Europe, and the former Soviet Union2 (>48 000 cases) and of cholera in South America3 (950 000 cases), Africa4,5 (12 000 deaths), and India6 (>150 000 cases). Recent outbreaks of whooping cough in the U.S.,7-9 Canada,10 Australia,11 the U.K.,12 Switzerland,13 and Spain14 demonstrate that the industrialized world is not exempt from such diseases. Each of these bacteria exert their toxicity through an exotoxin that uses NAD+ as an ADP-ribose donor to ADPribosylate a host protein. Diphtheria toxin ADP-ribosylates eukaryotic elongation factor 2 (EF-2)15 in vivo at diphthamide, a posttranslationally modified histidine residue, thereby preventing protein biosynthesis and killing the cell.16 Cholera and pertussis toxins ADP-ribosylate different G-proteins at arginine and cysteine residues, respectively. In addition to the potential for treating bacterial disease, inhibitors of enzymes that cleave N-ribosidic bonds (e.g., diphtheria,17,18 pseudomonas exotoxin,19 ricin,20 and gelonin21) have the potential to be used with immunotoxins in the treatment of cancer, to rescue normal cells from nonspecific killing by the immunotoxins.22,23 Enzymes catalyzing other ADP-ribosylation reactions of great biological interest have recently been described, such as poly(ADP-ribose) synthase, involved in DNA repair,24 and cyclic-ADP-ribose synthase,25 involved in intracellular signaling, plus other mono-ADP-ribosyl transferases.26 Determination of the transition state structures for diphtheria toxin-catalyzed reactions will be applicable to other biologically important systems.
In the absence of its physiological target, diphtheria toxin, like cholera and pertussis toxins, catalyzes a slow hydrolysis of NAD+ to ADP-ribose and nicotinamide.27 Although the reaction has no physiological significance, it can be exploited to measure the kinetic isotope effects (KIEs) of labeled NAD+ substrates (Figure 1). From KIEs determined at many labeled positions in the NAD+ molecule, it is possible to determine the transition state structure of the reaction using bond-energy/bond-order vibrational analysis. Knowing the transition state structure will permit further characterization of the mechanisms by which the enzyme stabilizes the enzymatic transition state complex to promote catalysis. The structure of the enzyme-stabilized transition state provides a target structure for the design of transition state analogues as inhibitors. Transition state analyses of NAD+ hydrolysis catalyzed by cholera28 and pertussis29 toxins have been reported. In the accompanying article,30 the transition state structure of solvolytic hydrolysis of NAD+ is reported and a new, structure interpolation method of transition state structure determination is described.
Figure 1.
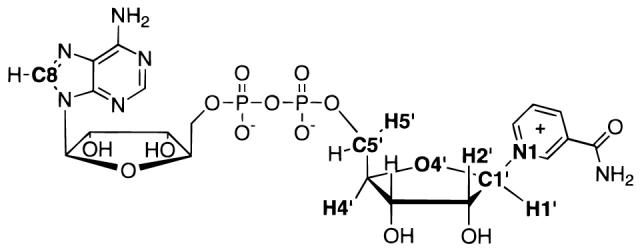
NAD+ molecule with positions of isotopic labels (3H, 14C, 15N, 18O) in bold type.
Materials and Methods
Materials
Hexokinase, myokinase, and glucose 6-phosphatase were from Sigma Chemical Co. (St. Louis, MO); [8-14C]ATP was from Amersham Life Sciences (Arlington Heights, IL). Except for 18O-labeled NAD+, isotopically labeled NAD+'s were synthesized as in Rising and Schramm.31
18O-NAD+'s. [5-18O]Glucose
Labeled glucose was synthesized from the ketone precursor (the generous gift of Michael Sinnott of University of Illinois at Chicago) similarly to the method described previously,32 except that the material was not recrystallized after LiAlH4 reduction. [5-18O]glucose was purified by sequential phosphorylation with hexokinase, anion-exchange chromatography, dephosphorylation with glucose 6-phosphatase, and repurification under the same conditions. Hexokinase and glucose 6-phosphatase were dialyzed against 50 mM potassium phosphate (pH 7.5) before use to remove unlabeled glucose. [5-18O]Glucose (55 μmol in 2 mL) was phosphorylated to glucose 6-phosphate with 2 u of hexokinase, 60 mM ATP, and 60 mM MgCl2 in 50 mM potassium phosphate (pH 7.5) for 2 h at room temperature. The reaction mixture was reduced to approximately half-volume under vacuum, applied to a 10 mL column of DEAE-Sephadex A-25 which had been equilibrated with H2O, then washed with 10 × 1 mL of H2O. [5-18O]Glucose 6-phosphate was eluted with 10 × 1 mL of 1 M NH4OAc. The fractions containing product were identified using the reducing sugar assay,33 pooled, frozen, and lyophilized twice. The [5-18O]glucose 6-phosphate was dephosphorlyated with 0.1 u of glucose 6-phosphatase in 50 mM potassium phosphate (pH 7.5) for 2 h at room temperature. Anion exchange chromatography was performed as above, with [5-18O]glucose eluting in the H2O fractions.
18O-NAD+
[4′-18O]NAD+ and [4′N-18O,8A-14C]NAD+34 were synthesized as described previously,31 with several modifications. The synthesis of nicotinic acid adenine dinucleotide (NaAD+) was done in two steps to allow incorporation of the 14C-label from [8-14C]ATP. In the first step, nicotinic acid mononucleotide (NaMN+) was synthesized,31 except that hexokinase, glucose 6-phosphate dehydrogenase, 6-phosphogluconate dehydrogenase, and phosphoriboisomerase were combined and dialyzed against 50 mM potassium phosphate (pH 7.5) to minimize addition of unlabeled intermediates from the enzyme preparations. The NH3 needed for the glutamate dehydrogenase reaction is normally supplied from the above enzyme preparations, which are (NH4)2SO4 suspensions; in this reaction, NH3HCO3 was added to 1.5 mM. After 9 h, the reaction was heated at 100 °C for 2 min to stop the enzyme reactions. Fructose (2 mM), 0.2 u of hexokinase, and 4 u of myokinase were added to convert ATP to AMP. NaMN+ was isolated by C18 reverse phase HPLC chromatography on a 7.8 × 300 mm column in 50 mM NH4OAc (pH 5.0) then lyophilized. NaAD+ was synthesized in two parallel reactions. To the lyophilized NaMN+ was added 1 mL of 4 mM ATP, 4 mM MgCl2, 50 mM KCl, 50 mM potassium phosphate (pH 7.5), and 0.25 u of NAD+ pyrophosphorylase, plus 10 μCi of [8-14C]ATP in one reaction mixture. The reactions were followed by HPLC for 15 h. The product NaAD+ was purified, and NAD+ was synthesized as described previously.31 Starting with water with an 18O content of 60% to make labeled glucose, the [4′-18O]NAD+ contained 37.1% 18O-label, as determined by mass spectrometry (see below). 4′-18O KIEs measured by the radiolabel technique were corrected for the extent of 18O-labeling.
Recombinant Diphtheria Toxin A-Chain (DTA). Recombinant DNA Procedures
An entirely synthetic gene encoding the catalytic domain of diphtheria toxin was used for expression of protein (S.R.B. and R. J. Collier, unpublished results). The synthetic gene was designed by altering the codon usage of the corynephage β-gene to reflect the bias exhibited by highly expressed proteins in Escherichia coli. The gene was divided into smaller, evenly spaced fragments by engineering unique restriction sites throughout the open reading frame. The DTA synthetic gene was cloned into pET-15b (Novagen, Inc.), replacing the NcoI-BamHI fragment, and transformed into the E. coli strain BL21 (DE3a) for expression of the proteins under transcriptional control of the T-7 promoter.
Fermentation and Harvest of E. coli
A 50 mL culture of L-broth (100 μg/mL ampicillin) was inoculated with a single colony from an LB-amp plate freshly streaked with BL21(DE3a) transformed with pET-15b-DTA. This inoculum was grown to an OD600 = 0.5 and then placed at 4 °C overnight. On the second day, 2 L baffled flasks, each containing 500 mL of L-broth (100 μg/mL ampicillin) prewarmed to 37 °C, were inoculated with 5 mL of the 50 mL overnight culture. The flasks were agitated on a rotary shaker at 37 °C. The cultures were induced at an OD600 = 1.0 with 1–2 mM isopropyl-β-d-thiogalactopyranoside (IPTG). The cells were harvested after 1–2 h, immediately chilled to 4 °C, and centrifuged at 3000g for 10 min at 4 °C. The pellets were resuspended in 5 mL of ice cold sonication buffer (50 mM Na2HPO4 (pH 8.0), 100 mM KCl, 0.1% Tween-20, 1.0 mM (phenylmethyl)sulfonyl fluoride, and 20 mM β-mercaptoethanol). The resuspended pellets were either frozen at −70 °C or sonicated immediately.
Purification of Mutant Toxins
The combined pellets were sonicated three times on ice for 30–45 s, using a Sonifier Cell Disruptor 350 (Branson Sonic Power Co.) with the power control at 5 and the duty cycle at 40%. The extracts were chilled on ice for at least 1 min between each sonication cycle. Cellular debris was pelleted by centrifuging at 5000g for 30 min at 4 °C. The supernatants were collected and chilled while the pellets were resuspended in 5–10 mL of sonication buffer and sonicated again as described above.
The synthetic gene encoding DTA was designed with a polyhistidine N-terminal fusion peptide, facilitating purification by nickel chelate affinity chromatography. The crude extracts were clarified immediately before chromatography by centrifuging at 20000g for 15 min The extracts were loaded directly onto a 3–5 mL nickel chelate affinity column (Qiagen) that had been preequilibrated with 10 bed volumes of sonication buffer. The column was washed with 5 bed volumes of sonication buffer plus 20 mM imidazole, followed by 2 bed volumes of 25 mM Tris•HCl (pH 8.0) plus 20 mM imidazole. The purified proteins were eluted with 5 bed volumes of 25 mM Tris•HCl (pH 8.0) plus 50 mM imidazole. The column fractions were analyzed by SDS–PAGE, and the purified protein was pooled.
Proteolytic Removal of the Polyhistidine Fusion Peptide
The synthetic gene was designed with a modified thrombin recognition sequence (Leu-Val-Pro-Arg-Gly-Ala) linking the C-terminus of the polyhistidine fusion peptide to the N-terminus of DTA. This design ensured that cleavage of the Arg–Gly peptide bond with thrombin results in production of DTA with an authentic amino-terminal sequence (Gly-Ala). Typically, 1 mg of DTA was incubated with 2–5 u of human thrombin (Novagen) for 1–5 days at 20 °C in 20 mM Tris•-HCl (pH 8.4), 150 mM NaCl, 2.5 mM CaCl2, and 2 mM DTT. The intact DTA was purified using a single anion-exchange FPLC chromatography fractionation step (FPLC: Mono-Q, Pharmacia).
Alternatively, the polyhistidine fusion peptide was removed by limited trypsin digestion, also yielding an authentic amino terminus. Generally, 1.5 mg of protein in 20 mM Tris•HCl (pH 7.4) and 10 mM β-mercaptoethanol was incubated with 7.5 μg of bovine trypsin (Sigma) for 60 min on ice. The entire incubation mixture was loaded on a 1.0 mL nickel chelation affinity column to bind uncut DTA as well as the cleaved polyhistidine peptide. The flow-through fractions were collected and combined with two 1.0 mL washes of 20 mM Tris•HCl (pH 7.4) and 10 mM β-mercaptoethanol. This protein was further purified using anion exchange chromatography (FPLC Mono Q from Pharmacia). Side fractions were pooled, desalted, and repurified using anion exchange chromatography.
KIE Measurement and Enzyme Kinetics. Kinetic Constants and Steady State Conditions
Hydrolysis of labeled NAD+'s by DTA was performed with 100 μM total NAD+ in 50 mM potassium phosphate (pH 6.0). The kinetic constants of hydrolysis were measured as described previously.28 Because the enzyme concentration was a significant fraction of the substrate concentration, Selwyn's test35 was used to ensure that steady state conditions still obtain. If steady state conditions hold, reactions performed at constant [NAD+] and varied [DTA] will give constant [product] for a given [DTA] × time; this was true up to the highest [DTA] tested, 16 μM (data not shown).
Commitment to Catalysis
The isotope trapping method was used to detect any commitment to catalysis. DTA (76 μM final concentration in 10 μL) was mixed with NAD+ (36–1000 μM) containing 2.4 × 105 cpm [4-3H]NAD+ in 50 mM potassium phosphate (pH 6.0) for 5s, then an excess of unlabeled NAD+ (100 μL of 10 mM) was added and the reaction allowed to proceed at 37 °C for 5kcat. [4-3H]-Nicotinamide released in the reaction was measured as described,28 and the commitment factor calculated by plotting 1/{[NAD+]trapped/[DTA-]total} versus 1/[NAD+]0. The y-intercept represents the fraction of NAD+ that would be trapped at infinite substrate concentration.
Radiolabel Technique
KIEs were measured by the competitive method with radiolabeled substrates by the same method as described previously,28 including the complete reaction with NAD+ glycohydrolase and purification and liquid scintillation counting of the product ADP-ribose. Hydrolysis of labeled NAD+'s by DTA was performed as above with 3 μM DTA for 3 h. The competitive radiolabel method entails measuring the relative rates of hydrolysis of an NAD+ isotopically labeled with 3H or 14C at the position of interest and one labeled at a remote site with the other radionuclide, which acts as a reporter for the natural isotope at the position of interest. The KIE is determined from the ratios of 14C/3H (for a 3H KIE) in the partial and complete reactions, with 14C acting as a reporter on 1H at the position of interest. Observed KIEs calculated this way are corrected to 0% reaction to allow for depletion of the faster reacting isotope.36 The remote label for determination of the 1′-14C, 4′-18O, and 1-15N KIEs was 4′-3H. Since the measured 4′-3H KIE ) 0.990 ± 0.002 was significantly different from unity, the heavy atom KIEs were corrected by multiplying by the measured 4′-3H KIE. All the 3H KIEs were measured using 5′-14C as the remote label, which was shown to have no measurable KIE for cholera toxin or solvolytic hydrolysis of NAD+.28 The 4′-18O and 1-15N KIEs were measured with doubly labeled NAD+'s, [4′-18ON,8-14CA] and [1-15N,5′-14C], with the remote radionuclide acting as a reporter for the stable heavy isotope.
Mass Spectrometry
The 4′-18O KIE was also measured by the competitive method using whole-molecule positive-ion electrospray mass spectrometry on residual NAD+ after reaction to approximately 50% completion. Anderson and co-workers have shown that KIEs can be determined by whole-molecule mass spectrometry with precision similar to the radiolabel method.37,38 [4′-18O]NAD+ (200 μM total concentration, 37.1% 4′-18O) with 6 μM DTA in 100 μL of 50 mM potassium phosphate (pH 6.0) was reacted at 37 °C for approximately 3 h, until the reaction was 50% complete. The extent of the reaction was determined by HPLC on a C18 reverse-phase column, 4 × 300 mm, in 50 mM ammonium acetate (pH 5.0). The relative peak areas (A260) of equimolar ADP-ribose and NAD+ under these conditions are 0.76(± 0.03):1. The remaining NAD+ was purified from the reaction mixture under the same HPLC conditions and >99% of the peak was collected and lyophilized overnight. The sample was redissolved in 2 mL of water and lyophilized again to remove volatile salts. The sample was dissolved in 100 μL of 0.1% aqueous trifluoroacetic acid for mass spectrometry. The substrate NAD+ (0% reaction) sample was prepared in the same way, except without DTA. Mass spectrometry of [4′-18O]-NAD+ without repurification gave identical results (not shown), demonstrating that the HPLC purification did not cause fractionation of the labeled NAD+.
Electrospray mass spectra of NAD+ were collected in single ion monitoring mode at m/z = 664.1 and 666.1, with a dwell time of 50 ms at each m/z. The former peak corresponds to unlabeled NAD+, the latter to [4′-18O]NAD+ plus molecules doubly substituted with natural abundance 2H, 13C, 15N, and natural abundance 18O. Samples were infused at 2 μL/min for ≥10 min per run, with three runs per KIE measurement.
Unlike KIEs measured by liquid scintillation counting, the molar amount of labeled material is not negligible compared with unlabeled material, so different equations are used to calculate the KIE. Also, it is necessary to account for the natural abundance isotopes in the peak at m/z = 666.1, which is 0.060 times the abundance of the isotopically unsubstituted peak at m/z = 664.1. The equation of Bigeleisen and Wolfsberg39 is
where [18P] is the concentration of 18O-labeled product and [18S]0 is the initial concentration of 18O-labeled substrate. This can be rearranged to
where f (= [P]/[S]0) is the fractional extent of reaction as determined by the HPLC assay, and ri and r0 are the ratio of peak intensities (I664.1, I666.1) at times t = i and 0, corrected for the natural abundance of m/z = 666.1, which was calculated from the natural abundances of elemental 13C, 15N, 2H, and 18O:
Since the majority of atoms of NAD+ are in isotopically insensitive positions, it was assumed that this ratio did not vary in the course of the reaction. In deriving this equation, we do not assume that [18S]/([18S] + [16S]) ≈ [18S]/[16S].40
Transition State Structure Determination. Bond-Energy/Bond-Order Vibrational Analysis
The transition state structure was determined by the structure interpolation method as described in the accompanying report. Briefly, trial transition state structures are generated automatically by the program CTBi30 for selected values of nLG,TS and nNu,TS as a function of the “oxocarbenium ion character” of the ribosyl moiety, and their KIEs are predicted using the program BEBOVIB.41 Reaction coordinates for concerted (with leaving group departure) and unimolecular attack of the nucleophile were investigated. Unimolecular departure of the leaving group is not a reasonable mechanism given the crystal structure but was investigated anyway. The predicted transition state structure was selected by plotting, for each isotopic label, the areas on a More-O'Ferrall-type reaction coordinate diagram (Figure 2) where the measured and predicted KIEs matched. The point where all the KIEs matched identifies the transition state structure.
Figure 2.
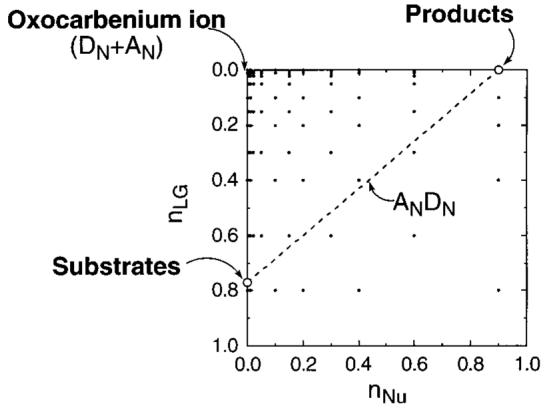
Reaction coordinate diagram. Positions in reaction coordinate space are illustrated by plotting the leaving group bond order (nLG) on the ordinate and nucleophile bond order on the abscissa (nNu). Thus, the reaction proceeds from the substrates in the lower left corner to products in the upper right. A classical DN + AN (SN1) reaction mechanism involves formation of an oxocarbenium ion intermediate, with complete loss of the leaving group, before the nucleophile bond order starts to increase. A concerted, synchronous ANDN (SN2) mechanism follows the dotted diagonal line, where increase in nNu at each point matches exactly the loss of nLG.
5′-3H KIE
Two sources for the large 5′-3H KIE were considered: distortion of the ∠C4′–C5′–O5′ bond angle and protonation of the α-phosphate. The distortional KIE was examined using ethanol as a model compound (Figure 3). The reactant model was ethanol optimized using an hybrid density functional theory minimization using Becke's exchange functional42 and Perdew and Wang's correlation functional43 with the 3-21+G** basis set using the program Gaussian 94.44 The effects of changes in the ∠C2–C1–O1 bond angle were analyzed by fixing it at 20° greater or less than the fully optimized structure at 106.3° and reoptimizing the rest of the ethanol molecule. Structures at values of ∠C2–C1–O1 between the extremes were calculated by varying the internal coordinates (bond lengths, bond angles, and torsional angles) between the optimal structure and the constrained structures with the program CTBi. 1-3H KIEs were calculated for each structure using BEBOVIB, with bond stretching and bond angle bending force constants taken from the AMBER force field of Kollman's group45 after conversion to appropriate units. The torsional force constants were 0.01 mdyn•Å/rad2 for the C-O bond and 0.02 mdyn•Å/rad2 for C–C.46
Figure 3.
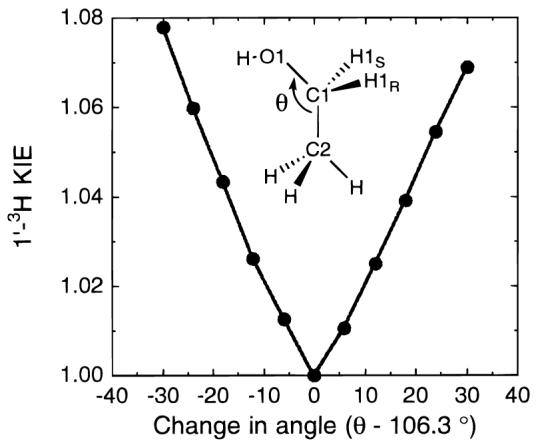
Distortional KIEs as modeled with EtOH. The bond angle, θ = ∠C2–C1–O1, is analogous to the bond angle ∠C4′–C5′–O5′ of NAD+ and the 1-3H KIE analogous to the 5′-3H KIE.
The effects of phosphate protonation were examined by optimizing ethyl phosphate in the neutral and monoanion forms at the same level of theory as ethanol. 1-3H KIEs were calculated from the fractionation factors derived by the program QUIVER47 from the optimized structures.
Results
Kinetic Constants
Hydrolysis of NAD+ by DTA was conducted in 50 mM potassium phosphate buffer (pH 6.0) at 37 °C. At this pH, the nonenzymatic, base-catalyzed hydrolysis which occurs above pH 7 was minimized. Under these conditions, DTA hydrolyzes NAD+ with kinetic constants of kcat = 3.0 (± 0.3) × 10−3 s−1, kcat/KM = 10.9 ± 0.4 M−1•s−1, and KM = 2.7 (± 0.3) × 10−4 M (Figure 4). KM closely approximates Kd, since there is no external commitment to catalysis (see below). The observed KM is greater than reported previously at pH 8.0, 2.0 (± 0.5) × 10−5 M,48 though kcat/KM = 12.5 M−1•s−1 is similar.
Figure 4.
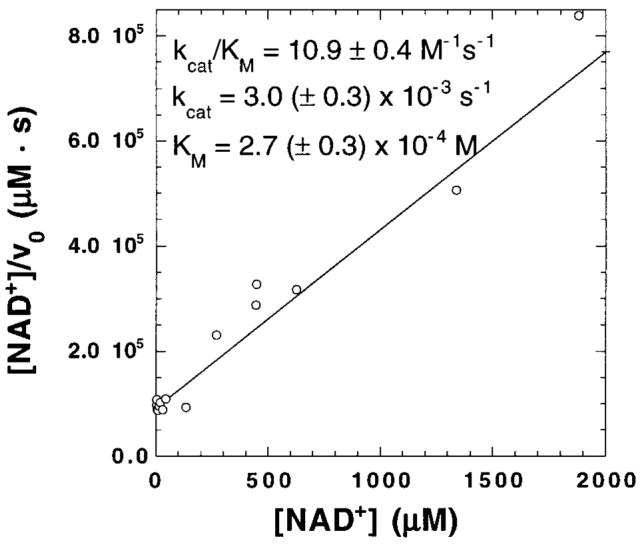
Hanes plot of kinetic constants for DTA-catalyzed NAD+ hydrolysis in 50 mM potassium phosphate (pH 6.0) at 37 °C.
Commitment to Catalysis
KIEs in kcat/KM report on the rate-limiting step (or steps if more than one is significantly rate-limiting) up to the first irreversible step of the reaction. Substrate molecules that bind to the enzyme and form products without dissociating from the Michaelis complex cause commitment to catalysis and decrease the experimentally measured KIEs. For full commitment, only binding isotope effects on formation of the Michaelis complex would be observed. The KIEs of the chemical step would be kinetically unobservable. The extent of commitment to catalysis was quantitated using an isotope trapping experiment.49 The results show that, at infinite substrate concentration, less than 0.3% of substrate would proceed forward to the chemical step without dissociation (Figure 5). Thus, the extent of forward commitment to catalysis is negligible.
Figure 5.
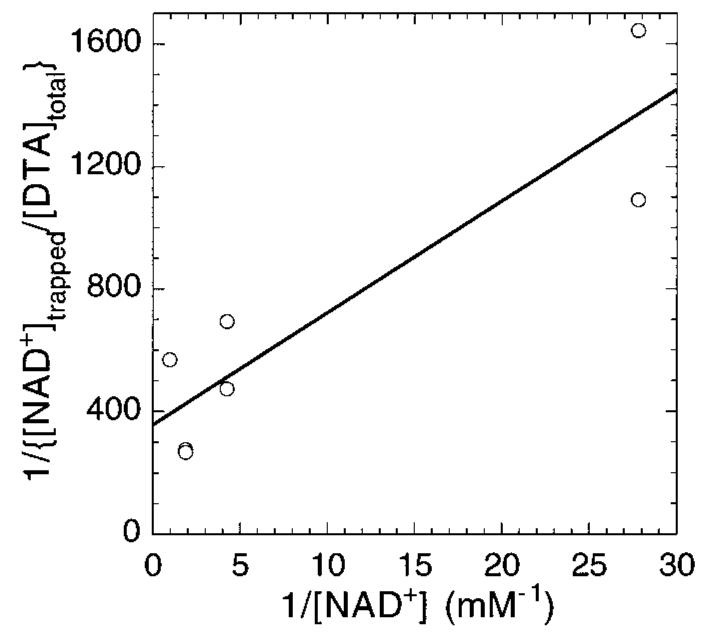
Commitment to catalysis. The ordinate intercept, 358, is the reciprocal of the fraction of NAD+ that would react with DTA, without dissociation, at infinite concentration of NAD+. This corresponds to a commitment factor of 0.0028.
In principle, product release could be rate-limiting and therefore reflected in the experimental KIEs. If it were, a burst of product formation would be observed under pre-steady-state conditions. In fact, the rate of product appearance is constant for reaction times as short as one-fifth of a turnover (not shown), demonstrating that product release is not rate-limiting. Further evidence comes from the kinetic constants for the ADP-ribosylation of EF-2. The lower limit on the rate of product release is set by kcat = 20 s−1 for the ADP-ribosylation of EF-2.48 Even if product release is fully rate-limiting in that reaction (for which there is no evidence for or against), that would be 7 × 103-fold faster than kcat = 3.0 × 10−3 s−1 for the hydrolysis reaction, further evidence that the chemical step is rate-limiting.
Measured KIEs
The KIEs measured in this study were determined as described previously28 using the competitive method with radiolabeled substrates (Table 1). The 4′-18O KIE was also determined by mass spectrometry. The KIEs measured by each technique were within experimental error of each other (Table 1, and see the Discussion).
Table 1.
Measured and Predicted KIEs of DTA Catalyzed NAD+ Hydrolysis
| label of interest | KIE type | measd KIE (± 95% confidence interval) |
na | predicted KIE at transition stateb |
|---|---|---|---|---|
| 1-15Nc | primary, leaving group |
1.030 ± 0.004 | 4 | 1.029 |
| 1′-14Cd | primary | 1.034 ± 0.004 | 4 | 1.034 |
| 1-15N,1′-14Ce | double primary | 1.062 ± 0.010 | 2 | |
| 1′-3Hf | α-secondary | 1.200 ± 0.005 | 4 | 1.186 |
| 2′-3Hf | β-secondary | 1.142 ± 0.005 | 3 | 1.141 |
| 4′-3Hf | γ-secondary | 0.990 ± 0.002 | 3 | –g |
| 5′-3Hf | δ-secondary | 1.032 ± 0.004 | 4 | –h |
| 4′-18O, mass spectrometryi |
α-secondary | 0.991 ± 0.003 | 3 | – |
| 4′-18O, radiolabeledj |
0.986 ± 0.003 | 3 | – | |
| 4′-18O, combined | 0.988 ± 0.003 | 6 | 0.985 |
Number of independent, quadruplicate determinations (triplicate for mass spectrometry).
nLG,TS = 0.02 and nNu,TS = 0.03.
Labeled substrate: [1-15N,5′-14C]NAD+. Remotely labeled substrate: [4′-3H]NAD+.
Remotely labeled substrate: [4′-3H]NAD+.
Labeled substrate: [1-15N,1′-14C]NAD+. Remotely labeled substrate: [4′-3H]NAD+.
Remotely labeled substrate: [5′-14C]NAD+.
4′-3H KIE was not modeled quantitatively.
5′-3H KIE could be matched by distorting the ∠C4′–C5′–O5′ bond angle or protonating the α-phosphate.
Measured by positive-ion whole-molecule mass spectrometry. Labeled substrate: [4′-18O]NAD+.
Labeled substrate: [4′N-18O,8A-14C]NAD+. Remotely labeled substrate: [4′-3H]NAD+.
Transition State Structure
The transition state structure that matched the experimental KIEs had high oxocarbenium ion character, with nLG,TS = 0.02 and nNu,TS = 0.03. This is a concerted ANDN50 (SN2) reaction, with both the leaving group and nucleophile participating in the reaction coordinate. No combination of nLG and nNu was found for DN + AN (SN1) or DN*AN (unimolecular attack of the nucleophile on the oxocarbenium ion) mechanisms that matched the experimental KIEs. The predicted transition state structure was identified from a contour plot of the area in reaction coordinate space in which the predicted KIEs for each label matched the measured one (Figure 6). The point where the contours converge indicates the transition state structure, at nLG = 0.02 and nNu = 0.03. The predicted KIEs for 4′-3H and 5′-3H were small throughout reaction coordinate space and are therefore not shown. This is consistent with the results from the solvolytic hydrolysis of NAD+, which shows that for a similar transition state structure (nLG,TS = 0.02, nNu,TS = 0.005) the experimental and predicted KIEs at H4′ and H5′ are negligible for the intrinsic chemical step. Thus the observed remote KIEs for the DTA reaction arise from the enzymatic stabilization of the transition state (see the Discussion).
Figure 6.
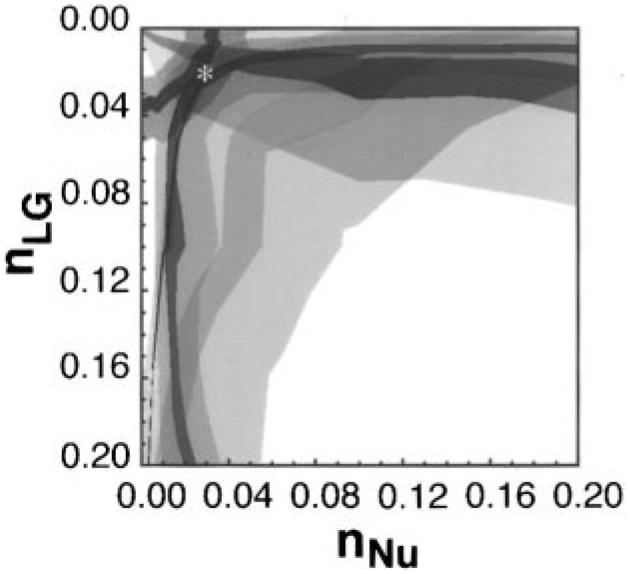
Match of predicted versus experimental KIEs. For each isotopic label, the colored area represents the match of the predicted with the experimental KIEs as a function of nLG and nNu in this More–O'Ferrall-type reaction coordinate diagram. The light shading represents the 95% confidence interval of each measured KIE, with dark shading representing the exact measured KIE (approximately ± 0.001): blue, 1-15N; red, 1′-14C; gray, 1′-3H; green, 2′-3H; orange, 4′-18O. The predicted transition state structure is indicated by *. Only the top left (dissociative) corner of reaction coordinate space is shown.
4′-3H KIE
The enzymatic 4′-3H KIE, 0.990 ± 0.002, was significantly more inverse than for the solvolytic hydrolysis (0.997 ± 0.001). Together with the 5′-3H KIE, these effects demonstrate that the enzyme is using binding energy remote from the catalytic site to promote catalysis. No attempt was made to quantitatively model the enzymatic 4′-3H KIE. A modest change in any of the bond angles between C4′ and O4′, C3′, or C5′ could cause a KIE of this relatively small magnitude.
5′-3H KIE
The experimental 5′-3H KIE of 1.032 ± 0.004 matched the predicted KIEs the ethanol model at ∠C2–C1–O1 angles −14° and +15° from the equilibrium value of 106°, that is, at 92° and 121°, respectively (Figure 3). The calculated secondary 1-3H KIE for the protonation of ethyl phosphate was 1.049, also of sufficient magnitude to account for the experimental result.
Discussion
Meaning of KIEs
KIEs reflect differences in the energy of each isotope between two states. The competitive method measures KIEs on kcat/KM (or V/K),51 where the relevant species are the reactant (free enzyme and free substrate in solution) and the enzymatic transition state complex. This is true both for radiolabeled substrates where the molar concentrations of the radiolabels are small fractions of the total NAD+ concentration and for the stable, nontrace 18O-labeled NAD+.
Mass Spectrometric Measurement of KIE
Because of the indirect nature of KIE measurements by the dual-radiolabel technique and the difficulty in checking the results by other means, as well as the susceptibility to interference and the small size of the effects being measured, the accuracy and precision of measured KIEs is always a source of concern. These concerns are compounded when dual remote labels must be used to measure KIEs of stable isotopes such as 15N and 18O. An important validation of the dual remote label method was obtained when the 4′-18O KIE measured by mass spectrometry was within experimental error of the one measured with dual remote radiolabels: 0.986 ± 0.003 using the radiolabel technique versus 0.991 ± 0.003 by mass spectrometry (Table 1).
The radiolabel technique is an inherently indirect measure, using liquid scintillation counting of radionuclides as reporters on 18O and 16O, whereas mass spectrometry directly measures the isotopically pure 18O- and 16O-containing NAD+ molecules (after compensating for the natural abundance of m/z = 666.1). With the radiolabel technique, isotope ratios were measured in the products of the reaction after isolation on ion exchange columns, while the mass spectrometry KIEs were measured from residual substrate after isolation by reverse phase HPLC. Given these differences in the measurement techniques, the identity of the measured KIEs within experimental error demonstrates the reliability of the measurement methods.
Description of KIEs
The predicted KIEs for the proposed transition state structure match all measured KIEs within the 95% confidence interval and are all within 0.002 of the exact measurement, with the sole exception of the 1′-3H KIE. Given the similar 1′-3H KIEs measured for NAD+ solvolysis (1.194)30 and hydrolysis by cholera (1.186)28 and pertussis (1.207)29 toxins, and the similarity to other N-riboglycoside hydrolyses,52 the measured KIE is also likely to be correct. Computational prediction of the 1′-3H KIE is difficult since the range of the predicted KIEs within reaction coordinate space varies from 0.60 to 1.36 and was larger than for any other label. Within this range, the difference between the predicted (1.186) and measured (1.200) KIEs at the transition state is small. The transition state structure derived with the structure interpolation method is consistent with a qualitative evaluation of the measured KIEs, with previously reported kinetic and structural studies of DTA (see below), and with other enzymatic N-riboside hydrolyses.28,29,53-58
[1-15N,1′-14C] KIE
The double primary, [1-15N,1′-14C] KIE = 1.062 ± 0.010 (n = 2), was measured and found to be, within experimental error, equal to the product of the individual KIEs, 1.065. This relationship was also observed for the solvolytic hydrolysis of NAD+, where the measured [1-15N,1′-14C] KIE = 1.034 ± 0.002 (n = 6) was equal to the product of the individual KIEs, 1.036. That the measured double KIE equals the product of the individual ones is a necessary consequence (though not diagnostic) of a mechanism where a single step is rate-limiting. The equality of those values demonstrates the accuracy and reliability of the KIE measurements.
Other KIEs
The combination of the relatively large 1-15N KIE, indicating large loss of C1′–N1 bond order, and small 1′-14C KIE, indicating low bond order to the approaching nucleophile, is diagnostic of a dissociative transition state. This is supported by the secondary KIEs. The large 1′-3H = 1.200 ± 0.005 is consistent with a dissociative transition state. Reybridization of C1′ toward sp2 plus a decrease in the steric crowding around H1′ led to a decrease in the out-of-plane bending forces, which results in a large, normal KIE.59 The large 2′-3H KIE = 1.142 is diagnostic of hyperconjugation, which is evidence for the ribose ring conformation in the transition state being 3′-exo. Hyperconjugation, as distinct from inductive effects, is highly sensitive to the angle between the C2′–H2′ bond and the scissile C1′–N1 bond,52,60 being maximal when the bonds are eclipsed or anti and zero when the dihedral angle is 90°. The planarity of the sp2-like O4′ and C1′ atoms forces ring atoms C4′–O4′–C1′–C2′ to be coplanar. The only conformational flexibility within the ribose ring is at C3′, which can be either 3′-exo or 3′-endo. In the 3′-exo conformation, the C2′–H2′ and C1′–N1 bonds are in nearly perfect eclipse, with a dihedral angle of 0.1°. In the 3′-endo conformation, the angle is 59.8° (not shown). The magnitude of the measured 2′-3H KIE is near the limit expected for a glycosidic ring system61 and similar to previously measured 2′-3H KIEs for ribosyl N-glycosides.28,29,52,55 The inverse 4′-18O KIE occurs because loss of C1′–N1 bond order is compensated for in the transition state by an increase in the C1′–O4′ bond order. This increased bond order to the ring oxygen atom restricts its vibrational environment, resulting in an inverse KIE.
The transition state structures of N-riboside hydrolyses for other enzymes derived in this lab28,29,53-58 have consistently indicated highly oxocarbenium ion-like transition state structures, including NAD+ hydrolysis catalyzed by cholera and pertussis toxins. Indeed, all evidence indicates that glycoside hydrolyses in general, enzymatic and nonenzymatic, proceed through oxocarbenium ion-like transition state structures.62-75
4′-3H and 5′-3H KIEs
In the solvolytic hydrolysis of NAD+, the measured KIEs at the remote sites are unmeasurably small (5′-3H KIE = 1.000 ± 0.003) or negligible (4′-3H KIE = 0.997 ± 0.001). Thus, the significant experimental measured KIEs for the enzymatic reaction (1.032 ± 0.004 and 0.990 ± 0.002, respectively) are not intrinsic to the chemical features of the transition state. They reflect the influence of the enzymatic binding energy at sites remote from the catalytic site to promote catalysis that results in structural changes at C4′ and C5′. A small, inverse 4′-3H and significant, normal 5′-3H KIE are becoming ubiquitous features of enzymatic N-riboglycoside hydrolysis.28,29,54-56 The remote 3H KIEs were analyzed in a separate step from the KIEs adjacent to the breaking bonds, since these effects are not inherent to the intrinsic chemical step of the reaction.
Ab initio calculations using small molecule models showed that the experimental 5′-3H KIE could arise from distortion of the ∠C4′–C5′–O5′ bond angle, by a change in the electrostatic environment of the α-phosphate, or some combination of these two effects. Protonation of ethyl phosphate gave a 1-3H KIE (1.049) larger than the experimental 5′-3H KIE. This KIE arises from inductive electron withdrawal toward the phosphate leading to weaker C–H bonds. This result demonstrates that a change in the electrostatic environment of the α-phosphate of NAD+ at the transition state, such as protonation or ion-pair formation by interaction with His21 of DTA, could account for the experimental KIE. Either increasing or decreasing the ∠C2–C1–O1 angle in ethanol results in normal KIEs, with the predicted KIEs matching the experimental 5′-3H KIE at angles of 92° and 121°. The calculated KIEs arise from a decrease in the C–C–H, O–C–H, and H–C–H bending force constants caused by the distortion of C1 of the model ethanol.55 It is not yet possible to distinguish between these two possibilities as the source of the experimental 5′-3H KIE.
Transition State Structure
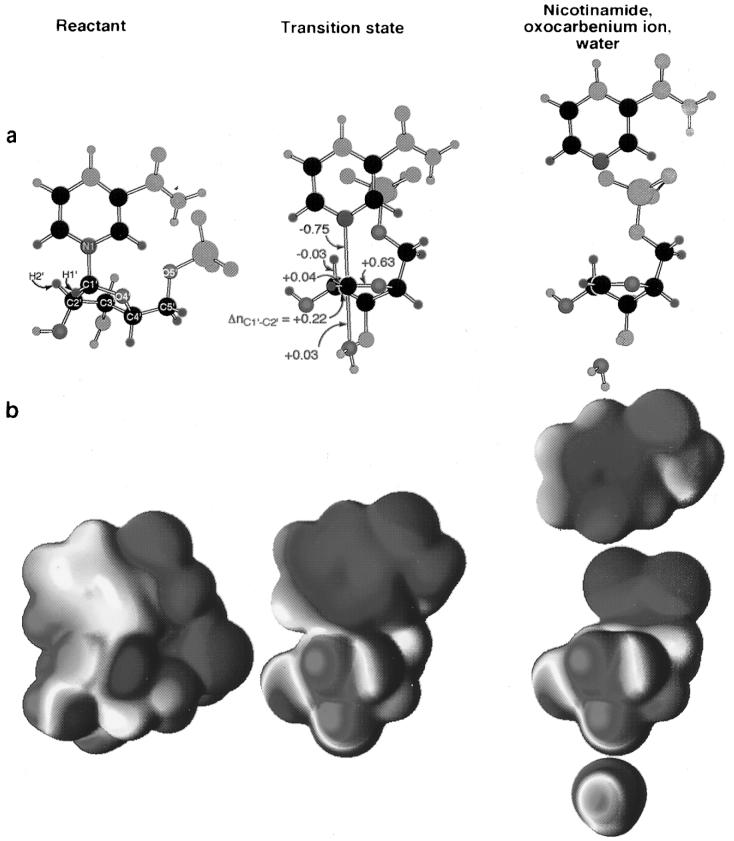
The following structural changes can be proposed as the NAD+ proceeds from the reactant (nLG,react = 0.77) to the transition state (nLG,TS = 0.02, nNu,TS = 0.03): The loss of bond order to the leaving group localizes the positive charge from the ground state onto the ribose ring. The loss of leaving group bond order, ΔnLG = −0.75, is compensated for by increases in bond orders within the ribose ring, ΔnC1′–O4′ = +0.63, ΔnC1′–C2′ = +0.22, and ΔnC1′–H1′ = +0.04, plus the appearance of the nucleophile, ΔnNu = +0.03. The sum of bond orders to C1′, ΣnC1′, is greater in the transition state (3.78) than in the reactant molecule (3.62). As discussed in the accompanying report, this change is likely due to the increased ability of C1′ to form π-bonding interactions with O4′ and C2′ when rehybridized toward sp2. This has also been observed in the transition state structures of cholera28 and pertussis29 toxin reactions. Another change that occurs is the flattening of the ribose ring. With the sp2 character of C1′, C2′, and O4′ increasing at the transition state, the atoms C4′–O4′–C2′–C1′ become coplanar. C3′ is the only ring atom that is not part of the plane; it projects below the plane in a 3′-exo conformation. Flattening of the ribose ring and the sp2 rehybridization of C1′ cause the nicotinamide ring and the phosphate to move closer together, above the plane of the ribose ring.
The charge distribution of NAD+ changes substantially between the reactant and transition states (Figure 7). In the reactant, the nitrogen of the nicotinamide ring bears a formal positive charge of 1+. At the electrostatic potential surface, the positive charge (red) is delocalized throughout the nicotinamide ring and into C1′ and H1′ of ribose. In the transition state, the nicotinamide ring becomes neutral and the positive charge transfers to the ribosyl ring. The electrostatic surface of the transition state is similar to that for a ribosyl oxocarbenium ion and nicotinamide which are not interacting with each other.
Figure 7.
Structures of reactant, transition state, and the hypothetical oxocarbenium ion, with independent, noninteracting nicotinamide and water molecules. (a) Atoms present in the cutoff models used in BEBOVIB calculations are colored by element; all others are colored gray. Changes in bond order between the reactant and the transition state are indicated. All atoms within two bonds of the isotopically labeled positions were included in KIE calculations, yielding “highly proper” cutoff models.89 (b) Electrostatic potentials projected onto the molecular surfaces of the full molecules in the same orientation as in part a, with red representing positive electrostatic potential and blue representing negative potential. Calculations were done at the RHF/6-31G** level. Molecular surfaces are at an electron density of 0.002 e/bohr3, and the electrostatic potential spectrum is from −0.1 (blue) to 0.1 hartree/e (red).
Comparison with Other Transition State Structures
The transition state structures for NAD+ hydrolysis by cholera toxin (nLG,TS = 0.09, nNu,TS = 0.005)28 and pertussis toxin (nLG,TS = 0.1, nNu,TS = 0.001)29 catalyzed hydrolysis of NAD+ have been reported. The reported leaving group bond orders were somewhat higher and the nucleophile bond orders somewhat lower than reported here for DTA. In those studies, the increase in C–N bond orders within the nicotinamide ring in the transition state was not included in the model, resulting in increased residual leaving group bond order in the transition state. The increase in predicted nLG's leads, in turn, to low predicted nNu's to match the ribosyl KIEs. Using the structure interpolation method, the predicted transition state bond orders for these reactions become nLG,TS = 0.02 and nNu,TS = 0.02 for the cholera toxin reaction and nLG,TS = 0.05, nNu,TS = 0.001 for the pertussis toxin reaction. These values are similar to the nLG,TS = 0.02 and nNu,TS = 0.03 for the DTA reaction. These are small changes in the predicted transition state structures that reflect refinement in the modeling procedure. In all cases, the transition state structures for toxin-catalyzed hydrolysis of NAD+ are highly oxocarbenium ion-like.
The DTA transition state structure is also similar to the transition state for the pH-independent solvolytic hydrolysis of NAD+, where nLG,TS = 0.02 and nNu,TS = 0.005. The difference in nNu, 0.025, between the enzymatic and solvolytic transition states represents a 6-fold difference in bond order. KIEs are exponential functions of bond order; therefore, this difference of 0.54 Å in bond length to the water nucleophile represents a real difference in the transition state structures. At the predicted transition state for the DTA reaction, the predicted KIEs are within the 95% confidence interval of all measured KIEs except the 1′-3H. The small difference of 1.200 and 1.186 between experimental and predicted KIEs at this position are easily explained by the well-documented difficulty in predicting α-secondary KIEs at this position.59,76
Catalytic Mechanism and the Structure of DTA
In considering the catalytic mechanism of DTA, it is worth noting that the toxin catalyzes NAD+ hydrolysis much more weakly than the ADP-ribosylation reaction. With kcat = 3.0 (± 0.3) × 10−3 s−1, compared with k = 5 × 10−7 s−1 for the uncatalyzed reaction at 37 °C,77 the rate enhancement is only 104-fold. The biologically relevant ADP-ribosylation of EF-2 exhibits a kcat = 20 s−1, a 4 × 107-fold rate enhancement.48 Much of the catalytic power brought to bear during the ADP-ribosylation reaction is evidently not operative in the hydrolytic reaction.
NAD+ Binding
The X-ray crystallographic structures of diphtheria toxin include ones with an endogenous inhibitor, ApUp, bound in the active site,78 with substrate NAD+ 79 and with the active site unoccupied.80 The nicotinamide ring of substrate NAD+ binds in a deep hydrophobic pocket on the enzyme, becoming desolvated. The low dielectric environment lowers the energy difference between the reactant and transition states by increasing the energy of the positively charged nicotinamide ring in the reactant relative to the neutral form at the transition state, a case of ground state destabilization. This deep pocket would make release of the product nicotinamide difficult before the ADP-ribosylation reaction was complete, consistent with the observed inversion of configuration of the anomeric carbon in the reaction with EF-2.81 The side chain of Glu148, which has been shown by photoaffinity labeling82 and mutagenesis83 to be crucial for catalysis, is located where it can stabilize the formation of the oxocarbenium ion-like transition state (see below). His21 is located near one of the phosphate groups of NAD+, where it could assist electrostatically in NAD+ binding. There are, however, some features of the X-ray crystallographic structure with bound NAD+ that appear unfavorable for catalysis.
“Anticatalytic” Structural Features
Several (apparently) favorable interactions between DTA and bound NAD+ in the crystal structure appear to be “anticatalytic”; that is, they appear to stabilize the reactant in preference to the transition state. The carboxamide nitrogen of the nicotinamide ring and one of the α-phosphate nonbridging oxygens are positioned to form an intramolecular hydrogen bond. This bond would need to be broken during C1′–N1 bond cleavage, making it an anticatalytic interaction. It would not be possible for the N–H⋯ O=P hydrogen bond to be a “fulcrum” about which the nicotinamide ring rotates as the C1′–N1 bond breaks because of the presence of an additional hydrogen bond from the carboxamide nitrogen to Gly22 C=O, which would need to be broken instead.
The closest contact the carboxylate of Glu148 makes with NAD+ is through the C5 atom of the nicotinamide ring (3.04 Å) and O2′ of the ribose ring (3.39 Å). The nicotinamide ring is positively charged in the reactant (Figure 7b) but becomes electroneutral in the transition state. Interaction of the reactant with a negatively charged carboxylate stabilizes the reactant relative to the transition state. Thus, a favorable interaction between Glu148 and the nicotinamide ring would be anticatalytic. In the crystal structure, the distance to C1′, the site of accumulation of positive charge at the transition state, is 3.96 Å, and the interaction is at an oblique angle, not ideally suited to forming a strong interaction (see below).
The presence of these “anticatalytic” features in the DTA/NAD+ crystal structure implies (a) that these favorable interactions must be broken, at some energetic cost, to attain the transition state and/or (b) that, although the general mode and orientation of binding of NAD+ are the same as in the productive Michaelis complex, some of the details are different.
Binding of the Transition State
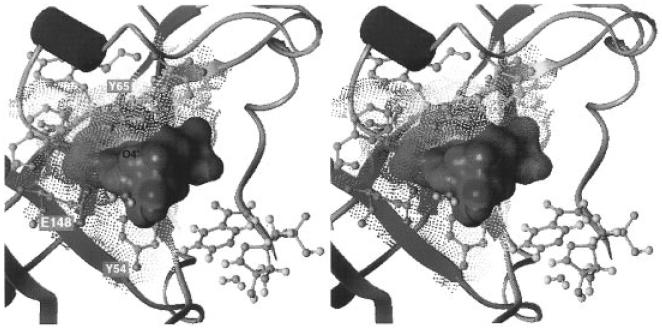
Docking the transition state structure with the nicotinamide ring superimposed on that of the crystallographically determined NAD+ in the active site cleft results in the ribosyl ring projecting into solution, with no contacts to DTA. While the sides of the nicotinamide binding pocket are well defined by the side chains of Tyr54 and Tyr65, the top of the pocket is less well defined, with contacts contributed by Tyr20, Gly22, Ser55, Thr56, Ala62, and Phe140. Only minor changes in protein conformation are necessary to accommodate binding the nicotinamide ring deeper in the pocket. In this way, the positively charged ribosyl ring at the transition state is in contact with the stabilizing negative charge of Glu148.
The transition state structure could be fitted into the active site of DTA, without modifying the protein structure, by changing the angle between the nicotinamide ring and the ribose ring and by varying the torsional angles about the C4′–C5′ and C5′–O5′ bonds. Torsional rotations have low energy and have negligible effects on KIEs. Similarly, because of the low bond order to the leaving group, nLG,TS = 0.02, a change in the angle between the nicotinamide ring and the ribosyl moiety also would have a negligible effect on the KIEs. The nicotinamide ring was positioned as deeply as possible in the binding pocket. The ribosyl portion was positioned with rC1′–N1 = 2.65 Å, with C1′ near the Glu148 carboxylate and with the position of the phosphate group adjusted to avoid steric clashes while remaining near the His21 side chain.
This docking experiment is a crude model of the enzyme/transition state interactions since no attempt was made to account for the unknown changes in protein structure that occur to form the transition state with the physiological second substrate, EF-2. However, with the transition state structure fitted in the active site and the electrostatic potential of the enzyme projected onto its solvent accessible surface, the electrostatic stabilization of the transition state becomes clear (Figure 8). The negative (blue dots) electrostatic potential of Glu148 is juxtaposed directly with the positive (solid red) electrostatic potential of the transition state at C1′. The positive electrostatic potential of His21 (red dots) complements the negative potential of the transition state's phosphate group (solid blue). With this orientation of the ribose ring, a perpendicular approach of the nucleophilic water brings it into close contact with Glu148. In this geometry, Glu148 can act as a general base catalyst or can electrostatically polarize the H–O bond of water to promote nucleophilic attack. Also, with this orientation, it becomes possible to form a C–H⋯O hydrogen bond between H1′ of NAD+ and a carboxylate oxygen of Glu148. C–H⋯O hydrogen bonds are weak, but biologically significant, interactions.84,85
Figure 8.
Stereodiagram of the transition state structure fitted into active site of DTA. Projection of the electrostatic potentials onto the molecular surface shows the complementarity of the contact site for the transition state. The ball-and-stick figure of the transition state on the lower right shows the orientation of the transition state in the active site. The ring oxygen, O4′, is labeled on the molecular surface. The region of positive potential (solid red) associated with C1′ of the TS is apposed with the negative potential (blue dots) of the carboxylate of Glu148. The negative electrostatic potential of the phosphate oxygens (solid blue) is near the positive potential (red dots) of His21 (not visible behind the phosphate). The proximity of the nucleophile water to the carboxylate of Glu148 raises the possibility that it promotes catalysis as a general base catalyst or by polarizing the H–O bond to enhance the nucleophilicity of the oxygen. The electrostatic potentials were calculated using the Delphi module of the program Insight II (Biosym Technologies, San Diego, CA). Charges were of 1+ were assigned to Lys, Arg, and His21 of DTA, 0.5+ to other His residues, and 1– to Glu and Asp. Point charges on the atoms of the transition state structure were assigned from the natural population analysis90 charges calculated from the wave function as in Figure 7. The molecular surfaces were calculated as the Connolly surfaces,91 but with the atomic radii reduced by a factor of 0.8 so that the surface approximates a smoothed van der Waals surface. The contact site of DTA includes all residues that contribute to the molecular surface surrounding the transition state: Tyr20, His21, Tyr54, Ser55, Thr56, Tyr65, Phe140, Glu148. Secondary structural elements of DTA, as calculated by the Kabsch and Sander criteria,92 are shown, with α-helices in purple and β-strands in blue. The transition state structure from Figure 7 was fitted into the active site cleft by allowing the bond angles between the nicotinamide and ribosyl moieties to vary, as well as the torsional angles about C4′–C5′ and C5′–O5′.
These features of the catalytic site suggest strategies for designing transition state inhibitors of diphtheria toxin. The transition state structure of the ribosyl group is similar to that for the hydrolysis of inosine catalyzed by nucleoside hydrolase from Crithidia fasiculata,55 with a highly dissociative, oxocarbenium ion-like transition state. For that enzyme, the electrostatic and geometric characters of the transition state were exploited to design and synthesize transition state analogue inhibitors with Ki's to 2 nM.86-88 Preliminary studies show that phenyliminoribitol and p-nitrophenyl amidrazone are modest inhibitors of DTA, with Ki's near 100 μM (data not shown). Given the extremely high specificity of DTA for the nicotinamide ring and adenosyl portion of the molecule, work is underway to incorporate these features into inhibitor structures. Work is also underway to characterize the transition state structure for the physiological reaction catalyzed by diphtheria toxin, the ADP-ribosylation of EF-2.
Conclusion
The transition state structure of DTA-catalyzed hydrolysis of NAD+ was determined by using the structure interpolation method of bond-energy/bond-order vibrational analysis of multiple KIEs. The transition state is oxocarbenium ion-like, with low residual bond order to the leaving group, nC1′–N1 = 0.02, and low bond order to the approaching nucleophilic water, nC1′–O = 0.03. The reaction mechanism is ANDN (i.e., concerted) and highly asynchronous, with both the leaving group and nucleophile participating in the reaction coordinate. The 4′-3H and 5′-3H KIEs indicate the use of binding energy remote from the scissile bond to promote catalysis, possibly through a change in the electrostatic environment of the α-phosphate and/or distortion of the ∠C4′–C5′–O5′ bond angle. KIEs were measured by the competitive radiolabel technique, with the [4′-18O] KIE also measured by whole-molecule positive ion mass spectrometry.
The transition state structure docked into the crystal structure of DTA suggests features of the catalytic mechanism. Desolvation of the nicotinamide ring in a hydrophobic pocket, electrostatic stabilization of the positive charge on the oxocarbenium ion-like transition state by the carboxylate group of Glu148, electrostatic stabilization of the pyrophosphoryl group by His21, and activation of the attacking water nucleophile can be proposed from the complex of DTA with the experimentally determined transition state structure.
Acknowledgment
The authors thank Mr. Edward Nieves and Dr. Ruth H. Angeletti for their invaluable help in developing the method of mass spectrometric determination of KIEs. We also thank Dr. R. John Collier for supporting the production of DTA and for his cooperation and encouragement for this study. Dr. Michael Sinnott generously provided the ketone precursor used in the synthesis of [5-18O]glucose.
Footnotes
This work was supported by NIH Research Grant AI34342 and a postdoctoral fellowship from the Natural Sciences and Engineering Research Council (Canada) to P.J.B.
Supporting Information Available: Summary of KIE calculations for the DTA-catalyzed hydrolysis transition state, plus the BEBOVIB input (9 pages). See any current masthead page for ordering and Internet access instructions
References
- 1.van Geldermalsen AA, Wenning U. Ann. Trop. Paediatr. 1993;13:13–19. doi: 10.1080/02724936.1993.11747620. [DOI] [PubMed] [Google Scholar]
- 2.Hardy IR, Dittmann S, Sutter RW. Lancet. 1996;347:1739–1744. doi: 10.1016/s0140-6736(96)90811-9. [DOI] [PubMed] [Google Scholar]
- 3.Koo D, Traverso H, Libel M, Drasbek C, Tauxe R, Brandling-Bennett D. Bull. Pan Am. Health Org. 1996;30:134–143. [PubMed] [Google Scholar]
- 4.Swerdlow DL, Levine O, Toole MJ, Waldman RJ, Tauxe RV. Lancet. 1994;344:1302–1303. doi: 10.1016/s0140-6736(94)90793-5. [DOI] [PubMed] [Google Scholar]
- 5.Siddique AK, Salam A, Islam MS, Akram K, Majumdar RN, Zaman K, Fronczak N, Laston S. Lancet. 1995;345:359–361. doi: 10.1016/s0140-6736(95)90344-5. [DOI] [PubMed] [Google Scholar]
- 6.Popovic T, Fields PI, Olsvik O, Wells JG, Evins GM, Cameron DN, Farmer J. J. r., Bopp CA, Wachsmuth K, Sack RB, et al. J. Infect. Dis. 1995;171:122–127. doi: 10.1093/infdis/171.1.122. [DOI] [PubMed] [Google Scholar]
- 7.Starke JR, Tan TQ, Chacko MR, Cleary TG, Connelly KK, Kline MW. Texas Med. 1994;90:35–45. [PubMed] [Google Scholar]
- 8.Christie CD, Marx ML, Marchant CD, Reising SF. New Engl. J. Med. 1994;331:16–21. doi: 10.1056/NEJM199407073310104. [DOI] [PubMed] [Google Scholar]
- 9.Rosenthal S, Strebel P, Cassiday P, Sanden G, Brusuelas K, Wharton M. J. Infect. Dis. 1995;171:1650–1652. doi: 10.1093/infdis/171.6.1650. [DOI] [PubMed] [Google Scholar]
- 10.De Serres G, Boulianne N, Douville Fradet M, Duval B. Canada Communicable Dis. Rep. 1995;21:45–48. [PubMed] [Google Scholar]
- 11.MacIntyre R, Hogg G. Aust. J. Public Health. 1994;18:21–24. doi: 10.1111/j.1753-6405.1994.tb00189.x. [DOI] [PubMed] [Google Scholar]
- 12.Syedabubakar SN, Matthews RC, Preston NW, Owen D, Hillier V. Epidemiol. Infect. 1995;115:101–113. doi: 10.1017/s0950268800058167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Matter HC, Schmidt-Schlapfer G, Zimmermann H. Schweiz. Med. Wochenschr. 1996;126:1423–1432. [PubMed] [Google Scholar]
- 14.Montiano Jorge JI, Lazcoz Huarte A, Amiama Perez de Villarreal C, Mendia Gutierrez M, Benito Fernandez J, Santiago Burruchaga M, Pocheville Guruceta I, Gutierrez Villamayor C, Gaztelurrutia Abaitua L. An. Esp. Pediatr. 1992;37:184–186. [PubMed] [Google Scholar]
- 15.Abbreviations: DTA, recombinant diphtheria toxin A chain; EF-2, eukaryotic elongation factor 2; HPLC, high-pressure liquid chromatography; IPTG, isopropyl-β-d-thiogalactopyranoside; KIE, kinetic isotope effect; NAD+, nicotinamide adenine dinucleotide (oxidized form); NaAD+, nicotinic acid adenine dinucleotide; NaMN+, nicotinic acid mononucleotide; nLG and nNu, bond orders to the leaving group and to the incipient nucleophile; nX-Y, bond order between atoms X and Y; rX-Y, bond length between atoms X and Y; SDS-PAGE, sodium dodecyl sulfate polyacrylamide gel electrophoresis; TS, transition state.
- 16.Wilson BA, Collier RJ. Curr. Top. Microbiol. Immunol. 1992;175:27–41. doi: 10.1007/978-3-642-76966-5_2. [DOI] [PubMed] [Google Scholar]
- 17.Li BYRS. J. Biol. Chem. 1994;269:2652–2658. [PubMed] [Google Scholar]
- 18.Murphy JR, vanderSpek JC. Sem. Cancer Biol. 1995;6:259–267. doi: 10.1006/scbi.1995.0034. [DOI] [PubMed] [Google Scholar]
- 19.Kreitman RJ, Pastan I. Sem. Cancer Biol. 1995;6:297–306. doi: 10.1006/scbi.1995.0038. [DOI] [PubMed] [Google Scholar]
- 20.Roy DC, Ouellet S, Le Houillier C, Ariniello PD, Perreault C, Lambert JM. J. Nat. Cancer Inst. 1996;88:1136–1145. doi: 10.1093/jnci/88.16.1136. [DOI] [PubMed] [Google Scholar]
- 21.French RR, Penney CA, Browning AC, Stirpe F, George AJ, Glennie MJ. Br. J. Cancer. 1995;71:986–994. doi: 10.1038/bjc.1995.190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gould BJ, Borowitz MJ, Groves ES, Carter PW, Anthony D, Weiner LM, Frankel AE. J. Nat. Cancer Inst. 1989;81:775–781. doi: 10.1093/jnci/81.10.775. [DOI] [PubMed] [Google Scholar]
- 23.Pai LH, Pastan I. In: Biologic Therapy of Cancer. 2nd ed. DeVita VT Jr., Hellman S, Rosenberg SA, editors. Lippincott; Philadelphia, PA: 1995. pp. 521–533. [Google Scholar]
- 24.Sugimura T, Miwa M. Mol. Cell. Biochem. 1994;138:5–12. doi: 10.1007/BF00928437. [DOI] [PubMed] [Google Scholar]
- 25.Lee HC, Galione A, Walseth TF. Vitam. Horm. 1994;48:199–257. doi: 10.1016/s0083-6729(08)60499-9. [DOI] [PubMed] [Google Scholar]
- 26.See: Poirier GG, Moreau P, editors. ADP-ribosylation reactions. Springer-Verlag; New York: 1992.
- 27.Kandel J, Collier RJ, Chung DW. J. Biol. Chem. 1974;249:2088–2097. [PubMed] [Google Scholar]
- 28.Rising KA, Schramm VL. J. Am. Chem. Soc. 1997;119:27–37. [Google Scholar]
- 29.Scheuring J, Schramm VL. Biochemistry. 1997;36:4526–4534. doi: 10.1021/bi962841h. [DOI] [PubMed] [Google Scholar]
- 30.Berti PJ, Schramm VL. J. Am. Chem. Soc. 1997;119:12069–12078. doi: 10.1021/ja971317a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Rising KA, Schramm VL. J. Am. Chem. Soc. 1994;116:6531–6536. [Google Scholar]
- 32.Bennet AJ, Sinnott ML. J. Am. Chem. Soc. 1986;108:7287–7294. [Google Scholar]
- 33.Parkin DW, Horenstein BA, Abdulah DR, Estupinan B, Schramm VL. J. Biol. Chem. 1991;266:20658–20665. [PubMed] [Google Scholar]
- 34.In this substrate (only), one of the labels occurs in the adenosyl portion of the NAD+ molecule, 8-14C of the adenine ring. This is indicated by the subscripted “A” in the label, to distinguish it from the 5′-18O label in the nicotinamidyl portion, “N”.
- 35.Selwyn MJ. Biochim. Biophys. Acta. 1965;105:193–195. doi: 10.1016/s0926-6593(65)80190-4. [DOI] [PubMed] [Google Scholar]
- 36.Parkin DW. In: Enzyme mechanism from isotope effects. Cook PF, editor. CRC Press Inc.; Boca Raton, FL: 1991. pp. 269–290. [Google Scholar]
- 37.Gawlita E, Paneth P, Anderson VE. Biochemistry. 1995;34:6050–6058. doi: 10.1021/bi00018a007. [DOI] [PubMed] [Google Scholar]
- 38.Bahnson BJ, Anderson VE. Biochemistry. 1991;30:5894–5906. doi: 10.1021/bi00238a013. [DOI] [PubMed] [Google Scholar]
- 39.Bigeleisen J, Wolfsberg M. Adv. Chem. Phys. 1958;1:15–76. [Google Scholar]
- 40.Melander L, Saunders WH., Jr. Reaction rates of isotopic molecules. John Wiley & Sons; New York: 1980. p. 98. [Google Scholar]
- 41.Sims LB, Burton GW, Lewis DE. BEBOVIB-IV, QCPE No. 337. Quantum Chemistry Program Exchange, Department of Chemistry, University of Indiana; Bloomington, IN: 1977. [Google Scholar]
- 42.Becke AD. Phys. Rev. A. 1988;38:3098–3100. doi: 10.1103/physreva.38.3098. [DOI] [PubMed] [Google Scholar]
- 43.Perdew JP, Wang Y. Phys. Rev. B. 1992;45:13244. doi: 10.1103/physrevb.45.13244. [DOI] [PubMed] [Google Scholar]
- 44.Frisch MJ, Trucks GW, Schlegel HB, Gill PMW, Johnson BG, Robb MA, Cheeseman JR, Keith T, Petersson GA, Montgomery JA, Raghavachari K, Al-Laham MA, Zakrzewski VG, Ortiz JV, Foresman JB, Cioslowski J, Stefanov BB, Nanayakkara A, Challacombe M, Peng CY, Ayala PY, Chen W, Wong MW, Andres JL, Replogle ES, Gomperts R, Martin RL, Fox DJ, Binkley JS, Defrees DJ, Baker J, Stewart JP, Head-Gordon M, Gonzalez C, Pople JA. Gaussian 94, Revision C.2. Gaussian, Inc.; Pittsburgh, PA: 1995. [Google Scholar]
- 45.Cornell WD, Cieplak P, Bayly CI, Gould IR, Merz KM, Jr., Ferguson DM, Spellmeyer DC, Fox T, Caldwell JW, Kollman PA. J. Am. Chem. Soc. 1995;117:5179–5197. [Google Scholar]
- 46.Eyster JM, Prohofsky EW. Spectrochim. Acta. 1974;30A:2041–2046. [Google Scholar]
- 47.Saunders M, Laidig KE, Wolfsberg M. J. Am. Chem. Soc. 1989;111:8989–8994. [Google Scholar]
- 48.Blanke SR, Huang K, Collier RJ. Biochemistry. 1994;33:15494–15500. doi: 10.1021/bi00255a031. [DOI] [PubMed] [Google Scholar]
- 49.Rose IW. Methods Enzymol. 1980;64:47–59. doi: 10.1016/s0076-6879(80)64004-x. [DOI] [PubMed] [Google Scholar]
- 50.Guthrie RD, Jencks WP. Acc. Chem. Res. 1989;22:343–349. [Google Scholar]
- 51.Northrop DB. Annu. Rev. Biochem. 1981;50:103–131. doi: 10.1146/annurev.bi.50.070181.000535. [DOI] [PubMed] [Google Scholar]
- 52.Schramm VL. In: Enzyme mechanism from isotope effects. Cook PF, editor. CRC Press Inc.; Boca Raton, FL: 1991. pp. 367–388. [Google Scholar]
- 53.Kline PC, Schramm VL. Biochemistry. 1995;34:1153–1162. doi: 10.1021/bi00004a008. [DOI] [PubMed] [Google Scholar]
- 54.Kline PC, Schramm VL. Biochemistry. 1993;32:13212–13219. doi: 10.1021/bi00211a033. [DOI] [PubMed] [Google Scholar]
- 55.Horenstein BA, Parkin DW, Estupinan B, Schramm VL. Biochemistry. 1991;30:10788–10795. doi: 10.1021/bi00108a026. [DOI] [PubMed] [Google Scholar]
- 56.Mentch F, Parkin DW, Schramm VL. Biochemistry. 1987;26:921–930. doi: 10.1021/bi00377a037. [DOI] [PubMed] [Google Scholar]
- 57.Parkin DW, Schramm VL. Biochemistry. 1987;26:913–920. doi: 10.1021/bi00377a036. [DOI] [PubMed] [Google Scholar]
- 58.Parkin DW, Leung HB, Schramm VL. J. Biol. Chem. 1984;259:9411–9417. [PubMed] [Google Scholar]
- 59.Poirier RA, Wang Y, Westaway KC. J. Am. Chem. Soc. 1994;116:2526–2533. [Google Scholar]
- 60.Sunko DE, Szele I, Hehre WJ. J. Am. Chem. Soc. 1977;99:5000–5004. [Google Scholar]
- 61.Ashwell M, Guo X, Sinnott ML. J. Am. Chem. Soc. 1992;114:10158–10166. [Google Scholar]
- 62.Sinnott ML. Chem. Rev. 1990;90:1171–1202. [Google Scholar]
- 63.Padmaperuma B, Sinnott ML. Carbohydr. Res. 1993;250:79–86. doi: 10.1016/0008-6215(93)84156-z. [DOI] [PubMed] [Google Scholar]
- 64.Tull D, Withers SG. Biochemistry. 1994;33:6363–6370. doi: 10.1021/bi00186a041. [DOI] [PubMed] [Google Scholar]
- 65.Tanaka Y, Tao W, Blanchard JS, Hehre EJ. J. Biol. Chem. 1994;269:32306–32312. [PubMed] [Google Scholar]
- 66.Wang QP, Graham RW, Trimbur D, Warren RAJ, Withers SG. J. Am. Chem. Soc. 1994;116:11594–11595. [Google Scholar]
- 67.Braun C, Brayer GD, Withers SG. J. Biol. Chem. 1995;270:26778–26781. doi: 10.1074/jbc.270.45.26778. [DOI] [PubMed] [Google Scholar]
- 68.McIntosh LP, Hand G, Johnson PE, Joshi MD, Korner M, Plesniak LA, Ziser L, Wakarchuk WW, Withers SG. Biochemistry. 1996;35:9958–9966. doi: 10.1021/bi9613234. [DOI] [PubMed] [Google Scholar]
- 69.Sinnott ML, Jencks WP. J. Am. Chem. Soc. 1980;102:2026–2032. [Google Scholar]
- 70.Kneir BL, Jencks WP. J. Am. Chem. Soc. 1980;102:6789–6798. [Google Scholar]
- 71.Amyes TL, Jencks WP. J. Am. Chem. Soc. 1989;111:7888–7900. [Google Scholar]
- 72.Banait NS, Jencks WP. J. Am. Chem. Soc. 1991;113:7951–7958. [Google Scholar]
- 73.Banait NS, Jencks WP. J. Am. Chem. Soc. 1991;113:7958–7963. [Google Scholar]
- 74.Cherian XM, Van Arman SA, Czarnick AW. J. Am. Chem. Soc. 1990;112:4490–4498. [Google Scholar]
- 75.Huang X, Surry C, Hiebert T, Bennet AJ. J. Am. Chem. Soc. 1995;117:10614–10621. [Google Scholar]
- 76.Westaway KC. Tetrahedron Lett. 1975;48:4229–4232. [Google Scholar]
- 77.Johnson RW, Marschner TM, Oppenheimer NJ. J. Am. Chem. Soc. 1988;110:2257–2263. [Google Scholar]
- 78.Choe S, Bennett MJ, Fujii G, Curmi PM, Kantardjieff KA, Collier RJ, Eisenberg D. Nature. 1992;357:216–222. doi: 10.1038/357216a0. [DOI] [PubMed] [Google Scholar]
- 79.Bell CE, Eisenberg D. Biochemistry. 1996;35:1137–1149. doi: 10.1021/bi9520848. [DOI] [PubMed] [Google Scholar]
- 80.Bell CE, Eisenberg D. Biochemistry. 1997;36:481–488. doi: 10.1021/bi962214s. [DOI] [PubMed] [Google Scholar]
- 81.Oppenheimer NJ, Bodley JW. J. Biol. Chem. 1981;256:8579–8581. [PubMed] [Google Scholar]
- 82.Carroll SF, McCloskey JA, Crain PF, Oppenheimer NJ, Marschner TM, Collier RJ. Proc. Natl. Acad. Sci. U.S.A. 1985;82:7237–7241. doi: 10.1073/pnas.82.21.7237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Wilson BA, Reich KA, Weinstein BR, Collier RJ. Biochemistry. 1990;29:8643–8651. doi: 10.1021/bi00489a021. [DOI] [PubMed] [Google Scholar]
- 84.Desiraju GR. Acc. Chem. Res. 1996;29:441–449. doi: 10.1021/ar950135n. [DOI] [PubMed] [Google Scholar]
- 85.Desiraju GR. Acc. Chem. Res. 1991;24:290–296. [Google Scholar]
- 86.Horenstein BA, Schramm VL. Biochemistry. 1993;32:7089–7097. doi: 10.1021/bi00079a004. [DOI] [PubMed] [Google Scholar]
- 87.Horenstein BA, Zabinski RF, Schramm VL. Tetrahedron Lett. 1993;34:7213–7216. [Google Scholar]
- 88.Horenstein BA, Schramm VL. Biochemistry. 1993;32:9917–9925. doi: 10.1021/bi00089a007. [DOI] [PubMed] [Google Scholar]
- 89.Sims LB, Lewis DE. In: Isotope effects: Recent developments in theory and experiment. Buncel E, Lee CC, editors. Vol. 6. Elsevier; New York: 1984. pp. 161–259. [Google Scholar]
- 90.Reed AE, Curtiss LA, Weinhold F. Chem. Rev. 1988;88:899–926. [Google Scholar]
- 91.Connolly ML. Science. 1983;221:709–713. doi: 10.1126/science.6879170. [DOI] [PubMed] [Google Scholar]
- 92.Kabsch W, Sander C. Biopolymers. 1983;22:2577–2637. doi: 10.1002/bip.360221211. [DOI] [PubMed] [Google Scholar]