Abstract
Biopolymers exhibit rough energy landscapes, thereby allowing biological processes to access a broad range of kinetic and thermodynamic states. In contrast to proteins, the energy landscapes of nucleic acids have been the subject of relatively few experimental investigations. In this study, we use calorimetric and spectroscopic observables to detect, resolve, and selectively enrich energetically discrete ensembles of microstates within metastable DNA structures. Our results are consistent with metastable, “native” DNA states being composed of an ensemble of discrete and kinetically stable microstates of differential stabilities, rather than exclusively being a single, discrete thermodynamic species. This conceptual construct is important for understanding the linkage between biopolymer conformational/configurational space and biological function, such as in protein folding, allosteric control of enzyme activity, RNA and DNA folding and function, DNA structure and biological regulation, etc. For the specific DNA sequences and structures studied here, the demonstration of discrete, kinetically stable microstates potentially has biological consequences for understanding the development and onset of DNA expansion and triplet repeat diseases.
Keywords: calorimetry, nucleic acid conformations
The concept of rough biopolymer energy landscapes is important for understanding biopolymer properties and function. Complex landscapes allow partial population of discrete, kinetically stable (metastable) species (1–12). These substates, in turn, may serve as biologically significant ligands, beyond the traditional, thermodynamically most stable, time-averaged, “native” macrostrate. Although it is well recognized that macroscopic states are composed of microscopic substates, it has been customary for experimentalists to think of a biologically relevant native state as a singular macrostate with a unique, well defined structure characterized by a homogeneous/smooth energy profile. Many biophysical measurements probe properties that are averaged over the ensemble of microstates that collectively correspond to a macroscopic native state. However, experimental evidence for the presence of, and dynamic interchange between, multiple states that constitute a global macrostate is provided by direct time-resolved measurements, and by structural dispersions in crystallographic and NMR studies (13–22). Such results underscore the potential importance as ligands or receptors in biological mechanisms of kinetically stable, trapped microstates embedded within the rough energy landscapes of purportedly singular macrostates. For example, the detection of transiently populated structural states in the native unbound protein ensemble that resemble those of the proteins in their bound state provides evidence for the so-called “conformational selection model” of protein binding, thereby suggesting significant biological functions for microstates in proteins (23–26).
By contrast with proteins, relatively few studies have probed the energy landscapes of nucleic acids, particularly via calorimetric techniques (27–35). As a result, the potential energetic/biological role(s), if any, of kinetically stable (metastable) microstates that make up the time-averaged, native state ensembles of macroscopic nucleic acid states remains to be determined.
As part of an effort to address this deficiency, we report here experimental evidence for the presence of discrete microstates in metastable triplet repeat bulge looped Ω-DNAs of potential biological significance. The specific triplet repeat bulge looped Ω-DNA species investigated mimic slipped DNA structures corresponding to intermediates in the processes that lead to DNA expansion in triplet repeat diseases (36). Incorrect processing by the cellular replication and repair machinery of such transiently formed slipped structures, in their macro and/or microstate ensembles, is believed to cause DNA expansion, the genotype that ultimately leads to the phenotype associated with DNA expansion diseases (37–50). The presence of discrete and kinetically stable microstates within the ensemble of the triplet repeat macrostate is therefore of potential significance for understanding the biology of triplet repeat diseases.
Results and Discussion
We have shown that the 2 complementary (CAG)6 and (CTG)6 triplet repeat bulge looped Ω-DNAs diagrammed in Fig. 1A do not spontaneously rearrange to their thermodynamically more stable duplex states when combined in solution, but rather remain trapped in their metastable looped structures (36).
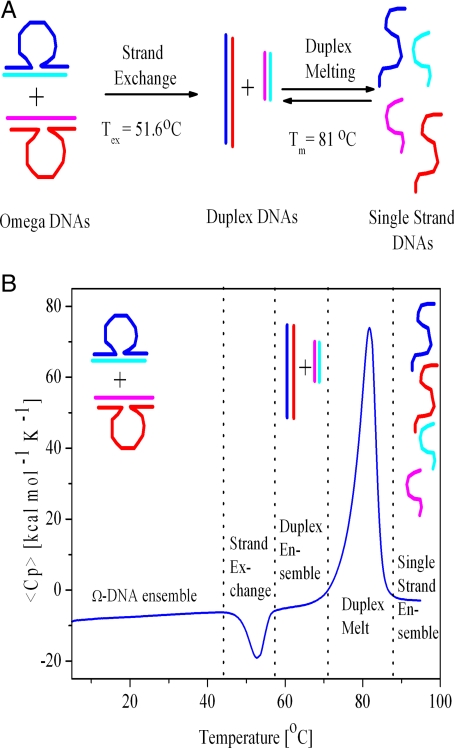
Fig. 1.
Interconversions of DNA states. (A) Schematic representation of the different DNA conformations and the transformations between them. (B) Calorimetric excess heat capacity curve for the first DSC heating scan of a 1:1 mixture of 2 complementary, triplet-repeat bulge looped Ω-DNAs. The dotted vertical lines delimit the thermal domains in which particular DNA conformations are selectively populated and the thermal regions in which conformational transformations are observed. The relevant DNA states are shown in diagram form. Note the unusual exothermic peak ≈50 °C, which is reflective of strand exchange between the 2 Ω-DNAs to form the 2 fully paired duplex states.
Strand exchange to the duplex state requires input of energy, occurring only at elevated temperatures. At the so-called exchange temperature, Tex, the strand exchange reaction proceeds irreversibly, with a release of heat energy. We detect this strand exchange between the 2 metastable bulge looped Ω-DNAs to form the 2 fully paired duplex states by monitoring the unusual exothermic peak in the DSC curves that, as expected for an irreversible process, is absent in the second heating scan (Fig. 1B).
These observations are consistent with the energy landscape of these looped, repeat sequences containing local minima (here the Ω-DNA structures), in addition to the global Watson and Crick duplex minima. Such metastable states may well present processing problems for the machinery of replication and repair. Further heating of the system results in conventional duplex melting, fully consistent with expectation.
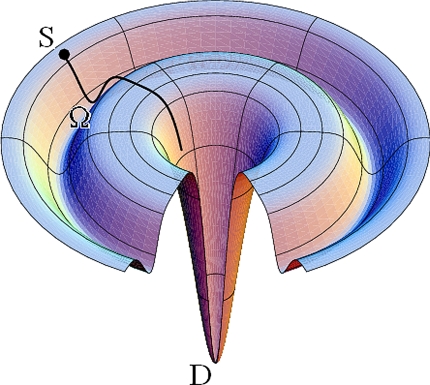
The landscape for these transformations is depicted in the energy funnel shown in Fig. 2. The arrow in this figure tracks the transformations noted above; namely, from the ensemble of high energy single strands (corresponding to the upper outer rim of the funnel), to the initial valley, which corresponds to the ensemble of metastable Ω-DNA structures (kinetically protected by a significant energy barrier), to the deep global minima associated with the ensemble of thermodynamically most stable duplex states.
Fig. 2.
Idealized representation of an energy landscape, showing features related to the triplet repeat DNA conformations investigated here (4). For clarity of presentation and ease of interpretation, the energy wells and the idealized trajectories between them are shown as smooth surfaces. The experimental data reported here, however, reveal that these surfaces are not smooth. The specific trajectory by which the DNA strands combine/fold and the shape of the folding landscape will depend on the temperature. At temperatures above exchange (landscape not shown), the barrier between the local Ω-DNA minimum, and the global duplex minimum would be diminished such that the Ω-DNA state no longer would be populated. [Reproduced with permission from ref. 4 (Copyright 1998, Wiley, New York).]
To further map the energy landscape of the metastable DNA molecules, we conducted a series of thermal incubations below the exchange temperature. Through such measurements we have been able to resolve populations of microstates of differential energetics that comprise the metastable Ω-DNA macrostate, consistent with a rough energy landscape (micro hills and valleys) within the upper “macro valley” representing the metastable Ω-DNA macrostate in Fig. 2. For each measurement needed to detect and energetically resolve this microstate fine structure, we incubated for an hour an equimolar mixture of the complementary CAG and CTG metastable Ω-DNAs at a series of temperatures below the exchange temperature, followed by cooling the sample down and rescanning. Because strand exchange between the 2 Ω-DNAs is irreversible, any exotherm detected in the postincubation second scan reflects the unreacted/unexchanged fractions of the original 2 Ω-DNAs. The results obtained here for different incubation temperatures are shown in Figs. 3A and 3B and are described below.
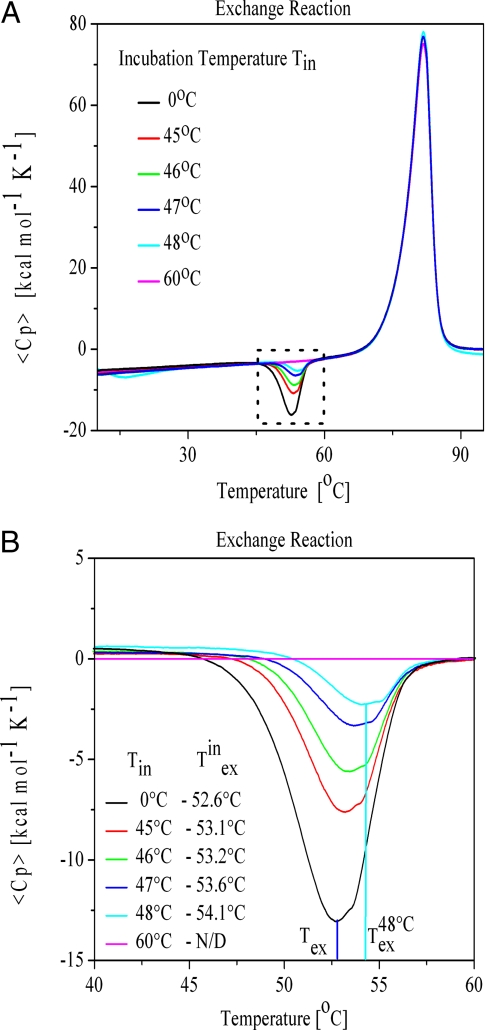
Fig. 3.
Incubation induced redistribution of DNA states. (A) Superposition of experimental excess heat capacity curves for a 1:1 mixture of the complementary, triplet repeat bulge looped Ω-DNAs after 1 h of preincubation at different temperatures. Incubation temperatures (Tin) are indicated in the figure. Note the differences in excess heat capacity curves in the temperature range where we observe the exothermic peak near 50 °C. Similar differences in the excess heat capacity curves are not observed at other temperatures. (B) Expanded view of the exothermic peak shown in Fig. 3A that highlights the incubation induced shift to higher temperatures of the exchange peak. The incubation temperatures (Tin) and the measured exchange temperature (Texin) are indicated in the figure.
We find that when the sample is incubated at temperatures well below the onset of the exchange reaction, the Ω-DNAs do not undergo strand exchange during the incubation period, as evidenced by the presence of the full exothermic peak in the DSC rescan curve (the black curve in Fig. 3A). Conversely, when the sample is incubated at temperatures above the exchange temperature, all of the Ω-DNA molecules undergo strand exchange, as evidenced by no signal being observed for residual, unreacted Ω-DNAs in the DSC rescan (the magenta curve in Fig. 3A). However, when the samples are incubated at a temperature close to the onset of the exchange exotherm, some residual fraction of the original exchange exotherm is detected upon rescan after cooling; evidence for some, but not all, of the Ω-DNA metastable state undergoing conversion to the more stable duplex state during incubation (the red, green, blue, and cyan curves in Fig. 3A) The fraction of the remaining Ω-DNA detected by the DSC exotherm scales with the incubation temperature, consistent with slow strand exchange kinetics, even close to the exchange temperature.
Most intriguing is that we observe shifts to higher exchange temperatures in the rescan of the incubated samples relative to the exchange temperatures of the exotherm in the initial scan of samples that were not preincubated (Fig. 3B). We propose that this increase in the exchange temperature for the residual/unexchanged Ω-DNA reflects the selective removal via strand exchange during preincubation of the low stability/high energy subfraction of the Ω-DNAs, thereby leaving the high stability/low energy substates unchanged. Our data are consistent with these low stability/high energy, unexchanged Ω- substates not being repopulated during the time course of our experiments. The lack of redistribution between the different microstates and the slow exchange kinetics at temperatures close to the exchange temperature may reflect energetically costly unfolding of a part of the loop domain before refolding to a new configuration or before strand exchange is possible (51, 52).
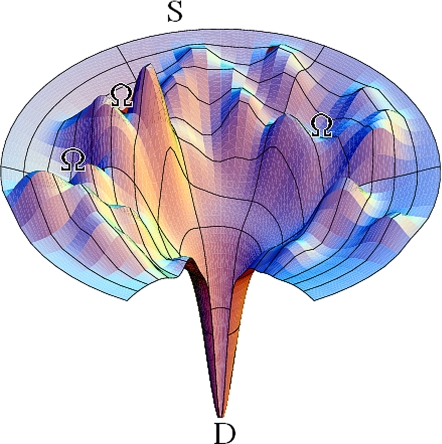
Collectively, our results suggest that preincubation leads to a selective enrichment of the high stability/low energy subpopulations of the microstate ensembles that constitute the macroscopic, metastable Ω-DNA states. We have made similar observations, using UV melting experiments (data not shown). In this case, our data show that a triplet repeat Ω-DNA metastable macrostate is populated by energetically discrete microstates separated by significant energy barriers. This conclusion means that the apparently smooth upper valley depicted in Fig. 2 for the metastable Ω-DNA states actually is quite rough, being itself composed of micro hills and valleys that constitute the ensemble of states corresponding to the 2 metastable Ω-DNA macrostates as indicated in Fig. 4.
Fig. 4.
Idealized representation of an energy landscape showing the micro hills and valleys that constitute the rough energy landscape of the metastable triplet repeat Ω-DNA macrostates investigated here (4). [Reproduced with permission from ref. 4 (Copyright 1998, Wiley, New York).]
For the CAG and CTG triple repeat bulge loop DNAs studied here, the presence of discrete microstates with significant energy barriers between them may contribute to the propensity of triplet DNA sequences to undergo DNA expansion. It has been suggested that DNA expansion is a consequence of challenges to the DNA replication and repair machinery, which has been optimized by evolution for dealing with duplex DNA, and therefore has difficulty processing bulge loop substrates (37–50, 53, 54). Our results suggest that in addition to an unusual metastable macrostate, the machinery of replication and repair also may need to recognize and process an ensemble of complex energetic and perhaps structural substates. Incorrect recognition, binding, and/or processing of some or all of these substates may challenge the DNA replication and repair machinery in a manner that facilitates expansion of the triplet repeat sequences. More generally, our results reveal the existence of a rough energy landscape for a metastable macrostate that is composed of an ensemble of energetically discrete microstates. This conclusion is also supported by strategically placed lesions within the Ω-DNA structure that modulate the distribution of microstates, while retaining the metastable macrostate (unpublished data).
In summary, we have shown via calorimetric measurements that the energy landscape of nucleic acids can be rough, and that some nucleic acid states, like those of proteins, can be composed of discrete microstates. It can be envisioned that discrete substates within the native state ensemble play important roles in the biology of other non-B-DNA secondary structures, such as G-quadruplexes (55–57), iDNAs (58–61), cruciforms (62–64), and triple helical H-DNA like structures (65–70), inter alia (41, 67, 71–76). Given the diverse range of secondary structural elements and highly folded 3 dimensional structures common to many biologically important macromolecules, the realization of rough energy landscapes and discrete microstates for nucleic acids should prove important for understanding the broad range of mechanisms that modulate nucleic acid biology.
Materials and Methods
Materials.
Oligonucleotides were synthesized on a 10 μmole scale by standard phosphoramidite chemistry, using an Äkta DNA synthesizer, and were purified by repeated DMT on/DMT off reverse phase HPLC, as described in refs. 52 and 61. The purities of the oligonucleotides were assessed by analytical HPLC and ion spray mass spectroscopy, and were found to be better than 98% by mass spectroscopy. Purified oligonucleotides were dialyzed against at least 2 changes of buffer containing NaCl, 10 mM Cacodylic acid/Na-Cacodylate, and 0.1 mM Na2 EDTA to yield a final concentration of 100 mM in Na+ cations, using dispo-dialyzers with MWCO 500 da (Spectrum). DNA extinction coefficients were determined by phosphate assay (77, 78) under denaturing conditions (90 °C) and were found to be: εX(CAG)6Y (260 nm, 90 °C) = 368,400 M−1·cm−1; εY′ (CTG)6X′ (260 nm, 90 °C) = 342,900 M−1·cm−1; εXY (260 nm, 90 °C) = 190,400 M−1·cm−1; εY′X′ (260 nm, 90 °C) = 186,200 M−1·cm−1.
DSC Studies.
DSC studies were conducted using a NanoDSCII differential scanning calorimeter (Calorimetry Science) with a nominal cell volume of 0.3 mL (79). Just before filling the DSC cell, equimolar concentrations of preformed complementary Ω-DNA oligonucleotides were combined to yield a final concentration 50 μM in strand. The sample was scanned once from 0 °C to the relevant incubation temperature at a rate of 1 °C/min, and then incubated at the incubation temperature for 1 h, followed by cooling back to 0 °C. The power needed to maintain sample and reference cells at constant temperature during incubation exhibited a complex multiexponential time dependence with a non-Arrhenius dependence on incubation temperature. After incubation, the sample was scanned at least twice from 0 °C to 100 °C at a constant heating rate of 1 °C/min, while recording the excess power required to keep sample cell and reference cells at the same temperature. After conversion to heat capacity units and subtractions of buffer/buffer scans, the raw DSC traces were normalized for DNA concentration and analyzed using Origin software.
UV Melting Studies.
UV absorption versus temperature studies were conducted using a Aviv DS14 UV/VIS spectrophotometer (Aviv Biomedical). Samples in 1-cm cells were heated from 0 °C to the incubation temperature in steps of 0.5 °C, and allowed to incubate for 1 h. Samples where than cooled back to 0 °C and heated in a second heating scan from 0 °C to 95 °C in steps of 0.5 °C. Upon reaching each set temperature, samples were equilibrated for 1 min before recording the absorption at 260 nm, with a 5-sec averaging time, resulting in a nominal heating rate of 0.1 °C/min. Oligonucleotide strand concentration was 1.5 μM.
UV Mixing Studies.
UV absorption versus time studies were conducted using a Varian 4000 UV/Vis spectrophotometer (Varian), equipped with a peltier controlled multicell cell holder. Complementary Ω-DNA samples were placed in separate compartments of a partitioned UV cuvette (path length 1 cm) and allowed to equilibrate at the relevant incubation temperature for a minimum of 10 min. After temperature equilibration, samples were rapidly mixed and the change in absorbance with time was recorded every second for 5 h. The UV absorption versus time profiles showed a complex multiexponential decay with non-Arrhenius temperature dependence, and an overall hypochromic change that depended on incubation temperature.
Acknowledgments.
We thank Drs. Roger Jones, Barbara Gaffney (Rutgers University), and G. Eric Plum (Rutgers University and IBET, Inc.) for advice and many helpful discussions. This work was supported by National Institutes of Health Grants GM23509, GM34469, and CA47995 (to K.J.B.)
Footnotes
The authors declare no conflict of interest.
References
- 1.Frauenfelder H, Sligar SG, Wolynes PG. The energy landscapes and motions of proteins. Science. 1991;254:1598–1603. doi: 10.1126/science.1749933. [DOI] [PubMed] [Google Scholar]
- 2.Frauenfelder H, McMahon B. Dynamics and function of proteins: The search for general concepts. Proc Natl Acad Sci USA. 1998;95:4795–4797. doi: 10.1073/pnas.95.9.4795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Frauenfelder H, Leeson DT. The energy landscape in non-biological and biological molecules. Nat Struct Biol. 1998;5:757–759. doi: 10.1038/1784. [DOI] [PubMed] [Google Scholar]
- 4.Chan HS, Dill KA. Protein folding in the landscape perspective: Chevron plots and non-Arrhenius kinetics. Proteins Struct Funct Genet. 1998;30:2–33. doi: 10.1002/(sici)1097-0134(19980101)30:1<2::aid-prot2>3.0.co;2-r. [DOI] [PubMed] [Google Scholar]
- 5.Bryngelson JD, Onuchic JN, Socci ND, Wolynes PG. Funnels, pathways, and the energy landscape of protein folding: A synthesis. Proteins. 1995;21:167–195. doi: 10.1002/prot.340210302. [DOI] [PubMed] [Google Scholar]
- 6.Wolynes PG, Onuchic JN, Thirumalai D. Navigating the folding routes. Science. 1995;267:1619–1620. doi: 10.1126/science.7886447. [DOI] [PubMed] [Google Scholar]
- 7.Onuchic JN, Luthey-Schulten Z, Wolynes PG. Theory of protein folding: The energy landscape perspective. Annu Rev Phys Chem. 1997;48:545–600. doi: 10.1146/annurev.physchem.48.1.545. [DOI] [PubMed] [Google Scholar]
- 8.Socci ND, Onuchic JN, Wolynes PG. Protein folding mechanisms and the multidimensional folding funnel. Proteins. 1998;32:136–158. [PubMed] [Google Scholar]
- 9.Onuchic JN, Wolynes PG. Theory of protein folding. Curr Opin Struct Biol. 2004;14:70–75. doi: 10.1016/j.sbi.2004.01.009. [DOI] [PubMed] [Google Scholar]
- 10.Wolynes PG. Recent successes of the energy landscape theory of protein folding and function. Q Rev Biophys. 2005;38:405–410. doi: 10.1017/S0033583505004075. [DOI] [PubMed] [Google Scholar]
- 11.Brooks CL, III, Onuchic JN, Wales DJ. Statistical thermodynamics. Taking a walk on a landscape. Science. 2001;293:612–613. doi: 10.1126/science.1062559. [DOI] [PubMed] [Google Scholar]
- 12.Lazaridis T, Karplus M. “New view” of protein folding reconciled with the old through multiple unfolding simulations. Science. 1997;278:1928–1931. doi: 10.1126/science.278.5345.1928. [DOI] [PubMed] [Google Scholar]
- 13.Faber HR, Matthews BW. A mutant T4 lysozyme displays five different crystal conformations. Nature. 1990;348:263–266. doi: 10.1038/348263a0. [DOI] [PubMed] [Google Scholar]
- 14.Boehr DD, Dyson HJ, Wright PE. An NMR perspective on enzyme dynamics. Chem Rev. 2006;106:3055–3079. doi: 10.1021/cr050312q. [DOI] [PubMed] [Google Scholar]
- 15.Palmer AG., 3rd Nmr probes of molecular dynamics: Overview and comparison with other techniques. Annu Rev Biophys Biomol Struct. 2001;30:129–155. doi: 10.1146/annurev.biophys.30.1.129. [DOI] [PubMed] [Google Scholar]
- 16.Moffat K. Time-resolved biochemical crystallography: A mechanistic perspective. Chem Rev. 2001;101:1569–1582. doi: 10.1021/cr990039q. [DOI] [PubMed] [Google Scholar]
- 17.Doniach S. Changes in biomolecular conformation seen by small angle X-ray scattering. Chem Rev. 2001;101:1763–1778. doi: 10.1021/cr990071k. [DOI] [PubMed] [Google Scholar]
- 18.Petsko GA, Ringe D. Fluctuations in protein structure from X-ray diffraction. Annu Rev Biophys Bioeng. 1984;13:331–371. doi: 10.1146/annurev.bb.13.060184.001555. [DOI] [PubMed] [Google Scholar]
- 19.Borgia A, Williams PM, Clarke J. Single-molecule studies of protein folding. Annu Rev Biochem. 2008;77:101–125. doi: 10.1146/annurev.biochem.77.060706.093102. [DOI] [PubMed] [Google Scholar]
- 20.Roder H, Maki K, Cheng H. Early events in protein folding explored by rapid mixing methods. Chem Rev. 2006;106:1836–1861. doi: 10.1021/cr040430y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Plaxco KW, Dobson CM. Time-resolved biophysical methods in the study of protein folding. Curr Opin Struct Biol. 1996;6:630–636. doi: 10.1016/s0959-440x(96)80029-7. [DOI] [PubMed] [Google Scholar]
- 22.Schuler B, Eaton WA. Protein folding studied by single-molecule FRET. Curr Opin Struct Biol. 2008;18:16–26. doi: 10.1016/j.sbi.2007.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Gsponer J, et al. A coupled equilibrium shift mechanism in calmodulin-mediated signal transduction. Structure. 2008;16:736–746. doi: 10.1016/j.str.2008.02.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Lange OF, et al. Recognition dynamics up to microseconds revealed from an RDC-derived ubiquitin ensemble in solution. Science. 2008;320:1471–1475. doi: 10.1126/science.1157092. [DOI] [PubMed] [Google Scholar]
- 25.Boehr DD, Wright PE. Biochemistry. How do proteins interact? Science. 2008;320:1429–1430. doi: 10.1126/science.1158818. [DOI] [PubMed] [Google Scholar]
- 26.Okazaki K.-i., Takada S. Dynamic energy landscape view of coupled binding and protein conformational change: Induced-fit versus population-shift mechanisms. Proc Natl Acad Sci USA. 2008;105:11182–11187. doi: 10.1073/pnas.0802524105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Woodside MT, et al. Direct measurement of the full, sequence-dependent folding landscape of a nucleic acid. Science. 2006;314:1001–1004. doi: 10.1126/science.1133601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lin MM, Meinhold L, Shorokhov D, Zewail AH. Unfolding and melting of DNA (RNA) hairpins: The concept of structure-specific 2D dynamic landscapes. Phys Chem Chem Phys. 2008;10:4227–4239. doi: 10.1039/b804675c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ma H, Wan C, Wu A, Zewail AH. DNA folding and melting observed in real time redefine the energy landscape. Proc Natl Acad Sci USA. 2007;104:712–716. doi: 10.1073/pnas.0610028104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ansari A, Kuznetsov SV, Shen Y. Configurational diffusion down a folding funnel describes the dynamics of DNA hairpins. Proc Natl Acad Sci USA. 2001;98:7771–7776. doi: 10.1073/pnas.131477798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Ansari A, Shen Y, Kuznetsov SV. Misfolded loops decrease the effective rate of DNA hairpin formation. Phys Rev Lett. 2002;88 doi: 10.1103/PhysRevLett.88.069801. 069801. [DOI] [PubMed] [Google Scholar]
- 32.Hyeon C, Thirumalai D. Multiple probes are required to explore and control the rugged energy landscape of RNA hairpins. J Am Chem Soc. 2008;130:1538–1539. doi: 10.1021/ja0771641. [DOI] [PubMed] [Google Scholar]
- 33.Hyeon C, Thirumalai D. Can energy landscape roughness of proteins and RNA be measured by using mechanical unfolding experiments? Proc Natl Acad Sci USA. 2003;100:10249–10253. doi: 10.1073/pnas.1833310100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Thirumalai D, Hyeon C. RNA and protein folding: Common themes and variations. Biochemistry. 2005;44:4957–4970. doi: 10.1021/bi047314+. [DOI] [PubMed] [Google Scholar]
- 35.Li PT, Bustamante C, Tinoco I., Jr Real-time control of the energy landscape by force directs the folding of RNA molecules. Proc Natl Acad Sci USA. 2007;104:7039–7044. doi: 10.1073/pnas.0702137104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Volker J, Klump HH, Breslauer KJ. DNA metastability and biological regulation: Conformational dynamics of metastable omega-DNA bulge loops. J Am Chem Soc. 2007;129:5272–5280. doi: 10.1021/ja070258q. [DOI] [PubMed] [Google Scholar]
- 37.Bowater RP, Wells RD. The intrinsically unstable life of DNA triplet repeats associated with human hereditary disorders. Prog Nucleic Acid Res Mol Biol. 2001;66:159–202. doi: 10.1016/s0079-6603(00)66029-4. [DOI] [PubMed] [Google Scholar]
- 38.Sinden RR. Neurodegenerative diseases: Origins of instability. Nature. 2001;411:757–758. doi: 10.1038/35081234. [DOI] [PubMed] [Google Scholar]
- 39.Sinden RR, et al. Triplet repeat DNA structures and human genetic disease: Dynamic mutations from dynamic DNA. J Biosci. 2002;27:53–65. doi: 10.1007/BF02703683. [DOI] [PubMed] [Google Scholar]
- 40.Cleary JD, Pearson CE. Replication fork dynamics and dynamic mutations: The fork-shift model of repeat instability. Trends Genet. 2005;21:272–280. doi: 10.1016/j.tig.2005.03.008. [DOI] [PubMed] [Google Scholar]
- 41.Wells RD, Dere R, Hebert ML, Napierala M, Son LS. Advances in mechanisms of genetic instability related to hereditary neurological diseases. Nucl Acids Res. 2005;33:3785–3798. doi: 10.1093/nar/gki697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Mirkin EV, Mirkin SM. Replication fork stalling at natural impediments. Microbiol Mol Biol Rev. 2007;71:13–35. doi: 10.1128/MMBR.00030-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Mirkin SM. Expandable DNA repeats and human disease. Nature. 2007;447:932–940. doi: 10.1038/nature05977. [DOI] [PubMed] [Google Scholar]
- 44.Lenzmeier BA, Freudenreich CH. Trinucleotide repeat instability: A hairpin curve at the crossroads of replication, recombination, and repair. Cytogenet Genome Res. 2003;100:7–24. doi: 10.1159/000072836. [DOI] [PubMed] [Google Scholar]
- 45.Mirkin SM. Toward a unified theory for repeat expansions. Nat Struct Mol Biol. 2005;12:635–637. doi: 10.1038/nsmb0805-635. [DOI] [PubMed] [Google Scholar]
- 46.McMurray CT. DNA secondary structure: A common and causative factor for expansion in human disease. Proc Natl Acad Sci USA. 1999;96:1823–1825. doi: 10.1073/pnas.96.5.1823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Panigrahi GB, Lau R, Montgomery SE, Leonard MR, Pearson CE. Slipped (CTG)*(CAG) repeats can be correctly repaired, escape repair or undergo error-prone repair. Nat Struct Mol Biol. 2005;12:654–662. doi: 10.1038/nsmb959. [DOI] [PubMed] [Google Scholar]
- 48.Pearson CE, Edamura KN, Cleary JD. Repeat instability: Mechanisms of dynamic mutations. Nat Rev Genet. 2005;6:729–742. doi: 10.1038/nrg1689. [DOI] [PubMed] [Google Scholar]
- 49.Kovtun IV, Goellner G, McMurray CT. Structural features of trinucleotide repeats associated with DNA expansion. Biochem Cell Biol. 2001;79:325–336. [PubMed] [Google Scholar]
- 50.Kovtun IV, McMurray CT. Features of trinucleotide repeat instability in vivo. Cell Res. 2008;18:198–213. doi: 10.1038/cr.2008.5. [DOI] [PubMed] [Google Scholar]
- 51.Lee BJ, Barch M, Castner EW, Jr, Volker J, Breslauer KJ. Structure and dynamics in DNA looped domains: CAG triplet repeat sequence dynamics probed by 2-aminopurine fluorescence. Biochemistry. 2007;46:10756–10766. doi: 10.1021/bi7005674. [DOI] [PubMed] [Google Scholar]
- 52.Volker J, Makube N, Plum GE, Klump HH, Breslauer KJ. Conformational energetics of stable and metastable states formed by DNA triplet repeat oligonucleotides: Implications for triplet expansion diseases. Proc Natl Acad Sci USA. 2002;99:14700–14705. doi: 10.1073/pnas.222519799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Richards RI. Dynamic mutations: A decade of unstable expanded repeats in human genetic disease. Hum Mol Genet. 2001;10:2187–2194. doi: 10.1093/hmg/10.20.2187. [DOI] [PubMed] [Google Scholar]
- 54.Richards RI. Fragile and unstable chromosomes in cancer: Causes and consequences. Trends Genet. 2001;17:339–345. doi: 10.1016/s0168-9525(01)02303-4. [DOI] [PubMed] [Google Scholar]
- 55.Bates P, Mergny JL, Yang D. Quartets in G-major. The First International Meeting on Quadruplex DNA. EMBO Rep. 2007;8:1003–1010. doi: 10.1038/sj.embor.7401073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Huppert JL. Four-stranded DNA: Cancer, gene regulation and drug development. Philos Trans R Soc London Ser A. 2007;365:2969–2984. doi: 10.1098/rsta.2007.0011. [DOI] [PubMed] [Google Scholar]
- 57.Lane AN, Chaires JB, Gray RD, Trent JO. Stability and kinetics of G-quadruplex structures. Nucleic Acids Res. 2008;36:5482–5515. doi: 10.1093/nar/gkn517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Gueron M, Leroy JL. The i-motif in nucleic acids. Curr Opin Struct Biol. 2000;10:326–331. doi: 10.1016/s0959-440x(00)00091-9. [DOI] [PubMed] [Google Scholar]
- 59.Gehring K, Leroy JL, Gueron M. A tetrameric DNA structure with protonated cytosine. cytosine base pairs. Nature. 1993;363:561–565. doi: 10.1038/363561a0. [DOI] [PubMed] [Google Scholar]
- 60.Volker J, Klump HH, Breslauer KJ. The energetics of i-DNA tetraplex structures formed intermolecularly by d(TC5) and intramolecularly by d[(C5T3)3C5] Biopolymers. 2007;86:136–147. doi: 10.1002/bip.20712. [DOI] [PubMed] [Google Scholar]
- 61.Volker J, Klump HH, Breslauer KJ. Communication between noncontacting macromolecules. Proc Natl Acad Sci USA. 2001;98:7694–7699. doi: 10.1073/pnas.141221298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Lilley DM, Clegg RM. The structure of branched DNA species. Q Rev Biophys. 1993;26:131–175. doi: 10.1017/s0033583500004054. [DOI] [PubMed] [Google Scholar]
- 63.Seeman NC, Kallenbach NR. DNA branched junctions. Annu Rev Biophys Biomol Struct. 1994;23:53–86. doi: 10.1146/annurev.bb.23.060194.000413. [DOI] [PubMed] [Google Scholar]
- 64.Timsit Y, Moras D. Cruciform structures and functions. Q Rev Biophys. 1996;29:279–307. doi: 10.1017/s0033583500005862. [DOI] [PubMed] [Google Scholar]
- 65.Frank-Kamenetskii MD, Mirkin SM. Triplex DNA structures. Annu Rev Biochem. 1995;64:65–95. doi: 10.1146/annurev.bi.64.070195.000433. [DOI] [PubMed] [Google Scholar]
- 66.Mirkin SM, Frank-Kamenetskii MD. H-DNA and related structures. Annu Rev Biophys Biomol Struct. 1994;23:541–576. doi: 10.1146/annurev.bb.23.060194.002545. [DOI] [PubMed] [Google Scholar]
- 67.Wang G, Vasquez KM. Non-B DNA structure-induced genetic instability. Mutat Res. 2006;598:103–119. doi: 10.1016/j.mrfmmm.2006.01.019. [DOI] [PubMed] [Google Scholar]
- 68.Jain A, Wang G, Vasquez KM. DNA triple helices: Biological consequences and therapeutic potential. Biochimie. 2008;90:1117–1130. doi: 10.1016/j.biochi.2008.02.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Pilch DS, Plum GE, Breslauer KJ. The thermodynamics of DNA structures that contain lesions or guanine tetrads. Curr Opin Struct Biol. 1995;5:334–342. doi: 10.1016/0959-440x(95)80095-6. [DOI] [PubMed] [Google Scholar]
- 70.Plum GE, Pilch DS, Singleton SF, Breslauer KJ. Nucleic acid hybridization: Triplex stability and energetics. Annu Rev Biophys Biomol Struct. 1995;24:319–350. doi: 10.1146/annurev.bb.24.060195.001535. [DOI] [PubMed] [Google Scholar]
- 71.Phan AT, Kuryavyi V, Patel DJ. DNA architecture: From G to Z. Curr Opin Struct Biol. 2006;16:288–298. doi: 10.1016/j.sbi.2006.05.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Wells RD. Non-B DNA conformations, mutagenesis and disease. Trends Biochem Sci. 2007;32:271–278. doi: 10.1016/j.tibs.2007.04.003. [DOI] [PubMed] [Google Scholar]
- 73.Pennisi E. Genetics: DNA's molecular gymnastics. Science. 2006;312:1467–1468. doi: 10.1126/science.312.5779.1467. [DOI] [PubMed] [Google Scholar]
- 74.Wells RD, Harvey SC. Unusual DNA Structures: Proceedings of the First Gulf Shores Symposium, Held at Gulf Shores State Park Resort; April 6-8, 1987; New York: Springer; 1988. [Google Scholar]
- 75.Bacolla A, Wojciechowska M, Kosmider B, Larson JE, Wells RD. The involvement of non-B DNA structures in gross chromosomal rearrangements. DNA Repair (Amsterdam) 2006;5:1161–1170. doi: 10.1016/j.dnarep.2006.05.032. [DOI] [PubMed] [Google Scholar]
- 76.Bacolla A, Wells RD. Non-B DNA conformations, genomic rearrangements, and human disease. J Biol Chem. 2004;279:47411–47414. doi: 10.1074/jbc.R400028200. [DOI] [PubMed] [Google Scholar]
- 77.Snell FD, Snell CT. Colorimetric Methods of Analysis, Including Some Turbidimetric and Nephelometric Methods. Huntington, NY: R. E. Krieger; 1972. [Google Scholar]
- 78.Plum GE. Current Protocols in Nucleic Acid Chemistry. Hoboken, NJ: John Wiley & Sons; 2000. pp. 7.3.1–7.3.17. [Google Scholar]
- 79.Privalov G, Kavina V, Freire E, Privalov PL. Precise scanning calorimeter for studying thermal properties of biological macromolecules in dilute solution. Anal Biochem. 1995;232:79–85. doi: 10.1006/abio.1995.9957. [DOI] [PubMed] [Google Scholar]