Abstract
A recently determined set of 20 NMR-derived conformations of a 48-residue all-α-helical protein, (PDB ID code 2JVD), is validated here by comparing the observed 13Cα chemical shifts with those computed at the density functional level of theory. In addition, a recently introduced physics-based method, aimed at determining protein structures by using NOE-derived distance constraints together with observed and computed 13Cα chemical shifts, was applied to determine a new set of 10 conformations, (Set-bt), as a blind test for the same protein. A cross-validation of these two sets of conformations in terms of the agreement between computed and observed 13Cα chemical shifts, several stereochemical quality factors, and some NMR quality assessment scores reveals the good quality of both sets of structures. We also carried out an analysis of the agreement between the observed and computed 13Cα chemical shifts for a slightly longer construct of the protein solved by x-ray crystallography at 2.0-Å resolution (PDB ID code 3BHP) with an identical amino acid residue sequence to the 2JVD structure for the first 46 residues. Our results reveal that both of the NMR-derived sets, namely 2JVD and Set-bt, are somewhat better representations of the observed 13Cα chemical shifts in solution than the 3BHP crystal structure. In addition, the 13Cα-based validation analysis appears to be more sensitive to subtle structural differences across the three sets of structures than any other NMR quality-assessment scores used here, and, although it is computationally intensive, this analysis has potential value as a standard procedure to determine, refine, and validate protein structures.
The 13Cα NMR nucleus is ubiquitous in proteins, making it an attractive candidate for computation of theoretical chemical shifts at the quantum chemical level of theory to determine, refine, and validate protein structures (1–4). The backbone and side-chain conformations of a residue are influenced by interactions with the rest of the protein, but once these conformations are established by these interactions, the 13Cα chemical shift of this residue depends mainly on its backbone (5–7) and side-chain (8–13) conformations, with no significant influence of either the amino acid sequence (8, 12, 13), the position of the given residue in the sequence (1), or the oligomerization state of the protein. Based on these properties, we recently introduced a physics-based method (1, 2) that relies on the hypothesis that an accurate protein structure determination can be carried out by simply identifying a set of conformations that simultaneously satisfies two sets of constraints: (i) a computed torsional set of constraints for all amino acid residues in the sequence, obtained from a comparison of 13Cα chemical shifts and computed at the density functional level of theory (DFT), with the experimental data and (ii) a fixed set of experimental nuclear Overhauser Effect (NOE)-derived distance constraints. In addition, an analysis of the disagreement between observed and DFT-computed 13Cα chemical shifts enables us to use this methodology to refine and validate existing structures (1). There are three main advantages of this methodology: (i) it can be used for proteins of any class or size for which backbone 13Cα chemical shift assignments and NOE-based distance constraints can be obtained; (ii) it provides a unified, self-consistent, method to determine (2, 3), refine (4), and validate (1) protein structures at a high-quality level; and (iii) it does not use any knowledge-based information and, hence, it is a physics-based method.
The 77-residue YnzC protein from Bacillus subtilis (SWISS-PROT ID code YNZC_BACSU) is part of the small yneA SOS response operon that regulates cell division in this organism (14). The solution NMR structures of both full-length (residues 1–77) and truncated forms (residues 1–46) of YnzC have recently been determined (PDB ID code 2JVD) (15). The N-terminal portion of the protein forms a stable antiparallel helix–loop–helix motif, whose structure is stabilized by numerous conserved residues involved in the hydrophobic core as well as by key interhelical salt bridges, whereas the C-terminal ≈35 residues are intrinsically disordered. The unique two-helix monomeric structure of YnzC, with no disulfide bonds, makes it an attractive subject for the development and testing of quantum chemical-based methods for protein structure determination.
The goal of this work was twofold: first, as a blind test, to determine whether it is possible to obtain an ensemble of conformations for which each individual conformer simultaneously satisfies the NOE-derived distance constraints and the 13Cα-derived torsional constraints for the YnzC protein in solution. Although the solution NMR structure (15) of this protein had been solved at the time of this (blind) test, the only information provided was a full set of both the observed 13Cα chemical shifts and the NOE-derived distance constraints. In particular, no information about the coordinates of the solved structures for the YnzC protein (15) or the heteronuclear 15N-1H NOE data were provided.
Our second goal was to carry out a cross-validation test of high-quality sets of conformations obtained for the YnzC protein in solution by using alternative determination methods, namely, the solution NMR set of conformations (PDB ID code 2JVD) obtained by using NOE-derived distance constraints, dihedral-angle constraints and hydrogen-bond constraints (15), and the 2.0-Å x-ray crystal structure (PDB ID code, 3BHP) (16). For this second goal, several validation scores were used, namely: (i) Recall, Precision, F-measure (RPF) analysis (17); (ii) several global quality score indicators provided by Verify3D (18), ProsaII (19), Procheck (20), and MolProbity (21, 22); (iii) the conformational-average rmsd (ca-rmsd) (1) and rmsd between observed 13Cα chemical shifts and those computed at the DFT level; and (iv) the backbone rmsd between these refined structures and the mathematical average coordinates of the ensemble of NMR structures of YnzC (1-48) deposited in the Protein Data Bank.
Results and Discussion
In this section, an analysis of the quality of 2JVD (20 conformations) (15), Set-bt (10 conformations), and 3BHP (3 conformations) (16) of the YnzC protein structures is carried out by considering (i) the agreement between observed and computed 13Cα chemical shifts in terms of both the rmsd for each conformer and ca-rmsd (1); (ii) the global structural quality of the conformations as indicated by the packing contacts, dihedral-angle distribution, etc. (23); and (iii) the global goodness-of-fit to the NMR-data in terms of RPF scores (17). The analysis of each of these criteria follows.
Analysis of the Observed and Computed 13Cα Chemical Shifts.
Determination of a set of 10 protein conformations for YnzC (Set-bt).
A physics-based method, aimed at determining protein structures by using NOE-derived distance constraints together with observed 13Cα chemical shifts and those computed at the density functional level of theory, was applied here to determine 10 conformations (Set-bt) of the YnzC protein. The C-terminal ≈35-residues of the YnzC protein is intrinsically disordered in solution (15). Accordingly, calculations were carried out on 46-residue (YnzC[1–46]) and 52-residue (YnzC[1–52]) constructs of the 77-residue YnzC protein, including the first 46 and 52 residues, respectively, of the native sequence together with an additional 8-residue LEHHHHHH C-terminal affinity purification tag; the (His)6 tag was omitted for quantum chemistry calculations, which were carried out only for the first 48 residues of YnzC[1–52]; i.e., including only ≈6 residues from the intrinsically-disordered C-terminal region. The determination of this structure was carried out in a “blind test” manner. Thus, the only information used (and provided) was the full set of NOE-derived distance constraints and the observed 13Cα chemical shifts. In other words, information about the atomic coordinates of structures previously solved by NMR spectroscopy (2JVD) (15) and x-ray crystallography (3BHP) (16), respectively, were not available to the investigators carrying out the quantum-chemical-based structure analysis at the time of the blind-test determination.
Data available for these quantum-chemical calculations included complete 13Cα chemical shift data along with 1,022 NOE-based distance constraints [supporting information (SI) Table S1 and SI Text]. Additional chemical shift data, although required for determining NOESY cross-peak assignments, were not used in the quantum-chemical structure determination and refinement process. The method for the determination of the 10 conformations (Set-bt) basically consists of three steps (see SI Text). The first of these steps is secondary-structure prediction based on 13Cα conformational shifts (CS), computed as described in Materials and Methods, that provides an initial abbreviated set of backbone torsional angles, namely, for those regions of secondary structure such as α-helix or β-sheet. Fig. S1 shows the corresponding distribution of 13Cα conformational shift (CS) values computed for the protein YnzC[1–48] using the observed 13Cα chemical shifts and statistical coil values from Wishart et al. (24). Two criteria were adopted for assigning the torsional constraints based on the conformational shifts. First, α-helical segments are those for which at least three consecutive residues possess CS values >1 ppm (green bars in Fig. S1), and second, for those residues that satisfied this condition, canonical backbone torsional-angle constraints were assigned, namely, φ = −60° ± 30° and ψ = −40° ± 30°. No torsional constraints were assigned for the remaining residues. Variations of the torsional angles within a tolerance range (±Λ) are not subject to energetic penalties; i.e., we use a flat-bottom pseudopotential-energy function. During the VTF procedure a tolerances range of Λ = 30° was adopted. However, a smaller tolerance range was adopted in the subsequent steps (see SI Text) allowing us to find a set of conformations that simultaneously satisfy a set of distance constraints derived from both the experimental NOEs and the 13Cα conformational shifts.
These torsional constraints were then used together with 1,022 NOE-derived distance constraints to generate 2,000 conformations by using the variable-target-function (VTF) procedure (25). From this ensemble, 10 conformations with lowest residual distance constraint violations (i.e., maximum distance violation <3.02 Å) were selected. For these 10 conformations, 13Cα chemical shifts were then computed by using the quantum-chemical DFT method, as explained in Materials and Methods. This calculation provided both backbone (φ and ψ) and all side-chain (χ) torsional constraints for all 48 residues in the sequence, as explained in SI Text.
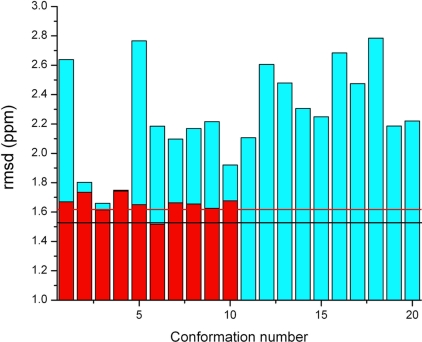
The 1,022 NOE-derived distance constraints plus the updated backbone torsional constraints for all the residues were then used to generate a new set of conformations with the ECEPP/3 force field. Two iterations of the procedure (steps 2 and 3) follow the steps illustrated in Fig. S2. During the first iteration, 10 conformations with maximum distance violations <0.2 Å were selected among 175 generated by using both the 1,022 NOE-derived distances and the set of backbone and side-chain torsional constraints derived from the VTF procedure. In this iteration, a tolerance range ±Λ, with Λ = 20°, for the torsional constraints was adopted. The calculated 13Cα chemical shifts for these conformations provide a new set of backbone and side-chain torsional constraints for all 48 residues in the sequence. During this second iteration, 10 conformations with maximum distance violations <0.09 Å were selected from 330 generated by using both the 1,022 NOE-derived distances and the new set of backbone and side-chain torsional constraints derived from the previous iteration. In this second iteration a tolerance range Λ = 10°, rather than Λ = 20° used in the previous iteration, for the torsional constraints was adopted. The 13Cα chemical shifts for each residue of Set-bt enabled us to compute the rmsd between calculated and observed 13Cα values for each of these 10 conformations (see red bars in Fig. 1). A superposition of this final set of 10 conformations is shown in Fig. 2A
Fig. 1.
Bars indicate the rmsd between computed and observed 13Cα chemical shifts for each of the 10 conformations of YnzC[1–46] from Set-bt (red bars) and the 20 conformations from the ensemble of NMR structures retrieved from the PDB, 2JVD (blue bars). Horizontal lines designate the ca-rmsds computed for each of these two sets as described in Materials and Methods. Black and red horizontal lines designate the ca-rmsd computed for residues 1–48 of 2JVD and Set-bt (including the first two residues of the C-terminal purification tag), respectively.
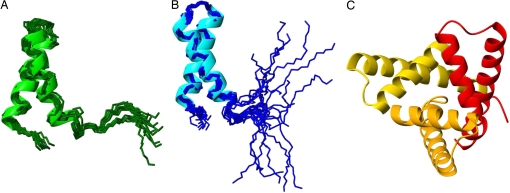
Fig. 2.
Ribbon diagrams of the superposition of 10 conformations obtained in Set-bt (A), the superposition of 20 conformations of 2JVD (B), and the x-ray structure (three monomers in the asymmetric unit) (C).
The significance of using 13Cα-derived torsional constraints for all residues.
To determine whether 13Cα-derived torsional constraints for all of the residues is a necessary condition to derive a good-quality set of conformations, such as Set-bt, the following test was carried out. The first iteration of our method (from here on referred to as run_A) was repeated twice. The additional two new runs differ from run_A only in the number, distribution, and type of torsional constraints used. In other words, all three runs start from the same initial conformation and with the same set of distance constraints, namely 1,022 NOE-derived distances. These different conditions were used to assess the specific contributions to the structure refinement of the specific types of torsional constraints based on quantum-chemical calculations. As a scoring function to judge the quality of the generated ensembles, for each set of conformations, we computed the maximum distance violation (using all of the 1,022 NOE-derived distances) and the backbone rmsd with respect to the average structure of the solution NMR structure (i.e., the 2JVD set) (15). Thus, the first test (from here on referred to as run_B) was carried out by removing all 13Cα-derived torsional constraints used in run_A, except those for the residues in the α-helix segments, namely for residues 4–18 and 24–39, which are indicated by green bars in Fig. S1. This experiment allowed us to assess the role of 13Cα-based torsional constraints in the turn region between the helices in determining the relative orientations of these helices. The second test (from here on referred to as run_C) was carried out by replacing all the chemical-shift constraints used in run_B by the set of backbone-torsional constraints used in the initial VTF step, namely, φ = −60° ± 30° and ψ = −40° ± 30°. This experiment allowed us to assess the value of the constraints generated by the DFT process in defining the accuracy of interhelical packing.
As discussed in the previous section, run_A yielded a set of 10 conformations with a maximum distance violation <0.2 Å and backbone rmsd of 1.7 Å relative to the average coordinates of the solution NMR structure ensemble 2JVD. The set of 10 conformations derived from run_B possessed a maximum distance violation <0.2 Å and a backbone rmsd relative to the average NMR structure coordinates of 2.6 Å. From this, we conclude that the torsional constraints on the loop region between the two helices contribute, but do not dominate, in defining the relative orientations of the two helices. On the other hand, the set of 10 conformations derived from run_C possessed a maximum distance violation <0.4 Å and a backbone rmsd relative to the NMR structure 2JVD of 1.9 Å. Accordingly, the constraints provided by the DFT calculations modestly improve the accuracy of the interhelical orientations, probably by providing somewhat more accurate side-chain packing. It should be noted that, although run_C provided a reasonably good structure, run_A could be further refined by iterative computation with DFT, to provide even better agreement with the combined chemical shift and NOE data. These results demonstrate that run_A, which makes use of the 13Cα-derived torsional constraints for all the residues in the sequence, provides a more accurate set of conformations than run_B or run_C in terms of the scoring functions used.
Validation of the 2JVD set of 20 conformations.
A superposition of the 20 conformations of 2JVD is shown in Fig. 2B. Computation of the 13Cα chemical shifts for each amino acid residue of the 20 conformations of the 2JVD set was carried out as described in Method Used to Compute the 13Cα Chemical Shifts in Materials and Methods. Blue bars in Fig. 1 show the mean rmsd between the observed and computed 13Cα chemical shifts of residues 1–48 for each of these 20 conformations. The black horizontal line (1.52 ppm) indicates the computed conformationally averaged ca-rmsd (1). Results obtained from each of the 10 conformations of Set-bt (red bars) are also shown in Fig. 1. The rmsd between calculated and observed 13Cα chemical shifts for each of the 20 conformations of 2JVD is higher, except for conformation no. 4 (for which these two conformations are indistinguishable), than those obtained from the Set-bt. This is not surprising because agreement between calculated and observed 13Cα chemical shifts was used as a constraint during the process of protein structure determination of the latter set. However, the ca-rmsd computed from 2JVD (1.52 ppm, black horizontal line in Fig. 1) is slightly better than the one computed from Set-bt (1.62 ppm, red horizontal line in Fig. 1). This is a consequence of the higher conformational dispersion in the C-terminal segment (residues 42–48) of the 2JVD structural ensemble as compared with Set-bt. This is clearly illustrated by comparing Fig. 2 A and B. The influence of this higher conformational dispersion at the C terminus on the ca-rmsd value is discussed below.
Analysis of the x-ray crystal structure of YnzC in terms of the 13Cα chemical shifts.
Although efforts to obtain diffraction-quality crystals of the same construct used in these NMR studies, YnzC[1–46], were not successful, diffraction-quality crystals were obtained for a slightly longer construct YnzC[1–52]. Both the YnzC[1–46] and YnzC[1–52] constructs are monomeric in solution (see Fig. S4), but YnzC[1–52] crystallized as a trimeric structure. A ribbon diagram of the 2.0-Å x-ray structure (16) (PDB ID code 3BPH, with three chains in the asymmetric unit) is shown in Fig. 2C. The three chains of this trimer, although essentially identical in conformation, exhibit some notable differences. In particular, in chains A and C, helix α2 extends through residue 52, whereas in chain B, helix α2 extends only to residue 48. The per-residue all-heavy atom rmsds (Å) between chains A–B and A–C, respectively, are shown in Fig. S3, illustrating the distribution of small structural differences among the three chains of the trimer observed in this crystal structure.
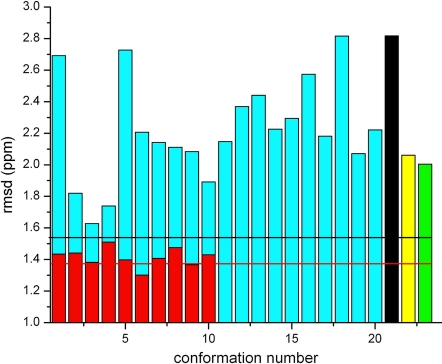
These subtle structural differences among the three chains of the 3BHP trimer result in small differences in calculated 13Cα chemical shift values. This is illustrated by the black, yellow and green bars, respectively, in Fig. 3. These calculations demonstrate that these 13Cα chemical shifts are very sensitive to the small conformational differences among the three chains of trimeric YnzC[1–52] observed in the crystal structure.
Fig. 3.
Bars indicate the rmsd (ppm) between computed and observed 13Cα chemical shifts for each of the 10 conformations of YnzC [1–46] from Set-bt (red bars), the 20 conformations from 2JVD (blue bars), and for each of the three chains in the 2.0-Å crystal structure of YnzC [1–52], 3BHP, namely chains A, B, and C (black, yellow, and green bars). Horizontal lines designate the ca-rmsds computed for each of the two sets of NMR-derived conformations as described in Materials and Methods. Black and red horizontal lines designate the ca-rmsd computed for residues 1–46 of 2JVD and Set-bt, respectively.
Although YnzC[1–52] is trimeric in the crystal structure, biophysical studies, including gel filtration, static light scattering, and 15N relaxation measurements, demonstrate that both YnzC[1–52] and YnzC[1–46] (used for NMR studies) are monomeric in solution (see Fig. S4); the full-length YnzC [1–77] is also monomeric in solution (15). Comparison of coordinates between the monomeric solution NMR structure and each monomer chain in the trimeric crystal structures reveals that residues 39–46 become more ordered (helical) in the crystal structure. This further extension of helix α2 in the crystalline environment is stabilized by intermolecular interactions within the trimeric structure (Fig. 2). However, for residues in the range 2–38, the NMR averaged (over all 20 models) and the x-ray averaged (over all three chains) structures are essentially identical (i.e., backbone rmsd between averaged coordinates of 0.57 Å).
Roles of ensemble averaging and protein flexibility.
The amino acid sequence of the YnzC[1–52] (3BHP) (16), YnzC[1–46] (2JVD) (15), and Set-bt structures are identical only for the first 46 residues. Hence, a straightforward comparison between these conformations requires that the rmsd and ca-rmsd for these sets of structures must be reevaluated by considering only the first 46 residues. Comparisons among these three sets are shown in Fig. 3. Some important conclusions can be derived from this analysis. First, the ca-rmsd of both 2JVD and Set-bt, black (1.54 ppm) and red (1.38 ppm) horizontal lines, respectively, in Fig. 3, are lower than the rmsd of any of the single chains of the crystal structure 3BHP (2.82, 2.06, and 2.00 ppm, for chains A, B, and C, respectively). This result is in line with a previous analysis of ubiquitin (1) showing that an ensemble of NMR-derived protein conformations provides better agreement, in terms of the ca-rmsd, than some single x-ray structures do. Fig. 3 also shows that 4 of 20 models of 2JVD (blue bars in Fig. 3) and all 10 conformations (red bars in Fig. 3) of Set-bt give lower rmsds than any of the three chains of 3BHP.
Heteronuclear 15N-1H NOE data obtained for YnzC[1–46] demonstrate that residues 41–46, along with the C-terminal eight-residue affinity purification tag, are quite flexible on the subnanosecond time scale (see Fig. S5). In considering only the first 46 residues, computation of the ca-rmsd for Set-bt (1.38 ppm, indicated by a red horizontal line in Fig. 3) is lower than the value obtained by considering the 48 residues (1.62 ppm, indicated by the red horizontal line in Fig. 1); this effect of dynamic regions on ca-rmsd is less pronounced in calculations carried out with the 20 conformations of 2JVD, i.e., considering only the first 46 residues gives a ca-rmsd of 1.54 ppm (black horizontal line in Fig. 3), whereas considering the first 48 residues gives a ca-rmsd of 1.52 ppm (black horizontal line in Fig. 1). These results are attributable to larger differences between observed and computed 13Cα chemical shifts for the two C-terminal residues of Set-bt than for the 2JVD set. In fact, the absolute values of the average error, and their SD (see Eqs. 1. and 2, in SI Text, for residues 47 and 48 are 0.36 ± 3.12 ppm and 1.54 ± 3.25 ppm for the 2JVD set, and 6.27 ± 0.39 ppm and 0.19 ± 0.17 for the Set-bt set, respectively, with the standard deviation reflecting the dispersion of the conformations in each ensemble. These results illustrate how highly flexible regions, such as the C-terminal residues of these YnzC constructs, are better represented by wide, rather than tight, sets of conformations. From this point of view, the flexible C-terminal region of YnzC[1–46] is better represented by the 2JVD set than by the Set-bt.
The ca-rmsd is lower when the extent of conformational sampling is more complete. For example, for the Set-bt, analysis of the dependence of the ca-rmsd on n, with 41 ≤ n ≤ 48 being the total number of residues considered for the computation of the ca-rmsd, reveals a constant ca-rmsd value of ≈1.4 ppm for 41 ≤ n ≤ 46, a higher ca-rmsd value (≈1.6 ppm) for n = 47, and no change after the inclusion of residue 48. Among all 48 residues, residue 47 exhibits both the highest absolute value of the average error, namely 6.27 ppm, and residue 47 has the lowest heteronuclear 15N-1H NOE values (see Fig. S5). It appears that for these two residues, the refinement protocol has resulted in an undersampling of the solution space contributing to the ca-rmsd.
In the protocol used here, the 13C-chemical shift-derived torsional constraints on the backbone and side-chain torsional angles used a tolerance of 10° in the last step of the procedure. Although this appears to be appropriate in well defined regions of the structure, in more poorly defined regions of the structure, these constraints are too tight and result in undersampling of the conformational space contributing to the observed chemical shift data. As we have pointed out previously, special care must be taken in using 13C chemical shift constraints in flexible regions of the protein structure (26). In retrospect, experimental data indicating structural flexibility, such as heteronuclear 15N-1H NOE data (see Fig. S5), could be used to identify regions of the structure where 13C constraints can be used only with looser tolerances. In this blind test case, however, these data were not provided nor used in the determination of the Set-bt.
A 13Cα-reference-dependent analysis.
Reference inaccuracy problems (1), which affect the ca-rmsd and the rmsd values, can be detected by computing the frequency distribution of the errors between observed and computed 13Cα chemical shifts. Such analysis (for the Set-bt) indicates that the resulting distribution can be modeled by a Normal (or Gaussian) function with a characteristic mean value (xo = 0.10 ppm) and standard deviation (σ = 1.08 ppm). The resulting mean value (xo = 0.10 ppm) is very close to the ideal one (xo = 0.0 ppm) indicating that there is no need for further reference corrections. Moreover, it also assures that 99.7% of these errors lie within 3σ (≈3.2 ppm).
A 13Cα-reference-independent analysis.
The Pearson coefficient R (27) provides a measure of the quality of the agreement in terms of the shielding (rather than the chemical shift) and, hence, is not affected by reference accuracy. The R values obtained for Set-bt, 2JVD, and chains A, B, and C of 3BHP are: 0.932, 0.917, 0.815, 0.881, and 0.865, respectively. These results confirm the conclusions derived from the 13Cα chemical shift analysis, namely through the comparison of rmsd and ca-rmsd shown in Fig. 3; the conformations of Set-bt are in best agreement with the 13Cα data, the conformations of set 2JVD are in good agreement, and the individual conformers of the x-ray crystal structure is in somewhat poorer agreement with these data.
Structure Quality Assessment.
Structural statistics for the solution NMR structures of YnzC[1–46] (2JVD), the x-ray structure of YnzC[1–52] (3BHP), and the structure of YnzC[1–46] determined by using DFT-based 13Cα chemical shift constraints (Set-bt) are presented in Table 1. All three sets of structures exhibit similar Ramachandran statistics and global structure quality factors, including Verify3D (18), ProsaII (19), Procheck (20), and MolProbity (21) scores. These results indicate the high quality of these protein structures determined by three different methods. This is not too surprising, because all three methods yield similar overall structures, although differing in structural details. Thus, the mean-to-mean rmsd values (from residues 4–38) for the backbone and heavy atoms are: (i) 0.39 Å and 0.91 Å for 2JVD vs. x-ray; (ii): 0.76 Å and 1.31 Å, for 2JVD vs. Set-bt; and (iii): 0.71 Å and 1.44 Å, for the x-ray vs. Set-bt, respectively.
Table 1.
Structural statistics for the solution NMR structures (2JVD), the X-ray structure (3BHP), and the computed structures (Set-bt) of protein YnzC[1–46]
| 2JVD | 3BHP | Set-bt | |
|---|---|---|---|
| Secondary structural elements | |||
| α1 | 4–19 | 3–19 | 4–19 |
| α2 | 24–38 | 23–49 | 24–38 |
| Ramachandran plot statistics†‡ | |||
| Most favored regions, % | 98.6 | 94.4 | 92.3 |
| Additional allowed regions, % | 1.4 | 5.6 | 7.7 |
| Generously allowed, % | 0.0 | 0.0 | 0.0 |
| Disallowed regions, % | 0.0 | 0.0 | 0.0 |
| Global quality scores† | |||
| Raw/Z score | |||
| Verify3D | 0.24/−3.53 | 0.41/−0.80 | 0.20/−4.17 |
| ProsaII | 0.91/1.08 | 1.37/2.98 | 0.71/0.25 |
| Procheck(φ-ψ)‡ | 0.53/2.40 | 0.44/2.05 | −0.20/−0.47 |
| Procheck(all)‡ | 0.50/2.96 | 0.41/2.42 | −0.35/−2.07 |
| Molprobity clash | 15.44/−1.12 | 14.59/−0.98 | 8.14/0.13 |
| RPF scores§ | |||
| Recall | 0.987 | 0.976 | 0.982 |
| Precision | 0.928 | 0.923 | 0.901 |
| F measure | 0.957 | 0.949 | 0.940 |
| 〈DP-score〉 | 0.732 (0.022) | 0.718 (0.047) | 0.717 (0.010) |
| Pairwise rmsd, Ŷ | |||
| Backbone atoms | 0.42 (0.10) | 0.21 (0.08) | 0.19 (0.06) |
| Heavy atoms | 1.08 (0.15) | 0.73 (0.26) | 0.41 (0.12) |
| rmsd from mean, Ŷ | |||
| Backbone atoms | 0.29 (0.07) | 0.15 (0.08) | 0.13 (0.05) |
| Heavy atoms | 0.77 (0.07) | 0.54 (0.11) | 0.29 (0.08) |
Computed for the following structural ensembles: 2JVD, 20 structures in PDB format; 3BHP, three structures in the asymmetric unit in PDB format; Set-bt, 10 structures converted from ECEPP/3 PDB format to IUPAC format by using PDBStat 5.0 (23).
†Calculated by using Protein Structure Validation Suite, version 1.3 (23).
‡Ordered residue ranges [S(φ) + S(ψ) > 1.8]: 2JVD: 2–38; Set-bt: 1–47. For 3BHP, all residues for the three structures in the asymmetric unit were included.
§RPF scores (17) reflecting the goodness-of-fit of the final ensemble of structures (including disordered residues) to the NMR data. For 2JVD and Set-bt, the coordinates for residues 1–46 of the structures in each ensemble were converted to IUPAC format by using PDBStat 5.0 (23). For 3BHP, hydrogen atoms were added to residues 1–46 of the three structures in the asymmetric unit with the Molprobity server (22), and the coordinates were converted to IUPAC format by using the WHATIF server (30). SDs for the average DP score over the individual models are given in parentheses.
¶Pairwise rmsds computed by using MOLMOL (31) for residues 4–38.
RPF Analysis.
We employ a formalism based on information-retrieval statistics, the RPF analysis, to represent the global goodness-of-fit of a structure or ensemble of structures with the experimental NOESY peak list data (17). Briefly, Recall measures the percentage of NOESY peaks that are consistent with the interproton distances in the 3D structure, Precision measures the percentage of close distance proton pairs (<5 Å) in the 3D structure whose back-calculated NOESY cross-peaks are observed in the NOESY peak lists, F-measure is the overall performance score calculated from the Recall and Precision, and Discriminating Power (DP)-score is a normalized F-measure that reflects how the query structure is distinguished from the freely rotating chain model. In practice, DP-scores and F-measures >0.7 and 0.9, respectively, indicate good global structure accuracy (17). Based on these criteria, all three sets of structures presented here, the solution NMR ensembles (2JVD and Set-bt) and the x-ray crystal structure (3BHP), display very good agreement with the experimental NOE data (see Table 1).
However, in contrast to the ca-rmsd metric discussed above, the global RPF analysis is less sensitive to subtle structural differences across the three sets of structures.
Conclusions
By carrying out a blind test, a distinction from previous structure determinations (2, 3), we demonstrate in this work that an accurate all-α-helix set of protein structures in solution can be determined by simply identifying a set of conformations that simultaneously satisfies a set of constraints, namely 13Cα-dynamically derived torsional angle constraints for all amino acid residues in the sequence and a fixed set of NOE-derived distance constraints. A comparative analysis of the ca-rmsd values computed among all three sets of conformations, namely those obtained by NMR (2JVD and Set-bt) and the x-ray crystallography structure (3BHP) reveals that the NMR-derived ensembles of structures are a better representation for the observed 13Cα chemical shifts in solution than any single conformer or any single chain of the x-ray structure. This result is in line with previous calculations on both 10 NMR-derived conformations (1D3Z) (28) and the x-ray structure (1UBQ) (29) of ubiquitin.
Because the ca-rmsd analysis might be biased by the fact that the 10 conformations of Set-bt were computed by a 13Cα-based method, whereas the others were not, a cross-validation quality test was also carried out. These structures consistently show good values for the RFP and DP-scores as well as for global structure quality factors. This analysis reveals that all three sets of structures analyzed here, namely the solution NMR ensembles (2JVD and Set-bt) and the x-ray crystal structure (3BHP), display very good agreement with the experimental NOE data, as well as dihedral angle distributions and atomic clash scores typical of good-quality protein structures. Taken together, these results indicate that the 20 conformations from the 2JVD set, the DFT-computed 10 conformations from Set-bt, and each of the three chains of the x-ray structure are highly-accurate sets of conformations that represent the YnzC protein in solution.
Some standard NMR structure-generation programs use the 13Cα and 13Cβ chemical shifts and chemical-shift database information for direct refinement of φ/ψ torsion angles (7) (see SI Text). These approaches are generally helpful in steering the structure away from high-energy φ/ψ conformations although less sophisticated than the protocols described here. In fact, a comparison among all of the quality factors used here, together with the validation analysis carried out with the quantum-chemical DFT-computed 13Cα chemical shifts, reveals that the latter method is more sensitive to subtle structural differences and, although computationally intensive, it has potential value as a standard procedure to determine, refine, and validate protein structures.
Materials and Methods
Experimental Set of Structures.
The cloning, expression, and purification of 13C,15N-enriched YnzC[1–46] (NMR) and selenomethionyl YnzC[1–52] (x-ray), as well as, the solution NMR structure and x-ray crystal structure determinations of YnzC[1–46] and YnzC[1–52], respectively (see Table S2), were performed by following standard protocols of the Northeast Structural Genomics consortium, as described (15, 32). Both constructs included additional eight-residue affinity tags (LEHHHHHH) at their C-termini. Coordinates of the 20 NMR-derived conformations of YnzC[1–46] (15) and the three monomer chains from the asymmetric unit of the 2.0-Å resolution x-ray structure of YnzC[1–52] (16) were obtained from the Protein Data Bank (33) under the PDB ID codes 2JVD (15) and 3BHP (16), respectively. The 48 13Cα chemical shifts and 1,022 NOE-derived distance constraints used in the NMR structure determination of YnzC[1–46] are available from the Biological Magnetic Resonance Data Bank (BMRB) under accession number 15476.
Conversion of the Experimental Structures from Flexible to Rigid ECEPP Geometry.
To carry out the present study, all of the experimentally determined conformations from 2JVD and 3BHP were regularized, i.e., all residues were replaced by the standard ECEPP/3 residues (34) (see SI Text).
Method Used to Compute the 13Cα Chemical Shifts.
The 13Cα chemical shifts for the conformations of Set-bt, 2JVD (15) and 3BHP (16) were computed by using a set of approximations described in recently published papers (1–4) and, hence, only salient information is provided in SI Text.
Conformational Shifts.
The 13Cα conformational shifts for each amino acid in the sequence were computed as the difference between the observed 13Cα chemical shifts and their corresponding statistical coil values, as reported by Wishart et al. (24).
Protein Structure Determination.
Details can be found in recently published papers (1–4) and, hence, only salient information is provided in SI Text.
Supplementary Material
Acknowledgments.
We thank Drs. R. Tejero and Y. J. Huang for valuable scientific discussions. This work was supported by National Institutes of Health Grants GM-14312, GM-24893, and Protein Structure Initiative Grant U54-GM074958 as a Community Outreach Project and by National Science Foundation Grant MCB05-41633). Support was also received from Consejo Nacional de Investigaciones Cientificas y Técnicas, Fondo para la Investigación Científica y Tecnológica–Agencia Nacional de Promoción Científica y Tecnológica Grant PAV 22642/22672 and from the Universidad Nacional de San Luis (P-328501), Argentina. The research was conducted by using the resources of a Beowulf-type cluster located at the Baker Laboratory of Chemistry and Chemical Biology, Cornell University, and the National Science Foundation Terascale Computing System at the Pittsburgh Supercomputer Center, Pittsburgh.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/cgi/content/full/0807105105/DCSupplemental.
References
- 1.Vila JA, Villegas ME, Baldoni HA, Scheraga HA. Predicting 13Cα chemical shifts for validation of protein structures. J Biomol NMR. 2007;38:221–235. doi: 10.1007/s10858-007-9162-x. [DOI] [PubMed] [Google Scholar]
- 2.Vila JA, Ripoll DR, Scheraga HA. Use of 13Cα chemical shifts in protein structure determination. J Phys Chem B. 2007;111:6577–6585. doi: 10.1021/jp0683871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Vila JA, Arnautova YA, Scheraga HA. Use of 13Cα chemical shifts for accurate determination of β-sheet structures in solution. Proc Natl Acad Sci USA. 2008;105:1891–1896. doi: 10.1073/pnas.0711022105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Vila JA, Scheraga HA. Factors affecting the use of 13Cα chemical shifts to determine, refine, and validate protein structures. Proteins Struct Funct Bioinf. 2008;71:641–654. doi: 10.1002/prot.21726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Spera S, Bax A. Empirical correlation between protein backbone conformation and Cα and Cβ 13C nuclear-magnetic-resonance chemical shifts. J Am Chem Soc. 1991;113:5490–5492. [Google Scholar]
- 6.deDios AC, Pearson JG, Oldfield E. Secondary and tertiary structural effects on protein NMR chemical shifts: An ab initio approach. Science. 1993;260:1491–1496. doi: 10.1126/science.8502992. [DOI] [PubMed] [Google Scholar]
- 7.Kuszewski J, Qin JA, Gronenborn AM, Clore GM. The impact on direct refinement against 13Cα and 13Cβ chemical shifts on protein structure determination by NMR. J Magn Reson Ser B. 1995;106:92–96. doi: 10.1006/jmrb.1995.1017. [DOI] [PubMed] [Google Scholar]
- 8.Pearson JG, et al. Predicting chemical shifts in proteins: Structure refinement of valine residues by using ab initio and empirical geometry optimizations. J Am Chem Soc. 1997;119:11941–11950. [Google Scholar]
- 9.Havlin RH, Le H, Laws DD, deDios AC, Oldfield E. An ab initio quantum chemical investigation of carbon-13 NMR shielding tensors in glycine, alanine, valine, isoleucine, serine, and threonine: Comparisons between helical and sheet tensors, and effects of χ1 on shielding. J Am Chem Soc. 1997;119:11951–11958. [Google Scholar]
- 10.Iwadate M, Asakura T, Williamson MP. Cα and Cβ carbon-13 chemical shifts in protein from an empirical database. J Biomol NMR. 1999;13:199–211. doi: 10.1023/a:1008376710086. [DOI] [PubMed] [Google Scholar]
- 11.Xu X-P, Case DAJ. Automatic prediction of 15N, 13Xα, 13Cβ and 13C′ chemical shifts in proteins using a density functional database. J Biomol NMR. 2001;21:321–333. doi: 10.1023/a:1013324104681. [DOI] [PubMed] [Google Scholar]
- 12.Sun H, Sanders LK, Oldfield E. Carbon-13 NMR shielding in the twenty common amino acids: Comparisons with experimental results in proteins. J Am Chem Soc. 2002;124:5486–5495. doi: 10.1021/ja011863a. [DOI] [PubMed] [Google Scholar]
- 13.Villegas ME, Vila JA, Scheraga HA. Effects of side-chain orientation on the 13C chemical shifts of antiparallel β-sheet model peptides. J Biomol NMR. 2007;37:137–146. doi: 10.1007/s10858-006-9118-6. [DOI] [PubMed] [Google Scholar]
- 14.Kawai Y, Moriya S, Ogasawara N. Identification of a protein, YneA, responsible for cell division suppression during the SOS response in Bacillus subtilis. Mol Microbiol. 2003;47:1113–1122. doi: 10.1046/j.1365-2958.2003.03360.x. [DOI] [PubMed] [Google Scholar]
- 15.Aramini JM, et al. Solution NMR structure of the SOS response protein YnzC from Bacillus subtilis. Proteins. 2008;72:526–530. doi: 10.1002/prot.22064. [DOI] [PubMed] [Google Scholar]
- 16.Kuzin AP, et al. Crystal structure of UPF0291 protein ynzC from Bacillus subtilis at resolution 2.0 A. Northeast Structural Genomics Consortium target SR384. 2008 doi: 10.2210/pdb3bhp/pdb. [DOI] [Google Scholar]
- 17.Huang YJ, Powers R, Montelione GT. Protein NMR recall, precision, and F-measure scores (RPF scores): Structure quality assessment measures based on information retrieval statistics. J Am Chem Soc. 2005;127:1665–1674. doi: 10.1021/ja047109h. [DOI] [PubMed] [Google Scholar]
- 18.Lüthy R, Bowie JU, Eisenberg D. Assessment of protein models with three-dimensional profiles. Nature. 1992;356:83–85. doi: 10.1038/356083a0. [DOI] [PubMed] [Google Scholar]
- 19.Sippl MJ. Recognition of errors in three-dimensional structures of proteins. Proteins. 1993;17:355–362. doi: 10.1002/prot.340170404. [DOI] [PubMed] [Google Scholar]
- 20.Laskowski RA, MacArthur MW, Moss DS, Thornton JM. PROCHECK: A program to check the stereochemical quality of protein structures. J Appl Crystallogr. 1993;26:283–291. [Google Scholar]
- 21.Lovell SC, et al. Structure validation by Cα geometry: φ, ψ, and Cβ deviation. Proteins. 2003;50:437–450. doi: 10.1002/prot.10286. [DOI] [PubMed] [Google Scholar]
- 22.Davis IW, et al. MolProbity: All-atom contacts and structure validation for proteins and nucleic acids. Nucleic Acids Res. 2007;35:W375–W383. doi: 10.1093/nar/gkm216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Bhattacharya A, Tejero R, Montelione GT. Evaluating protein structures determined by structural genomics consortia. Proteins. 2007;66:778–795. doi: 10.1002/prot.21165. [DOI] [PubMed] [Google Scholar]
- 24.Wishart DS, Bigam CG, Holm A, Hodges RS, Sykes BD. 1H, 13C and 15N random coil NMR chemical-shifts of the common amino-acids. 1. Investigations of nearest-neighbor effects. J Biomol NMR. 1995;5:67–81. doi: 10.1007/BF00227471. [DOI] [PubMed] [Google Scholar]
- 25.Vásquez M, Scheraga HA. Variable-target-function and buildup procedures for the calculation of protein conformation—Application to bovine pancreatic trypsin-inhibitor using limited simulated nuclear magnetic-resonance data. J Biomol Struct Dyn. 1988;5:757–784. doi: 10.1080/07391102.1988.10506426. [DOI] [PubMed] [Google Scholar]
- 26.Celda B, Biamonti C, Arnau MJ, Tejero R, Montelione GT. Combined use of 13C chemical shift and 1Hα-13Cα heteronuclear NOE data in monitoring a protein NMR structure refinement. J Biomol NMR. 1995;5:161–172. doi: 10.1007/BF00208807. [DOI] [PubMed] [Google Scholar]
- 27.Press HW, Teukolsky SA, Vetterling WT, Flannery BP. Numerical Recipes in Fortran 77. The Art of Scientific Computing. Second Ed. Cambridge, UK: Cambridge Univ Press; 1992. pp. 630–633. [Google Scholar]
- 28.Cornilescu G, Marquardt JL, Ottiger M, Bax A. Validation of protein structure from anisotropic carbonyl chemical shifts in a dilute liquid crystalline phase. J Am Chem Soc. 1998;120:6836–6837. [Google Scholar]
- 29.Vijay-Kumar S, Bugg CE, Cook WJ. Structure of ubiquitin refined at 1.8 Å resolution. J Mol Biol. 1987;194:531–544. doi: 10.1016/0022-2836(87)90679-6. [DOI] [PubMed] [Google Scholar]
- 30.Rodriguez R, Chinea G, Lopez N, Pons T, Vriend G. Homology modeling, model and software evaluation: Three related resources. Bioinformatics. 1998;14:523–528. doi: 10.1093/bioinformatics/14.6.523. [DOI] [PubMed] [Google Scholar]
- 31.Koradi R, Billeter M, Wüthrich K. MOLMOL: A program for display and analysis of macromolecular structures. J Mol Graphics. 1996;14:51–55. doi: 10.1016/0263-7855(96)00009-4. [DOI] [PubMed] [Google Scholar]
- 32.Acton TB, et al. Robotic cloning and protein production platform of the Northeast Structural Genomics Consortium. Methods Enzymol. 2005;394:210–243. doi: 10.1016/S0076-6879(05)94008-1. [DOI] [PubMed] [Google Scholar]
- 33.Berman HM, et al. The Protein Data Bank. Nucleic Acids Res. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Némethy G, et al. Energy parameters in polypeptides. 10. Improved geometrical parameters and nonbonded interactions for use in the ECEPP/3 algorithm, with application to proline-containing peptides. J Phys Chem. 1992;96:6472–6484. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.