Abstract
Kinetic isotope effects (KIEs) and computer modeling are used to approximate the transition state of S. pneumoniae 5′-methylthioadenosine/S-adenosylhomocysteine nucleosidase (MTAN). Experimental KIEs were measured and corrected for a small forward commitment factor. Intrinsic KIEs were obtained for [1′-3H], [1′-14C], [2′-3H], [4′-3H], [5′-3H2], [9-15N] and [Me-3H3] MTAs. The intrinsic KIEs suggest an SN1 transition state with no covalent participation of the adenine or the water nucleophile. The transition state was modeled as a stable ribooxacarbenium ion intermediate and was constrained to fit the intrinsic KIEs. The isotope effects predicted a 3-endo conformation for the ribosyl oxacarbenium-ion corresponding to H1′-C1′-C2′-H2′ torsional angle of 70°. Ab initio Hartree-Fock and DFT calculations were performed to study the effect of polarization of ribosyl hydroxyls, torsional angles and the effect of base orientation on isotope effects. Calculations suggest that the 4′-3H KIE arises from hyperconjugation between the lonepair (np) of O4′ and the σ* (C4′-H4′) antibonding orbital due to polarization of the 3′-hydroxyl by Glu174. A [methyl-3H3] KIE is due to hyperconjugation between np of sulphur and σ* of methyl C-H bonds. van der Waal contacts increase the 1′-3H KIE due to induced dipole-dipole interactions. The 1′-3H KIE is also influenced by the torsion angles of adjacent atoms and by polarization of the 2′-hydroxyl. Changing the virtual solvent (dielectric constant) does not influence the isotope effects. Unlike most N-ribosyltransferases, N7 of the leaving group adenine is not protonated at the transition state of S. pneumoniae MTAN. This feature differentiates the S. pneumoniae and E. coli transition states and explains the 103-fold decrease in the catalytic efficiency of S. pneumoniae MTAN relative to that from E. coli.
Keywords: 5’-methylthioadenosine, kinetic isotope effects, MTAN, 5′-methylthioadenosine nucleosidase, quorum sensing, nucleoside hydrolase, transition state, transition state analogue inhibitors, hyperconjugation
Introduction
Kinetic isotope effects (KIEs) have been useful in the study of kinetics,1-3 chemical equilibra,4-5 transition states,6-9 vibrational mode relaxations,10 tunneling,11-13 hyperconjugations14,15 and ionization.16-18 KIEs are particularly useful for studying transition states (TS) of enzymatic reactions. Multiple KIEs provide a boundary condition for the quantum chemistry calculations of a transition state. Iteratively applied constraints are then used to match the theoretical KIEs to the experimental ones. Transition state analogues capture catalytic forces imposed by enzymes and are powerful inhibitors.19-21 Knowledge of enzymatic transition states has lead to the design of some of the tightest binding non-covalent inhibitors known, with dissociation constants in the femtomolar range and some of which are in clinical trials.22-26
Isotope effects (IEs) arise from altered bond vibrational environments. Binding isotope effects (BIEs) report equilibrium bond changes, for example, on formation of a Michaelis complex. Competitive KIEs or isotope effects on (V/K) are the isotope effect associated with the first irreversible step in enzyme catalyzed reactions and they approximate intrinsic KIEs when the first irreversible step is the bond breaking step. Partially irreversible steps between the substrate and the transition state can suppress intrinsic KIEs, but suppressed isotope effects can be corrected by isotope partition methods.27 Intrinsic KIEs are directly associated with changes in the normal modes between reactants and the transition states.
In this study multiple isotopomers of MTA were used to study the transition state of 5′-methylthioadenosine/S-adenosylhomocysteine (MTAN) of S. pneumoniae, a bacterial enzyme involved in polyamine biosynthesis, quorum sensing, purine and methionine salvage.28-35 It catalyzes the physiologically irreversible hydrolytic cleavage of the N-glycosidic bonds of 5′-methylthioadenosine (MTA) or 5′-S-adenosylhomocysteine to 5′-methylthioribose, S-ribosylhomocysteine and adenine (Figure 1). Adenine is salvaged by adenine phosphoribosyltransferase (APRTase) and methylthioribose is converted to methionine in multiple steps.36 MTAN has been proposed to be a target for the design of antimicrobial agents because of its involvement in the synthesis of autoinducers2 (AI2). AI2s are quorum sensing molecules formed from S-ribosylhomocysteine and used by bacteria to signal biofilm formation, causing prolonged chronic infections. Mutational studies in Haemophilus influenzae, Streptococcus pneumoniae, Streptococcus pyogenes, and Enterococcus faecalis have suggested that mutations to the pfs gene (pfs gene encodes for MTAN) may reduce pathogenicity and the enzyme has been targeted for the design of antimicrobial agents.37-39
Figure 1.
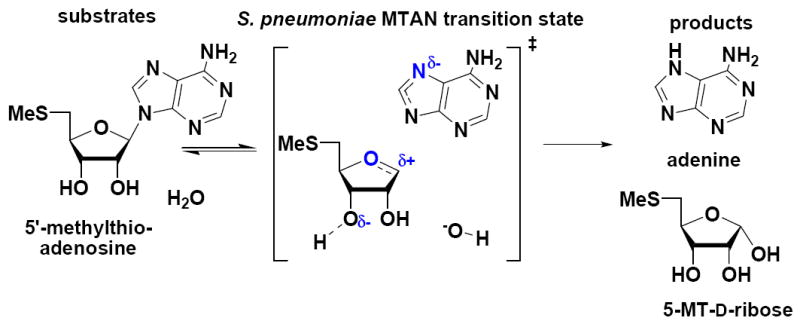
Hydrolysis of MTA by S. pneumoniae MTAN and the proposed transition state of the reaction. Features of the transition state that distinguish it from substrate are shown in blue.
E. coli MTAN has a dissociative SN1 transition state with full cleavage of the N-glycosidic bond and no participation of the attacking nucleophile. The adenine leaving group is activated by N7 protonation, a recurring theme in the acid-catalyzed cleavage of purine nucleosides. Other purine N-ribosyl transferases place an aspartate residue close of N7 (Asp197 for MTANs,22 Asp220 in MTAP40 and Asp198 in PNP41), which are proposed to protonate N7 at the transition states. Protonation of N7 makes the purine group electron deficient, weakening the N-ribosidic bond, and facilitates the reaction by forming neutral adenine as the leaving group.
In this study we explore the transition state of S. pneumoniae MTAN using 3H, 14C and 15N KIEs and model the transition state as an intermediate using density functional theory. The origin of remote KIEs, the effect of 2′- and 3′- hydroxyl ionizations, and the effects of altered torsion angles are investigated. The difficulty of explaining the large 1′-3H isotope effect (IE) observed in computational modeling of the dissociative SN1 transition states is addressed. Leaving group activation and hyperconjugation effects are explored to explain local and remote isotope effects.
Material and Methods
Expression of S. pneumoniae MTAN
Expression of S. pneumoniae MTAN in E. coli has been described.42 Briefly, the gene for S. pneumoniae MTAN was obtained by PCR amplification from genomic DNA and cloned into the pET23a(+) plasmid (Novagen). The MTAN gene was expressed in E. coli strain BL21 (DE3) at 37°C in the presence of 50 μg/mL carbenicillin for 4 hours after induction with IPTG. The expressed protein was purified on Ni2+-NTA His-Bind affinity columns and eluted with imidazole. Active fractions were further purified on a Superdex 200 gel filtration column. The purified protein was concentrated to 15 mg/mL and stored at -70° C.
Enzymes and reagents for ATP synthesis
The reagents and the enzymes used in the synthesis of ATPs from glucose have been described previously.7, 43-45
Synthesis of radiolabeled MTAs
Isotopically labeled [1′-3H] MTA, [1′-14C] MTA, [2′-3H] MTA, [3′-3H] MTA, [4′-3H] MTA, [5′-3H2] MTA and [Methyl-3H3] MTA were synthesized from the corresponding ATP molecules in two steps using a procedure described elsewhere.7
Kinetic isotope effect measurements
Competitive kinetic isotope effects (KIEs) were measured by comparing the products formed from pairs of isotopically labeled substrates, as described previously.7 The KIEs were corrected to 0% hydrolysis by the equation
Where f is the fraction of reaction progress and Rf and Ro are ratios of heavy to light isotope at partial and total completion of reaction, respectively.
Commitment to catalysis
The forward commitment to catalysis for S. pneumoniae MTAN was measured by the isotope-trapping pulse-chase method.27 The pulse solution (100 mM HEPES pH 7.5, 50 mM KCl, 170 μM of [8-14C] MTA) was mixed with enzyme (17 μM) to give a 100 μl reaction mixture. After 3 s (0.6 of one catalytic turnover at kcat of 12 min-1) the solution was diluted with 900 μL of solution containing 2.7 mM unlabeled MTA in 100 mM HEPES pH 8.5 and 50 mM KCl (the chase solution). Samples of 100 μL were quenched with 1 N HCl starting at 10 s up to 120 s (Figure 2). The adenine product was isolated by reverse phase HPLC using C-18 Deltapak column by 25% methanol in 50 mM ammonium acetate pH 5.0 and quantitated by scintillation counting. A control experiment was quenchedμ with 1 N HCl after 3 sec instead of addition of chase. The amount of product formed during this period was subtracted from each of the experimental values used to calculate commitment. The forward commitment was calculated from a plot of the amount of labeled adenine formed following addition of chase solution divided by the amount of labeled MTA at the active site before dilution with chase solution. This data was extrapolated to zero time. The forward commitment factor is quantitated from the y-intercept using the expression: (intercept/1-intercept).
Figure 2.
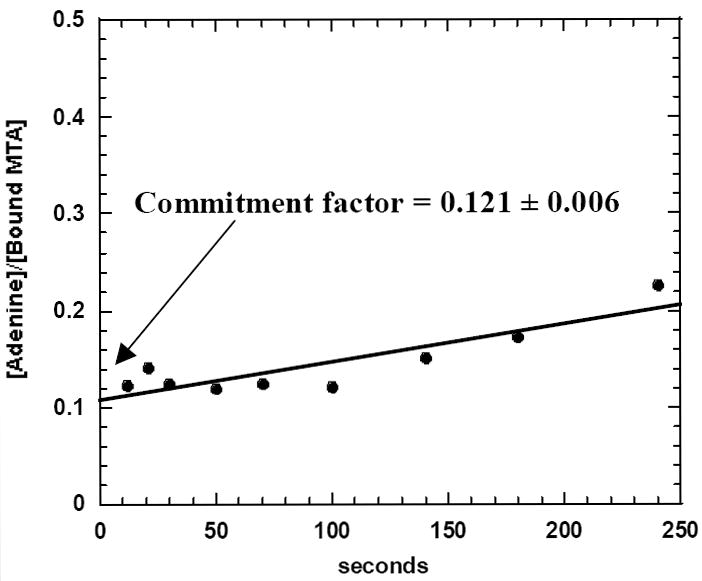
Forward commitment to catalysis for the MTAN-MTA complex. The complex of S. pneumoniae MTAN and [8-14C]MTA was diluted with a large excess of unlabeled MTA at 3 sec. Subsequent reaction partitions bound 14C-MTA to product (forward commitment) or permits release into free, unbound MTA. Zero commitment extrapolates through the origin while full (∞) commitment would intersect at 1.0 on the ordinate. Forward commitment was calculated by plotting the amount of labeled adenine formed following addition of chase solution divided by amount of labeled MTA on the active site before dilution with chase solution and extrapolating this ratio to zero time. The line is drawn from an ordinary least square fit of the data, y errors only. The intercept value is 0.108 ± 0.006. The forward commitment factor is calculated from the y-intercept using the expression: (intercept/1-intercept) and is 0.121 ± 0.006 for S. pneumoniae MTAN.
Computation of transition states
The in vacuo determination of the transition state for hydrolysis of MTA used hybrid density functional methods implemented in Gaussian03.46 The transition state was modeled as a ribooxacarbenium ion intermediate and a dissociated adenine leaving group using one-parameter Becke (B1) exchange functional, the LYP correlation functional and standard 6-31G* basis set.47 The same level of theory and basis set were used for optimization of substrate and products as well as for the computation of bond frequencies. The 5′-methylthio group was constrained during calculations by fixing the O4′-C4′-C5′-S and C4′-C5′-S-CS dihedral angles.
EIEs were calculated from the computed frequencies using ISOEFF 98 software.48 All calculated 3N-6 vibrational modes were used to calculate the isotope effects, but only those that exhibit shifts due to isotopic substitution contribute to the isotope effect. The isotope effects were calculated at the temperature of 298 K.
After each cycle of optimization, calculation of bond frequencies and isotope effects, geometric constraints applied to substrate and the transition state were optimized iteratively until the calculated equilibrium isotope effects for the transition state intermediate matched the experimental intrinsic KIEs. Constrained molecules impose energetically unfavorable positions relative to vacuum conditions for transition state searches. These reflect the forces imposed by the enzymatic environment.
Frequencies are obtained from the second derivative of the potential energy with respect to the reaction coordinate. For the unconstrained transition state a single imaginary frequency was obtained for the transition state. Standard frequency calculations are used to predicting isotope effects for the transition state. When multiple constraints are applied to the transition state additional imaginary frequencies (some not corresponding the reaction coordinate) can be generated. The standard frequency calculation does not discard bad imaginary frequencies and all 3N-6 normal modes are used for calculating the isotope effects. This can cause abnormal secondary KIEs. The solution was to model the transition state as an intermediate (no imaginary frequencies) and correlate EIEs to intrinsic KIEs to generate the transition state model. This method is a good approximation for the transition states of S. pneumoniae MTAN because of the complete loss of the C-N bond at the transition state. This gives an experimental intrinsic KIE and a calculated EIE of unity for the anomeric carbon. The KIE/EIE of unity supports loss of the C1′-N9 frequency completely compensated by increased frequencies to the neighboring C1′ atoms. Therefore, the transition states can be reasonably approximated as an intermediate. This way the generation of imaginary frequencies at remote sites following application of the multiple constraints can be avoided. Clearly, this approach yields an approximation of the transition state, as do all computational methods.
Natural Bond Orbital (NBO) calculations
The natural bond orbital (NBO) calculations were performed on optimized structures by including the pop = (nbo, full) keyword in the route section of input files.
Calculations of molecular electrostatic potential surface
The molecular electrostatic potential (MEP) surfaces were calculated by the CUBE subprogram of Gaussian03. The formatted checkpoint files used in the CUBE subprogram were generated by full or constrained geometry optimization at B1LYP level of theory and 6-31G* basis set. The MEP surfaces of the reactants and transition state were visualized using Molekel 4.049 at a density of 0.4 electron/Å3.50
Semiempirical, Ab initio and DFT calculations
The calculations described below were performed at density functional theory using B1LYP/6-31G* unless otherwise indicated. The output of NBO calculations was used to obtain the relative energy of hyperconjugation, sigma and sigma* orbital occupancy, charge and bond order.
A. 5-Methylthioribooxacarbenium ion
MTA at the transition state produced by S. pneumoniae MTAN was used to simulate the effect of rotation of the H1′-C1′-C2′-H2′ dihedral angle on the 2′-3H EIE. Remote geometry (O4′-C4′-C4′-S and C4′-C5′-S-CMe torsion angles) was constrained to ensure reasonable analogy between structures as the dihedral angle was varied. Isotope effects were computed for each torsion angle with respect to MTA.
B. 5’-Meththioribooxacarbenium 2′-hydroxyl polarization
The effect of 2′-hydroxyl polarization on 1′-3H and 2′-3H EIEs was explored by the computational methods described above. The H1′-C1′-C2′-H2′ torsion angle was fixed at 70°, where it generates a 2′-3H EIE similar to the intrinsic 2′-3H KIE. A hydroxyl anion was stepped closer to the 2′-OH to change the O-O bond distance in steps of 0.2 Å, each time performing an energy optimization. Interaction energy and isotope effect were determined for each distance. Remote geometry was constrained at the dihedral angles described above. A similar calculation explored the effect of polarization of the 3′-hydroxyl on the 4′-3H EIE. In these calculations the hydroxyl anion was positioned such that the Osugar-Hsugar-Ohydroxyl-Hhydroxyl torsion angle was 180°.
C. tetrahydro-2-((methylthio)-methyl)furan
This model molecule was used to study the effect of rotation of C4′-C5′-S-CMe torsion angle on the isotope effects of the methyl hydrogens. A 360° scan of the C4-C5-S-CMe torsion angle was performed. Isotope effects and NBO analyses were computed at each step. The O4′-C4′-C5′-S torsion angle was constrained to fix the 5′-methylthio relative to the furan ring and O4′-C1′-C2′-C3′ was constrained to prevent alteration in the ring pucker.
D. Solvation modeling
Solvation effects were examined by the Self Consistent Reaction Field (SCRF) method51 using the polarization continuum model implemented in Gaussin03.46 The homogenous dielectric environment is simulated by a virtual solvent characterized by the effective dielectric constant, εeff. Substrate was optimized in the dielectric environment of water with dielectric constant of 78.8, whereas the transition state was optimized in the presence of solvent with dielectric constants ranging from 4.9 of chloroform (similar to a dielectric constant of 4 assumed for the catalytic site) to that of 78.8 for water. A radius of 4.3 Å was used for the ribooxacarbenium ion transition state and for the substrate, a radius of 4.96 Å was used for the SCRF calculation. The recommended radii were obtained using the volume key word in the route section.
F. Effect of base orientation on 1′-3H EIE
The 1′-3H conformational equilibrium isotope effect was explored by examining the effect of the O4′-C1′-N9-C8 dihedral angle rotation in MTA on the 1′-3H EIE. The calculations were performed at the Hartree-Fock level of theory (HF/6-31G*). The output was used to evaluate the relative change in 1′-3H EIE with respect to orientation of base using scaled bond frequencies as described above. The ribose ring pucker and the 5′-methylthio group were constrained using the torsional angles described above.
G. 15N isotope effects and adenine protonation
Isotope effects (15N9, 15N7, 15N1, and 15N3) were calculated for adenine mono-protonated at N1, N3, N7 or N9 as well as for the unprotonated adenine. The isotope effects for adenine were calculated with respect to MTA. The structures for various adenines used in the calculation are included in the supplementary material.
Results
Experimental Kinetic Isotope Effects
Kinetic isotope effects were measured for the S. pneumoniae MTAN-catalyzed hydrolysis of MTA to adenine and 5-methylthioribose using substrate competition experiments. The observed isotope effects give (V/K) isotope effects that include a contribution from forward commitment factors. The hydrolytic reaction catalyzed by S. pneumoniae MTAN is physiologically irreversible; therefore reverse commitment is unlikely. Observed KIEs that include contribution from the forward commitment are listed in Table 1. These KIEs report vibrational changes between MTA free in solution and at the transition state. Irreversible steps before the bond breaking step obscure the intrinsic KIEs. Since the measured KIEs are in the range observed for intrinsic KIEs for other N-ribosyl transferases, forward commitment is modest.
Table 1.
Kinetic Isotope Effects (KIEs) measured at pH 7.5 for hydrolysis of MTA catalyzed by S. pneumoniae MTAN
| Substrate | Type of KIE | Experimental KIEa | Intrinsic KIEs |
|---|---|---|---|
| [1′-3H] and [5′-14C] MTA | α-secondary | 1.210 ± 0.002 | 1.235 ± 0.002 |
| [1′-14C] and [5′-3H2] MTA | primary | 1.000 ± 0.005b | 1.000 ± 0.005 |
| [2′-3H] and [5′-14C] MTA | β-secondary | 1.085 ± 0.002 | 1.095 ± 0.002 |
| [9-15N/5′-14C] /[5′-3H2]MTA | primary | 1.033 ± 0.004c | 1.037 ± 0.004 |
| [4′-3H] and [5′-14C] MTA | γ-secondary | 1.011 ± 0.005 | 1.012 ± 0.005 |
| [5′-3H2] and [5′-14C] MTA | δ-secondary | 1.017 ± 0.002 | 1.019 ± 0.002 |
| [Me-3H3] and [5′-14C] MTA | remote | 1.050 ± 0.002 | 1.056 ± 0.002 |
Experimental KIEs are corrected to 0% substrate depletion.
The 1′- 14C KIE was corrected for 5′- 3H KIE according to expression KIE= KIEobserved × 5′-3H2 KIE.
The 9-15N KIE was corrected for 5′-3H2 KIE according to expression KIE = KIEobserved × 5′-3H2 KIE. The intrinsic KIEs are obtained by correcting the KIEs on V/K for the forward commitment of 0.121.
KIEs were 1.21 for [1′-3H], 1.085 for [2′-3H], and 1.033 for [15N9]. These large isotope effects are indicative of a small commitment factor and substantial vibrational changes experienced by atoms close to the reaction center at the transition state compare to unbound substrate in solution.52 Surprisingly, a large intrinsic KIE of 1.050 was observed for the [Methyl-3H3] of the methylthio group, even though it is four bonds from the reaction center.
Commitment Correction and Intrinsic KIEs
Forward commitment for S. pneumoniae MTAN was measured at pH 7.5 using the isotope trapping method.27 The external forward commitment factor of 0.121 ± 0.006 for S. pneumoniae MTAN establishes that binding of MTA to the enzyme at pH 7.5 is partially committed (Figure 2). The TKeq for the MTAN reaction is assumed to be near unity since the anomeric carbon is sp3-hybridized in both reactant and product. The intrinsic isotope effects for reversible reaction are related to isotope effect on T(V/K) by the expression
Where T (V / K) is an observed (tritium or other isotope) isotope effect, Cf is the forward commitment for catalysis, Cr is the reverse commitment to catalysis, T Keq is the equilibrium isotope effect, and Tk is the intrinsic isotope effect.53 The reaction catalyzed by S. pneumoniae MTAN is irreversible under initial rate conditions therefore the above expression can be reduced to;
Intrinsic isotope effects can be obtained from the observed isotope effects (Table 1).
Correction for Remote Label KIEs
In experiments measuring the tritium KIEs, [5′-14C] MTA was used as a remote label for lighter isotopes. The isotope effect at 5′-14C was assumed to be unity because it is three bonds distant from the reaction center and 14C does not report isotope effects for geometric changes, unlike remote tritium labels.8,9 For measuring 1′-14C and 9-15N KIEs, [5′-3H2] MTA was used as remote label. The KIE for 1′-14C and 9-15N were corrected for the remote label KIE as significant remote KIEs are obtained with 5′-3H2 and 4′-3H, even though these atoms are four and three bonds away from the reaction center.
Computational Modeling of the Transition State for S. pneumoniae MTAN
The initial ab initio transition state of S. pneumoniae MTAN was modeled by including the leaving group and the nucleophile and had a single imaginary frequency of 397 i cm-1, corresponding to the decomposition mode. The transition state structure corresponding to this imaginary frequency had an SN2-like conformation with significant bonds to both the leaving group and the nucleophile. This transition state predicted a large isotope effect for [1′-14C] MTA, characteristic of SN2 transition states. The 1′-14C KIE of unity for S. pneumoniae MTAN establishes a transition state closely related to an isolated ribooxacarbenium-ion. Subsequent transition state calculations did not include the leaving group or the nucleophile.
Intrinsic KIEs of 1.037 for [9-15N] MTA, 1.00 for [1′-14C] MTA and a large α -secondary intrinsic KIE of 1.23 for [1′-3H] MTA suggest a fully-dissociative SN1 transition state for S. pneumoniae MTAN. The α-primary KIE of unity for [1′-14C] MTA indicates insignificant bond order to the leaving group and the attacking water nucleophile and little reaction coordinate motion. Fully-dissociative SN1 transition states can be modeled as oxacarbenium ion intermediates.9 The transition state was modeled using B1LYP level of theory and 6-31G(d) basis set implemented in Gaussian03. During the calculations the 5′-methylthio group was constrained using the torsion angle from the crystal structure of S. pneumoniae MTAN with a transition state analogue (MT-ImmA).54 The H1′-C1′-C2′-H2′, O4′-C4′-C5′-S and C4′-C5′-S-CS torsion angles were iteratively optimized until the calculated EIEs closely approximated the intrinsic KIEs. The leaving group adenine at the transition state was modeled separately (discussed below in context with 15N9). The effect of basis set and the level of theory on the calculated isotope effects are shown in Table 2 and properties of the transition state are listed in Table 3.
Table 2.
Effect of theory and basis set on calculated equilibrium isotope effects (EIEs) for the transition state of S. pneumoniae MTAN.
| Gas Phase
|
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| Hartree-Fock
|
B1LYP
|
B3LYP
|
|||||||
| Label | Expta | PM3 | 3-21G | 6-31G(d) | 6-31G(d, p) | 6-31G(d) | 6-31G(d, p) | 6-31G(d) | 6-31G(d, p) |
| [1′-3H] | 1.235 | 1.17 | 1.510 | 1.47 | 1.48 | 1.46 | 1.45 | 1.42 | 1.44 |
| [1′-14C] | 1.000 | 1.006 | 1.011 | 1.007 | 1.007 | 1.00 | 1.000 | 1.00 | 1.00 |
| [2’-3H] | 1.095 | 1.210 | 1.053 | 1.082 | 1.089 | 1.095 | 1.108 | 1.085 | 1.10 |
| [4′-3H] | 1.012 | 1.070 | 1.017 | 0.960 | 0.961 | 0.945 | 0.950 | 0.945 | 0.930 |
| [9-15N] | 1.037 | 1.021 | 1.035 | 1.031 | 1.024 | 1.035 | 1.030 | 1.028 | 1.028 |
| [5′-3H] | 1.019b | 1.009c | 1.031c | 0.989c | 0.985c | 1.002c | 1.00c | 0.992 | 0.990c |
| -pro(R) | 0.996 | 1.047 | 1.014 | 1.012 | 1.022 | 1.020 | 1.021 | 1.019 | |
| -pro(S) | 1.013 | 0.985 | 0.976 | 0.974 | 0.980 | 0.980 | 0.972 | 0.972 | |
| [Me-3H] | 1.056d | 1.053e | 1.079e | 1.050e | 1.067e | 1.045e | 1.035e | 1.017e | 1.034e |
| 1A | 0.980 | 1.015 | 0.975 | 0.994 | 0.990 | 0.99 | 0.980 | 0.990 | |
| 2B | 1.016 | 1.041 | 1.017 | 1.014 | 1.011 | 1.01 | 1.010 | 1.010 | |
| 3C | 1.057 | 1.022 | 1.059 | 1.059 | 1.044 | 1.035 | 1.028 | 1.034 | |
Experimental intrinsic KIEs,
Intrinsic [5′-3H2] KIE,
Overall calculated 5′-3H isotope effect obtained by multiplying 5′-proR and 5′-proS 3H isotope effects,
[Me-3H3] Intrinsic KIE,
Table 3.
Geometric and electronic changes in representative models of the substrate and the transition state for S. p. MTAN calculated using B1LYP/6-31G*.
| Bond Length
|
Bond Order Changea |
Hyperconjugation (kcals/mol)b |
Orbital Changesc |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bond Type | GS | TS | Δ(σ –σ*) | Substrate | TS | ΔΣ(TS-GS) | GS hybrid | Carbon cont.(%) | TS hybrid | Carbon cont.(%) | ||
| σ→ | →σ* | σ→ | →σ* | |||||||||
| C1′-H1′ | 1.0938 | 1.0905 | -0.01410 | 10.87 | 8.26 | 8.42 | 8.70 | -1.28 | sp2.82 | 62.80 | sp1.84 | 63.70 |
| C2′-H2′ | 1.0964 | 1.1003 | +0.02739 | 5.47 | 11.54 | 14.16d | 8.51 | -0.11 | sp2.69 | 62.18 | sp2.89 | 64.59 |
| C4′-H4′ | 1.0980 | 1.0883 | -0.01407 | 8.85 | 12.50e | 8.81 | 5.59 | 3.60 | sp3.01 | 61.81 | sp2.68 | 64.63 |
| C1′-N9 | 1.4564 | NA | NA | 9.02 | 27.41 | NA | NA | NA | sp3.26 | 35.72 | NA | NA |
| C5′-H5′ (R) | 1.0931 | 1.0957 | -0.01750 | 5.18 | 4.27 | 3.87 | 6.60g | 4.39 | sp3.04 | 63.81 | sp3.13 | 63.64 |
| C5′-H5′ (S) | 1.0935 | 1.0915 | -0.00092 | 3.62 | 5.21h | 4.29 | 3.77 | -0.30 | sp2.92 | 63.13 | sp2.79 | 64.57 |
| CS-H(A) | 1.0920 | 1.0902 | +0.00181 | 2.45 | 1.21 | 0.74 | 2.76i | 1.18 | sp2.96 | 62.78 | sp2.76 | 63.74 |
| CS-H(B) | 1.0926 | 1.0913 | -0.00629 | 0.00 | 4.20 | 0.58 | 1.20i | 0.01 | sp2.82 | 62.48 | sp2.84 | 62.31 |
| CS-H(C) | 1.0918 | 1.0902 | -0.00360 | 0.70 | 4.70j | 1.32 | 2.60i | -1.81 | sp2.78 | 62.36 | sp2.78 | 63.25 |
| C3′-H3′ | 1.0936 | 1.0892 | -0.00699 | 7.92 | 10.95 | 5.38 | 9.15k | 1.29 | sp2.72 | 63.13 | sp2.51 | 64.41 |
Calculated by subtracting the number of electrons occupying the σ* orbital from the number occupying the σ orbital and listed as change between Substrate and Transition state (TS) (Substrate-TS).
Sum of second order perturbation contributions calculated by NBO analysis. Cutoff = 0.5 kcals/mol.
Hybridization of the carbon atom and contribution of the carbon atom to the bond in percent. GS = ground state of substrate, TS = transition state. Lp1 is the sp-type lone pair; and Lp2 is p-type lone pair:
Lp2(C1’);
While Lp2(O4’);
Lp(O3’);
Lp2(S);
Lp2(S);
Lp2(S);
Lp2(S) are better acceptors in the substrate.
Lp2(O3’) are better acceptors in the transition state;
The H1′-C1′-C2′-H2′ dihedral angle and the 2′-3H EIE
The β-secondary 2′-3H isotope effect arises from the positive hyperconjugation of σ (C2′-H2′) bonding electrons to the partially empty p-orbital on the adjacent anomeric carbon in reactions involving carbocation-like transition states. The 2′-3H EIEs correlates inversely with the occupancy of σ (C2′-H2′) orbital on the anomeric carbon (Figure 3). The isotope effect is small inverse (~1%) between 0° and 45°, and increases steeply between 50° and 80° to a maximum value of 1.12 at a H1′-C1′-C2′-H2′ torsional angle of 90°, suggesting maximum overlap of σ (C2′-H2′) bonding orbitals with the p-orbital on the anomeric carbon.
Figure 3.
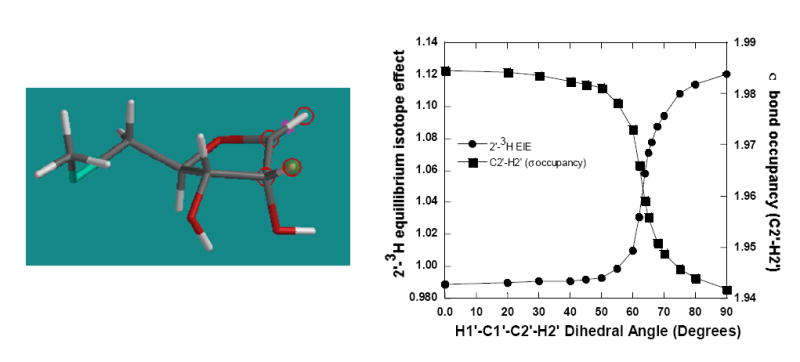
Geometry at the H1′-C1′-C2′-H2′ torsion angle alters the 2′-3H equilibrium isotope effect (EIE) and C2′-H2′ σ bond occupancy for the transition state of S. pneumoniae MTAN (upper right panel). The atoms of the H1′-C1′-C2′-H2′ torsion angle are circled in the model (upper left panel). The isotope effects are calculated with respect to MTA.
Polarization of the 2′-hydroxyl
Polarization of an OH bond generates an isotope effect on geminal CH bonds.52, 55 However, the effect of polarizing the OH bond adjacent to a carbocation has not been reported. The crystal structure of MT-ImmA, a proposed transition state analogue inhibitor, with S. pneumoniae MTAN suggests that the side chain of Glu174 forms a hydrogen bond to the 2′-OH (O-O distance 2.7 Å) and possibly polarizes the bond.42 The effect of 2′-OH polarization on the 2′-3H KIE was examined by moving a hydroxyl anion toward the 2′-OH from 4.0 Å to 2.4 Å in steps of 0.2 Å. Polarization of the 2′-OH sigma bond causes the 2′-3H IE to increase from 1.10 to 1.18 as the hydroxyl is stepped from 4.0 Å to 2.6 Å (Figure 4). The 2′-3H IE increases sharply from 1.18 to 1.40 as the OH- nucleophile is moved from 2.6 Å to 2.4 Å. The increase in 2′-3H IE with the polarization of 2′-OH expectedly correlates with the increase in C2′-H2′ bond length. The observed increase in C2′-H2′ bond length and the 2′-3H IE is most likely due to increased hyperconjugation from an enlarged sp-type lone pair at the 2′-oxygen due to polarization of the OH bond. The change in 2′-3H IE due to polarization is mainly in the decreased stretching frequency of C2′-H2′ since bending frequencies remain relatively unchanged during the process (data not shown).
Figure 4.
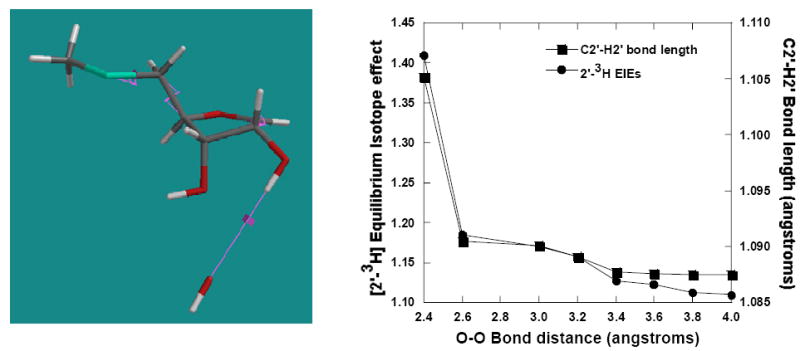
Polarization of the 2′-hydroxyl by a hydroxy anion alters the 2′-3H isotope effect. The change in 2′-3H IE and C2′-H2′ bond length is shown in right panel. The model on the left shows the geometry used in the calculation. The isotope effects are calculated with respect to MTA.
Ionization of glucose hydroxyls has been shown to cause significant isotope effects at geminal and adjacent CH centers.55 It was therefore expected that the ionization of the 2′-OH would cause an isotope effect at 1′-3H and at 3′-3H. The effect on 1′-3H is discussed under the 1′-3H IE section. The calculated 3′-3H IE increases to 1.060 upon ionization of the 2′-hydroxyl. Model calculations with isopropanol predict that the 3H isotope effect on vicinal CH bonds is approximately 1/3rd of that to the geminal CH bonds,52 similar to that found here.
Rotation of the H2′-C2′-O-H and H3′-C3′-O-H torsion angles and the 2′-3H IE
Variation of the 2′ -3H EIE in the transition state of S. pneumoniae MTAN due to rotation of H2′-C2′-O-H torsion angle is shown in Figure 5. The isotope effects were normalized with respect to the H2′-C2′-O-H torsion angle of 100°. The H1′-C1′-C2′-H2′, O4′-C4′-C5′-S and C4′-C5′-S-CS torsion angles were constrained to restrict the effect to the H2′-C2′-O-H torsion angle. At a H2′-C2′-O-H torsion angle of 70° a maximum isotope effect of 1.145 was observed for 2′ -3H. The variation in 2′ -3H EIE due to changes in the H2′-C2′-O-H torsion angle arises from the alignment of unhybridized p-type lone pair of the oxygen with the σ* (C2′-H2′) antibonding orbital (data not shown).
Figure 5.
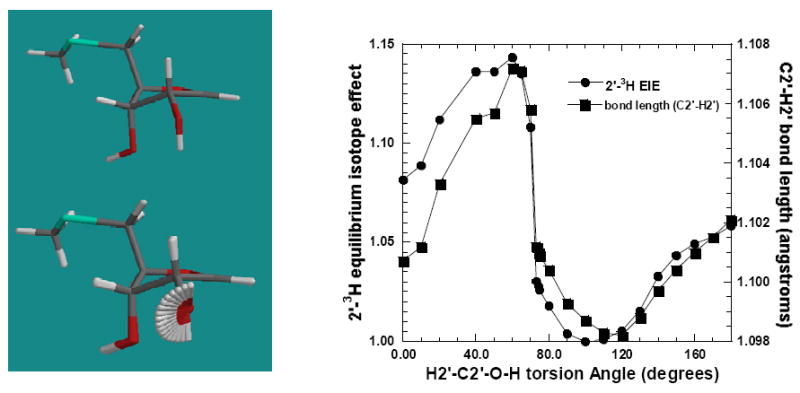
Relative change in 2′-3H isotope effects (IEs) and C2′-H2′ bond length due to rotation of the H2′-C2′-O-H torsion angle. The isotope effects are calculated with respect to a H2′-C2′-O-H torsion angle of 90°.
The rotation of the H3′-C3′-O-H torsion angle causes upto a 2% change in 2′-3H IE, with the maximum isotope effect induced at the torsion angle of 160° (supplementary material).
Modeling of 1′-3H
The in vacuo models of transition states of enzymatic reactions that proceed via dissociative SN1 transition states predict a larger value of 1′-3H IE than the experimental intrinsic value. For example, E. coli MTAN gave a 1′-3H intrinsic KIE of 1.16 compared to the calculated KIE of 1.38.7 Similarly, human and Plasmodium falciparum PNPs had intrinsic KIEs of 1.16 and 1.18, whereas as the calculated KIEs predicted a value of ~1.50.9 The rationale usually invoked to explain these large calculated isotope effects is that the interactions of C1′-H1′ with the catalytic site (or solvent) residues at the transition state dampens the out-of-plane bending motions (the major source of 1′-3H KIE), causing the suppression of the 1′-3H KIE. The absence of these effects in the in vacuo calculations gives a large value for the 1′-3H IE. In the following discussion we explore various factors, including the proposed dampening out-of-plane bending motions by van der Waal interactions, that may influence the 1′-3H IE:
a. Effect of the O4′-C1′-N9-C8 torsion angle
MTA has energetically preferred conformations for rotation around the N-glycosidic bond; a possible contribution to the 1′-3H IE. The effect of rotation of O4′-C1′-N9-C8 on 1′-3H IE was studied in MTA using the dihedral angle of 80° as the reference for calculating isotope effects. At an O4′-C1′-N9-C8 dihedral angle of 80° the C1′-H1′ bond is the shortest and the 1′-3H IE effects for all the other angles are normal with respect to the 80° torsion angle (Figure 6). At the O4′-C1′-N9-C8 torsion angle of 180°, adenine is syn to 5′-methylthioribose and at 0° it is in the anti conformation. Adenine prefers anticlinical and antiperiplanar conformations between 130°-180° as well syn-conformations between 30° and 60°, but the barrier for rotation around O4′-C1′-N9-C8 torsional angle is not large (~ 0.7 kcals/mol). The 1′-3H IE increases with the change in dihedral angle on either side of 80° and is largest (1.074) at 180°/anti conformation. The syn/0° conformation for adenine also gave a large normal isotope effect of 1.063. Thus, orientation of adenine, when immobilized by the enzyme, could change the calculated 1′-3H IE by as much as 1.074.
Figure 6.
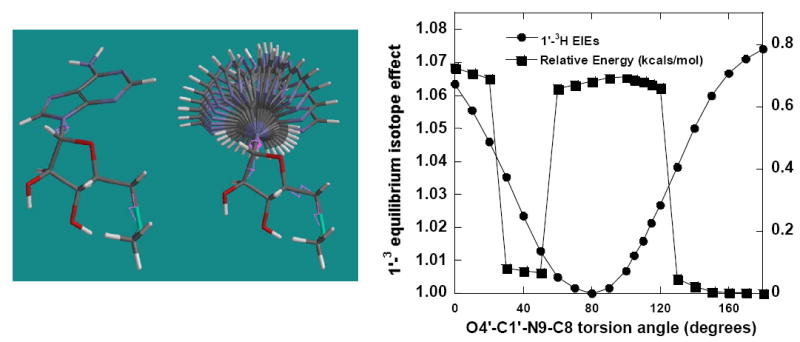
Relative change in 1′-3H EIEs and total relative energy due to rotation of the O4′-C1′-N9-C8 torsion angle in MTA. The isotope effects are calculated with respect to MTA with an O4′-C1′-N9-C8 torsion angle of 80°.
b. Effect of changing the dielectric constant
The dielectric constant (∊) experienced by reactant is significantly different when bound to enzyme relative to solvent. Proteins in solution can have localized microenvironments of high ∊, including the active sites of enzymes which are expected to have many polar groups.56 A range of dielectric constants from 4.9 to 78.8 was explored as a possible source of isotope effects. Changing the dielectric field has no influence on the 1′-3H isotope effect (Table 5). Isotope effects at other positions remain relatively unchanged as the ∊ is increased. Secondary isotope effects are vibrational effects and are sensitive to the distribution of electron density and behavior of electron density that depends on the geometrical structure of the molecule. The structure of the transition state remains relatively unchanged upon increasing the ∊.
Table 5.
Effect of Virtual Solvent on EIEs
| Dielectric constant | Equilibrium Isotope effects (EIEs)a |
|
|---|---|---|
| 1′-3H | 1′-14C | |
| 4.90 | 1.415 | 1.003 |
| 10.36 | 1.415 | 1.003 |
| 20.70 | 1.416 | 1.003 |
| 32.63 | 1.416 | 1.003 |
| 38.20 | 1.416 | 1.003 |
| 46.70 | 1.416 | 1.003 |
| 78.70 | 1.416 | 1.003 |
Isotope effects were calculated for the unconstrained fully dissociated 5′-methylribooxacarbenium ion at the indicated dielectric constants with respect to the 5′-methylthioadenosine (MTA) in water (ε = 78.8). Structures used for calculating the isotope effects are provided in the supplementary material.
c. van der Waal Interactions
The active sites of enzymes are proposed to be more constrained at the transition state than in the ground state. Thus, van der Waal clashes of C1′-H1′ with residues in the active site might dampen the out-of-plane bending motion of C1′-H1′ bond and reduce 1′-3H KIE. This proposal was evaluated using a minimal model of the S. pneumoniae MTAN transition state and a hydrogen molecule. The effect on 1′-3H IE was studied by impinging a hydrogen molecule on C1′-H1′ by bringing it (axially along the horizontal axis) from a distance of 3.0Å to 1.2 Å. The 1′-3H IE increased as the hydrogen approaches close to the van der Waal radii of H1′ (upper left panel (Figure 7)). The 1′-3H IE increased from 1.48 to 1.70 as the H1′-Hhydrogen distance was reduced from 1.8 Å to 1.2 Å (van der Waal radius of the hydrogen atom is 1.2 Å). The bond length of C1′-H1′ also increased progressively with the reduction in H1′-Hhydrogen distance and has the same general shape as the 1′-3H IE. The incoming hydrogen molecule induces a dipole in H1′ and the resulting induced dipole-dipole interaction weakened the C1′-H1′ bond, reduced stretching force constants and increased the 1′-3H IEs. This minimal model demonstrates that horizontal approach of a molecule to the van der Waal radii of H1′ would increase the 1′-3H IE. Similar results were obtained using oxygen or formaldehyde instead of hydrogen (supplementary material). Therefore, van der Waal interactions with the transition state are unlikely to decrease the 1′-3H IE by dampening the out-of-plane bending motion of C1′-H1′.
Figure 7.
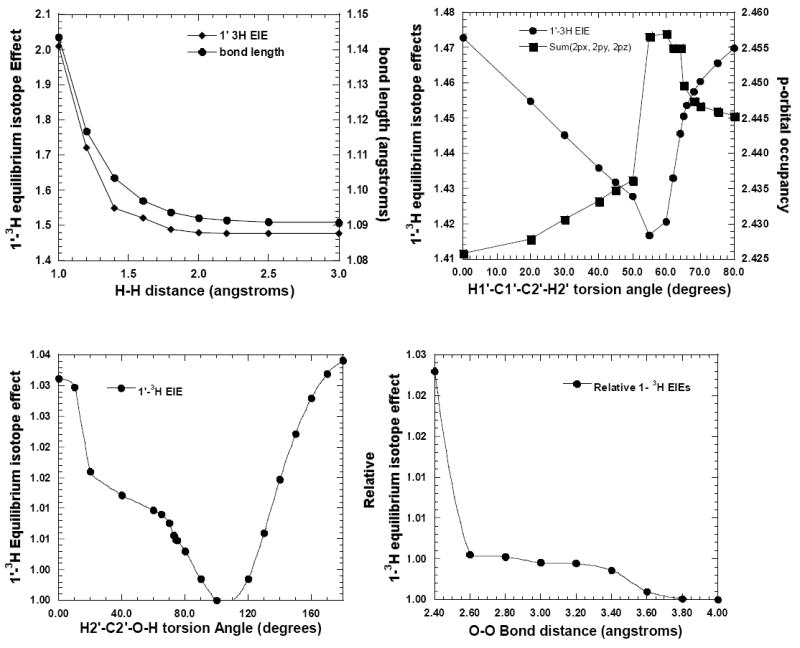
Calculations showing factors affecting 1′-3H EIEs. Changes in 1′-3H EIEs and length of the C1′-H1′ bond are shown due to steric imposition of a hydrogen molecule on the C1′-H1′ bond at the transition state of S. pneumoniae MTAN. A similar result with oxygen and formaldehyde (see supporting material) is shown in the upper left panel. The variation in 1′-3H EIEs and occupancy of the p-orbital (sum of px, py, and pz) of C1′ with altered H1′-C1′-C2′-H2′ torsion angle is shown in upper right panel. The 1′-3H EIEs in the upper panels are calculated with respect to MTA. Relative change in 1′-3 H EIEs by rotation of the H2′-C2′-O-H torsion angle at the transition state is shown in the lower left panel. The isotope effects are calculated with respect to a H2′-C2′-O-H torsion angle of 100°. The effect of polarization of the 2′-hydroxyl on relative 1′-3H EIEs is shown in the lower right panel. The IE are calculated with respect to a O2’hydroxyl-Oanion distance of 4.0 Å.
e. Varied H1′-C1′-C2′-H2′ and H2′-C2′-O-H torsion angles, polarization of the 2′-OH and 1′-3H isotope effect
Rotation of the H1′-C1′-C2′-H2′ and H2′-C2′-O-H torsion angles have a significant effect on the α-secondary 1′-3H IE. Orientation of the H1′-C1′-C2′-H2′ torsion angle can contribute a maximum of 1.05 to the 1′-3H IE (upper right and lower left, Figure 7), whereas the H2′-C2′-O-H torsion angle can contribute a maximum of 1.04. The 1′-3H IEs of 1.04 and 1.03 were observed for H2′-C2′-O-H torsion angle of 180° and 0°, respectively.
Polarization of the 2′-hydroxyl also influences the 1′-3H IE. A maximum change of 1.028 was observed for complete ionization of 2′-hydroxyl (lower right, Figure 7).
Protonation of adenine nitrogens and 15N EIEs
S. pneumoniae MTAN has a fully-dissociated transition state. Dissociation of the N-glycosidic bond in MTA causes increased electron density in adenine, increasing the pKa of adenine nitrogens. In most purine N-ribosyl transferases, protonation of the purine at N7 is proposed as a part of the transition state structure. Here 15N EIEs are explored for monoprotonated adenine at N1, N3, N7 or N9 and for the unprotonated adenine relative to unprotonated MTA (Table 4). Monoprotonation at N1 gives an inverse 15N1 IE of 0.987 and the isotope effects for 15N3 and 15N7 were close to unity but an IE of 1.028 at 15N9. The large normal isotope effect at N9 occurs because dissociation of the C1′-N9 bond causes increased vibrational freedom at N9. Protonation at N3 also gave IEs of unity for 15N3, 15N7 and 15N1, but a large normal isotope effect of 1.028 for 15N9, similar to N1 protonation. A small decrease in the 15N9 IE, from 1.028 to 1.025, was observed with N7 protonation. Protonation of N9 results in substantial decrease in the 15N9 isotope effect; from 1.028 to 1.010. The decrease is due to partial compensation of the lost C1′-N9 mode with the H-N9 mode. Significant changes in 15N IEs were also observed for unprotonated adenine. Conversion of MTA to anionic adenine gave 15N1 and 15N7 IE of 1.010 and 1.018, respectively whereas the isotope effect for 15N9 increased to 1.035, close to the theoretical maximum of 1.040 for 15N. The large 15N9 IE is due to the increased vibrational freedom following dissociation of N-glycosidic bond and due to the absence of compensatory increase in bond order in the absence of conjugated ring system. Disruption of conjugation in unprotonated adenine causes decrease in vibrational modes due to decrease in bond order to N9. Total bond length to N9 (C4-N9 and C8-N9) increased from 2.688 Å in protonated adenine to 2.714 Å in unprotonated adenine. Small normal 15N1 and 15N7 IEs were also observed in unprotonated adenine.
Table 4.
Effect of Adenine protonation on N1, N3, N7, N9 KIEs.
| Site of Protonation on Adenine | Calculated Kinetic Isotope Effectsa |
|||
|---|---|---|---|---|
| N1 | N3 | N7 | N9 | |
| N1 | 0.987 | 0.999 | 1.003 | 1.028 |
| N3 | 0.999 | 0.999 | 1.003 | 1.028 |
| N7 | 0.998 | 0.999 | 1.002 | 1.025 |
| N9 | 1.000 | 1.000 | 1.000 | 1.010 |
| Unprotonated | 1.010 | 1.002 | 1.018 | 1.035 |
The isotope effects are calculated with respect to MTA. The table reports the 15N isotope effects at four adenine nitrogens due to protonation of N1, N3, N7 or N9 and also for unprotonated adenine. The structures used in the calculations are given in the supplementary material.
Polarization of the 3′-hydroxyl and the 4′-3H EIE
Crystal structures of E. coli and S. pneumoniae MTAN with MT-ImmA, a transition state analogue inhibitor of MTAN, indicate that the 3′-hydroxyl of MT-ImmA is strongly hydrogen bonded to Glu174; suggesting partial or full polarization of the 3′-OH at the transition state. Polarization of the 2′-OH causes significant changes in the properties of the neighboring C2′-H2′, C1′-H1′, and C3′-H3′ bonds. However the effect on the C4′-H4′ bond is minimal. Polarization of the 3′-OH is expected to influence the 4′-3H and 2′-3H IEs. A hydroxyl anion was used to polarize the 3′-OH bond in the transition state of S. pneumoniae MTAN (Figure 8). The 4′-3H IE increased steadily from 0.94 to 1.015 as the hydroxyl nucleophile is stepped from 4.0 Å to 2.4 Å. Unlike the 2′-hydroxyl polarization, no sudden increase in isotope effect was observed between 2.5 Å and 2.4 Å (Figure 8). Complete ionization of the 3′-OH gives a maximum isotope effect of 1.015 for 4′-3H, an increase from 0.945 to 1.015. Although the 4′-3 H IE increased steadily, no increase in hyperconjugation between the lone pairs of O3 and the σ* (C4′-H4′) antibonding orbital was observed, suggesting an indirect mechanism of electron transfer. The change in 4′-3H IE correlates strongly with the increase in negative charge on ring oxygen (O4′) (Figure 8). Ionization of 3′-hydroxyl results in delocalization of electrons that are shared unequally by more electronegative or electron deficient atoms in the ribose ring. Unequal charge sharing due to ionization of a hydroxyl has been observed in glucose.55 These inductive electronic effects can result in increased hyperconjugation to the adjacent σ* (C4′-H4′) antibonding orbital, causing the 4′-3H IE and the 2′-3H IE to increase. The size of these remote IEs, calculated in vacuo, will be influenced by the nature of the contacts at the catalytic site. However they provide a useful indication of the origins of the intrinsic IEs.
Figure 8.
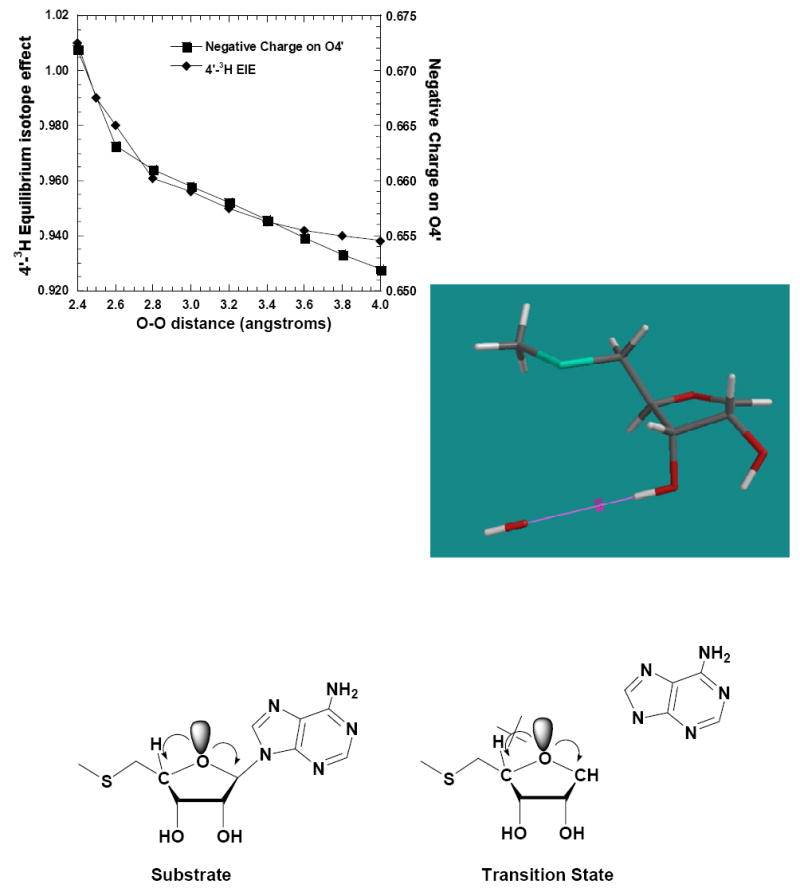
Variation of 4′-3H EIEs due to polarization of the 3′-OH by a hydroxyl anion. The altered charge on the ring oxygen is shown (upper right panel). The model at the bottom shows the difference in the hyperconjugation pattern of the lone pair of ring oxygen (O4′) in MTA and at the transition state. The 4′-3H EIEs are calculated relative to MTA.
Effect of the C4′-C5′-S-CMe torsion angle rotation on [Me-3H3] KIEs
The 5′-methylthio group of MTA is free to rotate about the C5′-S bond, altering the C4′-C5′-S-CMe torsional angle. This torsion angle is fixed near − 82.7° and − 87.7°, respectively in the active sites of S. pneumoniae42 and E. coli MTAN56 with MT-ImmA. Freezing of this torsion angle upon binding to enzyme could give the 1.056 isotope effect observed from the methyl hydrogens. Rotation of the C4′-C5′-S-CMe torsional angle was explored as a possible source of the isotope effect (Figure 9).
Figure 9.
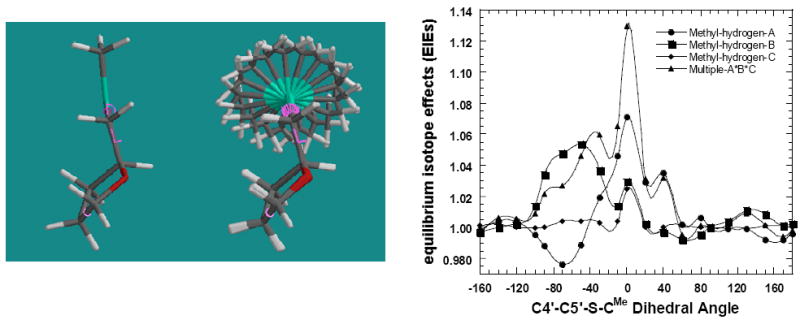
Rotation of C4′-C5′-S-CMe torsion angle in tetrahydro-2-((methylthio)-methyl) furan. The tritium isotope effects of the three methyl C-Hs and the overall EIEs are summarized in the upper right panel. The overall tritium isotope effect (3H3) for three methyl hydrogens was calculated by multiplying the individual 3H1 isotope effect for methyl hydrogens. The geometry is show in the left panel using in a tube model. The furan ring is numbered as in MTA with C4′ being the carbon to which the 5′-methylthiogroup is attached and the methyl hydrogens are indicated as HA, HB and HC.
Tetrahydro-2-((methylthio) methyl) furan provided a minimal model for rotation of the C4′-C5′-S-CMe torsion angle. The C-H bonds of the methyl group were not constrained during the calculation. Puckering of the furan ring was fixed during the calculation by constraining the O4′-C1′-C2′-C3′ torsion angle to 27°, while the C4′-C5′-S-CMe torsional angle was stepped through 360° in 20° increments (Figure 9). A C4′-C5′-S-CMe torsional angle of 0° gave the shortest overall average bond length and was used as the reference state. The methyl hydrogens show distinct angular variation of their isotope effects. Angular variation of the isotope effects is due to variation of negative hyperconjugation (np(S) to σ*(CH) antibonding orbital) upon rotation of the C4′-C5′-S-CMe bond. Three energetic mimina are found at -120°, between -40° to +20° and at +120°, although the barrier for rotation is relatively small at 0.76 kcal/mol (supplementary material).
Variation of isotope effects at methyl hydrogens in the cationic transition state was investigated by repeating the calculation with deprotonated tetrahydro-2-((methylthio) methyl)furan at C4, the atom corresponding to C1′ in MTA. Deprotonation at C4 reduced the maximum isotope effect from 1.13 to 1.044 (supplementary material). The observed decrease is mainly due to reduction in the negative hyperconjugation of the lone pair of sulphur.
Discussion
Transition state of S. pneumoniae MTAN and 1′-14C isotope effect
The α-primary 1′-14C KIE is the most diagnostic isotope effect for nucleophilic substitution reactions.57 It is sensitive to the bond orders of leaving group and the attacking nucleophile at the transition state. Associative SN2 transition states have an α-primary 1′-14C KIE of 1.080 to 1.13, whereas isotope effects of 1.03 to 1.08 correspond to small residual bond orders in SN1 transition states and fully dissociative SN1 transition states are characterized by 1′-14C KIEs close to unity. Most N-ribosyltransferases have 1′-14C KIE between 1.00 and 1.03 7, 9, and have dissociative SN1 mechanisms with significant ribooxacarbenium character. The primarya 1′-14C IE of unity for S. pneumoniae MTAN indicates a dissociative DN*AN mechanism. Loss of bond order to the leaving group is compensated by increased bond order to O4′, H1′ and C2′, since all 3N-6 vibrational modes in the reactant and oxacarbenium ion contribute the isotope effects (supplementary material).
Natural bond orbital analysis of the transition state and MTA indicates that the anomeric carbon is sp1.84 hybridized at the transition state relative to sp2.82 in the substrate (Table 2). These changes increase the cationic character at the transition state (positive charge on 04′ and C1′ increases by +0.14 and +0.34 respectively) relative to MTA. This sharing of charge is characteristic of ribooxacarbenium ions. 57 The transition state is also characterized by a partially empty p-orbital on the anomeric carbon that causes isotope effects at α-, β- and δ-positions.
Protonation of N7 and primary [9-15N] Isotope Effect (IE)
The maximum 9-15N theoretical KIE value predicted for loss of the C1′-N9 bond is 1.04. In MTA, loss of the N-glycosidic bond predicts a 9-15N IE of 1.035 (Table 4) and partial restoration of conjugation in the adenine ring system through protonation of N7 decreases the 9-15N IE from 1.035 to 1.025. The 9-15N intrinsic KIE of 1.037 measured for S. pneumoniae MTAN indicates a complete loss of the C1′-N9 bond at the transition state, a conclusion also supported by the 1′-14C KIE. Complete loss of the C1′-N9 bond causes significant re-hybridization of N9 and natural bond orbital analysis predicts N9 to be sp1.89 hybridized at the transition state compared to sp2.84 in MTA. The 9-15N intrinsic KIE of 1.037 indicates adenine is not protonated and therefore is anionic at the transition state. Protonation of adenine in S. pneumoniae MTAN occurs after the substrate has passed the transition state and breaking the N-glycosidic bond precedes adenine protonation. The transition state of S. pneumoniae MTAN differs from the transition state of MTAN from E. coli,7 which involves activation of the leaving group in the form of N7 protonation. Breaking the N-ribosidic without leaving group activation suggests that a major force in achieving the transition state is conversion of the ribosyl group to the ribooxacarbenium ion (discussed further with 4′-3H KIE).
Sugar puckering and the 2′-3H KIE
The β-secondary 2′-3H KIE is influenced by hyperconjugation of the σ (C2′-H2′) electrons to the partially empty 2pz orbital of C1′, polarization of the 2′-OH and orientation of the H2′-C2′-O-H torsion angle. The extent of hyperconjugation depends on overlap between the C2′-H2′ sigma bond and the electron-deficient p-orbital on the anomeric carbon. The KIE is greatest when the C2′-H2′ bond is parallel to the carbenium ion p-orbital and reaches a minimum when the C-H bond is perpendicular to the orbital. The isotope effect varies as a cos2θ function of this overlap. The extent of hyperconjugation is also affected by the amount of positive charge or the emptiness of the p-orbital on the anomeric carbon. For a fully-dissociated SN1 transition state a 2′-3H KIE of 1.12 was calculated for a 2pz-C1′-C2′-H2′ dihedral angle of 0° (Figure-3). The intrinsic KIE of 1.092 measured for S. pneumoniae MTAN corresponds to a H1′-C1′-C2′-H2′ torsion angle of 70° (or p-orbital-C1′-C2′-H2′ of 20°) indicating substantial overlap with the partially empty 2pz orbital at C1′. A H1′-C1′-C2′-H2′ torsion angle of 70° indicates 3-exo puckering for the ribosyl group and a O4′-C1′-C2′-C3′ dihedral angle of 13°. The magnitude of the 2′-3H KIE is also sensitive to polarization of the 2′-hydroxyl and orientation of the H2′-C2′-O-H torsion angle. Glu174 is within hydrogen bonding distance from the 2′-hydroxyl in S. pneumoniae and is conserved in MTANs, suggesting polarization of the 2′-OH may contribute to the 2′-3H KIE.7, 42 With the sugar pucker of the transition state fixed to that of MT-ImmA bound to MTAN,42 a H1′-C1′-C2′-H2′ torsion angle of 65° was obtained and corresponds to an isotope effect of 1.064 (Figure 3). Of the total 2′-3H KIE of 1.092, 1.064 comes from hyperconjugation and 1.028 is from polarization of 2′-hydroxyl or 3′-hydroxyl and/or orientation of the H2′-C2′-O-H torsion angle.
1′-3H KIE
The intrinsic 1′-3H KIE of 1.235 contains contributions from the out-of-plane bending modes58 of C1′-H1′ to give a normal KIE as well as altered C1′-H1′ stretching modes which contribute inversely to the KIE (inverse effects). The normal isotope effect caused by increased out-of-plane bending motion is always opposed by increased stretching mode force constants. Although both factors contribute to the magnitude of this KIE, the relative variation in the observed 1′-3H KIE for different enzymes is dominated by decreased force constants for bending modes at the transition state.
Computational modeling of the 1′-3H KIE to match experimental values is difficult and has been discussed.57 The computed isotope effect for 1′-3H MTA for the S. pneumoniae MTAN transition state at 298K in vacuum using the B1LYP/6-31G(d) level of theory is 1.47, almost double the intrinsic 1′-3H KIE of 1.23. Although van der Waal interactions have been implicated, these interactions have an opposite effect in the calculated 1′-3H IE (see above). Ground state effects including the O4′-C1′-N9-C8 torsion angle, polarization of the 2′-OH and rotation of the H2′-C2′-O-H bond can also influence the 1′-3H IE. Together they can contribute about 1.14 to the calculated 1′-3H IE, but still do not account for the large discrepancy in the calculated 1′-3H IE. Dampening of bending modes due to van der Waal interactions is also unlikely as these interactions increase the calculated isotope effect further due to a decrease in stretching modes. Crystal structures of MTANs from S. pneumoniae and E. coli show the region surrounding C1′-H1′ with no residue in van der Waal contact, although dynamic excursions involved in the transition state formation cannot be ruled out. It is also possible that the discrepancy between intrinsic and calculated 1′-3H isotope effects is due to the inaccuracy of density function theory (DFT) and Hartree-Fock (HF) methods in predicting the bending modes. For example, the semiempirical PM3 method predicts a value of 1.17 close to the intrinsic 1′-3H KIE of 1.23. The geometry of the transition state does not depend on matching the 1′-3H KIE and the value is consistent with KIEs measured for other ribooxacarbenium ion transition states.
The [4′-3H] KIE and transition state structure
The C4′-H4′ bond is three bonds from the reaction center and is alpha to the C4′-O4′ bond. In MTA the lone pair (np) of O4′ hyperconjugates with the σ* (C4′-H4′) antibonding orbital and decreases its bond order. The cationic transition state causes diversion of np of O4′ towards the cationic anomeric carbon (C1′). Hyperconjugation towards the C1′ at the transition state is compensated by decreased hyperconjugation of np of O4′ into the σ* (C4′-H4′) antibonding orbital, causing shortening of C4′-H4′ sigma bond (Figure 8). Natural bond orbital analysis predicted a large electron delocalization energy (6.59 kcal/mol) for the np (O4′) to σ* (C4′-H4′) hyperconjugation in MTA but less than <0.5 kcal/mol in the transition state. This change predicts a stiffer C4′-H4′ bond at the transition state to give an inverse 4′-3H KIE. An inverse 4′-3H IE of 0.945 was calculated for the transition state, in contrast to the experimental intrinsic KIE of 1.015. The 4′-3H KIE measured for S. pneumoniae MTAN is similar to that of 1.010 measured for E. coli MTAN. Based on calculations with on 2-propanol, it was argued that 3′-hydroxyl polarization would increase hyperconjugation between lone pairs of the 3′-hydroxyl oxygen and the σ*(C4′-H4′) antibonding orbital.7 The crystal structure of E. coli MTAN with MT-ImmA shows the Glu174 carboxylate 2.7Å from the 3′-hydroxyl.43 S. pneumoniae MTAN also has Glu174 interacting with the 3′-hydroxyl, therefore a similar mechanism of 3′-hydroxyl deprotonation at the transition state would explain the KIE. Using a hydroxyl anion to polarize the 3′-hydroxyl of the S. pneumoniae MTAN transition state gave an isotope effect of 1.015 for 4′-3H for complete ionization of the 3′-hydroxyl, due to increased np(O4′) to σ* (C4′-H4′) hyperconjugation and greater charge accumulation on O4′. The increased charge on O4′ also stabilizes the transition state by electron sharing with the cationic C1′.
Remote [Me-3H3] and [5′-3H2] KIEs
An intrinsic isotope effect of 1.056 was measured for methyl-3H3 MTA for S. pneumoniae MTAN. The methylthio group of 5′-methylthioadenosine is fixed in the active site of S. pneumoniae MTAN by hydrophobic interaction with non-polar residues including Met9, Ile50, Val102, Phe105 and Phe207.42 Freezing the C4′-C5′-S-CMe torsion angle subsequent to MTA binding gives rise to the observed isotope effect (Figure 9).
An intrinsic KIE of 1.019 for 5′-3H2 MTA in S. pneumoniae MTAN is small compared to other N-ribosyl transferases such as purine nucleoside phosphorylase and thymidine phosphorylase. The 5′-methylthio group of MTA differs from the hydroxymethyl of inosine in its lack of hydrogen bonding potential, which is responsible for most of the 5′-3H KIE observed in PNPs and thymidine phosphorylase.8 For S. pneumoniae MTAN the calculation predicted a 5′- 3H2 KIE of 1.00 (the product of 5′-pro-R and 5′-pro-S hydrogen isotope effects). The 5′-pro-R and 5′-pro-S hydrogens behave differently to give isotope effects of 1.022 and 0.98 respectively. The normal isotope effect for the 5′-pro-R hydrogen is due to hyperconjugation between lone pair of sulphur and its σ* antibonding orbital. For the 5′-proS hydrogen the inverse isotope effect is due to the change in hyperconjugation from the sigma bond of the C5′-H5′ proS hydrogen to the antibonding orbital of C4′-C5′. Freezing of the torsional angle upon binding and during the transition state gives rise to the observed 5′-3H KIE.
Ribose hydroxyls and the catalytic rate of S. pneumoniae MTAN
The transition state for S. pneumoniae MTAN has unprotonated adenine as the leaving group, uncoupling activation of the leaving group from N-glycosidic bond loss. Transition state analysis, mutation studies and kinetics of substrate analogues for E. coli MTAN have demonstrated the importance of ribose hydroxyls in catalysis. Mutation of Glu174 to Ala or Gln completely abolishes the catalytic activity in E. coli MTAN. Further 3′-deoxy-MTA is not a substrate whereas 2′-deoxy-MTA retains 82% of its catalytic activity. These studies imply that ionization of 3′-OH by Glu174 may be essential for catalysis in E. coli MTAN. Ionization of the 3′-OH by Glu174 releases electrons towards the purine ring, raising the pKa of N7, causing it to abstract a proton from the Asp197. Mutation of Asp197 completely abolishes catalytic activity in E. coli MTAN.
The crystal structure of S. pneumoniae MTAN with MT-ImmA shows complete conservation of active site residues supporting a similar mechanism. However the approximately 1000-fold decrease in catalytic efficiency by S. pneumoniae MTAN indicates an altered mechanism of transition state stabilization. The intrinsic KIE for 4′-3H KIE of 1.015 for S. pneumoniae MTAN and 1.010 for E. coli MTAN support ionization of the 3′-hydroxyl by Glu174 for transition states of both enzymes. Unlike E. coli MTAN, the N7 in S. pneumoniae MTAN is not protonated, indicating a high energy transition state for S. pneumoniae MTAN. The kcat/Kmof E. coli MTAN for hydrolysis of MTA is ~1000 times greater than the kcat/Km for S. pneumoniae MTAN, caused by the asynchronous loss of the N-ribosidic bond and proton donation to adenine.
Catalysis in S. pneumoniae MTAN is initiated by significant or complete polarization of the 3′-hydroxyl by Glu174, causing electron density to increase in the ribosyl group. The C1′-N9 bond strength weakens due to increased occupancy of σ*(C1′-N9) antibonding orbital. Cleavage of the N-ribosidic bond is slow in the absence of leaving group activation in S. pneumoniae MTAN. In contrast, the combination of 3′-OH ionization combined with the protonation of N7 accelerates the catalysis in E. coli MTAN.
Related purine N-ribosyltransferases achieve transition state with a neutral purine leaving group because of N7 protonation and a cationic ribooxacarbenium ion. In S. pneumoniae
MTAN, the leaving group adenine is anionic at the transition state. To compensate, the ribosyl becomes a charge neutral but strongly polarized zwitterion, anionic at the 3′-OH and cationic at C1′. In both mechanisms, the net charge difference between the ribosyl group and the leaving group is the same.
Conclusion
S. pneumoniae MTAN has a fully dissociative SN1 mechanism. The leaving group adenine is anionic at the transition state and therefore S. pneumoniae MTAN has a high energy transition state compared to the transition state of closely related E. coli MTAN. To achieve leaving group separation, the 3′-hydroxyl is deprotonated or strongly polarized at the transition state to form a zwitterionic ribosyl group. The dissociative transition state for S. pneumoniae MTAN predicts tighter binding of DADMe-Immucillins compared to Immucillins and this has been experimentally confirmed.42 Changing the dielectric field constant does not influence KIEs. van der Waal interactions between catalytic site residues and the transition state increases the 1′-3H KIE and does not explain computational anomaly of large KIE at this site. A general conclusion is that perturbation (deprotonation, formation of carbocation, rotation of torsion angles) in any part of the molecule influences all other atoms and is manifested in alterations in the isotope effects.
Supplementary Material
Figure 10.
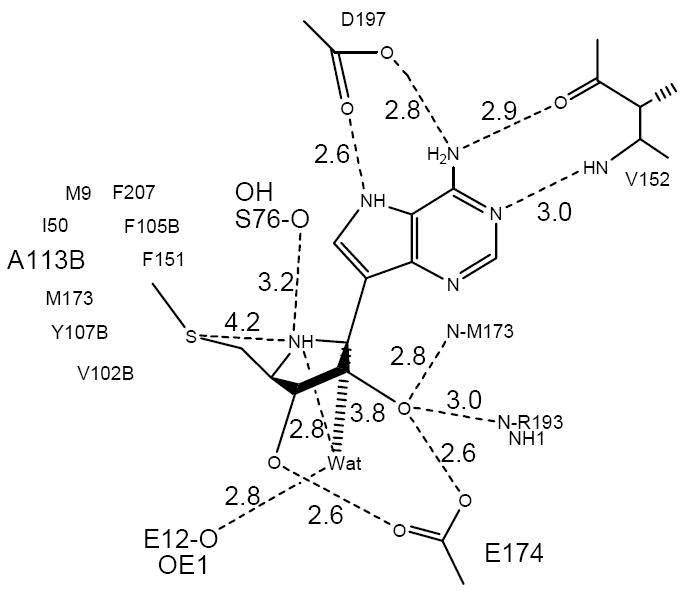
The contacts made by MT-ImmA, a transition state analogue with the residues in the active site of S. pneumoniae MTAN43.
Figure 11.
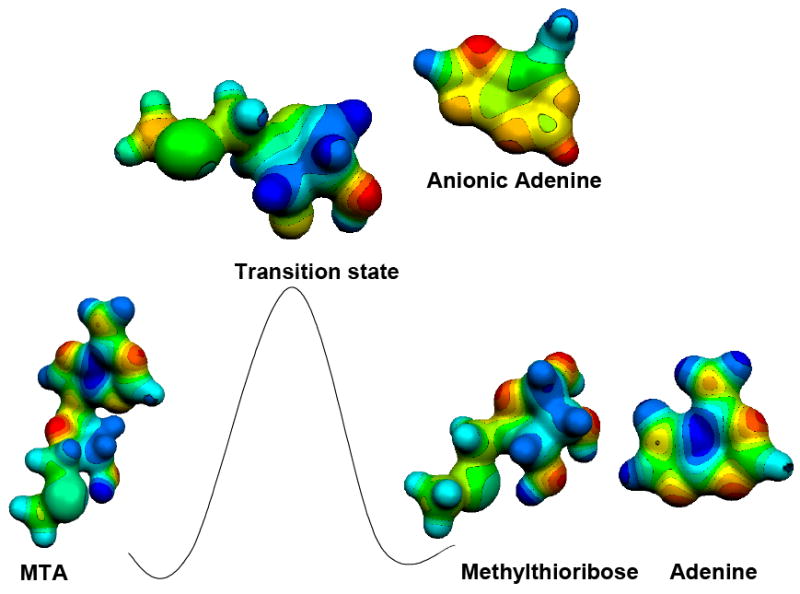
Reaction coordinate showing the molecular electrostatic surface potential of 5′-methylthioadenosine (a substrate), the transition state and adenine with 5-methylthioribose (products). MEPs were calculated at HF/STO3G (Gaussian 98/cube) for the geometry optimized at the B1LYP/6-31G(d) level of theory and visualized with Molekel 4.034 at a density of 0.4 electron/Å3.
Footnotes
This work was supported by NIH Research Grant GM 41916.
Abbreviations: MTA, 5′-methylthioadenosine; SAH, S-adenosylhomocysteine; SAM, 5-adenosylmethionine; MTR, 5-methylthioribose; MTAN, 5′methylthioadenosine/S-adenosylhomocysteine nucleosidase; MT-ImmA, MT-Immucillin-A, (1S)-1-(9-deazaadenin-9-yl)-1,4-dideoxy-1,4-imino-5-methylthio-D-ribitol; MT-DADMe-ImmA, 5′-methylthio-DADMe-Immucillin-A, (3R,4S)-1-[(9-deazaadenin-9-yl)methyl]-3-hydroxy-4-(methylthiomethyl)pyrrolidine;
Atoms of MT-ribose are numbered primed and of adenine are numbered unprimed in MTA both in the ground state as well as at the transition state. At the transition state’S. pneumoniae has no bond order to the adenine leaving group.
References
- 1.Cleland WW. Arch Biochem Biophy. 2005;433:2–12. doi: 10.1016/j.abb.2004.08.027. [DOI] [PubMed] [Google Scholar]
- 2.Bennet AJ, Sinnot ML. J Am Chem Soc. 1986;108:7287–7294. [Google Scholar]
- 3.Paneth B. Applications of Heavy Atom Isotope Effects. Synthesis and Applications of Isotopically Labeled Compounds. 1997 [Google Scholar]
- 4.Anet FAL, Basus VJ, Hewett APW, Saunders M. J Am Chem Soc. 1980;102:3945–3946. [Google Scholar]
- 5.Lewis BE, Schramm VL. J Am Chem Soc. 2001;123:1327–1336. doi: 10.1021/ja003291k. [DOI] [PubMed] [Google Scholar]
- 6.Craig BN, Janssen MU, Wickersham BM, Rabb DM, Chang PS, O’Leary DJ. J Org Chem. 1996;61:9610–9613. [Google Scholar]
- 7.Singh V, Lee JE, Nunez S, Howell LP, Schramm VL. Biochemistry. 2005;44:11647–11659. doi: 10.1021/bi050863a. [DOI] [PubMed] [Google Scholar]
- 8.Birck MR, Schramm VL. J Am Chem Soc. 2004;126:2447–2453. doi: 10.1021/ja039260h. [DOI] [PubMed] [Google Scholar]
- 9.Lewandowicz A, Schramm VL. Biochemistry. 2004;43:1458–1468. doi: 10.1021/bi0359123. [DOI] [PubMed] [Google Scholar]
- 10.Gambogi JE, L’Esperance RP, Lehmann KK, Pate BH, Scoles G. J Chem Phys. 1993;98:1116–1122. [Google Scholar]
- 11.Cha Y, Murray CJ, Klinman JP. Science. 1989;243:1325–1330. doi: 10.1126/science.2646716. [DOI] [PubMed] [Google Scholar]
- 12.Johnsson T, Edmondson DE, Klinmann JP. Biochemistry. 1994;33:14871–14878. doi: 10.1021/bi00253a026. [DOI] [PubMed] [Google Scholar]
- 13.Xue Q, Horsewill AJ, Johnson MR, Trommsdorff HP. J Chem Phys. 2004;120:11107–11119. doi: 10.1063/1.1738644. [DOI] [PubMed] [Google Scholar]
- 14.Lewis ES. Tetrahedron. 1959;5:143–148. [Google Scholar]
- 15.Shiner VJ., Jr Tetrahedron. 1959;5:243–252. [Google Scholar]
- 16.Northcott D, Robertson RE. J Phys Chem. 1969;73:1559–1563. [Google Scholar]
- 17.Heys JR. J Chromatogr. 1987;407:37–47. [Google Scholar]
- 18.Lewis ES, Boozer CE. J Am Chem Soc. 1952;74:6306–6307. [Google Scholar]
- 19.Wolfenden R. Nature. 1969;223:704–705. doi: 10.1038/223704a0. [DOI] [PubMed] [Google Scholar]
- 20.Wolfenden R, Snider MJ. Acc Chem Res. 2001;34:938–945. doi: 10.1021/ar000058i. [DOI] [PubMed] [Google Scholar]
- 21.Miller BG, Wolfenden R. Annu Rev Biochem. 2002;71:847–885. doi: 10.1146/annurev.biochem.71.110601.135446. [DOI] [PubMed] [Google Scholar]
- 22.Singh V, Evans GB, Lenz DH, Painter GF, Tyler PC, Furneaux RH, Lee JE, Howell PL, Schramm VL. J Biol Chem. 2005;280:18265–18273. doi: 10.1074/jbc.M414472200. [DOI] [PubMed] [Google Scholar]
- 23.Miles RW, Tyler PC, Furneaux RH, Bagdassarian CK, Schramm VL. Biochemistry. 1998;37:8615–8621. doi: 10.1021/bi980658d. [DOI] [PubMed] [Google Scholar]
- 24.Kicska GA, Tyler PC, Evans GB, Furneaux RH, Fedorov A, Lewandowicz A, Cahill SM, Almo SC, Schramm VL. Biochemistry. 2002;41:14489–14498. doi: 10.1021/bi026636f. [DOI] [PubMed] [Google Scholar]
- 25.Lewandowicz A, Tyler PC, Evans GB, Furneaux RH, Schramm VL. J Biol Chem. 2003;278:31465–31468. doi: 10.1074/jbc.C300259200. [DOI] [PubMed] [Google Scholar]
- 26.see http://www.biocryst.com
- 27.Rose IA. Methods Enzymol. 1980;64:47–59. doi: 10.1016/s0076-6879(80)64004-x. [DOI] [PubMed] [Google Scholar]
- 28.Schauder S, Shokat K, Surette MG, Bassler BL. Mol Microbiol. 2001;41:463–476. doi: 10.1046/j.1365-2958.2001.02532.x. [DOI] [PubMed] [Google Scholar]
- 29.Ragione D, Porcelli FM, Carteni-Farina M, Zappia V, Pegg AE. Biochem J. 1985;232:335–341. doi: 10.1042/bj2320335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Miller CH, Duerre JA. J Biol Chem. 1968;243:92–97. [PubMed] [Google Scholar]
- 31.Tabor CW, Tabor H. Methods Enzymol. 1983;94:294–297. [Google Scholar]
- 32.Xavier KB, Bassler BL. Curr Opin Microbiol Rev. 2003;6:191–197. doi: 10.1016/s1369-5274(03)00028-6. [DOI] [PubMed] [Google Scholar]
- 33.Parsek MR, Val DL, Hanzelka BL, Cronan JE, Jr, Greenberg EP. Proc Natl Acad Sci. 1999;96:4360–4365. doi: 10.1073/pnas.96.8.4360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Withers H, Swift HS, Williams P. Curr Opin Microbiol. 2001;4:186–193. doi: 10.1016/s1369-5274(00)00187-9. [DOI] [PubMed] [Google Scholar]
- 35.Miller MB, Skorupski K, Lenz DH, Taylor RK, Bassler BL. Cell. 2002;110:303–314. doi: 10.1016/s0092-8674(02)00829-2. [DOI] [PubMed] [Google Scholar]
- 36.Myers RW, Abeles RH. J Biol Chem. 1989;264:10547–10551. [PubMed] [Google Scholar]
- 37.Cadieux N, Bradbeer C, Reeger-Schneider E, Koster W, Mohanty AK, Wiener MC, Kadner RJ. J Bacteriol. 2002;184:706–717. doi: 10.1128/JB.184.3.706-717.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Riscoe MK, Ferro AJ, Fitchen JH. Parasitol Today. 1989;5:330–333. doi: 10.1016/0169-4758(89)90128-2. [DOI] [PubMed] [Google Scholar]
- 39.Sufrin JR, Meshnick SR, Spiess AJ, Garofalo-Hannman J, Pan XQ, Bacchi CJ. Antimicrob Agents Chemother. 1995;39:2511–2515. doi: 10.1128/aac.39.11.2511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Singh V, Shi W, Evans GB, Tyler PC, Furneaux RH, Schramm V. Biochemistry. 2004;43:9–18. doi: 10.1021/bi0358420. [DOI] [PubMed] [Google Scholar]
- 41.Shi W, Basso LA, Santos DS, Tyler PC, Furneaux RH, Blanchard JS, Almo AC, Schramm VL. Biochemistry. 2001;40:8204–8215. doi: 10.1021/bi010585p. [DOI] [PubMed] [Google Scholar]
- 42.Singh V, Shi W, Almo SC, Evans GB, Furneaux RH, Tyler PC, Zheng R, Schramm VL. Biochemistry. 2006 doi: 10.1021/bi061184i. submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Shi W, Tanaka KSE, Crother TR, Taylor MW, Almo SC, Schramm VL. Biochemistry. 2001;40:10800–10809. doi: 10.1021/bi010465h. [DOI] [PubMed] [Google Scholar]
- 44.Parkin DW, Leung HB, Schramm VL. J Biol Chem. 1984;259:9411–9417. [PubMed] [Google Scholar]
- 45.Rising KA, Schramm VL. J Am Chem Soc. 1994;116:6531–6536. [Google Scholar]
- 46.Frisch MJ, et al. Gaussian 03, Revision B.04. Gaussian, Inc.; Pittsburgh, PA: 2003. [Google Scholar]
- 47.Becke DA. J Chem Phys. 1996;104:1040–1046. [Google Scholar]
- 48.Anisimov V, Paneth P. ISOEFF98. J Math Chem. 1999;26:75–86. [Google Scholar]
- 49.Flükiger P, Lüthi HP, Portmann S, Weber J. MOLEKEL 4.0. Swiss Center for Scientific Computing, Manno; Switzerland: 2000. [Google Scholar]
- 50.Bagdassarian CK, Schramm VL, Schwartz SD. Biochemistry. 1996;37:8825–8836. [Google Scholar]
- 51.Cramer CJ, Truhlar DJ. Chem Rev. 1999;99:2161–2200. doi: 10.1021/cr960149m. [DOI] [PubMed] [Google Scholar]
- 52.Lewis BE, Schramm VL. J Am Chem Soc. 2003;125:4785–4798. doi: 10.1021/ja0298242. [DOI] [PubMed] [Google Scholar]
- 53.Northrop DB. Biochemistry. 1975;14:2644–2651. doi: 10.1021/bi00683a013. [DOI] [PubMed] [Google Scholar]
- 54.Lee JE, Singh V, Evans GB, Tyler PC, Furneaux RH, Cornell KA, Riscoe MK, Schramm VL, Howell LP. J Biol Chem. 2005;280:18274–82. doi: 10.1074/jbc.M414471200. [DOI] [PubMed] [Google Scholar]
- 55.Lewis BE, Schramm VL. J Am Chem Soc. 2003;125:7872–7877. doi: 10.1021/ja034983m. [DOI] [PubMed] [Google Scholar]
- 56.Dwyer JJ, Gittis AG, Karp DA, Lattman EE, Spencer DS, Stities WE, Garcia-Moreno BE. Biophysical Journal. 2000;79:1610–1620. doi: 10.1016/S0006-3495(00)76411-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Berti PJ, Tanaka KSE. Adv Phys Org Chem. 2002;37:239–314. [Google Scholar]
- 58.Pham TV, Fang YR, Westaway KC. J Am Chem Soc. 1997;119:227–232. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


