The presence of pseudosymmetry can cause problems in structure determination and refinement. The relevant background and representative examples are presented.
Keywords: pathology, twinning, pseudosymmetry
Abstract
It is not uncommon for protein crystals to crystallize with more than a single molecule per asymmetric unit. When more than a single molecule is present in the asymmetric unit, various pathological situations such as twinning, modulated crystals and pseudo translational or rotational symmetry can arise. The presence of pseudosymmetry can lead to uncertainties about the correct space group, especially in the presence of twinning. The background to certain common pathologies is presented and a new notation for space groups in unusual settings is introduced. The main concepts are illustrated with several examples from the literature and the Protein Data Bank.
1. Introduction
With the advent of automated methods in crystallography (Adams et al., 2002 ▶, 2004 ▶; Brunzelle et al., 2003 ▶; Lamzin & Perrakis, 2000 ▶; Lamzin et al., 2000 ▶; Snell et al., 2004 ▶), it is possible to solve a structure without visual inspection of the diffraction images (Winter, 2008 ▶; Holton & Alber, 2004 ▶), interpretation of the output of a molecular-replacement program (Read, 2001 ▶; Navaza, 1994 ▶; Vagin & Teplyakov, 2000 ▶) or, in extreme cases, manually building a model or even looking at the electron-density map (Emsley & Cowtan, 2004 ▶; Terwilliger, 2002a ▶,b ▶; Morris et al., 2003 ▶, 2004 ▶; Holton et al., 2000 ▶; Ioerger et al., 1999 ▶; McRee, 1999 ▶; Perrakis et al., 1999 ▶). Although automated methods often handle many routine structure-solution scenarios, pitfalls arising from certain pathologies are still outside the scope of most automated methods and often require human intervention to ensure smooth progress of structure solution or refinement.
This manuscript studies situations that arise when noncrystallographic symmetry (NCS) operators are close to true crystallographic symmetry, a situation known as pseudosymmetry. Pathologies of this type are often seen in protein crystallography (Dauter et al., 2005 ▶), since a large number of proteins crystallize with more than a single copy in the asymmetric unit or in various space groups.
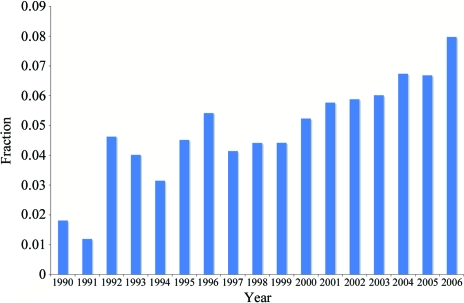
The distinction between ‘simple’ NCS and pseudosymmetry can be made in a number of ways. One way of defining pseudosymmetry is by idealizing NCS operators to crystallographic operators and determining the root-mean-square displacement (r.m.s.d.) between Cα atoms of the actual structure and the putative structure in which the pseudosymmetry is an exact symmetry. If the resulting r.m.s.d. is below a certain threshold value (say 3 Å), the structure can be called pseudosymmetric. Using this definition, we find that about 6% of the structures deposited in the PDB exhibit pseudosymmetry. This observation is in line with the observations of Wang & Janin (1993 ▶), who concluded that the alignment of NCS axes is biased towards crystallographic symmetry axes. On a year-to-year basis, there has been a slow increase in the fraction of new structures that exhibit pseudosymmetry (Fig. 1 ▶). This small increase is most likely to be the consequence of improvements in hardware and software that allow more routine detection, solution and refinement of structures with pseudosymmetry, as well as a general tendency to focus on more challenging proteins or protein complexes.
Figure 1.
Prevalence of structures with pseudosymmetry in the PDB since 1990. A 3 Å r.m.s.d. between NCS-related Cα was used. See text for details
In order to develop a better understanding of the consequences of pseudosymmetry, we review some basic concepts and introduce an efficient way of describing space groups in unusual settings. We furthermore ‘visualize’ relations between space groups via graphs similar to those generated by the Bilbao crystallographic server (Ivanchev et al., 2000 ▶). In contrast to these, the graphs presented here include the point groups or space groups in all orientations in which they occur in the supergroups, rather than just one representative per point-group or space-group type. This results in a more informative and complete overview of the relations between different groups.
A number of examples from the PDB (Berman et al., 2000 ▶; Bernstein et al., 1977 ▶) and literature are provided to illustrate common surprises and pitfalls arising from (pseudo) symmetry. We will describe structures with suspected incorrect symmetry, give an example of molecular replacement of twinned data with ambiguous space-group choices and illustrate the uses of group–subgroup relations.
2. Space groups, symmetry and approximate symmetry
2.1. Space groups in unusual settings
The standard reference for crystallographic space-group symmetry is International Tables for Crystallography Volume A (Hahn, 2002 ▶). In the following, we will use ITVA to refer to this work. ITVA Table 4.3.1 defines Hermann–Mauguin space-group symbols for 530 conventional settings of the 230 space-group types. This means that in general there are multiple settings for a given space-group type. For example, assume we are given an X-ray data set that can be integrated and scaled in space group P222. Further analysis of the data reveals systematic absences for (0, k, 0) with k odd. This suggests the space group is P2212. It may be useful or necessary (e.g. for compatibility with older software) to reindex the data set so that the twofold screw axis is parallel to a new c axis to obtain space group P2221. The space groups and unit cells before and after reindexing are said to be in different settings.
In the context of group–subgroup analysis with respect to a given metric (unit-cell parameters), unusual settings not tabulated in ITVA arise frequently. To be able to represent these with concise symbols, we have introduced universal Hermann–Mauguin symbols by borrowing an idea introduced in Shmueli et al. (2001 ▶): a change-of-basis symbol is appended to the conventional Hermann–Mauguin symbol. To obtain short symbols, two notations are used. For example (compare with Fig. 4 below),
These two symbols are equivalent, i.e. encode the same unconventional setting of space group No. 5. The change-of-basis matrix encoded with the x, y, z notation is the inverse transpose of the matrix encoded with the a, b, c notation. Often, for a given change of basis, one notation is significantly shorter than the other. The shortest symbol is used when composing the universal Hermann–Mauguin symbol.
Note that both change-of-basis notations have precedence in ITVA. The x, y, z notation is used to symbolize symmetry operators which act on coordinates. Similarly, the x, y, z change-of-basis symbol encodes a matrix that transforms coordinates from the reference setting to the unconventional setting. The a, b, c notation appears in ITVA §4.3, where it encodes basis-vector transformations. Our a, b, c notation is compatible with this convention. The a, b, c change-of-basis symbol encodes a matrix that transforms basis vectors from the reference setting to the unconventional setting. A comprehensive overview of transformation relations is given in and around Table 2.E.1 of Giacovazzo (1992 ▶).
2.2. Relations between groups
A subgroup H of a group G is a subset of the elements of G which also forms a (smaller) group. For instance, the symmetry operators of space group P222 can be described by {(x, y, z), (−x, y, −z), (x, −y, −z), (−x, −y, z)}. Subgroups of P222 can be constructed by selecting only certain operators. The full list of subgroups of P222 and the set of ‘remaining operators’ for each subgroup with respect to P222 are given in Table 1 ▶.
Table 1. Subgroups of P222.
For each subgroup, the symmetry operators are specified together with the operators that are elements of P222 but not of the subgroup.
| Space group | Operators | Remaining operators |
|---|---|---|
| P222 | (x, y, z), (−x, y, −z), (x, −y, −z), (−x, −y, z) | None |
| P211 | (x, y, z), (x, −y, −z) | (−x, y, −z), (−x, −y, z) |
| P121 | (x, y, z), (−x, y, −z) | (x, −y, −z), (−x, −y, z) |
| P112 | (x, y, z), (−x, −y, z) | (−x, y, −z), (x, −y, −z) |
| P1 | (x, y, z) | (−x, y, −z), (x, −y, −z), (−x, −y, z) |
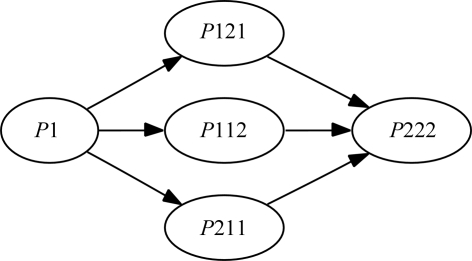
Note that if the operators of P211 are combined with one of the ‘remaining’ operators (−x, y, −z) or (−x, −y, z), the other operator is generated by group multiplication, leading to P222. A depiction of the relations between all subgroups of P222 is shown in Fig. 2 ▶. In this figure, nodes representing space groups are linked with arrows. The arrows between the space groups indicate that the multiplication of a single symmetry operator into a group results in the other group. For example, the arrow in Fig. 2 ▶ from P1 to P211 indicates that a single symmetry element [in this case (x, −y, −z)] combined with P1 results in the space group P211.
Figure 2.
A graphical representation of all group–subgroup relations for P222 and it subgroups. The arrows connecting two space groups represent the addition of a single operator to the parent space groups and its result.
2.3. Pseudosymmetry
As mentioned before, it is not uncommon that noncrystallographic symmetry can be approximated by crystallographic symmetry. A change of the space-group symmetry of a known crystal form, either a reduction or an increase of the symmetry, is often induced by ligand binding, the introduction of selenomethionine residues, halide or heavy-metal soaking or crystal growth under different conditions (Dauter et al., 2001 ▶; Poulsen et al., 2001 ▶; Parsons, 2003 ▶).
Group–subgroup relations and their graphical representations as outlined in §2.2 are a useful tool for understanding approximate symmetry and the resulting relations between the space groups of different crystal forms. The graphical representations can often provide an easy way of enumerating and illustrating all possible subgroups of a space group. This enumeration of possible space or point groups can be useful in the case of perfect merohedral twinning.
Constructing artificial structures with pseudosymmetry is straightforward. For example, given the asymmetric unit of a protein in P222, generate a symmetry-equivalent copy using the operator (−x, y, −z) or (−x, −y, z). If small random perturbations are applied to this new copy (e.g. a small overall rotation or small random shifts), then the two copies together can be considered as the asymmetric unit of a P211 structure with P222 pseudosymmetry. These two molecules are then related by an NCS operator that is close to a perfect twofold crystallographic rotation.
Note that in the previous example crystallographic symmetry operators were transformed into an NCS operator by the application of a small perturbation of the coordinates. The ‘remaining operators’ in Table 1 ▶ can be seen as NCS operators that are approximately equal to the listed operators.
3. Common pathologies
3.1. Rotational pseudosymmetry
Rotational pseudosymmetry (RPS) can arise if the (approximate) point-group symmetry of the lattice is higher than the point-group symmetry of the crystal. RPS is generated by an NCS operator parallel to a symmetry operator of the lattice that is not also a symmetry operator of the crystal space group. A prime example of such a case can be found in PDB entry 1q43 (Zagotta et al., 2003 ▶). The structure crystallizes in space group I4, with two molecules per asymmetric unit (ASU). The r.m.s.d. between the two copies in the ASU is 0.27 Å. The following NCS operator (in fractional coordinates) that relates one molecule to the other is
The rotational part R of the NCS operator can be recognized as being almost identical to a twofold axis in the xy plane. If the idealized operator (−y + ½, −x + ½, −z + 0.31) is combined with space group I4m we obtain space group I422 with an arbitrary origin shift along z, which is a polar axis in I4.
The R value between pseudosymmetry-related intensities as calculated from the coordinates is equal to 44%. For unrelated (independent) intensities, the R value is expected to be equal to 50% (Lebedev et al., 2006 ▶). In this case, it is clear that the correct symmetry is I4 rather than I422. However, there is a ‘grey area’ where it may be possible to merge the data with reasonable statistics in the higher symmetry. While this has the advantage of reducing the number of model parameters, over-idealization of the symmetry may lead to problems in structure solution and particularly refinement. Furthermore, information about biologically significant differences may be lost. In case of doubt, the best approach is to process and refine in both the lower and the higher symmetry and to compare the resulting R free values and model quality indicators.
3.2. Translational pseudosymmetry and pseudocentring
Translational pseudosymmetry (TPS) is generated by an NCS operator whose rotational part is close to a unit matrix. If a TPS operator or a combination of TPS operators is very similar to a group of lattice-centring operators, it can be denoted as pseudocentring. An example is PDB entry 1sct (Royer et al., 1995 ▶), where an NCS operator (x + ½, y + ½, z) mimics a C-centring operator. In this particular case, the true space group is P212121, but pseudosymmetric C2221.
In reciprocal space, the presence of pseudocentring operators translates into a systematic modulation of the observed intensities (e.g. Chook et al., 1998 ▶) and is most easily detected by inspection of the Patterson function (e.g. Zwart et al., 2005 ▶). The subset of reflections that would be systematically absent given idealized centring operators will have systematically low intensities. If these intensities are sufficiently low, data-processing programs may index and reduce the diffraction images in a unit cell that is too small. This situation is very similar to the case of higher rotational symmetry as discussed in the previous section. The ‘grey area’ considerations of the previous section also apply to TPS.
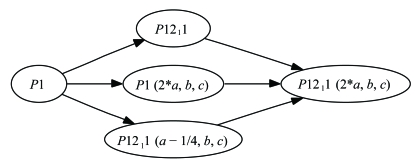
An interesting crystallographic pathology can arise when pseudocentring is present. An example is given by Isupov & Lebedev (2008 ▶). In this case, the space group is P21 with a pseudotranslation (x + ½, y, z). Consider two P21 cells stacked side by side on the bc face of the unit cell. The resulting symmetry is described by the universal Hermann–Mauguin symbol P1211 (2a, b, c). A full list of symmetry operators in this setting is shown in Table 2 ▶. From this set of operators, a number of subgroups can be constructed (Fig. 3 ▶). Operators not used in the construction of the subgroup can be regarded as NCS operators. If operators A and B are designated as crystallographic symmetry, the space group is P21 and operators C and D are NCS operators. If, however, operators A and D are designated to be crystallographic, the space group is P21 with an origin shift of (¼, 0, 0) and B and C are NCS operators. Both choices produce initially reasonable R values, but only choice one is correct and eventually leads to the best model.
Table 2. The presence of a pseudocentring operator (x + ½, y, z) in P21 can lead to an interesting pathology.
If all operators are crystallographic operators and (x + ½, y, z) is designated to be a lattice translation, then a number of groups can be formed. See Fig. 2 ▶ and the main text for details.
| Name | Operators | Description |
|---|---|---|
| A | (x, y, z) | Identity |
| B | (−x, y + ½, −z) | 21 through (0, 0, 0) |
| C | (x + ½, y, z) | Lattice translation |
| D | (−x + ½, y + ½, −z) | 21 through (¼, 0, 0) |
Figure 3.
A space-group graph showing all subgroups of space group P1211 (2a, b, c). Specifically, two distinct P21 subgroups are available with equal unit-cell parameters, related by an origin shift of ¼. See text and Table 2 ▶ for details.
3.3. Twinning
Twinning is the partial or full overlap of multiple reciprocal lattices. Each measured intensity is therefore the sum of the intensities of the individual domains with different orientations. The presence of twinning in an X-ray data set usually reveals itself by intensity statistics that deviate from theoretical distributions. However, the presence of pseudorotational symmetry (especially when parallel to the twin axis) or pseudotranslational symmetry can offset the effects of twinning on the intensity statistics, making it more difficult to detect the twinning. Basic intensity statistics elucidating the problems of pseudosymmetry in combination with twinning are explained thoroughly by Lebedev et al. (2006 ▶). Prime examples of problems with space-group assignment owing to the presence of pseudosymmetry and twinning are described by Abrescia & Subirana (2002 ▶), Lee et al. (2003 ▶), Rudiño-Piñera et al. (2004 ▶) and MacRae et al. (2006 ▶).
The relative sizes of the twin domains building up the crystal are the twin fractions. The sum of the twin fractions is 1. The situation where all twin fractions are all equal is called perfect twinning. A twin with an arbitrary ratio of twin fractions is denoted as a partial twin. A number of papers are available from the literature that deal with a basic introduction to twinning (Dauter, 2003 ▶; Parsons, 2003 ▶; Yeates, 1997 ▶; Yeates & Fam, 1999 ▶), as well as case studies of particular proteins (Barends et al., 2005 ▶; Barends & Dijkstra, 2003 ▶; Lehtiö et al., 2005 ▶; Rudolph et al., 2003 ▶, 2004 ▶; Wittmann & Rudolph, 2007 ▶; Yang et al., 2000 ▶).
3.3.1. Merohedral and pseudomerohedral twins
Merohederal or pseudomerohedral twinning is a form of twinning in which the (primitive) lattice has a higher symmetry than the symmetry of the unit-cell content. If this occurs, the arrangement of reciprocal-lattice points will have a higher symmetry than the symmetry of the intensities associated with the reciprocal-lattice points. The symmetry operators that belong to the point group of the reciprocal lattice, but not to the symmetry of the point group of the intensities, are potential twin laws.
If the reciprocal lattice is perfectly invariant under a given twin law (merohedral twinning), the presence of twinning can only be detected by inspection of the intensity statistics or model-based techniques. However, if the reciprocal lattice is only approximately invariant under a given twin law (pseudomerohedral twinning), twin-related intensities may be identified as individual reflections in the diffraction pattern. Examples of a number of (pseudo)merohedrally twinned structures are given in Table 3 ▶.
Table 3. Examples of (pseudo)merohedrally twinned structures.
| PDB code | Unit-cell parameters (Å, °) | Space group | Twin law | Fraction (%) | Type |
|---|---|---|---|---|---|
| 1q43 | a = b = 95, c = 125, α = β = γ = 90 | I4 | (−k, −h, −l) | 8 | M |
| 1eyx | a = b = 180, c = 36, α = β = 90, γ = 120 | R3:H | (h, −h − k, −l) | 45 | M |
| 1upp | a = 155.8, b = 156.2, c = 199.7,α = β = γ = 90 | C2221 | (h, k, −l) | 45 | PM |
| 1l2h | a = b = 53.9, c = 77.4, α = β = γ = 90 | P43 | (−h, k, −l) | 37 | M |
The presence of an NCS operator that is an approximate crystallographic operator provides a structural basis for the presence of twinning. Twin-domain interfaces have molecular contacts that are very similar to interfaces seen in nontwinned domains, which allows or promotes the growth of twinned crystals in general. In a similar manner, twinning can be introduced by the breaking of symmetry owing to a temperature-dependent phase transition (Helliwell et al., 2006 ▶; Herbst-Irmer & Sheldrick, 1998 ▶; Parsons, 2003 ▶) or by other external influences such as inclusion of a ligand or heavy-atom soaks. An example of such a phase transition is described by Dauter et al. (2001 ▶). In that particular case, however, the phase transition occurred in the other direction: the symmetry of the crystals before a halide soak had a lower symmetry than after the soak, eliminating the possibility of twinning.
Note that when a crystal is perfectly twinned or almost perfectly twinned, the data will scale well in a space group that is incorrect. The use of an incorrect space group often impedes a successful structure-solution procedure. A general theme in most cases studies involving difficulties with twinning (see references in §3.3) is that structure solution is possible once the correct space group has been found. Incorrect assignment of the space group for data sets with close to perfect twinning seems to be the most important factor hampering structure solution.
3.3.2. Twinning by reticular merohedry
Reticular merohedral twinning can be understood as merohedral twinning on a collection of unit cells, a so-called sublattice (Rutherford, 2006 ▶). In this type of twinning, only a fraction of the reflections will overlap with their twin-related counterpart. This results in a diffraction pattern that consists of intensity sums with contributions from a variable number of twin domains. A well known example of twinning by reticular merohedry is the obverse–reverse twinning in rhombohedral space groups. An excellent introduction to twinning by reticular merohedry is given by Parsons (2003 ▶). Examples of diffraction patterns can be found in Dauter (2003 ▶).
3.3.3. Order–disorder twinning
Order–disorder twinning (Dornberger-Schiff & Dunitz, 1965 ▶; Dornberger-Schiff & Grell-Niemann, 1961 ▶; Dornberger-Schiff, 1956 ▶, 1966 ▶) is a less well classified type of twinning, but has been observed for protein structures in a number of cases (Trame & McKay, 2001 ▶; Wang et al., 2005 ▶; Rye et al., 2007 ▶). Order–disorder twinning can occur when a crystal lattice is built up of successive layers of molecules, in such a manner that two or more different stacking vectors can relate neighboring layers to form geometrically identical interfaces between them. An irregular sequence of stacking vectors results in OD-twinning or partial crystal disorder dependent on the frequency of the defects. Such irregularity introduces a modulation of the intensities of specific reflections. A correction for this effect can be vital for structure solution and can result in lower R values during refinement (Trame & McKay, 2001 ▶). As noted by Nespolo et al. (2004 ▶), order–disorder phenomena in combination with twinning may easily go unnoticed during structure solution and refinement.
3.4. Common pitfalls
3.4.1. Misindexing
If the beam centre has not been defined accurately enough, autoindexing programs can return an indexing solution in which the (0, 0, 0) reflection (the direct beam) is, for instance, indexed as (0, 0, 1). Subsequent merging of the data will fail if the Miller indices are not corrected. Misindexing can be avoided by obtaining the position of the direct beam on the detector using powder methods or by using more robust autoindexing routines (Sauter et al., 2004 ▶).
3.4.2. Incorrect unit cell
When more than one single crystal is present or when the diffraction images are noisy in general, it is possible that autoindexing procedures will produce a unit cell that is too large. In the integrated and merged data, this issue can reveal itself as a prominent peak in the Patterson function. In contrast, if the structure under investigation has a strong pseudotranslation, it can occur that the indexing solution corresponds to a unit cell that is too small. In such a case, reflections that are systematically weak owing to the pseudotranslation are ignored and the pseudotranslation is mistaken for a lattice translation.
3.4.3. Incorrect space group
If an approximately correct unit cell has been obtained, the space group has to be determined based on the intensities. The presence of pseudosymmetry can make this choice difficult, but it can often be made automatically by programs such as phenix.xtriage (Zwart et al., 2005 ▶), XPREP (Sheldrick, 2000 ▶), POINTLESS (Evans, 2006 ▶) or LABELIT (Sauter et al., 2006 ▶). Assigning an incorrect space group can result in a number of difficulties. If the assigned symmetry is too low, structure solution and refinement is made artificially difficult because of the larger number of molecules in the asymmetric unit. Furthermore, differences between molecules can subsequently be overinterpreted, resulting in incorrect biological conclusions.
If the data are twinned and as a result the assigned symmetry is too high, it may not be possible to solve the structure. An excellent example that illustrates this (and other) pitfalls is given by Lee et al. (2003 ▶), where the presence of pseudotranslational symmetry and perfect twinning resulted in an incorrect choice of both the unit cell and the space group.
4. Examples
4.1. Interesting cases from the PDB
A number of data sets in the PDB show interesting pathologies such as twinning and pseudorotational and or pseudotranslational symmetry. A few examples are highlighted here.
4.1.1. 2bd1: incorrect symmetry
The structure of phospholipase A2 (Sekar et al., 2006 ▶) was indexed in C2 with unit-cell parameters a = 74.58, b = 48.69, c = 67.55 Å, α = 90, β = 102.3, γ = 90°. The Patterson function reveals a peak at (0, ½, 0) with a height approximately equal to that of the origin (99%). Correspondingly, the intensities of the reflections with Miller indices that would be equal to zero if the NCS operator was crystallographic barely rise above the noise as judged from their associated standard deviations. The r.m.s.d. between the Cα atoms of the two molecules related by the translational NCS operator obtained from the Patterson function is very small (0.08 Å). In comparison, the cross-validated estimate of the coordinate error is 0.19 Å, which strongly suggests that the unit cell is in fact too large.
4.1.2. 2a8y: incorrect symmetry
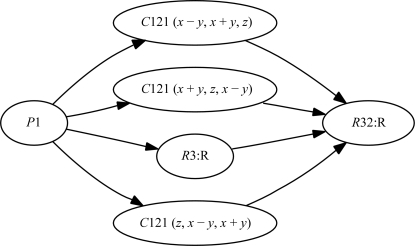
The unit-cell parameters for this structure are a = 96.60, b = 96.56, c = 96.63 Å, α = 91.57, β = 91.23, γ = 91.52°. The deposited space group is P1 (Zhang et al., 2006 ▶). Cursory analysis of the unit-cell parameters suggests that the highest possible symmetry is rhombohedral. An analysis of the merged intensities with phenix.xtriage reveals that the intensity symmetry corresponds to the space group C2, with unit-cell parameters a = 135.2, b = 138.1, c = 96.6 Å, α = 90, β = 92.2, γ = 90°. In this particular case, the authors did attempt to merge the data in various point groups (including C2), but the data only scaled well in space group P1 (Zhang et al., 2006 ▶). Given the pseudosymmetric nature of the lattice (pseudo-rhombohedral), C2 can be embedded in the higher symmetry lattice in three different ways (see Fig. 4 ▶), corresponding to the three orientations of the twofold axis in space group R32. The integration suite used to initially process the data only gave a single indexing choice for C2, which was unfortunately incorrect. Currently, the structure is being re-refined in the higher symmetry C2 space group (Ealick, private communication).
Figure 4.
A space-group graph showing all subgroups of space group R32:R. Specifically, three distinct C2 subgroups are available corresponding to the three possible directions the twofold axes can be oriented in R32.
4.1.3. 1upp: pseudotranslational symmetry and twinning
The structure of a spinach Rubisco complex (Karkehabadi et al., 2003 ▶) has associated unit-cell parameters a = 155.9, b = 156.3, c = 199.8 Å, α = 90, β = 90, γ = 90° and space group C2221. Obviously, a is approximately equal to b, resulting in the presence of the twin law (k, h, −l). Furthermore, the Patterson function indicates a translational NCS vector (½, 0, ½) with a height of 40% of the origin. The presence of pseudotranslational symmetry can make the detection of twinning difficult, but the results of the L test (Padilla & Yeates, 2003 ▶) are quite clear (Table 4 ▶). Refinement of the twin fraction given the deposited structure indicates that the twin fraction is approximately 45%. Including twinning in the R-value calculations (while keeping the model fixed) reduces the R value from 0.25 to 0.17.
Table 4. Intensity statistics of 1upp .
Only the L test indicates that the data might be twinned.
| Statistic | Observed | Theory (untwinned) | Theory (perfect twin) |
|---|---|---|---|
| 〈I2〉/〈I〉2 | 2.09 | 2 | 1.5 |
| 〈F〉2/〈F2〉 | 0.80 | 0.785 | 0.885 |
| 〈|E2 − 1|〉 | 0.731 | 0.736 | 0.541 |
| 〈L〉 | 0.43 | 0.50 | 0.375 |
4.2. Molecular replacement using twinned data
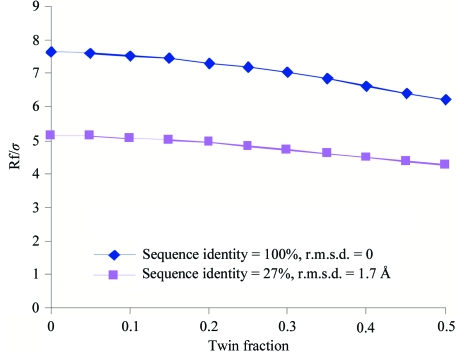
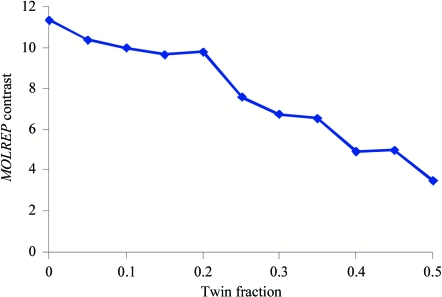
Using artificially twinned data, it can be demonstrated that the contrast of the rotation function decreases in proportion to the twin fraction (Fig. 5 ▶). A similar observation is made for the translation function (Fig. 6 ▶). However, from practical experience we know that molecular replacement based on twinned data is often successful if the quality of the search model is reasonable (e.g. Wittmann & Rudolph, 2007 ▶).
Figure 5.
The value of the largest peak in the rotation function using the program MOLREP for synthetically twinned data. The blue line shows the value for a model with 100% sequence identity, whereas the purple line indicates the results of the rotation function when the model has 27% sequence identity. In both runs, the search model compromised only one quarter of the total ASU content.
Figure 6.
The value of the contrast of the translation function using the program MOLREP for synthetically twinned data, given a correct orientation of the model. The search model was identical to the model used to compute the artificially twinned data.
In the case of perfect twinning, a data-reduction program may pick a symmetry that is too high (see §3.3.1). In this situation it is unlikely that molecular replacement will produce a solution, as the ASU is typically too small to contain the true contents of the crystal. Working with the data reprocessed in the lower symmetry may be successful, even though the data are perfectly twinned. This is illustrated by the following example.
The X-ray data set of Dicer crystals (MacRae et al., 2006 ▶; MacRae & Doudna, 2007 ▶) was initially processed in point group P422, but failed to give interpretable maps using experimental phasing methods in all P4x2y2 groups. Intensity statistics revealed that the data were twinned and reprocessing the data in point group P4 resulted in partially interpretable SAD maps in space group P41, assuming a twofold twin law along b. However, a complete and refinable model could not be obtained in any tetragonal space group. Collecting data from a new specimen revealed that the point-group symmetry was equal to P222 with almost perfect twinning, leading to a pseudo-tetragonal system. A successful structure solution via molecular replacement and SAD methods was obtained in space group P21221. Here, we repeat the structure solution using molecular replacement to determine the effect of different prior space-group hypotheses. To this end, data submitted to the PDB with accession code 2qwv were reindexed from P21212 to P21221 with operator (−a, c, b) to obtain a setting that corresponds to the standard setting if the data were merged in point group P422. The data with intensity symmetry P222 were then merged in P422. These merged data were then expanded out to point groups P4, C222 and P222, the three point groups directly ‘below’ point group P422 (see Fig. 1 in the supplementary material1). Molecular replacement with chain A of the deposited model was used to determine the structure in all possible space groups of the given point groups. The rotation function gave two clear solutions in point group P422 and four clear solutions in point groups P4, C222 and P222 (Table 5 ▶). Subsequent translation functions and refinement of the twin fraction resulted in three likely possible solutions in space groups P41, P21221 and P22121 (Table 6 ▶). Further rigid-body and group ADP refinement lowered the R values of the space-group candidates in the orthorhombic system to 25%, while the model in P41 had an R value of 29%.
Table 5. Rotation-function peaks of Dicer data.
| Point group | Top rotation-function peaks (Rf/σ) |
|---|---|
| P422 | 8.29 7.55 4.61 |
| P4 | 8.32 8.32 7.58 7.58 4.62 |
| C222 | 8.28 8.28 7.72 7.72 4.68 |
| P222 | 8.27 8.27 7.55 7.55 4.61 |
Table 6. Translation-function and refinement results for Dicer data.
Only molecular-replacement solutions with initial R values (R molrep) below 50% are shown. All other space groups results in values above 50%. R twin is the R value of the model to the data as obtained directly after molecular replacement, but taking into account the effects of twinning. R group is the R value of the model and the data after rigid-body refinement of individual chains and refinement of grouped ADPs. Twin fractions were refined to 50% for all cases.
| Space group | Copies | Rmolrep (%) | Rtwin (%) | Rgroup (%) |
|---|---|---|---|---|
| P4122 | 2 | 47 | NA | NA |
| P41212 | 2 | 48 | NA | NA |
| P41 | 4 | 43 | 38 | 29 |
| P2221 | 4 | 49 | 39 | NA |
| P21221 | 4 | 43 | 36 | 25 |
| P22121 | 4 | 43 | 37 | 25 |
| P212121 | 4 | 49 | 43 | NA |
Note that it is not surprising that P21221 and P22121 are both possible solutions since the data are perfectly twinned in point group P222 with twin law (−k, −h, −l) and the solutions correspond to the two different twin domains. Data with a lower twin fraction or the presence of anomalous differences can be used to determine the space group.
4.3. Manual molecular replacement using group–subgroup relations
It is not uncommon that protein molecules crystallize in various space groups (polymorphs). In some cases, the polymorphs are related and one can use the structure of one polymorph to solve the other without the aid of automated molecular-replacement software (Di Costanzo et al., 2003 ▶). An example structure solution utilizing group–subgroup relations is presented here.
The crystals of 1eix and 1jjk (Poulsen et al., 2001 ▶) were grown under similar conditions, but 1eix is a native protein structure while 1jjk is a selenomethionine derivative. The unit-cell parameters are listed in Table 7 ▶. The ratio of the unit-cell volumes is 2.12, suggesting the possibility of a relation between the two unit cells. Another piece of evidence suggesting a relation is found in the Patterson function of 1jjk: a large peak is located at (½, 0, ½), which can be interpreted as pseudocentring (translational NCS). If this NCS operator is idealized to a crystallographic operator, the unit-cell parameters of 1jjk become equal to the unit-cell parameters of 1eix (apart from a permutation of the basis vectors). It is thus clear that 1jjk is related to 1eix via pseudotranslational symmetry (as seen from the Patterson peak) and pseudorotational/screw symmetry (P21 versus P212121).
Table 7. Unit-cell parameters for structures 1eix and 1jjk .
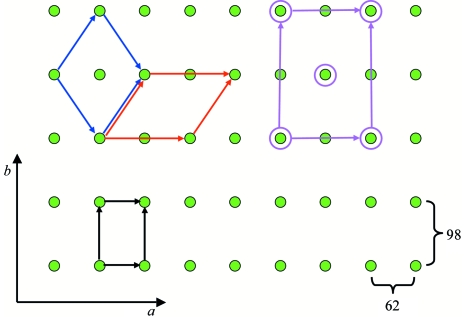
A relation between the two unit cells was identified with the tool iotbx.explore_metric_symmetry (Zwart et al., 2006 ▶) and is depicted in Fig. 7 ▶. The procedure used to solve the structure of 1jjk with the model of 1eix via group–subgroup relations is described in Di Costanzo et al. (2003 ▶). Firstly, the appropriate ASU is constructed by applying a twofold screw axis to the ASU of 1eix. Subsequently, a lattice translation along a is applied to these two molecules. An appropriate change of basis to bring the model into the correct orientation and a subsequent origin shift generates a possible solution. In this particular case, a group theoretical analysis reveals that two origin shifts are possible (see §3.2 and Fig. 2 in the supplementary material1). Rigid-body refinement of the two possible solutions, taking into account the presence of twinning, resulted in a single clear solution (Table 8 ▶).
Figure 7.
The relations between projections of the unit cells of 1eix and 1jjk. The basis vectors of the orthorhombic unit cell of 1eix are shown in black. The blue and red basis vectors are two equivalent choices for a unit cell of 1jjk. The purple vectors indicate that 1jjk is approximately C-centred orthorhombic.
Table 8. Results of the manual molecular replacement and subsequent rigid-body refinement.
| Origin shift | R value (start) | R value (rigid) | R value (twin) |
|---|---|---|---|
| Choice 1 | 0.54 | 0.34 | 0.30 (twin fraction: 0.43) |
| Choice 2 | 0.54 | 0.30 | 0.25 (twin fraction: 0.37) |
Using the same group–subgroup relations, one can test the presence of a relation between crystal forms by computing intensity correlations between reindexed data sets. If the crystal form with the smaller unit cell is reindexed to a unit cell that is related to the larger cell, the intensities can be compared relatively straightforwardly (Grosse-Kunstleve et al., 2005 ▶). This allows one to verify a possible relationship between two crystal forms before attempting manual molecular replacement.
5. Discussion and conclusions
There are numerous special cases and pitfalls arising from the interplay of crystallographic and noncrystallographic symmetry in macromolecular crystals. Clearly, this paper only touches the tip of the iceberg. Fortunately, there are now a number of tools that make it possible to identify many of the most common problems (Evans, 2006 ▶; Sheldrick, 2000 ▶; Vaguine et al., 1999 ▶; Zwart et al., 2005 ▶). In some situations it is possible to correct for the problem; in others, use of the appropriate algorithms in subsequent structure solution and refinement can lead to accurate final models that are suitable for biological interpretation. Experience suggests that it is initially best to treat all experimental data with suspicion and apply all available tests to identify possible pathologies as soon as possible after data collection and processing. In an ideal world, data would be stored in an unmerged form in space group P1 and certain decisions made automatically as more information becomes available. In the case of (close to) perfect twinning, knowledge of the proper space group can for instance only be available when a partial model has been built. A similar argument can be made for the detection of and dealing with order–disorder twinning. Note that this scheme assumes that the correct unit cell has been found by the autoindexing software. Incorporating decision-making schemes that include changes in the primitive unit-cell parameters will most likely require access to the raw data.
Although access to the raw data is preferred for decision-making procedures, the Dicer example (§4.2) illustrates that integrating the expansion of data into a lower space group in a molecular-replacement procedure can in some cases lead to a successful structure solution. Similar arguments can probably be made for structure-solution routes via experimental phasing techniques.
Supplementary Material
Supplementary material file. DOI: 10.1107/S090744490705531X/ba5111sup1.pdf
Acknowledgments
The authors would like to thank the NIH for generous support of the PHENIX project (1P01 GM063210). This work was partially supported by the US Department of Energy under Contract No. DE-AC02-05CH11231 (PHZ, RWGK and PDA), the Wellcome Trust (064405/Z/01/A, GNM) and NIH (1-RO1-GM069758-03, AAL) The programs mentioned here are available in the PHENIX (http://www.phenix-online.org) and CCP4 (http://www.ccp4.ac.uk) software suites.
Footnotes
Supplementary material has been deposited in the IUCr electronic archive (Reference: BA5111). Services for accessing this material are given at the back of the journal.
References
- Abrescia, N. G. A. & Subirana, J. A. (2002). Acta Cryst. D58, 2205–2208. [DOI] [PubMed]
- Adams, P. D., Gopal, K., Grosse-Kunstleve, R. W., Hung, L.-W., Ioerger, T. R., McCoy, A. J., Moriarty, N. W., Pai, R. K., Read, R. J., Romo, T. D., Sacchettini, J. C., Sauter, N. K., Storoni, L. C. & Terwilliger, T. C. (2004). J. Synchrotron Rad.11, 53–55. [DOI] [PubMed]
- Adams, P. D., Grosse-Kunstleve, R. W., Hung, L.-W., Ioerger, T. R., McCoy, A. J., Moriarty, N. W., Read, R. J., Sacchettini, J. C., Sauter, N. K. & Terwilliger, T. C. (2002). Acta Cryst. D58, 1948–1954. [DOI] [PubMed]
- Barends, T. R. M., de Jong, R. M., van Straaten, K. E., Thunnissen, A.-M. W. H. & Dijkstra, B. W. (2005). Acta Cryst. D61, 613–621. [DOI] [PubMed]
- Barends, T. R. M. & Dijkstra, B. W. (2003). Acta Cryst. D59, 2237–2241. [DOI] [PubMed]
- Berman, H. M., Westbrook, J., Feng, Z., Gilliland, G., Bhat, T. N., Weissig, H., Shindyalov, I. N. & Bourne, P. E. (2000). Nucleic Acids Res.28, 235–242. [DOI] [PMC free article] [PubMed]
- Bernstein, F. C., Koetzle, T. F., Williams, G. J., Meyer, E. F. Jr, Brice, M. D., Rodgers, J. R., Kennard, O., Shimanouchi, T. & Tasumi, M. (1977). J. Mol. Biol.112, 535–542. [DOI] [PubMed]
- Brunzelle, J. S., Shafaee, P., Yang, X., Weigand, S., Ren, Z. & Anderson, W. F. (2003). Acta Cryst. D59, 1138–1144. [DOI] [PubMed]
- Chook, Y. M., Lipscomb, W. N. & Ke, H. (1998). Acta Cryst. D54, 822–827. [DOI] [PubMed]
- Dauter, Z. (2003). Acta Cryst. D59, 2004–2016. [DOI] [PubMed]
- Dauter, Z., Botos, I., LaRonde-LeBlanc, N. & Wlodawer, A. (2005). Acta Cryst. D61, 967–975. [DOI] [PubMed]
- Dauter, Z., Li, M. & Wlodawer, A. (2001). Acta Cryst. D57, 239–249. [DOI] [PubMed]
- Di Costanzo, L., Forneris, F., Geremia, S. & Randaccio, L. (2003). Acta Cryst. D59, 1435–1439. [DOI] [PubMed]
- Dornberger-Schiff, K. (1956). Acta Cryst.9, 593–601.
- Dornberger-Schiff, K. (1966). Acta Cryst.21, 311–322.
- Dornberger-Schiff, K. & Dunitz, J. D. (1965). Acta Cryst.19, 471–472.
- Dornberger-Schiff, K. & Grell-Niemann, H. (1961). Acta Cryst.14, 167–177.
- Emsley, P. & Cowtan, K. (2004). Acta Cryst. D60, 2126–2132. [DOI] [PubMed]
- Evans, P. (2006). Acta Cryst. D62, 72–82. [DOI] [PubMed]
- Giacovazzo, C. (1992). Fundamentals of Crystallography. Oxford University Press.
- Grosse-Kunstleve, R. W., Afonine, P. V., Sauter, N. K. & Adams, P. D. (2005). IUCr Comput. Commission Newsl.5, 69–91.
- Hahn, T. (2002). International Tables for Crystallography, Vol. A, 5th ed. Dordrecht: Kluwer Academic Publishers.
- Helliwell, M., Collison, D., John, G. H., May, I., Sarsfield, M. J., Sharrad, C. A. & Sutton, A. D. (2006). Acta Cryst. B62, 68–85. [DOI] [PubMed]
- Herbst-Irmer, R. & Sheldrick, G. M. (1998). Acta Cryst. B54, 443–449.
- Holton, J. & Alber, T. (2004). Proc. Natl Acad. Sci. USA, 101, 1537–1542. [DOI] [PMC free article] [PubMed]
- Holton, T., Ioerger, T. R., Christopher, J. A. & Sacchettini, J. C. (2000). Acta Cryst. D56, 722–734. [DOI] [PubMed]
- Ioerger, T. R., Holton, T., Christopher, J. A. & Sacchettini, J. C. (1999). Proceedings of the Seventh International Conference on Intelligent Systems for Molecular Biology, pp. 130–137. Menlo Park: AAAI. [PubMed]
- Isupov, M. N. & Lebedev, A. A. (2008). Acta Cryst. D64, 90–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ivantchev, S., Kroumova, E., Madariaga, G., Pérez-Mato, J. M. & Aroyo, M. I. (2000). J. Appl. Cryst.33, 1190–1191.
- Karkehabadi, S., Taylor, T. C. & Andersson, I. (2003). J. Mol. Biol.334, 65–73. [DOI] [PubMed]
- Lamzin, V. S. & Perrakis, A. (2000). Nature Struct. Biol.7, Suppl., 978–981. [DOI] [PubMed]
- Lamzin, V. S., Perrakis, A., Bricogne, G., Jiang, J., Swaminathan, S. & Sussman, J. L. (2000). Acta Cryst. D56, 1510–1511. [DOI] [PubMed]
- Lebedev, A. A., Vagin, A. A. & Murshudov, G. N. (2006). Acta Cryst. D62, 83–95. [DOI] [PubMed]
- Lee, S., Sawaya, M. R. & Eisenberg, D. (2003). Acta Cryst. D59, 2191–2199. [DOI] [PubMed]
- Lehtiö, L., Fabrichniy, I., Hansen, T., Schönheit, P. & Goldman, A. (2005). Acta Cryst. D61, 350–354. [DOI] [PubMed]
- MacRae, I. J. & Doudna, J. A. (2007). Acta Cryst. D63, 993–999. [DOI] [PubMed]
- MacRae, I. J., Zhou, K., Li, F., Repic, A., Brooks, A. N., Cande, W. Z., Adams, P. D. & Doudna, J. A. (2006). Science, 311, 195–198. [DOI] [PubMed]
- McRee, D. E. (1999). J. Struct. Biol.125, 156–165. [DOI] [PubMed]
- Morris, R. J., Perrakis, A. & Lamzin, V. S. (2003). Methods Enzymol.374, 229–244. [DOI] [PubMed]
- Morris, R. J., Zwart, P. H., Cohen, S., Fernandez, F. J., Kakaris, M., Kirillova, O., Vonrhein, C., Perrakis, A. & Lamzin, V. S. (2004). J. Synchrotron Rad.11, 56–59. [DOI] [PubMed]
- Navaza, J. (1994). Acta Cryst. A50, 157–163.
- Nespolo, M., Ferraris, G., Durovic, S. & Takeuchi, Y. (2004). Z. Kristallogr.219, 773–778.
- Padilla, J. E. & Yeates, T. O. (2003). Acta Cryst. D59, 1124–1130. [DOI] [PubMed]
- Parsons, S. (2003). Acta Cryst. D59, 1995–2003. [DOI] [PubMed]
- Perrakis, A., Morris, R. & Lamzin, V. S. (1999). Nature Struct. Biol.6, 458–463. [DOI] [PubMed]
- Poulsen, J.-C. N., Harris, P., Jensen, K. F. & Larsen, S. (2001). Acta Cryst. D57, 1251–1259. [DOI] [PubMed]
- Read, R. J. (2001). Acta Cryst. D57, 1373–1382. [DOI] [PubMed]
- Royer, W. E. Jr, Heard, K. S., Harrington, D. J. & Chiancone, E. (1995). J. Mol. Biol.253, 168–186. [DOI] [PubMed]
- Rudiño-Piñera, E., Schwarz-Linek, U., Potts, J. R. & Garman, E. F. (2004). Acta Cryst. D60, 1341–1345. [DOI] [PubMed]
- Rudolph, M. G., Kelker, M. S., Schneider, T. R., Yeates, T. O., Oseroff, V., Heidary, D. K., Jennings, P. A. & Wilson, I. A. (2003). Acta Cryst. D59, 290–298. [DOI] [PubMed]
- Rudolph, M. G., Wingren, C., Crowley, M. P., Chien, Y. & Wilson, I. A. (2004). Acta Cryst. D60, 656–664. [DOI] [PubMed]
- Rutherford, J. S. (2006). Acta Cryst. A62, 93–97. [DOI] [PubMed]
- Rye, C. A., Isupov, M. N., Lebedev, A. A. & Littlechild, J. A. (2007). Acta Cryst. D63, 926–930. [DOI] [PubMed]
- Sauter, N. K., Grosse-Kunstleve, R. W. & Adams, P. D. (2004). J. Appl. Cryst.37, 399–409. [DOI] [PMC free article] [PubMed]
- Sauter, N. K., Grosse-Kunstleve, R. W. & Adams, P. D. (2006). J. Appl. Cryst.39, 158–168.
- Sekar, K., Yogavel, M., Kanaujia, S. P., Sharma, A., Velmurugan, D., Poi, M.-J., Dauter, Z. & Tsai, M.-D. (2006). Acta Cryst. D62, 717–724. [DOI] [PubMed]
- Sheldrick, G. M. (2000). XPREP Version 6.0. Bruker AXS Inc., Madison, Wisconsin, USA.
- Shmueli, U., Hall, S. R. & Grosse-Kunstleve, R. W. (2001). International Tables for Crystallography, Vol. B, edited by U. Shmueli, pp. 107–119. Dordrecht: Kluwer Academic Publishers.
- Snell, G., Cork, C., Nordmeyer, R., Cornell, E., Meigs, G., Yegian, D., Jaklevic, J., Jin, J., Stevens, R. C. & Earnest, T. (2004). Structure, 12, 537–545. [DOI] [PubMed]
- Terwilliger, T. (2002a). Acta Cryst. A58, C57.
- Terwilliger, T. C. (2002b). Acta Cryst. D58, 1937–1940. [DOI] [PubMed]
- Trame, C. B. & McKay, D. B. (2001). Acta Cryst. D57, 1079–1090. [DOI] [PubMed]
- Vagin, A. & Teplyakov, A. (2000). Acta Cryst. D56, 1622–1624. [DOI] [PubMed]
- Vaguine, A. A., Richelle, J. & Wodak, S. J. (1999). Acta Cryst. D55, 191–205. [DOI] [PubMed]
- Wang, J., Kamtekar, S., Berman, A. J. & Steitz, T. A. (2005). Acta Cryst. D61, 67–74. [DOI] [PubMed]
- Wang, X. & Janin, J. (1993). Acta Cryst. D49, 505–512. [DOI] [PubMed]
- Winter, G. M. (2008). In preparation.
- Wittmann, J. G. & Rudolph, M. G. (2007). Acta Cryst. D63, 744–749. [DOI] [PubMed]
- Yang, F., Dauter, Z. & Wlodawer, A. (2000). Acta Cryst. D56, 959–964. [DOI] [PubMed]
- Yeates, T. O. (1997). Methods Enzymol.276, 344–358. [PubMed]
- Yeates, T. O. & Fam, B. C. (1999). Structure, 7, R25–R29. [DOI] [PubMed]
- Zagotta, W. N., Olivier, N. B., Black, K. D., Young, E. C., Olson, R. & Gouaux, E. (2003). Nature (London), 425, 200–205. [DOI] [PubMed]
- Zhang, Y., Porcelli, M., Cacciapuoti, G. & Ealick, S. E. (2006). J. Mol. Biol.357, 252–262. [DOI] [PubMed]
- Zwart, P. H., Grosse-Kunstleve, R. W. & Adams, P. D. (2005). CCP4 Newsl.42, contribution 10.
- Zwart, P. H., Grosse-Kunstleve, R. W. & Adams, P. D. (2006). CCP4 Newsl.44, contribution 8.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material file. DOI: 10.1107/S090744490705531X/ba5111sup1.pdf