Skip to main content
NCBI home page
Protein Science : A Publication of the Protein Society logoLink to Protein Science : A Publication of the Protein Society
. 2003 Sep;12(9):2057–2062. doi: 10.1110/ps.0302503

Contact order revisited: Influence of protein size on the folding rate

Dmitry N Ivankov 1, Sergiy O Garbuzynskiy 1, Eric Alm 2, Kevin W Plaxco 3, David Baker 2, Alexei V Finkelstein 1
PMCID: PMC2324001  PMID: 12931003

Abstract

Guided by the recent success of empirical model predicting the folding rates of small two-state folding proteins from the relative contact order (CO) of their native structures, by a theoretical model of protein folding that predicts that logarithm of the folding rate decreases with the protein chain length L as L2/3, and by the finding that the folding rates of multistate folding proteins strongly correlate with their sizes and have very bad correlation with CO, we reexamined the dependence of folding rate on CO and L in attempt to find a structural parameter that determines folding rates for the totality of proteins. We show that the Abs_CO = CO × L, is able to predict rather accurately folding rates for both two-state and multistate folding proteins, as well as short peptides, and that this Abs_CO scales with the protein chain length as L0.70 ± 0.07 for the totality of studied single-domain proteins and peptides.

Keywords: Protein folding kinetics, two-state kinetics, multistate kinetics, contact order, protein size, protein topology, rate of folding

Many proteins fold and unfold by a simple two-state transition lacking observable intermediates at any solvent conditions (Jackson 1998). Many other proteins exhibit a more complicated multistate transition; namely, they have observable folding intermediates under physiological conditions. However, the boundary between these two groups of proteins is not as well defined.

It is known that some proteins can be switched from two-state to multistate folding, and vice versa, by point mutations or even by changing conditions such as the salt concentration or temperature (Jackson 1998). In addition, multistate folding is observed only far from the point of thermodynamic equilibrium between the native and denatured states, whereas, close to this point, all proteins fold without any observable intermediates (Privalov 1979; Jackson 1998; Finkelstein and Ptitsyn 2002).

Small two-state folding proteins have attracted particular attention of experimentalists and theorists. It was demonstrated that the logarithms of in-water folding rates of these proteins correlate with their gross topological parameter called relative contact order (CO; Plaxco et al. 1998b). The latter is defined as

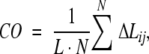graphic file with name M1.gif (1)

where N is the number of contacts (within 6 Å) between nonhydrogen atoms in the protein, L is the length of the protein in amino acid residues, and ΔLij is the number of residues separating the interacting pair of nonhydrogen atoms (adjacent residues are assumed to be separated by one residue, etc.).

CO is a renormalization of the perhaps more intuitive measure, absolute contact order (Abs_CO),

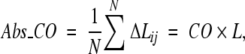graphic file with name M2.gif (2)

which, however, was found to be less correlated than CO with folding rates of the two-state folders (Plaxco et al. 1998b; Grantcharova et al. 2001).

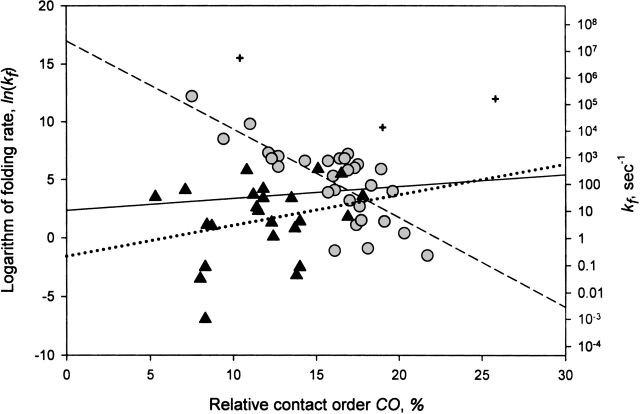
The CO was invented to compare differences in topology (rather than in size) between proteins of different length. This parameter is small for proteins stabilized mainly by local interactions and is large when residues in a protein interact frequently with partners far away in the protein sequence. The latter should lead to slower folding (Plaxco et al. 1998b; Fersht 2000). Indeed, negative correlation between the CO and the logarithm of folding rates was found to be very strong, ∼ −0.8 (Plaxco et al. 1998b; Fersht 2000) for two-state folding proteins (which also holds for all two-state folding proteins studied to date; Fig. 1 ▶, circles).

Figure 1.

Figure 1.

Open in a new tab

Natural logarithm of observed folding rate in water, ln(kf), versus relative contact order (CO) for various proteins and peptides: proteins having two-state folding kinetics at all the denaturant concentrations (circles ), proteins having multistate folding kinetics in water (and at low denaturant concentrations; triangles ), and short peptides (crosses ). The figure includes peptides and proteins listed in Table 1; CO is computed after Equation 1 from the PDB coordinates (Bernstein et al. 1977). If several folding rates are observed for some protein (see Table 1), ln(kf) is the mean value of their natural logarithms. The dashed line represents the best linear fit for two-state folders only (the negative correlation coefficient is as significant as −0.75; the fitted dependence is y = 16.94 − 0.76x); the dotted line represents the best linear fit for multistate folders only (the correlation coefficient is +0.26; namely, it has the opposite sign compared with that for the two-state folders; y = −1.55 + 0.26x); the solid line represents the best linear fit for the totality of all peptides and proteins presented (the correlation coefficient is insignificant, +0.10 only; y = 2.37 + 0.10x).

However, examining a whole set of proteins studied to date (Table 1), we see that CO, although it still gives good results for two-state folding proteins, fails to predict the folding rates of short peptides and large multistate folding proteins (Fig. 1 ▶). It seems the reason is that CO takes into account topology only and pays no explicit attention to the protein size.

Table 1.

List of proteins and polypeptides a

No. Protein Reference PDB L ln(kf) CO, % Abs_CO
    1 α-helixb Thompson et al. 1997 —b 21 15.5 10.4 2.2
    2 β-hairpinc Munoz et al. 1997 1PGB 16 12 25.8 4.1
    3 WW domaind Jager et al. 2001 1PIN 34 9.5 19.0 6.5
    4 E3/E1-binding domain of dihydrolipoyl acyltransferasee Spector and Raleigh 1999 2PDD 41 9.8 11.0 ± 0.4 4.5 ± 0.2
    5 ACBP Kragelund et al. 1995 2ABD 86 6.6 14.3 ± 0.3 12.3 ± 0.3
    6 Cytochrome b562f Wittung-Stafshede et al. 1999 256B 106 12.2 7.5 7.9
    7 Colicin E9 immunity protein Ferguson et al. 1999 1IMQ 86 7.3 12.1 10.4
    8 λ-Repressor Burton et al. 1996 1LMB 80 8.5 9.4 7.5
    9 Fibronectin ninth FN3 module Plaxco et al. 1997 1FNF 90 −0.9 18.1 16.3
10 Twitchin Clarke et al. 1999 1WIT 93 0.4 20.3 18.9
11 Tenascin (short form) Clarke et al. 1997 1TEN 90 (89) 1.1 17.4 15.4
12 SH3 domain (a-spectrin) Viguera et al. 1996 1SHG 62 (57) 1.4 19.1 10.9
13 SH3 domain (src) Grantcharova and Baker 1997 1SRL 64 (56) 4 19.6 11.0
14 SH3-domain (PI3 kinase)g Guijarro et al. 1998 1PNJ 90 (86) −1.1 16.1 13.9
15 SH3-domain (fyn) Plaxco et al. 1998a 1SHF 67 (59) 4.5 18.3 10.8
16 Photosystem I accessory protein P. Bowers and D. Baker, unpubl. 1PSF 69 3.2 17.0 11.7
17 CspB (Bacillus subtilis) Schindler et al. 1995 1CSP 67 7.0 16.4 11.0
Perl et al. 1998 6.5
18 CspB (B. caldolyticus) Perl et al. 1998 1C9O 66 7.2 7.5 7.9
19 CspB (Thermatoga maritima) Perl et al. 1998 1G6P 66 6.3 17.5 ± 0.4 11.4 ± 0.3
20 CspA Reid et al. 1998 1MJC 69 5.3 16.0 11.0
21 Cyclophilin A Ikura et al. 2000 1LOP 164 6.6 15.7 25.7
22 DNA-binding proteinh Guerois and Serrano 2000 1C8C 63 7 12.7 8.0
23 IgG binding domain of streptococcal protein Li Kim et al. 2000 1HZ6 62 4.1 16.1 10.0
24 Protein G McCallister et al. 2000 1PGB 57 (56) 6 17.3 9.7
25 FKBP12 Main et al. 1999 1FKB 107 1.5 17.7 18.9
26 Ci2 Jackson and Fersht 1991 2CI2 64 3.9 15.7 10.0
27 Activation domain procarboxypeptidase A2 Villegas et al. 1995 1AYE 80 6.8 16.7 13.4
28 Spliceosomal protein U1Aj Silow and Oliveberg 1997 1URN 102 (96) 5.8 16.9 16.2
29 Muscle-AcPk Van Nuland et al. 1998a 1APS 98 −1.5 21.7 ± 0.6 21.2 ± 0.6
Open in a new tab

The columns in this table are as follows: Protein , name of protein; Ref , reference to the original article on folding and unfolding kinetics; PDB , Protein Data Bank entry (Bernstein et al. 1977); L , number of residues in the protein used in the experimental study, and (in parentheses) the number of residues that have defined three-dimensional coordinates and contribute to the relative contact order ( ) calculations; ln(kf) , natural logarithm of the experimental folding rates in the water; and Abs_CO, absolute contact order.

a The list of single-domain proteins and peptides that lack both disulfide bonds and covalent bonds to ligands is taken from Galzitskaya et al. 2003). If folding of some protein was investigated at different temperatures, the experiment at the temperature closest to 25°C is presented in the Table; we took the slowest phase that is not considered as cis/trans proline isomerization phase in the original paper. If the three-dimensional structure of a protein whose folding was studied experimentally was absent in PDB, but PDB contains the structure of its mutant or very close homolog, the latter was used in our CO calculations; this is mentioned in a corresponding footnote. If several PDB entries are available for some protein, the best refined full-length X-ray structure is used in our CO calculation; in the absence of X-ray structure, the averaged NMR structure is used; in the absence of such, CO was averaged over all NMR models (in this case, the standard deviation is given). Nos. 1–3 indicate short peptides; 4–33, proteins with two-state folding within the whole range of experimental conditions; and 34–57, proteins with multistate folding in water.

b There is no PDB entry for the Ala-rich 21-residue α-helix studied; the ideal (Ala)21 α-helix was used in our contact order calculation.

cln(kf) value in water refers also to the midtransition point at 24°C

d Small WW domain consisting of one β-sheet is considered as a peptide. ln(kf) value refers to the temperature 41.7°C.

eln(kf) value is the investigators’ extrapolation of folding rate to 25°C.

f Two-state folding is assumed by long extrapolation made by investigators.

g Although the investigators of the experimental paper reported that the SH3 domain from PI3 kinase is 84 amino acids long, it was actually refolded by them with the additional two N-terminal residues and four C-terminal residues. The latter four are absent in the PDB entry.

Table 1.

List of proteins and polypeptides a

No. Protein Reference PDB L ln(kf) CO, % Abs_CO
30 S6 Otzen and Oliveberg 1999 1RIS 101 (97) 5.9 18.9 18.4
31 His-containing phosphocarrier protein Van Nuland et al. 1998b 1POH 85 2.7 17.6 15.0
32 N-terminal domain from L9 Kuhlman et al. 1998 1DIV 56 6.1 12.7 7.1
33 Villin 14T Choe et al. 1998 2VIK 126 6.8 12.3 15.4
34 Apomyoglobinl Cavagnero et al. 1999 1A6N 151 1.1 8.4 12.7
35 Colicin E7 immunity protein Ferguson et al. 1999 1CEI 87 (85) 5.8 10.8 9.2
36 Cro protein Laurents et al. 2000 2CRO 71 (65) 3.7 11.2 7.3
37 P16 protein Tang et al. 1999 2A5E 156 3.5 5.3 8.3
38 Twitching Ig repeat 27 Fowler and Clarke 2001 1TIT 89 3.6 17.8 15.8
39 CD2, 1st domain Parker et al. 1997 1HNG 98 (95) 1.8 16.9 16.0
40 Fibronectin tenth FN3 module Cota and Clarke 2000 1FNF 94 5.5 16.5 15.5
41 IFABP from rat Burns et al. 1998 1IFC 131 3.4 13.5 17.7
42 ILBPm Dalessio and Ropson 2000 1EAL 127 1.3 12.3 ± 0.5 15.7 ± 0.6
43 CRBP II Burns et al. 1998 1OPA 133 1.4 14.0 18.7
44 CRABP I Burns et al. 1998 1CBI 136 −3.2 13.8 18.8
45 tryptophan synthase α-subunitn Ogasahara and Yutani 1994 1QOP 268 (267) −2.5 8.3 22.3
46 GroEL apical domain (191–345) Golbik et al. 1998 1AON 155 0.8 13.7 21.2
47 Barstaro Schreiber and Fersht 1993 1BRS 89 3.4 11.8 10.5
48 Che Y Munoz et al. 1994 3CHY 129 (128) 1 8.7 11.2
49 Ribonuclease HIp Parker and Marqusee 1999 2RN2 155 0.1 12.4 19.3
50 DHFR (dihydrofolate reductase)q Jennings et al. 1993 1RA9 159 4.6 14.0 22.3
51 tryptophan synthase β2-subunitn Goldberg et al. 1990 1QOP 396 (390) −6.9 8.3 32.5
52 N-terminal domain from PGK Parker et al. 1995 1PHP 175 2.3 11.5 20.2
53 C-terminal domain from PGKr Parker et al. 1996 1PHP 219 −3.5 8.0 17.4
54 Barnase Matouschek et al. 1990 1BNI 110 (108) 2.6 11.4 12.3
55 T4 lysozymes Parker and Marqusee 1999 2LZM 164 4.1 7.1 11.6
56 Ubiquitint Khorasanizadeh et al. 1996 1UBQ 76 5.9 15.1 11.5
57 Suc 1u Schymkowitz et al. 2000 1SCE 113 (101) 4.2 11.8 11.9
Open in a new tab

h The folding of mutant protein Y34W was studied experimentally; we used the available PDB structure of wild type in our calculation of CO.

i The folding of mutant protein Y47W was studied experimentally; we used the available PDB structure of this mutant in our calculation of CO.

j The folding of mutant protein F56W was studied experimentally; we used the available PDB structure of mutant Y31H/Q36R in our calculation of CO.

k The folding of mutant protein C21S was studied experimentally; we used the available PDB structure of wild type protein in our calculation of CO.

l We used the available PDB structure of a holoform of myoglobin (but without heme) in our calculation of CO.

m We used the available PDB structure of mutant protein T118S from pig in our calculation of CO instead of the wild type protein from rat

n The folding of protein from Escherichia coli was studied experimentally. We used the available PDB structure of the same protein from Salmonella typhimurium in our calculation of CO.

o The folding of mutant protein C40A/C82A was studied experimentally; we used the available PDB structure of this mutant in our calculation of CO.

p The folding of mutant protein C13A/C63A/C133A was studied experimentally; we used the available PDB structure of wild type protein in our calculation of CO.

q The folding of wild type protein was studied. We used the available PDB structure of mutant protein N37D in our calculation of CO. ln(kf) value refers to the summary rate of two parallel pathways of refolding of DHFR.

r The folding of mutant protein W290Y was studied experimentally. We used the available PDB structure of wild type in our calculation of CO.

s The folding of Cys-free mutant was studied experimentally. We used the available PDB structure of wild-type protein in our calculation of CO.

t The folding of bovine protein F45W mutant was studied experimentally. We used the available PDB structure of WT human protein in our calculation of CO.

u There is only a strand-exchanged form of suc1 dimer in PDB. We used a concatenation of fragment 2–88 of chain C and fragment 89–102 of chain A as a tentative structure of monomeric protein in our calculation of CO.

A number of basic correlations between protein size and folding rate have been suggested (Thirumalai 1995; Gutin et al. 1996; Finkelstein and Badretdinov 1997a,b). All of them stress that, as might be expected, folding rate decreases monotonically with protein size, but all indicate different scaling laws for this decrease. It should be noted that some recent simulations of folding of off-lattice protein models with simplified potentials (Koga and Takada 2001) indicate that the logarithms of protein folding rate decrease with the chain length as L0.61 ± 0.18, which is in accordance with both Finkelstein and Badretdinov’s (1997a,b) and Thirumalai’s (1995) theories.

It has been shown, however, that the protein size by itself determines folding rates of only multistate folding proteins and fails to predict those for two-state folders (Galzitskaya et al. 2003): For multistate folders, the negative correlation between LP (L being the number of residues in the chain and P a free parameter) and the logarithm of folding rates is as high as −0.80 in the broad range of power P from zero to one, whereas for two-state folders any correlation between folding rate and size is virtually absent.

This study is aimed to develop a general parameter for predicting the protein folding rates of two-state folding proteins, multistate folding proteins, and small peptides. This general estimate, if found, would be useful for two reasons: (1) Attribution of proteins to two-state or multistate folders is somewhat arbitrary, at least for proteins which can be switched from the two-state to the multistate behavior by point mutations or changing solvent conditions, and (2) it is useful to estimate the folding rate of a protein when one does not know a priori if it is two-state or multistate folding protein.

Results and Discussion

The simplest way to obtain such a parameter is to take into account both the protein topology and its size, that is, to combine a length-based theory with empirical topology effect (Plaxco et al. 1998b). Here we describe such a combination.

Specifically, a theory of Finkelstein and Badretdinov’s (1997a,b) predicted that in a vicinity thermodynamic midtransition, folding rates of all single-domain proteins should decrease with their lengths, L as exp[−(0.5 ÷ 1.5) L2/3], and where the size-independent coefficient C = 0.5 ÷ 1.5 depends on the topology of the protein: C is close to 0.5 when a protein is stabilized mainly by local interactions, so that semifolded protein does not contain closed loops protruding from the folding nucleus, and C is close to 1.5 when a protein has many long-range contacts, so that many closed loops protrude from the nucleus. Later it was shown (Galzitskaya et al. 2001) that the range kf = exp(0.5L2/3) × 10ns ÷ exp(1.5L2/3) × 10ns is valid for all the studied peptides and single-domain proteins of a great variety of lengths, topologies, and folding behaviors.

Although Finkelstein and Badretdinov did not give an algorithm to compute their coefficient, C, from protein structure, it is clear that a physical sense of C is similar to those of the CO of Plaxco et al. Both are small for proteins with local contacts (i.e., α-helical proteins), and both are large for proteins with predominantly long-range contacts, which cannot avoid having many loops in a semifolded state. Therefore, the values of C and CO should correlate.

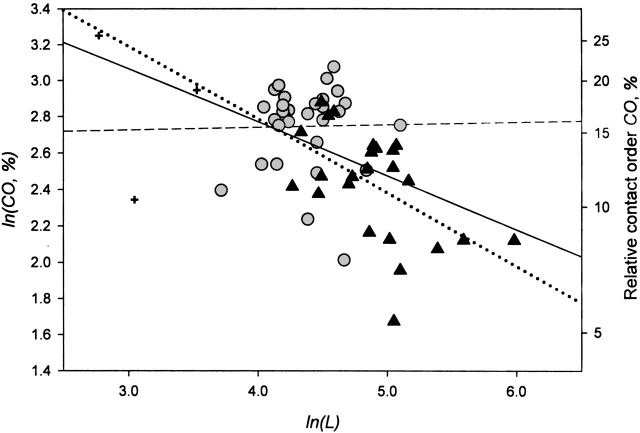
The simplest combination of CO and L, which seems to follow from theories of Plaxco et al. and Finkelstein and Badretdinov, may look like CO × L2/3. However, because we observe that CO is not a chain length–independent parameter (as the value C of Finkelstein and Badretdinov should be) but anticorrelates with the chain length, L (Fig. 2 ▶), for totality of proteins and peptides, we summarize CO and L in a general parameter, the "size-modified contact order" (SMCO), as

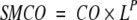graphic file with name M3.gif (3)

Figure 2.

Figure 2.

Open in a new tab

Logarithm of relative contact order versus logarithm of chain length. See legend to Figure 1 ▶ for specification of the symbols and other details. The dashed line represents the best linear fit for two-state folders only (the correlation coefficient is 0.02; y = 2.68 + 0.01x); the dotted line represents the best linear fit for multistate folders only (the correlation coefficient is −0.54; y = 4.41 − 0.40x); the solid line represents the best linear fit for the totality of all peptides and proteins (the correlation coefficient is −0.50; y = 3.95 − 0.30x). The linear regression coefficients 0.01, −0.40, and −0.30 are determined with errors ±0.16, ±0.13, and ±0.07, respectively.

One can see that P = 0 corresponds to SMCO = CO, whereas P = 1 corresponds to SMCO = Abs_CO.

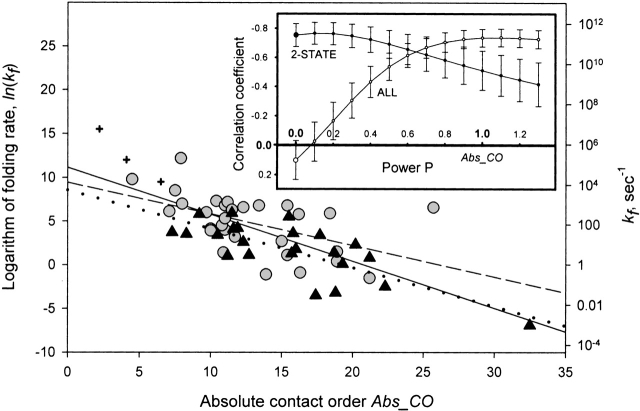
The correlation of SMCO and ln(kf), depending on the power P value, is presented in the inset in Figure 3 ▶. One can see that although any P > 0.7 results in approximately the same correlation for the totality of proteins and peptides, the best correlation is achieved at P ≈ 1, that is, when SMCO ≈ Abs_CO. The correlation of Abs_CO and ln(kf) is presented in Figure 3 ▶.

Figure 3.

Figure 3.

Open in a new tab

Logarithm of observed folding rate in water ln(kf) versus Abs_CO = CO × L. See legend to Figure 1 ▶ for specification of the symbols and other details. The dashed line represents the best linear fit for two-state folders only (the fitted dependence is y = 9.44 − 0.36x; the correlation coefficient is −0.51); the dotted line represents the best linear fit for multistate folders only (the fitted dependence is y = 8.56 − 0.44x; the correlation coefficient is −0.78); the solid line represents the best linear fit for the totality of all peptides and proteins presented (the fitted dependence is y = 11.15 − 0.54x; the correlation coefficient is −0.74). (Inset) Correlation coefficients between the logarithm of experimental folding rate in water and the value of CO × LP depending on the value of power P. Error bars, standard errors in correlation coefficients. The curve "2-STATE" concerns the two-state folding proteins only, and the curve "ALL" concerns the totality of all studied peptides and proteins; the curve for the multistate folding proteins is not shown because it is close to the curve "ALL" up to the standard error in correlation coefficients.

It should be mentioned, however, that for the two-state folders, the best ln(kf)–to–SMCO correlation is achieved when P = 0 ÷ 0.5 rather than 1 (Fig. 3 ▶, inset).

However, this difference between the scaling laws observed for two-state folders and the other proteins correlates, to a certain extent, with the finding (Fig. 2 ▶) that CO is independent on the chain length for the two-state folders, whereas it decreases with the chain length, L, in proportion to L−0.4 for multistate folders, and for the totality of proteins and peptides, CO decreases with their chain length, L, in proportion to L−0.30 ± 0.07 on the average.

It is noteworthy that CO scales namely as L−0.30 ± 0.07 for the totality of proteins and peptides (Fig. 2 ▶, dashed line). This means that the value Abs_CO = CO × L (which has the highest correlation with ln[kf] for the totality of proteins and peptides; Fig. 3 ▶, inset) scales with the chain length as L0.70 ± 0.07. This is in a very good concordance with a general scaling law L2/3 predicted by Finkelstein and Badretdinov 1997a,b; although the Thirumalai’s [1995] scaling law L0.5 has only a little worse correlation with experiment, and thus, cannot be ruled out; Fig. 3 ▶, inset), and agrees with an empirical scaling L0.61 ± 0.18 resulting from simplified off-lattice folding simulations of Koga and Takada (2001).

Acknowledgments

We are grateful to Blake Gillespie and Oxana Galzitskaya for discussions and some computations, and to David Thirumalai for discussions and his results on correlation of ln(kf) with CO × L1/2. This work was supported in part by the Russian Foundation for Basic Research, by an International Research Scholar’s Award to A.V.F. from the Howard Hughes Medical Institute, and by the Institute of Theoretical Physics (Santa Barbara University, ITP work no. NSF-ITP-01-173).

The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked "advertisement" in accordance with 18 USC section 1734 solely to indicate this fact.

Article and publication are at http://www.proteinscience.org/cgi/doi/10.1110/ps.0302503.

References

  1. Bernstein, F.C., Koetzle, T.F., Williams, G.J.B., Meyer, E.F., Brice, M.D., Rogers, J.R., Kennard, O., Shimanouchi, T., and Tasumi, M. 1977. The Protein Bank: A computer-based archival file for macromolecular structures. Eur. J. Biochem. 80 319–324. [DOI] [PubMed] [Google Scholar]
  2. Burns, L.L., Dalessio, P.M., and Ropson, I.J. 1998. Folding mechanism of three structurally similar β-sheet proteins. Proteins 33 107–118. [DOI] [PubMed] [Google Scholar]
  3. Burton, R.E., Huang, G.S., Daugherty, M.A., Fullbright, P.W., and Oas, T.G. 1996. Microsecond protein folding through a compact transition state. J. Mol. Biol. 263 311–322. [DOI] [PubMed] [Google Scholar]
  4. Cavagnero, S., Dyson, H.J., and Wright, P.E. 1999. Effect of H helix destabilizing mutations on the kinetic and equilibrium folding of apomyoglobin. J. Mol. Biol. 285 269–282. [DOI] [PubMed] [Google Scholar]
  5. Choe, S.E., Matsudaira, P.T., Osterhout, J., Wagner, G., and Shakhnovich, E.I. 1998. Folding kinetics of villin 14T, a protein domain with a central β-sheet and two hydrophobic cores. Biochemistry 37 14508–14518. [DOI] [PubMed] [Google Scholar]
  6. Clarke, J., Hamill, S.J., and Johnson, C.M. 1997. Folding and stability of a fibronectin type III domain of human tenascin. J. Mol. Biol. 270 771–778. [DOI] [PubMed] [Google Scholar]
  7. Clarke, J., Cota, E., Fowler, S.B., and Hamill, S.J. 1999. Folding studies of immunoglobulin-like β-sandwich proteins suggest that they share a common folding pathway. Struct. Fold. Des. 7 1145–1153. [DOI] [PubMed] [Google Scholar]
  8. Cota, E. and Clarke, J. 2000. Folding of β-sandwich proteins: Three-state transition of a fibronectin type III module. Protein Sci. 9 112–120. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Dalessio, P.M. and Ropson, I.J. 2000. β-Sheet proteins with nearly identical structures have different folding intermediates. Biochemistry 39 860–871. [DOI] [PubMed] [Google Scholar]
  10. Ferguson, N., Capaldi, A.P., James, R., Kleanthous, C., and Radford, S.E. 1999. Rapid folding with and without populated intermediates in the homologous four-helix proteins Im7 and Im9. J. Mol. Biol. 286 1597–1608. [DOI] [PubMed] [Google Scholar]
  11. Fersht, A.R. 2000. Transition-state structure as a unifying basis in protein-folding mechanisms: Contact order, chain topology, stability, and the extended nucleus mechanism. Proc. Natl. Acad. Sci. 97 1525–1529. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Finkelstein, A.V. and Badretdinov, A.Y. 1997a. Physical reasons for a rapid folding of stable protein structures: A solution of Levinthal’s paradox. Mol. Biol. 31 391–398. [PubMed] [Google Scholar]
  13. ———. 1997b. Rate of protein folding near the point of thermodynamic equilibrium between the coil and the most stable chain fold. Fold Des. 2 115–121. [DOI] [PubMed] [Google Scholar]
  14. Finkelstein, A.V and Ptitsyn, O.B. 2002. Protein physics. Lectures 19–21. Academic Press, New York.
  15. Fowler, S.B. and Clarke, J. 2001. Mapping the folding pathway of an immunoglobulin domain: Structural detail from φ value analysis and movement of the transition state. Struct. Fold Des. 9 355–366. [DOI] [PubMed] [Google Scholar]
  16. Galzitskaya, O.V., Ivankov, D.N., and Finkelstein, A.V. 2001. Folding nuclei in proteins. FEBS Lett. 489 113–118. [DOI] [PubMed] [Google Scholar]
  17. Galzitskaya, O.V., Garbuzynskiy, S.O., Ivankov, D.N., and Finkelstein, A.V. 2003. Chain length is the main determinant of the folding rate for proteins with three-state folding kinetics. Proteins 51 162–166. [DOI] [PubMed] [Google Scholar]
  18. Golbik, R., Zahn, R., Harding, S.E., and Fersht, A.R. 1998. Thermodynamic stability and folding of GroEL minichaperones. J. Mol. Biol. 276 505–515. [DOI] [PubMed] [Google Scholar]
  19. Goldberg, M.E., Semisotnov, G.V., Friguet, B., Kuwajima, K., Ptitsyn, O.B., and Sugai, S. 1990. An early immunoreactive folding intermediate of the tryptophan synthetase β2 subunit is a "molten globule." FEBS Lett. 263 51–56. [DOI] [PubMed] [Google Scholar]
  20. Grantcharova, V.P. and Baker, D. 1997. Folding dynamics of the src SH3 domain. Biochemistry 36 15685–15692. [DOI] [PubMed] [Google Scholar]
  21. Grantcharova, V., Alm, E.J., Baker, D., and Horwich, A.L. 2001. Mechanisms of protein folding. Curr. Opin. Struct. Biol. 11 70–82. [DOI] [PubMed] [Google Scholar]
  22. Guerois, R. and Serrano, L. 2000. The SH3-fold family: Experimental evidence and prediction of variations in the folding pathways. J. Mol. Biol. 304 967–982. [DOI] [PubMed] [Google Scholar]
  23. Guijarro, J.I., Morton, C.J., Plaxco, K.W., Campbell, I.D., and Dobson, C.M. 1998. Folding kinetics of the SH3 domain of PI3 kinase by real-time NMR combined with optical spectroscopy. J. Mol. Biol. 276 657–667. [DOI] [PubMed] [Google Scholar]
  24. Gutin, A.M., Abkevich, V.I., and Shakhnovich E.I. 1996. Chain length scaling of protein folding time. Phys. Rev. Lett. 77 5433–5436. [DOI] [PubMed] [Google Scholar]
  25. Ikura, T., Hayano, T., Takahashi, N., and Kuwajima, K. 2000. Fast folding of Escherichia coli cyclophilin A: A hypothesis of a unique hydrophobic core with a phenylalanine cluster. J. Mol. Biol. 297 791–802. [DOI] [PubMed] [Google Scholar]
  26. Jackson, S.E. 1998. How do small single-domain proteins fold? Fold. Des. 3 R81–R91. [DOI] [PubMed] [Google Scholar]
  27. Jackson, S.E. and Fersht, A.R. 1991. Folding of chymotrypsin inhibitor 2, 1: Evidence for a two-state transition. Biochemistry 30 10428–10435. [DOI] [PubMed] [Google Scholar]
  28. Jager, M., Nguyen, H., Crane, J.C., Kelly, J.W., and Gruebele, M. 2001. The folding mechanism of a β-sheet: The WW domain. J. Mol. Biol. 311 373–393. [DOI] [PubMed] [Google Scholar]
  29. Jennings, P.A., Finn, B.E., Jones, B.E., and Matthews, C.R. 1993. A reexamination of the folding mechanism of dihydrofolate reductase from Escherichia coli: Verification and refinement of a four-channel model. Biochemistry 32 3783–3789. [DOI] [PubMed] [Google Scholar]
  30. Khorasanizadeh, S., Peters, I.D., and Roder, H. 1996. Evidence for a three-state model of protein folding from kinetic analysis of ubiquitin variants with altered core residues. Nat. Struct. Biol. 3 193–205. [DOI] [PubMed] [Google Scholar]
  31. Kim, D.E., Fisher, C., and Baker, D. 2000. A breakdown of symmetry in the folding transition state of protein L. J. Mol. Biol. 298 971–984. [DOI] [PubMed] [Google Scholar]
  32. Koga, N., and Takada, S. 2001. Roles of native topology and chain-length scaling in protein folding: A simulation study with a Go-like model. J. Mol. Biol. 313 171–180. [DOI] [PubMed] [Google Scholar]
  33. Kragelund, B.B., Robinson, C.V., Knudsen, J., Dobson, C.M., and Poulsen, F.M. 1995. Folding of a four-helix bundle: Studies of acyl-coenzyme A binding protein. Biochemistry 34 7217–7224. [DOI] [PubMed] [Google Scholar]
  34. Kuhlman, B., Luisi, D.L., Evans, P.A., and Raleigh, D.P. 1998. Global analysis of the effects of temperature and denaturant on the folding and unfolding kinetics of the N-terminal domain of the protein L9. J. Mol. Biol. 284 1661–1670. [DOI] [PubMed] [Google Scholar]
  35. Laurents, D.V., Corrales, S., Elias-Arnanz, M., Sevilla, P., Rico, M., and Padmanabhan, S. 2000. Folding kinetics of phage 434 Cro protein. Biochemistry 39 13963–13973. [DOI] [PubMed] [Google Scholar]
  36. Main, E.R., Fulton, K.F., and Jackson, S.E. 1999. Folding pathway of FKBP12 and characterisation of the transition state. J. Mol. Biol. 291 429–444. [DOI] [PubMed] [Google Scholar]
  37. Matouschek, A., Kellis Jr., J.T., Serrano, L., Bycroft, M., and Fersht, A.R. 1990. Transient folding intermediates characterized by protein engineering. Nature 346 440–445. [DOI] [PubMed] [Google Scholar]
  38. McCallister, E.L., Alm, E., and Baker, D. 2000. Critical role of β-hairpin formation in protein G folding. Nat. Struct. Biol. 7 669–673. [DOI] [PubMed] [Google Scholar]
  39. Munoz, V., Lopez, E.M., Jager, M., and Serrano, L. 1994. Kinetic characterization of the chemotactic protein from Escherichia coli, CheY: Kinetic analysis of the inverse hydrophobic effect. Biochemistry 33 5858–5866. [DOI] [PubMed] [Google Scholar]
  40. Munoz, V., Thompson, P.A., Hofrichter, J., and Eaton, W.A. 1997. Folding dynamics and mechanism of β-hairpin formation. Nature 390 196–199. [DOI] [PubMed] [Google Scholar]
  41. Ogasahara, K. and Yutani, K. 1994. Unfolding-refolding kinetics of the tryptophan synthase α subunit by CD and fluorescence measurements. J. Mol. Biol. 236 1227–1240. [DOI] [PubMed] [Google Scholar]
  42. Otzen, D.E. and Oliveberg, M. 1999. Salt-induced detour through compact regions of the protein folding landscape. Proc. Natl. Acad. Sci. 96 11746–11751. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Parker, M.J. and Marqusee, S. 1999. The cooperativity of burst phase reactions explored. J. Mol. Biol. 293 1195–1210. [DOI] [PubMed] [Google Scholar]
  44. Parker, M.J., Spencer, J., and Clarke, A.R. 1995. An integrated kinetic analysis of intermediates and transition states in protein folding reactions. J. Mol. Biol. 253 771–786. [DOI] [PubMed] [Google Scholar]
  45. Parker, M.J., Sessions, R.B., Badcoe, I.G., and Clarke, A.R. 1996. The development of tertiary interactions during the folding of a large protein. Fold. Des. 1 145–156. [DOI] [PubMed] [Google Scholar]
  46. Parker, M.J., Dempsey, C.E., Lorch, M., and Clarke, A.R. 1997. Acquisition of native β-strand topology during the rapid collapse phase of protein folding. Biochemistry 36 13396–13405. [DOI] [PubMed] [Google Scholar]
  47. Perl, D., Welker, C., Schindler, T., Schroder, K., Marahiel, M.A., Jaenicke, R., and Schmid, F.X. 1998. Conservation of rapid two-state folding in mesophilic, thermophilic and hyperthermophilic cold shock proteins. Nat. Struct. Biol. 5 229–235. [DOI] [PubMed] [Google Scholar]
  48. Plaxco, K.W., Spitzfaden, C., Campbell, I.D., and Dobson, C.M. 1997. A comparison of the folding kinetics and thermodynamics of two homologous fibronectin type III modules. J. Mol. Biol. 270 763–770. [DOI] [PubMed] [Google Scholar]
  49. Plaxco, K.W., Guijarro, J.I., Morton, C.J., Pitkeathly, M., Campbell, I.D., and Dobson, C.M. 1998a. The folding kinetics and thermodynamics of the Fyn-SH3 domain. Biochemistry 37 2529–2537. [DOI] [PubMed] [Google Scholar]
  50. Plaxco, K.W., Simons, K.T., and Baker, D. 1998b. Contact order, transition state placement and the refolding rates of single domain proteins. J. Mol. Biol. 277 985–994. [DOI] [PubMed] [Google Scholar]
  51. Privalov, P.L. 1979. Stability of proteins: Small globular proteins. Adv. Protein Chem. 33 167–241. [DOI] [PubMed] [Google Scholar]
  52. Reid, K.L., Rodriguez, H.M., Hillier, B.J., and Gregoret, L.M. 1998. Stability and folding properties of a model β-sheet protein, Escherichia coli CspA. Protein Sci. 7 470–479. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Schindler, T., Herrler, M., Marahiel, M.A., and Schmid, F.X. 1995. Extremely rapid protein folding in the absence of intermediates. Nat. Struct. Biol. 2 663–673. [DOI] [PubMed] [Google Scholar]
  54. Schreiber, G. and Fersht, A.R. 1993. The refolding of cis- and trans-peptidylprolyl isomers of barstar. Biochemistry 32 11195–11203. [DOI] [PubMed] [Google Scholar]
  55. Schymkowitz, J.W., Rousseau, F., Irvine, L.R., and Itzhaki, L.S. 2000. The folding pathway of the cell-cycle regulatory protein p13suc1: Clues for the mechanism of domain swapping. Struct. Fold Des. 8 89–100. [DOI] [PubMed] [Google Scholar]
  56. Silow, M. and Oliveberg, M. 1997. High-energy channeling in protein folding. Biochemistry 36 7633–7637. [DOI] [PubMed] [Google Scholar]
  57. Spector, S. and Raleigh, D.P. 1999. Submillisecond folding of the peripheral subunit-binding domain. J. Mol. Biol. 293 763–768. [DOI] [PubMed] [Google Scholar]
  58. Tang, K.S., Guralnick, B.J., Wang, W.K., Fersht, A.R., and Itzhaki, L.S. 1999. Stability and folding of the tumour suppressor protein p16. J. Mol. Biol. 285 1869–1886. [DOI] [PubMed] [Google Scholar]
  59. Thirumalai, D. 1995. From minimal models to real proteins: Time scales for protein folding kinetics. J. Phys. 5 1457–1469. [Google Scholar]
  60. Thompson, P.A., Eaton, W.A., and Hofrichter, J. 1997. Laser temperature jump study of the helix⇔coil kinetics of an alanine peptide interpreted with a "kinetic zipper" model. Biochemistry 36 9200–9210. [DOI] [PubMed] [Google Scholar]
  61. Van Nuland, N.A., Chiti, F., Taddei, N., Raugei, G., Ramponi, G., and Dobson, C.M. 1998a. Slow folding of muscle acylphosphatase in the absence of intermediates. J. Mol. Biol. 283 883–891. [DOI] [PubMed] [Google Scholar]
  62. Van Nuland, N.A., Meijberg, W., Warner, J., Forge, V., Scheek, R.M., Robillard, G.T., and Dobson, C.M. 1998b. Slow cooperative folding of a small globular protein HPr. Biochemistry 37 622–637. [DOI] [PubMed] [Google Scholar]
  63. Viguera, A.R., Serrano, L., and Wilmanns, M. 1996. Different folding transition states may result in the same native structure. Nat. Struct. Biol. 3 874–880. [DOI] [PubMed] [Google Scholar]
  64. Villegas, V., Azuaga, A., Catasus, L., Reverter, D., Mateo, P.L., Aviles, F.X., and Serrano, L. 1995. Evidence for a two-state transition in the folding process of the activation domain of human procarboxypeptidase A2. Biochemistry 34 15105–15110. [DOI] [PubMed] [Google Scholar]
  65. Wittung-Stafshede, P., Lee, J.C., Winkler, J.R., and Gray, H.B. 1999. Cytochrome b562 folding triggered by electron transfer: Approaching the speed limit for formation of a four-helix–bundle protein. Proc. Natl. Acad. Sci. 96 6587–6590. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Protein Science : A Publication of the Protein Society are provided here courtesy of The Protein Society

RESOURCES