Abstract
PsiCSI is a highly accurate and automated method of assigning secondary structure from NMR data, which is a useful intermediate step in the determination of tertiary structures. The method combines information from chemical shifts and protein sequence using three layers of neural networks. Training and testing was performed on a suite of 92 proteins (9437 residues) with known secondary and tertiary structure. Using a stringent cross-validation procedure in which the target and homologous proteins were removed from the databases used for training the neural networks, an average 89% Q3 accuracy (per residue) was observed. This is an increase of 6.2% and 5.5% (representing 36% and 33% fewer errors) over methods that use chemical shifts (CSI) or sequence information (Psipred) alone. In addition, PsiCSI improves upon the translation of chemical shift information to secondary structure (Q3 = 87.4%) and is able to use sequence information as an effective substitute for sparse NMR data (Q3 = 86.9% without 13C shifts and Q3 = 86.8% with only Hα shifts available). Finally, errors made by PsiCSI almost exclusively involve the interchange of helix or strand with coil and not helix with strand (<2.5 occurrences per 10000 residues). The automation, increased accuracy, absence of gross errors, and robustness with regards to sparse data make PsiCSI ideal for high-throughput applications, and should improve the effectiveness of hybrid NMR/de novo structure determination methods. A Web server is available for users to submit data and have the assignment returned.
Keywords: NMR, chemical shifts, secondary structure, neural networks
The flood of data from the genomic sequencing projects has inspired structural genomic projects aimed at determining all of the possible protein folds (Burley 2000; Brenner 2001). Although the major methodology being used in these projects is X-ray crystallography, NMR is also being developed as an alternative for high-throughput applications (Montelione 2001). One of the major bottlenecks in NMR structure determinations is in the interpretation and analysis of the spectral data, which, with the possible exception of chemical-shift assignment (Bailey-Kellogg et al. 2000; Moseley et al. 2001), still requires considerable human intervention. One promising approach to this problem is to couple theoretical simulations with NMR methods to reduce the amount of data, effort, and time required to determine the fold of a protein (Delaglio et al. 2000; Rohl and Baker 2002). Automated and accurate secondary structure assignments are necessary for these methods to be effective.
Secondary structure from chemical shifts (CSI)
The first step of any NMR structure determination is the assignment of chemical shifts (CSI). Because this is also the only step that has been partially automated, a considerable amount of effort has been expended in translating chemical shifts into structural information (Wishart et al. 1992; Wishart and Sykes 1994; Cornilescu et al. 1999; Bonvin et al. 2001). There is a fairly simple, if noisy, relationship between secondary structure and the chemical shifts of certain nuclei (Spera and Bax 1991; Wishart et al. 1991). For example, Hα chemical shifts are higher than average (downfield) in extended structures and lower than average (upfield) in helices. The same is true for 15N and Cβ shifts, whereas the opposite relationship holds for C, and Cα shifts. To exploit this information, CSI (Chemical Shift Index) (Wishart et al. 1992; Wishart and Sykes 1994) assigned three indices, −1, 0, and 1, depending on whether the chemical shift was near the average value or at one of the extremes. Consecutive occurrences of like indices were used to identify the presence of secondary structure. To further increase accuracy, a jury system averaged assignments from multiple chemical shifts—C, Cα, Cβ, and Hα—to arrive at a consensus assignment.
Secondary structure from sequence (Psipred)
Early secondary structure prediction methods relied upon database (Chou and Fasman 1974; Garnier et al. 1978) or theoretically derived propensities (Lim 1974) for residue types to be in the three secondary structure states with Q3 (i.e., the percentage total number of residues correctly assigned to the three secondary structure states) accuracies in the 60% range. The current generation of methods exploits the information from multiple alignments to further enhance the accuracy (Krogh et al. 1994; Rost 1996; Jones 1999), which now approaches 80%. The use of neural nets, PHD (Rost 1996) and Psipred (Jones 1999), to interpret the large amount of data has been also instrumental in increasing the accuracy. One of the most accurate methods, Psipred, uses neural nets to convert PsiBlast (Altschul et al. 1997) profile data to secondary structure propensities. A second set of neural nets then takes into account local interactions to smooth the resulting secondary structure predictions and further increase accuracy.
Secondary structure from chemical shifts and sequence (PsiCSI)
PsiCSI combines both the chemical shift-based and sequence-based methods to further increase the accuracy of secondary structure assignments. It is also designed to best utilize whatever data is available. PsiCSI begins by refining the CSI methodology. Rather than three indices, three separate potentials ranging from 0 to 1 are assigned to reflect the relative likelihood of a given chemical-shift value being associated with a given secondary structure state. Like CSI, PsiCSI reduces noise by polling nearby shifts. PsiCSI examines a small window of shifts (three residues) centered around the residue in question. Potentials derived from these shifts, along with the estimated residue-dependent reliabilities (i.e., probability of the assignment being correct) of these potentials, are fed into a first layer of neural networks to derive a second set of refined potentials. Like CSI, multiple shifts are used to further increase accuracy. Additional information from 15N shifts and from Psipred predictions is also used. Rather than utilizing a simple jury system, PsiCSI trains a second layer of neural networks. Every possible combination of the available data for the residue (i.e., refined potentials from the first layer of networks and Psipred potentials) is fed into separate neural nets. Reliabilities for each combination are estimated and the best performing combination (for that residue type) is used to provide potentials for the next layer of neural networks. Finally, as with Psipred, the last neural net takes into account local interactions. This is similar to the first layer of neural nets used to average out chemical shift noise. However, because the accuracy of the inputs at this stage is much higher, it is possible to utilize a much larger window (17 vs. 3 residues) to take into account more subtle interactions between distant residues. The most reliable outputs from the second layer along with estimated reliablities are fed into this final neural net to ultimately obtain the PsiCSI prediction.
Results and Discussion
PsiCSI significantly improves upon existing methods
PsiCSI achieves a Q3 accuracy of 89% (per residue), which is a significant improvement over the 82.8% (z > 12) accuracy observed for CSI and the 83.5% (z > 11) accuracy observed for Psipred. The CSI accuracy observed for our dataset differs from the originally published accuracy of 92%. However, this figure was obtained using a small sample of proteins on the basis of a combination of subjective identification of secondary structures from NMR data (not structures) and on crystal structures. In addition, the dataset was not jackknifed, 8 of the 16 proteins used to evaluate CSI were also part of the set of 12 proteins used to determine the indices. The observed accuracy of Psipred also differs from the stated accuracy (80%) by more than can be accounted for by random chance (z > 8). The test set may include proteins and/or homologs to proteins used to train Psipred’s neural networks, which could account for the higher accuracy. However, the accuracy of the chemical shift alone version of PsiCSI (87.4%) indicates that the high accuracy of PsiCSI is not contingent upon the unusual accuracy of Psipred on the test set.
The distribution of Q3 accuracies of PsiCSI, CSI, and PsiPred, is shown in Figure 1 ▶. The distribution of PsiCSI accuracies is very tight, reflecting the consistency of the method. Some of the less accurate results come from large regions of coil being assigned as helix or extended (see Electronic Supplemental Material). It is possible that PsiCSI is detecting some residual structure in these regions. PsiCSI does better than CSI or Psipred in the majority of cases as is expected from the average per residue increase in accuracy. The existence of cases in which PsiCSI performs 40% better than CSI and 28% better than Psipred indicates that PsiCSI is able to compensate when the other methods do extremely poorly.
Fig. 1.
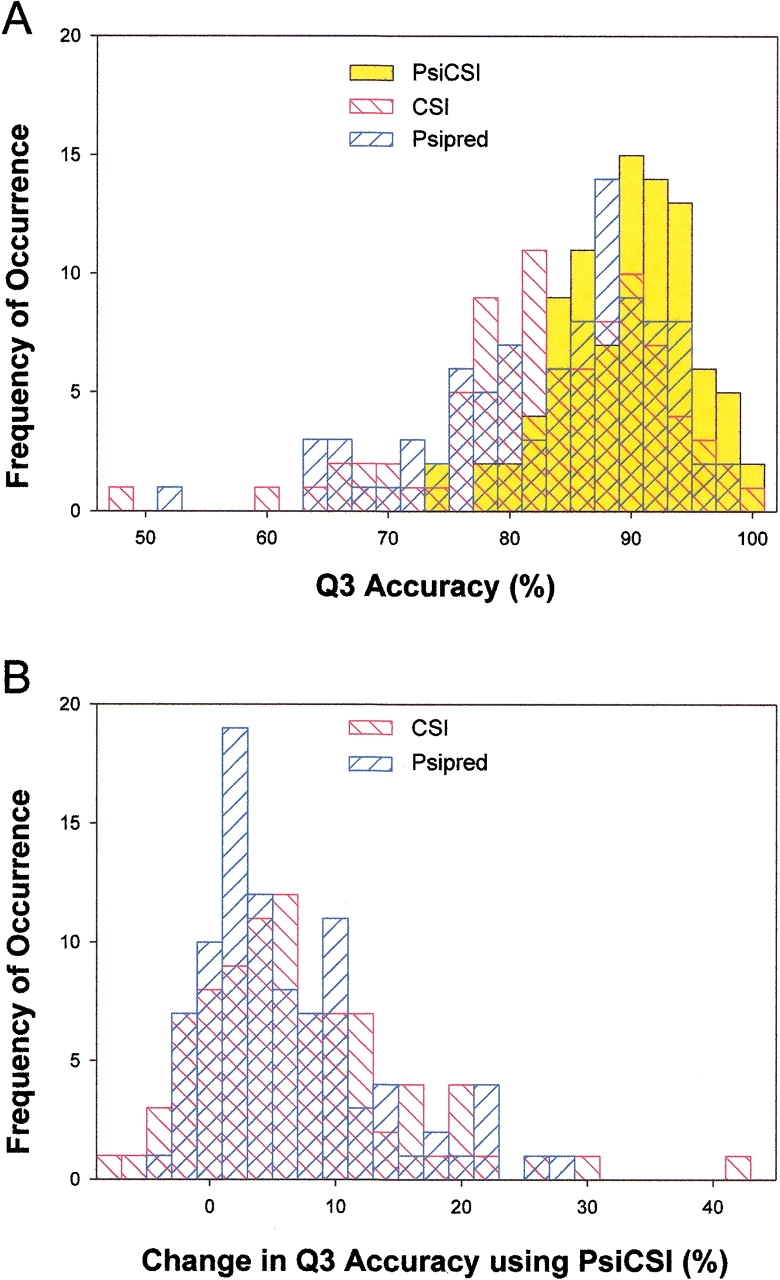
Distribution of Q3 accuracies. (A) The distribution of Q3 accuracies for the PsiCSI, CSI, and Psipred is shown. For CSI, consensus predictions were not available for two cases, and these were omitted. Not only is the increased accuracy readily apparent, but the consistency of PsiCSI is revealed by the a tight and nearly symmetrical distribution of accuracies. Both CSI and Psipred have significant populations in which the methods do relatively poorly in contrast to PsiCSI, in which no protein fares worse than 74%, and the average Q3 accuracy is 89%. (B) The distribution of the differences in the Q3 accuracy of PsiCSI is compared with that of CSI and Psipred for the same protein. As would be expected from the overall increased accuracy of PsiCSI, the distribution indicates that there are relatively few cases in which PsiCSI performs more poorly than CSI or Psipred, and only marginally so. Conversely, the improvement observed when using PsiCSI can be very large, indicating that the method can still be effective in cases in which CSI or Psipred do very poorly.
Table 1 lists different indices of accuracy. Although PsiCSI is most accurate for helical regions and less accurate for extended and coil regions, this is true for all methods, and PsiCSI is still the most accurate method in each category. For all three categories, the reliablities and accuracies for PsiCSI are virtually identical, indicating that PsiCSI strikes a good balance between underpredicting and overpredicting secondary structure elements.
Table 1.
Accuracy and reliability of PsiCSI, Psipred, and CSI
| Accuracy (%)a | Reliability (%)b | ||||||
| Overall (Q3)% | H | E | C | H | E | C | |
| PsiCSI | 89.0 | 91.8 | 84.4 | 89.1 | 93.3 | 84.0 | 88.3 |
| PsiCSI (shifts only) | 87.4 | 90.5 | 80.2 | 88.3 | 92.1 | 82.9 | 86.2 |
| PsiCSI (no 13C) | 86.9 | 87.0 | 82.6 | 88.7 | 90.6 | 86.0 | 85.1 |
| PsiCSI (no 13C/15N) | 86.8 | 87.0 | 81.6 | 88.7 | 90.6 | 85.9 | 84.4 |
| Psipred v2.3 | 83.5 | 88.7 | 79.3 | 81.8 | 83.1 | 77.2 | 86.6 |
| CSI (consensus) | 82.8 | 86.9 | 80.7 | 81.0 | 91.4 | 71.3 | 82.7 |
a Percentage of correct assignments of state/total number of residues that are actually in that state.
b Percentage of correct assignments of state/total number of residues assigned to that state.
Table 2 lists the frequencies of the different types of errors made by the different methods. Noteworthy is the near complete absence of helix to extended or extended to helix errors in assignments made by PsiCSI. In contrast, Psipred is 75 times more likely to make these sorts of errors and will occasionally interchange stretches of helix and strand. The major source of error for PsiCSI is the interchange of extended and coil states. This is understandable given that PsiCSI only takes into account local interactions, whereas extended regions are partially defined by hydrogen-bonding interactions that are not necessarily local.
Table 2.
Nature of assignment errors made by PsiCSI, Psipred, and CSI
| Number of Occurrences per 10000 residues | ||||||
| H → E | H → C | E → H | E → C | C → H | C → E | |
| PsiCSI | 2.1 | 258.8 | 0.0 | 309.7 | 211.1 | 317.1 |
| PsiCSI (shifts only) | 2.1 | 299.1 | 6.4 | 387.1 | 240.7 | 325.6 |
| PsiCSI (no 13C) | 2.1 | 411.5 | 5.3 | 340.5 | 283.2 | 264.1 |
| PsiCSI (no 13C/15N) | 3.2 | 405.2 | 5.3 | 359.6 | 282.1 | 263.0 |
| Psipred v2.3 | 84.9 | 274.7 | 73.2 | 337.3 | 498.5 | 379.7 |
| CSI (consensus) | 8.9 | 413.7 | 3.3 | 389.2 | 258.0 | 647.2 |
Multiple levels of neural nets progressively increase the accuracy of PsiCSI
The relationship between chemical shift and secondary structure is a very noisy one. Initial secondary structure potentials are rather poor predictors (Table 3). After application of the first set of neural nets, which reduces the noise by examining the shifts in a window of three consecutive residues, the correlation between secondary structure and chemical shift improves dramatically for all of the shifts. The effect of the second set of neural nets, which combine chemical shift data from different nuclei and Psipred data, is also shown in Table 3. Progressive addition of more input points improves accuracy. Although there are clearly diminishing returns with data combinations containing more than four sets of potentials, the identity of the inputs matters less as the number of inputs increases. The final neural net accounting for local interactions raises the accuracy to its final value of 89% when all available data is used. The system also is effective when only subsets of data are used as inputs with 87.4% accuracy when data is restricted to chemical shifts, 86.9% accuracy with only 15N, Hα, and Psipred data, and 86.8% with just Hα and Psipred data.
Table 3.
Accuracy of PsiCSI after each layer of neural networks
| Q3 Accuracy Range % | |
| Initial potentials | 51.7–69.6a |
| After first layer | 63.4–79.0a |
| After second layer | |
| 2 inputs | 73.5–86.0b |
| 3 inputs | 78.6–87.9b |
| 4 inputs | 82.9–88.4b |
| 5–6 inputs | 84.7–88.5b |
| After third layer | 89.0 |
a Accuracy depends on the nucleus that gave rise to the chemical shifts used for the initial potentials.
b Accuracy depends upon which inputs (chemical shifts and/or Psipred derived data) are combined.
The use of well-defined consensus secondary structures minimizes the variability introduced by NMR conformers
NMR structures consist of sets of conformers that satisfy the constraints derived from the spectral data (largely from NOEs). Because secondary structure is usually not explicitly constrained, there are variations in secondary structure between the different conformers. Previous studies correlating chemical shift with structure have largely avoided using NMR-derived structures to sidestep this problem. However, this limits the number of proteins that can be assayed to those with both NMR data and crystal structures. Furthermore, the use of crystal structures may mask true differences between solution and the crystal states. It was for this reason that solution structures were used whenever possible (85/92 structures).
Simple use of just the first conformer was attempted with some success (Q3 = 86.1% for 68 proteins; data not shown). However, the level of variation between conformers was sufficiently high (94% average pairwise concordance; 87% concordance between the most divergent pair) that significant errors in secondary structure identification were introduced. The variability was reduced by using a consensus secondary structure (96% concordance). A further difficulty arises that variability can be much higher in regions in which there are fewer experimental NMR constraints. The lack of constraints can be the result of true structural heterogeneity or the result of experimental factors (relaxation, exchange, chemical shift ambiguity), which preclude the observation and identification of NOEs. Thus, the training set was further restricted to residues in which the level of agreement on secondary structure was at least 90%, which accounted for a large majority (85%) of the residues.
The accuracies of the different methods over this subset of residues and over the entire set of residues are shown in Table 4. Table 5 lists all of the proteins in the test set and the Q3 accuracies using PsiCSI, CSI, and Psipred. All methods improve by ∼3% when the subset of well-defined regions is used. Large-scale analysis of secondary structure by EVA (Eyrich et al. 2001; Rost and Eyrich 2001) has also detected a 3% lower accuracy for prediction methods when the first conformer of an NMR structure is used rather than a crystal structure. One possible reason for this decrease is that disordered regions are generally not observed in crystal structures, whereas they are present in NMR structures. Our protocol seems to have restored this 3% difference in prediction accuracy by filtering out these regions and also by eliminating the noise introduced by utilizing first conformer structures rather than the consensus of all conformer structures. This type of strategy may be useful for other surveys of secondary structures that include NMR structures. All statistics have been calculated using this subset of residues (9437 residues) with well-defined secondary structure unless otherwise stated.
Table 4.
Accuracy of PsiCSI, CSI, and Psipred on the regions with well-defined secondary structure
| All regions (Q3%) | Well-defined regions (Q3%) | |
| PsiCSI | 85.9 | 89.0 |
| PsiCSI (shifts only) | 84.5 | 87.4 |
| Psipred v2.3 | 80.3 | 83.5 |
| CSI (consensus)a | 80.1 | 82.8 |
a Only proteins in which a consensus could be reached (90/92) by CSI were considered.
Table 5.
Q3 accuracies for members of the test set
| Protein | PsiCSI | CSI | Psipred |
| 1d6k A | 74.12 | 68.24 | 74.12 |
| 1ckv _ | 74.19 | 59.48 | 65.32 |
| 1dbd A | 77.00 | 76.00 | 75.00 |
| 1g4f A | 78.38 | 79.73 | 51.35 |
| 1cex _ | 79.70 | 76.41 | 79.19 |
| 1ckr A | 79.73 | 77.03 | 72.30 |
| 1mb1 _ | 81.63 | 83.16 | 83.67 |
| 2rsp A | 81.74 | 78.90 | 77.39 |
| 1g5v A | 81.82 | 81.82 | 83.64 |
| 2jhb A | 82.31 | 80.77 | 64.62 |
| 1hka _ | 83.54 | 81.20 | 81.65 |
| 1c54 A | 83.87 | 75.27 | 73.12 |
| 1d4b A | 84.21 | 84.62 | 64.04 |
| 1blr _ | 84.25 | 75.41 | 83.46 |
| 1omt _ | 84.31 | 80.00 | 84.31 |
| 1b64 _ | 84.38 | 88.89 | 71.88 |
| 1qlz A | 84.44 | 89.77 | 72.22 |
| 1cej A | 84.52 | 83.33 | 78.57 |
| 1d2b A | 84.76 | 79.21 | 75.24 |
| 1duj A | 85.03 | 77.22 | 79.68 |
| 1bb8 _ | 85.07 | 89.55 | 65.67 |
| 1cz5 A | 85.47 | 65.54 | 87.71 |
| 1bqv _ | 85.57 | 78.95 | 76.29 |
| 1qm3 A | 85.71 | 89.16 | 65.48 |
| 1osp O | 86.06 | 85.54 | 76.89 |
| 1bwm A | 86.12 | 66.27 | 83.25 |
| 1onc _ | 86.41 | 67.65 | 77.67 |
| 1myo _ | 86.41 | 79.21 | 84.47 |
| 1bf8 _ | 86.67 | 81.82 | 85.45 |
| 1ci5 A | 86.90 | 81.93 | 80.95 |
| 1fzt A | 87.10 | 77.71 | 87.10 |
| 2ife A | 87.67 | 47.89 | 79.45 |
| 1ssn _ | 87.85 | 82.24 | 75.70 |
| 1qm1 A | 88.17 | 89.01 | 63.44 |
| 1qhk A | 88.37 | 85.37 | 79.07 |
| 7i1b _ | 88.41 | 84.78 | 86.23 |
| 1qkh A | 88.89 | 78.33 | 79.37 |
| 1bnp _ | 89.04 | 84.51 | 86.30 |
| 1bld _ | 89.05 | 78.68 | 88.32 |
| 1dlx A | 89.22 | 87.25 | 92.16 |
| 1u9a A | 89.31 | 77.56 | 91.19 |
| 1ns1 A | 89.86 | 97.10 | 68.12 |
| 1e17 A | 89.87 | 70.89 | 86.08 |
| 1rch _ | 89.92 | _ | 93.28 |
| 1akp _ | 90.00 | 73.75 | 88.75 |
| 2ncm _ | 90.32 | 90.32 | 88.17 |
| 1tba A | 90.38 | 79.59 | 80.77 |
| 1h92 A | 90.38 | 72.00 | 90.38 |
| 1fo7 A | 90.53 | 91.58 | 70.53 |
| 1c15 A | 90.91 | 89.29 | 82.95 |
| 2tbd _ | 90.91 | 84.26 | 77.27 |
| 1eoq A | 90.91 | 82.89 | 89.61 |
| 1imp _ | 91.36 | 91.36 | 87.65 |
| 1aq5 A | 91.49 | 87.23 | 89.36 |
| 1oca _ | 91.56 | 82.12 | 90.26 |
| 1d7q A | 91.60 | 86.73 | 93.13 |
| 1inz A | 91.67 | 93.55 | 76.52 |
| 1br0 A | 91.92 | 93.94 | 94.95 |
| 1qjt A | 92.05 | 89.77 | 88.64 |
| 1bo0 _ | 92.11 | 82.99 | 92.11 |
| 1hdn _ | 92.21 | _ | 85.71 |
| 1itf _ | 92.57 | 86.49 | 87.84 |
| 3pdz A | 92.55 | 76.92 | 93.62 |
| 1khm A | 92.68 | 88.75 | 89.02 |
| 1g03 A | 92.86 | 95.54 | 87.50 |
| 3msp A | 92.92 | 81.42 | 86.73 |
| 1d1d A | 93.30 | 94.26 | 85.65 |
| 1eo0 A | 93.42 | 64.47 | 85.53 |
| 1ab2 _ | 93.62 | 90.00 | 92.55 |
| 3mef A | 93.62 | 78.72 | 91.49 |
| 1jwd A | 93.75 | 70.00 | 88.75 |
| 2bjx A | 93.94 | 88.89 | 94.95 |
| 1c06 A | 94.03 | 94.03 | 90.30 |
| 1mfn _ | 94.16 | 81.05 | 94.16 |
| 1b91 A | 94.17 | 91.58 | 90.29 |
| 1eiw A | 94.19 | 92.86 | 88.37 |
| 1ig6 A | 94.25 | 88.51 | 91.95 |
| 1jwe A | 94.74 | 92.47 | 92.63 |
| 1iti _ | 94.92 | 88.14 | 81.36 |
| 1bw5 _ | 95.16 | 86.89 | 77.42 |
| 1cfe _ | 95.24 | 82.86 | 95.24 |
| 1hkt _ | 95.77 | 80.60 | 88.73 |
| 1kqq A | 96.06 | 91.27 | 92.91 |
| 1du6 A | 96.49 | 98.25 | 94.74 |
| 2cpb _ | 96.77 | 96.77 | 87.10 |
| 1emw A | 97.22 | 86.11 | 93.06 |
| 1eih A | 98.44 | 89.06 | 95.31 |
| 1c0v A | 98.53 | 100.00 | 97.06 |
| 1qk9 A | 98.73 | 92.41 | 89.87 |
| 1ntc A | 98.78 | 95.65 | 89.02 |
| 1fr0 A | 99.07 | 90.48 | 88.79 |
| 1rpr A | 100.00 | 88.89 | 98.28 |
The accuracy of PsiCSI may be improved by additional data points and sources
Because secondary structures are somewhat artificial constructs, there is ambiguity in how they are defined. DSSP (Kabsch and Sander 1983, used in this study) and Stride (Frishman and Argos 1995), the two most popular identification protocols agree to a level of 95% of the three-state secondary structure assignments, mostly differing on the extent of secondary structures (Cuff and Barton 1999). DEFINE (Richards and Kundrot 1988), used with DSSP in the original CSI evaluation, agrees with DSSP and Stride at the level of 73% and 74%, respectively (Cuff and Barton 1999). An additional factor affecting the limit of accuracy are the limits of resolution of the models upon which the secondary structures are based. The dataset used in this study consisted of residues in which there is at least 90% agreement on the secondary structure between the different conformers, and presently, PsiCSI, at 89%, is close to this minimum accuracy. However, as the average pairwise concordance between the secondary structure of conformers is 94%, there is still room for improvement.
To further improve PsiCSI, more data points and more data sources will be required.
The present sample size (9437 residues) still places limits on the data processing scheme. For example, given a sufficient number of data points, it might be possible to improve upon the second layer of neural nets by training a separate set of nets for each residue type. More sample points would also reduce the noise in the original translation of chemical shifts to secondary structure. A larger training set would especially benefit the final neural network, which has many more connections than the other networks and, thus, is more difficult to train. As for data sources, additional NMR information could include more chemical shifts (e.g., from amides), J-coupling constants, and NOE data. These data could easily be incorporated as additional inputs to the neural nets. Because the major weakness of PsiCSI is in distinguishing coil from extended, NOE information, which could be used to infer the existence of non-local hydrogen bonding, is likely to be of greatest benefit. Finally, PsiCSI, has scrupulously avoided a major source of secondary structure information, homology. The secondary structure of close homologs is highly conserved and predictions based on close homology are much more accurate than any sequence-based method. Even in its present form, PsiCSI should perform better on proteins with homology to members of the training set. During prototyping, it was observed that overall accuracies, especially that of the first chemical shift to secondary structure potential translation and that of the final neural net layer, were significantly increased by the inclusion of homologs in the training set. PsiCSI could be easily modified to explicitly include homology information either directly as additional inputs, or indirectly through modifications of the secondary structure potential translations to weight data according to the degree of local sequence homology.
PsiCSI should expedite both experimental and theoretical applications
Presently, NMR secondary structure assignments require manual interpretation of several pieces of data, mainly chemical shifts, J-couplings, and NOEs. PsiCSI approaches the accuracy required to completely automate the process and certainly reduces the amount of additional data that needs to be gathered and interpreted before an assignment is made. The effectiveness of the method with sparse data also means that secondary structures can be confidently assigned at an earlier stage. The fact that PsiCSI does not require heteronuclear chemical shifts to be effective also makes it useful for proteins in which costs and/or poor expression preclude isotopic labeling. The very high accuracy and automated nature of PsiCSI also makes it potentially quite useful for rapid profiling of proteins in high-throughput structural genomic applications. The ability of PsiCSI to function without complete assignment of all of the backbone chemical shifts makes it particularly well suited for use in conjunction with automated chemical-shift assignment methods, which do not always provide complete assignments.
PsiCSI is one of a new generation of applications such as TALOS (Cornilescu et al. 1999), and Rosetta-NMR (Rohl and Baker 2002) that utilize the growing database of structural and sequence information to better interpret experimental data. Rosetta-NMR is an example of more ambitious attempts to marry de novo database-based protein structure simulations with NMR data to directly arrive at a tertiary fold. To reduce the search space, de novo programs often fix or bias secondary structures during the simulation (Ortiz et al. 1999; Samudrala et al. 1999; Bonneau et al. 2001). Small errors can impact upon the convergence of the final structures. However, gross errors, such as those in which large stretches of helix or strand are interchanged, can result in prediction of the wrong fold (Samudrala and Levitt 2002). PsiCSI should be of considerable help for these hybrid applications, not only because of the increase in overall accuracy, but also because of the virtual elimination of gross errors.
Materials and methods
Initial chemical shift secondary structure potentials are derived from a database
Because of the differences in referencing and calibrating chemical shifts, especially for earlier studies, chemical shifts were obtained from a database (RefDb) (http://redpoll.pharmacy.ualberta.ca/RefDB/) provided by David Wishart’s group, in which they have re-referenced the data points from the BBMR database (Seavey et al. 1991). Paramagnetic systems, unfolded proteins, proteins smaller than 35 residues, and proteins with large prosthetic groups or other ligands were excluded, giving a set of 92 proteins for which there were at least some 13C, 15N, and 1H shifts and a matching structure in the PDB. Where multiple structures were available, preference was given to the solution structure.
For each of the proteins in the final set of 92, the secondary structure was first determined using DSSP (treating H and G as helix, E and B as extended, and everything else as coil). For NMR ensembles, the secondary structure of all of the conformers were determined and a consensus structure obtained. Residues in which there was < 90% agreement between the conformers were excluded from further consideration. A database was made from the remaining residues, relating chemical shift to secondary structure and amino acid type. To translate a given chemical shift into secondary structure potentials, the database was searched for residues with chemical shifts (of the same residue type) that were within 0.4 ppm for C, 0.2 ppm for Cα, and Cβ, 0.3 ppm for N, and 0.04 ppm for Hα. If there were < 20 shifts, the next closest shifts were used until the minimum of 20 was obtained. Chemical shifts from the same protein or related proteins (see below) were excluded. The secondary structure of each residue within this set was tabulated. When there was partial disagreement among conformers as to the state of the residue, the proportion of conformers in each of the 3 states was used in the tabulation (e.g., for a residue in which 9 of 10 conformers are helical and 1 is coil, 0.9 would be added to the helix total, 0.1 would be added to the coil total). The final number of residues in helix, extended, and coil states were divided by the total number of chosen residues to obtain the secondary structure potentials. These potentials were then normalized to take into account the proportion of helix, extended, and coil states in the test set.
Psipred secondary structure potentials were obtained using Psipredv2.3. Two sets of secondary structure potentials can be obtained from Psipred. One set uses only the PsiBlast profiles, whereas the second set smooths the potentials by taking into account local interactions between residues. The first set of potentials was used, as the last neural net in PsiCSI also takes into account local interactions. However, the slightly more accurate smoothed set of potentials was used for all comparisons of accuracy.
Finally, for each potential, the number of correct assignments made using that potential were divided by the total number of assignments made. This was done for each of the three secondary structure states to give a set of three reliability estimates. Because of the strong dependence of these reliabilities on the residue type, the indices were calculated for each of the 20 amino acids to give 20 separate sets of reliability indices per potential.
First layer of neural nets reduce noise by considering shifts at neighboring residues
Because secondary structures involve more than a single residue, the accuracy of the initial set of potentials can be increased by examining the adjacent residues to see whether similar potentials are found. Thus, the potentials from the original residue, and the two adjacent residues, along with the estimates of reliability, provided inputs for the first layer of neural networks. A total of 7 inputs per residue (3 secondary structure potentials, 3 reliability indices, and 1 input to indicate the absence of data due to the window extending beyond the edge of the protein) or 21 total, led into 3 hidden inputs that fed into the final 3 output units. These outputs correspond to three new secondary potentials. The test set was balanced so that equal numbers of residues in the three states were present and then randomly split into two. One set was used to train the set and the other to evaluate the accuracy. Training was accomplished by resilient back-propagation until the evaluation set showed no improvement. This was done three times using a different set of initial values for the weights and the best performing net chosen. Different neural nets were trained for each of the five different chemical shifts. The SNNS (Stuttgart Neural Network System version 4.2) package (http://www-ra.informatik.unituebingen.de/SNNS/) was used to generate and train all of the networks. Reliabilities for the new set of potentials were also estimated.
Second layer of neural nets combine different chemical shift and Psipred potentials
To combine the chemical-shift and Psipred potentials, a second set of neural networks was used. Separate networks were trained for all possible combinations of chemical shift and Psipred data. Each neural network consisted of an input for each of the chemical shift derived secondary potentials (3–15), the reliability indices, and an input for each of the PsiPred potentials and reliability indices. These fed into a hidden layer of six units and a final output layer of three units again, corresponding to further refined helical, extended, and coil potentials. The second layer of neural nets were trained on balanced sets in the same manner as for the first layer.
Third neural net factors in local interactions
By use of the second layer of neural nets, secondary structure predictions were made with potentials obtained from each of the possible data combinations. These were compared with the actual secondary structure and ranked by their reliablity for each residue type. Outputs from the most reliable combinations were used to provide inputs for the final neural net. The purpose of this neural net was to account for local interactions between secondary structure elements. The architecture was similar to that used in the first layer of networks with seven inputs per residue corresponding to the secondary structure potentials and the reliability indices. However, due to the increased accuracy of the inputs at this point, a larger window of 17 residues could be used. The resulting 119 inputs fed into a hidden layer of 17 and an output layer of 3, corresponding to the 3 final secondary structure potentials. Training was done as before, except that sets were not balanced. Because the best available data nearly always includes a Psipred component, the final network optimizes itself to correct Psipred types of errors and underperforms when only chemical-shift information is available. Thus, estimates of accuracy when only chemical-shift information is available were obtained using a separate network that was trained on chemical shift data (resulting in a minor improvement of 0.5%).
Test sets and cross-validation
For stringent cross-validation, all of the calculations, including the chemical-shift translation, the calculation of reliability indices, the ranking of the performance of the different nets, and neural net training itself, were done by use of a subset that not only excluded the protein to be tested, but also any proteins in the same family [up to the T level as determined by CATH (Orengo et al. 1997)]. By use of software made publicly available by the researchers, CSI and Psipred were also used on the same dataset to predict secondary structure for comparison.
Electronic supplemental material
Figure S1 shows the relative performance of the three methods: PsiCSI, CSI, and PsiPred. The assignments for all the proteins used in the test set are listed.
Web server
A server that takes as input a sequence and chemical shift data and returns a secondary structure prediction is accessible via http://protinfo.compbio.washington.edu.
Acknowledgments
This work was supported in part by a Searle Scholar Award to R.S.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.
Article and publication are at http://www.proteinscience.org/cgi/doi/10.1110/ps.0222303.
Supplemental material: See www.proteinscience.org.
References
- Altschul, S.F., Madden, T.L., Schaffer, A.A., Zhang, J., Zhang, Z., Miller, W., and Lipman, D.J. 1997. Gapped BLAST and PSI-BLAST: A new generation of protein database search programs. Nucleic Acids Res. 25 3389–3402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bailey-Kellogg, C., Widge, A., Kelley, J.J., Berardi, M.J., Bushweller, J.H., and Donald, B.R. 2000. The NOESY jigsaw: Automated protein secondary structure and main-chain assignment from sparse, unassigned NMR data. J. Comput. Biol. 7 537–558. [DOI] [PubMed] [Google Scholar]
- Bonneau, R., Tsai, J., Ruczinski, I., Chivian, D., Rohl, C., Strauss, C.E., and Baker, D. 2001. Rosetta in CASP4: Progress in ab initio protein structure prediction. Proteins 45 119–126. [DOI] [PubMed] [Google Scholar]
- Bonvin, A.M., Houben, K., Guenneugues, M., Kaptein, R., and Boelens, R. 2001. Rapid protein fold determination using secondary chemical shifts and cross-hydrogen bond 15N-13C′ scalar couplings (3hbJNC′). J. Biomol. NMR 21 221–233. [DOI] [PubMed] [Google Scholar]
- Brenner, S.E. 2001. A tour of structural genomics. Nat. Rev. Genet. 2 801–809. [DOI] [PubMed] [Google Scholar]
- Burley, S.K. 2000. An overview of structural genomics. Nat. Struct. Biol. 7 932–934. [DOI] [PubMed] [Google Scholar]
- Chou, P.Y. and Fasman, G.D. 1974. Conformational parameters for amino acids in helical, β-sheet, and random coil regions calculated from proteins. Biochemistry 13 211–222. [DOI] [PubMed] [Google Scholar]
- Cornilescu, G., Delaglio, F., and Bax, A. 1999. Protein backbone angle restraints from searching a database for chemical shift and sequence homology. J. Biomol. NMR 13 289–302. [DOI] [PubMed] [Google Scholar]
- Cuff, J.A. and Barton, G.J. 1999. Evaluation and improvement of multiple sequence methods for protein secondary structure prediction. Proteins 34 508–519. [DOI] [PubMed] [Google Scholar]
- Delaglio, F., Kontaxis, G., and Bax, A. 2000. Protein structure determiniation using molecular fragment replacement and NMR dipolar couplings. J. Am. Chem. Soc. 122 2142–2143. [Google Scholar]
- Eyrich, V.A., Marti-Renom, M.A., Przybylski, D., Madhusudhan, M.S., Fiser, A., Pazos, F., Valencia, A., Sali, A., and Rost, B. 2001. EVA: Continuous automatic evaluation of protein structure prediction servers. Bioinformatics 17 1242–1243. [DOI] [PubMed] [Google Scholar]
- Frishman, D. and Argos, P. 1995. Knowledge-based protein secondary structure assignment. Proteins 23 566–579. [DOI] [PubMed] [Google Scholar]
- Garnier, J., Osguthorpe, D.J., and Robson, B. 1978. Analysis of the accuracy and implications of simple methods for predicting the secondary structure of globular proteins. J. Mol. Biol. 120 97–120. [DOI] [PubMed] [Google Scholar]
- Jones, D.T. 1999. Protein secondary structure prediction based on position-specific scoring matrices. J. Mol. Biol. 292 195–202. [DOI] [PubMed] [Google Scholar]
- Kabsch, W. and Sander, C. 1983. Dictionary of protein secondary structure: Pattern recognition of hydrogen-bonded and geometrical features. Biopolymers 22 2577–2637. [DOI] [PubMed] [Google Scholar]
- Krogh, A., Brown, M., Mian, I.S., Sjolander, K., and Haussler, D. 1994. Hidden Markov models in computational biology. Applications to protein modeling. J. Mol. Biol. 235 1501–1531. [DOI] [PubMed] [Google Scholar]
- Lim, V.I. 1974. Algorithms for prediction of α-helical and β-structural regions in globular proteins. J. Mol. Biol. 88 873–894. [DOI] [PubMed] [Google Scholar]
- Montelione, G.T. 2001. Structural genomics: An approach to the protein folding problem. Proc. Natl. Acad. Sci. 98 13488–13489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moseley, H.N., Monleon, D., and Montelione, G.T. 2001. Automatic determination of protein backbone resonance assignments from triple resonance nuclear magnetic resonance data. Methods Enzymol. 339 91–108. [DOI] [PubMed] [Google Scholar]
- Orengo, C.A., Michie, A.D., Jones, S., Jones, D.T., Swindells, M.B., and Thornton, J.M. 1997. CATH—a hierarchic classification of protein domain structures. Structure 5 1093–1108. [DOI] [PubMed] [Google Scholar]
- Ortiz, A.R., Kolinski, A., Rotkiewicz, P., Ilkowski, B., and Skolnick, J. 1999. Ab initio folding of proteins using restraints derived from evolutionary information. Proteins 37 177–185. [DOI] [PubMed] [Google Scholar]
- Richards, F.M. and Kundrot, C.E. 1988. Identification of structural motifs from protein coordinate data: Secondary structure and first-level supersecondary structure. Proteins 3 71–84. [DOI] [PubMed] [Google Scholar]
- Rohl, C.A. and Baker, D. 2002. De novo determination of protein backbone structure from residual dipolar couplings using rosetta. J. Am. Chem. Soc. 124 2723–2729. [DOI] [PubMed] [Google Scholar]
- Rost, B. 1996. PHD: Predicting one-dimensional protein structure by profile-based neural networks. Methods Enzymol. 266 525–539. [DOI] [PubMed] [Google Scholar]
- Rost, B. and Eyrich, V.A. 2001. EVA: Large-scale analysis of secondary structure prediction. Proteins (Suppl) 5 192–199. [DOI] [PubMed] [Google Scholar]
- Samudrala, R. and Levitt, M. 2002. A comprehensive analysis of 40 blind protein structure predictions. BMC Struct. Biol. 2 3–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Samudrala, R., Xia, Y., Huang, E., and Levitt, M. 1999. Ab initio protein structure prediction using a combined hierarchical approach. Proteins (Suppl) 3 194–198. [DOI] [PubMed] [Google Scholar]
- Seavey, B.R., Farr, E.A., Westler, W.M., and Markley, J.L. 1991. A relational database for sequence-specific protein NMR data. J. Biomol. NMR 1 217–236. [DOI] [PubMed] [Google Scholar]
- Spera, S. and Bax, A. 1991. Empirical correlation between protein backbone conformation and Cα and Cβ NMR chemical shifts. J. Am. Chem. Soc. 113 5490–5492. [Google Scholar]
- Wishart, D. and Sykes, B. 1994. The 13C chemical-shift index: A simple method for the identification of protein secondary structure using 13C chemical-shift data. J. Biolmol. NMR 4 171–180. [DOI] [PubMed] [Google Scholar]
- Wishart, D.S., Sykes, B.D., and Richards, F.M. 1991. Relationship between nuclear magnetic resonance chemical shift and protein secondary structure. J. Mol. Biol. 222 311–333. [DOI] [PubMed] [Google Scholar]
- ———. 1992. The chemical shift index: A fast and simple method for the assignment of protein secondary structure through NMR spectroscopy. Biochemistry 31 1647–1651. [DOI] [PubMed] [Google Scholar]


