Abstract
The rabbit Na+-glucose (SGLT1) and the human Na+-Cl−-GABA (GAT1) cotransporters were expressed in Xenopus laevis oocytes, and passive Na+ and water transport were studied using electrical and optical techniques. Passive water permeabilities (Lp) of the cotransporters were determined from the changes in oocyte volume in response to osmotic gradients. The specific SGLT1 and GAT1 Lp values were obtained by measuring Lp in the presence and absence of blockers (phlorizin and SKF89976A). In the presence of the blockers, the Lp values of oocytes expressing SGLT1 and GAT1 were indistinguishable from the Lp of control oocytes. Passive Na+ transport (Na+ leak) was obtained from the blocker-sensitive Na+ currents in the absence of substrates (glucose and GABA).
Passive Na+ and water transport through SGLT1 were blocked by phlorizin with the same sensitivity (inhibitory constant (Ki), 3-5 μM). When Na+ was replaced with Li+, phlorizin also inhibited Li+ and water transport, but with a lower affinity (Ki, 100 μM). When Na+ was replaced by choline, which is not transported, the SGLT1 Lp was indistinguishable from that in Na+ or Li+, but in this case water transport was less sensitive to phlorizin.
The activation energies (Ea) for passive Na+ and water transport through SGLT1 were 21 and 5 kcal mol−1, respectively. The high Ea for Na+ transport is comparable to that of Na+-glucose cotransport and indicates that the process is dependent on conformational changes of the protein, while the low Ea for water transport is similar to that of water channels (aquaporins).
GAT1 also behaved as an SKF89976A-sensitive water channel. We did not observe passive Na+ transport through GAT1.
We conclude that passive water and Na+ transport through cotransporters depend on different mechanisms: Na+ transport occurs by a saturable uniport mechanism, and water permeation is through a low conductance water channel. In the case of SGLT1, we suggest that both the water channel and water cotransport could contribute to isotonic fluid transport across the intestinal brush border membrane.
Cotransporters are membrane proteins which couple the downhill transport of cations (Na+ or H+) to the uphill transport of substrates (sugars, amino acids, neurotransmitters, vitamins and ions) into cells. In addition to the secondary active transport of solutes, many cotransporters exhibit a cationic leak current (uniporter mode), which is the passive transport of Na+ (or H+) in the absence of substrates (see Wright et al. 1996). We have previously suggested that cotransporters can function as passive (osmotic) and secondary active water transporters. For example, the Na+- glucose cotransporter SGLT1 exhibits an osmotic water permeability that is blocked by the inhibitor phlorizin (Zampighi et al. 1995; Loo et al. 1996; Loike et al. 1996; Meinild et al. 1998a). Under sugar-transporting conditions, SGLT1 transports 200-260 H2O molecules along with two sodium ions and one glucose molecule for every transport cycle. This solute-coupled water transport occurs in the absence of, and even against, an osmotic gradient (Loo et al. 1996; Zeuthen et al. 1997; Meinild et al. 1998a; Wright et al. 1998). Similar observations on the K+-Cl−, H+- lactate, Na+-Cl−-GABA, Na+-iodide and H+-amino acid transporters indicate that water transport may be a general phenomenon in this class of membrane transport proteins with coupling coefficients varying from 50 to 500 water molecules per substrate molecule (Zeuthen, 1991, 1994; Loo et al. 1996; Zeuthen et al. 1996; Meinild et al. 1998a).
The purpose of this study was to investigate the relationship between passive water and ion transport by cotransporters. We used the Na+-glucose (SGLT1) and the Na+-Cl−-GABA (GAT1) transporters as model systems. The two transporters belong to different families of Na+-dependent transport proteins. Our goal was to compare the passive water transport and the Na+ leak to determine whether these fluxes occur in parallel, or whether they occur by different ‘mechanisms’. We (i) examined the dependence of the leak current and passive water permeability on cations; (ii) compared the activation energies of the Na+ leak and the passive water pathway; and (iii) determined protein conformational states which allow passive Na+ and water leaks.
METHODS
Xenopus laevis oocytes were isolated, injected with 50 ng of rabbit SGLT1 (Hediger et al. 1987) or human GAT1 (Nelson et al. 1990) cRNA, and maintained in Barth's medium at 18°C for 5-14 days (Parent et al. 1992a; Loo et al. 1996). The frogs were chilled by immersion in 0°C ice water for 30 min and killed by an overdose of Nembutal (60 mg for 60 min) in accordance with the protocol approved by the UCLA Chancellor's Animal Protection Committee. Substrate (glucose, GABA) transport was monitored using the two-electrode voltage clamp (Loo et al. 1993).
The osmotic water permeability of oocytes was estimated from the rate of change of cell volume when an osmotic gradient (-20 mosmol l−1) was imposed by removal of mannitol from the superfusing solution. The oocyte cross-sectional area was measured every 0.5 s from bright-field images, and the images were digitized as previously described (Loo et al. 1996; Zeuthen et al. 1997; Meinild et al. 1998a). The relative volume of the oocytes (V/Vo) is related to the cross-sectional area A by: V/Vo = (A/Ao)3/2, where V is the volume, Vo is the initial volume and Ao is the initial cross-sectional area. Osmotic water permeability (Lp) is proportional to the rate of change of cell volume: Vo(d/dt V/Vo) =Lp×S × Vw×Δπ, where S is the oocyte surface area (0.4 cm2, Loo et al. 1996), Vw is the partial molar volume of water (18 cm3 mol−1) and Δπ is the osmotic gradient. Oocytes were impaled with microelectrodes during the course of all experiments. Impalement of the oocytes with microelectrodes had no effect on Lp (Loo et al. 1996; Meinild et al. 1998a,b). The experimental chamber had a functional volume of 15 μl, and all experiments were performed under continuous superfusion (at a rate of 17 μl s−1) of the bath solution, which was usually a NaCl buffer (mM: 90 NaCl, 20 mannitol, 2 KCl, 1 MgCl2, 1 CaCl2 and 10 Hepes (pH 7.4); osmolarity was 212 mosmol l−1). The osmolarity of all solutions was measured with a vapour pressure osmometer (Wescor, Logan, UT, USA). All experiments were repeated on at least three oocytes from different donor frogs. With the exception of experiments to determine the activation energies for the Na+ leak and osmotic water transport, all experiments were performed at 20-21°C.
RESULTS
The Na+ leak current of SGLT1 is illustrated in Fig. 1A. Shown are continuous current records for an oocyte expressing SGLT1 and a control non-injected oocyte. The holding potential was -50 mV. In the SGLT1 oocyte (Fig. 1A, left panel), external phlorizin (100 μM) blocked a component of the inward holding current in the presence of Na+. After phlorizin blockade, the holding current was the same as that of control oocytes. The Na+ leak, which was the current blocked by a saturating concentration of phlorizin, was 8 % (29 nA) of the maximum sugar-coupled Na+ current (Imax; 356 nA) measured in the presence of a saturating concentration of sugar (5 mM α-methyl-D-glucopyranoside, α-MDG). Phlorizin had no effect on the holding current when external Na+ was replaced by choline. The Na+ leak was not observed in control oocytes (Fig. 1A, right panel). The Na+ leak saturated with increasing external Na+ concentration and negative membrane voltages. At maximal transport rate (Vm, -150 mV), the apparent affinity constant (K0.5) for Na+ was 2.5 mM and the Hill coefficient was 2. For example, in one experiment, K0.5 for Na+ was 3.8 ± 0.4 mM and the Hill coefficient was 2.3 ± 0.5. The inhibitory constant (Ki) for phlorizin inhibition of the Na+ leak current was 3-5 μM (data not shown). In addition to Na+, Li+ and H+ also carried the leak current, and the Ki for phlorizin inhibition of the Li+ leak current was 100 μM (data not shown).
Figure 1. SGLT1 Na+ leak and passive water transport.
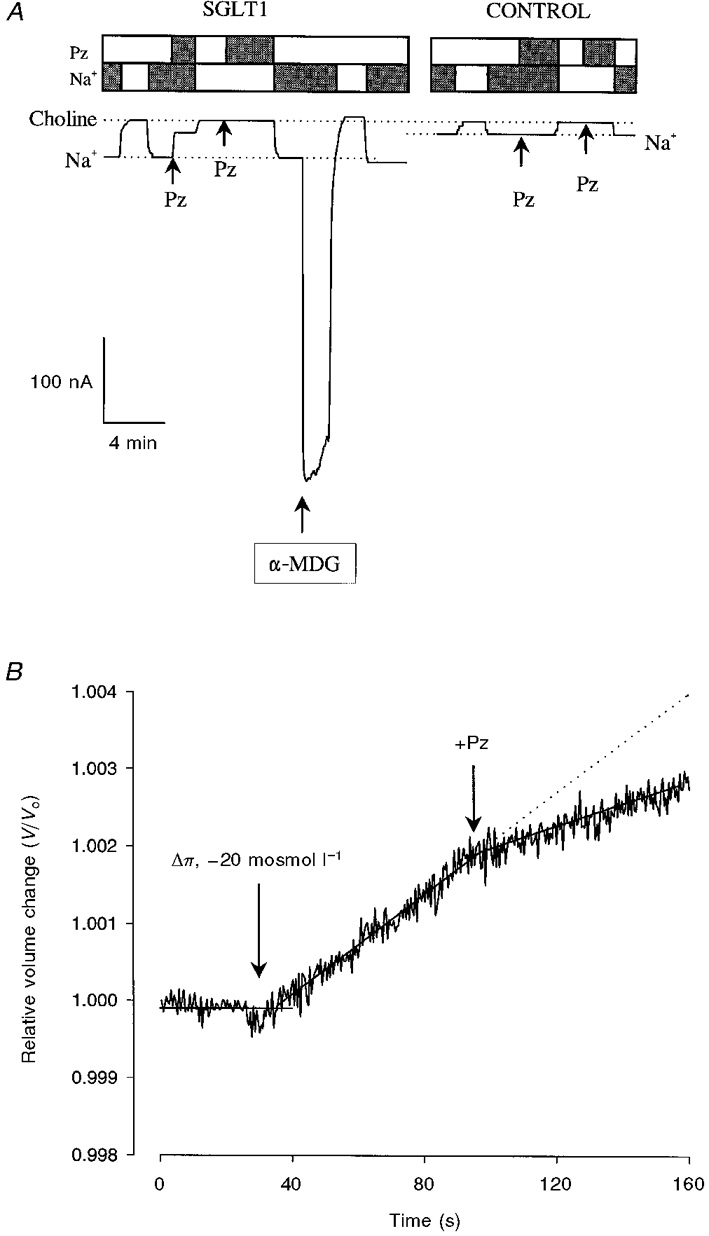
A, SGLT1 Na+ leak. Continuous current record from oocytes with membrane potential held at -50 mV. The dotted lines are the holding currents in the presence of Na+ and when Na+ was replaced by choline. The boxes above the current traces show the presence (filled bars) or absence (open bars) of 100 mM Na+, and 100 μM phlorizin (Pz). In the SGLT1-expressing oocyte, phlorizin (100 μM) blocked a component of the holding current in Na+ buffer. The magnitude of the phlorizin-blocked current (29 nA) was 8 % of the current (356 nA) generated by a saturating concentration of sugar (5 mM α-MDG). Phlorizin had no effect when Na+ was replaced with choline. The phlorizin-sensitive Na+ leak was not observed in control (non-injected) oocytes. In addition to Na+, Li+ supported the leak current. The Ki for phlorizin inhibition of the leak current was 5 μM in Na+ and 100 μM in Li+ (not shown). B, passive water transport by SGLT1. An osmotic gradient of -20 mosmol l−1 was imposed by removal of mannitol from the superperfusing buffer (see Methods). Phlorizin (100 μM) reduced the rate of swelling by 50 % (from 3.3 × 10−3 to 1.5 × 10−3% s−1), to that of control oocytes. The lines were drawn by linear regression.
The passive (osmotic) water permeability of SGLT1 is illustrated in Fig. 1B. Upon application of the osmotic gradient (-20 mosmol l−1), the oocyte volume increased linearly with time. The rate of swelling was reduced to that of control oocytes by the addition of 100 μM phlorizin to the external solution (this study; Loo et al. 1996).
The phlorizin-inhibited passive water permeability was related to the level of expression of SGLT1. Figure 2 shows the direct correlation between passive volume flow (Jv) and the density of SGLT1 in the membrane. Jv was the total water flux under an osmotic gradient of -20 mosmol l−1, and the number of transporters was obtained by dividing the maximal rate of sugar transport, Imax, in the presence of Na+ (the current induced by 5 mM α-MDG) by the turnover rate of rabbit SGLT1 (25 s−1, Panayotova-Heiermann et al. 1994, 1995). The data were pooled from experiments performed in bath solution containing Na+, Li+ and choline. Volume flows measured in saturating concentrations of phlorizin (100 μM) with Na+ were similar to those of control oocytes (this study; Loo et al. 1996). The collinearity of the data indicate that the passive water permeability of SGLT1 is independent of the external cation. The slope of the regression line was 1.4 (± 0.4) × 10−14 cm s−1 per transporter.
Figure 2. Dependence of the SGLT1 passive water transport on cations.
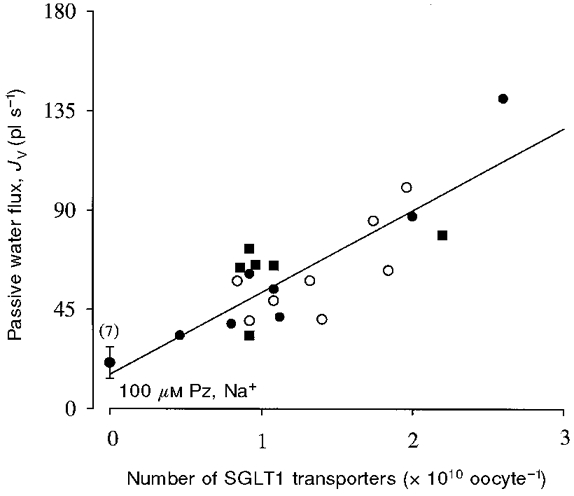
For each oocyte, the protocol was first to determine the level of expression of SGLT1 by measuring the maximal rate of sugar transport (Imax) with the addition of a saturating concentration (5 mM) of α-MDG in NaCl buffer at a Vm of -50 mV. Passive volume flow (Jv) was measured in the absence of sugar, under an osmotic gradient of -20 mosmol l−1 (see Fig. 1B). For each oocyte Jv was determined in Na+ (•) and in at least one of Li+ (○) or choline (▪). For each cation, the Lp was measured in the absence of phlorizin, and with 5, 10 and 100 μM phlorizin in the bath solution. The data plotted were from experiments performed in Na+, Li+ and choline in the absence of phlorizin. The abscissa is the number of transporters in the oocyte plasma membrane and was obtained for each oocyte by dividing Imax in the presence of Na+ by the turnover number of rabbit SGLT1 (25 s−1, Panayotova-Heiermann et al. 1994). The Li+- and choline-containing buffers were prepared by equiosmolar replacement of the 90 mM NaCl in the bath solution by LiCl and choline chloride. The slopes of the regression lines in Na+, Li+ and choline were 38 ± 4, 30 ± 4 and 34 ± 6 pl s−1 (1010 transporters)−1, respectively. Using Student's t test for the comparison of slopes, we found no statistically significant difference between the slopes of the plots obtained in Na+, Li+ and choline (P >> 0.05 for all comparisons). The slope of the regression line through all the data indicates that the Lp is 1.4 × 10−14 cm s−1 per transporter. The data obtained in 100 μM phlorizin in Na+ were identical to the Lp of control oocytes.
The blockade of the SGLT1 Lp by phlorizin (100 μM) in the presence of Na+, Li+ and choline is shown in Fig. 3. The Lp of the oocyte (the background Lp) has been subtracted. Phlorizin (100 μM) blocked 100 % of the SGLT1 Lp in Na+ buffer, but only 41 and 21 %, respectively, in Li+ and choline. The Ki for phlorizin blockade of the Lp was similar to the Ki for the leak currents: 3-5 μM in Na+ and ∼100 μM in Li+ (data not shown). The weak inhibition of the SGLT1 Lp by phlorizin in choline is consistent with the lack of effect of 100 μM phlorizin on current in choline (Fig. 1A).
Figure 3. Blockade of the SGLT1 Lp by phlorizin.
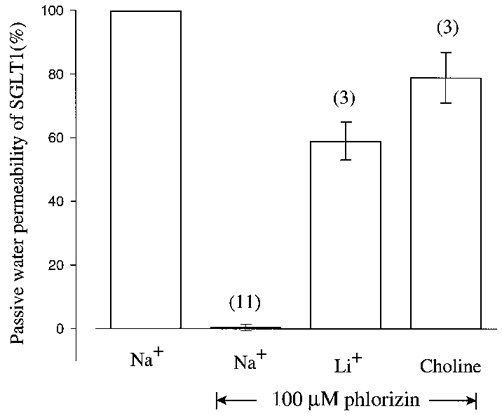
For each oocyte, the passive water permeability and its sensitivity to phlorizin were determined in Na+ and in at least one of Li+ or choline. Inhibition by phlorizin was measured using 5, 10 and 100 μM phlorizin, and shown are the results of the experiments in 100 μM phlorizin. The numbers in parentheses indicate the sample size and error bars are standard errors of the mean. Data were corrected for the water flow of control non-injected oocytes (see Fig. 1B). In Na+, 100 μM phlorizin blocked all the SGLT1 passive water transport (Ki, ≈5 μM), whereas it blocked 41 ± 6 % (n = 3) in Li+ and 21 ± 8 % (n = 3) in choline.
The Na+ leak and passive water permeability were also sensitive to phloretin. The apparent affinities were similar: 100 μM external phloretin blocked the SGLT1 Na+ leak current by 47 ± 6 % (n = 5) and the SGLT1 Lp by 36 ± 6 % (n = 6). In control oocytes, 100 μM phloretin increased the holding current slightly, by 9 ± 4 nA (n = 3) at -50 mV, but had no effect on the Lp. In three control oocytes, the Lp was 2.2 (± 0.4) × 10−4 cm s−1 in the absence, and 2.4 (± 0.2) × 10−4 cm s−1 in the presence, of 100 μM phloretin.
The activation energies (Ea) of the passive water permeability and the Na+ leak were compared. The Ea values were obtained by measuring the phlorizin-sensitive Na+ leak current, INa, and passive water permeability, Lp, as the bath temperature was varied between 10 and 30°C. Ea values were determined from the slope of the Arrhenius plot of INa and Lp (Fig. 4). Ea for the SGLT1 Lp was 5 ± 1 kcal mol−1 (n = 4); for the SGLT1 Na+ leak it was 19 ± 1 kcal mol−1 (n = 3).
Figure 4. Arrhenius plots of Na+ leak and passive water transport through SGLT1.
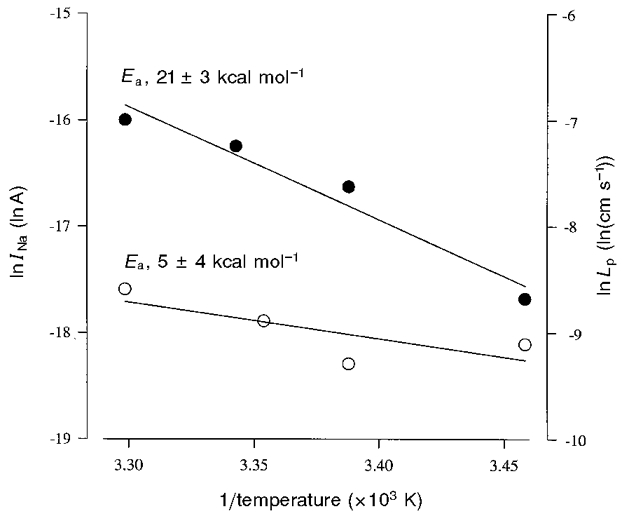
Na+ leak (INa; •) and passive water permeability (Lp; ○) were measured in a single oocyte expressing SGLT1 by determining the Na+ leak current and passive water transport in the presence and absence of phlorizin (100 μM) as bath temperature was varied from 10 to 30 °C. Membrane potential was held at -50 mV for the Na+ leak experiments. The lines were drawn by linear regression and correspond to an activation energy, Ea (Ea = -R× slope, where R is the gas constant) of 5 ± 4 kcal mol−1 for passive water transport, and 21 ± 3 kcal mol−1 for Na+ leak. From 4 experiments, Ea for the SGLT1 Lp was 5 ± 1 kcal mol−1; from 3 experiments, Ea for the SGLT1 Na+ leak was 19 ± 1 kcal mol−1.
We performed experiments on the human Na+-Cl−-GABA cotransporter GAT1 to examine the differences between the water and Na+ leak pathways. SKF89976A is a specific inhibitor of GABA transport by GAT1 (see Mager et al. 1993). Figure 5A shows that there was a water permeability associated with GAT1 which was blocked by SKF89976A (25 μM). After blockade by SKF89976A, Lp was the same as in control oocytes (Fig. 5B). GAT1 did not exhibit a Na+ leak: in four oocytes expressing GAT1 (the GABA-induced current at -50 mV was 325 ± 86 nA), 200 μM SKF89976A had no effect on the holding current. The background current carried by Na+, measured as the difference in current when external Na+ was replaced by choline when membrane potential was held at -50 mV, was slightly higher in oocytes expressing GAT1 (20 ± 4 nA, n = 4) than controls (12 ± 1 nA, n = 3). Phloretin (100 μM, n = 3) had no effect on the passive water permeability of oocytes expressing GAT1 (data not shown).
Figure 5. Passive water transport by GAT1.
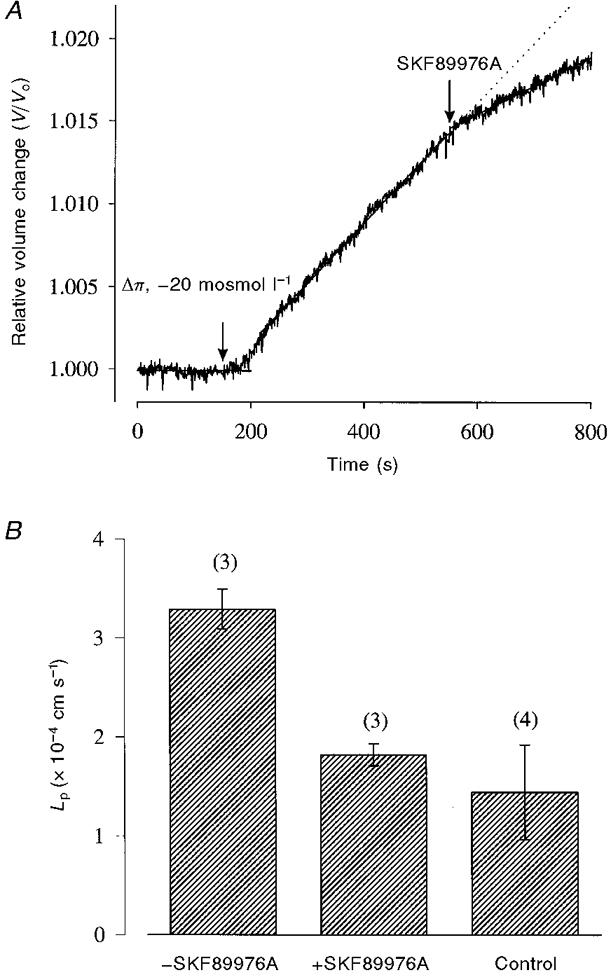
A, relative volume change of an oocyte expressing GAT1 subjected to an osmotic gradient of -20 mosmol l−1. Bath solution was the 90 mM NaCl buffer (same protocol as in Fig. 1B). B, this water permeability was blocked by the inhibitor SKF89976A (25 μM). After blockade by the inhibitor, Lp was reduced to that of control, non-injected oocytes.
DISCUSSION
The main conclusion of this study is that the Na+ leak and passive water transport through cotransporters exhibit very different characteristics. (1) Saturability. The Na+ leak saturates with increasing external Na+ concentration with an apparent affinity constant, K0.5, for Na+ of 2.5 mM and a Hill coefficient of 2 at -150 mV (present study; Panayotova-Heiermann et al. 1998). In contrast, passive volume flow is linear with the imposed osmotic gradient (Loo et al. 1996; Meinild et al. 1998a). (2) Activation energy. The Na+ leak has a high activation energy, Ea, of 19 kcal mol−1, while Ea was 5 kcal mol−1 for passive volume flow. (3) Ionic specificity. The ion leak pathway is supported by Na+, H+ and Li+ but not choline (this study; Umbach et al. 1990; Panayotova-Heiermann et al. 1998). In contrast, the SGLT1 Lp is identical in the presence of Na+, Li+ and choline (Fig. 2). (4) Functionality. Data from flux studies of radiolabelled glucose and Na+ under voltage clamp indicate that the Na+ leak is not present under saturating glucose conditions (Mackenzie et al. 1998). In contrast, SGLT1 passive water transport is present under saturating conditions (Loo et al. 1996; Meinild et al. 1998a). The observation that GAT1 exhibits a passive water permeability, but not a Na+ leak (Fig. 5) is also consistent with different mechanisms for Na+ leak and passive water transport. Passive water transport has also been reported for the cystic fibrosis transmembrane conductance regulator (CFTR) and, similar to SGLT1, the passive water pathway appears to be separate from the ion permeation pathway (Schreiber et al. 1997).
We have previously proposed a 6-state ordered kinetic model for Na+-glucose cotransport (Parent et al. 1992b; Loo et al. 1998). The model describes Na+-coupled sugar transport as a series of ligand-induced conformational changes (Fig. 6). On the external membrane surface, two sodium ions bind to the empty transporter (conformation 1, C1), forming the complex C2 before the binding of the sugar molecule. Sugar is transported via a conformational change (C3 ⇌ C4) of the fully loaded transporter (C3) between the external and internal faces of the membrane. After the dissociation of sugar and Na+ from the transporter at the internal surface, the empty transporter (C6) is returned to the external surface via another conformational change (C6 ⇌ C1). In the presence of Na+ and sugar, phlorizin locks the transporter protein in one conformation (the phlorizin-bound form of C3). The model also incorporates an uncoupled Na+ flux through SGLT1 (uniporter or Na+ leak mode, C2 ⇌ C5) in the absence of sugar. The data obtained in the present study provide further independent evidence for this kinetic model, namely that: (1) the Na+ leak (C2 ⇌ C5) saturates with external Na+ concentration (see also Panayotova-Heiermann et al. 1998); (2) the Na+ leak (C2 ⇌ C5) and Na+-glucose cotransport (C3 ⇌ C4) share high activation energies, 19 kcal mol−1 for Na+ leak and 26 kcal mol−1 for Na+-glucose cotransport (Loo et al. 1996); (3) the apparent affinity constant, K0.5, for Na+ (2.5 mM) and the Na+ Hill coefficient (nH = 2) are the same for Na+ leak as for Na+-glucose cotransport; and (4) the Na+ leak and Na+-glucose cotransport are both blocked by phlorizin with the same sensitivity (Ki, ∼5 μM). The model also provides a framework for accounting for the effects of phlorizin on the leak current and passive water transport in the presence of Na+ and Li+, i.e. the similar Ki values for phlorizin blockade of the leak currents and Lp in Na+ and Li+ (Fig. 3).
Figure 6. A 6-state ordered kinetic model for Na+-sugar, Na+ leak and passive water transport.
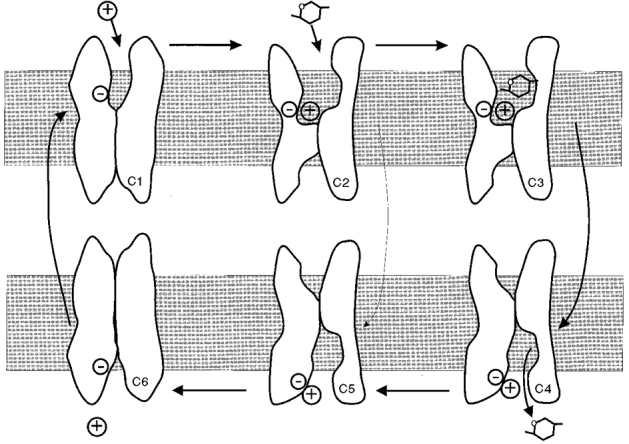
Model modified from Parent et al. (1992b) and (Loo et al. 1993, 1998). The model assumes that: (i) the transporter has a valency of -2 (for simplicity depicted by -); (ii) in the external membrane surface (with states C1, 2, 3), two sodium ions (depicted by +) bind to the transporter before the sugar molecule; (iii) sugar is transported simultaneously with Na+ via the conformational change C3 ⇌ C4; (iv) in the internal membrane surface (with states C4, 5, 6) the sugar molecule dissociates from the transporter before the sodium ions; and (v) membrane voltage affects the conformational change of the empty transporter C1 ⇌ C6, and Na+ binding to the transporter C1 ⇌ C2. The protein behaves as a Na+-sugar cotransporter (cycle C1, 2, 3, 4, 5, 6) in the presence of sugar. In the absence of sugar, the protein behaves as a Na+ uniporter (Na+ leak, cycle C1, 2, 5, 6). In the absence of Na+ (for example, in choline) the protein can behave as a passive water transporter (cycle C1, 6). Computer simulations were performed using the set of rate constants for rabbit SGLT1 from Panayotova-Heiermann et al. (1994) to estimate the probability of the transporter being in the different conformations. At -50 mV: (1) in the presence of choline, 60 % of the cotransporters were in C1 and 40 % in C6; (2) in the presence of Na+ but absence of sugar, 80 % were in C2, 10 % in C1 and 10 % in C3; and (3) in the presence of Na+ and sugar, 80 % were in C5 and 20 % in C6.
The Lp is the same in the active (sugar-transporting) and passive (Na+ uniporter) modes (Loo et al. 1996; Meinild et al. 1998a), as well as when Na+ is replaced by choline (present study). Computer simulations of the kinetic model (see legend to Fig. 6) showed that at -50 mV: (1) in the presence of choline, 60 % of the cotransporters were in C1 and 40 % were in C6; (2) in Na+ but in the absence of sugar, 80 % were in C2, 10 % were in C1 and 10 % were in C3; and (3) in the presence of Na+ and sugar, 80 % were in C5 and 20 % were in C6 (see also Parent et al. 1992b). Thus C1, C2, C5 and C6 may each contribute to passive water permeability. Phlorizin, which has been shown to block the conformational changes of SGLT1, locks the protein in the phlorizin-bound form of C3, and in this conformation the transporter is able neither to undergo conformational changes (Loo et al. 1993, 1998), nor to transport water passively. Thus passive water transport by SGLT1 depends on the conformational state of the protein.
The inhibitors of Lp in SGLT1 and GAT1 block the conformational changes in both transporters (Mager et al. 1993; Loo et al. 1998). The common action of these compounds in locking the proteins in a conformation that does not allow water transport suggests that SGLT1 and GAT1 share a common mechanism for passive water transport.
The low activation energy (5 kcal mol−1) of passive volume flow is comparable to that of aquaporins (3-4 kcal mol−1, Preston et al. 1992; 6-7 kcal mol−1, Meinild et al. 1998b), suggesting that passive water flow through SGLT1 is similar to water flow through an aqueous pore. It is noteworthy that the unitary Lp for SGLT1 is about 100 times lower than that of aquaporin1 (Zampighi et al. 1995; Loo et al. 1996). Aquaporin1 is strictly selective for water (Meinild et al. 1998b), implying that the pore is very narrow. The low SGLT1 Lp may be due to: (1) a longer effective pore length; (2) a lower mobility of H2O in the pore (for instance, more binding sites and hydrogen bonding); or (3) a lower open probability for the SGLT1 water channel.
A number of transport proteins appear to exhibit the ability to transport water passively. These include the facilitative glucose transporter GLUT1 (Fischbarg et al. 1990), the CFTR (Hasegawa et al. 1992; Schreiber et al. 1997), the Na+-glucose cotransporter (Zampighi et al. 1995; Loo et al. 1996; Loike et al. 1996; Zeuthen et al. 1997; Meinild et al. 1998a) and the Na+-Cl−-GABA cotransporter (this study). In preliminary experiments, we have also observed passive water transport in the Na+-dicarboxylate transporter NaDC1 (Pajor, 1995), and the plant H+-amino acid transporter AAP5 (Fischer et al. 1995). Loike et al. (1996) have found that the passive water permeability of rabbit SGLT1 depends on external Na+, contrary to our present finding of independence from the cation. The reason for this discrepancy is not clear but it may be that we measured initial rates (within 30 s) while the experiments of Loike et al. (1996) were considerably longer (up to 30 min). Meinild et al. (1998b) have recently found that osmotically induced volume changes in Xenopus oocytes exhibit significant time-dependent decreases. This would lead to large discrepancies between the Lp measured during initial rates (within 10 s) and that for longer periods.
What is the physiological relevance of passive water transport by SGLT1? The human small intestine absorbs 10 l of water a day, but the mechanism of water transport is not well understood. Fluid transport occurs in the absence of or even against bulk osmotic gradients, and is secondary to active solute transport. Water movement has been postulated to be driven by local osmotic gradients within the tissue (Diamond & Bossert, 1967). Since osmotic gradients have not been found within epithelial tissues and water channels have not yet been reported for the small intestine (overall, water permeabilities are low in the intestine), an alternative hypothesis has been proposed where water is transported across the intestine by cation-driven transporters, such as the Na+-glucose transporter in the apical and the K+-Cl− transporter in the basolateral membrane (Zeuthen, 1991; Loo et al. 1996; Zeuthen et al. 1997; Meinild et al. 1998a). Based on the stoichiometry of 200-250 water molecules transported with each glucose molecule, we estimated that approximately 4-5 l of water are transported across the brush border membrane of the intestine by SGLT1 by secondary active transport (Loo et al. 1996; Zeuthen et al. 1997; Meinild et al. 1998a). The accompaniment of 200-250 H2O molecules with two sodium ions and each glucose molecule is equivalent to a coupling ratio of 65-85 H2O molecules per solute molecule. Since isotonicity requires 275 H2O molecules per solute molecule, this results in a fluid which is hypertonic (Diamond, 1996). The finding that the passive water pathway is operational under sugar-transporting conditions (Meinild et al. 1998a) indicates that the hypertonic fluid transported across the apical membrane by SGLT1 per se would create an osmotic gradient, which could then provide a driving force for water movement through the passive water pathway of SGLT1. Thus according to our hypothesis, isotonic water transport across the brush border membrane of the intestine is the sum of secondary active water transport (coupled to Na+ and sugar transport) and a passive component through the SGLT1 water channel.
Acknowledgments
We thank Ms M. Contreras and D. Leung for assistance with the oocytes, Dr H. Sarkar for providing the GAT1 clone, S. Eskandari for critical comments on the manuscript, and W. Bondinell of SmithKline-Beecham Pharmaceuticals for kindly providing the SKF compound. This work was supported by National Institutes of Health grants DK19567, DK44602 and GM52094, National Science Foundation Grant MCB 9520599, EY-05661, the Danish Research Council and Novo Nordisk.
References
- Diamond JM. Wet transport proteins. Nature. 1996;384:611–612. doi: 10.1038/384611a0. 10.1038/384611a0. [DOI] [PubMed] [Google Scholar]
- Diamond JM, Bossert WH. Standing gradient osmotic flow. A mechanism for coupling of water and solute transport in epithelia. Journal of General Physiology. 1967;50:2061–2083. doi: 10.1085/jgp.50.8.2061. 10.1085/jgp.50.8.2061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischbarg J, Kuang K, Vera JC, Arant S, Silverstein SC, Loike JD, Rosen OM. Glucose transporters serve as water channels. Proceedings of the National Academy of Sciences of the USA. 1990;87:3244–3247. doi: 10.1073/pnas.87.8.3244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischer W-N, Kwart M, Hummel S, Frommer WB. Substrate specificity and expression profile of amino acid transporters (AAPS) in Arabidopsis. Journal of Biological Chemistry. 1995;270:16315–16320. doi: 10.1074/jbc.270.27.16315. 10.1074/jbc.270.27.16315. [DOI] [PubMed] [Google Scholar]
- Hasegawa H, Skach W, Baker O, Calayag MC, Lingappa V, Verkman AS. A multifunctional aqueous channel formed by CFTR. Science. 1992;258:1477–1479. doi: 10.1126/science.1279809. [DOI] [PubMed] [Google Scholar]
- Hediger MA, Coady MJ, Ikeda TS, Wright EM. Expression cloning and cDNA sequencing of the Na+/glucose cotransporter. Nature. 1987;330:379–381. doi: 10.1038/330379a0. 10.1038/330379a0. [DOI] [PubMed] [Google Scholar]
- Loike JD, Hickman S, Kuang K, Xu M, Cao L, Vera JC, Silverstein C, Fischbarg J. Sodium-glucose cotransporters display sodium- and phlorizin-dependent water permeability. American Journal of Physiology C. 1996;271:1774–1779. doi: 10.1152/ajpcell.1996.271.5.C1774. [DOI] [PubMed] [Google Scholar]
- Loo DDF, Hazama A, Supplisson S, Turk E, Wright EM. Relaxation kinetics of the Na+/glucose cotransporter. Proceedings of the National Academy of Sciences of the USA. 1993;90:5767–5771. doi: 10.1073/pnas.90.12.5767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loo DDF, Zeuthen T, Chandy G, Wright EM. Cotransport of water by the Na+/glucose cotransporter. Proceedings of the National Academy of Sciences of the USA. 1996;93:13367–13370. doi: 10.1073/pnas.93.23.13367. 10.1073/pnas.93.23.13367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKenzie B, Loo DDF, Wright EM. Relationship between Na+/glucose cotransporter (SGLT1) currents and fluxes. Journal of Membrane Biology. 1998;162:101–106. doi: 10.1007/s002329900347. 10.1007/s002329900347. [DOI] [PubMed] [Google Scholar]
- Mager S, Naeve J, Quick M, Labarca L, Davidson N, Lester HA. Steady states, charge movement, and rates for a cloned GABA ion-coupled transporter expressed in Xenopus oocytes. Neuron. 1993;10:177–188. doi: 10.1016/0896-6273(93)90309-f. 10.1016/0896-6273(93)90309-F. [DOI] [PubMed] [Google Scholar]
- Meinild A-K, Klaerke DA, Loo DDF, Wright EM, Zeuthen T. The human Na+-glucose cotransporter is a molecular water pump. The Journal of Physiology. 1998a;508:15–21. doi: 10.1111/j.1469-7793.1998.015br.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meinild A-K, Klaerke DA, Zeuthen T. Bidirectional water fluxes and specificity for small hydrophilic molecules in aquaporins 0-5. Journal of Biological Chemistry. 1998b;273:32446–32453. doi: 10.1074/jbc.273.49.32446. 10.1074/jbc.273.49.32446. [DOI] [PubMed] [Google Scholar]
- Nelson H, Mandiyan S, Nelson N. Cloning of the human brain GABA transporter. FEBS Letters. 1990;269:181–184. doi: 10.1016/0014-5793(90)81149-i. 10.1016/0014-5793(90)81149-I. [DOI] [PubMed] [Google Scholar]
- Pajor AM. Sequence and functional characterization of a renal sodium/dicarboxylate cotransporter. Journal of Biological Chemistry. 1995;270:5779–5785. doi: 10.1074/jbc.270.11.5779. [DOI] [PubMed] [Google Scholar]
- Panayotova-Heiermann M, Loo DDF, Lam JT, Wright EM. Neutralization of conserved charged transmembrane residues in the Na+/glucose cotransporter SGLT1. Biochemistry. 1998;37:10522–10528. doi: 10.1021/bi9800395. [DOI] [PubMed] [Google Scholar]
- Panayotova-Heiermann M, Loo DDF, Wright EM. Sodium/D-Glucose cotransporter charge movements involve polar residues. Journal of Biological Chemistry. 1994;269:21016–21020. [PubMed] [Google Scholar]
- Panayotova-Heiermann M, Loo DDF, Wright EM. Kinetics of steady-state currents and charge movements associated with the rat Na+/glucose cotransporter. Journal of Biological Chemistry. 1995;270:27099–27155. doi: 10.1074/jbc.270.45.27099. 10.1074/jbc.270.45.27099. [DOI] [PubMed] [Google Scholar]
- Parent L, Supplisson S, Loo DDF, Wright EM. Electrogenic properties of the cloned Na+/glucose cotransporter. Part I. Voltage clamp studies. Journal of Membrane Biology. 1992a;125:49–62. doi: 10.1007/BF00235797. [DOI] [PubMed] [Google Scholar]
- Parent L, Supplisson S, Loo DDF, Wright EM. Electrogenic properties of the cloned Na+/glucose cotransporter. Part II. A transport model under non-rapid equilibrium conditions. Journal of Membrane Biology. 1992b;125:63–79. doi: 10.1007/BF00235798. [DOI] [PubMed] [Google Scholar]
- Preston GM, Carroll TP, Guggino WB, Agre P. Appearance of water channels in Xenopus oocytes expressing red cell CHIP28 protein. Science. 1992;256:385–387. doi: 10.1126/science.256.5055.385. [DOI] [PubMed] [Google Scholar]
- Schreiber R, Greger R, Nitschke R, Kunzelmann K. Cystic fibrosis transmembrane conductance regulator activates water conductance in Xenopus oocytes. Pflügers Archiv. 1997;434:841–847. doi: 10.1007/s004240050473. [DOI] [PubMed] [Google Scholar]
- Umbach JA, Cody MJ, Wright EM. Intestinal Na+/glucose cotransporter expressed in Xenopus oocytes is electrogenic. Biophysical Journal. 1990;57:1217–1224. doi: 10.1016/S0006-3495(90)82640-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright EM, Loo DDF, Panayotova-Heiermann M, Hirayama BA, Turk E, Eskandari S, Lam J. Structure and function of the Na+/glucose cotransporter. Acta Physiologica Scandinavica. 1998;16:257–264. [PubMed] [Google Scholar]
- Wright EM, Loo DDF, Turk E, Hirayama BA. Sodium cotransporters. Current Opinion in Cell Biology. 1996;8:468–473. doi: 10.1016/s0955-0674(96)80022-6. [DOI] [PubMed] [Google Scholar]
- Zampighi GA, Kreman M, Boorer KJ, Loo DDF, Bezanilla F, Chandy G, Hall JE, Wright EM. A method for determining the unitary functional capacity of cloned channels and transporters expressed in Xenopus laevis oocytes. Journal of Membrane Biology. 1995;148:65–78. doi: 10.1007/BF00234157. [DOI] [PubMed] [Google Scholar]
- Zeuthen T. Secondary active transport of water across the ventricular cell membrane of choroid plexus epithelium of Necturus maculosus. The Journal of Physiology. 1991;444:153–173. doi: 10.1113/jphysiol.1991.sp018871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeuthen T. Cotransport of K+, Cl−and H2O by membrane proteins from choroid plexus epithelium of Necturus maculosus. The Journal of Physiology. 1994;478:203–219. doi: 10.1113/jphysiol.1994.sp020243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeuthen T, Hamann S, LaCour M. Cotransport of H+, lactate and H2O by membrane proteins in retinal pigment epithelium of bullfrog. The Journal of Physiology. 1996;497:3–17. doi: 10.1113/jphysiol.1996.sp021745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeuthen T, Meinild A-K, Klaerke DA, Loo DDF, Wright EM, Belhage B, Litman T. Water transport by the Na+/glucose cotransporter under isotonic conditions. Biology of the Cell. 1997;89:307–312. doi: 10.1016/s0248-4900(97)83383-7. [DOI] [PubMed] [Google Scholar]


