Abstract
Genome-wide detection of transcription start sites (TSSs) has revealed that RNA Polymerase II transcription initiates at millions of positions in mammalian genomes. Most core promoters do not have a single TSS, but an array of closely located TSSs with different rates of initiation. As a rule, genes have more than one such core promoter; however, defining the boundaries between core promoters is not trivial. These discoveries prompt a re-evaluation of our models for transcription initiation. We describe a new framework for understanding the organization of transcription initiation. We show that initiation events are clustered on the chromosomes at multiple scales—clusters within clusters—indicating multiple regulatory processes. Within the smallest of such clusters, which can be interpreted as core promoters, the local DNA sequence predicts the relative transcription start usage of each nucleotide with a remarkable 91% accuracy, implying the existence of a DNA code that determines TSS selection. Conversely, the total expression strength of such clusters is only partially determined by the local DNA sequence. Thus, the overall control of transcription can be understood as a combination of large- and small-scale effects; the selection of transcription start sites is largely governed by the local DNA sequence, whereas the transcriptional activity of a locus is regulated at a different level; it is affected by distal features or events such as enhancers and chromatin remodeling.
Since most genetic information is expressed via transcription by RNA Polymerase II, understanding the manner and mechanisms of transcription initiation by this enzyme is of fundamental importance to biology. Most of our knowledge of the transcription initiation process comes from detailed experiments on single-core promoters (for review, see Smale and Kadonaga 2003). As a consequence, the only reasonably detailed model of the process assumes that promoters have a TATA-box, which directs the positioning of the preinitiation complex—in effect initiating transcription from a single nucleotide (Hampsey 1998; Thomas and Chiang 2006). However, the fraction of promoters with clear TATA-boxes has been decreasing with the number of promoters discovered (Ohler et al. 2002; Gershenzon and Ioshikhes 2005; Molina and Grotewold 2005; Carninci et al. 2006; Cooper et al. 2006).
Indeed, the largest TSS identification study to date (Carninci et al. 2006), in which >12 million mRNA 5′ ends were sequenced, showed that the majority of strong human and mouse RNA Polymerase II core promoters have an array of close TSSs instead of the expected single TSS. That study used the Cap Analysis of Gene Expression (CAGE) technology, based on sequencing 5′ ends, “CAGE tags,” of CAP-selected full-length cDNAs. A particular strength of the CAGE method is that tags mapped to the genome show both the location and strength of transcription (the number of mapped tags at a given location) (Carninci et al. 2006; Kodzius et al. 2006). This means that most promoters can be accurately described as a distribution of initiation site events on a stretch of nucleotides. We have previously shown that broad TSS distributions are correlated with CpG islands and ubiquitously expressed genes, whereas promoters with a narrow TSS distribution frequently direct tissue-specific genes and often have a TATA box. For most promoters, the TSS distributions are highly conserved between human and mouse, suggesting a regulatory mechanism underlying the precise nucleotide selection even when a promoter has multiple TSS peaks (Carninci et al. 2006; see Supplemental Fig. S1 for examples of different TSS distributions in mouse and human promoters).
Moreover, most genes have several strong core promoters, which complements alternative splicing in generating different protein isoforms (Carninci et al. 2006; Kimura et al. 2006). Intriguingly, some, but not all genes have weak TSSs scattered over their exons (Carninci et al. 2006). As this has been observed with multiple technologies, it is unlikely to be an experimental artifact—in a recent study, internal TSSs were shown to be the start of transcripts bridging two genes separated by 300 kbp (The ENCODE Project Consortium 2007). Therefore, in many cases it is hard to judge where a given core promoter starts and ends. This issue is analogous to the difficulty of defining gene boundaries in mammalian genomes—in fact, >70% of all nucleotides are transcribed at some point (Carninci et al. 2005; The ENCODE Project Consortium 2007). These and other recent findings using high-throughput TSS-sequencing methods haven been reviewed in detail in Muller et al. (2007) and Sandelin et al. (2007). Thus, we are in a situation where we have an unprecedented depth of data describing TSS locations and their usage by the cell, but lack a quantitative model for how the cell selects these TSSs on larger scales and at the nucleotide level.
In this report, we show that initiation events are clustered hierarchically—clusters within clusters, likely reflecting different biological determinants working at different resolutions. We show that in the smallest of such clusters—which can be defined as core promoters—a local DNA code can predict the selection and usage of transcription start sites with nucleotide resolution. Conversely, both the expression strength of clusters and the shape of larger clusters are likely determined by distal effects in addition to the local code.
Results
Initiation events are organized in hierarchical clusters
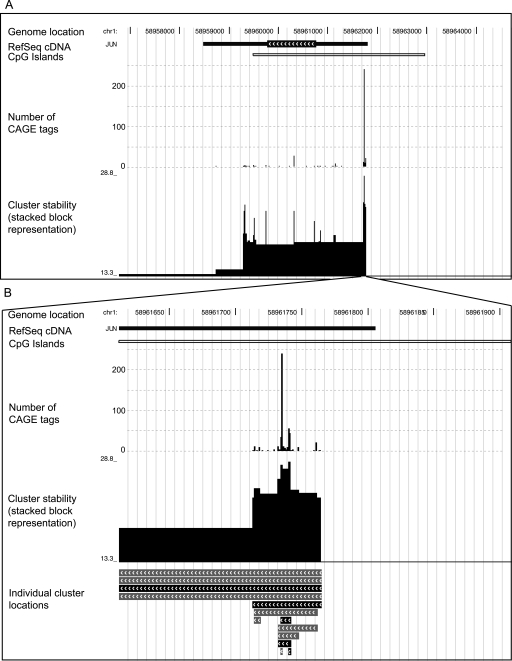
Older studies (Carninci et al. 2006; Kawaji et al. 2006; Ponjavic et al. 2006) used an arbitrary definition of TSS clusters, based on overlapping CAGE tags, in an attempt to recreate something resembling the expected single TSS per gene. A limitation with this approach is that the TSS distribution is reduced to one dimension—a nucleotide can only occur in one cluster, or none—whereas it is evident by eye that clusters within clusters exist within the genome. In Figure 1, we show an example of this: the JUN gene has a single exon that has a much greater density of CAGE tags than the surrounding genomic sequence, constituting one broad cluster. Looking more closely, we see a higher density of CAGE tags near its annotated 5′ end: a stronger cluster. Zooming in on the annotated 5′ end (Fig. 1B) shows that the strong 5′ cluster has a core region with even greater tag density. Thus, this locus has at least three layers of clusters within clusters.
Figure 1.
Multiple-scale clustering of transcription initiation events. (A) Clustering of transcription initiation events in a 9-kb region around the JUN oncogene in human chromosome 1. (B) Zoom-in on the main JUN promoter region. Each panel displays genomic features with a representation similar to that used by the UCSC Genome Browser (Kent et al. 2002). Different types of features are shown in different “tracks,” stacked from top to bottom in each panel. The topmost track shows the location in chromosome 1. Below this, the next track indicates the location of the single-exon JUN gene, according to RefSeq cDNAs in the UCSC database (Karolchik et al. 2003); the thicker part with chevrons is the protein-coding region, and the thinner parts are the 5′ and 3′ untranslated regions. Transcription is directed right-to-left. CpG island regions are shown below. The CAGE track (the first barplot) shows the number of CAGE tags initiating from each nucleotide. There is clearly a cluster of initiation events roughly covering the JUN gene, contrasted with a striking absence of initiation events on either side of the gene. Furthermore, this cluster clearly contains a much denser subcluster in the annotated promoter region, and the subcluster seems to contain a core region with an even greater density of initiation events (B). The clusters track (B, bottom) shows the clusters in the CAGE data picked out by our algorithm. Stable clusters (stability ≥2) are black and unstable clusters are gray. Only clusters >1 nt are shown in this track. For some of the clusters in this track, we only see one of their ends, as they extend further in the 3′ direction. Finally, the cluster-stability track shows these same clusters as blocks that are stacked on each other, where the height of each block reflects the cluster’s stability. (In fact, the logarithm of the d parameter from our algorithm is plotted on the Y-axis, so that the height of each block is proportional to the logarithm of the cluster’s stability. See the main text and Methods for definitions of stability and d.)
It would be useful to have an algorithm that can automatically identify clusters within clusters in genomic data such as this. This would allow us to describe the structure of the data, rather than merely observing that it is complex. We constructed such an algorithm, which can detect small, dense clusters as well as large, rarefied clusters. The algorithm uses a density parameter, d, and it reports the segments of each chromosome that maximize the value of the following formula: (number of events in the segment) − d × (size of the segment in nt). This formula favors segments with a large number of events, but disfavors large segments: the reported segments will be those with the best trade-off between these two factors. Thus, the segments reported by the algorithm can be considered clusters of the observed events. If the d parameter is large, the trade-off will tend to favor small and dense clusters, whereas if d is small, the trade-off will tend to favor large and rarefied clusters. In particular, for a given value of d, the clusters must have a density greater than d events per nucleotide (otherwise the formula would be negative). Our algorithm finds all clusters for all values of d (see Methods). We call this algorithm parametric clustering. The algorithm can be viewed as automating pattern recognition by the human eye.
Some clusters are more sensitive to the value of the d parameter than others. Each cluster has a minimum d, below which it becomes merged into a larger cluster, and a maximum d, above which it breaks up into smaller clusters. If a cluster’s minimum d is very close to its maximum d, then the cluster is not very strongly present in the data, and it could easily vanish entirely if the data were to change slightly. On the other hand, if a cluster’s minimum d is much less than its maximum d, then it is a prominent feature in the data. Accordingly, we define a cluster’s stability to be the ratio of its maximum d to its minimum d.
This clustering algorithm was applied to the human CAGE data. It was applied to pooled data from multiple cell types, and also to non-pooled data from specific cell types (Supplemental Table S1). As an example, the clustering results for pooled data at the JUN locus are shown in Figure 1. The algorithm indeed detects multiple clusters within clusters, and the most stable clusters correspond fairly well with the clusters identified by eye as described above.
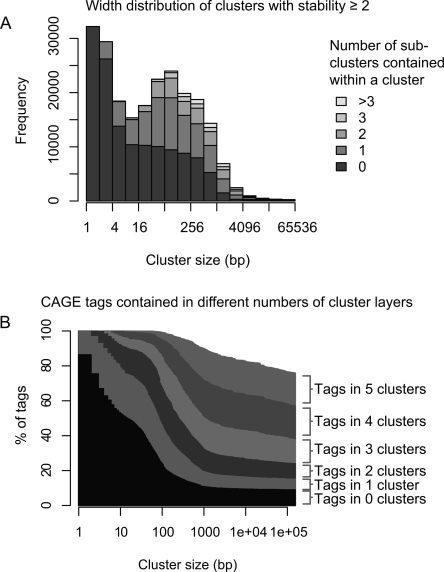
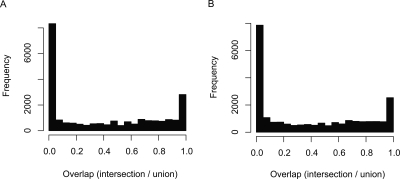
Generally, when assessing all clusters in the genome, the cluster-width distribution has two pronounced peaks at <4 and 100–150 nts (Fig. 2A), consistent with sharp and broad classes of promoters previously described (Carninci et al. 2006). The latter peak might be correlated to the length of DNA covered by the nucleosome (∼150 bp), since active human promoters are nucleosome depleted (Nishida et al. 2006). Clusters commonly contain up to three stable (i.e., prominent) subclusters, and most CAGE tags are covered by multiple levels of stable clusters (Fig. 2A,B). Presumably, these multiple layers of clustering reflect regulatory processes that have varying levels of resolution, such as histone acetylation, DNA methylation, and nucleosome spacing (Smale and Kadonaga 2003; Mito et al. 2005; Barrera and Ren 2006; Mellor 2006; Segal et al. 2006). Clusters of tags from different cell types tend to overlap one another either very closely or not at all (Fig. 3), implying that there is a set of underlying clusters that are either active or inactive in a given cell type.
Figure 2.
Properties of transcription initiation clusters. (A) Size distribution and numbers of subclusters. Clusters were binned according to their size, and the number of clusters in each size bin is plotted as a histogram. Within each size bin, the clusters are subdivided according to how many subclusters they contain (not counting sub-sub-clusters, etc). (B) Percentage of CAGE tags contained in multiple layers of clusters within clusters. The fraction of tags contained within 0, 1, or more clusters is shown for varying cluster sizes (X-axis); when only small clusters are considered, most tags are isolated, but when large clusters are considered, most tags lie in multiple layers of clusters. In both panels, only stable clusters (stability ≥2) are considered.
Figure 3.
Overlap of transcription initiation clusters from different cell lines. (A) Overlap between clusters from skin fibroblasts (HBM library) and clusters from HepG2 cells (HBY library). (B) Overlap between clusters from skin fibroblasts (HBM library) and clusters from cerebrum (HAM library). If two clusters overlap, the degree of overlap is measured as the number of nucleotides in the intersection of the clusters divided by the number of nucleotides in the union of the clusters. This value varies between one (perfect overlap) and zero (no overlap). Since we are dealing with nested hierarchies of clusters, it is not appropriate to compare every cluster from one cell line with all overlapping clusters in the other cell line. In each panel, the first mentioned library is designated as the “query,” and the second as the “reference.” For each query cluster, we wish to know whether there is a closely corresponding reference cluster. Only robust query clusters are considered, i.e., those with stability ≥2. For each query cluster, we find the reference cluster with the highest degree of overlap, and report this value. If there is no overlapping reference cluster, an overlap value of zero is reported. Cases with an intermediate degree of overlap are often caused by single, outlying CAGE tags that shift the cluster boundary in one library.
Position-specific signals define a TSS selection code
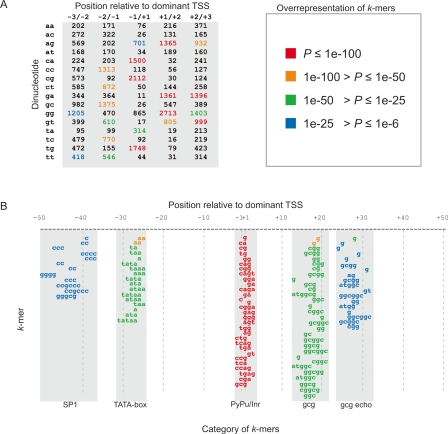
It is plausible that TSS organization at the smallest scale is determined by the local DNA sequence: a “TSS code” that directs the selection of TSSs by the RNA polymerase II initiation complex. We first investigated whether certain DNA patterns occur more often at a fixed distance from a strong TSS. We expect that many such patterns would correspond to known core-promoter elements, in particular the TATA-box (starting at ∼−34/−28) and Inr (covering −2/+5) (Smale and Kadonaga 2003). To find TSS positioning motifs, we counted all DNA “words” (oligonucleotides) of length k nucleotides (k-mers) at a given distance from locally dominant TSS in HepG2 cells, where k is 1–6. As an example, dinucleotide counts in the −3/+3 region are shown in Figure 4A. For a given k-mer and position, we assessed whether the number of occurrences at this position is over- or under-represented, compared with the frequency of the word regardless of position (see Methods). An over-representation implies that this word at the given position is important in some way for initiation of transcription: it might be bound by a transcription factor, or have some other unknown function.
Figure 4.
A code for transcription initiation. (A) Dinucleotide frequencies at fixed distances from dominant transcription start sites in HepG2 cells. Dinucleotide counts in the −3/+3 region around 7734 transcription start sites are shown as a table. These frequencies are highly non-random; each dinuceotide has a P-value describing its over-representation, where low P-values correspond to high over-representation. Dinucleotides are shaded by colors according to the P-value range they belong to, where red and blue represent the most and least significant categories, respectively (see legend at right of table). In general, oligonucleotide frequencies in the −50/+50 region constitute a code for TSS selection. The most frequent motifs in this region are shown in B. (B) Over-represented k-mers at fixed distances from dominant transcription start sites in HepG2 cells. This is a graphical representation of the same type of data as in A, but extended to all over-represented DNA words (or k-mers) in the −50 to +50 region around dominant transcription start sites. Statistically over-represented k-mers are displayed at the positions where they occur relative to the dominant TSS, whose first transcribed nucleotide is at +1. As in A, k-mers are colored according to their over-representation P-value. From left to right, the word columns can be described as SP1-like (at –50/−37), TATA-box (−32/−25), Inr/Pyrimidine-Purine (−2/+3), gcg-motif (+12/+21), and gcg echo (+25/+32). Each column (motif) is sorted by P-values independently of the other columns; for instance, the words in the Inr column are all more significantly over-represented than those in the gcg column. See Supplemental Figure S2 with legend for a more detailed description of each motif with corresponding statistics, sorted by overall P-value, and Supplemental Figures S3–S7 for corresponding figures using other cell lines from human and mouse.
Indeed, the most over-represented k-mers correspond to known functional promoter elements. The most strongly over-represented k-mers occur right at the TSS (Fig. 4B). They confirm preference for a Py-Pu dinucleotide at the −1/+1 position reported in Carninci et al. (2006), and are mostly consistent with the broader YYANWYY Inr motif (Smale and Kadonaga 2003), although the +1/+2 dinucleotide appears better represented by RR than AN. The second-strongest motif is the TATA box, in the −31/−23 region (Fig. 4B). The position of this motif is entirely consistent with previous studies using a multitude of experimental and statistical techniques (Kovacs and Butterworth 1986; Molina and Grotewold 2005; Ponjavic et al. 2006; Sandelin et al. 2007). Despite being significantly over-represented, the TATA k-mers only occur in a small fraction of the sequences (see Supplemental Figs. S2–S7). The low fraction of TATA-box promoters is consistent with recent studies identifying TSSs genome-wide (Ohler et al. 2002; Gershenzon and Ioshikhes 2005; Molina and Grotewold 2005; Carninci et al. 2006; Cooper et al. 2006). Third is a novel and very clear CG-rich motif in the downstream region (Fig. 4B). It is more specific than merely CG-rich: the k-mers are all variants of a GCG trinucleotide repeat. The weakest of the clearly visible motifs is an SP1-like element in the −50/−30 region, and an “echo” of the GCG repeat 10 nt downstream of the main GCG repeat. Since 10 nt is one turn of the double helix, the GCG repeat and its echo have the same phasing relative to the TSS. The over-representation of SP1 sites in this region was reported previously using mouse data (Carninci et al. 2006). The same motifs are consistently found using CAGE data from other human and mouse cell types, although the gcg echo is not always apparent (Supplemental Figs. S2–S7; Supplemental Table S1).
Importantly, correlation does not prove causation: it is possible that each of these motifs contributes to TSS selection (see also Discussion), or alternatively, have other functions. For instance, SP1 might regulate the level rather than the positioning of transcription, but binding to the −50/−30 region may be favorable for its interaction with the transcription machinery. In addition, the bound protein cannot always be identified with certainty based solely on the DNA patterns; for example, SP1 sites can be bound by both SP1 and SP3 proteins.
The Inr, SP1, gcg , and gcg echo motifs tend to co-occur with each other more often than expected by chance (Supplemental Table S2), but the TATA box is neither positively nor negatively correlated with the other motifs. This is consistent with there being two major promoter architectures, TATA box versus CG-rich, which are sometimes superimposed (Carninci et al. 2006).
Notably, we do not find any clear evidence of over-representation of the DPE, MTE, or BRE motifs discovered in Drosophila melanogaster, which all are reported to have positional preferences relative to the TSS (for review, see Smale and Kadonaga 2003). This does not necessarily mean that these elements are not ever used in human promoters, but they likely have a less prominent role than in D. melanogaster.
These findings confirm that certain known patterns at specific distances can be predictive of TSS locations, but also indicate that there might be uncharacterized patterns with similar functions present. Together, these patterns suggest the existence of a generic DNA code for mammalian TSS selection.
Local DNA sequence accurately predicts selection of initiation sites
A good test of whether the local DNA code organizes transcription initiation at small scales is to see whether TSS usage within small clusters can be predicted from the sequence. First, we tabulated all k-mer counts with a given distance from dominant TSSs, counted as above in the −50/+50 region. An example is shown in Figure 4A: the code is simply a table of characteristic oligonucleotide frequencies. From this, for a given word-length k, we built a statistical model that will score any 100-nt-long sequence based on the words observed at given positions in this sequence; it essentially evaluates the likelihood of this sequence, given the underlying word distribution, based on the known TSSs. In statistical terms, this is an inhomogeneous Markov model (MM) of order k − 1 (Borodovsky and Peresetsky 1994). The use of Markov models in sequence analysis is reviewed in Durbin et al. (2001). Sequences containing k-mers that are similarly positioned to those in the known TSS sequences will, if evaluated by the MM, have a higher MM score than other sequences; we will interpret this score (expressed as a likelihood ratio; see Methods) as the transcription initiation propensity of the center nucleotide in the query sequence. Thus, we can let this MM slide in 1-nt increments over sequences to predict the initiation propensity of each nucleotide. To test our method, we counted k-mers in the −50/+50 region around locally dominant TSSs from the whole genome, but excluded those from chromosome 1. Clusters from chromosome 1 (defined by the cluster method described previously) were used for testing.
First, we investigated whether nucleotides with different observed initiation usage within a cluster can be distinguished by their MM score. The initiation site usage of a nucleotide within a given cell sample can be measured by the number of tags whose 5′ ends map to that nucleotide. Importantly, however, CAGE is a sampling procedure (Carninci et al. 2006), and small differences in tag counts between two nucleotides might arise due to chance. Therefore, we only compared the scores of pairs of nucleotides within each cluster that have significantly different numbers of CAGE tags (one-sided binomial P ≤ 0.01). If the MM score was higher for the nucleotide that also had the higher CAGE tag count, we counted the case as “positive,” otherwise “negative.” The accuracy is the percentage of positives of all pairs tested. If the MM scores had no relation to the CAGE tag count, we would expect an accuracy of 50% by chance.
As an example, a TSS cluster from the MFSD4 gene has 278 pairs of nucleotides with significantly different tag counts; for every such pair, the nucleotide with more tags also has a higher TSS propensity according to the second-order MM (100% accuracy) (Fig. 5A,B). More generally, using the HepG2 data, the first-order MM makes correct predictions for 91% of nucleotide pairs, while second- and third-order MMs are marginally less accurate (Table 1). Since the −1/+1 dinucleotide seems especially important for TSS positioning (Carninci et al. 2006), we also tried a first-order MM based only on the −1/+1 regions of the training sequences. This model achieves 78% accuracy, confirming the importance of this dinucleotide, but also demonstrating a substantial contribution from the wider flanking region (Table 1).
Figure 5.
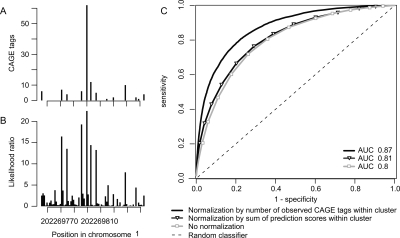
Predicting TSS usage. (A) Observed TSS usage in a TSS cluster at the start of the MFSD4 gene. The number of CAGE tags (from all libraries) initiating from each nucleotide is shown as a bar plot. This is for comparison with the predicted initiation propensity in the next panel. (B) Predicted TSS propensity of each nucleotide in the above TSS cluster. The transcription initiation propensity of each nucleotide, calculated as a likelihood ratio predicted from the surrounding DNA sequence using a second-order Markov model (see main text and Methods), is shown as a bar plot. Note the high correlation between predicted rates in this panel and the observed counts in A. (C) Classification of nucleotides within TSS clusters as active or inactive. The receiver operating characteristic (ROC) curve plots sensitivity vs. specificity (see Methods) for classification methods. The area under the curve (AUC) statistic is shown within the plot for the different prediction methods. An AUC of 100% corresponds to ideal performance, while a random classifier (shown as a dotted line) will have an AUC of 50%. We use the prediction scores, as exemplified in B, to classify each nucleotide in a cluster as active or inactive, for the test clusters on chromosome 1. With no additional scaling of these scores, the predictive power is adequate (gray line with boxes). Normalizing the nucleotide scores by the sum of prediction scores within the cluster (black line with triangles) does not improve the prediction. However, after scaling the prediction scores by the overall expression level (number of observed CAGE tags) of the cluster (black line), the AUC reaches an impressive 87%. Thus, knowing the expression output of a given promoter region adds additional predictive power.
Table 1.
Prediction of relative TSS propensity within HepG2 TSS clusters (HBY library)
TSS selection within clusters can vary between cell types, indicating subtle differences in sequence determinants (Kawaji et al. 2006). We identified other CAGE libraries from different tissues/cell lines (Supplemental Table S3), each of which is a different experiment in which the RNA libraries originate from different laboratories. We repeated the above analysis on each library, which gave accuracies similar to that of the HepG2 data set (Table 2; Supplemental Table S4). To test the universality of our model, we trained the MM on one CAGE library (using all chromosomes except chromosome 1), and evaluated it with CAGE clusters from another library (only using chromosome 1). Generally, training and evaluating using a single CAGE library gives higher accuracy than when training and evaluating with disparate libraries (Table 2; Supplemental Table S4), but the difference is not large. This strongly indicates that the model is applicable to different cellular contexts, and at the same time, shows that the initial results are unlikely to be due to some specific features of certain RNA libraries.
Table 2.
Prediction of relative TSS propensity within clusters from different cell lines, using a first-order Markov model trained on −50/+50 nucleotides
Cases where the training and evaluation process use data from the same cell line or set are in bold. HBY is a HepG2 liver cell library, HBM a skin cell line library, and HAM a cerebrum library. The datasets are described in detail in Supplemental Table S1.
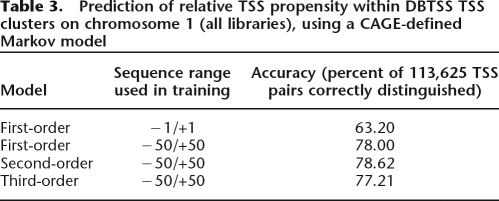
We sought to validate the model further, using TSS data from experimental techniques other than CAGE. Since we predict relative initiation-site usage on a genome scale, any such data must be able to measure initiation-site usage with nucleotide resolution in standardized experiments performed on a massive scale, since results otherwise would be anecdotal. This rules out low-throughput methods such as nuclease protection assays, which cannot give expression quantification with single-nucleotide resolution (Carninci et al. 2006), and are, as a rule, applied to single promoters in a given experiment. Given this, aside from the CAGE set, the most suitable data source is the oligo-capped expressed sequence tag (EST) datasets deposited in the DBTSS database (Yamashita et al. 2006), although even this is not ideal. The oligo-capping method has two known sources of expression bias: the RNA ligation step and the PCR amplification of full-length cDNAs. In oligo-capping, an oligonucleotide is ligated to full-length, 5′-phosphorylated mRNAs (Suzuki et al. 2001) with T4 RNA ligase. This enzyme has nucleotide preferences, so that some RNA sequences are ligated 10-fold more efficiently than others (Ohtsuka et al. 1980; Harada and Orgel 1993), causing some RNA sequences to be under-represented in the full-length cDNA library and others to be over-represented. An additional source of bias is the PCR reaction that is commonly used to amplify oligo-capped cDNA before cloning and sequencing. PCR often reduces cDNA diversity by amplifying some sequences more than others. For instance, when comparing two blastocyst full-length cDNA libraries, one of which was prepared without PCR and the other with PCR amplification, the former identified a much larger cDNA diversity than the latter (Carninci et al. 2003). In contrast, CAGE is prepared by cap-trapping, which is based on a chemical reaction to add a biotin group to the cap-site that has no nucleotide bias (Kodzius et al. 2006). Additionally, in CAGE, all of the 5′ ends are chopped to 20–21-nt-long tags, and only subsequently amplified by PCR before proceeding to cloning and sequencing. Amplifying tags of the same length minimizes amplification bias (Shiraki et al. 2003; Kodzius et al. 2006). Despite these biases, when we evaluated TSS clusters in human chromosome 1 made from all oligo-capped ESTs, using a first-order model trained on all CAGE data from all other chromosomes, we achieve an accuracy of 78% (Table 3), which is substantially higher than the 50% expected by chance. As with the CAGE data, using a model based only on the −1/+1 dinucleotide results in a ∼10% decrease in accuracy (Table 3), showing that the DNA code does not reside in the −1/+1 dinucleotide alone, but in the broader −50/+50 region. Thus, the DBTSS data also support the DNA code, albeit with more reservations than the CAGE data.
Table 3.
Prediction of relative TSS propensity within DBTSS TSS clusters on chromosome 1 (all libraries), using a CAGE-defined Markov model
As our method can distinguish between TSS with significantly different CAGE tag counts, we sought to extend it to predict the nucleotides that are experimentally detected TSSs within each cluster with the current sequencing depth (see Methods for details). For a TSS cluster as in Figure 5A, we use the corresponding MM prediction scores (Fig. 5B) to classify a nucleotide as “active” or “inactive.” We rescaled the MM scores on each nucleotide so that they sum up to the total number of tags within the cluster. Then, nucleotides with a rescaled score over a chosen threshold were predicted as “active.” We evaluate this method by plotting sensitivity against 1 − specificity (Fig. 5C); this is a receiver operating characteristic (ROC) curve, as reviewed in Akobeng (2007). The predictive power of a method can be judged by the area under the ROC curve (the AUC value). Essentially, the AUC is expected to be 50% with a random classifier and 100% with a perfect classifier. Using the first-order MM, the AUC is 87.1%, indicating high predictive performance.
Importantly, by rescaling the MM scores to the number of CAGE tags, we are predicting whether a certain nucleotide within a cluster is active given the expression strength of the cluster (the observed number of CAGE tags); since CAGE is a sampling procedure, the number of detected TSSs should be dependent on the number of sampled tags. If the normalization based on expression strength is not used, implicitly interpreting MM scores equally in any genomic location, the performance is adequate but lower (Fig. 5C). Thus, the chance of observing a particular nucleotide as a TSS will be dependent on both the local DNA sequence and the expression level of the cluster. In other words, the MM scores in themselves are describing TSS selection propensities and not absolute expression rates.
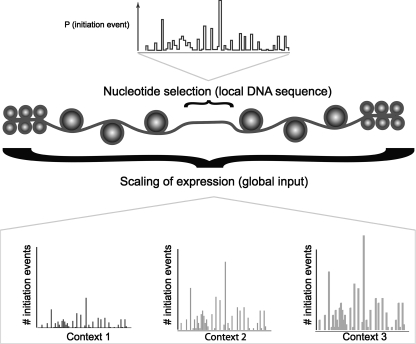
These results suggest a model where coarse-grained regulatory processes (enhancers, chromatin state, etc.) tune the expression level of an entire TSS cluster, and a code defined by the local DNA sequence determines relative TSS selection within the cluster (Fig. 6). This model predicts that DNA sequence alone should be less reliable at predicting relative TSS usage rates of nucleotides that are taken from two different, non-overlapping clusters, compared with our study above, which compares nucleotides from within the same cluster. This is because, according to our model, different distal elements will control the total expression output of the different clusters. We tested this by randomly shuffling the assignment of clusters to all of the nucleotides in the test set, and then re-running the initiation-site usage test as described above (see Methods). As expected, we observed an overall decrease in prediction accuracy (Table 1).
Figure 6.
A general model for the organization of transcription initiation. The underlying propensity for initiation of transcription by the RNA polymerase II enzyme is governed solely by local DNA sequence. The role of processes working distally (such as enhancers) or at larger scales is to stabilize the initiation process or regulate DNA accessibility. The global features can be viewed as a way to scale the underlying TSS selection distribution; these features can change due to context, while the local DNA code cannot. “Context” encompasses both distal DNA elements/chromatin state events and the state of the cell (e.g., which transcription factors are present). The total expression output from a TSS cluster is a product of the local and global factors.
Discussion
We have shown that, using relatively simple methods, TSS selection can be predicted with high accuracy within local regions just using DNA sequence. The model is based on the occurrence of sequence motifs with a given spacing to the TSS, where the most over-represented motifs have the greatest impact on TSS prediction. Three of the five most over-represented motifs are already established as significant determinants of initiation-site usage and/or positioning in multiple studies (Smale and Kadonaga 2003); this is particularly true for the TATA-box (see, for example, Kovacs and Butterworth 1986; O'Shea-Greenfield and Smale 1992; Zhu et al. 1995). The importance of the Inr/PyPu motif has been investigated in multiple studies (Grosschedl and Birnstiel 1980; Tokunaga et al. 1984; Smale and Baltimore 1989). In a previous study (Carninci et al. 2006), we have shown that naturally occurring mutations in PyPu motifs in orthologous mouse–human promoters changing them to PyPy, PuPu, or PuPy, on average, decrease initiation rates, which is entirely consistent with this study. Likewise, the SP1 transcription factor has been shown to bind in the −80 to −40 region and have an effect on initiation-site selection (Blake et al. 1990; Smale et al. 1990). All of these findings fit with our model. Elucidation of the role of the gcg repeats demands further experimental studies. At present, our study can only show that these motifs have a predictive effect, not that they are biologically active. A detailed investigation of their biological effects is beyond the scope of this work: to show that local DNA sequence can predict initiation rates.
A DNA code for transcription initiation fits with the previously suggested (Sandelin et al. 2007) picture, where RNA Polymerase II and associated factors scan accessible DNA, and initiation events are more likely to occur within sequence contexts that fit the word distribution depicted in Figure 4B. With this model, every genomic nucleotide is a potential transcription start site, although most are not used significantly.
Conversely, in this model, the total expression strength at a locus (equivalent to the number of initiation events) is determined also by active enhancers, cofactors, and the accessibility of DNA. The model suggests that that the primary function of distal elements is either to make DNA accessible for the transcription machinery, or to stabilize the formation of the preinitiation complex; these elements will then have limited function in the local selection of nucleotides once DNA is accessible (Fig. 6). Thus, integration of local and distal effects will be necessary to simultaneously model TSS selection and promoter expression.
The MM can be applied to any sequence that is indicated to be accessible to the transcription apparatus: accessibility data can be anything from acetylation status to immunoprecipitated components of the transcription-initiation complex. The corresponding MM scores will then be indicative of the relative initiation-site usage between the nucleotides that are assessed. However, as explained above, the MM scores alone cannot predict the scale of expression, as the regulatory determinants reside elsewhere. The expression of a given locus must then be assessed by other means, which would be dependent on the method used to indicate accessibility.
While the MM may be practically used to pinpoint the exact start sites from other technologies with lower resolution, such as ChIP-chip with antibodies targeting parts of the preinitiation complex, we consider the main utility of our method to be on the conceptual level; as we can predict the relative initiation site usage by just using local DNA sequence, it seems likely that the majority of the determinants for this process reside there.
An important caveat with our model is that it is bounded by the quality and depth of available experimental data; it requires massive sequencing of transcription start sites to be trained and evaluated, and these data sets are just becoming available to the field. Therefore, the current model should be viewed as a first trial to capture the main determinants in a DNA code for initiation, which has room for improvement both by experimental and computational means.
A DNA code for transcription initiation has important biomedical implications; it may be possible to identify polymorphisms that create or destroy strong transcription-initiation sites, and the code may help us understand how transcription start-site usage has evolved between species.
The key difference in our approach compared with earlier computational efforts to annotate TSSs lies in the changed view of core promoters made possible by high-throughput TSS sequencing data (Carninci et al. 2006). Smaller-scale studies (Suzuki et al. 2001; Smale and Kadonaga 2003) have shown these broad types of TSS architectures for single genes, but these examples were not generalized as principles applying to the rest of the genome. Thus, most efforts to annotate and predict core promoter locations have been targeted to identify a single TSS or the region around it, often defined by RefSeq cDNAs, modeled as sparsely distributed on-off switches (Ohler et al. 2000; Scherf et al. 2000; Davuluri et al. 2001; Down and Hubbard 2002; Werner 2003; Bajic et al. 2004, 2006; Gangal and Sharma 2005; Solovyev et al. 2006; Zhao et al. 2007) in otherwise presumed transcriptionally silent DNA. In contrast, our model considers multiple initiation sites and their relative usage, and distinguishes TSS selection propensity from absolute expression levels. Overall, the target of our analysis is conceptually different; given a known active promoter region and its expression strength, we assess the TSS propensity of each nucleotide within the region.
Together with recent studies showing that nucleosome positioning is predictable (Segal et al. 2006) and that TSSs can be inferred by chromatin signatures (Heintzman et al. 2007), our results suggest that an accurate model for genome-wide transcription-initiation events with nucleotide resolution is a realistic near-term goal instead of a distant aspiration.
Methods
Data sources
CAGE tags are 20–21 bp 5′ ends of full-length cDNAs that have been mapped to the corresponding (mouse or human) genome sequence. Protocols for CAGE were described by Kodzius et al. (2006). We used the human CAGE data mapped to the hg17 genome assembly as described in Carninci et al. (2006) for the majority of analyses—for Supplemental Figures S4–S7, mouse CAGE data from the same study mapped to the mm5 assembly was used. For clarity, aside from the alignment cut-offs described in Carninci et al. (2006), each CAGE tag must have a unique best-scoring mapping; each CAGE tag only maps to one single genomic location. We only used the 5′-end position of tags for all the analyses. Properties of the datasets are described within Supplemental Tables S1 and S3. An assessment of the reliability of the CAGE technology, using six lines of evidence, is described in detail in the Supplementary material of Carninci et al. (2006).
Defining locally dominant TSS
To learn the sequence features associated with high rates of initiation, we took locally dominant transcription start sites, i.e., nucleotides with at least five transcription initiation events in the CAGE data, and more events than any other nucleotide at a distance of ≤100 nt upstream or downstream. The two DNA strands (or directions of transcription) were considered separately. The number of cases retrieved is dependent on what library or libraries are used (see Supplemental Tables S1, S2). Dominant TSSs retrieved this way were used for both analyzing k-mer occurrences, and later to train the Markov model (in the latter case all TSS from chromosome 1 were removed, to allow for an independent test set).
Parametric clustering algorithm
The aim is to identify clusters, at multiple scales, among transcription initiation events observed at specific locations in the genome. The input data for our analysis is mappings of CAGE tags to unique sites in the genome as described above (Carninci et al. 2006), where each such defined TSS also is labeled with strand and the number of 5′ edges of CAGE tags mapped to it. Clusters among these datapoints are identified as follows: Clusters are defined to be maximal scoring segments of a chromosome, where the score is given by this formula: Score = (number of events in segment) − d × (segment size in nt).
Events on each strand of the chromosome were considered separately (as if each strand were a separate chromosome). Roughly speaking, clusters are maximal segments with a density of more than d events per nucleotide. More precisely, clusters are maximal segments where every prefix and suffix of the segment has a density of more than d events per nucleotide. (Otherwise, the segment would not be maximal scoring, because its score could be increased by removing the prefix or suffix.)
Maximal scoring segments are widely used to identify sequence features such as hydrophobic tracts in proteins and CpG islands in DNA, and they underlie sequence comparison algorithms such as BLAST (Karlin and Altschul 1990; Taylor et al. 2006). The definition of maximal scoring segments is discussed in Ruzzo and Tompa (1999). We use the same definition of maximal scoring segments as Ruzzo and Tompa (1999); in particular, ties are broken by disallowing zero-scoring prefixes or suffixes.
Our segment-scoring scheme can be interpreted as a log likelihood ratio. The simplest statistical model of a cluster is for events to occur randomly and uniformly in the cluster with average density p per nucleotide, and the simplest null model is for events to occur randomly and uniformly with average density q per nucleotide (where q < p) (a Poisson process). Then, the log likelihood ratio of observing n events in a segment of size s is:
This formula is equivalent to our segment-scoring scheme, with d = (p − q)/log(p/q). Multiplying the score by a fixed number such as log(p/q) does not change the maximal-scoring segments.
Clusters at different scales are found by varying the d parameter; large values of d produce small, dense clusters and small values of d produce large, loose clusters. The following algorithm finds all clusters for all values of d.
The algorithm begins at the largest scale, where d = 0, and all of the events are merged into one big cluster. It then calculates the density (events per nucleotide) of every prefix and suffix of the big cluster. The lowest value among all of these densities is the critical value of d, at which the big cluster ceases to be a maximal-scoring segment (because zero-scoring prefixes or suffixes are not allowed). This is the maximum d for the big cluster, and the minimum d for its subclusters. Furthermore, the corresponding prefix (or suffix) defines a breakpoint; at higher values of d, every maximal scoring segment must be either completely inside or completely outside of the prefix (or suffix).
To prove this, first assume, without loss of generality, that we are dealing with a prefix. At the critical value of d, every suffix of this prefix must have non-positive score; otherwise, an even lower density prefix could be obtained by removing this suffix. At higher values of d, the score of any segment can only decrease. Thus, at higher values of d there cannot be a maximal scoring segment that begins in the prefix and ends outside of it.
Given this breakpoint, we proceed by divide and conquer. The large cluster is broken into two parts: the lowest-density prefix (or suffix), and the remainder of the cluster. If several prefixes and/or suffixes are tied for the lowest density, one is chosen arbitrarily; the end result will be the same. Finally, the algorithm is reapplied recursively to each of the two parts. When applying the algorithm to each part, it is possible for its maximum d, i.e., the lowest density of any prefix or suffix, to be less than or equal to its minimum d (i.e., the maximum d of the parent cluster). In this case, there is no value of d at which the part is a maximal-scoring segment, and so the algorithm does not report any cluster, but the breaking-in-two and recursion proceed as normal.
This procedure returns all possible maximal scoring segments and also annotates each segment with the minimum and maximum values of d where it is maximal scoring. If a particular segment is maximal scoring over a large range of values for d, it is intuitively a “stable” cluster. Thus, the stability of each cluster is defined as max d/min d.
A Perl script implementing this algorithm is available at the supporting website. The average complexity is O(N logN), and the worst case O(N2), where N is the number of experimentally defined TSSs. In practice, it takes a few minutes on a standard desktop workstation to cluster the human genome-wide FANTOM3 CAGE data (Carninci et al. 2006). We call it “parametric” clustering based on an analogy with parametric alignment described in Waterman et al. (1992).
Finding over-represented k-mers at specific positions
For locally dominant TSS (see above), we counted all k-mers (k = 1–6) at each position from −100 to +100 on the same strand as the TSS. For a given k-mer and position, we tabulated the number of occurrences S, and calculated the likelihood of finding ≥S words at a given position based on the frequency of this k-mer in all positions (a Binomial test) in the range. P-values obtained were corrected for multiple testing bias by the Bonferroni method. Specifically, P-values were multiplied by 4k times the number of positions.
Position-specific Markov models
The aim is to predict the preponderance of transcription-initiation events at a given nucleotide, based on the DNA sequence surrounding the nucleotide. For locally dominant TSS (see above) we obtained the 100-nt genomic sequence beginning 50 nt upstream and ending 49 nt downstream (i.e., the −50 to +50 region relative to the transcription start site at +1). To allow for test cases independent of the training data, sequences from chromosome 1 were discarded at this point.
To obtain position-specific Markov models (MMs), also known as inhomogenous Markov models (Borodovsky and Peresetsky 1994), we simply counted the frequency of every k-mer (where k = 2, 3, or 4) at each position in the training sequences. This directly defines a MM of order k − 1. A MM of order n specifies the probability of observing a given symbol, given the n preceding symbols (in our cases, nucleotides). This is equal to the probability of the (n+1)-mer ending at the given nucleotide divided by the probability of the preceding n-mer; thus, all of these probabilities can be estimated from the position-specific k-mer frequencies above. Pseudocounts were not used, since there were no k-mers in the evaluation sets that did not occur in the training set when k = 2 or 3, and only a few cases when k = 4.
We also experimented with variable-order MMs, which use longer k-mers, when those k-mers are sufficiently common to get reliable frequencies, and shorter k-mers otherwise. Surprisingly, this did not lead to an improvement in prediction accuracy (data not shown).
Scoring sequences with Markov models
The position-specific Markov models were used to make predictions as follows. A window of size 100 nt was slid across the test sequence in 1-nt increments. The following likelihood ratio was calculated for each window: Prob(window|promoter model)/Prob(window|null model). The “promoter model” is the position-specific Markov model described above. The null model is a standard homogeneous Markov model (i.e., not position specific), derived from the promoter model by summing the counts of each k-mer over all positions. This likelihood ratio predicts the initiation rate at the 51st nucleotide in the window. Thus, in order to scan the whole test sequence, flanking genomic sequence of 50 nt upstream and 49 nt downstream was added first.
As a special case, a first-order Markov model was constructed just from the −1/+1 regions of the training sequences. This model only has one position, so the null model described above would be identical to the promoter model. So, in this case only, a null model of uniform k-mer frequencies was used.
Predicting TSS usage using Markov models
Predictions were made within small, stable clusters of transcription-initiation events on chromosome 1. Specifically, clusters wider than 100 bp, or with stability <2, were not considered. Of the remaining clusters, the outermost ones were used (i.e., if a stable cluster ≤100 bp lay within another stable cluster ≤100 bp, predictions were made for every nucleotide in the outer one). Note that the numbers for training and evaluation will vary depending on what CAGE libraries are used (see Supplemental Table S3).
The initiation rate predictions were interpreted in two ways: qualitative and binary. In the qualitative interpretation, if nucleotide X has a higher likelihood ratio value than nucleotide Y, then it is predicted to have a higher rate of transcription initiation. In the binary interpretation, we ask whether a given nucleotide within a cluster is used as a TSS, given the total expression level of the cluster (the sum of all observed tags within the cluster; for details, see below). To be clear, for all tests, the MM was applied to each nucleotide covered by the cluster, regardless of observed CAGE tag counts. Thus, each nucleotide will obtain a MM score.
Predicting relative initiation site usage within clusters (qualitative interpretation)
For a given TSS cluster, we assessed all pairs of nucleotides in the cluster that have significantly different tag counts, assuming a null model where tags at both nucleotides are equally likely. Note that such pairs can include nucleotides with 0 tags. Significance was determined using the one-sided Binomial test with an alpha value of ≤0.01. For each significant pair identified this way, we noted whether the nucleotide with the larger number of CAGE tags also had a higher MM score. These cases were defined as correct predictions, while any other cases were defined as incorrect. The accuracy reported is the overall number of correct predictions divided by all significant pairs tested in all clusters (as defined above) on chromosome 1.
Randomization (shuffling) test
One of our hypotheses in this work is that the total expression level of a TSS cluster (expressed as the total number of CAGE tags within the cluster) will be determined partially by events and/or elements outside of the cluster. If this is true, repeating the above analysis where nucleotide pairs are taken from different clusters should decrease performance, since the expression level of the two clusters will have different regulatory inputs. To test this, we randomly shuffled the assignments of cluster names to nucleotides in the test set. This results in a new, equally large cluster set with the same cluster widths as previously, but where the CAGE tag counts in each position in the clusters are randomly sampled from the original cluster set without replacement. We then applied the relative initiation site usage prediction test as described above for each newly defined cluster. An alternative strategy, exhaustive testing of all nucleotide pairs between all original clusters, is computationally intractable.
Classification of active TSS within a cluster (binary interpretation)
Each TSS cluster can be defined as a vector K with the same length as the cluster, in which Ki denotes the number of CAGE tags (≥0) at nucleotide i. Sliding the Markov model over the cluster will produce a vector T with the same length as K, where Ti is the likelihood ratio score of nucleotide i in the cluster. We normalized T to sum to 1, and then multiplied each element by the sum of K (in other words, we rescale T to the number of CAGE tags in the cluster). If a Ti ≥ a chosen cut-off c, the nucleotide i is labeled “active.” Note that this is different from just transforming the vector T to 1 (a probability distribution), as the sum of K will be different in different clusters, while the cut-off c is static. Using T as either a probability vector summing to 1 or the raw likelihood ratio scores as predictors gives adequate, but decreased predictive performance (see Fig. 5C).
True positives (TP) are defined as Ki > 0 and Ti ≥ c (where c is an arbitrary cutoff), while true negatives (TN) are defined as Ki = 0 and Ti < c. Increases in c will result in higher specificity, [TN/(TN+FP)] but lower sensitivity [TP/(TP+FN)]. The trade-off between specificity and sensitivity (a ROC) is shown in Figure 5C. The area under the ROC curve (area under curve [AUC]) can be interpreted as the predictive performance, where an area of 1 corresponds to perfect performance. AUC values were calculated using the trapz() function in the caTools R package (Ihaka and Gentleman 1996).
Evaluation of TSS predictions using oligo-capped ESTs
A collection of 1,562,911 oligo-capped ESTs mapped to the hg17 assembly were downloaded from the DBTSS (Suzuki et al. 2004) website. We treated these equivalently to CAGE tags; only the 5′ end nucleotide was assessed. We pooled all available EST libraries, and (as in the CAGE trial) assessed the expression of a single nucleotide by the number of exact 5′ ends that were mapped to this nucleotide. The parametric clustering algorithm was applied to this set; for our evaluations, we extracted clusters with a stability ≥2 from chromosome 1. We then used the MM trained by all CAGE tags from the other chromosomes to assess the oligo-capped-derived clusters.
Acknowledgments
We thank Tim Bailey, Christine Wells, Erik van Nimwegen, and Ole Winther for useful comments on our methods; Jasmina Ponjavic for help with images; and Ulla Hansen, Ann Karlsson, Troels Marstrand, Hui Gao, Charles Plessy, Valtteri Wirta, and Chris Frith for advice on the manuscript. This study was supported by a Research Grant for the RIKEN Genome Exploration Research Project from the Ministry of Education, Culture, Sports, Science and Technology of the Japanese Government to Y.H.; a grant of the Genome Network Project from the Ministry of Education, Culture, Sports, Science, and Technology, Japan; the Strategic Programs for R&D of RIKEN Grant for the RIKEN Frontier Research System, Functional RNA research program. A.S, E.V., and A.K are supported by a grant from the Novo Nordisk Foundation to the Bioinformatics Centre. M.C.F. was a University of Queensland Postdoctoral Fellow.
Footnotes
[Supplemental material is available online at www.genome.org. Perl scripts for parametric clustering and for making and scanning position-specific Markov models, are available together with datasets used in this work at http://binf.ku.dk/~albin/supplementary_data/tss_code/.]
Article published online before print. Article and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.6831208
Note added in proof
A recent publication (Xi et al. 2007) reported a novel core promoter motif, “motif8,” which matches the gcg repeat motif reported in the present study, in terms of both sequence and position relative to TSS.
References
- Akobeng A.K. Understanding diagnostic tests 3: Receiver operating characteristic curves. Acta Paediatr. 2007;96:644–647. doi: 10.1111/j.1651-2227.2006.00178.x. [DOI] [PubMed] [Google Scholar]
- Bajic V.B., Tan S.L., Suzuki Y., Sugano S., Tan S.L., Suzuki Y., Sugano S., Suzuki Y., Sugano S., Sugano S. Promoter prediction analysis on the whole human genome. Nat. Biotechnol. 2004;22:1467–1473. doi: 10.1038/nbt1032. [DOI] [PubMed] [Google Scholar]
- Bajic V.B., Brent M.R., Brown R.H., Frankish A., Harrow J., Ohler U., Solovyev V.V., Tan S.L., Brent M.R., Brown R.H., Frankish A., Harrow J., Ohler U., Solovyev V.V., Tan S.L., Brown R.H., Frankish A., Harrow J., Ohler U., Solovyev V.V., Tan S.L., Frankish A., Harrow J., Ohler U., Solovyev V.V., Tan S.L., Harrow J., Ohler U., Solovyev V.V., Tan S.L., Ohler U., Solovyev V.V., Tan S.L., Solovyev V.V., Tan S.L., Tan S.L. Performance assessment of promoter predictions on ENCODE regions in the EGASP experiment. Genome Biol. 2006;7:S1–S3. doi: 10.1186/gb-2006-7-S1-S3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrera L.O., Ren B., Ren B. The transcriptional regulatory code of eukaryotic cells - insights from genome-wide analysis of chromatin organization and transcription factor binding. Curr. Opin. Cell Biol. 2006;18:291–298. doi: 10.1016/j.ceb.2006.04.002. [DOI] [PubMed] [Google Scholar]
- Blake M.C., Jambou R.C., Swick A.G., Kahn J.W., Azizkhan J.C., Jambou R.C., Swick A.G., Kahn J.W., Azizkhan J.C., Swick A.G., Kahn J.W., Azizkhan J.C., Kahn J.W., Azizkhan J.C., Azizkhan J.C. Transcriptional initiation is controlled by upstream GC-box interactions in a TATAA-less promoter. Mol. Cell. Biol. 1990;10:6632–6641. doi: 10.1128/mcb.10.12.6632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borodovsky M., Peresetsky A., Peresetsky A. Deriving non-homogeneous DNA Markov chain models by cluster analysis algorithm minimizing multiple alignment entropy. Comput. Chem. 1994;18:259–267. doi: 10.1016/0097-8485(94)85022-4. [DOI] [PubMed] [Google Scholar]
- Carninci P., Waki K., Shiraki T., Konno H., Shibata K., Itoh M., Aizawa K., Arakawa T., Ishii Y., Sasaki D., Waki K., Shiraki T., Konno H., Shibata K., Itoh M., Aizawa K., Arakawa T., Ishii Y., Sasaki D., Shiraki T., Konno H., Shibata K., Itoh M., Aizawa K., Arakawa T., Ishii Y., Sasaki D., Konno H., Shibata K., Itoh M., Aizawa K., Arakawa T., Ishii Y., Sasaki D., Shibata K., Itoh M., Aizawa K., Arakawa T., Ishii Y., Sasaki D., Itoh M., Aizawa K., Arakawa T., Ishii Y., Sasaki D., Aizawa K., Arakawa T., Ishii Y., Sasaki D., Arakawa T., Ishii Y., Sasaki D., Ishii Y., Sasaki D., Sasaki D., et al. Targeting a complex transcriptome: The construction of the mouse full-length cDNA encyclopedia. Genome Res. 2003;13:1273–1289. doi: 10.1101/gr.1119703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carninci P., Kasukawa T., Katayama S., Gough J., Frith M.C., Maeda N., Oyama R., Ravasi T., Lenhard B., Wells C., Kasukawa T., Katayama S., Gough J., Frith M.C., Maeda N., Oyama R., Ravasi T., Lenhard B., Wells C., Katayama S., Gough J., Frith M.C., Maeda N., Oyama R., Ravasi T., Lenhard B., Wells C., Gough J., Frith M.C., Maeda N., Oyama R., Ravasi T., Lenhard B., Wells C., Frith M.C., Maeda N., Oyama R., Ravasi T., Lenhard B., Wells C., Maeda N., Oyama R., Ravasi T., Lenhard B., Wells C., Oyama R., Ravasi T., Lenhard B., Wells C., Ravasi T., Lenhard B., Wells C., Lenhard B., Wells C., Wells C., et al. The transcriptional landscape of the mammalian genome. Science. 2005;309:1559–1563. doi: 10.1126/science.1112014. [DOI] [PubMed] [Google Scholar]
- Carninci P., Sandelin A., Lenhard B., Katayama S., Shimokawa K., Ponjavic J., Semple C.A., Taylor M.S., Engstrom P.G., Frith M.C., Sandelin A., Lenhard B., Katayama S., Shimokawa K., Ponjavic J., Semple C.A., Taylor M.S., Engstrom P.G., Frith M.C., Lenhard B., Katayama S., Shimokawa K., Ponjavic J., Semple C.A., Taylor M.S., Engstrom P.G., Frith M.C., Katayama S., Shimokawa K., Ponjavic J., Semple C.A., Taylor M.S., Engstrom P.G., Frith M.C., Shimokawa K., Ponjavic J., Semple C.A., Taylor M.S., Engstrom P.G., Frith M.C., Ponjavic J., Semple C.A., Taylor M.S., Engstrom P.G., Frith M.C., Semple C.A., Taylor M.S., Engstrom P.G., Frith M.C., Taylor M.S., Engstrom P.G., Frith M.C., Engstrom P.G., Frith M.C., Frith M.C., et al. Genome-wide analysis of mammalian promoter architecture and evolution. Nat. Genet. 2006;38:626–635. doi: 10.1038/ng1789. [DOI] [PubMed] [Google Scholar]
- Cooper S.J., Trinklein N.D., Anton E.D., Nguyen L., Myers R.M., Trinklein N.D., Anton E.D., Nguyen L., Myers R.M., Anton E.D., Nguyen L., Myers R.M., Nguyen L., Myers R.M., Myers R.M. Comprehensive analysis of transcriptional promoter structure and function in 1% of the human genome. Genome Res. 2006;16:1–10. doi: 10.1101/gr.4222606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davuluri R.V., Grosse I., Zhang M.Q., Grosse I., Zhang M.Q., Zhang M.Q. Computational identification of promoters and first exons in the human genome. Nat. Genet. 2001;29:412–417. doi: 10.1038/ng780. [DOI] [PubMed] [Google Scholar]
- Down T.A., Hubbard T.J., Hubbard T.J. Computational detection and location of transcription start sites in mammalian genomic DNA. Genome Res. 2002;12:458–461. doi: 10.1101/gr.216102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durbin R., Eddy S.R., Krogh A., Mitchison G., Eddy S.R., Krogh A., Mitchison G., Krogh A., Mitchison G., Mitchison G. Biological sequence analysis. Cambridge University Press; Cambridge, UK: 2001. [Google Scholar]
- The ENCODE Project Consortium Identification and analysis of functional elements in 1% of the human genome by the ENCODE pilot project. Nature. 2007;447:799–816. doi: 10.1038/nature05874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gangal R., Sharma P., Sharma P. Human pol II promoter prediction: Time series descriptors and machine learning. Nucleic Acids Res. 2005;33:1332–1336. doi: 10.1093/nar/gki271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gershenzon N.I., Ioshikhes I.P., Ioshikhes I.P. Synergy of human Pol II core promoter elements revealed by statistical sequence analysis. Bioinformatics. 2005;21:1295–1300. doi: 10.1093/bioinformatics/bti172. [DOI] [PubMed] [Google Scholar]
- Grosschedl R., Birnstiel M.L., Birnstiel M.L. Identification of regulatory sequences in the prelude sequences of an H2A histone gene by the study of specific deletion mutants in vivo. Proc. Natl. Acad. Sci. 1980;77:1432–1436. doi: 10.1073/pnas.77.3.1432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hampsey M. Molecular genetics of the RNA polymerase II general transcriptional machinery. Microbiol. Mol. Biol. Rev. 1998;62:465–503. doi: 10.1128/mmbr.62.2.465-503.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harada K., Orgel L.E., Orgel L.E. In vitro selection of optimal DNA substrates for T4 RNA ligase. Proc. Natl. Acad. Sci. 1993;90:1576–1579. doi: 10.1073/pnas.90.4.1576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heintzman N.D., Stuart R.K., Hon G., Fu Y., Ching C.W., Hawkins R.D., Barrera L.O., Van Calcar S., Qu C., Ching K.A., Stuart R.K., Hon G., Fu Y., Ching C.W., Hawkins R.D., Barrera L.O., Van Calcar S., Qu C., Ching K.A., Hon G., Fu Y., Ching C.W., Hawkins R.D., Barrera L.O., Van Calcar S., Qu C., Ching K.A., Fu Y., Ching C.W., Hawkins R.D., Barrera L.O., Van Calcar S., Qu C., Ching K.A., Ching C.W., Hawkins R.D., Barrera L.O., Van Calcar S., Qu C., Ching K.A., Hawkins R.D., Barrera L.O., Van Calcar S., Qu C., Ching K.A., Barrera L.O., Van Calcar S., Qu C., Ching K.A., Van Calcar S., Qu C., Ching K.A., Qu C., Ching K.A., Ching K.A., et al. Distinct and predictive chromatin signatures of transcriptional promoters and enhancers in the human genome. Nat. Genet. 2007;39:311–318. doi: 10.1038/ng1966. [DOI] [PubMed] [Google Scholar]
- Ihaka R., Gentleman R., Gentleman R. R: A language for data analysis and graphics. J. Comput. Graph. Statist. 1996;5:299–314. [Google Scholar]
- Karlin S., Altschul S.F., Altschul S.F. Methods for assessing the statistical significance of molecular sequence features by using general scoring schemes. Proc. Natl. Acad. Sci. 1990;87:2264–2268. doi: 10.1073/pnas.87.6.2264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karolchik D., Baertsch R., Diekhans M., Furey T., Hinrichs A., Lu Y., Roskin K., Schwartz M., Sugnet C., Thomas D., Baertsch R., Diekhans M., Furey T., Hinrichs A., Lu Y., Roskin K., Schwartz M., Sugnet C., Thomas D., Diekhans M., Furey T., Hinrichs A., Lu Y., Roskin K., Schwartz M., Sugnet C., Thomas D., Furey T., Hinrichs A., Lu Y., Roskin K., Schwartz M., Sugnet C., Thomas D., Hinrichs A., Lu Y., Roskin K., Schwartz M., Sugnet C., Thomas D., Lu Y., Roskin K., Schwartz M., Sugnet C., Thomas D., Roskin K., Schwartz M., Sugnet C., Thomas D., Schwartz M., Sugnet C., Thomas D., Sugnet C., Thomas D., Thomas D., et al. The UCSC Genome Browser Database. Nucleic Acids Res. 2003;31:51–54. doi: 10.1093/nar/gkg129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kawaji H., Frith M.C., Katayama S., Sandelin A., Kai C., Kawai J., Carninci P., Hayashizaki Y., Frith M.C., Katayama S., Sandelin A., Kai C., Kawai J., Carninci P., Hayashizaki Y., Katayama S., Sandelin A., Kai C., Kawai J., Carninci P., Hayashizaki Y., Sandelin A., Kai C., Kawai J., Carninci P., Hayashizaki Y., Kai C., Kawai J., Carninci P., Hayashizaki Y., Kawai J., Carninci P., Hayashizaki Y., Carninci P., Hayashizaki Y., Hayashizaki Y. Dynamic usage of transcription start sites within core promoters. Genome Biol. 2006;7:R118. doi: 10.1186/gb-2006-7-12-r118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kent W.J., Sugnet C.W., Furey T.S., Roskin K.M., Pringle T.H., Zahler A.M., Haussler D., Sugnet C.W., Furey T.S., Roskin K.M., Pringle T.H., Zahler A.M., Haussler D., Furey T.S., Roskin K.M., Pringle T.H., Zahler A.M., Haussler D., Roskin K.M., Pringle T.H., Zahler A.M., Haussler D., Pringle T.H., Zahler A.M., Haussler D., Zahler A.M., Haussler D., Haussler D. The human genome browser at UCSC. Genome Res. 2002;12:996–1006. doi: 10.1101/gr.229102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura K., Wakamatsu A., Suzuki Y., Ota T., Nishikawa T., Yamashita R., Yamamoto J., Sekine M., Tsuritani K., Wakaguri H., Wakamatsu A., Suzuki Y., Ota T., Nishikawa T., Yamashita R., Yamamoto J., Sekine M., Tsuritani K., Wakaguri H., Suzuki Y., Ota T., Nishikawa T., Yamashita R., Yamamoto J., Sekine M., Tsuritani K., Wakaguri H., Ota T., Nishikawa T., Yamashita R., Yamamoto J., Sekine M., Tsuritani K., Wakaguri H., Nishikawa T., Yamashita R., Yamamoto J., Sekine M., Tsuritani K., Wakaguri H., Yamashita R., Yamamoto J., Sekine M., Tsuritani K., Wakaguri H., Yamamoto J., Sekine M., Tsuritani K., Wakaguri H., Sekine M., Tsuritani K., Wakaguri H., Tsuritani K., Wakaguri H., Wakaguri H., et al. Diversification of transcriptional modulation: Large-scale identification and characterization of putative alternative promoters of human genes. Genome Res. 2006;16:55–65. doi: 10.1101/gr.4039406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kodzius R., Kojima M., Nishiyori H., Nakamura M., Fukuda S., Tagami M., Sasaki D., Imamura K., Kai C., Harbers M., Kojima M., Nishiyori H., Nakamura M., Fukuda S., Tagami M., Sasaki D., Imamura K., Kai C., Harbers M., Nishiyori H., Nakamura M., Fukuda S., Tagami M., Sasaki D., Imamura K., Kai C., Harbers M., Nakamura M., Fukuda S., Tagami M., Sasaki D., Imamura K., Kai C., Harbers M., Fukuda S., Tagami M., Sasaki D., Imamura K., Kai C., Harbers M., Tagami M., Sasaki D., Imamura K., Kai C., Harbers M., Sasaki D., Imamura K., Kai C., Harbers M., Imamura K., Kai C., Harbers M., Kai C., Harbers M., Harbers M., et al. CAGE: Cap analysis of gene expression. Nat. Methods. 2006;3:211–222. doi: 10.1038/nmeth0306-211. [DOI] [PubMed] [Google Scholar]
- Kovacs B.J., Butterworth P.H., Butterworth P.H. The effect of changing the distance between the TATA-box and cap site by up to three base pairs on the selection of the transcriptional start site of a cloned eukaryotic gene in vitro and in vivo. Nucleic Acids Res. 1986;14:2429–2442. doi: 10.1093/nar/14.6.2429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mellor J. Dynamic nucleosomes and gene transcription. Trends Genet. 2006;22:320–329. doi: 10.1016/j.tig.2006.03.008. [DOI] [PubMed] [Google Scholar]
- Mito Y., Henikoff J.G., Henikoff S., Henikoff J.G., Henikoff S., Henikoff S. Genome-scale profiling of histone H3.3 replacement patterns. Nat. Genet. 2005;37:1090–1097. doi: 10.1038/ng1637. [DOI] [PubMed] [Google Scholar]
- Molina C., Grotewold E., Grotewold E. Genome wide analysis of Arabidopsis core promoters. BMC Genomics. 2005;6:25. doi: 10.1186/1471-2164-6-25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muller F., Demeny M.A., Tora L., Demeny M.A., Tora L., Tora L. New problems in RNA polymerase II transcription initiation: Matching the diversity of core promoters with a variety of promoter recognition factors. J. Biol. Chem. 2007;282:14685–14689. doi: 10.1074/jbc.R700012200. [DOI] [PubMed] [Google Scholar]
- Nishida H., Suzuki T., Kondo S., Miura H., Fujimura Y., Hayashizaki Y., Suzuki T., Kondo S., Miura H., Fujimura Y., Hayashizaki Y., Kondo S., Miura H., Fujimura Y., Hayashizaki Y., Miura H., Fujimura Y., Hayashizaki Y., Fujimura Y., Hayashizaki Y., Hayashizaki Y. Histone H3 acetylated at lysine 9 in promoter is associated with low nucleosome density in the vicinity of transcription start site in human cell. Chromosome Res. 2006;14:203–211. doi: 10.1007/s10577-006-1036-7. [DOI] [PubMed] [Google Scholar]
- Ohler U., Stemmer G., Harbeck S., Niemann H., Stemmer G., Harbeck S., Niemann H., Harbeck S., Niemann H., Niemann H. Stochastic segment models of eukaryotic promoter regions. Pac. Symp. Biocomput. 2000;5:377–388. doi: 10.1142/9789814447331_0036. [DOI] [PubMed] [Google Scholar]
- Ohler U., Liao G.C., Niemann H., Rubin G.M., Liao G.C., Niemann H., Rubin G.M., Niemann H., Rubin G.M., Rubin G.M. Computational analysis of core promoters in the Drosophila genome. Genome Biol. 2002;3 doi: 10.1186/gb-2002-3-12-research0087. RESEARCH0087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohtsuka E., Doi T., Uemura H., Taniyama Y., Ikehara M., Doi T., Uemura H., Taniyama Y., Ikehara M., Uemura H., Taniyama Y., Ikehara M., Taniyama Y., Ikehara M., Ikehara M. Comparison of substrate base sequences for RNA ligase reactions in the synthesis of a tetradecanucleotide corresponding to bases 21-34 of E. coli tRNAfMet 1. Nucleic Acids Res. 1980;8:3909–3916. doi: 10.1093/nar/8.17.3909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O'Shea-Greenfield A., Smale S.T., Smale S.T. Roles of TATA and initiator elements in determining the start site location and direction of RNA polymerase II transcription. J. Biol. Chem. 1992;267:1391–1402. [PubMed] [Google Scholar]
- Ponjavic J., Lenhard B., Kai C., Kawai J., Carninci P., Hayashizaki Y., Sandelin A., Lenhard B., Kai C., Kawai J., Carninci P., Hayashizaki Y., Sandelin A., Kai C., Kawai J., Carninci P., Hayashizaki Y., Sandelin A., Kawai J., Carninci P., Hayashizaki Y., Sandelin A., Carninci P., Hayashizaki Y., Sandelin A., Hayashizaki Y., Sandelin A., Sandelin A. Transcriptional and structural impact of TATA-initiation site spacing in mammalian core promoters. Genome Biol. 2006;7:R78. doi: 10.1186/gb-2006-7-8-r78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruzzo W.L., Tompa M., Tompa M.1999. A linear time algorithm for finding all maximal scoring subsequences. In The Seventh International Conference on Intelligent Systems for Molecular Biology, pp.234–241. . The AAAI Press, Menlo Park, CA [PubMed] [Google Scholar]
- Sandelin A., Carninci P., Lenhard B., Ponjavic J., Hayashizaki Y., Hume D.A., Carninci P., Lenhard B., Ponjavic J., Hayashizaki Y., Hume D.A., Lenhard B., Ponjavic J., Hayashizaki Y., Hume D.A., Ponjavic J., Hayashizaki Y., Hume D.A., Hayashizaki Y., Hume D.A., Hume D.A. Mammalian RNA polymerase II core promoters: Insights from genome-wide studies. Nat. Rev. Genet. 2007;8:424–436. doi: 10.1038/nrg2026. [DOI] [PubMed] [Google Scholar]
- Scherf M., Klingenhoff A., Werner T., Klingenhoff A., Werner T., Werner T. Highly specific localization of promoter regions in large genomic sequences by PromoterInspector: A novel context analysis approach. J. Mol. Biol. 2000;297:599–606. doi: 10.1006/jmbi.2000.3589. [DOI] [PubMed] [Google Scholar]
- Segal E., Fondufe-Mittendorf Y., Chen L., Thastrom A., Field Y., Moore I.K., Wang J.P., Widom J., Fondufe-Mittendorf Y., Chen L., Thastrom A., Field Y., Moore I.K., Wang J.P., Widom J., Chen L., Thastrom A., Field Y., Moore I.K., Wang J.P., Widom J., Thastrom A., Field Y., Moore I.K., Wang J.P., Widom J., Field Y., Moore I.K., Wang J.P., Widom J., Moore I.K., Wang J.P., Widom J., Wang J.P., Widom J., Widom J. A genomic code for nucleosome positioning. Nature. 2006;442:772–778. doi: 10.1038/nature04979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shiraki T., Kondo S., Katayama S., Waki K., Kasukawa T., Kawaji H., Kodzius R., Watahiki A., Nakamura M., Arakawa T., Kondo S., Katayama S., Waki K., Kasukawa T., Kawaji H., Kodzius R., Watahiki A., Nakamura M., Arakawa T., Katayama S., Waki K., Kasukawa T., Kawaji H., Kodzius R., Watahiki A., Nakamura M., Arakawa T., Waki K., Kasukawa T., Kawaji H., Kodzius R., Watahiki A., Nakamura M., Arakawa T., Kasukawa T., Kawaji H., Kodzius R., Watahiki A., Nakamura M., Arakawa T., Kawaji H., Kodzius R., Watahiki A., Nakamura M., Arakawa T., Kodzius R., Watahiki A., Nakamura M., Arakawa T., Watahiki A., Nakamura M., Arakawa T., Nakamura M., Arakawa T., Arakawa T., et al. Cap analysis gene expression for high-throughput analysis of transcriptional starting point and identification of promoter usage. Proc. Natl. Acad. Sci. 2003;100:15776–15781. doi: 10.1073/pnas.2136655100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smale S.T., Baltimore D., Baltimore D. The “initiator” as a transcription control element. Cell. 1989;57:103–113. doi: 10.1016/0092-8674(89)90176-1. [DOI] [PubMed] [Google Scholar]
- Smale S.T., Kadonaga J.T., Kadonaga J.T. The RNA polymerase II core promoter. Annu. Rev. Biochem. 2003;72:449–479. doi: 10.1146/annurev.biochem.72.121801.161520. [DOI] [PubMed] [Google Scholar]
- Smale S.T., Schmidt M.C., Berk A.J., Baltimore D., Schmidt M.C., Berk A.J., Baltimore D., Berk A.J., Baltimore D., Baltimore D. Transcriptional activation by Sp1 as directed through TATA or initiator: Specific requirement for mammalian transcription factor IID. Proc. Natl. Acad. Sci. 1990;87:4509–4513. doi: 10.1073/pnas.87.12.4509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Solovyev V., Kosarev P., Seledsov I., Vorobyev D., Kosarev P., Seledsov I., Vorobyev D., Seledsov I., Vorobyev D., Vorobyev D. Automatic annotation of eukaryotic genes, pseudogenes and promoters. Genome Biol. 2006;7:S1–S10. doi: 10.1186/gb-2006-7-S1-S10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suzuki Y., Taira H., Tsunoda T., Mizushima-Sugano J., Sese J., Hata H., Ota T., Isogai T., Tanaka T., Morishita S., Taira H., Tsunoda T., Mizushima-Sugano J., Sese J., Hata H., Ota T., Isogai T., Tanaka T., Morishita S., Tsunoda T., Mizushima-Sugano J., Sese J., Hata H., Ota T., Isogai T., Tanaka T., Morishita S., Mizushima-Sugano J., Sese J., Hata H., Ota T., Isogai T., Tanaka T., Morishita S., Sese J., Hata H., Ota T., Isogai T., Tanaka T., Morishita S., Hata H., Ota T., Isogai T., Tanaka T., Morishita S., Ota T., Isogai T., Tanaka T., Morishita S., Isogai T., Tanaka T., Morishita S., Tanaka T., Morishita S., Morishita S., et al. Diverse transcriptional initiation revealed by fine, large-scale mapping of mRNA start sites. EMBO Rep. 2001;2:388–393. doi: 10.1093/embo-reports/kve085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suzuki Y., Yamashita R., Sugano S., Nakai K., Yamashita R., Sugano S., Nakai K., Sugano S., Nakai K., Nakai K. DBTSS, DataBase of Transcriptional Start Sites: Progress report 2004. Nucleic Acids Res. 2004;32:D78–D81. doi: 10.1093/nar/gkh076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor T.D., Noguchi H., Totoki Y., Toyoda A., Kuroki Y., Dewar K., Lloyd C., Itoh T., Takeda T., Kim D.W., Noguchi H., Totoki Y., Toyoda A., Kuroki Y., Dewar K., Lloyd C., Itoh T., Takeda T., Kim D.W., Totoki Y., Toyoda A., Kuroki Y., Dewar K., Lloyd C., Itoh T., Takeda T., Kim D.W., Toyoda A., Kuroki Y., Dewar K., Lloyd C., Itoh T., Takeda T., Kim D.W., Kuroki Y., Dewar K., Lloyd C., Itoh T., Takeda T., Kim D.W., Dewar K., Lloyd C., Itoh T., Takeda T., Kim D.W., Lloyd C., Itoh T., Takeda T., Kim D.W., Itoh T., Takeda T., Kim D.W., Takeda T., Kim D.W., Kim D.W., et al. Human chromosome 11 DNA sequence and analysis including novel gene identification. Nature. 2006;440:497–500. doi: 10.1038/nature04632. [DOI] [PubMed] [Google Scholar]
- Thomas M.C., Chiang C.M., Chiang C.M. The general transcription machinery and general cofactors. Crit. Rev. Biochem. Mol. Biol. 2006;41:105–178. doi: 10.1080/10409230600648736. [DOI] [PubMed] [Google Scholar]
- Tokunaga K., Hirose S., Suzuki Y., Hirose S., Suzuki Y., Suzuki Y. In monkey COS cells only the TATA box and the cap site region are required for faithful and efficient initiation of the fibroin gene transcription. Nucleic Acids Res. 1984;12:1543–1558. doi: 10.1093/nar/12.3.1543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waterman M.S., Eggert M., Lander E., Eggert M., Lander E., Lander E. Parametric sequence comparisons. Proc. Natl. Acad. Sci. 1992;89:6090–6093. doi: 10.1073/pnas.89.13.6090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Werner T. The state of the art of mammalian promoter recognition. Brief. Bioinform. 2003;4:22–30. doi: 10.1093/bib/4.1.22. [DOI] [PubMed] [Google Scholar]
- Xi H., Yu Y., Fu Y., Foley J., Halees A., Weng Z., Yu Y., Fu Y., Foley J., Halees A., Weng Z., Fu Y., Foley J., Halees A., Weng Z., Foley J., Halees A., Weng Z., Halees A., Weng Z., Weng Z. Analysis of overrepresented motifs in human core promoters reveals dual regulatory roles of YY1. Genome Res. 2007;17:798–806. doi: 10.1101/gr.5754707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamashita R., Suzuki Y., Wakaguri H., Tsuritani K., Nakai K., Sugano S., Suzuki Y., Wakaguri H., Tsuritani K., Nakai K., Sugano S., Wakaguri H., Tsuritani K., Nakai K., Sugano S., Tsuritani K., Nakai K., Sugano S., Nakai K., Sugano S., Sugano S. DBTSS: DataBase of Human Transcription Start Sites, progress report 2006. Nucleic Acids Res. 2006;34:D86–D89. doi: 10.1093/nar/gkj129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao X., Xuan Z., Zhang M.Q., Xuan Z., Zhang M.Q., Zhang M.Q. Boosting with stumps for predicting transcription start sites. Genome Biol. 2007;8:R17. doi: 10.1186/gb-2007-8-2-r17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu Q., Dabi T., Lamb C., Dabi T., Lamb C., Lamb C. TATA box and initiator functions in the accurate transcription of a plant minimal promoter in vitro. Plant Cell. 1995;7:1681–1689. doi: 10.1105/tpc.7.10.1681. [DOI] [PMC free article] [PubMed] [Google Scholar]