Abstract
The rate-limiting step for nucleotide incorporation in the pre-steady state for most nucleic acid polymerases is thought to be a conformational change. As a result, very little information is available on the role of active-site residues in the chemistry of nucleotidyl transfer. For the poliovirus RNA-dependent RNA polymerase (3Dpol), chemistry is partially (Mg2+) or completely (Mn2+) rate limiting. Here we show that nucleotidyl transfer depends on two ionizable groups with pKa values of 7.0 or 8.2 and 10.5, depending upon the divalent cation used in the reaction. A solvent deuterium isotope effect of three to seven was observed on the rate constant for nucleotide incorporation in the pre-steady state; none was observed in the steady state. Proton-inventory experiments were consistent with two protons being transferred during the rate-limiting transition state of the reaction, suggesting that both deprotonation of the 3′-hydroxyl nucleophile and protonation of the pyrophosphate leaving group occur in the transition state for phosphodiester bond formation. Importantly, two proton transfers occur in the transition state for nucleotidyl-transfer reactions catalyzed by RB69 DNA-dependent DNA polymerase, T7 DNA-dependent RNA polymerase and HIV reverse transcriptase. Interpretation of these data in the context of known polymerase structures suggests the existence of a general base for deprotonation of the 3′-OH nucleophile, although use of a water molecule cannot be ruled out conclusively, and a general acid for protonation of the pyrophosphate leaving group in all nucleic acid polymerases. These data imply an associative-like transition-state structure.
Keywords: general-acid–base catalysis, phosphoryl transfer, two-metal-ion mechanism
Nucleic acid polymerases are essential for the maintenance and expression of the genomes of all organisms. All classes of polymerases use the same five-step kinetic scheme for nucleotide incorporation (1–6). The kinetic mechanism for the RNA-dependent RNA polymerase (RdRp1) from poliovirus (3Dpol) is shown in Scheme 1. One of the advantages of this system is that once 3Dpol assembles onto the primer–template substrate, this complex has a half-life of >2 h (7), greatly simplifying kinetic analysis. In step one, the enzyme–nucleic acid complex (ERn) binds the nucleoside triphosphate forming a ternary complex (ERnNTP). Step two involves a conformational change (*ERnNTP) that orients the triphosphate for catalysis. In step three, nucleotidyl transfer occurs (*ERn+1PPi), followed by a second conformational-change step (ERn+1PPi) and pyrophosphate release (ERn+1).
Scheme 1.
Kinetic mechanism for 3Dpol-catalyzed nucleotide incorporation. See text for details.
Although the sequence of events occurring during the nucleotide-addition cycle is identical for all polymerases, the rate-limiting step appears to be different. In most cases, the first conformational-change step (step two) is rate-limiting (2, 8, 9). In one, chemistry (step three) is rate-limiting (10), and in some (e.g., T4 and RB69 DNA polymerases), the rate-limiting step has not been established. For 3Dpol, both steps two and three are rate limiting when Mg2+ is used as the divalent cation cofactor, and step three is rate limiting when Mn2+ is used (1, 11). Therefore, the 3Dpol system provides a unique opportunity to interrogate the chemistry of polymerase catalyzed nucleotidyl transfer by using a nucleotide incorporation assay.
A two-metal ion mechanism has been proposed for polymerase-catalyzed nucleotidyl transfer reactions (12–14). In this mechanism (Fig. 1A), metal A increases the nucleophilicity of the primer 3′-OH by lowering its pKa value, metals A and B stabilize the oxyanion that forms in the pentacovalent transition state, and metal B may facilitate pyrophosphate release (13). During nucleotidyl transfer, the proton from the 3′-OH of the primer (Ha in Fig. 1B) must be removed. It is not known whether the pyrophosphate leaving group must be protonated (Hb in Fig. 1B) as the pKa value on the enzyme is not known and could range from 7.0 to 9.0 based on solution studies (15–17). Whether active-site residues function as acceptor or donor for these key proton-transfer reactions is not known. We report two proton transfer reactions during polymerase-catalyzed nucleotide incorporation. Our data provide evidence for use of a general acid in polymerase-catalyzed nucleotidyl-transfer reactions; the use of a general base is also suggested, but specific base catalysis cannot be ruled out at this time.
Fig. 1.
Polymerase-catalyzed nucleotidyl transfer. (A) Two-metal-ion mechanism. The nucleoside triphosphate enters the active site with a divalent cation (Mg2+, metal B). This metal is coordinated by the β- and γ-phosphates of the nucleotide, an Asp residue located in structural motif A of all polymerases, and likely water molecules (indicated as oxygen ligands to metal without specific designation). Metal B orients the triphosphate in the active site and may contribute to charge neutralization during catalysis. Once the nucleotide is in place, the second divalent cation binds (Mg2+, metal A). Metal A is coordinated by the 3′-OH, the α-phosphate, as well as Asp residues of structural motifs A and C. Metal A lowers the pKa of the 3′-OH (denoted as Ha) facilitating catalysis at physiological pH. Adapted from refs. 12 and 13. Coordinating Asp residues from 3Dpol are indicated (12). (B) Proton transfer reactions. During the nucleotidyl transfer reaction, two proton-transfer reactions may occur. The proton from the 3′-OH nucleophile (Ha) must be removed; a proton may be donated to the pyrophosphate leaving group (Hb).
Results
Two Ionizable Groups Are Required for RdRp-Catalyzed Nucleotidyl Transfer.
Because chemistry is at least partially rate limiting for 3Dpol-catalyzed nucleotide incorporation, we reasoned that it should be possible to obtain insight into the proton transfers occurring during the rate-limiting transition state by evaluating the pH dependence of the reaction. To maximize the amount of kinetic data obtained, we developed and validated a stopped-flow fluorescence assay for 3Dpol that employs an RNA template containing 2-aminopurine [supporting information (SI) Figs. 7 and 8]. To vary the pH of the reaction without varying the ionic strength, we chose the MTCN and MHCN buffer systems (18). The buffers were comparable, yielding KD,app and kpol values of 200 ± 20 μM and 50 ± 10 s−1, respectively, at pH 7.5 (SI Table 2). The higher KD,app value for ATP relative to previous buffer systems used was caused by the increased ionic strength of the MTCN and MHCN buffers (data not shown).
The KD,app and kpol values for nucleotide incorporation were measured at different pH values in Mg2+ or Mn2+ (SI Table 3). Experiments were limited to pH 10 in Mg2+ and pH 9 in Mn2+ due to complications of metal hydroxide precipitation at higher pH values. Values for kpol were plotted as a function of pH (Fig. 2). In Mg2+, a bell-shaped curve was observed, indicative of two ionizable groups. The data were fit to Eq. 3, yielding pKa values of 7.0 ± 0.1 and 10.5 ± 0.1.
Fig. 2.
Two ionizable groups are required for nucleotidyl transfer. Values for kpol were obtained for AMP incorporation into S/S-+1 using the stopped-flow assay (see SI Text) in 5 mM MgCl2 (A) or 5 mM MnCl2 (B). pH values >10 in Mg2+ and 9 in Mn2+ caused precipitation. The solid lines show the fit of the data to Eq. 3 for Mg2+, yielding pKa values of 7.0 ± 0.1 and 10.5 ± 0.1 and to Eq. 4 for Mn2+, yielding a pKa value of 8.2 ± 0.1. The dashed line in panel B shows the predicted curve should an ionizable group with a pKa of 10.5 exist in Mn2+.
In Mn2+, a similar pH dependence was observed for the acidic arm of the profile, but with a shift in pKa of about one pH unit to 8.2 ± 0.1. These data fit well to a single ionization model (Eq. 4). However, we could not rule out a two-ionization model in Mn2+. The pH rate profile that would be observed with pKa values of 8.2 and 10.5 is shown in Fig. 2B (dashed line). Data above pH 9 would be required to distinguish between the one- and two-ionization models.
Rate Limiting Steps as a Function of pH.
To determine whether rate-limiting steps were changing as a function of pH, we evaluated the phosphorothioate (thio) effect over the pH range evaluated above (SI Table 4). For 3Dpol, chemistry is partially rate limiting in Mg2+ at pH 7.5 (1). Under these conditions, the observed thio effect was 3 ± 0.3 (SI Table 4). At pH values <7.5, chemistry was clearly at least partially rate limiting as the value for the thio effect either did not change (pH 7.0) or increased (pH 6.0) (SI Table 4). A thio effect was also observed at pH values of 8.0 and 9.0; however, none was observed at pH 10 (SI Table 4). Interestingly, the decrease in the value of the thio effect above pH 7.5 was due to a specific increase in the observed rate constant for AMPαS incorporation without any significant effect on that for AMP incorporation (SI Table 4). In Mn2+ at pH 7.5, chemistry is exclusively rate limiting (11). From pH 6.0 to 9.0, the thio effect ranged from 7 to 5 (SI Table 4), consistent with chemistry remaining kinetically significant over this pH range.
Solvent Deuterium Isotope Effect as a Probe for Rate-Limiting Steps During Nucleotide Incorporation.
Because it was difficult to interpret the loss of the thio effect in Mg2+ at pH 10.0, we turned to the solvent deuterium isotope effect. Indeed, if proton transfers are occurring during the rate-limiting steps measured by our nucleotide incorporation assay, then an isotope effect should be apparent (19). In Mg2+ at pH 7.5, an isotope effect of 3 ± 0.5 was observed for AMP incorporation in the pre-steady-state (Fig. 3A). In Mn2+ at pH 7.5, an isotope effect of 7 ± 2 was observed (Fig. 3B). Essentially identical values were obtained by using the quench-flow instrument (SI Fig. 9A). The dependence of the magnitude of the isotope effect on the divalent cation used was consistent with previous observations that chemistry is partially rate limiting in Mg2+ but solely rate limiting in Mn2+ (1, 11). However, to rule out conformational perturbations as the cause of the observed isotope effects, AMP incorporation in the steady state was evaluated.
Fig. 3.
A solvent deuterium isotope effect on the kinetics of nucleotide incorporation in the pre-steady-state. Pre-steady-state incorporation of AMP into S/S-+1 in H2O (filled circles) or D2O (filled squares) in Mg2+ (A) or Mn2+ (B). The solid line is the fit of the data to Eq. 1, yielding rate constants, kobs, in Mg2+ of 30 ± 4 s−1, and 10 ± 1 s−1 for H2O and D2O, respectively; and of 10 ± 1 s−1 and 1.4 ± 0.3 s−1 in Mn2+. Steady state incorporation of AMP into S/S-+1 in H2O (filled circles) or D2O (filled squares) in Mg2+ (C) or Mn2+ (D). The lines are the fit of the data to a line, yielding rates in Mg2+ of 3.4 × 10−4 ± 1 × 10−5 μM s−1 and 2.9 × 10−4 ± 3 × 10−5 μM s−1 in H2O and D2O, respectively; and of 0.5 ± 0.1 μM s−1 and 0.3 ± 0.1 μM s−1 in Mn2+.
The rate-limiting step in the steady state is dissociation of enzyme from the primer–template substrate (7). An isotope effect on this step would not be expected. As shown in Fig. 3 C and D, an isotope effect was not observed. We conclude that the solvent deuterium isotope effect is a useful probe for chemistry as a rate-limiting step during nucleotide incorporation.
Evaluation of the pH dependence of the solvent deuterium isotope effect in Mg2+ showed values between 2 and 3 from pH 7.5 to 10.0 (SI Table 4). Therefore, chemistry is partially rate limiting over the entire pH range evaluated.
Two Proton-Transfer Reactions in the Rate-Limiting Transition State for RdRp-Catalyzed Nucleotidyl Transfer.
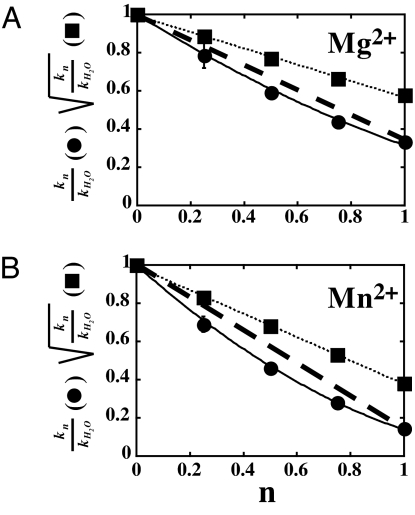
The existence of a solvent deuterium isotope effect on the rate constant for nucleotide incorporation permits quantitation of the number of protons transferred in the rate-limiting transition state (proton inventory) (19). In this experiment, the observed rate constant for nucleotide incorporation (kn) is measured in reactions containing different mole fractions of D2O (n). A plot of the quotient kn/kH2O (kH2O is the observed rate constant in H2O) as a function of n will fall on the line defined by kH2O/kH2O and k100%D2O/kH2O if a single proton is transferred. The data will fit to a second-order polynomial if two protons are transferred, to a third order polynomial if three protons are transferred, and so on. We performed a proton-inventory experiment for AMP incorporation by 3Dpol in Mg2+ (Fig. 4A) and in Mn2+ (Fig. 4B). In neither case did the data fall on the line (dashed lines in Fig. 4) that would define a single proton transfer (Eq. 6). However, the data fit well to a second-order polynomial, the Gross–Butler equation (Eq. 5) for two-proton transfers (solid lines in Fig. 4). A plot of the square root of the ratio of rate constants as a function of mole fraction was linear (dotted lines in Fig. 4), providing additional evidence for the quadratic nature of the data. Based upon these data, we conclude that two proton transfer reactions occur in the rate-limiting transition state for phosphodiester bond formation catalyzed by the poliovirus RdRp.
Fig. 4.
Two protons are transferred during nucleotidyl transfer. Proton inventory was performed in Mg2+ (A) or Mn2+ (B) as described in detail in SI Text. kn is the observed rate constant for nucleotide incorporation at a particular mole fraction of D2O. kH2O is the observed rate constant for nucleotide incorporation in H2O. n is the mole fraction of D2O. Values for kn/kH2O (filled circles) or the square root of kn/kH2O (filled squares) were plotted as a function of n. The solid lines represent the fit of the data to a two-proton-transfer model (Eq. 5) and the dashed lines represent the predicted line for a one-proton-transfer model (Eq. 6). The dotted lines represent the fit of the data to a line. Each data point represents the average of two to three independent experiments. The standard deviation was <10% in all cases.
Two Proton-Transfer Reactions in the Rate-Limiting Transition State for Nucleotidyl Transfer of Other Classes of Nucleic Acid Polymerases.
To determine whether the conclusions reached here for the RdRp applied to other classes of nucleic acid polymerases, we performed similar experiments with RB69 DdDp, T7 DdRp, and HIV RT. In all cases, a solvent deuterium isotope effect was observed (Fig. 5A) that ranged from two to five (Table 1). The magnitude of the effect was verified for RB69 DNA polymerase by using a quench-flow instrument (Fig. 9B). Importantly, proton-inventory experiments fit well to a two-proton model for these polymerases (Fig. 5B and Table 1). We conclude that two proton transfer reactions occur in the rate limiting transition state for nucleotidyl transfer catalyzed by all classes of nucleic acid polymerases.
Fig. 5.
Two protons are transferred during phosphodiester bond formation catalyzed by all polymerases. (A) Solvent deuterium isotope effect for other polymerases: RB69 DdDp (i), T7 DdRp (ii), and HIV RT (iii). Pre-steady-state rate constants for nucleotide incorporation were determined for all polymerases in H2O (filled circles) or D2O (filled squares) as described in detail in SI Text. The solid lines are the fits of the data to Eq. 1. The rate constants were: 240 ± 25 s−1 and 60 ± 6 s−1 in H2O and D2O, respectively, for RB69 DdDp; 40 ± 5 s−1 and 8 ± 1 s−1 in H2O and D2O, respectively, for T7 DdRp; 65 ± 5 s−1 and 30 ± 2 s−1 in H2O and D2O, respectively, for HIV RT. (B) Proton inventory for other polymerases: RB69 DdDp (i), T7 DdRp (ii), and HIV RT (iii). Experiments were performed as described in SI Text. Values for kn/kH2O (filled circles) or the square root of kn/kH2O (filled squares) were plotted as a function of n. The solid lines represent the fit of the data to a two-proton-transfer model (Eq. 5) and the dashed lines represent the predicted line for a one-proton-transfer model (Eq. 6). The dotted lines represent the fit of the data to a line. In all cases, a two-proton-transfer model fit the data best. Each data point represents the average of two to three independent experiments. The standard deviation was <10% in all cases.
Table 1.
Solvent deuterium isotope effect and two proton transfer reactions are observed during nucleotidyl transfer by all polymerases
| Enzyme | D2O effect | Proton inventory |
|---|---|---|
| PV RdRp | 3 ± 0.5 | 2 |
| RB69 DdDp | 4 ± 1 | 2 |
| T7 DdRp | 5 ± 1 | 2 |
| HIV RT | 2 ± 0.5 | 2 |
Discussion
It is well accepted that all nucleic acid polymerases employ a two-metal-ion mechanism (12, 13) as structural studies have revealed at least two divalent cations in the active site of polymerases poised for or undergoing catalysis (20–22). Divalent cations can clearly facilitate activation of the 3′-OH for nucleophilic attack under physiological conditions (pH 7.5) and can balance the negative charge that develops during formation of the pentavalent, phosphorane transition state. However, implicit in the formation and collapse of the proposed transition state for nucleotidyl transfer is the potential requirement for two proton transfer reactions: one from the 3′-OH nucleophile and one to the PPi leaving group (Fig. 1B). It should be noted that the protonation state of PPi during catalysis has been essentially ignored during most discussions of nucleotidyl transfer (13). Current dogma is that side chains at polymerase active sites do not participate in the chemistry of nucleotidyl transfer other than by serving as ligands for the two essential metal ions (23, 24), implying that water must serve as the proton acceptor and donor during nucleotidyl transfer. However, if this were the case, then one might expect these critical water molecules to appear in all complexes poised for or undergoing catalysis, which is not observed. The absence of these key water molecules could reflect the fact that most of these complexes have been solved by employing substrate and/or cofactor mimics: 3′-deoxy-terminated primers, nonhydrolyzable nucleotide analogues, and/or catalytically incompetent divalent cations such as Ca2+ (21, 22, 25–27).
Interrogation of the chemical mechanism for nucleotidyl transfer catalyzed by DNA polymerases has been discouraged by the general belief that a conformational change is completely rate limiting for nucleotide incorporation, a belief that has relied on interpreting the magnitude of the thio effect, a highly controversial parameter (28–30). Our studies of the RdRp from poliovirus, however, have shown that chemistry is at least partially rate limiting for nucleotide incorporation in Mg2+ and completely rate limiting in Mn2+. Therefore, this system permits interrogation of the chemical mechanism by employing a nucleotide incorporation assay.
Evaluation of the pH dependence of PV polymerase-catalyzed nucleotide incorporation in Mg2+ revealed a dependence of the reaction on two ionizable groups with apparent pKa values of 7.0 and 10.5 (Fig. 2A). Because a conformational change is partially rate limiting in Mg2+ (1), these values may not reflect true pKa values (31), preventing unambiguous assignment of these pKa values to specific proton-transfer reactions. In Mn2+, however, chemistry is completely rate limiting so the pKa value of 8.2 observed here (Fig. 2B) is likely a true pKa value for proton transfer from the 3′-OH to its acceptor. This pKa reflects a single ionization event as a plot of the logkobs as a function of pH yields a line with a slope of ≈1 (data not shown). The observed pKa value for the acidic limb of the pH rate profile, which likely contains some component related to 3′-OH activation, changed not only in response to the divalent cation used, but also in response to the nucleotide used (ATPαS or ATP) when Mg2+ was the divalent cation cofactor (compare Fig. 2B and SI Table 4). This observation is consistent with this pKa value measured in Mg2+ reflecting ionizations required for both a conformational change and chemistry. Because reactions employing ATPαS should have chemistry more rate limiting, the pKa value measured here (≈8.0, SI Table 4) may be a true pKa as it matches that observed in Mn2+.
The solvent deuterium isotope effect is a useful probe for chemistry in the rate-limiting step for nucleotide incorporation by the RdRp (Fig. 3 and SI Table 4). The observed values for the solvent deuterium isotope effect ranged from three in Mg2+ at pH 7.5 (Fig. 3A), where chemistry is only partially rate limiting (1), to seven in Mn2+ at pH 7.5 (Fig. 3B), where chemistry is completely rate limiting (11). No significant isotope effect was measured in steady state kinetic assays in the presence of either divalent cation (Fig. 3 C and D), consistent with the rate constant for polymerase-product dissociation being measured under these conditions (7). Application of the solvent deuterium isotope effect to other polymerase systems (Fig. 5A) revealed chemistry as partially rate limiting for nucleotide incorporation catalyzed by RB69 DdDp, T7 DdRp, and HIV RT and validated the solvent deuterium isotope effect as a useful mechanistic probe of rate-limiting steps for all polymerases tested (Table 1).
The observation of a solvent deuterium isotope effect permitted the quantification of the number of proton-transfer reactions occurring during the rate-limiting transition state for nucleotide incorporation catalyzed by the RdRp (Fig. 4) and other polymerases as well (Fig. 5B). In all cases, two proton-transfer reactions were observed (Table 1). This observation would suggest that conversion of the 3′-OH to the 3′-O− does not occur as a discrete step before attack on the α-phosphorous of the bound nucleotide and provides the first evidence that the PPi leaving group does, indeed, leave in a protonated form.
A solvent deuterium isotope effect of seven was observed for the RdRp under conditions in which chemistry is entirely rate limiting for nucleotide incorporation (Fig. 3), consistent with both protons being transferred simultaneously in the rate-limiting transition state. Efficient proton transfer would necessitate a suitable proton acceptor and donor. As discussed above, structural studies have not identified conserved water molecules to serve this function. We suggest that a general base and a general acid are used in nucleotidyl-transfer reactions catalyzed by all polymerases (Fig. 6). Specific base catalysis cannot be ruled out.
Fig. 6.
A general base and a general acid in polymerase-catalyzed nucleotidyl transfer reactions? The data are consistent with a model in which activation of the nucleophile and protonation of the leaving group occur coordinately in the transition state. The absence of conserved waters to serve as acceptor or donor for these proton-transfer reactions lead us to propose that a residue on the enzyme accepts the proton from the 3′-OH (B) and that a residue on the enzyme donates a proton to the PPi leaving group (A). If this is the case, then an associative-like transition state structure would be expected.
Over a decade ago, Pelletier and colleagues proposed the use of a general base for the nucleotidyl-transfer reaction catalyzed by DNA polymerase beta (polβ) (25). This proposal initiated a debate that has yet to be settled (32). In particular, Asp-256 of polβ is in a position relative to the sugar to accept the proton from the 3′-OH (25). The Pelletier structure contained dideoxy-terminated primer (25). However, more recent structures with an authentic primer terminus and a nonhydrolyzable nucleotide analogue continue to support this possibility (22).
There is a general consensus that the structural homologue of polβ Asp-256 in other systems is the evolutionarily conserved Asp residue of motif C (SI Table 5) (33). In many polymerase structures, this motif C residue is often found serving as a ligand for one or both metals (21, 26, 34, 35). This circumstance permits distance arguments to be used against this residue serving as a general base (32). However, in structures of a Bacillus stearothermophilus DNA polymerase I fragment (BF) undergoing catalysis, this motif C residue interacts with the primer 3′-OH after nucleotide binding but before binding of the second metal ion (metal A) (20). In addition, computational modeling of the nucleotidyl transfer reaction catalyzed by the T7 DdDp has suggested that the conserved motif C residue, Asp-654, serves as a general base (36). For the motif C Asp to function as a general base, it must dissociate from metal A as the transition state is approached.
Structural studies have revealed a basic amino acid, in most cases a lysine, in a position to serve as a general acid (SI Table 5) (21, 26, 34, 35). This residue is located on helix O of A-family polymerases, helix P of B-family polymerases and on the loop of structural motif D of RdRps and RTs. Motif D has been in search of a function other than structural scaffolding since solution of the first RT structures (37). In all cases in which this putative general acid has been changed, the observed rate of nucleotide incorporation has been diminished substantially (38–40). Particularly noteworthy is the observation that chemistry appears to become more rate-limiting by changing the putative general acid of RB69 DNA polymerase, Lys-560, to alanine (39). The pre-steady-state burst of nucleotide incorporation observed for the wild-type enzyme was lost with the Ala-560 derivative, and there was a 250-fold reduction in the observed rate constant for nucleotide incorporation and a 2-fold increase in the observed thio effect (39). Evaluation of the pH dependence and proton inventory for these and/or related derivatives will determine whether this residue is the general acid.
In conclusion, we have used the RdRp from PV as a model to produce the first comprehensive analysis of the chemical mechanism for a nucleic acid polymerase. This system has proven to be particularly attractive because of the extremely slow (0.0001 s−1) and pH-independent nature of the rate constant for dissociation of the primer-template substrate from the enzyme (7). These studies have provided evidence for a highly symmetrical transition state with proton transfers from the 3′-OH and to PPi occurring in a coordinated fashion. Pyrophosphate protonation was not expected. All classes of polymerase appear to have a similar transition-state structure. Coordinated proton transfer reactions necessitate a well-positioned acceptor and donor. The absence of ordered water molecules in the appropriate position in all cases forces us to consider the importance of general-acid–base-facilitated catalysis by all polymerases. The use of general-acid–base catalysis by polymerases in no way refutes the two-metal-ion mechanism (12–14). Metal B has the capacity to link the formation and stability of metal-A-binding site to the nature (correct vs. incorrect) of the bound nucleotide (11, 41–43). Once metal A binds, catalysis will be initiated. The two required proton-transfer reactions would be facilitated by active-site residues. Proof of the existence and function of a general acid and/or a general base in a polymerase remains to be obtained. If our hypothesis is correct, then an associative-like mechanism is likely used by polymerases for nucleotidyl transfer.
Materials and Methods
Materials.
All materials were of the highest grade available. A complete list is given in SI Text.
Expression and Purification of Polymerases.
All polymerases: 3Dpol RdRp, RB69 DdDp, T7 DdRp and HIV RT were expressed in E. coli and purified as described previously (44–46). All details, including modifications, are provided in SI Text.
Nucleotide Incorporation Experiments.
All pre-steady-state and steady-state experiments were performed as described (1, 7, 11, 39, 47). All details, including modifications, are provided in SI Text.
Data Analysis.
Data were fit by nonlinear regression using the program KaleidaGraph (Synergy Software, Reading, PA) Equations used are provided in SI Text.
Supplementary Material
Acknowledgments
We thank Steve Benkovic, Phil Bevilacqua, Marty Bollinger, Squire Booker, and Kevin Raney for invaluable discussions throughout the course of this study and/or for critical evaluation of the manuscript. This study was supported by National Institute of Allergy and Infectious Diseases/National Institutes of Health Grant AI45818 and the Canadian Institutes of Health Research (CIHR).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS direct submission.
This article contains supporting information online at www.pnas.org/cgi/content/full/0608952104/DC1.
References
- 1.Arnold JJ, Cameron CE. Biochemistry. 2004;43:5126–5137. doi: 10.1021/bi035212y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Fiala KA, Suo Z. Biochemistry. 2004;43:2116–2125. doi: 10.1021/bi035746z. [DOI] [PubMed] [Google Scholar]
- 3.Kati WM, Johnson KA, Jerva LF, Anderson KS. J Biol Chem. 1992;267:25988–25997. [PubMed] [Google Scholar]
- 4.Kuchta RD, Mizrahi V, Benkovic PA, Johnson KA, Benkovic SJ. Biochemistry. 1987;26:8410–8417. doi: 10.1021/bi00399a057. [DOI] [PubMed] [Google Scholar]
- 5.Patel SS, Wong I, Johnson KA. Biochemistry. 1991;30:511–525. doi: 10.1021/bi00216a029. [DOI] [PubMed] [Google Scholar]
- 6.Washington MT, Prakash L, Prakash S. Cell. 2001;107:917–927. doi: 10.1016/s0092-8674(01)00613-4. [DOI] [PubMed] [Google Scholar]
- 7.Arnold JJ, Cameron CE. J Biol Chem. 2000;275:5329–5336. doi: 10.1074/jbc.275.8.5329. [DOI] [PubMed] [Google Scholar]
- 8.Rittinger K, Divita G, Goody RS. Proc Natl Acad Sci USA. 1995;92:8046–8049. doi: 10.1073/pnas.92.17.8046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Eger BT, Benkovic SJ. Biochemistry. 1992;31:9227–9236. doi: 10.1021/bi00153a016. [DOI] [PubMed] [Google Scholar]
- 10.Arndt JW, Weimin G, Zhong X, Showalter AK, Liu J, Dunlap CA, Lin Z, Paxson C, Tsai M-D, Chan MK. Biochemistry. 2001;40:5368–5375. doi: 10.1021/bi002176j. [DOI] [PubMed] [Google Scholar]
- 11.Arnold JJ, Gohara DW, Cameron CE. Biochemistry. 2004;43:5138–5148. doi: 10.1021/bi035213q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Liu J, Tsai M-D. Biochemistry. 2001;40:9014–9022. doi: 10.1021/bi010646j. [DOI] [PubMed] [Google Scholar]
- 13.Steitz TA. Curr Opin Struct Biol. 1993;3:31–38. [Google Scholar]
- 14.Bolton EC, Mildvan AS, Boeke JD. Mol Cell. 2002;9:879–889. doi: 10.1016/s1097-2765(02)00495-1. [DOI] [PubMed] [Google Scholar]
- 15.Dawson RMC, Elliot DC, Elliot WH, Jones KM. Data for Biochemical Research. Oxford: Oxford Univ Press; 1989. [Google Scholar]
- 16.Frey CM, Stuehr JE. J Am Chem Soc. 1972;94:8898–8904. doi: 10.1021/ja00780a042. [DOI] [PubMed] [Google Scholar]
- 17.Hammes GG, Morrell ML. J Am Chem Soc. 1964;86:1497–1502. [Google Scholar]
- 18.Ellis KJ, Morrison JF. Methods Enzymol. 1982;87:405–426. doi: 10.1016/s0076-6879(82)87025-0. [DOI] [PubMed] [Google Scholar]
- 19.Schowen RL, Venkatasubban KS. CRC Crit Rev Biochem. 1985;17:1–44. doi: 10.3109/10409238409110268. [DOI] [PubMed] [Google Scholar]
- 20.Johnson SJ, Taylor JS, Beese LS. Proc Natl Acad Sci USA. 2003;100:3985–3900. doi: 10.1073/pnas.0630532100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Doublie S, Tabor S, Long AM, Richardson CC, Ellenberger T. Nature. 1998;391:251–258. doi: 10.1038/34593. [DOI] [PubMed] [Google Scholar]
- 22.Batra VK, Beard WA, Shock DD, Krahn JM, Pedersen LC, Wilson SH. Structure (London) 2006;14:757–766. doi: 10.1016/j.str.2006.01.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Brautigam CA, Steitz TA. Curr Opin Struct Biol. 1998;8:54–63. doi: 10.1016/s0959-440x(98)80010-9. [DOI] [PubMed] [Google Scholar]
- 24.Steitz TA. Nature. 1998;391:231–232. doi: 10.1038/34542. [DOI] [PubMed] [Google Scholar]
- 25.Pelletier H, Sawaya MR, Kumar A, Wilson SH, Kraut J. Science. 1994;264:1891–1903. [PubMed] [Google Scholar]
- 26.Franklin MC, Wang J, Steitz TA. Cell. 2001;105:657–667. doi: 10.1016/s0092-8674(01)00367-1. [DOI] [PubMed] [Google Scholar]
- 27.Yin YW, Steitz TA. Cell. 2004;116:393–404. doi: 10.1016/s0092-8674(04)00120-5. [DOI] [PubMed] [Google Scholar]
- 28.Joyce CM, Benkovic SJ. Biochemistry. 2004;43:14317–14324. doi: 10.1021/bi048422z. [DOI] [PubMed] [Google Scholar]
- 29.Showalter AK, Tsai MD. Biochemistry. 2002;41:10571–10576. doi: 10.1021/bi026021i. [DOI] [PubMed] [Google Scholar]
- 30.Herschlag D, Piccirilli JA, Cech TR. Biochemistry. 1991;30:4844–4854. doi: 10.1021/bi00234a003. [DOI] [PubMed] [Google Scholar]
- 31.Cleland WW. Adv Enzymol Relat Areas Mol Biol. 1977;45:273–387. doi: 10.1002/9780470122907.ch4. [DOI] [PubMed] [Google Scholar]
- 32.Steitz TA, Smerdon SJ, Jager J, Joyce CM. Science. 1994;266:2022–2025. doi: 10.1126/science.7528445. [DOI] [PubMed] [Google Scholar]
- 33.Singh K, Modak MJ. Trends Biochem Sci. 1998;23:277–281. doi: 10.1016/s0968-0004(98)01250-x. [DOI] [PubMed] [Google Scholar]
- 34.Kiefer JR, Mao C, Braman JC, Beese LS. Nature. 1998;391:304–307. doi: 10.1038/34693. [DOI] [PubMed] [Google Scholar]
- 35.Li Y, Korolev S, Waksman G. EMBO J. 1998;17:7514–7525. doi: 10.1093/emboj/17.24.7514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Florian J, Goodman MF, Warshel A. J Am Chem Soc. 2003;125:8163–8177. doi: 10.1021/ja028997o. [DOI] [PubMed] [Google Scholar]
- 37.Kohlstaedt LA, Wang J, Friedman JM, Rice PA, Steitz TA. Science. 1992;256:1783–1790. doi: 10.1126/science.1377403. [DOI] [PubMed] [Google Scholar]
- 38.Osumi-Davis PA, de Aguilera MC, Woody RW, Woody AY. J Mol Biol. 1992;226:37–45. doi: 10.1016/0022-2836(92)90122-z. [DOI] [PubMed] [Google Scholar]
- 39.Yang G, Franklin M, Li J, Lin TC, Konigsberg W. Biochemistry. 2002;41:2526–2534. doi: 10.1021/bi0119924. [DOI] [PubMed] [Google Scholar]
- 40.Pandey VN, Kaushik N, Modak MJ. J Biol Chem. 1994;269:13259–13265. [PubMed] [Google Scholar]
- 41.Yang W, Lee JY, Nowotny M. Mol Cell. 2006;22:5–13. doi: 10.1016/j.molcel.2006.03.013. [DOI] [PubMed] [Google Scholar]
- 42.Gohara DW, Arnold JJ, Cameron CE. Biochemistry. 2004;43:5149–5158. doi: 10.1021/bi035429s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Tsai YC, Johnson KA. Biochemistry. 2006;45:9675–9687. doi: 10.1021/bi060993z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Gohara DW, Ha CS, Kumar S, Ghosh B, Arnold JJ, Wisniewski TJ, Cameron CE. Protein Expr Purif. 1999;17:128–138. doi: 10.1006/prep.1999.1100. [DOI] [PubMed] [Google Scholar]
- 45.Yang G, Lin T, Karam J, Konigsberg WH. Biochemistry. 1999;38:8094–8101. doi: 10.1021/bi990653w. [DOI] [PubMed] [Google Scholar]
- 46.Le Grice SF, Gruninger-Leitch F. Eur J Biochem. 1990;187:307–314. doi: 10.1111/j.1432-1033.1990.tb15306.x. [DOI] [PubMed] [Google Scholar]
- 47.Götte M, Arion D, Parniak MA, Wainberg MA. J Virol. 2000;74:3579–3585. doi: 10.1128/jvi.74.8.3579-3585.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.