Abstract
Passive H+-ion mobility within eukaryotic cells is low, due to H+-ion binding to cytoplasmic buffers. A localized intracellular acidosis can therefore persist for seconds or even minutes. Because H+-ions modulate so many biological processes, spatial intracellular pH (pHi)-regulation becomes important for coordinating cellular activity. We have investigated spatial pHi-regulation in single and paired ventricular myocytes from rat heart by inducing a localized intracellular acid-load, while confocally imaging pHi using the pH-fluorophore, carboxy-SNARF-1. We present a novel method for localizing the acid-load. This involves the intracellular photolytic uncaging of H+-ions from a membrane-permeant acid-donor, 2-nitrobenzaldehyde. The subsequent spatial pHi-changes are consistent with intracellular H+-mobility and cell-to-cell H+-permeability constants measured using more conventional acid-loading techniques. We use the method to investigate the effect of reducing pHi on intrinsic (non-CO2/HCO3− buffer-dependent) and extrinsic (CO2/HCO3− buffer-dependent) components of Hi+-mobility. We find that although both components mediate spatial regulation of pH within the cell, their ability to do so declines sharply at low pHi. Thus acidosis severely slows intracellular H+-ion movement. This can result in spatial pHi nonuniformity, particularly during the stimulation of sarcolemmal Na+-H+ exchange. Intracellular acidosis thus presents a window of vulnerability in the spatial coordination of cellular function.
INTRODUCTION
Regulation of intracellular pH (pHi) is essential for the maintenance of normal cellular function. In the mammalian heart, modest displacements of pHi from its resting level of 7.1–7.2 occur physiologically, for example during increases in cardiac workload (1,2) and during extracellular acid-base disturbances (3,4). Because of the high chemical reactivity of H+-ions, notably with intracellular proteins, such displacements affect the electrical (5) and contractile (4, 6) behavior of the heart, and must eventually be corrected via regulatory processes. Larger displacements of pHi occur during clinical disorders such as myocardial ischemia (7) where they induce severe contractile dysfunction (6,8) and arrhythmia (9).
The regulation of cardiac pHi is achieved by means of ion transport proteins, which translocate H+, OH−, and HCO3− ions across the sarcolemma. Their ability to regulate pHi depends on adequate H+-ion mobility within the cytoplasmic compartment. H+-diffusion, however, is severely restricted because of high intracellular H+-buffering (∼50,000, equivalent to an intracellular buffering capacity of ∼50 mM). Most of this buffering occurs at histidine residues on intracellular proteins that, because of their large size, exhibit low mobility. We have shown that adequate H+-mobility within ventricular myocytes is furnished by a population of lower molecular weight diffusible buffers, such as the histidyl dipeptides acetylcarnosine, acetylanserine, and homocarnosine (10). These chaperone H+-ions around the cell on a mobile buffer shuttle, thereby enabling the spatial regulation of pHi. One important feature of the shuttle is that, although it distributes H+-ions within the cell, it results in an effective Hi+-mobility (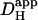 , the apparent H+-diffusion coefficient) more than two orders of magnitude lower than in unbuffered solution (11). Another important feature is that, when pHi decreases, many of the diffusible buffers approach saturation by H+-ions, causing a further fall in Hi+-mobility (12). Low Hi+-mobility can result in significant spatial nonuniformity of cytoplasmic pHi, particularly when large fluxes of acid occur across the sarcolemma (13).
, the apparent H+-diffusion coefficient) more than two orders of magnitude lower than in unbuffered solution (11). Another important feature is that, when pHi decreases, many of the diffusible buffers approach saturation by H+-ions, causing a further fall in Hi+-mobility (12). Low Hi+-mobility can result in significant spatial nonuniformity of cytoplasmic pHi, particularly when large fluxes of acid occur across the sarcolemma (13).
In addition to intrinsic buffers such as histidyl dipeptides, the major extrinsic buffer system, CO2/HCO3 (carbonic buffer), can also shuttle H+-ions spatially within a cell, particularly when catalyzed endogenously by the enzyme, carbonic anhydrase (14–16). It is not known, however, if this component of the buffer-shuttle is modulated by changes of pHi in a manner similar to that observed for the intrinsic shuttle. In this work we have therefore examined the relative roles of extrinsic and intrinsic buffer in setting Hi+-mobility in the ventricular myocyte, over a range of pHi values. This permits an assessment of their physiological importance in the spatial regulation of pHi.
To assess Hi+-mobility, a local rise of [H+]i is typically induced in one region of the cytoplasm and its spatial dissipation imaged confocally using an intracellular pH-fluorophore, such as carboxy-SNARF. Current methods for locally displacing pHi include H+ loading from an acid-filled patch-pipette (11), and local microperfusion of extracellular membrane-permeant acidic molecules such as CO2 or acetic acid (17,18). Such approaches can be technically demanding and may not be suitable for all cell-types. We have therefore tested a novel method for introducing H+-ions into a cell, by uncaging them from the membrane-permeant, proton-donor compound, 2-nitrobenzaldehyde (NBA), using ultraviolet (UV) flash-photolysis. Apart from a brief report for a neuronal preparation (19), this technique has not been applied previously in intact cells. In this work, we explore its potential in isolated ventricular myocytes. We assess the suitability of NBA for local and whole-cell intracellular proton uncaging, we estimate the photolytic efficiency of the process, and we gauge its usefulness for measuring Hi+-mobility in single cells, and cell-to-cell H+-permeability in cell-pairs. Having validated the technique, we then use it to elucidate the pHi-sensitivity of Hi+-shuttling via extrinsic and intrinsic buffer.
METHODS
Cell isolation
Cardiac myocytes were isolated from ∼300 g Sprague-Dawley rats (killed by cervical dislocation in accordance with UK Home Office guidelines) using a combination of mechanical and enzymatic (0.24 mg/ml Blendzymes III, Roche, UK) dispersion (11,16,20). Cells were stored in DMEM culture medium (Sigma, UK) at room temperature.
Solutions
HEPES-buffered normal Tyrode (NT) solution contained (in mM): NaCl (135), KCl (4.5), HEPES (20), CaCl2 (2), MgCl2 (1), glucose (10). Solution pH was adjusted to 7.4 using 4 M NaOH. CO2/bicarbonate-buffered NT contained (in mM): NaCl (120), KCl (4.5), NaHCO3 (22), CaCl2 (2), MgCl2 (1), glucose (10). Solution pH was adjusted to 7.4 by continuously bubbling with 5% CO2. Where indicated, 1 mM NBA (from 1 M stock dissolved in methanol) was included in solutions. In some experiments with coupled cell-pairs, 60 μM α-glycyrrhetinic acid (αGA) was included in superfusates to block gap junctional channels (20). In other experiments, the enzyme carbonic anhydrase was blocked with 100 μM acetazolamide (ATZ). All chemicals were obtained from Sigma.
Cell superfusion
Experiments were carried out in a 500-μl Plexiglas flow-through chamber with the base made from a thin, glass coverslip. To facilitate cell adhesion, the coverslip was coated before each experiment with 100 μl 0.01% poly-L-lysine (Sigma). After washing away poly-L-lysine, 200 μl of cells in culture medium were applied to the superfusion chamber, mixed with 1.5 μl 1.7 mM solution of an acetoxy-methyl (AM) carboxy-SNARF pH-fluorophore (Molecular Probes, Eugene, OR) in DMSO. For experiments at alkaline or resting pHi, carboxy-SNARF-1 was used (pK = 7.5), whereas at lower pHi, the recently developed analog, carboxy-SNARF-4F (pK = 6.4), was preferred (21). The physicochemical properties of the two dyes (e.g., their membrane permeability, molecular mass and chemical structure) are very similar, differing only by the pK shift in their emission spectra. After 10 min of dye-loading in darkness, cells were continuously supplied with superfusate. When required, two platinum wires along the length of the chamber were used to field-stimulate the cells.
Confocal pHi imaging
Cells were imaged using an inverted confocal microscope (TCS NT system on a DM IRBE microscope; Leica, Wetzlar, Germany) equipped with a ×63 plano-apochromat, water-immersion objective (NA 1.2) with UV correction. The carboxy-SNARF dyes were excited by the 514-nm line from an Argon laser, and fluorescence emission was measured at 580 ± 20 nm and 640 ± 20 nm (line scan speed = 400Hz). The ratio of fluorescence intensity measured at the two wavelengths was converted to pH using calibration curves obtained in separate experiments (22).
H+-uncaging from NBA
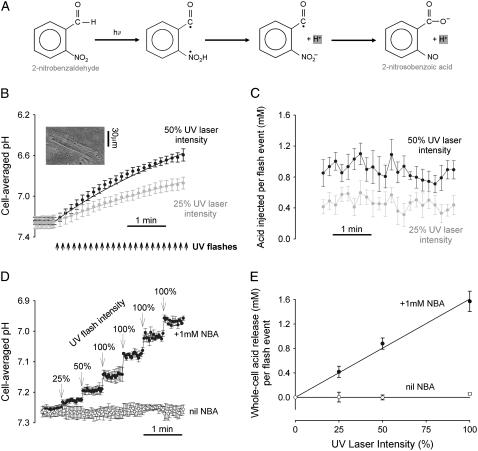
After loading with pH-fluorophore, the cells were then loaded with the H+-donor compound by including 1 mM NBA in all superfusates. This is highly membrane-permeant, superfusion typically commencing a few minutes before an experiment. Cells loaded with 1 mM NBA for 1 min produced the same magnitude of acid-uncaging as cells loaded for >3 min. When exposed to UV light-flashes at 351 nm from a 20-mW UV laser (Enterprise II Laser; Coherent, CA), NBA undergoes an intramolecular redox reaction (23) giving 2-nitrosobenzoic acid (Fig. 2 A). The pK of 2-nitrosobenzoic acid is ∼2.2 and so the product is fully dissociated in the physiological pHi range. Despite photolysis, the intracellular concentration of NBA remained constant owing to continued passive entry from the superfusate. Without electronic zoom, the ROI exposed to UV light could be as large as 150 × 150 μm (entire field of view) or as small as 5 × 5 μm (the smallest sweep length). At a pixel resolution of 256 × 256 and a line-scan speed of 400 Hz, the UV laser dwell-time per pixel was ∼10 μs. UV light intensity could be reduced by neutral-density filters to obtain the desired magnitude of intracellular acid-load. Since high-energy laser exposure tends to damage cells, two consecutive UV flashes of lower intensity, separated by 0.95 s (a flash-event), were preferred over a single, higher intensity exposure.
FIGURE 2.
H+-uncaging in whole-cell (A). The energy from UV light catalyzes the intramolecular redox between the nitryl and aldehyde group of 2-nitrobenzaldehyde, producing 2-nitrosobenzoic acid which dissociates to its anion and H+. (B) Inset shows rat myocyte superfused with HEPES-buffered NT containing 1mM NBA and 30 μM cariporide. (Main panel) repetitive exposure of entire myocyte to UV flash events at 0.11Hz (denoted by arrows) produces a cumulative acidification which was monitored in between flash-events using carboxy-SNARF fluorescence: acid-loading rate, 4.16 mM/min at 25% laser intensity (shaded circles; n = 10) and 8.14 mM/min at 50% laser intensity (solid circles; n = 10). The continuous curves show model-predictions for constant acid-injection rates into a compartment with a buffering capacity as defined in (16). (C) The amount of acid released per flash-event, calculated from the change in pHi after each flash-event multiplied by the intrinsic buffering capacity (n = 10). (D) Rat myocytes were superfused with HEPES-buffered NT containing 30 μM cariporide. In some experiments, 1 mM NBA was included in superfusates. Cells (n = 6 with NBA, n = 7 without NBA) were exposed to a UV flash-event of varying magnitude (25–100% of full power) every 30 s. Between flash events, pHi was imaged every 2.1 s. (E) The stepwise fall in pHi recorded in D was converted into a measure of acid released per flash-event (Jinj = −ΔpH × β), using values for buffering-capacity (β) measured previously (16). This has been plotted as a function of laser intensity. Data points in all panels shown as mean ± SE.
The excitation protocol could be programmed to switch automatically between Argon laser for carboxy-SNARF excitation and acquisition of pHi data, and UV laser for flash-photolysis. Due to time delays imposed by the changes in microscope optics, the shortest transition time between “acquisition mode” and “photolysis mode” was 3–4 s.
Presetting starting pHi
Superfusion with NT stabilizes pHi at 7.1–7.2. In some experiments, pHi was preset uniformly to different levels before starting an experiment. To manipulate starting pHi, cells were prepulsed (24,25) with solutions containing ammonium chloride or sodium acetate (based on NT solutions, with an appropriate reduction in [NaCl] to keep overall osmolarity constant at ∼310 mOsm/kg). After the prepulse, cells were returned to NT solutions containing no weak base or weak acid, resulting in an intracellular acidosis or alkalosis, respectively. By varying the dose of acetate (40–80 mM) or ammonium (10–30 mM) and the duration of the prepulse (4–8 min), it was possible to attain any desired pHi value in the range 6.2–7.8. To clamp the pHi to the new displaced level, measures were taken to block sarcolemmal acid/base transport pharmacologically or by ion-substitution. Na+-H+ exchange (NHE) was blocked by including 30 μM cariporide (Aventis, Germany) in superfusates (26,27). In CO2/bicarbonate-buffered superfusates, Na+-HCO3− cotransport (NBC) was 90% blocked by 10 μM S0859 (Aventis) (27); in CO2-free solutions, NBC was not active. In CO2/bicarbonate-buffered superfusates, acid-loading transporters (Cl−-HCO3− exchange and Cl−-OH− exchange) were blocked by replacing extracellular chloride salts with an equivalent concentration of gluconate salts (with an appropriate rise in total added [Ca2+] from 2 to 8.5 mM to account for the binding of Ca2+ to gluconate) (28). In CO2-free solutions, sarcolemmal H+-equivalent influx at high pHi is mediated by Cl−-OH− exchange (CHE) (25). Because this is kinetically slow (<1 mM/min), no inhibitory measures were taken in experiments that lasted up to 2 min.
Offline data processing
The confocal system produces three stacks of images: a spatial fluorescence map of the cell at 580 nm, a spatial fluorescence map at 640 nm, and the transmission image of the cell. The transmission image is used to describe the cell geometry, whereas the ratio of the fluorescence at 580 nm and 640 nm (after background offsetting) gives a measure of pHi. Raw data were processed into [H+]i time courses, averaged within rectangular ROIs (typically 15–20 μm by 15–20 μm), aligned along the length of the cell (macro written in Scion Image; Scion).
For H+-loading experiments using serial H+-ion uncaging, the mean time course of rise of [H+]i in each ROI was fitted with an algorithm for two-dimensional H+-diffusion from a constant source (defined by the UV-flash area). For single cells (16), the diffusion equation was solved over a single reflective compartment, defined by the geometrical boundary of the cell. The fitting procedure was solved using the finite element method, assuming a single value for the apparent intracellular H+-diffusion coefficient (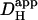 ) (29). By varying the starting level of [H+]i (see above) and restricting each best-fit to a fall in cell-averaged pHi of <0.3 pH-units, it was possible to discern the pHi-dependence of
) (29). By varying the starting level of [H+]i (see above) and restricting each best-fit to a fall in cell-averaged pHi of <0.3 pH-units, it was possible to discern the pHi-dependence of 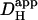 , as described in the Results section. The estimate of
, as described in the Results section. The estimate of 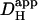 was assigned to a pHi value equal to the cell-averaged pHi at the mid-point of acid-loading. Different values for starting [H+]i were spaced as closely as 0.05 pH-units.
was assigned to a pHi value equal to the cell-averaged pHi at the mid-point of acid-loading. Different values for starting [H+]i were spaced as closely as 0.05 pH-units.
For experiments where the relaxation of a longitudinal pHi-gradient was imaged after terminating the local acid-uncaging sequence, [H+]i data were fitted to a two-dimensional reflective compartment model with a nonuniform initial condition. The entire relaxation period was used for best-fitting, and the estimate of 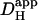 was assigned to the cell-averaged pHi at the midtime of relaxation.
was assigned to the cell-averaged pHi at the midtime of relaxation.
In the case where H+-uncaging was performed locally in a cell-pair, the two-dimensional diffusion equation was solved (20) over two reflective compartments, coupled across the junctional membrane by a passive permeation flux, described by an apparent permeability coefficient (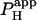 ). The boundary condition for this junctional membrane was: H+-Fluxcell1→2 =
). The boundary condition for this junctional membrane was: H+-Fluxcell1→2 = 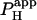 × ([H+]cell2 − [H+]cell1).
× ([H+]cell2 − [H+]cell1).
Statistical analysis of data was performed using Student's unpaired t-test or by one-factor analysis of variation. The level of significance was set to 5%. Data are presented as mean ± SE.
Measurements of cell-shortening and intracellular Ca2+
Experiments were carried out on an epifluorescence set-up built on a Nikon Diaphot microscope (Nikon, UK). Rat myocytes were AM-loaded with 10 μM of the Ca2+-indicator, Fluo-3 (Molecular Probes). During superfusion with HEPES-buffered NT, cells were electrically field-stimulated (60–70 V, 0.2-ms pulses at 1 Hz from an isolated DC stimulator). Intracellular fluorophore was excited by a Xenon lamp monochromator (Optoscan, Cairn, UK) at 488 nm and Ca2+-sensitive fluorescence >515 nm was measured with a photomultiplier tube. Cell contraction was measured simultaneously using an edge-detection device (Crescent Electronics, UT) that utilized the transmission image of the cell. Data were digitized with a CED 1401plus digitizer (Cambridge Electronic Design, UK) and recorded with Spike2 software (Cambridge Electronic Design). Ca2+ data are presented as a ratio, relative to diastolic Ca2+ (F/F0); cell-shortening has been normalized to the control value averaged over the first minute of stimulation.
RESULTS
Effect of 2-nitrobenzaldehyde on excitation-contraction coupling
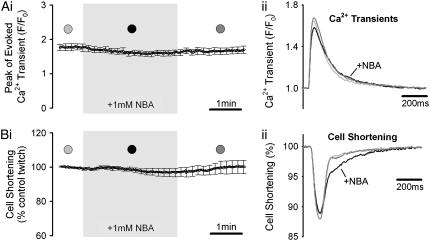
Isolated myocytes were electrically activated by field stimulation at 1 Hz. Fig. 1, Aii and Bii, show simultaneous recordings of the evoked Ca2+-transient and cell-shortening before, during, and after a 3-min exposure to 1 mM NBA. The caged H+-compound did not affect the time course or amplitude of the Cai2+-transient (Fig. 1 A), and had no influence on peak cell-shortening (Fig. 1 B), indicating that it does not disrupt excitation-contraction coupling. In 5 out of 10 cells, however, a reversible slowing of the late phase of relaxation was observed. We did not investigate this phenomenon further as it was not a consistent occurrence, and there was no other detectable effect of NBA. The slowing was most likely due to direct interference of NBA with the myofilaments or the cell's viscoelastic machinery, rather than an influence on intracellular Ca2+ dynamics, as relaxation of the Ca2+-transient was unaffected.
FIGURE 1.
Effect of 2-nitrobenzaldehyde on excitation-contraction coupling. Rat myocytes were superfused with HEPES-buffered media and field-stimulated at 1Hz. After a period of pacing (>1 min), cells were exposed to superfusates containing 1 mM NBA. The evoked Ca2+-transient (A) and cell-shortening (B) were measured simultaneously (mean ± SE; n = 10). (Ai) Peak systolic Cai2+-fluorescence is plotted versus time (peak systolic, F, normalized to diastolic Ca2+-fluorescence, F0). (Bi) Mean contraction amplitude (for each experiment, normalized to initial control contraction [averaged over 1 min]) is plotted versus time. (Aii) Superimposed time courses of Ca2+-transients from a representative experiment, taken at times indicated in panel Ai. (Bii) Superimposed time courses of cell-shortening, taken from same experiment as Aii.
When superfused with 1 mM NBA (n = 10), myocytes typically remained quiescent and rod-shaped for at least 10 min, whereas, with 5 mM NBA (n = 10), cells usually survived for no more than 5 min. At 10 mM NBA, cells rapidly developed membrane blebs and displayed hypercontracture within 1–2 min. NBA was therefore applied at 1 mM in all subsequent experiments.
Whole-cell flash-photolysis
When UV light is scanned across the entire area of a cell, pHi should decrease uniformly, provided the intracellular concentration of NBA is uniform. This assumption is likely to hold true because NBA is a membrane-permeant, low molecular-weight solute (151 Da) that is neither charged nor subject to transmembrane transport or metabolism. NBA had no effect on resting pHi until the cell was exposed to UV light (see Figs. 2 B, 4 Ai, 5 Ai, 6 A). Fig. 2 B shows data pooled from several experiments where the entire field of view encompassing a cell was exposed to UV flash-events at 0.11 Hz (indicated by the arrows), interposed by 2-s periods of pHi data-acquisition (with 2-frame averaging). Photolytic redox of extracellular NBA did not lead to accumulation of extracellular acid because uncaged protons were washed away by continuous superfusion. H+-ions uncaged within the cell, however, produced a cumulative fall of pHi of ∼0.65 pHi units within 3.5 min at 50% laser intensity (solid circles). This acid-load was not extruded, as the cell was superfused with a CO2/HCO3−-free solution (to inhibit NBC) containing 30 μM cariporide (to inhibit NHE).
FIGURE 4.
Local H+-uncaging in an isolated myocyte (Ai). Protocol 1: rat myocyte, superfused with HEPES-buffered Tyrode containing 1 mM NBA and 30 μM cariporide. Repetitive flash-events (0.11 Hz) were applied to a 5 × 5μm ROI positioned at the left end of the cell. [H+] was averaged in three ROIs every 2.1 s (colored circles, coded to match the colored ROIs shown in schematic diagram at top); points have been interpolated to form continuous time courses. Superimposed black traces show best-fit solutions to a constant-source diffusion equation with a 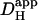 of 10 × 10−7 cm2/s. Inset shows a calibrated pH-map during acid-loading, taken at the time indicated. (Aii) Data from (i) are presented (colored traces) as longitudinal [H+]-profiles at consecutive times, together with best-fit model predictions (black lines). The shaded vertical bar indicates the position of the H+-uncaging site. (B) Protocol 2: rat myocyte, superfused with HEPES-buffered Tyrode containing 1 mM NBA and 30 μM cariporide. Six UV flash-events (0.5 Hz) were applied to a 15 × 15 μm ROI positioned toward the left end of the cell. After termination of flash sequence, the relaxation of [H+] averaged in three ROIs (traces color-coded to match ROIs shown in schematic diagram) is shown, along with superimposed best-fit model-predictions (black traces) for a
of 10 × 10−7 cm2/s. Inset shows a calibrated pH-map during acid-loading, taken at the time indicated. (Aii) Data from (i) are presented (colored traces) as longitudinal [H+]-profiles at consecutive times, together with best-fit model predictions (black lines). The shaded vertical bar indicates the position of the H+-uncaging site. (B) Protocol 2: rat myocyte, superfused with HEPES-buffered Tyrode containing 1 mM NBA and 30 μM cariporide. Six UV flash-events (0.5 Hz) were applied to a 15 × 15 μm ROI positioned toward the left end of the cell. After termination of flash sequence, the relaxation of [H+] averaged in three ROIs (traces color-coded to match ROIs shown in schematic diagram) is shown, along with superimposed best-fit model-predictions (black traces) for a 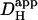 of 5.5 × 10−7 cm2/s.
of 5.5 × 10−7 cm2/s.
FIGURE 5.
Local H+-uncaging in a myocyte cell-pair (Ai). End-to-end rat myocyte cell-pair, superfused with HEPES-buffered Tyrode containing 1 mM NBA and 30 μM cariporide. Repetitive flash-events (0.11 Hz) were applied to a 5 × 5 μm ROI at the left end of the cell-pair. The color-coded time courses illustrate the cumulative rise in [H+]. The superimposed black traces show best-fit solutions to a constant-source diffusion equation with a 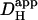 of 9.5 × 10−7 cm2/s and a
of 9.5 × 10−7 cm2/s and a 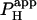 of 1.6 × 10−3 cm/s. Inset shows a calibrated pH-map during acid loading, taken at the time indicated. (Aii) Data from i are presented as longitudinal [H+]-profiles at consecutive times, together with best-fit model-predictions. The vertical solid-gray bar indicates position of the acid-release site; diagonally lined bar highlights a discontinuity in the [H+]-profile coincident with the gap junction. (B) Mean ±SE for
of 1.6 × 10−3 cm/s. Inset shows a calibrated pH-map during acid loading, taken at the time indicated. (Aii) Data from i are presented as longitudinal [H+]-profiles at consecutive times, together with best-fit model-predictions. The vertical solid-gray bar indicates position of the acid-release site; diagonally lined bar highlights a discontinuity in the [H+]-profile coincident with the gap junction. (B) Mean ±SE for 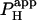 measured with (n = 6) and without (n = 7) 60 μM α-glycerrhetinic acid (αGA) in superfusates, derived from experiments like that shown in Ai. Asterisk denotes significant difference (P < 0.05).
measured with (n = 6) and without (n = 7) 60 μM α-glycerrhetinic acid (αGA) in superfusates, derived from experiments like that shown in Ai. Asterisk denotes significant difference (P < 0.05).
FIGURE 6.
Intrinsic and extrinsic components of Hi+-mobility are both pH-sensitive (A). A rat myocyte was superfused with CO2/HCO3−-buffered Tyrode containing 1 mM NBA and 30 μM cariporide. Repetitive flash-events (0.11 Hz) were applied to a 5 × 5μm ROI positioned at the left end of the cell (protocol 1). The colored circles show the rise of [H+] averaged in three ROIs (color-coded and positioned as shown in schematic diagram at top). Superimposed black traces show best-fit solutions to a constant-source diffusion equation with a 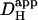 of 22 × 10−7 cm2/s. Inset at bottom shows a calibrated pH-map of the cell during acid-loading, taken at time indicated. (B) Experiments using either protocol 1 (solid triangles) or 2 (open squares) for local H+-uncaging (see text, and Fig. 3) in an isolated myocyte were performed from a range of starting pHi-values, while superfusing the cell with HEPES-buffered (blue symbols) or CO2/HCO3−-buffered (red symbols) solution. Starting pHi was preset using a weak acid/base prepulse technique (see Methods). Blue triangles, n = 4, 11, 34, 46, 98, 42, 25; blue open squares, n = 19, 22, 5; red triangles, n = 7, 10, 11, 10, 18, 37, 9, 8. The dashed line illustrates the pHi-dependence of
of 22 × 10−7 cm2/s. Inset at bottom shows a calibrated pH-map of the cell during acid-loading, taken at time indicated. (B) Experiments using either protocol 1 (solid triangles) or 2 (open squares) for local H+-uncaging (see text, and Fig. 3) in an isolated myocyte were performed from a range of starting pHi-values, while superfusing the cell with HEPES-buffered (blue symbols) or CO2/HCO3−-buffered (red symbols) solution. Starting pHi was preset using a weak acid/base prepulse technique (see Methods). Blue triangles, n = 4, 11, 34, 46, 98, 42, 25; blue open squares, n = 19, 22, 5; red triangles, n = 7, 10, 11, 10, 18, 37, 9, 8. The dashed line illustrates the pHi-dependence of 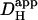 measured previously using a different technique (12). All red data-points are significantly different from the dashed line (z-test, 95% confidence level). In some experiments, 100 μM ATZ was added to CO2/HCO3− superfusates to block carbonic anhydrase (green triangles, n = 17,19). These data points were not significantly different from the dashed line (z-test, 95% confidence level). (C) The change in
measured previously using a different technique (12). All red data-points are significantly different from the dashed line (z-test, 95% confidence level). In some experiments, 100 μM ATZ was added to CO2/HCO3− superfusates to block carbonic anhydrase (green triangles, n = 17,19). These data points were not significantly different from the dashed line (z-test, 95% confidence level). (C) The change in 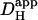 in the presence of CO2/HCO3− buffer is plotted as a function of pHi (red symbols, without ATZ; green symbols, with ATZ). The dashed red line represents the difference between the best-fit sigmoidal curve to the
in the presence of CO2/HCO3− buffer is plotted as a function of pHi (red symbols, without ATZ; green symbols, with ATZ). The dashed red line represents the difference between the best-fit sigmoidal curve to the 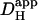 data in the presence and absence of carbonic buffer. (D) The fraction of
data in the presence and absence of carbonic buffer. (D) The fraction of 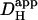 that is measured in CO2/HCO3−-buffered solution (in the absence of ATZ) that is attributable to carbonic (i.e., nonintrinsic) buffering. This fraction is close to 0.3 over the entire pHi-range studied. Data points in panels B and C show mean ± SE.
that is measured in CO2/HCO3−-buffered solution (in the absence of ATZ) that is attributable to carbonic (i.e., nonintrinsic) buffering. This fraction is close to 0.3 over the entire pHi-range studied. Data points in panels B and C show mean ± SE.
The change of pHi (ΔpHi) plotted for each flash-event in Fig. 2 B, when multiplied by an appropriate value of buffering capacity (16), reveals the quantum of acid uncaged (Jq). Fig. 2 C plots Jq as a function of time, for the successive flash-events illustrated in Fig. 2 B. Jq is relatively constant, indicating that the quantum was independent of the level of pHi. Note that the cumulative fall of pHi plotted in Fig. 2 B is curved rather than linear, because pH is a logarithmic function of [H+], and intrinsic buffering capacity increases as pHi falls (16,25). Thus, even though H+-release per flash-event is constant, the resulting ΔpHi is increasingly attenuated as pHi falls.
The magnitude of the cumulative acid-load depended on the intensity of UV light, which could be varied by means of neutral density filters. Halving the laser intensity from 50% to 25% (by introducing a higher neutral density filter) reduced the mean acid-loading rate during the flash-sequence (Fig. 2 B, shaded circles), and halved the quantum of acid released per event (Fig. 2 C). Jq could therefore be graded experimentally.
The amplitude and time course of ΔpHi during a flash-event is shown at higher resolution in Fig. 2 D. Here, rat myocytes were exposed to flash-events of different laser intensity (once at 25%, once at 50%, and then four times at 100% intensity), each followed by a 30-s period of pHi data acquisition. The superfusates were again HEPES-buffered and contained 30 μM cariporide to inhibit sarcolemmal acid-extrusion. Each flash-event produced a rapid and sustained fall of pHi, (solid circles) whereas the whole sequence induced a series of stepwise decreases of pHi. The results therefore indicate that H+-uncaging is both rapid and irreversible. Because of the delay between UV-exposure and pHi-recording in our apparatus, we were unable to resolve the kinetics of uncaging but, in aqueous solution, it is known to occur within nanoseconds (30). Note that the flash sequence produced no change of pHi in the absence of NBA (open circles), indicating that the source of acid was indeed NBA redox. It also confirms that UV laser-light itself did not influence the fluorescent signal from the pH reporter-dye.
The constancy of pHi immediately after a flash-event indicates that acid release was uniform along the vertical axis of the cell, and also that the photolytic product, 2-nitrosobenzoic acid, does not flux significantly from the cell (if this happened, the acid-load would be dissipated). Fig. 2 E plots the mean quantum of H+-release as a function of laser intensity. This increases linearly with UV light intensity, reaching 1.6 mM acid released per event for 100% laser power. This represents a quantum yield for an individual UV flash of ∼80% (1 flash-event = 2 individual flashes separated by 0.95 s; see Methods). The absence of saturation of acid-release with increasing laser power suggests that NBA photolyzed at the flash site is replenished rapidly i.e., sarcolemmal permeation of NBA is not a rate-limiting factor for intracellular H+-uncaging.
Regional flash-photolysis: modeling H+-uncaging protocols
By confining the UV laser-scanning area to a small region of the cell, a local acidosis can be produced. This local pHi change then drives dissipative H+-fluxes that obey Fickian diffusion. Two experimental protocols were used to drive these dissipative H+-fluxes: i), the H+-load was ramped up locally in a stepwise manner using a prolonged burst of identical flash-events, and the rise of H+-ion concentration in adjacent regions was monitored between flash-events; and ii), the local H+-load was established by a shorter rapid burst of flash-events, and its subsequent dissipation upon termination of the burst was monitored. The kinetics of the dissipative H+-fluxes, whether driven during or after the acid-load, were quantified in terms of an apparent H+-diffusion coefficient, 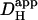 .
.
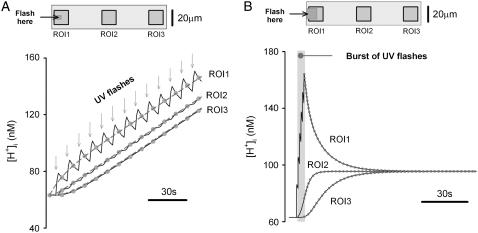
The validity of the two protocols was explored using a mathematical model, as shown in Fig. 3. In panel A, repetitive Hi+-uncaging at 0.11 Hz (Protocol 1) was simulated at the left end of a rectangular model-cell. For a given value of 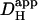 , this produces local stepwise increments in [H+]i, which start to dissipate into neighboring regions. The result is a saw-toothed rise of [H+]i averaged within an ROI positioned over the H+-uncaging region. The time course, however, becomes smoother the more distal the ROI is positioned from the release site. In actual experiments, data acquisition would normally take place at the midpoint between flash-events, as indicated by the solid circles. These points are readily fitted by a two-dimensional diffusion equation (dashed lines), taking the same value for
, this produces local stepwise increments in [H+]i, which start to dissipate into neighboring regions. The result is a saw-toothed rise of [H+]i averaged within an ROI positioned over the H+-uncaging region. The time course, however, becomes smoother the more distal the ROI is positioned from the release site. In actual experiments, data acquisition would normally take place at the midpoint between flash-events, as indicated by the solid circles. These points are readily fitted by a two-dimensional diffusion equation (dashed lines), taking the same value for 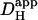 , but assuming a constant localized source of acid-injection at the release-site. We therefore used the simpler, constant-source model (16) when analyzing experimental data obtained with repetitive quantal uncaging.
, but assuming a constant localized source of acid-injection at the release-site. We therefore used the simpler, constant-source model (16) when analyzing experimental data obtained with repetitive quantal uncaging.
FIGURE 3.
Protocols for producing localized acid-loads. A computational model was used to simulate localized H+-uncaging within a rectangular model-cell (100 × 25 μm) featuring a 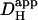 of 10−6 cm2/s. (A) Protocol 1: simulation of repetitive H+-uncaging at 0.11 Hz (denoted by arrows) in a small ROI (5 × 5 μm) positioned at the left end of the cell (see schematic diagram at top). The [H+]-rise averaged in three downstream 15 × 15 μm ROIs is plotted versus time. Solid circles denote the mid-times between flash-events. The dashed lines illustrate the solution to a constant-source diffusion equation. (B) Protocol 2: simulation of brief sequence of flash-events in a 10 × 10 μm ROI positioned at the left end of the model-cell (inset). After inducing a 150 nM longitudinal H+-gradient, flashing was stopped to allow the gradient to relax. Time courses of the rise and subsequent relaxation of [H+]i in three downstream 15 × 15 μm ROIs are plotted as the continuous curves. Solid symbols indicate the expected timing of pHi data acquisition during the relaxation phase.
of 10−6 cm2/s. (A) Protocol 1: simulation of repetitive H+-uncaging at 0.11 Hz (denoted by arrows) in a small ROI (5 × 5 μm) positioned at the left end of the cell (see schematic diagram at top). The [H+]-rise averaged in three downstream 15 × 15 μm ROIs is plotted versus time. Solid circles denote the mid-times between flash-events. The dashed lines illustrate the solution to a constant-source diffusion equation. (B) Protocol 2: simulation of brief sequence of flash-events in a 10 × 10 μm ROI positioned at the left end of the model-cell (inset). After inducing a 150 nM longitudinal H+-gradient, flashing was stopped to allow the gradient to relax. Time courses of the rise and subsequent relaxation of [H+]i in three downstream 15 × 15 μm ROIs are plotted as the continuous curves. Solid symbols indicate the expected timing of pHi data acquisition during the relaxation phase.
Fig. 3 B illustrates the results of modeling a brief burst of six flash-events and the subsequent relaxation of the pHi nonuniformity (Protocol 2). The solid symbols represent pHi at intervals, equivalent to the pH-sampling periods used during experiments (2.1 s), whereas the continuous lines are the full time courses predicted by the model. The relaxation phase can be simulated using a two-dimensional diffusion equation in a closed compartment, featuring a nonuniform initial condition given by the longitudinal pHi-profile predicted after the final flash-event.
Local H+-uncaging in isolated myocytes
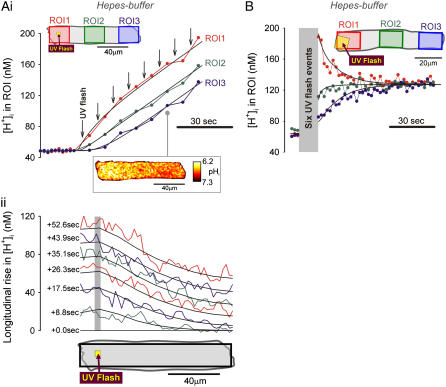
The two acid-loading protocols were applied in experiments on rat myocytes superfused with HEPES-buffered NT containing 30 μM cariporide. The myocyte illustrated schematically in Fig. 4 Ai was exposed at 0.11 Hz to flash-events over a small 5 × 5 μm ROI set toward the left end of the cell (Protocol 1). Spatial pHi data were acquired midway between flash-events, and these data points were interpolated to obtain [H+]i time courses in three ROIs, as shown in Fig. 4 Ai. The delay of ∼25 s between acidification in the proximal (red) and distal (blue) ROIs reflects a low mean value of 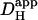 , estimated to be 10 × 10−7 cm2/s in that particular cell (curve best-fit to data is plotted in black, Fig. 4 Ai). The goodness-of-fit between the model and experimental data was confirmed by plotting the measured longitudinal elevation of [H+]i along a cell-wide ROI at different times after commencing the flash-sequence (Fig. 4 Aii), and superimposing this with model-predictions using the same mean value of
, estimated to be 10 × 10−7 cm2/s in that particular cell (curve best-fit to data is plotted in black, Fig. 4 Ai). The goodness-of-fit between the model and experimental data was confirmed by plotting the measured longitudinal elevation of [H+]i along a cell-wide ROI at different times after commencing the flash-sequence (Fig. 4 Aii), and superimposing this with model-predictions using the same mean value of 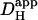 (black lines, Fig. 4 Aii).
(black lines, Fig. 4 Aii).
In a different myocyte, a 10 × 10 μm ROI was exposed to a burst of six flash-events within a period of 12 s (Protocol 2), giving rise to an acute longitudinal pHi nonuniformity. After the brief burst, the subsequent dissipation of the pHi gradient is illustrated by the convergence of [H+]i time courses measured in three ROIs (Fig. 4 B). When best-fitted with a diffusion equation, these data yielded a 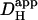 of 5.5 × 10−7 cm2/s.
of 5.5 × 10−7 cm2/s.
The spatiotemporal behavior of Hi+ in the sample experiments illustrated in Fig. 4 is consistent with that observed previously using a different technique where H+-ions were introduced locally into a ventricular myocyte through a cell-attached micropipette. It is indicative of a diffusive process. The values derived for 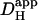 are also within the range of previous estimates, suggesting that Hi+-uncaging is a viable approach for investigating Hi+-mobility. Results derived for
are also within the range of previous estimates, suggesting that Hi+-uncaging is a viable approach for investigating Hi+-mobility. Results derived for 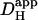 will be analyzed in more detail in a later section.
will be analyzed in more detail in a later section.
Local H+-uncaging in myocyte cell-pairs
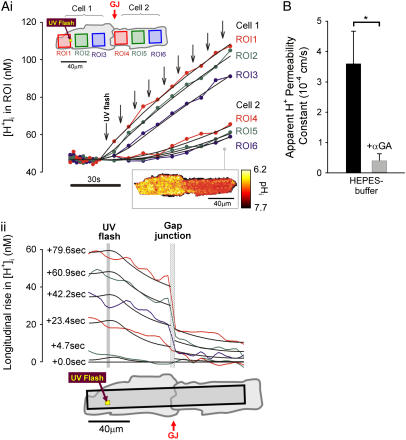
Photolytic uncaging of acid need not be limited to single cells. Fig. 5 illustrates the results of an experiment performed on a rat ventricular cell-pair superfused with HEPES-buffered NT containing 30 μM cariporide. A 5 × 5 μm region at the left end of one of the cells of the pair was exposed repetitively to flash-events (Protocol 1). As expected, the localized acid-load spread rightward along the proximal cell and permeated into the second cell across the gap junctional region (Fig. 5 Ai). This phenomenon has been demonstrated previously while using a micropipette to load acid directly into one cell of the pair (20). When the longitudinal elevation in [H+]i was measured at different times before and after commencement of the flash sequence, a large [H+]i-discontinuity was evident across the junction (Fig. 5 Aii), demonstrating that this region is rate-limiting for cell-to-cell H+-ion transmission (20,31). Using a coupled two-compartment diffusive model with a constant local source for H+-ions, and assuming H+-ion reflection at all but the junctional boundaries, the data in Fig. 5 A were deconvoluted to give an estimate of the apparent proton permeability constant (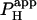 ) across the junction. Fig. 5 B pools results for
) across the junction. Fig. 5 B pools results for 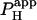 from several H+-uncaging experiments performed on myocyte cell-pairs. The mean
from several H+-uncaging experiments performed on myocyte cell-pairs. The mean 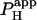 evaluated with this technique, 3.60(±1.07) × 10−4 cm/s, is similar to previous estimates of 2.03(±0.66) × 10−4 cm/s and 4.45(±0.21) × 10−4 cm/s measured using micropipette H+-injection (20) or local weak acid/base microperfusion techniques (31). The presence of the gap junctional inhibitor, α-glycyrrhetinic acid (αGA) at 60 μM reduced
evaluated with this technique, 3.60(±1.07) × 10−4 cm/s, is similar to previous estimates of 2.03(±0.66) × 10−4 cm/s and 4.45(±0.21) × 10−4 cm/s measured using micropipette H+-injection (20) or local weak acid/base microperfusion techniques (31). The presence of the gap junctional inhibitor, α-glycyrrhetinic acid (αGA) at 60 μM reduced 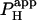 by 70–80% (Fig. 5 B), consistent with inhibition of H+-passage through ventricular connexin channels (20).
by 70–80% (Fig. 5 B), consistent with inhibition of H+-passage through ventricular connexin channels (20).
Results of local Hi+-uncaging in ventricular cell-pairs are thus comparable with those seen using other, more conventional acid-loading techniques (20,31). We conclude that H+-uncaging from NBA is suitable for estimating cell-to-cell H+-permeability as well as cytoplasmic H+-mobility. We also conclude that inclusion of 1 mM NBA within cardiac myocytes does not influence the spatial movement of H+ within the cell or its permeation through connexin channels.
pHi-dependence of intracellular H+-ion mobility
To resolve the pHi-dependence of H+-ion mobility, starting pHi was manipulated uniformly to different levels before locally uncaging H+ from NBA. Manipulation was achieved by prepulsing the cell with solutions containing the salt of a membrane-permeant weak acid (e.g., sodium acetate) or weak base (e.g., ammonium chloride), as described in the Methods section. On returning to normal Tyrode, pHi respectively alkalinized and acidified (25). The pHi was then stabilized at the new level by inhibiting sarcolemmal H+-equivalent transport (see Methods).
Hi+-uncaging experiments were repeated over a range of starting pHi-values in the presence and absence of extrinsic carbonic buffer. Cumulative acid-loading (Protocol 1) in the presence of carbonic buffer is illustrated in Fig. 6 A. As with HEPES-buffer, [H+]i increased fastest close to the site of H+-release, whereas it rose more slowly in downstream regions. The estimated 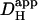 for the cell shown in Fig. 6 A was 22 × 10−7 cm2/s and was higher than that typically measured for cells superfused with HEPES-buffer.
for the cell shown in Fig. 6 A was 22 × 10−7 cm2/s and was higher than that typically measured for cells superfused with HEPES-buffer.
Values of 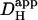 are plotted in Fig. 6 B versus the cell-averaged pHi measured during the cumulative acid-load (see Methods). Values derived from cumulative Hi+-loading (Protocol 1; red, blue triangles) as well as post-loading Hi+-relaxation (Protocol 2; open squares) have been included. In some H+-loading experiments performed in the presence of CO2/HCO3− buffer (green triangles), 100 μM acetazolamide (ATZ) was added to superfusates, to retard carbonic buffer equilibration. This is normally catalyzed by endogenous carbonic anhydrase (CA) (32–34).
are plotted in Fig. 6 B versus the cell-averaged pHi measured during the cumulative acid-load (see Methods). Values derived from cumulative Hi+-loading (Protocol 1; red, blue triangles) as well as post-loading Hi+-relaxation (Protocol 2; open squares) have been included. In some H+-loading experiments performed in the presence of CO2/HCO3− buffer (green triangles), 100 μM acetazolamide (ATZ) was added to superfusates, to retard carbonic buffer equilibration. This is normally catalyzed by endogenous carbonic anhydrase (CA) (32–34).
The data pooled in Fig. 6 B show that, for experiments performed under HEPES-buffered conditions, 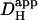 decreases by about sixfold as mean pHi decreases from 7.5 to 6.1. Results from the two acid-loading protocols were very similar when compared over a common pHi-range. The relationship between pHi and intrinsic
decreases by about sixfold as mean pHi decreases from 7.5 to 6.1. Results from the two acid-loading protocols were very similar when compared over a common pHi-range. The relationship between pHi and intrinsic 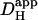 is similar to that deduced previously in rat and guinea pig ventricular myocytes (dashed line) using a dual microperfusion technique (12).
is similar to that deduced previously in rat and guinea pig ventricular myocytes (dashed line) using a dual microperfusion technique (12).
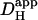 in the presence of CO2/bicarbonate-buffer was consistently higher than in HEPES, but its value still declined with pHi (Fig. 6 B). Fig. 6 C plots the carbonic-induced increment of
in the presence of CO2/bicarbonate-buffer was consistently higher than in HEPES, but its value still declined with pHi (Fig. 6 B). Fig. 6 C plots the carbonic-induced increment of 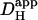 over the whole pHi range tested. It is largest at ∼7.5 and decreases monotonically as pHi falls. Interestingly, the decline is similar to that for intrinsic H+-mobility. This is confirmed in Fig. 6 D which plots the fraction of
over the whole pHi range tested. It is largest at ∼7.5 and decreases monotonically as pHi falls. Interestingly, the decline is similar to that for intrinsic H+-mobility. This is confirmed in Fig. 6 D which plots the fraction of 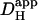 attributable to carbonic buffer alone. This fraction remains close to 30% over the pHi range. Thus the pHi-dependent properties of intrinsic and extrinsic Hi+-mobility show virtually identical pHi-sensitivity, resulting in near constant fractional contributions to Hi+-mobility as pHi is varied. The extrinsic component appeared to be dependent upon CA activity, as it was abolished by ATZ, leaving only the intrinsic component of
attributable to carbonic buffer alone. This fraction remains close to 30% over the pHi range. Thus the pHi-dependent properties of intrinsic and extrinsic Hi+-mobility show virtually identical pHi-sensitivity, resulting in near constant fractional contributions to Hi+-mobility as pHi is varied. The extrinsic component appeared to be dependent upon CA activity, as it was abolished by ATZ, leaving only the intrinsic component of 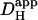 .
.
DISCUSSION
Hi+-uncaging reveals pH-sensitivity of Hi+-mobility
Photolytic uncaging of H+-ions from intracellular NBA provides a unique way of examining H+-ion dynamics in the cardiac ventricular myocyte. The technique has allowed us to assess the relative roles of intrinsic (non-CO2) and extrinsic (carbonic) buffer, in the regulation of Hi+-mobility. We find that the ability of both types of buffer to mediate intracellular H+-ion movement declines about sixfold as intracellular pH decreases from 7.5 to 6.1. As pHi falls, carbonic buffer's fractional contribution to 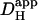 remains constant, at ∼30%. A comparable pHi-sensitivity of intrinsic
remains constant, at ∼30%. A comparable pHi-sensitivity of intrinsic 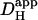 has been reported previously for rat and guinea pig myocytes (12), using a radically different technique (local pHi-displacement with membrane-permeant weak acid or base). In that work, however, experiments were not performed in the presence of carbonic buffer so the pHi-sensitivity of extrinsic Hi+-mobility could not be explored.
has been reported previously for rat and guinea pig myocytes (12), using a radically different technique (local pHi-displacement with membrane-permeant weak acid or base). In that work, however, experiments were not performed in the presence of carbonic buffer so the pHi-sensitivity of extrinsic Hi+-mobility could not be explored.
The physiological benefit of a decline in 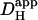 with pHi is unclear, but it may represent a strategy for slowing the spatial spread of a local intracellular acid insult, both within a cell and within a multicellular region. Intracellular acid-overload is potentially damaging to cardiac tissue, as it is associated with intracellular Ca2+-overload (35,36), leading to electrical and mechanical malfunction (6,8,9). Slow spatial spread of H+-ions may, for example, facilitate their local removal via sarcolemmal transport mechanisms, thus restricting their global impact on the myocardium.
with pHi is unclear, but it may represent a strategy for slowing the spatial spread of a local intracellular acid insult, both within a cell and within a multicellular region. Intracellular acid-overload is potentially damaging to cardiac tissue, as it is associated with intracellular Ca2+-overload (35,36), leading to electrical and mechanical malfunction (6,8,9). Slow spatial spread of H+-ions may, for example, facilitate their local removal via sarcolemmal transport mechanisms, thus restricting their global impact on the myocardium.
The pHi-dependence of 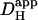 revealed using H+-uncaging, indicates that in the presence of CO2/HCO3−, total
revealed using H+-uncaging, indicates that in the presence of CO2/HCO3−, total 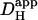 at pHi 6.1 is ∼4×10−7 cm2/s. This value is nearly 300-fold lower than H+-mobility in water (at 37°C, DH = 12 × 10−5 cm2/s). Such low mobility predicts that acidosis will predispose intracellular pH to spatial non-uniformity. Indeed such non-uniformity at low pHi has already been observed in the ventricular myocyte during stimulation of sarcolemmal Na+-H+ exchange (13). Intracellular pH nonuniformity induced by stimulation of H+-equivalent membrane transport has also been observed in epithelial cells (15), and in invertebrate and mammalian neurons (37,38). It seems likely that, in these cell-types, a similar decline of Hi+-mobility with pHi will contribute to the generation of local pHi microdomains.
at pHi 6.1 is ∼4×10−7 cm2/s. This value is nearly 300-fold lower than H+-mobility in water (at 37°C, DH = 12 × 10−5 cm2/s). Such low mobility predicts that acidosis will predispose intracellular pH to spatial non-uniformity. Indeed such non-uniformity at low pHi has already been observed in the ventricular myocyte during stimulation of sarcolemmal Na+-H+ exchange (13). Intracellular pH nonuniformity induced by stimulation of H+-equivalent membrane transport has also been observed in epithelial cells (15), and in invertebrate and mammalian neurons (37,38). It seems likely that, in these cell-types, a similar decline of Hi+-mobility with pHi will contribute to the generation of local pHi microdomains.
Flash-photolysis of NBA: a novel experimental tool
NBA appears suitable for intracellular proton uncaging. In the mammalian ventricular myocyte, its toxicity is minimal at the doses used. In the absence of UV flashing, 1 mM NBA had no effect on diastolic Cai2+ or on the time course and amplitude of an electrically-evoked Ca2+-transient. It also had no direct effect on cellular contraction, although an unexplained slowing of the later stage of relaxation was sometimes detected. Most importantly, 1 mM NBA had no effect on the mechanisms of spatial pHi regulation, as evidenced by a lack of effect on estimates of Hi+-mobility (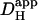 ) and cell-to-cell H+-permeability (
) and cell-to-cell H+-permeability (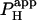 ). Flash-photolysis of intracellular NBA should therefore be an important new tool in the study of pHi regulation.
). Flash-photolysis of intracellular NBA should therefore be an important new tool in the study of pHi regulation.
Advantages of the technique
The technique can be used to produce whole-cell as well as local pHi-changes (cf. Fig. 2 with 4). Experiments need not be limited to single-cells but can be performed equally well on cell-pairs, and may also be suitable for tissue or whole-organ studies. UV flashing in the absence of NBA had no effect on pHi (Fig. 2 D), eliminating the possibility of an acid-source other than NBA, or of an artifactual UV-interaction with intracellular carboxy-SNARF. We assessed the technique as an alternative to previous approaches for inducing pHi nonuniformity. These have comprised localized myocyte-exposure to weak acids or bases (17,18,31) or localized acid-loading via a patch pipette (11,14,16,20). UV flash-photolysis of caged-H+ compounds was a simpler technique to use, with a much higher success rate experimentally. Furthermore, unlike the other two acid-loading techniques, the size, speed, and magnitude of intracellular loading could readily be varied during an experiment by adjusting the UV laser intensity.
Intracellular NBA photolysis has previously been tested in snail neurons (19) but the physicochemical properties of the technique were not quantified. In this work we monitored pHi ratiometrically and estimated the magnitude of local and whole-cell pHi-changes. When exposed to a dose of UV light, NBA releases a quantity of acid (Fig. 2 C) that is dependent on the laser intensity (Fig. 2 E). At 100% laser intensity (20 mW) the photolytic efficiency is very high, reaching 80% (i.e., during a single flash, 0.80 mM acid was released per 1 mM NBA). This is a considerably higher efficiency than that attained with other caged-H+ compounds such as 4-formyl-6-methoxy-3-nitrophenoxyacetic acid (39).
Since 2-nitrosobenzoic acid, the product of NBA photolysis, has a low pK, it will fully dissociate into H+ and 2-nitrosobenzoate in the physiological pH range and produce an acid-load that is independent of pHi. H+-ions are therefore trapped intracellularly, and the trapping becomes cumulative during a series of flash-events (Fig. 3). In this respect, NBA is better than a substance such as 2-hydroxyphenyl 1-(2-nitrophenyl)ethyl phosphate (40) which has a pK value near 5, and therefore does not fully dissociate, so that its acid-delivery will vary with pHi. Its anionic conjugate-base will also contribute to cytoplasmic H+-buffering capacity.
Owing to the high membrane-permeability of NBA, its inclusion in the superfusate effectively clamps its intracellular concentration. The compound is also rapidly replenished after photolysis and was never a limiting factor in this work (cf. the linearity of the relationship shown in Fig. 2 E between the concentration of acid uncaged and that of NBA). Some previously used H+-donors, e.g., 4-formyl-6-methoxy-3-nitrophenoxyacetic acid (39) are poorly membrane-permeant and therefore less suitable.
Disadvantages of the technique
These are fourfold. Firstly, as alluded to above, prolonged exposure to intense UV light causes cell damage, but we have defined experimental protocols that appear to minimize this. Secondly, NBA appeared to be cytotoxic at concentrations as high as 10 mM, although such effects were minimal at 1 mM. We have not specifically examined the nature of NBA-toxicity but, at high concentration, NBA has tissue-fixative properties. In view of this, it may be prudent to limit its dosage to no more than 1 mM. Thirdly, photolysis of NBA will cause intracellular accumulation of nitrosobenzoate and, at high concentration, this will impose an untoward osmotic stress on the cell. For modest whole-cell acid-loads or for spatially localized uncaging maneuvers, this is unlikely to present a serious problem. For example, a whole cell acid-load of 0.5 pHi units would release ∼25 mM nitrosobenzoate, causing an increase of intracellular osmolarity of ∼8%, which will induce osmotic swelling. This level of osmotic loading is well tolerated by cardiac myocytes. Indeed acid-loading by any experimental technique, or indeed metabolically by the cell itself, is likely to be accompanied by a comparable osmotic load, as protons must be added with an equivalent anionic charge, much of which will be osmotically active. The fact, however, that nitrosobenzoate is membrane impermeant, and therefore cannot escape from the cell, should be borne in mind when contemplating prolonged NBA-uncaging experiments. Fourthly, because it is so membrane permeant, NBA may well gain access to intracellular organelles. The uncaging procedure may therefore release H+-ions directly into the sarcoplasmic reticulum or into mitochondria, in addition to the cytoplasm. In our present single-photon excitation system, this effect may be amplified by photolytic H+-release within the cones of UV illumination above and below the confocal plane (this latter problem would be greatly reduced by multiphoton excitation exclusively in the confocal plane). Where H+-ion release into organelles is considered to be a potential problem, it may be prudent to compare results with those obtained using a cell-attached acid-filled micropipette (where H+-ions initially access only the cytoplasm). In the present determinations of intrinsic 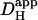 , for example, it is unlikely that possible H+-release into organelles was significantly interfering with measurements of cytoplasmic H+-movement, as
, for example, it is unlikely that possible H+-release into organelles was significantly interfering with measurements of cytoplasmic H+-movement, as 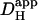 was comparable when measured by both techniques. Overall, when reviewing the use of intracellular NBA as an experimental tool it would seem that, for many experimental purposes, the advantages far outweigh the disadvantages.
was comparable when measured by both techniques. Overall, when reviewing the use of intracellular NBA as an experimental tool it would seem that, for many experimental purposes, the advantages far outweigh the disadvantages.
MECHANISM OF pH-SENSITIVE Hi+-MOBILITY
Intrinsic Hi+-mobility
We have shown previously that the pHi-dependence of intrinsic 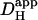 is consistent with two pooled populations of intrinsic buffer (12). One appears to have very low or zero mobility, most likely represented by buffer sites on intracellular proteins. The other appears to be more mobile, represented by lower molecular weight molecules such as the histidyl dipeptides (100–200 Da) that are prevalent in many tissues, including heart (41) and skeletal muscle (42). As described in the Introduction, Hi+-mobility is dependent on spatial H+-shuttling by these mobile buffer molecules. They are estimated to have a pooled diffusion coefficient, Dmob, equal to 49.9 × 10−7 cm2/s (12). Since the intrinsic buffers equilibrate rapidly (25), the apparent diffusion coefficient (
is consistent with two pooled populations of intrinsic buffer (12). One appears to have very low or zero mobility, most likely represented by buffer sites on intracellular proteins. The other appears to be more mobile, represented by lower molecular weight molecules such as the histidyl dipeptides (100–200 Da) that are prevalent in many tissues, including heart (41) and skeletal muscle (42). As described in the Introduction, Hi+-mobility is dependent on spatial H+-shuttling by these mobile buffer molecules. They are estimated to have a pooled diffusion coefficient, Dmob, equal to 49.9 × 10−7 cm2/s (12). Since the intrinsic buffers equilibrate rapidly (25), the apparent diffusion coefficient (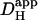 ) can be described using the equation:
) can be described using the equation:
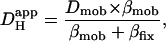 |
(1) |
where Dmob and βmob denote the intrinsic mobile buffer diffusion coefficient and capacity respectively, and where βfix denotes the intrinsic fixed buffer capacity (11,43). On this scheme, the pHi-dependence of intrinsic 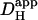 is consistent with a pHi-dependence of βmob and βfix, the former having a mean pK of ∼7.48 and the latter a much lower mean pK of 6.40 (12). Thus as pHi decreases from a resting value of ∼7.1, βmob also decreases as it becomes saturated with H+-ions, whereas βfix increases as ambient pH approaches its pK. The mobile fraction of intrinsic buffering thus decreases, resulting in a fall of Hi+-mobility.
is consistent with a pHi-dependence of βmob and βfix, the former having a mean pK of ∼7.48 and the latter a much lower mean pK of 6.40 (12). Thus as pHi decreases from a resting value of ∼7.1, βmob also decreases as it becomes saturated with H+-ions, whereas βfix increases as ambient pH approaches its pK. The mobile fraction of intrinsic buffering thus decreases, resulting in a fall of Hi+-mobility.
Extrinsic Hi+-mobility
Comparison with previous work
Introducing carbonic buffer into a rat myocyte increased 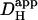 by ∼50% (i.e., the extrinsic component of
by ∼50% (i.e., the extrinsic component of 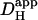 is ∼30% of total
is ∼30% of total 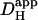 ). Although an increase was found in previous work on guinea-pig and rabbit ventricular myocytes, it appeared to be much larger (two- to fivefold). Some of this discrepancy may represent species differences, but there are other possible explanations. Firstly, initial work with CO2/HCO3− buffer (14) estimated
). Although an increase was found in previous work on guinea-pig and rabbit ventricular myocytes, it appeared to be much larger (two- to fivefold). Some of this discrepancy may represent species differences, but there are other possible explanations. Firstly, initial work with CO2/HCO3− buffer (14) estimated 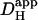 from the time delay for H+-ion diffusion down a cell, when injected locally from a micropipette. Unlike more recent analyses (16,29), the specific geometry of each cell was not taken into account (myocyte geometry was standardized as rectangular). As a result, errors in estimating
from the time delay for H+-ion diffusion down a cell, when injected locally from a micropipette. Unlike more recent analyses (16,29), the specific geometry of each cell was not taken into account (myocyte geometry was standardized as rectangular). As a result, errors in estimating 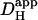 may have arisen, particularly when the time delay was small. Secondly, most previous work did not acknowledge the pHi-dependence of
may have arisen, particularly when the time delay was small. Secondly, most previous work did not acknowledge the pHi-dependence of 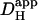 . The graph shown in Fig. 6 B illustrates that carbonic buffer's contribution is 2 × 10−7 cm2/s at pHi 6.1, rising to nearly 10 × 10−7 cm2/s at pHi 7.5. The intrinsic contribution varies from 2.5–22 × 10−7 cm2/s over the same range (Fig. 6 A), which encompasses the averaged values for intrinsic
. The graph shown in Fig. 6 B illustrates that carbonic buffer's contribution is 2 × 10−7 cm2/s at pHi 6.1, rising to nearly 10 × 10−7 cm2/s at pHi 7.5. The intrinsic contribution varies from 2.5–22 × 10−7 cm2/s over the same range (Fig. 6 A), which encompasses the averaged values for intrinsic 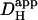 reported previously (typically ∼8 × 10−7 cm2/s). Thus, if Hi+-mobility values were not compared at a common pHi, the contribution of carbonic buffer would appear to range from 10% to 500%. Clearly the procedure of using a common pHi value when comparing
reported previously (typically ∼8 × 10−7 cm2/s). Thus, if Hi+-mobility values were not compared at a common pHi, the contribution of carbonic buffer would appear to range from 10% to 500%. Clearly the procedure of using a common pHi value when comparing 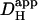 values must now be adopted. A final reason for differing estimates of carbonic buffer's contribution to Hi+-mobility may be its slow kinetics, which permit the buffer to mediate slow, but not fast, Hi+-shuttling reactions. We return to this point in a later section.
values must now be adopted. A final reason for differing estimates of carbonic buffer's contribution to Hi+-mobility may be its slow kinetics, which permit the buffer to mediate slow, but not fast, Hi+-shuttling reactions. We return to this point in a later section.
Extrinsic Hi+-mobility constrained by fixed buffers and [HCO3−]i
HCO3− anions, in concert with CO2, act as mobile buffers within the cell, shuttling H+-ions spatially (14,15). Like other mobile buffers, HCO3− ions must compete with fixed intrinsic buffers for H+-ion binding. Given that βfix rises steeply as pHi falls (12,16), part of the observed decline in the effectiveness of the extrinsic shuttle at low pHi (Fig. 6 C) can be attributed to increased competition from fixed buffers. This would predict a 1.7-fold decline in extrinsic H+-mobility, rather than the fivefold decline actually observed (Fig. 6 C). Thus other factors must also play a role.
Assuming that CO2 is freely permeant across the sarcolemma, so that [CO2]i is clamped by a constant extracellular [CO2], carbonic buffering capacity at equilibrium can be expressed as a function of intracellular bicarbonate concentration (24):
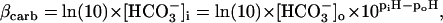 |
(2) |
where subscripts i and o denote the intracellular and extracellular compartments, respectively. Equation 1 has previously been modified to describe the Hi+-mobility constant in the presence of carbonic buffer (14) by including two extra terms, βcarb and Dcarb (the effective diffusion coefficient of carbonic buffer, a term lumped for the individual diffusion coefficients of intracellular CO2 and HCO3−, the constituents of carbonic buffer):
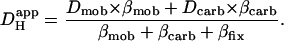 |
(3) |
Assuming the cell remains fully open to CO2, much of the pHi-dependence of extrinsic Hi+-mobility can be explained by a fall in [HCO3−]i, and hence a fall of βcarb as pHi declines. Over the pHi range from 7.5 to 6.1, βcarb at equilibrium falls 25-fold. This would be more than sufficient to account for the decline in the extrinsic component of Hi+-mobility (Fig. 6 C). During intracellular acidosis, H+-movement via the carbonic shuttle is therefore likely to be constrained by the H+-binding capacity of fixed buffers, and by the availability of intracellular bicarbonate.
Extrinsic Hi+-mobility also constrained by slow buffer-kinetics
Although extrinsic Hi+-mobility will be influenced by [HCO3−]i, quantifying this effect is not straightforward. Eq. 3 can be used to predict  in the presence of carbonic buffer, provided the effective value for βcarb is known. In this work, net Hi+-movement was observed over periods of 1–2 min. Unfortunately, on this timescale, βcarb cannot reliably be estimated from Eq. 2, as the CO2/HCO3− buffer system may not be close to equilibrium. CO2-hydration is slow and only moderately accelerated in cardiomyocytes by endogenous CA (34). As a result, intracellular carbonic buffering is also slow, often taking minutes to equilibrate. During this period, the effective value of βcarb may be significantly less than its equilibrium value. This raises difficulties for computing
in the presence of carbonic buffer, provided the effective value for βcarb is known. In this work, net Hi+-movement was observed over periods of 1–2 min. Unfortunately, on this timescale, βcarb cannot reliably be estimated from Eq. 2, as the CO2/HCO3− buffer system may not be close to equilibrium. CO2-hydration is slow and only moderately accelerated in cardiomyocytes by endogenous CA (34). As a result, intracellular carbonic buffering is also slow, often taking minutes to equilibrate. During this period, the effective value of βcarb may be significantly less than its equilibrium value. This raises difficulties for computing  .
.
By assigning a value to Dcarb, Eq. 3 can be used to explore the effective value of βcarb during spatial Hi+-movement. After correcting for temperature and macromolecular crowding in the cytosolic environment, the intracellular diffusion coefficients for CO2 and HCO3− (the constituents of carbonic buffer) have been estimated as 11 and 7.7 × 10−6 cm2/s, respectively (29). Dcarb can be represented by the lower of the two coefficients, i.e., 7.7 × 10−6 cm2/s. Best-fitting the data in Fig. 6 B with Eq. 3 yields estimates for βcarb, which rise from around 1 mM at pH 6.1 to 4 mM at pH 7.5. These are considerably smaller than the equilibrium values predicted from Eq. 2 (2.5 and 63 mM, respectively). The low effective values for βcarb are therefore suggestive of an out-of-equilibrium state, whereby carbonic buffer contributes only a fraction of its full capacity to the shuttling of intracellular H+-ions. The exact value of this fraction will depend on the buffer's catalytic acceleration by CA, the magnitude of the spatial acid-flux, and movements of CO2 across the sarcolemma. This conclusion is reinforced by the observation that extrinsic Hi+-mobility disappears entirely when CA is inhibited by acetazolamide (Fig. 6 B, green triangles).
The above calculations suggest that, during the intracellular acid-loading rate used in this study (∼15 mM/min averaged over the cell), the effective value of βcarb was reduced by 2.5–15-fold from its equilibrium value. Much larger spatial acid-fluxes (∼100 mM/min) have been induced previously in experiments involving partial exposure of a myocyte to ammonium chloride (18). In those experiments, the presence of carbonic buffer had virtually no effect on Hi+-mobility, suggesting the effective value of βcarb may have fallen to near zero.
The ability of the CO2/HCO3−-shuttle to mediate Hi+-movement in the cardiac myocyte will therefore be limited, not only by fixed buffers and the availability of intracellular bicarbonate, but also by the extrinsic buffer's slow kinetics. When spatial pHi nonuniformity is large, resulting in high intracellular H+-traffic, the buffer's fractional contribution will be reduced. The present estimate of 30% should therefore be viewed in the context of the size of the underlying spatial acid-flux. Significant differences in flux magnitude may account for reported differences in the buffer's contribution to Hi+-mobility (this work; (14,16,18)), and in its ability to minimize pHi nonuniformity (14–16,38).
Because of uncertainty regarding the effective value of βcarb during Hi+-shuttling, the mechanism for pH-dependent extrinsic Hi+-mobility has yet to be modeled quantitatively. Even if carbonic buffer is significantly out-of-equilibrium, as seems likely during some local Hi+-movement, the restricted availability of intracellular HCO3− during acidosis will be an important constraining factor. An additional factor may be a pHi-sensitivity of the CA enzyme, as this regulates the speed of buffer equilibration (32,34). CA isoforms I and II are known to be pH-sensitive (44), but the isoforms responsible for facilitating intracellular H+-ion movement in the cardiac myocyte have yet to be identified.
CONCLUSIONS
Flash-photolysis of intracellular NBA provides a convenient and novel tool for displacing intracellular pH. The approach is simple to implement and need not be restricted to single-cell preparations. It should prove useful in cell-types less amenable to conventional methods of local acid-injection. Using the method, we have demonstrated that, in ventricular cells, both extrinsic (carbonic) and intrinsic buffers regulate intracellular H+-ion movement. With these experimental protocols, extrinsic buffer accounts for ∼30% of Hi+-mobility over a wide pHi-range. The fact that this component relies upon the activity of CA indicates the important role of this enzyme in spatial pHi regulation. The remaining 70% of Hi+-movement is mediated by intrinsic mobile buffers. A key finding is that both extrinsic and intrinsic Hi+-mobility are severely reduced during intracellular acidosis. This will compromise the spatial uniformity of pHi, particularly when sarcolemmal H+-equivalent extruders are stimulated (13). The physiological consequences of spatial pHi nonuniformity are only now being investigated, but they are likely to include a spatial disruption of both Cai2+-signaling (45,46) and contraction (46). Severe intracellular acidosis in the cardiac myocyte may thus present a window of vulnerability in the spatial coordination of cell function.
Acknowledgments
The authors thank Mr. Philip Cobden for excellent technical assistance.
This work was supported by a British Heart Foundation Program grant to R.V.J, and a MERIT award from the National Institutes of Health to K.W.S. (5R37HL042873).
References
- 1.Bountra, C., K. Kaila, and R. D. Vaughan-Jones. 1988. Effect of repetitive activity upon intracellular pH, sodium and contraction in sheep cardiac Purkinje fibres. J. Physiol. 398:341–360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Elliott, A. C., G. L. Smith, and D. G. Allen. 1994. The metabolic consequences of an increase in the frequency of stimulation in isolated ferret hearts. J. Physiol. 474:147–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ellis, D., and R. C. Thomas. 1976. Microelectrode measurement of the intracellular pH of mammalian heart cells. Nature. 262:224–225. [DOI] [PubMed] [Google Scholar]
- 4.Bountra, C., and R. D. Vaughan-Jones. 1989. Effect of intracellular and extracellular pH on contraction in isolated, mammalian cardiac muscle. J. Physiol. 418:163–187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Komukai, K., F. Brette, C. Pascarel, and C. H. Orchard. 2002. Electrophysiological response of rat ventricular myocytes to acidosis. Am. J. Physiol. Heart Circ. Physiol. 283:H412–H422. [DOI] [PubMed] [Google Scholar]
- 6.Fabiato, A., and F. Fabiato. 1978. Effects of pH on the myofilaments and the sarcoplasmic reticulum of skinned cells from cardiace and skeletal muscles. J. Physiol. 276:233–255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Garlick, P. B., G. K. Radda, and P. J. Seeley. 1979. Studies of acidosis in the ischaemic heart by phosphorus nuclear magnetic resonance. Biochem. J. 184:547–554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Orchard, C. H., and J. C. Kentish. 1990. Effects of changes of pH on the contractile function of cardiac muscle. Am. J. Physiol. 258:C967–C981. [DOI] [PubMed] [Google Scholar]
- 9.Orchard, C. H., and H. E. Cingolani. 1994. Acidosis and arrhythmias in cardiac muscle. Cardiovasc. Res. 28:1312–1319. [DOI] [PubMed] [Google Scholar]
- 10.Vaughan-Jones, R. D., K. W. Spitzer, and P. Swietach. 2005. Spatial aspects of intracellular pH regulation in heart muscle. Prog. Biophys. Mol. Biol. 90:207–224. [DOI] [PubMed] [Google Scholar]
- 11.Vaughan-Jones, R. D., B. E. Peercy, J. P. Keener, and K. W. Spitzer. 2002. Intrinsic H+ ion mobility in the rabbit ventricular myocyte. J. Physiol. 541:139–158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Swietach, P., and R. D. Vaughan-Jones. 2005. Relationship between intracellular pH and proton mobility in rat and guinea-pig ventricular myocytes. J. Physiol. 566:793–806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Swietach, P., and R. D. Vaughan-Jones. 2005. Spatial regulation of intracellular pH in the ventricular myocyte. Ann. N. Y. Acad. Sci. 1047:271–282. [DOI] [PubMed] [Google Scholar]
- 14.Spitzer, K. W., R. L. Skolnick, B. E. Peercy, J. P. Keener, and R. D. Vaughan-Jones. 2002. Facilitation of intracellular H+ ion mobility by CO2/HCO3− in rabbit ventricular myocytes is regulated by carbonic anhydrase. J. Physiol. 541:159–167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Stewart, A. K., C. A. Boyd, and R. D. Vaughan-Jones. 1999. A novel role for carbonic anhydrase: cytoplasmic pH gradient dissipation in mouse small intestinal enterocytes. J. Physiol. 516:209–217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zaniboni, M., P. Swietach, A. Rossini, T. Yamamoto, K. W. Spitzer, and R. D. Vaughan-Jones. 2003. Intracellular proton mobility and buffering power in cardiac ventricular myocytes from rat, rabbit, and guinea pig. Am. J. Physiol. Heart Circ. Physiol. 285:H1236–H1246. [DOI] [PubMed] [Google Scholar]
- 17.Spitzer, K. W., P. R. Ershler, R. L. Skolnick, and R. D. Vaughan-Jones. 2000. Generation of intracellular pH gradients in single cardiac myocytes with a microperfusion system. Am. J. Physiol. Heart Circ. Physiol. 278:H1371–H1382. [DOI] [PubMed] [Google Scholar]
- 18.Swietach, P., C. H. Leem, K. W. Spitzer, and R. D. Vaughan-Jones. 2005. Experimental generation and computational modeling of intracellular pH gradients in cardiac myocytes. Biophys. J. 88:3018–3037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Schwiening, C. J. 2004. Rapid regionally restricted pHi shifts in neurons induced by the UV photolysis of 2-nitrobenzaldehyde. J. Physiol. 555P:D1.
- 20.Zaniboni, M., A. Rossini, P. Swietach, N. Banger, K. W. Spitzer, and R. D. Vaughan-Jones. 2003. Proton permeation through the myocardial gap junction. Circ. Res. 93:726–735. [DOI] [PubMed] [Google Scholar]
- 21.Haugland, R. P. 2002. Handbook of Fluorescent Probes and Research Products. Molecular Probes, Eugene, OR.
- 22.Thomas, J. A., R. N. Buchsbaum, A. Zimniak, and E. Racker. 1979. Intracellular pH measurements in Ehrlich ascites tumor cells utilizing spectroscopic probes generated in situ. Biochemistry. 18:2210–2218. [DOI] [PubMed] [Google Scholar]
- 23.Saxena, A. M., J. B. Udgaonkar, and G. Krishnamoorthy. 2005. Protein dynamics control proton transfer from bulk solvent to protein interior: a case study with a green fluorescent protein. Protein Sci. 14:1787–1799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Roos, A., and W. F. Boron. 1981. Intracellular pH. Physiol. Rev. 61:296–434. [DOI] [PubMed] [Google Scholar]
- 25.Leem, C. H., D. Lagadic-Gossmann, and R. D. Vaughan-Jones. 1999. Characterization of intracellular pH regulation in the guinea-pig ventricular myocyte. J. Physiol. 517:159–180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Scholz, W., U. Albus, L. Counillon, H. Gogelein, H. J. Lang, W. Linz, A. Weichert, and B. A. Scholkens. 1995. Protective effects of HOE642, a selective sodium-hydrogen exchange subtype 1 inhibitor, on cardiac ischaemia and reperfusion. Cardiovasc. Res. 29:260–268. [PubMed] [Google Scholar]
- 27.Yamamoto, T., P. Swietach, A. Rossini, S. H. Loh, R. D. Vaughan-Jones, and K. W. Spitzer. 2005. Functional diversity of electrogenic Na+-HCO3− cotransport in ventricular myocytes from rat, rabbit and guinea pig. J. Physiol. 562:455–475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Sun, B., C. H. Leem, and R. D. Vaughan-Jones. 1996. Novel chloride-dependent acid loader in the guinea-pig ventricular myocyte: part of a dual acid-loading mechanism. J. Physiol. 495:65–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Swietach, P., M. Zaniboni, A. K. Stewart, A. Rossini, K. W. Spitzer, and R. D. Vaughan-Jones. 2003. Modelling intracellular H+ ion diffusion. Prog. Biophys. Mol. Biol. 83:69–100. [DOI] [PubMed] [Google Scholar]
- 30.Abbruzzetti, S., E. Crema, L. Masino, A. Vecli, C. Viappiani, J. R. Small, L. J. Libertini, and E. W. Small. 2000. Fast events in protein folding: structural volume changes accompanying the early events in the N→I transition of apomyoglobin induced by ultrafast pH jump. Biophys. J. 78:405–415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Swietach, P., and R. D. Vaughan-Jones. 2004. Novel method for measuring junctional proton permeation in isolated ventricular myocyte cell pairs. Am. J. Physiol. Heart Circ. Physiol. 287:H2352–H2363. [DOI] [PubMed] [Google Scholar]
- 32.Geers, C., and G. Gros. 2000. Carbon dioxide transport and carbonic anhydrase in blood and muscle. Physiol. Rev. 80:681–715. [DOI] [PubMed] [Google Scholar]
- 33.Knuppel-Ruppert, A. S., G. Gros, W. Harringer, and H. P. Kubis. 2000. Immunochemical evidence for a unique GPI-anchored carbonic anhydrase isozyme in human cardiomyocytes. Am. J. Physiol. Heart Circ. Physiol. 278:H1335–H1344. [DOI] [PubMed] [Google Scholar]
- 34.Leem, C. H., and R. D. Vaughan-Jones. 1998. Out-of-equilibrium pH transients in the guinea-pig ventricular myocyte. J. Physiol. 509:471–485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Gambassi, G., R. G. Hansford, S. J. Sollott, B. A. Hogue, E. G. Lakatta, and M. C. Capogrossi. 1993. Effects of acidosis on resting cytosolic and mitochondrial Ca2+ in mammalian myocardium. J. Gen. Physiol. 102:575–597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kaila, K., and R. D. Vaughan-Jones. 1987. Influence of sodium-hydrogen exchange on intracellular pH, sodium and tension in sheep cardiac Purkinje fibres. J. Physiol. 390:93–118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Schwiening, C. J., and D. Willoughby. 2002. Depolarization-induced pH microdomains and their relationship to calcium transients in isolated snail neurones. J. Physiol. 538:371–382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Willoughby, D., and C. J. Schwiening. 2002. Electrically evoked dendritic pH transients in rat cerebellar Purkinje cells. J. Physiol. 544:487–499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Janko, K., and J. Reichert. 1987. Proton concentration jumps and generation of transmembrane pH-gradients by photolysis of 4-formyl-6-methoxy-3-nitrophenoxyacetic acid. Biochim. Biophys. Acta. 905:409–416. [DOI] [PubMed] [Google Scholar]
- 40.Khan, S., F. Castellano, J. L. Spudich, J. A. McCray, R. S. Goody, G. P. Reid, and D. R. Trentham. 1993. Excitatory signaling in bacterial probed by caged chemoeffectors. Biophys. J. 65:2368–2382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.O'Dowd, J. J., D. J. Robins, and D. J. Miller. 1988. Detection, characterization, and quantification of carnosine and other histidyl derivatives in cardiac and skeletal muscle. Biochim. Biophys. Acta. 967:241–249. [DOI] [PubMed] [Google Scholar]
- 42.Abe, H. 2000. Role of histidine-related compounds as intracellular proton buffering constituents in vertebrate muscle. Biochemistry (Mosc.). 65:757–765. [PubMed] [Google Scholar]
- 43.Irving, M., J. Maylie, N. L. Sizto, and W. K. Chandler. 1990. Intracellular diffusion in the presence of mobile buffers. Application to proton movement in muscle. Biophys. J. 57:717–721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Khalifah, R. G. 1971. The carbon dioxide hydration activity of carbonic anhydrase. I. Stop-flow kinetic studies on the native human isoenzymes B and C. J. Biol. Chem. 246:2561–2573. [PubMed] [Google Scholar]
- 45.Dilworth, E. L., P. Swietach, and R. D. Vaughan-Jones. 2006. Local control of ventricular Ca2+-signalling by intracellular pH. Biophysical Society 50th Annual Meeting. 2006:1552.
- 46.Spitzer, K. W., and R. D. Vaughan-Jones. 2006. Regional intracellular acidosis in ventricular myocytes creates spatial gradients in Ca2+ transients. Biophysical Society 50th Annual Meeting. 73A.